Abstract
Fault diagnosis plays an important role in complex and safety-critical systems such as nuclear power plants (NPPs). With the development of artificial intelligence (AI), extensive research has been carried out for fast and efficient fault diagnosis based on intelligent methods. This paper presents a review of various AI-based system-level fault diagnosis methods for NPPs. We first discuss the development history of AI. Based on this exposition, AI-based fault diagnosis techniques are classified into knowledge-driven and data-driven approaches. For knowledge-driven methods, we discuss both the early if–then-based fault diagnosis techniques and the current new theory-based ones. The principles, application, and comparative analysis of the representative methods are systematically described. For data-driven strategies, we discuss single-algorithm-based techniques such as ANN, SVM, PCA, DT, and clustering, as well as hybrid techniques that combine algorithms together. The advantages and disadvantages of both knowledge-driven and data-driven methods are compared, illustrating the tendency to combine the two approaches. Finally, we provide some possible future research directions and suggestions.
1. Introduction
Advances in technology have increased the level of automation in industry, but they have made systems increasingly complex, placing higher demands on system safety and reliability. One way to improve system safety and reliability is to improve the quality, reliability, and robustness of system components, but this still cannot eliminate the occurrence of faults [1,2]. Therefore, fault diagnosis has become an important technique to ensure the safety and reliability of industrial systems. For complex nuclear power plant systems, fault diagnosis techniques are designed to monitor whether the system and its components are functioning properly, detect the type of fault at an early stage, and determine the location and severity of the fault to avoid further damage [3].
Fault diagnosis includes fault monitoring, fault location, and fault analysis [4,5]. Fault monitoring determines whether there is a fault in the system and components. Fault location determines the location of the fault. Fault analysis performs the function of determining the type, severity, and cause of the fault. Traditional fault diagnosis techniques are generally divided into hardware-redundancy-based, model-based, and signal-processing-based methods [6,7,8]. The hardware-redundancy-based method is to use a redundant component design idea to detect component faults when the component outputs are different from those of the redundant components [9,10,11,12]. The model-based method requires a more accurate mathematical model of the system, similar to the concept of hardware redundancy, which is diagnosed by comparing the output of the mathematical model with that of the actual system [13,14,15,16]. The signal-processing-based method requires mathematical or statistical processing of the measured data to extract information related to the fault [17,18,19,20].
More than two-thirds of the nuclear reactors in service by the end of 2021 worldwide were pressurized water reactors (PWRs), and the typical pressurized water reactor system composition is shown in Figure 1. PWR nuclear power plants use light water as a coolant and moderator [21], which mainly consists of a nuclear steam supply system [21,22], a turbine generator system [23], and other auxiliary systems [24]. After the coolant absorbs the heat energy released from nuclear fuel fission, the heat is then transferred through the steam generator to the second circuit to generate steam, which then enters the turbine to do work and generate electricity [25]. Nuclear power plant systems contain hundreds of subsystems with potential radiological hazards. If a fault occurs during operation, the operator is required to accurately determine the fault type. Therefore, fault diagnosis is an important support technology to assist operators in making fault identification. Traditional fault diagnosis techniques for nuclear power plants rely mainly on expert experience, which is somewhat uncertain and subjective. With the advancement of instrumentation and control systems, nuclear power plants generate a large amount of data. Artificial intelligence can process the large amount of data, and the research on fault diagnosis technology based on AI is increasing.
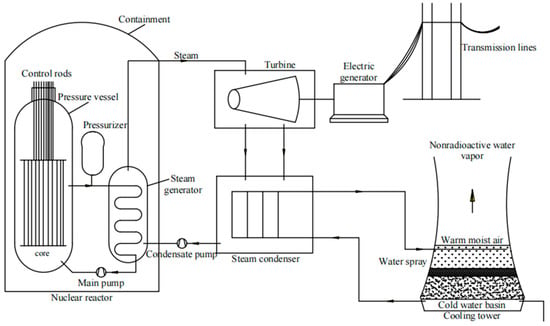
Figure 1.
Main structure of the pressurized water reactor [26].
System-level faults are one of the major causes of accidents in nuclear power plants. In the event of a fault, trained operators are faced with hundreds of subsystems and a large number of monitoring and control parameters, and the immense psychological stress can easily lead them to misjudgments, which can lead to serious radiological consequences. With the rise of AI, numerous studies on fault diagnosis based on AI have emerged. AI is a technology that resembles human intelligence through some programmed language of computers. AI has shown great advantages in some aspects. First, AI can process huge sources of information in a short period, helping operators extract critical information quickly after a fault occurs. Second, AI can also eliminate human error. Even the best experts in the nuclear field have the potential to make mistakes, while AI systems built on specific tasks do not suffer from such errors. Third, AI can work continuously, and continuous condition monitoring is essential for nuclear power plants. AI does not always work, e.g., some AI technologies that rely on training are unreliable if they encounter situations other than training.
With the development of AI technology, more and more scholars have focused on the application of AI in nuclear power plant fault diagnosis [3,27,28,29]. However, there is no systematic compendium of AI-based fault diagnosis methods for nuclear power plants. This paper aims to comprehensively review the progress of fault diagnosis techniques from an AI perspective and establish a new framework for fault diagnosis classification. Fault diagnosis technology is divided into two types: knowledge-driven and data-driven. The existing research is described and analyzed in detail under this framework. One of the purposes of this paper is to introduce existing nuclear power plant fault diagnosis problems to the research group of AI and to introduce AI concepts and techniques to the nuclear power industry, to make the combination of AI and fault diagnosis better. This paper also tries to identify the problems to be solved and the direction of future research. Note that this paper will not discuss all the techniques in the field of fault diagnoses, such as traditional signal-processing-based fault diagnosis techniques and component-level fault diagnosis. The reader may refer to [16,30] for more information on the history and methods of diagnosis techniques.
This paper is organized as follows: Section 2 is a fault diagnosis classification framework from the AI perspective. Section 3 introduces knowledge-driven fault diagnosis techniques and representative methods. Section 4 introduces data-driven fault diagnosis techniques and representative methods. Section 5 is the comparative analysis of the two methods. Section 6 provides the conclusions of this paper and the directions for future research.
2. Fault Diagnosis Classification from the AI Perspective
It is important to identify the history of AI development, which helps to establish a framework for AI-based fault diagnosis technology for nuclear power plants.
2.1. Development History of AI
Artificial intelligence (AI) was born in 1956, and there are two competing lines of development, namely, symbolism and connectionism [31]. As shown in Figure 2, connectionism, also known as data-driven methods, predates symbolism and originates in early computers and cybernetics [32]. The concept of neural networks was introduced by neuroscientist Warren McCulloch and logician Walter Pitts in 1943 [33]. The development trend in Figure 2 shows the dominance of connectionism in the early stages, and connectionism saw a major development in the late 1950s [34]. Frank Rosenblatt, inspired by the work of many parties, proposed a true connectionism system [35]. In the 1960s and 1970s, a variety of connectionist techniques were developed [36,37,38], such as statistical learning techniques based on decision theory [38] and reinforcement learning techniques [39], with representative works such as Samuel’s checkers program [40] and Nilsson’s “learning machines” [41].
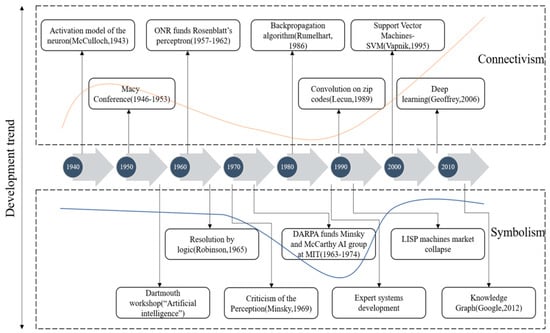
Figure 2.
History of AI, two lines of development, and the dominant situation in each period.
In the late 1970s, limited by the computing power of the time, the development of connectionism reached a low point, and the school of symbolism gradually emerged. Symbolism, also known as knowledge-driven methods, was defined as artificial intelligence at the Dartmouth Conference in 1956, and connectionism in cybernetics was introduced into AI years later [42]. Symbolism dominated the field of AI from the 1960s to the early 1990s. At the request of National Aeronautics and Space Administration (NASA) in 1965, Stanford University successfully developed the Dendritic Algorithm (DENRAL) expert system, which has a very rich knowledge of chemistry and can help chemists infer molecular structures from mass spectrometry data. The completion of this system marked the birth of expert systems [43]. By the mid-1970s, expert systems had gradually matured, the most representative of which was the Daptomycin (MYCIN) system by Sholtev et al., which was used to diagnose and treat bloodstream infections and encephalitis infections and could provide prescription recommendations [44]. Another highly successful expert system is the Prosecutor (PROSPECTOR) system, which was used to assist geologists in detecting mineral deposits and was the first to achieve significant economic benefits [45]. After the mid-1980s, expert systems have been widely put into commercial operation. One famous example is the eXpert CONfigurer (XCON)/R1 expert system developed by the Department of Environmental Conservation (DEC) in collaboration with Carnegie Mellon University, which saves millions of dollars per year [46]. Subsequently, symbolism went downhill due to its complex construction process and limited performance [47]. Since the 1990s, there has been a strong tendency for connectionism to replace symbolism due to improved algorithms, increased computing power, and improved data resources [48,49,50]. Geoffrey Hinton, the father of neural networks, and his student Ruslan proposed a solution to the problem of gradient disappearance in deep network training, starting the wave of deep learning in industry and academia [51]. However, in 2012, Google launched the Knowledge Graph project, which is essentially an improvement on the semantic web of the 1960s symbolism school and to some extent represents progress in the development of symbolism [52].
In conclusion, connectionism is dominant in the current development process of AI while symbolism is in a slow development stage. However, both AI routes have their one-sidedness. Connectionism lacks robustness and interpretability, while symbolism lacks data mining and relies excessively on expert subjective opinions and complex combinatorial rules. Therefore, the two schools have a strong complementarity, and the integration of the two schools will certainly become a major trend in the future development of AI. For the convenience of description, this paper refers to symbolism as the first-generation AI and connectionism as the second-generation AI.
2.2. AI-Based Fault Diagnosis Classification
Since the 1980s, AI-based fault diagnosis techniques have been applied in nuclear power plants [53], and subsequent developments have been closely linked to AI techniques. The nuclear accident diagnosis expert system [54] is a typical representative of the first-generation AI-based techniques, which consists of a fault diagnosis knowledge base, a comprehensive knowledge base, and a fault diagnosis inference machine. The system obtains fault types by importing the monitored physical symptoms into the inference machine and interacting with the diagnostic knowledge base. Early expert systems were mainly based on simple if–then rules in the computer domain [55], and new theories such as signed directed graphs (SDGs) [56], Bayesian networks (BNs) [57], and dynamic uncertain causality graphs (DUCGs) [58] were gradually introduced subsequently. Neural-network-based fault diagnosis technology is a typical application of second-generation AI, which uses historical data to train neural networks to obtain a diagnostic model capable of identifying faults [59]. In addition, scholars have conducted in-depth research on the applications of single and hybrid algorithms. Scholars applied a single algorithm including artificial neural networks, principal component analysis, support vector machine, decision tree, and unsupervised clustering to fault diagnosis and preliminarily verified the feasibility of these methods [60,61,62,63,64]. Subsequently, hybrid algorithms such as fuzzy logic–neural network, laminar model–neural network, principal component analysis–neural network, laminar model–support vector machine, and principal component analysis–convolution neural network are proposed, and these hybrid algorithms have been proven to have better diagnostic performances than single algorithms [65,66,67,68,69,70,71,72,73].
VOSviewer 1.6.17 is a software tool for constructing and visualizing bibliometric networks. In this paper, we use VOSviewer software to conduct statistical and cluster analyses of the literature to obtain the hot topics and frontier trends in the field of “nuclear power plant fault diagnosis”. A subject search was conducted by the keyword “fault diagnosis”, and the research direction was set to “nuclear science technology” based on all the databases subscribed to the Web of Science. The clustering view shown in Figure 3 was obtained by performing text analysis on 647 relevant papers. The brighter the node color in the graph, the more relevant papers are. Being closer to the center indicates that the research object receives more attention. The fault diagnosis methods related to AI can be divided into part A and part B as shown in Figure 3. In part A, “knowledge base”, “expert system”, “fuzzy logic”, and “fuzzy logic” can be seen, and they belong to the first generation of AI technology. Part A is located at the edge of the clustering diagram, which indicates that the current attention to the application of the first generation of AI technology is not high. In part B, “artificial neural network” and “training” can be seen, and they belong to the second generation of AI technology. It can be seen that part B has brighter color and higher centrality, which indicates that the fault diagnosis method based on second-generation AI is the current research hot spot.
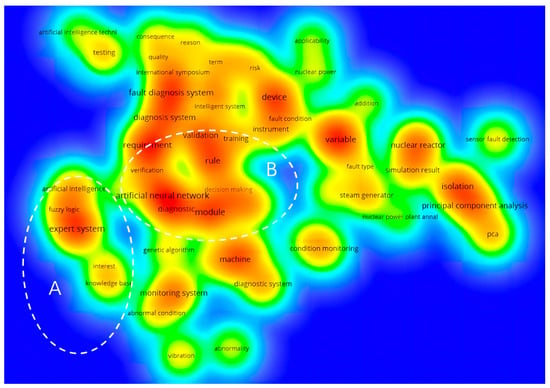
Figure 3.
Cluster diagram for fault diagnosis of nuclear power plants.
As shown in Figure 4, this paper establishes a new fault diagnosis classification framework from the AI perspective, that is, knowledge-driven and data-driven fault diagnosis methods. Knowledge-driven methods correspond to first-generation AI technology, and data-driven methods correspond to second-generation AI technology. Then, the development of the two methods is systematically combed to help readers understand the progress of fault diagnosis technology from the AI perspective.
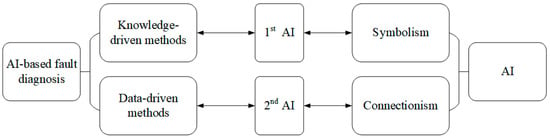
Figure 4.
Fault diagnosis classification framework.
3. Knowledge-Driven Fault Diagnosis Methods
Knowledge-driven fault diagnosis methods for nuclear power plants, also known as expert systems, can be regarded as a combination of the knowledge base and the inference machine. They mainly use the experience accumulated by domain experts in long-term practice. As shown in Figure 5, the knowledge-driven fault diagnosis methods can be divided into two types, the early if–then (Section 3.1) and the current new theories (Section 3.2). These new theories include signed directed graphs, Bayesian networks and dynamic uncertain causality graphs, etc. The inference mechanism is the main difference between them. Finally, we summarize the characteristics of these knowledge-driven methods (Section 3.3).
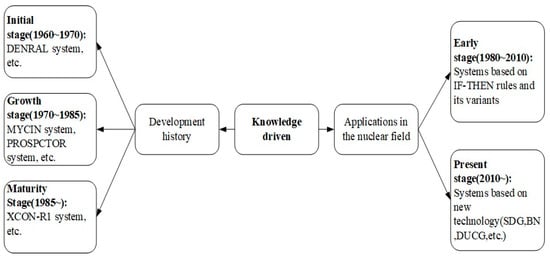
Figure 5.
History of knowledge-driven fault diagnosis methods and their application in the nuclear field.
3.1. Fault Diagnosis Methods Based on If–Then
The fault diagnosis technology based on if–then rules mainly includes the establishment of the knowledge base and the inference engine. William et al. built a fault diagnosis expert system by taking four types of typical accidents (LOFW, SGTR, LOCA, and MSLB) in nuclear power plants as the diagnosis objects [55]. They first established nine if–then rules (Table 1) based on domain knowledge and then constructed an expert system based on these rules. As shown in Figure 6, the system infers from known facts until the type of accident is obtained. If there is not enough information to conclude, the system infers backward to determine what information it needs to know. The system will then query the nuclear plant instrumentation or use the operator to fill in the knowledge gaps. Bergman et al. first used expert systems to diagnose faults in boiling water reactors [74]. Since expert knowledge has uncertainty, some scholars have introduced the concept of fuzzy membership in the representation of expert knowledge and used fuzzy logic for inference as a way to deal with the uncertainty of expert knowledge [75,76]. Sutton et al. developed a fuzzy expert system for the early detection of steam leakage faults in nuclear power plants [77]. Fuzzy theory is good at describing the uncertainty caused by imprecision, while evidence theory can describe the uncertainty caused by ignorance. Yang et al. proposed an expert system based on a confidence rule base based on fuzzy theory, evidence theory, and decision theory [78,79]. The confidence rule base adds the concept of confidence to the if–then rule, which can represent the complex causal relationship between various types of data with uncertainty. The above shows that the early expert systems in the nuclear field focused on the application and improvement under if–then rules.

Table 1.
If–then rules.
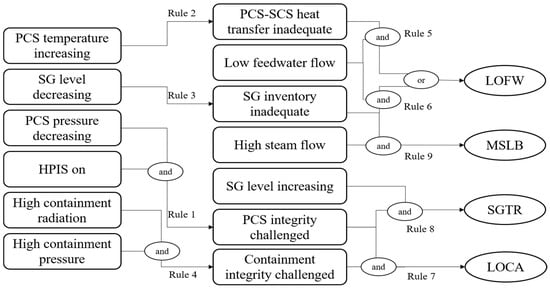
Figure 6.
Schematic diagram of an expert system based on if–then rules [55].
3.2. Fault Diagnosis Methods Based on New Theories
3.2.1. Signed Directed Graphs
Signed directed graphs (SDGs) are also knowledge-driven methods, which do not require an exact mathematical model. SDGs first originated in the chemical industry and were proposed by Iri et al. [80]. SDGs consist of nodes and directed arrows between nodes, which can effectively represent the relationships between elements within a system. As shown in Figure 7, the node representation in SDG is flexible. Nodes a, b, and c can represent not only physical variables, such as pressure and temperature, but also some parts of the system, such as switches and valves. Nodes R1 and R2 can represent an event, such as a specific fault cause or adverse consequence [10]. The relationships between nodes in SDG are expressed qualitatively, and it is not necessary to provide the exact quantitative relationships between system nodes. Therefore, it is easier to establish the model. For fault diagnosis of the SDG model, the means of combining reverse inference and forward inference are generally adopted. Assume that nodes a and b are abnormal and c is normal. According to the reverse inference, two compatible paths can be obtained: b → a → R1 and b → a → R2. R1 and R2 are the candidate fault sources. Then the forward inference is verified. If R1 is the fault source, node c should be large or small, but the state of node c is normal, which is not consistent with the observation. Therefore, the candidate fault source R1 is a false solution and should be discarded. Similarly, the forward inference for R2 is verified, and R2 is consistent with the actual observed value when R2 is the fault source, which means that R2 is a plausible fault source. More detailed information on the signed directed graph can be found in [81,82,83].
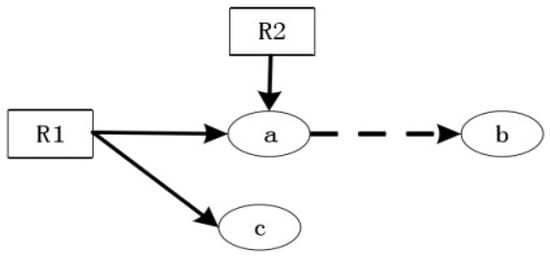
Figure 7.
Schematic representation of the structure of a symbolic directed graph. Nodes a and b are abnormal and c is normal. R1 and R2 are the candidate fault sources.
To improve SDGs’ accuracy and sensitivity, SDGs have been successively combined with other methods, such as SDGs–expert system [84], SDGs–principal component analysis [85], SDGs–qualitative trend analysis [86], SDGs–hazard and operability [87], SDGs–fuzzy logic [88,89], and SDGs–Bayesian networks [90].
In the nuclear field, Wu et al. thoroughly studied the application of SDGs methods for fault diagnosis and successively combined SDGs with fuzzy theory and correlation analysis for online monitoring and diagnosis of nuclear power plants [91,92,93]. The fault diagnosis technology based on SDGs can reveal the fault propagation path and comprehensively explain the fault cause, which is its remarkable feature. However, when the system is complex, the rule combination explosion problem will appear in accordance with the directed graph, which is one of the reasons why this method is not widely used at present.
3.2.2. Bayesian Networks
A Bayesian network is a directed acyclic network, which consists of nodes and directed edges. Nodes include parameter nodes and fault nodes, and the relationship between nodes is connected by directed edges. The uncertainty of the relationship between nodes is expressed by a conditional probability table [94]. Figure 8 shows a simple Bayesian network model in which is the fault nodes and has two states (“0” and “1”), and are parameter nodes, each of which has states. Assuming that the parameter nodes have two states, their conditional probability tables are shown in Table 2 and Table 3. The directed edges between the nodes indicate the dependencies between the parent and child nodes, such as with . More detailed information on Bayesian networks can be found in [95,96].
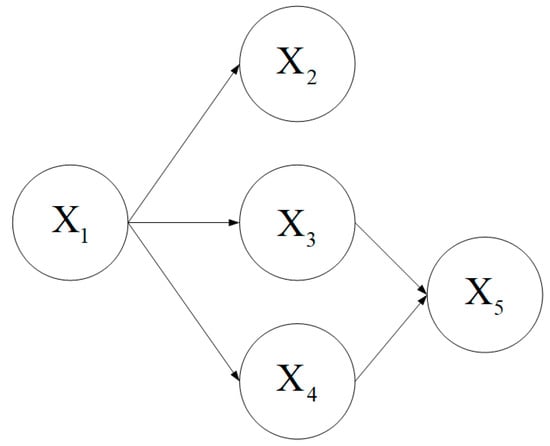
Figure 8.
Schematic representation of the structure of a Bayesian network.

Table 2.
CPT of parameters , , and .

Table 3.
CPT of parameter .
Assuming that the state information of the parameter node is currently obtained as , the probability that the faulty node is in state 1 (faulty state) is inferred from Equation (1).
Bayesian networks were first used to build regulatory systems and have been used in industrial systems since the 21st century, especially in the area of reliability. Lerner et al. proposed a dynamic Bayesian network (DBN) for tracking and diagnosing complex systems [97]. Przytula et al. proposed an efficient BN generation procedure for diagnosis and applied it to internal combustion locomotives, satellite communication systems, and satellite test equipment [98], which can handle continuous variables representing parameter states and discrete variables representing fault situations. Mahadevan et al. applied the BN concept to a new method for reassessing the reliability of structural systems [99].
In the nuclear field, Wu proposed a fault diagnosis framework for NPPs with BNs as the core, which combines PCA, data fusion, and fuzzy theory to achieve an online diagnosis of NPPs with multi-sensor information [100]. Jones et al. proposed a DBN system for diagnosing the state of nuclear power plants, which can predict the progress of an accident [101]. Oh et al. focused on the diagnostic performance under normal operating conditions and LOCA system states based on a dynamic Bayesian network and adopted the step-by-step diagnostic idea for system states and accident types [102]. Yi Ren et al. proposed a method of uncertainty reliability evaluation combining GO-FLOW and dynamic Bayesian network. This method uses sensitivity analysis to provide input information that contributes most to uncertainty. The uncertainty is then quantified using the DBN algorithm and Monte Carlo simulation to appropriately estimate the analysis results [103]. Zhao et al. combined Bayesian networks with a probabilistic risk assessment to achieve fast prediction of accident source terms. They used Bayesian networks for online fault diagnosis and matched the fault diagnosis results with the accident sequences in probabilistic risk assessment to obtain the source term release class [104,105,106]. Bayesian networks have advantages over if–then and SDG in accommodating missing information and uncertainty inference and quantifying diagnostic results.
3.2.3. Dynamic Uncertain Causality Graphs
In the 1990s, Zhang proposed a knowledge expression and inference model based on probability, the Dynamic Causality Diagram (DCD) [107]. Based on the DCD, Zhang further proposed the dynamic uncertain causality graphs (DUCGs), which added conditional action events and default events. It expressed the uncertain causality by independent random events and graphically. When predicting, the qualitative inference results are obtained first, and then the probability is calculated numerically [108]. Compared with BNs, the DUCG model is greatly simplified by removing unrelated independent events, and inference becomes very easy when evidence of independent connecting events or action events is introduced. In addition, DUCG overcomes the shortcomings that the concise expression of knowledge and inference methods of the BN applicable in the single-assignment case are not applicable in the multi-assignment case. The reason for describing the state of a variable is called an assignment. A single-assignment variable means that there is only one assignment for a variable, and a multiple-assignment variable means that there is more than one assignment for a variable. For detailed principles of DUCG theory, readers can refer to [58,109,110,111,112].
In the nuclear field, Deng was the first to establish a DUCG model for fault diagnosis in NPPs and validated the performance of the model with a second-loop feeder pipe leakage fault [113]. Zhang et al. proposed a DUCG method with fault diagnosis and fault process deduction [114]. Zhao et al. proposed a DUCG diagnosis system for CPR1000 reactor type and compared the method with other diagnosis methods, which promoted the development of an intelligent diagnosis system for the CPR1000 [115,116,117,118]. Dong et al. studied the new inference algorithm and industrial fault diagnostic system for nuclear power plants [119,120].
According to our literature study, the application of DUCG in the nuclear field is still in its infancy. There is a lack of specialized books on this theory, which hinders the promotion of DUCG technology to a certain extent. However, DUCG-based medical diagnosis technology is developing more rapidly, and Zhang’s team is also conducting related research and promotion [121,122,123,124,125,126].
3.3. Summary of Knowledge-Driven Fault Diagnosis Methods
This section focuses on knowledge-driven fault diagnosis methods for NPPs and classifies the existing methods into two types: if–then rule (Section 4.1) and new theories (Section 4.2). Expert systems (if–then), signed directed graphs, Bayesian networks, and dynamic uncertainty causal graphs are introduced in detail. The development characteristics of these four methods are shown in Figure 9. The earliest expert systems are based on if–then rules and rely on the rules stored in the expert knowledge base. The symbolic-directed graph method incorporates qualitative knowledge representation between nodes, which greatly improves the inference ability. The Bayesian network introduces uncertain inference technology, which can accommodate information loss and improve system robustness. Dynamic uncertainty causal graphs develop multi-assignment inference techniques based on Bayesian networks, which possess higher inference efficiency. These knowledge-driven methods share common drawbacks. They all need to establish a complete knowledge base first. Therefore, it is necessary to improve the efficiency of knowledge acquisition and the completeness of the knowledge base. In addition, the complex cause–effect relationships within nuclear power plants make the knowledge base complex and large, which requires improved reasoning efficiency.
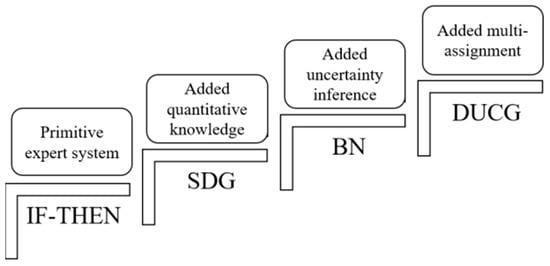
Figure 9.
Development characteristics of the four methods.
4. Data-Driven Fault Diagnosis Methods
The data-driven fault diagnosis method for nuclear power plants can be regarded as a combination of a “data base” and an “inference machine”. The “data base” is defined as the massive data resources required by the method, which should be distinguished from the concept of the database in the computer field. Additionally, the “inference machine” refers to a trained model based on large amounts of data, which is different from knowledge-driven “inference machines” (Section 3). As shown in Figure 10, the application of data-driven fault diagnosis methods in the nuclear field can be divided into two types: single algorithms (Section 4.1) and hybrid algorithms (Section 4.2). Most hybrid algorithms are improved based on single algorithms and have stronger diagnostic performance. To enable readers to understand the data-driven methods and their research progress in detail, the principles of several representative methods and their application progress in NPP fault diagnosis are introduced in Section 4.1. The research progress of fault diagnosis based on hybrid algorithms is introduced in Section 4.2. Finally, we summarize the characteristics of data-driven methods (Section 4.3).
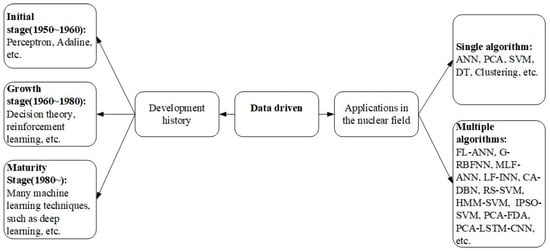
Figure 10.
History of data-driven development and its application in the nuclear field.
4.1. Fault Diagnosis Methods Based on Single Algorithms
In this section, we present several representative single algorithms and their research progress in the nuclear field and conclude with a brief comparison of these methods.
4.1.1. Artificial Neural Network
Artificial neural networks (ANNs) are mathematical models that mimic the structure and function of biological neural networks. They are used to approximate or evaluate functions [127]. An ANN is a system that can learn and summarize existing data to produce a system that can be automatically identified. The most common artificial neural network is a back propagation neural network (BPNN), as shown in Figure 11, which consists of an input layer, one or more hidden layers, and an output layer in which neurons are connected by weights. Each neuron contains two transformation steps internally [128,129,130]. First, the weighted sum of all input values connected to that neuron is calculated. Second, the weighted sum is nonlinearly transformed using an activation function.
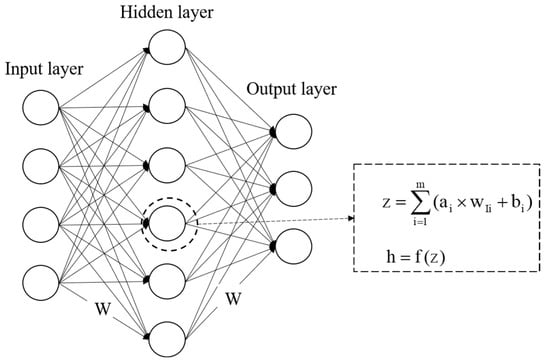
Figure 11.
BP neural network.
The training process of a BPNN is as follows: when a BPNN obtains a learning sample, the sample is transmitted from the input layer through the hidden layer to the output layer, which is the input response of the network. If the network fails to obtain the expected target output in the output layer, the error signal will enter the back-propagation phase and return to the input layer along the original connection path. The error signal can be reduced by modifying the weights of each layer. When errors are propagated repeatedly, the correct prediction of the output layer increases. The back-propagation process is stopped until the error is sufficiently small, and then a mapping is created between the input and output to obtain a model with predictive or diagnostic capabilities. With the development of technology, artificial neural networks have developed in various forms. The network architecture can be divided into three types: feed-forward neural networks [131], recurrent neural networks [132], and reinforcement networks [133].
Since artificial neural networks can handle complex multimodal, associative, inferential, and memory functions, this matches the fault diagnosis of complex nuclear power systems. The fault diagnosis method based on a neural network is to establish a mapping of the fault diagnosis based on the training data. The trained network is then used for new observations to judge anomalies. Zwingelstein et al. first applied the BPNN to the fault diagnosis of NPPs and preliminarily verified the feasibility [60,134,135]. In addition to BPNNs, such as recurrent neural networks (RNNs) [136], improved BPNNs [137], self-organizing neural networks [138], and Hopfield neural networks [139] have all been studied in applications. In general, research based on neural networks is mostly in the preliminary validation phase. The combination of neural networks with other algorithms for diagnosis is the mainstream trend. The related content will be presented in Section 4.2.
4.1.2. Support Vector Machine
The basic idea of support vector machines (SVMs) is to divide data into different categories using a hyperplane formed by formulas. Taking the simplest two classifications as an example, as shown in Figure 12, the formula represents different hyperplanes. For a linearly separable dataset, and denote the two boundaries of the hyperplane. All hyperplanes that can divide the dataset into two classes are within these two boundaries. Among all hyperplanes, the goal of SVM is to find an optimal decision boundary that is farthest from the nearest samples of different classes, that is, to obtain the most robust classification hyperplane. Since the nuclear power plant operation data are nonlinear, it is not possible to establish the hyperplane by the same method. The solution is to map the data from the low-dimensional space to the high-dimensional space and find the optimal hyperplane in the high-dimensional space, and the kernel function is the core of the method. More detailed principles about SVM can be found in [133,134,135].
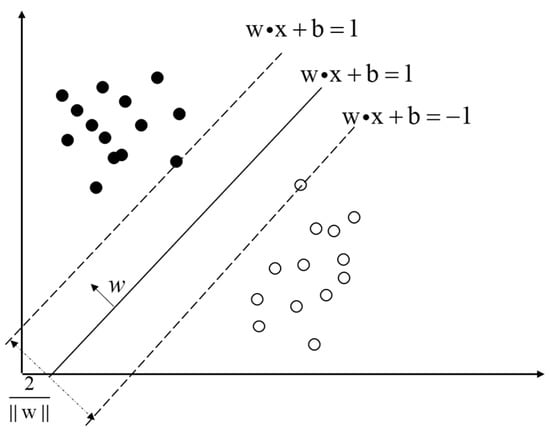
Figure 12.
Support vector machine.
Gottlieb et al. first used support vector machines for the diagnosis of NPP accidents and verified the feasibility of SVM for data classification [135]. Zio et al. used support vector machines in the diagnosis of subsystems such as feed water system [136], first-loop system [137], and other components of abnormal monitoring [138,139]. Kim et al. used support vector machines to predict the times of serious accidents to help operators better manage accidents [140]. Abiodun et al. established diagnostic models for different components of NPPs in the form of a support vector set for early fault diagnosis [141]. As with neural network methods, NPP fault diagnosis relying on SVM alone has been less studied. As a fundamental method, the current research involving SVMs is more in the area of hybrid algorithms, which will be presented in subsequent sections.
4.1.3. Decision Tree
The decision tree is a tree structure learned from data. The decision tree is based on a tree structure to make decisions. It selects one of several attributes of the training samples for determination each time and assigns the samples to different sets according to their values on that attribute, after which the next round of decisions is made until all the samples in the same set belong to the same class. Decision trees usually have three steps: feature selection, generation of decision trees, and pruning of decision trees. As shown in Figure 13, when using a decision tree for fault diagnosis, the fault feature parameters are tested starting from the root node, and the fault samples are assigned to their internal nodes based on the test results. Each internal node corresponds to a value of that feature, so the samples are tested and assigned recursively until they reach the leaf node, which is the type of fault. In fact, for complex industrial systems such as nuclear power plants, overly complex decision trees will lead to poor generalization performance. Readers can find more detailed information in [140,141,142,143].
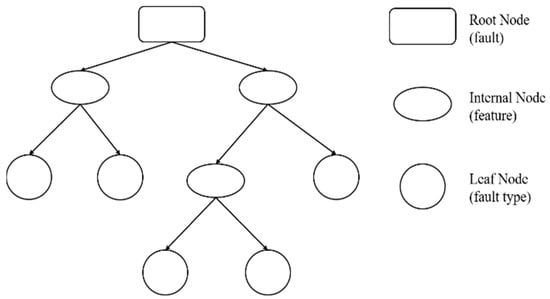
Figure 13.
Decision tree.
In the field of NPP fault diagnosis, decision trees are more intuitive and explanatory than other algorithms, but pure decision-tree-based fault diagnosis is less applied. Yu et al. first used a decision tree in the fault diagnosis of NPP and compared and combined it with other algorithms [63,144,145]. Sharanya et al. used decision trees for the diagnosis of cooling tower faults in NPPs. Based on the comparison of several algorithms, they concluded that decision trees have the potential to be combined with other algorithms to construct hybrid models [146].
4.1.4. Principal Component Analysis
Principal component analysis (PCA) is a statistical method that converts a set of potentially correlated variables into a set of linearly uncorrelated variables called principal components through an orthogonal transformation. PCA is often used for data dimensionality reduction. As shown in Figure 14, the first step is to move the center of the axes to the center of the data and then rotate the axes to maximize the variance of the data on the C1 axis to retain more information, where C1 is the first principal component. The second step is to find the second principal component C2 so that it has a covariance of 0 with C1 to avoid overlapping with C1 information and maximize the variance of the data in that direction. The third step is to use the same steps as the second step to continue to find the next principal component. Data containing m variables can have up to m principal components. More detailed principles of principal component analysis can be found in [147,148,149].
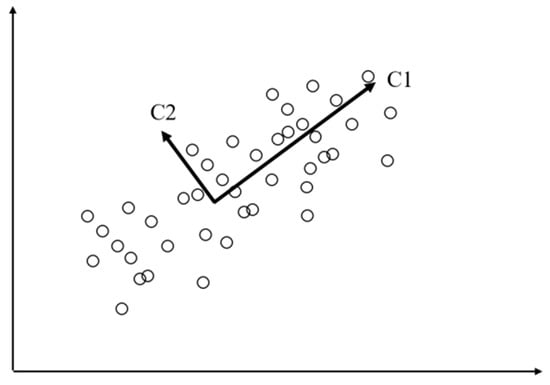
Figure 14.
Principal component analysis.
In the field of NPP fault diagnosis, PCA is generally used for fault monitoring. Lu et al. used PCA in the fault diagnosis of steam generators to extract the main features of faults and quantify the accuracy of fault identification by projecting normalized vectors into the fault space [147,148]. Zhao et al. used PCA for steam generators and considered the uncertainty of the simulation model, which improved the robustness of the PCA model diagnosis [149]. Wei et al. used the PCA method for status monitoring of the sensor in NPPs and calculated the non-detection area of the sensor in the model, which expanded the fault diagnosis scope of the PCA model [150,151,152,153,154]. Yu et al. proposed an improved PCA model to improve the diagnostic accuracy and the diagnostic capability of multi-sensors [155,156]. Zhang et al. systematically studied the fault detection performance of various PCA methods [157]. In addition, most of the fault diagnosis methods use PCA as a pre-technology to reduce the data dimension to improve the diagnostic performance of hybrid methods, which will be described in subsequent sections.
4.1.5. Clustering
Clustering is an emerging method, and the understanding of clustering is not systematic enough compared with the aforementioned algorithms. There is not even a chapter on clustering in the well-known textbook [158]. Clustering is an unsupervised learning method, that is, the labeling information of the training samples is unknown. The goal is to divide the samples in a dataset into several usually disjoint subsets, each called clusters. Note that clustering is significantly different from classification. The former algorithms (Section 4.1.1, Section 4.1.2, Section 4.1.3 and Section 4.1.4) essentially solve the classification problem, that is, the labels of each sample are known and the data are classified into known categories. Clustering divides the data into different subsets according to its inherent nature and rules. Clustering can be divided into partition-based methods, hierarchy-based methods, density-based methods, network-based methods, and model-based methods. More detailed principles of clustering can be found in [159,160,161].
In the field of NPP fault diagnosis, clustering is mainly used for fault monitoring. This method can be used to distinguish abnormal conditions from normal conditions even if they have not been trained. Talonen first developed a diagnostic model for early fault identification in NPPs based on a partition method [162]. Podofillini et al. established a dynamic process fault identification model based on model clustering [163]. Mercurio et al. simulated 60 accident samples and classified them into four categories using a clustering method, one of which was a new type of fault that was not trained beforehand [164]. Sameer et al. clustered turbine fault information from different NPPs and developed a generic fault diagnosis framework [165]. Baraldi et al. successively used clustering for fault diagnosis of different components of NPPs [61,166,167,168,169,170].
4.1.6. Comparison of Single Algorithms
Some data-driven methods have not been mentioned, such as logistic regression and naive Bayes. Due to their lack of applicability or application prospects, they are not further described in this paper. Table 4 summarizes the characteristic of the above five methods.

Table 4.
Comparison of single algorithms.
4.2. Fault Diagnosis Methods Based on Hybrid Algorithms
In the field of NPP fault diagnosis, hybrid algorithms combine the advantages of different single algorithms to obtain better diagnosis results. With the development of AI technology, almost all of the current methods are based on hybrid algorithms. As shown in Table 5, we conducted a detailed survey of the existing hybrid-algorithm-based fault diagnosis methods. In this table, we established six topics based on the five algorithms introduced in Section 4.1. In the first five topics, X stands for other auxiliary algorithms, such as ANN+X, which represents a hybrid diagnostic algorithm with ANN as the main algorithm. The sixth topic is the research literature involving the comparison of each algorithm. According to the literature research, the proportion of the literature on each topic and the distribution of the diagnostic objects are shown in Figure 15.
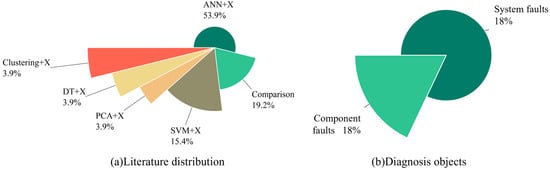
Figure 15.
Literature topic distribution (a) and diagnosis object (b).
In general, the current research of ANN+X algorithm occupies the mainstream direction, which is consistent with the development trend of AI, followed by SVM+X and comparison. In terms of diagnosis objects, system-level faults in NPPs, such as LOCA, SGTR, MSLB, and other initial events, are the vast majority of the diagnosis objects. However, component-level faults such as valves, feed pumps, inverters, etc. are less studied. One of the reasons is that most of the studies are conducted based on simulators due to the lack of real fault data, while simulation data for system-level faults are more readily available.
ANN+X. This topic is closely related to the development of neural network technology. For example, RNN is a very popular technique in recent years, which is good at processing time series data and has wide applications in natural language processing and artificial intelligence translation. Ye et al. introduced RNN with other algorithms into NPP fault diagnosis [171,172,173], making full use of the time series nature of the data. Some scholars considered the NPP data too complex, so they used other algorithms as front-end techniques to reduce the dimensionality and finally obtained better diagnostic performances [69,174,175]. Since there are various types of ANNs, each with unique advantages, integrated learning techniques combining multiple networks have been widely studied [158,159,160,161,162]. Ming et al. introduced multilayer flow models to improve the accuracy and interpretability of the neural network [67]. Qian et al. proposed a method to expand the fault diagnosis dataset based on generative adversarial networks (GANs) and demonstrated that the enhanced dataset can improve the performance of various models [163]. In addition, several scholars have studied the optimization of the hyperparameters of ANNs to obtain the parameter settings with the best diagnosis performance [172].
Comparison. In a comparative study, Yao et al. compared the performance of ANN with PCA, DT, and SVM methods in a more systematic way. He also transformed the state information of NPPs into image form and then used the advantages of convolutional neural networks in image recognition for the fault diagnosis [164]. In addition, Liu et al. built a hybrid model of SVM and SDG (the knowledge-driven method) and adopted different diagnostic methods for different objects [165]. To sum up, the relative research is relatively basic, and systematic comparative research is not yet available.
Other topics. The research directions of SVM+X include two main aspects. One is a combination of algorithms to reduce the data complexity with SVM. Another is to introduce algorithms related to the SVM parameter optimization [73,166,167]. The other three topics (PCA+X, DT+X, and Clustering +X) are less studied, and these three topics can be further studied in terms of integrated learning, interpretability, and hyperparameter optimization.

Table 5.
Fault diagnosis methods based on hybrid algorithm.
Table 5.
Fault diagnosis methods based on hybrid algorithm.
| Topic | Reference | Algorithm | Diagnosis Object | Highlights |
|---|---|---|---|---|
| ANN+X | [171] | WPT and LSTM | NPP converter | The operation mode of the power system is analyzed in depth when a failure occurs. |
| [174] | WPT and ANN | NPP system faults | Disturbing perturbations in training set are reduced by WPT. | |
| [173] | RNN, WOLP, and ARTD | NPP system faults | The paper improved the practical applicability and scalability of diagnosis systems to real processes and machinery. | |
| [69] | CN and DBN | NPP system faults | Correlation analysis is used for dimensionality reduction. | |
| [69] | FNN and MSIF | NPP system faults | The system is able to achieve a single-fault and some multiple-fault diagnoses. | |
| [172] | CGRN and EPSO | NPP system faults | The technical framework of digital twin model, deep learning, and heuristic algorithm is established. | |
| [158] | BPNN and RBF | NPP system faults | First adopts the BP-ANN for a rapid group pre-diagnosis, then uses the RBF ANNs to verify the results. | |
| [159] | FNN and RBF | NPP system faults | A combination of NN and fuzzy theory is proposed. | |
| [160] | ANN and VF | NPP system faults | Many neural networks diagnose the same fault, and the result is obtained by voting fusion. | |
| [161] | ANN and LF | NPP system faults | The logical fusion method was employed to fuse the diagnosing results of different neural networks. | |
| [162] | ELM and AdaBoost | NPP system faults | The paper verifies the feasibility and validity of the ensemble learning method for fault diagnosis. | |
| [168] | ANN and SW | NPP system faults | Adaptive feature learning using a sliding window strategy. | |
| [67] | ANN and MFM | NPP system faults | MFM can provide explanations on how the malfunctions originated and propagated to the current situation. | |
| [169] | ANN and FL | Small break loss of coolant accident | High sensitivity and superior prediction capabilities. | |
| SVM + X | [166] | LS-SVM and GPR | NPP system faults | PSO is applied to find the optimal GPR model to better assess the severity of the fault. |
| [170] | SVM and RS | NPP system faults | The uncertain data is reduced based on RS theory. | |
| [73] | SVM and EPSO | NPP system faults | The optimization of hyperparameters of SVM by improved PSO is compared with others. | |
| [167] | SVM and GA | Physical parameter | A new GASVM is proposed to classify multiple faults. | |
| PCA+ X | [72] | PCA and MFM | NPP system faults | Mechanism simulation is implemented to provide training data with fault signatures. |
| DT + X | [145] | DT and RS | NPP system faults | A parameter reduction method based on neighborhood rough sets was proposed. |
| Clustering +X | [176] | Clustering and FBS | NPP turbine | The paper developed a framework of unsupervised classification of transients. |
| Comparison | [164] | PCA and (SVM, KNN, LDA, DT, and LR) | NPP system fault s | The state information imaging is used to construct the different condition images. |
| [177] | PCA and SVM | NPP system fault s | A three-layer fault classification model was established to diagnose the fault type, location, and degree. | |
| [178] | PCA and ANN | SG tube; RCS pump | Radial basis network provides better prediction and diagnoses the faults faster than Elman neural network. | |
| [165] | ANN, D-S, and SDG | NPP system faults | To the different diagnostic object, we adopted the different diagnostic methods. | |
| [179] | ANN and SVM | Feed-water pump | A comparative analysis of ANN and SVM was performed. | |
| [147] | PCA and ANN | NPP system faults | The method utilizes the (PCA) technique to reduce the problem dimension. |
Abbreviations: WPT: wavelet packet transforms; LSTM: long short-term memory; RNN: recurrent neural network; WOLP: wavelet on-line pre-processing; ARTD: autonomous recursive task decomposition; CN: correlation analysis; DBN: deep belief network; FNN: fuzzy neural network; MSIF: multi-source information fusion; CGRN: convolutional gated recurrent network; EPSO: enhanced particle swarm optimization; RBF: dial basis function; VF: voting fusion; LF: logical fusion; ELM: extreme learning machine; SW: sliding window; MFM: multi-flow model; FL: fuzzy logic; RS: rough sets; GA: genetic algorithm; FBS: fuzzy-based slope.
4.3. Summary of Data-Driven Fault Diagnosis Techniques
This section provides a detailed survey of the data-driven NPP fault diagnosis methods based on a single and hybrid algorithm perspective. To help readers understand the basic principles of these methods more quickly, this part dilutes the relevant formulas and elaborates the core ideas in layman’s terms, and it includes an index of the relevant literature for readers who need to do further study. The study shows that the current research favors the application of hybrid algorithms. This is because a single algorithm often does not fully satisfy the needs of the fault diagnosis. ANN+X is a popular research direction, which is also driven by the current popular deep learning technology. However, for nuclear power plants with high safety and reliability requirements, the inherent uninterpretability of neural networks and the dependence on massive data will hinder their practical application.
5. Results
The advantage of knowledge-driven methods is that there is no need to establish a systematic analytical model, and the diagnosis results are highly interpretable and robust. However, there are shortcomings in these methods. First, it is difficult to obtain expert knowledge, and the accuracy depends on the richness of the knowledge base. Second, when there are many inference rules, matching conflicts may occur during the inference process, resulting in low inference efficiency. The advantages of the data-driven methods are that the modeling process is relatively simple, general, and in real time, but there are also some shortcomings. Second, it is difficult to obtain fault sample data, and it is almost impossible to obtain real fault sample data for NPPs. For example, a large amount of data is required to train a neural network, which is not friendly to nuclear power plants. Third, the generalization ability of the model is weak. Once the actual data are slightly different from the training data, it may lead to inaccurate diagnosis results. Fourth, its calculation process is not interpretable, and it is difficult to convince industry workers. Table 6 compares the advantages and disadvantages of the two types.

Table 6.
Comparison of fault diagnosis methods.
The table shows that the two types are highly complementary but that a way to truly integrate the two has not yet been achieved. In recent years, physics-informed neural networks (PINN) [180], which embed physical partial differential equations into neural networks for learning solutions, have effectively improved the generalization ability of models and compensated for the disadvantages of purely data-driven methods. The integration of knowledge-driven and data-driven methods represented by PINN brings new ideas to nuclear power plant fault diagnosis technology. How to combine the two organically and make full use of the knowledge and data resources of nuclear power plants is an important research direction.
6. Conclusions and Future Directions
This paper reviews the fault diagnosis techniques for NPPs from the perspective of AI. A new fault diagnosis classification framework is established. The fault diagnosis techniques are divided into two types: knowledge-driven and data-driven. The knowledge-driven methods are divided into the early if–then rules and current new theories (SDG, BN, DUCG, etc.). The principles, application, and comparative analysis of these methods are systematically described. The data-driven methods are divided into two research directions: single algorithms and hybrid algorithms. For single algorithms, the principles, application, and comparative analysis of the five representative algorithms (ANN, SVM, PCA, DT, and clustering) are also given. For the hybrid algorithm, a “topic + X” classification means is constructed in this paper. The existing fault diagnosis technology based on hybrid algorithms is investigated in detail, and the mainstream trend of current research is given. Finally, the advantages and disadvantages of both knowledge-driven and data-driven methods are compared, and an important research direction is how to combine data-driven and knowledge-driven methods. With the advancement of AI technology, NPP fault diagnosis methods are still being improved and developed forward, and the following are some possible research directions.
- The combination of data-driven and knowledge-driven fault methods. At present, their respective theories have become mature, but there is still a lack of theoretical research integrating their advantages. In the context of the digital transformation of NPPs, data resources can be easier to obtain, and knowledge resources can be obtained from NPP’s Deterministic Security Analysis Report (DSAR) and Probabilistic Risk Analysis Report (PRAR). DSAR and PRAR contain detailed knowledge descriptions of fault mechanisms, which can be used to build knowledge-driven models such as Bayesian network models, and data resources of nuclear power plants can help build data-driven models such as neural networks. For example, when strong interpretability of diagnostic results is required, it is necessary to consider incorporating knowledge into the model. We have explored the combination of knowledge-driven and data-driven methods by using PRAR and DASR to build Bayesian networks for fault type diagnoses as well as using data to build neural networks for fault severity diagnoses [181]. Studying new technologies to make full use of these two resources is a field worthy of research in the future.
- On-demand system fault diagnosis. In practice, Zhao et al. classify the types of NPP system-level faults into two types, operational faults and on-demand faults [106]. An operational fault is defined as an unexpected abnormal behavior during the operation of a nuclear power plant, such as a rupture of primary coolant pipes and a rupture of heat transfer pipes of steam generators. An on-demand fault is defined as the fault of the response system to perform a predetermined function after an operational fault occurs, such as high pressure in the primary circuit, which makes the pressure of the regulator higher than the set value and prevents the relief of the safety valve from opening. At present, there is little research on on-demand faults, but it is of great significance to nuclear safety.
- Introduction of digital twin technology. Digital twin refers to the simulation process of integrating multi-disciplinary, multi-physical quantity, multi-scale, and multi-probability technology by making full use of the data such as the physical model, sensor update, and operation history and finally completing the mapping in the virtual space, to reflect the whole life cycle process of the corresponding physical equipment [182]. At present, most studies are based on data from NPP simulators. These simulators are not high-fidelity models, which means that the application of the diagnostic model in actual NPP has great uncertainty. The digital twin technology can accurately simulate the actual equipment. The reliability and safety of its practical application will be greatly improved based on this technology. Nguyen et al. studied a digital twin approach to system-level fault detection and diagnosis for thermal hydraulic systems [183]. Therefore, it is of great significance to establish the digital twin model of NPPs.
- More detailed diagnostic hierarchy. As shown in Figure 15, most of the current studies focus on system-level faults in NPPs, while there are few studies on human factor faults, sensor faults, control room faults, network security faults, etc.
- Construction of the generalized model. In many cases, the fault diagnosis models we construct are only applicable to specific tasks. When encountering a new task, it is an important challenge to reuse the previous data and experiences. Transfer learning provides a possible solution [184]. Some related studies are in progress [185,186,187,188].
- Interdisciplinary cooperation. Fault diagnosis is a comprehensive technology involving multiple disciplines (modern control theory, mathematical statistics, signal processing, pattern recognition, artificial intelligence, etc.). Most of the current fault diagnosis research is limited intra-disciplinary exploration. An optimal fault diagnosis research should gather multidisciplinary knowledge as a way to drive the fault diagnosis technology in a more efficient, sensitive, and intelligent direction. Therefore, a cross-disciplinary perspective is crucial for researchers.
Author Contributions
Conceptualization, J.L. and J.T.; methodology, B.Q. and J.L.; investigation, B.Q.; writing—original draft preparation, B.Q.; writing—review and editing, J.L. and J.T.; funding acquisition, J.L. All authors have read and agreed to the published version of the manuscript.
Funding
The research was supported by the Innovation Funds of CNNC-Tsinghua Joint Center for Nuclear Energy R&D (Project No. 20202009032) and grant from National Natural Science Foundation of China (Grant No. T2192933).
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ding, S.X. Model-Based Fault Diagnosis Techniques: Design Schemes, Algorithms, and Tools; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Qian, Y.; Li, X.; Jiang, Y.; Wen, Y. An expert system for real-time fault diagnosis of complex chemical processes. Expert Syst. Appl. 2003, 24, 425–432. [Google Scholar] [CrossRef]
- Ma, J.; Jiang, J. Applications of fault diagnosis in nuclear power plants: An introductory survey. IFAC Proc. Vol. 2009, 42, 1150–1161. [Google Scholar] [CrossRef]
- Hwang, I.; Kim, S.; Kim, Y.; Seah, C.E. A survey of fault detection, isolation, and reconfiguration methods. IEEE Trans. Control Syst. Technol. 2009, 18, 636–653. [Google Scholar] [CrossRef]
- Dey, S.; Mohon, S.; Pisu, P.; Ayalew, B. Sensor fault detection, isolation, and estimation in lithium-ion batteries. IEEE Trans. Control Syst. Technol. 2016, 24, 2141–2149. [Google Scholar] [CrossRef]
- Kim, S.; Jung, I.; Kim, Y. Hybrid Fault Detection and Isolation Techniques for Aircraft Inertial Measurement Sensors. Int. J. Aeronaut. Space Sci. 2006, 7, 73–83. [Google Scholar] [CrossRef]
- Han, L.; De-Yun, X. Survey on data driven fault diagnosis methods. Control Decis. 2011, 26, 1–9. [Google Scholar]
- Dehestani, D.; Eftekhari, F.; Guo, Y.; Ling, S.; Su, S.; Nguyen, H. Online support vector machine application for model based fault detection and isolation of HVAC system. Int. J. Mach. Learn. Comput. 2011, 1, 66–72. [Google Scholar] [CrossRef]
- Andersson, M. Fault diagnosis of a fixed wing UAV using hardware and analytical redundancy. Dissertation 2013, 1, 92. [Google Scholar]
- Jacintha, V.; Shakthimurugan, K.; Kripakaran, V.; Lokeshwaran, S. FPGA Based Dual Redundancy CAN Controller with Fault Tolerance. In Proceedings of the 2018 4th International Conference on Electrical Energy Systems (ICEES), Chennai, India, 7–9 February 2018; pp. 667–671. [Google Scholar]
- Merrill, W.C.; Guo, T.-H.; Delaat, J.C.; Duyar, A. Real Time Fault Diagnosis for Propulsion Systems. IFAC Proc. Vol. 1991, 24, 491–496. [Google Scholar] [CrossRef]
- Cordoneanu, D.; Niţu, C. A Review of Fault Diagnosis in Mechatronics Systems. In Proceedings of the International Conference of Mechatronics and Cyber-Mixmechatronics, Bucharest, Romania, 6–7 September 2018; pp. 173–184. [Google Scholar]
- Simani, S.; Fantuzzi, C.; Patton, R.J. Model-based fault diagnosis techniques. In Model-based Fault Diagnosis in Dynamic Systems Using Identification Techniques; Springer: Berlin/Heidelberg, Germany, 2003; pp. 19–60. [Google Scholar]
- Wu, Q.; Saif, M. An overview of robust model-based fault diagnosis for satellite systems using sliding mode and learning approaches. In Proceedings of the 2007 IEEE International Conference on Systems, Man and Cybernetics, Montreal, QC, Canada, 7–10 October 2007; pp. 3159–3164. [Google Scholar]
- Marzat, J.; Piet-Lahanier, H.; Damongeot, F.; Walter, E. Model-based fault diagnosis for aerospace systems: A survey. Proc. Inst. Mech. Eng. Part G: J. Aerosp. Eng. 2012, 226, 1329–1360. [Google Scholar] [CrossRef]
- Gao, Z.; Cecati, C.; Ding, S.X. A survey of fault diagnosis and fault-tolerant techniques—Part I: Fault diagnosis with model-based and signal-based approaches. IEEE Trans. Ind. Electron. 2015, 62, 3757–3767. [Google Scholar] [CrossRef]
- Cong, X.; Zhang, C.; Jiang, J.; Zhang, W.; Jiang, Y.; Zhang, L. A Comprehensive Signal-Based Fault Diagnosis Method for Lithium-Ion Batteries in Electric Vehicles. Energies 2021, 14, 1221. [Google Scholar] [CrossRef]
- Chong, U.-P. Signal model-based fault detection and diagnosis for induction motors using features of vibration signal in two-dimension domain. Stroj. Vestn. 2011, 57, 655–666. [Google Scholar]
- Giantomassi, A.; Ferracuti, F.; Iarlori, S.; Ippoliti, G.; Longhi, S. Signal based fault detection and diagnosis for rotating electrical machines: Issues and solutions. In Complex System Modelling and Control through Intelligent Soft Computations; Springer: Berlin/Heidelberg, Germany, 2015; pp. 275–309. [Google Scholar]
- Wu, C.; Guo, C.; Xie, Z.; Ni, F.; Liu, H. A signal-based fault detection and tolerance control method of current sensor for PMSM drive. IEEE Trans. Ind. Electron. 2018, 65, 9646–9657. [Google Scholar] [CrossRef]
- Yan, C.; Wang, J.; Haifeng, G. Nuclear Reactor Structures and Materials; Harbin Engineering University Press: Harbin, China, 2015. [Google Scholar]
- Wan, J.; Song, H.; Yan, S.; Sun, J.; Zhao, F. Development of a simulation platform for dynamic simulation and control studies of AP1000 nuclear steam supply system. Ann. Nucl. Energy 2015, 85, 704–716. [Google Scholar] [CrossRef]
- Zhang, J.; Yin, S.; Chen, L.; Ma, Y.; Wang, M.; Fu, H.; Wu, Y.; Tian, W.; Qiu, S.; Su, G. A study on the dynamic characteristics of the secondary loop in nuclear power plant. Nucl. Eng. Technol. 2021, 53, 1436–1445. [Google Scholar] [CrossRef]
- Filippov, G.; Klemin, A. The role of auxiliary equipment in ensuring the reliability and safety of nuclear power plants. In Nuclear Power Performance and Safety. V. 2. Achievements in Construction and Operation; International Atomic Energy Agency (IAEA): Vienna, Austria, 1988. [Google Scholar]
- Hewitt, G.F.; Collier, J.G. Introduction to Nuclear Power; CRC Press: Boca Raton, FL, USA, 2000. [Google Scholar]
- Qi, B.; Xiao, X.; Liang, J.; Po, L.-c.C.; Zhang, L.; Tong, J. An open time-series simulated dataset covering various accidents for nuclear power plants. Sci. Data 2022, 9, 766. [Google Scholar] [CrossRef]
- Reifman, J. Survey of artificial intelligence methods for detection and identification of component faults in nuclear power plants. Nucl. Technol. 1997, 119, 76–97. [Google Scholar] [CrossRef]
- Ma, J. Methods and Systems for Fault Diagnosis in Nuclear Power Plants; The University of Western Ontario: London, ON, Canada, 2015. [Google Scholar]
- Patel, H.R.; Shah, V.A. Fault detection and diagnosis methods in power generation plants-the Indian power generation sector perspective: An introductory review. PDPU J. Energy Manag. 2018, 2, 31–49. [Google Scholar]
- Ma, J.; Jiang, J. Applications of fault detection and diagnosis methods in nuclear power plants: A review. Prog. Nucl. Energy 2011, 53, 255–266. [Google Scholar] [CrossRef]
- Zhang, B.; Zhu, J.; Su, H. Toward the third generation of articial intelligence. Sci. Sin. Inf. 2020, 50, 22. (In Chinese) [Google Scholar]
- De Blasio, G.; Moreno-Díaz, A.; Moreno-Díaz, R. McCulloch’s Relation to Connectionism and Artificial Intelligence. In Proceedings of the International Conference on Computer Aided Systems Theory, Las Palmas de Gran Canaria, Spain, 19–24 February 2017; pp. 41–48. [Google Scholar]
- McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Pias, C. Cybernetics–Kybernetik. In Proceedings of the The Macy-Conferences, New York, NA, USA, 8–9 March 1946. [Google Scholar]
- Rosenblatt, F. The perceptron: A probabilistic model for information storage and organization in the brain. Psychol. Rev. 1958, 65, 386. [Google Scholar] [CrossRef] [PubMed]
- Manheim, J.H.; Manheim, S.R. Connectionism and the teaching machine. Math. Teach. 1965, 58, 200–204. [Google Scholar] [CrossRef]
- Minsky, M.L.; Papert, S.A. Perceptrons. Am. J. Psychol. 1969, 84, 449–452. [Google Scholar]
- Mendel, J.; McLaren, R. 8 reinforcement-learning control and pattern recognition systems. In Mathematics in Science and Engineering; Elsevier: Amsterdam, The Netherlands, 1970; Volume 66, pp. 287–318. [Google Scholar]
- Chatam, S.L. Reinforced Study. In Proceedings of the Annual Conference of the Western College Reading Association, London, UK, 4–6 April 1972; Volume 5, pp. 21–24. [Google Scholar]
- Samuel, A.L. Some studies in machine learning using the game of checkers. II—Recent progress. IBM J. Res. Dev. 1967, 11, 601–617. [Google Scholar] [CrossRef]
- Nilsson, N.J. Learning Machines; McGraw-Hill: New York, NY, USA, 1965. [Google Scholar]
- McCarthy, J.; Minsky, M.L.; Rochester, N.; Shannon, C.E. A proposal for the dartmouth summer research project on artificial intelligence, august 31, 1955. AI Mag. 2006, 27, 12. [Google Scholar]
- Lederberg, J. How DENDRAL was conceived and born. In A History of Medical Informatics; American Medical Informatics Association (AMIA): Bethesda, MD, USA, 1990; pp. 14–44. [Google Scholar]
- Shortliffe, E.H.; Davis, R.; Axline, S.G.; Buchanan, B.G.; Green, C.C.; Cohen, S.N. Computer-based consultations in clinical therapeutics: Explanation and rule acquisition capabilities of the MYCIN system. Comput. Biomed. Res. 1975, 8, 303–320. [Google Scholar] [CrossRef]
- Duda, R.; Gaschnig, J.; Hart, P. Model design in the PROSPECTOR consultant system for mineral exploration. In Readings in Artificial Intelligence; Elsevier: Amsterdam, The Netherlands, 1981; pp. 334–348. [Google Scholar]
- Cheeseman, P.C.; Stutz, J.C. Bayesian classification (AutoClass): Theory and results. Adv. Knowl. Discov. Data Min. 1996, 180, 153–180. [Google Scholar]
- Cui, X.; Huang, Z.-X. Artificial Intelligence Research Program: Dilemma and Trend. J. Nanjing Univ. Aeronaut. Astronaut. (Soc. Sci.) 2011, 3, 1–15. [Google Scholar]
- Babbar, P.; Yadav, K.; Singhal, A.; Sharma, V. Connectionist model in artificial intelligence. Int. J. Appl. Eng. Res. 2018, 13, 5154–5159. [Google Scholar]
- Pierdicca, R.; Paolanti, M.; Felicetti, A.; Piccinini, F.; Zingaretti, P. Automatic Faults Detection of Photovoltaic Farms: solAIr, a Deep Learning-Based System for Thermal Images. Energies 2020, 13, 6496. [Google Scholar] [CrossRef]
- Li, W.; Zhang, L.; Wu, C.; Cui, Z.; Niu, C. A new lightweight deep neural network for surface scratch detection. Int. J. Adv. Manuf. Technol. 2022, 123, 1999–2015. [Google Scholar] [CrossRef] [PubMed]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the dimensionality of data with neural networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef] [PubMed]
- Qi, G.; Gao, H.; Wu, T. The research advances of knowledge graph. Technol. Intell. Eng. 2017, 3, 4–25. [Google Scholar]
- Zhou, G.; Yang, L. Advance in study of intelligent diagnostic method for nuclear power plant. At. Energy Sci. Technol. 2008, 42, 92–99. [Google Scholar]
- Yang, Y.O.; Chang, S.H. A diagnostic expert system for the nuclear power plant based on the hybrid knowledge approach. IEEE Trans. Nucl. Sci. 1989, 36, 2450–2458. [Google Scholar] [CrossRef]
- Nelson, W.R. REACTOR: An Expert System for Diagnosis and Treatment of Nuclear Reactor Accidents. In Proceedings of the AAAI, Pittsburgh, PA, USA, 22–26 August 1982; pp. 296–301. [Google Scholar]
- Chang, C.C.; Yu, C.C. On-line fault diagnosis using the signed directed graph. Ind. Eng. Chem. Res. 1990, 29, 1290–1299. [Google Scholar] [CrossRef]
- Pearl, J. Bayesian Networks; Cambridge University Press: London, UK, 2011. [Google Scholar]
- Zhang, Q.; Dong, C.; Cui, Y.; Yang, Z. Dynamic uncertain causality graph for knowledge representation and probabilistic reasoning: Statistics base, matrix, and application. IEEE Trans. Neural Netw. Learn. Syst. 2013, 25, 645–663. [Google Scholar] [CrossRef]
- Liu, Y.; Xia, H.; Shen, J.; Xie, C. Application of BP-RBF neural network to fault diagnosis of nuclear power plant. At. Energy Sci. Technol. 2008, 42, 193–199. [Google Scholar]
- Zwingelstein, G.; Georgel, B. Applications of expert systems and neural networks for the condition monitoring and inspection of french nuclear power plants. In Proceedings of the 52nd American Power Conference, Chicago, IL, USA, 28–29 October 1990; pp. 895–900. [Google Scholar]
- Shen, S.; Li, F. The Design of Rule-based Neural Network System for Fault Diagnosis of Nuclear Power Plant. Comput. Eng. Appl. 2003, 22, 2–5. [Google Scholar]
- Xia, H.; Zhang, N. Study on fault diagnosis technology based on support vector machine. In Proceedings of the Progress Report on Nuclear Science and Technology, Beijing, China, 18-20 November 2010; Volume 1, pp. 1068–1076. [Google Scholar]
- Mu, Y.; Xia, H. A study on fault diagnosis technology of nuclear power plant based on decision tree. In Proceedings of the International Conference on Nuclear Engineering, Xi’an, China, 17–21 May 2010; pp. 707–710. [Google Scholar]
- Baraldi, P.; Di Maio, F.; Zio, E.J. Unsupervised clustering for fault diagnosis in nuclear power plant components. Application. 2013, 6, 764–777. [Google Scholar] [CrossRef]
- Yong-Kuo, L.; Hong, X.; Chun-Li, X.J. Application of fuzzy neural network to the nuclear power plant in process fault diagnosis. Application 2005, 4, 34–38. [Google Scholar] [CrossRef]
- Shi, X.-C.; Xie, C.-L.; Wang, Y.H. Nuclear power plant fault diagnosis based on genetic-RBF neural network. Application 2006, 5, 57–62. [Google Scholar] [CrossRef]
- Ming, Y.; Jianfei, L.; Minjun, P.; Shengyuan, Y.; Zhijian, Z. A hybrid approach for fault diagnosis based on multilevel flow models and artificial neural network. In Proceedings of the 2006 International Conference on Computational Inteligence for Modelling Control and Automation and International Conference on Intelligent Agents Web Technologies and International Commerce (CIMCA’06), Sydney, Australia, 28 November 2006; p. 2. [Google Scholar]
- Liu, Y.; Xia, H.; Xie, C.; Chen, Z.; Chen, H.J. Study on intelligence fault diagnosis method for nuclear power plant equipment based on rough set and fuzzy neural network. Nucl. Power Eng. 2007, 28, 110–114. [Google Scholar]
- Peng, B.-S.; Xia, H.; Liu, Y.-K.; Yang, B.; Guo, D.; Zhu, S.-M. Research on intelligent fault diagnosis method for nuclear power plant based on correlation analysis and deep belief network. Prog. Nucl. Energy 2018, 108, 419–427. [Google Scholar] [CrossRef]
- Jamil, F.; Abid, M.; Haq, I.; Khan, A.Q.; Iqbal, M. Fault diagnosis of Pakistan Research Reactor-2 with data-driven techniques. Ann. Nucl. Energy 2016, 90, 433–440. [Google Scholar] [CrossRef]
- Saeed, H.A.; Peng, M.-J.; Wang, H.; Zhang, B.-W. Novel fault diagnosis scheme utilizing deep learning networks. Prog. Nucl. Energy 2020, 118, 103066. [Google Scholar] [CrossRef]
- Peng, M.-J.; Wang, H.; Chen, S.-S.; Xia, G.-L.; Liu, Y.-K.; Yang, X.; Ayodeji, A. Technology. An intelligent hybrid methodology of on-line system-level fault diagnosis for nuclear power plant. Nucl. Eng. Technol. 2018, 50, 396–410. [Google Scholar] [CrossRef]
- Wang, H.; Peng, M.-J.; Hines, J.W.; Zheng, G.-Y.; Liu, Y.-K.; Upadhyaya, B.R. A hybrid fault diagnosis methodology with support vector machine and improved particle swarm optimization for nuclear power plants. ISA Trans. 2019, 95, 358–371. [Google Scholar] [CrossRef]
- Bergman, S.; Åström, K.J. Fault Detection in Boiling Water Reactors by Noise Analysis; Department of Automatic Control, Lund Institute of Technology: Lund, Sweden, 1983. [Google Scholar]
- Rogulj, K.; Kilić Pamuković, J.; Jajac, N. Knowledge-Based Fuzzy Expert System to the Condition Assessment of Historic Road Bridges. Appl. Sci. 2021, 11, 1021. [Google Scholar] [CrossRef]
- Li, W.; Zhang, L.; Chen, X.; Wu, C.; Cui, Z.; Niu, C. Predicting the evolution of sheet metal surface scratching by the technique of artificial intelligence. Int. J. Adv. Manuf. Technol. 2021, 112, 853–865. [Google Scholar] [CrossRef]
- Sutton, R.; Parkins, M. Early detection of steam leaks in nuclear plant. In Proceedings of the International Conference on Control 1991. Control’91, Edinburgh, UK, 25–28 March 1991; pp. 75–80. [Google Scholar]
- Yang, J.-B.; Liu, J.; Wang, J.; Sii, H.-S.; Wang, H.W. Belief rule-base inference methodology using the evidential reasoning approach-RIMER. IEEE Trans. Syst. 2006, 36, 266–285. [Google Scholar]
- Yang, J.B.; Liu, J.; Xu, D.L.; Wang, J.; Wang, H. Optimization models for training belief-rule-based systems. IEEE Trans. Syst. Man Cybern.-Part A Syst. Hum. 2007, 37, 569–585. [Google Scholar] [CrossRef]
- Iri, M.; Aoki, K.; O’Shima, E.; Matsuyama, H. An algorithm for diagnosis of system failures in the chemical process. Comput. Chem. Eng. 1979, 3, 489–493. [Google Scholar] [CrossRef]
- VanderWeele, T.J.; Robins, J.M. Signed directed acyclic graphs for causal inference. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2010, 72, 111–127. [Google Scholar] [CrossRef] [PubMed]
- Tsuge, Y.; Shiozaki, J.; Matsuyama, H.; O’Shima, E. Fault diagnosis algorithms based on the signed directed graph and its modifications. In Proceedings of the PSE’85, Process Systems Engineering on the Use of Computers in Chemical Engineering, Cambridge, UK, 31 March–4 April 1985; pp. 133–144. [Google Scholar]
- Vedam, H.; Venkatasubramanian, V. Signed digraph based multiple fault diagnosis. Comput. Chem. Eng. 1997, 21, S655–S660. [Google Scholar] [CrossRef]
- Kramer, M.A.; Palowitch Jr, B. A rule-based approach to fault diagnosis using the signed directed graph. AIChE J. 1987, 33, 1067–1078. [Google Scholar] [CrossRef]
- Vedam, H.; Venkatasubramanian, V. PCA-SDG based process monitoring and fault diagnosis. Control Eng. Pract. 1999, 7, 903–917. [Google Scholar] [CrossRef]
- Dong, G.; Chongguang, W.; Zhang, B.; Xin, M. Signed directed graph and qualitative trend analysis based fault diagnosis in chemical industry. Chin. J. Chem. Eng. 2010, 18, 265–276. [Google Scholar]
- Wang, H.; Chen, B.; He, X.; Tong, Q.; Zhao, J. SDG-based HAZOP analysis of operating mistakes for PVC process. Process Saf. Environ. Prot. 2009, 87, 40–46. [Google Scholar] [CrossRef]
- Tarifa, E.E.; Scenna, N.J. Fault diagnosis for a MSF using a SDG and fuzzy logic. Desalination 2003, 152, 207–214. [Google Scholar] [CrossRef]
- He, B.; Chen, T.; Yang, X. Root cause analysis in multivariate statistical process monitoring: Integrating reconstruction-based multivariate contribution analysis with fuzzy-signed directed graphs. Comput. Chem. Eng. 2014, 64, 167–177. [Google Scholar] [CrossRef]
- Peng, D.; Geng, Z.; Zhu, Q. A multilogic probabilistic signed directed graph fault diagnosis approach based on Bayesian inference. Ind. Eng. Chem. Res. 2014, 53, 9792–9804. [Google Scholar] [CrossRef]
- Guohua, W.; Diping, Y.; Jiyao, Y.; Yiqing, X.; Dongxu, J. A Framework for Monitoring and Fault Diagnosis in Nuclear Power Plants Based on Signed Directed Graph Methods. Front. Energy Res. 2021, 9, 59. [Google Scholar] [CrossRef]
- Wu, G.; Zhang, L.; Tong, J. Online fault diagnosis of nuclear power plants using signed directed graph and fuzzy theory. In Proceedings of the International Conference on Nuclear Engineering, Shanghai, China, 2–6 July 2017; p. V004T006A011. [Google Scholar]
- Wu, G.; Wang, J.; Yuan, D.; Xiao, Y. Research on Fault Diagnosis Based on Hierarchical Signed Directed Graph for Nuclear Power Plants. In Proceedings of the International Conference on Nuclear Engineering, Virtual, 4–5 August 2020; p. V002T008A024. [Google Scholar]
- Cruz-Ramirez, N.; Acosta-Mesa, H.G.; Carrillo-Calvet, H.; Nava-Fernández, L.A.; Barrientos-Martínez, R.E. Diagnosis of breast cancer using Bayesian networks: A case study. Comput. Biol. Med. 2007, 37, 1553–1564. [Google Scholar] [CrossRef]
- Pearl, J. Fusion, propagation, and structuring in belief networks. Artif. Intell. 1986, 29, 241–288. [Google Scholar] [CrossRef]
- Murphy, K.P. Dynamic Bayesian Networks: Representation, Inference and Learning; University of California: Berkeley, CA, USA, 2002. [Google Scholar]
- Lerner, U.; Parr, R.; Koller, D.; Biswas, G. Bayesian fault detection and diagnosis in dynamic systems. In Proceedings of the AAAI/IAAI, Austin, TX, USA, 2000, July 30–August 3; pp. 531–537.
- Przytula, K.W.; Thompson, D. Construction of Bayesian networks for diagnostics. In Proceedings of the 2000 IEEE Aerospace Conference, Big Sky, MT, USA, 25–25 March 2000; pp. 193–200. [Google Scholar]
- Mahadevan, S.; Zhang, R.; Smith, N. Bayesian networks for system reliability reassessment. Struct. Saf. 2001, 23, 231–251. [Google Scholar] [CrossRef]
- Wu, G.; Tong, J.; Zhang, L.; Zhao, Y.; Duan, Z. Framework for fault diagnosis with multi-source sensor nodes in nuclear power plants based on a Bayesian network. Ann. Nucl. Energy. 2018, 122, 297–308. [Google Scholar] [CrossRef]
- Jones, T.B.; Darling, M.C.; Groth, K.M.; Denman, M.R.; Luger, G.F. A dynamic bayesian network for diagnosing nuclear power plant accidents. In Proceedings of the The Twenty-Ninth International Flairs Conference, Key Largo, FL, USA, 16–18 May 2016. [Google Scholar]
- Oh, C.; Lee, J.I. Real time nuclear power plant operating state cognitive algorithm development using dynamic Bayesian network. Reliab. Eng. Syst. Saf. 2020, 198, 106879. [Google Scholar] [CrossRef]
- Ren, Y.; Fan, D.; Ma, X.; Wang, Z.; Feng, Q.; Yang, D. A GO-FLOW and dynamic Bayesian network combination approach for reliability evaluation with uncertainty: A case study on a nuclear power plant. IEEE Access 2017, 6, 7177–7189. [Google Scholar] [CrossRef]
- Zhao, Y.; Tong, J.; Zhang, L. Rapid source term prediction in nuclear power plant accidents based on dynamic Bayesian networks and probabilistic risk assessment. Ann. Nucl. Energy 2021, 158, 108217. [Google Scholar] [CrossRef]
- Zhao, Y.; Di, F.; Zio, E.; Zhang, Q.; Dong, C.L.; Zhang, J. Techniques. Optimization of a dynamic uncertain causality graph for fault diagnosis in nuclear power plant. Nucl. Sci. Tech. 2017, 28, 34. [Google Scholar]
- Zhao, Y.; Tong, J.; Zhang, L.; Wu, G. Diagnosis of operational failures and on-demand failures in nuclear power plants: An approach based on dynamic Bayesian networks. Ann. Nucl. Energy 2020, 138, 107181. [Google Scholar] [CrossRef]
- Zhang, Q. Probabilistic reasoning based on dynamic causality trees/diagrams. Reliab. Eng. Syst. Saf. 1994, 46, 209–220. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhang, Q. Model event/fault trees with dynamic uncertain causality graph for better probabilistic safety assessment. IEEE Trans. Reliab. 2017, 66, 178–188. [Google Scholar] [CrossRef]
- Zhang, Q. Dynamic uncertain causality graph for knowledge representation and reasoning: Discrete DAG cases. J. Comput. Sci. Technol. 2012, 27, 1–23. [Google Scholar] [CrossRef]
- Zhang, Q. Dynamic uncertain causality graph for knowledge representation and probabilistic reasoning: Directed cyclic graph and joint probability distribution. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 1503–1517. [Google Scholar] [CrossRef]
- Zhang, Q.; Geng, S. Dynamic uncertain causality graph applied to dynamic fault diagnoses of large and complex systems. IEEE Trans. Reliab. 2015, 64, 910–927. [Google Scholar] [CrossRef]
- Zhang, Q. Dynamic uncertain causality graph for knowledge representation and reasoning: Continuous variable, uncertain evidence, and failure forecast. IEEE Trans. Syst. Man Cybern. Syst. 2015, 45, 990–1003. [Google Scholar] [CrossRef]
- Hong-chen, D.; Qin, Z.; Yue, Z.; Chun-ling, D. DUCG reasoning machine design and implementation in nuclear power plant fault diagnosis. At. Energy Sci. Technol. 2014, 48, 491. [Google Scholar]
- Zhang, Q.; Zhang, Z. Dynamic uncertain causality graph applied to dynamic fault diagnoses and predictions with negative feedbacks. IEEE Trans. Reliab. 2015, 65, 1030–1044. [Google Scholar] [CrossRef]
- Zhao, Y.; Dong, C.; Zhang, Q. Pilot Study of Diagnosis on CPR1000 With Dynamic Uncertain Causality Graph. In Proceedings of the International Conference on Nuclear Engineering, Charlotte Convention Center, Charlotte, NC, USA, 26–30 June 2016; p. V004T014A009. [Google Scholar]
- Zhao, Y.; Di Maio, F.; Zio, E.; Zhang, Q.; Dong, C. Genetic Algorithm Optimization of a Dynamic Uncertain Causality Graph (DUCG) for Fault Diagnosis in Nuclear Power Plants. In Proceedings of the International Conference on Nuclear Engineering, Charlotte Convention Center, Charlotte, NC, USA, 26–30 June 2016; p. V004T014A010. [Google Scholar]
- Zhao, Y.; Zhang, Q.; Deng, H.; Dong, C. Application of DUCG in fault diagnosis of nuclear power plant secondary loop. At. Energy Sci. Technol. 2014, 48, 496–501. [Google Scholar]
- Zhao, Y.; Zhang, Q.; Dong, C. Design and implementation of nuclear power plant fault diagnosis expert system based on DUCG. At. Energy Sci. Technol. 2016, 50, 1474–1479. [Google Scholar]
- Dong, C.; Zhou, J. A New Algorithm of Cubic Dynamic Uncertain Causality Graph for Speeding Up Temporal Causality Inference in Fault Diagnosis. IEEE Trans. Reliab. 2022, 1, 1–16. [Google Scholar] [CrossRef]
- Bu, X.; Nie, H.; Zhang, Z.; Zhang, Q. An Industrial Fault Diagnostic System Based on a Cubic Dynamic Uncertain Causality Graph. Sensors 2022, 22, 4118. [Google Scholar] [CrossRef]
- Bu, X.; Lu, L.; Zhang, Z.; Zhang, Q.; Zhu, Y. A general outpatient triage system based on dynamic uncertain causality graph. IEEE Access 2020, 8, 93249–93263. [Google Scholar] [CrossRef]
- Deng, N.; Zhang, Q. Towards Dynamic Uncertain Causality Graphs for the Intelligent Diagnosis and Treatment of Hepatitis B. Symmetry 2020, 12, 1690. [Google Scholar] [CrossRef]
- Geng, S.; Zhang, Q. Clinical diagnosis expert system based on dynamic uncertain causality graph. In Proceedings of the 2014 IEEE 7th Joint International Information Technology and Artificial Intelligence Conference, Chongqing, China, 20–21 December 2014; pp. 233–237. [Google Scholar]
- Hao, S.-R.; Geng, S.-C.; Fan, L.-X.; Chen, J.-J.; Zhang, Q.; Li, L.-J. Intelligent diagnosis of jaundice with dynamic uncertain causality graph model. J. Zhejiang Univ.-Sci. B 2017, 18, 393–401. [Google Scholar] [CrossRef]
- Bu, X.; Zhang, Z.; Zhang, Q. Clinical Assistant Diagnosis System Based on Dynamic Uncertain Causality Graph. In Proceedings of the International Conference on Mechatronics and Intelligent Robotics, Kunming, China, 19–20 May 2018; pp. 1030–1038. [Google Scholar]
- Dong, C.; Wang, Y.; Zhang, Q.; Wang, N. The methodology of dynamic uncertain causality graph for intelligent diagnosis of vertigo. Comput. Methods Programs Biomed. 2014, 113, 162–174. [Google Scholar] [CrossRef]
- Wang, S.-C. Artificial neural network. In Interdisciplinary Computing in Java Programming; Springer: Berlin/Heidelberg, Germany, 2003; pp. 81–100. [Google Scholar]
- Basheer, I.A.; Hajmeer, M. Artificial neural networks: Fundamentals, computing, design, and application. J. Microbiol. Methods 2000, 43, 3–31. [Google Scholar] [CrossRef] [PubMed]
- Gardner, M.W.; Dorling, S. Artificial neural networks (the multilayer perceptron)—A review of applications in the atmospheric sciences. Atmos. Environ. 1998, 32, 2627–2636. [Google Scholar] [CrossRef]
- Schalkoff, R.J. Artificial Neural Networks; McGraw-Hill Higher Education: New York, NY, USA, 1997. [Google Scholar]
- Fine, T.L. Feedforward Neural Network Methodology; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Medsker, L.; Jain, L.C. Recurrent Neural Networks: Design and Applications; CRC Press: Boca Raton, FL, USA, 1999. [Google Scholar]
- Baker, B.; Gupta, O.; Naik, N.; Raskar, R. Designing neural network architectures using reinforcement learning. arXiv 2016, arXiv:1611.02167. [Google Scholar]
- Kim, K.; Aljundi, T.; Bartlett, E. Nuclear Power Plant Fault-Diagnosis Using Artificial Neural Networks; Iowa State University of Science and Technology: Ames, IA, USA, 1992. [Google Scholar]
- Kim, K.; Bartlett, E.B. Error prediction for a nuclear power plant fault-diagnostic advisor using neural networks. Nucl. Technol. 1994, 108, 283–297. [Google Scholar] [CrossRef]
- Şeker, S.; Ayaz, E.; Türkcan, E. Elman’s recurrent neural network applications to condition monitoring in nuclear power plant and rotating machinery. Eng. Appl. Artif. Intell. 2003, 16, 647–656. [Google Scholar] [CrossRef]
- Li, J.Y.; Xia, H.; Cheng, S.Y. Study on Sensor with Mechanical Properties in Nuclear Power Plant with Application of BP Neural Network to Fault Tolerant Control. Adv. Mater. Res. 2013, 644, 56–59. [Google Scholar] [CrossRef]
- Qi, Z.; Li, W.; Zhang, Y.; Hong, J.; Yuan, Y.; Ma, W. Sensor fault detection in nuclear power plant using Auto-Associative Neural Network. In Proceedings of the International Conference on Nuclear Engineering (ICONE), Tsukuba, Japan, 19–24 May 2019; p. 2134. [Google Scholar]
- Messai, A.; Mellit, A.; Abdellani, I.; Pavan, A.M. On-line fault detection of a fuel rod temperature measurement sensor in a nuclear reactor core using ANNs. Prog. Nucl. Energy 2015, 79, 8–21. [Google Scholar] [CrossRef]
- Safavian, S.R.; Landgrebe, D. A survey of decision tree classifier methodology. IEEE Trans. Syst. Man Cybern. 1991, 21, 660–674. [Google Scholar] [CrossRef]
- Myles, A.J.; Feudale, R.N.; Liu, Y.; Woody, N.A.; Brown, S.D. An introduction to decision tree modeling. J. Chemom. A J. Chemom. Soc. 2004, 18, 275–285. [Google Scholar] [CrossRef]
- Freund, Y.; Mason, L. The alternating decision tree learning algorithm. In Proceedings of the ICML, Bled, Slovenia, 27–30 July 1999; pp. 124–133. [Google Scholar]
- Song, Y.-Y.; Ying, L. Decision tree methods: Applications for classification and prediction. Shanghai Arch. Psychiatry 2015, 27, 130. [Google Scholar]
- Mu, Y.; Sheng, G.M.; Xia, H.; Sun, P.N.; Qian, Y. Study on Fault Diagnosis Method for Nuclear Power Plant Based on Fuzzy Rough Sets and Decision Tree. Adv. Mater. Res. 2014, 981, 701–705. [Google Scholar] [CrossRef]
- Mu, Y.; Xia, H.; Liu, Y.-K. Fault diagnosis method for nuclear power plant based on decision tree and neighborhood rough sets. At. Energy Sci. Technol. 2011, 45, 44. [Google Scholar]
- Sharanya, S.; Venkataraman, R. Empirical Analysis of Machine Learning Algorithms in Fault Diagnosis of Coolant Tower in Nuclear Power Plants. In Proceedings of the International Conference on Computational Vision and Bio Inspired Computing, Coimbatore, India, 21–22 September 2018; pp. 1325–1332. [Google Scholar]
- Hadad, K.; Mortazavi, M.; Mastali, M.; Safavi, A.A. Enhanced neural network based fault detection of a VVER nuclear power plant with the aid of principal component analysis. IEEE Trans. Nucl. Sci. 2008, 55, 3611–3619. [Google Scholar] [CrossRef]
- Kaistha, N.; Upadhyaya], B.R. Incipient fault detection and isolation of field devices in nuclear power systems using principal component analysis. Nucl. Technol. 2001, 136, 221–230. [Google Scholar] [CrossRef]
- Zhao, K.; Upadhyaya, B.R. Model based approach for fault detection and isolation of helical coil steam generator systems using principal component analysis. IEEE Trans. Nucl. Sci. 2006, 53, 2343–2352. [Google Scholar] [CrossRef]
- Ma, J.; Jiang, J. Detection and identification of faults in npp instruments using kernel principal component analysis. J. Eng. Gas Turbines Power 2012, 134, 032901. [Google Scholar] [CrossRef]
- Li, W.; Peng, M.; Wang, Q. Fault detectability analysis in PCA method during condition monitoring of sensors in a nuclear power plant. Ann. Nucl. Energy 2018, 119, 342–351. [Google Scholar] [CrossRef]
- Li, W.; Peng, M.; Liu, Y.; Jiang, N.; Wang, H.; Duan, Z. Fault detection, identification and reconstruction of sensors in nuclear power plant with optimized PCA method. Ann. Nucl. Energy 2018, 113, 105–117. [Google Scholar] [CrossRef]
- Li, W.; Peng, M.; Wang, Q.J. Improved PCA method for sensor fault detection and isolation in a nuclear power plant. Technology. 2019, 51, 146–154. [Google Scholar] [CrossRef]
- Qi, S.M.C. Sensor Fault Detection for Nuclear Power Plant Based on Dynamic Principal Component Analysis. J. Wuhan Univ. Technol. (Transp. Sci. Eng.) 2012, 6, 1–6. [Google Scholar]
- Yu, Y.; Peng, M.-j.; Wang, H.; Ma, Z.-g.; Li, W. Improved PCA model for multiple fault detection, isolation and reconstruction of sensors in nuclear power plant. Ann. Nucl. Energy 2020, 148, 107662. [Google Scholar] [CrossRef]
- Li, W.; Peng, M.; Liu, Y.; Cheng, S.; Jiang, N.; Wang, H. Condition Monitoring of Sensors in a NPP Using Optimized PCA. Sci. Technol. Nucl. Install. 2018, 2018, 1–16. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, X.; Lou, C.; Jiang, J. Principal Component Analysis Methods for Fault Detection Evaluated on a Nuclear Power Plant Simulation Platform. In Proceedings of the 2019 5th International Conference on Control Science and Systems Engineering (ICCSSE), Shanghai, China, 14–16 August 2019; pp. 45–48. [Google Scholar]
- Yu, R.; Liu, F. An online fault diagnosis method for nuclear power plant based on combined artificial neural network. In Proceedings of the 2010 Asia-Pacific Power and Energy Engineering Conference, Chengdu, China, 28–31 March 2010; pp. 1–4. [Google Scholar]
- Sun, P.; Liu, Y.; Wu, G.; Duan, Z. Research on Fault Diagnosis of Reactor Coolant Accident in Nuclear Power Plant Based on Radial Basis Function and Fuzzy Neural Network. In Proceedings of the International Conference on Nuclear Engineering, Online, 4-5 August 2020; p. V001T006A005. [Google Scholar]
- Zhou, G.; Ge, S.; Yang, L. Fault diagnosis method for nuclear power plants based on neural networks and voting fusion. At. Energy Sci. Technol. 2010, 44, 367–372. [Google Scholar]
- Gang, Z.; Long, H.; Li, Y. Fault diagnosis method for nuclear power plants based on integrated neural networks and logical fusion. In Proceedings of the 2013 IEEE 11th International Conference on Electronic Measurement & Instruments, Harbin, China, 16–19 August 2013; pp. 839–843. [Google Scholar]
- Li, C.; Yu, R.; Wang, T. The Research of Fault Diagnosis of Nuclear Power Plant Based on ELM-AdaBoost. SAMME. Sci. Technol. Nucl. Install. 2020, 2020, 1–9. [Google Scholar]
- Qian, G.; Liu, J. Fault diagnosis based on conditional generative adversarial networks in nuclear power plants. Ann. Nucl. Energy 2022, 176, 109267. [Google Scholar] [CrossRef]
- Yao, Y.; Wang, J.; Xie, M.; Hu, L.; Wang, J. A new approach for fault diagnosis with full-scope simulator based on state information imaging in nuclear power plant. Ann. Nucl. Energy 2020, 141, 107274. [Google Scholar] [CrossRef]
- Liu, Y.-k.; Xie, C.-l.; Peng, M.-j.; Ling, S.-h. Improvement of fault diagnosis efficiency in nuclear power plants using hybrid intelligence approach. Prog. Nucl. Energy 2014, 76, 122–136. [Google Scholar] [CrossRef]
- Wang, Z.; Xia, H.; Peng, B.; Yang, B.; Zhu, S.; Zhang, J.; Annor-Nyarko, M. A multi-stage hybrid fault diagnosis approach for operating conditions of nuclear power plant. Ann. Nucl. Energy 2021, 153, 108015. [Google Scholar] [CrossRef]
- Amer, F.Z.; El-Garhy, A.M.; Awadalla, M.H.; Rashad, S.M.; Abdien, A.K. A real-valued genetic algorithm to optimize the parameters of support vector machine for classification of multiple faults in NPP. Nukleonika 2011, 56, 323–332. [Google Scholar]
- Saeed, H.A.; Wang, H.; Peng, M.; Hussain, A.; Nawaz, A. Online fault monitoring based on deep neural network & sliding window technique. Prog. Nucl. Energy 2020, 121, 103236. [Google Scholar] [CrossRef]
- Mwangi, M.A.; Yong-Kuo, L.; Ochieng, A.S. Small Break Loss of Coolant Accident (SB-LOCA) fault diagnosis using Adaptive Neuro-Fuzzy Inference System (ANFIS). IOP Conf. Ser. Earth Environ. Sci. 2021, 675, 012034. [Google Scholar] [CrossRef]
- Xu, J.; Chen, W.; Tang, Y. Study on fault diagnosis in nuclear power plant based on Rough Sets and Support Vector Machine. Nucl. Power Eng. 2009, 30, 51–54. [Google Scholar]
- Ye, S.; Jiang, J.; Li, J.; Liu, Y.; Zhou, Z.; Liu, C. Fault diagnosis and tolerance control of five-level nested NPP converter using wavelet packet and LSTM. IEEE Trans. Power Electron. 2019, 35, 1907–1921. [Google Scholar] [CrossRef]
- Wang, H.; Peng, M.-j.; Ayodeji, A.; Xia, H.; Wang, X.-k.; Li, Z.-k. Advanced fault diagnosis method for nuclear power plant based on convolutional gated recurrent network and enhanced particle swarm optimization. Ann. Nucl. Energy 2021, 151, 107934. [Google Scholar] [CrossRef]
- Roverso, D. Fault diagnosis with the aladdin transient classifier. In Proceedings of the System Diagnosis and Prognosis: Security and Condition Monitoring Issues III, Orlando, FL, USA, 21 April 2003; pp. 162–172. [Google Scholar]
- Hadad, K.; Pourahmadi, M.; Majidi-Maraghi, H. Fault diagnosis and classification based on wavelet transform and neural network. Prog. Nucl. Energy 2011, 53, 41–47. [Google Scholar] [CrossRef]
- Liu, Y.-K.; Peng, M.-J.; Xie, C.-L.; Dong, Y.-X. Research and design of distributed fault diagnosis system in nuclear power plant. Prog. Nucl. Energy 2013, 68, 97–110. [Google Scholar]
- Baraldi, P.; Di Maio, F.; Rigamonti, M.; Zio, E.; Seraoui, R. Transients analysis of a nuclear power plant component for fault diagnosis. Chem. Eng. Trans. 2013, 33, 895–900. [Google Scholar]
- Cao, H.; Sun, P.; Zhao, L. PCA-SVM method with sliding window for online fault diagnosis of a small pressurized water reactor. Ann. Nucl. Energy 2022, 171, 109036. [Google Scholar] [CrossRef]
- Ayodeji, A.; Liu, Y.-k.; Xia, H. Knowledge base operator support system for nuclear power plant fault diagnosis. Prog. Nucl. Energy 2018, 105, 42–50. [Google Scholar] [CrossRef]
- Ke, Z.; Hu, X.; Teng, D.; Tao, M. Intelligent Fault Diagnosis Method Based on Operating Parameters in Nuclear Power Plant. In Proceedings of the International Conference on Nuclear Engineering, Shanghai, China, 2–6 July 2017; p. V001T004A015. [Google Scholar]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Qi, B.; Zhang, L.; Liang, J.; Tong, J. Combinatorial Techniques for Fault Diagnosis in Nuclear Power Plants Based on Bayesian Neural Network and Simplified Bayesian Network-Artificial Neural Network. Front. Energy Res. 2022, 10, 920194. [Google Scholar] [CrossRef]
- El Saddik, A. Digital twins: The convergence of multimedia technologies. IEEE Multimed. 2018, 25, 87–92. [Google Scholar] [CrossRef]
- Nguyen, T.N.; Ponciroli, R.; Bruck, P.; Esselman, T.C.; Rigatti, J.A.; Vilim, R.B. A digital twin approach to system-level fault detection and diagnosis for improved equipment health monitoring. Ann. Nucl. Energy 2022, 170, 109002. [Google Scholar] [CrossRef]
- Pan, S.J.; Yang, Q. A Survey on Transfer Learning. IEEE Trans. Knowl. Data Eng. 2010, 22, 1345–1359. [Google Scholar] [CrossRef]
- Zhong, X.; Ban, H. Pre-trained network-based transfer learning: A small-sample machine learning approach to nuclear power plant classification problem. Ann. Nucl. Energy 2022, 175, 109201. [Google Scholar] [CrossRef]
- Yao, Y.; Ge, D.; Yu, J.; Xie, M. Model-Based Deep Transfer Learning Method to Fault Detection and Diagnosis in Nuclear Power Plants. Front. Energy Res. 2022, 10, 823395. [Google Scholar] [CrossRef]
- Li, J.; Lin, M.; Li, Y.; Wang, X. Transfer learning with limited labeled data for fault diagnosis in nuclear power plants. Nucl. Eng. Des. 2022, 390, 111690. [Google Scholar] [CrossRef]
- Li, J.; Lin, M.; Li, Y.; Wang, X. Transfer learning network for nuclear power plant fault diagnosis with unlabeled data under varying operating conditions. Energy 2022, 254, 124358. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).