1. Introduction
Wind energy is becoming an essential pillar of the energy mix, helping to decarbonize the energy system and to improve energy independence and security of supply in many countries [
1,
2]. Most commercial wind farms today are remotely monitored around the clock to keep the operation and maintenance costs low. The continuous monitoring allows for early detection of potential operation problems and facilitates proactive condition-based maintenance. Gearboxes and generators are of particular interest in the monitoring of wind turbines (WT), because they are especially costly to replace, and associated replacement work tends to entail long downtimes [
3,
4,
5,
6]. Thus, more and more wind turbine drivetrains are monitored with accelerometers. This makes it possible to derive and track the vibration spectra of critical components such as gearbox parts and generator bearings.
Previous studies have proposed various methods and features for vibration-based fault detection in the drivetrains of wind turbines. The proposed frequency-domain methods include the monitoring and analysis of particular frequencies, their harmonics, sidebands and the signal envelope. Recent studies in this area applied to wind turbine gearboxes include [
7], in which conventional filtering, Hilbert transform and cepstrum methods are applied for detecting broken teeth faults of gears. To extract features for weak faults however, complex wavelet transform providing multi-scale enveloping spectrograms from which bearing failure can be detected is introduced. The work in [
8] proposed a method based on the Vold–Kalman filter and higher order energy separation. In [
9], a method based on sparse representation theory is outlined, with the stated advantages over conventional methods being in alleviating background noise, handling the coupling effect and a more intuitive fault diagnosis process. Similarly, Ref. [
10] introduced a structured sparsity method, highlighting and demonstrating the same advantages. A novel modulation model for the diagnosis of compound faults is shown in [
11]. The presented approach enables adaptive decomposition of the signal, with the authors presenting superior performance compared to classic empirical mode decomposition methods. In the time domain, the existing methods focus on analysing the amplitudes of the vibration time series and tracking statistical properties of the vibration response distribution. Recent contributions include [
12], presenting a fault diagnostic method based on measurement indicators such as root mean square analysis (RMS), skewness, kurtosis or the crest factor. Experimental results on a fixed-speed planetary gearbox test rig indicated that promising results in discriminating fault conditions could be obtained using RMS analysis when compared with other indicators. However, the author notes the indicator’s sensitivity to variable operational conditions. In [
13], mean vibration signatures were extracted from recordings of a group of healthy identical WTs. The resulting measurements were used as reference, and by detecting deviations, faults can be identified, as presented in their case study. A different approach is outlined in [
14], where these traditional vibration-based features such as RMS or peak-to-peak were replaced with linear regression parameters of the feature-generator power relationship, allowing for load-independent evaluations and higher interpretability. Methods based on extracting features from multiple domains have also been proposed: Most recently, in [
15], a fault diagnosis method based on fused features is presented, of which an optimal subset is chosen by a statistical feature selection. In [
16], features from the time, frequency, and time–frequency domains are extracted and combined as well. A random forest is used to reduce the dimensionality of the feature set and to select an optimal subset for the fault diagnosis model. We refer to [
17,
18] for comprehensive reviews of the state-of-the-art methods of vibration-based fault detection in wind turbine drivetrains.
The existing methods require the upfront development and extraction of component-specific features from the accelerometer measurements by condition-monitoring engineers. The upfront definition of spectral features for the monitoring constitutes a major time investment before commissioning and operating the turbine. For instance, in-depth information about the respective gearbox design and composition are needed to this end. The characteristic frequencies of the monitored components need to be determined if the corresponding spectral lines are supposed to be tracked. Collecting this spectral information for every monitored component in every monitored wind turbine and model constitutes a major effort. The extracted spectral features tend to be turbine- and component-specific. Therefore, they can generally not be reused for new wind turbine types or when components have been updated. Moreover, feature engineering can result in more and in less effective features for fault detection. For example, in a case study by [
19], spectral line and cepstrum analyses resulted in higher fault detection accuracies than time synchronous averaging and spectral kurtosis methods. Thus, depending on the chosen feature engineering approach, one may end up with more or less satisfactory fault detection accuracies.
Recently, first studies have proposed the application of fault detection methods that do not require any feature engineering. The work in [
20] demonstrated the application of autoencoders for detecting blade damage in wind turbines based on the blade stress and strain signals obtained from strain gauge sensors. In a similar application, Ref. [
21] made use of a convolutional autoencoder for detecting blade damages. To this end, they employed data from the wind turbine’s supervisory control and data acquisition (SCADA) system to identify changes in the dynamics of the blade system. In [
22], an autoencoder is applied for the transfer learning of fault diagnosis tasks on SCADA and failure status datasets. They investigated different fault types and focused on the transfer of fault diagnostics models to target turbines with few available SCADA data. When vibration sensors are unavailable, SCADA-based modelling of the turbine’s normal behaviour can enable the detection of operation faults in drivetrain components (e.g., [
23,
24,
25,
26,
27,
28]).
The goal of our study is to develop and demonstrate a fault detection method for vibration-monitored drivetrain components in wind turbines that does not require any feature engineering but is able to learn the characteristic spectral features of the monitored components without any human assistance from a continuous range of the spectrum, such as the full half spectrum. The method should enable simple model architectures to facilitate its adoption by practitioners. At the same time, it should neither be restricted to monitoring specific frequencies, nor should it require a comprehensive set of gearbox- and fault-type-specific observations. The latter would be needed for fault detection methods based on supervised machine learning, but in practice, such datasets are usually not available or not accessible to wind turbine operators.
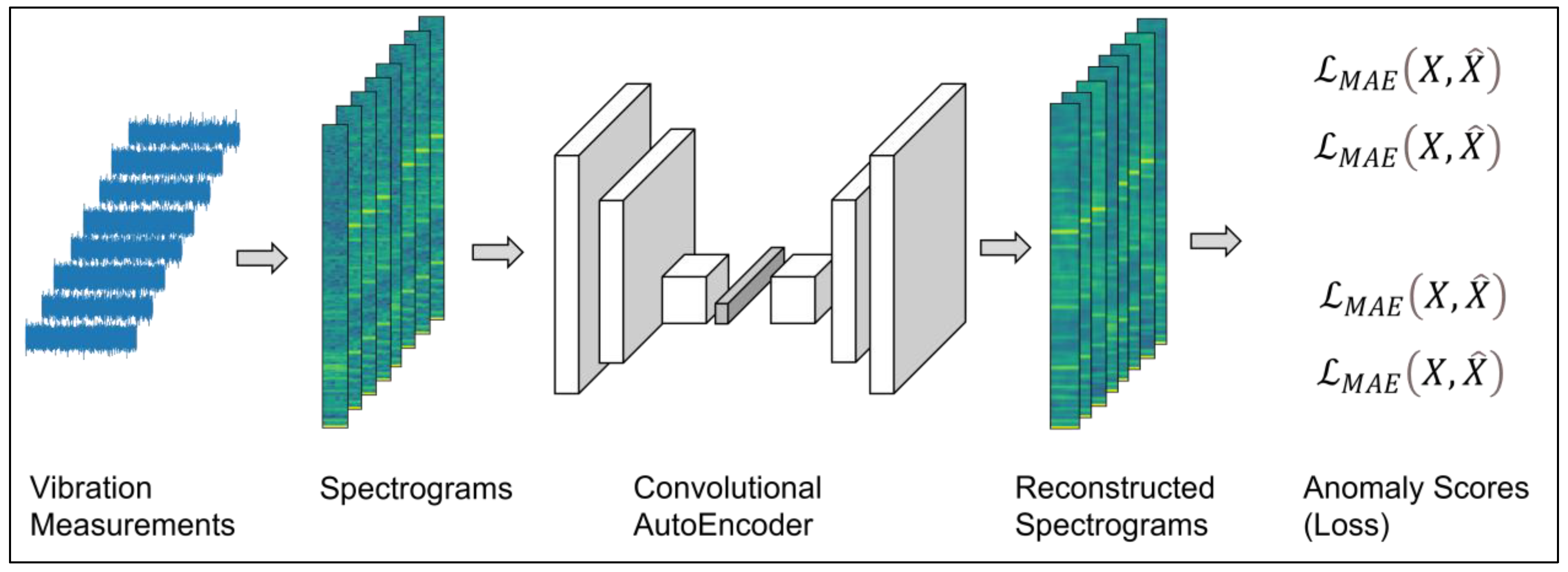
To achieve this goal, the present study proposes and demonstrates the application of convolutional autoencoders for the feature learning, extraction and early detection of faults in vibration-monitored wind turbine gearboxes and generators. This study is the first to propose spectral normal-behaviour models constructed without feature engineering for the purpose of vibration-based fault detection in wind turbine drivetrains, to the best of our knowledge.
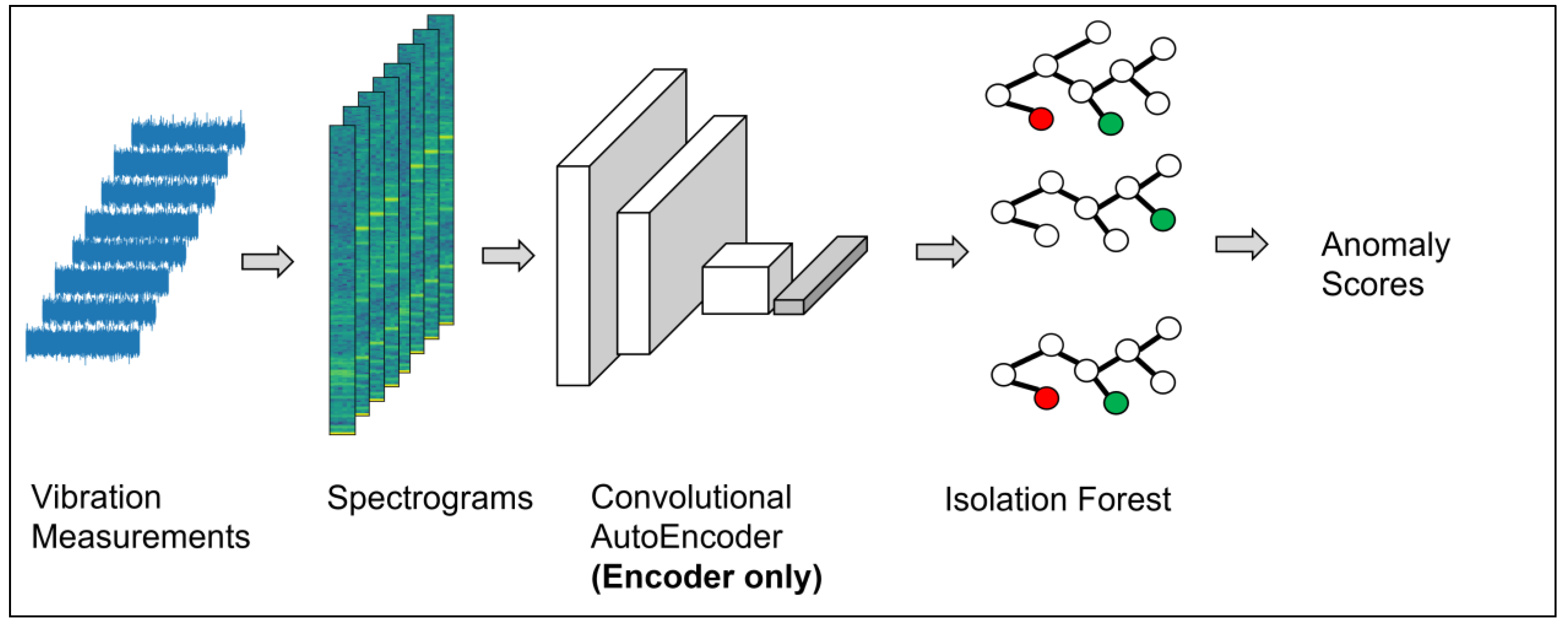
In this study, we also propose and investigate fault detection based on non-convolutional autoencoders. Moreover, we compare the performance of reconstruction-error-based gearbox and generator health indices to health indices derived by one-class classification with an isolation forest model.
This paper is organized as follows.
Section 2 describes our new fault detection methods.
Section 3 introduces the gearbox and generator datasets and models used for demonstrating the methods. The results of our study are discussed in
Section 4, and our conclusions follow in
Section 5.
4. Results and Discussion
In the following sections, we will first present and discuss the results of our proposed methods for our case study with two commercially operated wind turbines (
Section 3.1). To convert the accelerometer measurements into spectrograms, we applied a short-time Fourier transform (STFT; [
38]) with window sizes of 250 ms and an overlap of 100 ms. Fault detection was performed based on spectrogram segments of 1 s duration and considering frequencies up to 1000 Hz. These parameters were chosen so as to enable sufficient temporal evolution and frequency resolution of the signal and at the same time allow for large enough training, validation and test sets. Our results are robust against modifications of these parameters. Prior to the model training, we applied a log-transformation to each spectrogram and a min–max normalization, such that all data points fall in the range of [0, 1].
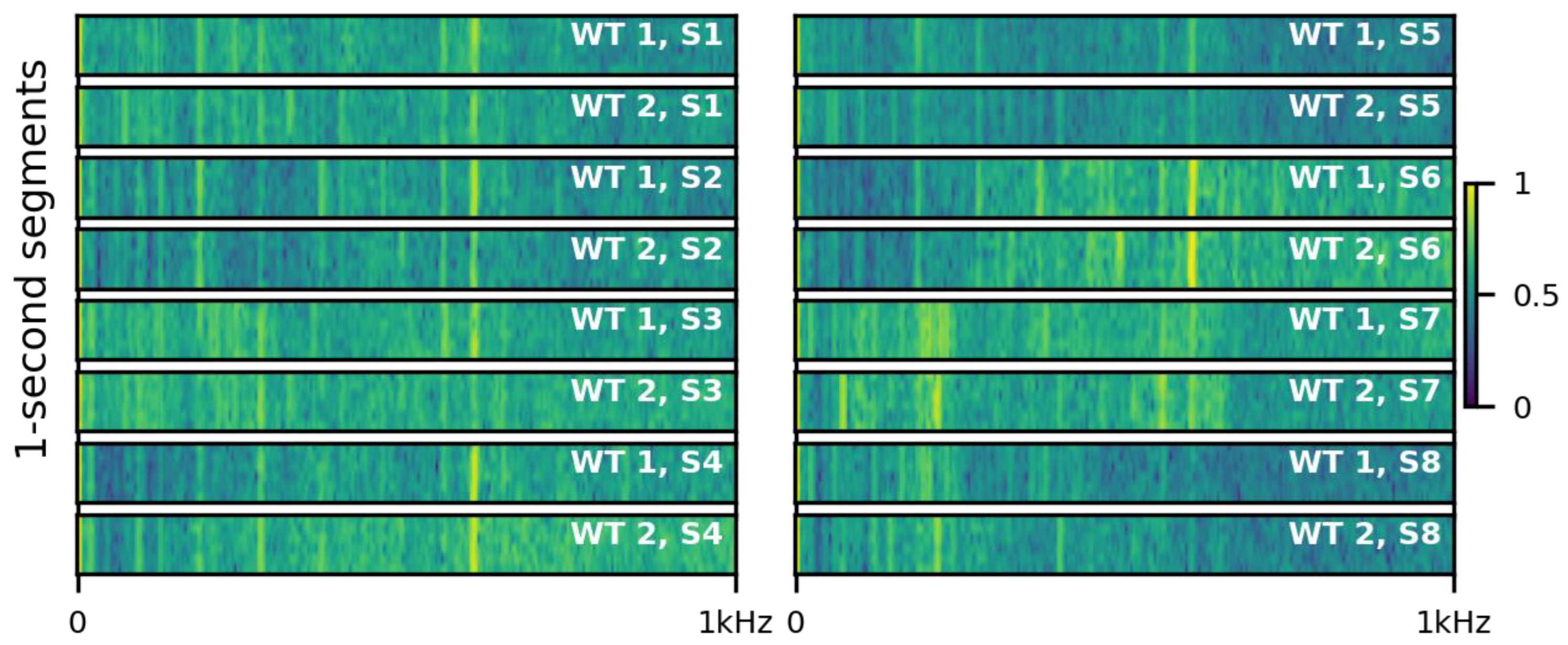
Figure 4 shows examples of the resulting spectrograms for the components monitored with the accelerometers S1–S8 in both wind turbines.
Dataset splits. For our case study, we created a separate model for each accelerometer. We split the recordings of WT1 into a 70% training set, a 15% validation set and a 15% test set for each accelerometer. A sliding window was applied to extract multiple 1 s segments from each 2 s recording. The resulting segments of the training set were used to train the autoencoders and the isolation forests, while the validation set was used for the model selection and early stopping. All data from WT2 served as an additional separate test set, so we could obtain fault notifications for each component.
Model selection. We performed a preliminary model search using the Hyperband hyperparameter optimization algorithm [
39] in order to find an optimal convolutional autoencoder architecture. We evaluated architectures consisting of only convolutional and pooling layers which resulted in a bottleneck size of 128 units (the flattened size of the last encoder layer). This dimension requirement was set beforehand by us. Choosing a bottleneck size significantly smaller than the input size forces the network to learn a compressed representation of the inputs. This compressed representation serves as input to the isolation forest. In terms of configurations, we evaluated models with up to five encoding layers with either four, eight, or sixteen feature maps, with kernel sizes (height, width) of either (1, 3), (1, 5), (3, 3), (3, 5), or (5, 5) and with varying learning rates between 3 × 10
−2 and 1 × 10
−4. The decoder architecture was always symmetrical to the encoder. The network weights were optimized using the adaptive moment estimation (Adam) optimization algorithm [
40], minimizing the mean absolute error (MAE) between the reconstruction output and the original input. Further, we applied an early stopping mechanism to stop training when the validation loss had not improved within 15 epochs.
This hyperparameter optimization was performed only on the training and validation set of accelerometer S1. The Hyperband search algorithm resulted in the best-performing convolutional architecture (“conv-AE”) outlined in
Table 3. Additionally, we compared the reconstruction performance to a minimal dense architecture (“dense-AE”) described in
Table 3, i.e., to the smallest possible model configuration in terms of parameters with at least one hidden fully connected layer and the same bottleneck size.
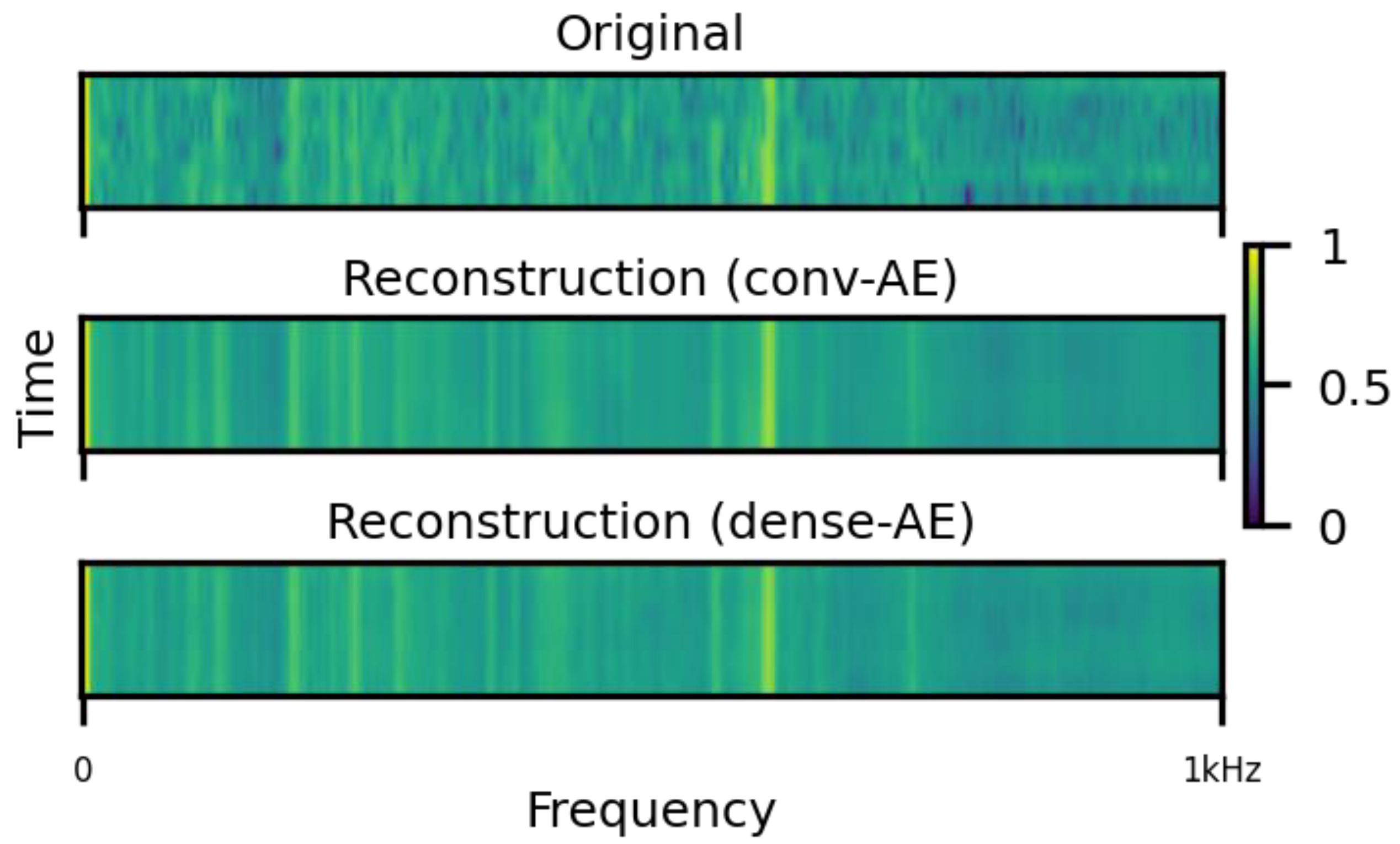
Both the convolutional and the dense model architectures evaluated by us are capable of reconstructing visually similar spectrogram segments after finished training, as shown by the autoencoder reconstructions in
Figure 5. While the training loss was lower using the dense autoencoder model (3.55 × 10
−2) compared to the convolutional autoencoder (3.63 × 10
−2), the validation loss was higher (3.82 × 10
−2) compared to the convolutional autoencoder model (3.70 × 10
−2), indicating a poorer reconstruction performance of the dense autoencoder model on the same unseen dataset. We attribute the divergence of the training and validation losses observed in the case of the dense autoencoder to its overfitting on the training set, due to the dense autoencoder’s large number of parameters. Our case study showed that the convolution-based architecture can achieve a better reconstruction performance on unseen data with a comparably small number of parameters, specifically with only 2.5% of the dense autoencoder model’s number of parameters. At the same time, the convolutional autoencoder maintained a good correspondence between training and validation losses. This suggests that the convolutional autoencoder network learns more generalizable features and is less prone to overfitting in this application. In addition, the dense autoencoder has a large number of parameters, so its training can quickly become computationally expensive when considering multiple models or larger datasets with even more components and wind turbines. Based on these results, we determined that the convolutional architecture is better suited for our task. Consequently, we proceeded by using this configuration for all further experiments.
Fault detection based on autoencoder reconstruction losses. We trained a separate convolutional autoencoder network with the conv-AE configuration for each accelerometer, using 70% of the measurements of the monitored healthy component from WT1 as the training set and 15% as the validation set. The networks were trained with the same procedure as outlined in the model selection experiment. During the training, all eight autoencoders achieved similar performances in terms of their validation losses (3.48 × 10−2–4.68 × 10−2). We evaluated the reconstruction errors obtained from the reconstructions of the segments in the training, validation, and test sets of WT1 and the test data from WT2. A threshold was determined based on the training errors, and if it was exceeded, we considered the segment as anomalous.
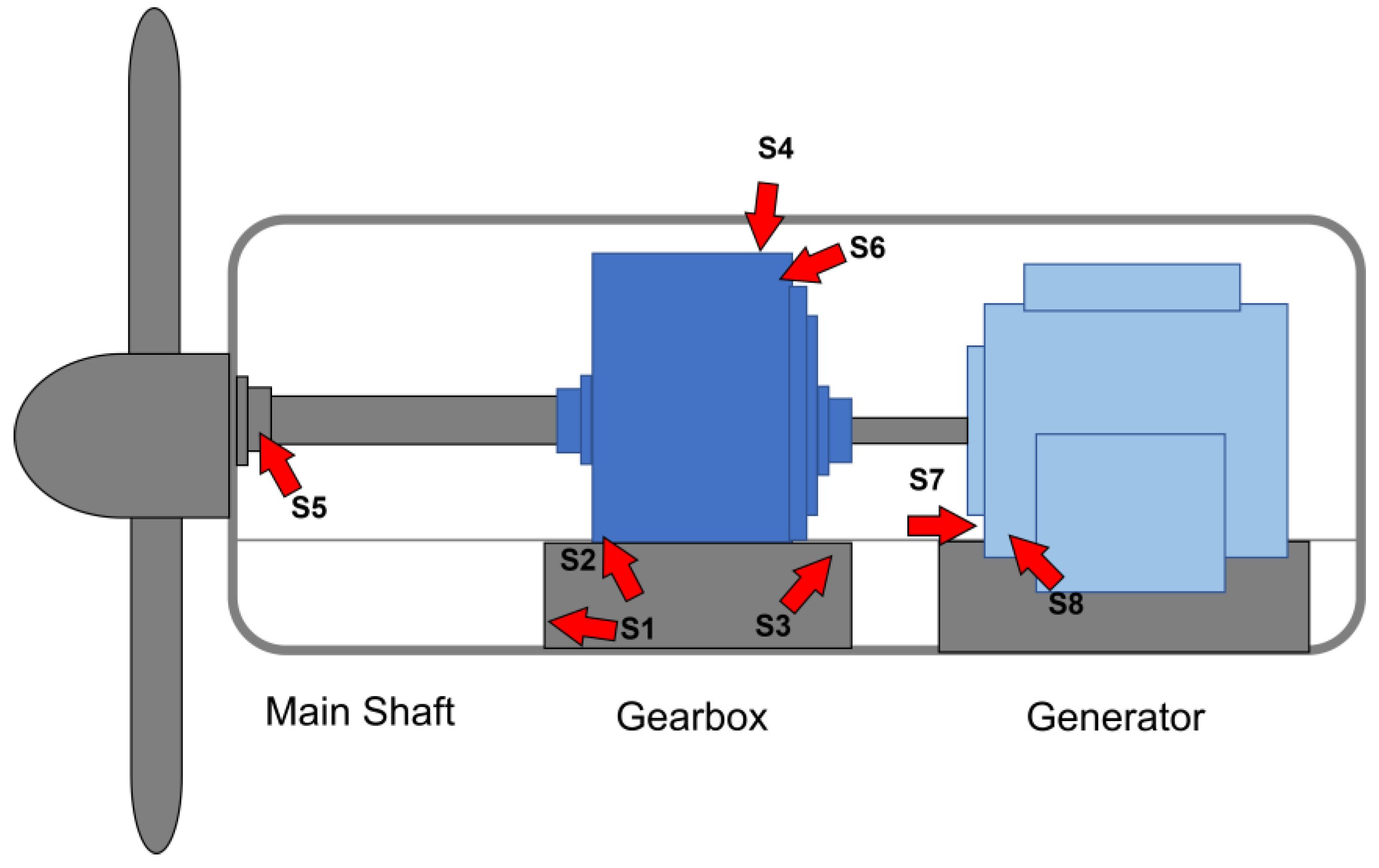
Our autoencoder-based fault detection method found increased reconstruction errors for the spectrograms derived from accelerometers S7 and S8, as shown in
Figure 6 and
Figure 7. These sensors monitor the generator component coupling to the gearbox, as shown in
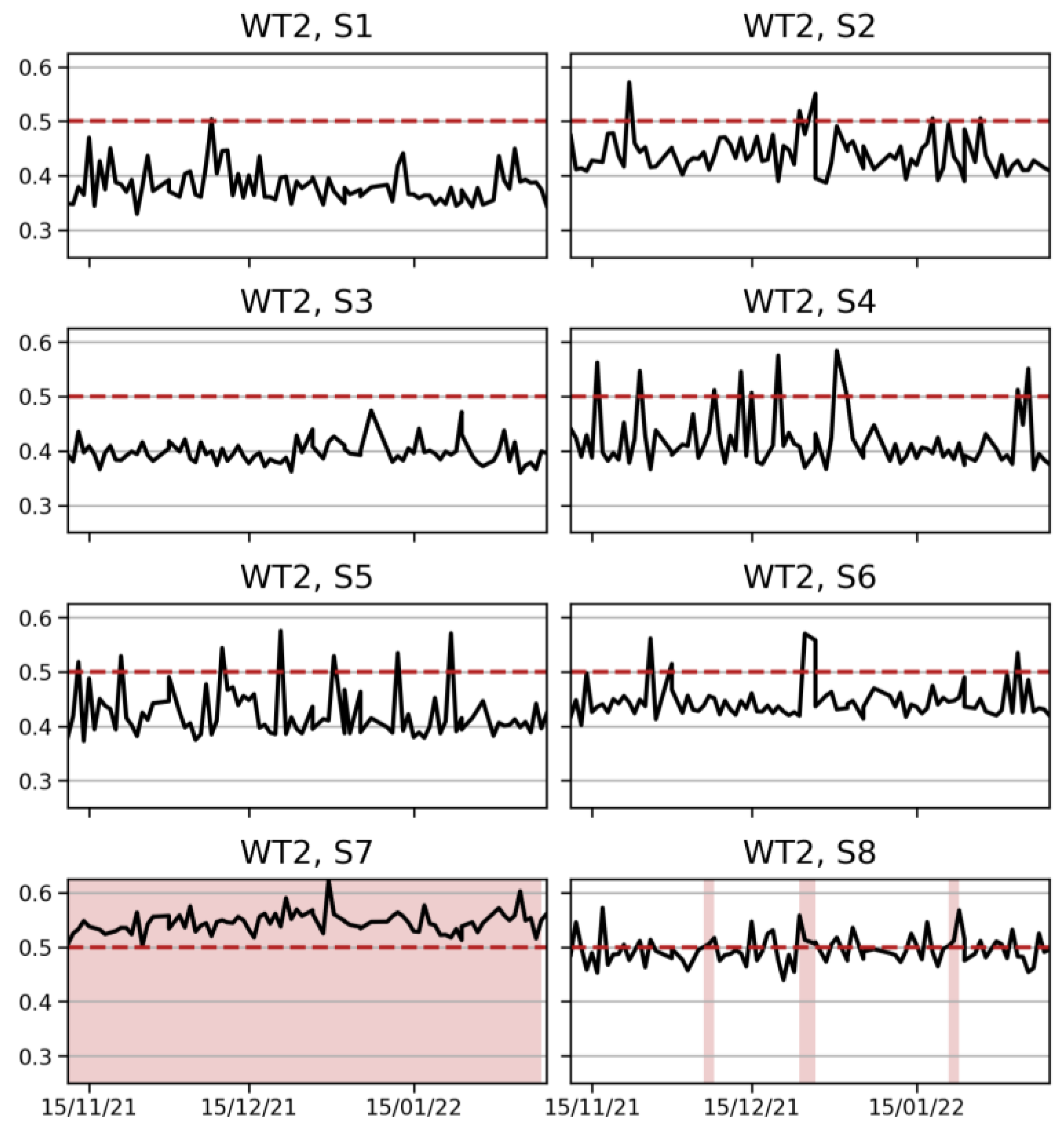
Figure 3. The health index in
Figure 7 displays the evolution of the health of each monitored component and the degree of anomaly of the component’s vibrational response. Based on the sensors from WT1, we estimated that an appropriate threshold value for bounding the reconstruction errors of normal-vibration-response spectrograms is around 0.6. To estimate this threshold more accurately, a larger number of fault instances would be needed. Based on the health index, we defined a custom rule for notifying the wind turbine operators when a certain number of anomalies were detected within a given timeframe. Specifically, a fault alarm was generated in our case study if the threshold was exceeded three times in a row, as shown by the shaded areas in
Figure 7. No alarm was triggered for the components associated with S1–S6. Our findings indicate unusual and persistent spectral changes likely to result from fault-affected vibration responses of the monitored generator. We confirmed this finding by investigating the logs of the affected WT2. The logs specified that WT2 had suffered incipient generator damage without further detailing the type of damage. Thus, we could confirm that our proposed fault detection method is sufficiently sensitive to detect incipient generator damage from accelerometer measurements in commercial wind turbines. Note that we arrived at our diagnosis without any feature engineering but, rather, by letting the autoencoder itself learn what spectrograms look like in the normal operation of healthy components.
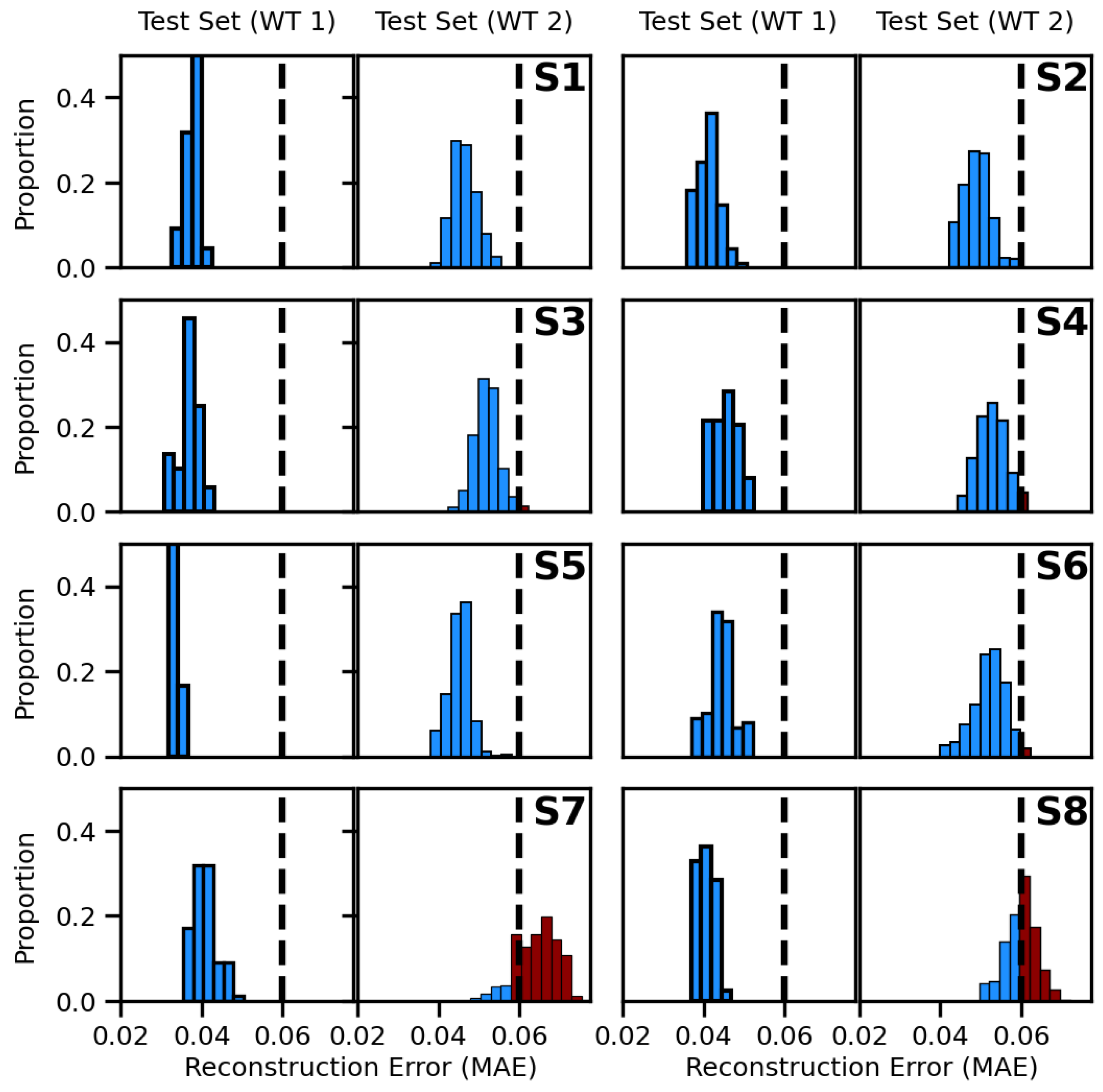
Fault detection based on isolation forests. We applied the previously trained autoencoders for isolation-forest-based fault detection by using only their encoder parts. Each encoder part outputs a compressed feature representation in a vector of size 128 (the bottleneck layer output) which was then input into the isolation forests. For each accelerometer, we trained an isolation forest (IF) using the extracted feature vectors of spectrogram segments from the training set.
Each isolation forest was evaluated on unseen spectrograms from the test set of healthy WT1 and with spectrograms from WT2, as shown in
Figure 8. The isolation forest models also provided an anomaly score (health index) for each spectrogram segment. Across all eight evaluated models, the isolation forests have consistently and correctly classified the WT1 test sets as healthy, just like the reconstruction-error-based method, as shown in
Figure 6 and
Figure 8. When evaluating the spectrograms from WT2, the isolation forest models assigned elevated anomaly scores to the generator (accelerometers S7, S8 in
Figure 8 and
Figure 9).
Figure 9 displays the health index for all monitored components. As shown in
Figure 8 and
Figure 9, fault detection based on isolation forests resulted in larger anomaly scores for the spectrograms derived from the accelerometers S7 and S8. This indicates a fault in the generator, which is consistent with the results of our reconstruction-error-based fault detection method.
We applied a rule to trigger a fault alarm if three consecutive anomalies occurred, as indicated by the shaded areas in
Figure 9. No alarm was triggered for the components associated with S1–S6. A small number of spectrograms from other components exceeded the threshold of 0.5 according to the isolation forest models, as shown by sensors S2 and S4–S6 in
Figure 8, but these did not result in persistently abnormal health scores, as shown in
Figure 9. On the other hand, multiple persistent fault alarms were triggered for the generator coupling side towards the gearbox (S7, S8).
After detecting the fault-affected vibration responses from sensors S7 and S8, a consultation of the WT2 operation logs confirmed that the generator coupling side towards the gearbox had suffered incipient damage. Thus, both presented fault detection methods successfully detected a fault in the generator from the spectral features learnt by the convolutional autoencoder.
Our study makes use of multiple model parameter values, such as the bottleneck size of the autoencoder, the number of trees in the isolation forests, or the number of maximal consecutive days with anomalies in the health index. We optimized the parameter values related to the autoencoder architecture and training, specifically the number of layers, their sizes, and learning parameters, based on a hyperparameter optimization approach as described above. Optimizing these values is possible because the autoencoder training can be considered a supervised task, in which the input spectrograms are taken to be the target outputs. Therefore, a loss value can be optimized by the choice of the autoencoder architecture and network parameters in the training process. On the other hand, the fault detection methods based on the spectrogram reconstruction error and based on the isolation forest perform unsupervised tasks because of the absence of a comprehensive set of labelled fault observations.
The optimal choice of parameters in the fault detection models is not within the scope of this study. Specifically, this includes the optimal number of trees in the isolation forest, the optimal contamination parameter in the isolation forest model, and the optimal reconstruction error threshold. We propose future studies to investigate in more detail the optimal choice of the parameter values based on additional fault observation datasets.
We also investigated the effectiveness of the presented fault detection methods for detecting known gearbox damages in one of the two 750 kW turbines from NREL (
Section 3.2). Applying the same procedures as outlined for the commercial wind turbines above, we found that both fault detection methods were successful in detecting the fault-affected components in the damaged NREL wind turbine from their vibration responses. Our results from the NREL wind turbines confirm the effectiveness of both the reconstruction-based and the isolation-forest-based fault detection approach.
5. Conclusions
Wind energy continues to expand strongly in Europe and around the world. The operation and maintenance costs of wind turbines account for a major fraction of the levelized cost of energy. Condition monitoring and artificial intelligence constitute powerful means for automating the early detection of incipient damage in wind turbines under various operating conditions. Machine learning methods enable early notification of wind turbine operators based on the vibration responses of the monitored components.
However, the existing vibration-based fault detection methods rely on the upfront definition of features in the frequency or time domains. This study has introduced two new fault detection methods for vibration-monitored parts that do not require any feature engineering. The proposed methods make use of convolutional autoencoders to detect unusual operation behaviour from the spectrograms of the monitored parts. The autoencoders learn and extract spectral features customized to the monitored components in an autonomous manner, without requiring any human assistance. In doing so, the autoencoders learn a spectral model of the component’s normal behaviour from past accelerometer measurements.
We have demonstrated the new fault detection approaches—based on reconstruction errors and based on isolation forests—in four wind turbine drivetrains. We showed that both methods can successfully distinguish damaged from healthy vibration-monitored parts. First, we demonstrated their performances in detecting incipient generator damage from the vibration responses of the generators in two multi-MW onshore wind turbines. In addition, we confirmed the effectiveness of our presented fault detection methods in test rig measurements from NREL, where they successfully detected gearbox damage.
Comparing convolutional and dense autoencoders for feature extraction and reconstruction, we found that convolutional autoencoders can accomplish the spectrogram reconstructions with a drastically lower number of parameters as compared to dense autoencoders. Thus, the proposed convolutional autoencoders avoid overfitting and can generalize better to unseen data.
Importantly, both presented fault detection methods do not require any feature engineering. We discussed how convolutional autoencoders can autonomously extract the most relevant features from a continuous range of the spectrum. We demonstrated this for the range of [0, 1000] Hz, because many characteristic frequencies fall in this range. In principle, however, the proposed method can also be applied to the full half spectrum. The autoencoders learn the normal vibration responses without requiring any upfront definition of features, thereby saving time and effort. An additional advantage of the presented methods is that a broad continuous range of the spectrum can be monitored instead of the usual focus on individual frequencies and harmonics.
The obtained results are very promising. While we demonstrated the new fault detection approach by means of gearbox and generator vibration responses, it can in principle also be applied to the structural health monitoring of other subsystems such as at the wind turbine tower. Further studies are needed for applications beyond the drivetrain to investigate the effect of variable operation conditions and how to account for them in the preprocessing and feature extraction in applications beyond the drivetrain. In the present study, we account for the effects of variable operation conditions by investigating the vibration responses at constant generator and drivetrain loads. The requirement to measure the vibration responses at constant loads can be easily accomplished in practical applications. For example, time-slice vibration measurements can be triggered whenever a specified load condition is met, e.g., by triggering the acquisition system at a certain rotational speed of the generator.
In addition to applications in other subsystems, future research should also investigate the proposed approach with more comprehensive datasets of vibration responses from damaged drivetrain components. It would be worthwhile to apply and investigate it for different damage types and intensities. It will also be interesting to study the temporal development of the proposed health indices in view of progressively increasing damage.