Abstract
Availability of reliable and extended datasets of recorded power output from renewables is nowadays seen as one of the key drivers to improve the design and control of smart energy systems. In particular, these datasets are needed to train artificial intelligence methods. Very often, however, datasets can be corrupted due to lack of records connected to failures of the acquisition system, maintenance downtime periods, etc. Several recovery (imputation) methods have been used to guess and replace missing data. In this paper, we exploit the matrix completion approach. The available measures of several variables referring to a real onshore wind farm are organized into a matrix in a daily range and the Singular Value Thresholding method is used to carry out the matrix completion process. Numerical results show that matrix completion is a reliable and parameter-free tuning tool to impute missing data in these applications.
1. Introduction
1.1. Background and Motivation
Wind energy will play a central role in achieving the Paris Agreement target of limiting global warming to by 2100. In 2021, 94 GW of wind power was added all over the world, approaching a global capacity of 850 GW [1]. The International Renewable Energy Agency (IRENA) suggests reaching 8000 GW of wind energy capacity by 2050 to reach decarbonization goals by that date [2]. Research and technical advancement are key to increase the penetration of wind power in the world energy mix. In particular, planning of energy fluxes in wind-fed grids and power management strategies usually requires historical datasets of previous installations to build upon, especially in support of the development of advanced techniques based on data-driven methods [3]. Reliable records for wind speed and/or power production of a given turbine are also beneficial for many other areas of wind energy, such as power curve estimation [4], fatigue assessment [5] and tests of new individual turbine control methods [3]. They can also be used to estimate the suitability of coupling wind energy with different types of energy demand [6]. Operational data of wind turbines are harvested by the supervisory control and data acquisition (SCADA) system. However, the measurement system may be interfered with by several events: sensor failures, communication congestion [7], communications errors, delays, maintenance operations, icing and curtailments [8]. Research may struggle in managing and evaluating the problem in the presence of missing data [9], leading to incomplete analyses and biased results. Moreover, historical datasets are crucial for the techno-economic optimization of new installations and for the simulation of different layouts. Missing data can have an impact when calculating the monthly or annual yield [10], key for the performance estimation of new plants. For example, in [11] it is shown that missing data due to icing can bias wind resource estimates downwards by more than 3.8%. Data-driven algorithms also play a crucial role in the management of the electrical network, affected by new issues brought by the increasing penetration of wind energy. Wind resources are intermittent and fluctuating, hence the power produced by wind turbines may have a significant impact on the power system operation [12]. Wind speed and power predictions are now crucial for correct management of power fluxes [13]. Forecast methods rely on historical data collected by the SCADA system of the wind farm, and loss of data may severely impact model estimation and operation. Missing values represent a huge problem for forecasting wind power and thus the correct management of the system [14]. One option is simply to omit the missing values in forecast model training. However, this may bias model estimates [8]. Effective methods to fill missing data could also be useful for studies that aim to investigate the power production stability [15] or to correctly evaluate their performance in complex terrain [16].
1.2. Related Studies
As discussed, there is a strong interest in developing reliable tools to impute missing or corrupted data in wind farms datasets, and several strategies have been implemented to this end lately. To properly contextualize the present study, here we briefly discuss the main data imputation strategies for time series and their employment for missing data from wind farm datasets. In [17], an extensive comparison among a number of different procedures for recovering missing values in time series is carried out. More precisely, matrix completion approaches and pattern-based methods are described and applied for the recovery of large missing blocks in real-words time series. Results show that the performance of the methods depend on the characteristics of the time series, and there is not a single algorithm able to ensure high accuracy in all cases. The matrix completion approach has also been used in nuclear forensic analysis [18], where authors compared five different missing value algorithms and found that the matrix completion produced the best results. Time series arising in traffic congestion analysis are considered in [19], where the data are organized in a tensor, and the joint matrix factorization method is used to model the tensor and predict missing data. The idea of filling missing data with the values of its neighbors that share the same/similar information is exploited in [20]. In this paper, similarity rules are used allowing a tolerance to small variations. A different approach is explored in [21], where the proposed heuristic data imputation algorithm exploits attribute correlations expressed in terms of relaxed functional dependencies. In [22], a data cleaning system that relies on statistical learning and inference is proposed. Concerning the specific case of missing data in wind farms’ datasets, several approaches have been tested. In [8], the multiple imputation approach is used, while in [9,14] deep learning approaches are exploited. More precisely, in [9] BP neural networks are used to predict missing power data. Interestingly, an adaptive procedure is proposed that automatically selects the minimum number of neurons from the training error. The study presented in [14] addresses the problem of filling missing data of wind farms via the context encoder neural networks. Finally, in [23] the issue of missing data in wind farm datasets is analyzed and faced with moving average approaches, namely moving average based on autoregressive order and moving average representation.
2. Materials and Methods
2.1. Theoretical Approach
In this paper, we want to develop an easy-to-use, yet effective method for missing data imputation. In particular, we focus on the matrix estimation reformulation of wind and power data reconstruction. Measurements collected by the SCADA system can be rearranged into a matrix where each column corresponds to a particular measured quantity (for example, wind speed, generated power, etc.), and each row corresponds to a particular timestamp. In this scenario, the incomplete measurements correspond to the missing matrix entries we aim at reconstructing, exploiting the observed ones, i.e., the collected data.
When it comes to time series, both univariate and multivariate, it is common to look for a reconstruction of all variables exploiting the information in the series itself (or its lagged copies [23]). In the matrix completion approach it means we have to rearrange the series (which can be seen as one or more vectors) into a matrix, usually wrapping the vectors column (row)-wise (as in [14,24]). On the other hand, in the context of neural networks it is common to use many attributes to predict a single output (e.g., [9]).
In the present work, we try to merge these two aspects in our data imputation procedure. Indeed, our focus is on reconstructing the mean generated power (even if we reconstruct all attributes together) to carry on further analysis on the wind farm; to improve the reconstruction, we exploit the measurements of several variables from the database in a daily range. We arrange data into a matrix (stacking data of each turbine in the farm), and finally we wrap column-wise to make the matrix dimension more manageable for the numerical algorithm. A clear advantage of our method, based on the matrix completion approach, compared, for example, to methods based on neural network [9] is its simplicity; indeed, in matrix completion, there is no model to design as in neural networks, and the optimization method needed to solve the problem does not need parameter tuning. This results in a reliable and easy to use method.
2.2. The Matrix Completion Problem
As discussed, we organize our data in a matrix, and the imputation of missing data is then reduced to a matrix completion problem, i.e., on the problem of reconstructing a matrix given only a portion of observed entries. Since matrices are ubiquitous and versatile in science and engineering, the matrix completion approach has been applied in many fields, such as collaborative filtering [25], bioinformatics [26], image reconstruction [27] and data imputation [24]. Researchers in numerical optimization and statistics have worked on matrix completion problems under a variety of modeling assumptions [24,25].
A popular convex relaxation of the problem consists of finding the minimum of the nuclear norm of the matrix that has to be reconstructed subject to linear constraints in order to exactly recover the observed data [28,29]. This approach has the advantage of exactly, rather than approximately, recovering the entries of the matrix when a suitable low rank assumption is satisfied, together with another assumption called “incoherence”. A number of papers in statistics follow a different approach and propose estimators of the true matrix providing bounds on the expected value of the estimation error [24,30]. All these approaches use, in a different form, the singular value decomposition (SVD) of the observed matrix and a matrix shrinkage operator (see, for example, [30,31,32]). An alternative strategy for the matrix completion problem relies on the semidefinite programming (SDP) problem reformulation (see [28,33,34]).
Here, we adopt the nuclear norm minimization model and employ for its solution the SVD-based algorithm proposed by Cai and Candès in [31]. In the next sections, we will describe in detail the model and the algorithm, and then we will show its application to the recovery of power data.
We now introduce the notation and the definitions we will use. Let be the matrix of data and the entry of i-th row and j-th column. Suppose we observe only m entries of M with indexes in . So, we have and formally
We denote with the complementary of , i.e., the set of indexes of not observed entries. We introduce the operator defined as follows:
Moreover, in what follows we will make use of the singular value decomposition of a matrix.
Definition 1.
Given a matrix , it can be factorized as where and is a diagonal matrix. The are called singular values of A. They are non-negative, and we suppose them in decreasing order . The matrices U and V are orthornormal, i.e., , where I is the identity matrix, and the column vectors of U and V are called left and right singular vectors of A, respectively. We note that the rank of A corresponds to the number of non-zero singular values. The factorization is the singular value decomposition (from now on SVD) of the matrix A.
We finally introduce the Froebenius norm of a given matrix that is defined as and the nuclear norm that is the sum of its singular values, i.e., .
Now, we have all the elements at hand to introduce the matrix completion problem. Given a matrix where we observe m entries with indexes in , we want to fully reconstruct M from the observed entries. Given a set of m observed entries, there are infinitely many matrices with those entries. A common hypothesis is to assume that the matrix M has low rank [29]. With this assumption, the matrix completion problem can be stated as the constrained minimization problem:
where the linear constraint imposes equality element-wise. Unfortunately, this problem is NP-hard and exponential in time. A popular convex relaxation of the problem (see [29]) consists of finding the minimum nuclear norm of X that satisfies the linear constraints in (2), that is, solving the following heuristic optimization:
Candès and Recht proved in [29] that if , sampled uniformly at random among all subsets of cardinality m and M, obeys a low coherence condition, then with large probability, the unique solution to (3) is exactly M, provided that the number of samples obeys , for some positive numerical constant C. In other words, problem (3) is “formally equivalent” to problem (2), and M can be exactly reconstructed.
Several methods [31,33,35,36,37,38] have been proposed to compute an approximate solution X to the optimization problem (3). Once X has been computed, the entries of X that do not belong to are used to impute the missing data in M.
2.3. The Singular Value Thresholding Method
In [31], the authors proposed the singular value thresholding (SVT) method to solve the problem (3). In the following, we describe its key elements, the algorithm and the main theoretical results. We begin defining the singular value shrinkage operator of a given matrix A.
Definition 2.
Given a matrix , its SVD decomposition and a constant , we define the operator
In words, the operator sets to 0 all singular values less than and reduces the others of a quantity equal to . This procedure is also known as soft thresholding. We note that if A has many singular values less than , then has rank much smaller than A.
The SVT is an iterative method. Given a starting point and a sequence of steps at each iteration, it computes the matrices as follows:
The following theorems state that the sequence converges to the solution of a minimization problem which is strictly correlated to problem (3).
Theorem 1.
Suppose the sequence of steps satisfies . Then, the sequence generated by (5) converges to , for , where is a unique solution of the minimization problem
Theorem 2.
Then,
These results can be interpreted as follows: for big values of , the solution to problem (6) is “close” to the solution of (3). So, we expect that if we choose big enough, the numerical solution provided by the iterative process (5) is a good approximation of the original matrix M.
We highlight two crucial properties of the algorithm: low-rank property and sparsity. About the former, an empirical fact is that the matrices in the sequence have low rank. The reason is that we are interested in large values of (as suggested by Theorem 2), and it happens that many singular values are set to 0 during the thresholding step. About the latter property, we have that at each iteration is sparse. It can be proved by induction that vanishes outside . These two properties enable reducing the overall computational cost of the SVD decomposition and saving memory storage.
The SVT algorithm is sketched in Section 3.4, page 12. In Section 3, we specify the stopping criteria implemented in our experimentation and our choice of the input parameters .
2.4. Data Reduction
2.4.1. Turbine Functioning
The matrix completion method was applied to the historical dataset coming from the SCADA system of a real wind farm located in Kedros, Greece. The system includes six Enercon E-82 (2.3 MW) wind turbines. The manufacturer provides a datasheet containing the ideal turbine power curve, i.e., how the generated power depends on the wind speed. The ideal power curve is plotted in black in Figure 1, overlapping the real measured data (blue dots).
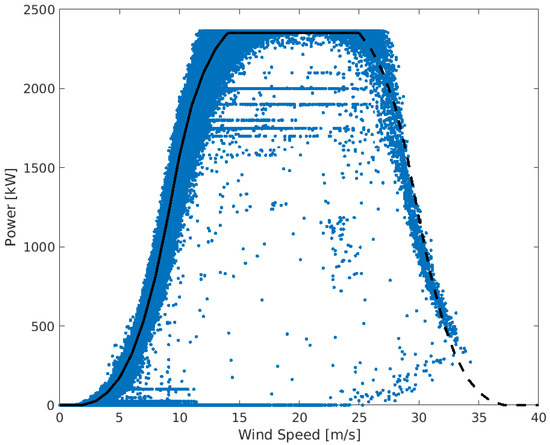
Figure 1.
Plot of measured power vs. measured wind speed of all data points (blue dots) and power curve provided by constructor (black solid line). In the storm region (), the dashed curve represents the trend presumed by the constructor but not guaranteed.
We highlight three key properties of the curve:
- There is a cut–in speed below which the turbine is not activated, hence the generated power is 0 kW;
- Above the cut–in speed, the curve has a cubic trend until reaches a rated speed . Above this value, the power generation is kept constant;
- Finally, the turbine is braked and the power generation stopped when the wind speed is above the cut–off speed .
In our case study, the three speed values are , and . Most wind turbines interrupt the power generation when the wind speed exceeds the cut–off value. This model is instead provided with the Enercon storm control that slows the wind turbine down so that it can continue to operate even at high wind velocities. The produced power is gradually reduced, starting from a defined value (25 m/s) until the actual cut–off (38 m/s). Real measurement data validate the behaviour, following the predicted curve even in this high wind speed area.
2.4.2. Data Collection
We have at our disposal data of one year of operation. The SCADA system harvests data each 10 min, recording mean, maximum and minimum values of several quantities during the time interval. The outside temperature is collected too. Our set of data could have missing values, i.e., due to blackout or failure in the remote monitoring system, or inconsistent data, that is, wind speed and generated power inconsistent with the ideal power curve. This can happen due to sensors malfunctioning. Since we aim to carry out an energy analysis of the wind farm, our goal is to achieve consistent data as much as possible. Therefore, we will proceed to recover inconsistent data as well as missing data.
In our case study, we will focus on and exploit only a subset of all the measurements collected, in particular: mean, maximum and minimum values of the wind speed, rotor speed and generated power data. For the classification of the data, we will make use of the outside temperature too.
2.4.3. Classification Criteria
Now, we present the criteria used to classify inconsistent data. These consider the outside temperature recorded and a comparison between generated power and the ideal power curve.
Icing
When the outside temperature is extremely low, we can have the formation of ice on the anemometer or on the blades of the turbines. Even small amounts of ice can cause significant power loss due to the aerodynamic inefficiency of the modified blade shape. This phenomenon is called icing. Icing is a phenomenon which is characteristic of a specific site and of course needs to be accounted for in the estimation of the actual annual energy production (AEP) of a wind farm; to this end, losses (annual average percentage reduction of AEP) are usually introduced when siting analyses are carried out. In the present case, however, the scope of the analysis was to recreate a complete time history of wind/power data for external use, e.g., in energy management systems. For this reason, data subject to icing (thus dependent of the specific year of measurement) are considered as inconsistent, as common practice by the industrial partner EUNICE WIND that supported this activity. However, they could be easily included again in the case of a specific year needing to be analyzed. In our procedure, we classified as icing all timestamps corresponding with measured temperature less than .
Power Band
During the operation, due to the interaction of the turbine with unpredictable phenomena, real production data may not match the exact ideal production that we may expect utilizing the ideal power curve from the manufacturer’s datasheet. Little discrepancies are within the norm. However, sensor failure may cause actually abnormal measurements with that must be rejected. Usually, the most reliable measurements are the ones of wind speed (except in the case of icing we discussed before), while other data, such as rotor speed or generated power, are more uncertain. So, in our classification, we assume that wind data are always reliable. Then, we define a band around the power curve and check if the pair mean values of wind speed and generated power is inside the band. If the check is passed, we maintain all the data; otherwise, we maintain only the wind data and go on recovering the other data. The red lines in Figure 2 represent the power band width. The power band is defined as follows:
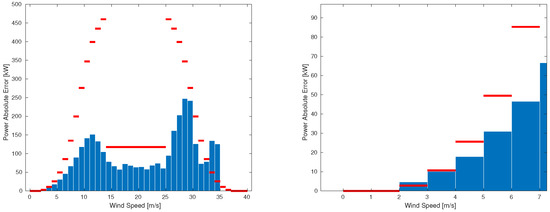
Figure 2.
Histograms of the mean absolute error (MAE) of measured power. On the X-axes, we have a range of wind speed; each interval is 1 m/s wide. The red lines represents the band width.
- For wind speed values below the cut–in speed , we consider consistent only the data with generated power null, so the band is exactly the power curve;
- For wind speed values included between and , the band is limited by of the theoretical generated power;
- For values included between and , the generated power is kept constant, and the band is limited by +10%/−5% of the theoretical generated power;
- For speed above , the curve is symmetrically extended and the same for the band.
Figure 2 shows that the mean average error (MAE) is within the power band, represented by the red lines, except for data corresponding to wind speed of the order of . The MAE is computed with respect to the ideal value in the power curve.
2.5. Recovery Workflow
We now discuss the procedure for data recovery. More precisely, we describe how we arrange the data into a matrix, the reconstruction procedure and how we evaluate the obtained outcome.
2.5.1. Building the Data Matrix M
Our goal is to recover the mean generated power of the 6 turbines for an efficiency analysis of the wind farm. For the reconstruction, we use the data of wind speed, rotor speed and generated electrical power divided by day. For each of these three quantities, we use the average value and the maximum and minimum values of the 10 min interval. We also use the theoretical value of generated power given the wind speed. As a result, at each timestamp, we have 10 values per turbine. In each day, we have 144 timestamps per turbine, for a total of 864. We rearrange these data in a matrix M of dimension . At a generic row i of the matrix, we have the collected data at timestamp . The values relative the k-th turbine are stored in columns of index with , i.e., the first turbine values are stored in and so on.
In this framework, the data of rotor speed and maximum/minimum values of the three quantities are used as additional information to “help” the reconstruction. The same is true for the theoretical generated power.
2.5.2. The Training, Validation and Testing Sets
Our classification procedure gives rise to the set of the indices of observed entries, where we include indices corresponding to all consistent data and discard all missing or inconsistent data. More specifically, whereas we have consistent data in a timestamp, we observe all 10 values of that interval, while when they are inconsistent, we only observe the three values of wind speed (since we decided to consider them always reliable, except for the case of icing) and the theoretical generated power, while the other six are unobserved.
We also consider a validation set that we will use to evaluate the reconstruction. We consider a portion (in our case sampled randomly) of all “consistent timestamps” and discard them too as described before. The remaining data are referred to as the training set. Using this approach, we can compare the reconstruction of the data in the validation set with the actual values and obtain a further evaluation criterion of the procedure. We will denote as and the sets of indices associated to the training set and the validation set, respectively. The testing set is given by the complementary set to , i.e., the set of indices that do not belong to . We will also compare the value of the rebuilt power data that clearly belong to the testing set, with the theoretical value of the generated power given the corresponding wind speed. Then, we will make use of the sets and that denote the set of indices corresponding to the power measures in the validation and testing set, respectively.
2.5.3. Reconstruction Procedure
As mentioned before, we recover the data one day at a time. We skip the day and do not even try the reconstruction if one of the following situations occurs:
- There is at least one interval at which icing occurs. In this case, we have no reliable information for the particular turbine in that timestamp. So, the reconstruction is too hard;
- All the data of one turbine are missing. This can happen due to a blackout or a failure during the whole day.
- After the classification procedure, it happens that the day has less than of consistent timestamps.
In the other cases, we use the SVT algorithm, described in Section 2.3, to reconstruct the matrix M. Before that, we have to normalize the data. Indeed, wind speed, rotor speed and generated power have three different ranges which differ up to two orders of magnitude (indeed, the wind speed maximum value is approximately , while the maximum generated power is over ). We opted for a constant normalization, i.e., we choose three values greater than the maximum values of wind speed, rotor speed and generated power of the whole year, respectively. Then, each day the data are normalized, we divide by the appropriate value. In our case, the study values are m/s for the wind speed, min−1 for the rotor speed and 2715 kW for the power. The entries of the normalized matrix are in the range . Then, the reconstruction is carried out, and finally the data are denormalized multiplying by the same constants.
3. Results
3.1. Implemented Workflow
Here, we briefly summarize the steps of our recovery strategy described in Section 2.5. For every chosen day, we perform the following steps in order to obtain the rebuilt matrix .
- IF there is icing or all data from a turbine are missing: discard the day and skip to Step 3.ELSEClassify the data and build the set .
- IF the data are all consistent, or less than the 50% of data are consistent: discard the day and skip to Step 3.ELSEproceed with recovery:
- (a)
- Rearrange data in matrix M and normalize them to obtain .
- (b)
- Divide consistent data in the training and the validation set. Let be the matrix with 0 entries out of .
- (c)
- Apply the SVT Algorithm 1 with as input matrix. Let be the outcome of the SVT Algorithm.
- (d)
- Denormalize and obtain .
- RETURN
3.2. Summary of Days in 2015
As already mentioned, we applied our reconstruction procedure only to data of days in which the corresponding matrix completion problem was a well-posed problem. More precisely, we discarded days with icing, days with all missing data of a turbine or less than of consistent timestamps. (We calculate the ratio of consistent timestamps over the total, i.e., 864.) In our case study, we have:
- One day with icing;
- One day with all data missing from a turbine;
- Four days with less than of consistent data;
- Seven days with of consistent data.
Overall, the available database accounts for 352 out of 365 days.
Then, we divide the remaining days according to the following two different criteria.
- Percentage of consistent data.
- We consider three groups: Sample_75, days with a percentage of consistent data greater or equal to and less than ; Sample_90, days with a percentage greater or equal to and less than ; Sample_100, days with a percentage greater or equal to .
- Wind speed zone.
- We divide the range of wind speed in three zones: Zone_1 up to ; Zone_2 from to and Zone_3 from on. Then, the days are divided based on in which wind zone the majority of the mean wind speed of inconsistent/missing measurements are.
In Figure 3, we show the heatmap of the days with respect to the two criteria. Zone_1 is empty and Zone_3 contains a small amount of days. So, we can ignore those days and consider only Zone_2 days.
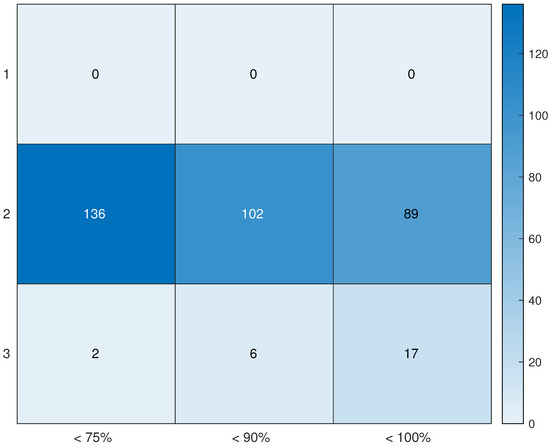
Figure 3.
Heatmap of number of days divided by percentage of consistent data (column) and zone with most of the data in (row).
3.3. Reconstruction Evaluation
To evaluate the reconstruction, we count how many consistent data we obtain after the matrix completion process. More precisely, we consider the power data which were previously classified as unobserved (i.e., inconsistent or missing in the training set) and are then reconstructed inside the band. Then, denoting as the number of such data, we compute the following values:
- Total Reconstruction Ratei.e., the percentage of reconstructed values of the generated power with respect to all data.
- Relative Reconstruction Ratewhere is the cardinality of the set of rejected timestamps. In other words, is the percentage of reconstructed values of the generated power with respect to the discarded timestamps.
- In order to give more insights on the accuracy of the computed reconstruction, in addition to the total and relative reconstruction rate we provide the value of the following RMSEs:
- -
- RMSE on the training set:
- -
- RMSE on the validation set:
- -
- RMSE of the power data on the testing set:
- -
- RMSE of the power data on the testing set:where is the column index of the theoretical generated power values corresponding to values in the j-th column. (With our arrangement of the data, the theoretical values of generated power are 18 columns ahead of the mean generated power values, i.e., ).
3.4. Numerical Experimentation
Now, we report the results of our numerical simulations. All the reported numerical results were obtained by implementing the SVT Algorithm 1 in MATLAB R2020b and performing the numerical experiments on an Intel Core i7-9700T CPU 2.00–1.99 GHz with an 16 GB RAM.
| Algorithm 1 SVT Algorithm |
| Input: |
| Output: |
| 1: for to do |
| 2: Compute the SVD of |
| 3: Set |
| 4: if the stopping criterion is satisfied then |
| 5: return |
| 6: end if |
| 7: Set |
| 8: end for |
| 9: return |
In all our experimentation, we used the following values for parameters and initial point: the sequence of steps is chosen equal to a constant value , the threshold and the initial guess are chosen as follows: and , where . For motivation and discussion on the choice of parameters see Section 5.1 in [31].
As stopping criterion, we set the maximum number of iterations . We also implemented a criterion on the relative error evaluated on training data
and a criterion on the relative error between two consecutive iterations
with , . We note that in our experiments the above criteria on relative errors never activated, and the algorithm always reached the maximum number of iterations.
Since the computation of the SVD is the most CPU -intense part of the SVT algorithm, we employed the cheaper truncated SVD as described in [31]. For its computation in our Matlab implementation, we used the Matlab built-in function svds.
We chose five random days for each of the three groups: Sample_75, Sample_90 and Sample_100, and we tried 50 reconstructions with different training and validation sets.
Table 1, Table 2 and Table 3 report the results for Sample_75, Sample_90 and Sample_100, respectively. The reported data are the following: the first column shows the day considered; columns from 2 to 4 report the number of rejected timestamps and the cardinality of the training and validation sets; in the subsequent two columns we report the total and relative reconstruction rate and averaged over 50 runs; in the next columns we report , , and averaged over 50 runs. Finally, we report the average CPU time.

Table 1.
Reconstruction results on days from the Sample_75 group. The reported statistics are averaged over 50 runs.

Table 2.
Reconstruction results on days from the Sample_90 group. The reported statistics are averaged over 50 runs.

Table 3.
Reconstruction results on days from the Sample_100 group. The reported statistics are averaged over 50 runs.
The three Tables show that the relative reconstruction rate is around 50% or higher in Sample_90 and Sample_100, while it is lower (around the 20%) in Sample_75, highlighting that problems with percentage of discarded data between 25% and 50% are difficult to solve. In addition, we note that in all the cases, the RMSE on the validation test is of the order of , and we observe that is always greater than the RMSE evaluated only on the power data of the validation. This means that power reconstruction (which is our final goal) is slightly better than general reconstruction. We also note that an increase in the number of consistent data produces an increase in the RMSE values.
The statistics reported in the tables are not enough to give a complete picture of the obtained results. Then, in order to give more insight into the quality of the reconstruction, we also illustrate the results through a number of graphics for each examined day. In the following, we show these for a specific day of each group, and further graphics are given in the Appendix A. We plot the power rejected data (red dots), power validation data (green triangles) and power reconstructed data (blue squares) both versus wind speed and versus ideal power. The gray area represents the acceptance band.
We underscore that in the plots in the first and second lines of the figures of each day, the more points we have inside the band of the right plot, the better the procedure is. In the bottom line pictures, if the points lie near the diagonal, it means that the reconstruction method provides data close to the ideal value.
In Figure 4, we plot the results corresponding to 26 February. Many rejected points are reconstructed inside the band, and in general, all the data points are closer to the band than the original ones.
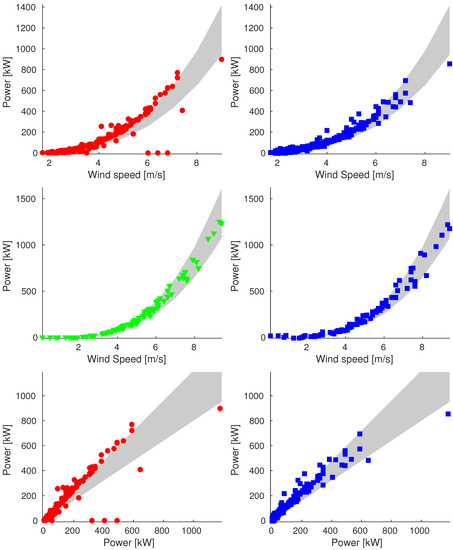
Figure 4.
Plot of reconstructions for data points of 26 February (Sample_75). We compare original data (on the left) and reconstructed values (on the right). We show plots of power vs. wind speed of rejected and validation data (up and middle, respectively) and plot of power vs. ideal power of rejected data (bottom).
Analogous plots are reported in Figure 5 for 16 May in Sample_90. Similar to the Sample_75 case, the quality of the reconstructed data seems good. Moreover, the method shows extremely good performance on the validation set. We note that only a few reconstructed data are not correctly rebuilt as they are far away from the band.
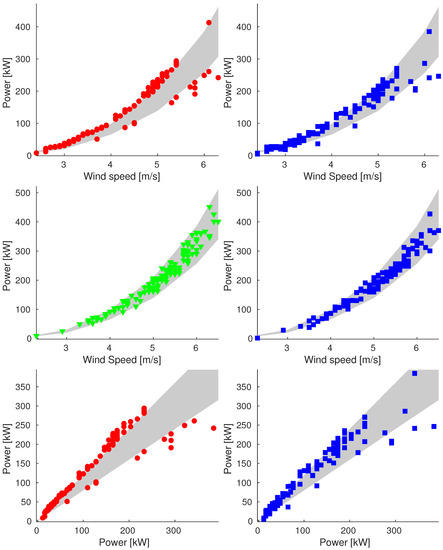
Figure 5.
Plot of reconstructions for data points of 16 May (Sample_90). We compare original data (on the left) and reconstructed values (on the right). We show plots of power vs. wind speed of rejected and validation data (up and middle, respectively) and plot of power vs. ideal power of rejected data (bottom).
In Figure 6, we report the results for 15 September in Sample_100. In this last case, the number of rejected data is smaller. We can observe that we have extremely good performance for the validation set, and again the reconstructed data are closer to the power curve than the discarded data except for data with wind speed near 4 m/s.
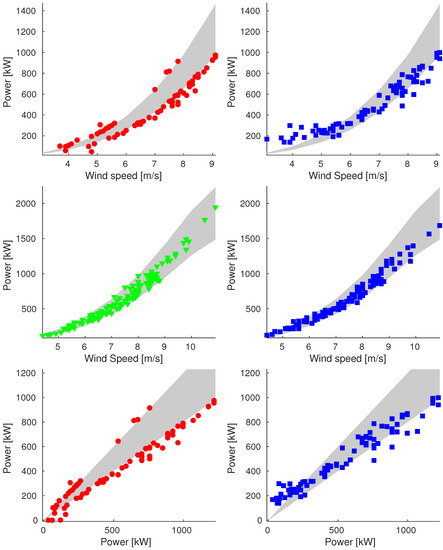
Figure 6.
Plot of reconstructions for data points of 15 September 15 (Sample_100). We compare original data (on the left) and reconstructed values (on the right). We show plots of power vs. wind speed of rejected and validation data (up and middle, respectively) and plot of power vs. ideal power of rejected data (bottom).
Looking at the validation data, some of the measures corresponding to have been imputed with power value greater than 0 kW, while for data in that range, we expect a null generated power (see Section 2.4.3, Power band paragraph). This is clear, for example, in Figure A2, Figure A3, Figure A4 and Figure A6. We note this is not a big issue as it is always possible to implement a post–reconstruction procedure to set the power values to 0 kW for the data with .
Let us comment on another aspect of the proposed procedure. In Table 2 and Table 3, the most difficult days are 10 April and 18 August. Indeed, we have which is much less than other days in the groups. Looking at Figure A5 and Figure A9, we can see that the majority of the data corresponds to low wind speed values. Indeed, for low speed data, the generated power is small, and the band is narrow, making the reconstruction task difficult. For these data, the absolute error is relatively small, but looking at the Figures, we can see how the reconstructed data form a cloud around the band and do not reproduce the trend well.
4. Discussion
4.1. Comments on Numerical Results
Upon examination of the numerical results presented in Section 3 and in the Appendix A, it can be noticed that our procedure is able to reconstruct the data trend in most of the cases. The reported statistics confirm that the procedure imputes power data with sufficient accuracy.
A weak point is that with our acceptance criteria, many points with high wind speed are really close to the band, but theoretically out of it (e.g., see Figure A1, Figure A5, Figure A7 and Figure A11), and thus they are rejected. This yields values of the relative reconstruction rate that are not as high as desirable. Nonetheless, we can consider those points as an improvement compared to the original rejected data. In addition, we highlight that in our experimentation, the acceptance criteria are suggested by the particular real case scenario, but they can be modified (e.g., enlarging the band) according to the application case.
Another downside of the procedure concerns the reconstruction of data in the area of low wind speed (<5 m/s). Data with wind speed less than have already been labeled as non-critical, since they can be dealt with in a post-processing procedure, which sets the generated power to 0 kW, according to our discussion in Section 2.4.3. On the other hand, data with wind speed slightly higher than are often reconstructed as a cloud around the band. This can be due to the small generated power of these data compared to the whole operative range. Indeed, despite data normalization, the wide power range makes it harder to reconstruct the power corresponding to low speeds. Future developments could enhance the reconstruction with an ad hoc procedure for these particular data.
As a final remark, results demonstrate that, different from many machine learning procedures, the matrix completion approach does not require parameter tuning. Indeed, our experimentation shows that SVT is reliable with the standard choice of the three parameters suggested in [31], and it does not require tuning them problem by problem. This could make our procedure an easy and ready-to-use tool to be used in many contexts, even only for preliminary processing of the data.
4.2. Conclusions and Perspectives
We focused on the imputation of missing power measures in data provided by the SCADA system of a real wind farm. For the estimation of the missing data we employed measures of several quantities: wind speed, rotor speed and generated power (mean, maximum and minimum) and adopted the matrix completion reformulation. For the numerical solution of the arising optimization problem, we employed the SVT method.
The practical performance of this approach was investigated on real data, i.e., those provided by a wind farm located in Kedros, Greece. The obtained results show that this approach is able to impute power data with sufficient accuracy. In order to increase the reconstruction quality, it could be useful to employ specifically designed second order methods for the numerical solution of the optimization problem (3) and the computation of the reconstructed matrix [33]. It is worth remarking that, as outlined in [17], performance of data imputation strategies depends on the specific characteristics of the data involved. A neural networks model, if properly tuned, provides high accuracy (potentially the highest) [9]. However, the model’s fine-tuning is highly time-consuming as it involves the choice of the net architecture (layer, nodes, activation functions), the loss function and the optimizer used for the training, which by itself requires parameter tuning (learning rate and batch size) [14]. Conversely, the approach proposed in the present study does not require any tuning of either the model or the parameters.
Further aspects that are worth being investigated in the near future are the adopted strategy for scaling the matrix and the choice of the measures that are used to build it and to drive the imputation of the missing power data. In addition, it is interesting to consider a modification to the acceptance criteria (according to different applied scenarios) and improvements of our method with ad hoc procedures to deal with the reconstruction of low speed data.
Author Contributions
Conceptualization, A.B. and S.B.; methodology, M.S. and S.B.; software, M.S.; validation, M.S., S.B. and F.S.; investigation, M.S. and S.B.; data curation, M.S. and F.S.; writing—original draft preparation, M.S.; writing—review and editing, M.S., S.B., F.S. and A.B.; supervision, A.B and S.B.; project administration, S.B. and A.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data used for the study are proprietary of EUNICE WIND.
Acknowledgments
The authors would like to acknowledge the company EUNICE WIND for providing the experimental data of the Kedros wind farm. The second author acknowledges the financial support received by the INdAM GNCS project “Ottimizzazione adattiva per il machine learning” (CUP_E55F22000270001).
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Additional Images
For the sake of clarity, we showed images of only a day for each group in the main body of the paper. We report here the results of the other days considered in the discussion above.
Appendix A.1. Sample_75
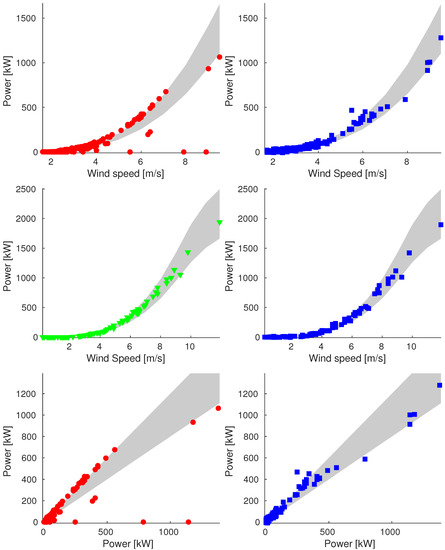
Figure A1.
Plot of reconstructions for data points of 7 May (Sample_75). We compare original data (on the left) and reconstructed values (on the right). We show plots of power vs. wind speed of rejected and validation data (up and middle respectively) and plot of power vs. ideal power of rejected data (bottom).
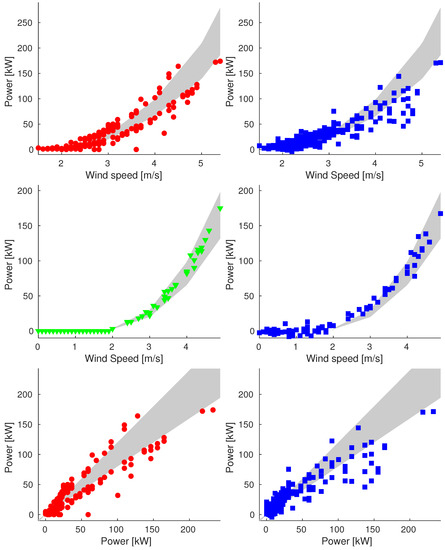
Figure A2.
Plot of reconstructions for data points of 26 July (Sample_75). We compare original data (on the left) and reconstructed values (on the right). We show plots of power vs. wind speed of rejected and validation data (up and middle respectively) and plot of power vs. ideal power of rejected data (bottom).
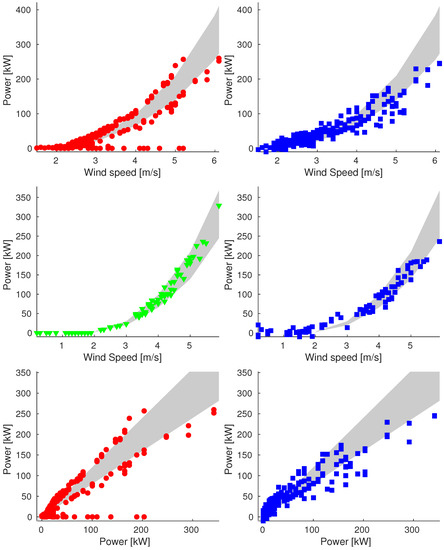
Figure A3.
Plot of reconstructions for data points of 19 August (Sample_75). We compare original data (on the left) and reconstructed values (on the right). We show plots of power vs. wind speed of rejected and validation data (up and middle respectively) and plot of power vs. ideal power of rejected data (bottom).
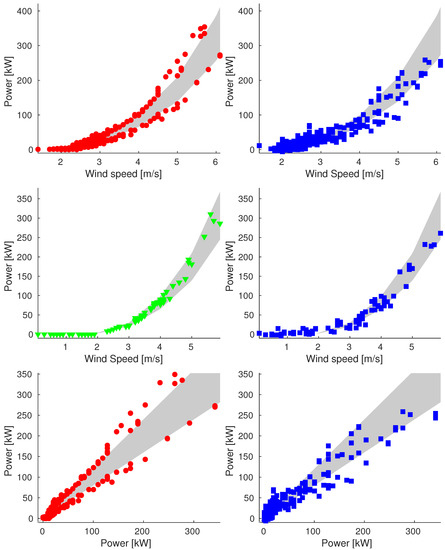
Figure A4.
Plot of reconstructions for data points of 2 September (Sample_75). We compare original data (on the left) and reconstructed values (on the right). We show plots of power vs. wind speed of rejected and validation data (up and middle respectively) and plot of power vs. ideal power of rejected data (bottom).
Appendix A.2. Sample_90
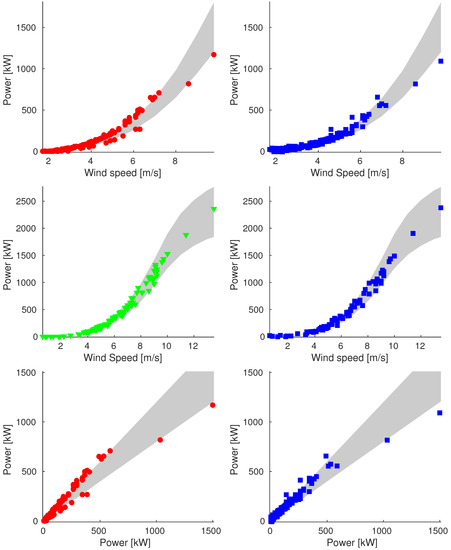
Figure A5.
Plot of reconstructions for data points of 18 June (Sample_90). We compare original data (on the left) and reconstructed values (on the right). We show plots of power vs. wind speed of rejected and validation data (up and middle respectively) and plot of power vs. ideal power of rejected data (bottom).
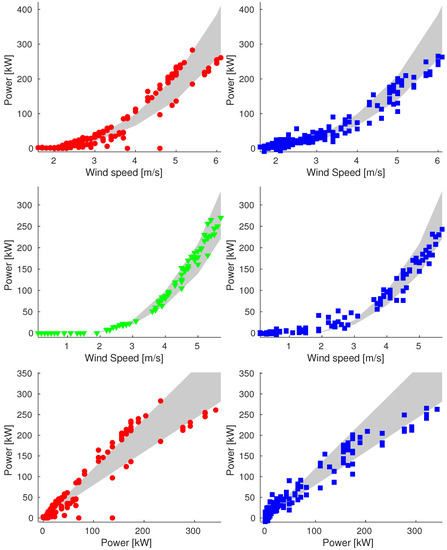
Figure A6.
Plot of reconstructions for data points of 18 August (Sample_90). We compare original data (on the left) and reconstructed values (on the right). We show plots of power vs. wind speed of rejected and validation data (up and middle respectively) and plot of power vs. ideal power of rejected data (bottom).
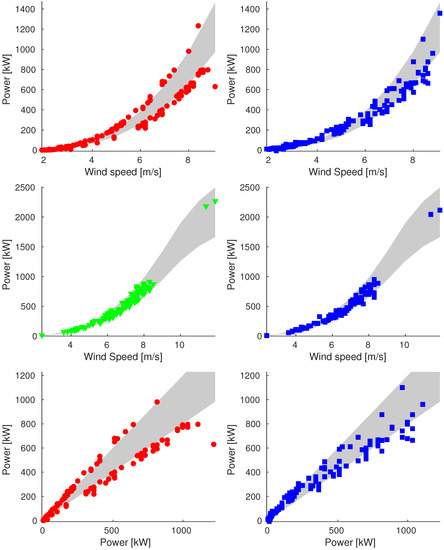
Figure A7.
Plot of reconstructions for data points of 23 August (Sample_90). We compare original data (on the left) and reconstructed values (on the right). We show plots of power vs. wind speed of rejected and validation data (up and middle respectively) and plot of power vs. ideal power of rejected data (bottom).
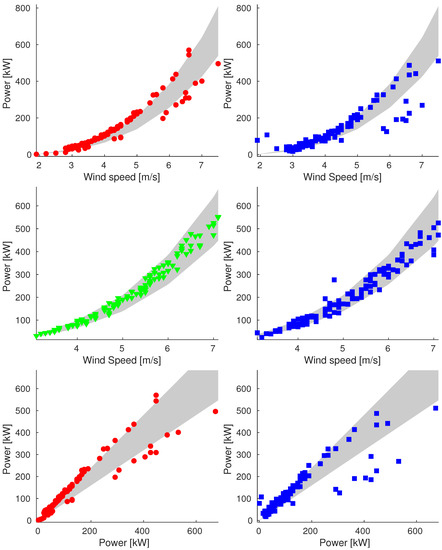
Figure A8.
Plot of reconstructions for data points of 24 September (Sample_90). We compare original data (on the left) and reconstructed values (on the right). We show plots of power vs. wind speed of rejected and validation data (up and middle respectively) and plot of power vs. ideal power of rejected data (bottom).
Appendix A.3. Sample_100
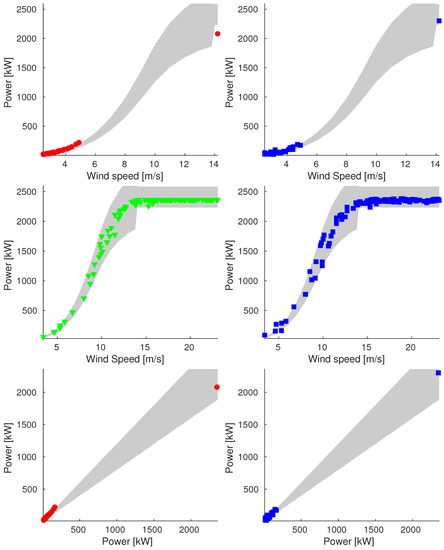
Figure A9.
Plot of reconstructions for data points of 10 April (Sample_100). We compare original data (on the left) and reconstructed values (on the right). We show plots of power vs. wind speed of rejected and validation data (up and middle respectively) and plot of power vs. ideal power of rejected data (bottom).
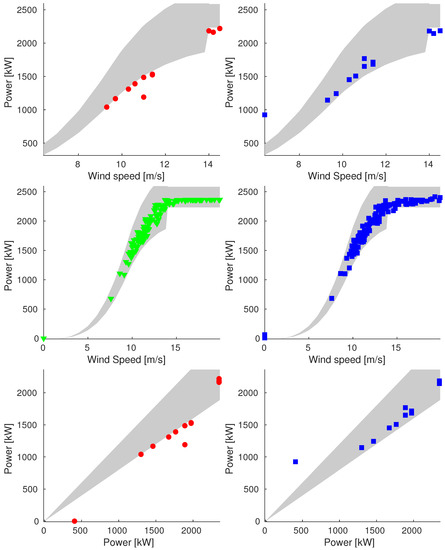
Figure A10.
Plot of reconstructions for data points of 2 June (Sample_100). We compare original data (on the left) and reconstructed values (on the right). We show plots of power vs. wind speed of rejected and validation data (up and middle respectively) and plot of power vs. ideal power of rejected data (bottom).
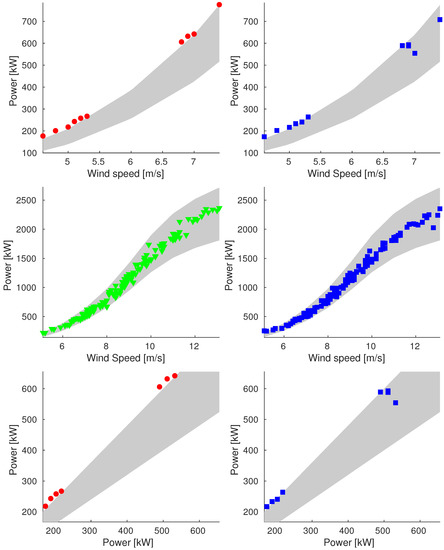
Figure A11.
Plot of reconstructions for data points of 16 October (Sample_100). We compare original data (on the left) and reconstructed values (on the right). We show plots of power vs. wind speed of rejected and validation data (up and middle respectively) and plot of power vs. ideal power of rejected data (bottom).
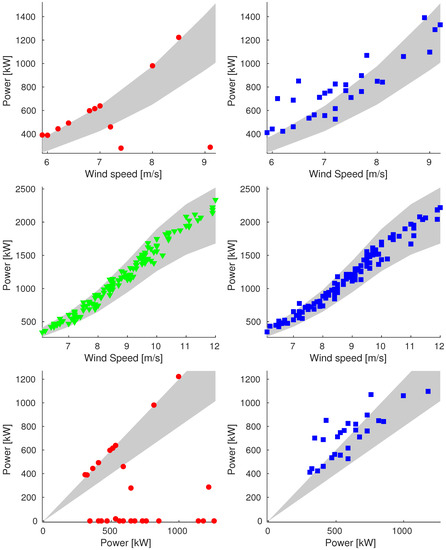
Figure A12.
Plot of reconstructions for data points of 11 December (Sample_100). We compare original data (on the left) and reconstructed values (on the right). We show plots of power vs. wind speed of rejected and validation data (up and middle respectively) and plot of power vs. ideal power of rejected data (bottom).
References
- Global Wind Report 2022. Global Wind Energy Council. 2022. Available online: https://gwec.net/global-wind-report-2022/ (accessed on 25 November 2022).
- World Energy Transitions Outlook: 1.5 °C Pathway. IRENA. 2022. Available online: https://www.irena.org/publications/2022/mar/world-energy-transitions-outlook-2022 (accessed on 25 November 2022).
- Meyers, J.; Bottasso, C.; Dykes, K.; Fleming, P.; Gebraad, P.; Giebel, G.; Göçmen, T.; van Wingerden, J.W. Wind farm flow control: Prospects and challenges. Wind. Energy Sci. Discuss. 2022, 7, 2271–2306. [Google Scholar] [CrossRef]
- Hu, Y.; Qiao, Y.; Liu, J.; Zhu, H. Adaptive Confidence Boundary Modeling of Wind Turbine Power Curve Using SCADA Data and Its Application. IEEE Trans. Sustain. Energy 2019, 10, 1330–1341. [Google Scholar] [CrossRef]
- Pacheco, J.; Pimenta, F.; Pereira, S.; Cunha, Á.; Magalhães, F. Fatigue Assessment of Wind Turbine Towers: Review of Processing Strategies with Illustrative Case Study. Energies 2022, 15, 4782. [Google Scholar] [CrossRef]
- Superchi, F.; Mati, A.; Pasqui, M.; Carcasci, C.; Bianchini, A. Techno-economic study on green hydrogen production and use in hard-to-abate industrial sectors. IOP J. Phys. Conf. Ser. 2022, 2385, 012054. [Google Scholar] [CrossRef]
- Li, Q.; Cheng, L.; Gao, W.; Gao, D.W. Fully Distributed State Estimation for Power System with Information Propagation Algorithm. J. Mod. Power Syst. Clean Energy 2020, 8, 627–635. [Google Scholar] [CrossRef]
- Tawn, R.; Browell, J.; Dinwoodie, I. Missing data in wind farm time series: Properties and effect on forecasts. Electr. Power Syst. Res. 2020, 189, 106640. [Google Scholar] [CrossRef]
- Mao, Y.; Jian, M. Data completing of missing wind power data based on adaptive BP neural network. In Proceedings of the 2016 International Conference on Probabilistic Methods Applied to Power Systems (PMAPS), Beijing, China, 16–20 October 2016; pp. 1–6. [Google Scholar]
- Salmon, J.; Taylor, P. Errors and uncertainties associated with missing wind data and short records. Wind Energy 2014, 17, 1111–1118. [Google Scholar] [CrossRef]
- Aidan, C.; Afzal, S.; Klaus-Ole, V. The effect of missing data on wind resource estimation. Energy 2011, 36, 4505–4517. [Google Scholar]
- Pinson, P. Wind Energy: Forecasting Challenges for Its Operational Management. Stat. Sci. 2013, 28, 564–585. [Google Scholar] [CrossRef]
- Wang, J.; Song, Y.; Liu, F.; Hou, R. Analysis and application of forecasting models in wind power integration: A review of multi-step-ahead wind speed forecasting models. Renew. Sustain. Energy Rev. 2016, 60, 960–981. [Google Scholar] [CrossRef]
- Liao, W.; Bak-Jensen, B.; Pillai, J.R.; Yang, D.; Wang, Y. Data-Driven Missing Data Imputation for Wind Farms Using Context Encoder. J. Mod. Power Syst. Clean Energy 2021, 10, 964–976. [Google Scholar] [CrossRef]
- Wang, Q.; Luo, K.; Wu, C.; Mu, Y.; Tan, J.; Fan, J. Diurnal impact of atmospheric stability on inter-farm wake and power generation efficiency at neighboring onshore wind farms in complex terrain. Energy Convers. Manag. 2022, 267, 115897. [Google Scholar] [CrossRef]
- Wang, Q.; Luo, K.; Yuan, R.; Wang, S.; Fan, J.; Cen, K. A multiscale numerical framework coupled with control strategies for simulating a wind farm in complex terrain. Energy 2020, 203, 117913. [Google Scholar] [CrossRef]
- Khayati, M.; Lerner, A.; Tymchenko, Z.; Cudré-Mauroux, P. Mind the gap: An experimental evaluation of imputation of missing values techniques in time series. In Proceedings of the VLDB Endowment, Tokyo, Japan, 30 August–4 September 2020; Volume 13, pp. 768–782. [Google Scholar]
- Jones, A.; Keatley, A.; Goulermas, J.; Scott, T.; Turner, P.; Awbery, R.; Stapleton, M. Machine learning techniques to repurpose Uranium Ore Concentrate (UOC) industrial records and their application to nuclear forensic investigation. Appl. Geochem. 2018, 91, 221–227. [Google Scholar] [CrossRef]
- Jia, X.; Dong, X.; Chen, M.; Yu, X. Missing data imputation for traffic congestion data based on joint matrix factorization. Knowl.-Based Syst. 2021, 225, 107114. [Google Scholar] [CrossRef]
- Song, S.; Sun, Y.; Zhang, A.; Chen, L.; Wang, J. Enriching Data Imputation under Similarity Rule Constraints. IEEE Trans. Knowl. Data Eng. 2020, 32, 275–287. [Google Scholar] [CrossRef]
- Breve, B.; Caruccio, L.; Deufemia, V.; Polese, G. RENUVER: A Missing Value Imputation Algorithm based on Relaxed Functional Dependencies. In Proceedings of the EDBT, Edinburgh, UK, 29 March–1 April 2022; pp. 1–52. [Google Scholar]
- Rekatsinas, T.; Chu, X.; Ilyas, I.F.; Ré, C. HoloClean: Holistic Data Repairs with Probabilistic Inference. arXiv 2017, arXiv:1702.00820. [Google Scholar] [CrossRef]
- Lotfi, B.; Mourad, M.; Najiba, M.B.; Mohamed, E. Treatment methodology of erroneous and missing data in wind farm dataset. In Proceedings of the Eighth International Multi-Conference on Systems, Signals & Devices, Sousse, Tunisia, 22–25 March 2011; pp. 1–6. [Google Scholar]
- Agarwal, A.; Amjad, M.J.; Shah, D.; Shen, D. Model agnostic time series analysis via matrix estimation. arXiv 2018, arXiv:1802.09064. [Google Scholar] [CrossRef]
- Ramlatchan, A.; Yang, M.; Liu, Q.; Li, M.; Wang, J.; Li, Y. A survey of matrix completion methods for recommendation systems. Big Data Min. Anal. 2018, 1, 308–323. [Google Scholar]
- Troyanskaya, O.; Cantor, M.; Sherlock, G.; Brown, P.; Hastie, T.; Tibshirani, R.; Botstein, D.; Altman, R.B. Missing value estimation methods for DNA microarrays. Bioinformatics 2001, 17, 520–525. [Google Scholar] [CrossRef]
- Nguyen, L.T.; Kim, J.; Shim, B. Low-rank matrix completion: A contemporary survey. IEEE Access 2019, 7, 94215–94237. [Google Scholar] [CrossRef]
- Fazel, M. Matrix Rank Minimization with Applications. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2002. [Google Scholar]
- Candès, E.J.; Recht, B. Exact matrix completion via convex optimization. Found. Comput. Math. 2009, 9, 717–772. [Google Scholar] [CrossRef]
- Chatterjee, S. Matrix estimation by universal singular value thresholding. Ann. Stat. 2015, 43, 177–214. [Google Scholar] [CrossRef]
- Cai, J.F.; Candès, E.J.; Shen, Z. A singular value thresholding algorithm for matrix completion. SIAM J. Optim. 2010, 20, 1956–1982. [Google Scholar] [CrossRef]
- Mazumder, R.; Hastie, T.; Tibshirani, R. Spectral regularization algorithms for learning large incomplete matrices. J. Mach. Learn. Res. 2010, 11, 2287–2322. [Google Scholar]
- Bellavia, S.; Gondzio, J.; Porcelli, M. A Relaxed Interior Point Method for Low-Rank Semidefinite Programming Problems with Applications to Matrix Completion. J. Sci. Comput. 2021, 89, 46. [Google Scholar] [CrossRef]
- Bellavia, S.; Gondzio, J.; Porcelli, M. An inexact dual logarithmic barrier method for solving sparse semidefinite programs. Math. Program. 2019, 178, 109–143. [Google Scholar] [CrossRef]
- Recht, B.; Fazel, M.; Parrilo, P.A. Guaranteed minimum-rank solutions of linear matrix equations via nuclear norm minimization. SIAM Rev. 2010, 52, 471–501. [Google Scholar] [CrossRef]
- Toh, K.C.; Yun, S. An accelerated proximal gradient algorithm for nuclear norm regularized linear least squares problems. Pac. J. Optim. 2010, 6, 15. [Google Scholar]
- Ma, S.; Goldfarb, D.; Chen, L. Fixed point and Bregman iterative methods for matrix rank minimization. Math. Program. 2011, 128, 321–353. [Google Scholar] [CrossRef]
- Keshavan, R.H.; Montanari, A.; Oh, S. Matrix completion from a few entries. IEEE Trans. Inf. Theory 2010, 56, 2980–2998. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).