Investigating Empirical Mode Decomposition in the Parameter Estimation of a Three-Section Winding Model †
Abstract
:1. Introduction
2. Transformer Winding Model
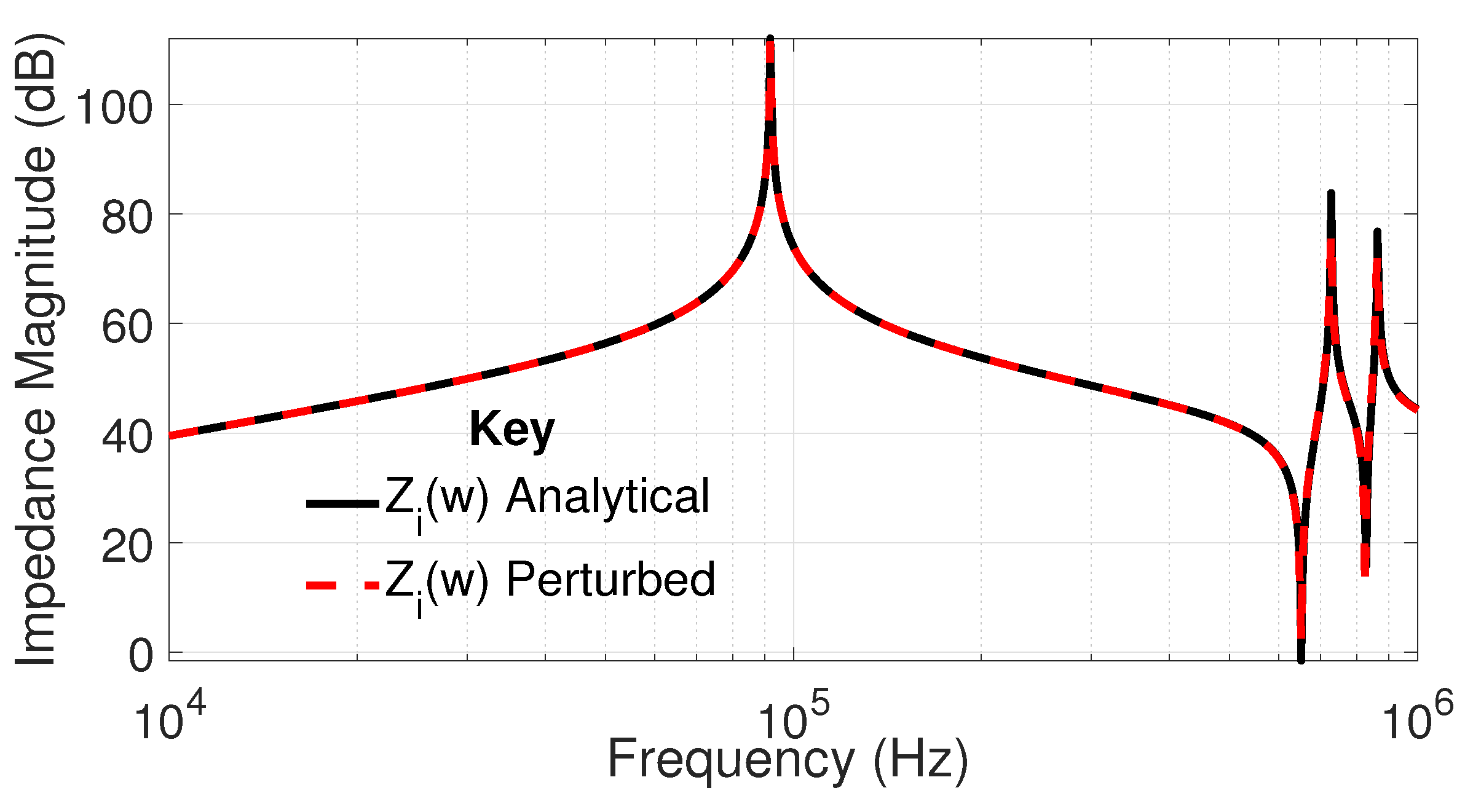
Analytical Input Impedance Frequency Response
3. Target Model Perturbation
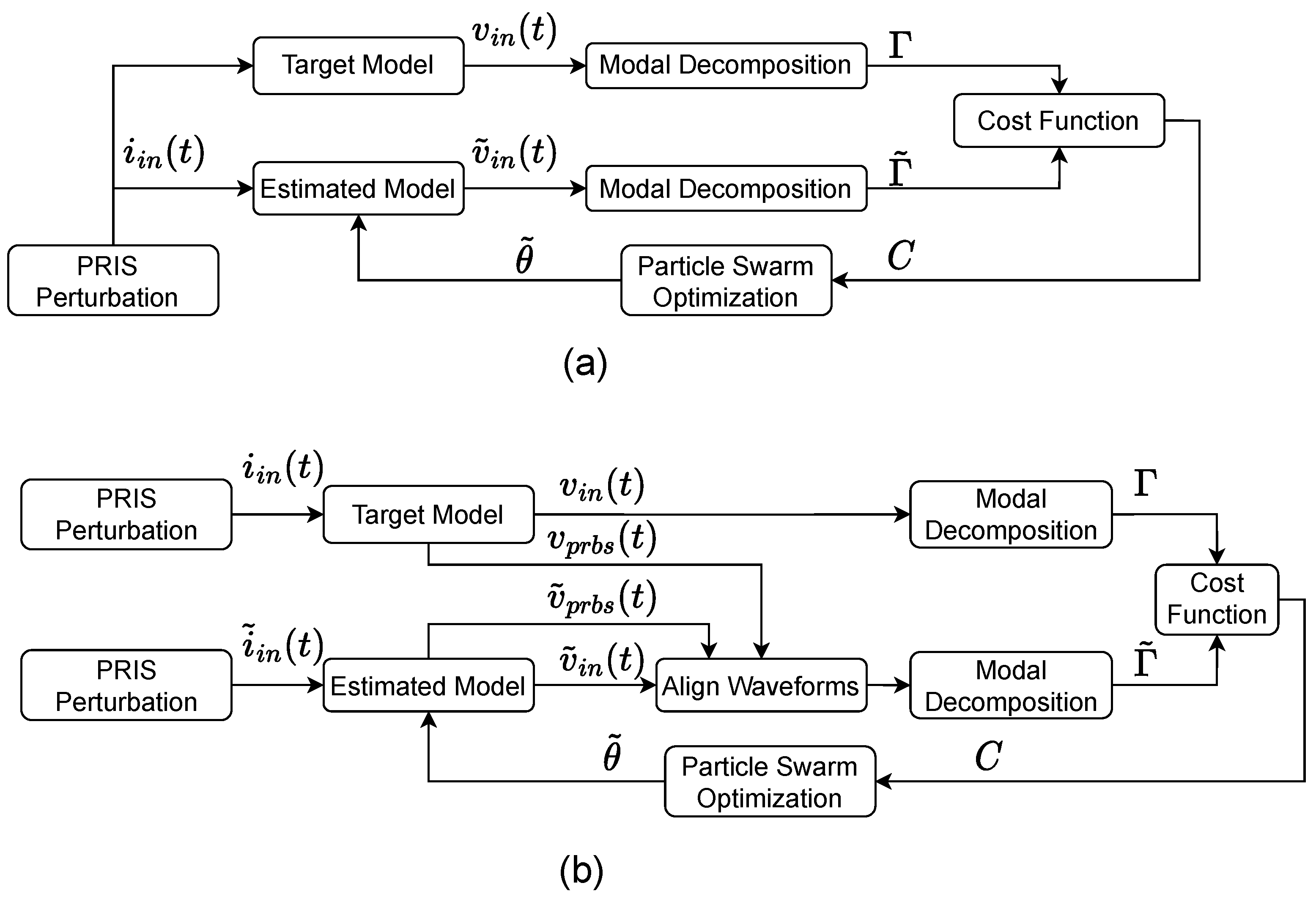
4. Parameter Estimation Methodology
5. Parameter Estimation Cost Function Formulations
5.1. Frequency-Domain Approach
5.2. Time-Domain Approach
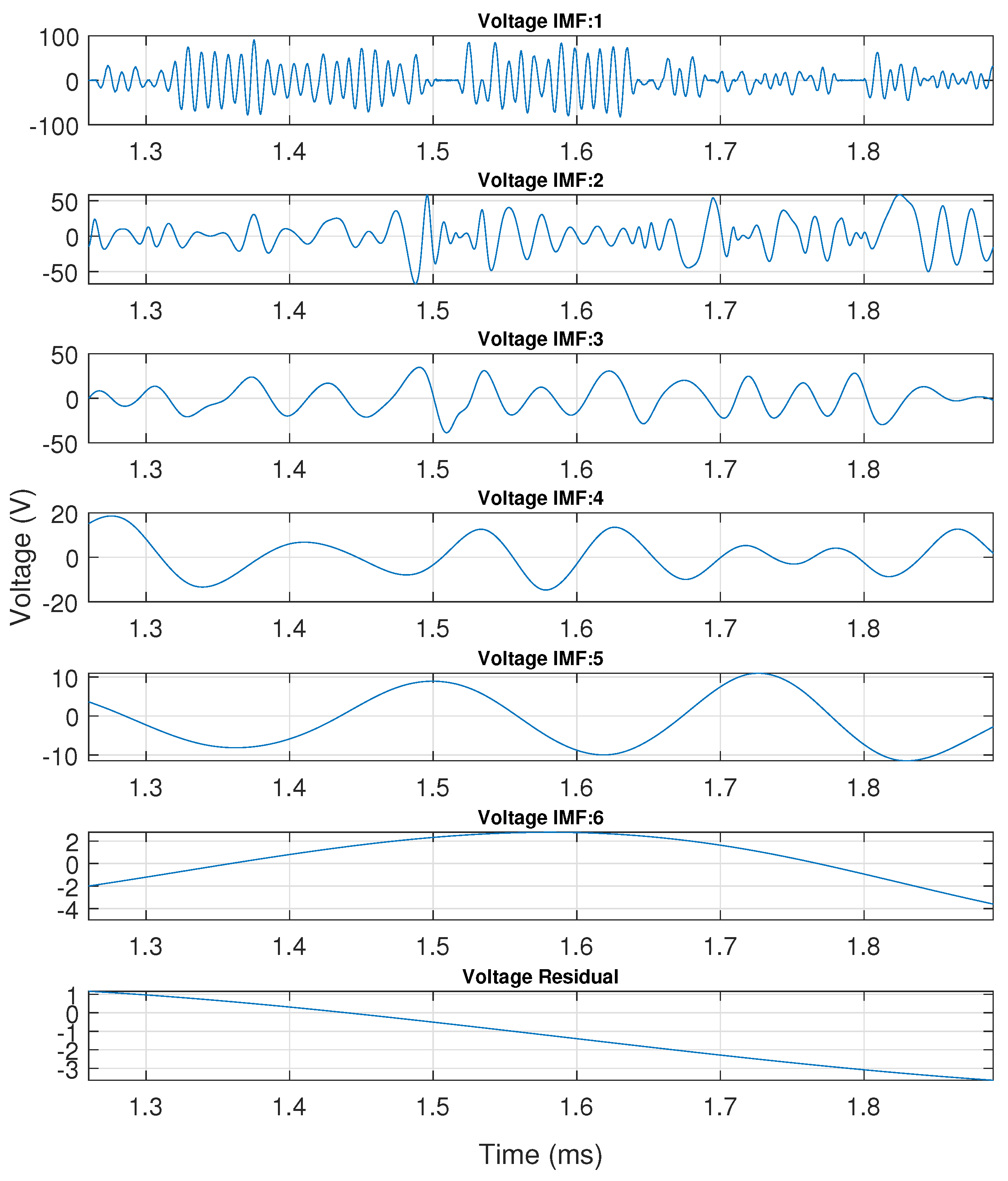
5.3. Empirical Mode Decomposition Approach
5.4. Inferred Empirical Mode Decomposition
5.5. Weighted Inferred Empirical Mode Decomposition
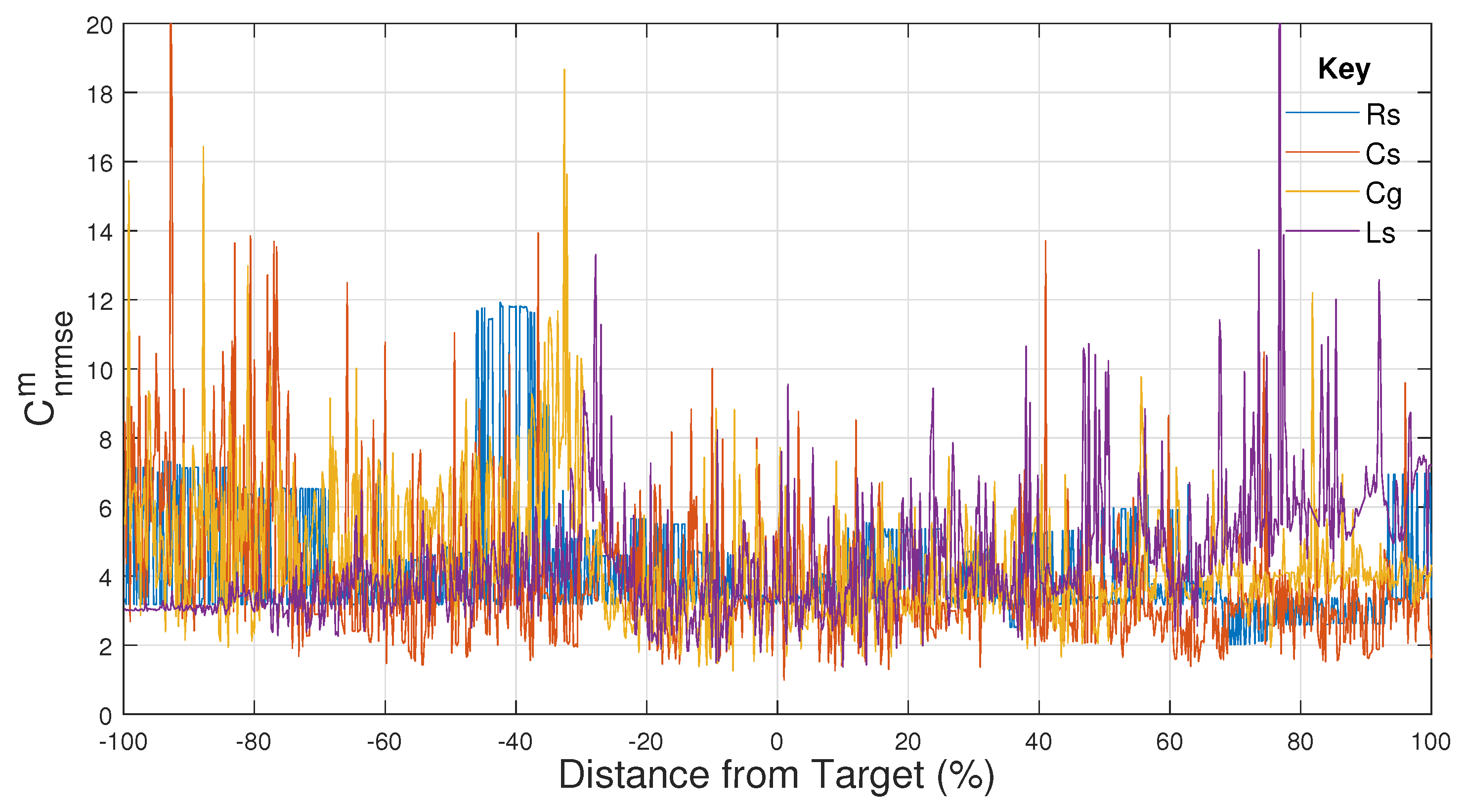
6. Results
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Peterson, B.; Rens, J.; Botha, M.G.; Desmet, J. On Harmonic Emission Assessment: A Discriminative Approach. Saiee Afr. Res. J. 2017, 108, 165–173. [Google Scholar] [CrossRef]
- Gomez-Luna, E.; Aponte, M.G.; Gonzalez-Garcia, C.; Pleite, G.J. Current Status and Future Trends in Frequency-Response Analysis With a Transformer in Service. IEEE Trans. Power Deliv. 2013, 28, 1024–1031. [Google Scholar] [CrossRef]
- Aguglia, D.; Viarouge, P.; de Almeida Martins, C. Frequency-Domain Maximum-Likelihood Estimation of High-Voltage Pulse Transformer Model Parameters. IEEE Trans. Ind. Appl. 2013, 49, 2552–2561. [Google Scholar] [CrossRef]
- Keyhani, A.; Chua, S.W.; Sebo, S.A. Maximum likelihood estimation of transformer high frequency parameters from test data. IEEE Trans. Power Deliv. 1991, 6, 858–865. [Google Scholar] [CrossRef]
- Brozio, C.C.; Vermeulen, H.J. Wideband equivalent circuit modelling and parameter estimation methodology for two-winding transformers. IEE Proc.-Gener. Transm. Distrib. 2003, 6, 487–492. [Google Scholar] [CrossRef]
- Keyhani, A.; Tsai, H.; Abur, A. Maximum likelihood estimation of high frequency machine and transformer winding parameters. IEEE Trans. Power Deliv. 1990, 5, 212–219. [Google Scholar] [CrossRef]
- Chanane, A.; Houassine, H.; Bouchhida, O. Enhanced modelling of the transformer winding high frequency parameters identification from measured frequency response analysis. IET Gener. Transm. Distrib. 2019, 13, 1339–1345. [Google Scholar] [CrossRef]
- Chanane, A.; Bouchhida, O.; Houassine, H. Investigation of the transformer winding high-frequency parameters identification using particle swarm optimisation method. IET Electr. Power Appl. 2016, 10, 923–931. [Google Scholar] [CrossRef]
- Chanane, A.; Belazzoug, M. On accuracy of a mutually coupled ladder network model high-frequency parameters identification for a transformer winding using gray wolf optimizer method. COMPEL-Int. J. Comput. Math. Electr. Electron. Eng. 2019, 40, 40–50. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995. [Google Scholar]
- Askarzadeh, A. A novel metaheuristic method for solving constrained engineering optimization problems: Crow search algorithm. Comp. Struct. 2016, 169, 1–12. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis. Proc.-Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Stallone, A.; Cicone, A.; Materassi, M. New insights and best practices for the successful use of Empirical Mode Decomposition, Iterative Filtering and derived algorithms. Sci. Rep. 2020, 10, 15161. [Google Scholar] [CrossRef] [PubMed]
- Deering, R.; Kaiser, J.F. The use of a masking signal to improve empirical mode decomposition. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, Philadelphia, PA, USA, 18–23 March 2005. [Google Scholar]
- Geng, C.; Wang, F.; Zhang, J.; Zhijian, J. Modal parameters identification of power transformer winding based on improved Empirical Mode Decomposition method. Electr. Power Syst. Res. 2014, 108, 331–339. [Google Scholar] [CrossRef]
- Yu, H.; Kong, L. Research on Modal Parameter Identification Method of Power Transformer Winding. In Proceedings of the 37th Chinese Control Conference (CCC), Wuhan, China, 25–27 July 2018. [Google Scholar]
- Xiong, W.; Li, J.; Pan, H. Analysis of transformer winding vibration based on modified empirical mode decomposition. In Proceedings of the 8th World Congress on Intelligent Control and Automation, Jinan, China, 7–9 July 2010. [Google Scholar]
- Xiong, W.; Pan, H. Transformer Winding Vibration Enveloping for Empirical Mode Decomposition Based on Non-uniform B-Spline Fitting. In Proceedings of the Second International Symposium on Knowledge Acquisition and Modeling, Wuhan, China, 30 November–1 December 2009. [Google Scholar]
- Mwaniki, F.M.; Vermeulen, H.J. Characterization and Application of a Pseudo-random Impulse Sequence for Parameter Estimation Applications. IEEE Trans. Instrum. Meas. 2020, 69, 3917–3927. [Google Scholar] [CrossRef]
- Gerber, I.P.; Mwaniki, F.M.; Vermeulen, H.J. Parameter Estimation of a Ferro-Resonance Damping Circuit using Pseudo-Random Impulse Sequence Perturbations. In Proceedings of the 56th International Universities Power Engineering Conference (UPEC), Middlesbrough, UK, 31 August–3 September 2021. [Google Scholar]
- Banks, D.M.; Bekker, J.C.; Vermeulen, H.J. Parameter Estimation of a Two-Section Transformer Winding Model using Pseudo-Random Impulse Sequence Perturbation. In Proceedings of the 56th International Universities Power Engineering Conference (UPEC), Middlesbrough, UK, 31 August–3 September 2021. [Google Scholar]
- Satish, L.; Sahoo, S.K. Locating faults in a transformer winding: An experimental study. Electr. Power Syst. Res. 2009, 79, 89–97. [Google Scholar] [CrossRef]
- Mukherjee, P.; Satish, L. Construction of equivalent circuit of a transformer winding from driving-point impedance function-analytical approach. IET Electr. Power Appl. 2012, 6, 172–180. [Google Scholar] [CrossRef]
- Ragavan, K.; Satish, L. Localization of Changes in a Model Winding Based on Terminal Measurements: Experimental Study. IEEE Trans. Power Deliv. 2007, 22, 1557–1565. [Google Scholar] [CrossRef]
- Wang, F.; Ren, R.; Yin, X.; Yu, N.; Yang, Y. A transformer with high coupling coefficient and small area based on TSV. Integration 2021, 81, 211–220. [Google Scholar] [CrossRef]
- MATLAB Signal Processing Toolbox. Available online: https://www.mathworks.com/products/dsp-system.html (accessed on 12 June 2022).
- Banks, D.M.; Bekker, J.C.; Vermeulen, H.J. Parameter Estimation of a Three-Section Winding Model using Intrinsic Mode Functions. In Proceedings of the IEEE International Conference on Environment and Electrical Engineering and IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Prague, Czech Republic, 28 June–1 July 2022. [Google Scholar]
- Franklin, G.F.; Powell, D.J.; Emami-Naeini, A. Feedback Control of Dynamic Systems, 4th ed.; Prentice Hall PTR: Hoboken, NJ, USA, 2001. [Google Scholar]




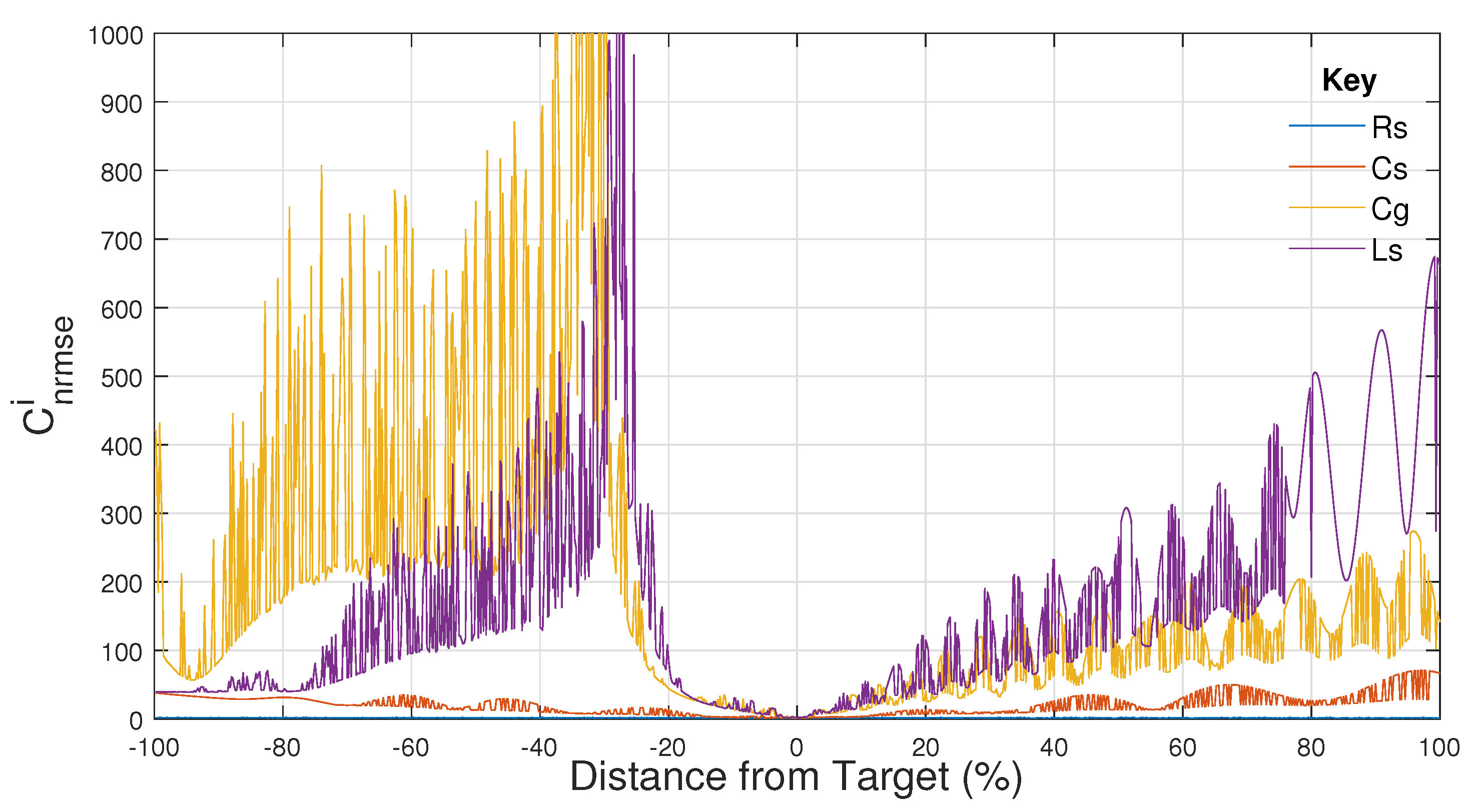
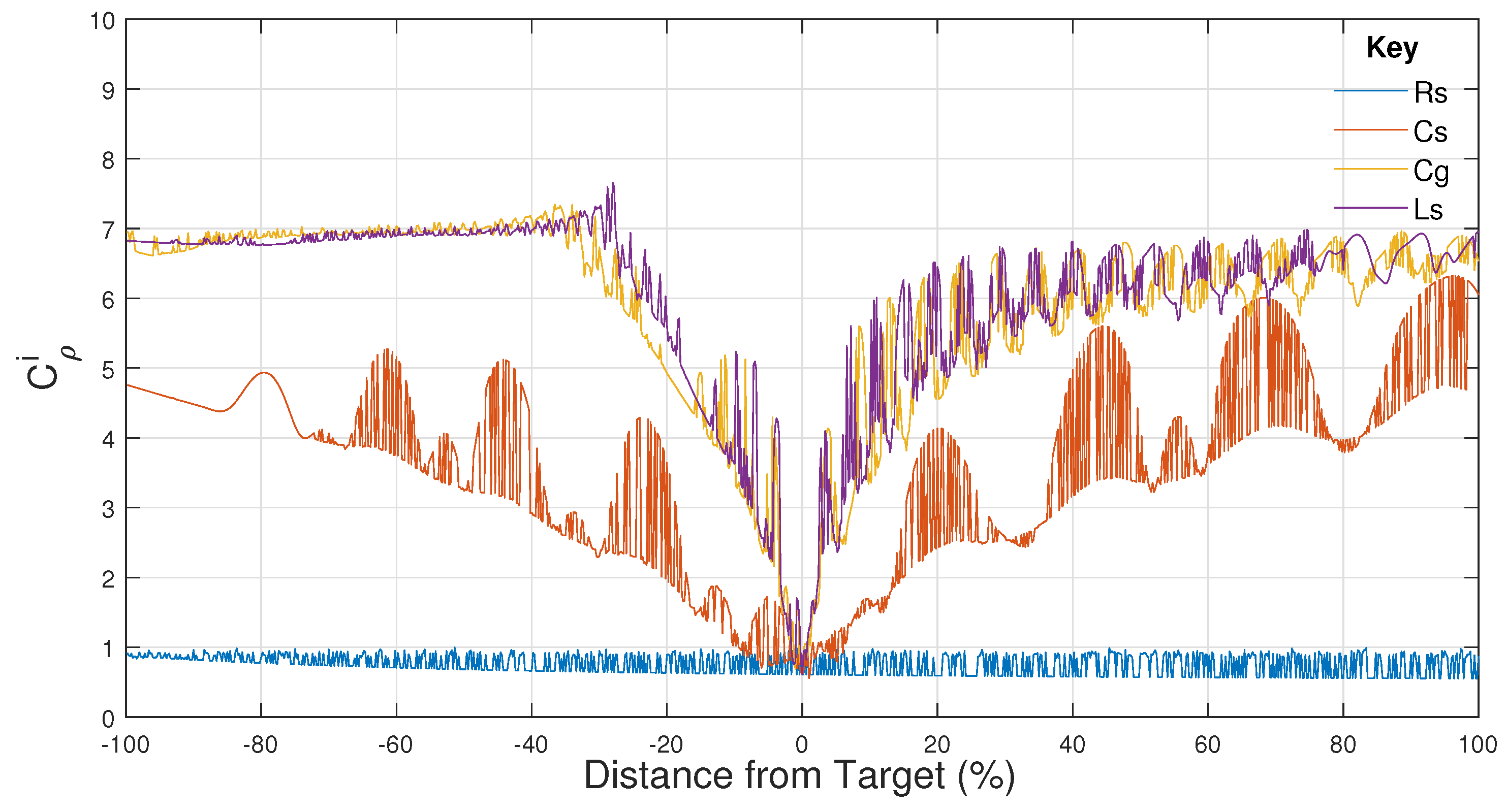

| Parameters | |||||||
|---|---|---|---|---|---|---|---|
| Lower Bound | 1 | 1 | 1 | 1 | 85 | 85 | 85 |
| Upper Bound | 1000 | 1000 | 1000 | 1000 | 95 | 95 | 95 |
| Approach | Frequency-Domain | |
|---|---|---|
| Cost Function | ||
| −242.50 | 45.23 | |
| −3.09 | −0.50 | |
| 0.67 | 37.50 | |
| 2.55 | −40.25 | |
| −8.83 | −3.73 | |
| 0.03 | -8.80 | |
| −5.29 | −6.70 | |
| Runtime (h) | 29.88 | 11.81 |
| Approach | Time-Domain | Empirical Mode Decomposition | Inferred Empirical Model Decomposition | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Alignment | Strategy 1 | Strategy 2 | Strategy 1 | Strategy 2 | Strategy 1 | Strategy 2 | ||||||
| Cost Function | ||||||||||||
| 1.14 | 83.13 | −392.75 | 4.62 | 36.90 | −941.37 | −575.99 | −395.22 | 1.14 | −84.61 | −392.63 | −101.221 | |
| −1.91 | 47.17 | −2.01 | −0.93 | −3.03 | 25.25 | −2.30 | −3.03 | −1.91 | 21.58 | 0.99 | 10.62 | |
| −0.59 | −723.11 | 1.30 | 8.31 | −59.55 | 37.50 | −33.19 | 34.50 | −0.59 | −3.74 | −0.17 | −1.45 | |
| 1.73 | 86.26 | 1.90 | −8.80 | 33.47 | −51.22 | 26.99 | −74.00 | 1.73 | −0.91 | 1.77 | 1.47 | |
| −4.78 | −4.85 | −3.60 | 2.31 | −5.03 | 0.42 | −5.03 | −5.66 | −4.78 | 0.67 | −1.15 | −2.24 | |
| −3.15 | −5.45 | 2.63 | 1.15 | 2.50 | −3.10 | −7.94 | 0.33 | −3.15 | 1.88 | −3.64 | 2.43 | |
| 0.53 | −8.03 | −8.63 | −4.93 | −0.50 | −0.41 | −6.46 | 0.65 | 0.53 | 0.74 | −3.66 | −6.36 | |
| Runtime (h) | 12.32 | 4.31 | 6.66 | 6.22 | 5.92 | 1.76 | 14.65 | 9.07 | 8.33 | 8.87 | 6.72 | 9.49 |
| Cost Function | ||
|---|---|---|
| Alignment | Strategy 1 | Strategy 2 |
| –52.55 | –133.64 | |
| 17.23 | 10.82 | |
| –3.28 | –2.11 | |
| 0.038 | 1.62 | |
| –2.35 | –6.63 | |
| 0.24 | 0.54 | |
| 0.73 | –2.99 | |
| Runtime (h) | 297.68 | 487.35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Banks, D.M.; Bekker, J.C.; Vermeulen, H.J. Investigating Empirical Mode Decomposition in the Parameter Estimation of a Three-Section Winding Model. Energies 2023, 16, 1668. https://doi.org/10.3390/en16041668
Banks DM, Bekker JC, Vermeulen HJ. Investigating Empirical Mode Decomposition in the Parameter Estimation of a Three-Section Winding Model. Energies. 2023; 16(4):1668. https://doi.org/10.3390/en16041668
Chicago/Turabian StyleBanks, Daniel Marc, Johannes Cornelius Bekker, and Hendrik Johannes Vermeulen. 2023. "Investigating Empirical Mode Decomposition in the Parameter Estimation of a Three-Section Winding Model" Energies 16, no. 4: 1668. https://doi.org/10.3390/en16041668
APA StyleBanks, D. M., Bekker, J. C., & Vermeulen, H. J. (2023). Investigating Empirical Mode Decomposition in the Parameter Estimation of a Three-Section Winding Model. Energies, 16(4), 1668. https://doi.org/10.3390/en16041668






