Insights into the Application of Machine Learning in Reservoir Engineering: Current Developments and Future Trends
Abstract
1. Introduction
2. Application Status of ML in Reservoir Engineering
2.1. Production Prediction
2.2. Well Test Analysis
2.3. Reservoir Characterization
3. Future Trends for ML in Reservoir Engineering
3.1. Data Quality and Quantity
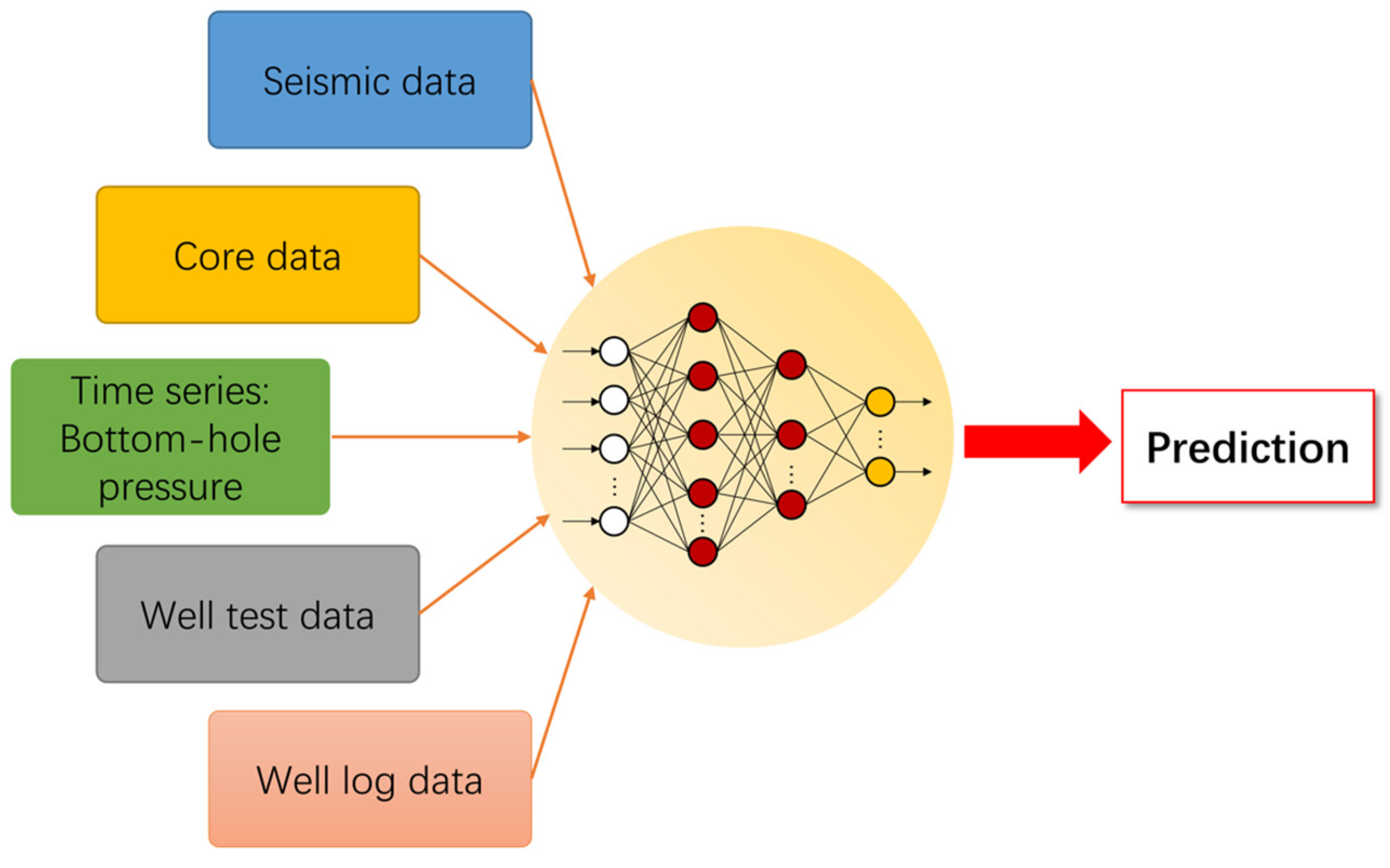
3.2. Fusion of Multiple Data Sources
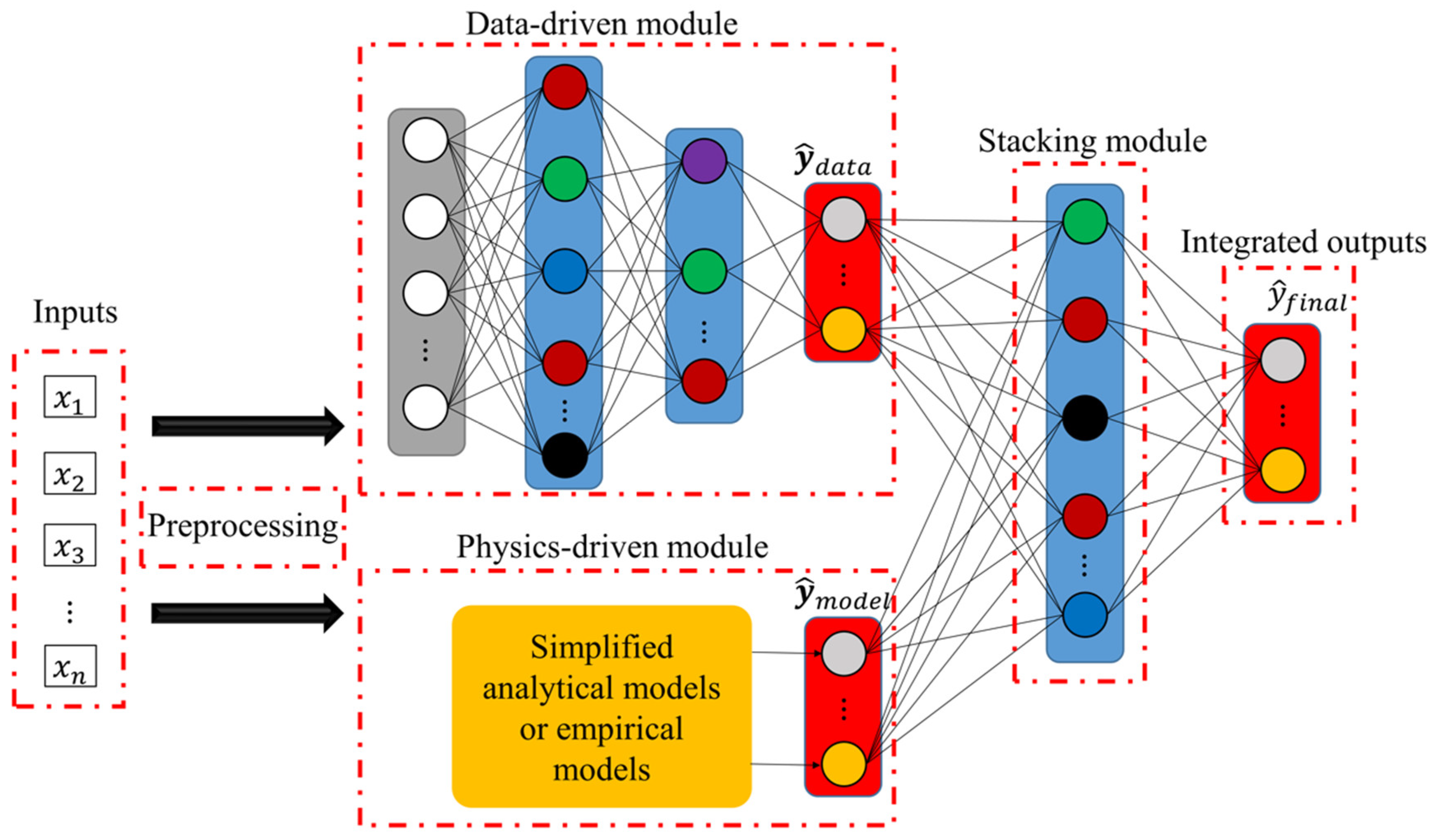
3.3. Coupling Physics Laws with ML
4. Conclusions
- Machine learning (ML) techniques have numerous applications in reservoir engineering with acceptable accuracy, including the estimation of reservoir properties, well test interpretation, and investigation of production behaviors.
- A variety of machine learning algorithms have been adopted in the field of reservoir engineering, among which neural networks (e.g., FCNN, RNN and its variant LSTM, CNNs) are the most popular models because of their powerful nonlinear mapping capacity and flexibility in addressing different data formats.
- The current application of ML in reservoir engineering is still in its infancy, and further research is needed to enhance the ability to draw reliable inferences from sparse data and to develop strategies for integrating data from multiple sources/formats.
- More attention should be given to the integration of physical laws with current data-driven models for the purpose of improving model interpretability and generalization, and PINN is a promising approach to address this problem.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Karniadakis, G.E.; Kevrekidis, I.G.; Lu, L.; Perdikaris, P.; Wang, S.; Yang, L. Physics-informed machine learning. Nat. Rev. Phys. 2021, 3, 422–440. [Google Scholar] [CrossRef]
- Choubey, S.; Karmakar, G.P. Artificial intelligence techniques and their application in oil and gas industry. Artif. Intell. Rev. 2021, 54, 3665–3683. [Google Scholar] [CrossRef]
- Jordan, M.I.; Mitchell, T.M. Machine learning: Trends, perspectives, and prospects. Science 2015, 349, 255–260. [Google Scholar] [CrossRef] [PubMed]
- Silver, D.; Schrittwieser, J.; Simonyan, K.; Antonoglou, I.; Huang, A.; Guez, A.; Hubert, T.; Baker, L.; Lai, M.; Bolton, A.; et al. Mastering the game of Go without human knowledge. Nature 2017, 550, 354–359. [Google Scholar] [CrossRef] [PubMed]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Noshi, C.I.; Schubert, J.J. The Role of Machine Learning in Drilling Operations; A Review. In Proceedings of the SPE/AAPG Eastern Regional Meeting, Pittsburgh, PA, USA, 7–11 October 2018. [Google Scholar] [CrossRef]
- Purbey, R.; Parijat, H.; Agarwal, D.; Mitra, D.; Agarwal, R.; Pandey, R.K.; Dahiya, A.K. Machine learning and data mining assisted petroleum reservoir engineering: A comprehensive review. Int. J. Oil Gas Coal Technol. 2022, 30, 359–387. [Google Scholar] [CrossRef]
- Graczyk, K.M.; Matyka, M. Predicting porosity, permeability, and tortuosity of porous media from images by deep learning. Sci. Rep. 2020, 10, 21488. [Google Scholar] [CrossRef]
- Hui, G.; Chen, S.; He, Y.; Wang, H.; Gu, F. Machine learning-based production forecast for shale gas in unconventional reservoirs via integration of geological and operational factors. J. Nat. Gas Sci. Eng. 2021, 94, 104045. [Google Scholar] [CrossRef]
- Liu, X.; Ge, Q.; Chen, X.; Li, J.; Chen, Y. Extreme learning machine for multivariate reservoir characterization. J. Pet. Sci. Eng. 2021, 205, 108869. [Google Scholar] [CrossRef]
- Bai, Y.; Berezovsky, V.; Popov, V. Digital core 3d reconstruction based on micro-CT images via a deep learning method. In Proceedings of the 2020 International Conference on High Performance Big Data and Intelligent Systems (HPBD&IS), Shenzhen, China, 23–25 May 2020; pp. 1–6. [Google Scholar]
- Xue, L.; Gu, S.; Mi, L.; Zhao, L.; Liu, Y.; Liao, Q. An automated data-driven pressure transient analysis of water-drive gas reservoir through the coupled machine learning and ensemble Kalman filter method. J. Pet. Sci. Eng. 2022, 208, 109492. [Google Scholar] [CrossRef]
- Wang, H.; Qiao, L.; Lu, S.; Chen, F.; Fang, Z.; He, X.; Zhang, J.; He, T. A Novel Shale Gas Production Prediction Model Based on Machine Learning and Its Application in Optimization of Multistage Fractured Horizontal Wells. Front. Earth Sci. 2021, 9, 726537. [Google Scholar] [CrossRef]
- Qiao, L.; Wang, H.; Lu, S.; Liu, Y.; He, T. Novel Self-Adaptive Shale Gas Production Proxy Model and Its Practical Application. ACS Omega 2022, 7, 8294–8305. [Google Scholar] [CrossRef]
- Wu, P.-Y.; Jain, V.; Kulkarni, M.S.; Abubakar, A. Machine learning–based method for automated well-log processing and interpretation. In Proceedings of the 2018 SEG International Exposition and Annual Meeting, Anaheim, CA, USA, 14–19 October 2018. [Google Scholar] [CrossRef]
- Jo, H.; Pan, W.; Santos, J.E.; Jung, H.; Pyrcz, M.J. Machine learning assisted history matching for a deepwater lobe system. J. Pet. Sci. Eng. 2021, 207, 109086. [Google Scholar] [CrossRef]
- Ray, S. A quick review of machine learning algorithms. In Proceedings of the 2019 International Conference on Machine Learning, Big Data, Cloud and Parallel Computing (COMITCon), Faridabad, India, 14–16 February 2019; pp. 35–39. [Google Scholar]
- Mahesh, B. Machine learning algorithms—A review. Int. J. Sci. Res. 2020, 9, 381–386. [Google Scholar]
- Wang, H.; Chen, Z.; Chen, S.; Hui, G.; Kong, B. Production forecast and optimization for parent-child well pattern in unconventional reservoirs. J. Pet. Sci. Eng. 2021, 203, 108899. [Google Scholar] [CrossRef]
- Chu, H.; Liao, X.; Dong, P.; Chen, Z.; Zhao, X.; Zou, J. An Automatic Classification Method of Well Testing Plot Based on Convolutional Neural Network (CNN). Energies 2019, 12, 2846. [Google Scholar] [CrossRef]
- Kong, B.; Chen, Z.; Chen, S.; Qin, T. Machine learning-assisted production data analysis in liquid-rich Duvernay Formation. J. Pet. Sci. Eng. 2021, 200, 108377. [Google Scholar] [CrossRef]
- Ibrahim, A.F.; Al-Dhaif, R.; Elkatatny, S.; Al Shehri, D. Machine Learning Applications to Predict Surface Oil Rates for High Gas Oil Ratio Reservoirs. J. Energy Resour. Technol. 2022, 144, 1–19. [Google Scholar] [CrossRef]
- Anifowose, F.; Abdulraheem, A.; Al-Shuhail, A. A parametric study of machine learning techniques in petroleum reservoir permeability prediction by integrating seismic attributes and wireline data. J. Pet. Sci. Eng. 2019, 176, 762–774. [Google Scholar] [CrossRef]
- Guo, Z.; Wang, H.; Kong, X.; Shen, L.; Jia, Y. Machine Learning-Based Production Prediction Model and Its Application in Duvernay Formation. Energies 2021, 14, 5509. [Google Scholar] [CrossRef]
- Duan, Y.; Wang, H.; Wei, M.; Tan, L.; Yue, T. Application of ARIMA-RTS optimal smoothing algorithm in gas well production prediction. Petroleum 2022, 8, 270–277. [Google Scholar] [CrossRef]
- Fan, D.; Sun, H.; Yao, J.; Zhang, K.; Yan, X.; Sun, Z. Well production forecasting based on ARIMA-LSTM model considering manual operations. Energy 2021, 220, 119708. [Google Scholar] [CrossRef]
- Song, X.; Liu, Y.; Xue, L.; Wang, J.; Zhang, J.; Wang, J.; Jiang, L.; Cheng, Z. Time-series well performance prediction based on Long Short-Term Memory (LSTM) neural network model. J. Pet. Sci. Eng. 2020, 186, 106682. [Google Scholar] [CrossRef]
- Zha, W.; Liu, Y.; Wan, Y.; Luo, R.; Li, D.; Yang, S.; Xu, Y. Forecasting monthly gas field production based on the CNN-LSTM model. Energy 2022, 260, 124889. [Google Scholar] [CrossRef]
- Nagaraj, G.; Pillai, P.; Kulkarni, M. Deep Similarity Learning for Well Test Model Identification. In Proceedings of the SPE Middle East Oil & Gas Show and Conference, Event Canceled. 28 November–1 December 2021. [Google Scholar] [CrossRef]
- Wang, S.; Chen, S. Application of the long short-term memory networks for well-testing data interpretation in tight reservoirs. J. Pet. Sci. Eng. 2019, 183, 106391. [Google Scholar] [CrossRef]
- Li, D.; Liu, X.; Zha, W.; Yang, J.; Lu, D. Automatic well test interpretation based on convolutional neural network for a radial composite reservoir. Pet. Explor. Dev. 2020, 47, 623–631. [Google Scholar] [CrossRef]
- Liu, X.; Li, D.; Yang, J.; Zha, W.; Zhou, Z.; Gao, L.; Han, J. Automatic well test interpretation based on convolutional neural network for infinite reservoir. J. Pet. Sci. Eng. 2020, 195, 107618. [Google Scholar] [CrossRef]
- Dong, P.; Chen, Z.; Liao, X.; Yu, W. Application of deep learning on well-test interpretation for identifying pressure behavior and characterizing reservoirs. J. Pet. Sci. Eng. 2022, 208, 109264. [Google Scholar] [CrossRef]
- Zhou, W.; Gupta, S.; Banerjee, R.; Poe, B.; Spath, J.; Thambynayagam, M. Production forecasting and analysis for unconventional resources. In Proceedings of the International Petroleum Technology Conference, Beijing, China, 26–28 March 2013. [Google Scholar]
- Khan, M.R.; Alnuaim, S.; Tariq, Z.; Abdulraheem, A. Machine Learning Application for Oil Rate Prediction in Artificial Gas Lift Wells. In Proceedings of the SPE Middle East Oil and Gas Show and Conference, Manama, Bahrain, 18–21 March 2019. [Google Scholar] [CrossRef]
- Wang, W.; Wong, A.K. Autoregressive Model-Based Gear Fault Diagnosis. J. Vib. Acoust. 2002, 124, 172–179. [Google Scholar] [CrossRef]
- Lee, N.-U.; Shim, J.-S.; Ju, Y.-W.; Park, S.-C. Design and implementation of the SARIMA–SVM time series analysis algorithm for the improvement of atmospheric environment forecast accuracy. Soft Comput. 2018, 22, 4275–4281. [Google Scholar] [CrossRef]
- Valipour, M.; Banihabib, M.E.; Behbahani, S.M.R. Comparison of the ARMA, ARIMA, and the autoregressive artificial neural network models in forecasting the monthly inflow of Dez dam reservoir. J. Hydrol. 2013, 476, 433–441. [Google Scholar] [CrossRef]
- Tadjer, A.; Hong, A.; Bratvold, R.B. Machine learning based decline curve analysis for short-term oil production forecast. Energy Explor. Exploit. 2021, 39, 1747–1769. [Google Scholar] [CrossRef]
- Zhong, Z.; Sun, A.Y.; Wang, Y.; Ren, B. Predicting field production rates for waterflooding using a machine learning-based proxy model. J. Pet. Sci. Eng. 2020, 194, 107574. [Google Scholar] [CrossRef]
- Horne, R.N. Modern Well Test Analysis; Petroway Inc.: Palo Alto, CA, USA, 1995; p. 926. [Google Scholar]
- Bourdet, D. Well Test Analysis: The Use of Advanced Interpretation Models; Elsevier: Amsterdam, The Netherlands, 2002. [Google Scholar]
- Shun, L.; Feng-Rui, H.; Kai, Z.; Ze-Wei, T. Well Test Interpretation Model on Power-law Non-linear Percolation Pattern in Low-permeability Reservoirs. In Proceedings of the International Oil and Gas Conference and Exhibition in China, Beijing, China, 8–10 June 2010. [Google Scholar] [CrossRef]
- Bourdet, D.; Ayoub, J.A.; Plrard, Y.M. Use of Pressure Derivative in Well-Test Interpretation. SPE Form. Eval. 1989, 4, 293–302. [Google Scholar] [CrossRef]
- Pandey, R.K.; Aggarwal, S.; Nath, G.; Kumar, A.; Vaferi, B. Metaheuristic algorithm integrated neural networks for well-test analyses of petroleum reservoirs. Sci. Rep. 2022, 12, 16551. [Google Scholar] [CrossRef]
- Anifowose, F.A.; Labadin, J.; Abdulraheem, A. Hybrid intelligent systems in petroleum reservoir characterization and modeling: The journey so far and the challenges ahead. J. Pet. Explor. Prod. Technol. 2017, 7, 251–263. [Google Scholar] [CrossRef]
- Vallabhaneni, S.; Saraf, R.; Priyadarshy, S. Machine-Learning-Based Petrophysical Property Modeling. In Proceedings of the SPE Europec Featured at 81st EAGE Conference and Exhibition, London, UK, 3–6 June 2019. [Google Scholar]
- Grana, D.; Azevedo, L.; Liu, M. A comparison of deep machine learning and Monte Carlo methods for facies classification from seismic data. Geophysics 2020, 85, WA41–WA52. [Google Scholar] [CrossRef]
- Liu, M.; Nivlet, P.; Smith, R.; BenHasan, N.; Grana, D. Recurrent neural network for seismic reservoir characterization. In Advances in Subsurface Data Analytics; Elsevier: Amsterdam, The Netherlands, 2022; pp. 95–116. [Google Scholar] [CrossRef]
- Feng, R.; Hansen, T.M.; Grana, D.; Balling, N. An unsupervised deep-learning method for porosity estimation based on poststack seismic dataDeep learning for porosity estimation. Geophysics 2020, 85, M97–M105. [Google Scholar] [CrossRef]
- Lee, J.; Lumley, D.E.; Lim, U.Y. Improving total organic carbon estimation for unconventional shale reservoirs using Shapley value regression and deep machine learning methods. AAPG Bull. 2022, 106, 2297–2314. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, L.; Pan, J.; Li, C.; Li, K.; Zhang, F.; Geng, J. Machine learning based deep carbonate reservoir characterization with physical constraints. In Proceedings of the 82nd EAGE Annual Conference & Exhibition, Online, 18–21 October 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Feng, R. Estimation of reservoir porosity based on seismic inversion results using deep learning methods. J. Nat. Gas Sci. Eng. 2020, 77, 103270. [Google Scholar] [CrossRef]
- Saikia, P.; Baruah, R.D.; Singh, S.K.; Chaudhuri, P.K. Artificial Neural Networks in the domain of reservoir characterization: A review from shallow to deep models. Comput. Geosci. 2020, 135, 104357. [Google Scholar] [CrossRef]
- Chaki, S.; Routray, A.; Mohanty, W.K. Well-Log and Seismic Data Integration for Reservoir Characterization: A Signal Processing and Machine-Learning Perspective. IEEE Signal Process. Mag. 2018, 35, 72–81. [Google Scholar] [CrossRef]
- Katterbauer, K.; Qasim, A.; Al Shehri, A.; Al Zaidy, R. A Deep Learning Formation Image Log Classification Framework for Fracture Identification—A Study on Carbon Dioxide Injection Performance for the New Zealand Pohokura Field. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 3–5 October 2022. [Google Scholar] [CrossRef]
- Tian, X.; Daigle, H. Machine-learning-based object detection in images for reservoir characterization: A case study of fracture detection in shales. Lead Edge 2018, 37, 435–442. [Google Scholar] [CrossRef]
- Le Ravalec, M.; Nouvelles, I.E.; Doligez, B.; Lerat, O. Integrated Reservoir Characterization and Modeling; IFP Energies Nouvelles: Rueil-Malmaison, France, 2014. [Google Scholar] [CrossRef]
- Abdi, Y. Integrated reservoir characterization and modeling of one Iranian naturally fractured reservoir using laboratory and field data. In Proceedings of the SPE/EAGE Reservoir Characterization and Simulation Conference, Abu Dhabi, United Arab Emirates, 28–31 October 2007. [Google Scholar]
- Priezzhev, I.; Stanislav, E. Application of Machine Learning Algorithms Using Seismic Data and Well Logs to Predict Reservoir Properties. In Proceedings of the 80th EAGE Conference and Exhibition 2018, Copenhagen, Denmark, 11–14 June 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Dixit, N.; McColgan, P.; Kusler, K. Machine Learning-Based Probabilistic Lithofacies Prediction from Conventional Well Logs: A Case from the Umiat Oil Field of Alaska. Energies 2020, 13, 4862. [Google Scholar] [CrossRef]
- Polyzotis, N.; Zinkevich, M.; Roy, S.; Breck, E.; Whang, S. Data validation for machine learning. Proc. Mach. Learn. Syst. 2019, 1, 334–347. [Google Scholar]
- Gudivada, V.; Apon, A.; Ding, J. Data quality considerations for big data and machine learning: Going beyond data cleaning and transformations. Int. J. Adv. Softw. 2017, 10, 1–20. [Google Scholar]
- Konečný, J.; McMahan, H.B.; Yu, F.X.; Richtárik, P.; Suresh, A.T.; Bacon, D. Federated learning: Strategies for improving communication efficiency. arXiv 2016, arXiv:1610.05492. [Google Scholar]
- Weiss, K.; Khoshgoftaar, T.M.; Wang, D.D. A survey of transfer learning. J. Big Data 2016, 3, 9. [Google Scholar] [CrossRef]
- Wang, Y.; Yao, Q.; Kwok, J.T.; Ni, L.M. Generalizing from a few examples: A survey on few-shot learning. ACM Comput. Surv. 2020, 53, 63. [Google Scholar] [CrossRef]
- Razak, S.M.; Cornelio, J.; Cho, Y.; Liu, H.-H.; Vaidya, R.; Jafarpour, B. Transfer Learning with Recurrent Neural Networks for Long-Term Production Forecasting in Unconventional Reservoirs. SPE J. 2022, 27, 2425–2442. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Willard, J.; Jia, X.; Xu, S.; Steinbach, M.; Kumar, V. Integrating physics-based modeling with machine learning: A survey. arXiv 2020, arXiv:2003.04919. [Google Scholar]
- Lu, L.; Meng, X.; Mao, Z.; Karniadakis, G.E. DeepXDE: A Deep Learning Library for Solving Differential Equations. SIAM Rev. 2021, 63, 208–228. [Google Scholar] [CrossRef]
- Zhang, L.; Han, J.; Wang, H.; Saidi, W.; Car, R. End-to-end symmetry preserving inter-atomic potential energy model for finite and extended systems. In Proceedings of the 32nd Conference on Neural Information Processing Systems (NeurIPS 2018), Montréal, QC, Canada, 3–8 December 2018. [Google Scholar]

| Model | Application | Reference | Advantage |
|---|---|---|---|
| LR | Cumulative production forecast | [19] | Easy to implement and interpret |
| FCNN | Well test interpretation | [20] | Powerful non-linear mapping capacity; flexibility in various tasks; good generalization |
| XGBoost | Cumulative production forecast | [21] | High accuracy; robust; missing values are acceptable |
| RF | Water invasion pattern identification; properties estimation | [12] | Parallelizable; robust |
| SVM | Surface oil rates prediction; permeability estimation | [22,23] | Robust to noise; Effective for small datasets |
| GPR | Early oil and gas production | [24] | Probabilistic approach; uncertainty estimation; Prior knowledge included |
| ARIMA | Production dynamics | [25,26] | Interpretability; applicable to multiple temporal patterns; |
| LSTM | Production dynamics; reservoir models identification; | [27,28,29,30] | Capture long-term dependencies; powerful non-linear mapping capacity |
| CNN | Well test interpretation; production dynamics | [28,31,32,33] | Capture spatial dependencies; translation invariance |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Chen, S. Insights into the Application of Machine Learning in Reservoir Engineering: Current Developments and Future Trends. Energies 2023, 16, 1392. https://doi.org/10.3390/en16031392
Wang H, Chen S. Insights into the Application of Machine Learning in Reservoir Engineering: Current Developments and Future Trends. Energies. 2023; 16(3):1392. https://doi.org/10.3390/en16031392
Chicago/Turabian StyleWang, Hai, and Shengnan Chen. 2023. "Insights into the Application of Machine Learning in Reservoir Engineering: Current Developments and Future Trends" Energies 16, no. 3: 1392. https://doi.org/10.3390/en16031392
APA StyleWang, H., & Chen, S. (2023). Insights into the Application of Machine Learning in Reservoir Engineering: Current Developments and Future Trends. Energies, 16(3), 1392. https://doi.org/10.3390/en16031392







