Economic Optimization Control Method of Grid-Connected Microgrid Based on Improved Pinning Consensus
Abstract
:1. Introduction
- To establish the economic optimization model of grid-connected microgrids based on MAS.
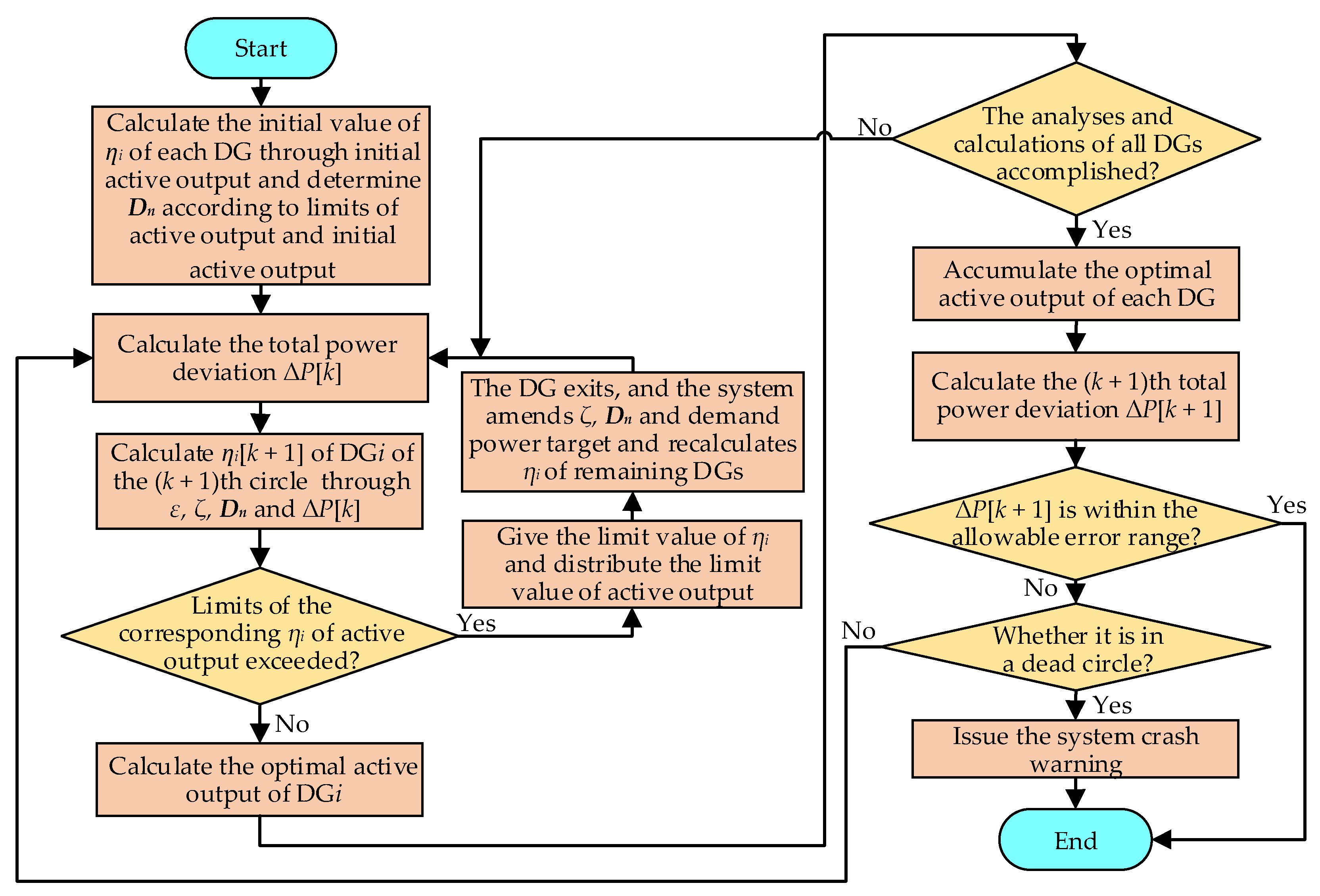
- To propose an improved pinning consensus algorithm based on ICR, quickly eliminating the total power deviation and achieving the convergence of ICR to reference value.
- To construct a distributed hierarchical control architecture and put forward an economic optimization control method of grid-connected microgrids based on improved pinning consensus. The impact of grid electricity price, pinning coefficient, power deviation elimination term coefficient, communication connection topology, DG plug-and-play, initial condition, and DLR constraint on control performance and operation state of the system is simulated. It is proven that the proposed method still possesses the superior overall response performance and can achieve the goal of economic optimization under the influence of different factors.
2. Economic Optimization Model of Grid-Connected Microgrid
3. Improved Pinning Consensus Algorithm Based on ICR
3.1. Traditional Mean Consensus and Pinning Consensus
3.2. Improved Pinning Consensus Algorithm Based on ICR
4. Distributed Hierarchical Optimization Control Method
5. Experiments and Analyses
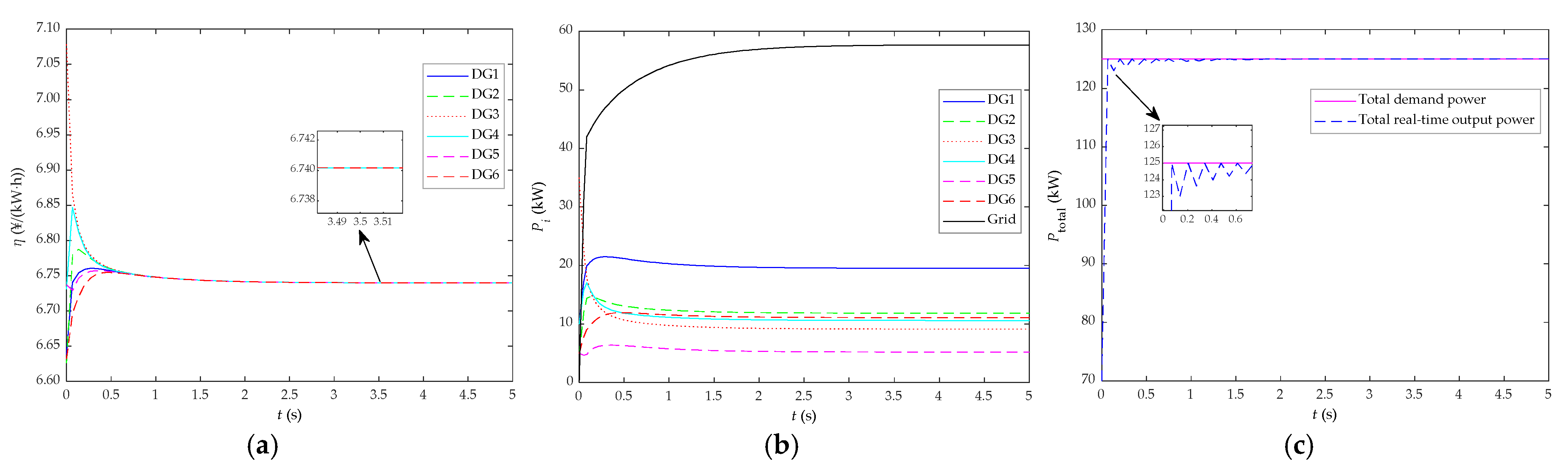
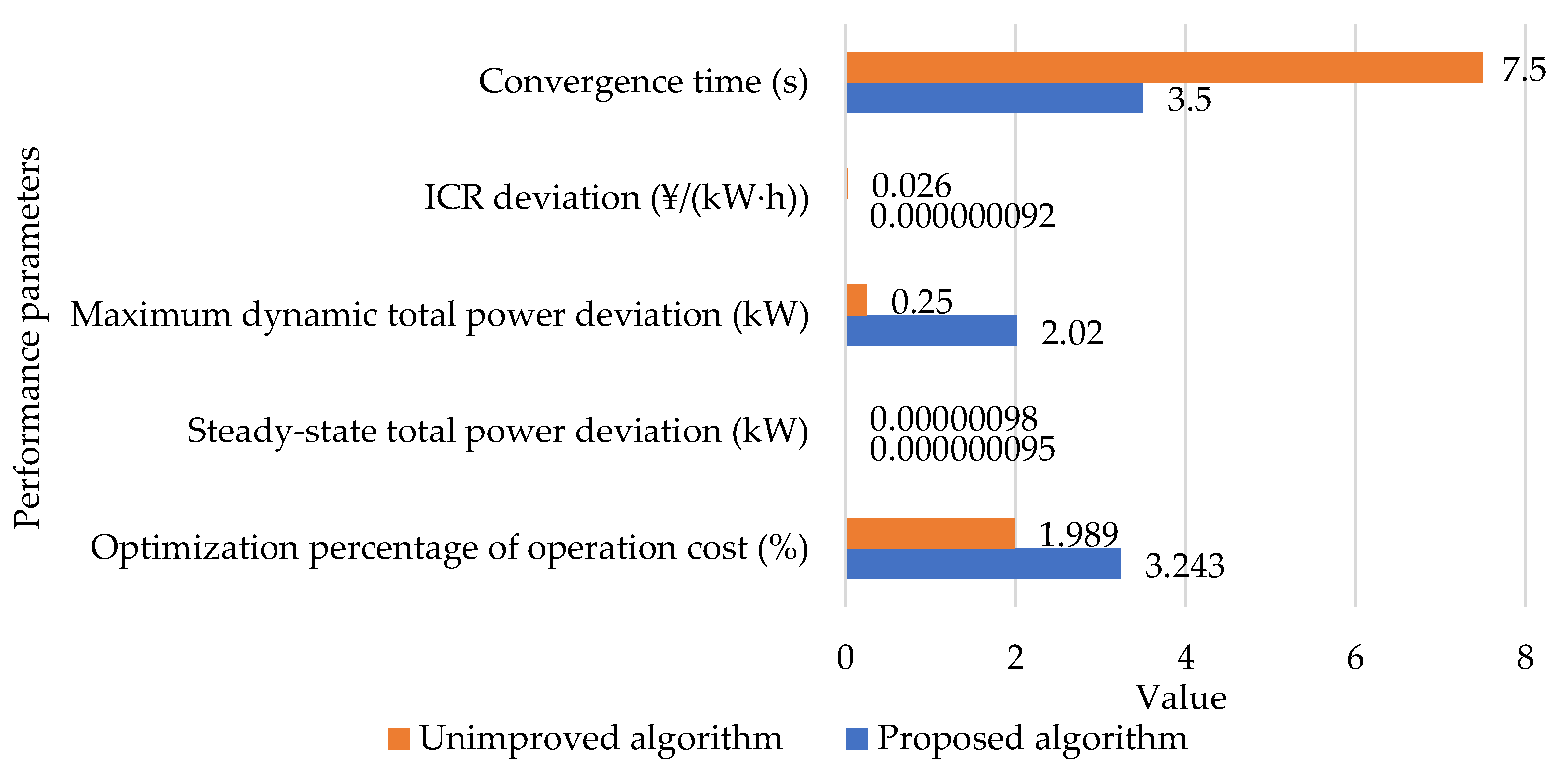
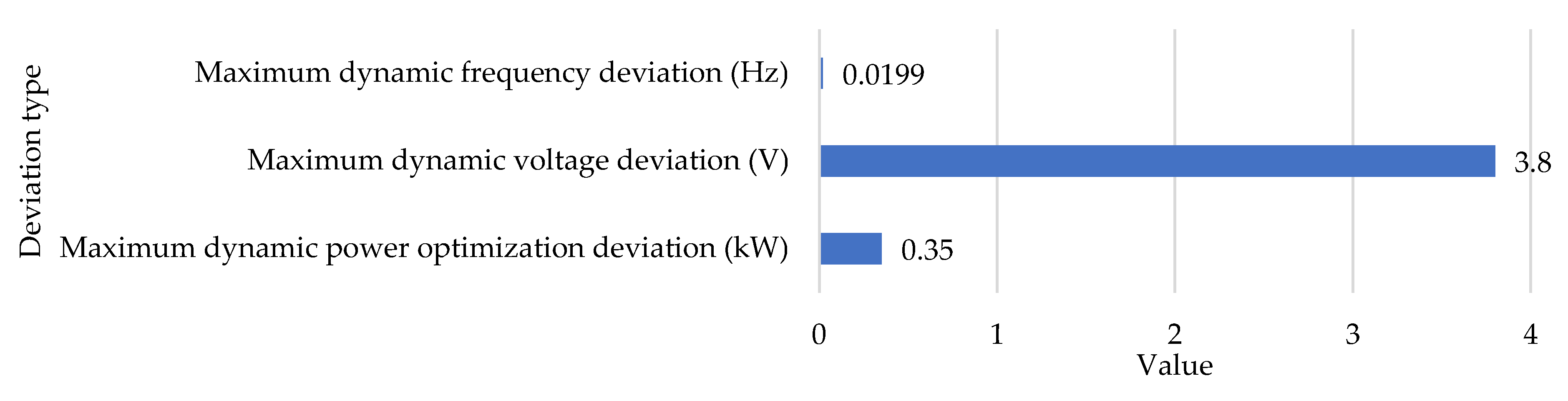
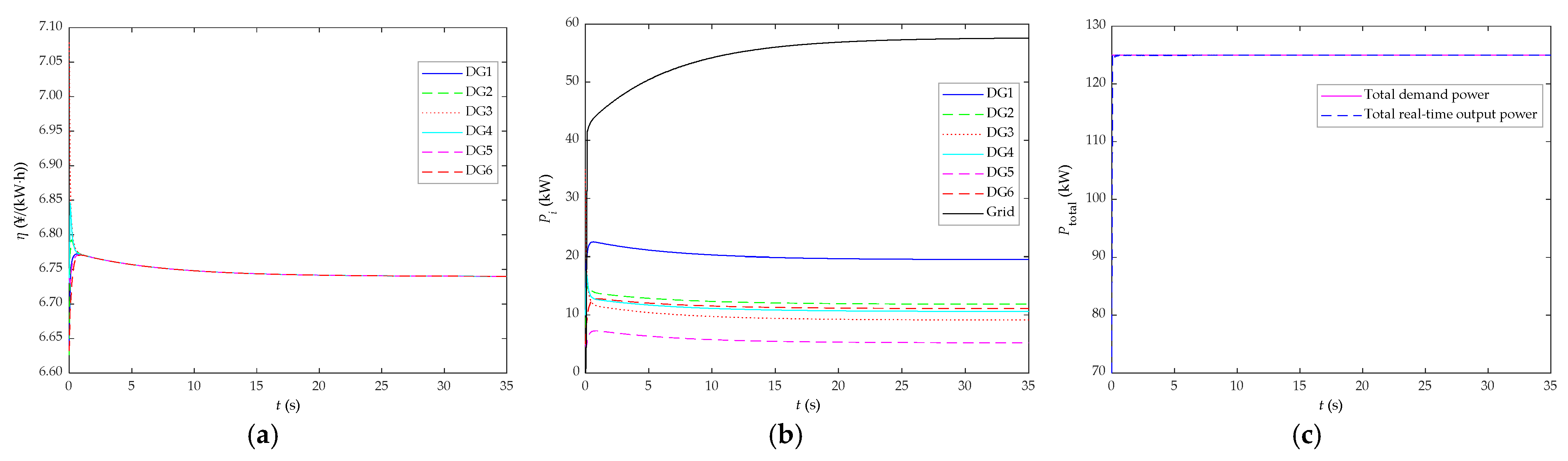
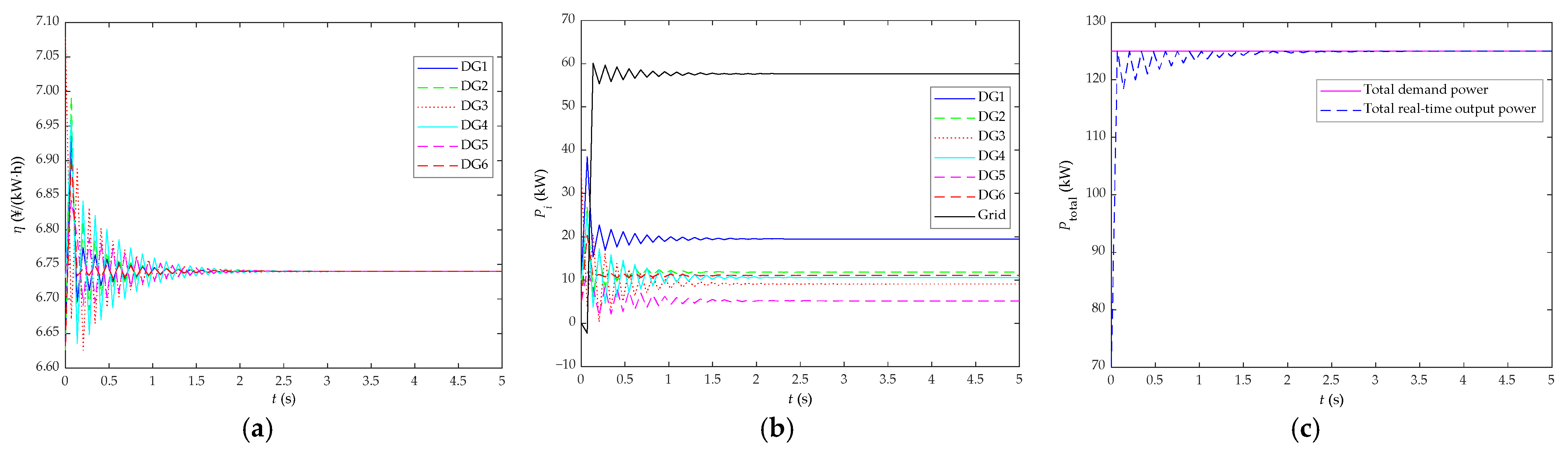
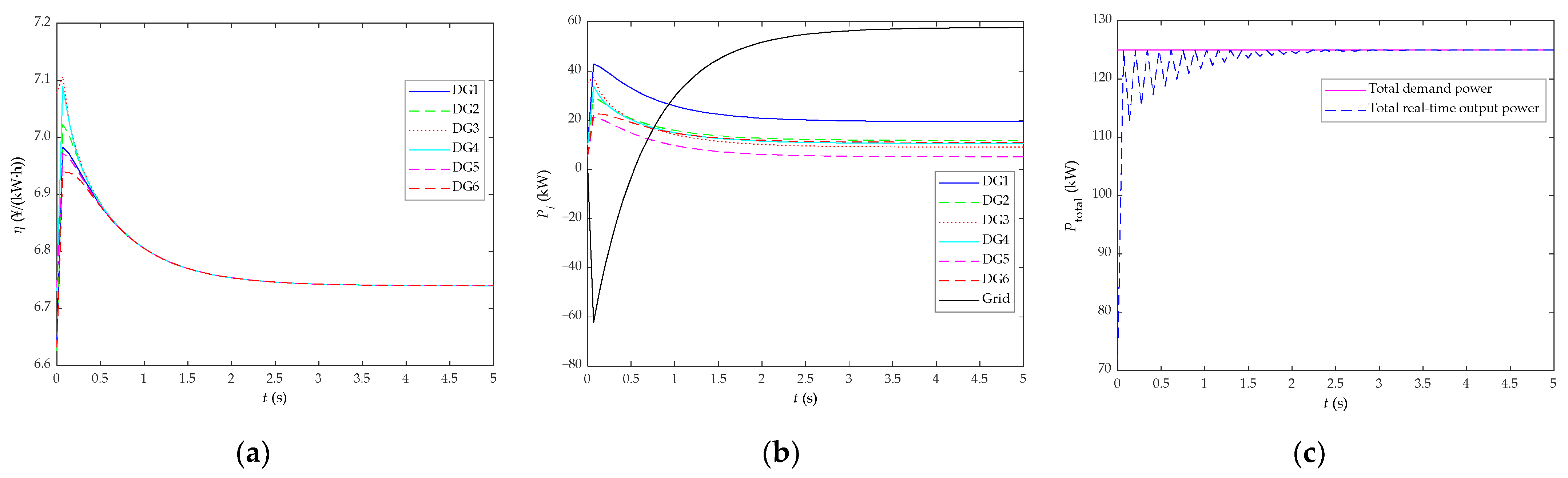
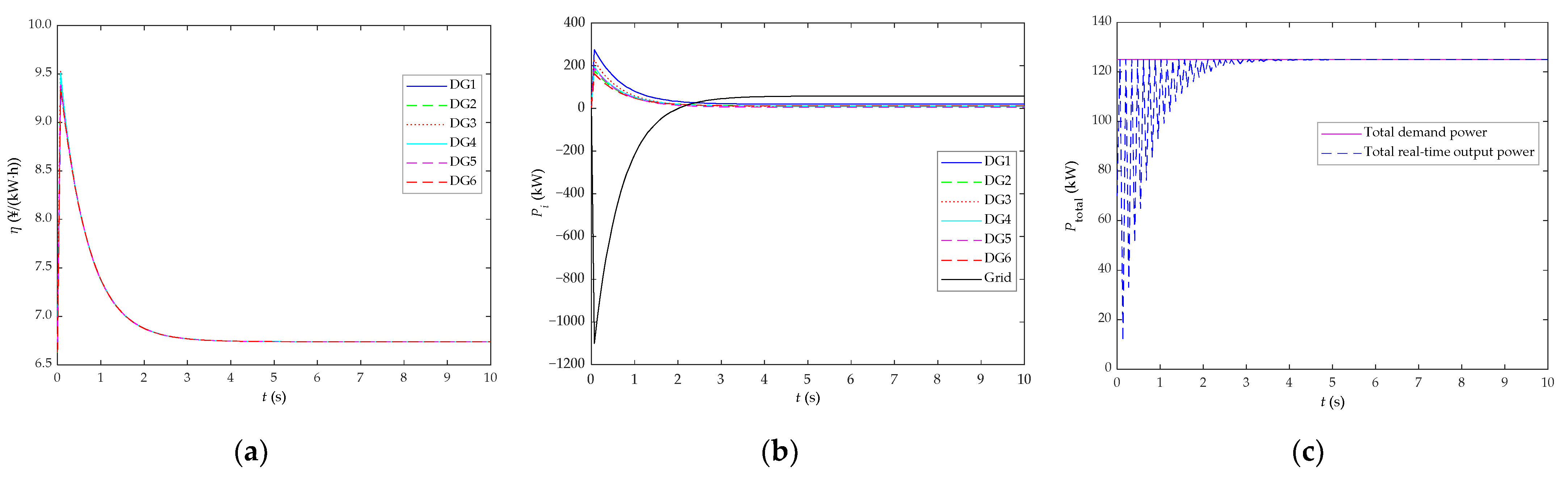
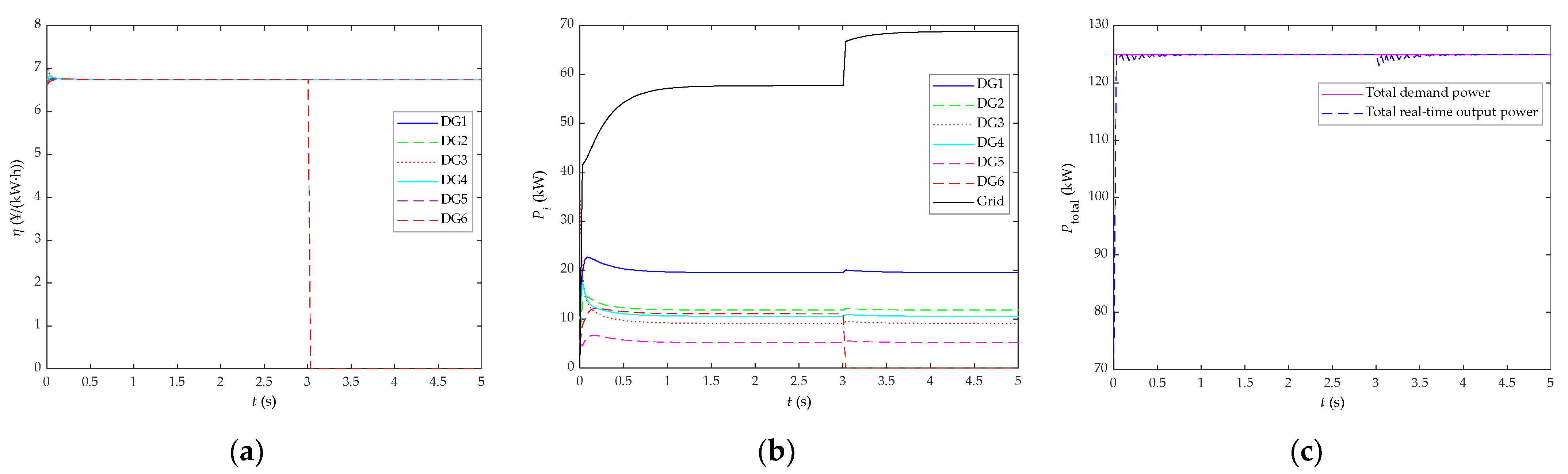
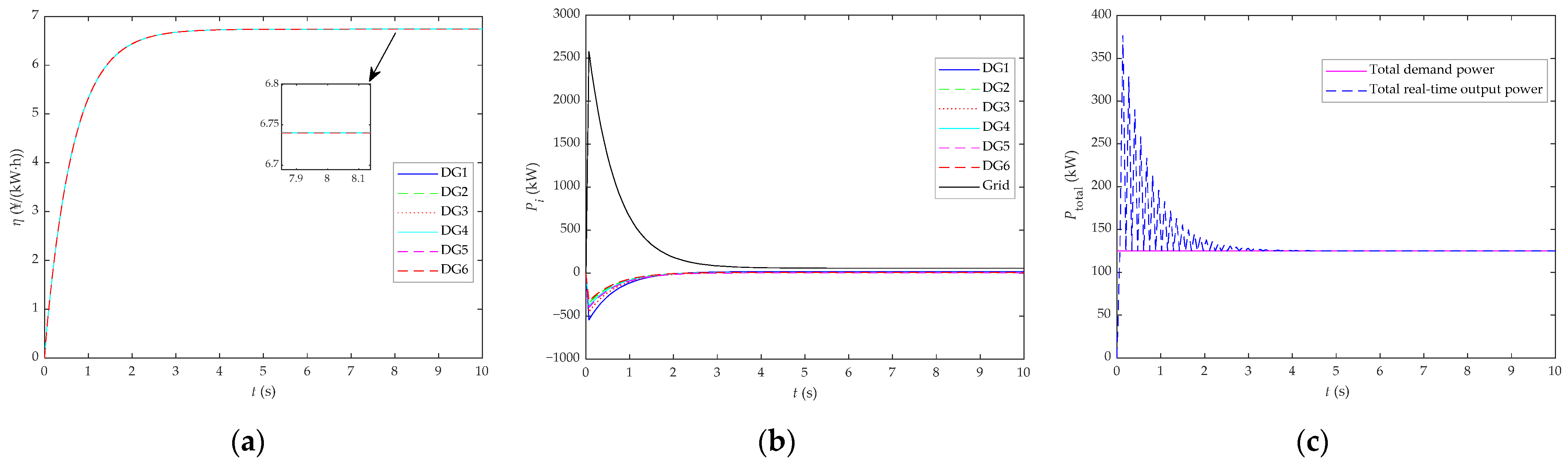
5.1. Comparative Analysis before/after Algorithm Improvement and Research on the Load Response Performance
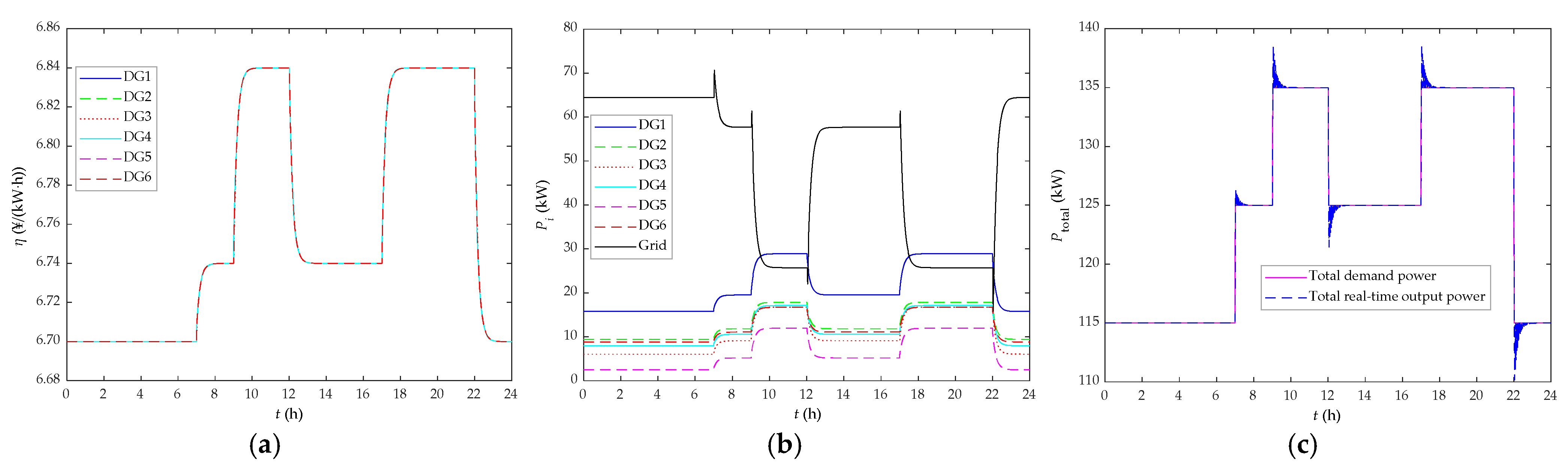
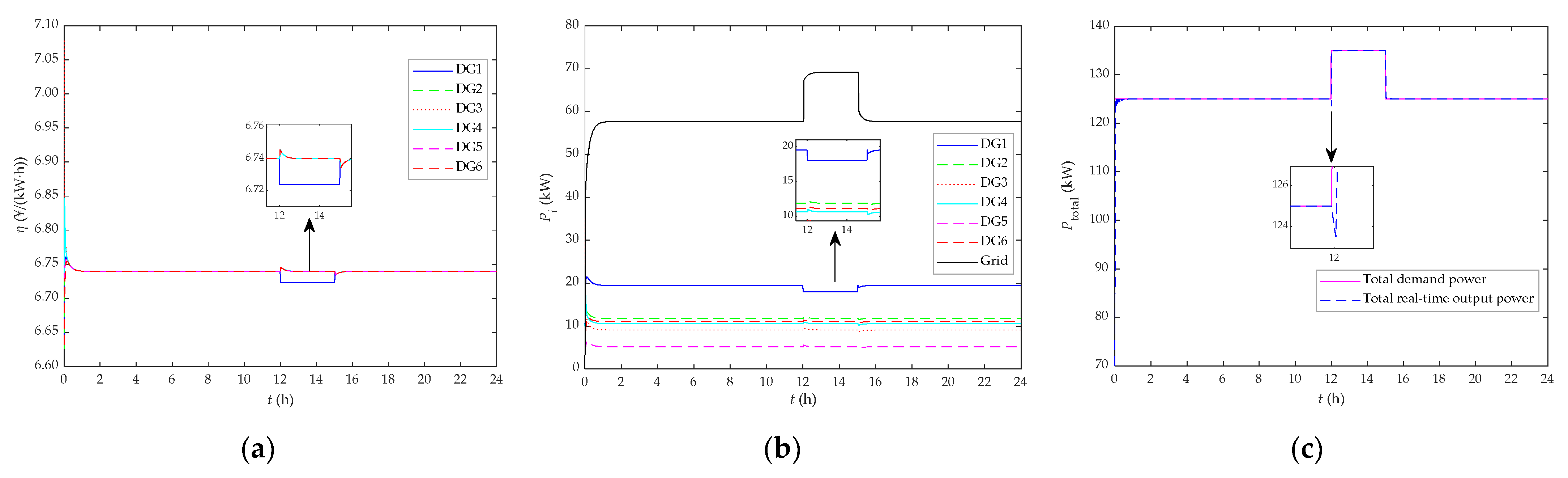
5.2. Research on the Effect of TOUP of Whole Day
5.3. Research on the Effect of Pinning Coefficient ζ
5.4. Research on the Effect of Power Deviation Elimination Term Coefficient ε
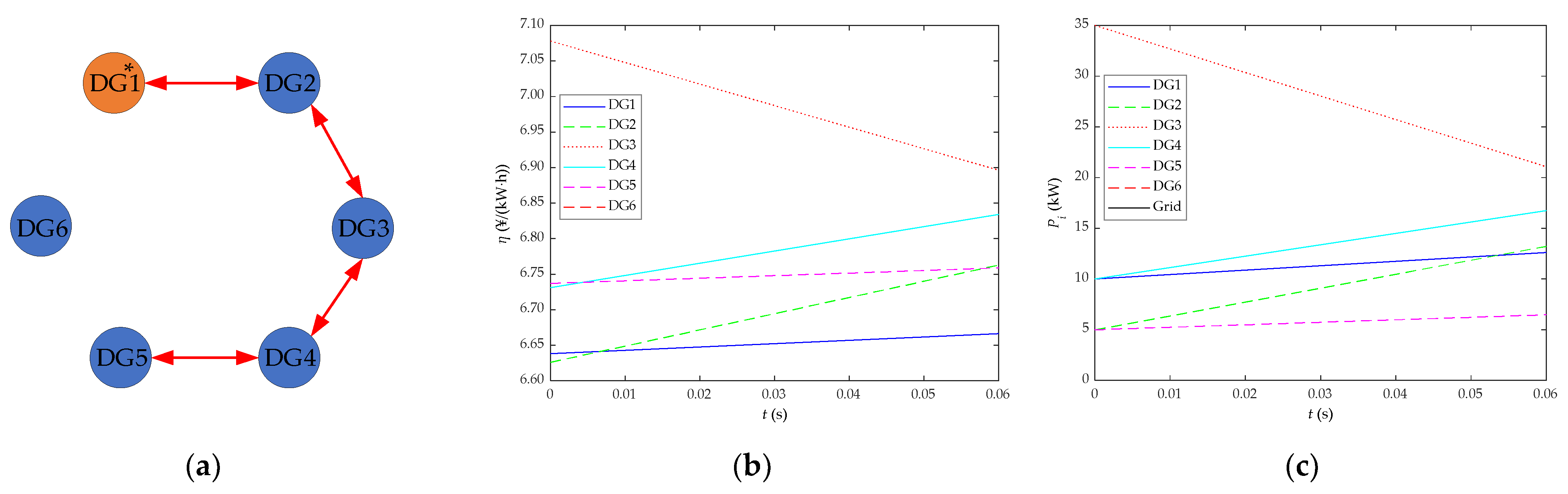
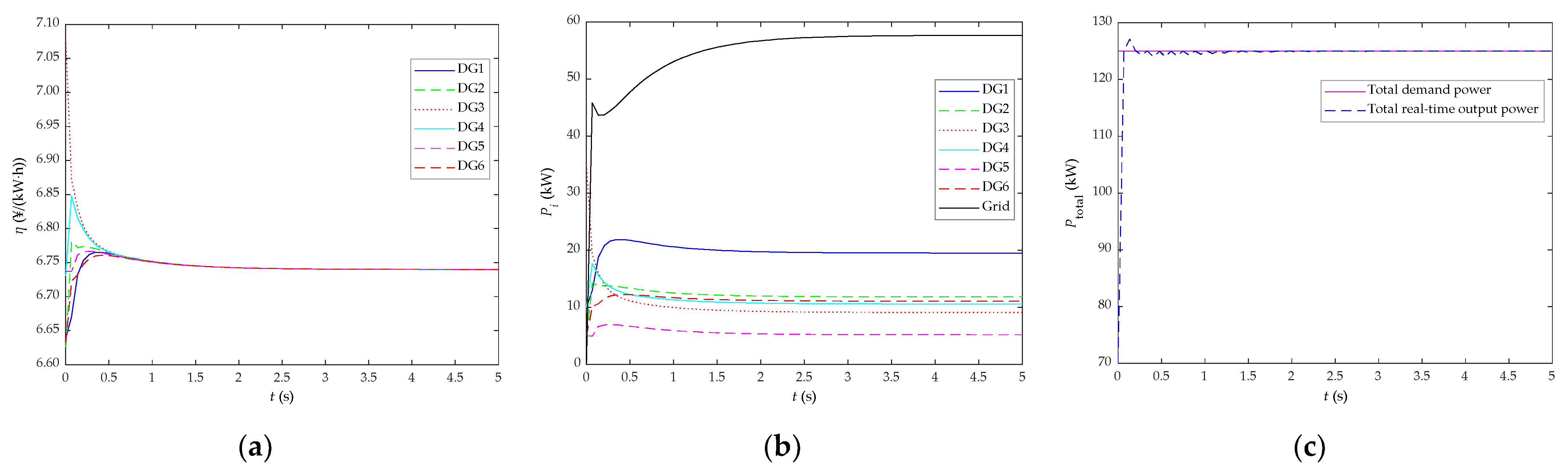
5.5. Research on the Effect of Communication Topology Change
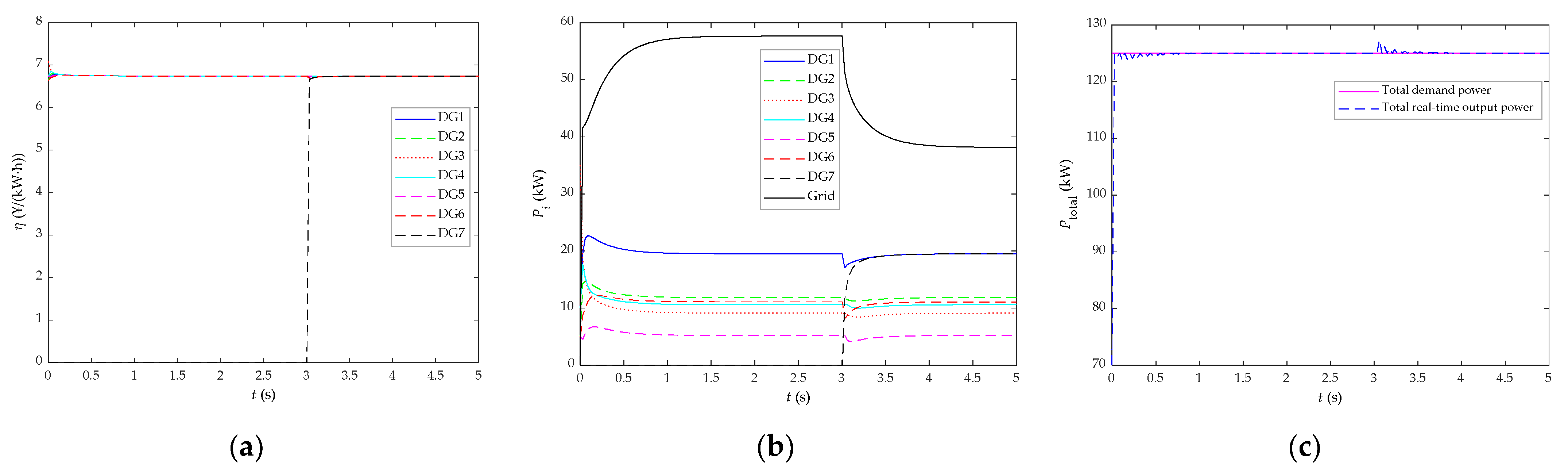
5.6. Research on the Effect of DG Plug-of-Play
5.7. Research on the Effect of Initial Condition
5.8. Research on the Effect of DLR
6. Discussions
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AT | Ambient Temperature |
| BESS | Battery Energy Storage System |
| DG | Distributed Generation |
| DLR | Dynamic Line Rating |
| ETESs | Electric-Thermal Energy Storages |
| ICR | Incremental Cost Rate |
| MAS | Multi-Agent System |
| TOUP | Time-of-Use Price |
References
- Wang, J.J.; Dong, C.Y.; Jin, C. Distributed Uniform Control for Parallel Bidirectional Interlinking Converters for Resilient Operation of Hybrid AC/DC Microgrid. IEEE Trans. Sustain. Energy 2022, 13, 3–13. [Google Scholar]
- Jabr, R.A. Economic Operation of Droop-Controlled AC Microgrids. IEEE Trans. Power Syst. 2022, 37, 3119–3128. [Google Scholar] [CrossRef]
- Chen, C.; Duan, S. Microgrid Economic Operation Considering Plug-in Hybrid Electric Vehicles Integration. J. Mod. Power Syst. Clean Energy 2015, 3, 221–231. [Google Scholar] [CrossRef] [Green Version]
- Nisha, K.S.; Gaonkar, D.N. Model Predictive Controlled Three-Level Bidirectional Converter with Voltage Balancing Capability for Setting up EV Fast Charging Stations in Bipolar DC Microgrid. Electr. Eng. 2022, 104, 2653–2665. [Google Scholar] [CrossRef]
- Zhang, J.; Qin, D.; Ye, Y. Multi-Time Scale Economic Scheduling Method Based on Day-Ahead Robust Optimization and Intraday MPC Rolling Optimization for Microgrid. IEEE Access 2021, 9, 140315–140324. [Google Scholar] [CrossRef]
- Dey, B.; Basak, S.; Pal, A. Demand-Side Management Based Optimal Scheduling of Distributed Generators for Clean and Economic Operation of a Microgrid System. Int. J. Energy Res. 2022, 46, 8817–8837. [Google Scholar] [CrossRef]
- Akbari, R.; Tajalli, S.Z.; Kavousi-Fard, A. Economic Operation of Utility-Connected Microgrids in a Fast and Flexible Framework Considering Non-Dispatchable Energy Sources. Energies 2022, 15, 2894. [Google Scholar]
- Lyu, C.; Jia, Y.; Xu, Z. A Novel Communication-Less Approach to Economic Dispatch for Microgrids. IEEE Trans. Smart Grid 2021, 12, 901–904. [Google Scholar] [CrossRef]
- Zhao, C.; Sun, W.; Wang, J.; Fang, Z. Distributed Robust Secondary Voltage Control for Islanded Microgrid with Nonuniform Time Delays. Electr. Eng. 2021, 103, 2625–2635. [Google Scholar]
- Li, Y.; Yang, Z.; Li, G.; Zhao, D.; Tian, W. Optimal Scheduling of an Isolated Microgrid with Battery Storage Considering Load and Renewable Generation Uncertainties. IEEE Trans. Ind. Electron. 2019, 66, 1565–1575. [Google Scholar] [CrossRef] [Green Version]
- Harsh, P.; Das, D. Optimal Coordination Strategy of Demand Response and Electric Vehicle Aggregators for the Energy Management of Reconfigured Grid-Connected Microgrid. Renew. Sustain. Energy Rev. 2022, 160, 112251. [Google Scholar] [CrossRef]
- Zhang, Y.; Liang, C.; Shi, J.; Lim, G.; Wu, Y. Optimal Port Microgrid Scheduling Incorporating Onshore Power Supply and Berth Allocation Under Uncertainty. Appl. Energy 2022, 313, 118856. [Google Scholar] [CrossRef]
- Yang, M.; Cui, Y.; Wang, J. Multi-Objective Optimal Scheduling of Island Microgrids Considering the Uncertainty of Renewable Energy Output. Int. J. Electr. Power Energy Syst. 2023, 144, 108619. [Google Scholar] [CrossRef]
- Das, D.; Hossain, M.J.; Mishra, S. Bidirectional Power Sharing of Modular Dabs to Improve Voltage Stability in DC Microgrids. IEEE Trans. Ind. Appl. 2022, 58, 2369–2377. [Google Scholar] [CrossRef]
- Pham, X.H.T. An Improved Controller for Reactive Power Sharing in Islanded Microgrid. Electr. Eng. 2021, 103, 1679–1689. [Google Scholar] [CrossRef]
- Alghamdi, B.; Claudio, C. Frequency and Voltage Coordinated Control of a Grid of AC/DC Microgrids. Appl. Energy 2022, 310, 118427. [Google Scholar] [CrossRef]
- Dashtaki, A.A.; Hakimi, S.M.; Hasankhani, A.; Derakhshani, G.; Abdi, B. Optimal Management Algorithm of Microgrid Connected to the Distribution Network Considering Renewable Energy System Uncertainties. Int. J. Electr. Power Energy Syst. 2023, 145, 108633. [Google Scholar] [CrossRef]
- Guo, J.; Meng, Z.; Chen, Y. Harmonic Transfer-Function-Based αβ-Frame SISO Impedance Modeling of Droop Inverters-Based Islanded Microgrid with Unbalanced Loads. IEEE Trans. Ind. Electron. 2023, 70, 452–464. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, Y.; Li, X. Adaptive Harmonic Impedance Reshaping Control Strategy Based on a Consensus Algorithm for Harmonic Sharing and Power Quality Improvement in Microgrids with Complex Feeder Networks. IEEE Trans. Smart Grid 2022, 13, 47–57. [Google Scholar] [CrossRef]
- Dabbaghjamanesh, M.; Kavousi-Fard, A.; Mehraeen, S.; Zhang, J.; Yang Dong, Z. Sensitivity Analysis of Renewable Energy Integration on Stochastic Energy Management of Automated Reconfigurable Hybrid AC-DC Microgrid Considering DLR Security Constraint. IEEE Trans. Ind. Inf. 2020, 16, 120–131. [Google Scholar] [CrossRef]
- Mohammed, N.; Lashab, A.; Ciobotaru, M.; Guerrero, J.M. Accurate Reactive Power Sharing Strategy for Droop-Based Islanded AC Microgrids. IEEE Trans. Ind. Electron. 2023, 70, 2696–2707. [Google Scholar] [CrossRef]
- Tightiz, L.; Yang, H.; Bevrani, H. An Interoperable Communication Framework for Grid Frequency Regulation Support from Microgrids. Sensors 2021, 21, 4555. [Google Scholar] [CrossRef] [PubMed]
- Dabbaghjamanesh, M.; Wang, B.; Kavousi-Fard, A.; Hatziargyriou, N.D.; Zhang, J. Blockchain-Based Stochastic Energy Management of Interconnected Microgrids Considering Incentive Price. IEEE Trans. Control. Netw. Syst. 2021, 8, 1201–1211. [Google Scholar] [CrossRef]
- Bucolo, M.; Buscarino, A.; Famoso, C.; Fortuna, L. Chaos Addresses Energy in Networks of Electrical Oscillators. IEEE Access 2021, 9, 153258–153265. [Google Scholar] [CrossRef]
- Zuo, K.; Wu, L. Enhanced Power and Energy Coordination for Batteries under the Real-Time Closed-Loop, Distributed Microgrid Control. IEEE Trans. Sustain. Energy 2022, 13, 2027–2040. [Google Scholar] [CrossRef]
- Ali, S.; Kazmi, S.A.A.; Malik, M.M. Energy Management in High RER Multi-Microgrid System via Energy Trading and Storage Optimization. IEEE Access 2022, 10, 6541–6554. [Google Scholar] [CrossRef]
- Dong, H.; Fu, Y.; Jia, Q.; Wen, X. Optimal Dispatch of Integrated Energy Microgrid Considering Hybrid Structured Electric-Thermal Energy Storage. Renew. Energy 2022, 199, 628–639. [Google Scholar] [CrossRef]
- Li, L.; Han, Y.; Li, Q.; Pu, Y.; Sun, C.; Chen, W. Event-Triggered Decentralized Coordinated Control Method for Economic Operation of an Islanded Electric-Hydrogen Hybrid DC Microgrid. J. Energy Storage 2022, 45, 103704. [Google Scholar] [CrossRef]
- Wang, H.; Li, W.; Yue, Y.; Zhao, H. Distributed Economic Control for AC/DC Hybrid Microgrid. Electronics 2022, 11, 13. [Google Scholar] [CrossRef]
- Jiang, K.; Wu, F.; Zong, X.; Shi, L.; Lin, K. Distributed Dynamic Economic Dispatch of an Isolated AC/DC Hybrid Microgrid Based on a Finite-Step Consensus Algorithm. Energies 2019, 12, 4637. [Google Scholar] [CrossRef] [Green Version]
- Maslak, G.; Orlowski, P. Microgrid Operation Optimization Using Hybrid System Modeling and Switched Model Predictive Control. Energies 2022, 15, 833. [Google Scholar] [CrossRef]
- Dabbaghjamanesh, M.; Kavousi-Fard, A.; Mehraeen, S. Effective Scheduling of Reconfigurable Microgrids With Dynamic Thermal Line Rating. IEEE Trans. Ind. Electron. 2018, 66, 1552–1564. [Google Scholar] [CrossRef]
- Su, W.; Yu, S.S.; Li, H.; Iu, H.H.-C.; Fernando, T. An MPC-Based Dual-Solver Optimization Method for DC Microgrids with Simultaneous Consideration of Operation Cost and Power Loss. IEEE Trans. Power Syst. 2021, 36, 936–947. [Google Scholar] [CrossRef]
- Tao, H.; Zhou, L.; Hao, S.; Paszke, W.; Yang, H. Output Feedback Based PD-Type Robust Iterative Learning Control for Uncertain Spatially Interconnected Systems. Int. J. Robust Nonlinear Control 2021, 31, 5962–5983. [Google Scholar] [CrossRef]
- Wei, J.; Tao, H.; Hao, S.; Paszke, W.; Gałkowski, K. Output Feedback Based Robust Iterative Learning Control via a Heuristic Approach for Batch Processes with Time-Varying State Delays and Uncertainties. J. Process Control. 2022, 116, 159–171. [Google Scholar] [CrossRef]
- Zhuang, Z.; Tao, H.; Chen, Y.; Stojanovic, V.; Paszke, W. An Optimal Iterative Learning Control Approach for Linear Systems with Nonuniform Trial Lengths Under Input Constraints. IEEE Trans. Syst. Man. Cybern. Syst. 2022, 1–13. [Google Scholar] [CrossRef]
- Zhou, L.; Tao, H.; Paszke, W.; Stojanovic, V.; Yang, H. PD-Type Iterative Learning Control for Uncertain Spatially Interconnected Systems. Mathematics 2020, 8, 1528. [Google Scholar] [CrossRef]
- Wang, P.; Chen, W.; Lin, S.; Liu, L.; Sun, Z.; Zhang, F. Consensus Algorithm Based on Verifiable Quantum Random Numbers. Int. J. Intell. Syst. 2022, 37, 6857–6876. [Google Scholar] [CrossRef]
- Olfati-Saber, R.; Murray, R.M. Consensus Problems in Networks of Agents with Switching Topology and Time-Delays. IEEE Trans. Autom. Control 2004, 49, 1520–1533. [Google Scholar] [CrossRef]















| DG | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Rated active power Pe | 30/kW | 15/kW | 40/kW | 15/kW | 15/kW | 30/kW |
| Power limits Pmin, Pmax | 5/kW, 35/kW | 5/kW, 20/kW | 5/kW, 50/kW | 0/kW, 20/kW | 0/kW, 20/kW | 5/kW, 35/kW |
| Initial active power P0 | 10/kW | 5/kW | 35/kW | 10/kW | 5/kW | 5/kW |
| Filter Resistance Rf | 0.12/Ω | 0.1/Ω | 0.15/Ω | 0.1/Ω | 0.1/Ω | 0.12/Ω |
| Filter Inductance Lf | 1.4/mH | 1.2/mH | 1.8/mH | 1.2/mH | 1.2/mH | 1.4/mH |
| Filter Capacitance Cf | 25/μF | 20/μF | 30/μF | 20/μF | 20/μF | 25/μF |
| Droop coefficient of active power m | 4 × 10−4 /(Hz/kW) | 8 × 10−4 /(Hz/kW) | 3 × 10−4 /(Hz/kW) | 8 × 10−4 /(Hz/kW) | 8 × 10−4 /(Hz/kW) | 4 × 10−4 /(Hz/kW) |
| Droop coefficient of reactive power n | 2 × 10−4 /(V/kvar) | 4 × 10−4 /(V/kvar) | 1.5 × 10−4 /(V/kvar) | 4 × 10−4 /(V/kvar) | 4 × 10−4 /(V/kvar) | 2 × 10−4 /(V/kvar) |
| Proportional and integral parameters of voltage controller kPu, kIu | 1, 150 | 0.8, 140 | 1.2, 160 | 0.8, 140 | 0.8, 140 | 1, 150 |
| Proportional and integral parameters of current controller kPc, kIc | 25, 80 | 22, 70 | 28, 90 | 22, 70 | 22, 70 | 25, 80 |
| Proportional and integral parameters of frequency optimization controller kf1, kf2 | 0.1, 25 | 0.9, 23 | 0.11, 28 | 0.9, 23 | 0.9, 23 | 0.1, 25 |
| Proportional and integral parameters of voltage optimization controller ku1, ku2 | 1, 50 | 0.8, 40 | 1.2, 60 | 0.8, 40 | 0.8, 40 | 1, 50 |
| Primary term coefficient of cost model a | 0.00533 /(¥/(kW·h)) | 0.00832 /(¥/(kW·h)) | 0.00653 /(¥/(kW·h)) | 0.00765 /(¥/(kW·h)) | 0.00741 /(¥/(kW·h)) | 0.00889 /(¥/(kW·h)) |
| Secondary term coefficient of cost model b | 6.532 /(¥/(kW·h)) | 6.543 /(¥/(kW·h)) | 6.621 /(¥/(kW·h)) | 6.578 /(¥/(kW·h)) | 6.663 /(¥/(kW·h)) | 6.543 /(¥/(kW·h)) |
| Constant term coefficient of cost model c | 213.1 /(¥/(kW·h)) | 200.0 /(¥/(kW·h)) | 10.0 /(¥/(kW·h)) | 15.0 /(¥/(kW·h)) | 240.0 /(¥/(kW·h)) | 200.0 /(¥/(kW·h)) |
| Variable | Value |
|---|---|
| DC side voltage Vdc | 600/V |
| Line voltage Uab | 380/V |
| Frequency f | 50/Hz |
| Switching frequency fsw | 10/kHz |
| Line impedance Z12 | 0.13/Ω + 1.7/mH |
| Line impedance Z23 | 0.10/Ω + 1.2/mH |
| Line impedance Z34 | 0.08/Ω + 1.0/mH |
| Line impedance Z45 | 0.15/Ω + 2.0/mH |
| Line impedance Z56 | 0.16/Ω + 2.1/mH |
| Line impedance Z61 | 0.14/Ω + 1.8/mH |
| Load 1 Pload1, Qload1 | 70/kW, 0.5/kvar |
| Load 2 Pload2, Qload2 | 40/kW, 0.3/kvar |
| Load 3 Pload3, Qload3 | 10/kW, 0.1/kvar |
| Load 4 Pload4, Qload4 | 10/kW, 0.1/kvar |
| Transmission loss power | 5/kW, 5/kvar |
| Deviation elimination term coefficient ε | 0.0005 |
| Pinning coefficient ζ | 0.1 |
| Electricity price in peak period, flat-valley period, and valley period pr | 6.84, 6.74, 6.70/(¥/(kW·h)) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tong, Z.; Zhang, C.; Wu, X.; Gao, P.; Wu, S.; Li, H. Economic Optimization Control Method of Grid-Connected Microgrid Based on Improved Pinning Consensus. Energies 2023, 16, 1203. https://doi.org/10.3390/en16031203
Tong Z, Zhang C, Wu X, Gao P, Wu S, Li H. Economic Optimization Control Method of Grid-Connected Microgrid Based on Improved Pinning Consensus. Energies. 2023; 16(3):1203. https://doi.org/10.3390/en16031203
Chicago/Turabian StyleTong, Zejun, Chun Zhang, Xiaotai Wu, Pengcheng Gao, Shuang Wu, and Haoyu Li. 2023. "Economic Optimization Control Method of Grid-Connected Microgrid Based on Improved Pinning Consensus" Energies 16, no. 3: 1203. https://doi.org/10.3390/en16031203
APA StyleTong, Z., Zhang, C., Wu, X., Gao, P., Wu, S., & Li, H. (2023). Economic Optimization Control Method of Grid-Connected Microgrid Based on Improved Pinning Consensus. Energies, 16(3), 1203. https://doi.org/10.3390/en16031203





