Wind-Tunnel Experiments on the Interactions among a Pair/Trio of Closely Spaced Vertical-Axis Wind Turbines

Abstract

To elucidate the wind-direction dependence of the rotor performance in closely spaced vertical-axis wind turbines, wind-tunnel experiments were performed at a uniform wind velocity. In the experiments, a pair/trio of three-dimensional printed model turbines with a diameter of D = 50 mm was used. The experiments were performed systematically by applying incremental adjustments to the rotor gap g and rotational direction of each rotor and by changing the wind direction. For tandem layouts, the rotational speed of the downwind rotor is 75–80% that of an isolated rotor, even at g/D = 10. For the average rotational speed of the rotor pair, an origin-symmetrical and a line-symmetrical distribution are observed in the co-rotating and inverse-rotating configurations, respectively, thereby demonstrating the wind-direction dependence for the rotor pair. The inverse-rotating trio configuration yields a higher average rotational speed than the co-rotating trio configuration for any rotor spacing under the ideal bidirectional wind conditions. The maximum average rotational speed should be obtained for a wind direction of θ = 0° in the inverse-rotating trio configuration. The wind-direction dependence of the rotational speeds of the three turbines was explained via flow visualization using a smoke-wire method and velocity field study using two-dimensional computational fluid dynamics.

1. Introduction

For both onshore and offshore wind farms, studies on the optimal layout of several closely placed vertical-axis wind turbines (VAWTs), using beneficial interactions between turbines in an array [1], are important issues that reflect a great demand for effective usage of abundant wind energy. As a fundamental step in the allocation of VAWTs in a wind farm, this study explores the wind-direction dependence of closely spaced two and three VAWTs by wind-tunnel experiments with miniature model turbines. The aspect ratio of the model turbine, i.e., the ratio of the height H to the diameter D, was set to a widely used value of approximately 1. Shamsoddin et al. [2] reported the effect of the aspect ratio on VAWT wakes.

Dabiri [3] conducted experiments at a field site in Los Angeles; in the experiment, many couples of inverse-rotating rotors were set like a fish schooling. The turbines were a modified version of a commercially available model with H/D = 3.42. Hezaveh et al. [4] showed that “the wind-farm design with staggered-triangle clusters is the optimal design in terms of cost per unit power produced.” Li et al. [5] showed that the power output is higher in the staggered wind farms (horizontal-axis wind turbines) than in the aligned ones.

From a set of field experiments conducted by Dabiri [3], with a three-VAWT configuration in which the third turbine was placed a distance of 4D downstream from the second turbine (i.e., the spacing of the rotors, g, between the surfaces of the second and third rotors is 3D) in an elbow-like layout, the performance was recovered to within 5% of the single-turbine performance. Zanforlin and Nishino [6] reported the power enhancement in closely arranged VAWTs with two-dimensional (2D) numerical simulation assuming fixed rotational speeds.

However, the studies by [3] and [6] did not adopt a co-rotating (CO) configuration. The results of the former include unnatural increases in power in the case near the tandem layout for a rotor gap ratio of g/D = 0.65, despite the unpreferred wake interaction between the turbines. The latter assumed that only the upstream turbine is working, regardless of the value of g/D within the range of 0.5–2. Therefore, well-controlled tandem experiments are necessary to clarify these points prior to investigating the wind-direction dependence of VAWT performance.

For the CO configuration, Dessoky et al. [7] performed a numerical simulation for a tandem layout of a pair of VAWTs. They reported that the downwind turbine shows better performance if the upwind turbine is operated at a high tip speed ratio and reported the effect of the turbine spacing on the downwind turbine performance. Recently, Kuang et al. [8] conducted a three-dimensional (3D) improved delayed detached-eddy simulation (IDDES) on two tandem CO offshore floating VAWTs. They reported that as the turbine spacing increased, the performance, an increase, and the optimal tip speed ratio of the downwind turbine were enhanced. These results confirm the previous findings reported by Dessoky et al. [7], who explained the improvement in turbine performance as an effect of the reduction in vorticity with the shifting of the downwind rotor in the downstream direction. However, these simulations with fixed rotational speeds still seem to be impractical in variable-speed VAWT operation, which depends on wind direction and flow speed. The importance of the 3D effects of blade geometry on VAWT wakes was reported experimentally (Wei et al. [9]) and numerically (Kuang et al. [8]). Furthermore, Jin et al. [10] reported the 3D structure of the wake behind twin VAWTs placed side-by-side and showed that the azimuth angle change has little effect on the rotor performance.

In a study on the wind-direction dependence of a pair of turbines, Sahebzadeh et al. [11] investigated 119 unique turbine arrangements with seven gaps in the range of g/D = 0.25–9 and 17 wind directions covering ±90°, and reported the effect of relative distance and angle on the individual and overall power performance of the two rotors.

However, their numerical study was also limited to a CO pair with fixed rotational speed. De Tavernier et al. [12] reported both CO and inverse-rotating (IR) double-rotor configurations in a study using a 2D panel/vortex model. From the wind-direction dependence of the power coefficient of two IR turbines, they reported a specific wind direction in which the downwind turbine performs better than the upwind turbine and explained it due to increased mass flow through the rotor because of the induced velocity caused by the first rotor on the second rotor. Regrettably, they intentionally left out the results for the CO configuration, merely stating that “very similar trends can be observed”. Therefore, their report does not contain any results on the wind-direction dependence with CO turbines, except for a side-by-side layout.

Although Hezaveh et al. [4] demonstrated an approximate 10% increase in the power generation of a single rotor in well-designed clusters, they reported the gap dependence of the power coefficient only for a wind direction of 60° (one upwind rotor and two downwind rotors) in a triangular-cluster configuration (see their Figures 8 and 9) in a study of a trio of turbines. Among other studies in three-VAWT arrays [13,14,15], Ahmadi-Baloutaki et al. [15] concluded that “the optimum range of the streamwise distance of the downstream turbine from the counter-rotating pair and the spacing between the pair was determined to be about three and one rotor diameters, respectively,” though they only considered a wind direction of 0° (an upwind counter-rotating rotor pair and one downwind rotor) for a nonequilateral-triangular cluster configuration.

Hara et al. [13] performed a 2D computational fluid dynamics (hereafter, 2D CFD) study. The strong point of their study was that the rotational speed of each rotor could change according to the interaction between each rotor and flow around it. Yoshino et al. [16] reported the wind-direction dependence of the rotational speed of three VAWTs.

Many studies explored multi-VAWT arrays, such as Zhang et al. [17] with 5 Savonius-type VAWTs (2D CFD), Mereu et al. [18] with 16 Savonius-type VAWTs (2D CFD), Bangga et al. [19] with 6 VAWTs (2D CFD with NACA 0021), Dabiri [3] with 6 VAWTs (field experiment), and Hezaveh et al. [4] with 96 VAWTs (large-eddy simulation).

Therefore, the objectives of this study using two and three miniature VAWTs are to explore the effects of the:

• Rotational directions;
• Gap ratios;
• Wind direction over 360°;

on the arrayed-turbine performance.

The significance of the investigation is:

• Wind-tunnel experiments equivalent to the operation of small variable-speed VAWTs;
• Comparison with the cutting-edge 2D CFD with the DFBI method [13,16];
• Well-supported flow patterns obtained by flow visualization.

The rotational speeds of the rotors were simulated in the 2D CFD with software STAR-CCM+ by solving an equation of continuity and Reynolds-averaged Navier–Stokes equations in an unsteady incompressible flow, in which the numerical setup was the same as that used in Hara et al. [13] for two rotors and Yoshino et al. [16] for three rotors.

2. Methods

2.1. Configuration of the Flow Field

The wind tunnel used had an outlet area 600 (width) × 350 (height) mm. The speed and direction of the wind were held constant for each experiment. The uniformity of the mean velocity and the turbulent intensity of the flow field are detailed in [20]. Figure 1 shows a model rotor named a butterfly wind turbine (BWT) used in the experiments. Each model rotor was printed on a 3D printer. The miniature models were also used in our previous experiments on a pair of VAWTs arranged side-by-side (Jodai and Hara [20]). A BWT is a lift-type VAWT with straight-blade portions, such as a high-performance H-Darrieus wind turbine, which features an armless rotor with looped blades. The height H and diameter D of the miniature model were 43.4 and 50 mm, respectively. Figure 1b is the cross-section of the model along the equatorial plane.

The measurements were conducted on a pair/trio of rotors in an open space beyond the wind-tunnel exit for layouts with 16 or 12 wind directions. An independent tandem experiment was also conducted at a uniform velocity V = 10 and 12 m/s prior to the multiple wind-direction experiments. The centers of the two or three turbines were located at the 3D-position (i.e., 150 mm) from the wind-tunnel outlet, except for the independent tandem experiments in which the upwind rotor was fixed 50 mm upstream of the center point. The solidity of the turbine model defined by Bc/(πD) was σ = 0.382. The Reynolds number based on D and the tip speed ratio at a rotational speed of N~4000 rpm were R_eD~4.7 × 10⁴ and λ~0.75, respectively, for the experiments on a pair of turbines with a wind speed of V = 14 m/s. On the other hand, in experiments on a trio of turbines with a wind speed of V = 12 m/s (N~3400 rpm), the corresponding values were R_eD~4.0 × 10⁴ and λ~0.74. The Reynolds number using the length of the chord c was R_ec~1.9/1.6 × 10⁴ for the experiments on a pair or trio of turbines. More details about the effect of a Reynolds number on the performance in a VAWT are given in [20] with relevant references. The error in the model rotational speed measurements was ±10 rpm, which corresponds to ±0.25% or ±0.29% of the rotational speed N (~4000 rpm or ~3400 rpm) of a single rotor with an isolated setting at a uniform wind velocity of V = 14/12 m/s.

Table 1. Comparison of the parameters of the vertical-axis turbine. CO and IR represent co-rotating and inverse-rotating configurations, respectively. U is the uniform speed; D is the rotor diameter; R_ec is the chord-based Reynolds number; λ = Rω/V is the tip speed ratio; and σ = Bc/(πD) is the solidity. Values marked with † are examples of nonequilateral-triangular cluster design consisting of three VAWTs.

Study	Layout	U (m/s)	D (m)	Rec/104 (-)	λ (-)	σ (-)	gmin/D (-)
Ahmadi-Baloutaki et al. [15]	0° trio (IR)	6–14	0.30	1.8–4.2	~0.05–0.3	0.239	0.5 †
Bangga et al. [19]	six-parallel (CO&IR)	8.0	2.0	14	1.5–3.0	0.0844	1.0
Dabiri [3]	$$\{\begin{array}{c}\mathrm{over} 360° \mathrm{over}\mathrm{pair} \left(\mathrm{IR}\right)\\ \mathrm{elbow}-\mathrm{like} \mathrm{trio} \left(\mathrm{IR}\right)\\ \mathrm{six}-\mathrm{staggered} \left(\mathrm{IR}\right)\end{array}$$	5.7 (7.8)	1.2	4.2 (6)	1.5–3.0	0.102	0.65 0.65 3.0
Dessoky et al. [7]	tandem pair (CO)	8.0	2	14	0.75	0.0844	1.5
De Tavernier et al. [12]	over 360° pair (CO&IR)	1.0	20	6.7	2.5, 3.5	0.032	0.01
Hezaveh et al. [4]	0°, 20°, 40°, 60° trio (CO)	12	1.2	8.8	2.18	0.0875	2.0
Kuang et al. [8]	tandem pair (CO)	8.0	0.8	10.7	0.4–1.5	0.239	1.0
Sahebzadeh et al. [11,21]	over ±90° pair (CO)	9.3	1	15.7	4	0.0191	0.25
Zanforlin and Nishino [6]	over 360° pair (IR)	8.0	1.2	6.8	2.3–3.2	0.102	0.5
Zanforlin [22] (tidal turbines)	over 360° trio (CO)	1.5	1.0	27	1.75	0.175	2.0
Zhang et al. [14]	0°, 60° trio (CO)	4.01	1.48	2	3.7	0.0323	2.0 †
Zheng et al. [23]	0°, 60° trio (IR)	10.6	1.2	9	2.3	0.102	0.6
Present	$$\{\begin{array}{c}\mathrm{tandem} \mathrm{pair} (\mathrm{CO}\&\mathrm{IR})\\ \mathrm{over} 360° \mathrm{pair}(\mathrm{CO}\&\mathrm{IR})\\ \mathrm{over} 360° \mathrm{trio}(\mathrm{CO}\&\mathrm{IR})\end{array}$$	10, 12 14 12	0.050	1.3, 1.6 1.9 1.6	~0.8	0.382	1.0 0.5 0.5

provides a comparison of the parameters adopted in related studies with those used in ours, including the cases of multiple rotors with more than three turbines. In Table 1, g_min/D is the minimum rotor gap ratio investigated and ω indicates the angular velocity of the rotor.

2.2. Tandem Layouts of a Pair of VAWTs

Figure 2 explains two tandem arrangements using two turbines according to Hara et al. [13] (see Figure 3 in [13]; the rotational direction in the present experiments is opposite to that adopted in their CFD study). In the tandem co-rotating (TCO) layout, the two rotors turn in the same rotational direction (Figure 2a), while in the tandem inverse-rotating (TIR) layout, the two rotors rotate in opposite rotational directions (Figure 2b). Rotor 1 and Rotor 2 are denoted as R1 and R2, respectively. The space between the two rotors is indicated by g. Results were obtained for six gap ratios of g/D = 1, 2, 4, 6, 8, and 10 (g = 50, 100, 200, 300, 400, and 500 mm) in the tandem arrangement. The experiments were performed at a uniform velocity V = 10 or 12 m/s. The x-coordinate represents the direction of the wind parallel to the array. The direction normal to x is y. In Figure 2, red arrows show the rotational directions of the rotors.

2.3. Wind Directions of a Pair of VAWTs (16 Wind Directions)

Figure 3 shows the definition of 16-wind-direction configurations of a closely spaced VAWT pair according to Sogo et al. [24] (see their Figure 2) or Hara et al. [13] (see their Figure 4). In the co-rotation (CO) configuration, the two rotors rotate in the same rotational direction, as illustrated in Figure 3a. In the inverse-rotation (IR) configuration, the two rotors turn in opposite rotational directions, as shown in Figure 3b. The space between Rotor 1 (R1) and Rotor 2 (R2) is indicated by g. The two gap ratios of g/D = 0.5 and 1 (g = 25 and 50 mm) were investigated in the configurations. The uniform velocity for the 16-wind-direction experiments was V = 14 m/s. θ is the wind-direction angle.

In Figure 3a, the CO layout at θ = 0° or 180° corresponds to the specific layout called CO in a side-by-side arrangement. The tandem co-rotating (TCO) layout at θ = 90° or 270° is introduced in Figure 2a. Although the same layout exists in the symmetric direction with respect to the center of the rotor pair (i.e., origin symmetry) in the CO configuration, as seen in Figure 3a, the wind-tunnel experiment was conducted for all cases of the 16-wind-direction configurations to ensure the repeatability of the experiment.

In Figure 3b, the counter-down layout at θ = 0°and counter-up layout at θ = 180° are called CD and CU, respectively, in a side-by-side arrangement. The TIR layout at θ = 90° or 270° is shown in Figure 2b. In contrast to the CO configuration in Figure 3a, equivalent cases exist in the symmetrical direction with respect to the x-axis (i.e., line symmetry) in the IR configuration in Figure 3b. Nevertheless, we still executed the experiment for all 16-wind-direction cases in the IR configuration, since there are no comparable systematic experiments on the wind-direction dependence.

2.4. Wind Directions of a Trio of VAWTs (12 Wind Directions)

Figure 4 shows the definition of 12-wind-direction configurations of a closely spaced VAWT trio. In the co-rotation trio (3CO) configuration, the three rotors turn in the same rotational direction, as illustrated in Figure 4a. In the inverse-rotation trio (3IR) configuration, one of the three rotors (R2) turns in an opposite direction, as shown in Figure 4b. The space between two of the three rotors (R1, R2, and R3) is indicated by g. The three gap ratios of g/D = 0.5, 1, and 2 (g = 25, 50, and 100 mm) were investigated in these configurations. The uniform velocity for the 12-wind-direction experiments was V = 12 m/s.

In Figure 4a, the layout at θ = 0° comprises a pair of CO rotors in a parallel arrangement (θ = 0° in Figure 3a) and an additional CO rotor (R3). Since the additional rotor R3 is placed behind the other rotors, we define this layout as 3COB. The label of number 3 was added to distinguish this layout from the 2COB layout, which is one of the layouts in the 3IR configuration (θ = 120° in Figure 4b), as explained later. The layout at θ = 90° is constituted by a pair of TCO rotors in a tandem arrangement (θ = 90° in Figure 3a) and an additional CO rotor (R3). We define this layout as 3TCOD, because the blades of the additional rotor R3 move downwind in the gap region (center of three turbines). Again, the label of number 3 was added in order to distinguish this layout from the 2TCOD layout, which is one of the layouts in the 3IR configuration (θ = 30° in Figure 4b).

Note that the blades of the other rotors, R1 and R2, move upwind in the gap region in the former layout (3TCOD). Similarly, the layouts at θ = 30° and 60° in the 3CO configuration are specific layouts, including a pair of tandem rotors or a pair of parallel rotors, and we define them as TCOU or 3COF, respectively. Since the same layout occurs at every 120° in the wind direction, the number of the independent layouts in the 3CO configuration is four (two parallel-like layouts and two tandem-like layouts). However, to obtain reliable experimental results, the wind-tunnel experiment was conducted for all cases of the 12-wind-direction configurations, as shown in Figure 4a. The three rotors are set on the corners of an equilateral triangle shown in lavender dash-dotted line. The length of the sides of the triangle is g + D.

In Figure 4b, the layout at θ = 0° comprises a pair of CD rotors in a parallel arrangement (θ = 0° in Figure 3b) and an additional rotor (R3). Since the additional rotor R3 is placed behind the other rotors, we define this layout as CDB. The layout at θ = 90° is comprised of a pair of TIR rotors in a tandem arrangement (θ = 90° in Figure 3b) and an additional rotor (R3). We define this layout as TIRD-CO, because the blades of the additional rotor R3 turn downwind in the gap region in addition to the fact that R3 rotates in the same direction as R1. This layout differs from the TIRU-CO layout at θ = 150° in Figure 4b, in which the blades of the additional rotor R1 move upwind in the gap region.

In the same way, the layouts at θ = 60° (CDF), 120° (2COB), 180° (CUF), 240° (CUB), and 300° (2COF) are specific layouts that include a pair of side-by-side rotors. On the other hand, the layouts at θ = 30° (2TCOD), 210° (2TCOU), 270° (TIRU-CU), and 330° (TIRD-CD) are additional specific layouts that include a pair of tandem rotors. Note that the same layout does not exist in the 3IR configuration. In other words, there are 12 independent layouts in the 3IR configuration (six parallel-like layouts and six tandem-like layouts). Therefore, we also conducted the experiment for all 12-wind-direction cases in the 3IR configuration.

In summary, there are 16 independent layouts (see

Table 2. Definition of the names of specific layouts in 12-wind-direction configurations (3CO and 3IR) in a closely spaced VAWT trio. Layouts with * are repeated every 120°.

Wind Direction (°)	3CO (Co-Rotation Trio)	3IR (Inverse-Rotation Trio)
0	3COB	CDB
30	TCOU	2TCOD
60	3COF	CDF
90	3TCOD	TIRD-CO
120	3COB *	2COB
150	TCOU *	TIRU-CO
180	3COF *	CUF
210	3TCOD *	2TCOU
240	3COB *	CUB
270	TCOU *	TIRU-CU
300	3COF *	2COF
330	3TCOD *	TIRD-CD

and Figure 4). To our knowledge, the present study is the first comprehensive measurement of the wind-direction dependence on the basis of a wind-tunnel experiment for three closely allocated VAWTs arranged equilaterally without omitting any wind directions, and with not only the 3CO configuration but also the 3IR configuration.

2.5. Characteristics of a Single Rotor Configuration

The aim of this subsection is to briefly describe the properties of the miniature turbine. Details of the torque measurement for the power calculation have been shown in Jodai and Hara [20]. Figure 5a shows the variation in the power coefficient C_p with the tip speed ratio λ of a wind turbine (see Table 1). The relationship between the rotational speed N and the motor power (power P of the model turbine at equilibrium) is shown in Figure 5b, where the red circles are points interpolated from the experiment. The approximate black curve (P vs. N) in Figure 5b is expressed by Equation (1).

$$P\stackrel{}{}[\mathrm{mW}]=0.2047{\left(\frac{N\left[\mathrm{rpm}\right]}{1000}\right)}^3+0.0442{\left(\frac{N\left[\mathrm{rpm}\right]}{1000}\right)}^2+21.042\left(\frac{N\left[\mathrm{rpm}\right]}{1000}\right)-0.0851$$

(1)

In the present experiments, a direct current motor was used only to start the rotation of a turbine in a uniform wind. The model rotational speed N [rpm] was measured using a noncontact-type digital tachometer with an accuracy of ±1 rpm, from a distance of 250–300 mm from the rotors (see [20] for details).

2.6. Experimental Setup of a Pair of VAWTs and a Trio of VAWTs

Figure 6 shows the normalized rotational speed in the case of the isolated turbine N_SI/N_SI0 placed y = 0 mm (see Figure 2, Figure 3 and Figure 4) at a uniform velocity V = 10 or 12 m/s. Here, N_SI is the rotational speed of the single rotor and N_SI0 is that located at x/D = 0. Hereafter, the rotational speed in the experimental result means the value measured in the case without a power supply to the startup motor, i.e., the free rotational speed (see Figure 7). The origins of the x- and y-axes correspond to the centers of the two/three rotors. Note that the upstream rotor (R1) is fixed at x/D = –1 and only the streamwise position of the downstream rotor (R2) was adjusted according to the rotor gap g in the tandem experiment (Figure 2). We confirmed the constant rotational speed within the error of ±2% in the range of 0 ≤ x/D ≤ 12 (Figure 6). This 600 mm streamwise range covers the full length of the tandem experiment, including a pair of two rotors at the maximum gap of 10D = 500 mm.

Figure 7 shows the setup of two VAWT models with a 200 mm gap (g/D = 4) arranged in tandem. Rotor 1 and Rotor 2 are aligned with the wind direction, as seen in Figure 2. The rotors can easily move along the rail in the ± x direction to realize the required spacing between the two rotors.

Figure 8 is the setup of two VAWT models with a 50 mm gap (g/D = 1) in IR configuration at θ = 112.5°. The figure shows the view from the top (see Figure 3b). The wind direction can be adjusted by using a rotating stage.

Figure 9 shows the experimental setup of a trio of 3D-printed VAWT models with a 50 mm gap (g/D = 1) in 3IR configuration at θ = 120°, viewed from the top (see Figure 4b).

3. Results and Discussion

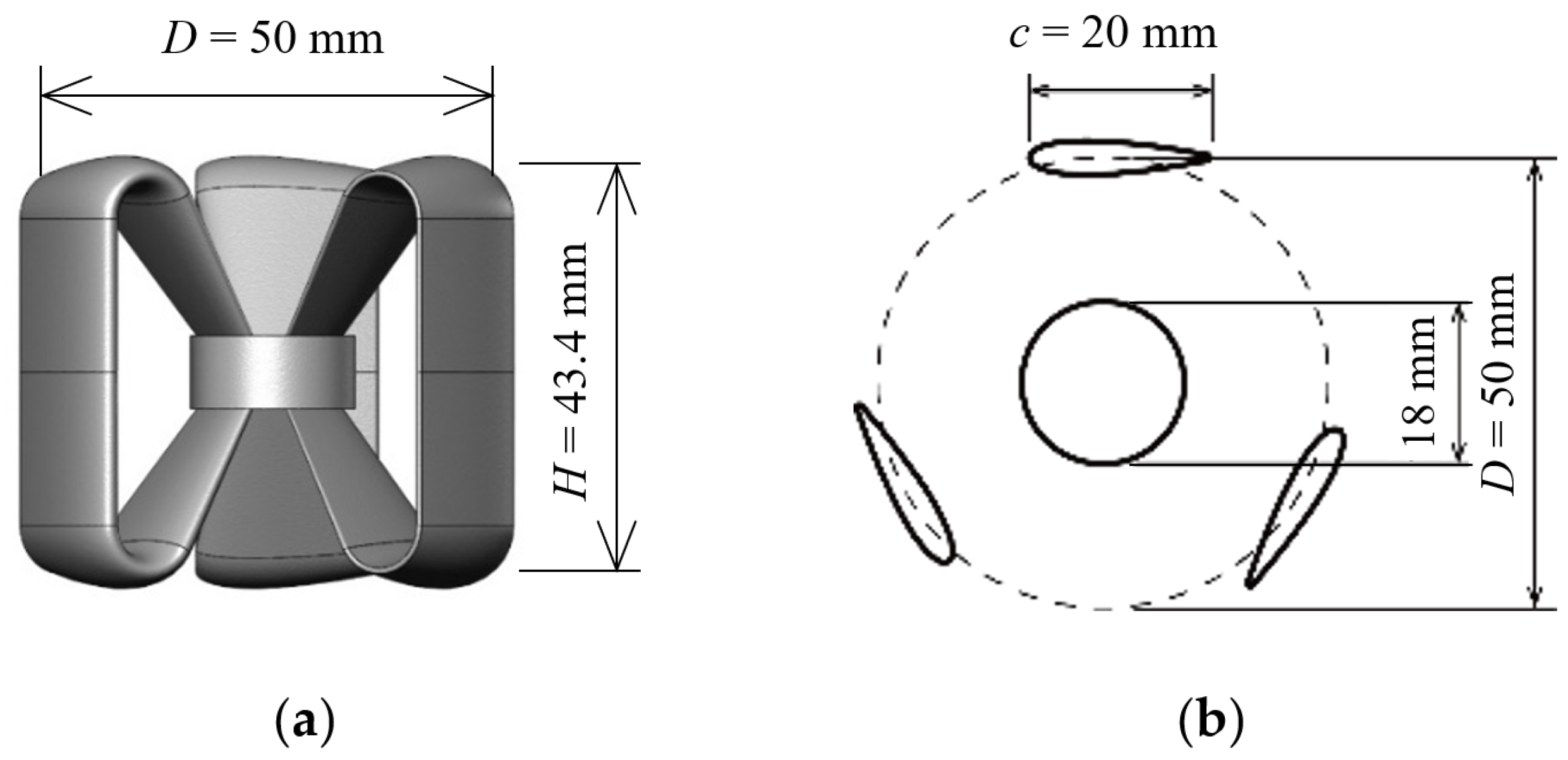
3.1. Rotational Speeds and Power of Closely Spaced VAWTs in Tandem Layouts

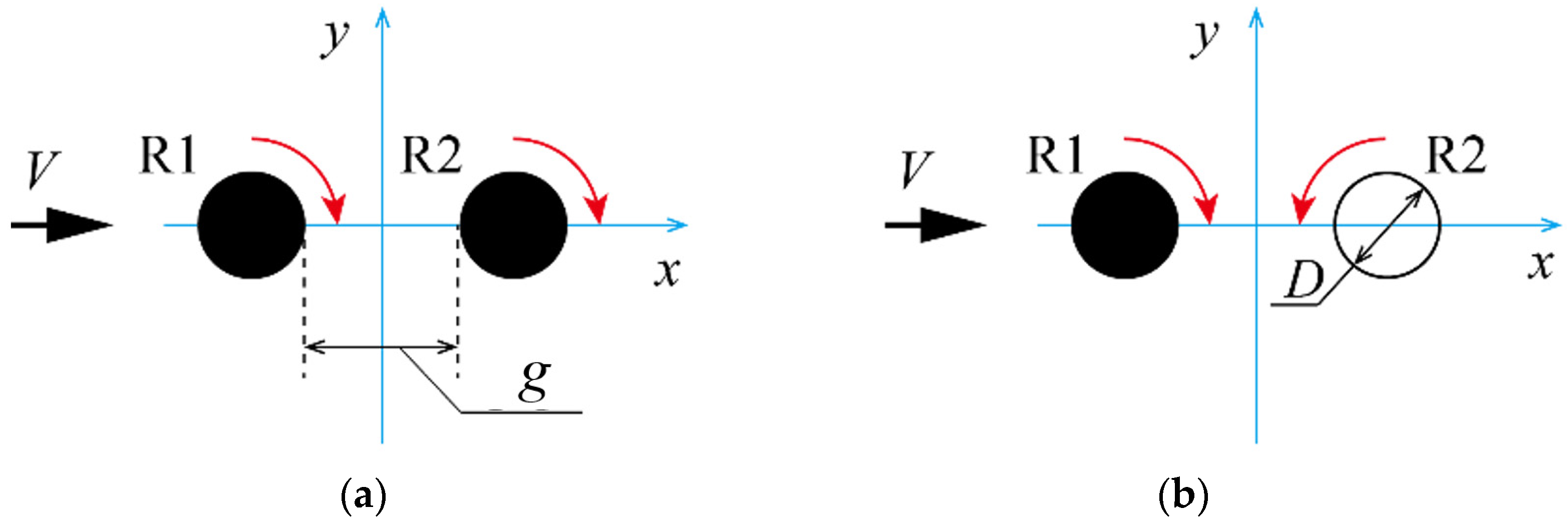
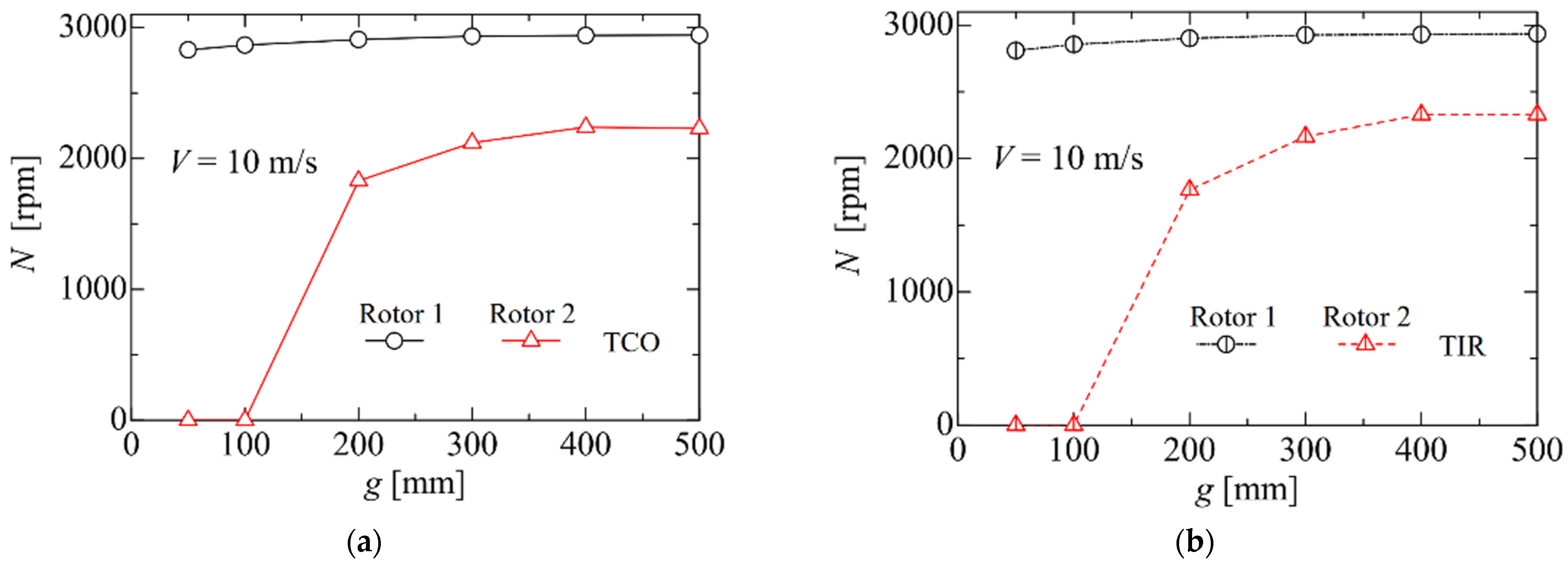
Figure 10 shows the variations in the rotational speed N [rpm] with the gap g between the two rotors. The results for the TCO layout (Figure 2a) and for the TIR layout (Figure 2b) are shown in Figure 10a and Figure 10b, respectively. The rotational speed of the single turbine obtained in the experiment was 2900 rpm at V = 10 m/s.

In the TCO layout in Figure 10a, the rotational speeds N of Rotor 1 in the upwind location and Rotor 2 in the downwind location decreased as the gap decreased because of the interaction between the rotors. Similarly, in the TIR layout (Figure 10b), the rotational speeds of Rotor 1 and Rotor 2 decreased as the gap decreased. In particular, the decreasing tendency in the case of Rotor 2 for smaller gaps is remarkable. As seen in Figure 10, the gap dependence of the rotational speed is almost the same for the TCO and TIR layouts: (1) at the smallest gap of g = 50 mm (g/D = 1), the value of the rotational speed of Rotor 1 is 97% of that of an isolated rotor; (2) even at g = 500 mm (g/D = 10), the value of the rotational speed of Rotor 2 is 75–80% of that of an isolated rotor. Note that for smaller gaps of g = 50 and 100 mm (g/D = 1 and 2), downwind Rotor 2 cannot continue to rotate due to the decelerated wake flow behind the upwind Rotor 1 at V = 10 m/s. Zanforlin and Nishino [6] presented the reduction of the power of the upstream turbine under the assumption that only this turbine is working in the case of the TIR layout at g/D = 0.5, 1, 1.5, and 2, using 2D CFD. However, their results showing the same power coefficient as that of an isolated turbine seem to be unexpected (see 90° in their Figures 15, 17, and 18). De Tavernier et al. [12] showed a power reduction of both turbines in the case of the TIR layout at g/D = 0.2, based on a 2D simulation with a panel/vortex model. According to their Figure 9, the power values of Rotor 1 and Rotor 2 are approximately 80% and 30% of that of an isolated rotor, respectively.

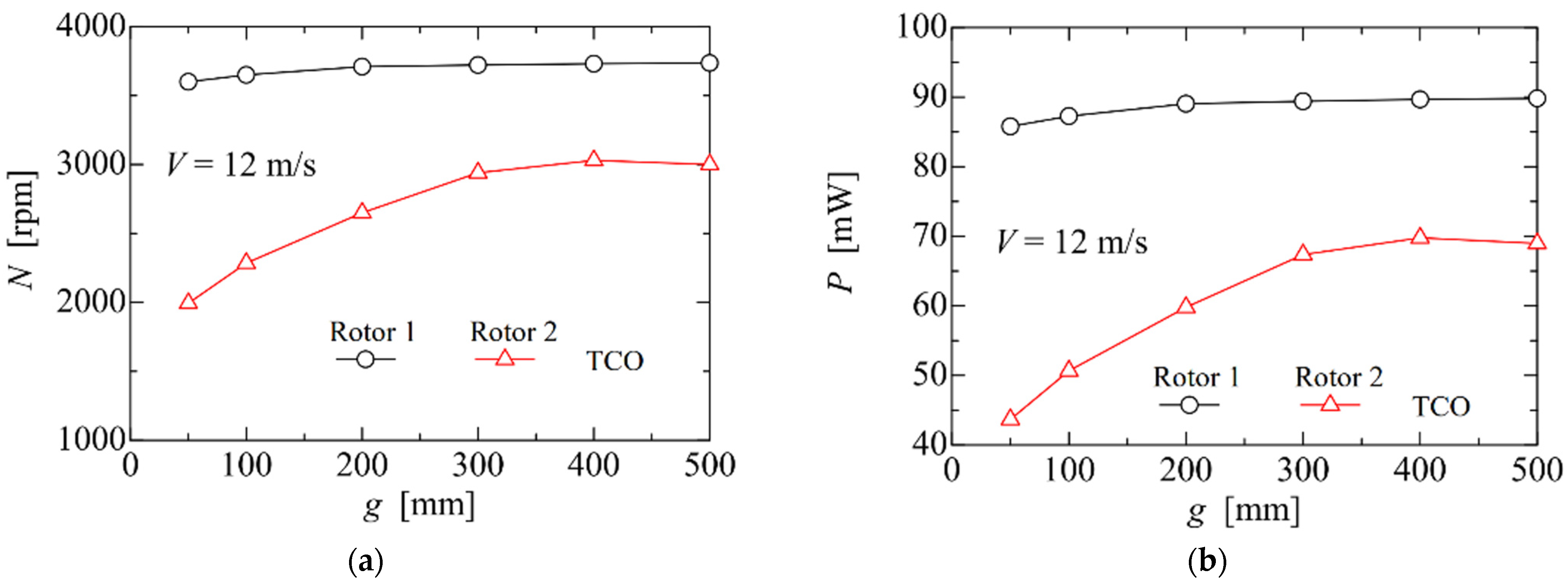
To investigate the decreasing tendency in smaller gaps, we also experimented with the TCO layout at a higher wind speed, as shown in Figure 11a. At the smallest gap of g = 50 mm, the value of N of Rotor 1 is 97% of that of an isolated rotor (3700 rpm for V = 12 m/s) and at g = 500 mm, the value of N of Rotor 2 is approximately 80% of that of an isolated rotor, as in the case of V = 10 m/s. At this higher uniform wind speed, the downwind Rotor 2 continued to rotate at 54% and 62% of rotational speed of an isolated rotor, even at smaller gaps of g = 50 and 100 mm, respectively. 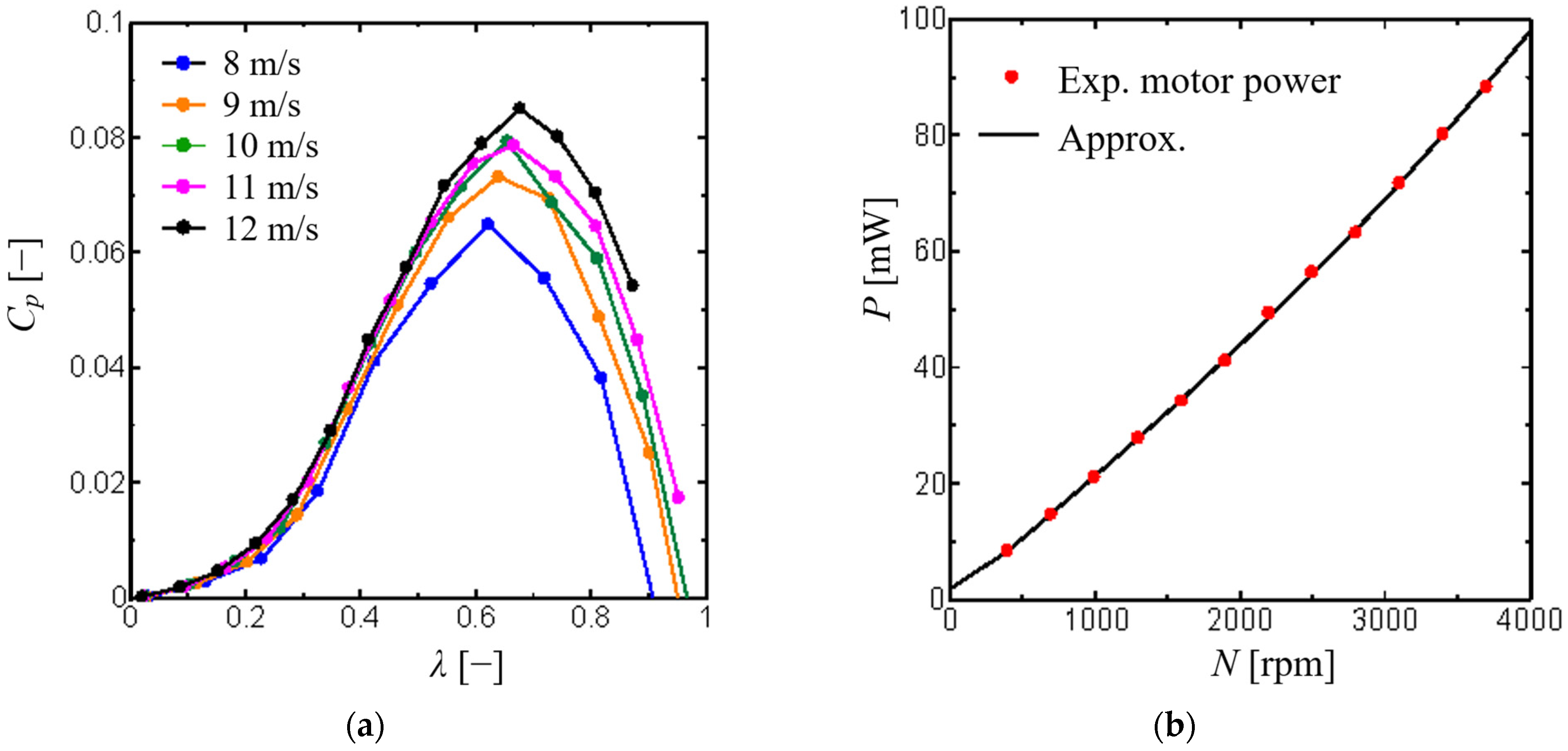Figure 11b shows the gap dependence of the power P obtained using Equation (1) explained in Section 2.5. The main results are as follows: (1) At g = 50 mm (g/D = 1), the power values of Rotor 1 and Rotor 2 are 97% and 49% of that of an isolated rotor (88.7 mW for V = 12 m/s); (2) at g = 500 mm (g/D = 10), the power of Rotor 2 is 78% of an isolated rotor. At the largest gap ratio, the power of Rotor 1 recovers to the value of a single rotor. According to Figure 6b,c in Sahebzadeh et al. [21], in the TCO layout for V = 9.3 m/s, the power values of Rotor 1 and Rotor 2 are 92% and 44%, respectively, of that of an isolated rotor at g/D = 0.5; these values changed to 95% and 40%, respectively, at g/D = 1.25. These values are qualitatively consistent with our experimental values for g/D = 1. Since the gap dependence of N is similar to that of P, as shown in Figure 11, hereafter, we will only use N for the discussion on the gap/wind-direction dependence for all configurations.

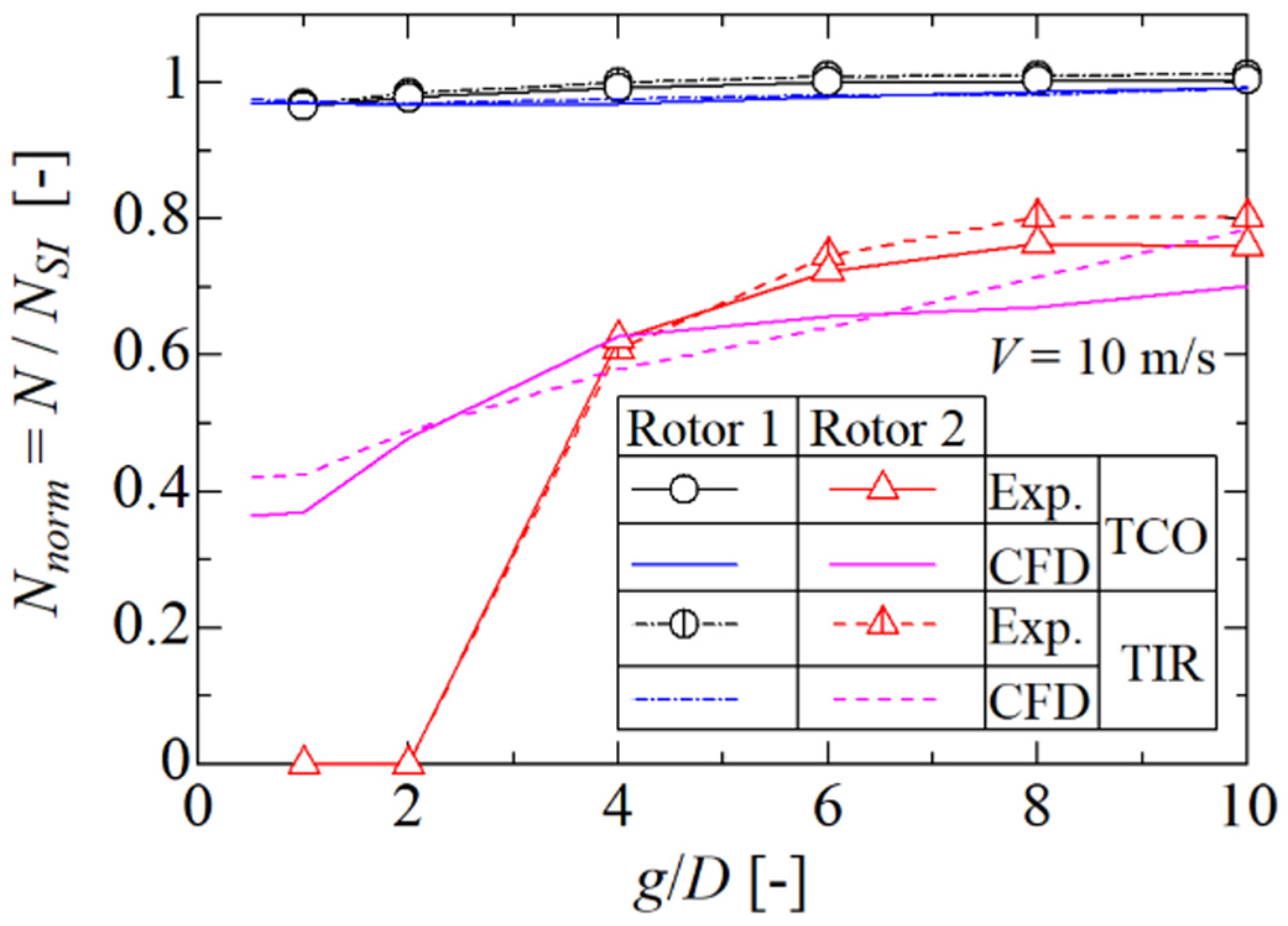
Next, we examine the normalized rotational speed N_norm, defined in Equation (2).

$$N_{norm}=\frac{N}{N_{SI}}$$

(2)

Figure 12 compares the results of N_norm obtained from the wind-tunnel experiment (Figure 10) with those obtained by Hara et al. [13] via 2D CFD analysis using the dynamic fluid body interaction (DFBI) method. The gap between the two rotors (g on the abscissa) is also nondimensionalized using the diameter of each rotor D. Regardless of the layout type (TCO and TIR), the normalized rotational speed decreased as the gap decreased in the experimental and CFD results.

Dessoky et al. [7] have reported the importance of the rotor spacing on the pair performance. This is based on the CFD code developed at their institute for wind turbine applications using 2 m diameter Darrieus turbine rotors of the two-bladed NACA 0021 airfoil. Sahebzadeh et al. [11] showed that the turbine wake is broken at a downstream distance of approximately 8D for the TCO layout based on the unsteady Reynolds-averaged Navier–Stokes (URANS) simulations with one-bladed turbines of an NACA 0018 airfoil. Their results also show a decreasing tendency of power for both rotors with decreasing g/D. They stated that the drop was caused by the upstream induction of the downstream turbine. However, their downstream rotor starts generating higher power at 0.25 ≤ g/D ≤ 1.25 in an unexpected manner; the minimum power is obtained at g/D = 2 and 4 in their simulation (see their Figure 6a). The parameter g in our work corresponds to their R-d (R is the center-to-center distance of two rotors and d is the diameter of the rotor in Sahebzadeh et al. [11]). Recently, Kuang et al. [8] reported that “the gap ratio of g/D = 5 can appropriately balance the power and space cost” only in the case of the TCO layout. Our experimental result (Figure 12), showing a slight change in the N_norm with the gap at g/D > 5, substantiates their appropriate gap ratio.

3.2. Wind-Direction Dependence of a Pair of VAWTs (16 Wind Directions)

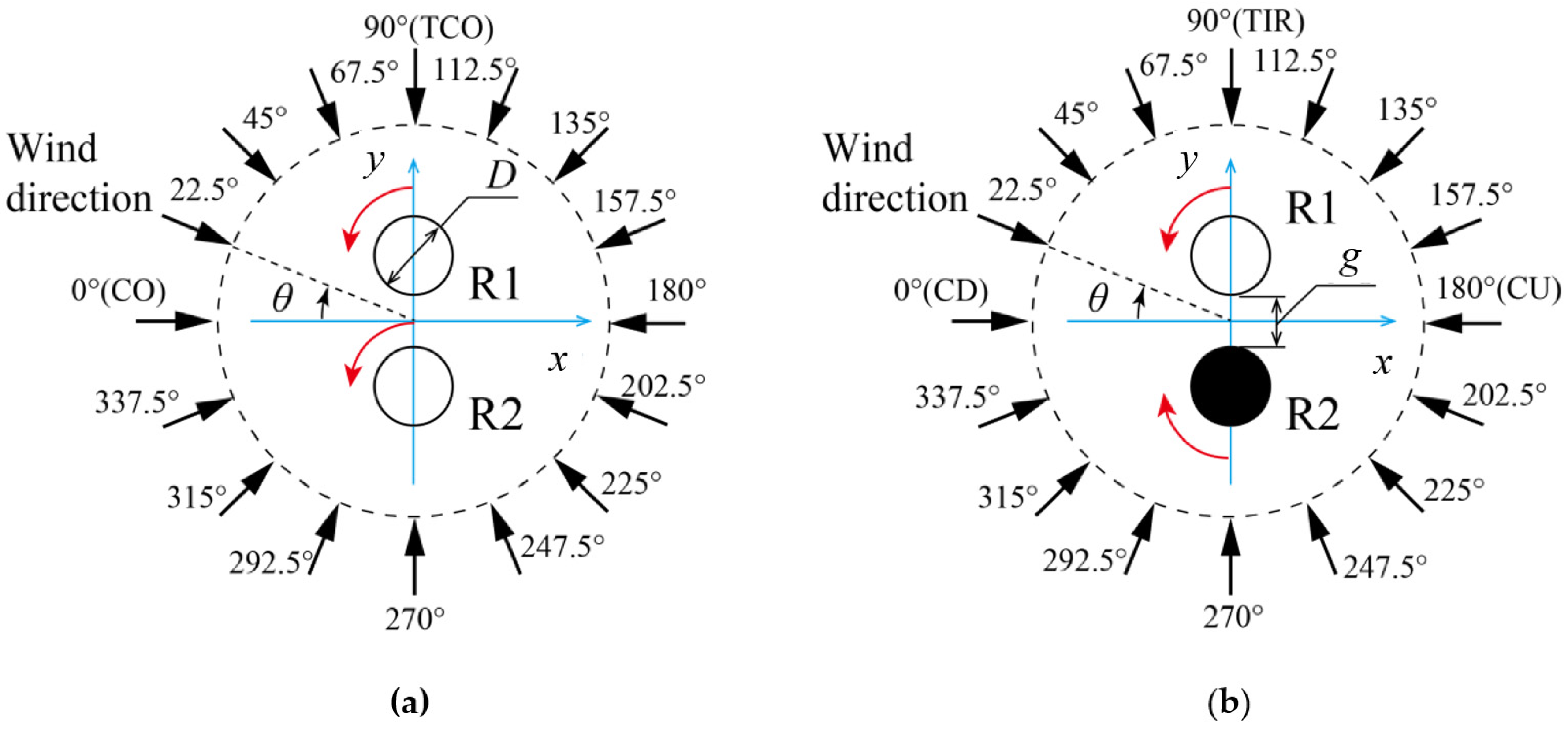
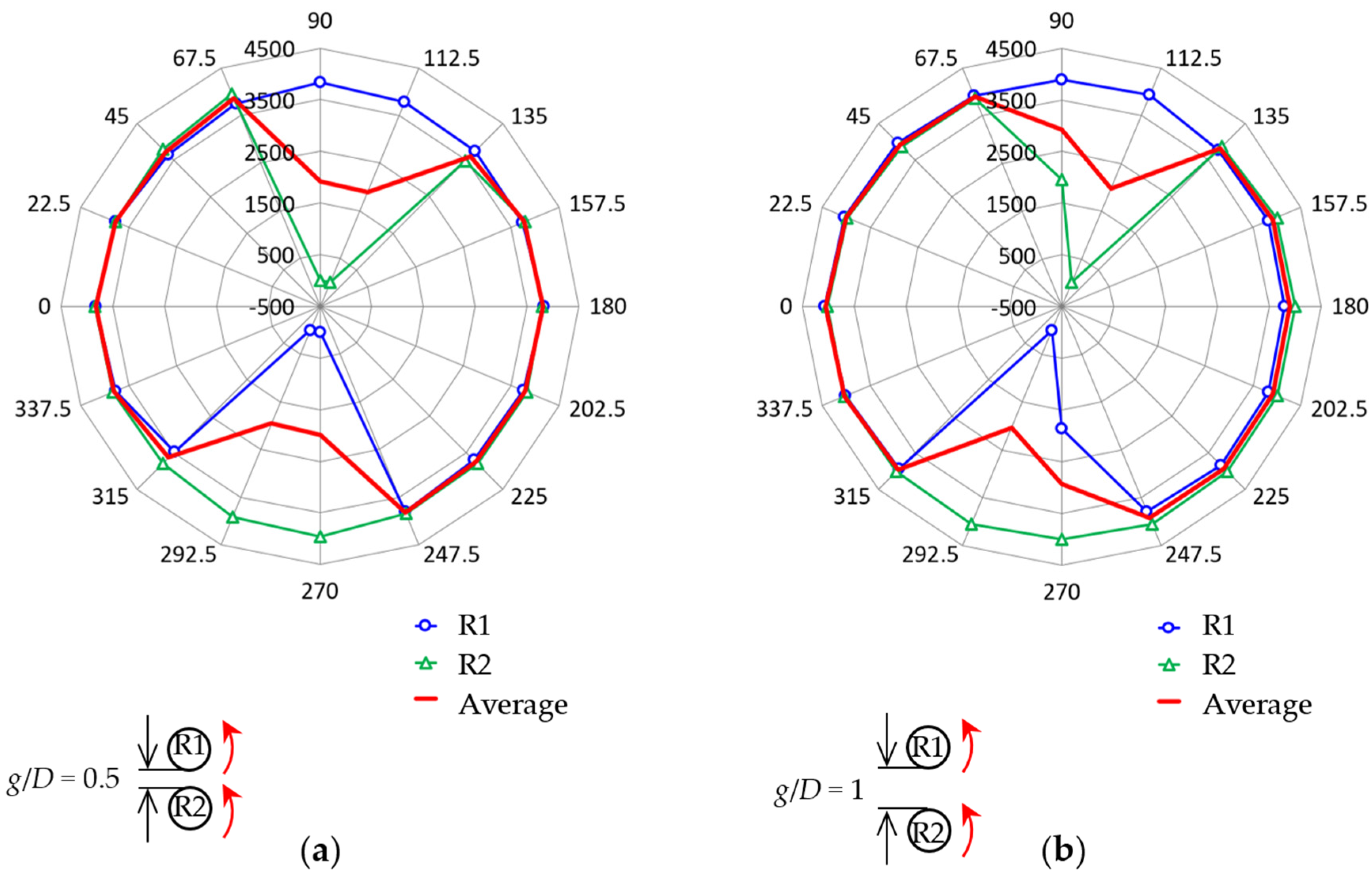
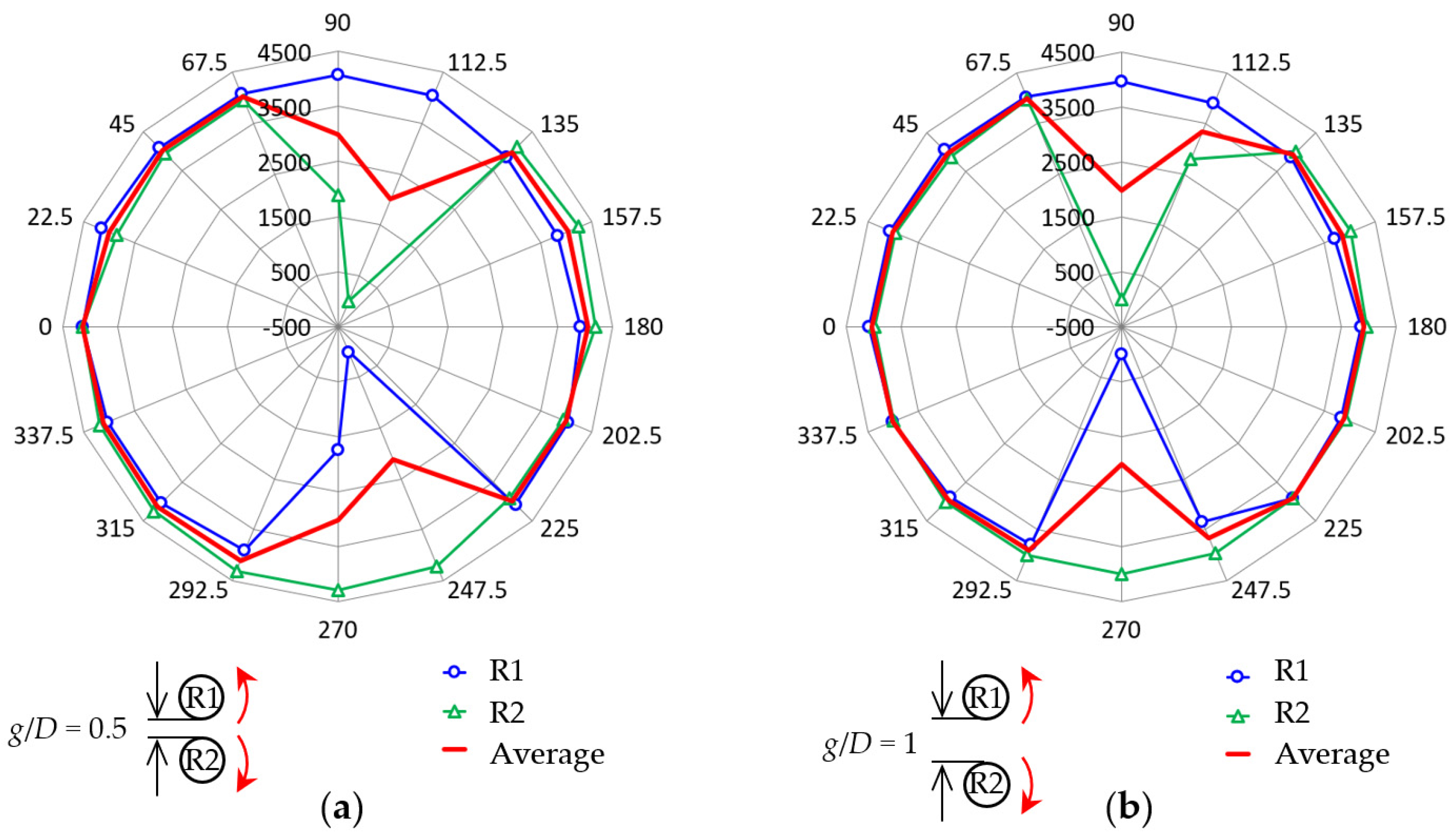
Figure 13 shows the 16-wind-direction dependence of the rotational speed in the CO configuration. The surrounding numbers indicate the wind direction θ (°). At wind direction θ = 90°, called the tandem co-rotating (TCO) layout, the rotational speed of the downwind rotor R2 decreases considerably (Figure 13b) or R2 stops (Figure 13a). This happens because of the wake of upstream rotor R1, as in the cases in Figure 11a (V = 12 m/s) and Figure 10a (V = 10 m/s). Interestingly, R2 also stops at θ = 112.5°. This can be explained by the existence of a deflected wake flow of R1 toward R2 by the Magnus effect [25]. Huang et al. [26] reported “wake shape deformation and deflection” of a VAWT using advanced robotic PIV. Strom et al. [1] have shown coherent structures in the wake of a vertical-axis turbine in a water channel experiment, in addition to the wake deflection (see their Figure 5). Furthermore, they have explained the mechanisms for the wake asymmetry using forces acting on the blade (see their Figure 6).

Sogo et al. [24] have reported this deflected wake in the cases of TCO and TIR layouts by visualizing the streak lines with a smoke-wire method in their Figure 4 and Figure 5. In Figure 13, the same phenomena (decrease in rotational speed of R1 or stoppage of R1) can be confirmed at θ = 270° and 292.5°, which are in origin symmetry for θ = 90° and 112.5°, respectively. Therefore, these phenomena ensure the repeatability of the experiment explained in Section 2.3. Sahebzadeh et al. [21] have defined the wind direction near the TCO layout (θ = 90–120° or θ = 270–300° and g/D < 4 in our coordinate) as the “wake-interaction regime” with low total performance in the TCO layout. This concurs well with our findings showing an origin-symmetrical distribution in the CO configuration.

Figure 14 shows the 16-wind-direction dependence of the rotational speed in the IR configuration. At wind direction θ = 90°, called the tandem inverse-rotating (TIR) layout, the rotational speed of the downwind rotor R2 decreases considerably (Figure 14a) or R2 stops (Figure 14b). This is the result of a wake interference, caused by the upwind rotor R1, with downwind rotor R2, as in the case in Figure 10b (V = 10 m/s). At θ = 112.5°, although R2 stops in the case of g/D = 0.5, it continues to rotate in the case of g/D = 1. In Figure 14, a slowdown in rotational speed or stopping of R1 can also be confirmed at θ = 270° and 247.5°, which are in line symmetry for θ = 90° and 112.5°, respectively.

This line symmetry is seen with respect to the line connecting the wind direction of θ = 0° and 180°. Consequently, the size of the left half area surrounded by red lines (indicating the average rotor speed of R1 and R2) and the line connecting the wind direction of θ = 90° and 270° is larger than the size of the corresponding right half area. This imbalance is emphasized with the decrease in g/D, as predicted by the numerical simulation by Hara et al. [13] (see their Figure 13b,d,f). In contrast, unnatural increases in power in the case of tandem layout are reported by Dabiri [3], based on field measurements (see their Figure 4), and Zanforlin and Nishino [6] (see their Figure 15), conducted by 2D numerical simulation. The former is seen in a wind direction of approximately θ = 110° and 290° (approximately 20° and 200° in their coordinates). The latter is seen in a wind direction of approximately θ = 90° (approximately γ = 90° in their coordinate). The line-symmetrical distribution of the wind-direction dependence in the IR configuration was also seen in the results of De Tavernier et al. [12], obtained using the 2D panel/vortex method (see their Figure 9), though they do not mention it. However, increases seen in their results for approximately θ = 45°, 135°, 225°, or 315° are unexplained.

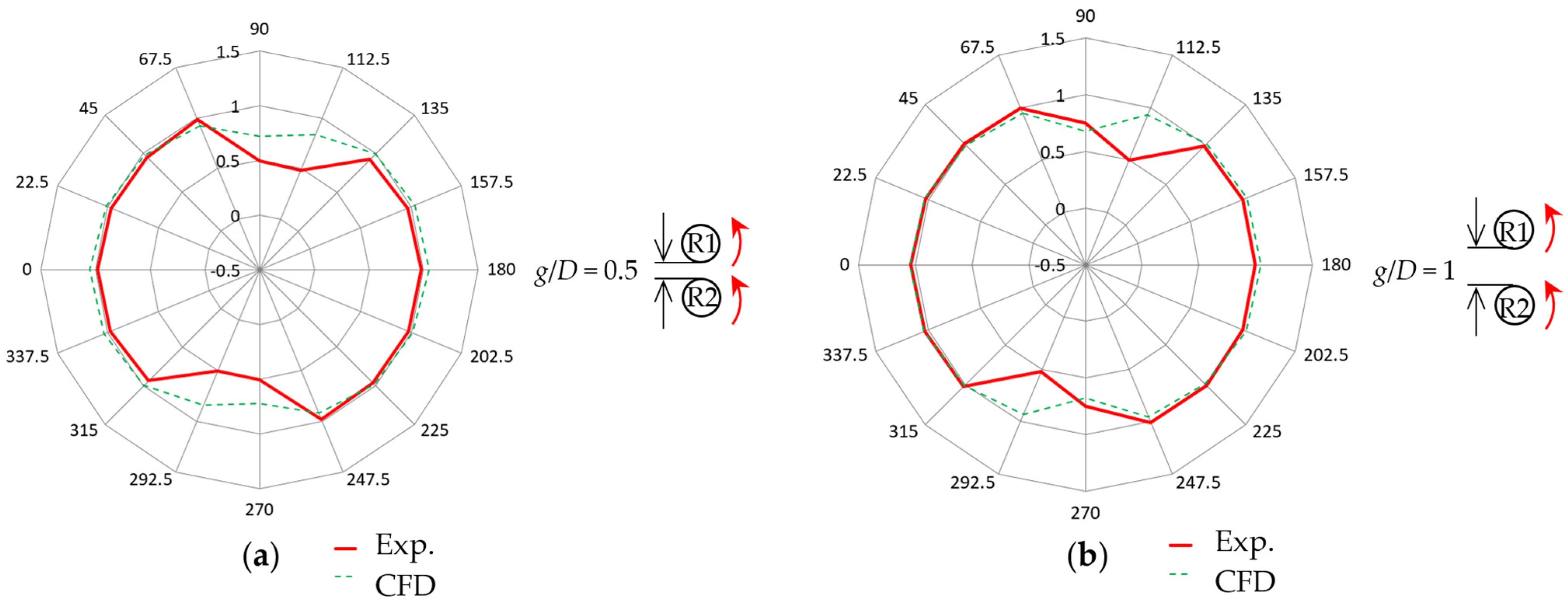
Next, we compare the experimental results with those obtained by 2D CFD [13] conducted by our group. Figure 15 depicts the comparison between the experimental and CFD results on 16-wind-direction dependence of the average normalized rotational speed in the CO configuration. In each figure, the red line represents the experimental results and the green dotted line shows the CFD results. Decreases in the average rotational speed on the TCO layout (θ = 90° and 270°) and near the tandem layout (θ = 112.5° and 292.5°) are seen in both the experimental and CFD results. This origin-symmetrical distribution on 16-wind-direction dependence in the CO configuration can be confirmed for g/D = 0.5 and 1. At θ = 112.5° and 292.5°, the decrease in rotational speed occurs more explicitly in the experimental results compared to the CFD results. This implies that the wake deflection, accompanied by the stopping of a downwind rotor, in the 3D experiment is stronger than that of the 2D CFD.

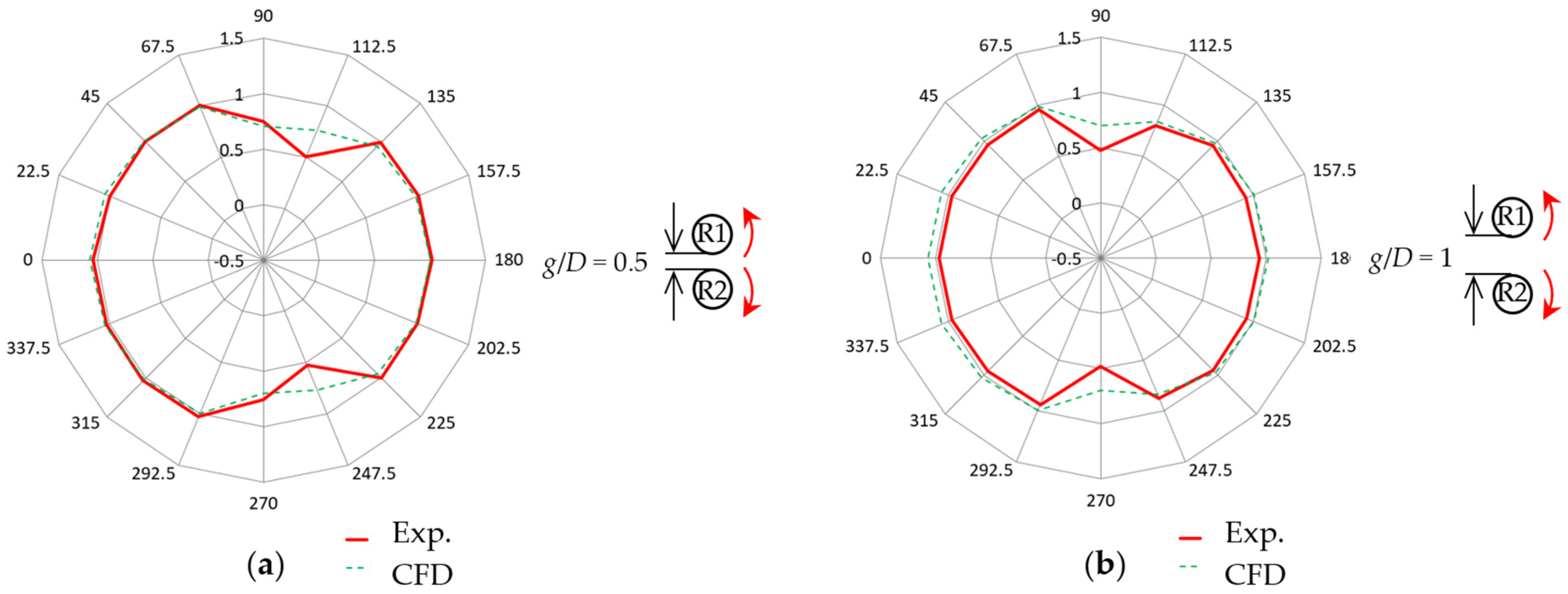
Figure 16 presents a comparison between the experimental and CFD results on the 16-wind-direction dependence of the average normalized rotational speed in the IR configuration. The CFD results also show an obvious slowdown in the average rotational speed in the TIR layout (θ = 90° and 270°) and near the tandem layout (θ = 112.5° and 247.5°). This supports the experimental results showing the line-symmetrical distribution on 16-wind-direction dependence in the IR configuration.

3.3. Wind-Direction Dependence of a Trio of VAWTs (12 Wind Directions)

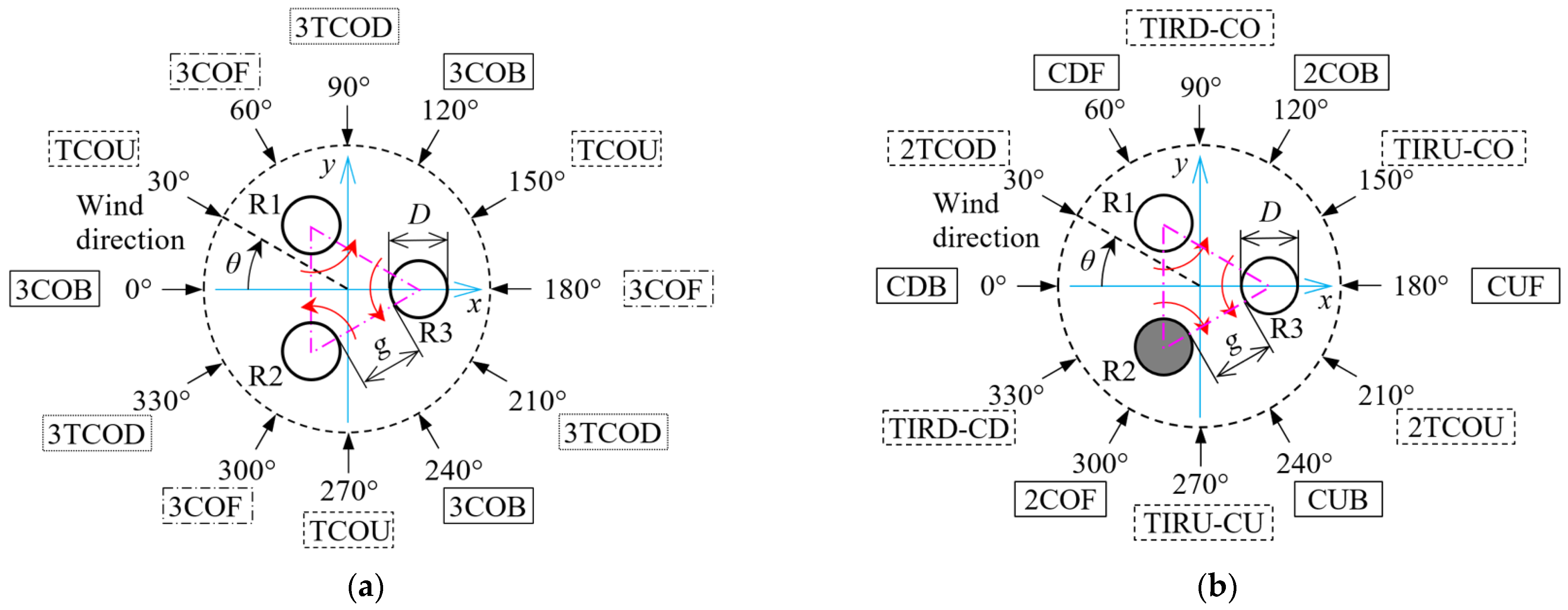
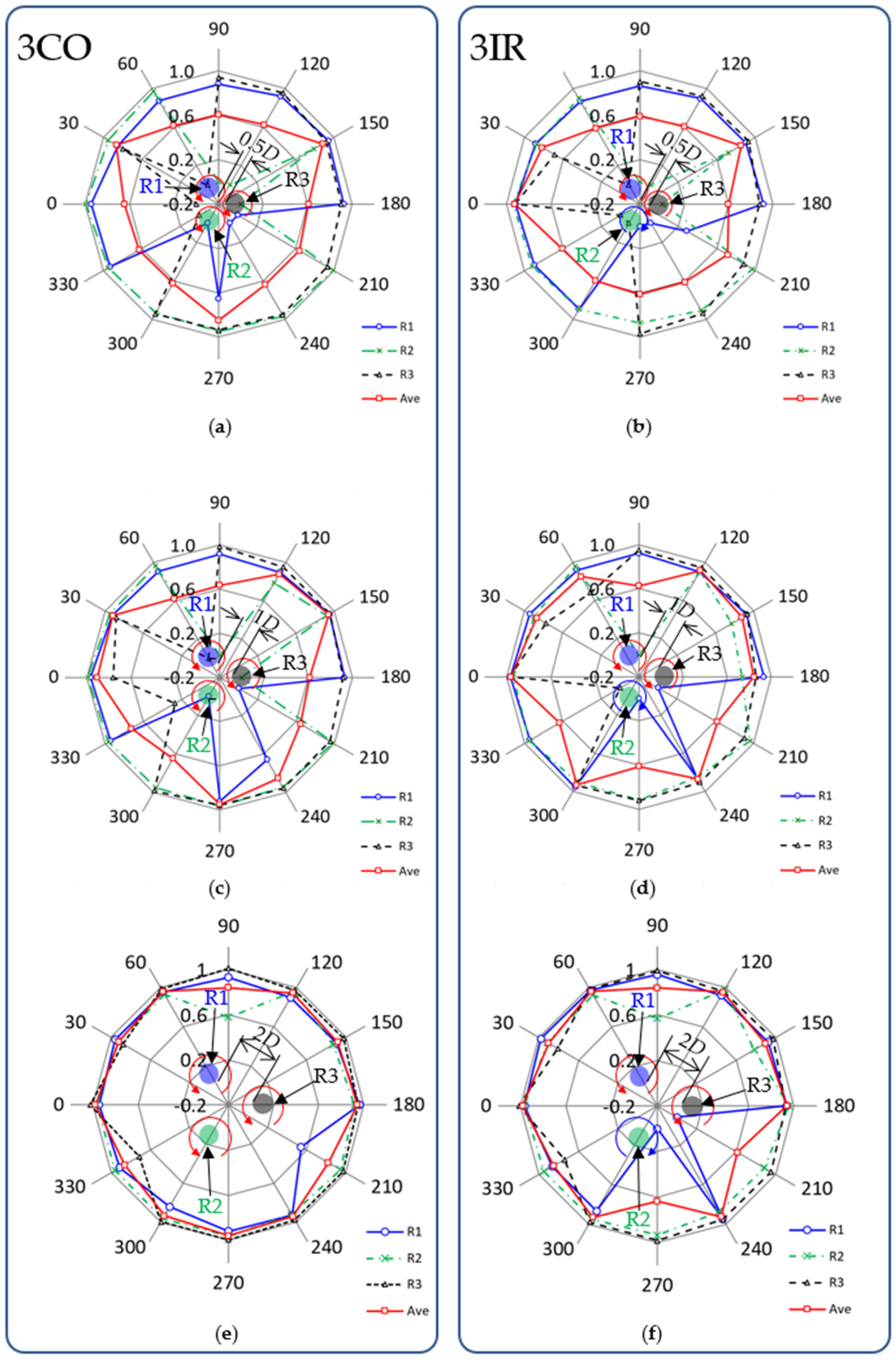
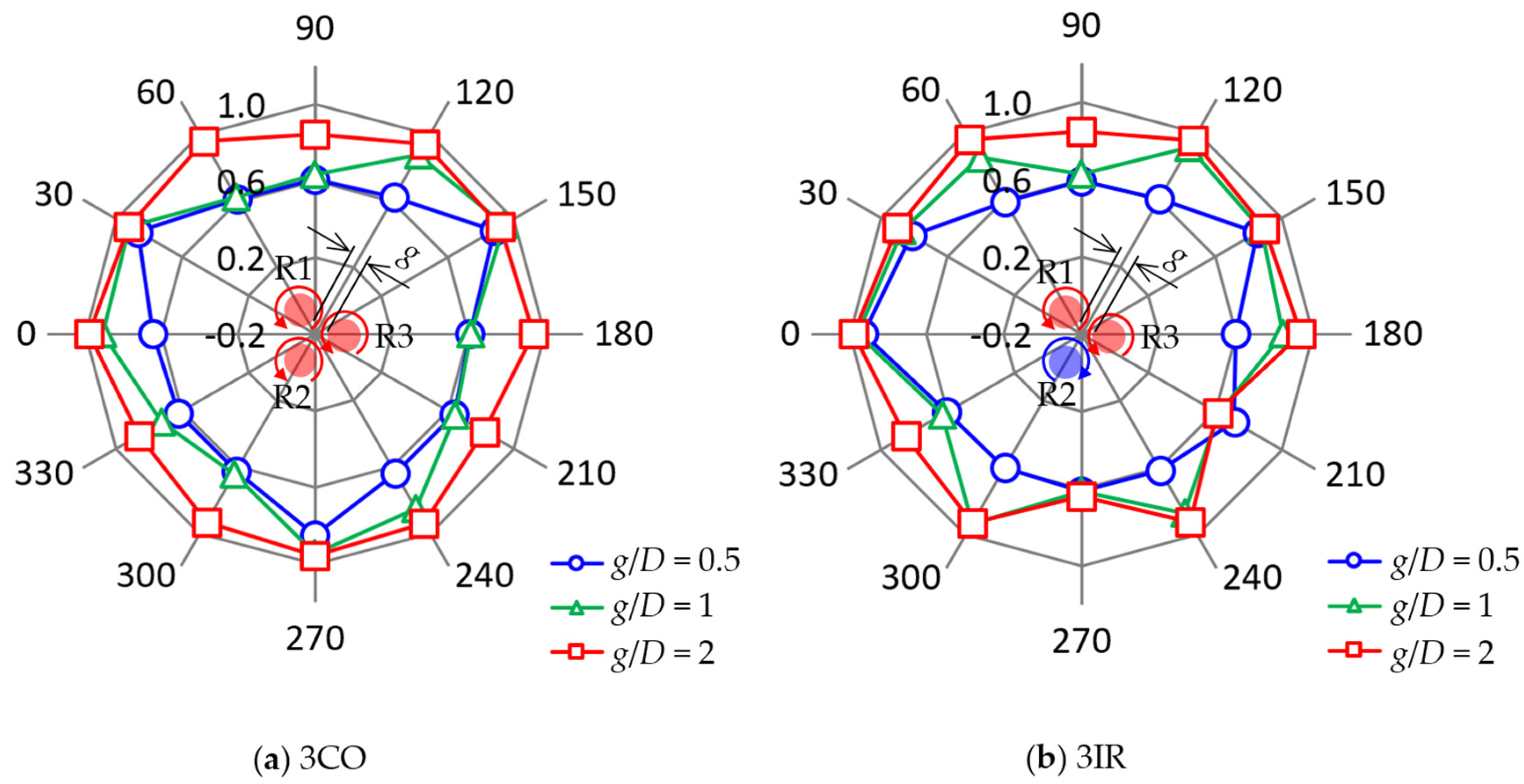
Figure 17 shows the 12-wind-direction dependence of the normalized rotational speed N_norm in the 3CO and 3IR configurations. In each figure, the blue circles indicate the rotational speed N of Rotor 1 (R1), the green crosses plot the N of Rotor 2 (R2), and the black triangles show the N of Rotor 3 (R3). The red squares represent the average rotor speed of R1, R2, and R3, defined as N_norm, ave.

First, we investigate the 3CO configuration in Figure 17a,c,e. At wind direction θ = 0°, called 3COB (see Figure 4a), the downwind rotor R3 stops at the smallest gap of g/D = 0.5 (Figure 17a) but R3 rotates faster with increasing the gap (Figure 17c,e). At wind direction θ = 30°, called TCOU, all rotors rotate at a relatively high speed, with the average rotational speed of the three rotors (N_norm,ave) reaching a maximum value at g/D = 0.5 and 1 (Figure 17a,c). At θ = 60°, called 3COF, one of the downwind rotors, R3, stops rotating at g/D = 0.5 and 1 (Figure 17a,c). Similarly, at θ = 90°, called 3TCOD, the downwind rotor R2 stops at g/D = 0.5 and 1 (Figure 17a,c). In this layout, a significant decrease in the rotational speed of R2 occurs, even in the largest gap of g/D = 2 (Figure 17e). As a result, the average rotational speed N_norm,ave is remarkably low in the 3TCOD. As explained in Section 2.4, the same layout occurs in every 120° in the 3CO configuration. In fact, the experimental results (Figure 17a,c,e) show the excellent rotational symmetry for the average normalized rotational speed N_norm,ave.

Second, we examine the 3IR configuration in Figure 17b,d,f. At wind direction θ = 0° (CDB; see Figure 4b), the downwind rotor R3, in addition to the upwind rotors (R1 and R2), continues to rotate even at the smallest gap of g/D = 0.5 (Figure 17b). This completely differs from the result in 3COB (θ = 0° in the 3CO layout). The average rotational speed of the three rotors, N_norm,ave, in the 3IR configuration reaches its maximum value at θ = 0° (i.e., CDB) at g/D = 0.5, 1, and 2 (Figure 17b,d,f). Hence, N_norm,ave in other layouts tends to have a much smaller value than it does in CDB, especially in the cases with a smaller gap distance. Although we do not explain all the layouts in detail here, the experimental results shown in Figure 17b,d,f prove that there is no rotationally symmetric distribution in N_norm,ave, as expected by the 12 independent layouts in the 3IR configuration explained in Section 2.4.

Hezaveh et al. [4] termed the mean value of three turbines as “cluster-averaged power.” For θ = 60°, they suggested the best gap ratios of 2, 3, and 4 with the highest cluster-averaged power value (see their Figure 8). These values support our results that the best gap ratio is g/D = 2 with maximum N_norm,ave value (Figure 17).

Here, we define the footprint radius R_foot and the footprint area A_foot of a trio of rotors, as in Equations (3) and (4). R_foot is the radius of the circular region that connotes the three rotors with a gap distance of g. The second term of the right hand of Equation (3) represents a distance from the center of the rotor trio to the corner of an equilateral triangle (lavender dash-dotted line in Figure 4). Since the diameter of each rotor D is 50 mm, the values of R_foot at g = 25, 50, and 100 mm are 68.30, 82.74, and 111.60 mm, respectively. The A_foot values at g = 25, 50, and 100 mm are then 0.01466, 0.02150, and 0.03913 m², respectively. We define the simple average of the N_norm,ave of the 12 wind directions as the N_{norm, 12-wind}.

Table 3. Comparison of average normalized rotational speed N_{norm, 12-wind} and 3N_{norm, 12-wind}/A_foot in a trio of VAWT models in an isotropic 12-directional wind speed.

Average Speed	g/D = 0.5		g/D = 1		g/D = 2
	3CO	3IR	3CO	3IR	3CO	3IR
Nnorm, 12-wind (-)	0.686	0.677	0.778	0.801	0.918	0.869
3Nnorm, 12-wind/Afoot (-/m2)	140.4	138.6	108.5	111.7	70.4	66.6

lists the values of N_{norm, 12-wind} based on the wind-tunnel experiments and those multiplied by 3 (i.e., the number of rotors) divided by the corresponding A_foot.

By referring to Table 3, the value of N_{norm, 12-wind} increases with an increase in g/D. This gap dependence is emphasized by the plots in Figure 18, in which N_norm,ave of the different rotor spacings are presented in one radar chart for 3CO and 3IR, respectively. In each figure, the blue circles indicate the average normalized rotational speed N_norm,ave at g/D = 0.5, the green triangles plot the N_norm,ave at g/D = 1, and the red squares show the N_norm,ave at g/D = 2.

In contrast, the performance indicated by 3N_{norm, 12-wind}/A_foot in a unit footprint area shows the opposite tendency, i.e., the advantage of a smaller rotor spacing (see Table 3). However, it is crucial to contemplate not only the performance (wind-direction dependence in N_{norm, 12-wind} or 3N_{norm, 12-wind}/A_foot) of a trio of turbines, but also the velocity deficit of the wake flow.

This interference between a trio and the other trios is essential for future research on the design of an optimal layout of the three-turbine array or multi rotor systems with very many rotors (e.g., [27]).

$$R_{foot}=\frac{D}{2}+\frac{g+D}{\sqrt{3}}$$

(3)

$$A_{foot}=\pi R_{foot}{}^2$$

(4)

Now, we define another normalized rotational speed, N_norm,bi-wind, in Equation (5). Here, N_{norm,ave, 0°} and N_{norm,ave, 180°} are average normalized rotational speeds of parallel-like layouts at θ = 0° and θ = 180°, respectively. Therefore, N_norm,bi-wind indicates the performance of a trio of turbines in an isotropic bidirectional wind speed. An example of the bi-wind in nature is a daytime sea breeze or a nighttime land breeze.

Table 4. Comparison of normalized rotational speed N_norm,bi-wind and 3N_norm,bi-wind/A_foot in a trio of VAWT models in an isotropic bidirectional wind speed.

Average Speed	g/D = 0.5		g/D = 1		g/D = 2
	3CO	3IR	3CO	3IR	3CO	3IR
Nnorm,bi-wind (-)	0.629	0.763	0.762	0.903	0.960	0.961
3Nnorm,bi-wind/Afoot (-/m2)	128.8	156.1	106.3	126.0	73.6	73.7

shows the values of N_norm,bi-wind for different gap ratios. Table 4 also contains the values of 3N_norm,bi-wind/A_foot, which indicates the advantage of a smaller rotor spacing. As shown in Table 4, the 3IR configuration yielded a higher average rotational speed than the 3CO arrangement at any rotor spacing in the ideal bidirectional wind conditions. It is interesting that the change in wind from 12-wind-direction (Table 3) to 2-wind-direction (Table 4) acts negatively in the 3CO configuration but positively in the 3IR configuration, on VAWT performance.

$$N_{norm, bi-wind}=\frac{N_{norm, ave, 0°}+N_{norm, ave, 180°}}{2}$$

(5)

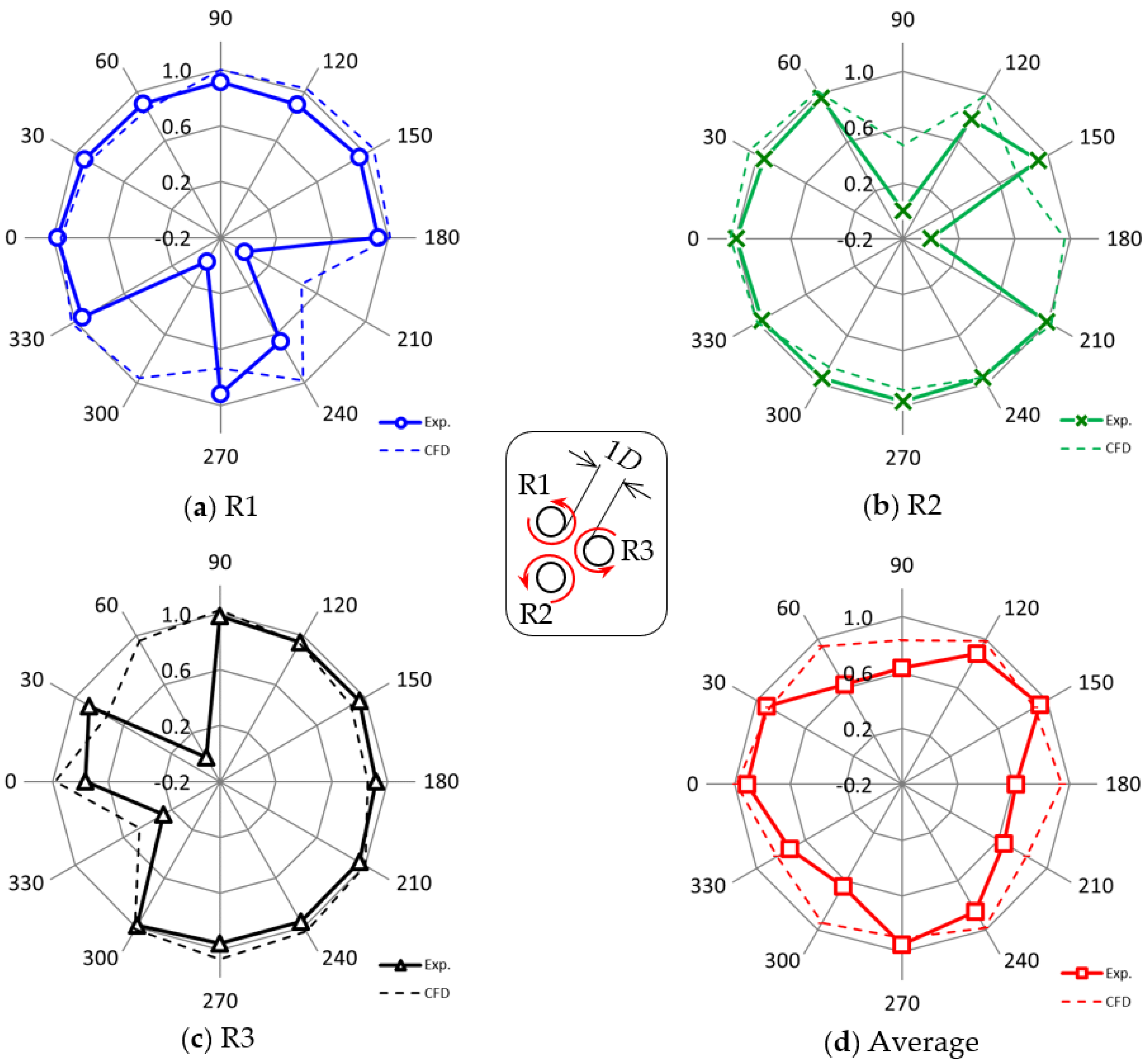
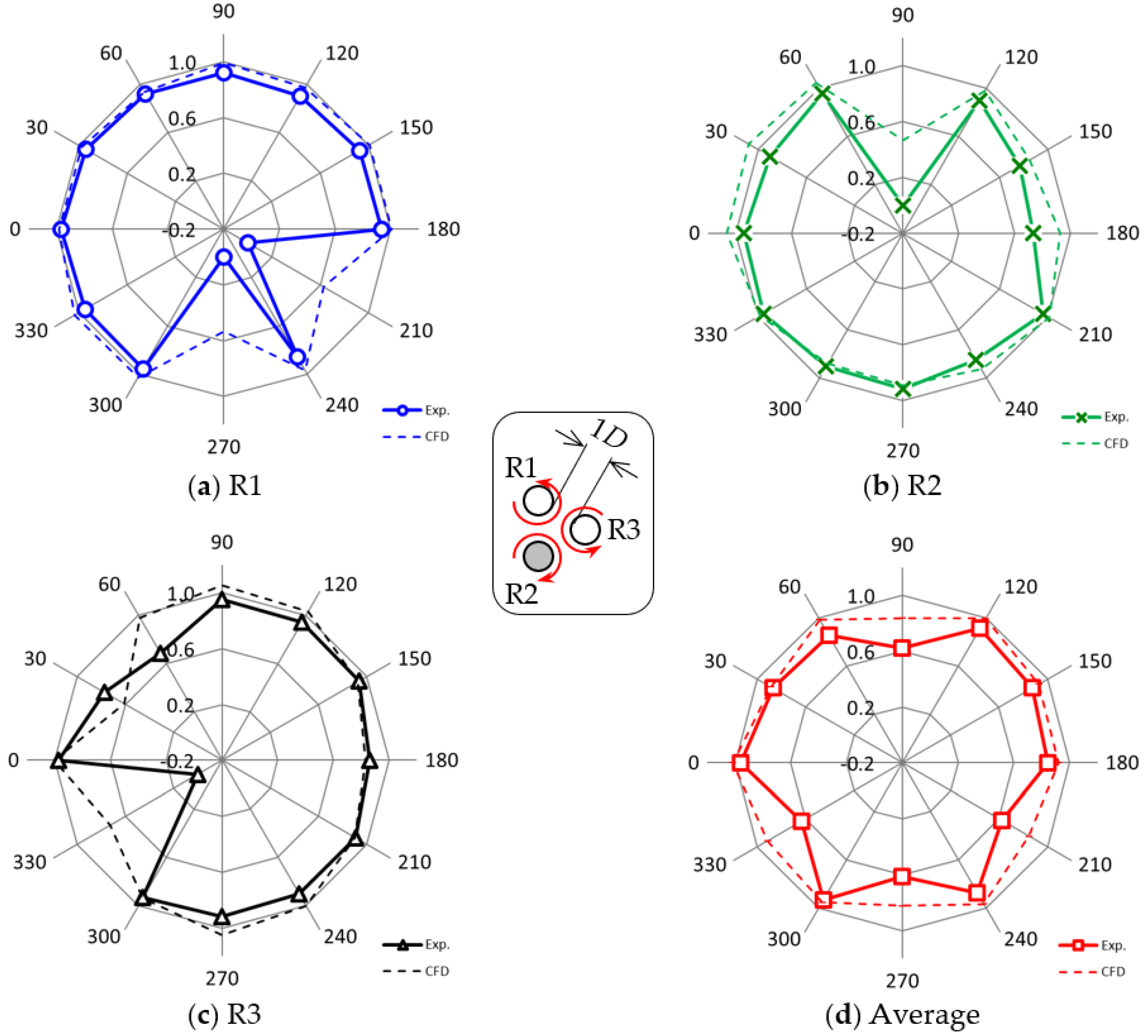
Figure 19 and Figure 20 compare the experimental results with corresponding 2D CFD results with the DFBI method [16] for the 3CO configuration and the 3IR configuration, respectively. As for the rotational direction and the gap length (g/D = 1), refer to the inset in Figure 19 and Figure 20. Broadly speaking, the speed-down tendencies of the downwind rotor are confirmed in both the experimental and the CFD results.

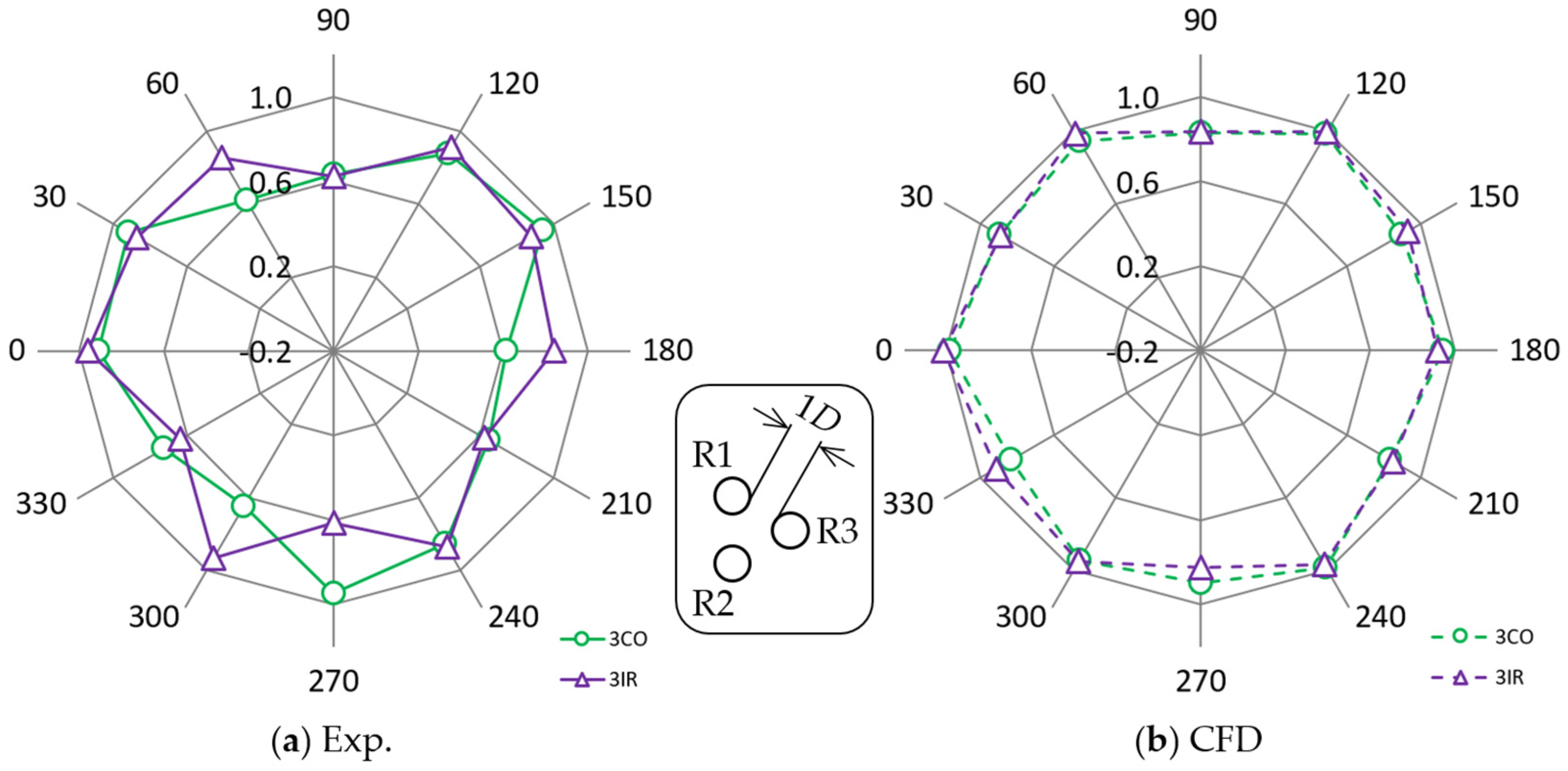
Next, we examine the difference between the 3CO and 3IR configurations. Figure 21 plots average normalized rotational speed in a trio of VAWT models at g/D = 1. The green circle and the purple triangle indicate the 3CO and 3IR, respectively. Figure 21a shows the experimental results with solid lines, while Figure 21b presents the CFD results with broken lines. It is worth noting that θ = 60° in 3IR (CDF) with a higher N_norm,ave value is an advantageous wind direction against θ = 60° in the 3CO (3COF).

On the other hand, θ = 270° in 3IR (TIRU-CU) with a lower N_norm,ave value is a disadvantageous wind direction against θ = 270° in 3CO (TCOF). In total, the value of N_{norm, 12-wind} (the simple average of the N_norm,ave of the 12 wind directions) of 0.801 of the 3IR is 3% larger than 0.778 of the 3CO (see Table 3).

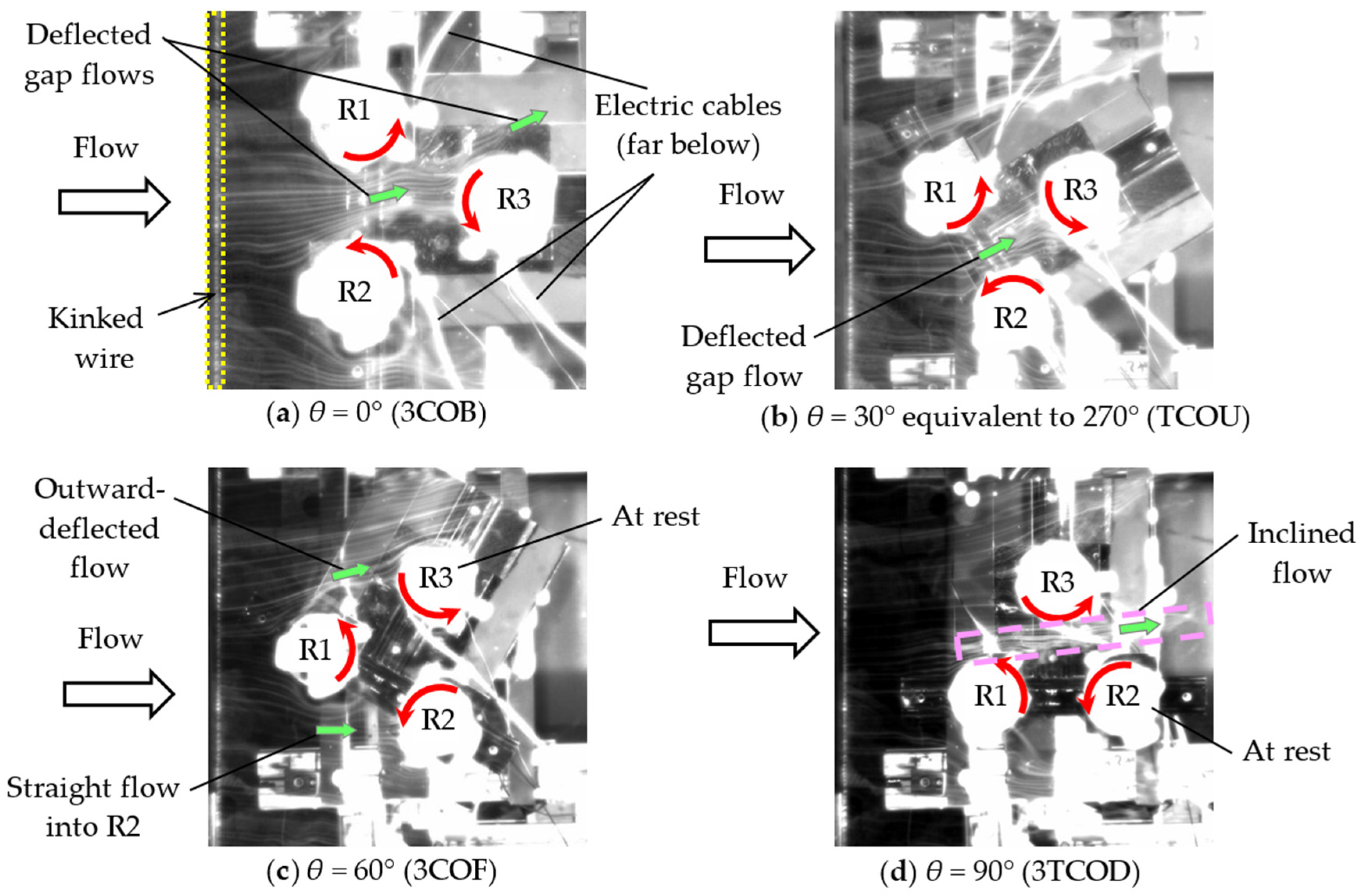
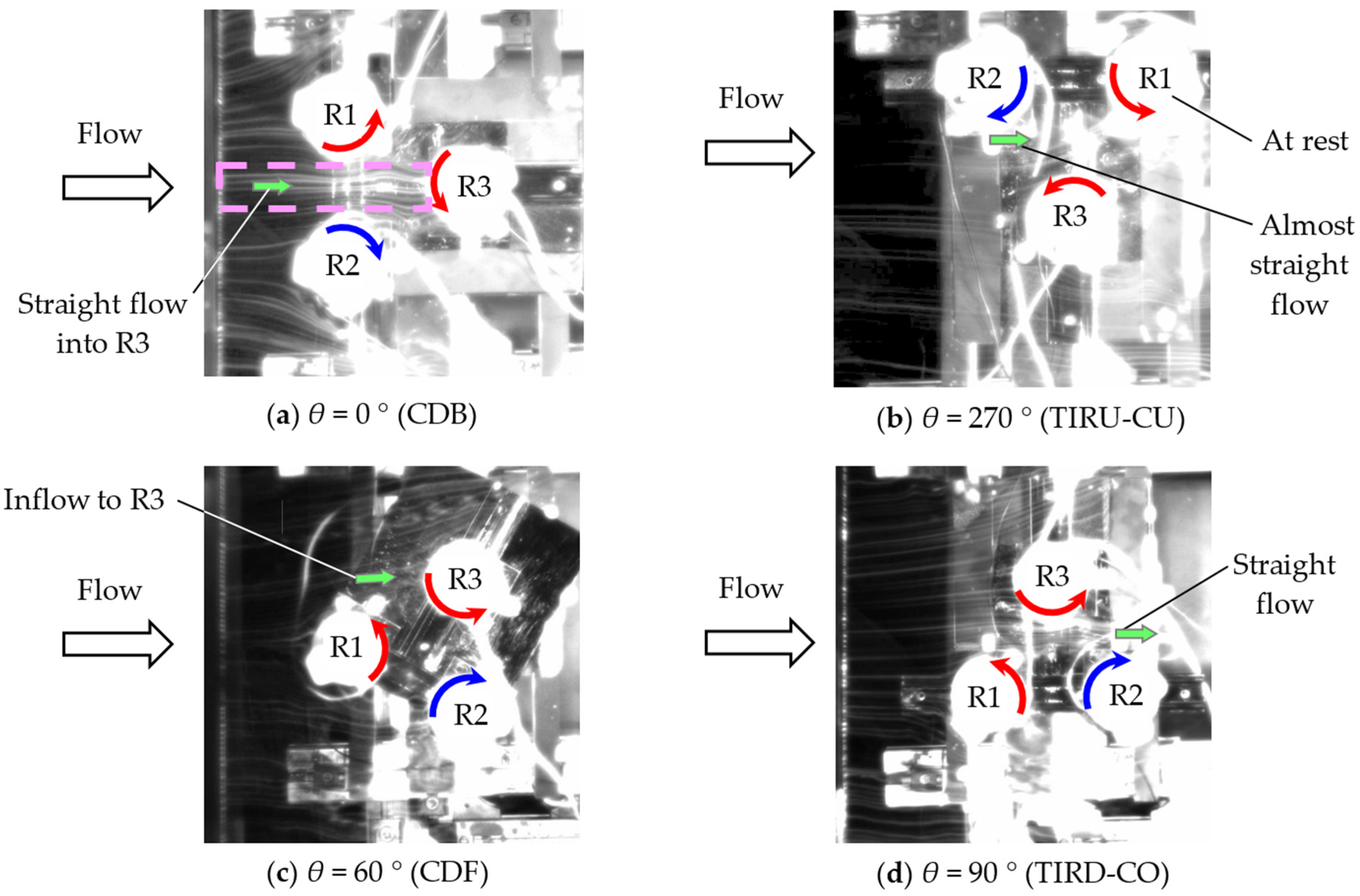
Figure 22 and Figure 23 show the streak lines observed using a smoke-wire method in the cases of the 3CO configuration and 3IR configuration, respectively. A stainless-steel wire, which is enclosed in the yellow dotted frame in Figure 22a, was horizontally set 2.7D upstream of the center of a trio of rotors. The apparatus is the same as that used in [20]. The critical parameter in the visualization of the flow is the rotational speed N of each rotor in order to maintain the tip speed ratio λ = πDN/(60V). Since the ratio of a uniform velocity in visualization to rotational speed measurements at 12 m/s is 1/6, each rotor speed is precisely adjusted one-sixth of the rotational speed presented in Figure 17 by using a variable external resistance. Electric cables located far below the trio of turbines are also seen in the visualization, as shown in Figure 22a.

Figure 24 and Figure 25 present the distributions of the streamwise component of flow velocity conducted by the corresponding 2D CFD with the DFBI method [16] in the cases of the 3CO and 3IR configurations, respectively. The color in Figure 24 and Figure 25 indicates the magnitude of the velocity.

First, we explore the flow patterns in the 3CO configuration in Figure 22. At wind direction θ = 0°, called 3COB (see Figure 22a), the distances of the adjacent streak lines contract between the upwind rotors (R1 and R2), which implies the flow acceleration between R1 and R2. This is also confirmed in the CFD results in Figure 24a. Subsequently, the accelerated gap flow deflects toward the R1 side (upper-side) and flows partially into the downwind rotor (R3).

At wind direction θ = 30°, called TCOU, in which all rotors rotate relatively fast, the accelerated flow between R1 and R2 deflects toward the center of R3 in Figure 22b (see the relatively high-speed inflow shown in yellow just in front of R3 in Figure 24b).

At θ = 60°, called 3COF, the outward-deflected flow in front of R3 glanced off the outer edge (upper-side) of R3, as shown in Figure 22c and Figure 24c. Furthermore, the flow in front of R3 receives a negative effect from R2-driven induced velocity. This outward deflection is caused by R1- and R2-driven induced velocities, resulting in deceleration in front of R3. On the other hand, R1- and R3-driven induced velocities have an accelerating effect on the flow in front of R2. These results imply that much momentum flows into R2; subsequently, asymmetric wakes (accompanied by deflected gap flow between them) are generated behind R2 and R3, as shown in Figure 24c. These are the reasons for the stoppage of R3 (black triangle in Figure 17c).

The deflected gap flow from R2 to R3 can also be seen in a 3CO-like layout (not in an equilateral triangle) using three Savonius turbines conducted by Shaheen et al. [28] (see their Figure 19).

Similarly, at θ = 90°, called 3TCOD, the downwind rotor R2 stops, indicated by the green cross in Figure 17c (a remarkable decrease in the speed in CFD in Figure 19b), since the flow between R2 and R3 diverges toward the opposite side (upper-side) of R2 enclosed by the lavender broken frame in Figure 22d. This can be seen in the inclined high-speed zone shown in the red contour in the CFD results in Figure 24d. Note that the low-speed inflow shown in green just in front of R2 in Figure 24d contrasts to the high-speed inflow in front of R3 seen in Figure 24b. Furthermore, the remarkably inclined wake zone enclosed by a red solid frame behind R2 is also contrastive to the straight wake zone, which is investigated later in Figure 25d in the opposite rotational direction of R2.

The above-mentioned flow deflection occurs through the combinational results of the Magnus effect and induced-velocity effect, originating from the three rotating turbines. Regarding the two parallel-like layouts in the 3CO configuration, the average rotational speed performance in the 3COB layout (θ = 0°) is greater than that in the 3COF layout (θ = 60°). Regarding the two tandem-like layouts in the 3CO configuration, the TCOU layout (θ = 30°) shows better performance compared with that in the 3TCOD layout (θ = 90°). These two relationships are common results obtained by the experiments and the CFD.

The former relationship (3COB > 3COF) is also confirmed in the normalized overall power coefficient by Zanforlin [22] for gap/D = 2 (see her Figure 10b), by Shaheen et al. [28] (see their Figures 22 (3COF-like layout) and 26 (3COB-like layout)), and by Silva and Danao [29] for gap/D = 1 (see their Table 6), with all based on 2D CFD.

Regarding the order of rotational speed N_norm, ave at θ = 60° in the 3CO configuration (i.e., 3COF), R2 rotates at the fastest speed for the gap/D = 0.5 and 1. This is the same result in three Savonius turbines in a 3COF-like layout independent of rotor gap ratio conducted by Shaheen et al. [27] (see their Figure 21) and on three Darrieus turbines in a 3COF layout by Silva and Danao [28] for gap/D = 1.

Next, we examine the flow patterns in the 3IR configuration in Figure 23. At wind direction θ = 0°, called CDB (see Figure 23a), the contracted streak lines between the upwind rotors (R1 and R2) directly flow into the downwind rotor (R3). The large high-speed zone surrounded by the three rotors is seen in the CFD results in Figure 25a. Therefore, the value of N_norm,ave in this layout takes the maximum value of 0.9618 among the whole 16 independent layouts (see Table 2). This value is 106% of 0.9087 obtained in the case of 3COB (θ = 0° in the 3CO layout). The corresponding 2D CFD shows 103% in this comparison (CDB to 3COB).

The order of rotational speed N_norm, ave at θ = 0° in the 3IR configuration (i.e., CDB) is R1 > Ave. > R2/R3, as seen in Figure 17d or Figure 17f for gap/D = 1 or 2. This agrees with the order of the power coefficient for CDB obtained by Zheng et al. [23] (see their Figure 19) based on 2D CFD.

At wind direction θ = 60°, called CDF, although the induced velocity of the upwind rotor (R1) causes negative effects on the flow before the downwind rotor (R3), the opposite rotation of R2 produces positive effects on the flow in front of R3. The wakes behind R2 and R3 show a relatively symmetric straight flow pattern enclosed by black solid frames in Figure 25c.

This indicates that the upper-side flow of R1 gives its streamwise momentum relatively directly into R3. This flow pattern is clearly different from that in the largely outward-deflected wake flow in the 3CO configuration at the same wind direction of θ = 60° (3COF). Hence, R3 continues to rotate in the case of CDF, which is in contrast to the result (R3 stopped) in the case of 3COF. This leads to a significant advantage in the N_norm,ave at the CDF layout (θ = 60° in the 3IR configuration) over N_norm,ave at 3COF, as seen in Figure 21 (indicated by CDF > 3COF).

At θ = 90°, called TIRD-CO, both flows of the upper and lower sides of R2 straightly move downstream, generating the above-mentioned streamwise wake zone behind R2 (Figure 25d).

At θ = 270°, called TIRU-CU (see Figure 23b), since the gap flow between R2 and R3 is almost straight in contrast to the largely deflected flow in Figure 22b, the gap flow in the TIRU-CU layout does not flow fully into the downwind rotor R1 but glances off the inner edge (lower-side) of R1.

Consequently, R1 stops to rotate in the experiment, or R1 takes the minimum N_norm,ave value in the CFD (see Figure 20a). Remember that the TCOU layout in Figure 22b for θ = 30° is equivalent to that in θ = 150° and 270° only for the 3CO configuration, as explained in Table 2. There is a remarkable difference in N_norm,ave between the TIRU-CU layout and the TCOU layout in the same wind direction (see Figure 21).

Finally, it is interesting to note that among the six parallel-like layouts (θ = 0°, 60°, 120°, 180°, 240°, and 300°), the N_norm,ave value in the 3IR configuration always exceeds that in the 3CO configuration in the experiments (see Figure 21a). In contrast, the N_norm,ave value in the 3IR configuration falls below that in the 3CO configuration regarding the six tandem-like layouts (θ = 30°, 90°, 150°, 210°, 270°, and 330°).

4. Conclusions

Our wind-tunnel experiments on the interaction between a pair/trio of closely spaced VAWTs have revealed a wind-direction dependence at a uniform wind speed.

For both the tandem co-rotating (TCO) and the tandem inverse-rotating (TIR) pair:

• The decrease in the rotational speed and rotor power of a pair of turbines arranged in tandem was demonstrated;
• The amount of decrease depended on the g/D ratio, with the value of the rotational speed of the downwind rotor 75–80% of that of an isolated rotor even at g/D = 10, although the value of the upstream rotor was 100%;
• The corresponding power value of the downwind rotor was approximately 80%.

In the 16-wind-direction experiments on a pair of VAWTs:

• The “origin-symmetrical” distribution of the average rotational speed of two rotors in the CO pair configuration and the “line-symmetrical” distribution in the IR pair configuration were demonstrated;
• The existence of a deflected wake flow accounted for the decreasing tendency of the rotational speed at θ = 90°, 112.5°, 270°, and 292.5° (showing the origin symmetry) in the CO pair configuration;
• A wake interaction caused a slowdown tendency at θ = 90°, 112.5°, 270°, and 247.5° (showing the line symmetry) in the IR pair configuration.

We examined 16 independent layouts (eight parallel-like layouts and eight tandem-like layouts) in the experiments on a trio of VAWTs:

• The performance in a unit footprint area demonstrated the advantage of a smaller rotor spacing for not only the average of 12-directional wind (Table 3) but also the average of bidirectional wind (Table 4);
• The inverse-rotating trio (3IR) configuration takes a higher average rotational speed than the co-rotating trio (3CO) configuration at any rotor gap under the ideal bidirectional wind conditions;
• The maximum average rotational speed can be obtained at a wind direction of θ = 0° in the 3IR configuration, which is 6% faster than that in the 3CO configuration;
• The average rotor speed of the three rotors N_norm, ave is remarkably low at θ = 90°, 210°, and 330° in the 3CO configuration (3TCOD). The 3CO configuration demonstrates the “rotational symmetry” for N_norm, ave in every 120°;
• The 3IR configuration does not show the rotational symmetry for N_norm, ave, as expected.

The corresponding flow patterns and velocity fields have been discussed in detail, along with flow visualization and 2D CFD results obtained by adopting the DFBI method:

• The relationship 3COB > 3COF for N_norm, ave is explained by accelerated gap flows at θ = 0° and the decelerating effect on the flow at θ = 60°, in the 3CO configuration;
• The relationship CDF > 3COF for N_norm, ave is explained by straight wakes at θ = 60° in the 3IR configuration and asymmetric wakes at θ = 60° in the 3CO configuration.

For future work:

• We are confident that our research will serve as a base for future studies on designing a wind farm consisting of sets of these turbine pairs and trios. Further investigation on the wake interference between them is essential for future research on the design. We are currently making preparations for the wind-tunnel experiments with 12 BWTs to determine the optimal arrangement, supported by JSPS KAKENHI below.