Distributed Integral Convex Optimization-Based Current Control for Power Loss Optimization in Direct Current Microgrids
Abstract
:1. Introduction
2. DC Microgrid and Objective Function
2.1. Modeling of the DC Microgrid
2.2. Loss Modelling of the DC Microgrid
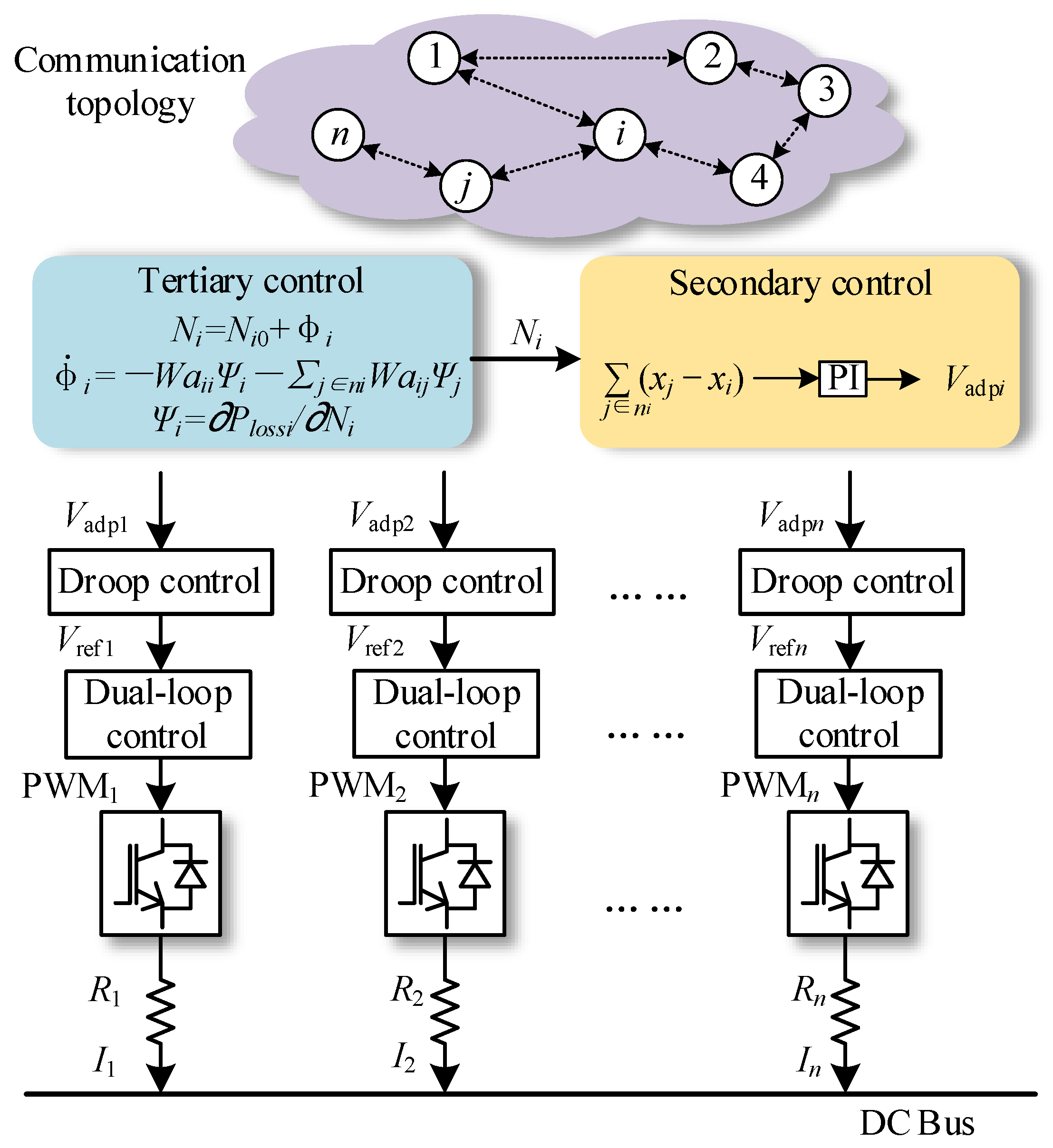
3. Hierarchical Control Design
3.1. DICOA
3.2. Lower Control Layers
- (1)
- With the use of the optimal current distribution coefficients derived by the DICOA, the current sharing error of the i-th DER can be calculated by
- (2)
- In the droop control part, the output voltage reference can be calculated as
- (3)
- For the voltage–current control, both the DC source current and the duty ratio are required to be regulated within the tolerances.
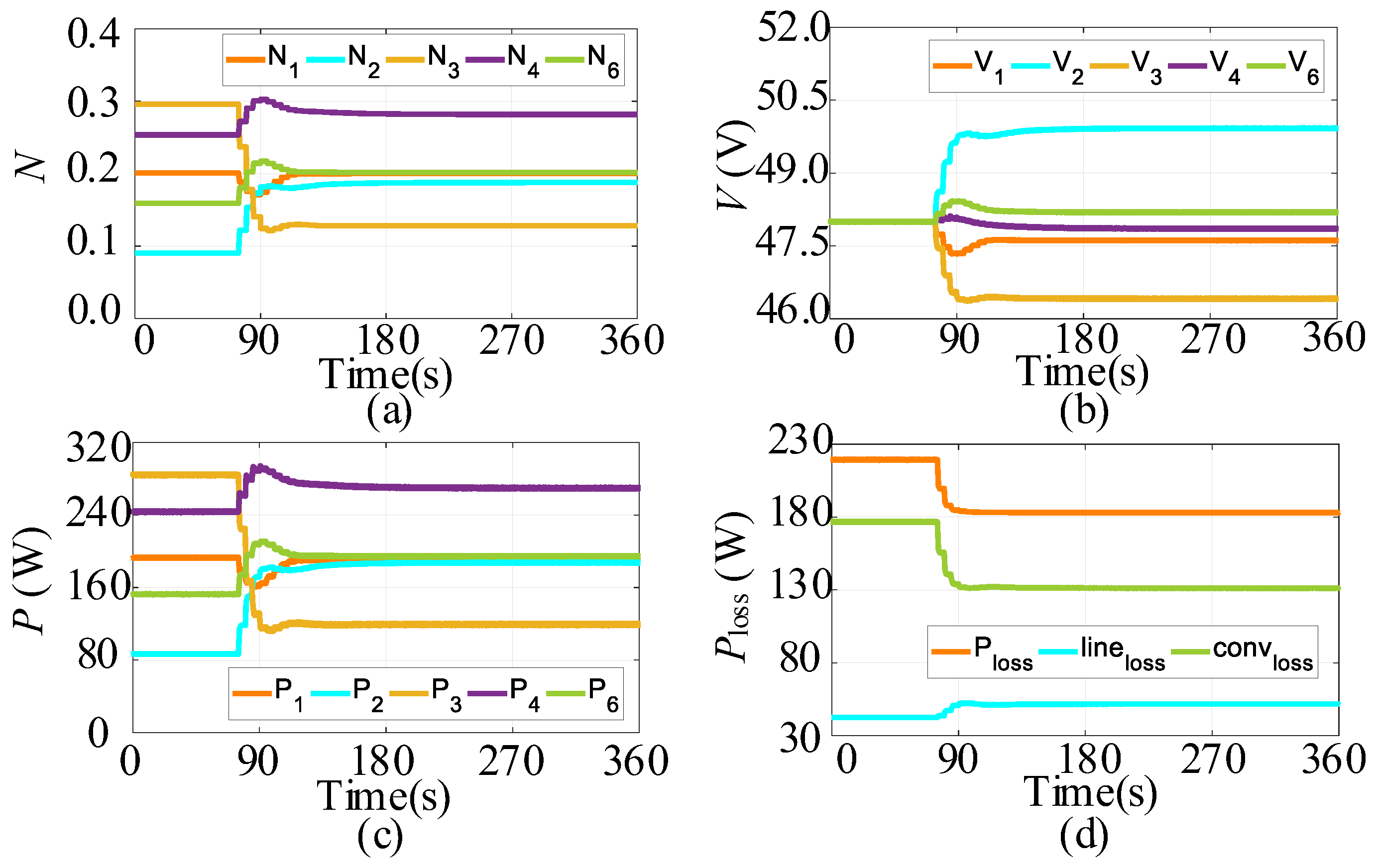
4. Simulation Results
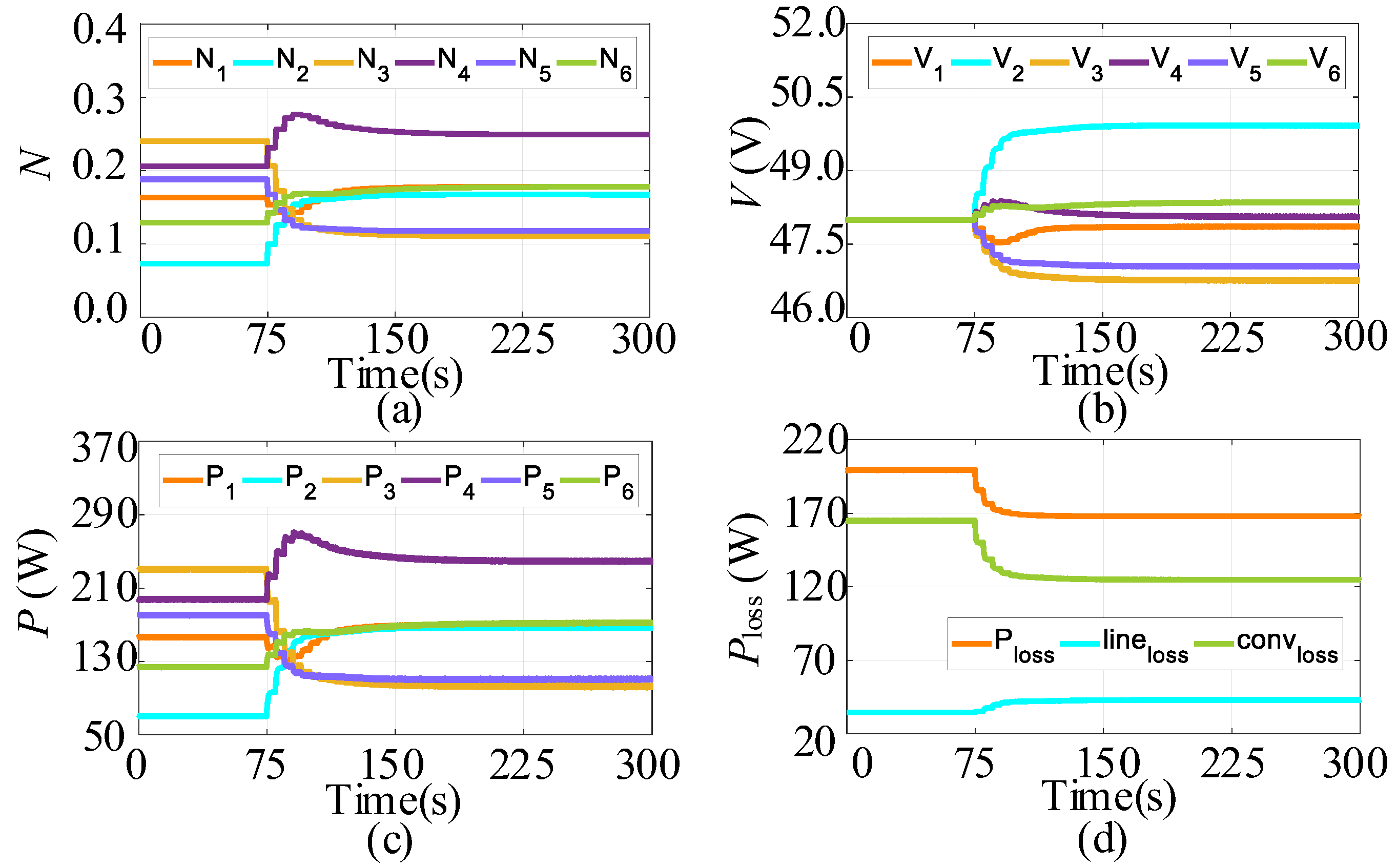
- Case 1: System Operation of the DC Electric Network Based on Six DERs
- Case 2: Output Power Limitation
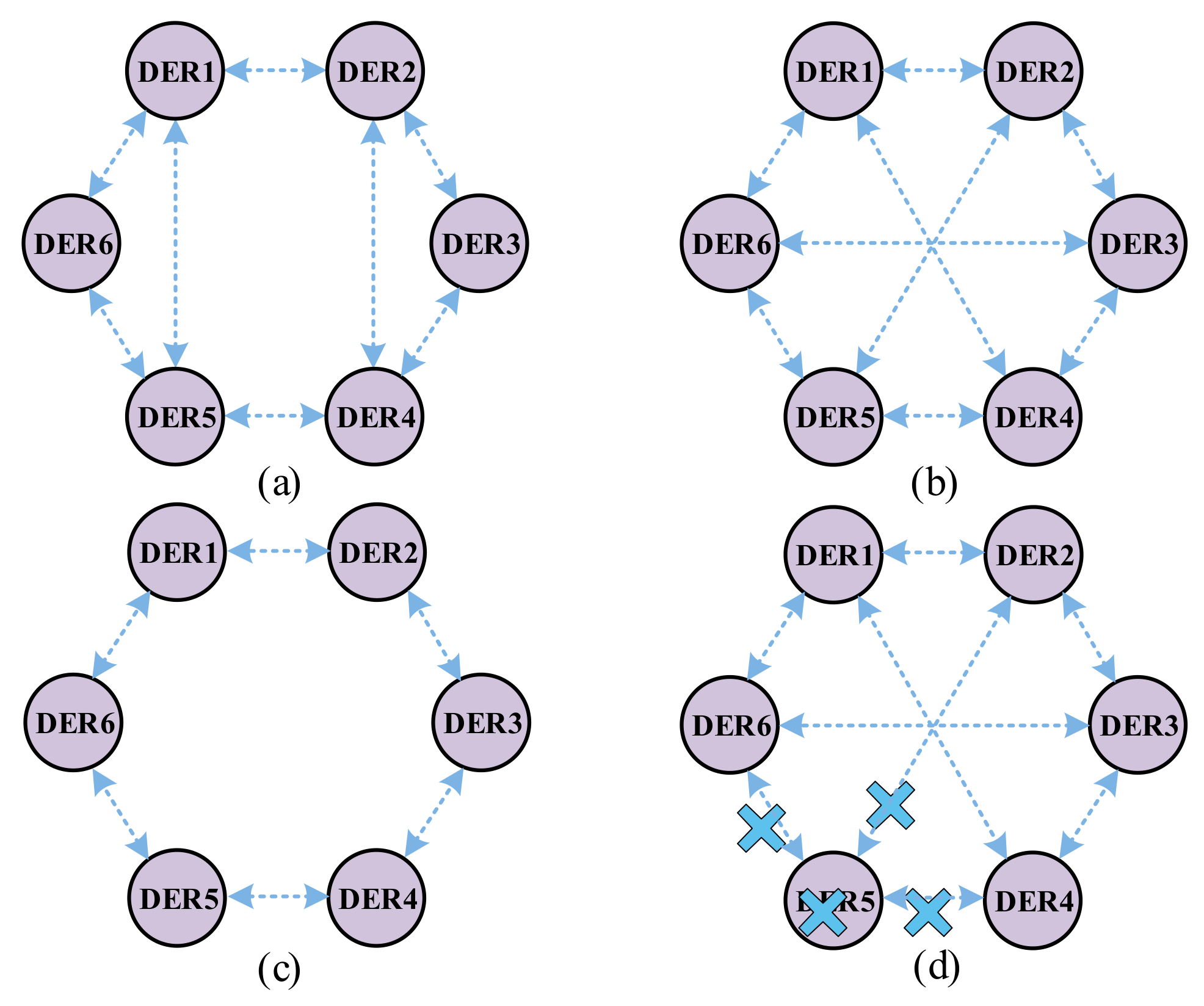
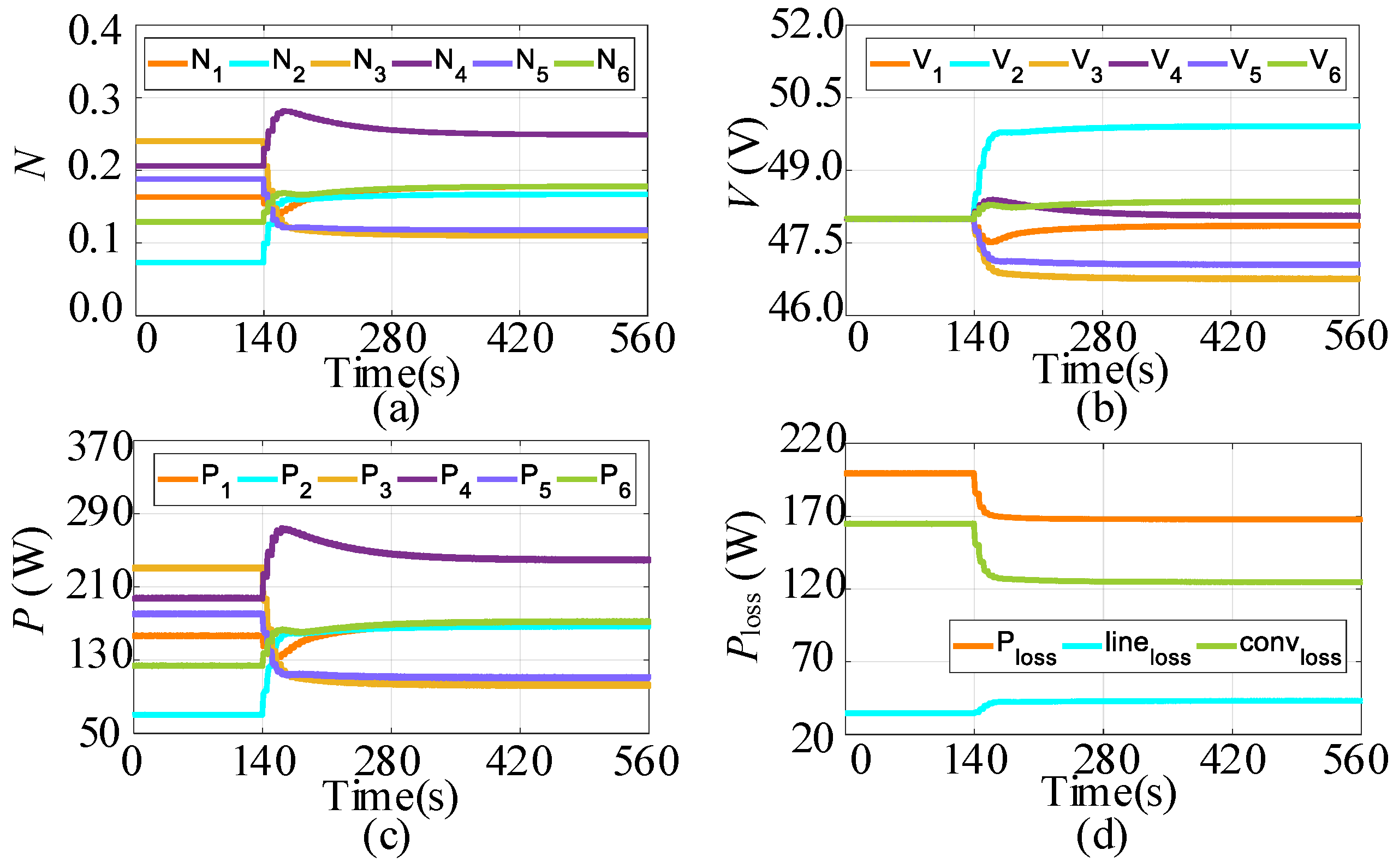
- Case 3: Communication Failure
- Case 4: Plug-Out of One DER
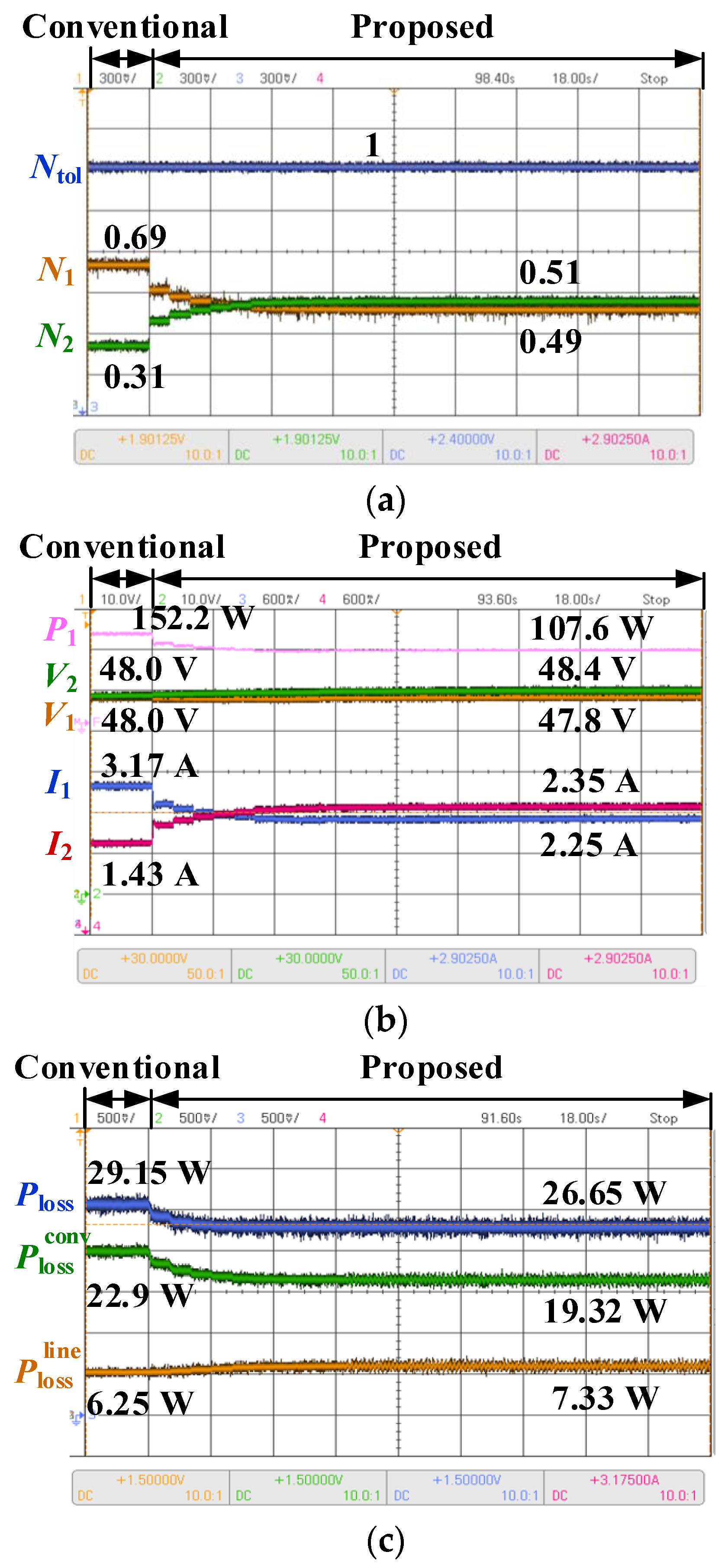
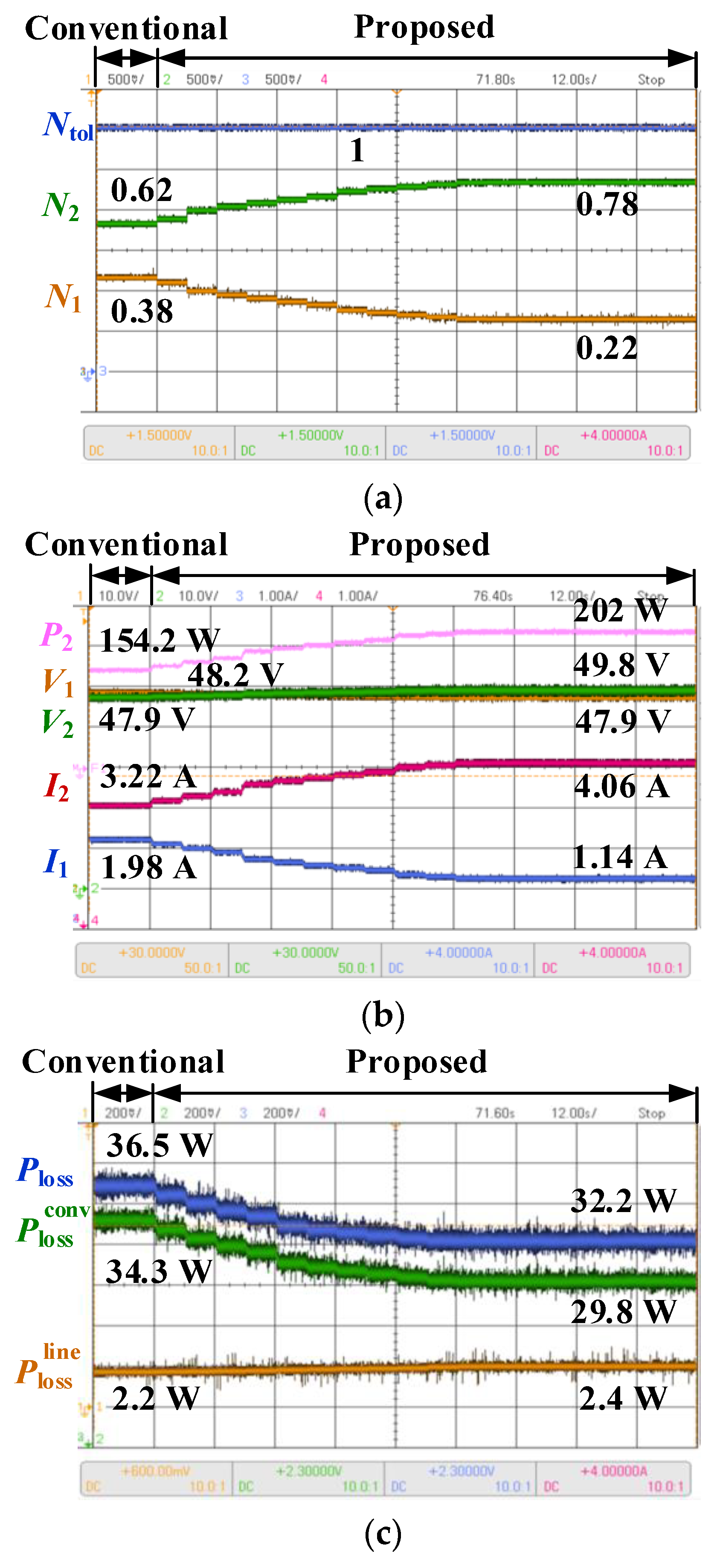
5. Experimental Results
- Scenario 1: Normal Operation
- Scenario 2: Injection Power Limitation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Babazadeh-Dizaji, R.; Hamzeh, M. Distributed hierarchical control for optimal power dispatch in multiple DC microgrids. IEEE Syst. J. 2020, 14, 1015–1023. [Google Scholar] [CrossRef]
- Jiang, Y.; Yang, Y.; Tan, S.C.; Hui, S.Y.R. Dual-ascent hierarchical control-based distribution power loss reduction of parallel-connected distributed energy storage systems in dc microgrids. IEEE J. Emer. Sel. Top. Ind. Electron. 2023, 4, 137–146. [Google Scholar] [CrossRef]
- Yang, Y.; Tan, S.C.; Hui, S.Y.R. Mitigating distribution power loss of DC microgrids with DC electric springs. IEEE Trans. Smart Grid 2018, 9, 5897–5906. [Google Scholar] [CrossRef]
- Pires, V.F.; Pires, A.; Cordeiro, A. DC Microgrids: Benefits, Architectures, Perspectives and Challenges. Energies 2023, 16, 1217. [Google Scholar] [CrossRef]
- Su, W.; Yun, S.; Li, H.; Lu, H.H.C.; Fernando, T. An MPC-based dual-solver optimization method for DC microgrids with simultaneous consideration of operation cost and power loss. IEEE Trans. Power Syst. 2021, 36, 936–947. [Google Scholar] [CrossRef]
- Fan, Z.; Fan, B.; Peng, J.; Liu, W. Operation loss minimization targeted distributed optimal control of DC microgrids. IEEE Syst. J. Early Access 2021, 15, 5186–5196. [Google Scholar] [CrossRef]
- Ren, Y.; Xu, M.; Zhou, J.; Lee, F.C. Analytical loss model of power MOSFET. IEEE Trans. Power Electron. 2006, 21, 310–319. [Google Scholar]
- Rodríguez, M.; Rodríguez, A.; Miaja, P.F.; Lamar, D.G.; Zúniga, J.S. An insight into the switching process of power MOSFETs: An improved analytical losses model. IEEE Trans. Power Electron. 2010, 25, 1626–1640. [Google Scholar] [CrossRef]
- Yuan, W.; Wang, Y.; Liu, D.; Deng, F.; Chen, Z. Efficiency-prioritized droop control strategy of AC microgrid. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 3, 2936–2950. [Google Scholar] [CrossRef]
- Wang, H.; Khambadkone, A.M.; Yu, X. Control of parallel connected power converters for low voltage microgrid-part II: Dynamic electrothermal modeling. IEEE Trans. Power Electron. 2010, 25, 2971–2980. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, D.L.Z.; Liu, P. A hierarchical control strategy of microgrids toward reliability enhancement. In Proceedings of the International Conference on Smart Grid (icSmartGrid), Nagasaki, Japan, 4–6 December 2018; pp. 123–128. [Google Scholar]
- Bartal, P.; Nagy, I. Game theoretic approach for achieving optimum overall efficiency in DC/DC converters. IEEE Trans. Ind. Electron. 2014, 61, 3202–3209. [Google Scholar] [CrossRef]
- Jiang, Y.; Yang, Y.; Tan, S.C.; Hui, S.Y.R. Power loss minimization of parallel-connected DERs in dc microgrids using a distributed hierarchical control. IEEE Trans. Smart Grid 2022, 13, 4538–4550. [Google Scholar] [CrossRef]
- Jiang, Y.; Yang, Y.; Tan, S.C.; Hui, S.Y.R. Distribution power loss mitigation of parallel-connected distributed energy resources in low-voltage DC microgrids using a Lagrange multiplier-based adaptive droop control. IEEE Trans. Power Electron. 2021, 36, 9105–9118. [Google Scholar] [CrossRef]
- Shi, M.; Chen, X.; Zhou, J.; Chen, Y.; Wen, J.; He, H. Advanced secondary voltage recovery control for multiple HESSs in a droop-controlled DC microgrid. IEEE Trans. Smart Grid 2019, 10, 3828–3839. [Google Scholar] [CrossRef]
- Cevher, V.; Becker, S.; Schmidt, M. Convex optimization for big data: Scalable, randomized, and parallel algorithms for big data analytics. IEEE Signal Process. Mag. 2014, 31, 32–43. [Google Scholar] [CrossRef]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Ali, S.; Zheng, Z.; Aillerie, M.; Sawicki, J.P.; Pera, M.C.; Hissel, D. A review of DC Microgrid energy management systems dedicated to residential applications. Energies 2021, 14, 4308. [Google Scholar] [CrossRef]
- Meng, L.; Shafiee, Q.; Trecate, G.F.; Karimi, H.; Fulwani, D.; Lu, X.; Guerrero, J.M. Review on control of DC microgrids and multiple microgrid clusters. IEEE J. Emerg. Sel. Topics Power Electron. 2017, 5, 928–948. [Google Scholar]
- Sahoo, S.; Mishra, S. A distributed finite-time secondary average voltage regulation and current sharing controller for DC microgrids. IEEE Trans. Smart Grid 2019, 10, 282–292. [Google Scholar] [CrossRef]
- Nasirian, V.; Davoudi, A.; Lewis, F.L.; Guerrero, J.M. Distributed adaptive droop control for DC distribution systems. IEEE Trans. Energy Convers. 2014, 29, 944–956. [Google Scholar] [CrossRef]
- Guo, F.; Wang, L.; Wen, C.; Zhang, D.; Xu, Q. Distributed voltage restoration and current sharing control in islanded DC microgrid systems without continuous communication. IEEE Trans. Ind. Electron. 2020, 67, 3043–3053. [Google Scholar] [CrossRef]
- Xing, L.; Xu, Q.; Guo, F.; Wu, Z.G.; Liu, M. Distributed secondary control for DC microgrid with event-triggered signal transmissions. IEEE Trans. Sustain. Energy 2021, 12, 1801–1810. [Google Scholar] [CrossRef]
- Poursafar, N.; Taghizadeh, S.; Hossain, M.J.; Guerrero, J.M. An optimized distributed cooperative control to improve the charging performance of battery energy storage in a multiphotovoltaic islanded DC microgrid. IEEE Syst. J. 2022, 16, 1170–1181. [Google Scholar] [CrossRef]
- Xiao, L.; Boyd, S. Optimal scaling of a gradient method for distributed resource allocation. J. Optimiz. Theory Appl. 2006, 29, 469–488. [Google Scholar] [CrossRef]



| Algorithms/Methods | Division | Iteration |
|---|---|---|
| Lagrange Multiplier method | ✓ | ✕ |
| Dual ascent algorithm | ✓ | ✓ |
| DICOA | ✕ | ✓ |
| Descriptions | Symbol | Value |
|---|---|---|
| Nominal DC bus voltage | Vnom | 48 V |
| Lower limit of the DC bus voltage | Vmin | 45.6 V |
| Upper limit of the DC bus voltage | Vmax | 50.4 V |
| Lower output power limit of the DERs | Pmin | 0 W |
| Upper output power limit of the DERs | Pmax | 350 W |
| Source voltage of the DERs | VSi | 24 V |
| Inductances of the converters | Li | 460 μH |
| Output capacitances of the converters | Ci | 10.1 μF |
| Line resistance of the DER1 | R1 | 0.53 Ω |
| Line resistance of the DER2 | R2 | 1.18 Ω |
| Line resistance of the DER3 | R3 | 0.16 Ω |
| Line resistance of the DER4 | R4 | 0.64 Ω |
| Line resistance of the DER5 | R5 | 0.46 Ω |
| Line resistance of the DER6 | R6 | 0.67 Ω |
| Communication delay | τ | 0.01 s |
| Descriptions | Symbol | Value |
|---|---|---|
| Mutual weights | Wij | 0.0002 |
| Virtual resistances | Rdi | 0.05 Ω |
| Conversion loss coefficients of DER1 | α | 1.161 |
| β | 0.730 | |
| γ | 1.693 | |
| Conversion loss coefficients of DER2 | α | 0.641 |
| β | 0.547 | |
| γ | 5.260 | |
| Conversion loss coefficients of DER3 | α | 1.693 |
| β | 5.260 | |
| γ | 3.540 | |
| Conversion loss coefficients of DER4 | α | 0.730 |
| β | 1.620 | |
| γ | 2.800 | |
| Conversion loss coefficients of DER5 | α | 1.939 |
| β | 1.830 | |
| γ | 2.693 | |
| Conversion loss coefficients of DER6 | α | 0.917 |
| β | 1.847 | |
| γ | 3.260 | |
| Switching frequency of the converters | fs | 100 kHz |
| Updating frequency of the DICOA | f3 | 0.2 Hz |
| Sampling frequency of the distributed secondary control | f2 | 1 kHz |
| Sampling frequency of the local control | f1 | 100 kHz |
| Scenarios | Line Resistances | PI Compensators | ||||||
|---|---|---|---|---|---|---|---|---|
| R1 (Ω) | R2 (Ω) | KPi | KIi | KP1i | KI1i | KP2i | KI2i | |
| 1 | 0.43 | 0.94 | 0.2 | 1.0 | 0.025 | 0.1 | 0.05 | 0.1 |
| 2 | 0.2 | 0.2 | 0.2 | 1.0 | 0.025 | 0.1 | 0.05 | 0.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Y.; Cheng, S.; Wang, H. Distributed Integral Convex Optimization-Based Current Control for Power Loss Optimization in Direct Current Microgrids. Energies 2023, 16, 8106. https://doi.org/10.3390/en16248106
Jiang Y, Cheng S, Wang H. Distributed Integral Convex Optimization-Based Current Control for Power Loss Optimization in Direct Current Microgrids. Energies. 2023; 16(24):8106. https://doi.org/10.3390/en16248106
Chicago/Turabian StyleJiang, Yajie, Siyuan Cheng, and Haoze Wang. 2023. "Distributed Integral Convex Optimization-Based Current Control for Power Loss Optimization in Direct Current Microgrids" Energies 16, no. 24: 8106. https://doi.org/10.3390/en16248106
APA StyleJiang, Y., Cheng, S., & Wang, H. (2023). Distributed Integral Convex Optimization-Based Current Control for Power Loss Optimization in Direct Current Microgrids. Energies, 16(24), 8106. https://doi.org/10.3390/en16248106






