Abstract
Coalbed methane (CBM) reservoirs’ permeability is the result of dynamic variations influenced by tectonics, hydrology and the CBM production process. Taking samples from the southeastern Ordos Basin, China, the permeability evolution of bituminous coal and its control were analyzed in three steps: (1) the coal fracture permeability evolution was acquired via X-ray CT scanning and permeability evolution experiments; (2) the permeability variation was determined while considering the coupling characteristics effective stress, gas slippage, and matrix shrinkage effect and its influencing factors; and (3) a dynamic permeability model was built while considering those effects. For samples in which neither fractures nor bedding developed, the permeability decreased first and then increased as the gas pressure increased. For samples with fractures that developed parallel to the axial direction, with a gradual increase in gas pressure, the permeability also increased. As the gas pressure decreased, the matrix shrinkage effect became positive, resulting in a permeability increase. The gas slippage effect was positive in the low-pressure stage, which also resulted in a permeability increase.
1. Introduction
Permeability is an important parameter for coalbed methane (CBM) desorption, migration, and production, and the permeability of coal reservoirs is affected by the reservoir pressure changed during its whole tectonic-burial evolution [1]. Desorbed gas transport in coal is generally recognized as having two transport mechanisms in dual porosity media, i.e., diffusion in the coal matrix and subsequent laminar or non-laminar flow in the cleat system [2,3,4]. A series of experimental and theoretical studies about coal permeability and its evolution have been carried out in academia [5].
Harpalani et al. [6] investigated the correlation between gas pressure and permeability, as well as the relationship between gas pressure and the gas desorption of coal samples, through physical simulation experiments. Seidle et al. [7] found that coal matrix shrinkage was related to gas content. Bustin [8] found that the permeability of bituminous coals is affected by the micro lithotype and effective stress. Harpalani et al. [6] studied the impact of various factors, including effective stress, gas slippage, and volumetric strain, on permeability changes in coal samples via experiments. Fu et al. [9,10] carried out experimental studies to investigate the mechanical properties of coal in multiphase media and the effect of coal matrix shrinkage on permeability and analyzed the coupling relationship between the mechanical effects of a matrix and the permeability of high-ranking coal. Somerton et al. [11] investigated the effect of effective stress on coal permeability. Clarkson et al. [12] found that the permeability of coal reservoirs is more susceptible to sensitivity injuries by comparing coal reservoirs to other types of reservoirs. Qu et al. [13] calculated the relationship between the width of a cleat and ground stress with the change in formation pressure on the basis of the elastoplastic constitutive equation of coal and focused on analyzing the application of the equation in underbalanced drilling and overbalanced drilling. Palmer et al. [14] and Shi et al. [15] investigated the permeability of a coal reservoir under the triaxial stress conditions and proposed a permeability model under the influence of two factors, stress and the internal and external pore pressure, and discovered the effect of gas pressure on the permeability under uniaxial pressure. Li et al. [16], Shao et al. [17], Meng et al. [18], and Yang et al. [19] studied the relationship between the water content and stress sensitivity of coal samples. The results showed that the samples containing bound water exhibited a greater sensitivity to stress, which resulted in more significant decreases in permeability and higher levels of permeability damage under stress. Chen et al. [20] found that the permeability of the coal increased with an increase in internal pore pressure when the actual stress was low and constant and that the permeability of the coal samples reduced with a decrease in the effective strain and an increase in pore internal pressure when the perimeter pressure was constant. Li et al. [21] concluded through an experimental study that as the effective stress increases, the width of a coal fracture decreases, leading to a decrease in permeability. Fu et al. [22] and Liu et al. [23] conducted impact loading experiments on coal samples at different strain rates and discovered that the original elastic modulus as well as the two strengths, i.e., ultimate strength and yield strength, varied positively with the strain rate in the anterior part of the constitutive curve and that plastic deformation exhibits characteristics such as increases in the previous stage and decreases in the later stage. Energy increases positively with strain rate during impact, and the dissipated energy and strain rate mostly exhibit insignificant power or linear functional relationships. Wei et al. [24] found that the dimensionless permeability of the coal samples as well as the permeability damage coefficient decrease with an increase in the confining pressure and that the stress sensitivity coefficient also increases with an increase in water content in the coal seam using a loaded coal gas seepage experiment system. Shang et al. [25] carried out experiments on seepage in fractured coal under a triaxial stress state, and their results showed that there is a negative correlation between coal porosity and confining pressure, both of which basically followed the logarithmic function relationship under the condition of multistage axial displacement. That study laid the foundation for coal reservoir stress sensitivity research. Wang et al. [26] studied the fracture evolution and nonlinear seepage characteristics of gas-bearing coals based on X-ray computed tomography combined with the lattice Boltzmann method. Shi et al. [27] used CT technology to study the microstructure evolution characteristics of bituminous coal. He et al. [28] found that bituminous coal has a higher acid sensitivity than anthracite. Li et al. [29] studied the permeability evolution characteristics of lignite under pyrolysis conditions. Li et al. [30] found through experimental methods that supercritical CO2 fracturing causes relaxation of the macromolecular structure of coal. Wang et al. [31] quantified coal uniaxial and triaxial fracture evolution on the basis of CT scanning and fractal theory. Wu et al. [32,33] analyzed and modeled the structural damage evolution in coal by combining X-ray CTs and gray-level co-occurrence matrix methods. Huang et al. [34] believed that the permeability of a coal matrix is vectorial and controlled by confining pressure and pore pressure. Song et al. [35] analyzed the adsorption/desorption mechanism of nitrogen on bituminous coal [36]. Su et al. [37] found through experimental research that a change in the pore structure of a coal matrix is the main reason for its change in mechanical properties. Liu et al. [38,39,40] focused on the Qinshui Block and studied the mechanisms of coalbed methane occurrence, accumulation, and production and systematically developed a block scale theory of coalbed methane migration and accumulation.
In summary, the permeability of a coal reservoir is always dynamically changing due to CBM formation evolution and exploitation and has an important influence on the state of CBM storage and the exploitation effect. Reservoir pressure is the fluid pressure acting on the pore and fracture space of the coal reservoir, which affects the methane adsorption and desorption and flow characteristics of the coal reservoir. Effective stress is the difference between the in situ stress and the fluid pressure in the pore space of the coal reservoir. Coal reservoir permeability is affected by the coal matrix shrinkage and expansion, fluid pressure and effective stress. For this reason, firstly, the experiments on the permeability evolution of coal fracture were carried out to study the characteristics of coal fracture deformation and permeability evolution. Secondly, the coupling characteristics of effective stress, slippage effect, and matrix shrinkage effect were considered to reveal the dynamic control of fracture permeability in coalbed methane reservoirs. Finally, based on the experimental data, a dynamic permeability model which considers the joint control conditions of effective stress, gas slippage effect, and matrix shrinkage, is established.
2. Samples and Methods
2.1. Samples and Experiments
Coal samples were collected from five representative mining areas located in the Weibei region of the Ordos Basin, and cylindrical cores with diameters of 25 mm were drilled along the direction of parallel laminations of the coal samples (Table 1) for the permeability evolution experiment. This experiment was completed with instrumentation such as the TAW100 (2010) deepwater pore pressure servo experiment system in the Rock Mechanics Laboratory of China University of Petroleum (Beijing) (Figure 1). The axial and radial pressures on the specimen were provided by a cylinder and loaded with hydraulic pump control. Both axial and confining pressures were stabilized by the hydraulic pump, and the gas permeation pressure was manually controlled using a gas cylinder with a pressure control valve. The gas permeability of the coal samples was tested with He and CO2 under different pressure conditions successively. The gas was injected into the samples from the top of the instrument through the gas injection port, and the volume of the gas exuded at the bottom could be measured using the drainage method. For each combination of pressure conditions, it generally took tens of minutes to hours from the beginning of the application of the inlet pressure to the observation of gas seepage, and once the gas flow reached stability, the gas seepage flow was continuously measured for 10–30 min to ensure that stable seepage characterization data were obtained for each of the stress conditions. The gas inlet pressure for the experiment was applied in steps from low to high according to the design scheme. The ambient temperature of this experiment was room temperature, and the effect of temperature on permeability was not considered in this study.

Table 1.
Basic information of experimental samples.
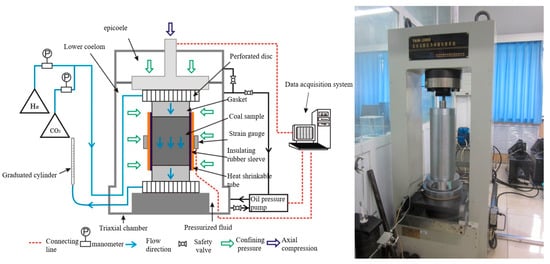
Figure 1.
Experimental principles and devices.
The gas permeability evolution experiment of the triaxial coal rock was carried out at room temperature (25 °C) using He and CO2 gases, and the selected coal samples were in the natural dry state. The experiment was divided into three parts and four groups of cyclic experiments. The specific experimental steps were as follows:
- (1)
- The confining pressure was held constant at 2.1 MPa unlike the other three cycling experiments which had confining pressures of 4.1 MPa, 5.3 MPa, and 6.3 MPa. Firstly, the experiment was carried out with He. The inlet gas pressure was gradually increased to test the steady flow rate of He at each experimental pressure point, and the permeability of He was then calculated. The above experiment was then repeated with CO2 gas on the same sample, and the permeability of CO2 was calculated.
- (2)
- The effective stress for the particular experiment was set constantly at 2 MPa (the effective stresses of the other three cyclic experiments were 3 MPa, 4 MPa, and 5 MPa). The inlet pressure and the confining pressure were increased at the same time, and the experiments with He and CO2 were performed successively, followed by the measurement of the gas permeability at each pressure point;
- (3)
- X-ray CT scans were performed on the coal samples before and after the four cycles of experiments in order to investigate the development of fractures in the coal rock.
Throughout the experiment, the confining pressure remained below 7.3 MPa, while the inlet pressure remained below 4.5 MPa. Additionally, the inlet pressure always remained lower than the confining pressure.
2.2. Permeability Variation Calculations
The experiments were performed using the steady state method, which involves applying a steady pressure difference between the upstream and downstream ends of the samples. The permeability was calculated based on Darcy’s Law by measuring the flow rate through the sample. The formula for calculating the permeability is as follows:
where Kg is the gas permeability, 10−3 µm2; p0 is the atmospheric pressure, MPa; qg is the gas flow rate at atmospheric pressure, cm3/s; µg is the viscosity of the gas at the measurement temperature, mPa·s; L is the length of the coal sample, cm; A is the cross-sectional area of the coal sample, cm2; and p1 is the inlet pressure, MPa.
3. Results
3.1. Coal Fracture and Permeability Evolution Characteristics
The results of five cycles of X-ray CT scanning experiments are depicted in Figure 2. It shows that as the confining pressure gradually increases, the effective stress also increases correspondingly, which results in a closure of the coal fracture. A typical fracture width, as shown in the figure, was selected for the measurement. The width of the fracture in the CT image of the layer was 0.3 mm when the confining pressure was 0.1 MPa. As the confining pressure increased, the width of the fracture began to decrease. When the confining pressure was 6 MPa, the width of the fracture was narrowed down to 0.25 mm, making the fracture unrecognizable to the naked eye on the CT image. This indicates that the increase in effective stress caused the fracture of the coal to gradually close, which eventually lead to a reduction in the permeability of the coal.
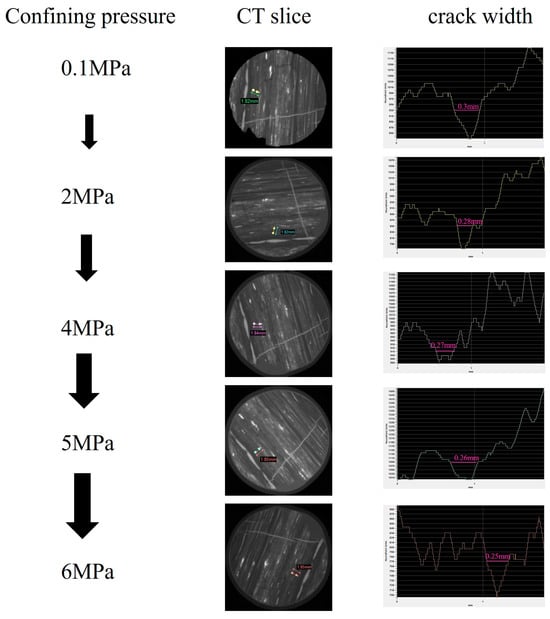
Figure 2.
Variation characteristics of crack width under different effective stresses.
From the CT slices, it can be clearly seen that the cracks are compressed, and from the curves, it can be seen that the width of the cracks decreases with an increase in the peripheral pressure, which shows that the permeability is negatively correlated with the peripheral pressure, while at a certain peripheral pressure, the permeability is positively correlated with the gas pressure.
The results of the permeability evolution experiments show that as the gas pressure increased under the condition of constant confining pressure, the effective stress decreased and permeability gradually increased. As the effective stress was held, an increase in confining pressure led to a reduction in permeability.
The changes in permeability have different patterns for samples with different coal structures. For samples with dense coal rock structures (Figure 3), where neither fractures nor bedding developed, the permeability decreased first and then increased as the gas pressure increased.
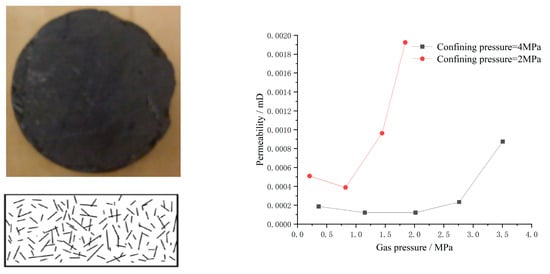
Figure 3.
He permeability evolution characteristic curve of densely structured XS5 coal sample.
Under the enclosing pressure of 2 MPa and 4 MPa, the permeability shows the trend of decreasing and then increasing, in which, the permeability first decreases rapidly, then increases rapidly under the enclosing pressure of 2 MPa, and reaches the minimum at a gas pressure of 0.8 MPa; under the enclosing pressure of 4 MPa, the permeability decreases slowly with the gas pressure, then increases rapidly at a gas pressure of 2.8 MPa, and increases rapidly at a gas pressure of 1.7. The permeability reaches the minimum value when the gas pressure is 1.7 MPa.
For coal samples with fractures that developed parallel to the axial direction (Figure 4), the gas will preferentially flow along the wider fractures because of the larger permeable space provided for gas flow. In these samples, with the gradual increase in gas pressure, the permeability also increases.
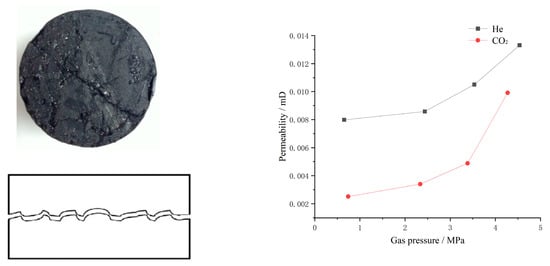
Figure 4.
Permeability evolution characteristic curve of XS5-1 coal sample with axially developed fractures.
With the increase in gas pressure, the permeability of both gases increased slowly and then rapidly under the condition of a surrounding pressure of 6 MPa, among which, the permeability of CO2 was obviously lower than that of He, and both gases increased faster when the gas pressure was 3.5 MPa.
3.2. Factors Influencing Permeability Evolution
3.2.1. Effective Stress Effect
The effective stress refers to the difference between the in situ stress acting on coal reservoirs and the fluid pressure in the pores and fractures. So, the relationship of effective stress, confining pressure, and gas pressure can be expressed as follows [3]:
where σe is the effective stress, MPa; σc is the confining pressure, MPa; pm is the gas pressure, MPa; and α is the effective stress coefficient. At pressures below 10.3 MPa, α values approach 1 [41]. The α value is almost constant for coal samples with relatively developed cleats [42]. Therefore, in this paper, α = 1 is more reasonable [5,43].
At the peripheral pressure of 4 MPa and 5 MPa, with the increase in gas injection pressure, the permeability of the two gases increased significantly, among which the permeability of He was significantly stronger than that of CO2 and the permeability curves of He all had a turning point, after which the increase in gas permeability became slower.
Increasing the confining pressure can result in a higher effective stress and can lead to the closure of fractures, so the permeability can be decreased (Figure 5). According to CT observations, the fractures in coal samples began to close when the confining pressure increased, resulting in a decrease in permeability.
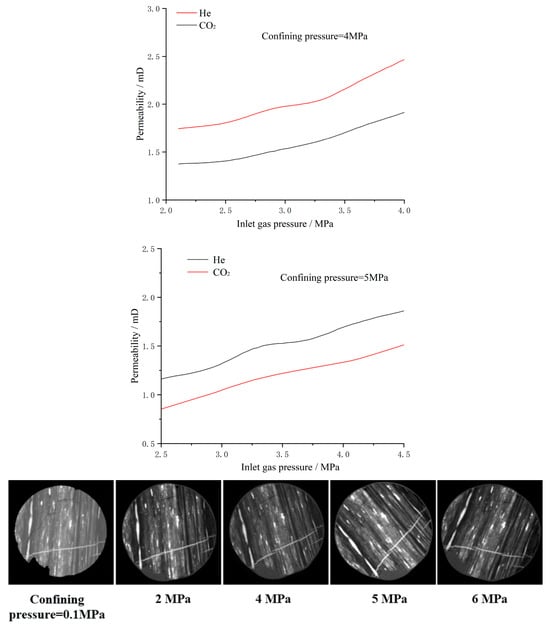
Figure 5.
Permeability evolution characteristics of effective stress control.
The increase in the effective stress effect on permeability can be expressed as follows [15,39]:
where ke is the permeability when the effective stress is σ, mD; k0 is the permeability under the initial effective stress σ0, mD; c is the compression coefficient of coal and rock cleat, which can be obtained by fitting; and ∆σ is the effective stress difference, MPa.
3.2.2. Gas Slippage Effect
The gas slippage effect is a phenomenon in which the flow velocity of gas molecules near the surface of the pore wall is not zero when the gas flows in a small capillary or a low-permeability, porous medium during the process of gas pressure reduction, which makes the measured permeability of the gas greater than that of a liquid. When the gas pressure of the XS5 coal sample was lower than 1.5 MPa under different confining pressure conditions, the permeability decreased with the increase in gas pressure (Figure 6). Since He is a non-adsorbed gas, it is believed that there is a gas slippage effect at this pressure stage, so the gas permeability was increased under low pressure.
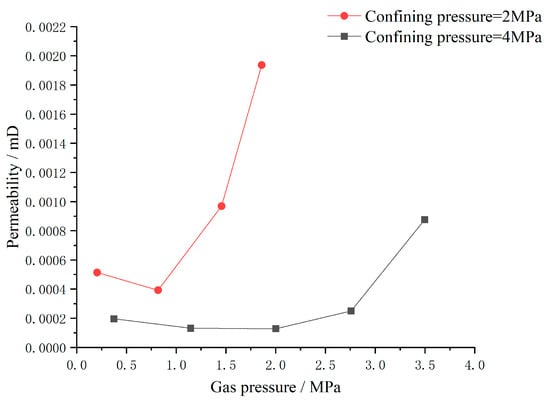
Figure 6.
Evolution characteristics of He permeability controlled by slippage effect.
Under the conditions of 2 MPa and 4 MPa, with the increase in gas pressure, the permeability showed the trend of decreasing and then increasing: under 2 MPa pressure, the permeability changes were more rapid, and the permeability reached the minimum value at a gas pressure of about 0.7 MPa and then increased rapidly; under 4 MPa pressure, the permeability changed gently, reached the minimum value at a gas pressure of about 1.5 MPa, and then increased rapidly at the inflection point at a gas pressure of about 2.7 MPa. At 4 MPa, the permeability changed gently, reaching a minimum value at about 1.5 MPa and then increasing rapidly at an inflection point at about 2.7 MPa.
The gas permeability can be increased under a low pressure because of the gas slippage effect when the experiments were performed with He and CO2. The permeability while considering the gas slippage effect can be expressed as follows [44]:
where kg is the gas permeability under average gas pressure conditions, which can be calculated with Equation (1); k0 is the gas Kjeldahl permeability, sometimes referred to as the equivalent liquid permeability; c is the scaling factor; λ is the average free path of gas molecules; and r is the average radius of the channel. The average free path of a gas is inversely proportional to the average gas pressure pm, so Equation (4) can be rewritten as follows [45]:
where pm is the average gas pressure, MPa, and b is the gas slippage factor or Klinkenberg coefficient, MPa, defined as .
3.2.3. Matrix Shrinkage Effect
When gas is injected into the coal samples, the gas (CO2) is adsorbed, causing matrix expansion, and while the reservoir pressure is reduced, adsorbed gas will undergo desorption, leading to matrix shrinkage. Here, the effective stress was kept constant while increasing the confining pressure and gas pressure, and the effect of matrix shrinkage on permeability was observed. The results have shown that as gas pressure increased and adsorption tended to saturate, and the influence of matrix shrinkage on permeability gradually weakened (Figure 7).
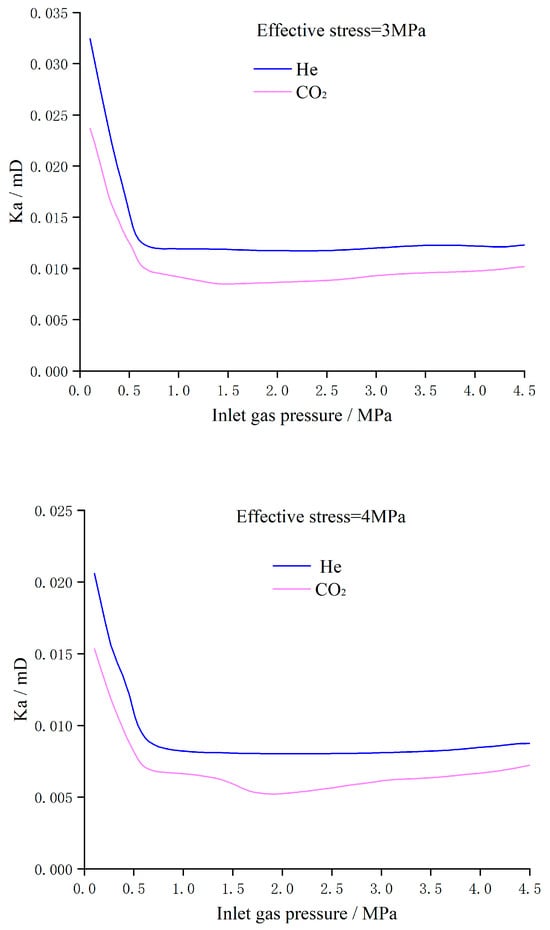
Figure 7.
Evolution characteristics of CO2 permeability controlled by matrix shrinkage effect.
At the initial stage of gas injection, with the increase in pressure, matrix adsorption, and matrix expansion, permeability decreased rapidly, and the lowest value appeared at a gas injection pressure of about 0.6 MPa, with the Sovereignty region flattened; the reason for this is that with the increase in gas pressure, matrix expansion has a weaker effect on permeability.
3.2.4. Comprehensive Control of Permeability Variation
The evolutionary characteristics of the gas permeability of the coal samples are shown in Figure 8. It can be seen that when the gas pressure exceeded the low-pressure range, where gas slippage occurs in the early stage of gas injection, the permeability of He continued to increase as the gas pressure increased under the condition in which the confining pressure was kept constant, while the gas permeability of CO2 decreased first because the CO2 was initially adsorbed, which caused the matrix to expand. And then, with the gradually increase in gas pressure, the effective stress decreased, which resulted in the permeability of CO2 increasing later.
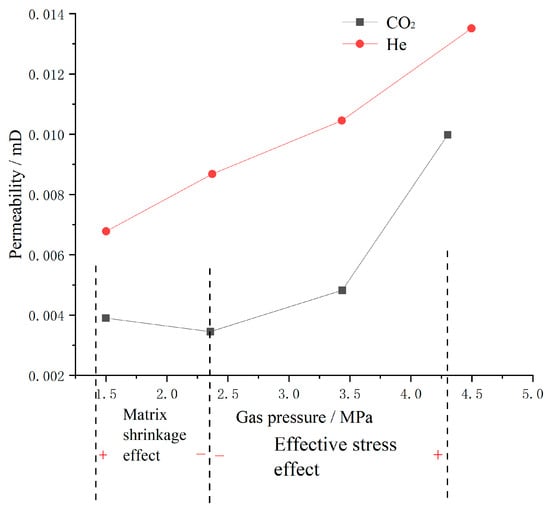
Figure 8.
Evolution of CO2 permeability under the joint control of matrix shrinkage and effective stress.
Therefore, the evolution of gas permeability is controlled by the shrinkage of the coal matrix and the effective stress when a slip-off no longer occurs beyond a certain low-pressure range. When the gas pressure decreases, the matrix shrinkage effect is positive, leading to an increase in permeability, and an effective stress effect that is negative leads to a decrease in permeability.
In the early stages of the experiment, the permeability decreased because adsorbent gases such as CO2 have an adsorptive effect, leading to a matrix expansion of the coal, which makes the cracks smaller. As the gas pressure increased, effective stress dominated and permeability gradually increased. Therefore, a decrease in gas pressure results in a positive effect of matrix shrinkage, resulting in an increase in permeability. The slippage effect has a positive effect in the low-pressure stage and leads to an increase in permeability; an effective stress effect that is negative leads to decreased permeability. Gas slippage, matrix shrinkage, and effective stress jointly control the evolution of permeability (Figure 9).
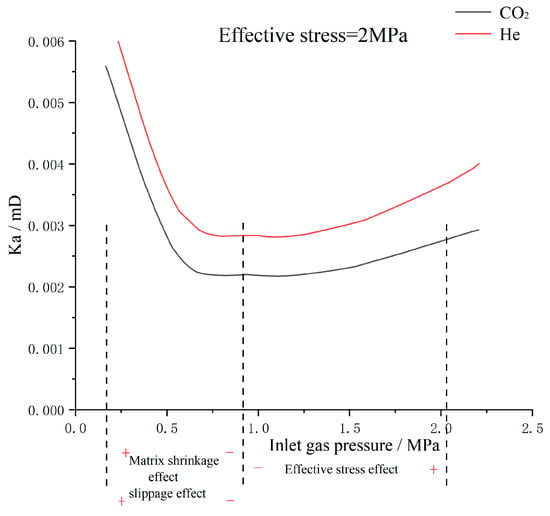
Figure 9.
Permeability evolution controlled by gas slippage, matrix shrinkage, and effective stress.
Therefore, when the effective stress is kept constant, the permeability increase in the gas slippage effect can be expressed as follows [3]:
4. Discussion
By analyzing the experimental data of six groups of samples, a series of correlation data between permeability and three geological effects are obtained. Taking the XS5 sample as an example, a mathematical model of coal permeability evolution controlled by dynamic effects is established.
4.1. Model of Effective Stress Controlling Permeability
It can be seen from Equation (3) that the relationship between gas permeability and effective stress is exponential, so the expression can be rewritten as follows:
By fitting the relationship between effective stress and permeability, the cleat compression coefficient c of coal can be calculated.
As shown in Figure 10, it can be seen that under different gas pressures, the permeability of He and CO2, and effective stress exhibit a significant exponential relationship. The correlation between the exponential fitting curve is extremely high, and the fitting formula is in accordance with the classical permeability model controlled by the effective stress effect.
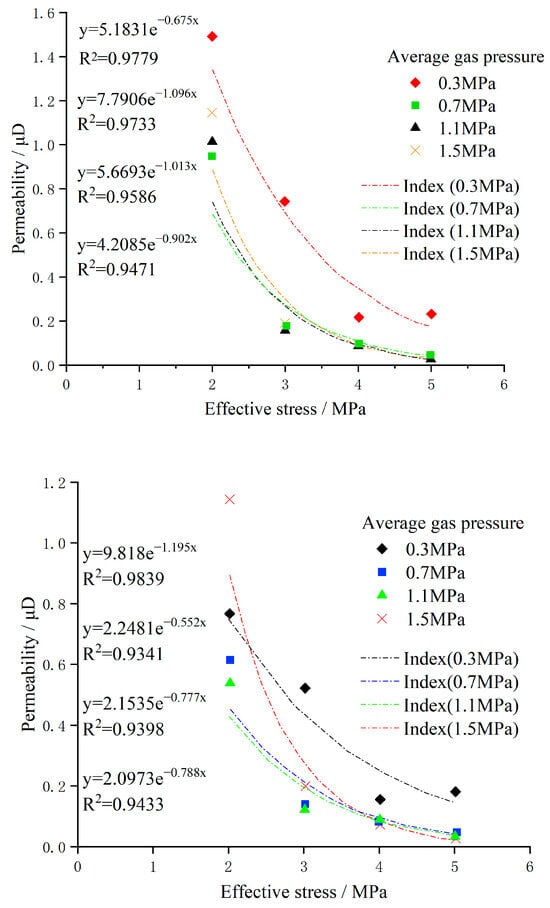
Figure 10.
Permeability evolution of He (upper) and CO2 (lower) under effective stress control under different gas pressures.
As shown in Figure 11, there is a high correlation between the effective stress and permeability. The slope of the fitted line is the cleat compression coefficient c of coal under different gas pressures. A mathematical model and related parameters for the evolution of permeability under effective stress control were obtained for the XS5 coal samples via calculations under different gas pressures (Table 2). From the table, it can be seen that the correlation between permeability and effective stress fitting increases as the gas pressure increases, indicating that a higher gas pressure results in more obvious control of the effective stress effect on permeability.
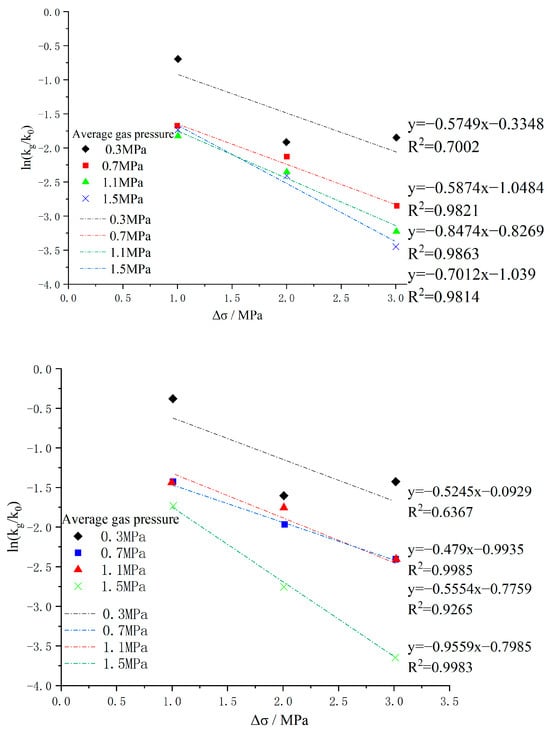
Figure 11.
Splitting compressibility coefficients of He (upper) and CO2 (lower) under effective stress control under different gas pressures.

Table 2.
Effective stress-controlled permeability model and parameters of XS5 sample.
4.2. Model of Gas Slippage Effect and Effective Stress-Controlled Permeability
Because He is a non-adsorbent gas, only the slippage effect and effective stress effect exist under pressure changes. Therefore, under the condition of constant effective stress, the permeability model of He controlled by the slippage effect can be calculated.
From Equation (5), it can be seen that gas permeability is positively correlated with the reciprocal of average gas pressure. Therefore, by fitting the relationship between the reciprocal of average gas pressure and permeability, the slip factor b and the Coriolis permeability k0 can be calculated.
The permeability evolution of He controlled by the gas slippage effect under the conditions of maintaining effective stress at 2 MPa and 4 MPa is illustrated in Figure 12. It can be seen that in the small range where the average gas pressure is close to 1 MPa, there is a turning point of permeability increase and decrease. Before the turning point, a significant gas slippage effect occurs during the low-pressure stage. Linear fitting was then performed on the data points during the gas slippage effect stage (Figure 13) to obtain the intercept from the Y-axis, which represents the k0 permeability under this effective stress; the slope of the fitted straight line is k0b, from which the slippage factor b value can be calculated.
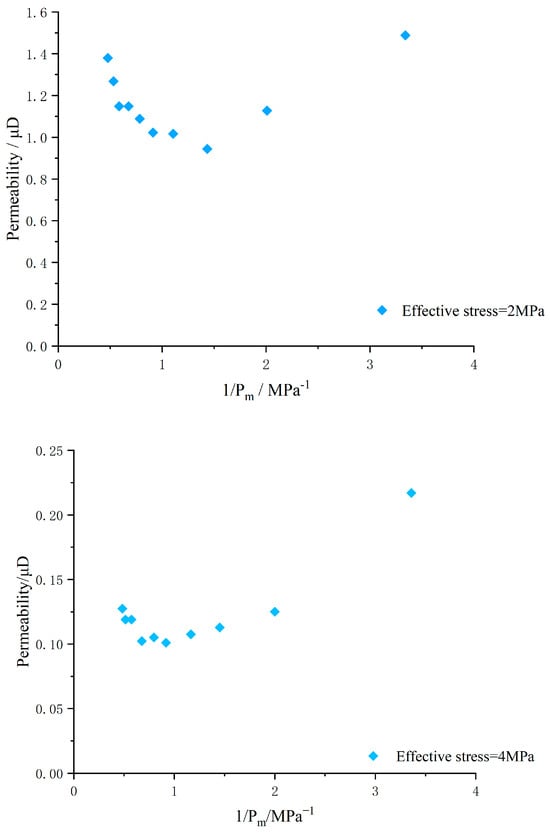
Figure 12.
Permeability evolution of He controlled by different effective stress slippage effects.
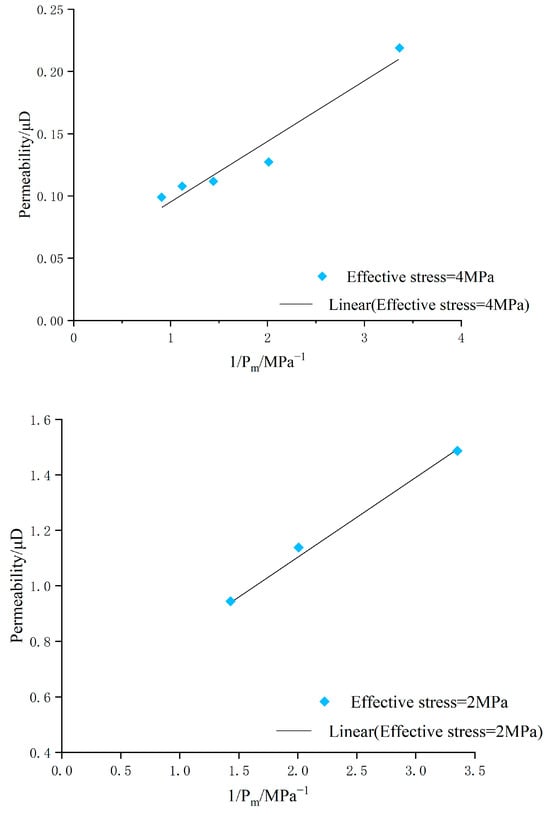
Figure 13.
Fitting of permeability and gas pressure reciprocal under different effective stresses.
According to Equation (6), the mathematical model and related parameters of the permeability evolution controlled by the slippage effect of He were obtained for the XS5 coal samples under different effective stresses. As shown in Table 3, as the effective stress increases, the Kjeldahl permeability decreases and the effective stress has a negative impact on gas permeability.

Table 3.
He permeability model and parameters controlled by gas slippage effect of XS5 samples.
4.3. Model for Controlling Permeability by Slippage Effect and Matrix Shrinkage Effect
Unlike the non-adsorptive gases, the gas slippage effect and matrix shrinkage effect occur when the experiments were performed with CO2. Based on the permeability evolution characteristics of He and CO2 measured simultaneously, the permeability model of CO2 controlled by the slippage effect can be obtained.
The slippage factor b can be further expressed as follows [3,26,41]:
where c is a constant; μ is the gas viscosity; w is the width of the fracture; R is the universal gas constant; T is the absolute temperature; and M is the molecular weight of the gas.
By transforming Equation (9), the slippage factor of CO2 gas can be expressed as follows:
where μC and μH is the gas viscosity of CO2 and He, and MC and MH are the gas molecular masses of CO2 and He.
So, according to the relationship between He and CO2, the slippage factor of CO2 can be calculated from He’s slippage factor (Table 4).

Table 4.
CO2 permeability model and parameters controlled by slippage effect and matrix shrinkage effect of XS5 samples.
Therefore, when the effective stress is kept constant, the permeability increase in CO2 caused by the gas slippage effect can be further expressed as follows:
The permeability increase caused by the matrix shrinkage effect can be further expressed as follows:
So, a mathematical model and the related parameters for the permeability evolution controlled by the slippage effect and the matrix shrinkage effect of CO2 gas under different effective stresses were obtained for the XS5 coal samples (Table 4).
5. Conclusions
Through X-ray CT scanning and permeability evolution experiments, it is concluded that the increase in confining pressure leads to a closure of coal fractures and a decrease in permeability. For samples in which neither fractures nor bedding developed, the permeability decreased first and then increased as the gas pressure increased. For samples with fractures that developed parallel to the axial direction, with the gradual increase in gas pressure, the permeability also increased.
The permeability evolution experiment of coal shows that as the gas pressure decreases, the matrix shrinkage effect is positive, leading to a permeability increase. The slippage effect is positive in the low-pressure stage, which increases the permeability. The effective stress effect is negative, resulting in lower permeability. Thus, the evolution of permeability is controlled by three effects: gas slippage, matrix shrinkage, and effective stress.
The dynamic permeability model established under the joint control conditions of effective stress, slip effect, and matrix shrinkage based on the experimental data should be carefully considered during CBM production.
Author Contributions
Methodology, Y.Q., D.C., A.A. and Y.C.; Validation, Y.Q. and F.S.; Formal analysis, Y.Q.; Investigation, Y.Q.; Writing—original draft, Y.Q., D.C., F.S., A.A. and Y.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (42102227; 42130806).
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
Author Abulaitijiang Abuduerxiti was employed by the company Xinjiang Oilfield Company, CNPC. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Bai, M.; Elsworth, D. Coupled processes in subsurface deformation. ASCE Press Flow Transp. 2000, 336–337. [Google Scholar]
- Elsworth, D.; Bai, M. Flow-deformation response of dual porosity media. Geotech. Eng. 1992, 118, 107–124. [Google Scholar] [CrossRef]
- Sun, F.; Liu, D.; Cai, Y.; Qiu, Y. Coal rank-pressure coupling control mechanism on gas adsorption/desorption in coalbed methane reservoirs. Energy 2023, 270, 126849. [Google Scholar] [CrossRef]
- Sun, F.; Liu, D.; Cai, Y.; Qiu, Y. A micro-macro coupled permeability model for gas transport in coalbed methane reservoirs. Energy 2023, 284, 128604. [Google Scholar] [CrossRef]
- Liu, D.; Yao, Y.; Chang, Y. Measurement of adsorption phase densities with respect to different pressure: Potential application for determination of free and adsorbed methane in coalbed methane reservoir. Chem. Eng. J. 2022, 446 Pt 3, 137103. [Google Scholar] [CrossRef]
- Harpalani, S.; Schraufnagel, R.A. Shrinkage of coal matrix with release of gas and its impact on permeability of coal. Fuel 1990, 69, 551–556. [Google Scholar] [CrossRef]
- Seidle, J.P.; Huitt, L.G. Experimental measurement of coal matrix shrinkage due to gas desorption and implications for cleat permeability increases. In Proceedings of the International Meeting on Petroleum Engineering, v 2. Richardson: Soc of Petroleum Engineers, Beijing, China, 14–17 November 1995; pp. 575–582. [Google Scholar]
- Bustin, R.M. Importance of fabric and composition on the stress sensitivity of permeability in some coals, northern Sydney basin: Relevance to coalbed methane exploitation. AAPG Bull. 1997, 81, 1894–1908. [Google Scholar]
- Fu, X.H.; Li, D.H.; Qin, Y.; Song, X. Experimental study on the effect of coal matrix shrinkage on permeability. J. China Univ. Min. Technol. 2002, 31, 129–131. [Google Scholar]
- Fu, X.H.; Qin, Y.; Zhang, W.H. Analysis of the coupling relationship between the mechanical effects of high rank coal matrix and coal reservoir permeability. J. Univ. Geol. 2003, 9, 373–377. [Google Scholar]
- Somerton, W.H.; Soylemezoglu, I.M.; Dudley, R.C. Effect of stress on permeability of coal. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1975, 12, 129–145. [Google Scholar] [CrossRef]
- Clarkson, C.R.; Jordan, C.L.; Gierhart, R.; Seidle, J.P. Production data analysis of CBM wells. Soc. Pet. Eng. 2007. [Google Scholar] [CrossRef]
- Qu, P.; Shen, R.C.; Yuan, J.P. Theoretical study on stress sensitivity of coal reservoirs. Pet. Drill. Tech. 2007, 35, 68–71. [Google Scholar]
- Palmer, I.; Mansoori, J. How permeability depends on stress and pore pressure in coalbeds: A New Model. Spe Reservoir. Eval. Eng. 1998, 1, 539–544. [Google Scholar] [CrossRef]
- Shi, J.Q.; Durucan, S. Drawdown induced changes in permeability of coalbeds: A New Interpretation of the Reservoir Response to Primary Recovery. Transp. Porous Media 2004, 56, 1–16. [Google Scholar] [CrossRef]
- Li, Q.M. Research on the Seepage Characteristics of Coal and Rock Damage under Multiple Protection Conditions and the Rationality Evaluation of Mining Deployment; Chongqing University: Chongqing, China, 2019. [Google Scholar]
- Shao, Z.B.; Zhang, H.; Zhong, Y.; Li, G.F.; She, J.P.; Li, Z.Z. Study on liquid phase detention and stress sensitive superimposed damage of tight sandstone gas reservoirs with multiple fractures: Taking the tight sandstone of Penglaizhen formation in western Sichuan as an example. J. Xi’an Pet. Univ. 2015, 30, 59–62. [Google Scholar]
- Meng, Z.P.; Hou, Q.L. Experimental analysis of stress sensitivity and influencing factors in coal reservoirs. J. Coal Sci. 2012, 37, 430–437. [Google Scholar]
- Yang, M.P.; Li, Y.; Li, Z.P. Experimental study on stress sensitivity of gas reservoirs rocks containing bound water. Nat. Gas Geosci. 2004, 15, 227–229. [Google Scholar]
- Chen, Z.H.; Wang, Y.B.; Guo, K. Study on stress sensitivity of high rank coalbed methane reservoirs. J. Geol. 2008, 82, 1390–1395. [Google Scholar]
- Li, X.C.; Kang, Y.L.; Luo, P.Y. The effect of stress on the width and permeability of coal and rock fractures. Coal Field Geol. Explor. 2009, 37, 29–37. [Google Scholar]
- Fu, Y.K.; Xie, B.J.; Wang, Q.F. Dynamic mechanical constitutive model of coal. J. Coal Sci. 2013, 38, 1769–1774. [Google Scholar]
- Liu, X.H.; Zhang, R.; Liu, J.F. Experimental study on coal rock impact dynamics under different strain rates. J. Coal Sci. 2012, 1528–1534. [Google Scholar]
- Wei, J.P.; Li, M.Z.; Wang, D.K.; Qin, H.J. Experimental study on sensitivity of coal sample permeability to confining pressure. Coal Sci. Technol. 2014, 42, 76–80. [Google Scholar]
- Shang, H.B.; Jin, D.W.; Zhang, T.J.; Tang, J. Evolution law of permeability characteristics of fractured coal under triaxial stress. J. Coal Sci. 2019, 044, 1066–1075. [Google Scholar]
- Wang, D.K.; Zeng, F.C.; Wei, J.P.; Zhang, H.T.; Wu, Y.; Wei, Q. Quantitative analysis of fracture dynamic evolution in coal subjected to uniaxial and triaxial compression loads based on industrial CT and fractal theory. J. Pet. Sci. Eng. 2021, 196, 108051. [Google Scholar] [CrossRef]
- Shi, J.; Feng, Z.; Zhou, D.; Meng, Q. Analysis of the permeability evolution law of in situ steam pyrolysis of bituminous coal combing with in situ CT technology. Energy 2023, 263, 126009. [Google Scholar] [CrossRef]
- He, J.; Li, H.; Yang, W.; Lu, J.; Lu, Y.; Liu, T.; Shi, S. Experimental study on erosion mechanism and pore structure evolution of bituminous and anthracite coal under matrix acidification and its significance to coalbed methane recovery. Energy 2023, 283, 128485. [Google Scholar] [CrossRef]
- Li, X.; Tian, J.; Ju, Y.; Chen, Y. Permeability variations of lignite and bituminous coals under elevated pyrolysis temperatures (35–600 °C): An experimental study. Energy 2022, 254, 124187. [Google Scholar] [CrossRef]
- Li, Y.; Ji, H.; Li, G.; Hu, S.; Liu, X. Effect of supercritical CO2 transient high-pressure fracturing on bituminous coal microstructure. Energy 2023, 282, 128975. [Google Scholar] [CrossRef]
- Huang, H.; Wang, E. A laboratory investigation of the impact of solvent treatment on the permeability of bituminous coal from Western Canada with a focus on microbial in-situ processing of coals. Energy 2020, 210, 118542. [Google Scholar] [CrossRef]
- Wang, D.K.; Tian, X.R.; Wei, J.P.; Zhang, H.T.; Yao, B.H.; Zhang, H.; Chen, C.Y. Fracture evolution and nonlinear seepage characteristic of gas-bearing coal using X-ray computed tomography and the lattice Boltzmann method. J. Pet. Sci. Eng. 2022, 211, 110144. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, D.K.; Wang, L.; Shang, Z.; Zhu, C.; Wei, J.; Yuan, A.; Zhang, H.; Zeng, F. An analysis of the meso-structural damage evolution of coal using X-ray CT and a gray-scale level co-occurrence matrix method. Int. J. Rock Mech. Min. Sci. 2022, 152, 105062. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, D.K.; Wang Wei, J.P.; Yao, B.; Zhang, H.; Fu, J.; Zeng, F. Damage constitutive model of gas-bearing coal using industrial CT scanning technology. J. Nat. Gas Sci. Eng. 2022, 101, 104543. [Google Scholar] [CrossRef]
- Song, B.; Zhai, X.; Ma, T.; Wang, B.; Hao, L.; Zhou, Y. Effect of water immersion on pore structure of bituminous coal with different metamorphic degrees. Energy 2023, 274, 127449. [Google Scholar] [CrossRef]
- Su, E.; Liang, Y.; Chen, X.; Wang, Z.; Ni, X.; Zou, Q.; Chen, H.; Wei, J. Relationship between pore structure and mechanical properties of bituminous coal under sub-critical and super-critical CO2 treatment. Energy 2023, 280, 128155. [Google Scholar] [CrossRef]
- Liu, D.M.; Jia, Q.F.; Cai, Y.D.; Gao, C.J.; Qiu, F.; Zhao, Z.; Chen, S.Y. A new insight into coalbed methane occurrence and accumulation in the Qinshui Basin, China. Gondwana Res. 2022, 111, 280–297. [Google Scholar] [CrossRef]
- Liu, D.M.; Yao, Y.B.; Wang, H. Structural compartmentalization and its relationships with gas accumulation and gas production in the Zhengzhuang Field, southern Qinshui Basin. Int. J. Coal Geol. 2022, 259, 104055. [Google Scholar] [CrossRef]
- Liu, D.M.; Yao, Y.B.; Yuan, X.H.; Yang, Y.H. Experimental evaluation of the dynamic water-blocking effect in coalbed methane reservoir. J. Pet. Sci. Eng. 2022, 217, 110887. [Google Scholar] [CrossRef]
- Randolph, P.L.; Soeder, D.J.; Chowdiah, P. Porosity and permeability of tight sands. In Spe Unconventional Gas Recovery Symposium; OnePetro: Richardson, TX, USA, 1984. [Google Scholar]
- Zhao, Y.S.; Hu, Y.Q.; Wei, J.P.; Yang, D. The experimental approach to effective stress law of coal mass by effect of methane. Transp. Porous Media 2003, 53, 235–244. [Google Scholar]
- Li, J.Q.; Liu, D.M.; Yao, Y.B.; Cai, Y.D.; Wang, L. The control effect of gas slippage and effective stress on the gas phase permeability of coal and rock. Nat. Gas Geosci. 2013, 24, 1074–1078. [Google Scholar]
- Shi, J.; Durucan, S. A model for changes in coalbed permeability during primary and enhanced methane recovery. SPE Reserv. Eval. Eng. 2005, 8, 291–299. [Google Scholar] [CrossRef]
- Klinkenberg, L.J. The permeability of porous media to liquids and gases. Drill. Prod. Pract. 1941, 2, 200–213. [Google Scholar] [CrossRef]
- Li, J.; Liu, D.; Yao, Y.; Cai, Y.; Chen, Y. Evaluation and modeling of gas permeability changes in anthracite coals. Fuel 2013, 111, 606–612. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).