Autonomous Wireless Power Transfer System with Constant Output Voltage in a Wide Load Range

Abstract

In this paper, an autonomous wireless power transfer (WPT) system with constant voltage output in a wide load range is presented. Here, combining self-oscillating control and phase-shift control, a new implementation of the autonomous WPT system is proposed. The proposed autonomous WPT system operates using a self-oscillating control method in the strong coupling region, which can automatically maintain the constant output voltage. In the weak coupling region, a phase-shift control method with a fixed frequency and a variable duty cycle is implemented, and a control strategy based on output voltage estimation is proposed to obtain the constant output voltage. In addition, according to the operating frequency characteristic of the proposed autonomous WPT system, a corresponding coupling region judgment method is presented to guarantee the realization of switching between the two control methods. An experimental prototype with a 24 V output voltage is constructed to validate the practicability of the proposed method. The experimental results show the proposed autonomous WPT system can obtain constant output voltage in a wide load range.

1. Introduction

Wireless power transfer (WPT) technology has become a widespread concern in the past decade and has significant commercial applications [1,2]. In particular, compared with magnetic inductive wireless power transfer (IPT), magnetically coupled resonant wireless power transfer (MCR-WPT) technology can transfer power in the middle distance and has significant advantages that have higher transfer efficiency and less electromagnetic interference caused by non-resonant frequencies [3]. Nowadays, MCR-WPT technology is applied to biomedical implants [4,5], mobile electronic products [6,7], electrical vehicles (EVs) [8,9], and other fields where wired contact is impossible or inconvenient.

To guarantee the lifetime and safety of batteries, it is essential to maintain constant current (CC) charging and constant voltage (CV) charging during the charging process. Until now, there have been three ways to obtain CC and CV outputs in the existing research. First, CC and CV outputs can be achieved by applying variable inductors [10,11] or designing a compensation topology [12,13,14]. However, variable inductors or additional power switches and auxiliary capacitors are employed in these methods, which will lead to a reduction in overall efficiency and affect the lightweight nature of the system. Second, CC and CV outputs can be implemented via the application of control strategies on the receiving side [15,16,17,18]. In [15], during the overall charging process, a 31.5 A CC output was gained at a transfer distance of 150 mm by utilizing a DC/DC converter in the receiver. In [16], CC and CV outputs were acquired via the employment of a battery management system composed of four DC/DC converters. Additional DC/DC converters are used to achieve the regulation of output voltage and current, which increases hardware costs and reduces power density. To eliminate additional DC/DC converters at the receiver, the uncontrolled rectifier is replaced with an active rectifier at the receiver to acquire a CC-CV charging profile [17,18]. In order to achieve accurate CC and CV outputs, the authors of [17] employed an active rectifier at the receiver and regulated the phase shift angle of the active rectifier, which could realize zero-voltage switching (ZVS) simultaneously. In [18], they utilized a semiactive rectifier on the receiving side to maintain the CC-CV charging mode and applied a phase shift control to improve efficiency. Third, CC and CV outputs can be realized via the adoption of control methods based on the transmitting side [19,20,21,22]. The authors of [19] analyzed the load-independent output characteristics of a bilateral LCC resonant network in the zero-phase angle (ZPA) condition and derived operating angle frequency solutions for the CC output and the CV output, employing a PI control to choose the corresponding operating angle frequency to maintain the CC-CV charging profile. In [20], to obtain the CC-CV charging profile, a three-coil WPT system based on an S/S/P resonant network was proposed, and operating angle frequency solutions for load-independent outputs in the ZPA condition were deduced. However, bilateral communication between the transmitting side and receiving side is necessary, which could have an effect on the stability of the WPT system because of delay problems or even interruption issues. To avoid bilateral communication, a load identification method on the transmitting side was proposed in [21,22]. By calculating the reflected impedance and active input power, the equivalent AC resistance can be estimated. According to these estimation values, a phase-shift control method based on a transmitter was employed to maintain CC and CV outputs in two types of resonant networks [21]. Considering the fundamental wave and third harmonic wave, an identification of the load current and load voltage was presented, and a linear control strategy based on these parameters was proposed to achieve CC and CV outputs [22].

Recently, a lot of autonomous WPT systems based on parity–time (PT)-symmetric theory have been proposed. PT-symmetric theory was first proposed in non-Hermitian physics and is now widely used in many fields. In 2017, scholars from Stanford University first introduced PT-symmetric theory to the field of WPT and proposed an autonomous WPT system with strong robustness [23], achieving efficient and stable power transmission over a distance variation of 0.7 m. However, since the proposed autonomous WPT system utilizes operational amplifiers to construct a negative resistor, both transfer efficiency and output power are limited.

Subsequently, Zhou et al. [24] proposed an autonomous WPT system without using operational amplifiers, consisting of a half-bridge inverter based on a self-oscillating control. Compared with the system using operational amplifiers, the overall efficiency of the proposed system had a significant improvement. Wu et al. [25] employed the phase synchronization method to establish an autonomous WPT system, where a negative resistor whose output power can be adjusted is built by a phase-shift-controlled full-bridge inverter. Within a transfer distance of 0.1–0.25 m, the CC and CV outputs can be maintained during the charging process. In [26], an autonomous WPT system using a combination of self-oscillating and pulse width modulation was presented, and constant output power was realized in the whole coupling region. Based on an S/S/PS resonant network, Qu et al. [27] proposed a three-coil autonomous WPT system that further extended the operational coupling region.

Nevertheless, the existing autonomous WPT systems have not addressed CV output in light loads. Therefore, this paper proposes a new autonomous WPT system with CV output in a wide load range. A new construction measure of negative resistors using a combination of the self-oscillating control method and the phase-shift control method is presented that highly extends the operational coupling region of the autonomous WPT system. Meanwhile, based on the characteristics of operating frequency solutions, a coupling region estimation method is proposed to ensure that the autonomous WPT system can correctly switch the corresponding control methods in different coupling regions. In addition, a CV control strategy based on reflected impedance is presented. Compared with the existing CV control strategies, the advantages of the proposed autonomous WPT system are as follows:

(1)

No additional DC/DC converter is necessary at the transmitter and receiver.

(2)

No bilateral communication is needed between the transmitter and receiver.

(3)

Constant voltage can be achieved in a wide load range.

The rest of this paper is organized as follows: The system circuit structure and theoretical analysis are provided in Section 2. The coupling region estimation method and CV control strategy are proposed in Section 3. The experimental verification of the proposed strategy is conducted in Section 4. Finally, the conclusions are offered in Section 5.

2. System Circuit Structure and Output Voltage Characteristics

2.1. System Circuit Structure

To analyze the mentioned autonomous WPT system, a series–series (SS) resonant network is selected owing to its simple structure and low loss. The system circuit structure of the mentioned autonomous WPT system using an SS resonant network is depicted in Figure 1 and is made up of a full-bridge inverter, an SS resonant network, and an uncontrolled rectifier. As shown in Figure 1, S₁–S₄ are four power MOSFETs that comprise the inverter at the transmitter. D₁-D₄ are four rectifier diodes at the receiver. L_p and L_s are the coil self-inductances of the transmitter and receiver, respectively. C_p and C_s are the corresponding resonant capacitors of the transmitter and receiver, respectively. R_p and R_s are the coil internal resistances of the transmitter and receiver, respectively. R_load is the equivalent load resistance. R_eq is the equivalent AC resistance of the uncontrolled rectifier and satisfies R_eq = 8 R_load/π². M is the mutual inductance between the coils of the transmitter and receiver. The coupling coefficient is denoted as k = M/(L_pL_s)^0.5. I_p and I_s are resonant currents of the transmitter and receiver, respectively.

Given the filtering properties of the resonant network, the resonant currents are approximatively sine waves. Therefore, the equivalent circuit model that is established via fundamental harmonic approximation is adequately precise and can simplify the analysis. A fundamental harmonic equivalent circuit model for the aforementioned autonomous WPT system using an SS resonant network is depicted in Figure 2. As illustrated by Figure 2, the phase difference between the output voltage of the inverter, V_ab, and the resonant current of the transmitter, I_p, is always zero, so the autonomous WPT system power source is modeled as a negative resistance: −R_N = −V_ab/I_p.

2.2. Output Voltage Characteristic

According to circuit theory, the autonomous WPT system can be described by

$$\left\{\begin{array}{c}\left(R_{\mathrm{p}}-R_{\mathrm{N}}+j\omega L_{\mathrm{p}}+\frac{1}{j\omega C_{\mathrm{p}}}\right)·\stackrel{ꔷ}{I_{\mathrm{p}}}-j\omega M\stackrel{ꔷ}{I_{\mathrm{s}}}=0\\ \left(R_{\mathrm{s}}+R_{\mathrm{eq}}+j\omega L_{\mathrm{s}}+\frac{1}{j\omega C_{\mathrm{s}}}\right)·\stackrel{ꔷ}{I_{\mathrm{s}}}-j\omega M\stackrel{ꔷ}{I_{\mathrm{p}}}=0\end{array}\right.$$

(1)

where İ_p and İ_s are phasors of the resonant current of the transmitter and receiver, respectively. ω is the operating angle frequency. j is the imaginary unit.

Equation (1) can be expressed in a matrix as

$$\left(\begin{array}{cc}\frac{R_{\mathrm{p}}-R_{\mathrm{N}}}{L_{\mathrm{p}}}+j\omega -j\frac{{\omega }_1^2}{\omega }& j\omega k\sqrt{\frac{L_{\mathrm{s}}}{L_{\mathrm{p}}}}\\ j\omega k\sqrt{\frac{L_{\mathrm{s}}}{L_{\mathrm{p}}}}& \frac{R_{\mathrm{s}}+R_{\mathrm{eq}}}{L_{\mathrm{s}}}+j\omega -j\frac{{\omega }_2^2}{\omega }\end{array}\right)\left(\begin{array}{c}\stackrel{ꔷ}{I_{\mathrm{p}}}\\ \stackrel{ꔷ}{I_{\mathrm{s}}}\end{array}\right)=0$$

(2)

where ω₁ and ω₂ are the natural resonant angle frequencies of the transmitter and receiver, respectively, which are defined as ω₁ = 1/(L_pC_p)^0.5 and ω₂ = 1/(L_sC_s)^0.5.

When the determinant of the coefficient matrix of Equation (2) is zero, that is, the real part and imaginary part are both zero, Equation (2) has non-zero solutions. To solve the operating angle frequency of the autonomous WPT system, the determinant of the system coefficient matrix can be calculated with

$$\left|\begin{array}{cc}\frac{R_{\mathrm{p}}-R_{\mathrm{N}}}{L_{\mathrm{p}}}+j\omega -j\frac{{\omega }_1^2}{\omega }& j\omega k\sqrt{\frac{L_{\mathrm{s}}}{L_{\mathrm{p}}}}\\ j\omega k\sqrt{\frac{L_{\mathrm{s}}}{L_{\mathrm{p}}}}& \frac{R_{\mathrm{s}}+R_{\mathrm{eq}}}{L_{\mathrm{s}}}+j\omega -j\frac{{\omega }_2^2}{\omega }\end{array}\right|=0$$

(3)

Furthermore, the autonomous WPT system needs to meet the primary condition, that is, ω₁ = ω₂ = ω₀. Based on the primary condition, taking ω as a real number and separating the real part and the imaginary part, the conditions wherein Equation (2) has non-zero solutions can be obtained as

$$\left\{\begin{array}{c}\frac{\left(R_{\mathrm{p}}-R_{\mathrm{N}}\right)\left(R_{\mathrm{s}}+R_{\mathrm{eq}}\right)}{{\omega }_0^2{L}_{\mathrm{p}}{L}_{\mathrm{s}}}-{\left(\frac{\omega }{{\omega }_0}-\frac{{\omega }_0}{\omega }\right)}^2+\frac{{\omega }^2{k}^2}{{\omega }_0^2}=0\\ \left(\frac{\omega }{{\omega }_0}-\frac{{\omega }_0}{\omega }\right)\left(\frac{R_{\mathrm{p}}-R_{\mathrm{N}}}{{\omega }_0{L}_{\mathrm{p}}}+\frac{R_{\mathrm{s}}+R_{\mathrm{eq}}}{{\omega }_0{L}_{\mathrm{s}}}\right)=0\end{array}\right.$$

(4)

Based on Equation (4), the conditions of the autonomous WPT system can be described as [25]

$$\left\{\begin{array}{c}\omega ={\omega }_0\\ \frac{R_{\mathrm{p}}-R_{\mathrm{N}}}{L_{\mathrm{p}}}=-\frac{R_{\mathrm{s}}+R_{\mathrm{eq}}}{L_{\mathrm{s}}}\end{array}\right.$$

(5)

Given Equation (5), there are two different operating regions for the autonomous WPT system, which are the weak coupling region and the strong coupling region. Only one operating angle frequency solution in the weak coupling region is ω = ω₀. In the strong coupling region, there are two operating angle frequency solutions. Submitting Equation (5) to Equation (4), the operating angle frequency of the system in the strong coupling region can be solved as

$$\omega =\left\{\begin{array}{l}\frac{{\omega }_0}{\sqrt{2\left(1-k^2\right)}}\sqrt{2-{\left(\frac{R_{\mathrm{s}}+R_{\mathrm{eq}}}{{\omega }_0{L}_{\mathrm{s}}}\right)}^2-\sqrt{{\left(2-{\left(\frac{R_{\mathrm{s}}+R_{\mathrm{eq}}}{{\omega }_0{L}_{\mathrm{s}}}\right)}^2\right)}^2+4\left(k^2-1\right)}}\\ \frac{{\omega }_0}{\sqrt{2\left(1-k^2\right)}}\sqrt{2-{\left(\frac{R_{\mathrm{s}}+R_{\mathrm{eq}}}{{\omega }_0{L}_{\mathrm{s}}}\right)}^2+\sqrt{{\left(2-{\left(\frac{R_{\mathrm{s}}+R_{\mathrm{eq}}}{{\omega }_0{L}_{\mathrm{s}}}\right)}^2\right)}^2+4\left(k^2-1\right)}}\end{array}\right.$$

(6)

If the autonomous WPT system always operates in the strong coupling region, it is necessary to meet the conditions as follows:

$${\left(2-{\left(\frac{R_{\mathrm{s}}+R_{\mathrm{eq}}}{{\omega }_0{L}_{\mathrm{s}}}\right)}^2\right)}^2+4\left(k^2-1\right)\ge 0$$

(7)

The curve of the operating frequency of the autonomous WPT system with variation in the coupling coefficient, k, is drawn in Figure 3. As depicted in Figure 3, the blue lines, which represent the operating frequency, can be divided between the weak coupling region (0 < k < k_c) and the strong coupling region (k_c ≤ k < 1). Furthermore, the transparent red region represents the strong coupling region, and the transparent blue region represents the weak coupling region.

According to Equation (7), the critical coupling coefficient, k_c, can be calculated with [25]

$$k_{\mathrm{c}}=\sqrt{1-\frac{1}{4}{\left(2-{\left(\frac{R_{\mathrm{s}}+R_{\mathrm{eq}}}{{\omega }_0{L}_{\mathrm{s}}}\right)}^2\right)}^2}$$

(8)

According to Equations (2) and (4), when the autonomous WPT system operates in two different coupling regions, the output current gain of the system can be calculated as [26]

$$\left\{\begin{array}{l}\frac{I_{\mathrm{s}}}{I_{\mathrm{p}}}=\frac{{\omega }_{0}k{L}_{\mathrm{s}}}{R_{\mathrm{s}}+R_{\mathrm{eq}}}\sqrt{\frac{L_{\mathrm{p}}}{L_{\mathrm{s}}}},0<k<k_{\mathrm{c}}\\ \frac{I_{\mathrm{s}}}{I_{\mathrm{p}}}=\sqrt{\frac{L_{\mathrm{p}}}{L_{\mathrm{s}}}},k_{\mathrm{c}}\le k<1\end{array}\right.$$

(9)

According to Equations (4) and (9), the output voltage gain of the system can be calculated as [26]

$$\left\{\begin{array}{l}\frac{V_{\mathrm{o}}}{V_{\mathrm{in}}}=\frac{{\omega }_{0}k{L}_{\mathrm{s}}{R}_{\mathrm{eq}}}{{\omega }_0^2{k}^2{L}_{\mathrm{p}}{L}_{\mathrm{s}}+R_{\mathrm{p}}\left(R_{\mathrm{s}}+R_{\mathrm{eq}}\right)}\sqrt{\frac{L_{\mathrm{p}}}{L_{\mathrm{s}}}},0<k<k_{\mathrm{c}}\\ \frac{V_{\mathrm{o}}}{V_{\mathrm{in}}}=\frac{1}{\sqrt{\frac{L_{\mathrm{p}}}{L_{\mathrm{s}}}}\left(1+\frac{R_{\mathrm{s}}}{R_{\mathrm{eq}}}\right)+\sqrt{\frac{L_{\mathrm{s}}}{L_{\mathrm{p}}}}\frac{R_{\mathrm{p}}}{R_{\mathrm{eq}}}},k_{\mathrm{c}}\le k<1\end{array}\right.$$

(10)

In practical applications, compared with coil internal resistances, the equivalent AC resistance, R_eq, is generally far larger. Hence, coil internal resistances can be neglected; then, the output voltage gain of the system can be simplified as

$$\left\{\begin{array}{l}\frac{V_{\mathrm{o}}}{V_{\mathrm{in}}}=\frac{R_{\mathrm{eq}}}{{\omega }_{0}k\sqrt{L_{\mathrm{p}}{L}_{\mathrm{s}}}},0<k<k_{\mathrm{c}}\\ \frac{V_{\mathrm{o}}}{V_{\mathrm{in}}}=\sqrt{\frac{L_{\mathrm{s}}}{L_{\mathrm{p}}}},k_{\mathrm{c}}\le k<1\end{array}\right.$$

(11)

According to Equation (11), the autonomous WPT system operating in the strong coupling region can maintain the constant output voltage without an additional control method. In other words, only the output control method in the weak coupling region needs to be considered.

The curve of the output voltage of the autonomous WPT system with variation in equivalent AC resistance, R_eq, is depicted in Figure 4. As seen in Figure 4, given the equivalent AC resistance, R_eq, the blue line, which represents the transfer characteristic of the output voltage, can also be divided between two regions, namely, the constant voltage region (0 < R_eq ≤ R_c) and the non-constant voltage region (R_eq > R_c). It is worth noting that the constant voltage region is equivalent to the strong coupling region, and the non-constant voltage region is equivalent to the weak coupling region.

According to Equation (7), the critical equivalent AC resistance, R_c, is defined as [26]

$$R_{\mathrm{c}}={\omega }_0{L}_{\mathrm{s}}\sqrt{2\left(1-\sqrt{\left(1-k^2\right)}\right)}-R_{\mathrm{s}}$$

(12)

3. Proposed Control Strategy for the Autonomous System

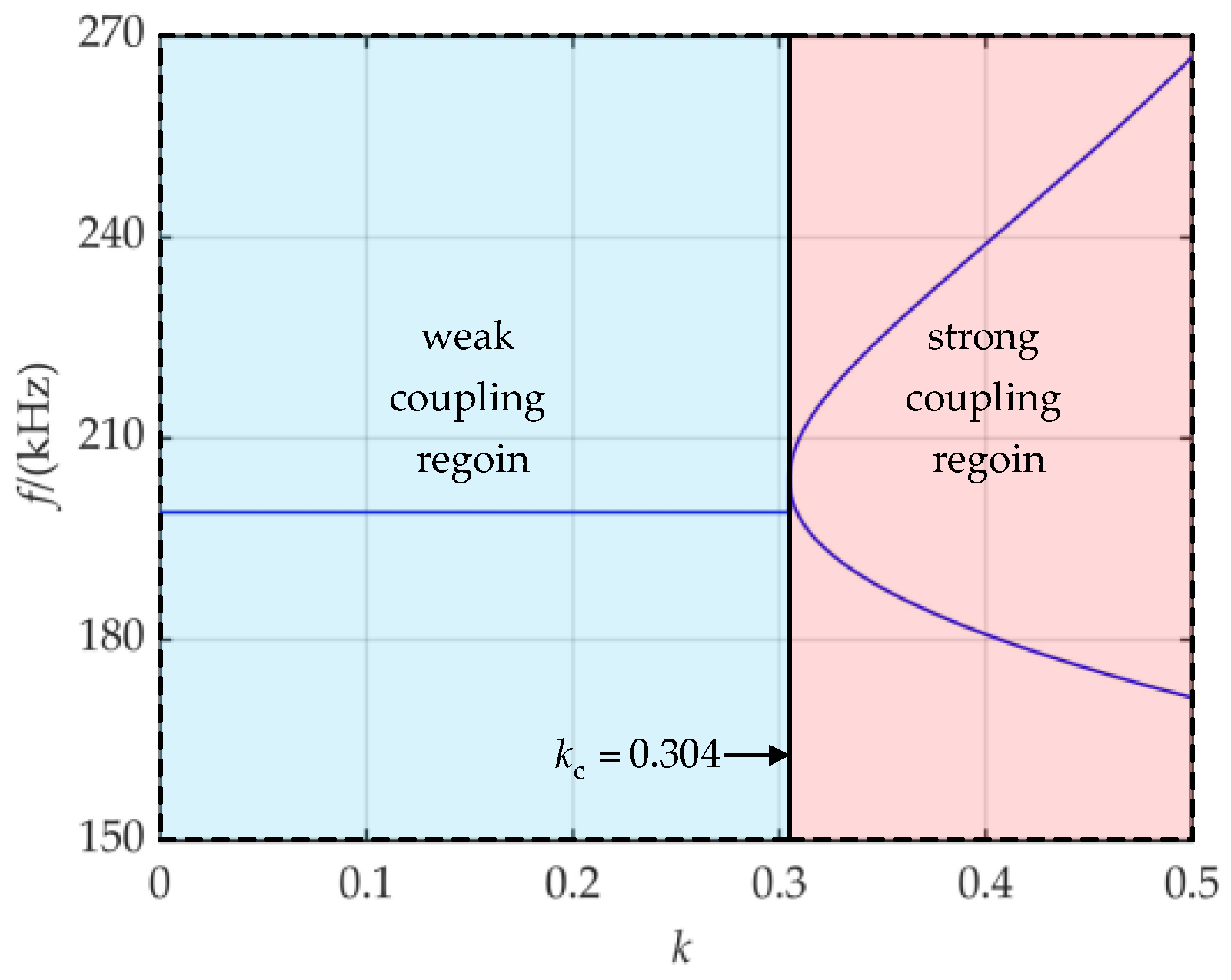
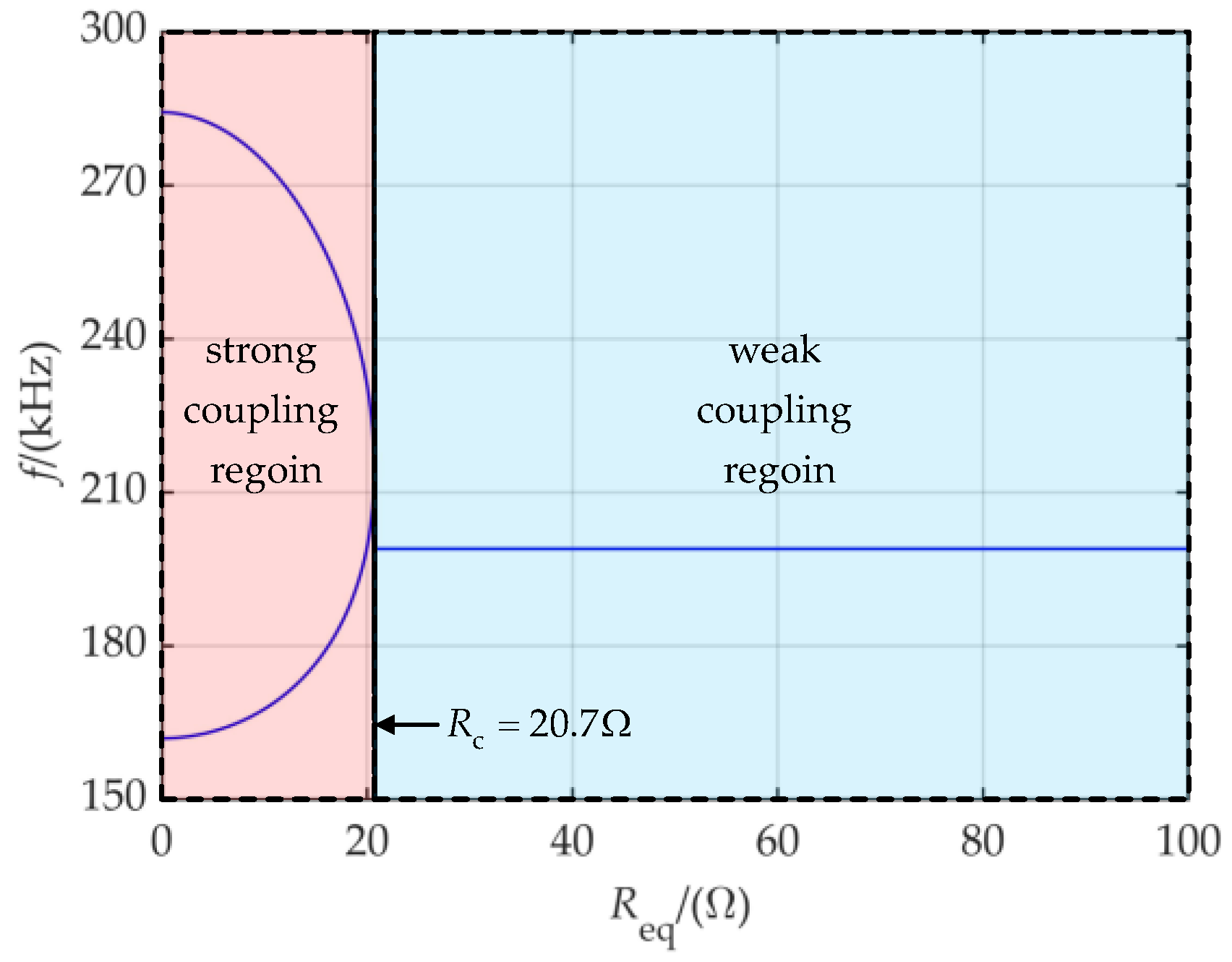
3.1. Coupling Region Estimation

Based on the preceding theoretical analysis, the mentioned autonomous WPT system can only maintain the CV output of the strong coupling region. Therefore, to expand the operating range of the CV output, the CV output of the weak coupling region is necessary to achieve. Because of the application of the additional control method in the weak coupling region, it is essential for acquiring CV output in a wide load range to estimate the operating coupling region. Hence, this section presents a novel method of estimating the operating coupling region. Moreover, the fundamental principle of the method is briefly interpreted as follows.

The curve of the operating frequency with variation in equivalent AC resistance is shown in Figure 5. According to Figure 5, the blue lines, which represent the operating frequency, can be divided between the strong coupling region (0 < R_eq ≤ R_c) and the weak coupling region (R_eq > R_c). When the operating frequency deviates from the natural resonant frequency, the operating coupling region of the system is the strong coupling region; when the operating frequency is the natural resonant frequency, the operating coupling region of the system is the weak coupling region. Therefore, the operating coupling region can be estimated as long as it is determined whether the operating frequency deviates from the natural resonant frequency.

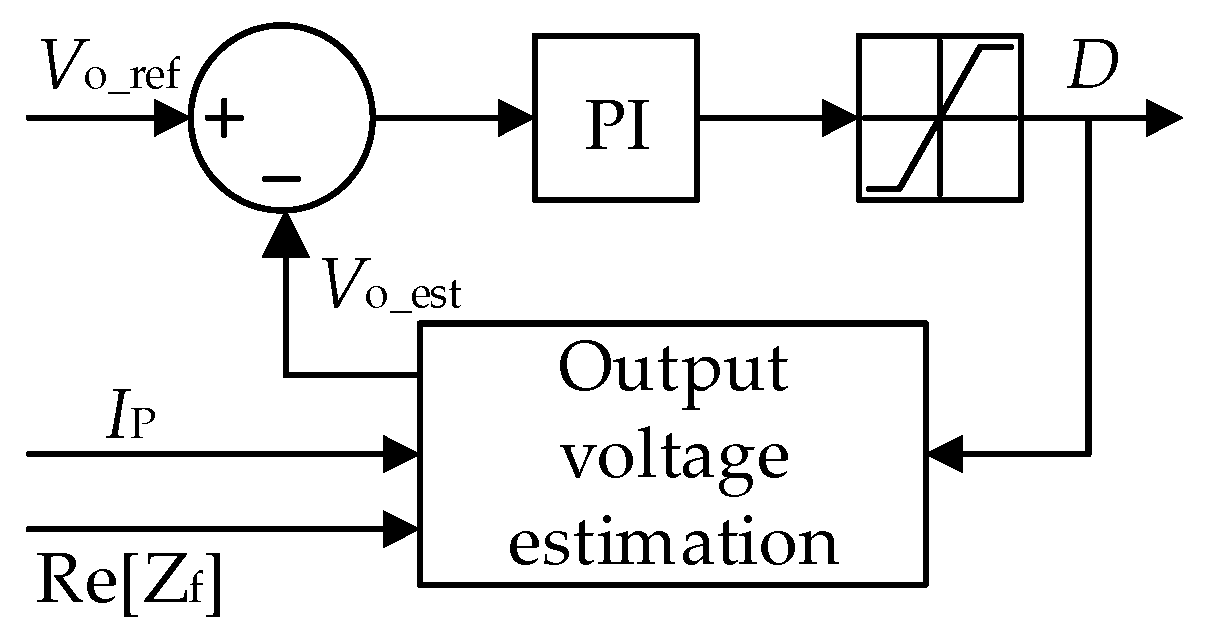
3.2. Output Voltage Estimation in the Weak Coupling Region

Because of the CV characteristics of the autonomous WPT system of the strong coupling region, the autonomous WPT system of the strong coupling region does not require an additional control method. However, the autonomous WPT system of the weak coupling region is the same as the traditional MCR-WPT system, in which the CV output cannot be maintained. In order to maintain the CV output of the weak coupling region, correctly estimating the output voltage of the autonomous WPT system is critical when the system operates in the weak coupling region. Therefore, this section proposes a new method of estimating the output voltage of the weak coupling region. Moreover, the fundamental principle of the method is briefly explained as follows.

The fundamental harmonic equivalent circuit model of the autonomous WPT system based on reflected impedance is characterized in Figure 6. According to circuit theory, the reflected impedance of the autonomous WPT system can be expressed as

$$Z_{\mathrm{f}}=\frac{{\omega }^2{k}^2{L}_{\mathrm{p}}{L}_{\mathrm{s}}}{R_{\mathrm{s}}+R_{\mathrm{eq}}+j\left(\omega L_{\mathrm{s}}-\frac{1}{\omega C_{\mathrm{s}}}\right)}=\frac{{\omega }^2{k}^2{L}_{\mathrm{p}}{L}_{\mathrm{s}}\left(R_{\mathrm{s}}+R_{\mathrm{eq}}\right)}{{\left(R_{\mathrm{s}}+R_{\mathrm{eq}}\right)}^2+{\left(\omega L_{\mathrm{s}}-\frac{1}{\omega C_{\mathrm{s}}}\right)}^2}-j\frac{{\omega }^2{k}^2{L}_{\mathrm{p}}{L}_{\mathrm{s}}\left(\omega L_{\mathrm{s}}-\frac{1}{\omega C_{\mathrm{s}}}\right)}{{\left(R_{\mathrm{s}}+R_{\mathrm{eq}}\right)}^2+{\left(\omega L_{\mathrm{s}}-\frac{1}{\omega C_{\mathrm{s}}}\right)}^2}$$

(13)

The operating angle frequency, ω, of the autonomous WPT system is equal to ω₀ when the operating coupling region of the system is the weak coupling region. Therefore, when ignoring the coil internal resistance of the receiving side, the real part of the reflected impedance, Re[Z_f], of the weak coupling region is simplified as

$$\mathrm{Re}\left[Z_{\mathrm{f}}\right]=\frac{{\omega }^2{k}^2{L}_{\mathrm{p}}{L}_{\mathrm{s}}}{R_{\mathrm{eq}}}=R_{\mathrm{N}}-R_{\mathrm{p}}$$

(14)

According to Figure 6, the estimation value of the output voltage can be calculated with

$$V_{\mathrm{o}}=I_{\mathrm{p}}\mathrm{Re}\left[Z_{\mathrm{f}}\right]=I_{\mathrm{p}}\left(R_{\mathrm{N}}-R_{\mathrm{p}}\right)$$

(15)

3.3. Control Strategy

According to the output voltage characteristics of the autonomous WPT system, a self-oscillating control method is applied in the strong coupling region, and an additional phase shift control method is employed in the weak coupling region to obtain a CV output in a wide load range. In order to precisely switch the corresponding control methods in different coupling regions, this section proposes a novel control strategy based on coupling region estimation. Figure 7 presents a flowchart of the proposed control strategy.

First of all, negative resistance, R_N, is calculated based on its definition. Secondly, according to Equation (14), the real part of the reflected impedance, Re[Z_f], is calculated. Then, according to the operating frequency characteristic of the autonomous WPT system, the operating coupling region of the system is judged by comparing the natural resonant frequency with the operating frequency to choose an appropriate control method. When the autonomous WPT system operates at the natural resonant frequency, the control method for the strong coupling region is selected, and we return to the first step. When the autonomous WPT system operates at a non-natural resonant frequency, an additional control method for the weak coupling region based on output voltage estimation is chosen. Next, the estimation value of the output voltage, V_{o_est}, is calculated according to Equation (15). Finally, after comparing the values of V_{o_est} and V_{o_ref}, a PI control is implemented to adjust the duty cycle of the full-bridge inverter, which maintains the constant output voltage, and we return to the first step. Figure 8 describes a constant output voltage control diagram of the weak coupling region at the transmitter.

4. Experiment Verification

In order to validate the practicability of theoretical analysis, an experimental prototype of the autonomous WPT system with 24 V constant output in a wide load range is built. The planar spiral coils of the transmitter and the receiver are tightly wound using a multistrand Litz wire of 200 × 0.1 mm with 16 turns, an inner diameter of 34.4 mm, and an outer diameter of 97.4 mm. In addition, to enhance coupling and flux guidance, a 10 mm × 10 mm × 5 mm ferrite layer composed of four 5 mm × 5 mm ferrites is added to the underside of the coil. The other parameters of the experimental prototype are shown in

Table 1. Parameters of the experimental prototype.

Symbol	Parameter	Value
LP	Coil self-inductance of the transmitter	31.9 μH
LS	Coil self-inductance of the receiver	31.6 μH
RP	Coil internal resistance of the transmitter	0.19 Ω
RS	Coil internal resistance of the receiver	0.19 Ω
CP	Resonant capacitance of LP	20.05 nF
CS	Resonant capacitance of LS	20.24 nF
f0	Natural resonant frequency	199 kHz
Vin	DC input voltage	24 V
k	Coupling coefficient	0.51

. In the experiment, in order to facilitate load switching, this paper makes use of the DC electronic load as the load for testing. For the convenience of testing, the range of the experimental load resistance is 7 to 100 Ω (strong coupling region: 7–24 Ω; weak coupling region: 24–100 Ω).

4.1. Steady-State Performance

The proposed system—either using the self-oscillating control method or the additional phase shift control method to maintain constant output voltage—is verified in this section. Figure 9 and Figure 10 describe the steady-state operating waveforms of the DC output voltage, the output voltage of the inverter, and the transmitting current.

Figure 9 presents the steady-state operating waveforms of the proposed system operating at a non-natural resonant frequency. When the load resistance, R_load, is equal to 12 Ω, the operating frequency of the proposed system is regulated to 166.4 kHz. The operating frequency of the proposed system is modulated to 168.9 kHz when the load resistance, R_load, is 14 Ω. As shown in Figure 9a,b, employing the self-oscillating control method, the operating frequency can be automatically adjusted to maintain the constant output voltage.

Figure 10 depicts the steady-state waveforms of the proposed system operating at a natural resonant frequency. When the load resistance, R_load, is 40 Ω, the duty cycle of the inverter is regulated to 0.41. The operating frequency of the proposed system is regulated to 0.28 when the load resistance, R_load, is equal to 60 Ω. As shown in Figure 10a,b by applying the additional phase-shift control method, the duty cycle of the inverter is adjusted by the PI control to realize constant output voltage.

In addition, the phase difference between the transmitting fundamental voltage and the transmitting current should be 180°. As illustrated in Figure 9 and Figure 10, the experimental results are consistent with the theoretical results.

4.2. Dynamic Performance

Load resistance mutation experiments in three different situations are conducted to test the dynamic performance of the proposed autonomous WPT system. Figure 11 describes the dynamic operating waveforms of the DC output voltage, the output voltage of the inverter, and the transmitting current.

The load resistance is altered from 12 Ω to 14 Ω; thus, the dynamic operating waveform of the proposed system, operating at a non-natural resonant frequency, is depicted in Figure 11a. In Figure 11a, the operating frequency of the autonomous WPT system changes from 166.4 kHz to 168.9 kHz, and the output voltage changes from 23.9 V to 24.01 V. In this process, the autonomous WPT system operates under the self-oscillating control method, which can self-select the optimal operating frequency to reach the steady state, and its output voltage is maintained at a constant value. The load resistance is altered from 40 Ω to 60 Ω; thus, the dynamic operating waveform of the proposed system, operating at a natural resonant frequency, is presented in Figure 11b. In Figure 11b, the autonomous WPT system operates at a fixed frequency, which is the natural frequency, and the output voltage changes from 24.08 V to 24.1 V. In the process, the autonomous WPT system under the phase-shift control method adjusts the duty cycle of the inverter to obtain a constant output voltage according to the estimation value of the output voltage. As shown in Figure 11a,b, when the proposed system operates at both a non-natural resonant frequency and a natural resonant frequency, the DC output voltage can be approximately maintained at 24 V.

Figure 11c shows the dynamic waveform of the proposed system when it transitions from a non-natural resonant frequency to a natural resonant frequency. In Figure 11c, given the coupling region judgment method, when altering the load resistance from 12 Ω to 14 Ω, the phase-shift control can be applied to the autonomous WPT system, which is under the self-oscillating control. As depicted in Figure 11c, when the operating coupling region changes, the CV output of the proposed autonomous WPT system can also be achieved.

4.3. Output Voltage and Overall Efficiency in a Wide Load Range

The theoretical and experimental operating frequencies of the autonomous WPT system under different equivalent AC resistances are compared in Figure 12. Because the theoretical operating frequency does not consider the actual duty cycle of the inverter, it will lead to additional errors. As seen in Figure 12, the experimental results for the operating frequency are approximately consistent with the theoretical results for the operating frequency.

The experimental results for the output voltage and overall efficiency under different equivalent load resistances are characterized in Figure 13. When the self-oscillating control method of the strong coupling region is employed, the variation in the output voltage is within 3%. When the additional phase shift control method of the weak coupling region is applied, the variation in the output voltage is within 2%. Therefore, the variation in the output voltage in a wide load range is relatively small and acceptable. The overall efficiency can be calculated using the output power, P_o, divided by the input power, P_in, where P_o and P_in are shown in the electronic load and the DC power supply, respectively. In addition, the output voltage of the traditional autonomous WPT system is also depicted in Figure 13. As shown in Figure 13, the traditional autonomous WPT system operating in the weak coupling region cannot maintain constant output voltage.

5. Conclusions

In conclusion, a new implementation method for an autonomous WPT system combining self-oscillating control and phase-shift control is proposed. Based on circuit theory, a system circuit model and a fundamental harmonic equivalent circuit model for the proposed system are established, and the transfer characteristics of the proposed system are derived and analyzed. By applying different control methods in different coupling regions, the output voltage can be maintained at a constant value. Furthermore, the proposed coupling region judgment method, based on the characteristics of operating frequency solutions, does not require an additional DC/DC converter or bilateral communication, which reduces the volume and hardware costs of the system. Finally, the feasibility of the theoretical analysis is validated by experiments. Therefore, the proposed autonomous WPT system can be employed in applications that require CV output in a wide load range.