1. Introduction
Recently, economic expansion has posed an unprecedented surge in electrical energy demand, owing to rapid urbanization and industrialization. Also, increasing global concerns over environmental sustainability have motivated a shift towards renewable energy sources (RESs) [
1]. Thus, there has been an urgent reformation in the grid structures towards smaller grids able to integrate RESs and control their generations to maintain acceptable voltage and frequency ranges. Therefore, MGs have emerged as a key element in power system architectures due to their ability to cope with high RES penetration and facilitate its integration. MG is a localized grouping of sources and loads that operates as a single controllable entity [
2]. MGs can disconnect from the main grid to operate autonomously when the main grid suffers disturbances [
3]. Distributed generators (DGs), such as wind turbines [
4], solar panels, and diesel generators, are the generation units. Also, MGs may include an energy storage system (ESS) like a battery bank or a flywheel as a rapid backup energy supplier. These MGs are attached to the grid by the point of common coupling (PCC), where MG units are attached as well. The integration of various DGs into a single system presents serious technical challenges. Efficient power sharing among the DGs is needed to ensure stable operation during transient disturbances while maintaining power quality and stability [
5].
In MG control, droop at the primary level responds to system operation to retain fast regulation. It is realized through droop, inner voltage, and current control loops, with the objective of DG power sharing, power quality, and voltage and frequency stabilization [
6]. The primary layer does not communicate with anything else, so it can react quickly to changes in the system on the millisecond level. This lets it quickly change reference values that come from voltage and frequency amplitudes processed in the inner loops. The relevant drawbacks associated with conventional droop control are the following: frequency and voltage deviations from nominal values past each disturbance. To address these deviations, the secondary controller operates as a compensator. These disturbances are common in low inertia and high RES penetration generation [
7]. The transient performance exhibits a gradual response, potentially leading to instability. The extent of this instability is contingent on disparities in the droop coefficients. The active and reactive powers are in a coupled relationship related to the MG lines and DGs’ R/X ratio (the ratio of resistance to inductive impedance).
The secondary level ensures that deviations remain within specified limits. Compared to the primary level, it exhibits a slow dynamic response to variations. The secondary level is categorized into centralized and decentralized controls [
8]. The tertiary level is the ultimate and slowest, governing the voltage and frequency of the MG interconnected with the main grid. This regulation relies on the measurement of power driven from the main grid. Traditional control strategies often fail to handle these tasks due to the highly dynamic and non-linear nature of MG loads and generation. Many optimization mechanisms to enhance energy management have been proposed to build a rigid control system [
9]. A review of MG control optimization methods is shown in
Table 1.
This conventional methodology typically relies on single-objective optimization techniques to derive the requisite parameters. However, it tends to overlook the inherent trade-offs within the optimization process. So, this study comes up with a new way to control multi-objective optimization using the multi-objective algorithm-based droop framework [
10], which works especially well for autonomous units.
This paper undertakes the derivation of a comprehensive model for autonomous MG operations. Leveraging the established mathematical model, power sharing analysis is employed to identify the parameters exerting influence over the system’s stability and delineate the stable parameter boundaries. Subsequently, the research proceeds to optimize these parameters by employing the CF-GSA. During the optimization process, due consideration is accorded to three competing objectives: the overarching regulation of the system’s voltage, the minimization of discrepancies in system power sharing, and the enhancement of system stability over time [
11]. The objective is to minimize these diverse criteria simultaneously, yielding a set of parameters for each DG within the system.
The CF-GSA is a new meta-heuristic optimization algorithm that was built on top of the Gravity Search Algorithm (GSA). It has a better model that makes convergence more accurate and faster and avoids local optimum points [
12]. CF-GSA has proven effective in learning and handling complex, high-dimensional data and making accurate and robust predictions, offering a potential solution to MG power sharing. It is a predictive control that may contribute to stability, energy management, and power dispatch optimization. Few studies have focused on optimized droop controllers specifically designed for optimal power sharing following a disturbance.
This paper proposes a CF-GSA-based droop controller to address MGs’ complex, adaptable, and dynamic control requirements. This research shows the CF-GSA-based droop efficacy and robustness in improving power sharing, voltage and frequency deviations, and power quality. Improving MG resilience and stability is essential to future energy systems. This research effectively provides a framework for enhancing MGs’ resilience, adaptability, and stability [
13,
14]. CF-GSA optimization can be applied to droop control in MGs with the following measures:
Objective Function Formulation: It defines an objective function that represents the performance criteria of the microgrid concerning voltage and frequency stability. This function should encapsulate the droop control parameters.
Parameter Representation: This represents the droop control parameters as variables in the optimization problem. These parameters include droop coefficients and reference voltage and frequency levels.
Fitness Evaluation: It utilizes CF-GSA to iteratively explore the solution space of Droop control parameters. The centripetal force concept helps guide the search towards optimal solutions.
Optimization Process: CF-GSA will iteratively evaluate different sets of droop control parameters based on the defined objective function. The algorithm will refine its search over several iterations, converging towards the optimal parameter values.
Optimal Solution: Once the optimization process converges, the resulting set of droop control parameters represent the optimized configuration for the microgrid’s stable operation under varying load and generation conditions.
This research paper is organized as follows: Initially, the paper introduces and discusses the MG primary control mathematical model and illustrates how frequency and voltage deviations are linked to conventional droop control. Second, it describes droop optimization and how the optimizer tunes certain parameters to improve droop performance. Third, this paper explains the CF-GSA algorithm and describes dynamic control optimization. Finally, the model performance results are demonstrated under the effect of the most common disturbances confronting the MG control, such as load fluctuations, DG disconnection, and secondary control failure due to communication delays. As each case unfolds, the CF-GSA-optimized droop is shown to be effective in maintaining stability [
15]. It has demonstrated robustness to effectively handle power sharing and stability issues during transient disturbances [
16]. In the subsequent sections, MGs modeling, the design and functionality of the proposed work, and the promising results are presented and discussed.
2. Microgrid Modelling
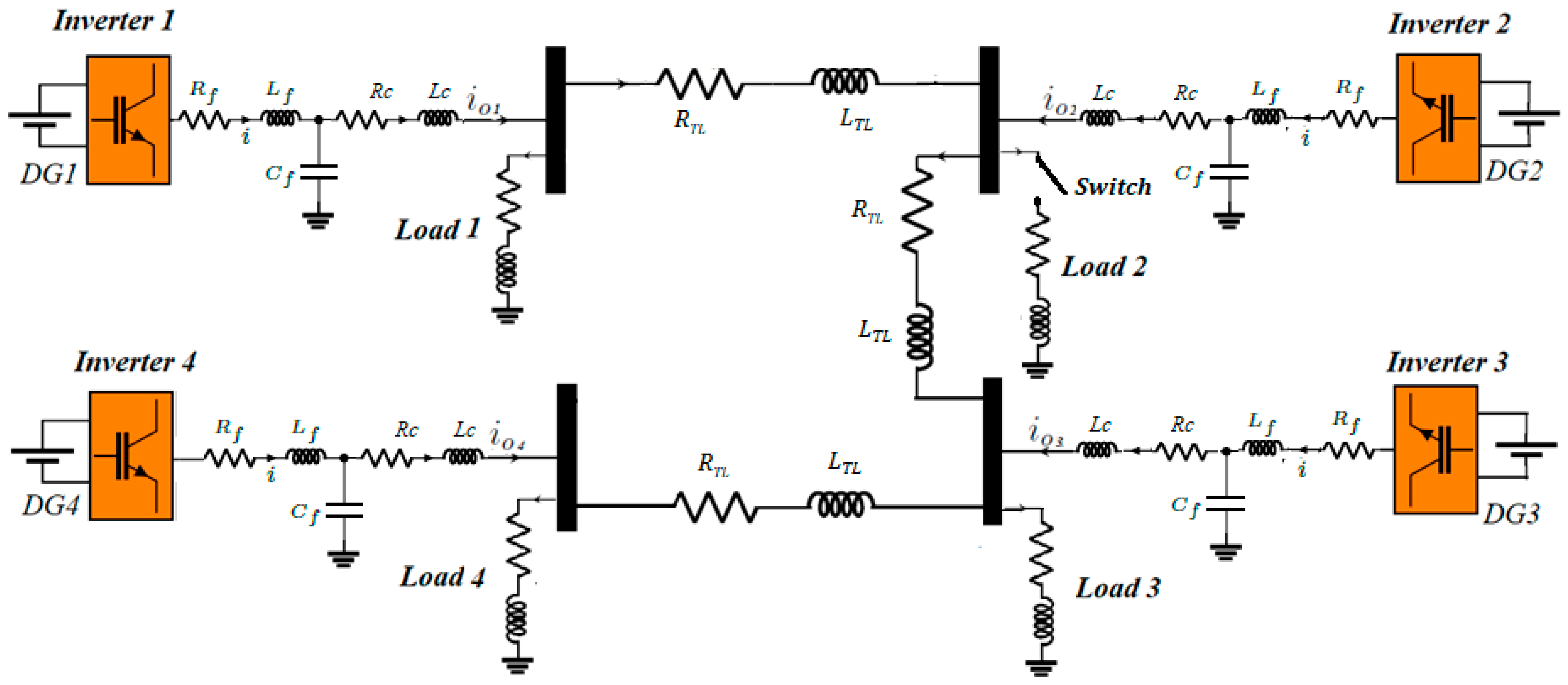
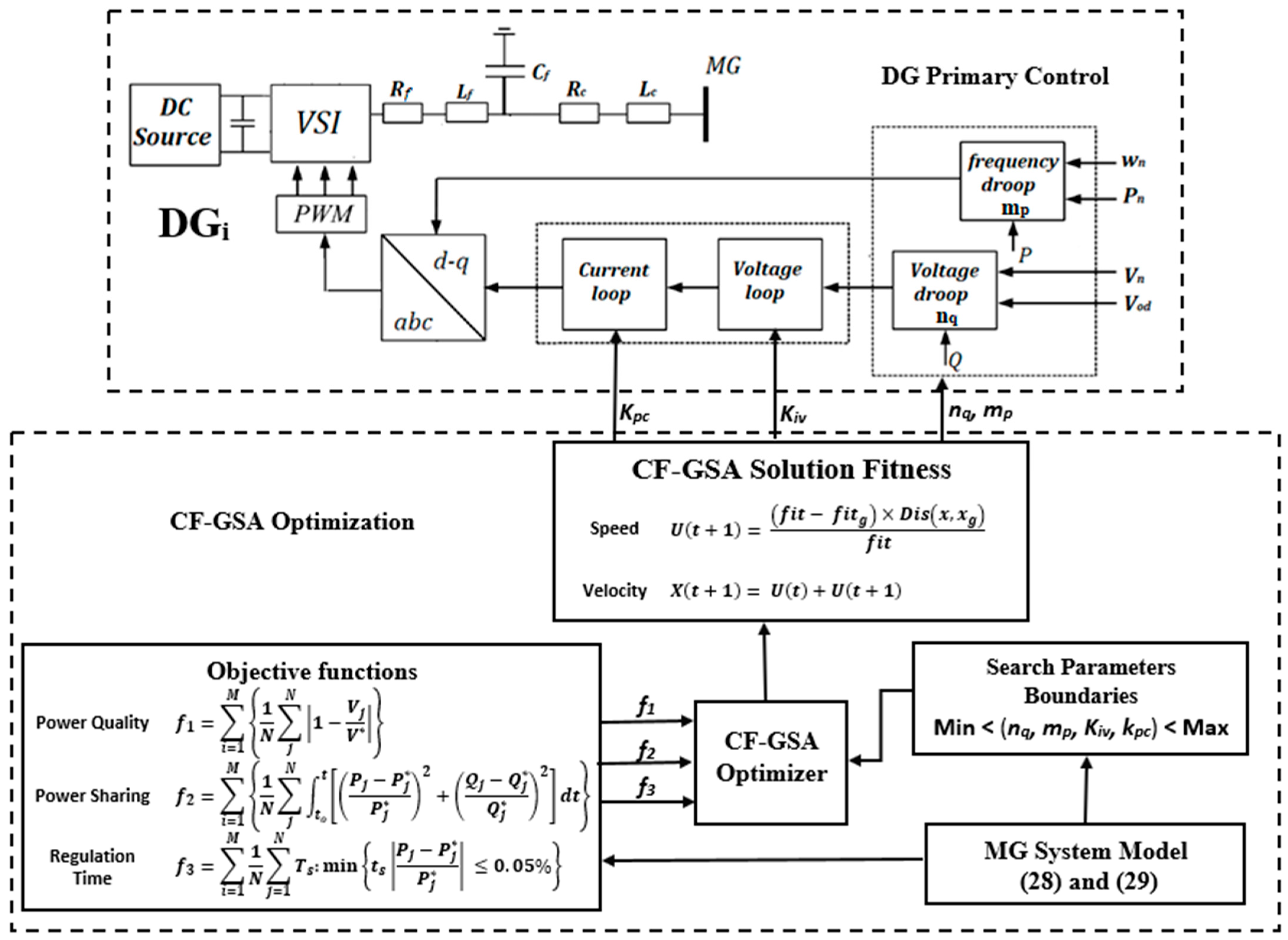
In this paper, a radial connection MG consisting of four DGs with separate distribution buses was built. The schematic representation of the MG system is shown in
Figure 1. The load capacity of the control area was 5.8 MW and 200 VAR (in each bus). DGs were made as DC RESs with voltage source inverters (VSIs) to make them act like they have low inertia and are easily affected by changes in MG performance and the weather outside. The power generated by these DGs was subject to sporadic interruptions, leading to voltage and frequency variations. Aside from this, the frequency and voltage deviations were caused by the dynamic changes in the switched load’s resistive and inductive loads in bus 2. The frequency and voltage limits must be maintained by sharing the generation gap and fulfilling the load demand. Thus, the optimized droop to control operating VSIs in active and reactive power (PQ) mode was feasible if they were connected to a medium-voltage MG that specifies the voltage and frequency references [
17].
However, a sudden disconnection of the grid power source would collapse the MG system because balance is absent in load and generation power, affecting the frequency and voltage control. VSIs’ capability to establish voltage and frequency references enabled MGs to operate in autonomous mode without any communication or mode control requirements. This is possible due to the VSI’s ability to operate and coordinate in parallel with other voltage sources alongside other VSIs during autonomous operation. Using reference voltage and frequency to control VSIs [
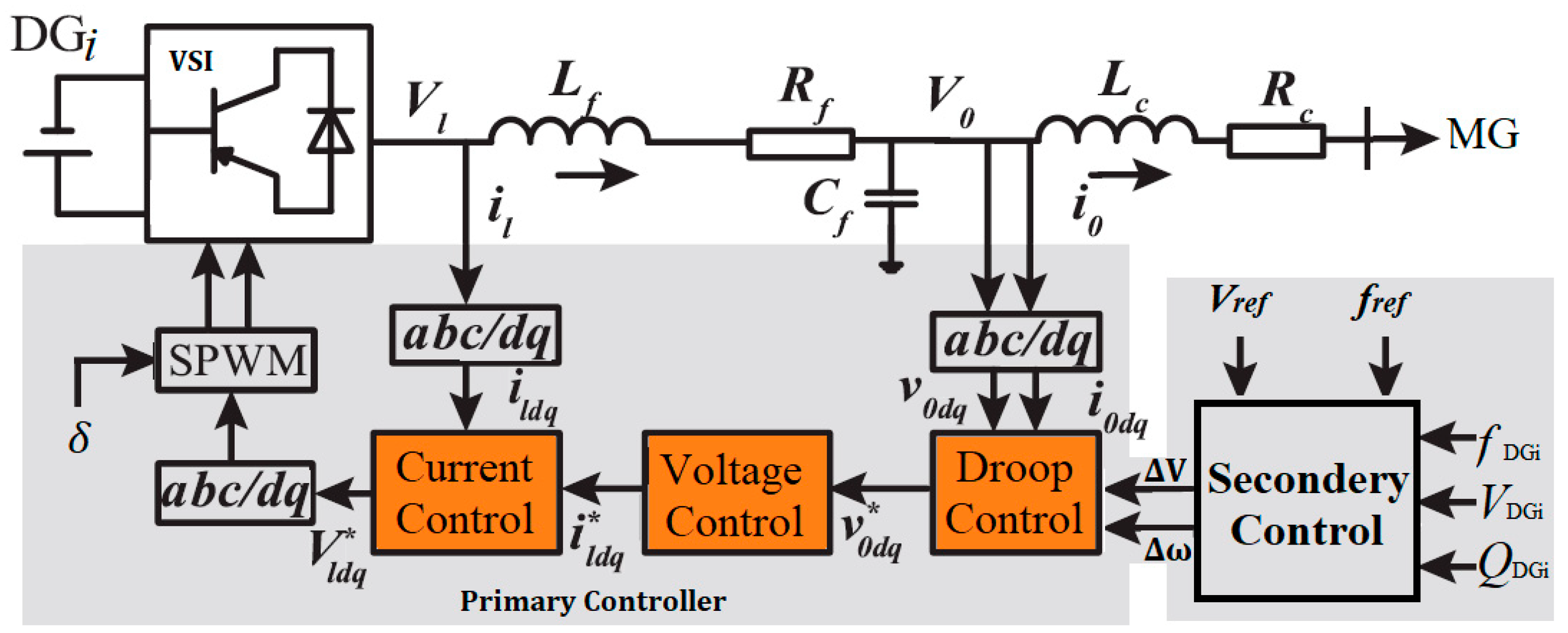
18], DGs can be put under a primary control to spread the load demand among several DGs in a way that is proportional to their ratings. VSIs are mostly controlled by the Sinusoidal Pulse Width Modulation (SPWM) switching technique, controlled by primary controller signals as shown in
Figure 2.
The load and line currents were modeled in the common d–q frame to facilitate the interconnection of multiple inverters. Tackling power sharing issues was addressed by employing model predictive controllers, an automatically tuned controller that performs optimization in real-time. It is dependent on several fundamental requirements, which will be discussed further below, to generate its controlled variables in the control system to tackle the dynamic fluctuation of frequency and voltage.
The proposed control strategy endeavors to achieve the goal by using prediction criteria across a forecast horizon as well as adhering to the restrictions of MG performance. The model was used to compute the next control action to be taken based on bus ratings, ensuring closed-loop stability, and reducing performance uncertainty. The future trajectory was predicted in advance while using an optimized controller. The control loops of the primary control layer were targeted for optimization in this paper; these loops were droop, voltage, and current loops [
19]. The droop loop was used in power systems to regulate frequency and voltage. It adjusts the DG inverter frequency and voltage based on the load [
20]. In a droop control strategy, as the load increases, the frequency decreases, and vice versa. The voltage control loop ensures that the output voltage remains within specified bounds. It regulates the voltage level to prevent overvoltage or undervoltage conditions, harming connected equipment [
21]. The current loop regulated the flow of electrical current in power electronics and converter systems. It ensured that the current supplied to the load or grid followed a desired reference. To improve these loops, a multi-objective optimization algorithm was used to generate the coefficients and gains of the models in these loops.
2.1. Primary Control Modelling
The primary control, including the droop control, inspired by traditional synchronous generator governor principles, independently regulates MG-connected VSI’s power output for precise distribution among distributed power sources during minor system disturbances. An MG, as depicted in
Figure 3, is comprised of distributed generation, network infrastructure, and load models.
The four-DG model from the reference was used in this paper. It includes droop controllers, voltage and current control models, LC filters, and coupled inductors. A full-system model was considered to comprehensively analyze stability factors within the system. Unlike previous models that neglected inverter gains, they were considered in this model to enhance model accuracy [
22].
2.1.1. Droop Model
The fundamental concept behind power sharing is to maintain load equilibrium by adjusting voltage and frequency amplitude by the droop characteristics. In the parallel VSI system, fundamental frequency (
ω) and voltage (
) are determined by the droop coefficients, frequency droop coefficient (
), and voltage droop coefficient (
), which are defined as follows:
where
,
, and
represent nominal set-points for frequency, voltage, and active power, while the nominal value for reactive power is considered zero. The calculation of reactive
and active power
relies on the measured voltage and current represented the by
d–
q reference frame, denoted by
,
,
, and
. To ensure high-quality power delivery, the average power is obtained through the utilization of a low-pass impedance filter featuring a cut-off frequency of
:
The droop control model is derived through linearization at the equilibrium point:
To facilitate the conversion of each reference inverter system to the common frame, the angular difference between the frames, denoted as
δ, is introduced. The frequency of the first VSI is established as the DG1 frequency,
. Consequently, the model for
δ is expressed as follows:
2.1.2. Voltage Control
The voltage control loop generates a reference current vector, denoted as
and
, within the
d–
q coordinate system. Illustrated in
Figure 3 is the block diagram of the voltage controller, which encompasses two conventional proportional–integral (PI) controllers featuring proportional (
Kpv) and integral (
Kiv) coefficients with a feed-forward term characterized by gain
F. The small signal
model for voltage control is represented as:
In these equations, corresponds to output voltage, and signifies the reference provided by the power controller. is filter capacitance.
2.1.3. Current Control
The current loop functions by deriving the output reference SPWM voltage, denoted as
and
. This is achieved through a comparison between the current sample values,
and
, and the filtered current reference, employing a PI controller and
is the filter inductance of the DG. The small signal
model for current loop is represented as:
2.1.4. LC Impedance Filter and Coupling Inductance Model
The impedance LC filter of
and
, along with the DG coupling line inductance
LC, and
RC serves to eliminate harmonics of switching frequency when the VSI is tied to the MG. Some references assume that
equals
. However, it is crucial to consider the inverter gain, particularly when the SPWM magnitude is significant, as neglecting it can lead to inaccurate results. The relationship between these factors is defined as follows:
The PWM gain, denoted as
, is equivalent to carrier amplitude and DC source voltage. This relationship is directly relevant when the VSI PWM sampling period, denoted as
TS, approaches a minimal value:
The impedance model for this scenario is as follows:
2.1.5. Inverter Mathematical Model
To integrate the inverter into the entire system, it is essential to transform the output variables
and the input variable
into a shared reference system. This transformation results in the output and input variables, as represented by the equations below:
To explain the droop performance from another perspective, it reduces the local power imbalance in autonomous mode, causing variations in frequency and voltage due to the corresponding droop characteristics [
23]. By letting the VSIs handle system problems with the information on their terminals, this control principle gets rid of the need for urgent communication between the DGs and the central controller (secondary layer) [
24]. If an unexpected disturbance happens in these situations, the VSIs that are controlled by droop functions will fix any power imbalances and spread out changes in power based on how their droop functions work. The droop coefficients
and
are effective in the trade of power balance and voltage/frequency stability. Equation (5) determines the power sharing while considering that power unbalance
P is represented by:
where
is the power change of load and
is power injected by
n the number of DGs.
where
is post-disturbance frequency and
is the pre-disturbance frequency.
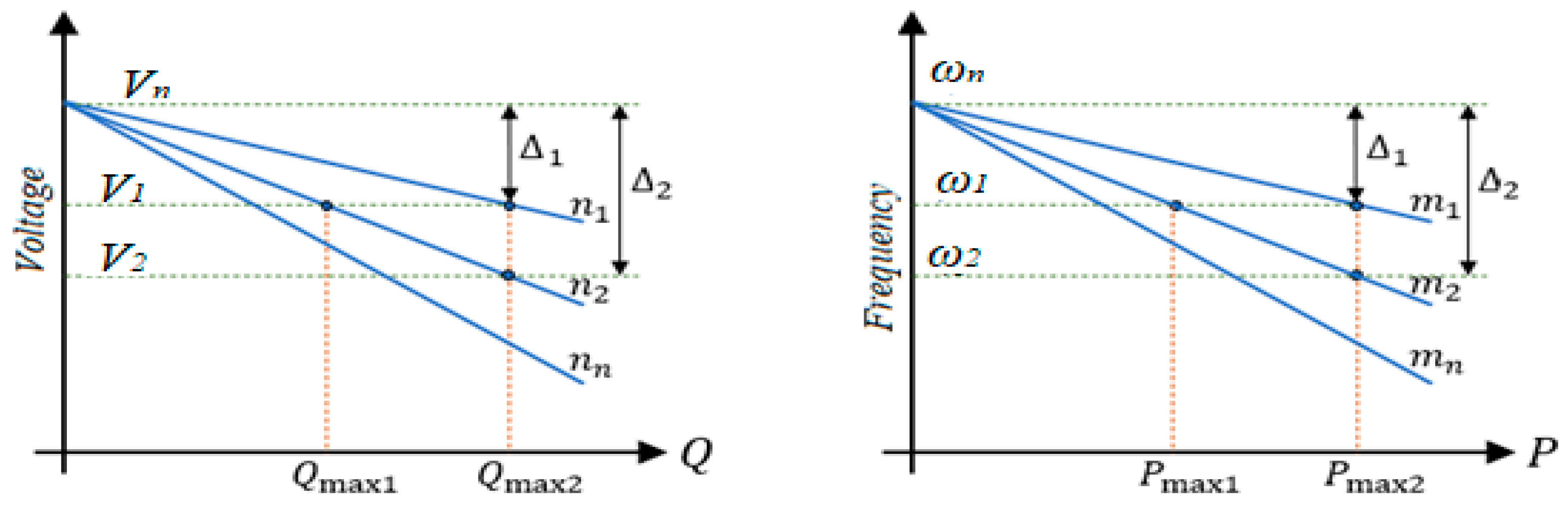
Therefore, droop coefficients are essential to ensure optimal power sharing. Thus, updating them enhances the response and adaptability to confront various transient disturbances. The advantage of droop control is that it enables power sharing without necessitating a communication link, thereby conferring flexibility and autonomy [
25]. As shown in
Figure 4, the droop curves demonstrate the deviation after each disturbance.
3. Methodology
3.1. Centripetal Force–Gravity Search Algorithm
Gravity force is directly proportional to the product of objects’ masses and inversely proportional to the distance between them. This law implies the existence of an attraction among particles within the search space, causing them to gravitate towards regions with higher mass. The object’s movement within this search space adheres to Newton’s second law, which relates the object’s acceleration to the force acting upon it and its mass [
26,
27]. Through repeated iterations, the entire population congregates around individuals of superior quality. Conversely, centripetal force denotes the resultant force experienced by an object undergoing circular motion, directed towards the circle center. In celestial motion, such as a star orbiting another, gravity serves as the centripetal force (CF). CF concept is giving rise to the innovative CF-GSA optimization, where CF is proportionate to an object’s linear velocity and mass while being inversely related to the spacing between objects. As mass increases, orbiting objects (planets) move toward the center (sun), expediting the discovery of the global optimum. Similarly, higher linear velocity and reduced distance yield the same effect. The physical expression of CF is given in Formula (32):
where
F is the centripetal force between two or more objects,
is the object’s linear velocity, and
R denotes the spacing between the objects. To simplify computational processes, the equation of
is simplified (removing root square) to the below expression:
In gravitation search, the object (planet) with higher mass moves faster to the optimal solution in the center (sun). Thus, mass
M defines the fitness of the search agent. The spacing
R defines the distance of the search agent from the optimal solution. Therefore, during the iterations, the formula for velocity update is reformulated in Formula (34):
where
fit denotes the current search agent fitness value,
fitg is iteration fitness, and
Dis(
x,
xg) represents the space between the current search agent and global optimum. Thus, the position update formula in Equation (35) is derived according to the
expression.
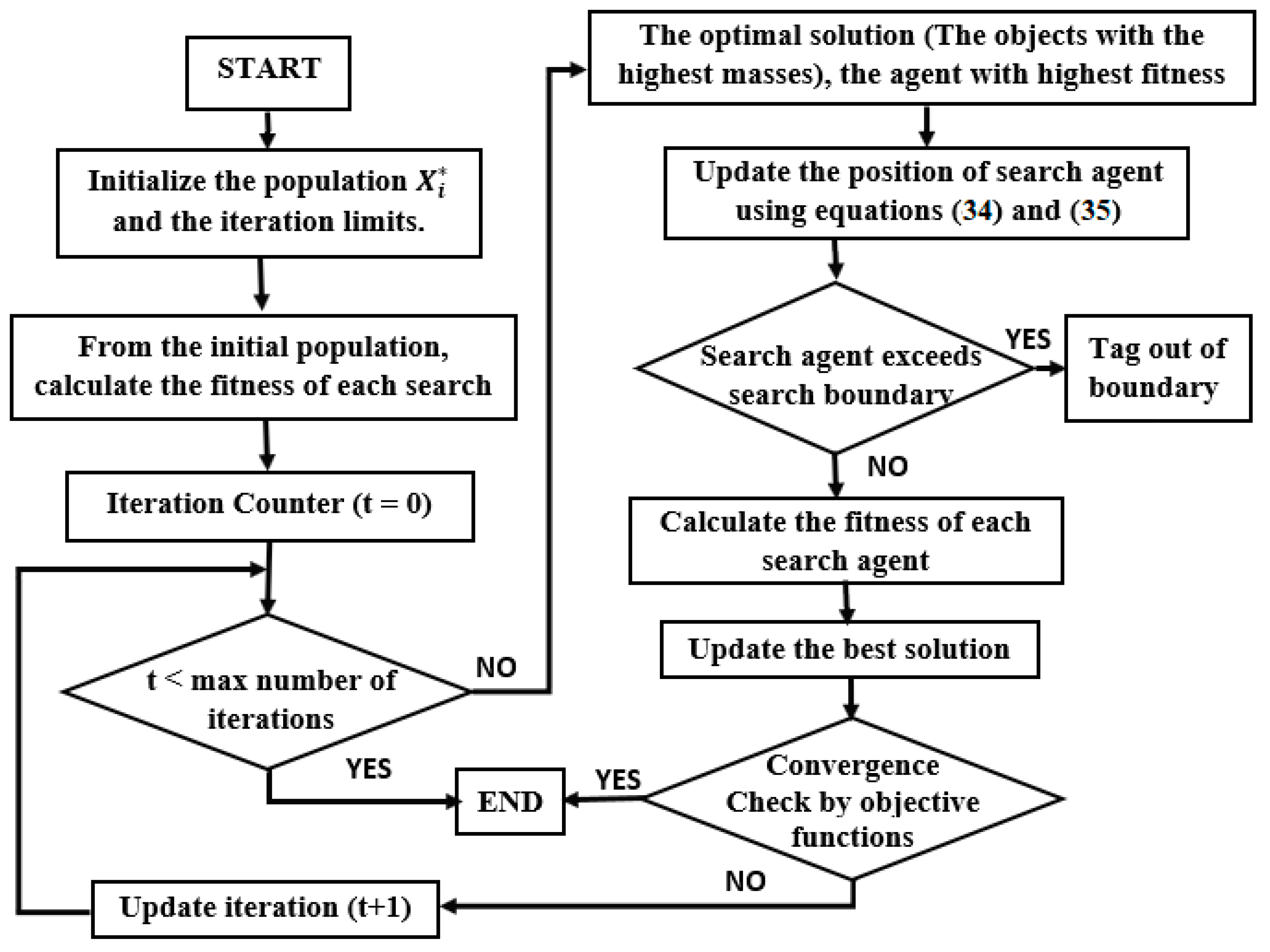
CF-GSA uses local search, rather than random search, of a neighborhood of solutions to find a single solution. Therefore, a population of candidate solutions is first generated, optimized, and updated for a certain problem. Then, an intensive search is carried out to find the best solution with the highest fitness (the nearest global optimum). As shown in
Figure 5, the track of required droop coefficients is based on the procedural steps of the CF-GSA, which are outlined as follows:
Initializing the candidate solution population , here is the best solution.
Calculating the value of fitness for each search agent and update
Determining the deviation for the agent in the generated population. The best solution is to adjust (mp, nq, Kpc, and Kiv) that leads to the lowest possible deviation.
Updating the position and velocity of the search agent using Equations (34) and (35).
Checking if any search agent exceeds the search space boundary.
Checking the solution using the objective functions to avoid local solutions.
Calculating the agents’ fitness, update the global optimum if there is better fitness.
3.2. Multi-Objective Function Optimization
The case study under consideration encompasses three optimization objectives. Given the MG capability to transition between many operation scenarios, it necessitates the establishment of an objective function that accounts for stability and seamless switching between these distinct operational modes, denoted as
M. It is essential to consider metrics for stability evaluating, encompassing adjustment time, voltage fluctuations, and power sharing [
28]. The raw deviations as the objective function would introduce a bias towards minimizing power share errors. Consequently, the power sharing error and voltage deviation are standardized to the order of 10
−3. Within this framework, this paper formulates three distinct objective functions, assessing the MG power quality, power sharing, and minimum regulation time, respectively.
3.2.1. The Power Quality Objective
This paper assesses MG power quality using voltage as a key indicator. Droop control, while effective in power regulation, can lead to voltage fluctuations relative to the rated value [
29]. These deviations, whether high or low, have the potential to damage components, thus undermining power quality. To quantify this, voltage deviation from the rated value was measured and normalized to establish the power quality loss rate. The goal is to minimize the loss rate of the power quality, focusing on the gap between each DG voltage
and the nominal voltage
(311), represented by the equation:
where
M denotes the system’s operational status, including grid-connected and autonomous scenarios, while
N signifies the number of DGs in the system.
3.2.2. Power Sharing Objective
The DG’s generated power is a vital system performance indicator, and droop control aims to distribute active and reactive power among inverters [
30]. Accurate power sharing signifies good system performance, but impedance mismatches cause reactive power distribution errors. This paper minimizes deviations in active and reactive power to assess power distribution, ensuring quick responses, according to the objective function is:
where
and
are output power, and
and
are reference values for various modes, given by:
where
is DG power capacity, and
,
, and
are total MG loads.
3.2.3. The Regulation Time Objective
To optimize the droop control, regulation time is adapted as an objective, defined based on the conventional control concept, where a minimum duration of
is required for instantaneous power to reach and maintain a voltage and frequency range within ±1% and ±0.1% of the median value, respectively [
31]. The Criterion (40) ensures the desired control of the optimized droop.
The objective function is then formulated as:
Solving multi-objective optimization problems involving objectives (36)–(41) necessitates the application of multi-objective optimization techniques.
Furthermore, this multi-objective optimization depends on an intensification mechanism to determine the search space associated with these objectives, as detailed in
Table 2. The intensification mechanism, depending on the expertise of the designer, is used to reduce the search time to the minimum as it intensifies the research on the promising research space rather than exploring a wide range of search space as it is required in the exploration mechanism.
3.3. Proposed Multi-Objectives CF-GSA Optimized Droop Control
This manuscript proposes and investigates a smart droop control for DGs to manage optimal power sharing among the DGs in the MG using CF-GSA to maintain optimal power sharing during operation and following disturbance events. The primary control layer is mainly responsible for power sharing, power quality, as well as voltage and frequency stability tasks. Also, the primary layer contains current and voltage loops controlled by PI controllers that are tuned consistently with the MG conditions and dynamics. The optimization involves collecting and preprocessing data, including information about each DG, the load demand, and the voltage and frequency levels at MG buses. This model depends on the following: the MG model to be regulated, a history of previous MG occurrences of control, and the cost functions of the control.
Two main gains will be tuned by the CF-GSA optimizer, the proportional coefficient for the current loop and the integral coefficient for the voltage loop. and are turned into constant values equal to 6.35 and 0.0029, respectively, as they cause no considerable change over the droop control performance.
As shown in
Figure 6, the optimizer continuously monitors the system state and adjusts the control coefficients as needed, providing a dynamic and adaptive control solution that can handle varying operating conditions and disturbances. This optimization structure generates the predicted control signal using an improved algorithm model, and its inputs consist of the previous control moves, the current state of the system, and the desired referenced control moves.
The tuning method is responsible for carrying out this task. Considering the cost function as well as the manipulated input and output constraints, the predicted output of the optimized droop as well as the actual error are incorporated into the production of the optimal power sharing control. The essential goal of the optimized droop is to bring the actual error as close to zero as possible with the minimum value for the cost function that is being considered, which can be expressed as a weighted sum of the squares of future error values and forecasted output. The data are collected over a certain period under various operating conditions to capture the system’s dynamic behavior. To prepare the data for the CF-GSA model, preprocessing steps such as normalization or standardization are performed to ensure the data are on a similar scale. Also, any missing or inconsistent data are handled to ensure the quality of the dataset. Optimization of the CF-GSA model involves applying the collected dataset to the MG parameters and resulting performance to accurately predict the control actions for a given system state. The model is evaluated using a separate part of the dataset. This optimization involves optimizing the objective functions, ensuring power sharing to maintain acceptable voltage and frequency levels at the MG buses. This CF-GSA optimizing model must fulfill the performance objectives and confront MG dynamics.
4. Results and Discussion
A radial connection MG model and simulation were carried out using MATLAB Simulink version 2023a for execution of simulations, providing a robust foundation for the derivation and interpretation of results. Based on the achieved optimal control parameters, this section aims to assess the system’s performance under conditions such as load disturbance, unequal line impedance, and plug-and-play scenarios. The outcomes of the multi-objective optimization strategy demonstrate the superior performance of CFGSA. Also, the precision of the experimental outcomes across all compared algorithms was ensured, and a uniform configuration was adopted. The population size was fixed at 30, the iteration count was set to 500, and each test function underwent 30 runs. These metrics serve to assess the algorithm’s accuracy and stability effectively. The satisfactory solution values customized by the objective functions were used to observe and control the MG parameters outlined in Equations (28) and (29). The performance of the proposed control was evaluated using the MG structure described in
Figure 1, the MG model ratings and specifications are outlined in
Table 3.
The validation scenarios encompass a broad range of conditions and cases that occur in the daily operation of MGs, including variations in inductive load demand, system disturbances such as the unexpected trip of a DG, and finally, secondary distributed failure due to weak communication topology and communication delay. These cases were combined to pose a complex challenge to the MG performance and verify the robustness and adaptability of the optimized droop. It is worth mentioning that the radial connection was the most challenging configuration among ring and mesh MG connections to control successfully since it was unable to confront voltage and frequency deviations due to the difficulty of power delivery and high aggregate line impedance, which resist natural power sharing. Therefore, this MG configuration was used to pose a control complexity to validate the optimized droop robustness against the worst-case scenarios. In Case 1, the optimization model was put through its paces by load fluctuations. Case 2 examined the robustness of the proposed control by subjecting it to a sudden DG disconnection and simulating its effects. Case 3 shed light on the robustness of the proposed system when a failure takes place in the secondary control and the ability of the primary layer to mitigate it,
is no longer zero as stated in Equation (3). The secondary layer is responsible for ensuring voltage and frequency stability. Therefore, with delayed information to the secondary, the secondary control was out-of-order, hence the voltage stability [
32,
33].
The proposed optimizer was designed and optimized to mitigate faulty compensation. In secondary control, the communication link was needed to send the instantaneous ratings (V, P, and Q) from the MG nodes and buses to the distributed secondary controllers of each DG. In the first and second cases, the secondary controller communication topology was an all-to-all mesh topology. However, in Case 3, a weak daisy chain topology is used to test the adaptability of the proposed optimizer.
4.1. Load Power Sharing
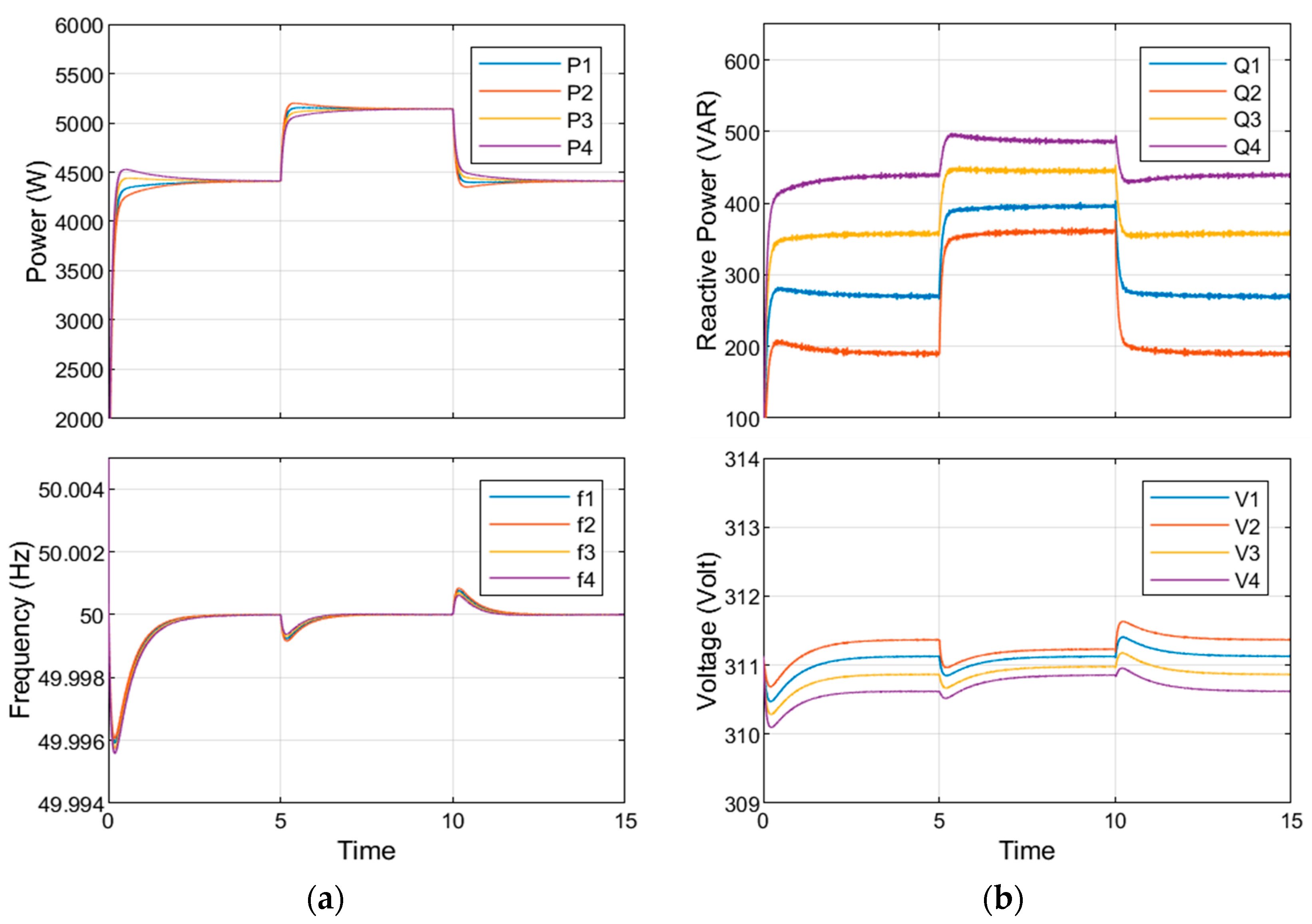
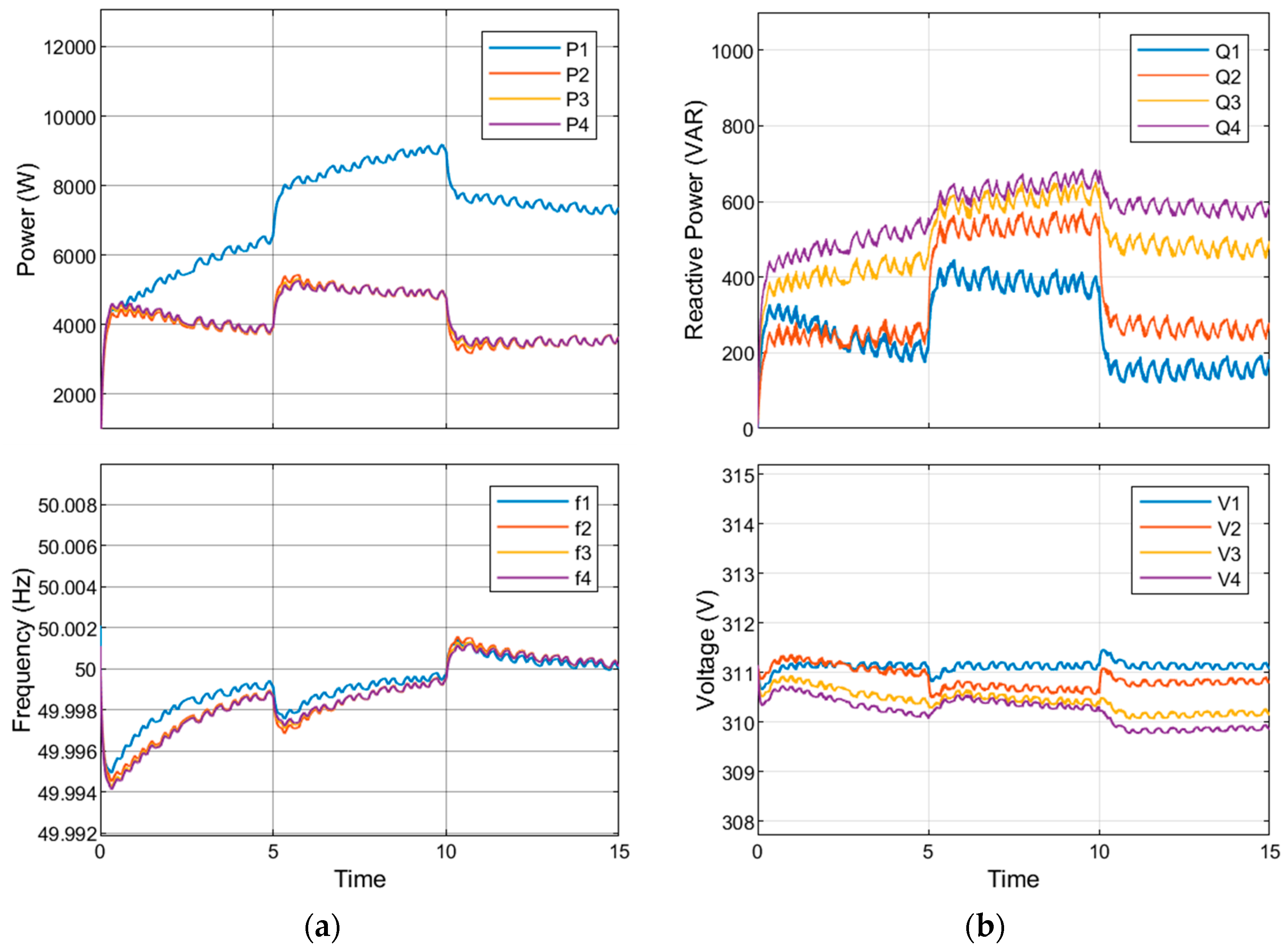
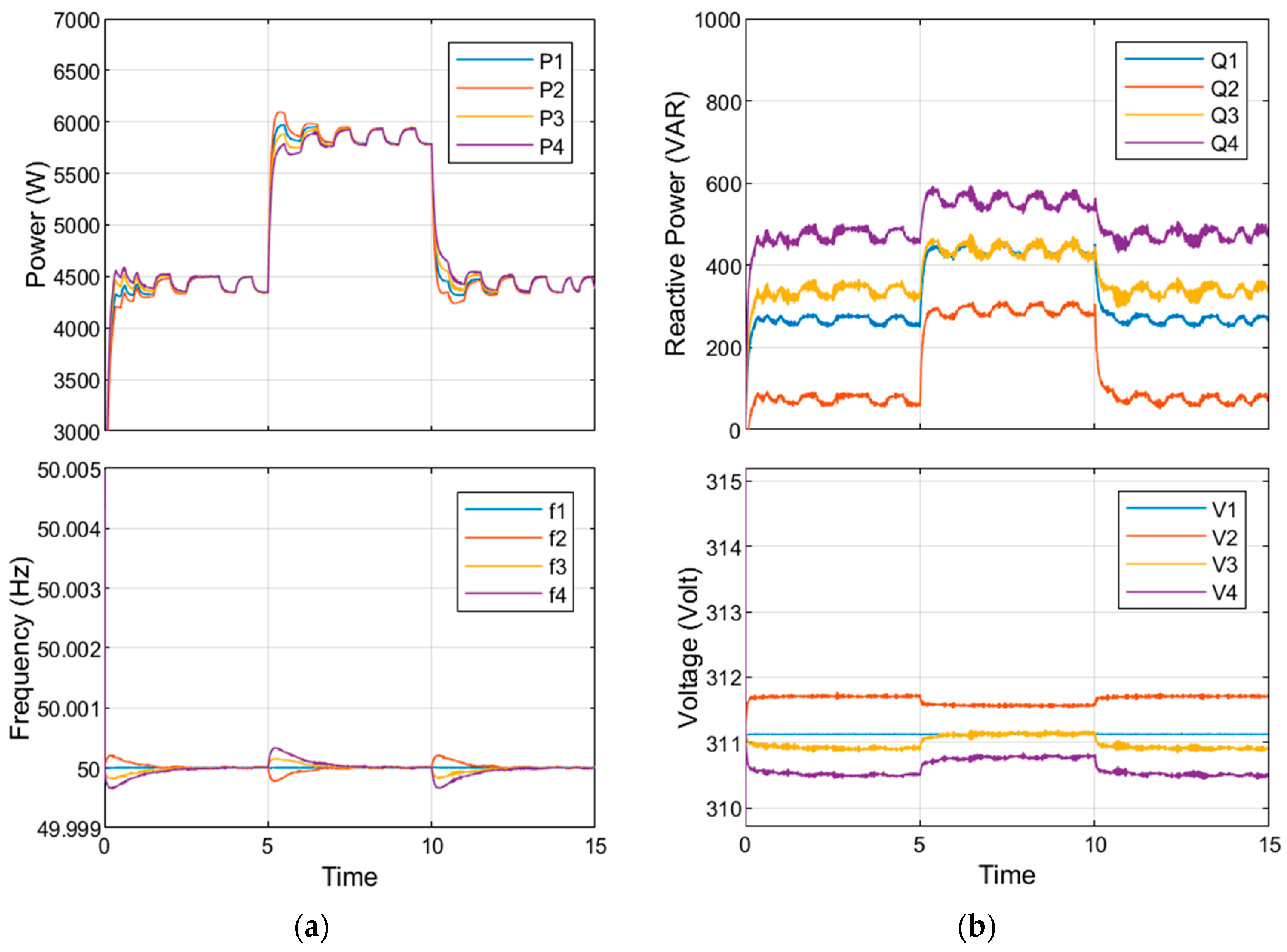
This section presents, in
Figure 7 and
Figure 8, a recent PSO-optimized droop with a model predictive control approach and the proposed CF-GSA-optimized droop, respectively. In (a) figures, the active power sharing regulates the frequency, while (b) figures demonstrate the reactive power sharing regulating voltage. Initially, the radial MG connection operates under inductive loads 1, 2, and 3, while load 2 is off. At a time of 5 to 10 s, load 2 is attached to the system to examine MG performance under additional critical inductive load changes.
The results, as shown in
Figure 8, showed that the proposed optimizer reduced the voltage and frequency deviation before, during, and after attaching load 2. The voltage deviation was 0.4 volts, and the restoration time was less than 1 s under the optimization. In frequency regulation, the optimized system reduced the frequency deviation (0.0002) at the operation startup, load added at t = 5 s, and load isolation at t = 10 s. Compared with the frequency restoration in [
34], the deviation was reduced significantly from 0.006 to 0.00025 Hz with the same restoration time of 1.5 s.
4.2. Inductive Load Sharing under DG Trip Scienario
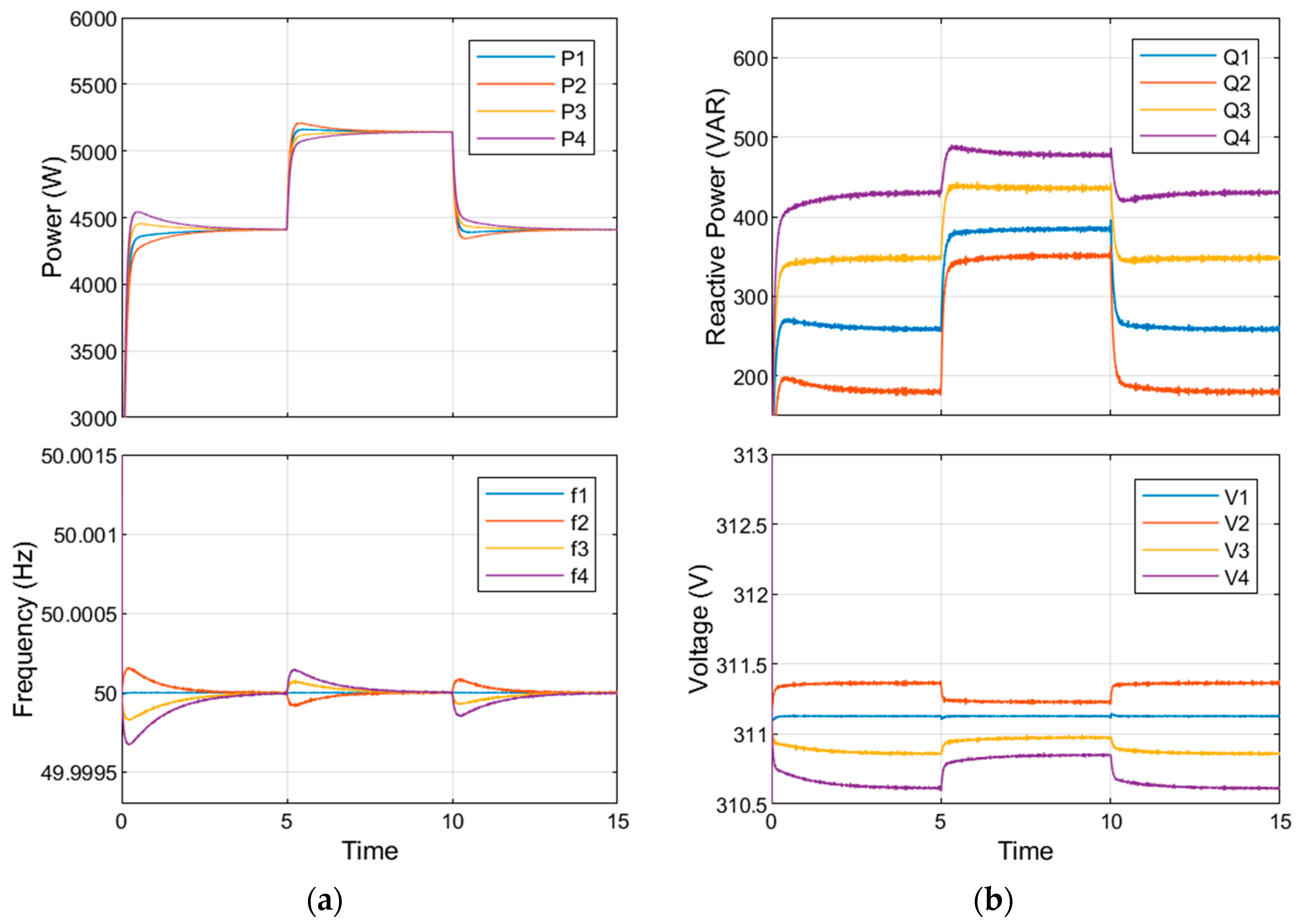
When confronted with an abrupt failure of a DG, the proposed optimized control shows agility in managing and compensating for the power shortage. It directs the operating DGs to increase their power output to cover the generation shortage due to a DG tripping at t = 5 s. This response minimizes the disturbance impact on the MG bus, avoiding any failure due to high voltage and frequency deviations. In
Figure 9, the proposed control offers a robust and adaptable response.
While DG4 was disconnected at t = 5 s, other DGs successfully compensated for the power shortage, even after an inductive load (load 2) was added at t = 10 s. Due to the radial MG line impedances, the closest source (DG3) was under the most pressure compared to the other DGs. The voltage in DG3 temporarily dropped by 0.4 V, which was fine. From t = 5 s on, the DG4 no-load voltage and frequency increased by 0.7 V and 0.01 Hz, respectively, which is acceptable under all governing protocols for MG performance. After t = 10 s, the DG no-load ratings increased since the additional load triggered the optimized droop to adjust DG4 to contribute to the new load sharing. In this case, load 4 successfully stayed in service. The controller performed without serious transient fluctuations on MG buses. This control approach demonstrates notable protective efficiency and enhances the reliability of MG.
4.3. Secondary Layer Failure (Communication Delay) Case
This section aims to demonstrate how the proposed system mitigates the severe and challenging secondary control failure. Thus, a simple graph daisy chain topology was used instead of the mesh (all-to-all) topology used in the previous cases. Daisy chain topology’s limited connectivity causes problems such as congestion and communication delays, so it cannot send instantaneous information to all of the secondary controllers in the MG in the right order. Also, the secondary control shared information for each DG is limited only to the neighboring units in the graph structure. These direct paths
aij of simple graph daisy chain topology with vertices are represented by a (4 × 4) matrix known as the adjacency matrix (
A), where all paths’ weights are set to unity [
35,
36].
The diagonal entries
i =
j represent the number of edges associated with a node (
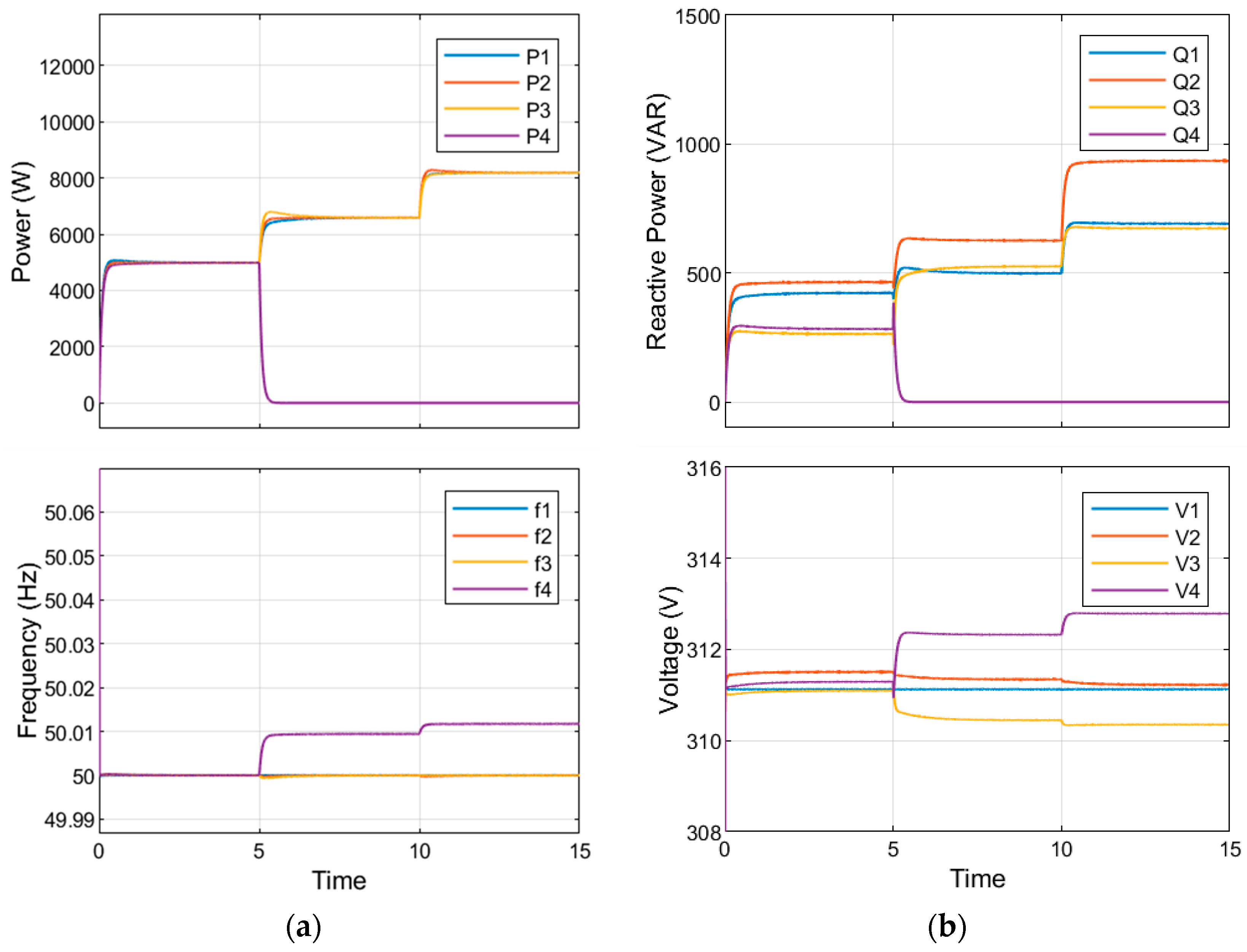
i). The adjacency matrix represents the communication topology and connectivity among all graph nodes. The communication delay employed on each communication link was 50 ms to cause a notable failure in the secondary control. The system operates on unbalanced loads on buses 1, 3, and 4. At t = (5 to 10) s, load 2 is added to examine the controller performance under two complex concurrent tasks. The failure of the secondary controller severely affected the stability of MG due to the inability of conventional droop controllers. The response is very poor, with intolerable voltage and frequency deviations, according to the results shown in
Figure 10. On the other hand, as shown in
Figure 11, under daisy chain topology and communication delay, the response of optimized droop is in the tolerated range. Moderate frequency (less than 0.0005 Hz) and voltage (less than 0.7 V) deviations were noticed, demonstrating robustness very close to (all to all) normal performance.
5. Conclusions
In this paper, a CF-GSA-optimized droop for improved MG power sharing is proposed. The MG includes four DGs, buses, and loads connected in radial connection. The proposed optimized control is designed to confront challenging, complex MG dynamics. Four parameters (mp, nq, Kpv, and Kic) in the primary layer are supervised and updated by the proposed optimized droop controller. Afterward, it was tested under various combined operational scenarios and disturbances. It exhibits robust, adaptable performance and has managed to improve power sharing among the DGs, maintaining system stability and regulating voltage and frequency. The three cases demonstrate the effectiveness of the proposed optimized droop control for radial microgrid configurations. In Case 1, load fluctuations were handled with optimized droop, showcasing improved frequency and voltage regulation compared to traditional methods. Case 2, involving a sudden DG disconnection, highlights the optimized droop’s agility in compensating for power shortage, ensuring stable performance. Case 3 explored a secondary control failure scenario, demonstrating the robustness of the proposed system under communication delays and topology changes, maintaining acceptable frequency and voltage deviations.