Numerical Simulation of Environmental Characteristics of Containment in Severe Accident of Marine Nuclear Power Plant
Abstract
:1. Introduction
2. Physical Model
2.1. Governing Equation
2.2. Buoyancy Force Model
2.3. Wall Condensation Model
3. Numerical Calculation Model Verification
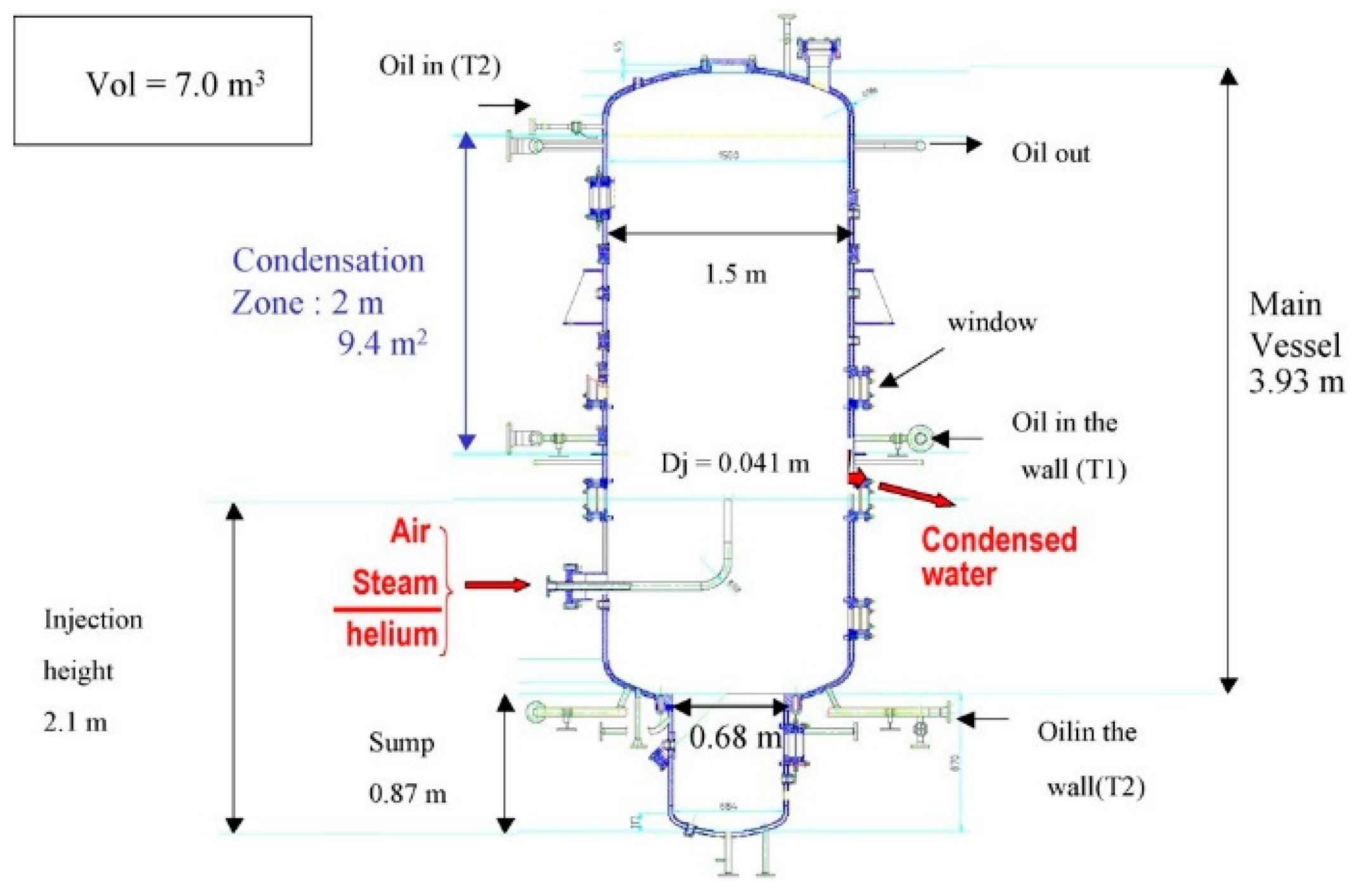
3.1. TOSQAN Experimental Device
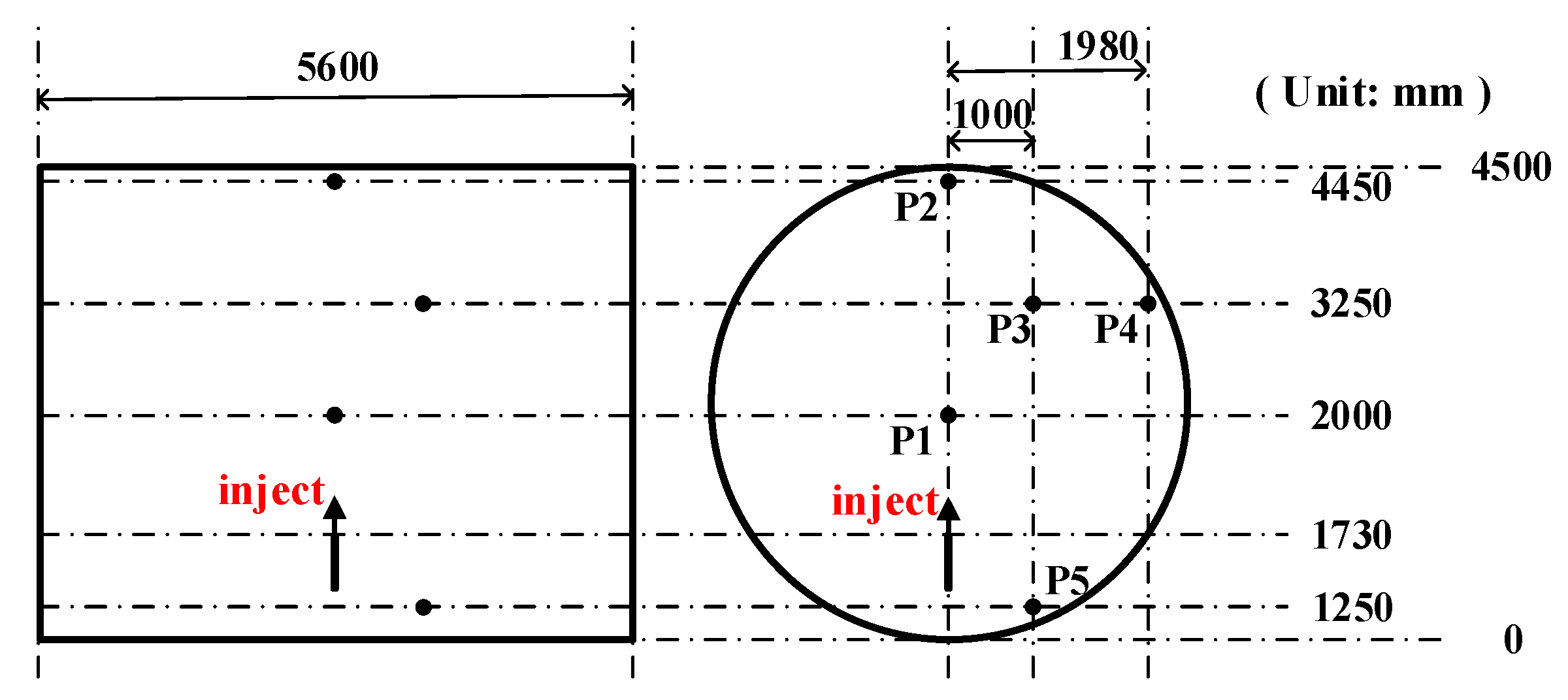
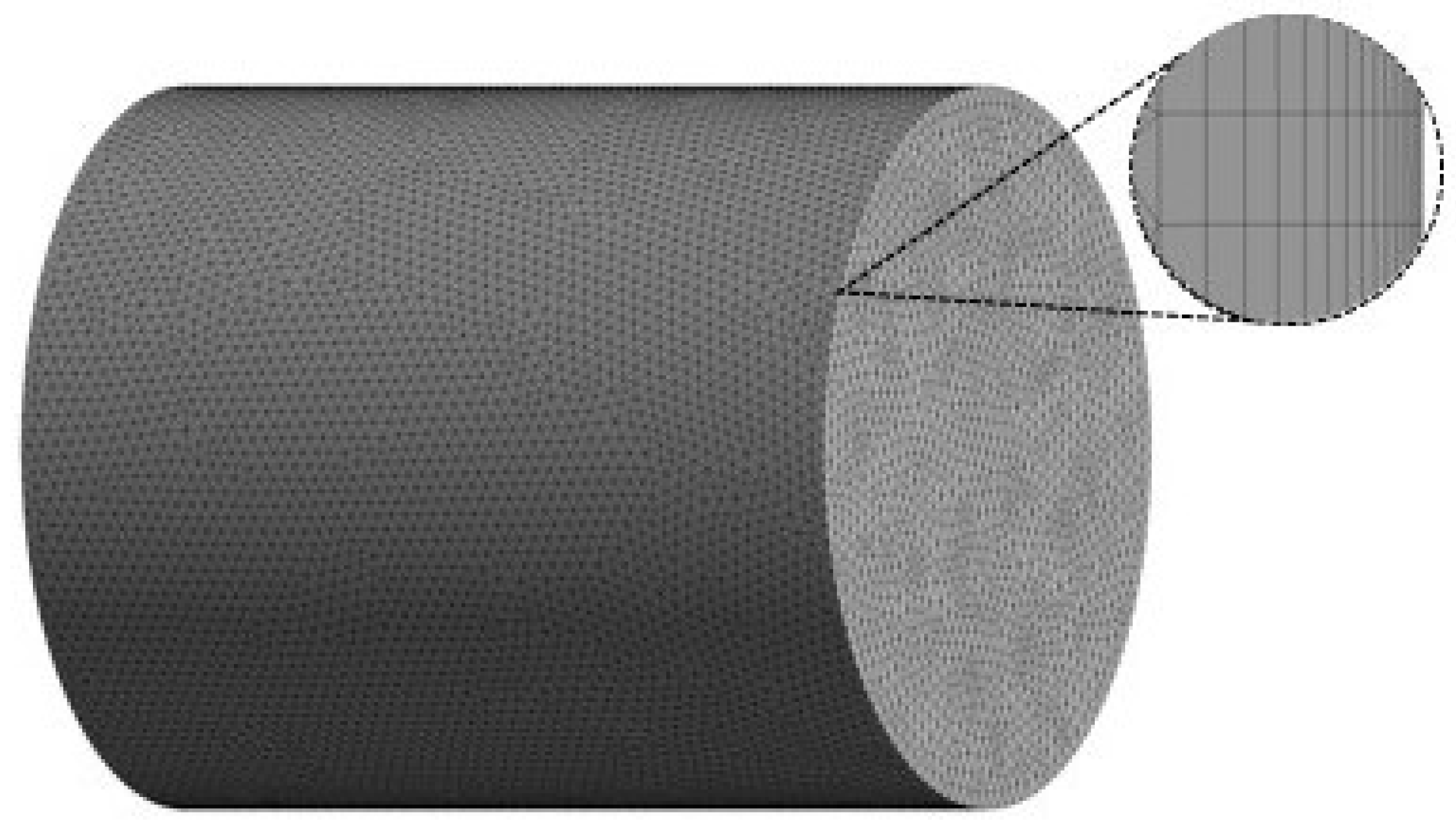
3.2. Geometric Model and Mesh Division
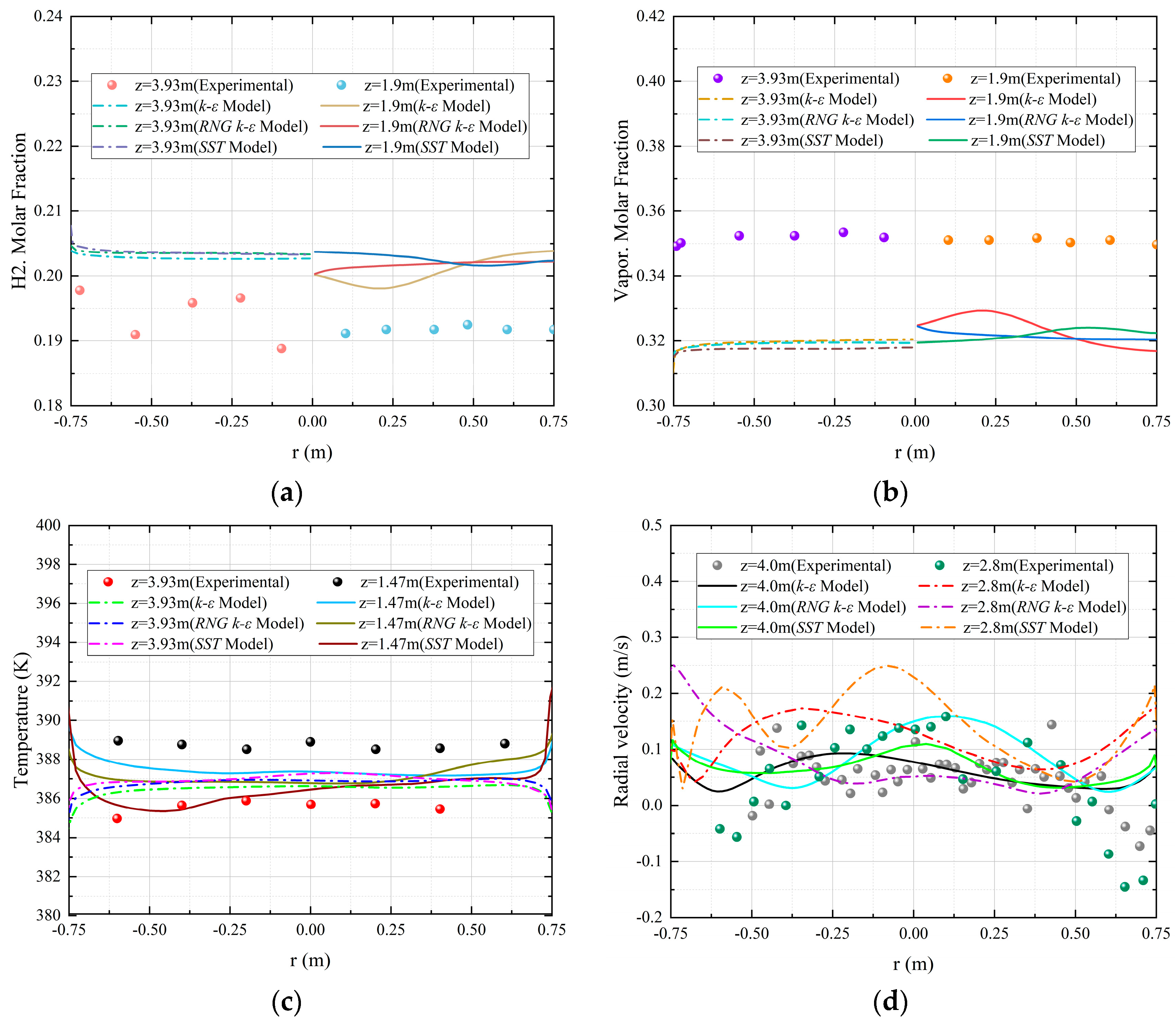
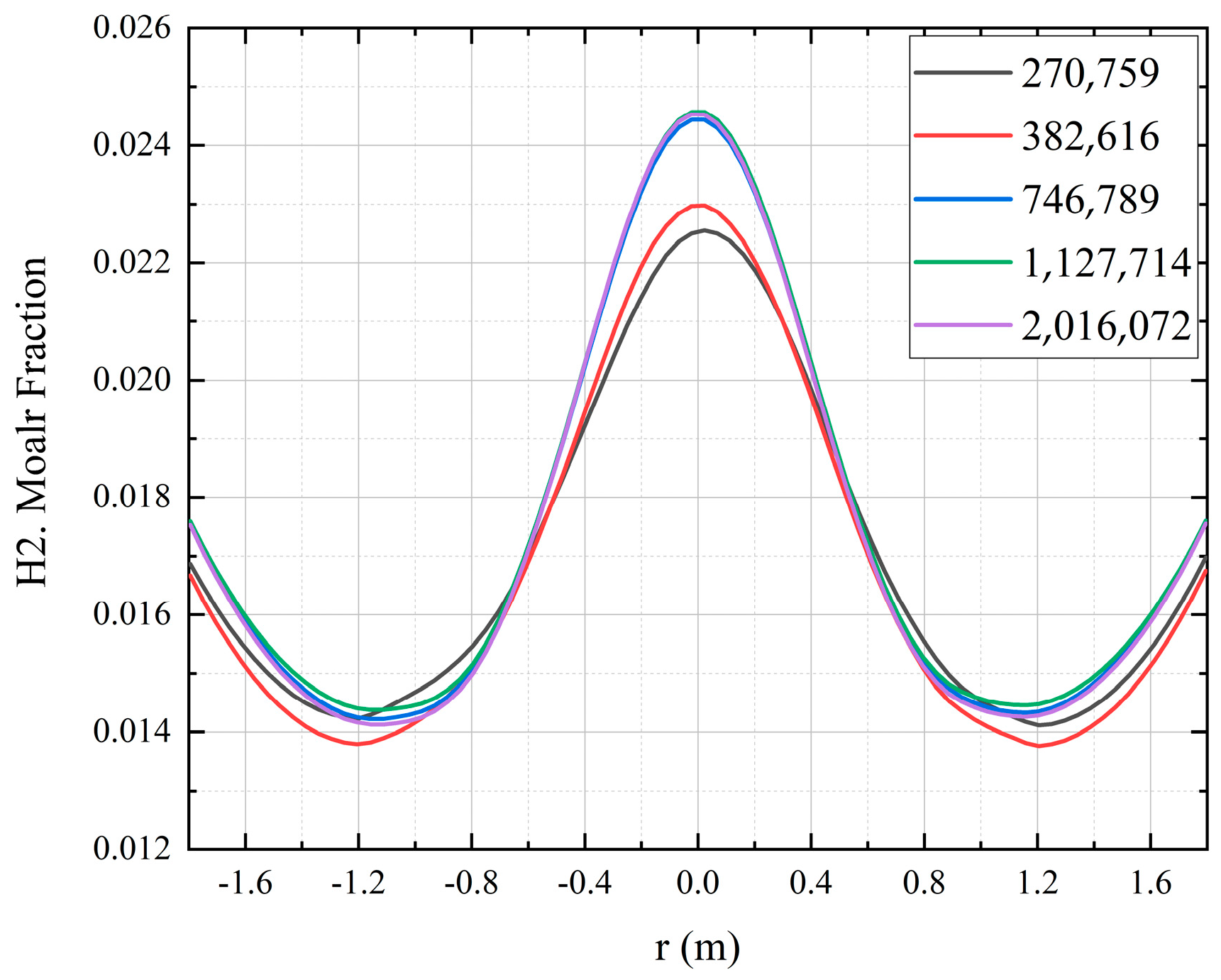
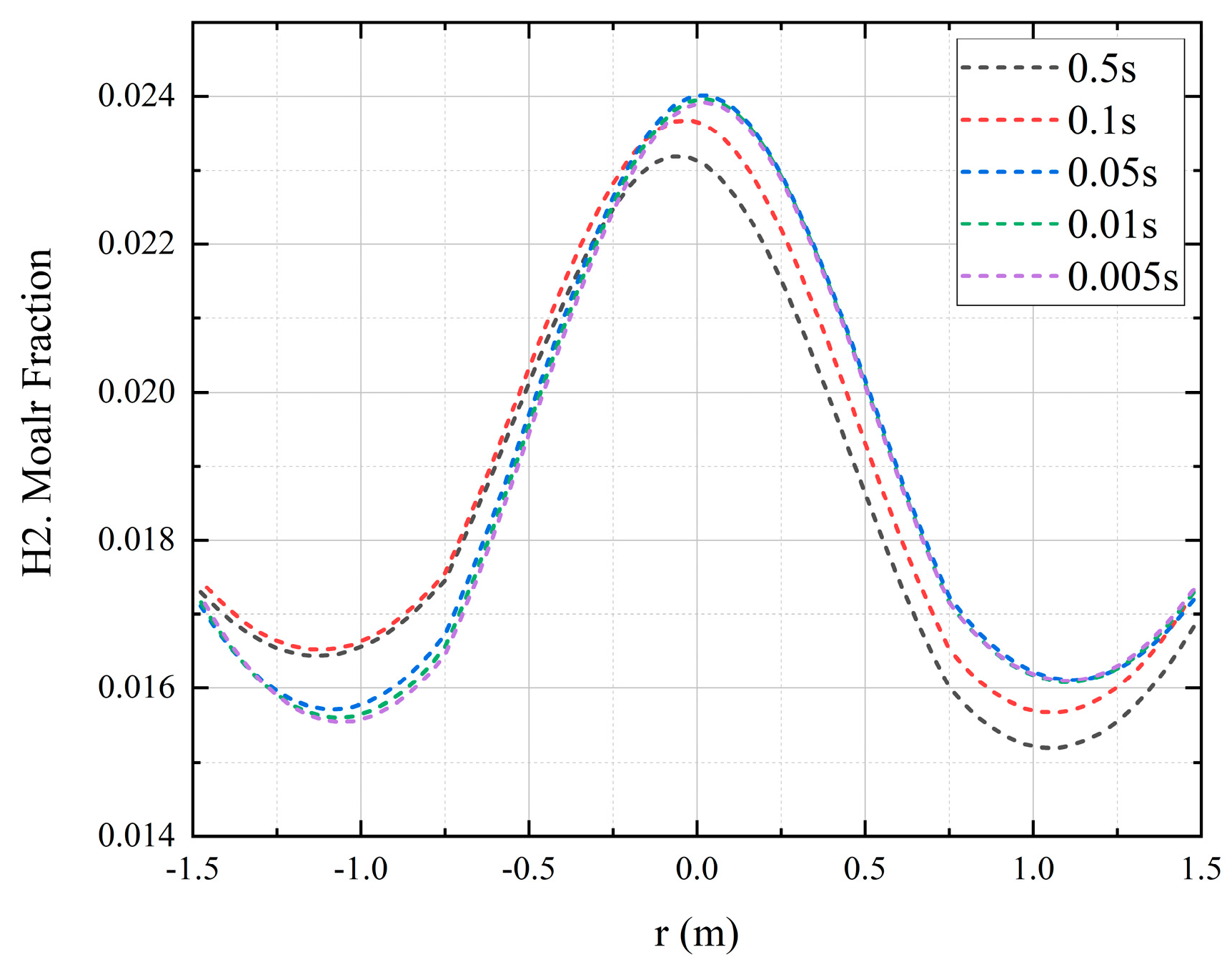
3.3. Adaptability Analysis of Turbulence Model
4. Containment Space Model
4.1. Geometric Model and Mesh Division
4.2. Initial Conditions and Basic Assumptions
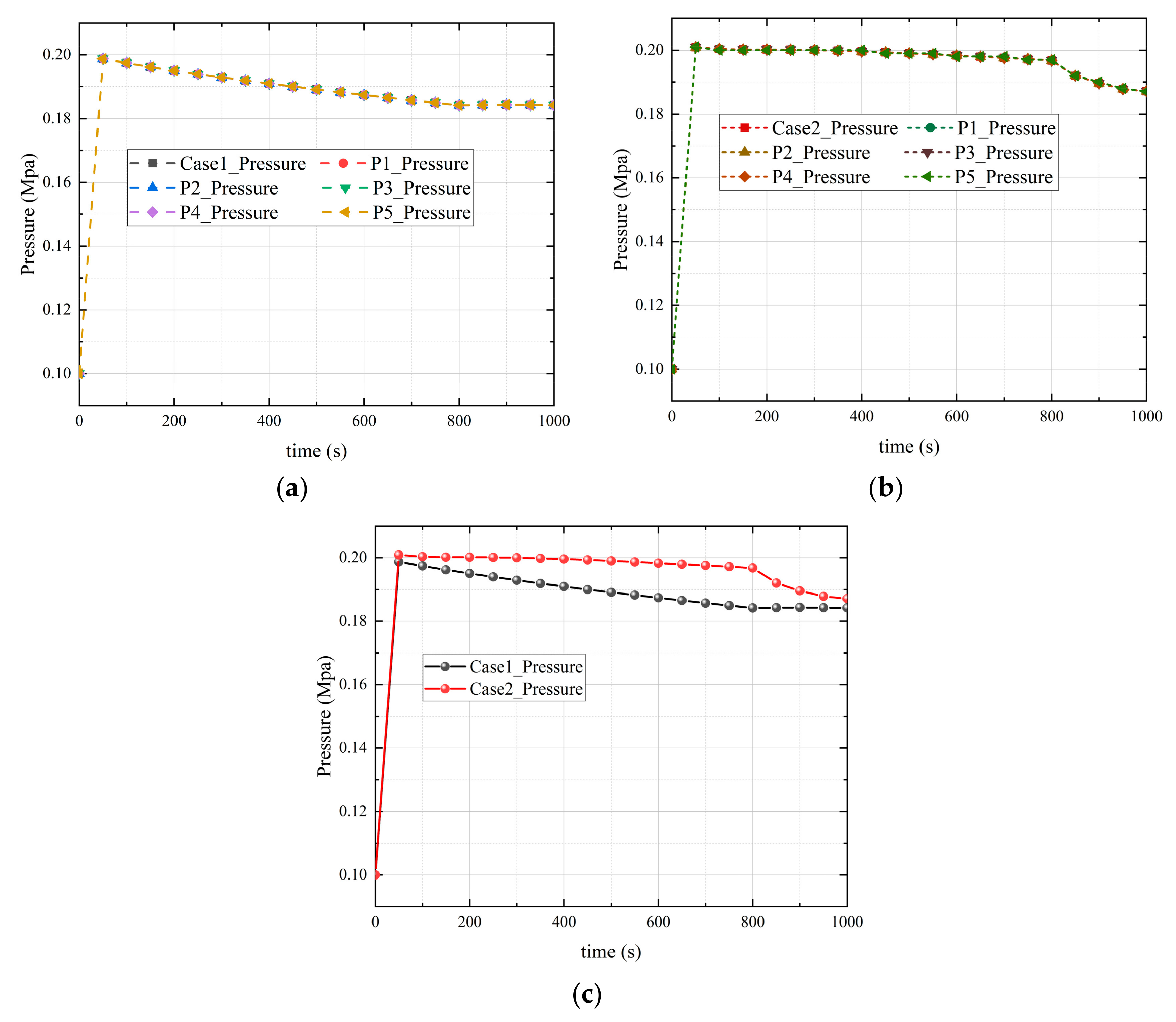
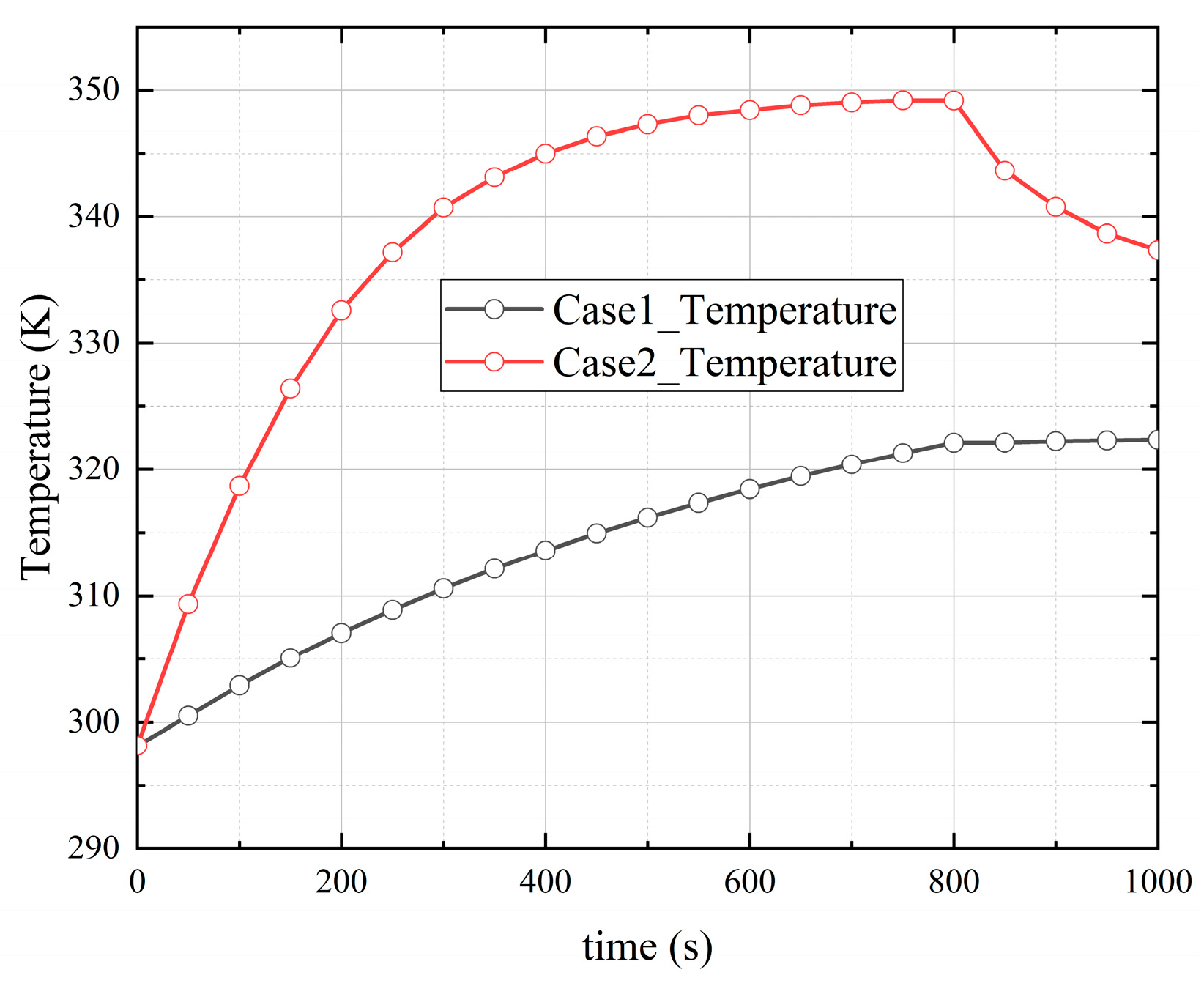
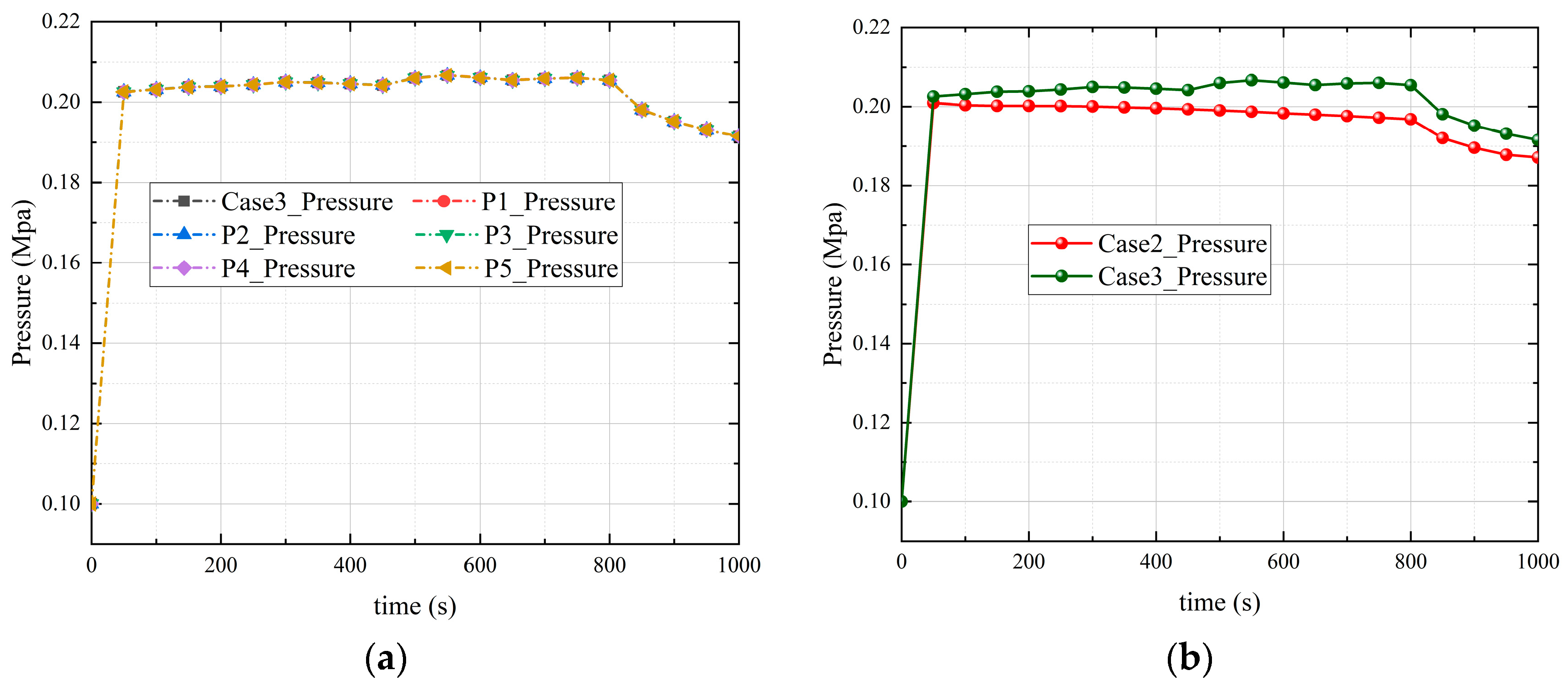
5. Numerical Simulation Results Analysis
5.1. Analysis of the Influence of Vapor
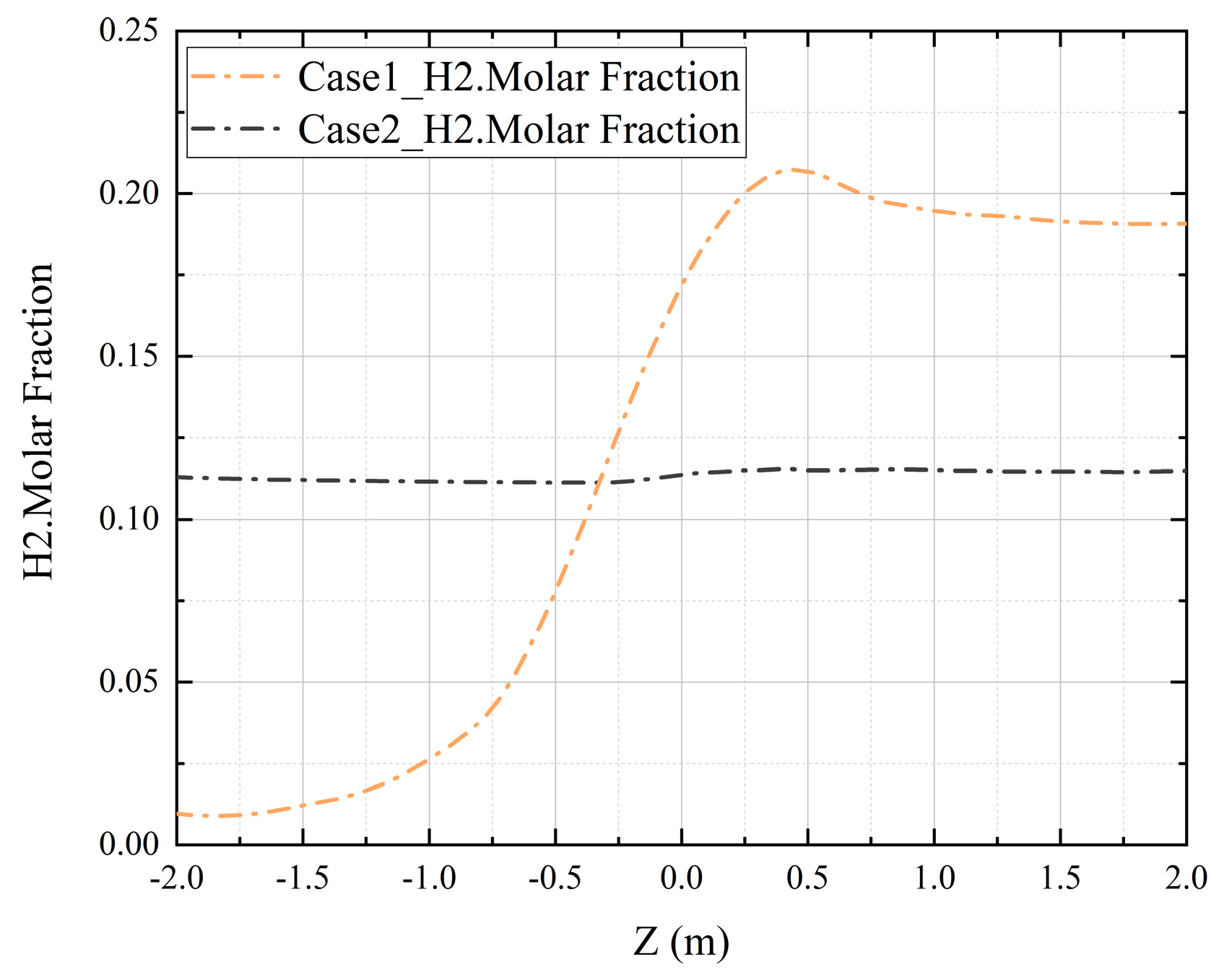
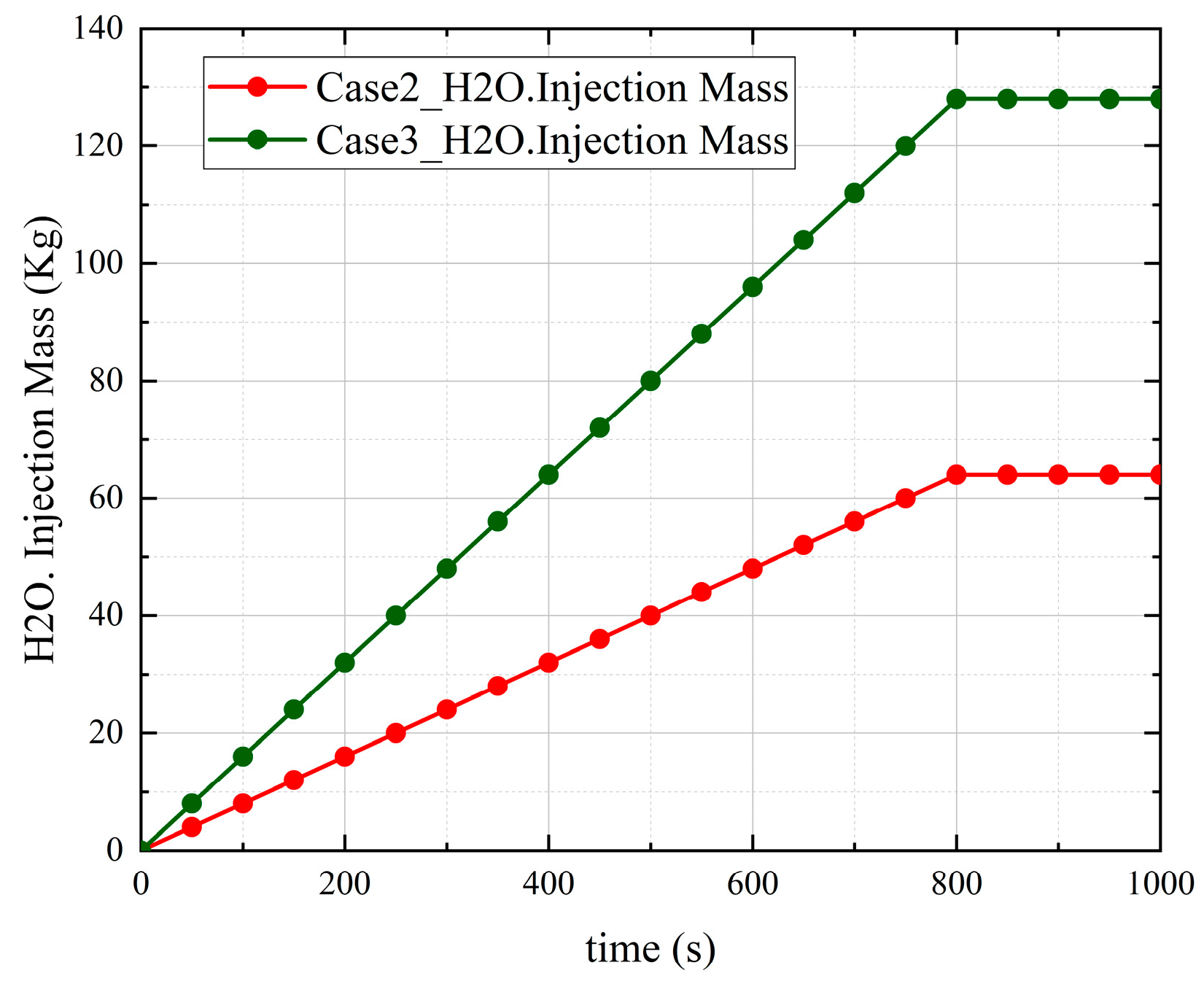
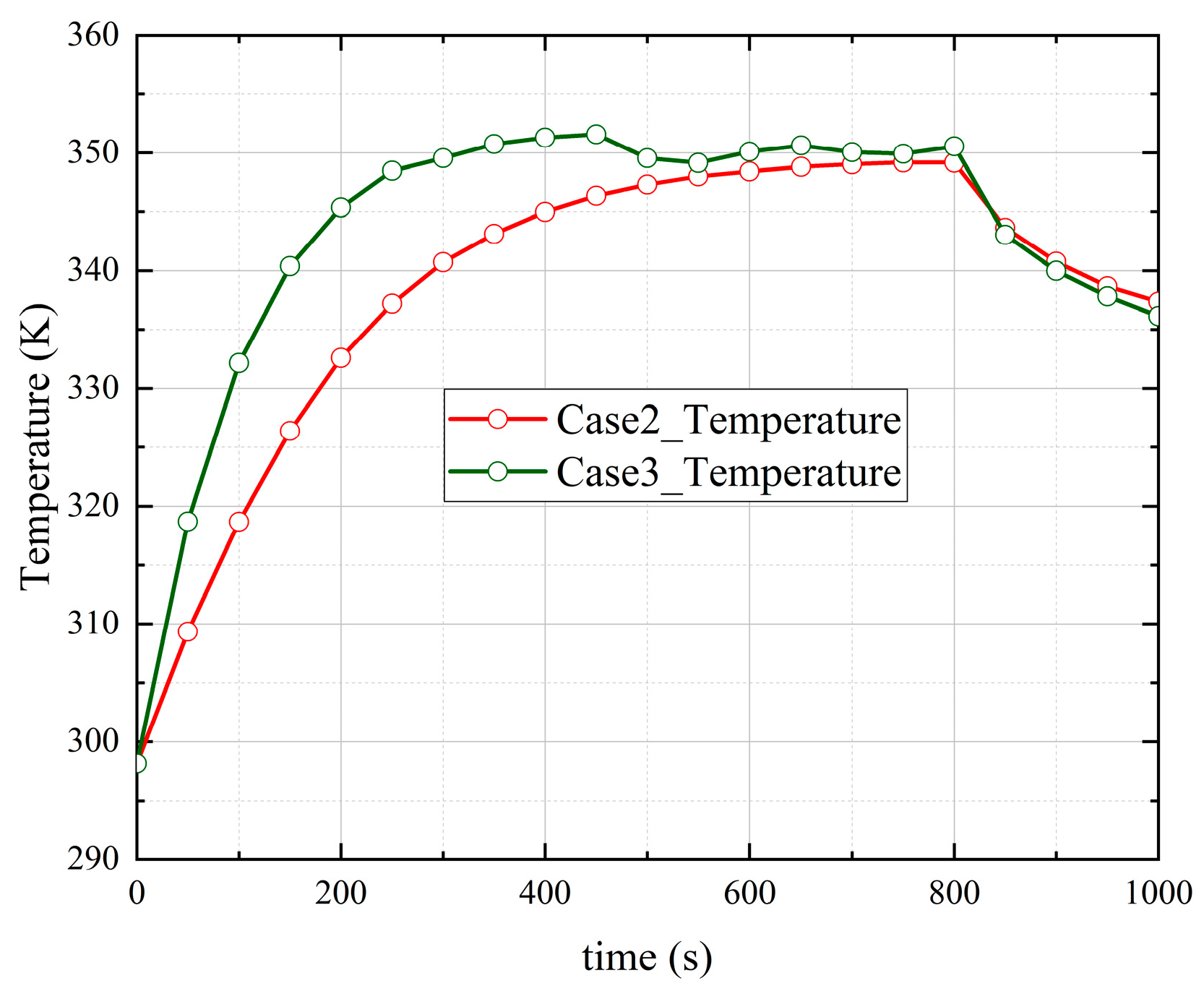
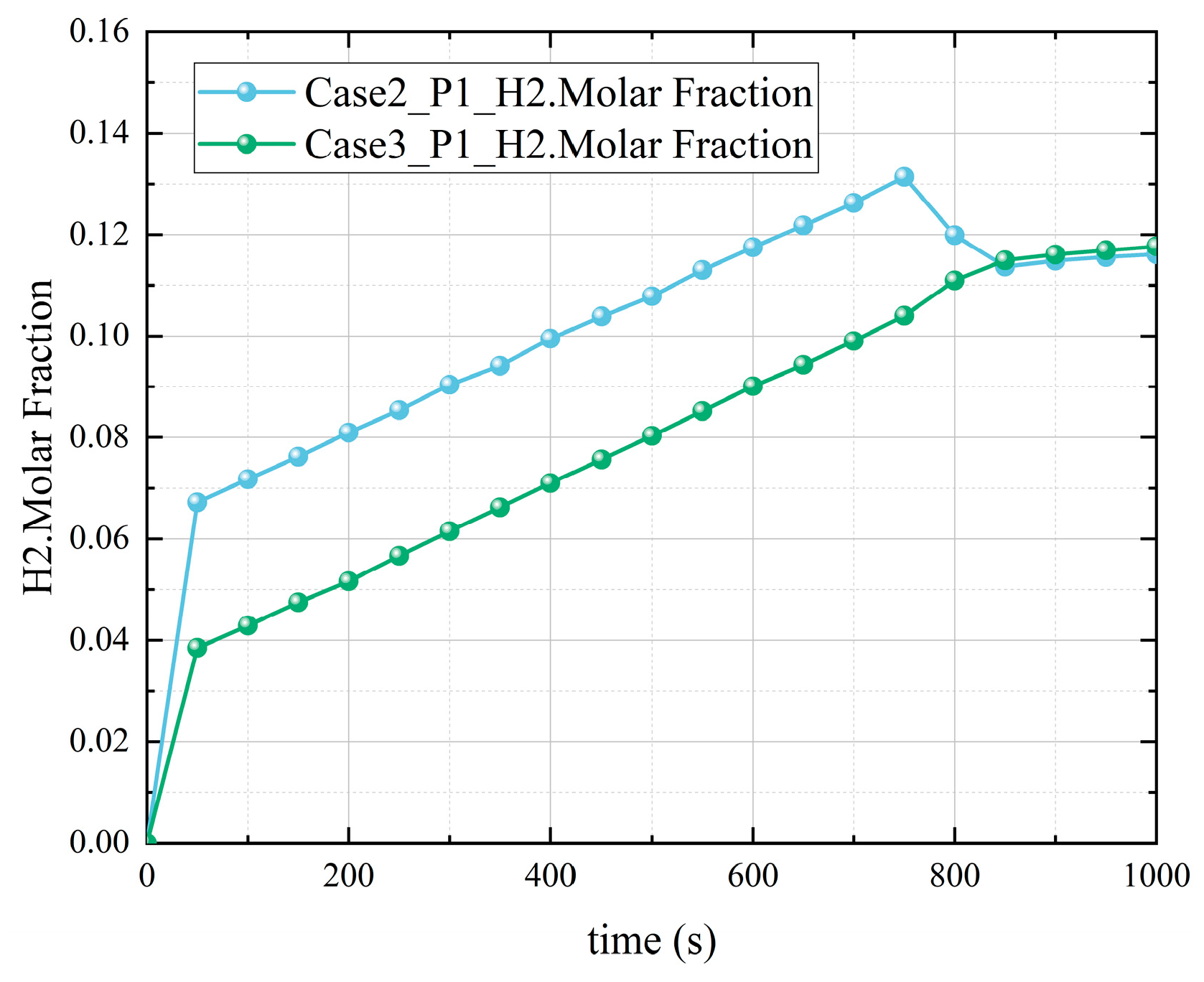
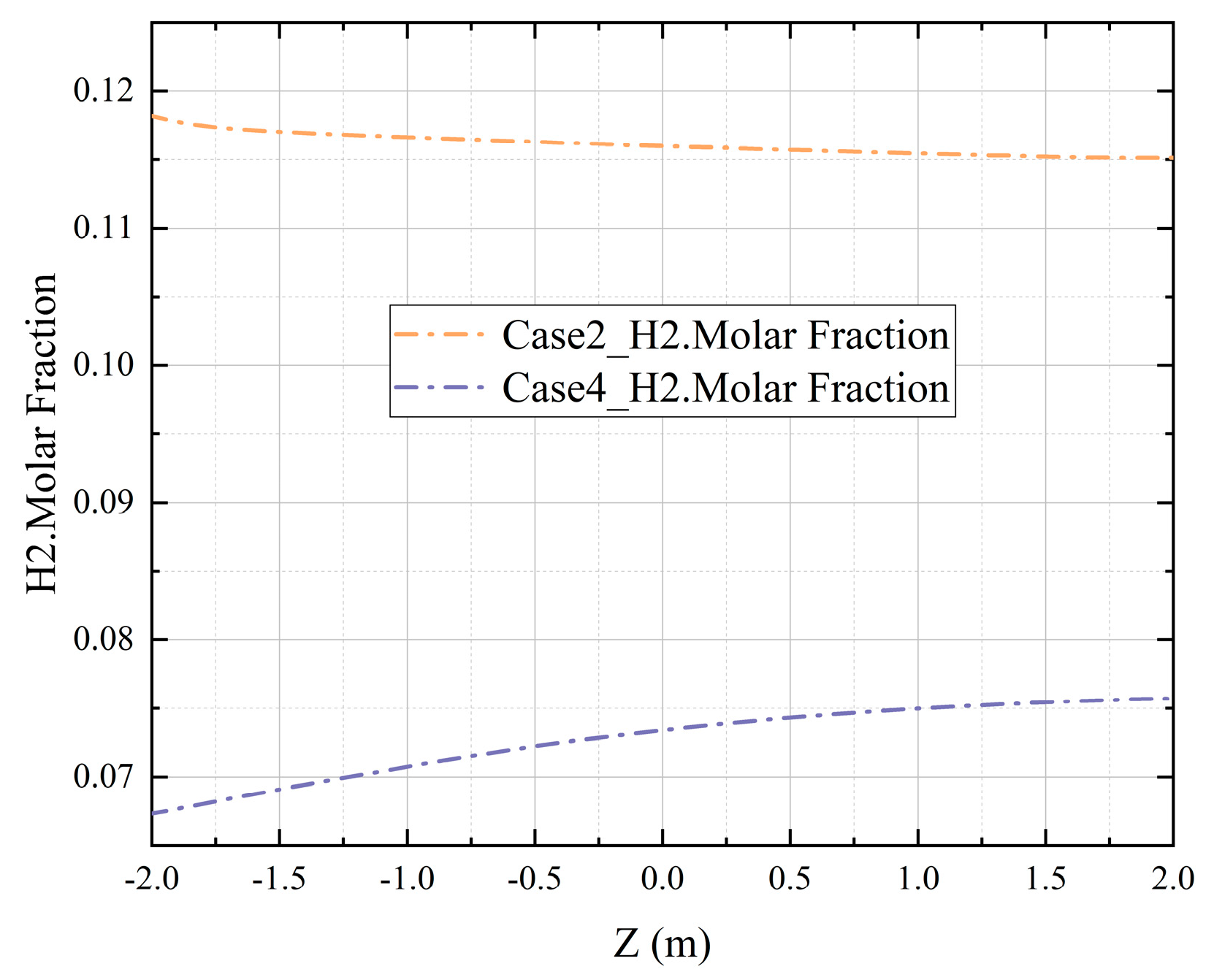
5.2. Analysis of the Influence of Vapor Concentration
5.3. Analysis of the Effect of Vapor Condensation
6. Conclusions
- (1)
- The turbulence model can be used to simulate the hydrogen distribution in the containment space during the hypothetical severe accident of the marine nuclear power plant.
- (2)
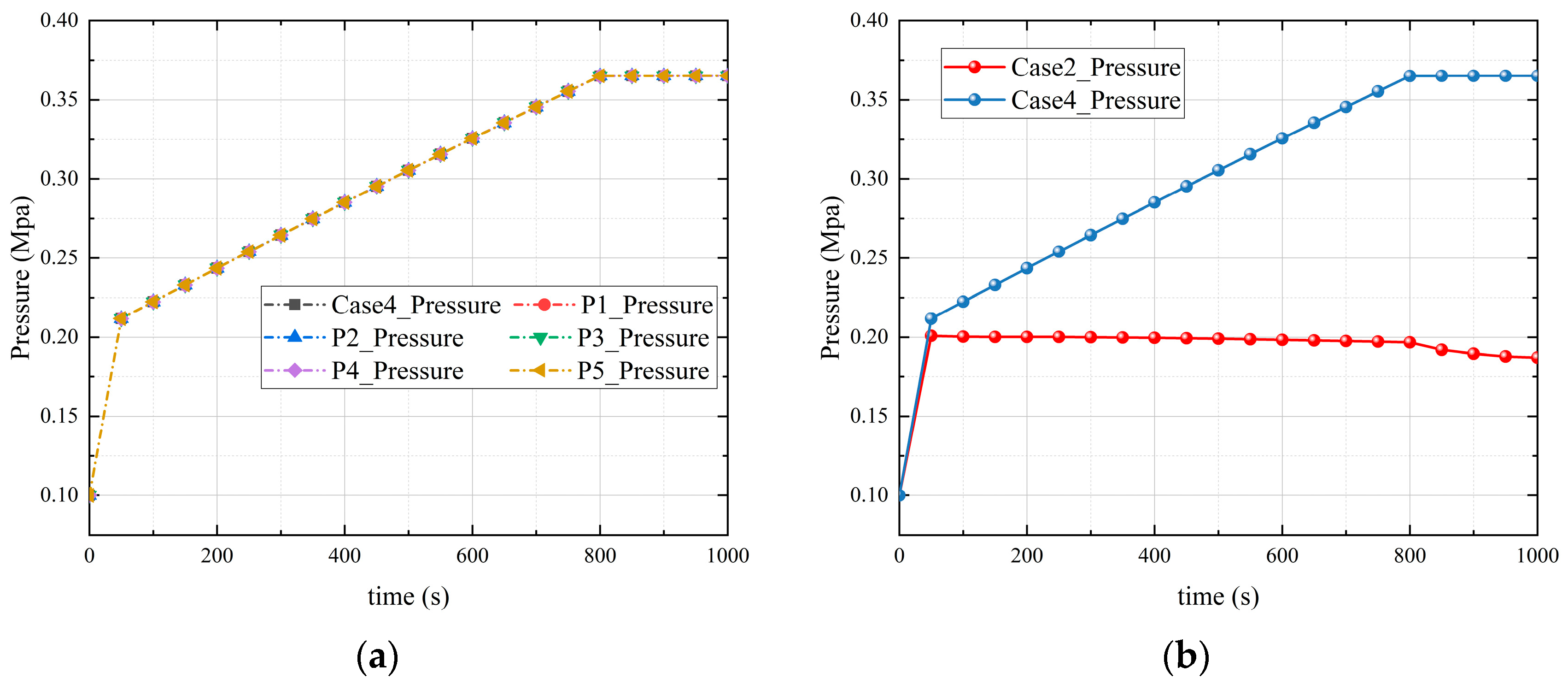
- During the serious accident of the marine nuclear power plant, the pressure response in the closed finite volume containment space is very rapid. Whether there is vapor, vapor concentration, and vapor condensation has no significant effect on the response speed of the pressure at each position in the containment space to reach the equilibrium state. The condensation of vapor can significantly reduce the pressure in the containment space. Compared to condensation without vapor, the peak pressure is reduced by about 44.99%, which can effectively reduce the risk of high pressure in the containment space.
- (3)
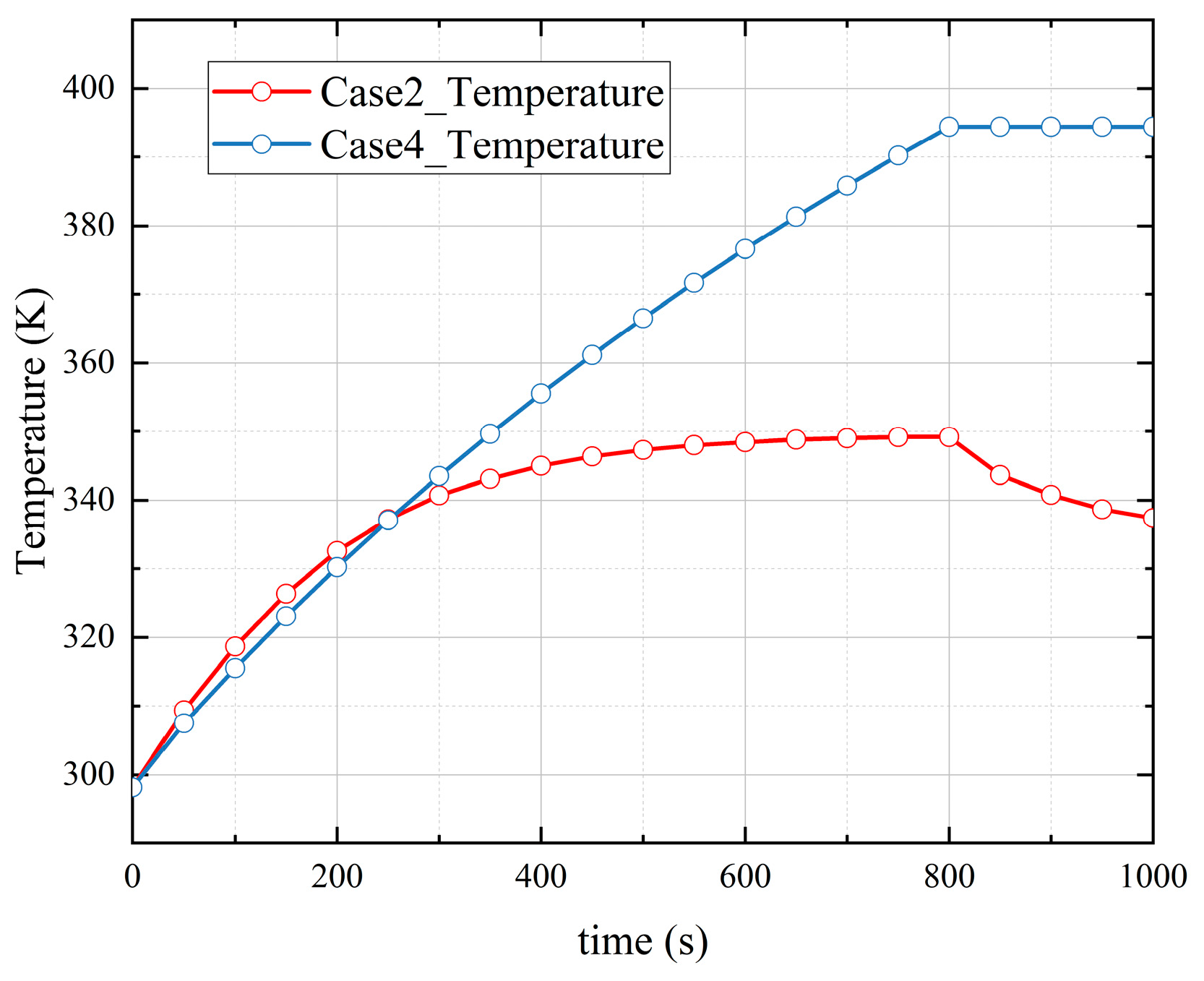
- The presence of vapor and the increase in vapor concentration will increase the temperature in the containment space during the severe accident of the marine nuclear power plant. The condensation of vapor makes the temperature in the containment space have a peak value during the accident, which is about 11.47% lower than the peak temperature in the containment space without vapor condensation. In the stage without gas injection, the condensation of vapor will make the temperature in the containment space continue to decrease, which can effectively reduce the high-temperature risk in the containment space during a serious accident.
- (4)
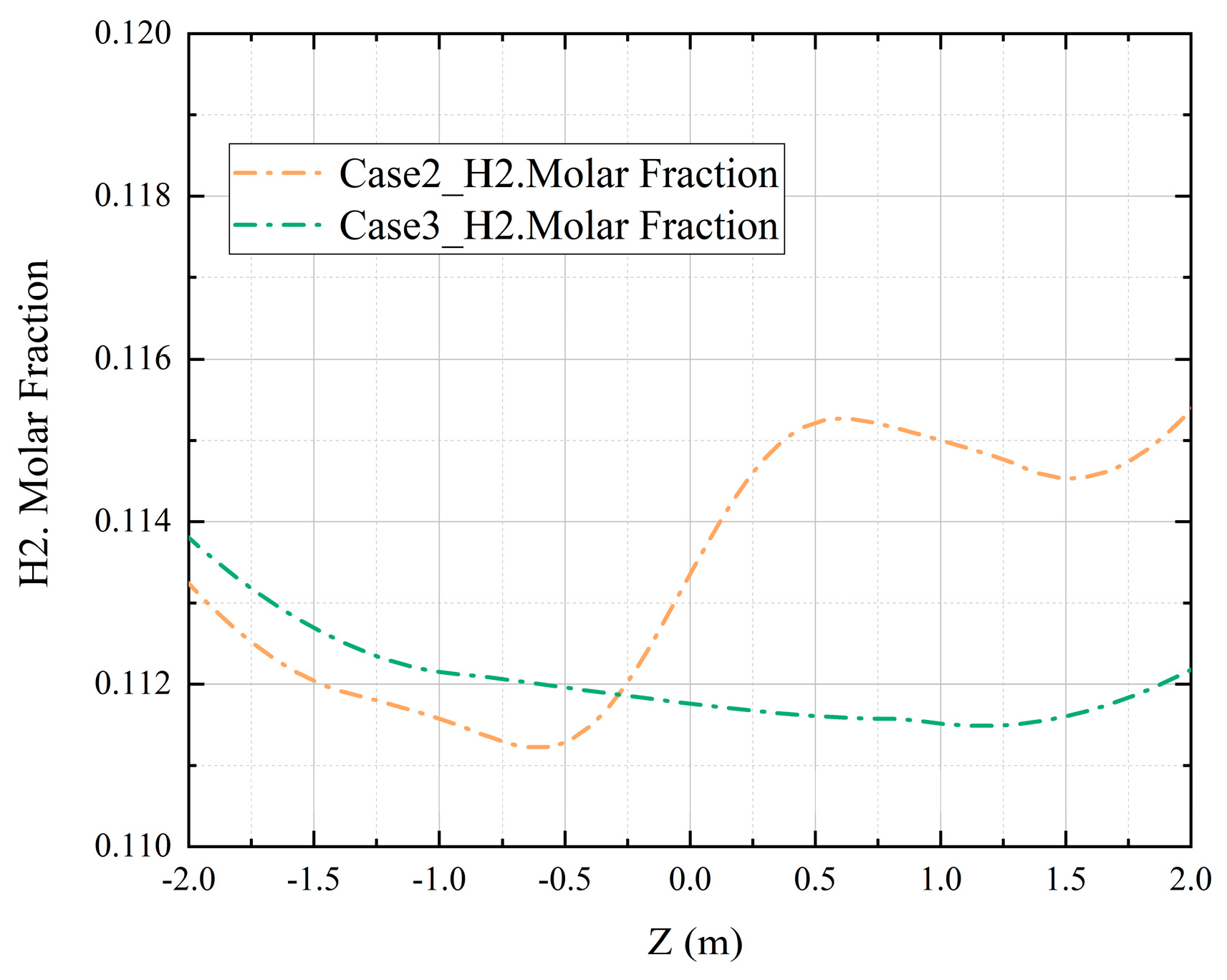
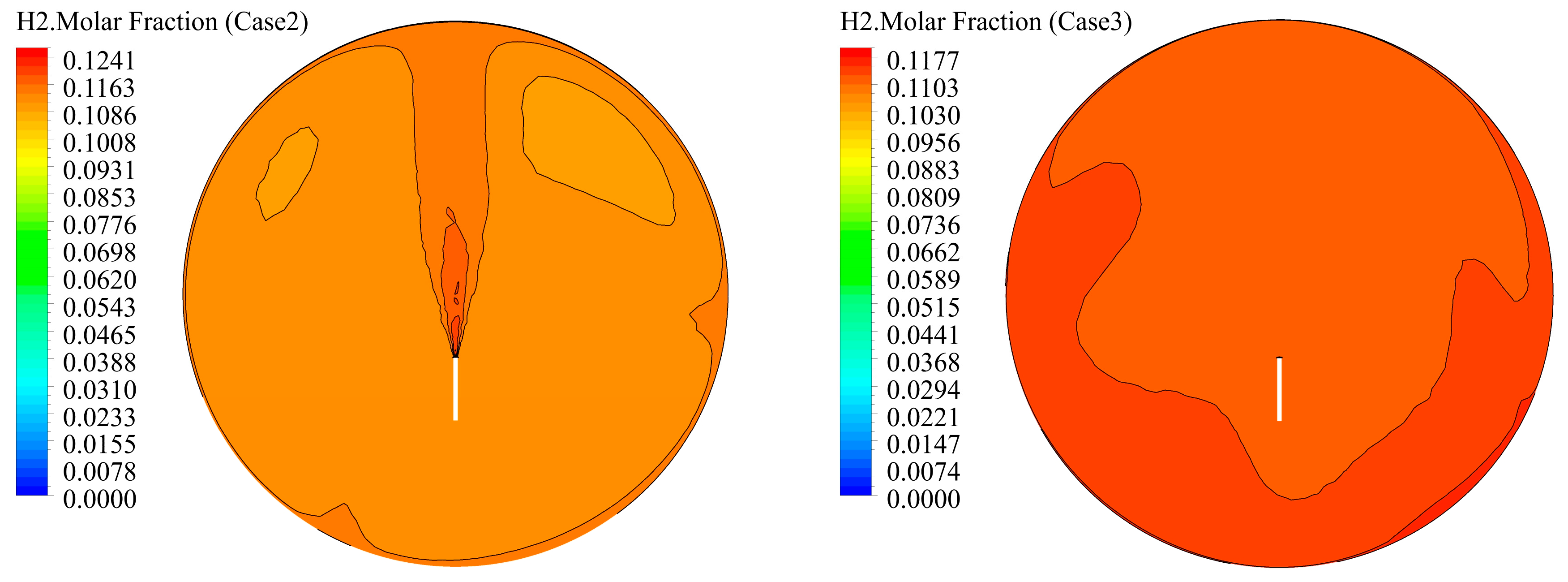
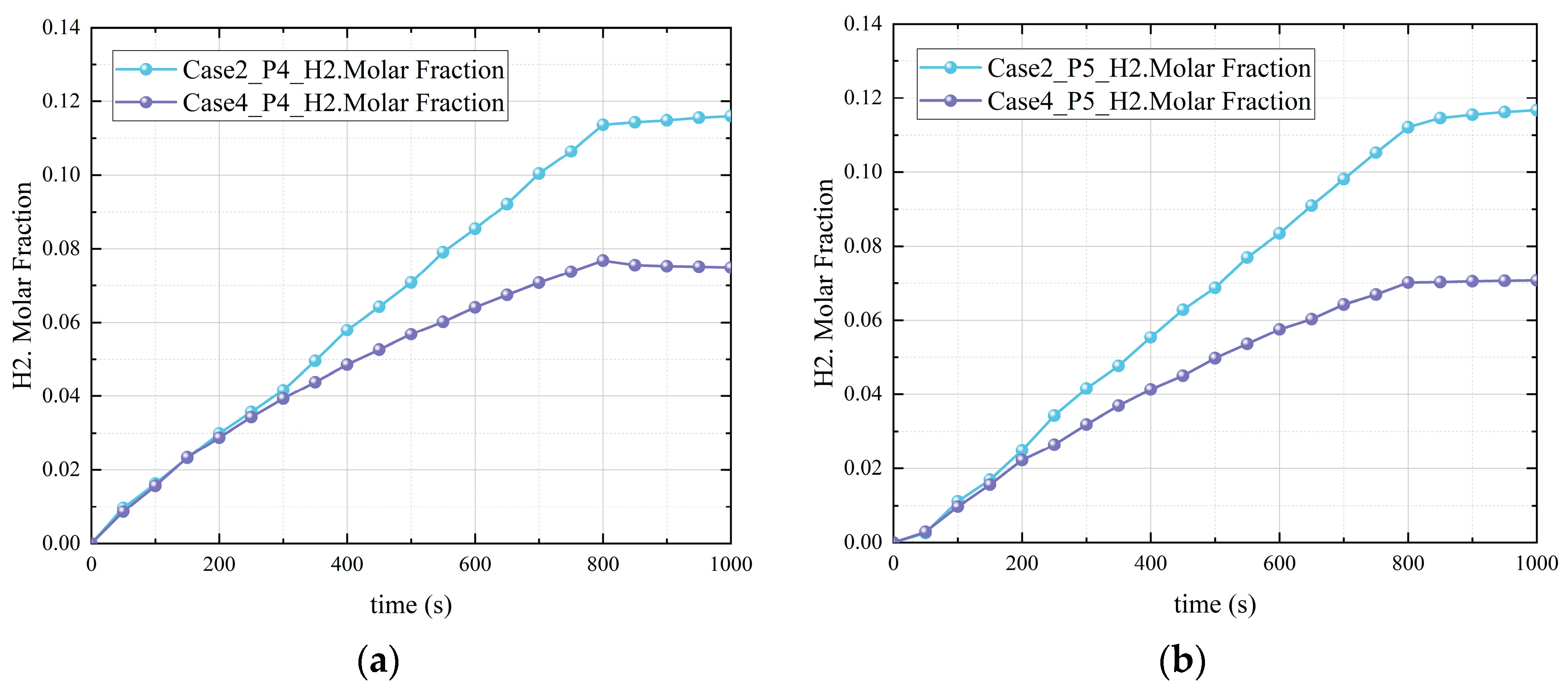
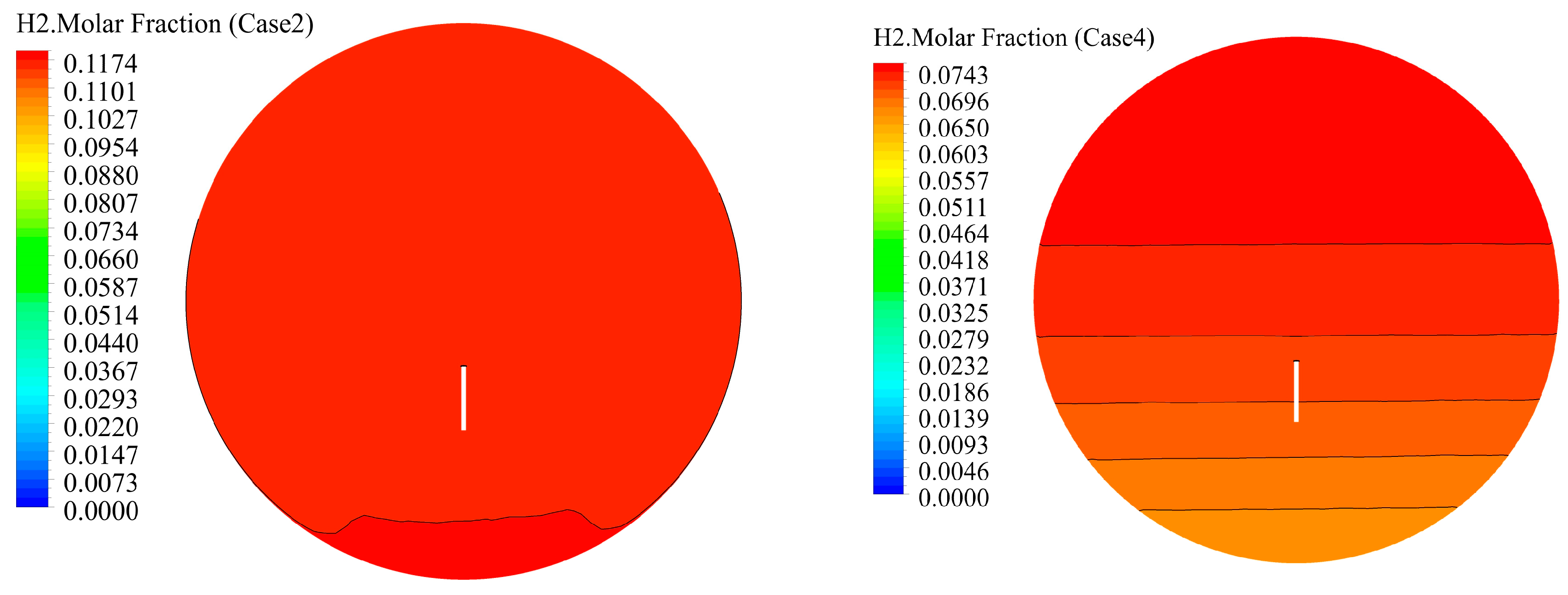
- The presence of vapor and the increase in vapor concentration can reduce the hydrogen concentration near the nozzle during the gas injection process. The reduction effect is significant when there is vapor, which is about 77.17% lower than that without vapor. The condensation of vapor on the wall surface will cause hydrogen to accumulate near the inner wall of the containment and increase the hydrogen concentration near the wall surface.
- (4)
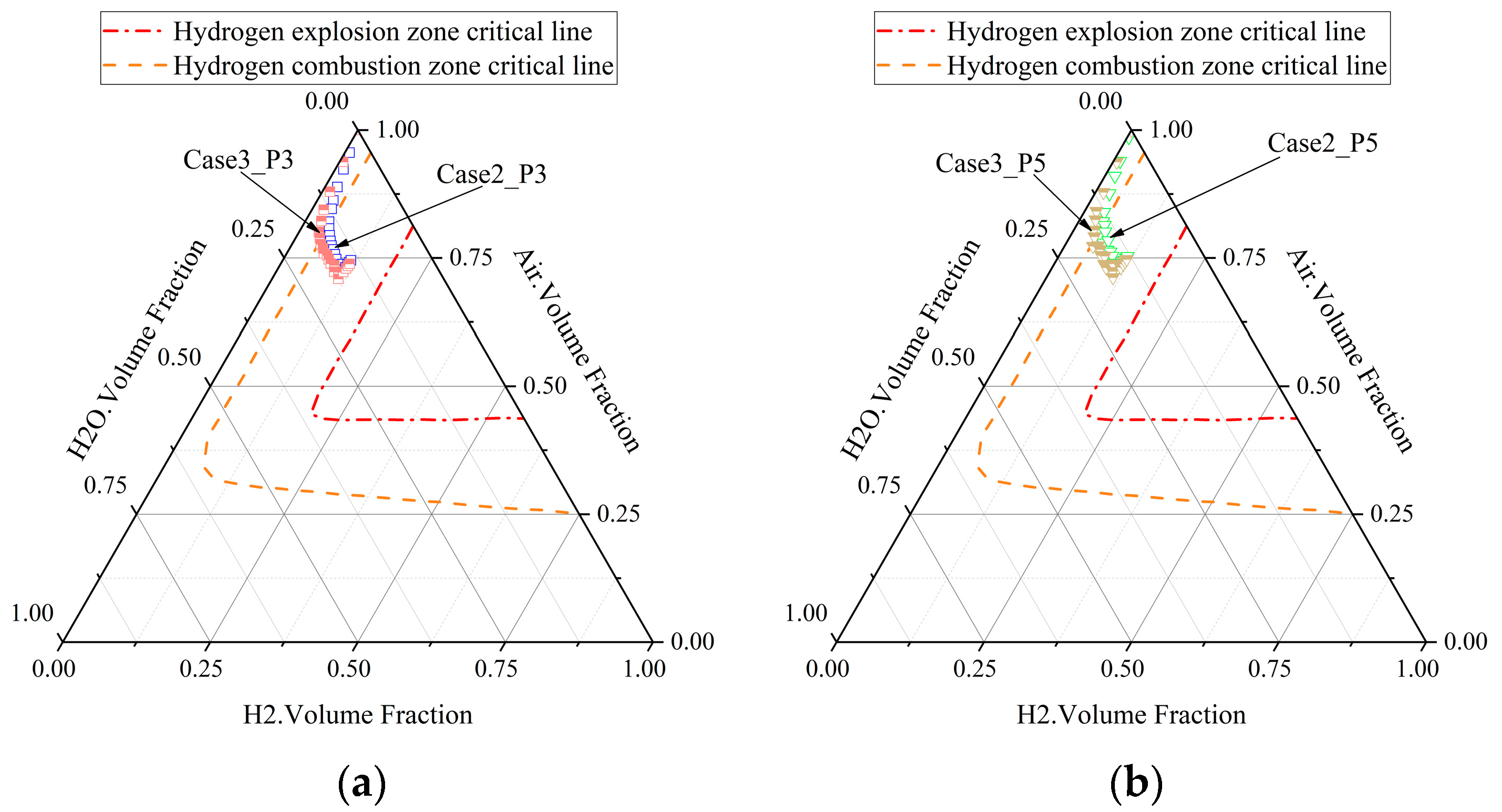
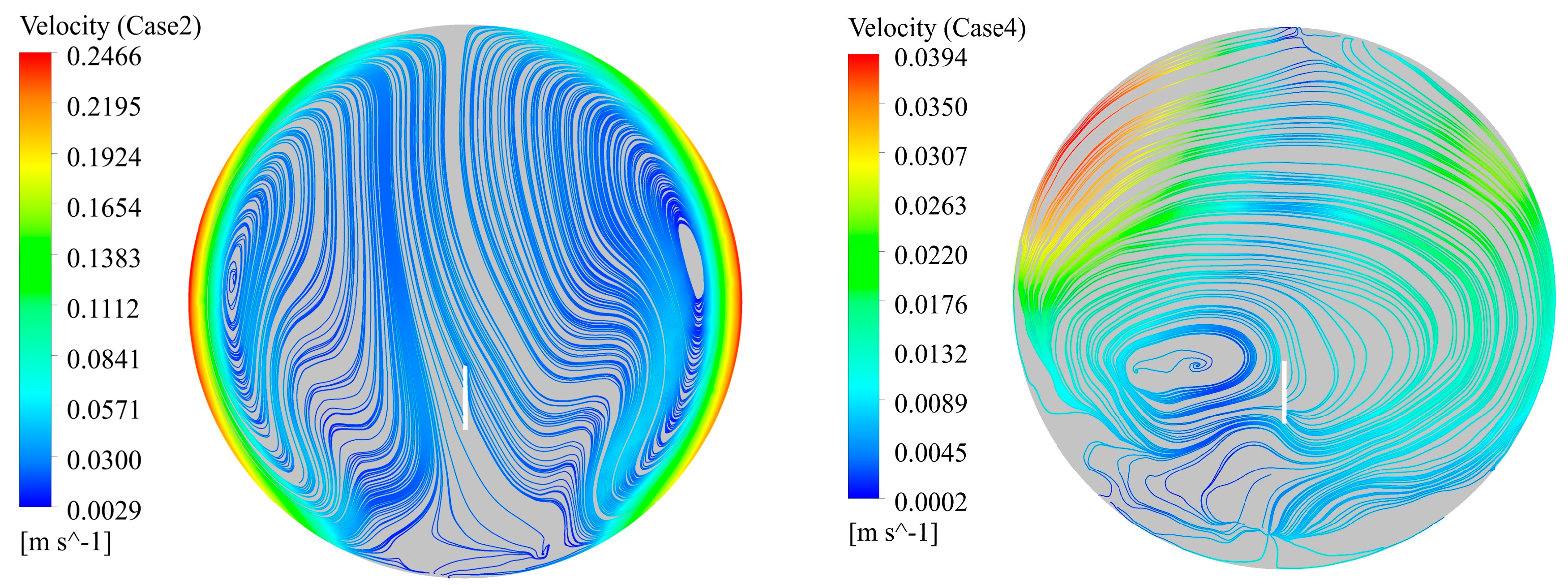
- The existence of vapor, the increase in vapor concentration, and the condensation of vapor will stir the gas environment in the closed containment space of the marine nuclear power plant, promote the mixing of gas in the containment space during the severe accident, and make the distribution of hydrogen in the containment space tend to be uniform. The presence of vapor and the increase in vapor concentration can reduce the hydrogen risk in the containment space during the accident, but the condensation of vapor will increase the hydrogen concentration in the containment space, which may also increase the hydrogen risk.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lee, K.; Lee, K.H.; Lee, J.I.; Jeong, Y.H.; Lee, P.S. A new design concept for offshore nuclear power plants with enhanced safety features. Nucl. Eng. Des. 2013, 254, 129–141. [Google Scholar] [CrossRef]
- Santinello, M.; Ricotti, M.E.; Ninokata, H.; Haratyk, G.; Ingremeau, J.J.; Gourmel, V. External heat transfer capability of a submerged SMR containment: The Flexblue case. Prog. Nucl. Energy 2017, 96, 62–75. [Google Scholar] [CrossRef]
- Lee, K.H.; Kim, M.G.; Lee, J.I.; Lee, P.S. Recent Advances in Ocean Nuclear Power Plants. Energies 2015, 8, 11470–11492. [Google Scholar] [CrossRef]
- Buongiorno, J.; Jurewicz, J.; Golay, M.; Todreas, N. The Offshore Floating Nuclear Plant Concept. Nucl. Technol. 2016, 194, 1–14. [Google Scholar] [CrossRef]
- Tong, L.L.; Zou, J.; Cao, X.W. Analysis on hydrogen risk mitigation in severe accidents for Pressurized Heavy Water Reactor. Prog. Nucl. Energy 2015, 80, 128–135. [Google Scholar] [CrossRef]
- Bentaib, A.; Meynet, N.; Bleyer, A. Overview on Hydrogen Risk Research and Development Activities: Methodology and Open Issues. Nucl. Eng. Technol. 2015, 47, 26–32. [Google Scholar] [CrossRef]
- Yanez, J.; Kuznetsav, M.; Souto-Iglesias, A. An analysis of the hydrogen explosion in the Fukushima-Daiichi accident. Int. J. Hydrog. Energy 2015, 40, 8261–8280. [Google Scholar] [CrossRef]
- Peng, C.; Tong, L.L.; Cao, X.W. Numerical analysis on hydrogen stratification and post-inerting of hydrogen risk. Ann. Nucl. Energy 2016, 94, 451–460. [Google Scholar] [CrossRef]
- Wilkening, H.; Ammirabile, L. Simulation of helium release in the Battelle Model Containment facility using OpenFOAM. Nucl. Eng. Des. 2013, 265, 402–410. [Google Scholar] [CrossRef]
- Agrawal, N.; Prabhakar, A.; Das, S.K. Hydrogen Distribution in Nuclear Reactor Containment During Accidents and Associated Heat and Mass Transfer Issues—A Review. Heat Transf. Eng. 2015, 36, 859–879. [Google Scholar] [CrossRef]
- Malet, J.; Porcheron, E.; Vendel, J. OECD International Standard Problem ISP-47 on containment thermal-hydraulics-Conclusions of the TOSQAN part. Nucl. Eng. Des. 2010, 240, 3209–3220. [Google Scholar] [CrossRef]
- Filippov, A.S.; Grigoryev, S.Y.; Tarasov, O.V. On the possible role of thermal radiation in containment thermal-hydraulics experiments by the example of CFD analysis of TOSQAN T114 air-He test. Nucl. Eng. Des. 2016, 310, 175–186. [Google Scholar] [CrossRef]
- Visser, D.C.; Siccama, N.B.; Jayaraju, S.T.; Komen, E.M.J. Application of a CFD based containment model to different large-scale hydrogen distribution experiments. Nucl. Eng. Des. 2014, 278, 491–502. [Google Scholar] [CrossRef]
- Malet, J.; Laissac, R. CFD calculations of stratification build-up tests of light gas in a closed vessel under controlled boundary conditions. Comput. Fluids 2015, 107, 224–241. [Google Scholar] [CrossRef]
- Gupta, S.; Schmidt, E.; von Laufenberg, B.; Freitag, M.; Poss, G.; Funke, F.; Weber, G. THAI test facility for experimental research on hydrogen and fission product behaviour in light water reactor containments. Nucl. Eng. Des. 2015, 294, 183–201. [Google Scholar] [CrossRef]
- Dehbi, A.; Kelm, S.; Kalilainen, J.; Mueller, H. The influence of thermal radiation on the free convection inside enclosures. Nucl. Eng. Des. 2019, 341, 176–185. [Google Scholar] [CrossRef]
- Prabhakar, A.; Agrawal, N.; Raghavan, V.; Das, S.K. Experimental investigations on the evolution of stratified layer of helium in the unventilated vertical cylindrical enclosure of AIHMS facility under wall temperature induced natural convection. Nucl. Eng. Des. 2017, 323, 367–375. [Google Scholar] [CrossRef]
- Prabhakar, A.; Agrawal, N.; Raghavan, V.; Das, S.K. An experimental study on the effect of coaxial circular disk obstacle on helium jet distribution inside the unventilated enclosure of AIHMS facility. Ann. Nucl. Energy 2018, 116, 347–359. [Google Scholar] [CrossRef]
- Filippov, A.S.; Grigoryev, S.Y.; Tarasov, O.V.; Iudina, T.A. Cfd Simulation of Panda And Mistra Cooler Tests of Ercosam-Samara Project. In Proceedings of the 22nd International Conference on Nuclear Engineering (ICONE22), Prague, Czech Republic, 7–11 July 2014; Amer Soc Mechanical Engineers: New York, NY, USA, 2014. [Google Scholar]
- Bakhmet’ev, A.M.; Bol’shukhin, M.A.; Kamnev, M.A.; Khizbullin, A.M.; Tyurikov, O.V. Computational and Experimental Studies of Mixing of a Light Gas in the ERCOSAM-SAMARA Projects. Atom. Energy 2017, 123, 1–9. [Google Scholar] [CrossRef]
- Fernandez-Cosials, M.K.; Jimenez, G.; Lopez-Alonso, E. Analysis of a gas stratification break-up by a vertical jet using the GOTHIC code. Nucl. Eng. Des. 2016, 297, 123–135. [Google Scholar] [CrossRef]
- Kelm, S.; Lehmkuhl, J.; Jahn, W.; Allelein, H.J. A comparative assessment of different experiments on buoyancy driven mixing processes by means of CFD. Ann. Nucl. Energy 2016, 93, 50–57. [Google Scholar] [CrossRef]
- Povilaitis, M.; Urbonavicius, E.; Rimkevicius, S. Validation of special nodalisation features for lumped-parameter injection modelling based on MISTRA facility tests from ISP-47 and SARNET. Nucl. Eng. Des. 2014, 278, 86–96. [Google Scholar] [CrossRef]
- Visser, D.C.; Houkema, M.; Siccama, N.B.; Komen, E.M. Validation of a FLUENT CFD model for hydrogen distribution in a containment. Nucl. Eng. Des. 2012, 245, 161–171. [Google Scholar] [CrossRef]
- Kim, J.; Jung, E.; Kang, S. Large eddy simulation of hydrogen dispersion from leakage in a nuclear containment model. Int. J. Hydrogen Energy 2015, 40, 11762–11770. [Google Scholar] [CrossRef]
- Liu, F.; Sun, Z.N.; Cao, B.Y.; Bian, H.Z.; Ding, M. Numerical investigations on the component separation phenomenon and transport behavior of steam-air-hydrogen mixture induced by condensation. Int. J. Therm. Sci. 2022, 172, 16. [Google Scholar] [CrossRef]

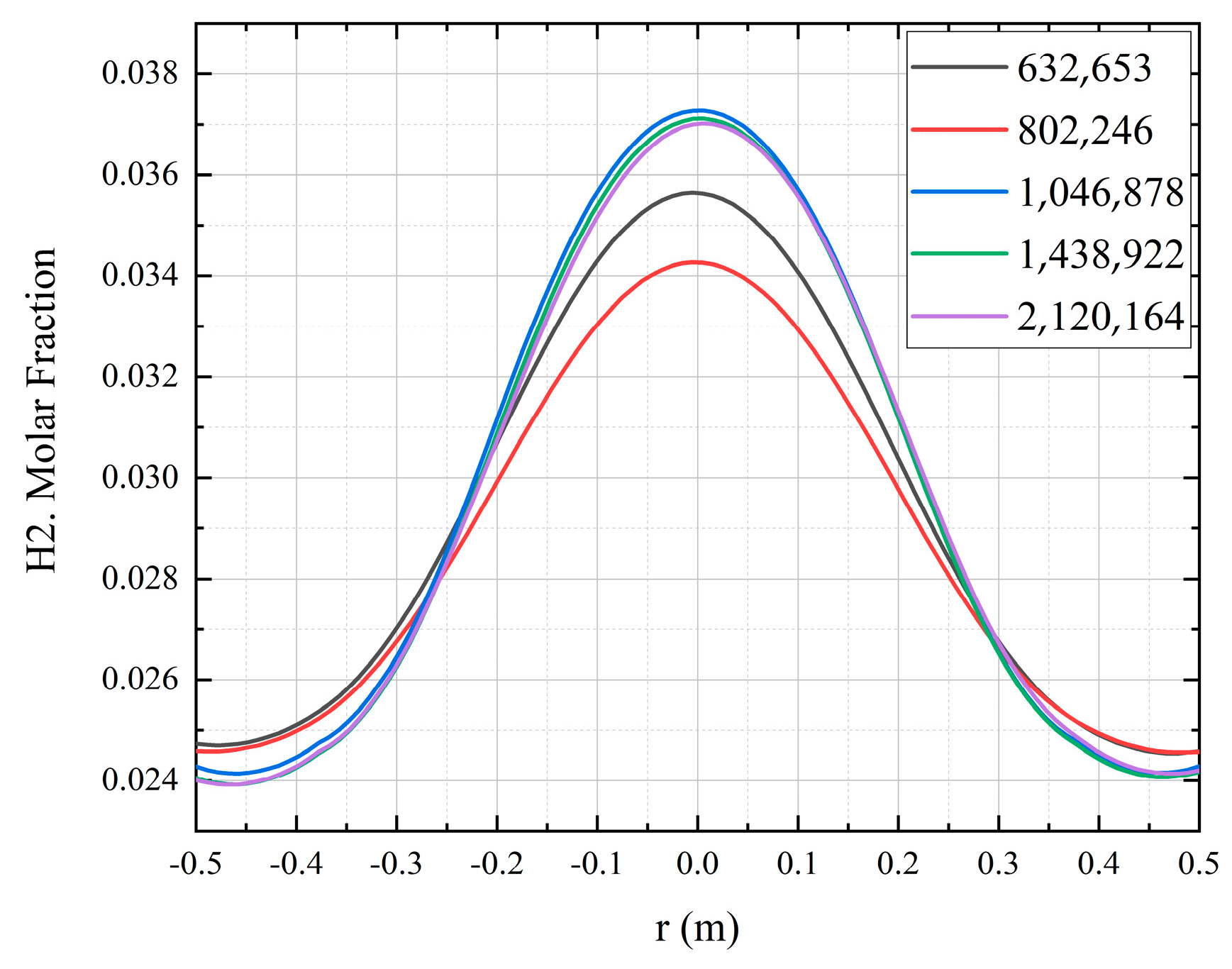
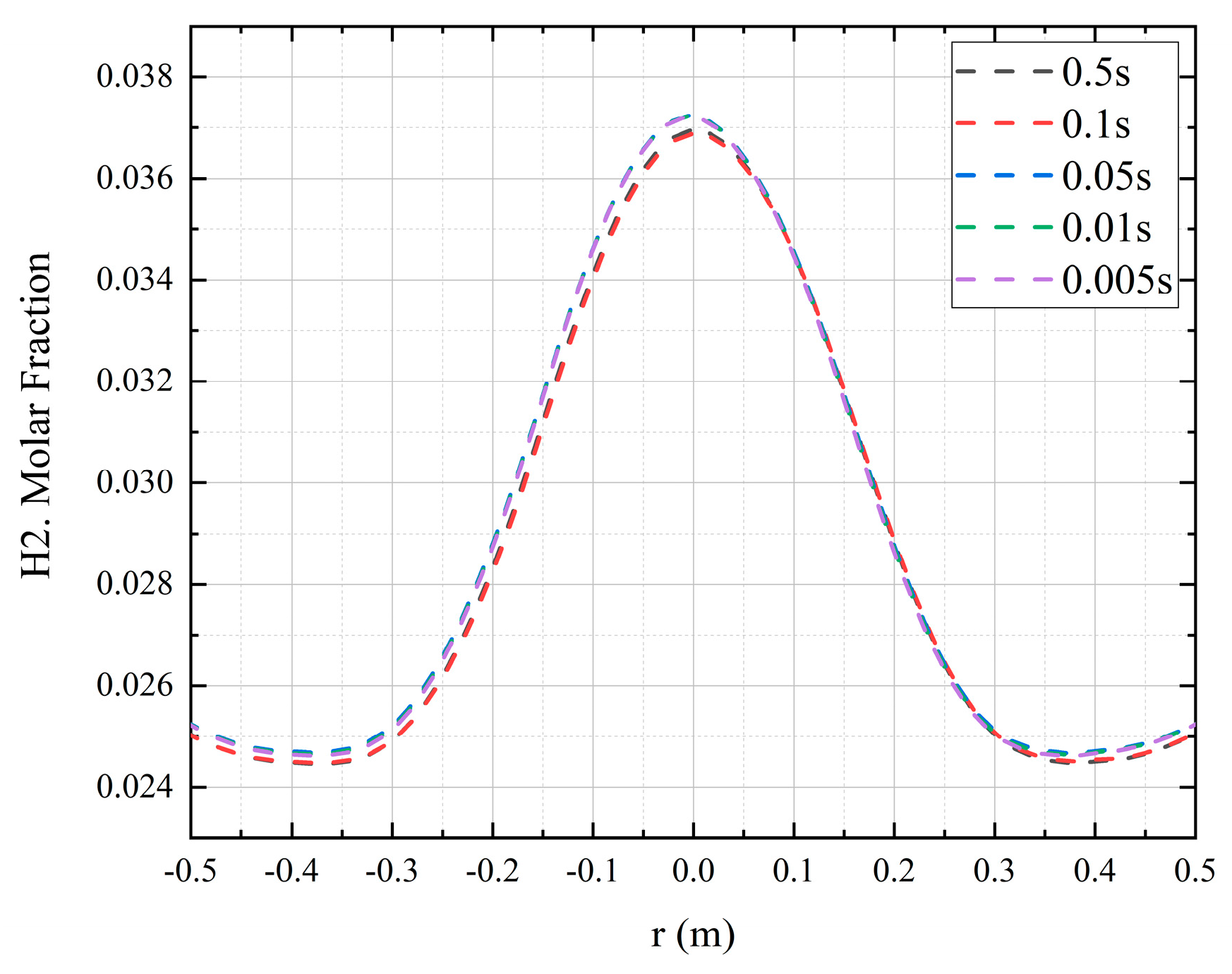





| Total Elements | Total Nodes | Mesh Size | Maximum Skewness | Average Skewness | Standard Deviation |
|---|---|---|---|---|---|
| 632,653 | 243,085 | 0.045 | 0.78455 | 0.14952 | 0.11938 |
| 802,246 | 307,848 | 0.04 | 0.80993 | 0.14778 | 0.11980 |
| 1,046,878 | 403,067 | 0.035 | 0.81553 | 0.14652 | 0.12140 |
| 1,438,922 | 550,412 | 0.03 | 0.83569 | 0.14707 | 0.12208 |
| 2,120,164 | 802,898 | 0.025 | 0.84632 | 0.14697 | 0.12245 |
| Total Elements | Total Nodes | Mesh Size | Maximum Skewness | Average Skewness | Standard Deviation |
|---|---|---|---|---|---|
| 270,759 | 80,041 | 0.2 | 0.79292 | 0.20843 | 0.13136 |
| 382,616 | 124,234 | 0.15 | 0.79230 | 0.19508 | 0.13447 |
| 746,789 | 261,168 | 0.1 | 0.84889 | 0.18221 | 0.13024 |
| 1,127,714 | 399,741 | 0.08 | 0.82073 | 0.17435 | 0.12857 |
| 2,016,072 | 710,252 | 0.06 | 0.81322 | 0.16598 | 0.12533 |
| Parameters | Case 1 | Case 2 | Case 3 | Case 4 |
|---|---|---|---|---|
| vapor mass flow rate /kg·s−1 | 0 | 0.08 | 0.16 | 0.08 |
| hydrogen mass flow rate /kg·s−1 | 0.002 | 0.002 | 0.002 | 0.002 |
| injection temperature /°C | 230 | 230 | 230 | 230 |
| injection time /s | 800 | 800 | 800 | 800 |
| dwell time /s | 200 | 200 | 200 | 200 |
| jet size /mm | 38 | 38 | 38 | 38 |
| initial gas composition | Air | Air | Air | Air |
| initial temperature /℃ | 25 | 25 | 25 | 25 |
| initial pressure /Mpa | 0.1 | 0.1 | 0.1 | 0.1 |
| wall temperature /℃ | 50 | 50 | 50 | adiabatic |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Z.; Liu, J.; Chen, Y.; Li, A. Numerical Simulation of Environmental Characteristics of Containment in Severe Accident of Marine Nuclear Power Plant. Energies 2023, 16, 7821. https://doi.org/10.3390/en16237821
Xu Z, Liu J, Chen Y, Li A. Numerical Simulation of Environmental Characteristics of Containment in Severe Accident of Marine Nuclear Power Plant. Energies. 2023; 16(23):7821. https://doi.org/10.3390/en16237821
Chicago/Turabian StyleXu, Zhiyong, Jialei Liu, Yuqing Chen, and Ang Li. 2023. "Numerical Simulation of Environmental Characteristics of Containment in Severe Accident of Marine Nuclear Power Plant" Energies 16, no. 23: 7821. https://doi.org/10.3390/en16237821
APA StyleXu, Z., Liu, J., Chen, Y., & Li, A. (2023). Numerical Simulation of Environmental Characteristics of Containment in Severe Accident of Marine Nuclear Power Plant. Energies, 16(23), 7821. https://doi.org/10.3390/en16237821







