A Two-Stage Scheduling Strategy for Electric Vehicles Based on Model Predictive Control
Abstract
:1. Introduction
- A two-stage optimal scheduling framework for EVs is proposed. Moreover, a charging and discharging power scheduling strategy, which includes day-ahead scheduling and real-time scheduling, is introduced to solve the problem of inaccurate power control in EVs.
- In the day-ahead scheduling stage, a distributionally robust optimization method is adopted to deal with the uncertainty of EVs. And the day-ahead scheduling model is established with the objective of minimizing charging and discharging costs. Therefore, the day-ahead power curve can be obtained.
- In the real-time scheduling stage, considering the dynamic connectivity of EVs, a real-time scheduling model based on MPC is established for tracking the day-ahead scheduling curve.
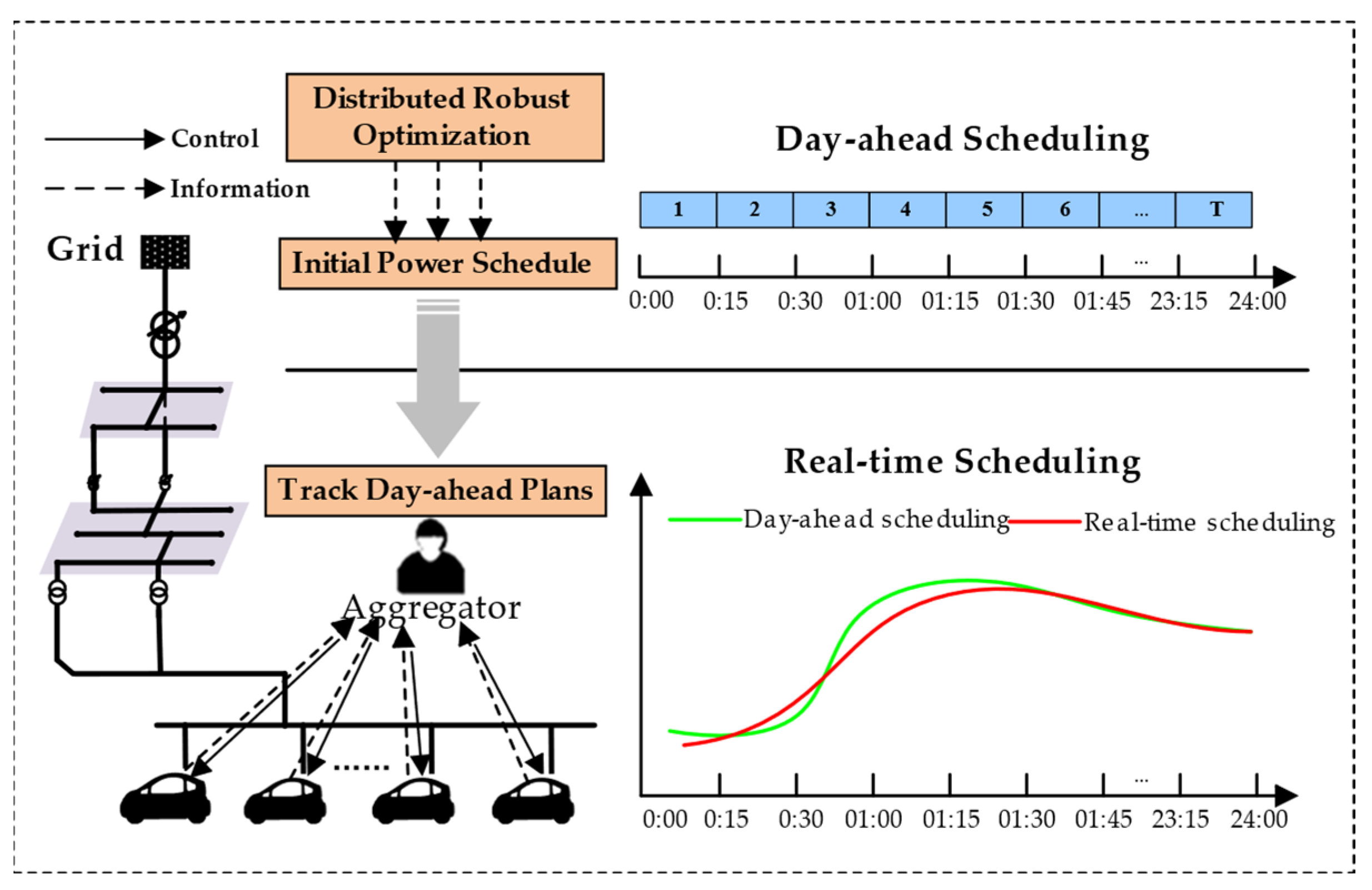
2. The Control Framework for EVs
2.1. Day-Ahead Scheduling
2.2. Real-Time Scheduling
3. Mathematical Modeling
3.1. The Day-Ahead Scheduling Based on Distributionally Robust Optimization
3.1.1. Uncertainty Set
3.1.2. Distributionally Robust Optimization Model for Electric Vehicle Scheduling
3.1.3. Power Constraints
3.1.4. Constraints for SOC
3.1.5. Constraints for Transformer
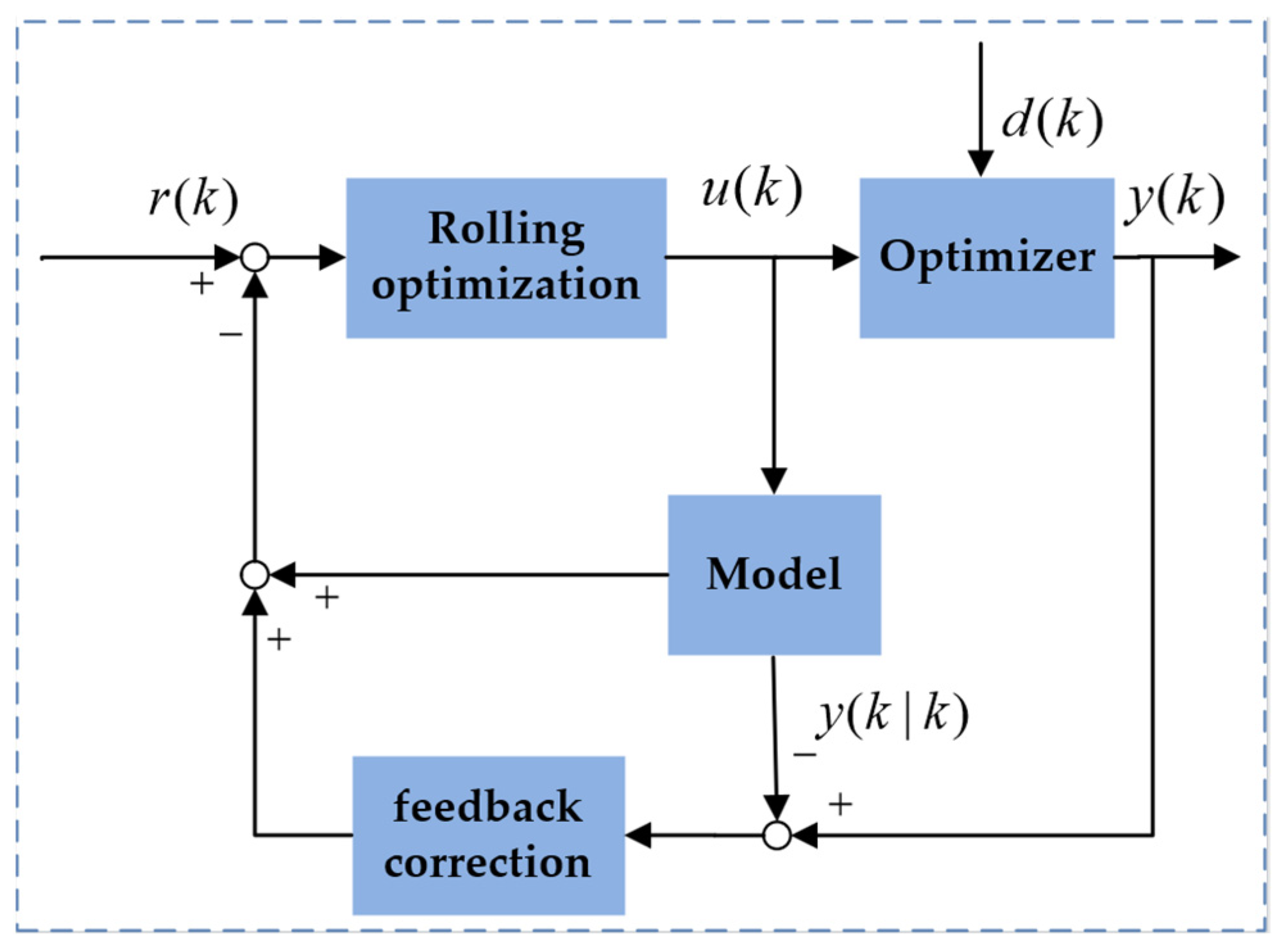
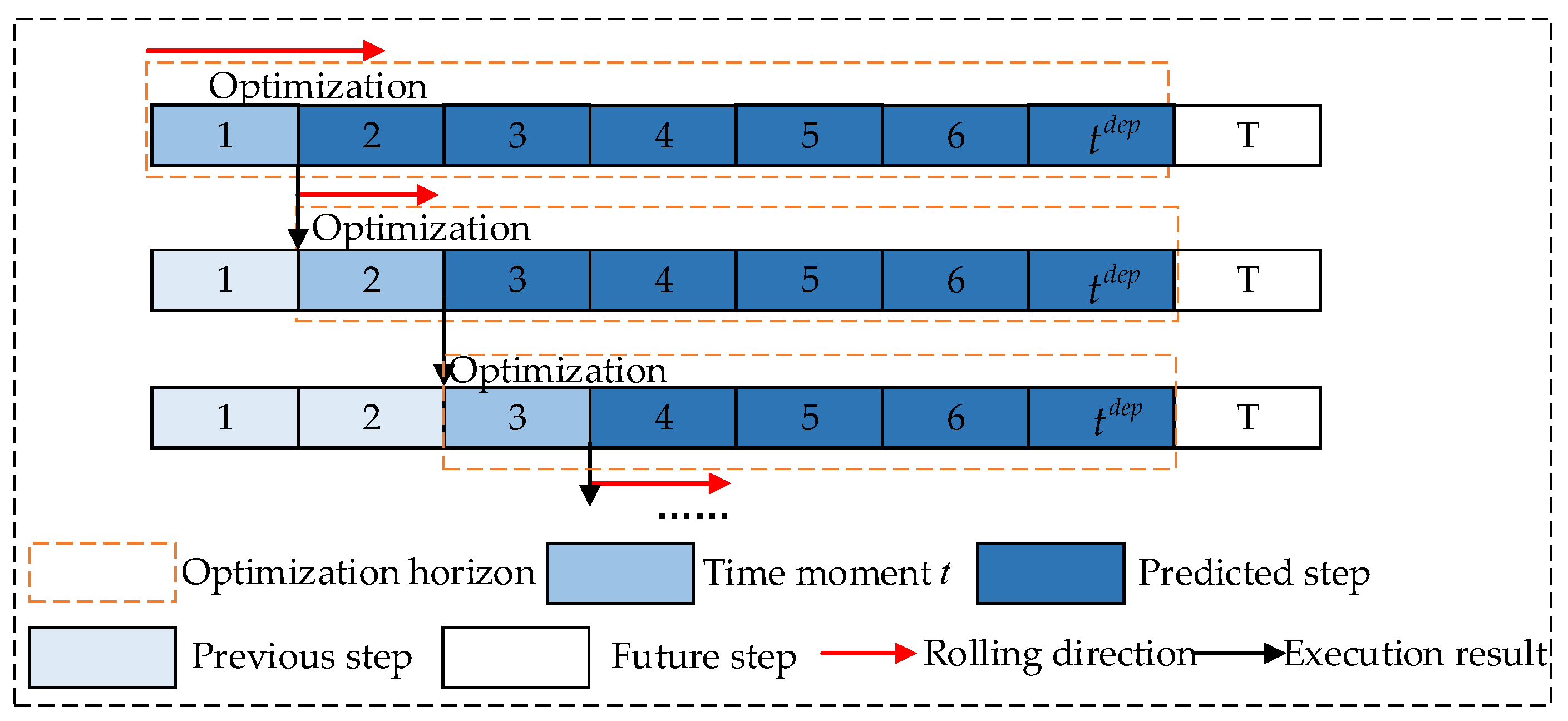
3.2. The Real-Time Scheduling Model Based on Model Predictive Control
3.2.1. Model Predictive Control
3.2.2. Objective Function
3.2.3. Constraints
4. Case Study
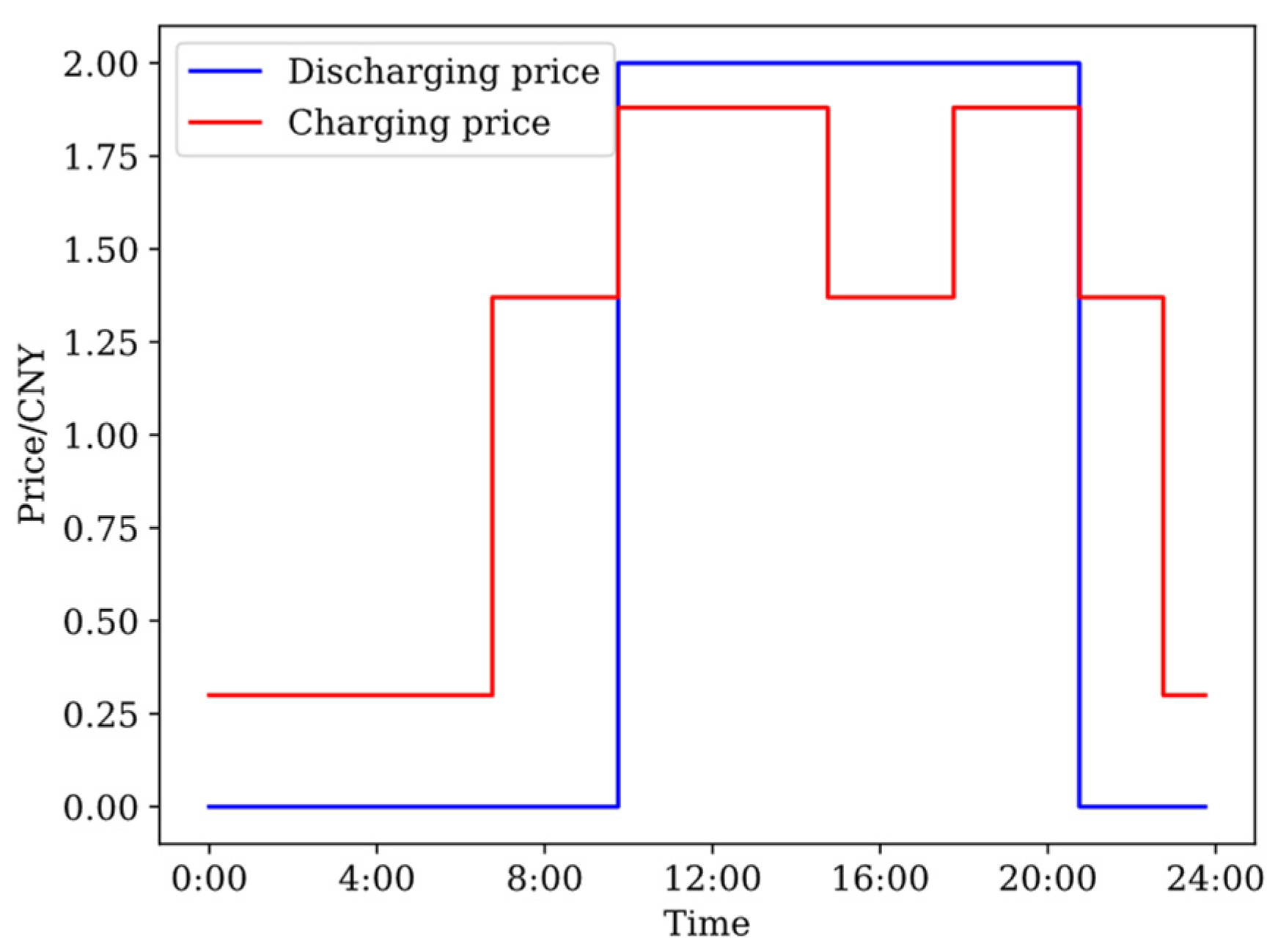
4.1. Simulation Parameter Settings
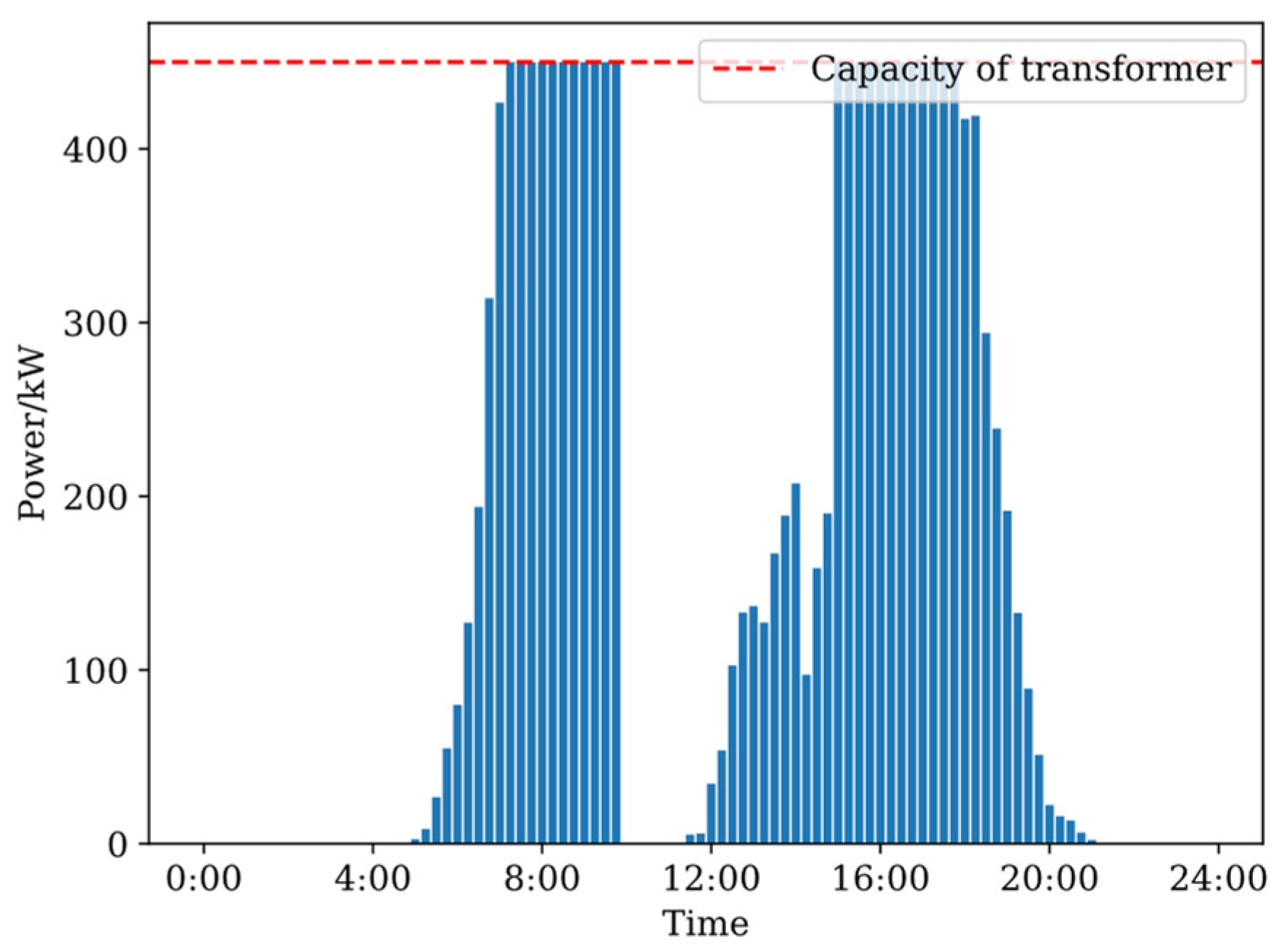
4.2. Results of Day-Ahead Scheduling
4.2.1. Power Curve
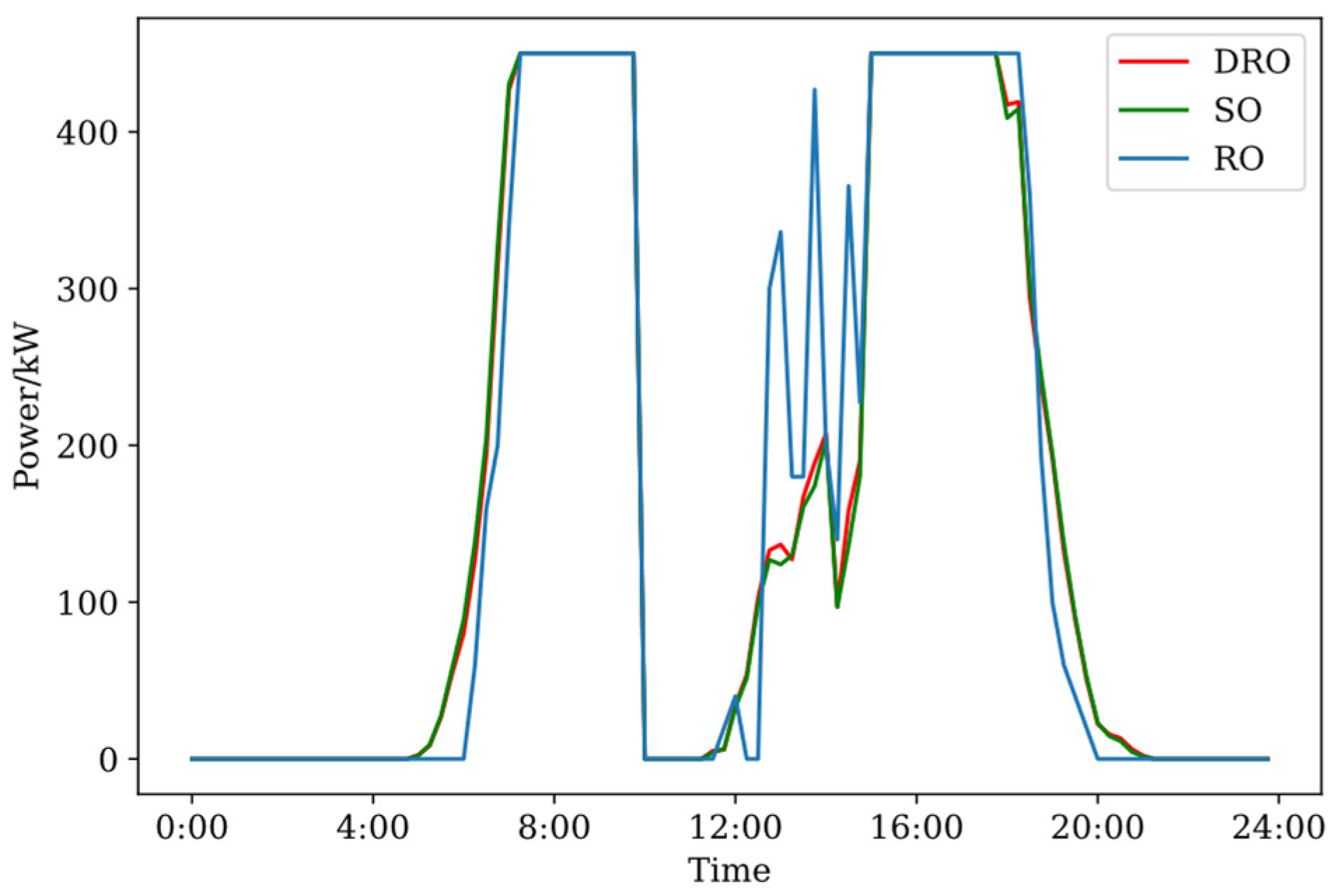
4.2.2. Comparative Analysis with Other Uncertainty Methods
4.2.3. Impact of Confidence on Robustness
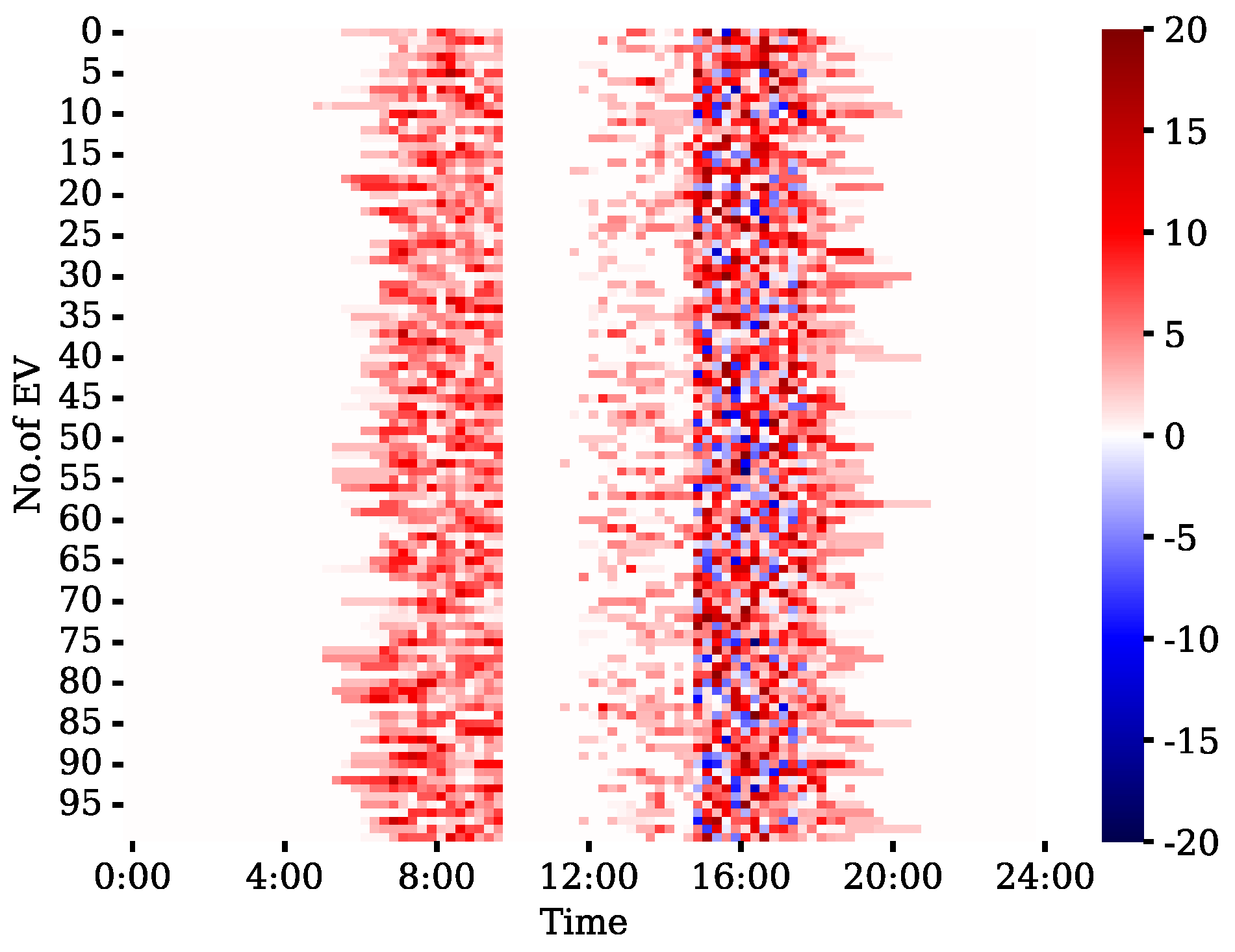
4.3. Results of Real-Time Scheduling
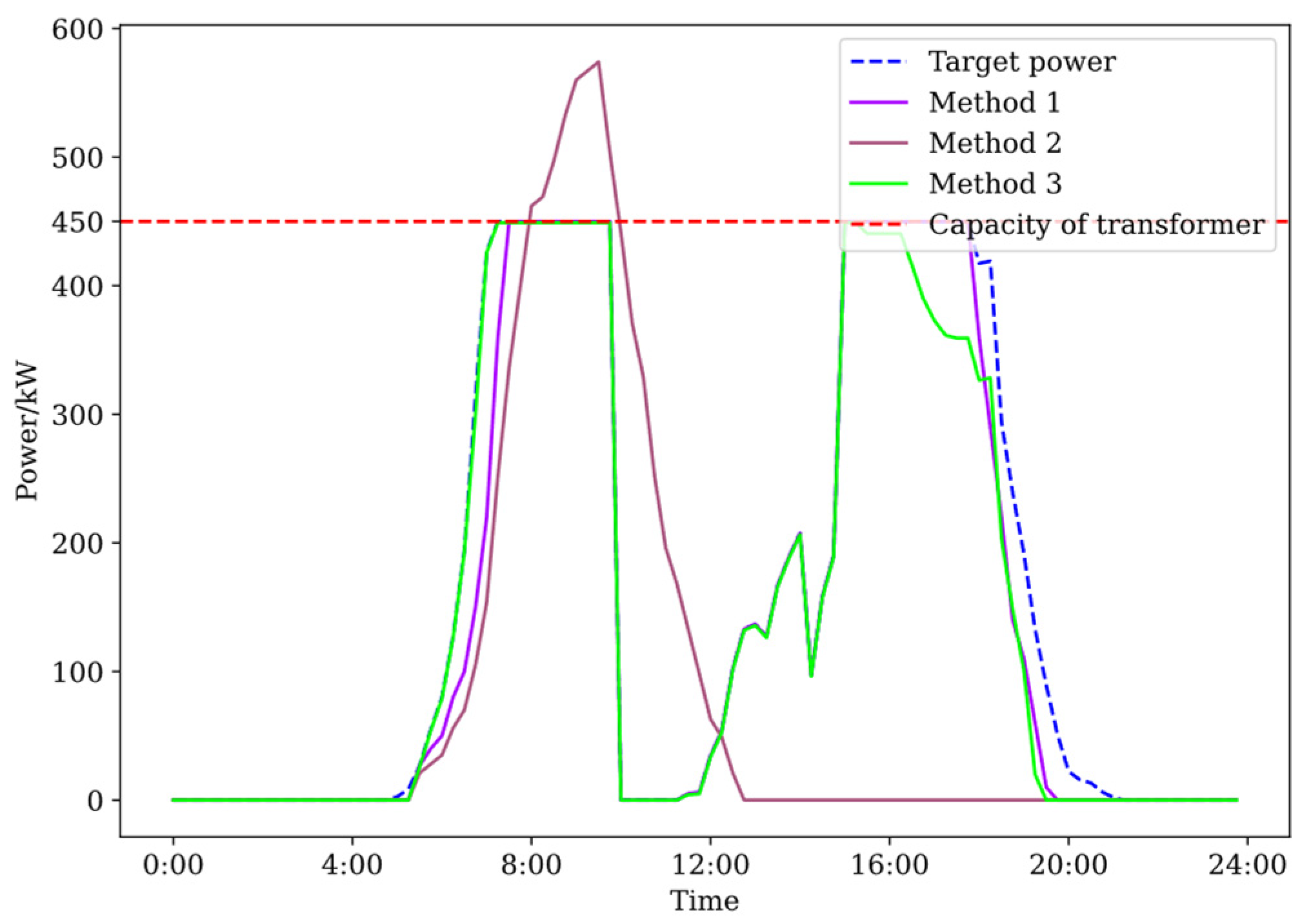
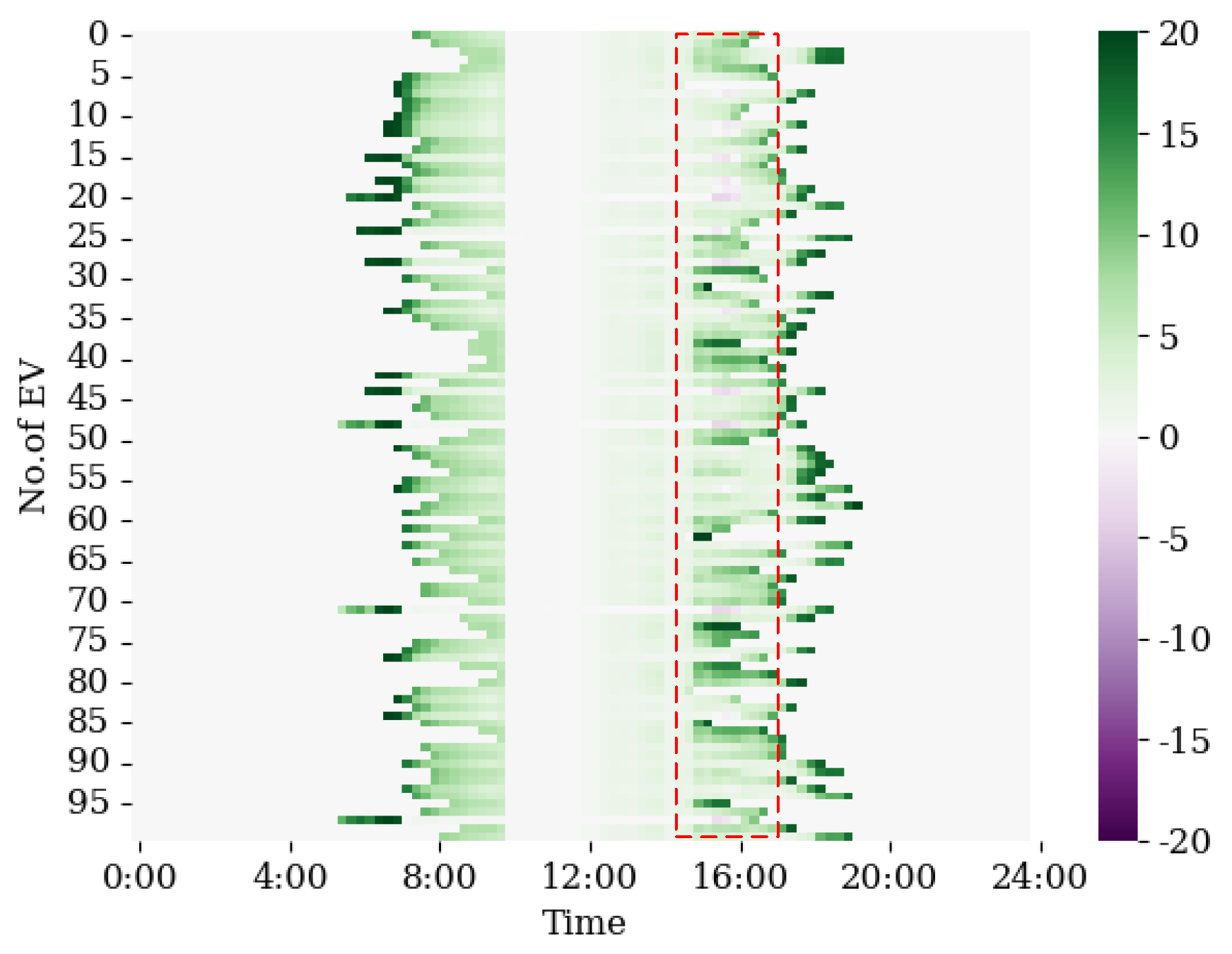
4.3.1. Power of Real-Time Scheduling
- (1)
- Method 1: Global optimization. Optimal solution with perfect information. The information about EVs is all known in advance.
- (2)
- Method 2: Disorderly charging. The EVs are charged at the maximum power of the chargers immediately after being connected to the grid. The charging of EVs stops when the expected SOC is reached.
- (3)
- Method 3: The proposed real-time scheduling strategy.
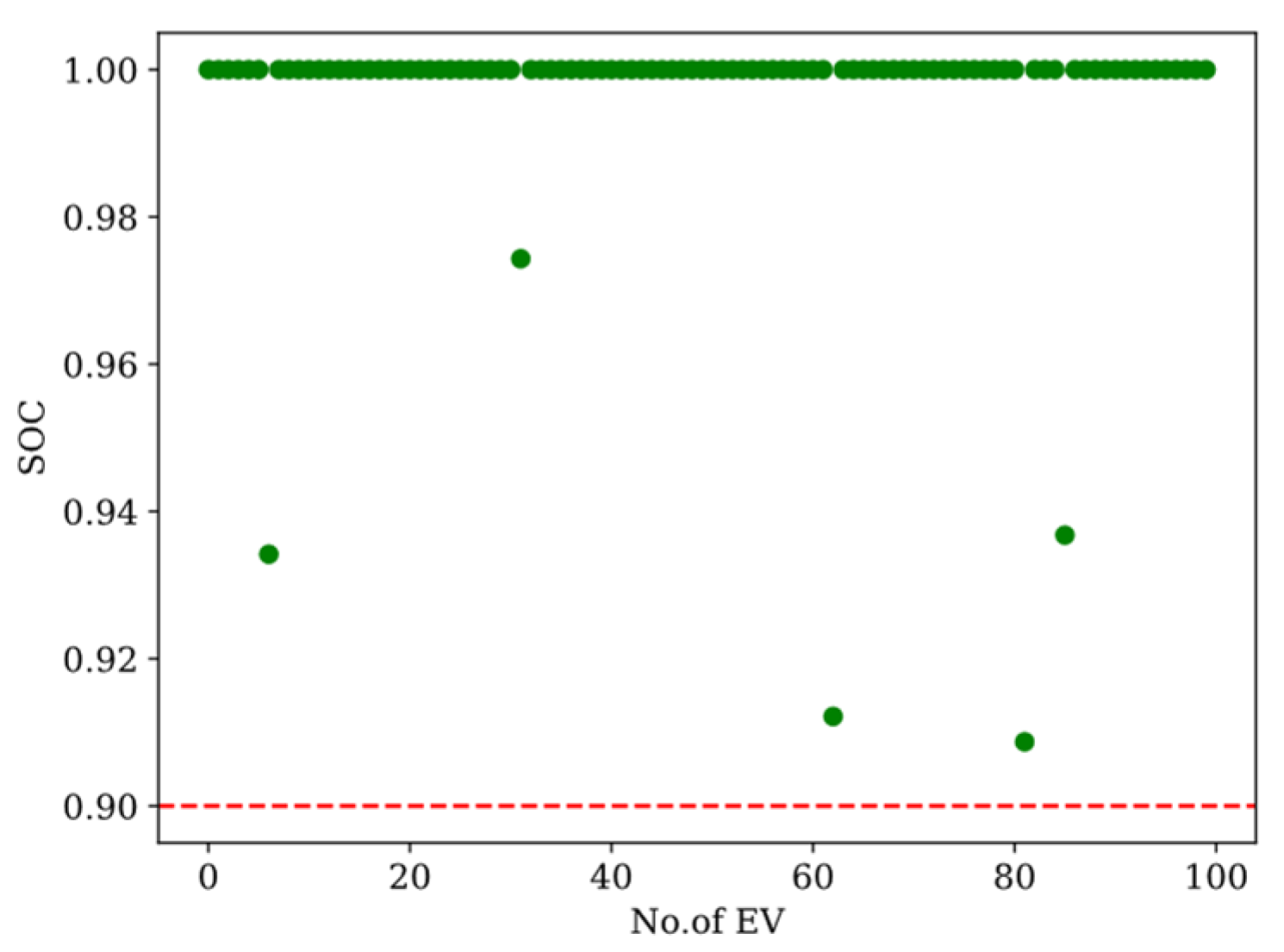
4.3.2. SOC at Departure Time
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Poongavanam, P.; Chand, A.A.; Tai, V.B.; Gupta, Y.M.; Kuppusamy, M.; Dhanraj, J.A.; Velmurugan, K.; Rajagopal, R.; Ramachandran, T.; Prasad, K.A.; et al. Annual Thermal Management of the Photovoltaic Module to Enhance Electrical Power and Efficiency Using Heat Batteries. Energies 2023, 16, 4049. [Google Scholar] [CrossRef]
- Tao, Y.; Chen, Y.; Huang, M.; Yang, L. Data-Based Orderly Charging Strategy Considering Users’ Charging Choices. Energies 2023, 16, 6923. [Google Scholar] [CrossRef]
- Zou, M.; Yang, Y.; Liu, M.; Wang, W.; Jia, H.; Peng, X.; Su, S.; Liu, D. Optimization Model of Electric Vehicles Charging and Discharging Strategy Considering the Safe Operation of Distribution Network. World Electr. Veh. J. 2022, 13, 117. [Google Scholar] [CrossRef]
- Hübner, M.; Zhao, L.; Mirbach, T.; Haubrich, H.-J.; Moser, A. Impact of Large-Scale Electric Vehicle Application on the Power Supply. In Proceedings of the 2009 IEEE Electrical Power & Energy Conference (EPEC), Montreal, QC, Canada, 22–23 October 2009; pp. 1–6. [Google Scholar] [CrossRef]
- You, P.; Yang, Z.; Chow, M.-Y.; Sun, Y. Optimal Cooperative Charging Strategy for a Smart Charging Station of Electric Vehicles. IEEE Trans. Power Syst. 2016, 31, 2946–2956. [Google Scholar] [CrossRef]
- Chen, X.; Wang, X.; Jian, J.; Tan, Z.; Li, Y.; Crossley, P. Novel Islanding Detection Method for Inverter-Based Distributed Generators Based on Adaptive Reactive Power Control. J. Eng. 2019, 2019, 3890–3894. [Google Scholar] [CrossRef]
- Das, H.S.; Rahman, M.M.; Li, S.; Tan, C.W. Electric Vehicles Standards, Charging Infrastructure, and Impact on Grid Integration: A Technological Review. Renew. Sustain. Energy Rev. 2020, 120, 109618. [Google Scholar] [CrossRef]
- Liu, C.; Chau, K.T.; Wu, D.; Gao, S. Opportunities and Challenges of Vehicle-to-Home, Vehicle-to-Vehicle, and Vehicle-to-Grid Technologies. Proc. IEEE 2013, 101, 2409–2427. [Google Scholar] [CrossRef]
- Liu, H.; Qi, J.; Wang, J.; Li, P.; Li, C.; Wei, H. EV Dispatch Control for Supplementary Frequency Regulation Considering the Expectation of EV Owners. IEEE Trans. Smart Grid 2018, 9, 3763–3772. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, D.; Li, Y.; Jiao, W.; Wang, G.; Zhao, J.; Qiang, Y.; Li, K. Enhancing Power Grid Resilience with Blockchain-Enabled Vehicle-to-Vehicle Energy Trading in Renewable Energy Integration. IEEE Trans. Ind. Appl. 2023, 1–16. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, B.; Wang, W.; Wang, M.; Peng, X. Development Pathway and Practices for Integration of Electric Vehicles and Internet of Energy. In Proceedings of the 2020 IEEE Sustainable Power and Energy Conference (iSPEC), Chengdu, China, 23–25 November 2020; pp. 2128–2134. [Google Scholar] [CrossRef]
- Peng, X.; Yang, Y.; Meng, D.; Cheng, H.; Dai, Y.; Zhang, X.; Zhong, Y. Research on Orderly Charging Control Strategy in Demond Response. In Proceedings of the 2021 IEEE 4th International Conference on Renewable Energy and Power Engineering (REPE), Beijing, China, 9–11 October 2021; pp. 216–220. [Google Scholar] [CrossRef]
- Lu, X.; Li, K.; Wang, F.; Mi, Z.; Sun, R.; Wang, X.; Lai, J. Optimal Bidding Strategy of DER Aggregator Considering Dual Uncertainty via Information Gap Decision Theory. IEEE Trans. Ind. Appl. 2021, 57, 158–169. [Google Scholar] [CrossRef]
- Porras, Á.; Fernández-Blanco, R.; Morales, J.M.; Pineda, S. An Efficient Robust Approach to the Day-Ahead Operation of an Aggregator of Electric Vehicles. IEEE Trans. Smart Grid 2020, 11, 4960–4970. [Google Scholar] [CrossRef]
- Zhou, W.; Xu, C.; Yang, D.; Peng, F.; Guo, X.; Wang, S. Research on Demand Response Strategy of Electric Vehicles Considering Dynamic Adjustment of Willingness Under P2P Energy Sharing. Proc. CSEE 2022, 1–14. [Google Scholar]
- Li, H.; Li, K.; Wang, Y.; Gao, F.; Zhang, Y.; Xie, H. Robust Optimal Scheduling Model of Grid-connected Electric Vehicle Clusters Based on SVC. High Volt. Eng. 2023, 1–9. [Google Scholar] [CrossRef]
- Nojavan, S.; Mohammadi-Ivatloo, B.; Zare, K. Optimal Bidding Strategy of Electricity Retailers Using Robust Optimisation Approach Considering Time-of-Use Rate Demand Response Programs under Market Price Uncertainties. IET Gener. Transm. Distrib. 2015, 9, 328–338. [Google Scholar] [CrossRef]
- Ning, C.; You, F. Data-Driven Decision Making under Uncertainty Integrating Robust Optimization with Principal Component Analysis and Kernel Smoothing Methods. Comput. Chem. Eng. 2018, 112, 190–210. [Google Scholar] [CrossRef]
- Shang, C.; Huang, X.; You, F. Data-Driven Robust Optimization Based on Kernel Learning. Comput. Chem. Eng. 2017, 106, 464–479. [Google Scholar] [CrossRef]
- Shi, W.; Lu, L.; Gao, H.; Li, H.; Liu, Y.; Liu, J. Economic Dispatch of Active Distribution Network with Participation of Demand Response and Electric Vehicle. Autom. Electr. Power Syst. 2020, 44, 41–51. [Google Scholar]
- Chen, L.; Pan, Z.; Yu, T.; Wang, K. Real-time Optimal Dispatch for Large-scale Electric Vehicles Based on Dynamic Non-cooperative Game Theory. Autom. Electr. Power Syst. 2019, 43, 32–40+66. [Google Scholar]
- Li, H.; Li, G.; Wang, K. Real-time Dispatch Strategy for Electric Vehicles Based on Deep Reinforcement Learning. Autom. Electr. Power Syst. 2020, 44, 161–167. [Google Scholar]
- Hu, J.; Zhou, H.; Li, Y. Real-time Dispatching Strategy for Aggregated Electric Vehicles to Smooth Power Fluctuation of Photovoltaics. Power Syst. Technol. 2019, 43, 2552–2560. [Google Scholar] [CrossRef]
- Tang, J.; Wang, D.; Jia, H.; Gao, S.; Song, Y.; Li, J.; Sun, C.; Fan, M. A Study of V2G Control Strategies of Aggregated Electric Vehicles for Real-Time Demand Response Based on Hysteresis Model. Power Syst. Technol. 2017, 41, 2155–2165. [Google Scholar] [CrossRef]
- Diaz, C.; Mazza, A.; Ruiz, F.; Patino, D.; Chicco, G. Understanding Model Predictive Control for Electric Vehicle Charging Dispatch. In Proceedings of the 2018 53rd International Universities Power Engineering Conference (UPEC), Glasgow, UK, 4–7 September 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Shi, Y.; Tuan, H.D.; Savkin, A.V.; Duong, T.Q.; Poor, H.V. Model Predictive Control for Smart Grids with Multiple Electric-Vehicle Charging Stations. IEEE Trans. Smart Grid 2019, 10, 2127–2136. [Google Scholar] [CrossRef]
- Zheng, Y.; Song, Y.; Hill, D.J.; Meng, K. Online Distributed MPC-Based Optimal Scheduling for EV Charging Stations in Distribution Systems. IEEE Trans. Ind. Inform. 2019, 15, 638–649. [Google Scholar] [CrossRef]
- Zhao, C.; Guan, Y. Data-Driven Stochastic Unit Commitment for Integrating Wind Generation. IEEE Trans. Power Syst. 2016, 31, 2587–2596. [Google Scholar] [CrossRef]
- Hackl, H.; Freiberger, M.; Matzick, P.; Stoiber, M.; Auinger, B. Energy Management Algorithm for Battery Sharing Based on Model Predictive Control Integrating Electro-Thermal Simulation and Demand Forecast. In Proceedings of the 2023 International Conference on Electrical Drives and Power Electronics (EDPE), The High Tatras, Slovakia, 25–27 September 2023; pp. 1–7. [Google Scholar] [CrossRef]
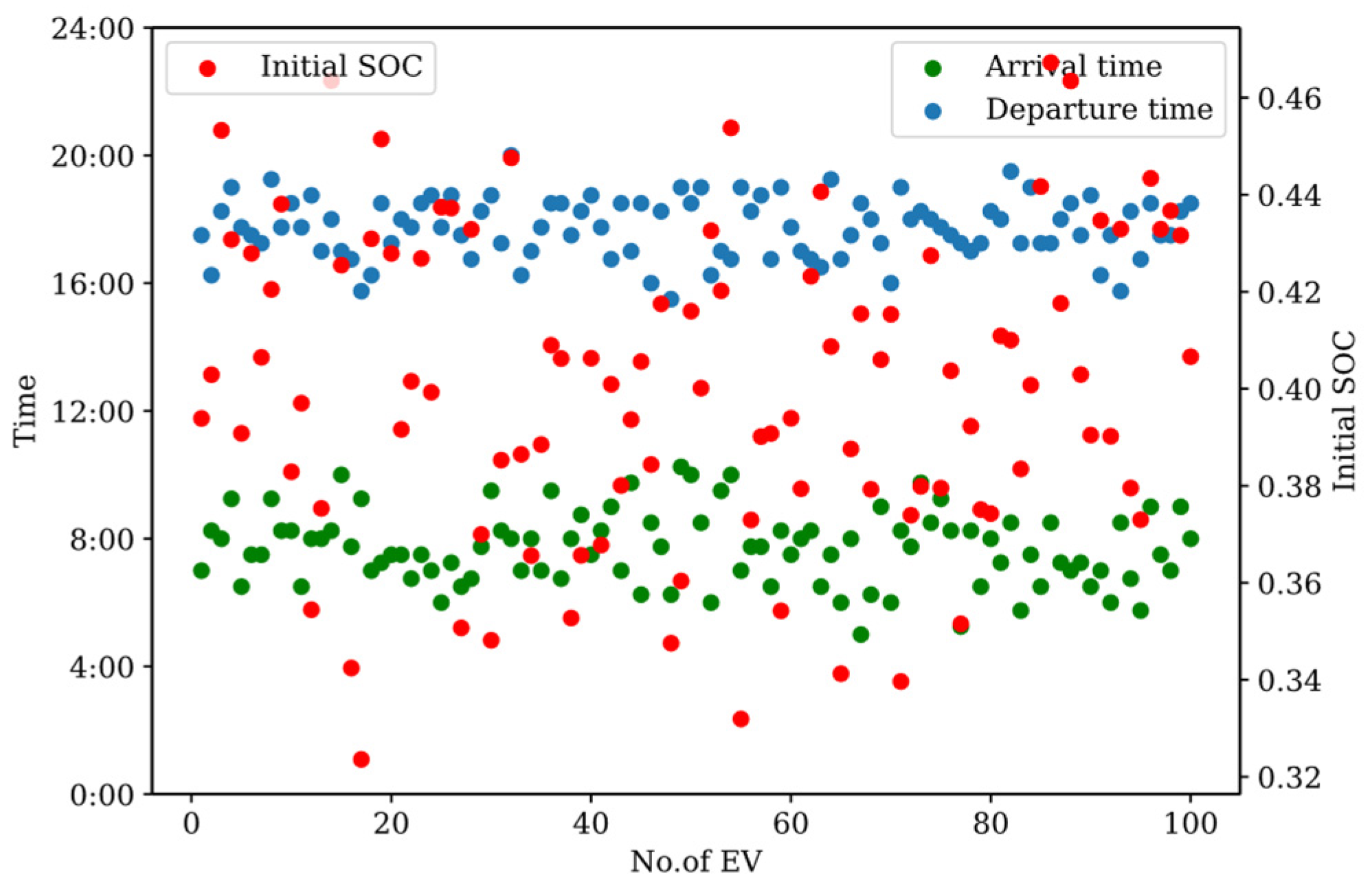
| Parameter | Value |
|---|---|
| Maximum charging/discharging power (kW) | 20 |
| Initial SOC | |
| Expected departure SOC | 0.9 |
| Charging/discharging efficiency | 0.9 |
| Battery capacity (kWh) | 60 |
| Minimum value of SOC | 0.2 |
| 0.95 | |
| (CNY/kWh) | 0.15 |
| , | 1 |
| (kW) | 450 |
| Arrival time | |
| Departure time |
| Method | Cost (CNY) |
|---|---|
| RO | 4493.48 |
| DRO | 4245.23 |
| SO | 4218.46 |
| 0.8 | 0.95 | |
|---|---|---|
| 0.3 | 4238.71 (CNY) | 4242.11 (CNY) |
| 0.6 | 4239.16 (CNY) | 4243.87 (CNY) |
| 0.95 | 4239.22 (CNY) | 4245.23 (CNY) |
| Number of Typical Scenarios | Cost (CNY) |
|---|---|
| 5 | 4156.73 |
| 10 | 4245.23 |
| 15 | 4620.58 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Chen, J.; Pan, Y.; Yang, Y.; Hu, J. A Two-Stage Scheduling Strategy for Electric Vehicles Based on Model Predictive Control. Energies 2023, 16, 7737. https://doi.org/10.3390/en16237737
Wang W, Chen J, Pan Y, Yang Y, Hu J. A Two-Stage Scheduling Strategy for Electric Vehicles Based on Model Predictive Control. Energies. 2023; 16(23):7737. https://doi.org/10.3390/en16237737
Chicago/Turabian StyleWang, Wen, Jiaqi Chen, Yi Pan, Ye Yang, and Junjie Hu. 2023. "A Two-Stage Scheduling Strategy for Electric Vehicles Based on Model Predictive Control" Energies 16, no. 23: 7737. https://doi.org/10.3390/en16237737
APA StyleWang, W., Chen, J., Pan, Y., Yang, Y., & Hu, J. (2023). A Two-Stage Scheduling Strategy for Electric Vehicles Based on Model Predictive Control. Energies, 16(23), 7737. https://doi.org/10.3390/en16237737






