Abstract
With the rapid development of new power systems, power usage stations are becoming more diverse and complex. Fine-grained management of demand-side power load has become increasingly crucial. To address the accurate load forecasting needs for various demand-side power consumption types and provide data support for load management in diverse stations, this study proposes a load sequence noise reduction method. Initially, wavelet noise reduction is performed on the multiple types of load sequences collected by the power system. Subsequently, the northern goshawk optimization is employed to optimize the parameters of variational mode decomposition, ensuring the selection of the most suitable modal decomposition parameters for different load sequences. Next, the SSA–KELM model is employed to independently predict each sub-modal component. The predicted values for each sub-modal component are then aggregated to yield short-term load prediction results. The proposed load forecasting method has been verified using actual data collected from various types of power terminals. A comparison with popular load forecasting methods demonstrates the proposed method’s higher prediction accuracy and versatility. The average prediction results of load data in industrial stations can reach RMSE = 0.0098, MAE = 0.0078, MAPE = 1.3897%, and R2 = 0.9949. This method can be effectively applied to short-term load forecasting in multiple types of power stations, providing a reliable basis for accurate demand-side power load management and decision-making.
1. Introduction
With the construction of a new power system and the gradual development of fine-grained power load management [1,2,3], the diversified load short-term prediction technology for the demand side of the power system plays an important role in accurate management decision-making for diversified stations and load types [4]. Fine-grained management of power load [5] refers to the real-time monitoring and analysis, regulation, and optimization of power load to achieve accurate management of the power load, effectively improving the efficiency and stability of the power system and reducing energy consumption and pollution emissions, which is the trend and direction of the development of the modern power industry [6]. However, due to the different effects of load evolution characteristics on different power market participants [7], the large amount of data collected in the diversified platform environment is highly complex, low real-time, and difficult data analysis, resulting in inconsistency and low accuracy of power load forecasting. Therefore, there is a certain resistance to accurate power load management. In areas where power resources are scarce [8,9,10], problems such as over-budget energy consumption, long outages, and high load risks at each station are frequent. The power systems need to upgrade their power demand-side response capabilities to improve the efficiency of power usage and maximize retailer profits [11]. In this study, we improve the accuracy of forecasting multiple loads in the short-term future for accurate scheduling and distribution efforts.
At present, short-term load forecasting technology is developing rapidly, and there are three mainstream load forecasting methods:
- (a)
- Traditional statistical models. These include the ARIMA (autoregressive integrated moving average) model [12], the Kalman filter model [13], the hidden Markov model [14], the Bayesian model [15], and the regression model [16] etc. However, such models lack the mining of the potential features of time series, and the predicted results are often quite different from the actual power load changes.
- (b)
- Predictive models based on machine learning. With a more powerful data mining performance than statistical models, it has been widely used, including in backpropagation (BP) [17], long short-term memory (LSTM) [18], extreme learning machine (ELM) [19], and gated recurrent unit (GRU) [20], etc. These algorithms have powerful functions in processing nonlinear data like load sequences. However, because they easily fall into the local optimal solution or overfitting, the prediction accuracy still needs to be improved. In the comparison of various algorithms, it is found that the prediction training speed of ELM is faster and more stable [21], which is more suitable for the prediction of power load series.
- (c)
- Hybrid predictive model. By combining the advantages of multiple forecasting models or using intelligent optimization algorithms, fully mining load sequence information to maximize the accuracy of load forecasting has been the mainstream research direction of forecasting technology over the past two years. Literature [22] The sequence-to-sequence (Seq2Seq) model is improved by convolutional neural network, attention mechanism, and Bayesian optimization, which improves the accuracy of load forecasting, but excessive algorithm optimization and feature data use leads to too high complexity of the prediction model and too long training time, which means that it is difficult to meet the real-time requirements of the power system load forecasting. Literature [23] Aiming at the integrated energy system of distributed energy resources, a prediction method based on EEMD combined with the LSTM–SVR–BO model is proposed to predict photovoltaic power. Literature [24] incorporates the attention mechanism into the traditional CNN-LSTM model to carry out short-term power load prediction for cogeneration. In most of the remaining literature [25,26,27,28], effective prediction methods are proposed for different objects in the power system, but there is a problem of insufficient applicability.
In summary, most existing short-term load forecasting methods focus on specific load types and rely heavily on load-related characteristic data. However, these methods require a significant amount of data samples for accurate load forecasting. Furthermore, the accuracy of load prediction heavily relies on these indicators, which may not be applicable across different industries due to the varying impacts of load-related features on power load. As a result, the lack of sufficient load characteristic data samples limits the applicability and accuracy of load prediction, especially for the precise control of demand-side load in the new power system. In contrast to existing methods, the research aims to overcome the limitations of current short-term load forecasting approaches. By recognizing the high dependence on load-related characteristic data and the inadequate collection of load-characteristic data samples, this study strives to develop a novel approach that extends beyond the conventional reliance on such indicators. This innovative method intends to provide highly applicable load predictions for accurate demand-side load control in the emerging power system, thereby addressing the challenges posed by varying load types and the insufficiency of load characteristic data.
Therefore, this study focuses on a new type of electric load management system. To address the issue of insufficient data samples regarding the diverse station electric load characteristics, a combined model based on the modified variational mode decomposition of the North Goshawk Optimization algorithm and the modified kernel extreme learning machine of the sparrow algorithm is proposed for demand-side electric load time-series forecasting. Firstly, based on the intelligent distribution sensing terminal of the power system in a certain area, the load data of various station types is collected, and the load time series data set of each station type is constructed by the preliminary noise reduction of the load data by wavelet decomposition. Secondly, the Northern Goshawk Optimization algorithm is used to optimize the number of decomposition layers and penalty factors of variational mode decomposition, and the optimal combination of VMD parameters for specific types of loads is calculated. Based on the modal decomposition results of VMD excluding residual terms, the SSA–KEM model is established to predict each sub-mode separately and superimpose the predicted value of each sub-mode to obtain the prediction result of the load series. Finally, on the data of multiple load types, the combination of various algorithms is compared to verify the high accuracy and applicability of the prediction results. It can provide reliable data support and a scientific decision-making basis for the precise load management of new power systems.
2. Load Sequence Decomposition
In order to tackle the challenges posed by the high complexity and volatility of power load sequences, limitations of the traditional empirical mode decomposition (EMD) method have been identified [29]. To address these limitations, this study proposes a load sequence decomposition method based on the Northern Goshawk Optimization algorithm (NGO) to optimize the variational mode decomposition (VMD). In this method, the NGO is employed to identify optimal parameter combinations and optimize the VMD algorithm. By decomposing the load sequence using the optimized VMD algorithm, the fluctuations and complexity in the original load sequence are reduced, and the distinctive characteristics of each modal component are emphasized. Furthermore, this approach fully harnesses the potential information within the original load data. Consequently, these modifications effectively mitigate the challenges associated with load forecasting, leading to enhanced precision and accuracy in predictions.
2.1. Variational Mode Decomposition
For power load time series data, VMD is performed based on a time–frequency analysis. VMD can perform adaptive load decomposition of non-stationary signals, decomposing the original multi-component signal into multiple amplitude-modulated frequency-modulated single-component signals, thereby effectively avoiding problems such as endpoint effects that may occur during iteration [30]. After decomposition, each mode exhibits a distinct finite bandwidth. The objective of the decomposition is to minimize the sum of estimated bandwidths of these decomposed modes using the variational model expression.
where is the sum of the decomposed K modes; is the center frequency corresponding to the kth sub mode k; is the original load sequence; is the Dirac distribution function; is the partial derivative operator at time t. Construct an augmented Lagrange function to solve Equation (1):
Iterative updates of , , and are made using the alternate direction method of multipliers (ADMM). The Fourier transforms of , , and are represented by , , and . Given , , , update the Fourier transform of first:
Next, update the center frequency:
where the center frequency of the current mode is ; The Wiener filter with the current margin is . Finally, update the Fourier transform of with step , as shown in the following Equation (5):
2.2. Northern Goshawk Optimization Algorithm
In the process of load sequence decomposition, the selection of the penalty factor “a” and decomposition layer “K” significantly impact the effectiveness of the VMD method. To optimize this selection process, the Northern Goshawk Optimization algorithm (NGO) [31] is introduced. The NGO is a novel swarm intelligent optimization algorithm that emulates the hunting behavior of northern goshawks. It demonstrates exceptional optimization performance as well as high accuracy and stability. The parameter lookup model for the NGO is as follows:
- Step 1: Population initialization
First, the population matrix X for the northern goshawk population is constructed, and the population members are randomly initialized in the search space:
In the population matrix: Xi is the position of the i-th northern goshawk; the population of northern goshawks is N; set the highest dimension m of the solution, and the i-th northern goshawk is represented as when it is in the j-th dimension; the objective function value of the northern goshawk population is expressed by the vector F; Fi is the objective function value of the i-th northern goshawk, and the expression formula is:
- Step 2: Identify prey and attack
The first stage of hunting prey in imitating the northern goshawk is to select the prey and conduct a quick pursuit, first randomly. That is, in the parameter search space, the goal is to identify the optimal region, and the global search is carried out. Set the i-th northern goshawk prey to and the i-th northern goshawk to in the new position of dimension j; the parameters r and I are random numbers for the search iteration; , are the positions of the goshawk and its prey, and their objective function value is Fi;
After the first stage of the attack, obtain the updated prey position P1, northern goshawk position , objective function value :
- Step 3: Pursuit and escape
When the northern goshawk attacks its prey, the prey will try to escape, and the northern goshawk needs to continue chasing its prey. The northern goshawk, characterized by its speed, can capture prey in almost any situation. The simulation of this behavior increases the algorithm’s ability to utilize local searches of the search space. Suppose the northern goshawk has a hunting radius of about R, the maximum number of iterations T, and the current iteration number t. The position of the j-th dimension of the i-th goshawk after the second stage update can be obtained as:
The position of the i-th northern goshawk after the iterative update is , and the objective function value of the i-th goshawk after the second stage update is , i.e.:
2.3. Load Sequence Decomposition of VMD Is Optimized Based on NGO
The accuracy and effectiveness of VMD decomposition may be influenced to a certain extent by manually set parameters, which have certain limitations. In this study, the Northern Goshawk Optimization algorithm (NGO) was employed to optimize the decomposition layer (K) and the penalty factor (α) of VMD. The fitness function utilized in the optimization process is the local minimum envelope entropy.
The envelope entropy reflects the sparsity characteristics of the original load signal. A smaller envelope entropy indicates that the decomposed subcomponents contain more informative features and less noise, whereas a larger envelope entropy is observed conversely. Consequently, the envelope entropy is utilized to measure the level of characteristic information and noise in the decomposed load sequence. Incorporating the envelope entropy as a fitness function for parameter optimization facilitates the identification of the optimal number of decomposition layers and penalty factors, consequently enhancing the accuracy and efficacy of the decomposition process.
where is the result of normalization, is the envelope signal of the K subcomponents of the VMD solution after Hilbert demodulation, and the flow chart of the NGO–VMD algorithm is shown in Figure 1:

Figure 1.
The flow chart of the NGO–VMD model.
3. Power Load Forecasting
3.1. Kernel Extreme Learning Machine Model
The kernel extreme learning machine (KELM) [32] is a single hidden layer feedforward neural network that consists of an input layer, a hidden layer, and an output layer. It was proposed based on ELM [27], and the network structure is illustrated in Figure 2. The introduction of the kernel function provides advantages in terms of generalization ability and performance. Additionally, it exhibits faster processing speed compared to other prediction methods, such as BP. It effectively addresses the challenge of handling a large volume of data resulting from the variational mode decomposition, thereby enhancing the demand-side load forecasting response capability. Hence, KELM is chosen for load forecasting in this study.

Figure 2.
The structure diagram of the KELM model.
The basic ELM model function can be expressed in the following:
where represents the output of the ELM; represents the weight matrix from the hidden layer to the output layer; is the number of hidden layer nodes; is the number of nodes in the output layer; represents the input vector; and represent input weight and output weight, respectively; represents the sigmoid function. After introducing the regularization term, the optimization form is:
where is the target matrix of the training data; is the regularization parameter. The optimal solution is obtained as:
The optimal solution is influenced by the initial input weights. The paper uses KELM to solve this problem. The output of KELM is:
where represents kernel matrix; represents kernel function. This paper adopts the radial basis kernel function RBF, the specific form is as follows:
3.2. KELM Optimized for SSA
In the case of utilizing the KELM model for prediction, the choice of the regularization factor and kernel parameter significantly influences the prediction accuracy. Moreover, the SSA algorithm offers the advantage of fast convergence, thereby reducing the execution time required for parameter-seeking optimization of the KELM model.
The SSA algorithm simulates the foraging behavior of sparrows to optimize parameters [33]. The population comprises producers, joiners, and vigilantes. Producers search for food, joiners retrieve food, and vigilantes detect potential dangers:
In Equation (23), is the number of iterations, denotes the j-dimension value of sparrow individual , is a random number in the interval , is the constant with the highest number of iterations, the alarm value is , and the safety threshold is . When the alarm value exceeds the safety threshold, the sparrow population will quickly leave and thus fly into the safe area; if it is less than the safety threshold, they will engage in extensive foraging. The movement rule of the joiner is:
In Equation (24), is the globally optimal position, which is occupied by the producer, is the globally worst position, and is a d-order matrix with matrix elements 1 or −1. If , the joiner fails to forage and travels to other areas to forage. The movement rule of the vigilant is:
When the current sparrow adaptation value is greater than the globally optimal adaptation value , the vigilante will approach the central safety zone from the edge of the hazardous population; when it is equal, it will approach the other individual sparrows. The flow chart of the SSA–KELM algorithm is shown in Figure 3:

Figure 3.
The flow chart of the SSA–KELM model.
3.3. Power Load Forecasting Modal
The proposed short-term power load forecasting method based on variational mode decomposition is shown in Figure 4.

Figure 4.
Modeling process for forecasting.
Step 1: The power distribution terminals in each station collect the power load data and obtain the diversified load data set through preliminary data preprocessing.
Step 2: Optimize the parameters of variational mode decomposition for different original demand-side load sequences.
Step 3: Based on improved variational mode decomposition, the load series is decomposed into multiple IMF modes for different original demand-side load sequences, and the residual terms are removed to reduce the impact on the accuracy of load forecasting.
Step 4: The parameter finding model of KEM is constructed for each IMF modal, and the initialization parameters of KEM are optimized by using the SSA optimization algorithm.
Step 5: Predict each modal component based on the parameter finding results of SSA–KELM.
Step 6: Reconstruct the prediction results of each modal component, obtain the load prediction results, and calculate the error of the training results.
4. Data Preprocessing
4.1. Load Sequence Data Acquisition from Multiple Stations
This study collected load data from various typical areas in a city in southwest China that lacked electricity. The data was then categorized based on local electricity consumption types, which included heavy industrial electricity in industrial parks, general industrial electricity, industrial and commercial electricity, non-industrial electricity, commercial electricity in commercial parks, single-sale electricity, residential electricity in residential parks, non-residential electricity, agricultural production electricity in agricultural parks, agricultural drainage and irrigation electricity, and other electricity consumption, resulting in a total of 11 types. To ensure an accurate reflection of demand-side characteristics, factors such as user type, load variations, data stability, and data reliability were comprehensively considered when selecting the data.
For this study, four types of electricity consumption were chosen, namely heavy industry electricity, commercial electricity, residential electricity, and agricultural production electricity. Additionally, three station load datasets were selected for prediction and analysis. Demand-side load data typically incorporates consumer electricity demand and behavior in the electricity market, providing valuable insights for load forecasting.
The load sequence data was collected at a granularity of one data point every 15 min, resulting in a total of 8640 data points collected from March to May at each station. The dataset was then divided into training and testing sets in an 8:2 ratio, yielding a total of 12 load forecast datasets.
4.2. Data Noise Reduction
The wavelet transform is a signal processing method that possesses multi-scale analysis capabilities, allowing for the decomposition of signals into detailed information and trend components of varying frequencies. Through the selection of an appropriate wavelet function and threshold, noise in the high-frequency portion of the load timing data can be effectively filtered, thereby preserving the main components of the signal. The utilization of wavelet transform denoising enables the reduction of random fluctuations and abnormal noise in the load data, minimizing interference with the VMD decomposition results. Consequently, VMD can more accurately capture the true trends and periodicity of the load data, ultimately enhancing the accuracy and reliability of load forecasting.
To eliminate the noise present in the 12 sets of load prediction data mentioned above, wavelet noise reduction is employed as a preliminary step, effectively diminishing the noise present in the load sequence. The noise reduction effect is visually presented in Figure 5.
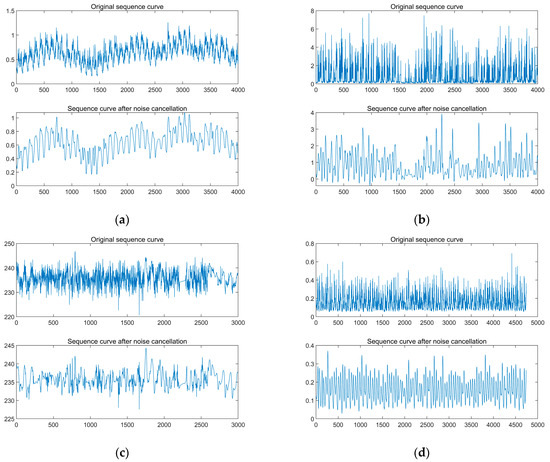
Figure 5.
Noise reduction results for each station type load profile: (a) industrial type; (b) business type; (c) agricultural production type; (d) residential electricity.
The demand side of the power system comprises four main types of load stations, each exhibiting distinct curve fluctuation characteristics. The modal decomposition method can effectively decompose and analyze each characteristic, reducing the difficulty of forecasting load fluctuations for each station type:
- (a)
- Industrial stations: Load curves are primarily influenced by production process changes and demand fluctuations. Less affected by seasonal and weather-related factors. Exhibits continuous fluctuation characteristics with noticeable cyclical changes. Short-term prediction results for industrial stations are usually more accurate.
- (b)
- Commercial stations: Load curves are mainly influenced by time of day and holidays. Higher load peaks during commercial time periods, while the load curve stabilizes during non-commercial times.
- (c)
- Agricultural stations: Load curves affected by seasonal and weather factors. Highly impacted by random factors such as sudden weather changes, agricultural disasters, and induction loads from irrigation systems and refrigeration equipment. Numerous factors causing random fluctuations make short-term load forecasting and control more challenging for agricultural stations.
- (d)
- Residential living stations: Exhibit cyclical fluctuation characteristics. Specific fluctuation characteristics may vary depending on geographical and social factors.
5. Result and Discussion
5.1. Algorithm Parameterization
In this study, the NGO algorithm was used to set the population size to 5. The maximum number of iterations was set to 20. The optimal number of decomposition layers (K) for searching variational mode decomposition (VMD) was tested within the range of 3 to 15. The optimal penalty factor was also tested within the range of 10 to 3000. The maximum number of iterations for VMD optimization was set to 200, while the rest of the parameters were kept at their default values. For the SSA algorithm, the population size was set to 20, the maximum number of iterations was set to 30, and the KELM parameter was set to its default value.
Based on the aforementioned parameter settings, the study performed multiple searches for multiple sets of load timing data corresponding to different station load types in order to determine the average optimal combinations of VMD parameters for each load type. The results are presented in Table 1.

Table 1.
VMD parameter combinations.
5.2. VMD Decomposition Results
The decomposition yields the NGO–VMD decomposition results for each load type, as shown in Figure 6.
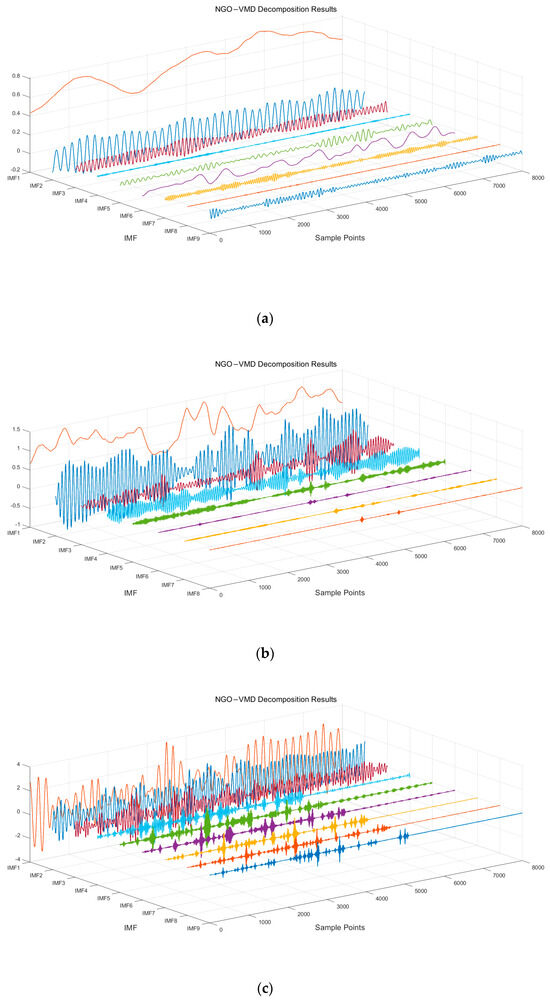
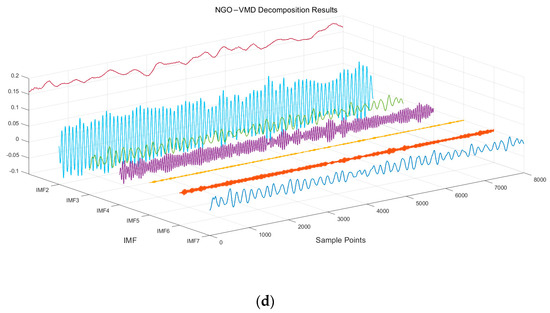
Figure 6.
NGO–VMD decomposition results: (a) industrial type; (b) business type; (c) agricultural production type; (d) residential electricity.
After eliminating the residual terms among the obtained modal components, the IMF1 component can capture the data patterns of different original load types and has the most significant contribution to the overall load prediction results. Whereas the high-frequency components, specifically IMF2 to IMF4, depict the cyclic fluctuation pattern of the electric power load more accurately. These components are separated, predicted individually, and then combined to enhance the overall prediction accuracy.
5.3. Forecast Results
Utilizing the pre-defined SSA–KELM parameters, combined with the multimodal decomposition results from NGO–VMD, the training and test sets are divided in an 8:2 ratio to predict each sub-modal component individually. The prediction results of each sub-modal component are combined to yield the final load sequence prediction. Figure 7 displays the prediction results of the test set:
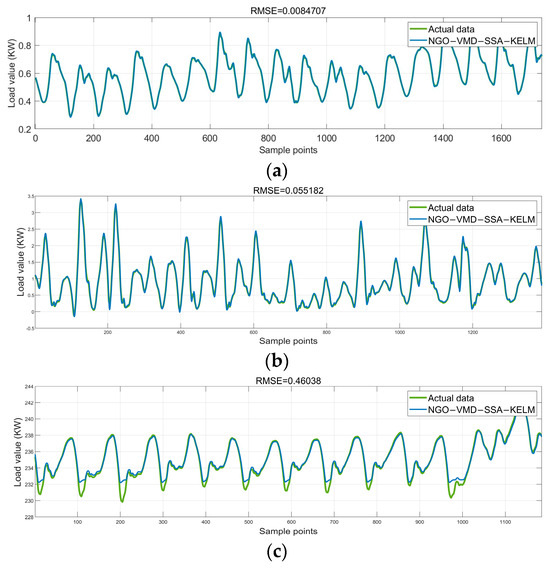
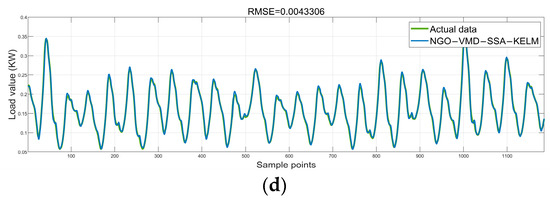
Figure 7.
Forecast results: (a) industrial type; (b) business type; (c) agricultural production type; (d) residential electricity.
The results demonstrate that the proposed model achieves accurate prediction results regardless of the type of electricity consumption or station load data encountered, indicating the universal applicability of the proposed model. To demonstrate the model’s superiority, additional commonly used forecasting models are selected for comparative validation.
5.4. Comparative Verification
LSTM, BP, KELM, and VMD–LSTM network models are established to predict for each set of electric load data to further validate the ability of the NGO−VMD−SSA−KELM algorithm to predict for loads of multiple station types on the demand side and a comparison of the average prediction errors of the five models for load data of different station types of electricity consumption is shown in Table 2:

Table 2.
Accuracy comparison.
Furthermore, the comparison reveals that the predictions of the NGO−VMD−SSA−KELM model exhibit greater accuracy and universality. In summary, the load timing prediction model developed in this study demonstrates a high level of prediction stability and accuracy.
6. Conclusions
This paper proposes a time series prediction model called VMD–KELM, which combines the Northern Goshawk Optimization method with the Sparrow Optimization algorithm. The proposed model provides a highly accurate and versatile load forecasting method for various types of power systems.
1. The NGO and SSA optimization algorithms are employed to intelligently search for parameters in VMD and KELM, reducing the impact of parameter selection on prediction accuracy.
2. By comparing the algorithm’s performance with other popular algorithms such as LSTM, BP, KELM, and VMD–LSTM, using actual load timing data of different power consumption types for simulation verification, it is evident that the proposed algorithm exhibits significant advantages.
3. Despite the potential presence of abnormal events in the actual collected power consumption data, the model exhibits an exceptional ability to generalize and accurately predict load data. The average prediction results for load data in industrial stations yield impressive values of RMSE = 0.0098, MAE = 0.0078, MAPE = 1.3897%, and R2 = 0.9949.
The NGO–VMD-SSA–KELM approach demonstrates high feasibility in addressing load forecasting challenges across multiple stations. Despite challenges in collecting complete load data in practical engineering applications, the prediction method proposed in this study can still facilitate accurate load management for diversified power stations. It enables timely response to load risk events, such as load adjustment, equipment switching, and stand-by plan activation, thereby ensuring the stable operation of the power system.
Author Contributions
Conceptualization, methodology, validation, resources and formal analysis, L.S.; methodology, software, writing—original draft preparation, writing—review and editing, visualization, Y.L.; validation, project administration, funding acquisition, Q.F.; writing—original draft preparation, L.C.; conceptualization, resources, supervision, N.P.; data curation, visualization, J.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Science and Technology Project of China Southern Power Grid Co., Ltd., under Grants YNKJXM20240002, the Technical Reform Project of China Southern Power Grid Co., Ltd., under Grants CG0500022001574137 and the National Key Research and Development Program of China under Grants 2023YFB2407300.
Data Availability Statement
The desensitized data supporting this study’s findings are available from the corresponding author upon reasonable request. The data are not publicly available due to company secrets.
Conflicts of Interest
The authors declare that this study was funded by the above project. The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article or the decision to submit it for publication.
References
- Liu, W.; Li, X.; Chen, R.; Zhu, J. Online emergency demand response mechanism for new power system. Comput. Electr. Eng. 2023, 109, 108746. [Google Scholar] [CrossRef]
- Shi, Q.; Yang, P.; Tang, B.; Lin, J.; Yu, G.; Muyeen, S.M. Active distribution network type identification method of high proportion new energy power system based on source-load matching. Int. J. Electr. Power Energy Syst. 2023, 153, 109411. [Google Scholar] [CrossRef]
- Hong, J.; Liang, F.; Yang, H. Research progress, trends, and prospects of big data technology for new energy power and energy storage system. Energy Rev. 2023, 2, 100036. [Google Scholar] [CrossRef]
- Wang, W.; Yu, T.; Huang, Y.; Han, Y.; Liu, D.; Shen, Y. The situation and suggestions of the new energy power system under the background of carbon reduction in China. Energy Rep. 2021, 7 (Suppl. 7), 1477. [Google Scholar] [CrossRef]
- Esmaeili, M.; Ahmadi, A.; Nateghi, A.; Shafie-khah, M. Robust power management system with generation and demand prediction and critical loads in DC microgrid. J. Clean. Prod. 2023, 384, 135490. [Google Scholar] [CrossRef]
- Cerna, F.; Coêlho, J.; Fantesia, M.P.; Naderi, E.; Marzband, M.; Contreras, J. Load Factor Improvement of the Electricity Grid Considering Distributed Energy Resources Operation and Regulation of Peak Load. Sustain. Cities Soc. 2023, 98, 104802. [Google Scholar] [CrossRef]
- Chen, H.; Zhu, M.; Hu, X.; Wang, J.; Sun, Y.; Yang, J. Research on short-term load forecasting of new-type power system based on GCN-LSTM considering multiple influencing factors. Energy Rep. 2023, 9 (Suppl. 10), 1022–1031. [Google Scholar] [CrossRef]
- Islam, A.; Al-tabatabaie, K.; Karmaker, A.; Hossain, B.; Islam, K. Assessing energy diversification policy and sustainability: Bangladesh standpoints. Energy Strategy Rev. 2022, 40, 100803. [Google Scholar] [CrossRef]
- Gebremeskel, D.; Ahlgren, E.; Beyene, G. Long-term electricity supply modelling in the context of developing countries: The OSeMOSYS-LEAP soft-linking approach for Ethiopia. Energy Strategy Rev. 2023, 45, 101045. [Google Scholar] [CrossRef]
- Wabukala, B.; Bergland, O.; Rudaheranwa, N.; Watundu, S.; Adaramola, M.S.; Ngoma, M.; Rwaheru, A. Unbundling barriers to electricity security in Uganda: A review. Energy Strategy Rev. 2022, 44, 100984. [Google Scholar] [CrossRef]
- Ahmed, E.M.; Rathinam, R.; Dayalan, S.; Fernandez, G.S.; Ali, Z.M.; Abdel Aleem, S.H.E.; Omar, A.I. A Comprehensive Analysis of Demand Response Pricing Strategies in a Smart Grid Environment Using Particle Swarm Optimization and the Strawberry Optimization Algorithm. Mathematics 2021, 9, 2338. [Google Scholar] [CrossRef]
- Dey, B.; Roy, B.; Datta, S.; Ustun, T. Forecasting ethanol demand in India to meet future blending targets: A comparison of ARIMA and various regression models. Energy Rep. 2023, 9, 411–418. [Google Scholar] [CrossRef]
- Lyu, C.; Song, Y.; Yang, D.; Wang, W.; Ge, Y.; Wang, L. Online prediction for heat generation rate and temperature of lithium-ion battery using multi-step-ahead extended Kalman filtering. Appl. Therm. Eng. 2023, 231, 120890. [Google Scholar] [CrossRef]
- Li, D.; Sun, Y.; Sun, J.; Wang, X.; Zhang, X. An advanced approach for the precise prediction of water quality using a discrete hidden markov model. J. Hydrol. 2022, 609, 127659. [Google Scholar] [CrossRef]
- Xiao, F.; Wang, X.; Hou, W.; Zhang, X.; Wang, J. An attention-based Bayesian sequence to sequence model for short-term solar power generation prediction within decomposition-ensemble strategy. J. Clean. Prod. 2023, 416, 137827. [Google Scholar] [CrossRef]
- Xu, N.; Wang, Z.; Dai, Y.; Li, Q.; Zhu, W.; Wang, R.; Finkelman, R. Prediction of higher heating value of coal based on gradient boosting regression tree model. Int. J. Coal Geol. 2023, 274, 104293. [Google Scholar] [CrossRef]
- Han, Y.; Liu, Y.; Lu, S.; Basalike, P.; Zhang, J. Electrical performance and power prediction of a roll-bond photovoltaic thermal array under dewing and frosting conditions. Energy 2021, 237, 121587. [Google Scholar] [CrossRef]
- Yan, Y.; Wang, X.; Ren, F.; Shao, Z.; Tian, C. Wind speed prediction using a hybrid model of EEMD and LSTM considering seasonal features. Energy Rep. 2022, 8, 8965–8980. [Google Scholar] [CrossRef]
- Wu, C.; Li, J.; Liu, W.; He, Y.; Nourmohammadi, S. Short-term electricity demand forecasting using a hybrid ANFIS–ELM network optimised by an improved parasitism–predation algorithm. Appl. Energy 2023, 345, 121316. [Google Scholar] [CrossRef]
- Guo, X.; Zhan, Y.; Zheng, D.; Li, L.; Qi, Q. Research on short-term forecasting method of photovoltaic power generation based on clustering SO-GRU method. Energy Rep. 2023, 9, 786–793. [Google Scholar] [CrossRef]
- Sahu, R.; Shaw, B.; Nayak, J.; Shashikant. Short/medium term solar power forecasting of Chhattisgarh state of India using modified TLBO optimized ELM. Eng. Sci. Technol. Int. J. 2021, 24, 1180–1200. [Google Scholar] [CrossRef]
- Dai, Y.; Yang, X.; Leng, M. Optimized Seq2Seq model based on multiple methods for short-term power load forecasting. Appl. Soft Comput. 2023, 142, 110335. [Google Scholar] [CrossRef]
- Wang, L.; Mao, M.; Xie, J.; Liao, Z.; Zhang, H.; Li, H. Accurate solar PV power prediction interval method based on frequency-domain decomposition and LSTM model. Energy 2023, 262, 125592. [Google Scholar] [CrossRef]
- Wan, A.; Chang, Q.; AL-Bukhaiti, K.; He, J. Short-term power load forecasting for combined heat and power using CNN-LSTM enhanced by attention mechanism. Energy 2023, 282, 128274. [Google Scholar] [CrossRef]
- Morais, L.; Aquila, G.; Faria, V.; Lima, L.; Lima, J.; Queiroz, A. Short-term load forecasting using neural networks and global climate models: An application to a large-scale electrical power system. Appl. Energy 2023, 348, 121439. [Google Scholar] [CrossRef]
- Aseeri, A. Effective RNN-Based Forecasting Methodology Design for Improving Short-Term Power Load Forecasts: Application to Large-Scale Power-Grid Time Series. J. Comput. Sci. 2023, 68, 101984. [Google Scholar] [CrossRef]
- Han, X.; Shi, Y.; Tong, R.; Wang, S.; Zhang, Y. Research on short-term load forecasting of power system based on IWOA-KELM. Energy Rep. 2023, 9, 238–246. [Google Scholar] [CrossRef]
- Wang, J.; Wang, K.; Li, Z.; Lu, H.; Jiang, H. Short-term power load forecasting system based on rough set, information granule and multi-objective optimization. Appl. Soft Comput. 2023, 146, 110692. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, B.; Pan, G.; Zhao, Y. A novel hybrid model based on VMD-WT and PCA-BP-RBF neural network for short-term wind speed forecasting. Energy Convers. Manag. 2019, 195, 180–197. [Google Scholar] [CrossRef]
- Zhao, Z.; Yun, S.; Jia, L.; Guo, J.; Meng, Y.; He, N.; Li, X.; Shi, J.; Yang, L. Hybrid VMD-CNN-GRU-based model for short-term forecasting of wind power considering spatio-temporal features. Eng. Appl. Artif. Intell. 2023, 121, 105982. [Google Scholar] [CrossRef]
- Dehghani, M.; Hubálovský, Š.; Trojovský, P. Northern Goshawk Optimization: A New Swarm-Based Algorithm for Solving Optimization Problems. IEEE Access 2023, 9, 162059–162080. [Google Scholar] [CrossRef]
- Fu, W.; Wang, K.; Tan, J.; Zhang, K. A composite framework coupling multiple feature selection, compound prediction models and novel hybrid swarm optimizer-based synchronization optimization strategy for multi-step ahead short-term wind speed forecasting. Energy Convers. Manag. 2020, 205, 112461. [Google Scholar] [CrossRef]
- Lu, S.; Gao, W.; Hong, C.; Sun, Y. A newly-designed fault diagnostic method for transformers via improved empirical wavelet transform and kernel extreme learning machine. Adv. Eng. Inform. 2021, 49, 101320. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).