Two-Dimensional Geothermal Model of the Peruvian Andes above the Nazca Ridge Subduction
Abstract
:1. Introduction
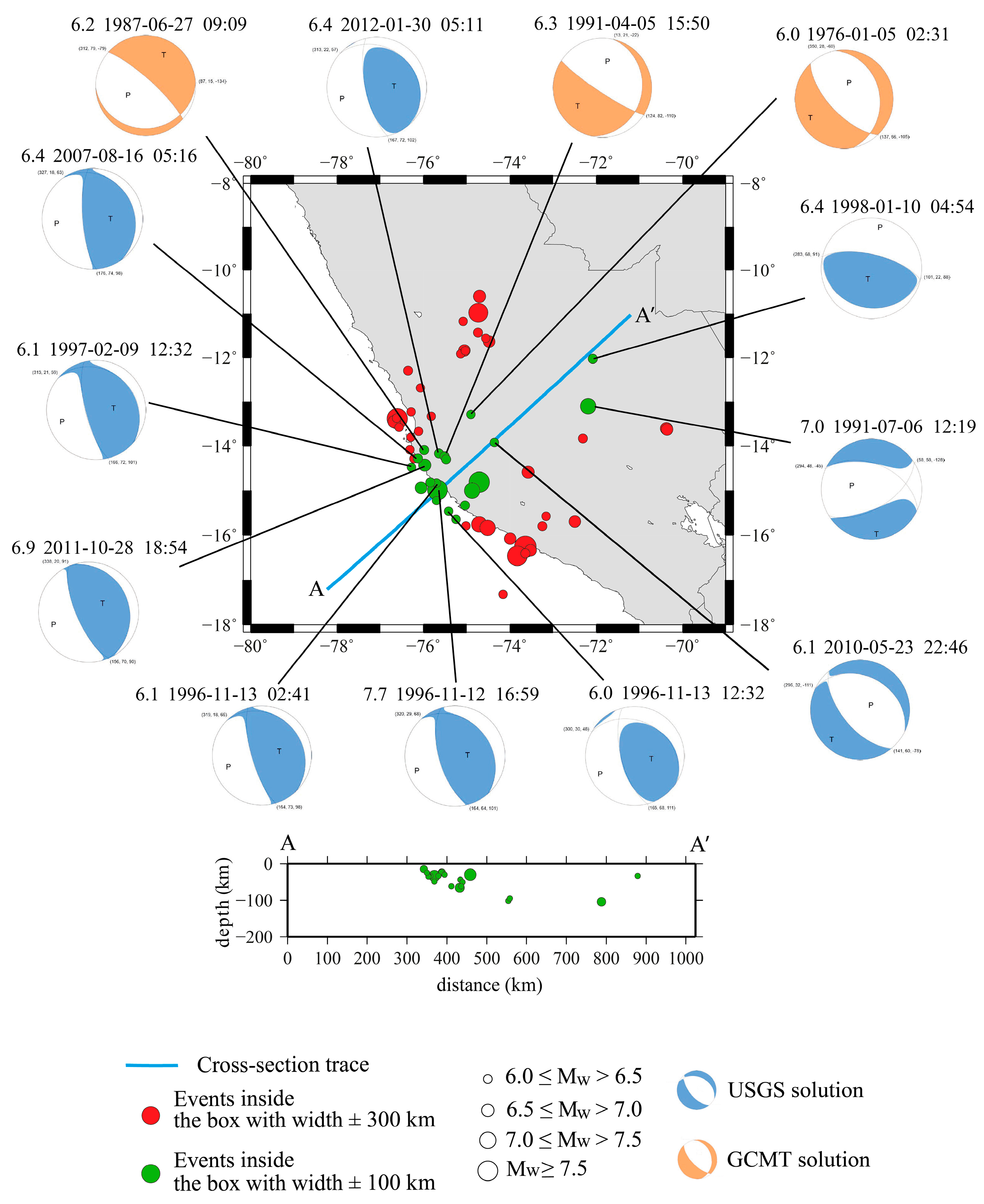
2. Geological Background
3. Materials and Methods
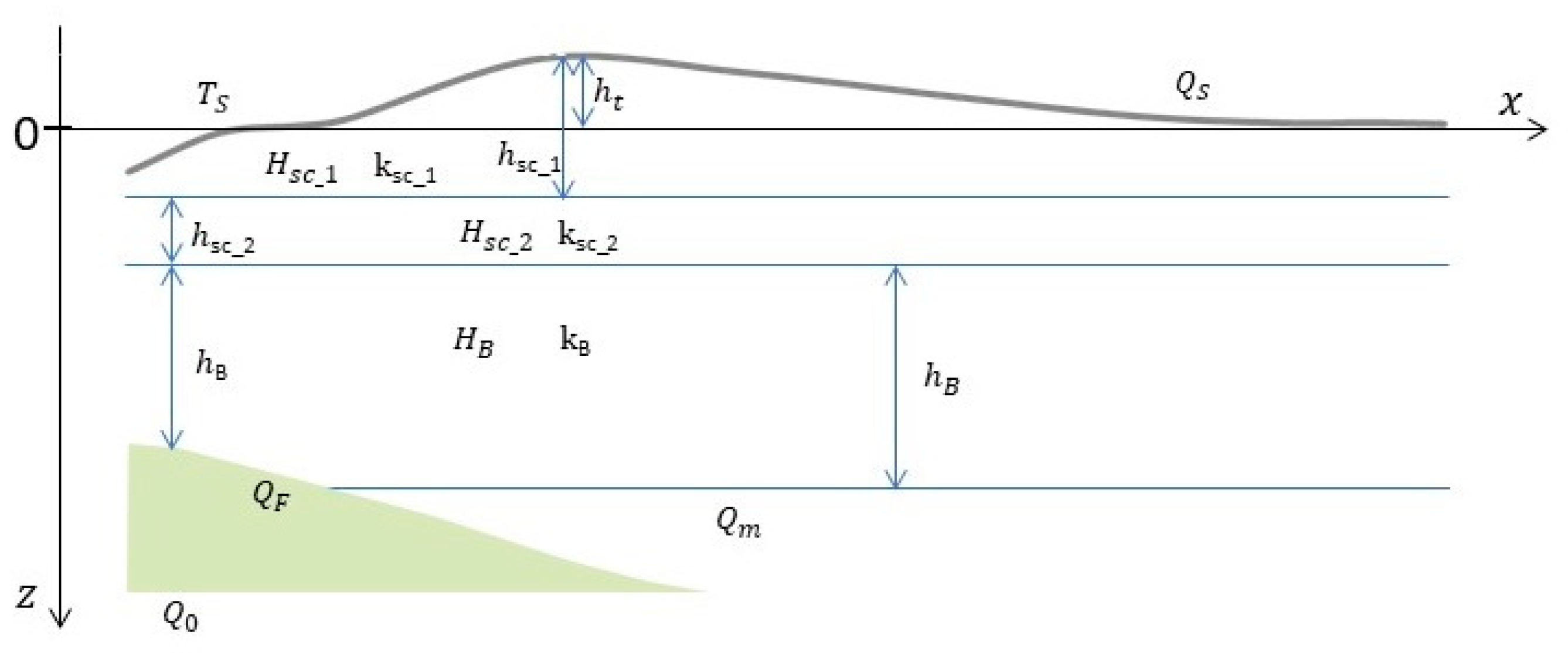
3.1. Lithospheric Model
3.2. Thermal Modelling
| (m) | Ground elevation (negative) or sea depth (positive) related to m.s.l. | |
| (m) | Sedimentary cover (Cenozoic-Mesozoic) thickness | |
| (m) | Sedimentary cover (Paleozoic) thickness | |
| (m) | Basement thickness | |
| RHP * of sedimentary cover (Cenozoic-Mesozoic) | [36] | |
| RHP * of sedimentary cover (Paleozoic) | [36] | |
| RHP * of basement thickness | [36] | |
| Thermal conductivity of sedimentary cover (Cenozoic-Mesozoic) | [42] | |
| Thermal conductivity of sedimentary cover (Paleozoic) | [42] | |
| Thermal conductivity of the basement | [42] | |
| Thermal diffusivity | [43] | |
| Coefficient of static friction | [43] | |
| Density of sedimentary cover (Cenozoic-Mesozoic) | [44] | |
| Density of sedimentary cover (Paleozoic) | [44] | |
| Density of the basement | [44] | |
| Depth scale | [45] | |
| Horizontal coordinate for points on the megathrust fault | ||
| Vertical coordinate for points on the megathrust fault | ||
| Dip angle of the megathrust fault | ||
| Pore fluid factor | [46] | |
| Relative plate velocity | [46] | |
| Fritional heat flow density | ||
| Oceanic heat flow density from the mantle | [47] | |
| Continental heat flow density from the mantle | [47] | |
| ) | Surface heat flow density | |
| Surface temperature |
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Woods, M.T.; Okal, E.A. The structure of the Nazca ridge and Sala y Gomez seamount chain from the dispersion of Rayleigh waves. Geophys. J. Int. 1994, 117, 205–222. [Google Scholar] [CrossRef]
- Macharé, J.; Ortlieb, L. Plio-Quaternary vertical motions and the subduction of the Nazca Ridge, central coast of Peru. Tectonophysics 1992, 205, 97–108. [Google Scholar] [CrossRef]
- Hampel, A. The migration history of the Nazca Ridge along the Peruvian active margin: A re-evaluation. Earth Planet. Sci. Lett. 2002, 203, 665–679. [Google Scholar] [CrossRef]
- Zeumann, S.; Hampel, A. Deformation of erosive and accretive forearcs during subduction of migrating and non-migrating aseismic ridges: Results from 3-D finite element models and application to the Central American, Peruvian, and Ryukyu margins. Tectonics 2015, 34, 1769–1791. [Google Scholar] [CrossRef]
- Li, C.; Clark, A.L. Tectonic effects of the subducting Nazca Ridge on the southern Peru continental margin. Mar. Pet. Geol. 1994, 11, 575–586. [Google Scholar]
- Hagen, R.A.; Moberly, R. Tectonic effects of a subducting aseismic ridge: The subduction of the Nazca Ridge at the Peru Trench. Mar. Geophys. Res. 1994, 16, 145–161. [Google Scholar] [CrossRef]
- Gutscher, M.A. Andean subduction styles and their effect on thermal structure and interplate coupling. J. South Am. Earth Sci. 2002, 15, 3–10. [Google Scholar] [CrossRef]
- Hampel, A.; Kukowski, N.; Bialas, J.; Huebscher, C.; Heinbockel, R. Ridge subduction at an erosive margin: The collision zone of the Nazca Ridge in southern Peru. J. Geophys. Res. Solid Earth 2004, 109, B02101. [Google Scholar] [CrossRef]
- Antonijevic, S.K.; Wagner, L.S.; Kumar, A.; Beck, S.L.; Long, M.D.; Zandt, G.; Tavera, H.; Condori, C. The role of ridges in the formation and longevity of flat slabs. Nature 2015, 524, 212–215. [Google Scholar] [CrossRef]
- Flórez-Rodríguez, A.G.; Schellart, W.P.; Strak, V. Impact of aseismic ridges on subduction systems: Insights from analog modeling. J. Geophys. Res. Solid Earth 2019, 124, 5951–5969. [Google Scholar] [CrossRef]
- Kumar, A.; Wagner, L.S.; Beck, S.L.; Long, M.D.; Zandt, G.; Young, B.; Tavera, H.; Minaya, E. Seismicity and state of stress in the central and southern Peruvian flat slab. Earth Planet. Sci. Lett. 2016, 441, 71–80. [Google Scholar] [CrossRef]
- Dragoni, M.; Doglioni, C.; Mongelli, F.; Zito, G. Evaluation of Stresses in Two Geodynamically Different Areas: Stable Foreland and Extensional Backarc. Pure Appl. Geophys. 1996, 146, 319–341. [Google Scholar] [CrossRef]
- Basilici, M.; Mazzoli, S.; Megna, A.; Santini, S.; Tavani, S. 3-D Geothermal Model of the Lurestan Sector of the Zagros Thrust Belt, Iran. Energies 2020, 13, 2140. [Google Scholar] [CrossRef]
- Santini, S.; Basilici, M.; Invernizzi, C.; Mazzoli, S.; Megna, A.; Pierantoni, P.P.; Spina, V.; Teloni, S. Thermal Structure of the Northern Outer Albanides and Adjacent Adriatic Crustal Sector, and Implications for Geothermal Energy Systems. Energies 2020, 13, 6028. [Google Scholar] [CrossRef]
- Santini, S.; Basilici, M.; Invernizzi, C.; Jablonska, D.; Mazzoli, S.; Megna, A.; Pierantoni, P.P. Controls of Radiogenic Heat and Moho Geometry on the Thermal Setting of the Marche Region (Central Italy): An Analytical 3D Geothermal Model. Energies 2021, 14, 6511. [Google Scholar] [CrossRef]
- Uyeda, S.; Watanabe, T.; Ozasayama, Y.; Ibaragi, K. Report of heat flow measurements in Peru and Ecuador. Bull. Earthq. Res. Inst 1980, 55, 55–74. [Google Scholar]
- Henry, S.G.; Pollack, H.N. Terrestrial heat flow above the Andean subduction zone in Bolivia and Peru. J. Geophys. Res. Solid Earth 1988, 93, 15153–15162. [Google Scholar] [CrossRef]
- Molnar, P.; England, P. Temperatures, heat flux, and frictional stress near major thrust faults. J. Geophys. Res. Solid Earth 1990, 95, 4833–4856. [Google Scholar] [CrossRef]
- Ramos, V.A.; Aleman, A. Tectonic evolution of the Andes. In Tectonic Evolution of South America, Proceeding of the 31st International Geological Congress, Rio de Janeiro, Brazil, 6–17 August 2000; Cordani, U.G., Milani, E.J., Filho, A.T., Campos, A.D., Eds.; Geological Society: London, UK, 2000; pp. 635–685. [Google Scholar]
- Sempere, T.; Folguera, A.; Gerbault, M. New insights into Andean evolution: An introduction to contributions from the 6th ISAG symposium (Barcelona, 2005). Tectonophysics 2008, 459, 1–13. [Google Scholar] [CrossRef]
- Mégard, F.; Schaer, J.; Rodgers, J. Structure and evolution of the Peruvian Andes. In The Anatomy of Mountain Ranges; Schaer, J.-P., Rodgers, J., Eds.; Princeton University Press: Princeton, NJ, USA, 1987; pp. 179–210. [Google Scholar]
- Kulm, L.D.; Thornburg, T.M.; Schrader, H.J.; Resig, J.M. Cenozoic structure, stratigraphy and tectonics of the central Peru forearc. Geol. Soc. Lond. Spec. Publ. 1982, 10, 151–169. [Google Scholar] [CrossRef]
- Scherrenberg, A.F.; Holcombe, R.J.; Rosenbaum, G. The persistence and role of basin structures on the 3D architecture of the Marañón Fold-Thrust Belt, Peru. J. South Am. Earth Sci. 2014, 51, 45–58. [Google Scholar] [CrossRef]
- Sempere, T.; Carlier, G.; Soler, P.; Fornari, M.; Carlotto, V.; Jacay, J.; Arispe, O.; Néraudeau, D.; Cárdenas, J.; Rosas, S.; et al. Late Permian–Middle Jurassic lithospheric thinning in Peru and Bolivia, and its bearing on Andean-age tectonics. Tectonophysics 2002, 345, 153–181. [Google Scholar] [CrossRef]
- Bishop, B.T.; Beck, S.L.; Zandt, G.; Wagner, L.S.; Long, M.D.; Tavera, H. Foreland uplift during flat subduction: Insights from the Peruvian Andes and Fitzcarrald Arch. Tectonophysics 2018, 731, 73–84. [Google Scholar] [CrossRef]
- Espurt, N.; Baby, P.; Brusset, S.; Roddaz, M.; Hermoza, W.; Regard, V.; Antoine, P.O.; Salas-Gismondi, R.; Bolanos, R. How does the Nazca Ridge subduction influence the modern Amazonian foreland basin? Geology 2007, 35, 515–518. [Google Scholar] [CrossRef]
- Van der Meijde, M.; Julià, J.; Assumpção, M. Gravity derived Moho for South America. Tectonophysics 2013, 609, 456–467. [Google Scholar] [CrossRef]
- Scire, A.; Zandt, G.; Beck, S.; Long, M.; Wagner, L.; Minaya, E.; Tavera, H. Imaging the transition from flat to normal subduction: Variations in the structure of the Nazca slab and upper mantle under southern Peru and northwestern Bolivia. Geophys. J. Int. 2016, 204, 457–479. [Google Scholar] [CrossRef]
- Bishop, B.T.; Beck, S.L.; Zandt, G.; Wagner, L.; Long, M.; Antonijevic, S.K.; Kumar, A.; Tavera, H. Causes and consequences of flat-slab subduction in southern Peru. Geosphere 2017, 13, 1392–1407. [Google Scholar] [CrossRef]
- Scire, A.; Zandt, G.; Beck, S.; Long, M.; Wagner, L. The deforming Nazca slab in the mantle transition zone and lower mantle: Constraints from teleseismic tomography on the deeply subducted slab between 6 S and 32 S. Geosphere 2017, 13, 665–680. [Google Scholar] [CrossRef]
- Hayes, G.P.; Moore, G.L.; Portner, D.E.; Hearne, M.; Flamme, H.; Furtney, M.; Smoczyk, G.M. Slab2, a comprehensive subduction zone geometry model. Science 2018, 362, 58–61. [Google Scholar] [CrossRef]
- Contreras-Reyes, E.; Muñoz-Linford, P.; Cortés-Rivas, V.; Bello-González, J.P.; Ruiz, J.A.; Krabbenhoeft, A. Structure of the collision zone between the Nazca Ridge and the Peruvian convergent margin: Geodynamic and seismotectonic implications. Tectonics 2019, 38, 3416–3435. [Google Scholar] [CrossRef]
- USGS.gov. Science for a Changing World. Available online: https://www.usgs.gov/ (accessed on 29 June 2023).
- Pfiffner, O.A.; Gonzalez, L. Mesozoic–Cenozoic evolution of the western margin of South America: Case study of the Peruvian Andes. Geosciences 2013, 3, 262–310. [Google Scholar] [CrossRef]
- Di Celma, C.; Pierantoni, P.P.; Volatili, T.; Molli, G.; Mazzoli, S.; Sarti, G.; Ciattoni, S.; Bosio, G.; Malinverno, E.; Collareta, A.; et al. Towards deciphering the Cenozoic evolution of the East Pisco Basin (southern Peru). J. Maps 2022, 18, 397–412. [Google Scholar] [CrossRef]
- Vilà, M.; Fernández, M.; Jiménez-Munt, I. Radiogenic heat production variability of some common lithological groups and its significance to lithospheric thermal modeling. Tectonophysics 2010, 490, 152–164. [Google Scholar] [CrossRef]
- Global CMT Catalog. Available online: https://www.globalcmt.org (accessed on 29 June 2023).
- Valdenegro, P.; Muñoz, M.; Yáñez, G.; Parada, M.A.; Morata, D. A model for thermal gradient and heat flow in central Chile: The role of thermal properties. J. South Am. Earth Sci. 2019, 91, 88–101. [Google Scholar] [CrossRef]
- Luo, T.; Leng, W. Thermal structure of continental subduction zone: High temperature caused by the removal of the preceding oceanic slab. Earth Planet. Phys. 2021, 5, 290–295. [Google Scholar] [CrossRef]
- Molnar, P.; Chen, W.P.; Padovani, E. Calculated temperatures in overthrust terrains and possible combinations of heat sources responsible for the tertiary granites in the greater Himalaya. J. Geophys. Res. 1983, 88, 6415–6429. [Google Scholar]
- Megna, A.; Candela, S.; Mazzoli, S.; Santini, S. An analytical model for the geotherm in the Basilicata oil fields area (southern Italy). Ital. J. Geosci. 2014, 133, 204–213. [Google Scholar] [CrossRef]
- Cermak, V.; Rybach, L. Thermal Conductivity and Specific Heat of Mineral and Rocks. In Landolt–Bornstein: Numerical Data and Functional Relationships in Science and Technology, Physical Properties of Rocks; Angenheister, G., Ed.; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1982; Volume 1, pp. 305–343. [Google Scholar]
- Dragoni, M.; Santini, S. Contribution of the 2010 Maule Megathrust Earthquake to the Heat Flow at the Peru-Chile Trench. Energies 2022, 15, 2253. [Google Scholar] [CrossRef]
- Rodriguez Piceda, C.; Scheck Wenderoth, M.; Gomez Dacal, M.L.; Bott, J.; Prezzi, C.B.; Strecker, M.R. Lithospheric density structure of the southern Central Andes constrained by 3D data-integrative gravity modeling. Int. J. Earth Sci. 2021, 110, 2333–2359. [Google Scholar] [CrossRef]
- Cermak, V.; Haenel, R. Geothermal maps. In Handbook of Terrestrial Heat-Flow Density Determination; Haenel, R., Rybach, L., Stegena, L., Eds.; Kluwer: Dordrecht, The Netherlands, 1988; pp. 261–300. [Google Scholar]
- Seno, T. Determination of the pore fluid pressure ratio at seismogenic megathrusts in subduction zones: Implications for strength of asperities and Andean-type Mountain building. J. Geophys. Res. 2009, 114, B05405. [Google Scholar] [CrossRef]
- Hamza, V.M.; Vieira, F.P. Global distribution of the lithosphere-asthenosphere boundary: A new look. Solid Earth 2012, 3, 199–212. [Google Scholar] [CrossRef]
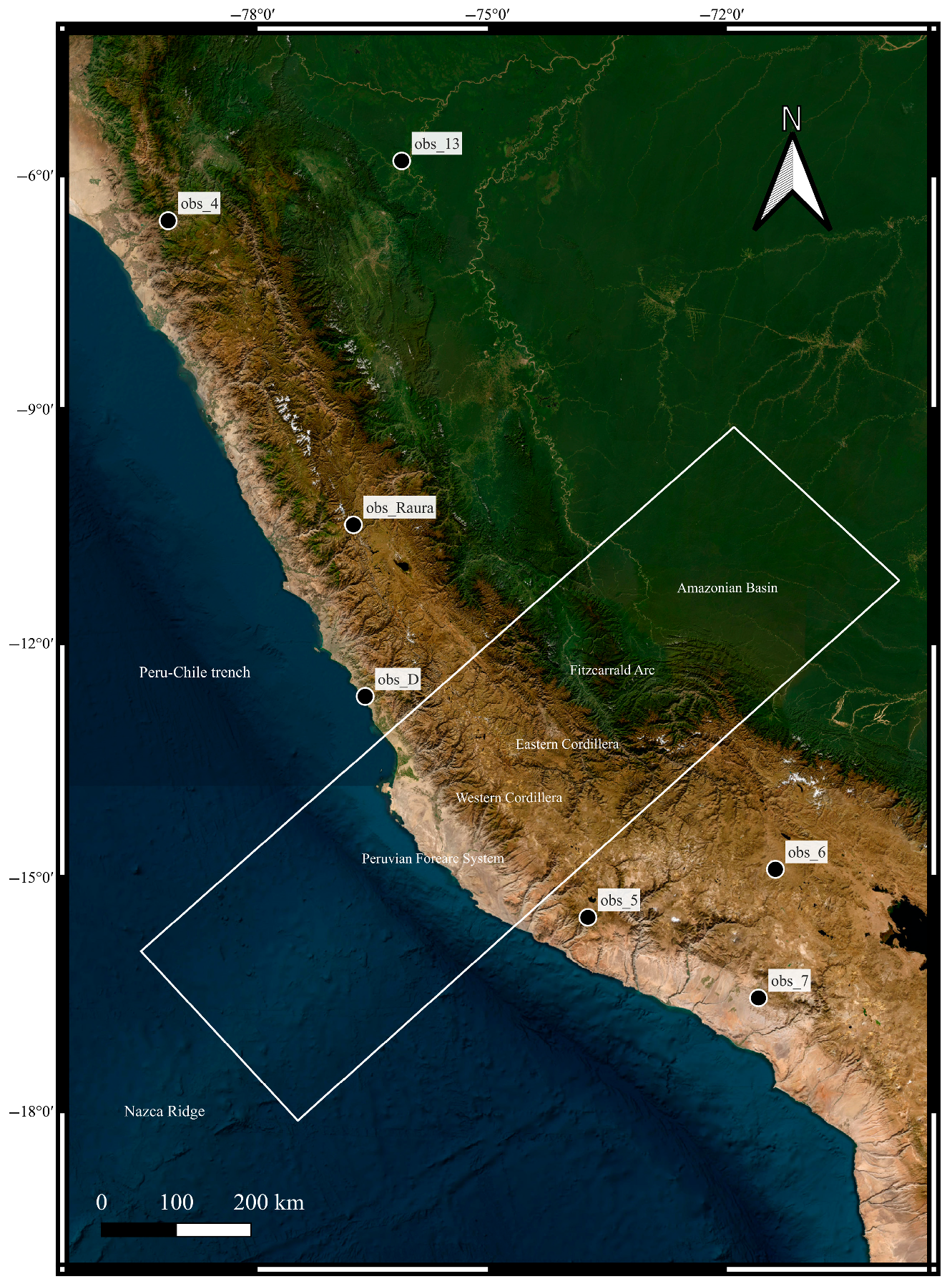



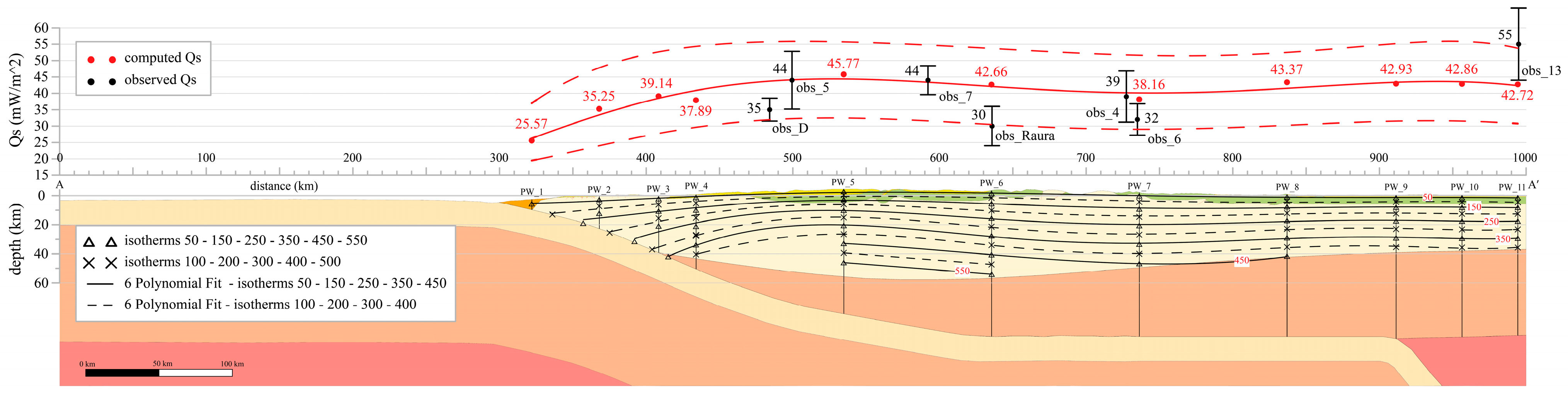
| Acronym | Site Name | S Lat | W Long | Observed Qs (mW/m2) | |
|---|---|---|---|---|---|
| obs_Raura | Raura | 10°29′ | 76°45′ | 30 ± 6.0 | [16] |
| obs_D | Condestable | 12°41′ | 76°36′ | 35 ± 3.5 | [17] |
| obs_4 | La Granja | 6°35′ | 79°07′ | 39 ± 7.8 | [17] |
| obs_5 | Marcahui | 15°31′ | 73°45′ | 44 ± 8.8 | [17] |
| obs_6 | Tintaya | 14°54′ | 71°21′ | 32 ± 4.8 | [17] |
| obs_7 | Cerro Verde | 16°33′ | 71°34′ | 44 ± 4.4 | [17] |
| obs_13 | Yurimaguas | 5°49′ | 76°08′ | 55 ±11.0 | [17] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ciattoni, S.; Mazzoli, S.; Megna, A.; Basilici, M.; Santini, S. Two-Dimensional Geothermal Model of the Peruvian Andes above the Nazca Ridge Subduction. Energies 2023, 16, 7697. https://doi.org/10.3390/en16237697
Ciattoni S, Mazzoli S, Megna A, Basilici M, Santini S. Two-Dimensional Geothermal Model of the Peruvian Andes above the Nazca Ridge Subduction. Energies. 2023; 16(23):7697. https://doi.org/10.3390/en16237697
Chicago/Turabian StyleCiattoni, Sara, Stefano Mazzoli, Antonella Megna, Matteo Basilici, and Stefano Santini. 2023. "Two-Dimensional Geothermal Model of the Peruvian Andes above the Nazca Ridge Subduction" Energies 16, no. 23: 7697. https://doi.org/10.3390/en16237697
APA StyleCiattoni, S., Mazzoli, S., Megna, A., Basilici, M., & Santini, S. (2023). Two-Dimensional Geothermal Model of the Peruvian Andes above the Nazca Ridge Subduction. Energies, 16(23), 7697. https://doi.org/10.3390/en16237697






