1. Introduction
Taiwan is located between 22° N and 25° N latitudes, making it close to the equator, and thus, it has a smaller solar angle deviation. Its advantageous geographical location provides stable sunshine, making Taiwan highly suitable for solar power development. However, Taiwan relies heavily on imported fossil fuels such as oil, coal, and natural gas, accounting for up to 92% of its energy sources, while renewable energy currently only contributes 5.5% of the total electricity generation. Within this renewable energy mix, as of 2021, solar photovoltaic power accounts for 64.8%, wind power 10.7%, and other sources, such as hydroelectric and geothermal power, make up 24.5% [
1]. Therefore, the more efficient development of solar energy generation has the potential to increase energy efficiency and enhance power supply reliability.
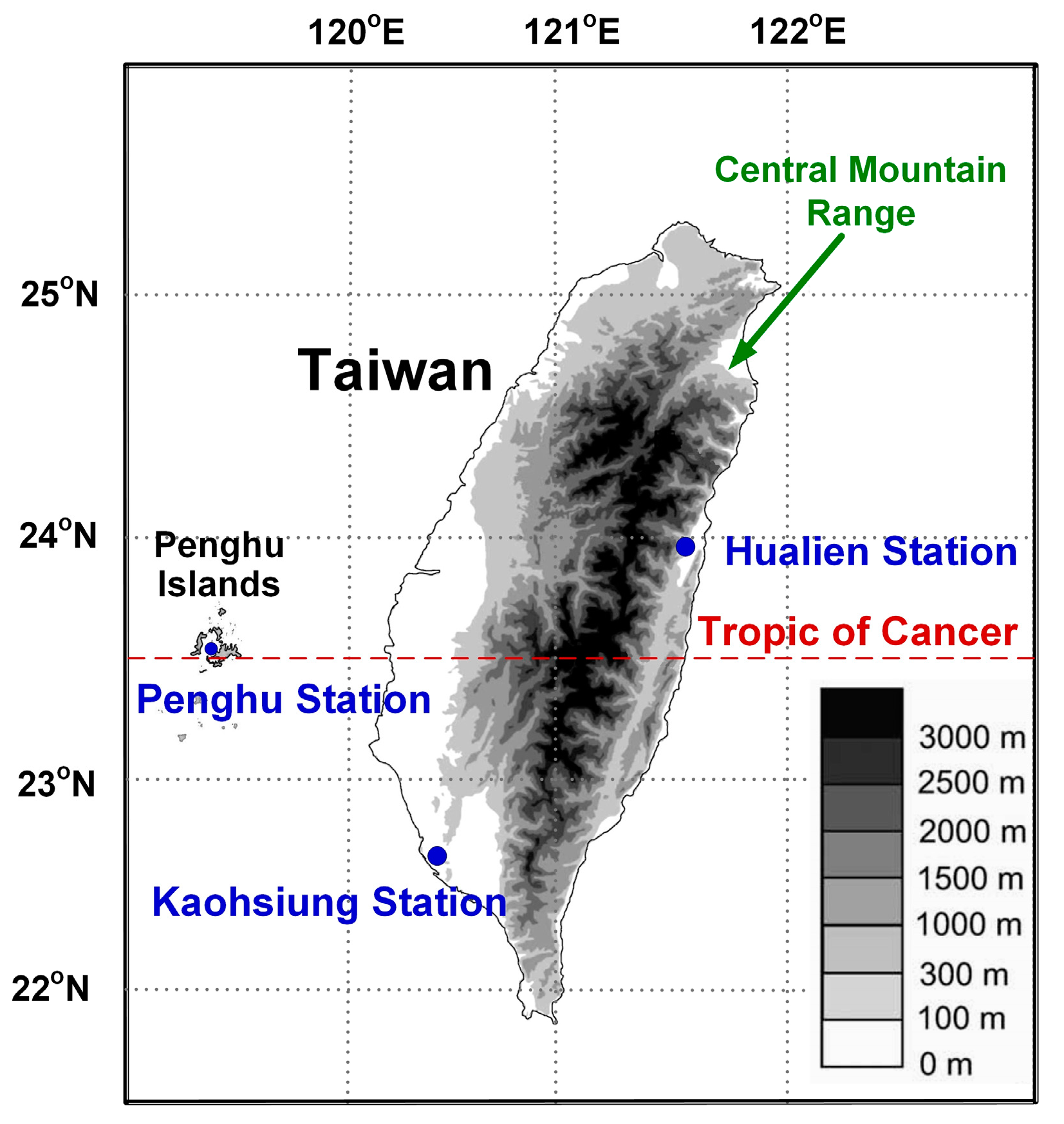
In Taiwan, the development of solar energy generation needs to take into account factors such as the angle and timing of sunlight, cloud cover, and topographical features. As a result, the energy received from solar radiation varies slightly across different regions, for example, in the southern part of Taiwan, at Kaohsiung Station (120.32° E, 22.57° N), in the eastern region at Hualien Station (121.61° E, 23.98° N), and on the outlying Penghu Islands at Penghu Station (119.56° E, 23.57° N)—as shown in
Figure 1.
Geographically, Kaohsiung Station is located south of the Tropic of Cancer, Hualien Station is situated north of the Tropic of Cancer, and Penghu Station is located approximately on the Tropic of Cancer. Regarding topographical conditions, as shown in
Figure 1, the average elevation of the Central Mountain Range (CMR) in Taiwan is about 2500 m [
2]. The CMR divides Taiwan into two regions, with Hualien Station to the right of the CMR and Kaohsiung Station to the left. According to Taipower [
1], the solar photovoltaic electricity generation at these three meteorological stations in 2020 was 3.41, 2.85, and 3.60 kWh-d, respectively. Although these three locations are geographically close, there is a significant difference in their solar energy generation capacity.
In recent years, due to the flourishing development of machine learning, the accuracy of climate prediction has significantly improved [
3,
4,
5,
6,
7,
8,
9]. Lauret et al. [
10] used a model to predict solar radiation in island environments and proposed the use of machine learning models to enhance the performance of linear regression models. They also suggested that machine learning performs better in less stable weather conditions. Wei [
11] studied various machine learning models, such as multilayer perceptron and random forest, to analyze solar energy predictions for meteorological stations in southern Taiwan. The study compared the influence of input data from satellites, ground stations, and solar angle data on predictions. Additionally, it calculated the optimal placement angle for solar panels based on hourly solar angle data to maximize solar energy generation efficiency. Voyant et al. [
12] also utilized various machine learning methods to predict solar radiation for the next 1–6 h. The study compared methods such as random forest, Gaussian processes, persistence, artificial neural networks, and support vector regressions to assess their strengths and weaknesses. The authors suggested that there is no one-size-fits-all best model, and combining multiple models in a hybrid prediction system yields superior results. Wei [
13] conducted research on the application of deep neural networks to predict solar radiation. The study compared the results of backpropagation neural networks and linear regression. It also examined the impacts of different types of solar panels on electricity generation efficiency. Ali et al. [
14] optimized the design of artificial neural networks for accurate global solar radiation forecasting while minimizing computational requirements. This paper reports on a new hybrid deep residual learning and gated long–short-term memory recurrent network boosted via a differential covariance matrix adaptation evolution strategy (ADCMA) to forecast solar radiation one hour ahead. Neshat et al. [
15] reported on a hybrid deep residual learning and gated long–short-term memory recurrent network boosted by a differential covariance matrix adaptation evolution strategy to forecast solar radiation one hour ahead.
In recent years, the recurrent neural network (RNN) architecture, which has been thriving, has found widespread applications in various fields [
16,
17,
18,
19,
20,
21,
22,
23]. Qing and Niu [
24] proposed the use of long–short-term memory neural networks (LSTMs) to predict solar radiation and compared the results with linear regression and backpropagation neural networks. Ultimately, they reported a 42.9% reduction in the root mean square error (RMSE) for the LSTM networks compared to backpropagation neural networks in predicting solar radiation. Li et al. [
25] utilized a prediction model based on RNNs to forecast the short-term output power of a generating system. This model took only electrical data as an input, without weather information, and they compared its performance within a 90-min horizon against BPNN, persistence, SVM, LSTM, and other methods. In recent times, many scholars have proposed the application of LSTM neural networks to predict weather changes. It has been noted in the literature that most of these studies have achieved favorable forecasting results. Therefore, in this study, to enhance the accuracy of predicting long-term outcomes, the decision was made to incorporate the LSTM neural network model.
Ghofrani et al. [
26] used a clustering approach to improve the performance of Bayesian neural networks and introduced an innovative, game-theoretic, self-organizing map (SOM) clustering method. They incorporated game theory to enhance the clustering effectiveness of the basic SOM clustering method. They also compared the results of Windows NT clustering, k-means clustering, and SOM clustering with machine-learning-derived predictions. Azimi et al. [
27] proposed a k-means cluster-based algorithm to enhance the predictive performance of multilayer perceptrons. Their approach altered the initialization method of the k-means clustering algorithm to ensure consistent results each time it is trained, referred to as TB k-means. They assessed the performance of different data analysis clustering algorithms and compared the processing time required for training with different feature data. Ultimately, they suggested that this clustering approach provides better predictive results compared to directly using multilayer perceptrons.
The purpose of this study is to establish a solar radiation prediction model to accurately predict solar radiation levels. Given that solar radiation prediction is a time series problem with highly nonlinear characteristics, this research employed various algorithmic techniques, including both unsupervised and supervised algorithms, to effectively construct suitable localized prediction models. With supervised-based algorithms, this study utilized deep neural networks (DNN) and LSTM neural networks. The selection of specific deep learning models, namely DNN and LSTM, was guided by several considerations. Firstly, these models have demonstrated robust performance in similar tasks, as evidenced by studies such as [
17,
18,
21,
25]. Their architectures are well suited for effectively learning intricate patterns within our dataset, aligning with the complexity of the problem we aimed to address. Additionally, for unsupervised-based algorithms, clustering methods such as k-means clustering and fuzzy C-means clustering were employed. After clustering, subsets of data were created for each cluster, and neural-network-based prediction models were established for each group. Consequently, under the DNN model, we could establish a k-means DNN (referred to as k_DNN) and a fuzzy C-means DNN (fc_DNN). Similarly, under the LSTM model, we could create a k-means LSTM (k_LSTM) and a fuzzy C-means LSTM (fc_LSTM).
2. Study Area and Material
This study was conducted in Taiwan with test locations at Kaohsiung Station, Hualien Station, and Penghu Station (
Figure 1). The research collected ten ground-level climate parameters related to solar radiation, including atmospheric pressure, surface temperature, dew temperature, relative humidity, water vapor, average wind speed, precipitation, rainfall duration, insolation duration, and global solar radiation. The above climate parameters have been suggested for use in predictive models in many studies, such as [
28,
29,
30,
31]. Therefore, we collected data on these meteorological factors as features for predicting solar radiation. The data source for these parameters was the Central Weather Administration (CWA), and the data were recorded at an hourly frequency. The data span from 1993 to 2021, totaling 29 years, resulting in a total of 254,184 hourly records.
Table 1 presents the attributes, along with their respective units and statistical values.
According to [
11,
32,
33], the addition of solar angle parameters can be used to improve the prediction of global solar radiation. Therefore, this study included five solar angle parameters, namely the declination angle, hour angle, zenith angle, elevation angle, and azimuth angle [
33]. Firstly, the declination angle (
δ) is the angle between the line connecting the Sun and the center of the Earth and the plane of the equator. The formula for this angle is as follows:
The hour angle (
ω) represents the angle at which the Sun moves relative to the position of the station per hour, and it can be calculated as follows:
The zenith angle (
θ) is the angle between the Sun and the vertical line to the horizontal plane, and it can be calculated using the following formula:
The elevation angle (
α) is the angle between the line connecting the Sun to the observation point and the horizontal plane.
The azimuth angle (
ξ) is the angle between the Sun’s position in its orbit and the horizontal plane. It can be calculated using the following formula:
In Equations (1)–(5) mentioned above: nd represents the day of the year, ranging from 1 to a maximum of 365; H represents the hour of the day when the angle is calculated, ranging from 1 to 24 h; and λ denotes the latitude of the test location.
3. A Real-Time Prediction System
As predicting solar radiation cannot guarantee that a single model will provide the best forecast [
12], this study established a real-time solar radiation prediction system. It aimed to integrate simulation results from different models, following the concept of an ensemble model to jointly determine the optimal solution.
Figure 2 illustrates the real-time prediction concept process designed for this study. The simulation interval was 1 h, and the solar radiation forecast horizon ranged from 1 to 12 h. The steps are described as follows:
- (1)
At sunrise, set the time as t;
- (2)
Receive the real-time ground weather data;
- (3)
Generate model input patterns, including the global solar radiation attribute {S}, weather attributes {W}, and solar position attributes {P}. The dataset {P} {δ, ω, θ, α, ξ} can be derived from Equations (1)–(5);
- (4)
Execute a model selection ensemble tabular (abbreviated as MSET);
- (5)
Retrieve the set of optimal suggested neural-network-based models from the MSET lookup table for the future at 1 to 12 h;
- (6)
Is it necessary to execute clustering models based on the suggested neural network-based models? If “yes”, proceed to Step 7; if “no”, continue with Step 9;
- (7)
Calculate the distances between a current sample and cluster centers for cluster models;
- (8)
Execute the cluster-based models (i.e., k_DNN, fc_DNN, k_LSTM, and fc_LSTM) and generate 1–12 h predictions;
- (9)
Execute the DNN and LSTM models and generate 1–12 h predictions;
- (10)
Generate a set of suggested neural-network-based models for 1 to 12 h in the future;
- (11)
Is it sunset? If “yes”, conclude the analysis procedure (Step 12); if “no”, return to Step 2 and set the time to t + 1.
In Step 4, the lookup table from MSET was used to determine the optimal model for real-time predictions at each forecasting time (1 to 12 h). Compared to having a single model decide the forecast, the collaborative decision of all models could enhance accuracy. In steps 8 and 9, the methods for establishing each model are explained as follows.
3.1. Supervised Models
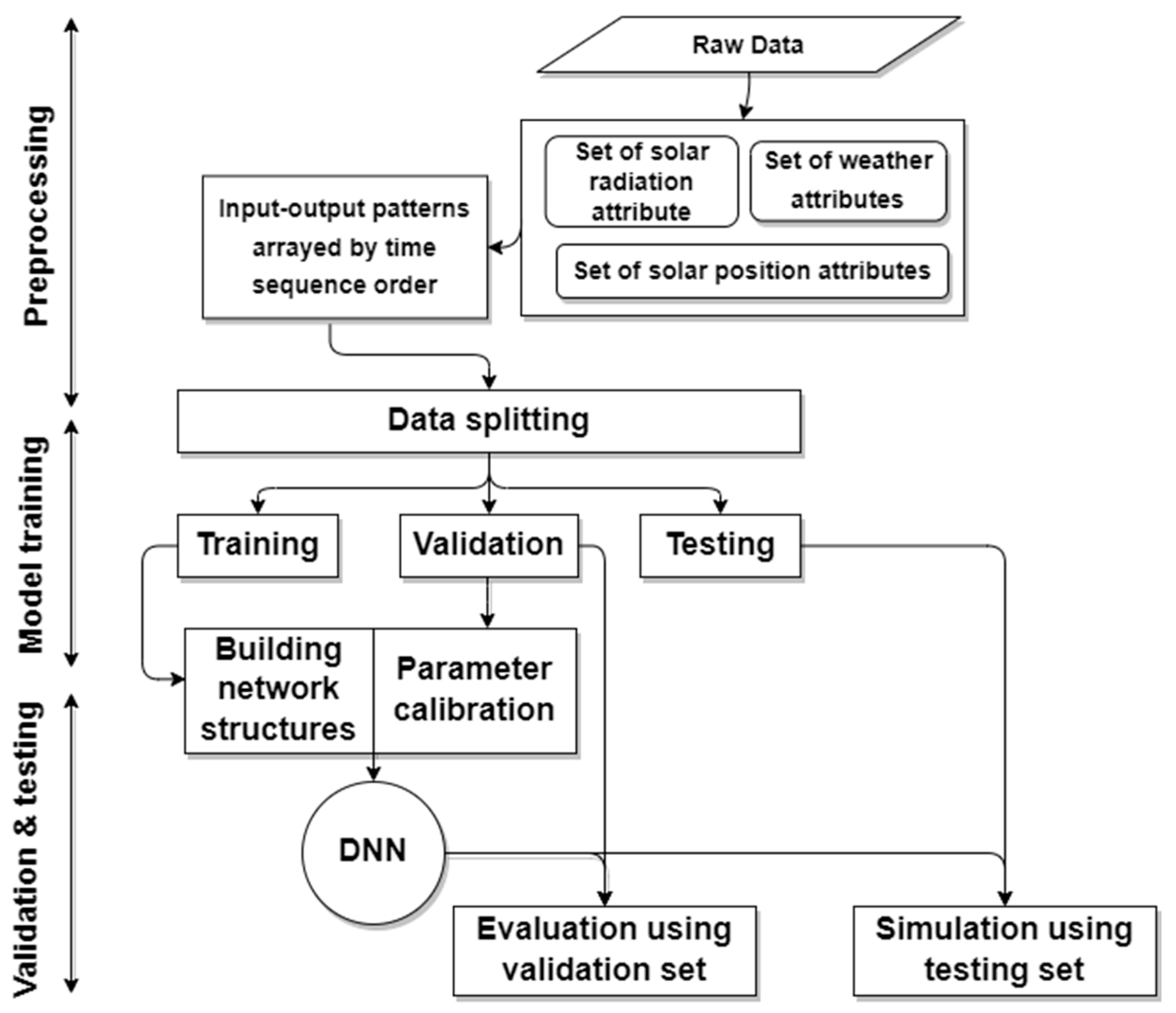
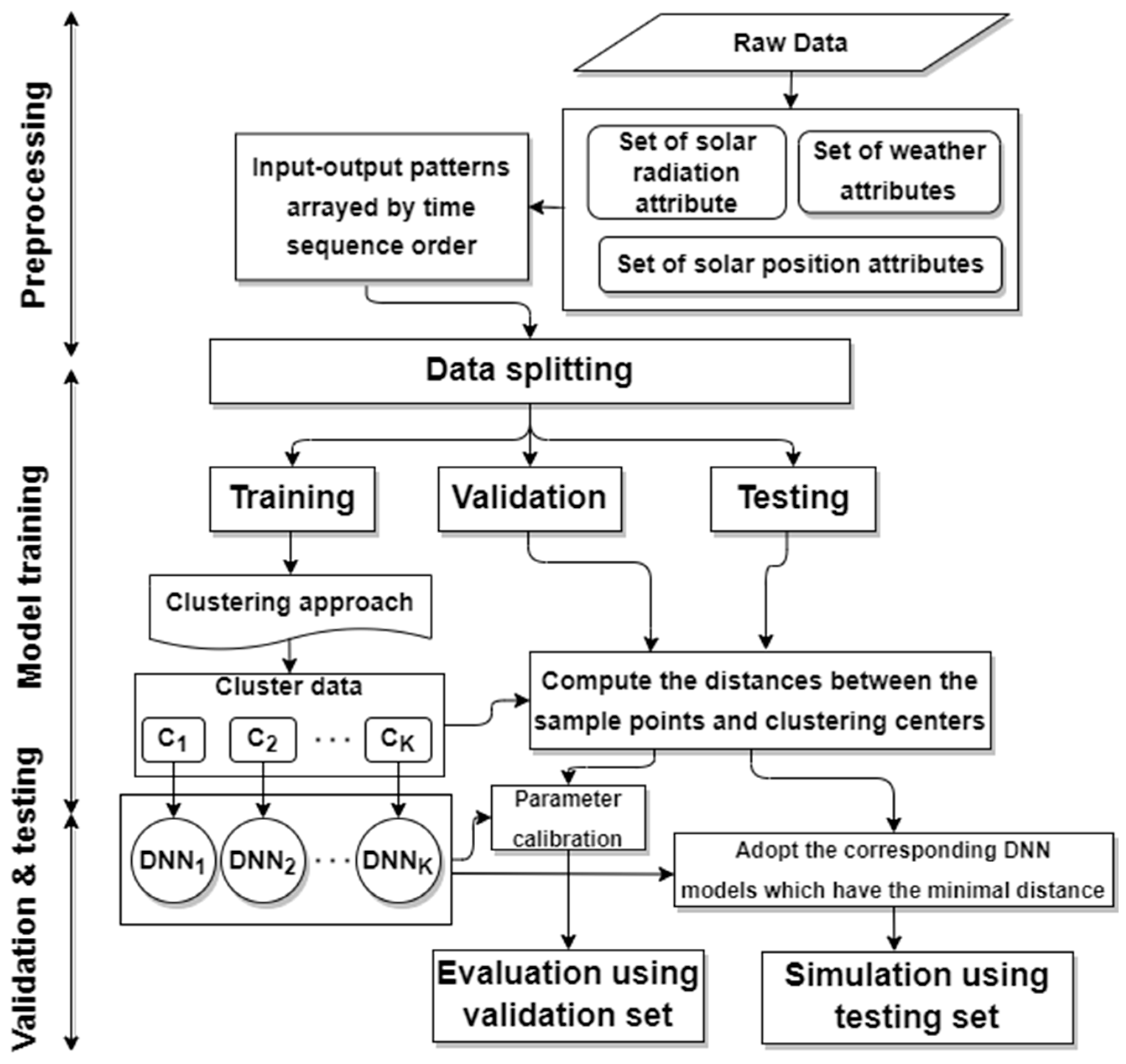
Figure 3 illustrates the modeling process for supervised models. Taking DNN as an example, DNN was developed based on the structure of deep neural networks. A deep neural network is a model with multiple layers and the advanced development of the multilayer perceptron based on the principles of the multilayer perceptron. The multilayer perceptron included an input layer, hidden layers, and an output layer. The input layer of the multilayer perceptron served as the interface for external input information, while the hidden layers and the output layer performed the actual computations. The flowchart in
Figure 3 explains that the data sets consisted of the solar radiation attribute {
S}, weather attributes {
W}, and solar position attributes {
P}. These three data sets were organized in a time sequence and then divided into a training set, a validation set, and a testing set. The training set and validation set were used for building prediction models, while the testing set was used to evaluate the model’s performance.
As shown in
Figure 4, O() represents a collection of observed values, including datasets of {
S}, {
W}, and {
P}. S
P() represents a collection of predicted solar radiation values. The predictive function of the model can be written as follows:
where S
P(
t +
k) represents the predicted solar radiation value for the future
k hours, O(
t − Δ
t) denotes past observed data,
d is the input delay time for the model,
N is the maximum prediction time length (set as a constant value in this study,
N = 12 h), and
n and
k are parameters (indices) for the prediction time length.
In Equation (6), when predicting the solar radiation SP(t + 1) for the next 1 h, the current time data (Δt = 0) and the observation set of the past d hours were used. For predictions beyond t + 2 in the future, the previous predicted values for each time step were also incorporated.
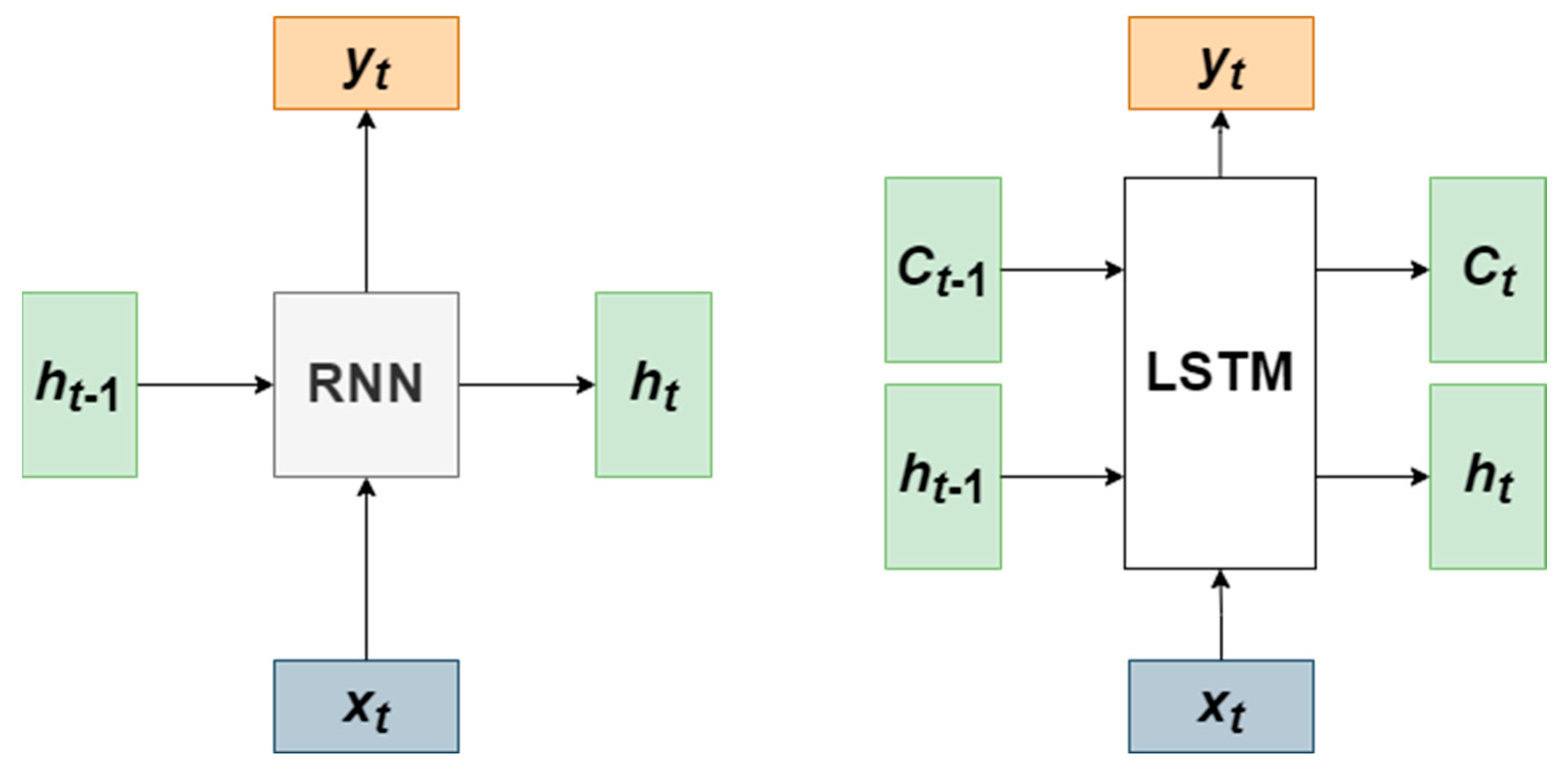
Additionally, in this study, another supervised model was employed, namely LSTM. LSTM is an advanced model within an RNN. RNNs are recurrent networks commonly used for handling time- and sequence-related problems. However, during the modeling process, the issue of vanishing gradients or exploding gradients may occur. To address this problem, Hochreiter and Schmidhuber [
34] introduced the LSTM neural network, which is an improved model incorporating memory blocks within the hidden layers of the RNN. As shown in
Figure 5, while traditional RNNs have a single hidden state,
ht, LSTM networks introduce memory blocks,
Ct, allowing them to retain longer memories and forget less relevant information.
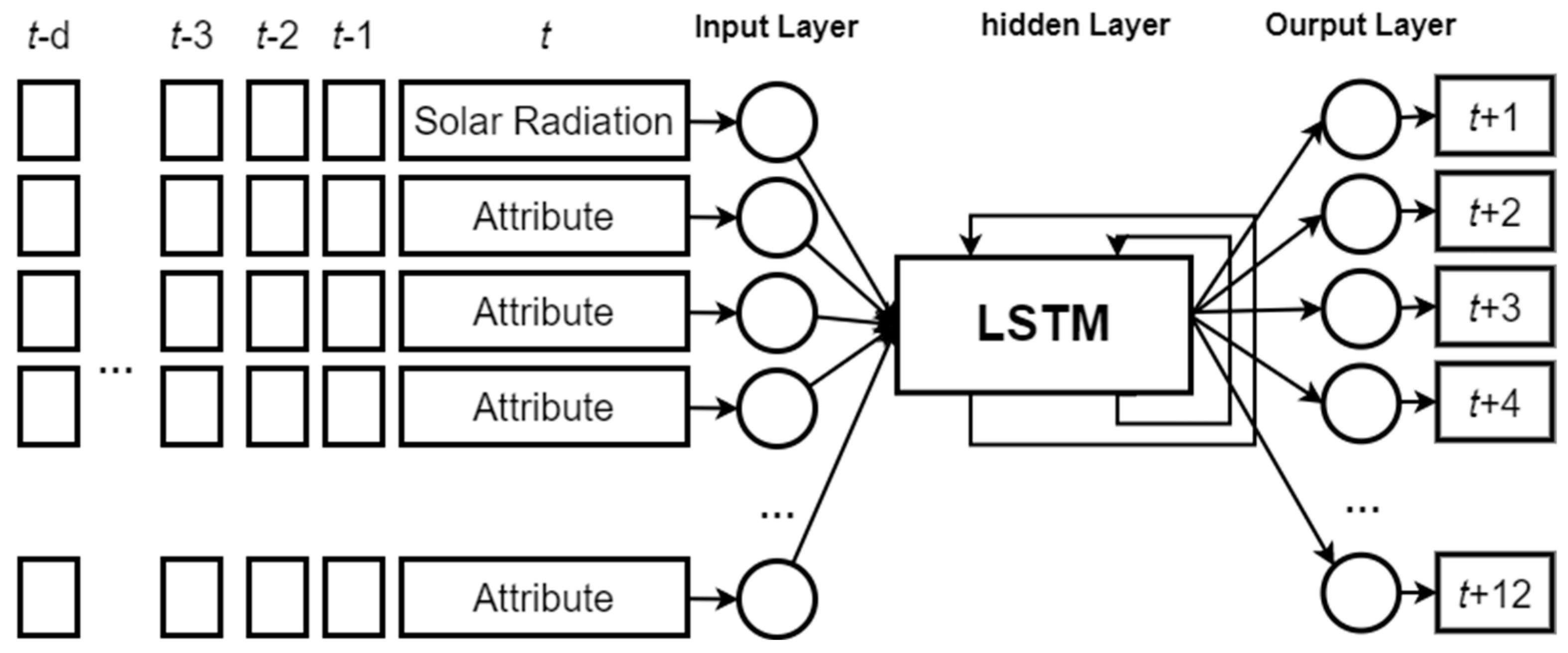
In the construction of the LSTM model in this study, the input data comprised the current solar radiation {
S} and attributes {
W} and {
P}. The input–output format of the model, as shown in
Figure 6, involved sequentially feeding data into the model based on the time sequence. The LSTM model was trained to predict 12 target values (i.e., solar radiation for the next 12 h), with each input data entry having a time length of
d′. The model directly output predictions for the next 12 h. To assess accuracy, the data were split into three sets for training, validation, and testing, as illustrated in
Figure 3, to evaluate the model’s performance.
3.2. Unsupervised Combined with Supervised Models
The unsupervised combined with supervised models in this study utilized unsupervised clustering algorithms in conjunction with supervised neural networks to form an integrated framework. The modularized process is depicted in
Figure 7. Initially, the three data sets of {
S}, {
W}, and {
P} were arranged based on the time sequence, and then they underwent data splitting. Subsequently, the training set was clustered, and each group of data was used to train a single supervised model (such as DNN and LSTM). After the model construction was complete, each data point in the validation set identified the cluster center with the shortest distance and utilized the corresponding ANN model for that cluster to predict solar radiation.
This study utilized two clustering methods: k-means and fuzzy C-means. The k-means method is a clustering algorithm that groups n data points into k clusters by minimizing the sum of the squared distances between all data points and their respective cluster centroids. The objective function J
K is the sum of the squared distances between all the data points and their cluster centroids, and the mathematical expression is as follows:
where K is the number of clusters,
k is the cluster index,
n is the number of data points,
xj is the
j-th input data sample,
Ci is the centroid of the
i-th cluster, and
wji is a weight, which is 1 if the data belongs to the
i-th cluster and 0 otherwise.
The fuzzy C-means algorithm applies fuzzy theory concepts to clustering methods [
35]. Unlike k-means, in fuzzy C-means, the weights,
W, are not binary; instead, each attribute datum is represented by a membership function to indicate the degree of belonging to each cluster. The objective function J
C is the sum of the squared distances between all data points and their cluster centroids, as shown in the following equation:
where K is the number of clusters,
n is the number of data points,
xj represents the
j-th sample data,
Ci is the centroid of the
i-th cluster,
is the weight (ranging from 0 to 1), indicating the degree of truth for its fuzzy set, and
m is the exponent coefficient, typically set to 2.
The sum of the weight coefficients should satisfy the constraint as follows:
The weight formula is as follows:
The number of clusters K mentioned above was determined using a trial and error method.
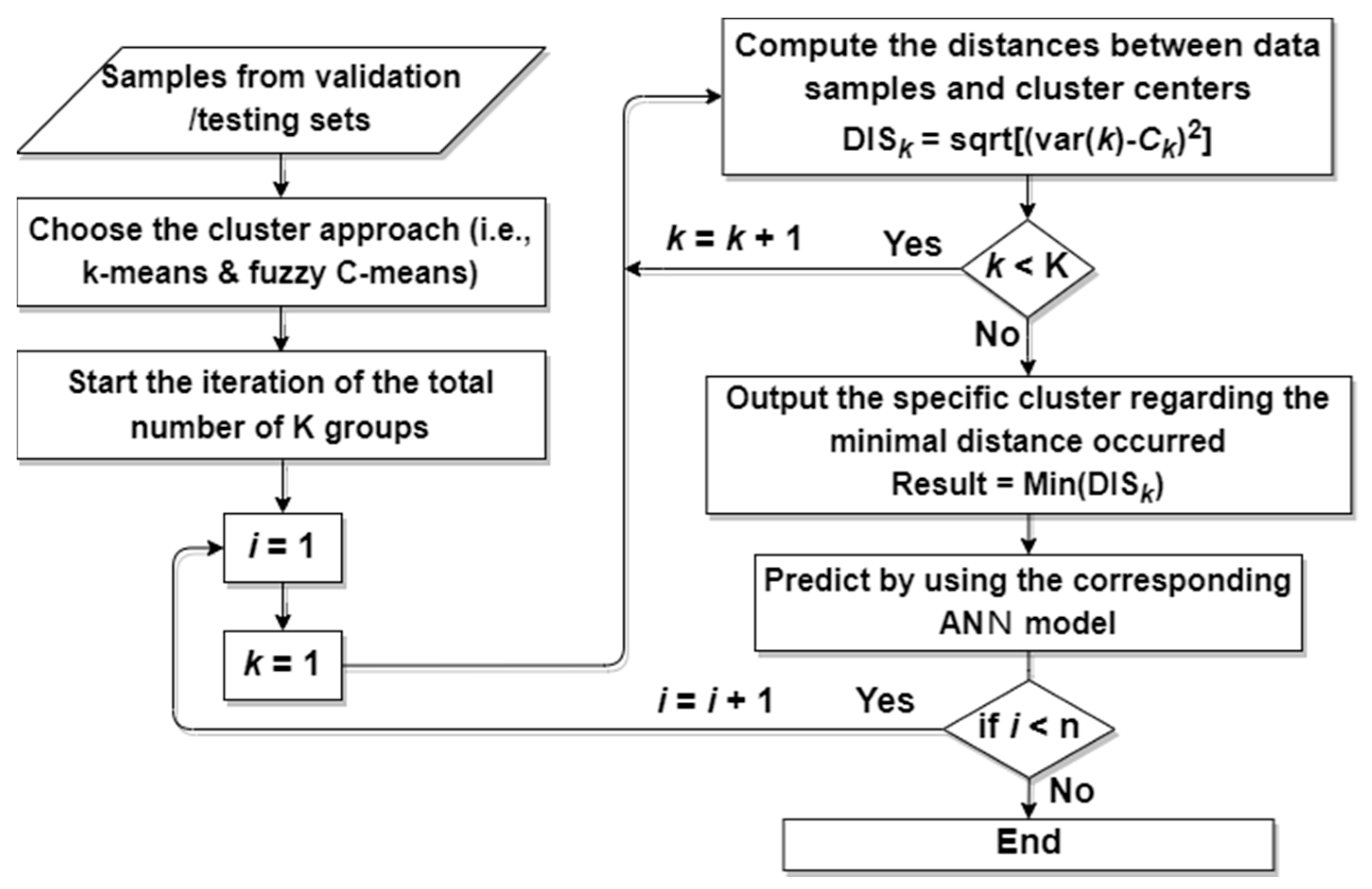
Figure 8 illustrates the process of selecting a cluster and predicting solar radiation based on the data in the validation set and testing set. After selecting the clustering method, the distance DIS between sample point
i and cluster center
Ck was calculated.
kmin_dis represents the shortest distance to a certain cluster. Based on the
kmin_dis result, you could use the predictive model associated with that cluster to estimate solar radiation.
5. Simulation
This study evaluated the DNN, LSTM, k_DNN, fc_DNN, k_LSTM, and fc_LSTM models using the testing set.
Figure 13 presents the evaluation results using the testing set, showing the rRMSE performance of each model for lead times ranging from 1 to 12 h. From
Figure 13a, it can be observed that at Kaohsiung Station, for lead times of 1 to 2 h, the different models had similar rRMSE values. However, for lead times greater than 3 h, fc_LSTM exhibited superior prediction performance. In
Figure 13b, at Hualien Station, for lead times of 1 to 3 h, LSTM, fc_DNN, and fc_LSTM showed comparable rRMSE values. For lead times greater than 4 h, fc_LSTM demonstrated better prediction performance.
Figure 13c shows the results for Penghu Station, where, for lead times of 1 to 2 h, the k_DNN, LSTM, k_LSTM, fc_DNN, and fc_LSTM models achieved similar rRMSE values. However, for lead times greater than 3 h, fc_LSTM exhibited a more significant advantage in terms of prediction performance.
Based on the rRMSE results of the DNN model, this study defined a “model improvement rate”, as described below:
After calculation, it was found that, at all three stations, the fc_LSTM model had the highest improvement rate (improving by 37.27%, 30.41%, and 29.08%, respectively) (see
Table 3), followed by the k_LSTM model with the second-highest improvement rate (improving by 20.81%, 19.54%, and 29.08%, respectively).
Model Selection Ensemble Tabular (MSET)
From
Section 3 of the real-time prediction system, the lookup table from MSET was used for real-time predictions to determine the best model for each forecast time (1 to 12 h).
Table 4 presents the results obtained from testing data simulations. It was observed that, for short-term predictions (lead time ≤ 3 h), a combination of clustering algorithms with DNN or LSTM models performed better at all three stations. However, for long-term predictions (lead time ≥ 4 h), combining clustering algorithms with LSTM models was the most stable choice.
This study used test data from 2017 to simulate a real-time prediction system. The best models selected from the MSET table for different forecast periods were further utilized for real-time updates in predicting solar radiation. To assess the system, ground station data and solar angle data obtained through k-means and fuzzy C-means clustering were used. Each set of data belonged to a cluster with cluster center coordinates. The model selection set table can be updated based on the required time intervals to ensure the accuracy of clustering and statistical results. In practice, current data are imported into the database every hour. The best forecast models for each upcoming hour are defined according to the model selection set table, and the results of all models are computed. Finally, the required forecast values are combined, and the current time is adjusted, enabling continuous predictions until the user terminates the process.
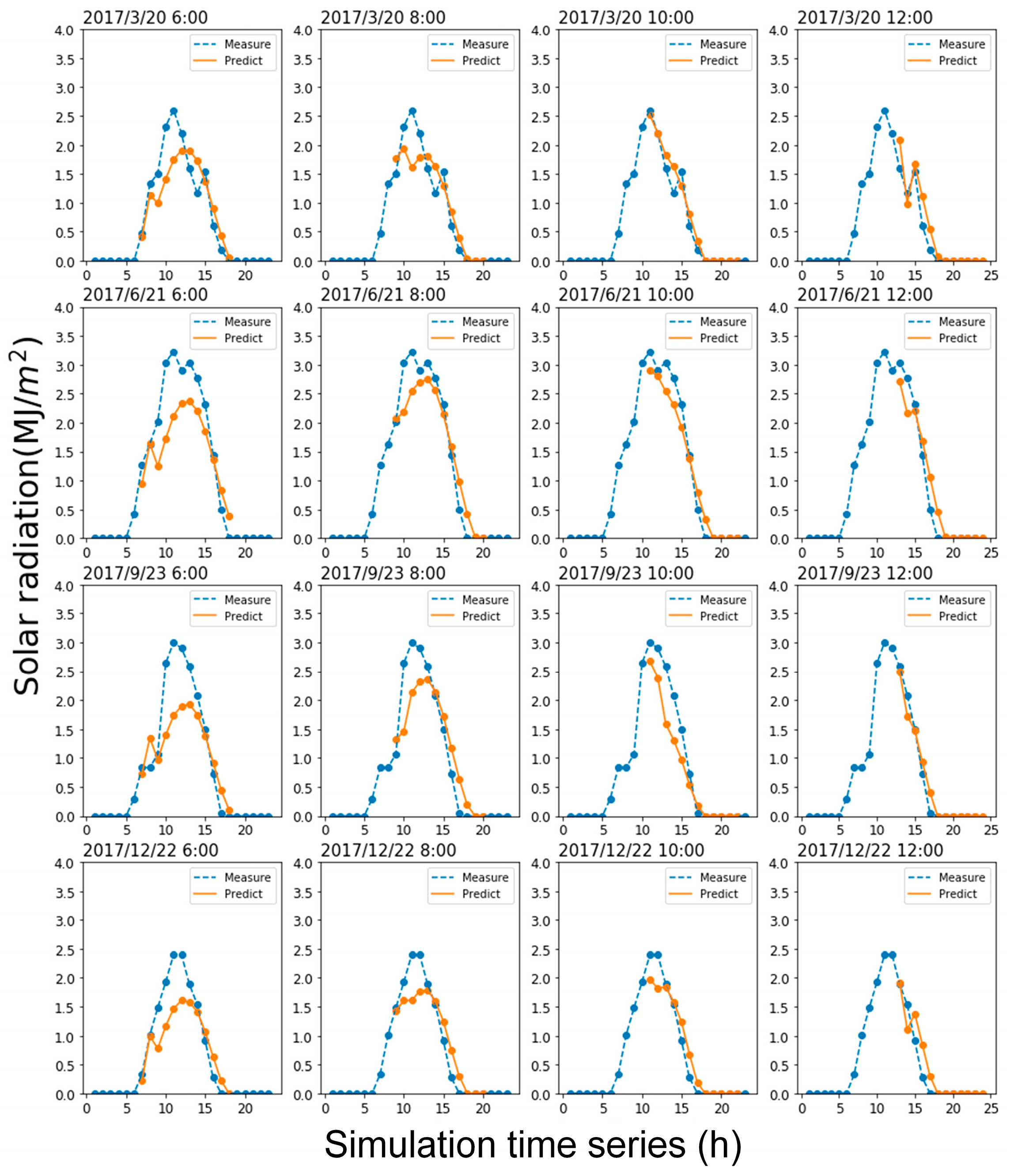
This study has established a real-time prediction system for solar radiation. The system’s performance was demonstrated using representative days chosen in this study: 03/20 (spring equinox), 06/21 (summer solstice), 09/22 (autumn equinox), and 12/21 (winter solstice).
Figure 14,
Figure 15 and
Figure 16 show the real-time predictions for Kaohsiung Station, Hualien Station, and Penghu Station during these four major seasonal transitions in 2017. The orange line represents the prediction results, while the blue line represents the observed solar radiation. Each prediction starts from 6:00 AM and looks ahead to the next 12 h. The figure titles indicate the time of the current prediction, starting at 6:00 AM, and the results are updated every two hours until noon, demonstrating the results up to that time.
It was evident that, at 6:00 AM, some stations tend to underestimate the peak around noon. However, after updating the data every two hours, by 10:00 AM, the results significantly improved and could reasonably predict the noon peak. The results demonstrate that the real-time predictions roughly aligned with the actual values. Based on the results, most errors were concentrated around the high values during the day. The accurate prediction of peak values can only be achieved as the current time approaches noon due to the error propagation over the long-term forecast. In such cases, the model’s output becomes increasingly conservative, leading to the observed underestimation. The study suggests that using more precise cluster selection methods to accurately choose the deep neural network trained by the noon cluster could potentially resolve this underestimation issue.
6. Conclusions
The aim of this study was to establish a prediction model for solar radiation and develop a hybrid real-time solar energy prediction system to obtain reliable daily solar radiation forecasts every morning. The system was designed to provide hourly updates and corrections to the predictions, assisting in determining the future electricity generation from solar energy and the optimal timing for energy generation. The study covered three regions, namely Kaohsiung, Hualien, and Penghu, each equipped with an independent real-time prediction system, forecasting solar radiation for the next 1 to 12 h.
In the model development phase, multiple models were employed, including a deep neural network (DNN) and a long–short-term memory neural network (LSTM). Additionally, unsupervised-based algorithms were used, which involved clustering methods such as k-means clustering and fuzzy C-means clustering. After clustering the data, neural-network-based prediction models were established for each cluster. As a result, in the DNN model, the following models were created: k-means DNN (k_DNN) and fuzzy C-means DNN (fc_DNN). In the case of the LSTM model, the following models were developed: k-means LSTM (k_LSTM) and fuzzy C-means LSTM (fc_LSTM).
Based on the predictions of various models, this study evaluated the best models for different forecasting time intervals and proposed a real-time solar radiation prediction system. This system is capable of providing real-time predictions of solar radiation in the range of 1 to 12 h ahead. To test its practicality, simulations were conducted using data from the year 2017. The results of the research’s prediction system demonstrated strong predictive performance. Even with increased errors in long-term predictions, the system was able to dynamically adjust the predictions in real time, effectively forecasting solar radiation for the next 12 h.