Abstract
Power batteries generate a large amount of heat during the charging and discharging processes, which seriously affects the operation safety and service life. An efficient cooling system is crucial for the batteries. This paper numerically simulated a power battery pack composed of 8 lithium-ion cells immersed in the coolant AmpCool AC-110 to study the effects of different coolants, different discharge rates, different coolant mass flow rates, different inlet temperatures and different inlet and outlet settings on the maximum temperature, the maximum temperature difference, the pressure drop, and the required pump power in the battery pack. Among the five coolants studied, W-E in water-based fluids has the best cooling effect, but because of high electric conductivity, it requires special considerations to avoid electric leakage. Increasing the mass flow rate of the coolant can significantly decrease Tmax and ΔTmax, but when the mass flow rate is already high, the decrease is limited and not obvious. Both Δp and the required pump power increase as the mass flow rate increases, and the required pump power increases faster. The inlet temperature will affect the physical properties of the coolant, and choosing the appropriate inlet temperature can not only decrease ΔTmax, but also decrease Δp and the required pump power in the battery pack. The range of 25~27 °C of the coolant AC-110 inlet temperature is recommended. For different inlet and outlet settings, the two-inlet two-outlet setting used in Case 7 has the best cooling effect, and the results indicate uniform distribution is very important to decrease temperature.
1. Introduction
The power battery is a key component for the current development of new energy vehicles, and it will continuously generate a large amount of heat during operation. As the main energy storage and power supply components of new energy vehicles, power batteries are usually made of lithium ions and have the advantages of high specific energy density, high discharge power, and mature production technology. The optimum operating temperature range of lithium-ion batteries is 25–40 °C, and the maximum temperature difference in the battery pack should not exceed 5 °C [1,2]. Therefore, the usage of an efficient battery thermal management system (BTMS) is an important condition to ensure the performance and safety of power batteries. At present, the thermal management systems of power batteries mainly include air cooling systems, liquid cooling systems, and phase-change material (PCM) cooling systems. The air cooling systems have the advantages of simple structures, low design difficulty, and low manufacturing cost, and are suitable for small battery-cooling systems [3,4]. The heat transfer coefficient of the liquid cooling systems is higher than the air cooling systems. Compared with the indirect liquid cooling, the cooling performance of the immersed liquid cooling technology is better [5,6,7,8,9]. The phase-change material cooling systems also have better cooling performance and thermal uniformity than air cooling systems, and if combined with air cooling systems or liquid cooling systems, their cooling ability can be further improved [10,11].
The immersed liquid cooling technology, also known as liquid direct cooling technology, usually uses non-conductive and non-flammable working fluids as coolants, such as mineral oil, silicone oil, fluorinated liquids, and refrigerants, etc. In the immersed liquid cooling technology, the batteries are fully immersed in the coolants or partially in direct contact with the coolants to minimize the thermal resistance between the batteries and the coolants, so that heat produced by batteries can be directly and effectively transferred to the coolants, and the temperature of batteries is controlled within a safe range. It is an efficient cooling method for power batteries. Compared with the indirect liquid cooling, in which the heat can only be transferred through the tubes or cooling plates, the battery pack with immersed liquid cooling technology has less auxiliary equipment and lower structural complexity. Scholars have conducted a significant amount of research on the immersed liquid cooling technology. LUO [12] conducted experiments and simulation methods to verify that the direct liquid cooling effect is obvious at 1C–4C discharge rate using transformer oil. Zhang et al. [13] studied the effect on temperature rise characteristics in battery pack of the oil immersion amount and ambient temperature in the static liquid cooling conditions at different discharge rates, as well as the oil immersion amount, oil flow rate, and inlet and outlet position changes in the dynamic liquid cooling conditions. The results show with the increase in the oil immersion amount and flow rate, and the change in the inlet and outlet positions, the thermal management effect of the battery pack is obviously improved. Qin [14] proposed a manifold-type immersion cooling structure, in which the jet flow formed by the manifold and the baffle is used to scour the surface of the battery, leading to a high local convective heat transfer coefficient. But, it is also pointed out that vortexes would be produced in the jet flow, which is not good to heat transfer, and vortexes should be weakened. Tan et al. [15] selected HFE-6120 as the single-phase coolant, and modelled and simulated different coolant channels and different flow directions to study the effect, finding that the maximum temperature and maximum temperature difference would decrease as the height of the flow channel increases, and the power consumption of the system would increase as the flow rate increases. Suresh Patil et al. [16] evaluated four cooling methods through experiments and simulations, that is, natural convection, no coolant flow and no tab cooling assistance, no coolant flow but with tab cooling assistance, and coolant flow with tab cooling assistance. It was found that the coolant flow with tab cooling assistance achieved the best cooling effect. Al-Zareer et al. studied and simulated the heat dissipation capacity of a battery pack that was immersed in cooling liquid. And, the coolants, for example, R134a [17], ammonia [18], and propane [2] were at different liquid levels in CFD simulation. The simulation results show that although the heat dissipation performance of these different coolants is different, there is a positive correlation between the heat dissipation capacity of the battery pack and the liquid level of the coolant. Li et al. [19] proposed a new battery immersion proposal, that is, the surface of the battery was coated with a layer of waterproof silicone sealant, which was a SS/BN composite material, and then the coated battery was directly immersed in water. The thermal properties and protective properties of different composite materials with different BN ratios were studied experimentally, and it was finally concluded that the composite material with 10 wt% BN content should be the best choice for battery surface coating materials. The research [20] gave five types of dielectric fluids commonly used at present, electronic fluorinated fluids, hydrocarbons, esters, silicone oils, and water-based fluids, and pointed out the advantages and disadvantages of these dielectric fluids. Then, based on the operating temperature characteristics of the battery system, the research progresses of immersion cooling in low temperature preheating, room-temperature cooling, and thermal runaway suppression were reviewed in detail.
This paper takes the eight rectangular lithium-ion cells, which are immersed in liquid coolant AmpCool AC-110, as the research object. The effects on heat dissipation performance of different coolants, different discharge rates, different coolant mass flow rates, different inlet temperatures of coolant, and different inlet and outlet settings are studied in this paper through numerical simulation technology. The main evaluation indicators are the maximum temperature, the maximum temperature difference, the pressure drop, and the required pump power.
2. Methodology
2.1. Lithium-Ion Battery Heat Generation Model
The heat generation principle of lithium-ion batteries during charging and discharging is due to the lots of redox reactions inside the battery in the working process, and a significant amount of of heat is released at the same time. In order to simplify the calculation, according to D. Bernardi’s battery heat generation theory [21], the heat generated by the battery is mainly divided into four parts: the chemical reaction heat Qr, the polarization heat Qp, Joule heat Qj and the side reaction heat Qs. The chemical reaction heat refers to the heat generated by the chemical reactions inside the battery. In lithium-ion batteries, it can be understood as the heat generated during the migration of lithium ions, so this part of the heat is reversible. The polarization heat can be divided into ohmic polarization heat and electrochemical polarization heat. The polarization heat caused by the ohmic internal resistance of the lithium-ion battery is ohmic polarization heat, while the polarization heat caused by the result of electrochemical reaction speed on the positive and negative electrodes lower than the electron movement speed is electrochemical polarization heat. The polarization heat is irreversible. Joule heat is mainly due to the heat generated by the Joule effect when the current passes through the poles of the battery, the electrolytes, the diaphragms, and other parts where there is usually resistance. The side reaction heat is the heat generated by the internal decomposition of the battery due to improper operation of the lithium-ion batteries. Under normal working conditions, this part of the heat is very small and can be ignored. Therefore, the total heat produced in lithium-ion batteries can be expressed as Equation (1).
In the formula,
- I—current during charging and discharging, A;
- Ro—internal ohmic resistance of battery, Ω;
- n—the number of batteries;
- m—the mass of each battery, kg;
- Q—total chemical reaction heat, J;
- M—molar mass, kg/mol;
- F—Faraday constant, 6485.4 C/mol;
- Rp—internal polarization resistance of battery, Ω.
2.2. Physical Model
In the simulation, a battery pack composed of 8 rectangular lithium-ion cells was used. The nominal capacity of the single cell was 55 Ah, and the single cell was regarded as an orthotropic material, with its thermal conductivity taken to be 30.6 W/(m·K) in the plane direction and thermal conductivity taken to be 3.06 W/(m·K) in the thickness direction. The internal structure of the battery pack is shown in Figure 1. The distance between adjacent cells was 30 mm, and the distances between the cells and the inner surface of the battery pack were also 30 mm. An immersed liquid cooling system was used in the battery pack, and the coolant was AmpCool AC-110. At 20 °C, the density of AC-110 was 820 kg/m3, the thermal conductivity was 0.14 W/(m·K), the specific heat capacity was 2060 J/(kg·K), and the dynamic viscosity was 0.020172 kg/(m·s). There was a coolant inlet on the left side of the battery pack and a coolant outlet on the right side, and the diameters of the inlet and outlet were both 10 mm. The length of the battery pack was 390 mm, the height of the pack was 292 mm, and the thickness was 157.5 mm.
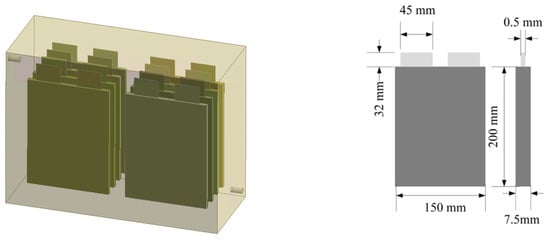
Figure 1.
Schematic diagram of the battery pack model.
Among the indicators selected in this paper, the maximum temperature in the battery pack is Tmax captured in the simulation in the battery pack, and the maximum temperature difference is ΔTmax, the difference between the maximum temperature Tmax and the minimum temperature Tmin captured in the simulation, shown in Equation (2). To ensure the working performance of the battery pack, Tmax should not exceed 50 °C and ΔTmax should not exceed 5 °C.
ΔTmax = Tmax − Tmin
The pressure drop is the pressure loss when the AC-110 coolant flows through the battery pack, that is, Δp, the difference in pressure between the inlet pin and the outlet pout of the coolant shown in Equation (3).
Δp = pin − pout
The required pump power is the product of the pressure drop Δp and volumetric flow rate V of the coolant, shown in Equation (4).
Pump Power = Δp × V
2.3. Governing Equations
This paper used software Solidworks (Visualize 2020) to build the physical model, shown in Figure 1, Geometry (2020 R2) to mesh and Fluent (2020 R2) for numerical simulation and data analysis, and divided the immersed liquid cooling battery pack composed of the coolant and the cells into fluid region and solid region. In the software Geometry, at the interface between the fluid region and solid region, the two regions were combined to form a new part to share nodes, so that there was only one set of edges in the model, which was both the boundary of the fluid and the solid. The fluid region was set to three-dimensional, steady state, incompressible flow with the energy equation turned on, and the influence of gravity on fluid flow was considered. The inlet of the coolant was set to the velocity inlet, and the outlet of the coolant was set to the pressure outlet. Since the velocity of the inlet was low, the laminar flow model was selected. The governing equations of fluid flow and heat transfer processes included the continuity equation shown in Equation (5), the three-dimensional momentum conservation equations shown in Equation (6), and the energy conservation equation shown in Equation (7).
Since the fluid flow of the coolant can be approximately considered to be an incompressible flow state in the immersed liquid cooling system, a pressure-based solver was used for the solution, and the SIMPLEC algorithm with a faster convergence speed was selected. The basic principle of the algorithm is to use the assumed pressure field to solve the momentum conservation equations and obtain the flux at the boundary point. However, since the assumed pressure field is not necessarily accurate, the obtained flux may not satisfy the continuity equation. By adding corrections into the original flux to obtain a new pressure field, the SIMPLEC algorithm continues to iterate through the pressure field and velocity field until the calculations converge.
2.4. The Grid Independent Analysis of Numerical Simulations
In order to ensure calculation accuracy and save time, the polyhedral mesh with simple structure, stability, and good quality was selected for discretization of the model regions, and the local mesh refinement approach was used to identify the smaller size. A grid independent analysis was performed to ensure that the number of the grids was independent of the calculation results in the simulation processes. Figure 2 shows the relationships between Tmax, ΔTmax, and the number of grids in the battery pack when the coolant AC-110 flows at an inlet temperature of 20 °C, with a a mass flow rate of 0.05 kg/s at a discharge rate of 1C. It can be seen from Figure 2 that as the number of grids increases, Tmax and ΔTmax in the battery pack firstly increase and then remain essentially unchanged. Taking both accuracy and the time of the calculation into account, 640,000 grids can already be seen to be the optimal number in this paper. With 640,000 grids, the change interval of Tmax is ≤0.04 °C, and the change interval of ΔTmax is ≤0.06 °C.
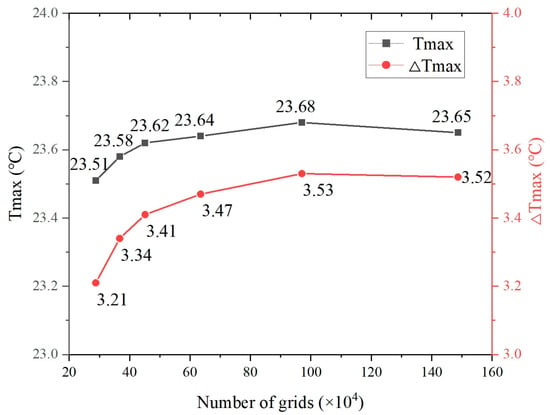
Figure 2.
The grid independent analysis.
3. Numerical Investigations
3.1. Effect of Different Coolants
It is pointed out in the literature [20] that the immersed liquid coolant should have the following properties: low dielectric value, high specific heat capacity, high thermal conductivity, low freezing point, non-flammable or high flash point, non-corrosive, low viscosity, low density, non-toxic and harmless, long life, economic, suitable operating temperature range, and other advantages. Currently, commonly used coolants can be divided into five types: electronic fluorinated fluids, hydrocarbons, esters, silicone oils, and water-based fluids. Among them, electronic fluorinated liquids usually have a low boiling point and can easily change the phase after absorbing heat, so they are often used as phase-change cooling materials. This paper selected the other four types to carry out numerical simulation studies, for example, PAO and AC-110 in hydrocarbons, DF-7 in esters, Si-oil in silicone oils, and 50% water + 50% ethylene glycol (W-E) in water-based fluids. The physical properties of these coolants are shown in Table 1. Figure 3 compares the impact of different coolants on system cooling performance at the 2C discharge rate with inlet temperature of 20 °C and velocity of 0.777 m/s.

Table 1.
Physical properties of different coolants.
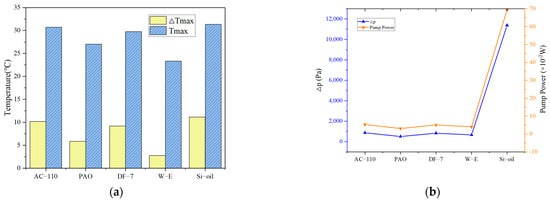
Figure 3.
(a) Tmax and ΔTmax, (b) Δp and the required pump power of different coolants.
It can be seen from Figure 3a that W-E in water-based fluids has the best cooling performance among the five coolants studied, and Tmax and ΔTmax are the smallest. The order of Tmax is Si-oil (31.4 °C) > AC-110 (30.7 °C) > DF-7 (29.8 °C) > PAO (27.0 °C) > W-E (23.3 °C), and the order of ΔTmax is Si-oil (11.2 °C) > AC-110 (10.2 °C) > DF-7 (9.2 °C) > PAO (5.9 °C) > W-E(2.7 °C). This is because W-E is a water-based fluid and has a higher thermal conductivity and specific heat capacity, which can take away more heat. However, because the water-based fluids usually have a higher electrical conductivity, special considerations need to be taken when using this type of coolant for surface anti-leakage treatment of the battery pack.
It can be seen from Figure 3b that PAO in hydrocarbons has the lowest Δp, as well as the lowest required pump power. Except for Si-oil, the required pump power is all less than 6 × 10−2 W, but the required pump power of Si-oil is about 0.7 W, mainly because the dynamic viscosity of Si-oil is the largest. The coolants with higher viscosity will cause higher flow resistance when coolants are passing through the battery pack. Therefore, when selecting a coolant, we should focus on the viscosity of the coolant, as viscosity will have a great impact on Δp and pump power. By comparing the results, except for water-based fluids, PAO in hydrocarbons has the best cooling performance under the same conditions, and requires the least pump power because of its higher specific heat capacity, higher thermal conductivity, and lower viscosity.
However, in order to find the effective liquid cooling methods, this paper selects AC-110, whose cooling capacity is moderate and environmental impact is zero [22], as the coolant on which to continue the research below to exploit a greater cooling potential.
3.2. Effect of Different Discharge Rates
The nominal capacity of the single cell in the battery pack studied in this paper is 55 Ah. Based on the battery heat generation model established previously, the thermal power of the battery pack under different discharge rates can be theoretically calculated, shown in Table 2. It can be seen when the battery pack is discharged at different rates, the corresponding thermal powers are different, and increase with the increased discharge rates. In this paper, the battery pack is set to the volumetric heat source, and the volume can be calculated from the size of the single cell. Therefore, the values of corresponding volumetric heat source can also be calculated at different discharge rates, which can also be found in Table 2.

Table 2.
Volumetric heat sources of the battery pack at different discharge rates.
Firstly, the temperature of the entire calculation region was set to 20 °C, and the mass flow rate of the coolant was set to 0.05 kg/s (the corresponding velocity of AC-110 was 0.777 m/s). It can be seen from Figure 4a that as the discharge rate increases, the heat production of the battery pack increases, and Tmax and ΔTmax in the battery pack increase accordingly. At 1C discharge rate, Tmax is 23.6 °C and ΔTmax is 3.5 °C. At high discharge rates (2C, 3C, 4C, and 5C), Tmax is increased by 7.1 °C, 15.2 °C, 21.9 °C, and 29.1 °C, respectively, compared with the 1C discharge rate; ΔTmax is increased by 6.7 °C, 14.4 °C, 20.9 °C, and 27.7 °C, respectively, compared with the 1C discharge rate. At this time, at the 5C discharge rate, Tmax in the battery pack exceeded the 50 °C criteria, and at the 2C–5C discharge rate; ΔTmax exceeded the 5 °C criteria, which will seriously affect the performance and life of the power battery. This is because at higher discharge rates, operating current is larger, causing the temperature inside the battery pack to rise faster, and the immersed liquid cooling method in the condition of 20 °C inlet temperature and 0.05 kg/s mass flow rate of the coolant cannot meet the requirements for the optimal operating temperature in the battery pack.
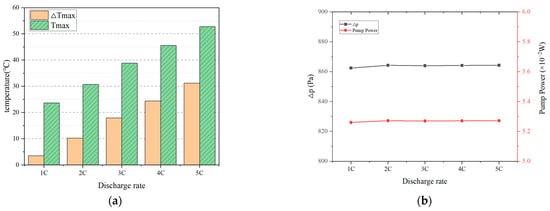
Figure 4.
(a) Tmax and ΔTmax, (b) Δp and the required pump power at different discharge rates.
As can be seen from Figure 4b, in terms of Δp and the required pump power in the battery pack, different discharge rates have almost no impact on Δp and the required pump power. At discharge rates from 1C to 5C, Δp is around 864 Pa and the required pump power is around 5.27 × 10−2 W. The main reason is that the main factors that affect Δp and the required pump power are the inlet area, the mass flow rate, and the viscosity of the coolant. Under the same conditions as above, Δp and the required pump power remain unchanged.
3.3. Effect of Different Flow Rates
From the above analysis, it can be seen at high discharge rates, when the mass flow rate of the coolant is only 0.05 kg/s, the corresponding flow velocity is very low, and there is a risk of overheating of the battery pack. Therefore, this paper studied the changes of Tmax, ΔTmax, Δp, and required pump power when the mass flow rate was ranging from 0.05 kg/s to 0.30 kg/s. The numerical results at discharge rates of 2C, 3C, and 4C, with inlet temperature of 20 °C, are shown in Figure 5.
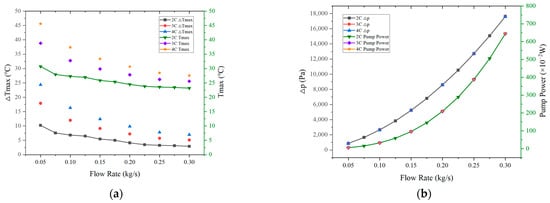
Figure 5.
(a) Tmax and ΔTmax, (b) Δp and the required pump power in different mass flow rate.
It can be seen from Figure 5a that at the 2C discharge rate, Tmax in the battery pack decreases as the mass flow rate increases. Furthermore, when the mass flow rate changes in the low range, there is a more obvious impact on Tmax than in the high range. For example, when the mass flow rate is increased from 0.05 kg/s to 0.10 kg/s, Tmax decreases from 30.7 °C to 27.3 °C, a decrease of 3.4 °C, while when the mass flow rate is increased from 0.25 kg/s to 0.30 kg/s, Tmax decreases from 23.5 °C to 23.2 °C, which is only a decrease of 0.3 °C. This is because the increase in mass flow rate significantly enhances the convective heat transfer effect. However, when the inlet mass flow rate is further increased, the decrease in Tmax is no longer obvious, indicating the impact of the inlet mass flow rate on Tmax in the current battery pack structure reaches the limit, and the cooling method that only relies on increasing the inlet mass flow rate to decrease Tmax is limited. At the same time, ΔTmax in the battery pack decreases as the mass flow rate increases. When different inlet mass flow rates are compared, it can be found that when the mass flow rate is increased from 0.05 kg/s to 0.20 kg/s, ΔTmax in the battery pack decreases significantly. However, when the inlet mass flow rate is further increased, the decrease in ΔTmax of different flow rates is no longer obvious. This can be explained by the fact that when the inlet mass flow rate increases, the temperature of battery near the inlet remains basically unchanged and is the minimum temperature in the battery pack. However, Tmax does not drop significantly in high mass flow rates. Therefore, the difference between the two temperatures (the minimum temperature and the maximum temperature) does not decrease significantly in high flow rates, indicating that the cooling method that only relies on increasing the inlet mass flow rate to control ΔTmax also has limitations in the current battery pack structure, and the mass flow rate is not the only factor that matters. At the discharge rates of 3C and 4C, Tmax and ΔTmax also have similar changing phenomenon with the 2C discharge rate.
It can be seen from Figure 5b that both Δp and the required pump power at 2C discharge rate increase with the increase in mass flow rate, in which the required pump power increases faster than Δp under the same mass flow rate gradient. At the same time, the change at high mass flow rates has a more obvious impact on Δp and the required pump power. For example, when the mass flow rate is increased from 0.05 kg/s to 0.10 kg/s, Δp increases from 864 Pa to 2654 Pa with an increase of 1790 Pa, and the required pump power increases from 5.27 × 10−2 W to 32.36 × 10−2 W with an increase of 27.09 × 10−2 W; when the flow rate is increased from 0.25 kg/s to 0.30 kg/s, Δp increases from 12,718 Pa to 17,623 Pa with an increase of 4905 Pa, and the required pump power increases from 3.88 W to 6.45 W with an increase of 2.57 W. At the discharge rates of 3C and 4C, Δp and the required pump power also have the same changing phenomenon because the discharge rate does not affect Δp and the required pump power, as discussed above. As the mass flow rate is increased, the velocity of the coolant is increased, and higher pressure at the coolant inlet is required, while the coolant outlet is a pressure outlet with a certain value, so Δp between inlet and outlet increases. And the required pump power is equal to the product of Δp and volumetric flow rate, so it will be more obviously affected by the mass flow rate and faster increasing than Δp under the same mass flow rate gradient.
3.4. Effect of Different Inlet Temperatures
The temperature of the fluid has an important influence on convective heat transfer. On the one hand, the temperature difference between fluid and the battery surface is one of the main factors driving convective heat transfer. On the other hand, changes in fluid temperature will also affect the fluid’s physical properties, such as density, viscosity, and thermal conductivity, and changes in these physical properties will affect the heat transfer characteristics of the fluid. Therefore, this paper studied the changes of the Tmax, ΔTmax, Δp and required pump power when the coolant with a mass flow rate of 0.05 kg/s enters the battery pack at different inlet temperatures with a range of 15–30 °C at the discharge rate of 2C. The physical properties of the coolant AC-110 used in the simulation are shown in Table 3.

Table 3.
The physical properties of the coolant AC-110 at different inlet temperatures.
It can be seen from Figure 6a that as the inlet temperature increases, Tmax in the battery pack noticeably increases. When the inlet temperature is increased from 15 °C to 30 °C, Tmax increases from 25.7 °C to 39.5 °C; therefore, the inlet temperature with a lower value can provide better cooling effect. As the coolant flows through the battery pack, it absorbs and carries away the heat generated in the battery pack. If the coolant inlet temperature is lower, the heat inside the battery can be taken away faster, allowing the battery pack to maintain a lower operating temperature. However, ΔTmax shows different changing phenomenon. When the inlet temperature is between 15 °C and 20 °C, the density, thermal conductivity, and specific heat capacity of the coolant are all the same, so ΔTmax is basically the same, at around 10 °C. When the inlet temperature exceeds 20 °C, ΔTmax begins to decrease, reaches its lowest value at 26 °C, and then slowly rises again. This is mainly because as the inlet temperature is increased, the specific heat capacity of the coolant begins to increase, which can absorb more heat with the same temperature rise. At the same time, the minimum temperature in the battery pack near the inlet is also increasing, and its difference from the maximum temperature in the battery pack is reduced, thereby decreasing ΔTmax. When the inlet temperature is too high, Tmax rises faster than the minimum temperature, and ΔTmax increases.
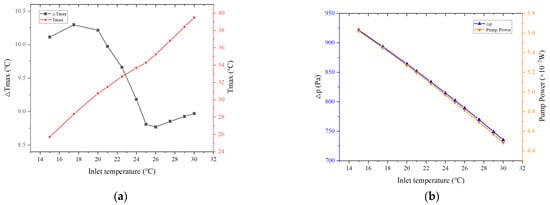
Figure 6.
(a) Tmax and ΔTmax, (b) Δp and the required pump power at different inlet temperatures.
It can be seen from Figure 6b that both Δp and the required pump power decrease as the inlet temperature increases. When the inlet temperature is increased from 15 °C to 30 °C, Δp decreases from 922 Pa to 735 Pa with a decrease of 187 Pa, 20.2%; the pump power decreases from 5.62 × 10−2 W to 4.48 × 10−2 W, which also decreases by 1.14 × 10−2 W, 20.2%. This is because the viscosity of the coolant decreases as the inlet temperature increases, and the viscosity affect Δp and the required pump power. Thereby, decreased viscosity results in low Δp and pump power in the battery pack. As above, when the inlet temperature is 26 °C, ΔTmax is the smallest; meanwhile, Δp and the required pump power are 789 Pa and 4.81 × 10−2 W, respectively, both decreasing by 14% compared with Δp and the required pump power with inlet temperature of 15 °C. Therefore, choosing the appropriate coolant temperature can not only decrease ΔTmax in the battery pack, but also decrease Δp and the required pump power of the system. This paper recommends that the inlet temperature of the coolant AC-110 in 25~27 °C is suitable to select.
3.5. Effect of Different Inlet and Outlet Settings
In order to study the impact of inlet and outlet settings on system cooling performance, this paper designed 8 different inlet and outlet settings. The mass flow rates of the coolants in Case 1–Case 8 were the same, and the cross-sectional area of the single inlet remained unchanged in Case 1–Case 5, while the inlet velocity was controlled by the number of inlets; Case 6–Case 8 keep the inlet velocity constant, while the cross-sectional area of the single inlet was controlled by the number of inlets, as shown in Table 4. Figure 7 compares the impact of different inlet and outlet settings on system performance at the 2C discharge rate with inlet temperature of 20 °C and mass flow rate of AC-110 of 0.05 kg/s.

Table 4.
Different inlet and outlet settings.
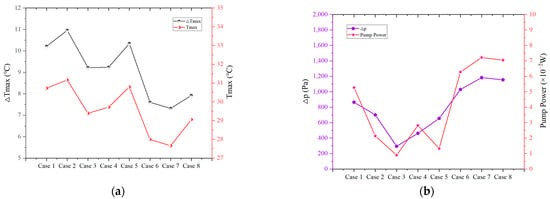
Figure 7.
(a) Tmax and ΔTmax, (b) Δp and the required pump power for different inlet and outlet settings.
It can be seen from Figure 7a that different inlet and outlet settings have different cooling effects. The temperature in Case 3 (2 inlets and 2 outlets) and Case 7 (2 inlets and 2 outlets) are low, indicating that uniform distribution is very important. The inlet velocity in Case 4 and Case 6–Case 8 is larger, which has better cooling effect and indicates that velocity has a more important effect than the number of inlets. Tmax and ΔTmax are the lowest in Case 7 (2 inlets and 2 outlets). Tmax is 27.7 °C, which is a decrease of 9.8% compared with 30.7 °C in Case 1. ΔTmax is 7.3 °C, compared with 10.1 °C in Case 1, a decrease of 28.4%. The settings and temperature distribution contours in Case 1 and Case 7 are shown in Figure 8. Since the inlets are set up at different positions without changing their velocities, the flow distribution is more uniform in Case 7.
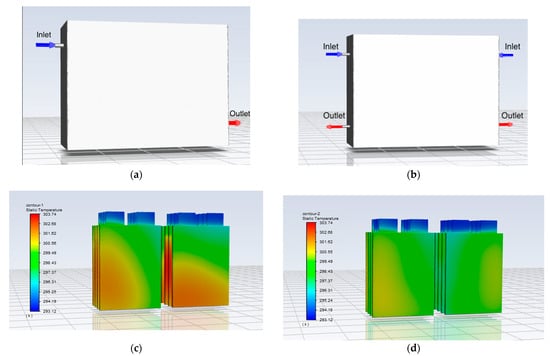
Figure 8.
The inlet and outlet settings in (a) Case 1 (b) Case 7 and temperature distribution contours in (c) Case 1 (d) Case 7.
However, from Figure 7b, we can see Δp and the required pump power are the highest in Case 7 (2 inlets and 2 outlets). Its Δp is 1183 Pa, which is an increase of 36.9% compared with 864 Pa in Case 1, and the required pump power is 7.22 × 10−2 W, an increase of 37.0% compared with 5.27 × 10−2 W in Case 1. Therefore, although this setting in Case 7 enhances cooling effect, it consumes more pump power. If the inlet temperature is set to 26 °C in Case 7, ΔTmax drops to 6.8 °C, and Δp and pump power also drop to 1068 Pa and 6.52 × 10−2 W, respectively, which performs better than inlet temperature of 20 °C. And, if the velocity is further increased, the Tmax drops to 31.3 °C and ΔTmax drops to 4.8 °C (2C discharge rate, inlet temperature of 26 °C, and mass flow rate of 0.10 kg/s), both below 50 °C criterion and 5 °C criterion, respectively.
4. Conclusions
This paper takes a power battery pack composed of eight lithium-ion cells as the research object, and uses numerical simulation technology to study the performance of an immersed liquid cooling system, the change in Tmax, ΔTmax, Δp, and the required pump power with different coolants, as well as different discharge rates, different mass flow rates, different inlet temperatures and different inlet and outlet settings.
- (1)
- Among the five coolants studied, W-E in water-based fluids has the best cooling effect, but its electric conductivity is high and requires special considerations to avoid electric leakage. Except for water-based fluids, PAO in hydrocarbon has the best cooling performance and requires the smallest pump power under the same conditions because of its higher specific heat capacity, higher thermal conductivity, and lower viscosity.
- (2)
- As the discharge rate increases, the heat production of the battery pack increases, Tmax and ΔTmax in the battery pack increase, and Δp and the required pump power remain basically unchanged.
- (3)
- Tmax and ΔTmax in the battery pack decrease as the inlet mass flow rate increases, but the method that only relies on increasing the inlet mass flow rate to control Tmax and ΔTmax is limited. Both Δp and the required pump power increase as the inlet mass flow rate increases, and the required pump power increases faster than Δp under the same mass flow rate gradient.
- (4)
- The inlet temperature of the coolant will affect physical properties such as density, specific heat capacity, thermal conductivity, and viscosity. Choosing the appropriate coolant temperature can not only decrease ΔTmax in the battery pack, but also decrease Δp and the required pump power of the system. This paper recommends that the inlet temperature of the coolant AC-110 should be in 25~27 °C.
- (5)
- For different inlet and outlet settings, The temperature in Case 3 (2 inlets and 2 outlets) and Case 7 (2 inlets and 2 outlets) are low, indicating that uniform distribution is very important. And, the 2 inlet and 2 outlet setting used in Case 7 has the best cooling effect. Compared with Case 1, Tmax decreases by 11.3% and ΔTmax decreases by 28.7%; however, Δp increases by 37.7% and the required pump power increases by 38.0%. Therefore, different inlet and outlet settings need to be considered comprehensively.
Author Contributions
Conceptualization, P.F. and Z.X.; methodology, Z.X. and J.S.; software, P.F.; validation, S.J. and L.F.; formal analysis, P.F.; investigation, S.J. and L.F.; resources, J.S.; data curation, P.F.; writing—original draft preparation, P.F.; writing—review and editing, J.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
Author Liwei Fang and Shouyi Jiao are employed by the company Shandong Lurun Heat Energy Science & Technology Co., Ltd. The remaining authors declare that the research is conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Lyu, Y.; Siddique, A.R.M.; Majid, S.H.; Biglarbegian, M.; Gadsden, S.A.; Mahmud, S. Electric vehicle battery thermal management system with thermoelectric cooling. Energy Rep. 2019, 5, 822–827. [Google Scholar] [CrossRef]
- Al-Zareer, M.; Dincer, I.; Rosen, M.A. A novel phase change based cooling system for prismatic lithium ion batteries. Int. J. Refrig. 2018, 86, 203–217. [Google Scholar] [CrossRef]
- Kim, G.-H.; Pesaran, A. Battery Thermal Management System Design Modeling; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2006. [Google Scholar]
- Yu, X.; Lu, Z.; Zhang, L.; Wei, L.; Cui, X.; Jin, L. Experimental study on transient thermal characteristics of stagger-arranged lithium-ion battery pack with air cooling strategy. Int. J. Heat Mass Transf. 2019, 143, 118576. [Google Scholar] [CrossRef]
- Qian, Z.; Li, Y.; Rao, Z. Thermal Performance of Lithium-Ion Battery Thermal Management System by Using Mini-Channel Cooling. Energy Convers. Manag. 2016, 126, 622–631. [Google Scholar] [CrossRef]
- Wu, W.; Wang, S.; Wu, W.; Chen, K.; Hong, S.; Lai, Y. A Critical Review of Battery Thermal Performance and Liquid Based Battery Thermal Management. Energy Convers. Manag. 2019, 182, 262–281. [Google Scholar] [CrossRef]
- Wu, S.; Lao, L.; Wu, L.; Liu, L.; Lin, C.; Zhang, Q. Effect analysis on integration efficiency and safety performance of a battery thermal management system based on direct contact liquid cooling. Appl. Therm. Eng. 2022, 201, 117788. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, X.; Meng, H.; Guo, L.; Zhang, Z. Numerical analysis of the thermal performance of a liquid cooling battery module based on the gradient ratio of a liquid cooling battery module based on the gradient ratio flow velocity and gradient increment tube diameter. Int. J. Heat Mass Transf. 2021, 175, 121338. [Google Scholar] [CrossRef]
- Safdari, M.; Ahmadi, R.; Sadeghzadeh, S. Numerical Investigation on PCM Encapsulation Shape Used in the Passive-Active Battery Thermal Management. Energy 2020, 193, 116840. [Google Scholar] [CrossRef]
- Cao, J.; Ling, Z.; Fang, X.; Zhang, Z. Delayed Liquid Cooling Strategy with Phase Change Material to Achieve High Temperature Uniformity of Li-Ion Battery under High-Rate Discharge. J. Power Sources 2020, 450, 227673. [Google Scholar] [CrossRef]
- Zhang, W.; Qiu, J.; Yin, X.; Wang, D. A novel heat pipe assisted separation type battery thermal management system based on phase change material. Appl. Therm. Eng. 2019, 165, 114571. [Google Scholar] [CrossRef]
- Luo, B. Research of Electric Vehicle Liquid Cooling System Which Directly Contact with Battery Pack. Master’s Thesis, University of Technology, Guangzhou, China, 2016. [Google Scholar]
- Jinqiang, Z.; Haimin, W.; Nan, L. Temperature field characteristics of a small NCM811 traction battery module cooled by insulating oil immersion. Energy Storage Sci. Technol. 2022, 11, 2612–2619. [Google Scholar]
- Le, Q.; Shi, Q.; Liu, Q.; Yao, X.; Ju, X.; Xu, C. Numerical investigation on manifold immersion cooling scheme for lithium ion battery thermal management application. Int. J. Heat Mass Transf. 2022, 190, 122750. [Google Scholar] [CrossRef]
- Wang, Y.; Rao, Z.; Liu, S.; Li, X.; Li, H.; Xiong, R. Evaluating the performance of liquid immersing preheating system for lithium-ion battery pack. Appl. Therm. Eng. 2021, 190, 116811. [Google Scholar] [CrossRef]
- Patil, M.S.; Seo, J.-H.; Lee, M.-Y. A Novel Dielectric Fluid Immersion Cooling Technology for Li-Ion Battery Thermal Management. Energy Convers. Manag. 2021, 229, 113715. [Google Scholar] [CrossRef]
- Al-Zareer, M.; Dincer, I.; Rosen, M.A. Heat and Mass Transfer Modeling and Assessment of a New Battery Cooling System. Int. J. Heat Mass Transf. 2018, 126, 765–778. [Google Scholar] [CrossRef]
- Al-Zareer, M.; Dincer, I.; Rosen, M.A. Electrochemical Modeling and Performance Evaluation of a New Ammonia-Based Battery Thermal Management System for Electric and Hybrid Electric Vehicles. Electrochim. Acta 2017, 247, 171–182. [Google Scholar] [CrossRef]
- Li, X.; Huang, Q.; Deng, J.; Zhang, G.; Zhong, Z.; He, F. Evaluation of Lithium Battery Thermal Management Using Sealant Made of Boron Nitride and Silicone. J. Power Sources 2020, 451, 227820. [Google Scholar] [CrossRef]
- Zeng, S.; Wu, W.; Liu, J.; Wang, S.; Ye, S.; Feng, Z. A review of research on immersion cooling technology for lithium-ion batteries. Energy Storage Sci. Technol. 2023, 5, 2888. [Google Scholar]
- Bernardi, D.; Pawlikowski, E.; Newman, J. A general energy balance for battery systems. J. Electrochem. Soc. 1985, 132, 5–12. [Google Scholar] [CrossRef]
- AmpCool Dielectric Coolant|Engineered Fluids. Available online: https://www.engineeredfluids.com/ampcool (accessed on 1 August 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).