Three-Phase Transformer Optimization Based on the Multi-Objective Particle Swarm Optimization and Non-Dominated Sorting Genetic Algorithm-3 Hybrid Algorithm
Abstract
:1. Introduction
2. Model Building
2.1. Impedance Analysis Equation
2.2. Transformer Loss Equation
2.3. Model building
2.4. Sensitivity Analysis
2.5. Model Validating
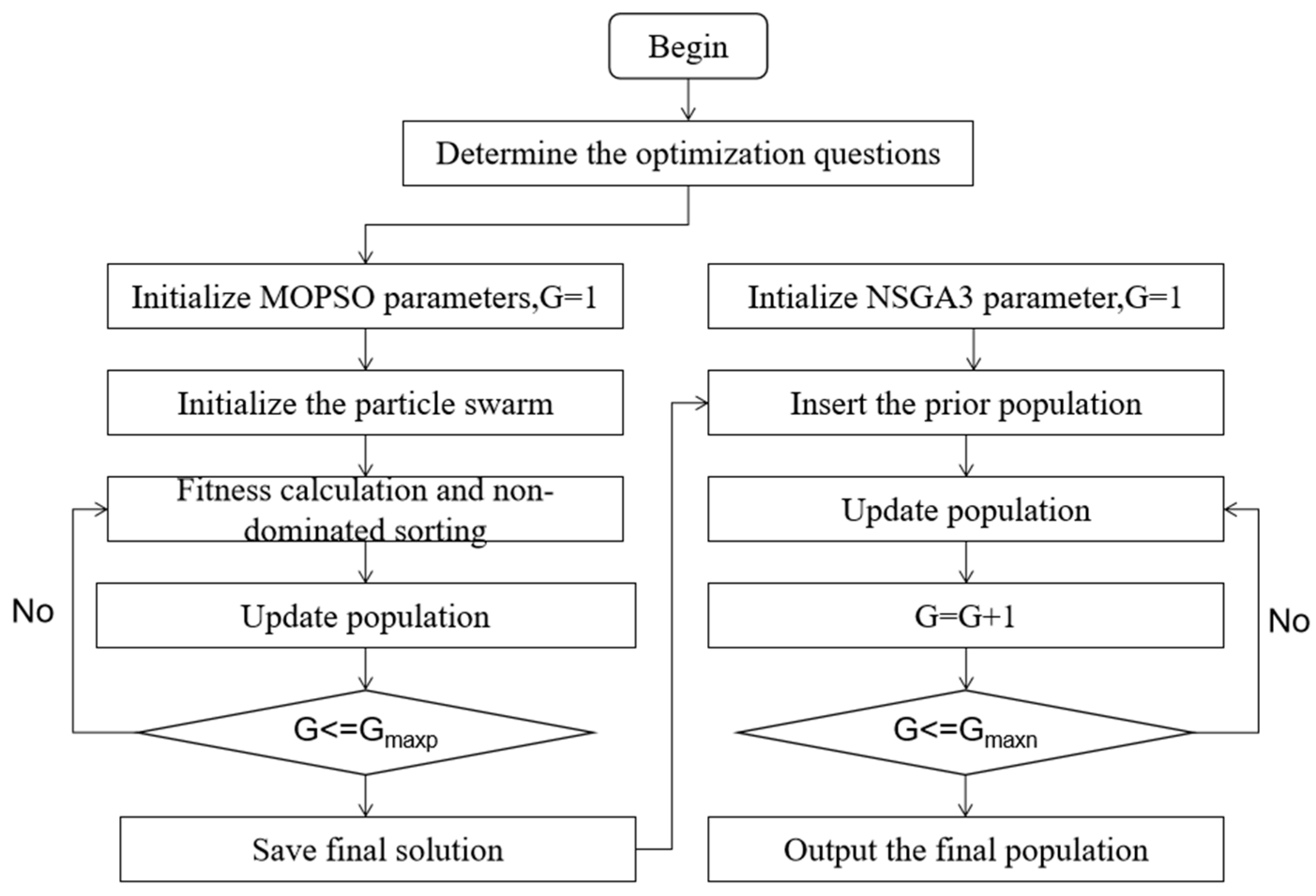
3. MOPSO-NSGA-III Algorithm
3.1. MOPSO
3.2. NSGA-III Algorithm
3.3. MOPSO-NSGA3 Hybrid Algorithm
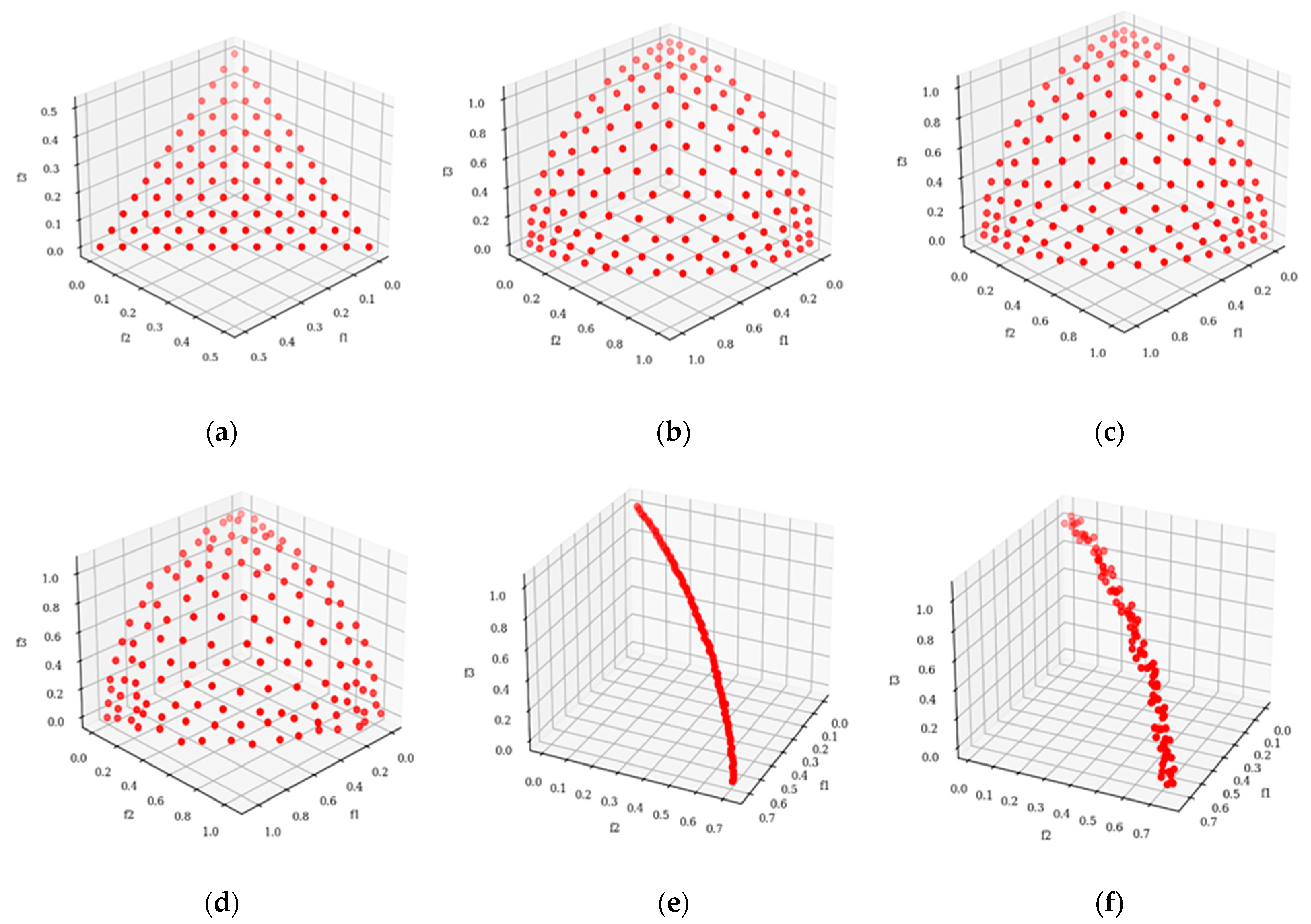
4. Experimental Test
Comparison of Results of Different Optimization Algorithms
5. Optimization
Result Comparisons
6. Conclusions
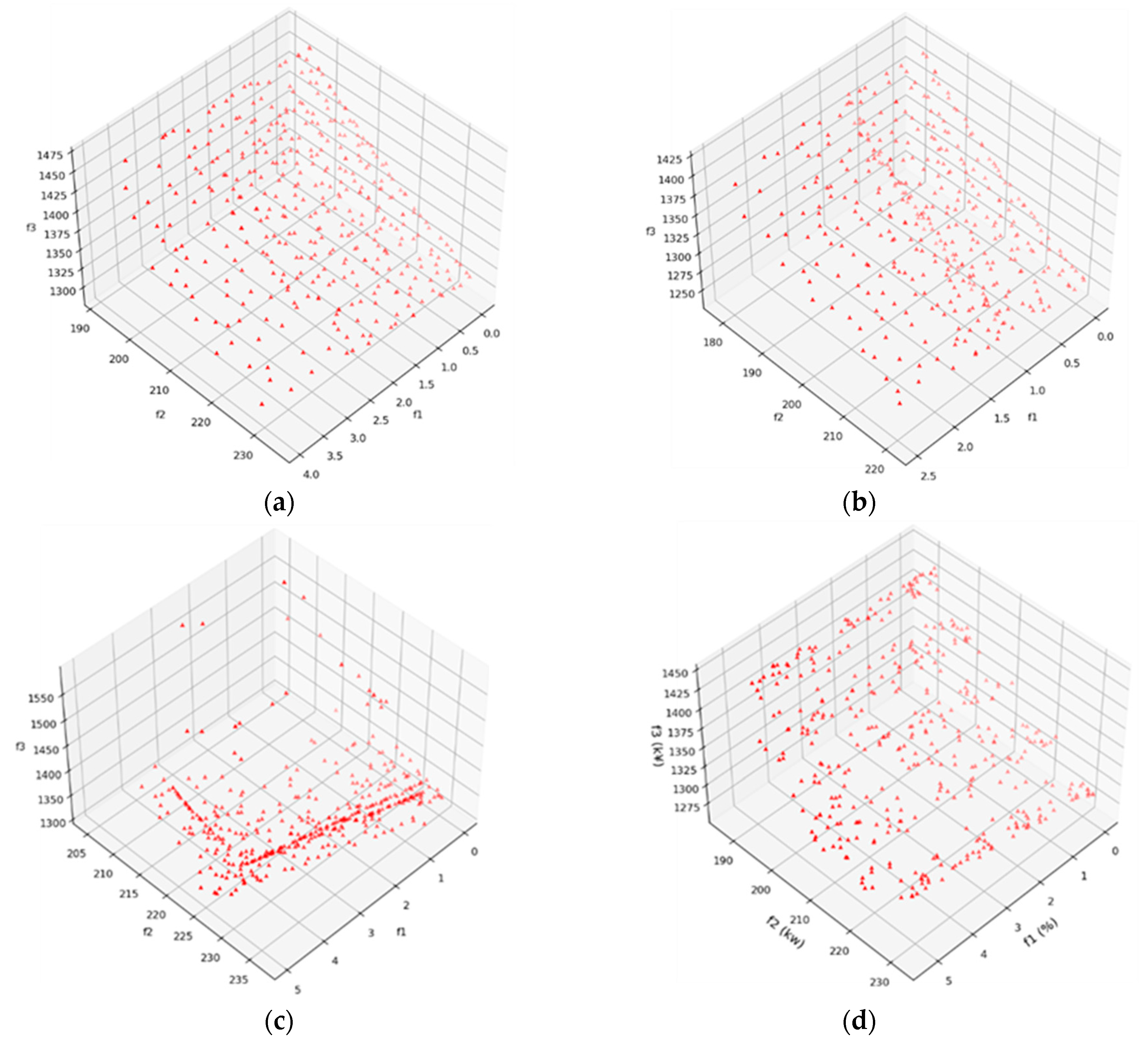
- (a)
- The multi-objective optimization model was built, and the accuracy model was validated via two transformers with the electrical specifications of 110 kV/50 MVA and 110 kV/63 MVA.
- (b)
- Sensitive analysis was carried out to analyze the interaction relationship between transformer design parameters and each optimization object.
- (c)
- The optimization work of the transformer with 110 kV electrical specifications has been carried out.
- (a)
- The analytical method was utilized to calculate short-circuit impedance in this paper, but this method is insufficient to consider the affections of material nonlinearity and core saturation characteristics. However, the finite element method is time-consuming and accompanied by a large computational quantity, which is unrealistic to operate in massively parallel computing. The lightweight machine learning (LN) and deep learning (DL) models will be used as the object function in the future to decrease the error from model prediction.
- (b)
- The flux leakage control, insulation requirements, and heat-dissipating method differ sharply for transformers with different voltage levels and operating capacities. The present multi-objective model needs to be improved to cover other types of transformers.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| U | Induced voltage | Equivalent magnetic leakage area | |
| f | Current frequency | Equivalent reactance height | |
| Bm | Peak flux density | T1 | Breadth of low-voltage winding |
| Afe | Sectional area of the core | T2 | Breadth of high-voltage winding |
| R | The radius of the core | Density of rolled steel | |
| N | Turns of the Winding | Tg | Breadth of clearance |
| SN | Transformer rated capacity | D1 | mean diameter size of low-voltage winding |
| f0 | Effective section coefficient | D2 | mean diameter size of high-voltage winding |
| KR | Rogowski factor | Dg | mean diameter size of clearance |
| Required short-circuit impedance | X | Short-circuit impedance | |
| Density of copper | Turns of low-voltage winding | ||
| Turns of high-voltage winding | Sl | Conductor cross-section area of low-voltage winding | |
| SH | Conductor cross-section area of high-voltage winding | Density of silicon steel | |
| Effective cross-sectional area of the core | bmax | Maximum stage width of core | |
| bmin | Minimum stage width of core | Height of the window | |
| Length of the tank | Width of the tank | ||
| Height of the tank | δ1 | Thickness of tank wall | |
| δ2 | Thickness of tank cover | δ3 | Thickness of tank bottom |
| Unit loss of silicon steel | Thickness of the core lamination | ||
| Eddy loss | Additional loss coefficient | ||
| b1~b5 | Stray loss regression coefficient | k1, k2 | Material dependent coefficients |
| hysteresis loss | Eddy loss coefficient of winding | ||
| Additional winding loss coefficient | Pnl | No-load loss | |
| Stray loss of the transformer | Winding resistance loss | ||
| cm | Transposition coefficient of winding | Variance of variable i | |
| First-order sensitivity of variable i | Total sensitivity of variable i | ||
| PSO | Particle swarm optimization | NSGA | Non-dominated sorting genetic algorithm |
| MOA | Multi-objective algorithm | MOP | Multi-objective problem |
| MO | Multi-objective | GA | Genetic algorithm |
References
- Georgilakis, P.S. Transformer Design Optimization. Power Syst. 2009, 38, 331–376. [Google Scholar]
- Ćalasan, M.P.; Jovanović, A.; Rubežić, V.; Mujičić, D.; Deriszadeh, A. Notes on Parameter Estimation for Single-Phase Transformer. IEEE Trans. Ind. Appl. 2020, 56, 3710–3718. [Google Scholar] [CrossRef]
- Cai, Z.; Zha, C.; Zhan, R.; Huang, G. Analysis and calculation of magnetic flux density distribution and core loss of nanocrystalline transformer. Energy Rep. 2022, 8, 218–225. [Google Scholar] [CrossRef]
- Li, S.; Sun, F.; Li, M.; Wang, C.; Li, X.; Yuan, P.; Zeng, H. The Research of 220kV Transformer Optimization Design Based on Finite Element Analysis Method. In Proceedings of the 2019 Chinese Automation Congress (CAC), Hangzhou, China, 22–24 November 2019; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA; pp. 5800–5803. [Google Scholar]
- Qin, J.; Yang, D.; Wang, N.; Ni, X. Convolutional sparse filter with data and mechanism fusion: A few-shot fault diagnosis method for power transformer. Eng. Appl. Artif. Intell. 2023, 124, 106606. [Google Scholar] [CrossRef]
- Zou, D.; Xiang, Y.; Zhou, T.; Peng, Q.; Dai, W.; Hong, Z.; Shi, Y.; Wang, S.; Yin, J.; Quan, H. Outlier detection and data filling based on KNN and LOF for power transformer operation data classification. Energy Rep. 2023, 9, 698–711. [Google Scholar] [CrossRef]
- Hernandez, A.; Canedo, J.M.; Olivares-Galvan, J.C.; Betancourt, E. Novel technique to compute the leakage reactance of three-phase power transformers. IEEE Trans. Power Deliv. 2016, 31, 437–444. [Google Scholar] [CrossRef]
- Kulkarni, S.V.; Khaparde, S.A. Transformer Engineering Design and Practice, 2nd ed.; CRC Press: New York, NY, USA, 2017. [Google Scholar]
- Dawood, K.; Kmirgz, G. A simple analytical method foraccurate prediction of the leakage reactance and leakage energyin high voltage transformers. J. King Saud Univ. Eng. Sci. 2022, in press. [Google Scholar] [CrossRef]
- Adly, A.A.; Abd-El-Hafiz, S.K. Automated transformer design and core rewinding using neural networks. J. Eng. Appl. Sci. 1999, 46, 351–364. [Google Scholar]
- Georgilakis, P.S. Recursive genetic algorithm-finite element method technique for the solution of transformer manufacturing cost minimization problem. IET Electr. Power Appl. 2009, 3, 514–519. [Google Scholar] [CrossRef]
- Hernández, C.; Arjona, M.A. Design of distribution transformers based on a knowledge-based system and 2D finite elements. Finite Elem. Anal. Des. 2007, 43, 659–665. [Google Scholar] [CrossRef]
- Hengsi, Q.; Kimball, J.W.; Venayagamoorthy, G.K. Particle swarm optimization of high-frequency transformer. In Proceedings of the 36th Annual Conference on IEEE Industrial Electronics Society (IECON), Glendale, AZ, USA, 7–10 November 2010; pp. 2914–2919. [Google Scholar]
- Tsili, M.A.; Kladas, A.G.; Georgilakis, P.S. Computer aided analysis and design of power transformers. Comput. Ind. 2008, 59, 338–350. [Google Scholar] [CrossRef]
- Balci, S.; Sefa, I.; Altin, N. Design and analysis of a 35 kVA medium frequency power transformer with the nanocrystalline core material. Int. J. Hydrogen Energy 2017, 42, 17895–17909. [Google Scholar] [CrossRef]
- Gu, S.; Han, L.; Liu, D.; Yu, W.; Xiao, Z.; Feng, T. Design and applicability analysis of independent double acquisition circuit of all-fiber optical current transformer. Glob. Energy Interconnect. 2019, 2, 531–540. [Google Scholar] [CrossRef]
- Orosz, T. FEM-Based Power Transformer Model for Superconducting and Conventional Power Transformer Optimization. Energies 2022, 15, 6177. [Google Scholar] [CrossRef]
- Janjua, A.K.; Mughal, S.N.; Khan, A.Z. Transformer’s Core Size Optimizaiton Using Genetic Algorithm. Conference Transformer’s Core Size Optimizaiton Using Genetic Algorithm. In Proceedings of the 2015 6th International Conference on Intelligent Systems, Modelling and Simulation, Kuala Lumpur, Malaysia, 9–12 February 2015; pp. 179–183. [Google Scholar]
- Marinov, A.; Bekov, E.; Feradov, F.; Papanchev, T. Genetic Algorithm for Optimized Design of Flyback Transformers. In Proceedings of the Conference Genetic Algorithm for Optimized Design of Flyback Transformers, Bourgas, Bulgaria, 3–6 June 2020; pp. 1–4. [Google Scholar]
- Shintemirov, A.; Tang, W.H.; Wu, Q.H. Construction of transformer core model for frequency response analysis with genetic Algorithm. In Proceedings of the Conference Construction of Transformer Core Model for Frequency Response Analysis with Genetic Algorithm, Calgary, AB, Canada, 26–30 July 2009; pp. 1–5. [Google Scholar]
- Zhang, S.; Hu, Q.; Wang, X.; Zhu, Z. Application of Chaos Genetic Algorithm to Transformer Optimal Design. In Proceedings of the Conference Application of Chaos Genetic Algorithm to Transformer Optimal Design, Shenyang, China, 6–8 November 2009; pp. 108–111. [Google Scholar]
- Zheng, R.R.; Zhao, J.Y.; Wu, B.C. Transformer Oil Dissolved Gas Concentration Prediction Based on Genetic Algorithm and Improved Gray Verhulst Model. In Proceedings of the Conference Transformer Oil Dissolved Gas Concentration Prediction Based on Genetic Algorithm and Improved Gray Verhulst Model, Shanghai, China, 7–8 November 2009; Volume 4, pp. 575–579. [Google Scholar]
- Ajour, M.N.; Abu-Hamdeh, N.H.; Mostafa, M.E. Optimizing and simulating cooling of electric transformer room utilizing genetic algorithm to reduce electricity/water demand by incorporating borehole ground heat exchangers. J. Taiwan Inst. Chem. Eng. 2023, 148, 104907. [Google Scholar] [CrossRef]
- Abdelwanis, M.I.; Abaza, A.; El-Sehiemy, R.A.; Ibrahim, M.N.; Rezk, H. Parameter Estimation of Electric Power Transformers Using Coyote Optimization Algorithm with Experimental Verification. IEEE Access 2020, 8, 50036–50044. [Google Scholar] [CrossRef]
- Guo, Z.; Yu, R.; Xu, W.; Feng, X.; Huang, A.Q. Design and Optimization of a 200-kW Medium-Frequency Transformer for Medium Voltage SiC PV Inverters. IEEE Trans. Power Electron. 2021, 36, 10548–10560. [Google Scholar] [CrossRef]
- Cheema, M.A.M.; Fletcher, J.E.; Dorrell, D. A Practical Approach for the Global Optimization of Electromagnetic Design of 3-Phase Core-Type Distribution Transformer Allowing for Capitalization of Losses. IEEE Trans. Magn. 2013, 49, 2117–2120. [Google Scholar] [CrossRef]
- Fei, S.-W.; Wang, M.-J.; Miao, Y.-B.; Tu, J.; Liu, C.-L. Particle swarm optimization-based support vector machine for forecasting dissolved gases content in power transformer oil. Energy Convers. Manag. 2009, 50, 1604–1609. [Google Scholar] [CrossRef]
- Illias, H.A.; Chai, X.R.; Abu Bakar, A.H. Hybrid modified evolutionary particle swarm optimisation-time varying acceleration coefficient-artificial neural network for power transformer fault diagnosis. Measurement 2016, 90, 94–102. [Google Scholar] [CrossRef]
- Korab, R.; Połomski, M.; Owczarek, R. Application of particle swarm optimization for optimal setting of Phase Shifting Transformers to minimize unscheduled active power flows. Appl. Soft Comput. 2021, 105, 107243. [Google Scholar] [CrossRef]
- Liao, R.; Zheng, H.; Grzybowski, S.; Yang, L. Particle swarm optimization-least squares support vector regression based forecasting model on dissolved gases in oil-filled power transformers. Electr. Power Syst. Res. 2011, 81, 2074–2080. [Google Scholar] [CrossRef]
- Lren, M. Optimization of transformer parameters at distribution and power levels with hybrid Grey wolf-whale optimization algorithm. Eng. Sci. Technol. Int. J. 2023, 43, 101439. [Google Scholar]
- Kotb, M.F.; El-Fergany, A.A.; Gouda, E.A. Estimation of electrical transformer parameters with reference to saturation behavior using artificial hummingbird optimizer. Sci. Rep. 2022, 12, 19623. [Google Scholar] [CrossRef] [PubMed]
- Orosz, T.; Karban, P.; Pánek, D.; Doleel, I. FEM-based transformer design optimization technique with evolutionary algorithms and geometric programming. Int. J. Appl. Electromagn. Mech. 2020, 64, 1–9. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Li, K.; Ding, Y.-Z.; Ai, C.; Sun, H.; Xu, Y.-P.; Nedaei, N. Multi-objective optimization and multi-aspect analysis of an innovative geothermal-based multi-generation energy system for power, cooling, hydrogen, and freshwater production. Energy 2022, 245, 123198. [Google Scholar] [CrossRef]
- Marghny, M.H.; Zanaty, E.A.; Dukhan, W.H.; Reyad, O. A hybrid multi-objective optimization algorithm for software requirement problem. Alex. Eng. J. 2022, 61, 6991–7005. [Google Scholar] [CrossRef]
- Shen, X.; Yu, G.; Chen, Q.; Hu, W. A multi-objective optimization co-evolutionary algorithm with dynamically varying number of subpopulations. Control. Decis. 2007, 22, 1011–1016. [Google Scholar]
- Wang, Y.; Chen, C.; Tao, Y.; Wen, Z.; Chen, B.; Zhang, H. A many-objective optimization of industrial environmental management using NSGA-III: A case of China’s iron and steel industry. Appl. Energy 2019, 242, 46–56. [Google Scholar] [CrossRef]
- Wu, X.; Li, X.; Qin, Y.; Xu, W.; Liu, Y. Intelligent multiobjective optimization design for NZEBs in China: Four climatic regions. Appl. Energy 2023, 339, 120934. [Google Scholar] [CrossRef]
- Solís-Pérez, J.E.; Gómez-Aguilar, J.F.; Hernández, J.A.; Escobar-Jiménez, R.F.; Viera-Martin, E.; Conde-Gutiérrez, R.A.; Cruz-Jacobo, U. Global optimization algorithms applied to solve a multi-variable inverse artificial neural network to improve the performance of an absorption heat transformer with energy recycling. Appl. Soft Comput. 2019, 85, 105801. [Google Scholar] [CrossRef]
- Mohammed, M.S.; Vural, R.A. NSGA-II+FEM Based Loss Optimization of Three-Phase Transformer. IEEE Trans. Ind. Electron. 2019, 66, 7417–7425. [Google Scholar] [CrossRef]
- Al-Dori, O.; Sakar, B.; Dnik, A. Comprehensive analysis of losses and leakage reactance of distribution transformers. Arab. J. Sci. Eng. 2022, 47, 14163–14171. [Google Scholar] [CrossRef]
- Bai, L.C.; Yan, G.Z. Theory and Calculation of Power Transformers, 2nd ed.; China Science and Technology Press: Liaoning, China, 2006. [Google Scholar]
- Chen, L.; Shang, K.; Ishibuchi, H. Performance Comparison of Multi-Objective Evolutionary Algorithms on Simple and Difficult Many-Objective Test Problems. In Proceedings of the 2020 IEEE Symposium Series on Computational Intelligence (SSCI), Canberra, Australia, 1–4 December 2020; pp. 2461–2468. [Google Scholar] [CrossRef]
- Kabakcioglu, F.; Bayraktarkatal, E. SOBOL sensitivity analysis and acoustic solid coupling approach to underwater explosion. Ocean. Eng. 2023, 281, 114752. [Google Scholar] [CrossRef]
- Vuillod, B.; Montemurro, M.; Panettieri, E.; Hallo, L. A comparison between Sobol’s indices and Shapley’s effect for global sensitivity analysis of systems with independent input variables. Reliab. Eng. Syst. Saf. 2023, 234, 109177. [Google Scholar] [CrossRef]
- Saltelli, A.; Annoni, P.; Azzini, I.; Campolongo, F.; Ratto, M.; Tarantola, S. Variance based sensitivity analysis of model output. Design and estimator for the total sensitivity index. Comput. Phys. Commun. 2010, 181, 259–270. [Google Scholar] [CrossRef]
- Jain, H.; Deb, K. An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point Based Nondominated Sorting Approach, Part II: Handling Constraints and Extending to an Adaptive Approach. IEEE Trans. Evol. Comput. 2014, 18, 577–601. [Google Scholar] [CrossRef]
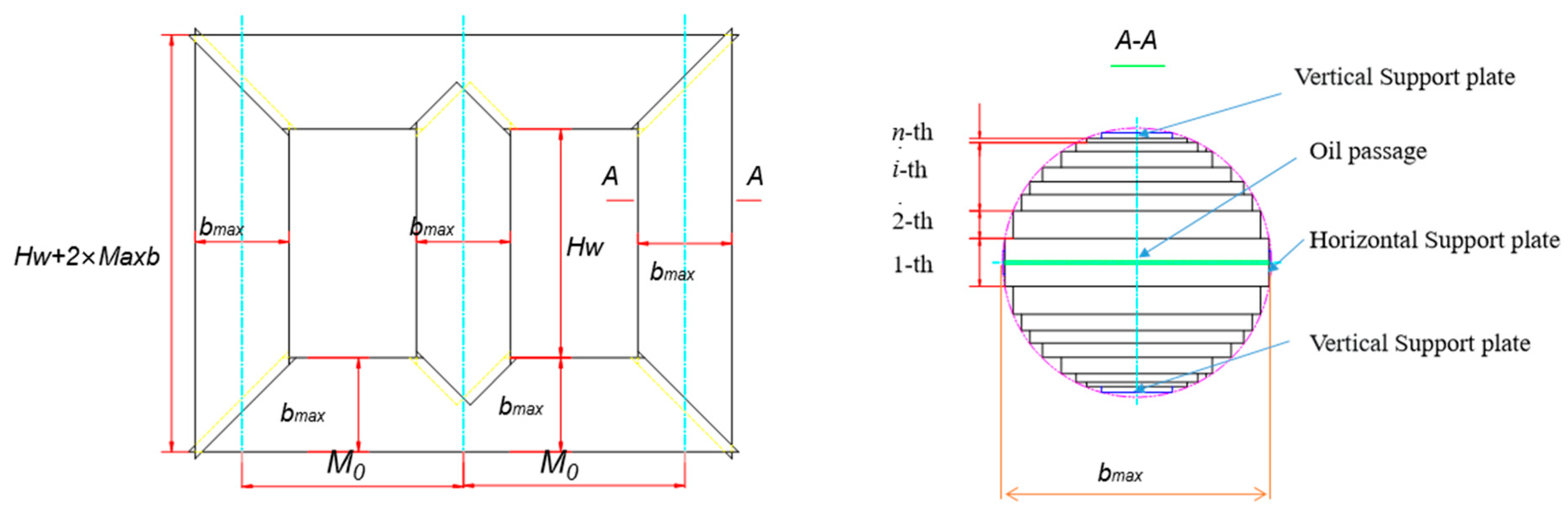
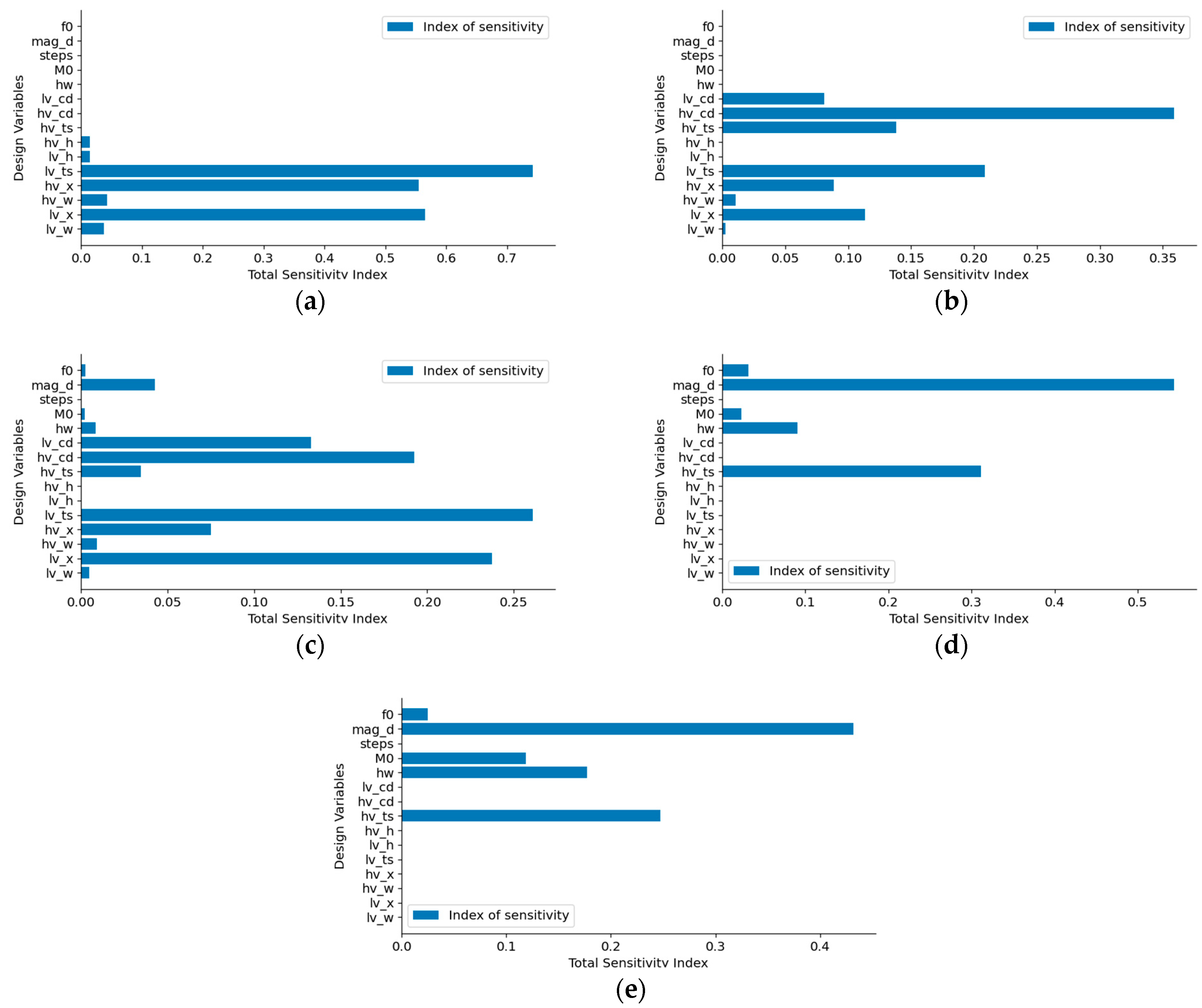
| Index | Descriptions of Object |
|---|---|
| minfcop | Minimize the usage of copper |
| minfrs | Minimize the usage of rolled steel |
| minfsc | Minimize the deviation between design impedance and required impedance. |
| minfss | Minimize the usage of silicon steel |
| minP | Minimize the on-load loss of the transformer |
| Design Variables | Down Bound | Up Bound | Descriptions |
|---|---|---|---|
| Tl | 70 | 110 | The width of low-voltage winding |
| Dl | 300 | 360 | Locating size of low-voltage winding |
| Hl | 750 | 925 | The height of low-voltage winding |
| TNl | 70 | 95 | The turns of low-voltage winding |
| Jl | 3.2 | 4.0 | Currency density of low-voltage winding |
| Th | 450 | 550 | Width of high-voltage winding |
| Dh | 470 | 510 | Locating size of high-voltage winding |
| Hh | 750 | 925 | Height of high-voltage winding |
| TNh | 475 | 525 | Turns of high-voltage winding |
| Jh | 2.5 | 3.3 | Currency density of high-voltage winding |
| M0 | 1300 | 1500 | Phase distances |
| Hw | 950 | 1050 | Window height |
| nsp | 14 | 25 | Steps of core |
| Brmp | 1.63 | 1.94 | Designed magnetic density |
| f0 | 0.95 | 0.975 | Lamination factor |
| Index | Measured Value | Calculated Value | Absolute Error |
|---|---|---|---|
| fcop (kg) | 10,757 | 10,455 | 2.81% |
| fsc (%) | 16.57 | 16.38 | 1.15% |
| P (W) | 216,360 | 234,718 | 8.48% |
| fss (kg) | 26,415 | 25,974 | 1.67% |
| frs (kg) | 24,518 | 26,784 | 9.24% |
| Index | Measured Value | Calculated Value | Absolute Error |
|---|---|---|---|
| fcop (kg) | 7348 | 7124 | 3.05% |
| fsc (%) | 16.94 | 16.66 | 1.65% |
| P (W) | 17,497 | 18,743 | 6.65% |
| fss (kg) | 17,834 | 17,461 | 7.12% |
| frs (kg) | 21,471 | 22,397 | 4.31% |
| Input: Vt and Xt of Particle swarm population and Archive set At |
| Output: Vt+1 and Xt+1 of Particle swarm population, Archive set At+1 |
| 1. Calculate the fitness of the population F |
| 2. Find non-dominated set ND and other swarm set D 3. At+1 = AtUND |
| 4. Find pbt based on crowding density |
| 5. For each d in set D |
| 6. Update the velocity Vi and position xi based on Equation (23) 7. Out-of-bounds handling |
| 8. End for |
| 9. Delete superfluous particles in At+1 |
| Input: H ← structured reference points, Z(s)←supplied aspiration, Pt ← parent population |
| Output: Pt+1 |
| 1. |
| 2. |
| 3. |
| 4. {ND1,ND2,…} = Fast − non − dominated − sort (Rt) 5. while |
| 6. 7. , record l = r |
| 8. if then #All next generation populations have been identified 9. , return , break 10. else: 11. #Add the satisfied population to the next iteration 12. Points to be chosen from 13. K = N − |Pt+1| #remaining need K pop to constitute the next group 14. Normalize the population members 15. Associate each member s with a reference point 16. Compute niche count of reference point 17. Chose K members from the to construct the next 18. generation; keep the niche obtained solutions for next iteration 19. end if |
| Problems | Algorithm | Hv | IGDmax | IGDmin | IGDmean |
|---|---|---|---|---|---|
| DTLZ1 | Ours | 0.9474 | 2.3641 | 0.078 | 0.7461 |
| NSGA3 | 0.8473 | 4.7792 | 0.3129 | 1.8472 | |
| NSGA2 | 0.8781 | 4.0767 | 0.2471 | 1.7496 | |
| MOPSO | 0.7271 | 6.3744 | 0.1846 | 3.4487 | |
| DTLZ2 | Ours | 0.5787 | 0.1074 | 0.0189 | 0.0441 |
| NSGA3 | 0.5586 | 0.1164 | 0.0497 | 0.0671 | |
| NSGA2 | 0.6392 | 0.2733 | 0.0258 | 0.0766 | |
| MOPSO | 0.4137 | 0.3615 | 0.0971 | 0.1479 | |
| DTLZ3 | Ours | 0.8471 | 4.5741 | 1.7544 | 2.1033 |
| NSGA3 | 0.7824 | 8.6473 | 2.5476 | 6.1078 | |
| NSGA2 | 0.7487 | 10.951 | 1.9748 | 8.1467 | |
| MOPSO | 0.03271 | 19.6734 | 2.0766 | 10.6983 | |
| DTLZ4 | Ours | 0.6974 | 0.9487 | 0.5455 | 0.7095 |
| NSGA3 | 0.6287 | 0.9507 | 0.5474 | 0.6674 | |
| NSGA2 | 0.9017 | 0.9503 | 0.4783 | 0.6771 | |
| MOPSO | 0.5187 | 0.9987 | 0.3741 | 0.689 | |
| DTLZ5 | Ours | 0.2217 | 0.1562 | 0.0294 | 0.0654 |
| NSGA3 | 0.2061 | 0.4329 | 0.1471 | 0.3987 | |
| NSGA2 | 0.1844 | 0.5474 | 0.2417 | 0.3479 | |
| MOPSO | 0.0327 | 0.7844 | 0.3374 | 0.5077 | |
| DTLZ6 | Ours | 0.2177 | 2.6573 | 1.9471 | 2.1287 |
| NSGA3 | 0.2014 | 4.3371 | 2.4476 | 3.1789 | |
| NSGA2 | 0.1764 | 6.1750 | 3.9743 | 4.1746 | |
| MOPSO | 0.1271 | 10.5767 | 4.6547 | 6.5479 |
| Indicator | Value | Indicator | Value |
|---|---|---|---|
| Capacity (kVA) | 50,000 | No-load Loss (kW) | 184 |
| Transformer Ratio | 110 kV/10.5 kV | Load Loss (kW) | 34.3 |
| Leakage Impedance | 17 ± 3 (%) | No-load Current (%) | 0.3 |
| Length (mm) | 5800 | Width (mm) | 2200 |
| Height (mm) | 2500 | Weight (mm) | 75,000 |
| f1 | Avg | Min | Max | Std |
| Present Algorithm | 1334.9 | 1235.5 | 1428.7 | 78.4 |
| NSGA2 | 1367.4 | 1277.4 | 1546.7 | 101.8 |
| NSGA3 | 1387.2 | 1274.4 | 1479.4 | 104.6 |
| MOPSO | 1369.9 | 1287.4 | 1557.4 | 54.6 |
| f2 | Avg | Min | Max | Std |
| Present Algorithm | 201.7 | 178.3 | 219.4 | 17.6 |
| NSGA2 | 208.4 | 184.7 | 228.7 | 15.4 |
| NSGA3 | 204.3 | 190.4 | 231.3 | 18.7 |
| MOPSO | 210.7 | 201.9 | 234.8 | 27.9 |
| f3 | Avg | Min | Max | Std |
| Present Algorithm | 1.32 | 0.17 | 2.41 | 1.41 |
| NSGA2 | 2.37 | 0.24 | 4.85 | 2.34 |
| NSGA3 | 1.97 | 0.14 | 3.94 | 1.94 |
| MOPSO | 2.19 | 0.29 | 4.93 | 2.53 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, B.; Zhang, L.; Jiang, Y.; Li, Z.; Xiao, W.; Shang, J.; Chen, X.; Li, M. Three-Phase Transformer Optimization Based on the Multi-Objective Particle Swarm Optimization and Non-Dominated Sorting Genetic Algorithm-3 Hybrid Algorithm. Energies 2023, 16, 7575. https://doi.org/10.3390/en16227575
Shi B, Zhang L, Jiang Y, Li Z, Xiao W, Shang J, Chen X, Li M. Three-Phase Transformer Optimization Based on the Multi-Objective Particle Swarm Optimization and Non-Dominated Sorting Genetic Algorithm-3 Hybrid Algorithm. Energies. 2023; 16(22):7575. https://doi.org/10.3390/en16227575
Chicago/Turabian StyleShi, Baidi, Liangxian Zhang, Yongfeng Jiang, Zixing Li, Wei Xiao, Jingyu Shang, Xinfu Chen, and Meng Li. 2023. "Three-Phase Transformer Optimization Based on the Multi-Objective Particle Swarm Optimization and Non-Dominated Sorting Genetic Algorithm-3 Hybrid Algorithm" Energies 16, no. 22: 7575. https://doi.org/10.3390/en16227575
APA StyleShi, B., Zhang, L., Jiang, Y., Li, Z., Xiao, W., Shang, J., Chen, X., & Li, M. (2023). Three-Phase Transformer Optimization Based on the Multi-Objective Particle Swarm Optimization and Non-Dominated Sorting Genetic Algorithm-3 Hybrid Algorithm. Energies, 16(22), 7575. https://doi.org/10.3390/en16227575






