Flame Structure at Elevated Pressure Values and Reduced Reaction Mechanisms for the Combustion of CH4/H2 Mixtures
Abstract
:1. Introduction
2. Experimental Methods
3. Modeling Details
3.1. Chemical Kinetics Simulations
3.2. Reduction in Kinetics Mechanism
- (1)
- A set of species and reactions that are only important during low-temperature oxidation, namely, CH3O2H and CH3O2, were removed;
- (2)
- According to our previous studies [48], there are two most important reaction pathways of methane transformation in flames: CH4 → CH3 → CH3O → CH2O → HCO → CO → CO2, and CH4 → CH3 → C2H6 → C2H5 → C2H4 → C2H3 → C2H2 → HCCO → CO → CO2. The second pathway becomes important only in fuel-rich flames and was therefore removed. This included C2 hydrocarbons, singlet CH2(s) and all reactions involving them;
- (3)
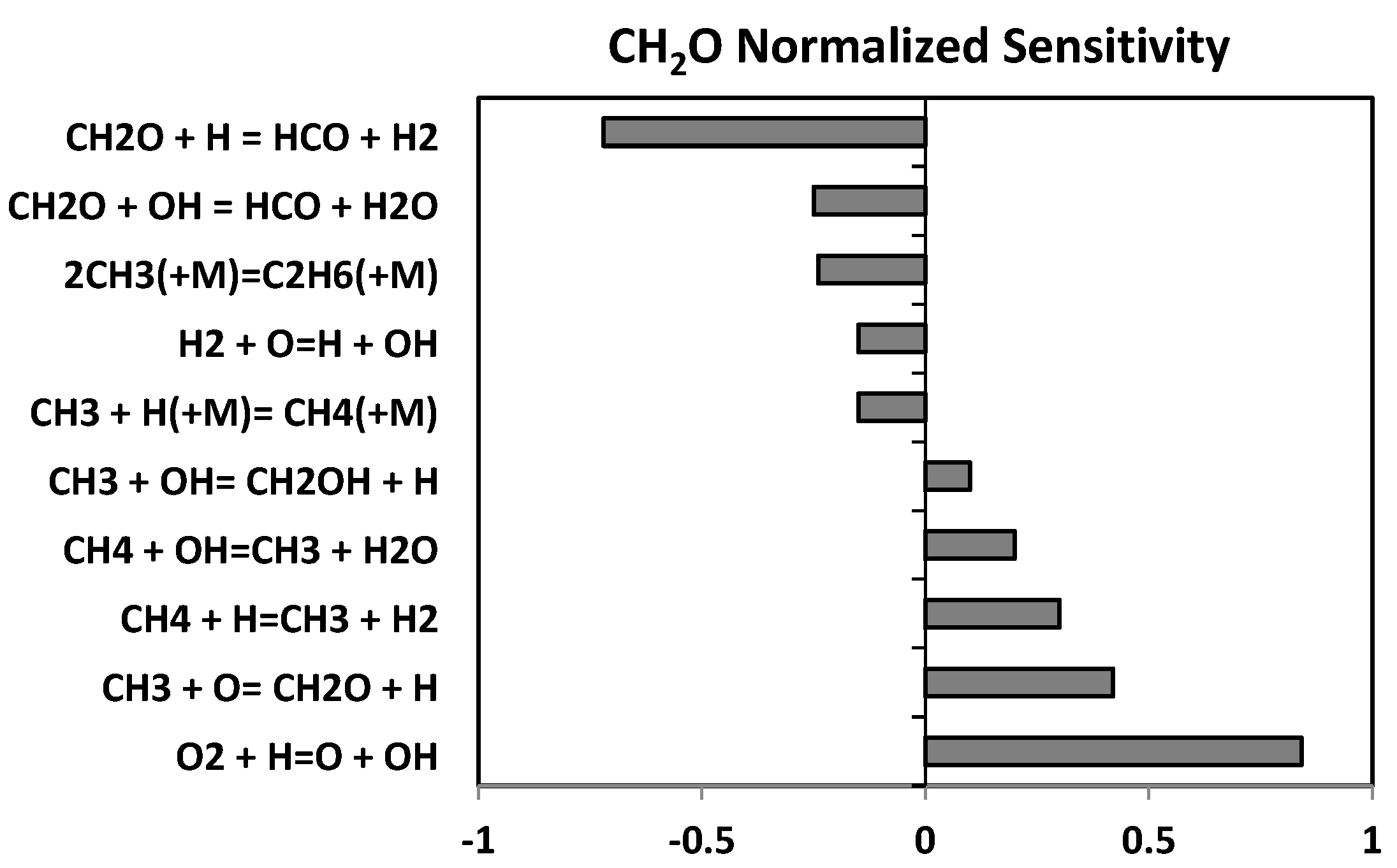
- Since several paths of CH3 consumption in the previous modification were deleted, the concentration of CH3 concentration increased considerably. This resulted in higher flame speed values, particularly at elevated pressures. To compensate this effect, the pre-exponential factors of 3 reactions, identified via a sensitivity analysis, were modified. The rate constant of reaction CH3 + HO2 ↔ CH4 + O2 (R14) was increased 2 times, while the rate constant of CH3 + HO2 ↔ CH3O + OH (R19) were reduced by a factor of 2. Also, for the reaction CH3 + OH ↔ CH2OH + H (R17), the rate constants were reduced by a factor of 2, but only for pressures above 1 atm;
- (4)
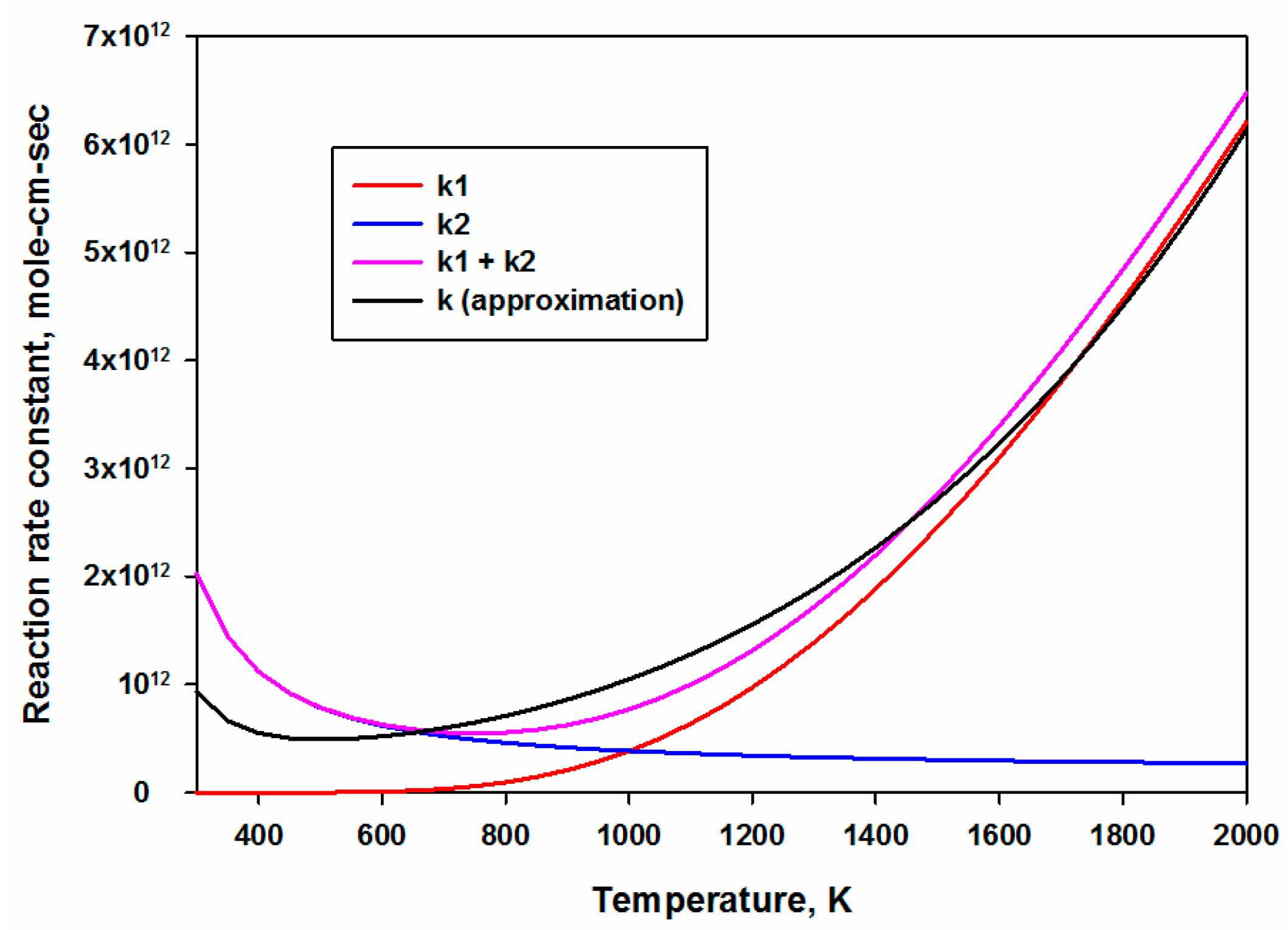
- The reaction rate constant of HO2 + HO2 ↔ H2O2 + O2 (R7) was initially expressed by two sets of reaction rate parameters, responsible for low and high temperature ranges. Both sets were merged and then approximated as a single set of reaction rate constants. Figure 1 shows the comparison between the sum of original reaction rates and the new approximated reaction rate.
3.3. Validation of the Reduced Models against LBV and IDT
4. Results and Discussion
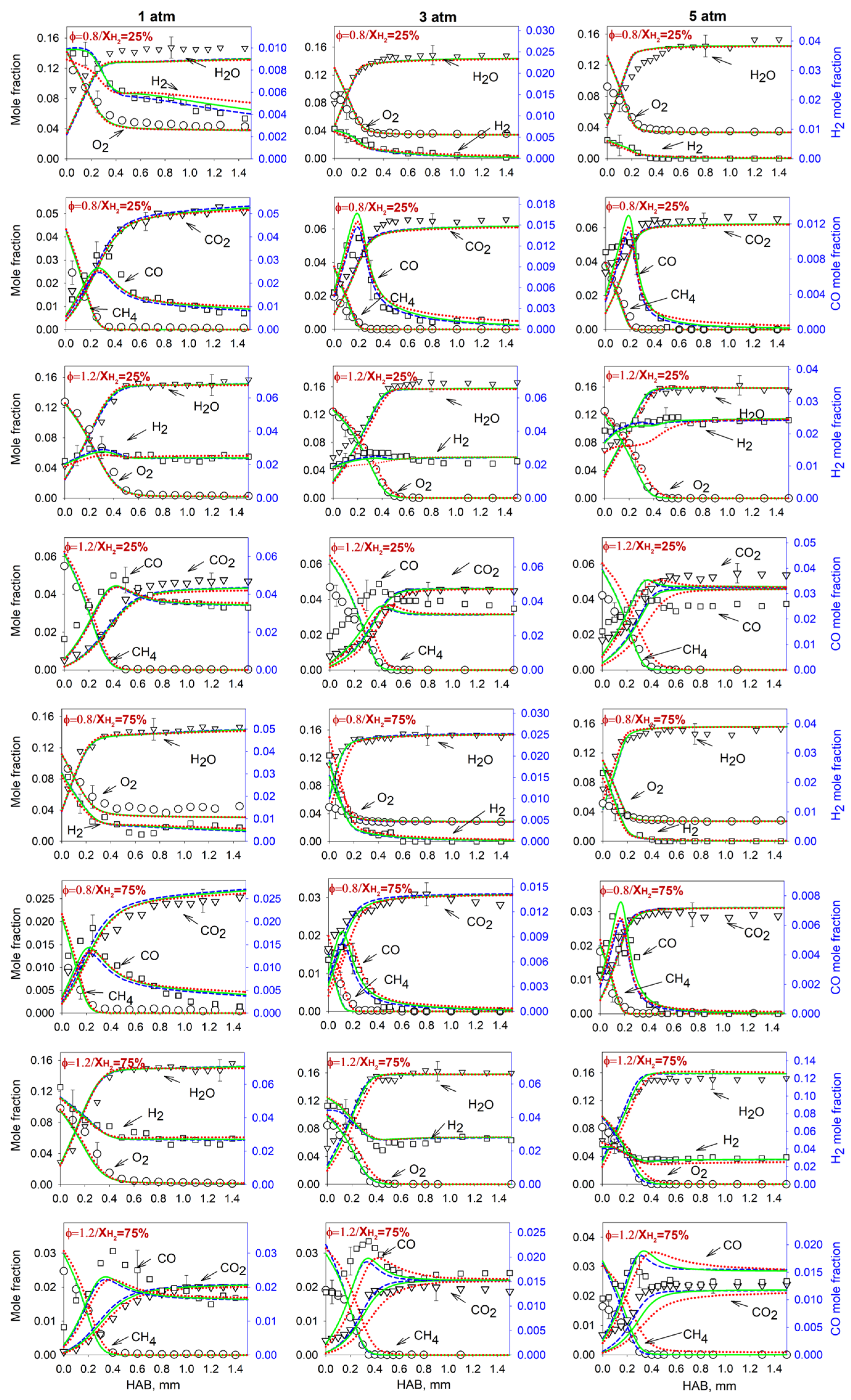
4.1. Flame Temperature and Mole Fraction Profiles of Major Flame Species
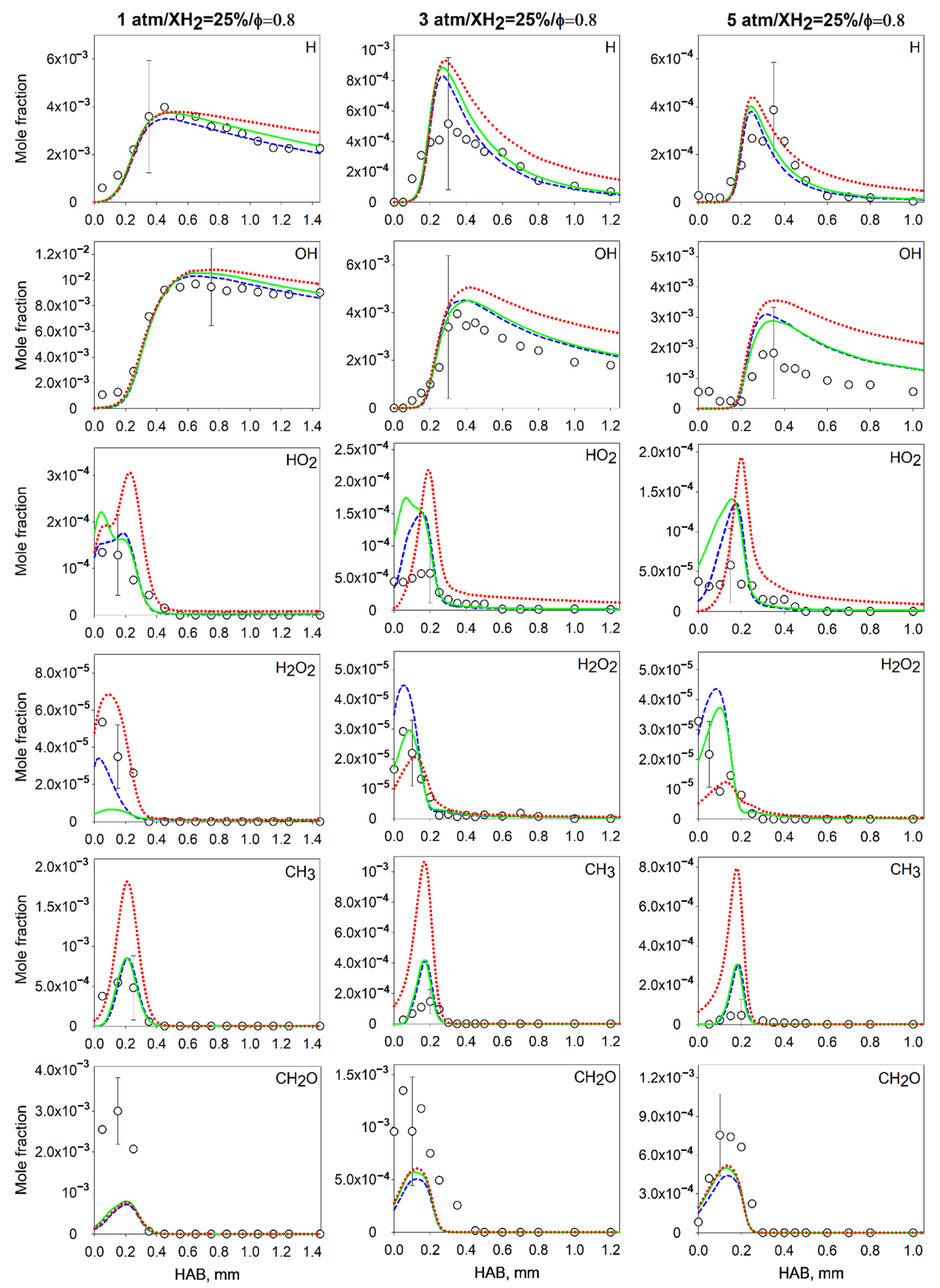
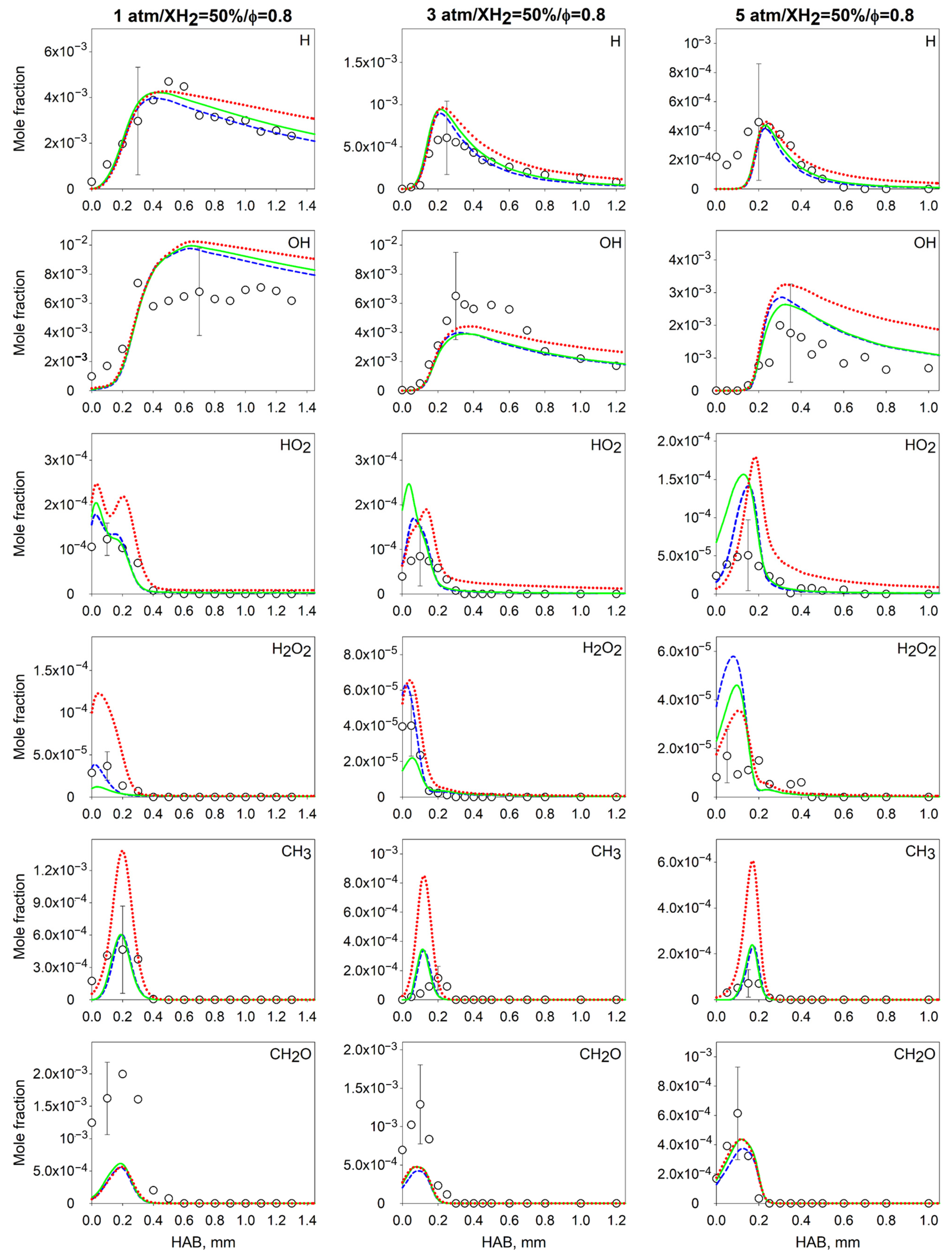
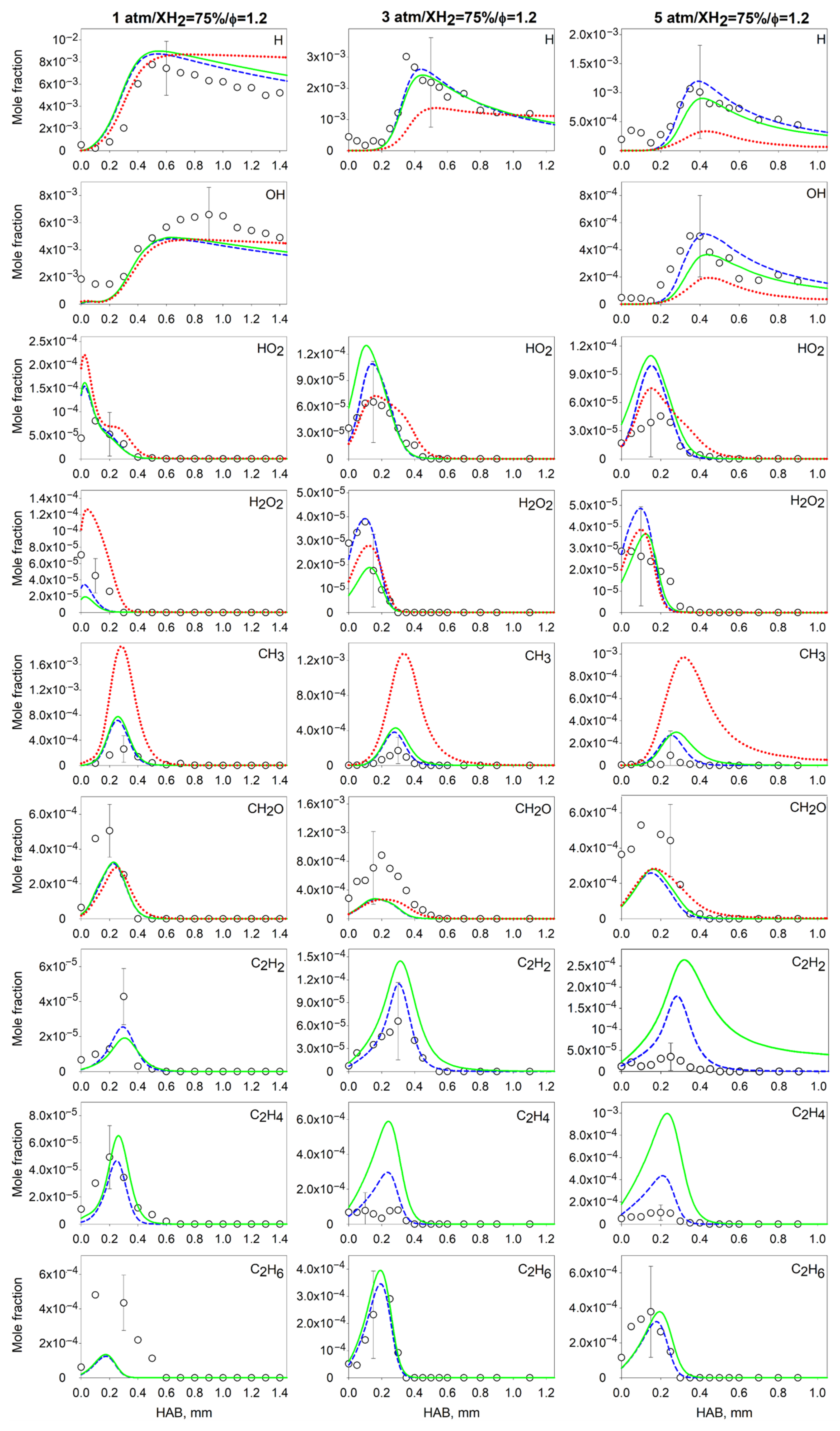
4.2. Measurements and Predictions of the Mole Fractions of Intermediates
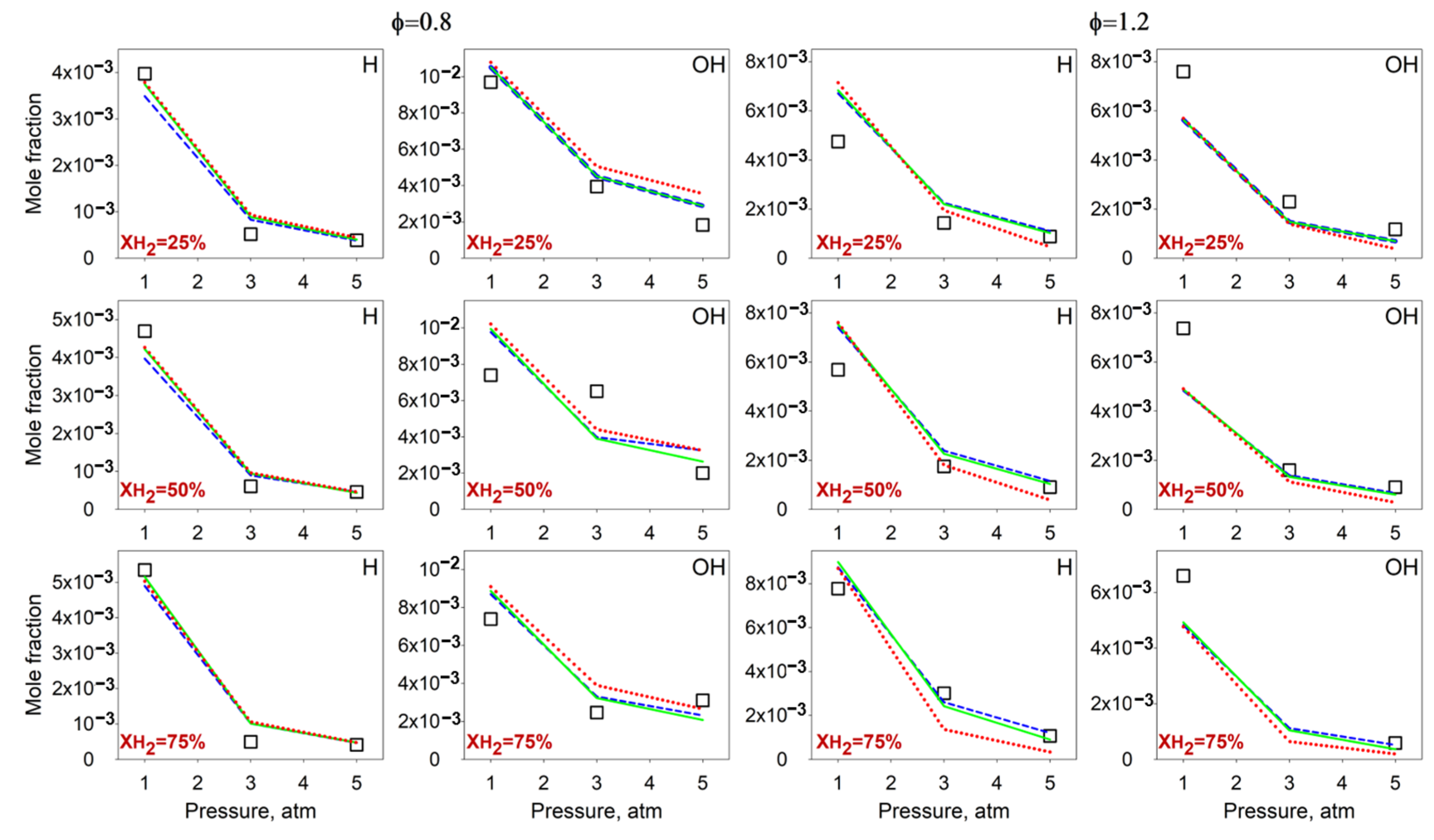
4.3. Effect of the Pressure on the Flame Intermediates
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A


References
- Lefebvre, A.H.; Ballal, D.R. Gas Turbine Combustion: Alternative Fuels and Emissions, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2010; ISBN 978-1-4200-8605-8. [Google Scholar]
- Taamallah, S.; Vogiatzaki, K.; Alzahrani, F.M.; Mokheimer, E.M.A.; Habib, M.A.; Ghoniem, A.F. Fuel Flexibility, Stability and Emissions in Premixed Hydrogen-Rich Gas Turbine Combustion: Technology, Fundamentals, and Numerical Simulations. Appl. Energy 2015, 154, 1020–1047. [Google Scholar] [CrossRef]
- Ozturk, M.; Dincer, I. System Development and Assessment for Green Hydrogen Generation and Blending with Natural Gas. Energy 2022, 261, 125233. [Google Scholar] [CrossRef]
- Makaryan, I.A.; Sedov, I.V.; Salgansky, E.A.; Arutyunov, A.V.; Arutyunov, V.S. A Comprehensive Review on the Prospects of Using Hydrogen–Methane Blends: Challenges and Opportunities. Energies 2022, 15, 2265. [Google Scholar] [CrossRef]
- Yan, F.; Xu, L.; Wang, Y. Application of Hydrogen Enriched Natural Gas in Spark Ignition IC Engines: From Fundamental Fuel Properties to Engine Performances and Emissions. Renew. Sustain. Energy Rev. 2018, 82, 1457–1488. [Google Scholar] [CrossRef]
- Xiang, L.; Jiang, H.; Ren, F.; Chu, H.; Wang, P. Numerical Study of the Physical and Chemical Effects of Hydrogen Addition on Laminar Premixed Combustion Characteristics of Methane and Ethane. Int. J. Hydrogen Energy 2020, 45, 20501–20514. [Google Scholar] [CrossRef]
- Dong, H.; Li, R.; Zhao, W.; Zhang, Y.; Chen, X.; Zhang, Q.; Cao, M.; Liu, F. Chemical Kinetics Properties and the Influences of Different Hydrogen Blending Ratios on Reactions of Natural Gas. Case Stud. Therm. Eng. 2023, 41, 102676. [Google Scholar] [CrossRef]
- Ghenai, C. Combustion of Sustainable and Renewable Biohythane Fuel in Trapped Vortex Combustor. Case Stud. Therm. Eng. 2019, 14, 100498. [Google Scholar] [CrossRef]
- Agostinelli, P.W.; Laera, D.; Chterev, I.; Boxx, I.; Gicquel, L.; Poinsot, T. Large Eddy Simulations of Mean Pressure and H2 Addition Effects on the Stabilization and Dynamics of a Partially-Premixed Swirled-Stabilized Methane Flame. Combust. Flame 2023, 249, 112592. [Google Scholar] [CrossRef]
- Lu, T.; Law, C.K. A Directed Relation Graph Method for Mechanism Reduction. Proc. Combust. Inst. 2005, 30, 1333–1341. [Google Scholar] [CrossRef]
- Franzelli, B.; Riber, E.; Cuenot, B. Impact of the Chemical Description on a Large Eddy Simulation of a Lean Partially Premixed Swirled Flame. Comptes Rendus Mécanique 2013, 341, 247–256. [Google Scholar] [CrossRef]
- Drost, S.; Eckart, S.; Yu, C.; Schießl, R.; Krause, H.; Maas, U. Numerical and Experimental Investigations of CH4/H2 Mixtures: Ignition Delay Times, Laminar Burning Velocity and Extinction Limits. Energies 2023, 16, 2621. [Google Scholar] [CrossRef]
- Davazdah Emami, S.; Kasmani, R.M.; Hamid, M.D.; Che Hassan, C.R.; Mokhtar, K.M. Kinetic and Dynamic Analysis of Hydrogen-Enrichment Mixtures in Combustor Systems—A Review Paper. Renew. Sustain. Energy Rev. 2016, 62, 1072–1082. [Google Scholar] [CrossRef]
- Eckart, S.; Zsély, I.G.; Krause, H.; Turányi, T. Effect of the Variation of Oxygen Concentration on the Laminar Burning Velocities of Hydrogen-Enriched Methane Flames. Int. J. Hydrogen Energy 2023, in press. [CrossRef]
- AL-Khafaji, M.; Yang, J.; Tomlin, A.S.; Thompson, H.M.; de Boer, G.; Liu, K.; Morsy, M.E. Laminar Burning Velocities and Markstein Numbers for Pure Hydrogen and Methane/Hydrogen/Air Mixtures at Elevated Pressures. Fuel 2023, 354, 129331. [Google Scholar] [CrossRef]
- Nilsson, E.J.K.; van Sprang, A.; Larfeldt, J.; Konnov, A.A. The Comparative and Combined Effects of Hydrogen Addition on the Laminar Burning Velocities of Methane and Its Blends with Ethane and Propane. Fuel 2017, 189, 369–376. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, X.; Wei, L.; Zhang, J.; Tang, C.; Huang, Z. Experimental and Modeling Study on Auto-Ignition Characteristics of Methane/Hydrogen Blends under Engine Relevant Pressure. Int. J. Hydrogen Energy 2012, 37, 19168–19176. [Google Scholar] [CrossRef]
- Petersen, E.L.; Hall, J.M.; Smith, S.D.; de Vries, J.; Amadio, A.R.; Crofton, M.W. Ignition of Lean Methane-Based Fuel Blends at Gas Turbine Pressures. J. Eng. Gas Turbines Power 2007, 129, 937–944. [Google Scholar] [CrossRef]
- Jin, H.; Yuan, W.; Li, W.; Yang, J.; Zhou, Z.; Zhao, L.; Li, Y.; Qi, F. Combustion Chemistry of Aromatic Hydrocarbons. Prog. Energy Combust. Sci. 2023, 96, 101076. [Google Scholar] [CrossRef]
- Yang, X.; Wang, T.; Zhang, Y.; Zhang, H.; Wu, Y.; Zhang, J. Hydrogen Effect on Flame Extinction of Hydrogen-Enriched Methane/Air Premixed Flames: An Assessment from the Combustion Safety Point of View. Energy 2022, 239, 122248. [Google Scholar] [CrossRef]
- Long, A.E.; Burbano, H.; Speth, R.L.; Movaghar, A.; Egolfopoulos, F.N.; Green, W.H. An Apparatus-Independent Extinction Strain Rate in Counterflow Flames. Proc. Combust. Inst. 2019, 37, 1979–1987. [Google Scholar] [CrossRef]
- Fotache, C.G.; Kreutz, T.G.; Law, C.K. Ignition of Hydrogen-Enriched Methane by Heated Air. Combust. Flame 1997, 110, 429–440. [Google Scholar] [CrossRef]
- Wang, J.; Hu, E.; Huang, Z.; Ma, Z.; Tian, Z.; Wang, J.; Li, Y. An Experimental Study of Premixed Laminar Methane/Oxygen/Argon Flames Doped with Hydrogen at Low Pressure with Synchrotron Photoionization. Chin. Sci. Bull. 2008, 53, 1262–1269. [Google Scholar] [CrossRef]
- Cong, T.L.; Dagaut, P. Experimental and Detailed Kinetic Modeling of the Oxidation of Methane and Methane/Syngas Mixtures and Effect of Carbon Dioxide Addition. Combust. Sci. Technol. 2008, 180, 2046–2091. [Google Scholar] [CrossRef]
- Katoh, A.; Oyama, H.; Kitagawa, K.; Gupta, A.K. Visualization of OH Radical Distribution in a Methane-Hydrogen Mixture Flame by Isotope Shift/Planar Laser Induced Fluorescence Spectroscopy. Combust. Sci. Technol. 2006, 178, 2061–2074. [Google Scholar] [CrossRef]
- GRI-Mech 3.0. Available online: http://combustion.berkeley.edu/gri-mech/version30/text30.html#cite (accessed on 5 January 2022).
- Sun, Y.; Zhang, Y.; Huang, M.; Li, Q.; Wang, W.; Zhao, D.; Cheng, S.; Deng, H.; Du, J.; Song, Y.; et al. Effect of Hydrogen Addition on the Combustion and Emission Characteristics of Methane under Gas Turbine Relevant Operating Condition. Fuel 2022, 324, 124707. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, X.; Wang, T.; Hou, X.; Zhang, J.; Zheng, S. Numerical Study of the Chemical, Thermal and Diffusion Effects of H2 and CO Addition on the Laminar Flame Speeds of Methane–Air Mixture. Int. J. Hydrogen Energy 2015, 40, 8475–8483. [Google Scholar] [CrossRef]
- Park, J.-W.; Oh, C.B. Flame Structure and Global Flame Response to the Equivalence Ratios of Interacting Partially Premixed Methane and Hydrogen Flames. Int. J. Hydrogen Energy 2012, 37, 7877–7888. [Google Scholar] [CrossRef]
- Wang, J.; Huang, Z.; Tang, C.; Miao, H.; Wang, X. Numerical Study of the Effect of Hydrogen Addition on Methane–Air Mixtures Combustion. Int. J. Hydrogen Energy 2009, 34, 1084–1096. [Google Scholar] [CrossRef]
- Stylianidis, N.; Azimov, U.; Birkett, M. Investigation of the Effect of Hydrogen and Methane on Combustion of Multicomponent Syngas Mixtures Using a Constructed Reduced Chemical Kinetics Mechanism. Energies 2019, 12, 2442. [Google Scholar] [CrossRef]
- Felden, A.; Esclapez, L.; Riber, E.; Cuenot, B.; Wang, H. Including Real Fuel Chemistry in LES of Turbulent Spray Combustion. Combust. Flame 2018, 193, 397–416. [Google Scholar] [CrossRef]
- Felden, A.; Pepiot, P.; Esclapez, L.; Riber, E.; Cuenot, B. Including Analytically Reduced Chemistry (ARC) in CFD Applications. Acta Astronaut. 2019, 158, 444–459. [Google Scholar] [CrossRef]
- Mulla, I.A.; Dowlut, A.; Hussain, T.; Nikolaou, Z.M.; Chakravarthy, S.R.; Swaminathan, N.; Balachandran, R. Heat Release Rate Estimation in Laminar Premixed Flames Using Laser-Induced Fluorescence of CH2O and H-Atom. Combust. Flame 2016, 165, 373–383. [Google Scholar] [CrossRef]
- Carter, C.D.; Skiba, A.W.; Boxx, I.; Allison, P.M. Optimal Approaches to Formaldehyde Planar Laser-Induced Fluorescence. Combust. Flame 2022, 246, 112431. [Google Scholar] [CrossRef]
- Wan, M.; Sun, M.; Wu, G.; Gao, Q.; Li, B.; Wang, H.; Sun, Y.; Zhu, J. Simultaneous CH3 and CH2O Imaging in Premixed Turbulent Flames for Instantaneous Flame Structure Visualization. Acta Astronaut. 2022, 191, 317–325. [Google Scholar] [CrossRef]
- Osipova, K.N.; Sarathy, S.M.; Korobeinichev, O.P.; Shmakov, A.G. Chemical Structure of Premixed Ammonia/Hydrogen Flames at Elevated Pressures. Combust. Flame 2022, 246, 112419. [Google Scholar] [CrossRef]
- Botha, J.P.; Spalding, D.B. The Laminar Flame Speed of Propane/Air Mixtures with Heat Extraction from the Flame. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1954, 225, 71–96. [Google Scholar] [CrossRef]
- Kim, Y.-K.; Irikura, K.K.; Rudd, M.E.; Ali, M.A.; Stone, P.M. Electron-Impact Cross Sections for Ionization and Excitation Database. Available online: https://www.nist.gov/pml/electron-impact-cross-sections-ionization-and-excitation-database (accessed on 26 October 2016).
- Cool, T.A.; Nakajima, K.; Taatjes, C.A.; McIlroy, A.; Westmoreland, P.R.; Law, M.E.; Morel, A. Studies of a Fuel-Rich Propane Flame with Photoionization Mass Spectrometry. Proc. Combust. Inst. 2005, 30, 1681–1688. [Google Scholar] [CrossRef]
- Dmitriev, A.M.; Agafontsev, M.V.; Loboda, E.L.; Knyazkov, D.A.; Korobeinichev, O.P. Measuring the Surface Temperature of a Molecular Beam Probe in the Flame Front at Pressures of 1–5 Atm. Combust. Explos. Shock Waves 2019, 55, 555–561. [Google Scholar] [CrossRef]
- Tereshchenko, A.G.; Knyazkov, D.A.; Skovorodko, P.A.; Paletsky, A.A.; Korobeinichev, O.P. Perturbations of the Flame Structure Due to a Thermocouple. I. Experiment. Combust. Explos. Shock Waves 2011, 47, 403–413. [Google Scholar] [CrossRef]
- Shaddix, C.R. Correcting Thermocouple Measurements for Radiation Loss: A Critical Review; Sandia National Labs.: Livermore, CA, USA, 1999. [Google Scholar]
- Ansys Chemkin-Pro: Combustion Simulation Software. Available online: https://www.ansys.com/products/fluids/ansys-chemkin-pro (accessed on 13 March 2020).
- Sarathy, S.M.; Thomson, M.J.; Togbé, C.; Dagaut, P.; Halter, F.; Mounaim-Rousselle, C. An Experimental and Kinetic Modeling Study of N-Butanol Combustion. Combust. Flame 2009, 156, 852–864. [Google Scholar] [CrossRef]
- Li, Y.; Zhou, C.-W.; Somers, K.P.; Zhang, K.; Curran, H.J. The Oxidation of 2-Butene: A High Pressure Ignition Delay, Kinetic Modeling Study and Reactivity Comparison with Isobutene and 1-Butene. Proc. Combust. Inst. 2017, 36, 403–411. [Google Scholar] [CrossRef]
- Mechanism Workbench—Kintech Laboratory—R&D Service and Software for Predicitve Physical Chemical Modeling. Available online: https://www.kintechlab.com/products/mechanism-workbench/ (accessed on 29 August 2023).
- Dmitriev, A.M.; Knyazkov, D.A.; Bolshova, T.A.; Tereshchenko, A.G.; Paletsky, A.A.; Shmakov, A.G.; Korobeinichev, O.P. Structure of CH4/O2/Ar Flames at Elevated Pressures Studied by Flame Sampling Molecular Beam Mass Spectrometry and Numerical Simulation. Combust. Flame 2015, 162, 3946–3959. [Google Scholar] [CrossRef]
- Moccia, V.; D’Alessio, J. Burning Behaviour of High-Pressure CH4-H2-Air Mixtures. Energies 2013, 6, 97–116. [Google Scholar] [CrossRef]
- Dirrenberger, P.; Le Gall, H.; Bounaceur, R.; Herbinet, O.; Glaude, P.-A.; Konnov, A.; Battin-Leclerc, F. Measurements of Laminar Flame Velocity for Components of Natural Gas. Energy Fuels 2011, 25, 3875–3884. [Google Scholar] [CrossRef]
- Cheng, R.K.; Oppenheim, A.K. Autoignition in Methane hydrogen Mixtures. Combust. Flame 1984, 58, 125–139. [Google Scholar] [CrossRef]
- Mei, B.; Zhang, J.; Ma, S.; Li, W.; Dmitriev, A.; Shmakov, A.; Bolshova, T.; Knyazkov, D.; Li, Y. Revisit Flame Chemistry of Propene at Elevated Pressures: Insight into Pressure Effects on Chemical Structure and Laminar Flame Propagation. Combust. Flame 2023, 251, 112725. [Google Scholar] [CrossRef]
- Knyazkov, D.A.; Dmitriev, A.M.; Shvartsberg, V.M.; Osipova, K.N.; Shmakov, A.G.; Korobeinichev, O.P. Study of the Chemical Structure of Laminar Premixed H2/CH4/C3H8/O2/Ar Flames at 1–5 Atm. Energy Fuels 2017, 31, 11377–11390. [Google Scholar] [CrossRef]
- Knyazkov, D.A.; Dmitriev, A.M.; Bolshova, T.A.; Shvartsberg, V.M.; Shmakov, A.G.; Korobeinichev, O.P. Structure of Premixed H2/O2/Ar Flames at 1–5atm Studied by Molecular Beam Mass Spectrometry and Numerical Simulation. Proc. Combust. Inst. 2017, 36, 1233–1240. [Google Scholar] [CrossRef]
- Abhinavam Kailasanathan, R.K.; Yelverton, T.L.B.; Fang, T.; Roberts, W.L. Effect of Diluents on Soot Precursor Formation and Temperature in Ethylene Laminar Diffusion Flames. Combust. Flame 2013, 160, 656–670. [Google Scholar] [CrossRef]
- Dmitriev, A.M.; Osipova, K.N.; Knyazkov, D.A.; Shmakov, A.G. Propylene Oxide Addition Effect on the Chemical Speciation of a Fuel-Rich Premixed n-Heptane/Toluene Flame. ACS Omega 2022, 7, 46900–46914. [Google Scholar] [CrossRef]
- Miller, J.A.; Klippenstein, S.J. The H + C2H2 (+M) ⇄ C2H3 (+M) and H + C2H2 (+M) ⇄ C2H5 (+M) Reactions: Electronic Structure, Variational Transition-State Theory, and Solutions to a Two-Dimensional Master Equation. Phys. Chem. Chem. Phys. 2004, 6, 1192–1202. [Google Scholar] [CrossRef]
- Wang, K.; Villano, S.M.; Dean, A.M. Experimental and Kinetic Modeling Study of Butene Isomer Pyrolysis: Part I. 1- and 2-Butene. Combust. Flame 2016, 173, 347–369. [Google Scholar] [CrossRef]




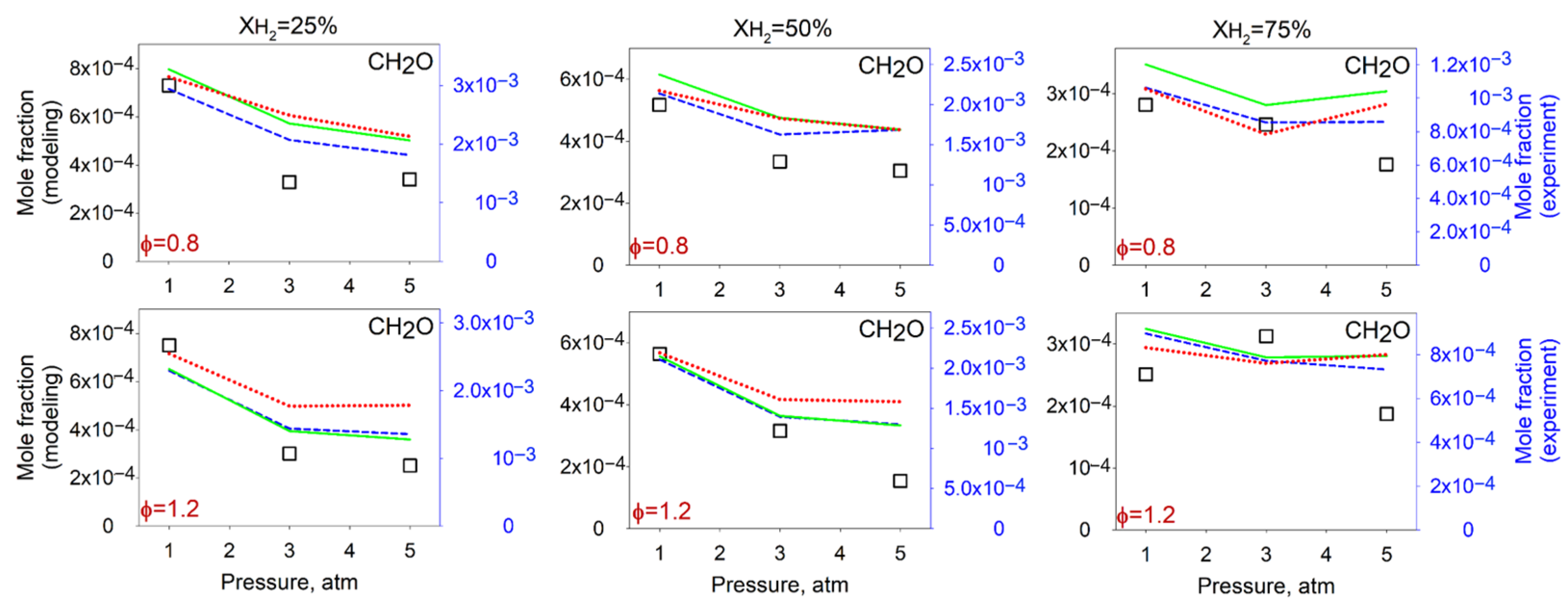

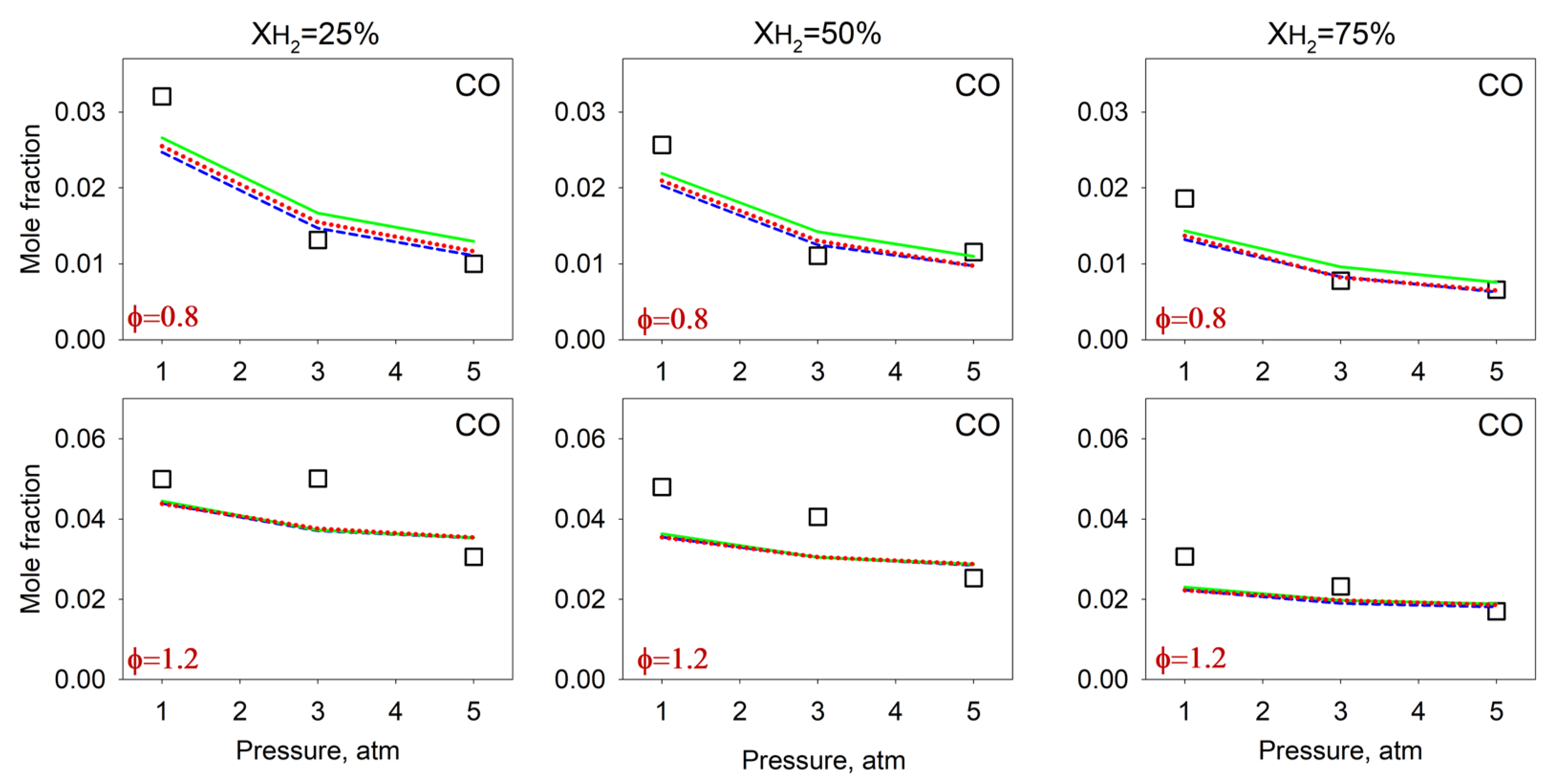
| φ | Reactant Mole Fraction | Mass Flow Rate (g/(cm2 s)) | XH2, % * | |||
|---|---|---|---|---|---|---|
| CH4 | H2 | O2 | Ar | |||
| 0.8 | 0.049 | 0.049 | 0.152 | 0.75 | 0.04513 | 50 |
| 1.2 | 0.061 | 0.061 | 0.128 | 0.75 | 0.04534 | 50 |
| 0.8 | 0.03 | 0.09 | 0.131 | 0.75 | 0.04797 | 75 |
| 1.2 | 0.036 | 0.108 | 0.105 | 0.75 | 0.05226 | 75 |
| 0.8 | 0.062 | 0.021 | 0.168 | 0.75 | 0.04285 | 25 |
| 1.2 | 0.08 | 0.027 | 0.144 | 0.75 | 0.04098 | 25 |
| m/z | Formula | Species Name | IE (eV) | E (eV) | Calibration | Accuracy |
|---|---|---|---|---|---|---|
| 1 | H | atomic hydrogen | 13.6 | 16.2 | RICS * vs. H2 | ±50% |
| 2 | H2 | hydrogen | 15.43 | 16.65 | Balance O | ±20% |
| 15 | CH3 | methyl radical | 9.84 | 12.3 | RICS vs. CH4 | ±50% |
| 16 | CH4 | methane | 12.71 | 14.35 | Direct | ±20% |
| 17 | OH | hydroxyl radical | 13.02 | 16.2 | RICS vs. H2O | ±50% |
| 18 | H2O | water | 12.62 | 15.4 | Balance O | ±20% |
| 26 | C2H2 | acetylene | 11.41 | 12.3 | Direct | ±50% |
| 28 | C2H4 | ethylene | 10.53 | 12.3 | Direct | ±50% |
| 28 | CO | carbon monoxide | 14.01 | 15.4 | Balance O | ±20% |
| 30 | CH2O | formaldehyde | 10.88 | 11.5 | RICS vs. C2H6 | ±50% |
| 30 | C2H6 | ethane | 11.52 | 12.3 | Direct | ±50% |
| 32 | O2 | oxygen | 12.07 | 14.35 | Direct | ±20% |
| 33 | HO2 | peroxide radical | 11.35 | 16.65 | RICS vs. O2 | ±50% |
| 34 | H2O2 | hydrogen peroxide | 10.58 | 14.35 | Direct | ±50% |
| 40 | Ar | argon | 15.76 | 16.3 | Direct | ±10% |
| 44 | CO2 | carbon dioxide | 13.77 | 15.4 | Balance O | ±20% |
| N | Reaction | A, mole-cm-sec-K | b | E, cal/mole |
|---|---|---|---|---|
| R1 | H2 + O ↔ H + OH | 5.08 × 104 | 2.67 | 6292.0 |
| R2 | H2 + OH ↔ H + H2O | 4.38 × 1013 | 0.0 | 6990.0 |
| R3 | O2 + H ↔ O + OH | 1.04 × 1014 | 0.0 | 15,286.0 |
| R4 | H2O2 (+M) ↔ 2OH (+M) Low-pressure limit: TROE centering: 0.43, 1.0 × 10−30, 1.0 × 1030 Enhanced third-body efficiencies: O2 = 1.2, H2 = 3.7, H2O = 7.65, CO = 2.8, CO2 = 1.6, H2O2 = 7.7 | 2.00 × 1012 2.49 × 1024 | 0.9 −2.3 | 48,749.0 48,749.0 |
| R5 | HO2 + H ↔ 2OH | 7.079 × 1013 | 0.0 | 295.0 |
| R6 | H + O2 (+M) ↔ HO2 (+M) Low-pressure limit: TROE centering: 0.67, 1.0 × 10−30, 1.0 × 1030, 1.0 × 1030 Enhanced third-body efficiencies: H2 = 1.3, H2O = 10, CO = 1.9, CO2 = 3.8, CH4 = 2, AR = 0.5 | 4.65 × 1012 1.737 × 1019 | 0.44 −1.23 | 0.0 0.0 |
| R7 | HO2 + HO2 ↔ H2O2 + O2 | 1.40 × 10−1 | 4.0 | −4000.0 |
| R8 | CH3 + O ↔ CH2O + H | 1.00 × 1013 | 0.1 | −136.0 |
| R9 | CO + OH ↔ CO2 + H | 7.015 × 104 | 2.053 | −355.7 |
| R10 | CH3 + H (+M) ↔ CH4 (+M) Low-pressure limit: TROE centering: 0.783, 74.0, 2941.0, 6964.0 Enhanced third-body efficiencies: H2 = 2, H2O = 6, CO = 1.5, CO2 = 2, CH4 = 2, AR = 0.7, N2 = 1.5 | 1.27 × 1016 2.477 × 1033 | −0.63 −4.76 | 383.0 2440.0 |
| R11 | CH4 + H ↔ CH3 + H2 | 6.14 × 105 | 2.5 | 9587.0 |
| R12 | CH4 + O ↔ CH3 + OH | 1.02 × 109 | 1.5 | 8600.0 |
| R13 | CH4 + OH ↔ CH3 + H2O | 5.83 × 104 | 2.6 | 2190.0 |
| R14 | CH3 + HO2 ↔ CH4 + O2 | 2.32 × 105 | 2.23 | −3022.0 |
| R15 | CH2 + O2 ↔ HCO + OH | 1.06 × 1013 | 0.0 | 1500.0 |
| R16 | CH3 + O2↔CH2O + OH | 2.641 | 3.283 | 8105.0 |
| R17 | CH3 + OH ↔ CH2OH + H | |||
| P = 1 atm: | 4.686 × 1010 | 0.833 | 3566.0 | |
| P = 10 atm: | 7.00 × 1012 | 0.134 | 5641.0 | |
| P = 100 atm: | 1.259 × 1014 | −0.186 | 8601.0 | |
| R18 | CH3 + OH ↔ CH2 + H2O | 4.293 × 104 | 2.56 | 3997.8 |
| R19 | CH3 + HO2 ↔ CH3O + OH | 5.00 × 1011 | 0.269 | −687.5 |
| R20 | CH2OH + O2 ↔ CH2O + HO2 | 2.41 × 1014 | 0.0 | 5017.0 |
| R21 | CH3O + O2 ↔ CH2O + HO2 | 4.38 × 10−19 | 9.5 | −5501.0 |
| R22 | CH2O + H ↔ HCO + H2 | 5.74 × 107 | 1.9 | 2740.0 |
| R23 | CH2O + OH ↔ HCO + H2O | 7.82 × 107 | 1.63 | −1055.0 |
| R24 | CH2O + CH3 ↔ HCO + CH4 | 3.83 × 10 | 3.36 | 4312.0 |
| R25 | HCO (+M) ↔ H + CO (+M) Enhanced third-body efficiencies: H2 = 2, H2O = 6, CO = 1.5, CO2 = 2, CH4 = 2 | 5.70 × 1011 | 0.66 | 14,870.0 |
| R26 | HCO + O2 ↔ CO + HO2 | 7.58 × 1012 | 0.0 | 410.0 |
| R27 | HCO + H ↔ CO + H2 | 7.34 × 1013 | 0.0 | 0.0 |
| R28 | HCO + OH ↔ CO + H2O | 3.011 × 1013 | 0.0 | 0.0 |
| R29 | HCO + CH3 ↔ CH4 + CO | 2.65 × 1013 | 0.0 | 0.0 |
| R30 | CH2O + H (+M) ↔ CH2OH (+M) Low-pressure limit: TROE centering: 0.7187, 103.0, 1291.0, 4160.0 Enhanced third-body efficiencies: H2 = 2, H2O = 6, CO = 1.5, CO2 = 2, CH4 = 2 | 5.40 × 1011 1.27 × 1032 | 0.454 −4.82 | 3600.0 6530.0 |
| R31 | CH3O (+M) ↔ CH2O + H (+M) Low-pressure limit: TROE centering: 0.9, 2500.0, 1300.0, 1.0 × 1099 Enhanced third-body efficiencies: H2 = 2, H2O = 6, CO = 1.5, CO2 = 2, CH4 = 2 | 6.80 × 1013 1.867 × 1025 | 0.0 −3.0 | 26,170.0 24,307.0 |
| φ | XH2, % | Laminar Burning Velocity, cm/s | |||
|---|---|---|---|---|---|
| Experiment [50] | AramcoMech 2.0 | RMech1 | RMech2 | ||
| 0.8 | 67 | 58.8 | 54.9 | 55.2 | 55.3 |
| 1.0 | 67 | 89.0 | 75.3 | 76.9 | 76.7 |
| 1.2 | 67 | 95.6 | 80.3 | 82.0 | 78.2 |
| 0.8 | 50 | 42.8 | 40.0 | 39.9 | 40.8 |
| 1.0 | 50 | 62.0 | 56.1 | 57.3 | 58.5 |
| 1.2 | 50 | 66.2 | 56.2 | 57.8 | 56.6 |
| 0.8 | 30 | 31.9 | 32.2 | 31.9 | 33.4 |
| 1.0 | 30 | 47.5 | 44.3 | 45.1 | 46.9 |
| 1.2 | 30 | 49.1 | 42.8 | 44.2 | 44.0 |
| P, atm | XH2, % | H | CH3 | OH | HO2 | H2O2 | CO | CH2O |
|---|---|---|---|---|---|---|---|---|
| 1 | 25 | −14 | 36 | 6 | 24 | −50 | −30 | −320 |
| 3 | 25 | 38 | 65 | 13 | 62 | 20 | 11 | −168 |
| 5 | 25 | −2 | 85 | 41 | 57 | 25 | 10 | −81 |
| 1 | 50 | −18 | 23 | 24 | 31 | −72 | −26 | −260 |
| 3 | 50 | 32 | 56 | −63 | 50 | 37 | 12 | −206 |
| 5 | 50 | −10 | 69 | 30 | 64 | 55 | −24 | −61 |
| 1 | 75 | −9 | 51 | 15 | 21 | −6 | −41 | −209 |
| 3 | 75 | 51 | 44 | 25 | 59 | 47 | 6 | −100 |
| 5 | 75 | 33 | 48 | −35 | 55 | 52 | −5 | −100 |
| P, atm | XH2, % | H | CH3 | OH | HO2 | H2O2 | CO | CH2O | C2H2 | C2H4 | C2H6 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 25 | 29 | 59 | −40 | 35 | −148 | −14 | −313 | 63 | 58 | −19 |
| 3 | 25 | 36 | 68 | −51 | 46 | −139 | −35 | −164 | 67 | 73 | 41 |
| 5 | 25 | 21 | 79 | −55 | 40 | 3 | 13 | −133 | 80 | 79 | 32 |
| 1 | 50 | 23 | 61 | −53 | 33 | −130 | −35 | −223 | 63 | 54 | −120 |
| 3 | 50 | 27 | 73 | −15 | 40 | −5 | −33 | −237 | 73 | 72 | 43 |
| 5 | 50 | 22 | 73 | −35 | 51 | 12 | 11 | −76 | 80 | 80 | 19 |
| 1 | 75 | 11 | 64 | −37 | 47 | −106 | −37 | −61 | −68 | −6 | −244 |
| 3 | 75 | −16 | 56 | 40 | −32 | −22 | −224 | 43 | 73 | 16 | |
| 5 | 75 | 11 | 67 | −13 | 54 | 41 | 6 | −104 | 80 | 76 | −18 |
| φ | P, atm | XH2, % | H | CH3 | OH | HO2 | H2O2 | CO | CH2O | C2H2 | C2H4 | C2H6 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.8 | 1 | 25 | 7 | 0 | 2 | 26 | −81 | 8 | 11 | −54 | 93 | 24 |
| 0.8 | 3 | 25 | 7 | 1 | 0 | 16 | −34 | 14 | 13 | −52 | 117 | 10 |
| 0.8 | 5 | 25 | 6 | 0 | −7 | 4 | −14 | 17 | 14 | −64 | 122 | 7 |
| 0.8 | 1 | 50 | 6 | 0 | 2 | 15 | −69 | 8 | 11 | −59 | 77 | 22 |
| 0.8 | 3 | 50 | 5 | 3 | −2 | 45 | −65 | 14 | 13 | −51 | 123 | 16 |
| 0.8 | 5 | 50 | 5 | 3 | −8 | 10 | −20 | 18 | 17 | −60 | 135 | 12 |
| 0.8 | 1 | 75 | 5 | 2 | 2 | −1 | 9 | 8 | 13 | −63 | 46 | 24 |
| 0.8 | 3 | 75 | 0 | −2 | −2 | 29 | −83 | 16 | 12 | −60 | 126 | 30 |
| 0.8 | 5 | 75 | 2 | 6 | −10 | 19 | −32 | 20 | 21 | −55 | 164 | 20 |
| 1.2 | 1 | 25 | 2 | 6 | 4 | 62 | −77 | 1 | 1 | −7 | 68 | 16 |
| 1.2 | 3 | 25 | −2 | 7 | −3 | −2 | −30 | 1 | −3 | 9 | 82 | 9 |
| 1.2 | 5 | 25 | −8 | 9 | −8 | −6 | −33 | 0 | −6 | 17 | 90 | 10 |
| 1.2 | 1 | 50 | 2 | 8 | 1 | 50 | −89 | 2 | 2 | −8 | 66 | 18 |
| 1.2 | 3 | 50 | −5 | −4 | −4 | 13 | −49 | 0 | 1 | 7 | 87 | −8 |
| 1.2 | 5 | 50 | −10 | 9 | −10 | 6 | −29 | 1 | −1 | 23 | 95 | 11 |
| 1.2 | 1 | 75 | 3 | 9 | 2 | 5 | −44 | 3 | 2 | −25 | 40 | 8 |
| 1.2 | 3 | 75 | −7 | 13 | −7 | 19 | −52 | 4 | 2 | 25 | 98 | 14 |
| 1.2 | 5 | 75 | −25 | 10 | −30 | 11 | −25 | 4 | 8 | 48 | 128 | 18 |
| φ | P, atm | XH2, % | H | CH3 | OH | HO2 | H2O2 | CO | CH2O |
|---|---|---|---|---|---|---|---|---|---|
| 0.8 | 1 | 25 | 9 | 113 | 5 | 74 | 101 | 3 | 7 |
| 0.8 | 3 | 25 | 12 | 158 | 12 | 44 | −54 | 5 | 20 |
| 0.8 | 5 | 25 | 16 | 160 | 14 | 42 | −72 | 5 | 18 |
| 0.8 | 1 | 50 | 8 | 129 | 5 | 38 | 219 | 3 | 2 |
| 0.8 | 3 | 50 | 8 | 153 | 11 | 12 | 4 | 4 | 12 |
| 0.8 | 5 | 50 | 11 | 161 | 14 | 27 | −39 | 5 | 17 |
| 0.8 | 1 | 75 | 3 | 172 | 5 | 71 | 984 | 4 | −1 |
| 0.8 | 3 | 75 | 5 | 121 | 18 | 4 | 118 | −1 | −8 |
| 0.8 | 5 | 75 | 2 | 163 | 15 | 15 | 80 | 3 | 12 |
| 1.2 | 1 | 25 | 6 | 126 | 5 | 36 | −44 | 0 | 11 |
| 1.2 | 3 | 25 | −13 | 218 | −9 | −15 | −87 | 1 | 23 |
| 1.2 | 5 | 25 | −58 | 237 | −50 | −44 | −78 | 0 | 31 |
| 1.2 | 1 | 50 | 3 | 134 | 2 | 7 | 1 | 0 | 4 |
| 1.2 | 3 | 50 | −25 | 189 | −19 | −33 | −84 | 0 | 16 |
| 1.2 | 5 | 50 | −67 | 248 | −58 | −44 | −67 | 1 | 22 |
| 1.2 | 1 | 75 | −1 | 165 | −1 | 44 | 267 | 0 | −7 |
| 1.2 | 3 | 75 | −48 | 236 | −43 | −34 | −29 | 4 | −1 |
| 1.2 | 5 | 75 | −72 | 258 | −63 | −24 | −20 | 3 | 9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gerasimov, I.E.; Bolshova, T.A.; Osipova, K.N.; Dmitriev, A.M.; Knyazkov, D.A.; Shmakov, A.G. Flame Structure at Elevated Pressure Values and Reduced Reaction Mechanisms for the Combustion of CH4/H2 Mixtures. Energies 2023, 16, 7489. https://doi.org/10.3390/en16227489
Gerasimov IE, Bolshova TA, Osipova KN, Dmitriev AM, Knyazkov DA, Shmakov AG. Flame Structure at Elevated Pressure Values and Reduced Reaction Mechanisms for the Combustion of CH4/H2 Mixtures. Energies. 2023; 16(22):7489. https://doi.org/10.3390/en16227489
Chicago/Turabian StyleGerasimov, Ilya E., Tatyana A. Bolshova, Ksenia N. Osipova, Artëm M. Dmitriev, Denis A. Knyazkov, and Andrey G. Shmakov. 2023. "Flame Structure at Elevated Pressure Values and Reduced Reaction Mechanisms for the Combustion of CH4/H2 Mixtures" Energies 16, no. 22: 7489. https://doi.org/10.3390/en16227489
APA StyleGerasimov, I. E., Bolshova, T. A., Osipova, K. N., Dmitriev, A. M., Knyazkov, D. A., & Shmakov, A. G. (2023). Flame Structure at Elevated Pressure Values and Reduced Reaction Mechanisms for the Combustion of CH4/H2 Mixtures. Energies, 16(22), 7489. https://doi.org/10.3390/en16227489






