Abstract
A reactor is an important piece of equipment used for reactive power compensation in power system and has a significant impact on the safe operation of power system. Thermal behavior is one of the main causes of reactor failures. For an accurate analysis of the thermal behavior of reactors, electromagnetic–thermal–fluid multi-physics coupling modeling is chosen. However, there is a huge difference in size between the overall structure of the reactor and its insulating material, which makes it difficult to perform mesh generation, resulting in dense mesh and significantly increased solution degrees of freedom, thus making the solution of the reactor’s multi-physics field model very time-consuming. To address this, this paper proposes a simplified processing method to accelerate the solution calculation of the reactor’s multi-physics model. This method calculates the equivalent turns of each encapsulate with parallel coils in the reactor, simplifying the encapsulate into a single-layer coil, thereby greatly reducing the division and solution degrees of freedom of the multi-physics model, and thus accelerating the simulation calculation. Taking a BKDCKL-20000/35 dry-type air-core shunt reactor as an example, the outer diameter of the coil is nearly 12,000 times bigger than the coil insulation, which is a huge size difference. Both refined models and simplified models are established. Compared to the simulation results of the detailed model, the simplified model demonstrates good accuracy; the maximum relative error of temperature is just 2.19%. Meanwhile, the computational time of the simplified model is reduced by 35.7%, which shows promising effectiveness and significant potential for applying the optimization design and operation prediction of dry-type air-core shunt reactors for enhanced thermal performance.
1. Introduction
Dry-type air-core reactors are widely used in power systems to regulate current flows, mitigate voltage fluctuations, and enhance the stability of electrical networks [1,2,3,4]. Unlike traditional oil-filled reactors, dry-type reactors utilize air as a cooling medium and do not rely on any insulating liquids. This feature eliminates the risk of leakage, making them environmentally friendly and safe for indoor installations. Dry-type air-core reactors have gained popularity due to their various advantages, such as low maintenance, compactness and space efficiency, low noise, good reliability, etc., making them a good choice in modern power transmission and distribution systems. The accurate calculation of temperature distribution plays a crucial role in design and optimization procedures. Alternatively, operational concerns might lead to instances of localized overheating within the reactors. Temperature rise computation involves multi-physics coupling characteristics, including electromagnetic losses, fluid dynamics, and thermal behavior.
In previous studies, three main ways to calculate the temperature rise of the reactor have been used (the average temperature rise method [5], the finite difference method (FDM) [6], and the finite element method (FEM) [7]), features and drawbacks of which are compared and presented in Table 1. The average temperature method typically estimates a rise in winding temperature using an empirical formula. However, this formula lacks the ability to predict the highest temperature rise or pinpoint the locations of maximum temperature within dry-type air-core reactors [7]. The FDM approach effectively illustrates the heat transfer process, but it lacks precision in acquiring accurate localized fluid temperature data and identifying reactor hotspots [8]. With regards to the FEM, there are two ways of predicting temperature fields based on dry-type air-core reactors. One method involves calculating heat convection using a convection coefficient [9,10], but the calculation accuracy depends on the convection heat transfer coefficient, which limits its actual application [11]. Another approach entails constructing a fluid–thermal coupled FEM model to compute the temperature distributions within the air-core reactor without requiring a convection coefficient.

Table 1.
Comparison of methods used to calculate temperature rises in the reactor.
A two-way coupled multi-physics model is created in [7] which integrates electromagnetic, thermal, and fluid dynamics aspects to simulate the reactor’s behavior and takes into account the impact of temperature on electrical conductivity within the conductor region. It also simplifies the governing equations of coupled fluid–temperature fields in these reactors by employing dimensional analysis. The authors of [8] focus on simulating the temperature field of a dry-type air-core reactor. The study aims to understand how temperature is distributed within the reactor under different conditions. Through simulation, the researchers aim to gain insight into the factors that affect temperature distribution and how the reactor’s design can be optimized for efficient cooling and reliable operation. Losses are calculated in an air-core reactor using 2D and 3D magnetic field analyses, whereby temperature distribution is calculated through 2D and 3D fluid–thermal coupled FEM models in [12], and researchers have also examined the influence of sustaining bars and spider arms on the reactor’s behavior. The authors of [13] analyze the temperature rise in a forced air-cooled dry-type air-core reactor based on the coupling of magnetic, thermal, and fluid fields. The magnetic–thermal coupling analysis of a saturable reactor is presented in [14], and a fast-mapping interpolation technique between heterogeneous meshes is employed to transfer core loss information from the electromagnetic field to the fluid field, which enhances the realism of the distribution of heat sources. The magnetic field and temperature distribution patterns across the reactor body winding, as well as the upper and lower supports, is revealed in [15] using a mathematical approach that integrates reactor loss and the fluid–temperature field. A temperature field solution model that combines fluid flow and thermal effects is constructed in [16]. This model is based on a laminar–turbulent flow state and takes into account the influence of attitude and climate conditions. It provides insights into the temperature field characteristics of the reactor at varying altitudes, capturing a hotspot temperature rise pattern. A fluid–solid coupled heat transfer + radiation heat transfer model is built and compared with some experimental tests in [17]. Moreover, the variation law of the axial temperature in the encapsulations is investigated.
In practical operation, the air-core reactor can experience overheating or even reach a point of combustion, directly impacting the safety and stability of the power system. Research indicates that elevated temperatures in the encapsulation coils substantially degrade the electrical and insulating characteristics of insulation materials [15]. This phenomenon stands as a key contributor to reactor burnout. In order to improve the thermal efficiency and realize the safe operation of the reactor, different methods are proposed to optimize the structure parameters of it. An optimization method based on the orthogonal experiment design and the FEM is proposed in [11] in order to reduce the temperature rise in a dry-type air-core reactor with the rain cover, in which a fluid–thermal coupled model is established according to the design parameters of the reactor so that the specific temperature distribution can be attained. A thermal load optimization technique based on the heat dissipation characteristics of the encapsulations of the air-core reactor is introduced in [18] to enhance metal conductor utilization, whereby a fluid–thermal coupled FEM model is built to obtain detailed temperature field distribution results. The structure parameters of rain cover and the ventilation duct of the air-core reactor under forced air cooling are optimized based on a quantum genetic algorithm, with a fluid field–temperature coupled FEM model established to estimate the temperature distribution in [19]. A thermal efficiency optimization method using a dry-type core reactor based on the particle swarm optimization algorithm is proposed in [20]. This method enhances thermal efficiency and simultaneously reduces the metal conductor usage by optimizing the structure parameters of coils. In addition, a fluid–thermal coupled FEM model is also constructed to estimate the temperature rise in the reactor. According to the aforementioned analysis, following both an analysis of the reactor’s temperature rises under different operation conditions and an improvement in the thermal efficiency of air-core reactor using structure parameters optimization, a fluid–temperature model is required to estimate the temperature distribution of the reactor. However, both require significant computational efforts due to the multi-physics coupling problem. This is more obvious when a reactor has more than a dozen encapsulates, each of which consist of several coil layers because the coil layer usually coated with insulating material is relatively thin compared to the radius of the conductor. The relatively small size of the covered insulation of the conductor compared to the size of the reactor makes divide mesh in the reactors more difficult. To be more specific, the thin-layer insulation between the coils requires small mesh to guarantee the accuracy and convergence of the model, which makes the mesh around the coil rather dense, increasing the computation time. Therefore, a method used to compute the equivalent turns of encapsulates is proposed, combined with the formula used to compute the equivalent thermodynamic parameter characteristics of polyesterimide film-coated aluminum wire. As such, each encapsulate can be simplified as a single-layer coil wound with glass fiber dipped using epoxy, which is helpful in order to lessen the calculation burden and reduce the simulation time.
In this paper, a multi-physics FEM model based on electromagnetic–fluid–thermal coupling is established according to the structure parameters of a dry-type air-core reactor. At first, the electromagnetic losses, associated with the heat sources of the temperature rise, are computed using a field–circuit coupling method whereby the electrical conductivity of the conductor is defined as a function that is dependent on temperature. Then, a fluid–thermal coupling model is built to determine the temperature distribution within the reactor, in which a turbulent k-ε model is used for calculations. Furthermore, simulation results of the electromagnetic field, the temperature field, and the fluid field, obtained with the multi-physics refined model (each encapsulate consists of several coil layers), are presented. Finally, the temperature distribution obtained with the multi-physics simplified model (each encapsulate is simplified as a single-layer coil) is compared with the multi-physics refined model, which validates the accuracy and effectiveness of the method proposed. In the following sections, the methodology, simulation techniques, and results obtained from the multi-physics coupling analysis of dry-type air-core reactors will be examined.
2. Materials and Methods
2.1. Basic Theory
The electromagnetic losses of coils in the dry-type air-core reactor are the heat sources of the temperature field analysis. These losses consist of resistance losses () and eddy current losses () [11]. The formula for calculating resistance losses [21] in the reactor is shown in Equation (1).
where , , , , and represent the current, resistance, spatial diameter, number of turns, and wire cross-sectional area of the jth coil in the ith layer, respectively. σ is the electrical conductivity of the coil. m represents the number of layers in the reactor and represents the number of coils in the ith layer.
Since the diameter of the conductor in the reactor coil is much smaller than the spatial diameter of the coil, the magnetic flux density within the cross-section of a single-turn conductor can be considered to be uniformly distributed. Then, the calculation of the eddy current losses is based on the magnetic flux density at the center of the cross-section of a single-turn coil, using the principle of superposition. The formula of eddy current losses [22] in the reactor is shown in Equation (2).
where dij represents the conductor diameter of the jth coil in the ith layer, ω is the angular frequency, and B represents the magnetic flux density at the center of the cross-section of a single-turn coil.
Considering that the electrical conductivity in the conductor region of coil is dependent on temperature, their relationship is as follows [23]:
where is the electrical conductivity at the reference temperature, is the temperature coefficient, T is the actual temperature of the metal, and is the reference temperature.
According to heat transfer principles, the heat of a dry-type air-core reactor is primarily dissipated through three modes: conduction, convection, and radiation. Heat conduction is the main mode of heat transfer in the same encapsulate between different parts of the coil conductor, the coil conductor, and insulating materials. Its control equation is as follows [12]:
where represents the heat flux density, k is the thermal conductivity, ∇T represents the temperature gradient in the direction of heat transfer, and the negative sign indicates the heat flows from higher temperatures to lower temperatures.
Heat convection is the primary mode of heat transfer between the surface of the coils and the surrounding air. In this paper, the heat dissipation of the dry-type air-core reactor is achieved through air self-cooling, which refers to the heat transfer of natural convection. Due to the low flow velocity of buoyancy-driven natural convection, the Boussinesq assumption is satisfied in the fluid dynamics model, which allows the density term to be treated as a constant, simplifying the equations and facilitating the analysis of natural convection phenomena. The mass conservation equation, the momentum conservation equation, and the energy conservation equation are all satisfied at the same time, ensuring the conservation of mass, momentum, and energy within the fluid system. These equations are as follows [7]:
where ∇· denotes the divergence operator, ρ is the density of the fluid, u is the velocity vector, ∇p represents the pressure gradient, μ is the dynamic viscosity, ∇2u represents the Laplacian operator applied to the velocity vector, g is the gravitational acceleration (which is equal to ), Cp is the heat capacity at a constant pressure, k is the thermal conductivity, and Q represents volumetric heat sources or sinks.
Since natural convection is generated by the buoyancy of air due to density differences caused by the heat source under the influence of gravity, a fluid dynamics model based on the Rayleigh number needs to be determined through Equation (6) [24]:
where ρ is the air density, is the thermal expansion coefficient, L is the characteristic length, and Δ is the temperature change.
If , the buoyancy-driven convection is laminar, and the transition from laminar to turbulent flow occurs within the Rayleigh number range of . When the Rayleigh number exceeds , the buoyancy-driven flow becomes turbulent flow. In this paper, a turbulent flow model is chosen.
The fluid inside the air passage between the encapsulates absorbs heat, resulting in an increase in temperature and a decrease in air density, causing it to flow upwards. Due to the effect of viscosity, the fluid temperature in the air passage near the upper part of the encapsulates is higher, leading to poorer heat dissipation performance. The flow pattern transitions from laminar flow to turbulent flow. In the simulation, the turbulent k-ε model is used for calculations. It calculates the transport equations for turbulent kinetic energy (k) and dissipation rates (ε) in order to accurately simulate the turbulent flow characteristics. By solving these equations, the model can predict the turbulence intensity, turbulent eddies, and other flow parameters to provide insights into the convective heat transfer and fluid dynamics within the system.
In this paper, heat radiation occurs between different encapsulates, as well as between the coils and the external environment. Its control equation is as follows [12]:
where ε is the emissivity of the emitting surface, which is set to be 0.9 for encapsulate surfaces. is the Stefan–Boltzmann constant, which is equal to . T1 and T2 are the absolute temperatures of the two surfaces involved in the heat transfer.
The investigated reactor has 13 encapsulates and 44 coil layers, each of which has a different size. Moreover, on both sides of each encapsulate is the wound with glass fiber dipped using epoxy. Each layer of the aluminum conductor is wound with polyesterimide film-coated aluminum wire. To achieve modeling simplification, coils with hundreds of turns and a round cross-section are equivalently represented as rectangular coils with the same turns. Therefore, the polyesterimide and aluminum wire can be integrated into a new material and their thermodynamic properties can be computed based on those of polyesterimide and aluminum, as follows [25]:
where subscripts 1 and 2 represent two different materials (polyesterimide and aluminum) within the composite.
Furthermore, since polyesterimide film is rather thin compared to the aluminum wire, this will greatly increase the degrees of freedom to solve, leading to a longer computation time. Thus, in order to simplify the model of each encapsulate, this paper proposes a method to replace these parallel coils within certain encapsulates to a single-layer coil. The coil wire cross-section area is equal to the original cross-sectional area of the wire multiplied by the number of coil layers. The equivalent number of turns for this single-layer coil of the kth encapsulate is proposed as follows:
where is the equivalent turns of the kth encapsulate; are the first, second, etc., turns; and the jth coil of the kth encapsulate.
2.2. Boundary Conditions
Determining the reactor’s temperature distribution relies on the establishment of appropriate boundary conditions. By utilizing the aforementioned simulation model, the reactor’s boundary conditions are configured as follows:
- (1)
- Due to the axial symmetry of the physical model, the reactor is simplified to a 1/2 model to facilitate the analysis of temperature rises within the reactor.
- (2)
- Since a multi-physics electromagnetic–fluid–thermal coupling model is built, the magnetic potential vector, temperature, pressure, turbulent kinetic energy, turbulent dissipation rate, and fluid velocity are dependent variables need to solved in each field. The initial temperature and ambient temperature are set to °C.
- (3)
- As shown in Figure 1, the boundary of the upper and lower surface (including surfaces 27 to 39 and surfaces 40 to 52) of each encapsulate and the right surface of encapsulate 13 are set as surface-to-ambient radiation, while the boundary of the surfaces 1 to 25 are set as surface-to-surface radiation.
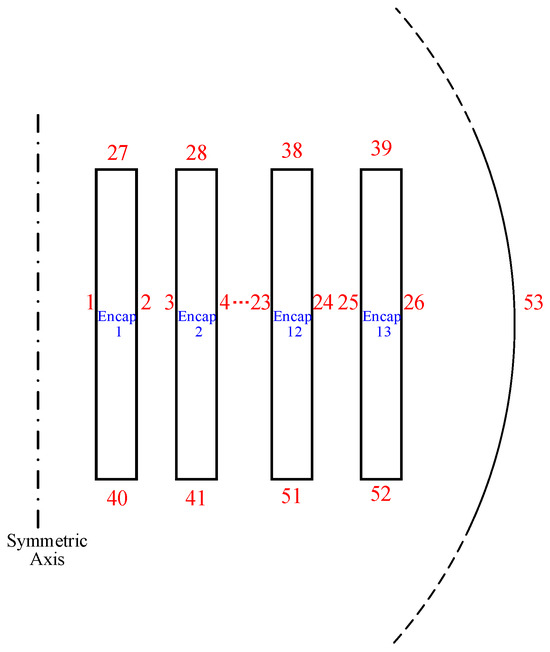 Figure 1. Diagram of boundary numbering for each encapsulate of the reactor.
Figure 1. Diagram of boundary numbering for each encapsulate of the reactor. - (4)
- The interfaces between the encapsulate surfaces and air (including surfaces 1–52) are set as non-slip boundary conditions. Surface 53 is set as an open boundary condition.
- (5)
- The buoyancy of the model is caused by the temperature difference in the axial direction. During simulation, the gravitational acceleration value in the axial direction is set to −9.8 m/s2.
A detailed model diagram of the reactor is presented in Figure 2. To build a model with the finite element method (FEM) and obtain the simulation results, six steps are required. Firstly, a geometric model needs to be built based on the geometric parameters of the investigated reactor, such as the height and width of each coil, the width of the air passage, the thickness of the insulation, and so on. Then, the material properties can be set, including electromagnetic and thermodynamic properties, such as electrical conductivity, density, heat capacity, thermal conductivity, and so on. After that, mesh setting should be completed based on the geometric size of different parts of the reactor, and the mesh size for each part should be chosen carefully to guarantee both the accuracy and divergence of the model. Next, the boundary conditions of the reactor are applied, and the symmetry boundary, radiation boundary, and wall condition all need to be set in this process. The load should be applied to the coils, and the number of coil turns, the radius of the coil, and the connection and relationship between the coils should be set during this step. Furthermore, to solve the multi-physics model that is built, the solver configuration needs to be set further. The solving time, solving method, and time step for the simulation can also be set during this step. Finally, the simulation results, including the temperature at any position, the temperature distribution curve of any path, the color nephogram of the flux density/temperature/fluid velocity, etc., can be obtained with post-processing.
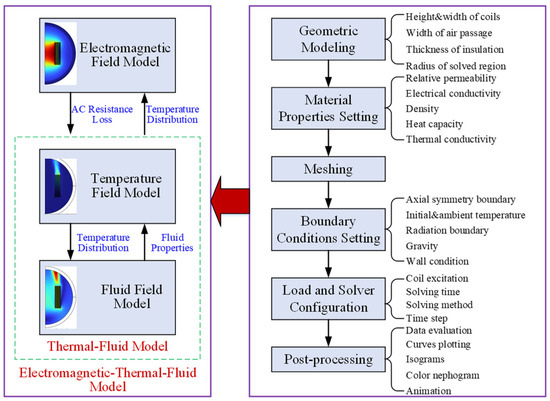
Figure 2.
A diagram of multi-physics modeling and modeling processes.
According to Figure 2, the multi-physics model consists of three parts, including an electromagnetic field model, a temperature field model, and a fluid field model. As the heat source for the temperature field model, the electromagnetic losses is equal to the AC resistance losses of coils, which can be obtained with an electromagnetic field model, in which the electrical conductivity of the coil is expressed as a function dependent on temperature to consider the effect of the temperature on the conductor region. Since the heat convection properties vary with temperature, the temperature distribution of the reactor is also dependent on the natural convection, which is related to the fluid properties. A thermal–fluid coupled model is built, whereby the turbulent k-ε model is used to simulate the turbulent flow characteristics within the air passage. Moreover, the heat radiation that occurs between the different encapsulates, as well as between the coils and the external environment, is also taken into account by setting proper boundary conditions. Therefore, a two-way coupled multi-physics model can be built and simulated by following the modeling process on the right-hand side of Figure 2, and the simulation results found with the multi-physics model are presented in the next section.
3. Results
3.1. The Electromagnetic Field Simulation Results of the Encapsulate Refined Model
The electromagnetic losses of coils in the dry-type air-core reactor are the heat sources for the temperature field analysis. Therefore, it is firstly necessary to compute the magnetic field and the winding current, realized by the 2D FEM coupled with an electric circuit, whereby a AC voltage source is applied to the electric circuit that is connected (in series) to the reactor whose coils in each capsulate are connected (in parallel) in the electric circuit. Figure 3 shows the magnetic flux density distribution. It can be seen that the magnetic field is symmetrically distributed around the center height and the maximum magnetic flux density located at the middle of the first encapsulate in the axial direction. According to Figure 3b, the magnetic flux density along the center line of encapsulate 1 shows an increasing trend from both ends towards the center height position, while in the other encapsulates, it is the opposite. This is attributed to the superposition of the magnetic field produced by the current of each coil. According to the winding currents and magnetic field obtained, resistance losses and eddy current losses in the windings can be computed.
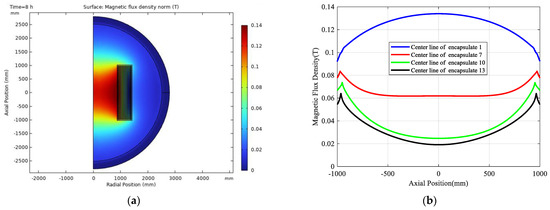
Figure 3.
The magnetic flux density distribution of the reactor. (a) Magnetic flux density nephogram; (b) axial distribution of magnetic flux density in the encapsulate.
3.2. The Temperature Field Simulation Results of the Encapsulate Refined Model
The temperature field simulation results when the temperature is stable are shown in Figure 4. The global and local view of the temperature distribution is shown in Figure 4a,b.
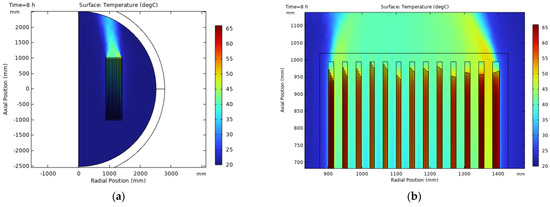
Figure 4.
Temperature distribution nephogram of the reactor. (a) Global view of temperature distribution; (b) local view of temperature distribution.
According to Figure 4a, the temperature of the air above the reactor and that within the air passage between the encapsulates is higher than elsewhere, which is attributed to the fact that normal temperature air enters from the lower side of the air passage and absorbs heat, which leads to a decrease in density, resulting in an upward flow caused by buoyant. Moreover, Figure 4b shows that the temperature of the 12th encapsulate is the highest, with a maximum temperature of 65.5 °C and a temperature rise of 45.5 °C. The temperature of the reactor is higher than that of the surrounding air because the electromagnetic loss is produced by the reactor, which is the heat source.
The temperature distribution of the reactor is shown in Figure 5. As shown in Figure 5a, both the inner and external encapsulates of the reactor have higher temperatures at the same height, and the temperature is lower for the middle encapsulates. In the same encapsulate, the temperature remains relatively constant along the radial direction at the same height. Significant temperature gradients occur within the internal air passage because of natural convection. Furthermore, there is a slight temperature difference along the radial direction between the 1st and 13th encapsulate layers at each height. This is because the left surface of the 1st layer of the encapsulate and the right surface of the 13th layer of the encapsulate are exposed to partially open and fully open environments, facilitating better heat dissipation. As a result, the temperature slightly decreases towards the outer side. The encapsulate temperature is significantly higher than the airflow temperature. Furthermore, within the same air passage, the temperature distribution along the radial direction is not uniform. The air temperature is higher near the encapsulate wall and lower away from the encapsulate wall, which is the result of convective heat transfer between the air and the encapsulate surface. In addition, the temperature at the same radial position increases from Height 1 to Height 4, where Heigh 1 represents in the middle of the reactor in the axial direction, while Height 2–Height 4 represents 1/8, 2/8, 3/8 height of the reactor away from the middle in the axial direction.
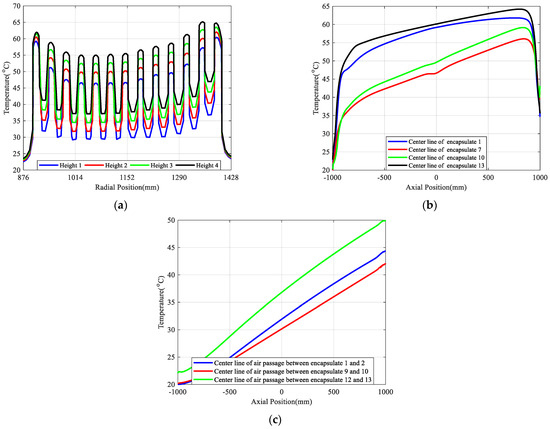
Figure 5.
The simulation results of temperature in radial and axial directions. (a) Radial temperature distribution at different heights; (b) axial temperature distribution in different encapsulates; (c) axial temperature distribution of air passages between different encapsulates.
In order to study the temperature distribution in the encapsulates, the center lines of encapsulates 1, 7, 10, and 13 are taken as the research objective, and the axial simulation results are presented in Figure 5b. Since the heights of each capsulate are different, the axial temperature gradually increases with a rise in height, and the highest temperature is located at about 75% of the height of reactor and is close to °C. At the same time, the temperature curves can be divided into three segments with different rise rates. In the initial segment, the temperature rise rate experiences a rapid increase owing to the significant decrease in convection heat transfer coefficient as the height rises. In the second segment, the temperature rise rate exhibits a slow acceleration, attributed to the gentle decline in convection heat transfer coefficient with increasing height. Conversely, in the final segment, temperature decreases with height due to improved heat dissipation conditions caused by the end effect, resulting in an elevation in the convection heat transfer coefficient with increasing height.
Figure 5c shows the temperature distribution along the axial direction along the center line of the air passage between encapsulates 1–2, 9–10, and 12–13. The temperature within each air passage almost increases linearly with the increase in axial position. This is because the normal temperature air enters from the lower side of the air passage and absorbs heat, which leads to a decrease in density, resulting in upward flow caused by buoyant. In the process of air flow, the heat emitted by the encapsulate is continuously absorbed. Therefore, the air temperature increases monotonously along the axial direction. The highest temperature is located at the top of encapsulates and is close to .
3.3. The Fluid Field Simulation Results of the Encapsulate Refined Model
The velocity distribution of the axial direction along the center line of the air passage between encapsulates 1–2, 9–10, and 12–13 is shown in Figure 6.
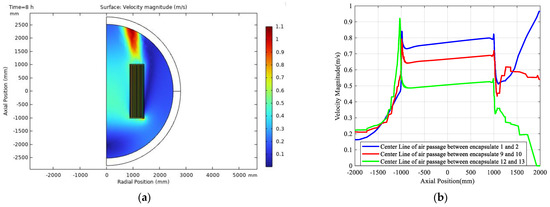
Figure 6.
Simulation results of fluid velocities for the reactor. (a) Fluid velocity distribution nephogram; (b) axial fluid velocity of air passage between different encapsulates.
The fluid velocity increase approaches the air passage between the encapsulates from the bottom of the reactor and is almost stable within the air passage along the axial direction, whereas the fluid flow is highly turbulent near the upper end of the reactor to the point of leaving the reactor, as shown in Figure 6b.
3.4. The Multi-Physics Simulation Results of the Encapsulate Simplified Model
The temperature distribution along the radial direction at the same height in the simplified model compared with refined model is presented in Figure 7, which shows good agreement. Since different coil layers within the same encapsulate are simplified as a single-layer coil, there is small temperature difference along the radial direction within the same coil. Only a slight decrease in temperature is observed in the insulation material on both sides of the encapsulate.
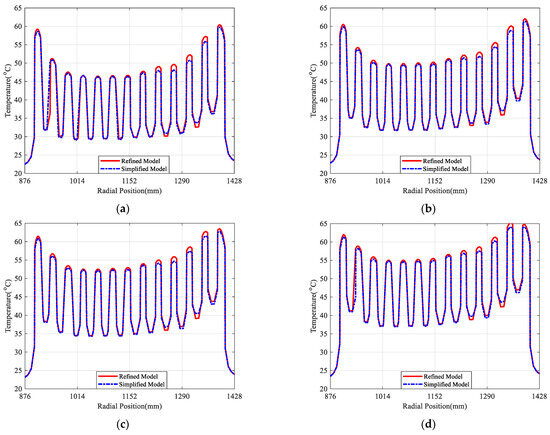
Figure 7.
Temperature comparisons between the multi-physics refined model and the simplified model in the radial direction at different heights. (a) Temperature comparisons between multi-physics refined model and simplified model based on the radial direction at Height 1; (b) temperature comparisons between the multi-physics refined model and the simplified model based on the radial direction at Height 2; (c) temperature comparisons between the multi-physics refined model and the simplified model based on the radial direction at Height 3; (d) temperature comparisons between the multi-physics refined model and the simplified model based on the radial direction at Height 4.
The relative error of the maximum and average temperatures of each encapsulate obtained from the simplified model compared to the refined model can also be computed, as presented in Table 2. As shown in the table, the maximum relative error is less than 2.2%, which indicates a high level of accuracy. Additionally, the computation time for solving the simplified model is 23 min, with a reduction rate of 35.7% compared to the computation time of the refined model. An improvement in the time consumption of the simplified model is helpful to optimize reactor using an intelligent algorithm considering the rise in temperature.

Table 2.
The comparison between the encapsulate refined model and the encapsulate simplified model.
Table 3 presents comparison results of electromagnetic parameters among the refined multi-physics model, simplified multi-physics model, and refined electromagnetic model.

Table 3.
Comparison of electrical parameters.
It can be seen that parameters computed with the proposed simplified model, including equivalent resistance, equivalent inductance, bus current, active power, and reactive power, closely agree with those obtained with the refined model, and the absolute value of the maximum relative error is 1.21%, which shows good accuracy. Meanwhile, the relative error between those obtained with the refined multi-physics model and the refined electromagnetic model is relatively higher, and its maximum absolute relative error value is up to 11.65%, which is attributed to the constant equivalent resistance independent of temperature in the electromagnetic model. This proves the importance of considering electrical conductivity variations in the conductor under different temperatures, as both the refined multi-physics model and the simplified multi-physics model did.
4. Conclusions
This paper establishes a 2D simulation model for the electromagnetic–fluid–thermal multi-physics coupling of the dry-type air-core reactor. Through simulations and in-depth analyses, the paper aims to identify potential hotspots and predict temperature profiles, which is vital for ensuring safe and reliable operation, extending the reactor’s lifespan and contributing to the overall efficiency and sustainability of power systems. By considering the losses in each layer of the reactor as the heat source, the temperature field distribution characteristics are obtained. The following conclusions are drawn:
- (1)
- The overall temperature distribution of the reactor encapsulates exhibits a trend where the upper region is higher than the lower region, and the central envelope experiences higher temperatures than the side envelopes. The highest temperature location in the upper region of the 12th encapsulate of the reactor is °C.
- (2)
- In the radial direction, the temperature distributions of encapsulates exhibit similar trends, and the middle ones are lower than those on the left and right sides. In the axial direction, temperatures gradually increase from the bottom to the top within the encapsulates, with the highest thermal location occurring at around 75% of the axial height of the reactor.
- (3)
- The temperature within each air passage almost linearly increases with an increase in the axial position. Within the same air passage, the temperature distribution along the radial direction is not uniform, and the air temperature is higher near the encapsulate wall and lower away from the encapsulate wall.
- (4)
- The simulation results obtained from the multi-physics simplified model are compared with the multi-physics refined model, showing good consistency. The maximum relative errors of temperature and the electromagnetic parameter are 2.19% and 1.21%, respectively. The relative error of equivalent inductance is just 0.08‰, whereas the time consumption is reduced by up to 35.7%, which verifies the effectiveness of the proposed method.
In future studies, we will apply the proposed simplified encapsulate multi-physics model to different structural dry-type air-core reactors in order to verify its performance and explore its application potential in optimizing the reactor’s thermal efficiency.
Author Contributions
Conceptualization, J.W., Z.C. and H.Z.; methodology, J.W. and M.Z.; validation, M.Z. and Y.P.; formal analysis, H.Z. and Y.P.; investigation, Z.C.; data curation, Y.P., J.L. and Q.H.; writing—original draft preparation, M.Z.; writing—review and editing, J.W., Z.C., H.Z., Y.P., J.L. and Q.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the State Grid Sichuan Electric Power Company scientific project, under grant number 52199722000T.
Data Availability Statement
The data included in the article that supports the results of this study can be obtained by contacting the corresponding author of this article.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Abbreviations | |||
| FDM | Finite difference method | ||
| FEM | Finite element method | ||
| Physics Constant | |||
| g | Gravity acceleration | ||
| Stefan–Boltzmann constant | |||
| Symbols | |||
| Temperature coefficient of resistivity | |||
| Thermal expansion coefficient | |||
| Emissivity of the emitting surface | |||
| ρ | Density | ||
| μ | Dynamic viscosity | ||
| ω | Angular frequency | ||
| σ | Electrical conductivity | ||
| Electrical conductivity at the reference temperature | |||
| ∇· | Divergence operator | ||
| ∇T | Temperature gradient in the direction of heat transfer | ||
| ∇p | Pressure gradient | ||
| ∇2u | Laplacian operator applied to the velocity vector | ||
| B | Magnetic flux density | ||
| Cp | Heat capacity | ||
| Spatial diameter of the jth coil in the ith layer | |||
| Current of the jth coil in the ith layer | |||
| L | Characteristic length | ||
| Equivalent turns of the kth encapsulate | |||
| The number of turns of the jth coil in the ith layer | |||
| The number of turns of the jth coil in the kth encapsulate | |||
| Resistance losses | |||
| Eddy current losses | |||
| Q | Heat source | ||
| Rayleigh number | |||
| Wire cross-sectional area of the jth coil in the ith layer | |||
| T | Temperature | ||
| Reference temperature | |||
| Conductor diameter of the jth coil in the ith layer | |||
| m | The number of layers in the reactor | ||
| The number of coils in the ith layer | |||
| k | Thermal conductivity | ||
| q | Heat flux density | ||
| u | Velocity | ||
References
- Levieux, L.I.; Inthamoussou, F.A.; De Battista, H. Power dispatch assessment of a wind farm and a hydropower plant: A case study in Argentina. Energy Convers. Manag. 2019, 180, 391–400. [Google Scholar] [CrossRef]
- Nie, H.; Liu, X.; Wang, Y.; Yao, Y.; Gu, Z.; Zhang, C. Breaking overvoltage of dry-type air-core shunt reactors and its cumulative effect on the interturn insulation. IEEE Access 2019, 7, 55707–55720. [Google Scholar] [CrossRef]
- Velásquez, R.M.A.; Lara, J.V.M. Life estimation of shunt power reactors considering a failure core heating by floating potentials. Eng. Fail. Anal. 2018, 86, 142–157. [Google Scholar] [CrossRef]
- Gning, P.; Lanfranchi, V.; Dauchez, N. Influence of the multi-component electrical feed of air-core industrial reactors on their sound radiation. Acta Acust. 2020, 4, 14. [Google Scholar] [CrossRef]
- Luo, S. Discussion on calculation of temperature rise of dry-type transformer. Transformer 2006, 43, 27–30. [Google Scholar] [CrossRef]
- Simonson, E.A.; Lapworth, J.A. Thermal capability assessment for transformers. In Proceedings of the 2nd International Conference on the Reliability of Transmission and Distribution Equipment, Coventry, UK, 29–31 March 1995. [Google Scholar] [CrossRef]
- Chen, F.; Zhao, Y.; Ma, X. An efficient calculation for the temperature of dry air-core reactor based on coupled multi-physics model. In Proceedings of the 2012 Sixth International Conference on Electromagnetic Field Problems and Applications, Dalian, China, 19–21 June 2012. [Google Scholar] [CrossRef]
- Yuan, F.T.; Yuan, Z.; Liu, J.X.; Wang, Y.; Mo, W.X.; He, J.J. Research on temperature field simulation of dry type air core reactor. In Proceedings of the 2017 20th International Conference on Electrical Machines and Systems, Sydney, Australia, 11–14 August 2017. [Google Scholar] [CrossRef]
- Zhu, J.; Zhang, W.; Huang, K.; Wang, S.; Sun, X.; Zhao, L. Research on temperature field of large capacity bridge arm reactor’s busbar based on circuit-magnetic-thermal field coupling calculation. In Proceedings of the 2020 IEEE International Conference on High Voltage Engineering and Application, Beijing, China, 6–10 September 2020. [Google Scholar] [CrossRef]
- Wan, X.; Wang, H.; Li, Y.; Li, C.; Zhao, Z.; Cui, Z. A study of encapsulation temperature field of dry-type air-core reactor with the structure of equivalent and aluminum wire-insulation. Distrib. Gener. Altern. Energy J. 2022, 37, 1665–1680. [Google Scholar] [CrossRef]
- Yuan, F.T.; Yang, S.W.; Qin, S.H.; Lv, K.; Tang, B.; Han, S.S. Thermal performance analysis and optimization design of dry type air core reactor with the double rain cover. Therm. Sci. 2022, 26 Pt A, 273–286. [Google Scholar] [CrossRef]
- Yan, X.; Dai, Z.; Zhang, Y.; Yu, C. Fluid-thermal field coupled analysis of air core power reactor. In Proceedings of the 2012 Sixth International Conference on Electromagnetic Field Problems and Applications, Dalian, China, 19–21 June 2012. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Qin, W.N.; Wu, G.L.; Ruan, J.J.; Huang, T. Analysis of temperature rise in reactors using coupled multi-physics simulations. In Proceedings of the 2013 IEEE International Conference on Applied Superconductivity and Electromagnetic Devices, Beijing, China, 25–27 October 2013. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, Q.; Zhang, C.; Li, Y.; Wang, J. Magnetic-thermal coupling analysis of saturable reactor. IEEE Trans. Magn. 2022, 58, 6300705. [Google Scholar] [CrossRef]
- Yu, G.; Yao, W.; Qingsong, L.; Teng, X.P.; Bo, Z.; Shi, J. Research on finite element model of air-core reactor based on magnetic-thermal coupling simulation. In Proceedings of the 2022 Asia Power and Electrical Technology Conference, Shanghai, China, 11–13 November 2022. [Google Scholar] [CrossRef]
- Li, C.; Wang, H.; Luo, C.; Zhang, D.; Wan, X.; Zhao, Z.; Li, Y. Numerical simulation and detection of dry-type air-core reactor temperature field based on laminar–turbulent model. AIP Adv. 2021, 11, 035002. [Google Scholar] [CrossRef]
- Wu, J.; Ou, Z.; Huo, F. Test analysis and simulation calculation of temperature field for dry-type air-core reactor. J. Phys. Conf. Ser. 2020, 1601, 022036. [Google Scholar] [CrossRef]
- Yuan, F.; Wu, K.; Yuan, Z.; Liu, J.; Ding, C.; Wang, Y.; He, J. Thermal optimization for dry type air core reactor base on FEM. In Proceedings of the 2018 21st International Conference on Electrical Machines and Systems, Jeju, Republic of Korea, 7–10 October 2018. [Google Scholar] [CrossRef]
- Liu, J.; Yuan, F.; Zhou, B.; Yang, S.; Lv, K.; Tang, B. Structure parameters optimization of the rain cover and ventilation duct of dry air core reactor under the forced air cooling condition. IEEJ Trans. Electr. Electron. Eng. 2022, 17, 792–800. [Google Scholar] [CrossRef]
- Yuan, F.; Lv, K.; Qin, S.; Tang, B.; Yang, S.; Han, S.; Ding, C. Electromagnetic−thermal characteristics analysis of dry−type core reactor and optimization design based on the particle swarm algorithm. IEEJ Trans. Electr. Electron. Eng. 2021, 16, 536–544. [Google Scholar] [CrossRef]
- Pusch, D.; Smajic, J.; Andjelic, Z.; Ostrowski, J.M. Comparison between BEM and classical FEM for a 3D low-frequency eddy-current analysis. IEEE Trans. Magn. 2010, 46, 2919–2922. [Google Scholar] [CrossRef]
- Yan, X.; Yu, X.; Shen, M.; Xie, D.; Bai, B. Research on calculating eddy-current losses in power transformer tank walls using finite-element method combined with analytical method. IEEE Trans. Magn. 2016, 52, 6300704. [Google Scholar] [CrossRef]
- Raymond, A.; John, W. Principles of Physics, 2nd ed.; Fort Worth: New York, NY, USA, 1998; p. 604. [Google Scholar]
- Liu, C.; Zhang, M.; Xi, J.; Sun, G.; Han, Y.; Liu, X. Study on temperature field of high capacity dry-type reactor based on fluid-thermodynamic coupling. High Volt. Appar. 2021, 57, 84–89. [Google Scholar] [CrossRef]
- Yu, Q.; Zhao, C.; Lin, H.; Wang, Y.; Si, C.; Yang, D. Damage mechanism of inter-turn insulation of dry-type air-core reactor based on temperature field. High Volt. Appar. 2022, 58, 94–100. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).