Robust Constant Exponent Coefficient Fixed-Time Control Based on Finite-Time Extended Sliding Mode Observer of Permanent Magnet Synchronous Motors
Abstract
:1. Introduction
- (1)
- A constant exponent coefficient fixed-time SMC (CECFSMC) will be used in this research. To the best of the authors’ knowledge, it is probably one of the simplest methods to regulate nonlinear systems and is easy to tune with respect to other fixed-time control methods. The controller has only six parameters to tune. A stability proof of the designed controller will be given, demonstrating that the closed-loop error responses converge to zero in a fixed amount of time. An additional feature of the designed controller also includes the chattering reduction.
- (2)
- An extended sliding mode observer (ESMO) is designed to estimate the PMSM velocity and lumped load disturbances at the same time. This is so the sliding mode controller can work as expected when disturbances are limited. The semi-global practical finite-time stable with finite reach time Treach is also theoretically proven.
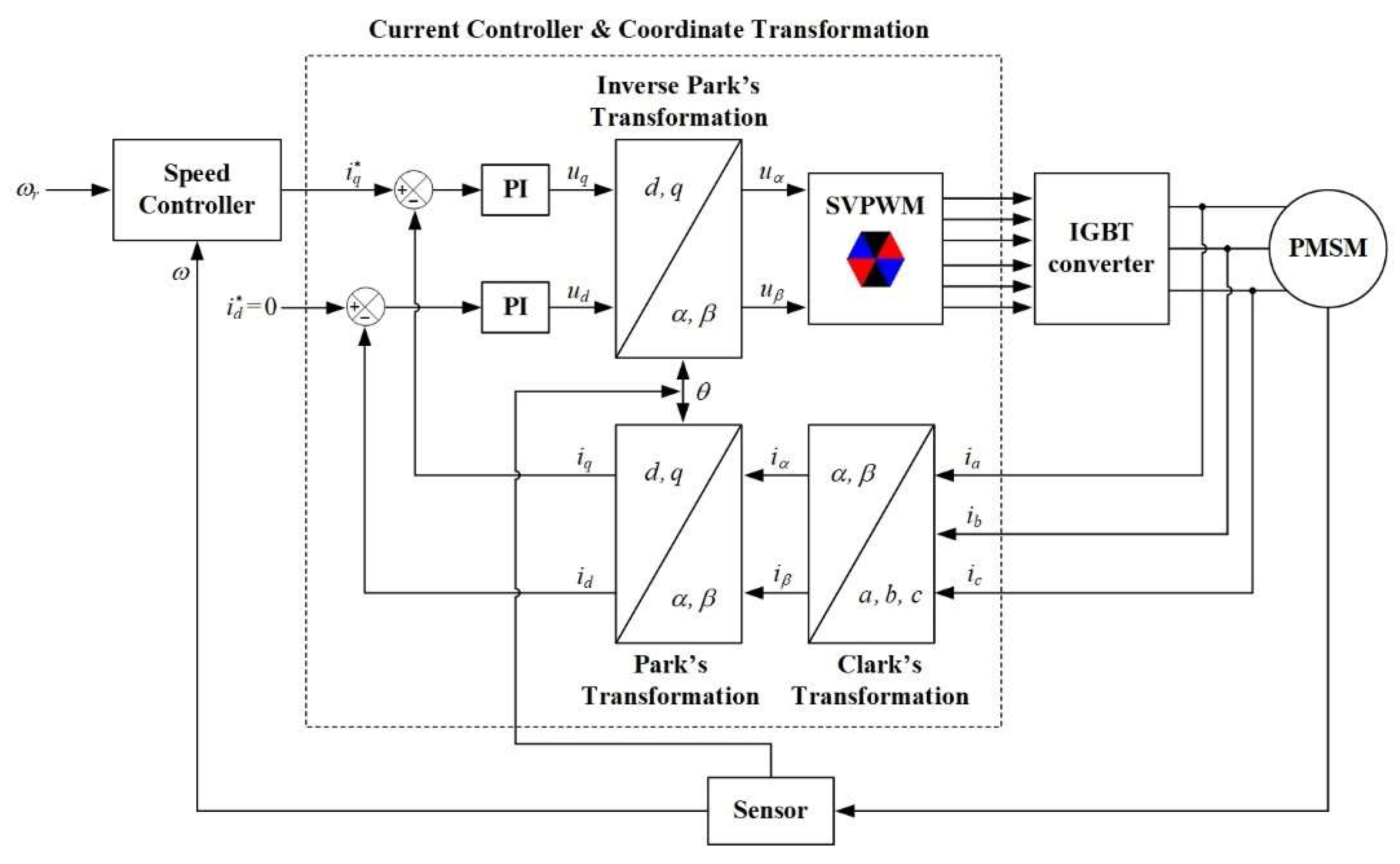
2. Control Model and PMSM Dynamical System
2.1. PMSM Mathematical Model
2.2. Robust Fixed-Time Stability and Constant Exponent Coefficient
3. Design of Speed Controller
3.1. Controller Design
3.2. Fixed-Time Sliding Mode Controller with State Disturbance Estimation
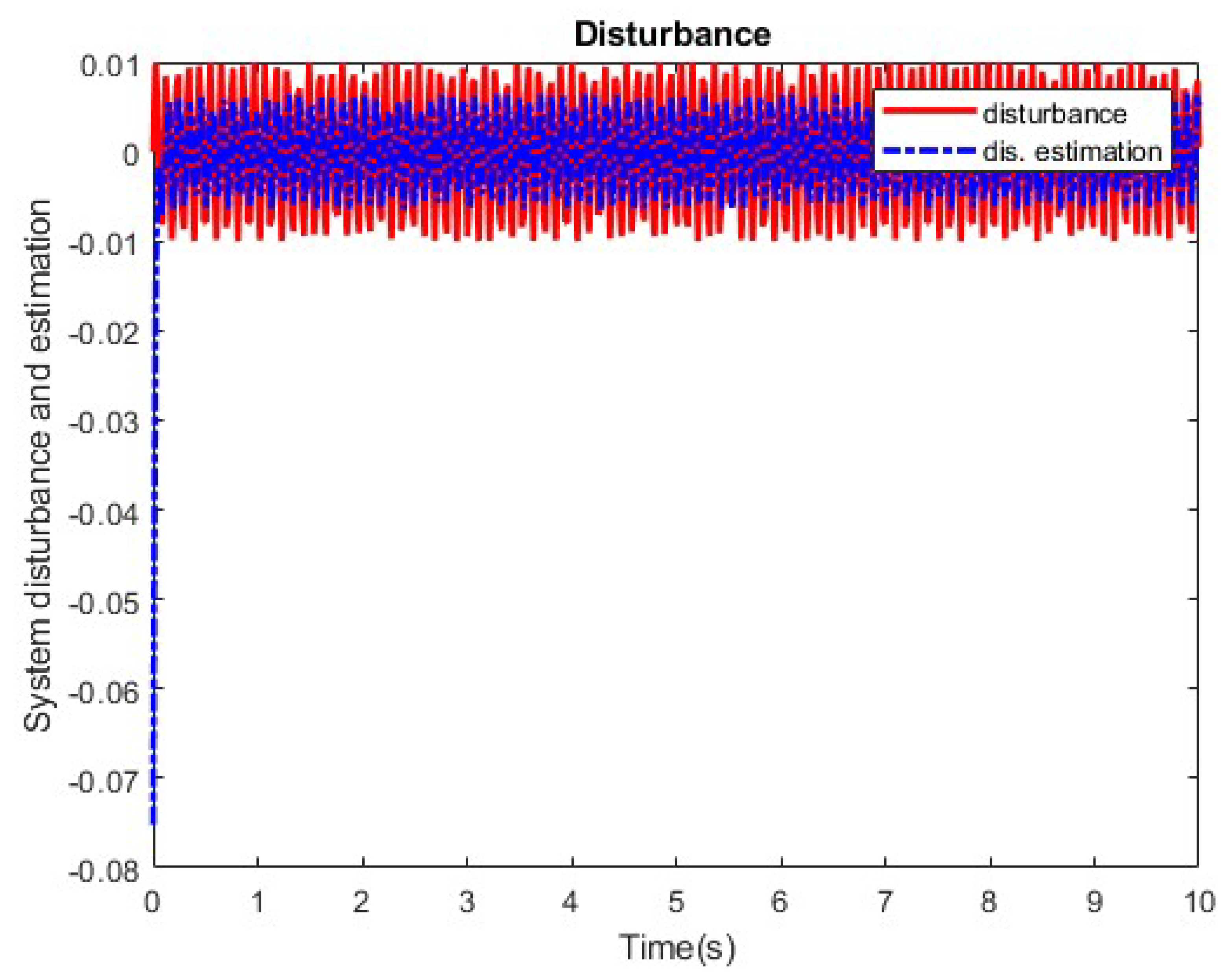
3.2.1. Extended Sliding Mode Observer (ESMO)
- (1)
- Consider the system , which is given by neglecting the terms in (31) and in (31):
- (2)
- Consider the system β which is given by neglecting the terms in (31) and in (31):
3.2.2. Extended Sliding Mode Observer-Based Fixed-Time Controller Design
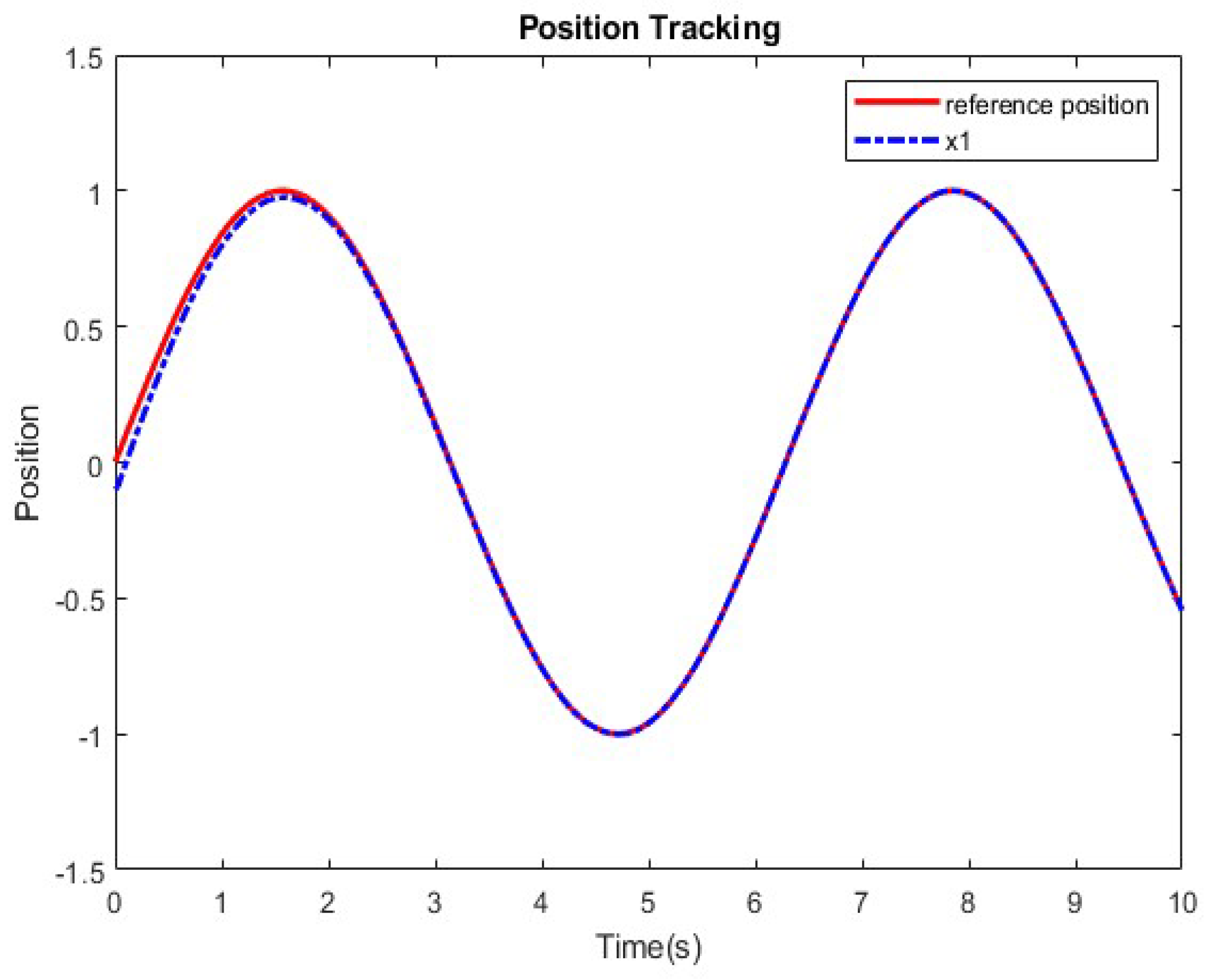
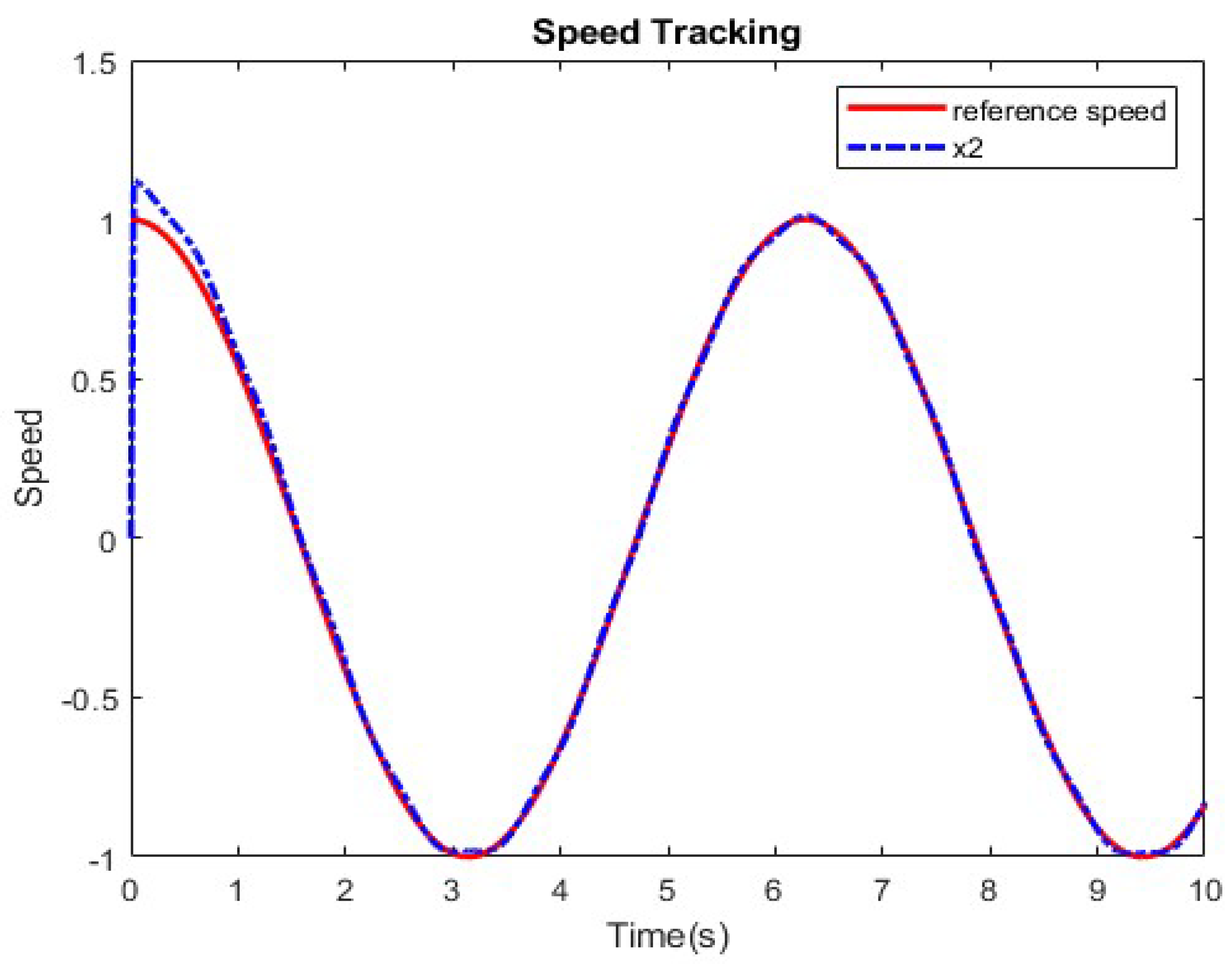
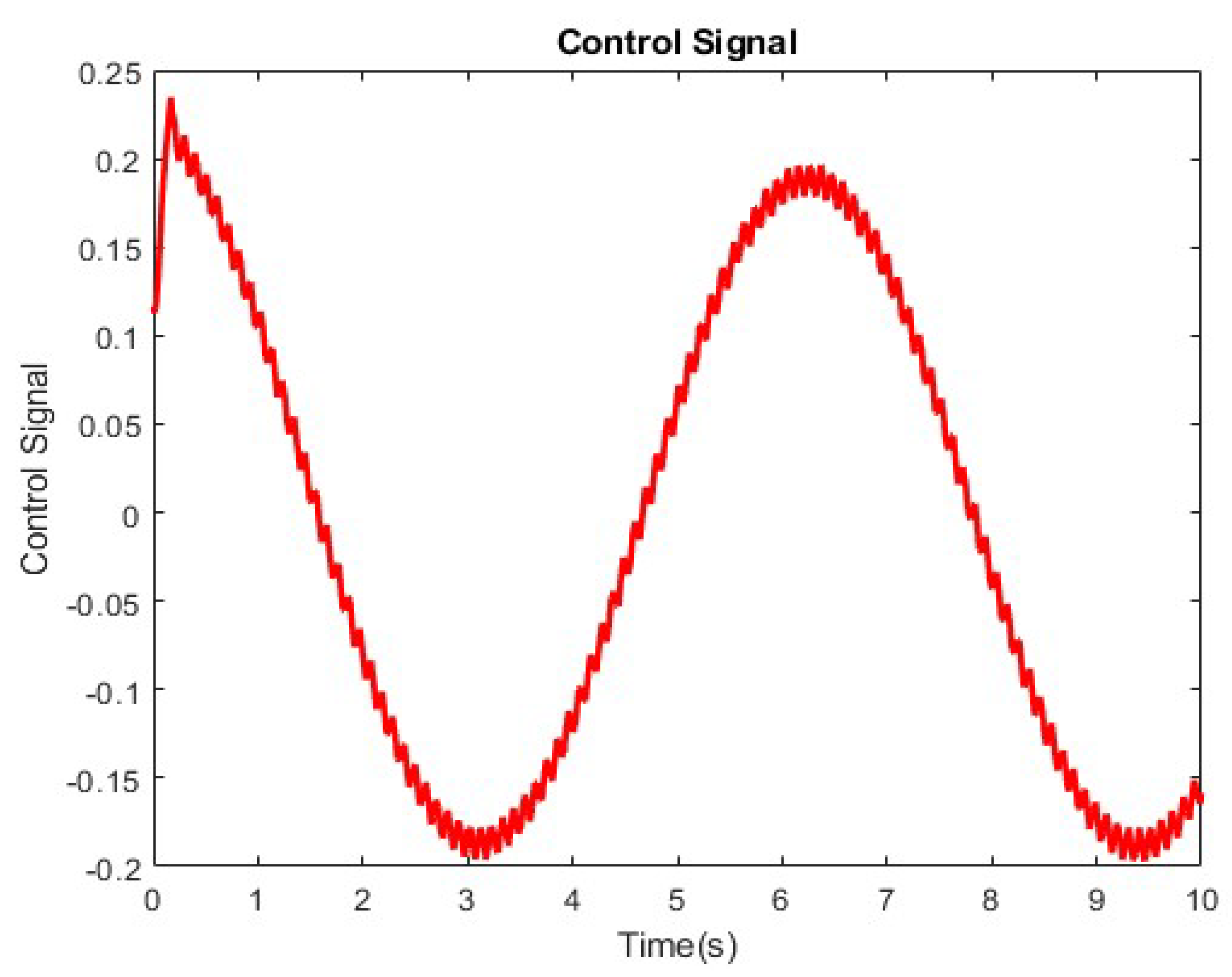
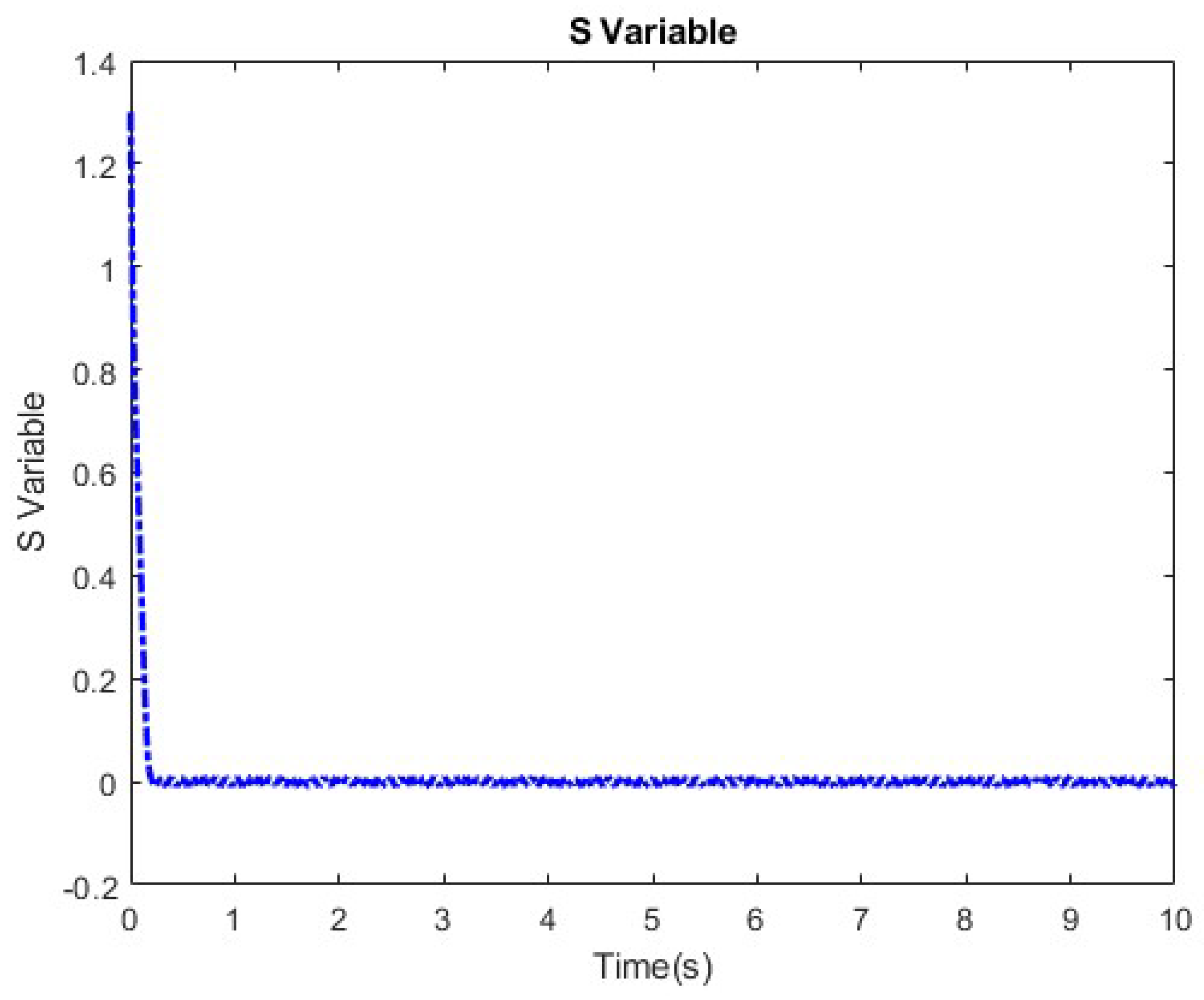
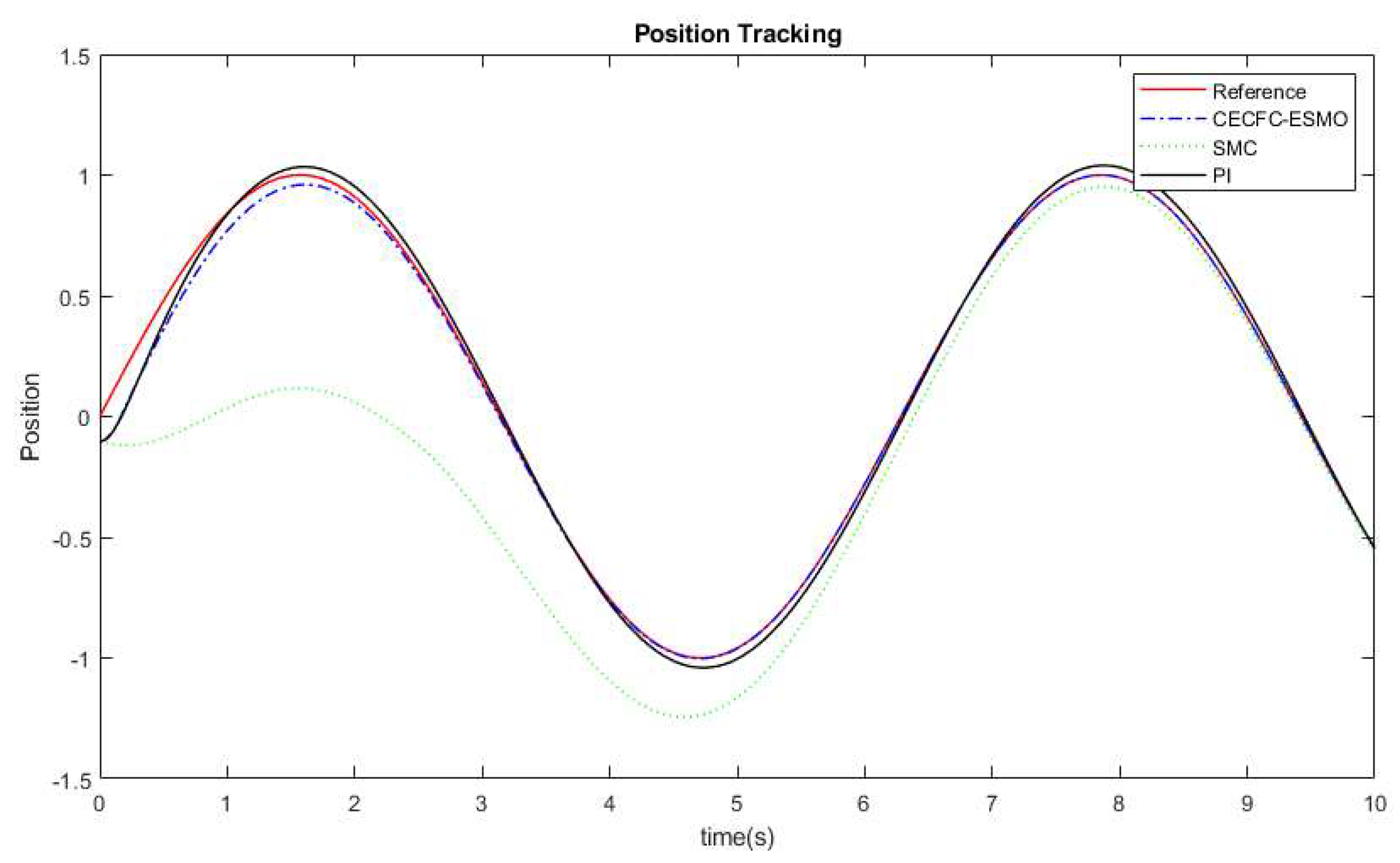
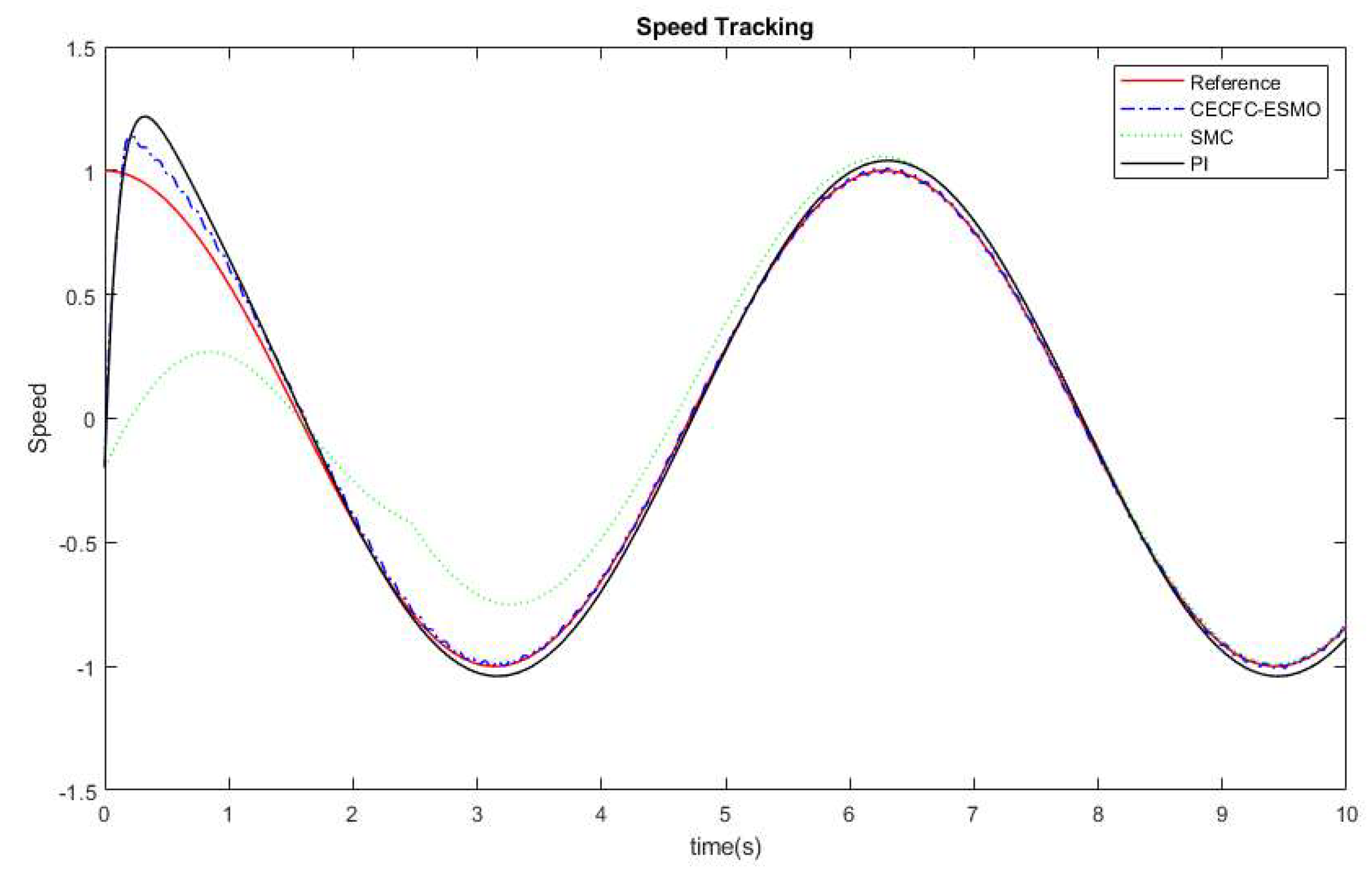
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, Y.; Xu, Y.; Zou, J. Sliding-mode sensorless control of PMSM with inverter nonlinear compensation. IEEE Trans. Power Electron. 2019, 34, 10206–10220. [Google Scholar] [CrossRef]
- Ruuskanen, V.; Nerg, J.; Rilla, M.; Pyrhonen, J. Iron loss analysis of the permanent-magnet synchronous machine based on finite-element analysis over the electrical vehicle drive cycle. IEEE Trans. Ind. Electron. 2016, 63, 4129–4136. [Google Scholar] [CrossRef]
- Sheng, L.; Li, W.; Wang, Y.; Fan, M.; Yang, X. Sensorless control of shearer short-range cutting interior permanent magnet synchronous motor based on a new sliding mode observer. IEEE Access 2017, 5, 18439–18450. [Google Scholar] [CrossRef]
- Fan, S.; Tong, C. Model predictive current control method for PMSM drives based on an improved prediction model. J. Power Electron. 2020, 20, 1456–1466. [Google Scholar] [CrossRef]
- Jiang, C.; Wang, Q.; Li, Z.; Zhang, N.; Ding, H. Nonsingular terminal sliding mode control of PMSM based on improved exponential reaching law. Electronics 2021, 10, 1776. [Google Scholar] [CrossRef]
- Wang, C.; Zhu, Q. Fuzzy logic speed control of Permanent magnet synchronous machine and feedback voltage ripple reduction in flux-weakening operation region. IEEE Trans. Ind. Appl. 2022, 56, 1505–1517. [Google Scholar] [CrossRef]
- Lin, F.-J.; Yang, K.-J.; Sun, I.-F.; Chang, J.-F. Intelligent position control of permanent magnet synchronous motor using recurrent fuzzy neural cerebellar model articulation network. IET Electr. Power Appl. 2015, 9, 248–264. [Google Scholar] [CrossRef]
- Nguyen, A.T.; Rafaq, M.S.; Choi, H.H.; Jung, J.-W. A model reference adaptive control-based speed controller for a surface-mounted permanent magnet synchronous motor drive. IEEE Trans. Ind. Electrons 2018, 65, 9399–9409. [Google Scholar] [CrossRef]
- Zhanga, G.; Gao, L.; Yang, H.; Mei, L. A novel method of model predictive control on permanent magnet synchronous machine with Laguerre function. Alex. Eng. J. 2021, 6, 5485–5494. [Google Scholar] [CrossRef]
- Wang, T.; Li, J.; Liu, Y. Synergetic control of permanent magnet synchronous motor based on load torque observer. Proc. Inst. Mech. Eng. Pt. I J. Syst. Contr. Eng. 2018, 233, 980–993. [Google Scholar] [CrossRef]
- Mu, C.; Xu, W.; Sun, C. On switching manifold design for terminal sliding mode control. J. Frankl. Inst. 2016, 353, 1553–1572. [Google Scholar] [CrossRef]
- Zaihidee, F.M.; Mekhilef, S.; Mubin, M. Robust speed control of PMSM using sliding mode control (SMC)—A Review. Energies 2019, 12, 1669. [Google Scholar] [CrossRef]
- Lin, Y.; Hu, K.; Yeh, T.; Liaw, C.-M. An electric-vehicle IPMSM drive with interleaved front-end DC/DC converter. IEEE Trans. Veh. Technol. 2016, 6, 4493–4505. [Google Scholar] [CrossRef]
- Napole, C.; Derbeli, M.; Barambones, O. A global integral terminal sliding mode control based on a novel reaching law for a proton exchange membrane fuel cell system. Appl. Energy. 2021, 301, 11743–11757. [Google Scholar] [CrossRef]
- Benosman, M.; Lum, K.Y. Passive actuators’ fault-tolerant control for affine nonlinear control systems. IEEE Trans. Control Syst. Technol. 2010, 18, 152–163. [Google Scholar] [CrossRef]
- Yang, Y.; Yan, Y. Neural network approximation-based nonsingular terminal sliding mode control for trajectory tracking of robotic ariships. Aerosp. Sci. Technol. 2016, 54, 192–197. [Google Scholar] [CrossRef]
- Bartoszewicz, A.; Lesniewskil, P. New switching and nonswitching type reaching laws for SMC of discrete time systems. IEEE Trans. Control Syst. 2016, 24, 670–677. [Google Scholar] [CrossRef]
- Wang, Y.; Feng, Y.; Zhang, Z.; Liang, J. A new reaching law for antidisturbance sliding-mode control of PMSM speed regulation system. IEEE Trans. Power Electron. 2020, 35, 4117–4126. [Google Scholar] [CrossRef]
- Ma, H.; Li, Y. Multi-power reaching law based discrete-time sliding-mode control. IEEE Access 2019, 7, 49822–49829. [Google Scholar] [CrossRef]
- Polykov, A. nonlinear feedback design for fixed-time stabilization of linear control system. IEEE Trans. Autom. Control. 2012, 57, 2106–2110. [Google Scholar] [CrossRef]
- Chen, C.; Li, L.; Peng, H.; Yang, Y.; Mi, L.; Zhao, H. A new fixed-time stability theorem and its application to the fixed-time synchronization of neural networks. Neural Netw. 2020, 123, 412–419. [Google Scholar] [CrossRef]
- Hu, C.; Yu, J.; Chen, Z.; Jiang, H.; Huang, T. Fixed-time stability of dynamical systems and fixed-time synchronization of coupled discontinuous neural networks. Neural Netw. 2017, 89, 74–83. [Google Scholar] [CrossRef]
- Parsegov, S.; Polyakov, A.; Shcherbako, V. Nonlinear fixed-time control protocol for uniform allocation of agents on segment. In Proceedings of the 51st IEEE Conference on Decision and Control, Maui, HI, USA, 10–13 December 2012; pp. 7732–7737. [Google Scholar] [CrossRef]
- Polyakov, A.; Fridman, L. Stablity notion and Lyapunov functions for sliding mode control systems. J. Frankl. Inst. 2014, 351, 1831–1865. [Google Scholar] [CrossRef]
- Moulay, E.; Lechappe, V.; Bernau, E.; Plestan, F. Robust fixed-time stability: Application to sliding mode control. IEEE Trans. Autom. Control. 2022, 67, 1061–1066. [Google Scholar] [CrossRef]
- Junejo, A.; Liu, Y.; Islam, M.D. Improved continuous fast terminal sliding mode control with extended state observer for speed regulation of PMSM drive system. IEEE Trans. Veh. Technol. 2019, 68, 10465–10476. [Google Scholar] [CrossRef]
- Xu, W.; Junejo, A.K.; Xu, W. Adaptive speed control of PMSM drive system based a new sliding-mode reaching law. IEEE Trans. Power Electron. 2020, 35, 12110–12121. [Google Scholar] [CrossRef]
- Liu, Y.-C.; Laghrouche, S.; Depernet, D.; N’Diaye, A.; Djerdir, A.; Cirrincione, M. Super-twisting sliding-mode observer-based model reference adaptive speed control of PMSM drives. J. Frankl. Inst. 2023, 360, 985–1004. [Google Scholar] [CrossRef]
- Zhang, L.; Tao, R.; Zhang, Z.-X.; Chien, Y.-R.; Bai, J. PMSM non-singular fast terminal sliding mode control with disturbance compensation. Inf. Sci. 2023, 642, 119040. [Google Scholar] [CrossRef]
- Yacef, F.; Rizoug, N.; Degaa, L.; Bouhali, O.; Hamerlain, M. Extended state observer-based adaptive fuzzy tracking control for a quadrotor UAV. In Proceedings of the 2018 5th International Conference on Control, Decision and Information Technologies (CoDIT), Thessaloniki, Greece, 10–13 April 2018; pp. 1023–1028. [Google Scholar] [CrossRef]
- Liu, K.; Wang, R. Antisaturation adaptive fixed-time sliding mode controller design to achieve faster convergence rate and its application. IEEE Trans. Circuits Syst. II Express Briefs. 2022, 69, 3555–3559. [Google Scholar] [CrossRef]
- Liu, K.; Wang, Y.; Ji, H. Adaptive finite-time tracking control for spacecraft proximity operations under actuator saturation. In Proceedings of the 2020 International Conference on Unmanned Aircraft Systems (ICUAS), Athens, Greece, 1–4 September 2020; pp. 1344–1349. [Google Scholar] [CrossRef]
- Lara, J.; Xu, J.; Chandra, A. Effects of rotor position error in the performance of field-oriented-controlled PMSM drives for electric vehicle traction applications. IEEE Trans. Ind. Electron. 2016, 63, 4738–4751. [Google Scholar] [CrossRef]
- Li, S.; Zhou, M.; Yu, X. Design and implementation of terminal sliding mode control method for PMSM speed regulation system. IEEE Trans. Ind. Inform. 2013, 9, 1879–1891. [Google Scholar] [CrossRef]
- Baht, S.; Berstein, D. Finite-time stability of continuous autonomous systems. SIAM J. Control Optim. 2000, 38, 751–766. [Google Scholar] [CrossRef]
- Moulay, E.; Perruquetti, W. Finite time stability and stabilization of a class of continuous systems. J. Math. Anal. Appl. 2006, 323, 1430–1433. [Google Scholar] [CrossRef]
- Polyakov, A.; Efimov, D.; Perruquetti, W. Finite-time and fixed-time stabilization: Implicit Lyapunov function approach. Automatica 2015, 51, 332–340. [Google Scholar] [CrossRef]
- Zou, Z.; Han, Q.; Ning, B. Fixed-Time Cooperative Control of Multi-Agent Systemsi; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Han, J. From PID to active disturbance rejection control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Kawski, M. Geometric homogeneity and stabilization. IFAC Proc. Vol. 1995, 28, 147–153. [Google Scholar] [CrossRef]
- Bhat, S.P.; Bernstein, D.S. Geometric to homogeneity with applications finite-time. Math. Control. Signals Syst. 2005, 17, 101–127. [Google Scholar] [CrossRef]
- Wongvanich, N.; Roongmuanpha, N.; Tangsrirat, W. Finite-time integral backstepping nonsingular terminal sliding mode control to synchronize a new six-term chaotic system and its circuit implementation. IEEE Access 2023, 11, 22233–22249. [Google Scholar] [CrossRef]
- Halledj, S.E.; Bouafassa, A. Anti-disturbance GITSMC with quick reaching law for speed control of PMSM drive. Bull. Electr. Eng. Inform. 2022, 11, 3228–3238. [Google Scholar] [CrossRef]
- Wan, Q.; Wang, H.; Sun, X. Position tracking control of PMSM system based on continuous sliding mode control and sliding mode observer. In Proceedings of the 2022 41st Chinese Control Conference (CCC), Hefei, China, 25–27 July 2022; pp. 2917–2922. [Google Scholar] [CrossRef]



| Parameter | Value | Unit |
|---|---|---|
| Number of pole pairs np | 6 | - |
| Rated power P | 0.4 | kW |
| Stator resistance Rs | 1.55 | |
| dq-axis inductance L | 6.71 | mH |
| Rotational inertia J | 0.0054 | kg.m2 |
| flux linkage φf | 0.174 | Wb |
| Viscous damping B | 0.00072 | N.m.s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cholahan, V.; Wongvanich, N.; Tangsrirat, W. Robust Constant Exponent Coefficient Fixed-Time Control Based on Finite-Time Extended Sliding Mode Observer of Permanent Magnet Synchronous Motors. Energies 2023, 16, 7454. https://doi.org/10.3390/en16217454
Cholahan V, Wongvanich N, Tangsrirat W. Robust Constant Exponent Coefficient Fixed-Time Control Based on Finite-Time Extended Sliding Mode Observer of Permanent Magnet Synchronous Motors. Energies. 2023; 16(21):7454. https://doi.org/10.3390/en16217454
Chicago/Turabian StyleCholahan, Varin, Napasool Wongvanich, and Worapong Tangsrirat. 2023. "Robust Constant Exponent Coefficient Fixed-Time Control Based on Finite-Time Extended Sliding Mode Observer of Permanent Magnet Synchronous Motors" Energies 16, no. 21: 7454. https://doi.org/10.3390/en16217454
APA StyleCholahan, V., Wongvanich, N., & Tangsrirat, W. (2023). Robust Constant Exponent Coefficient Fixed-Time Control Based on Finite-Time Extended Sliding Mode Observer of Permanent Magnet Synchronous Motors. Energies, 16(21), 7454. https://doi.org/10.3390/en16217454






