Power-System Flexibility: A Necessary Complement to Variable Renewable Energy Optimal Capacity Configuration
Abstract
1. Introduction
2. Model Formulation: Algorithm and Input Assumptions
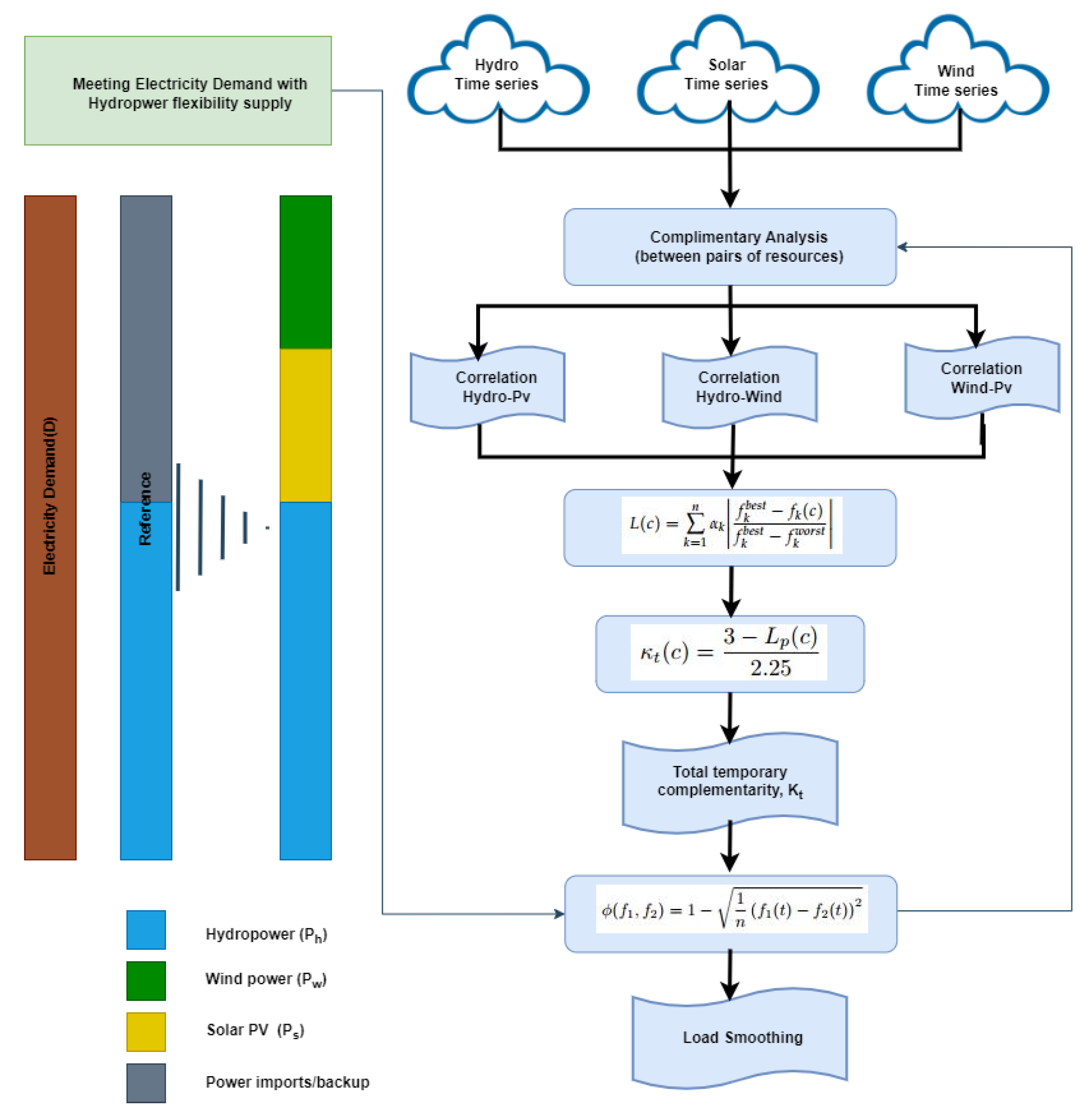
2.1. Complementary Characteristics by Means of the Correlation Coefficients
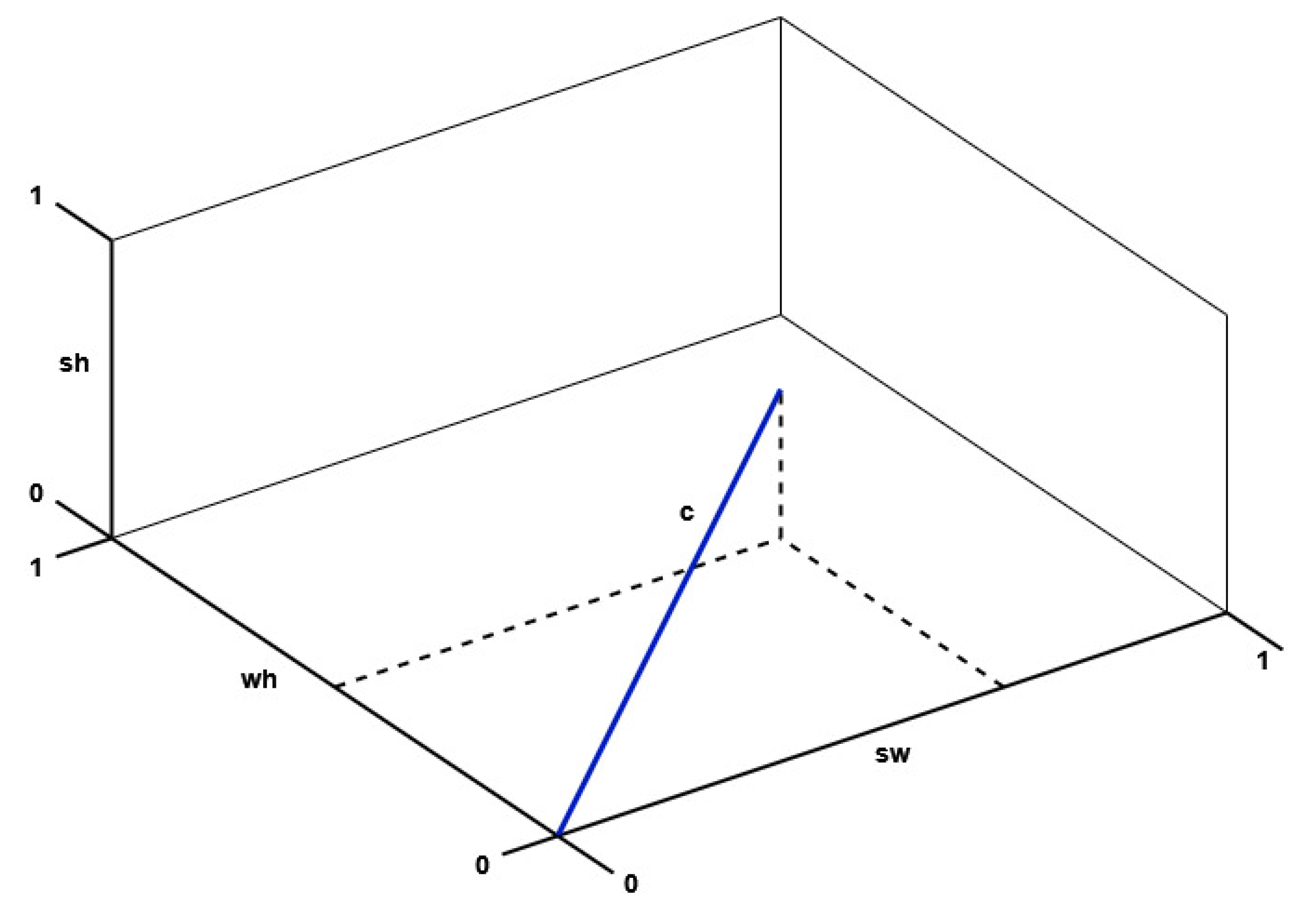
2.2. Space-Vector-Based Multidimensional Complementary Index
2.3. Load Smoothing through Complementarity
- Highly ratings for areas with complementary resources even when the strength of the actual resource is too weak for practical exploitation.
- Undervaluing areas with less complementary resources though strong enough to be useful for economic exploitation.
2.4. Power Generation Modeling
- (i)
- Hydropower Model
- (ii)
- Solar PV Model
- (iii)
- Wind Power Model
- (iv)
- Normalized generation configuration
3. Case Study and Datasets
3.1. Kenyan Electricity Sector
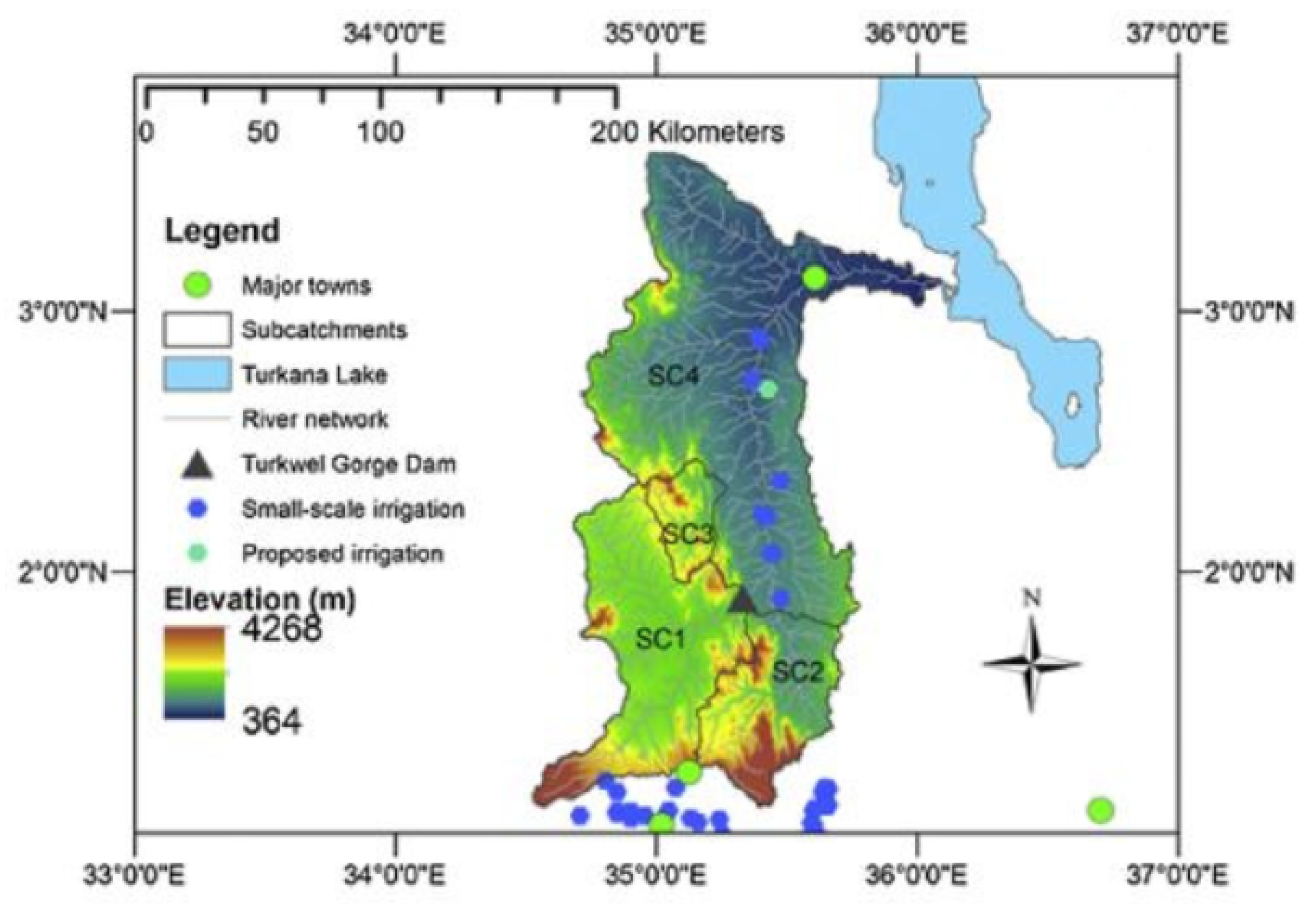
3.2. The Turkwel River Basin
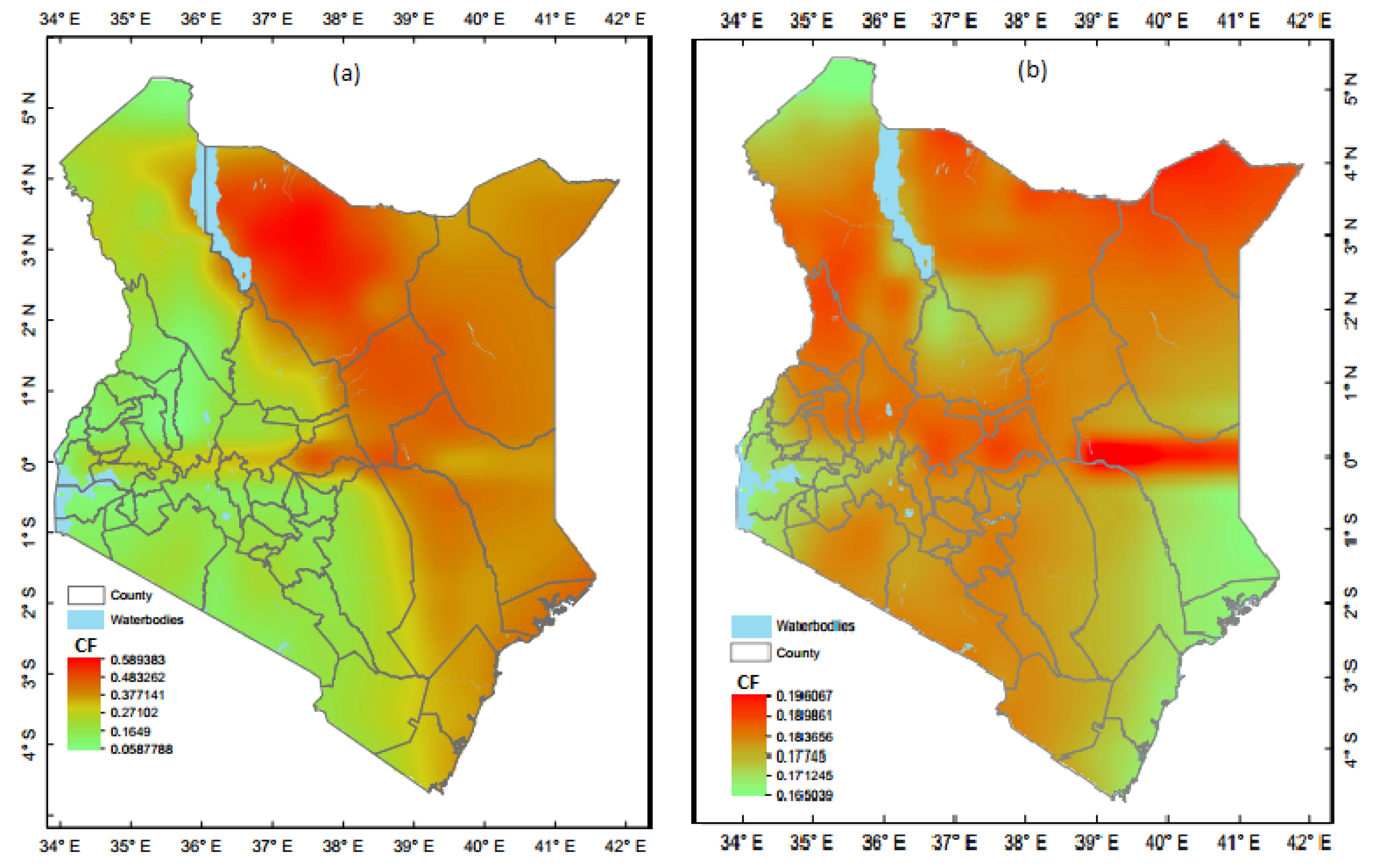
3.3. Wind and Solar Time Series
3.4. Power System Flexibility
4. Results and Discussion
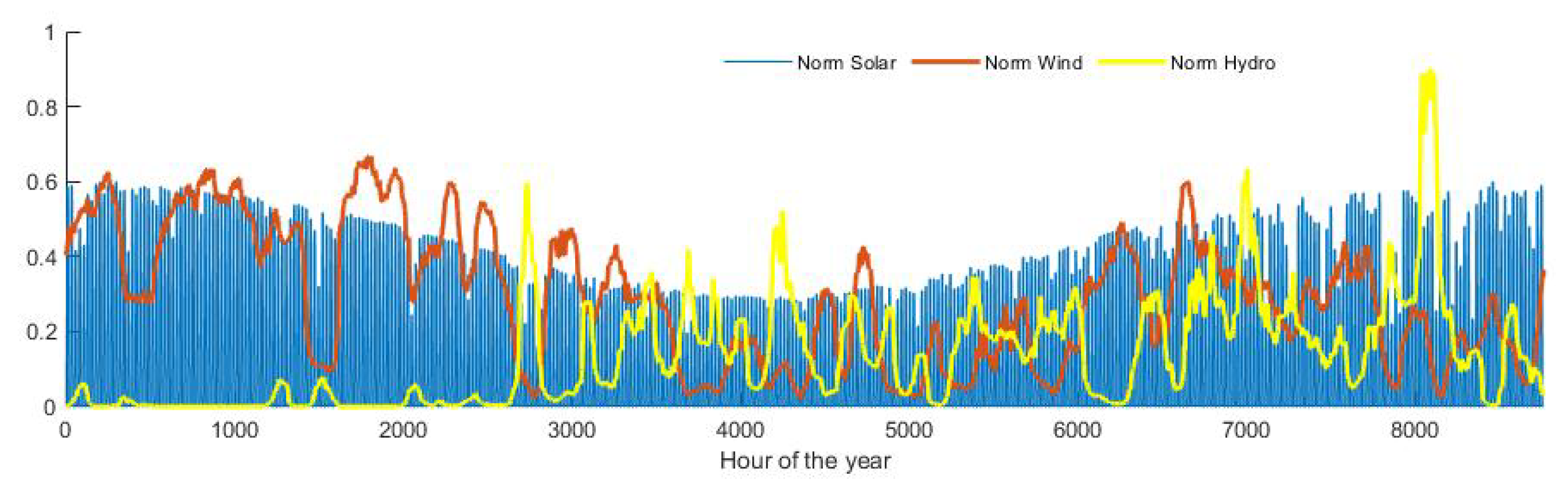
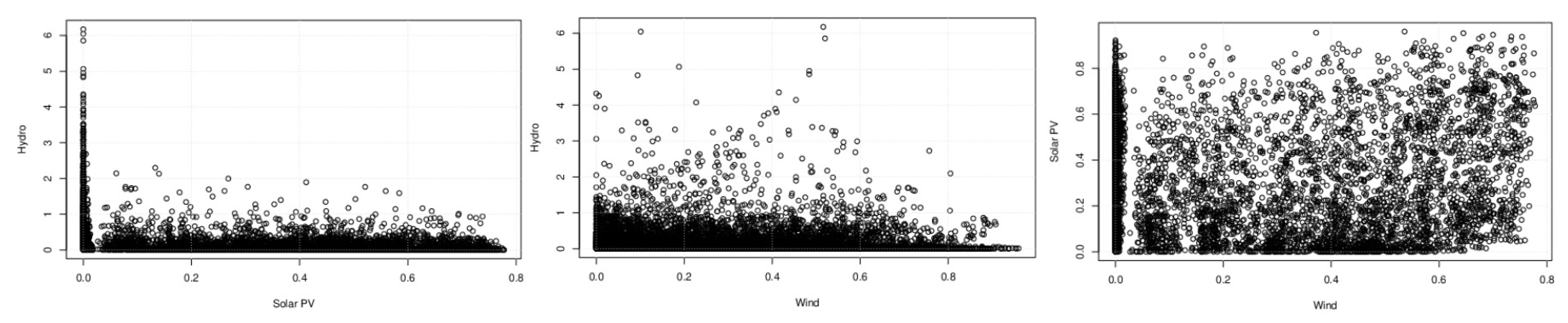
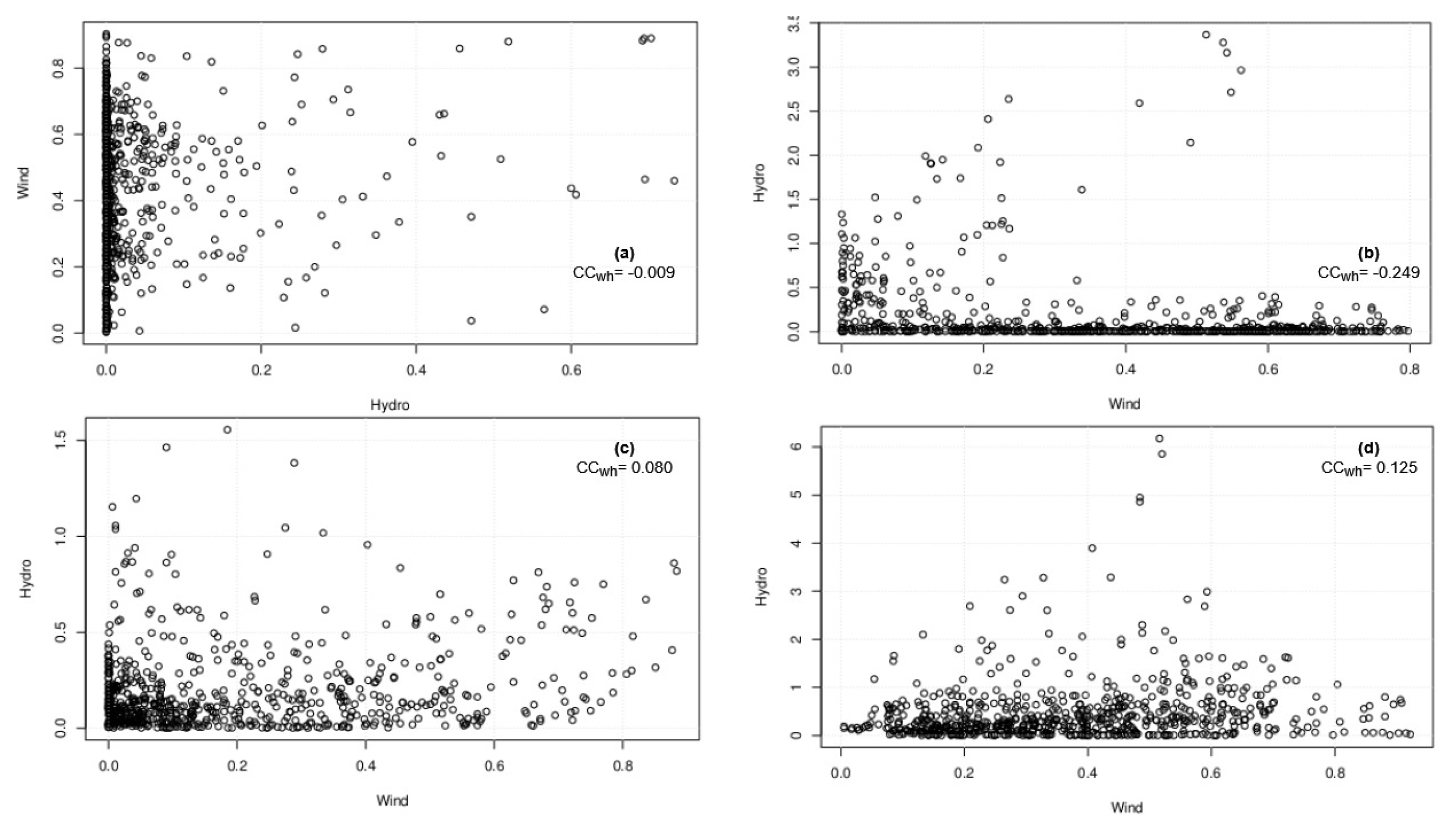
4.1. Early Evidence of Complementarity
4.2. Analysis of W-H-S Complementary Characteristics on Annual Scale
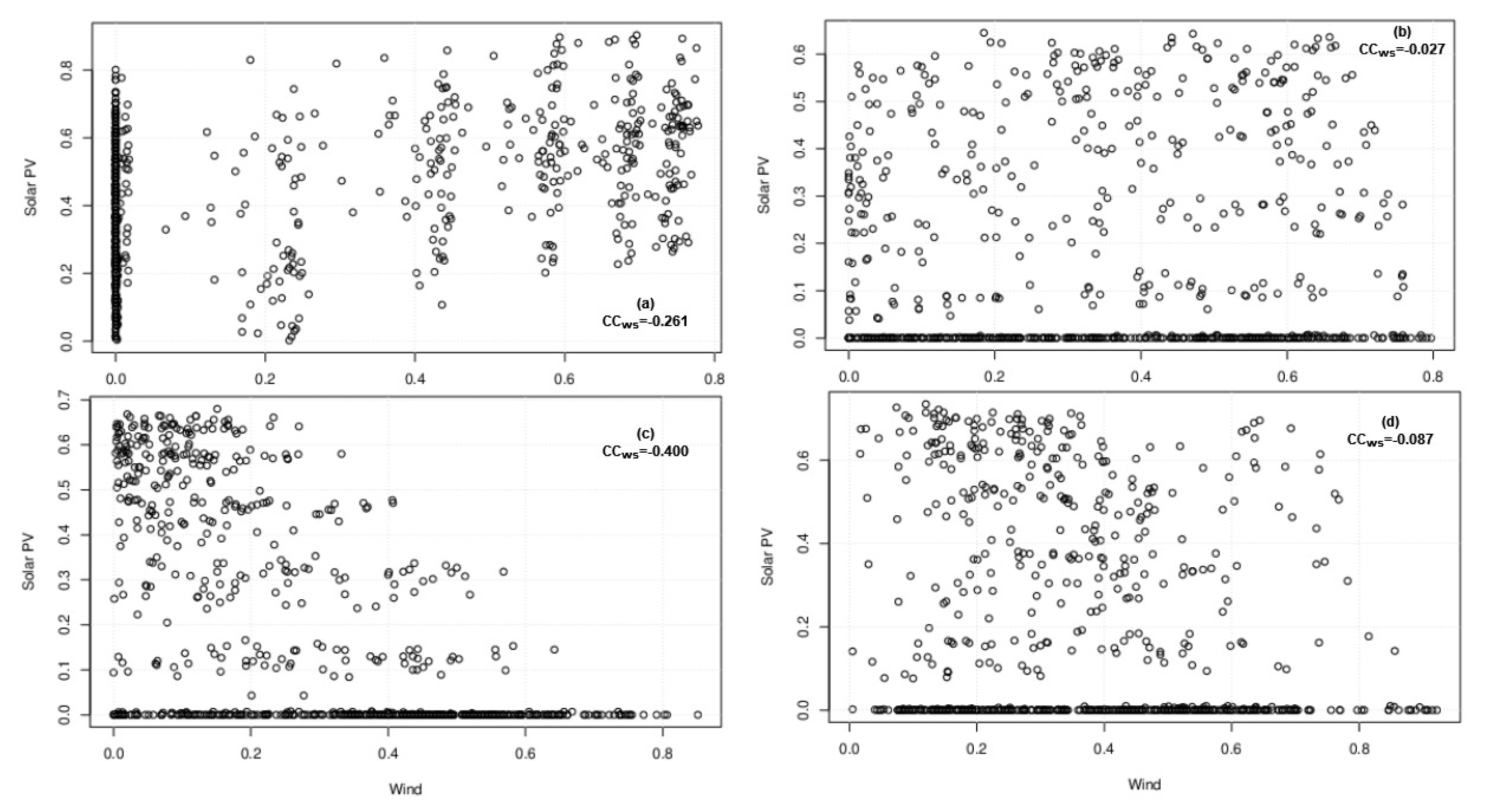
4.3. Complementary Characteristics of W-H-S on Monthly Timescale
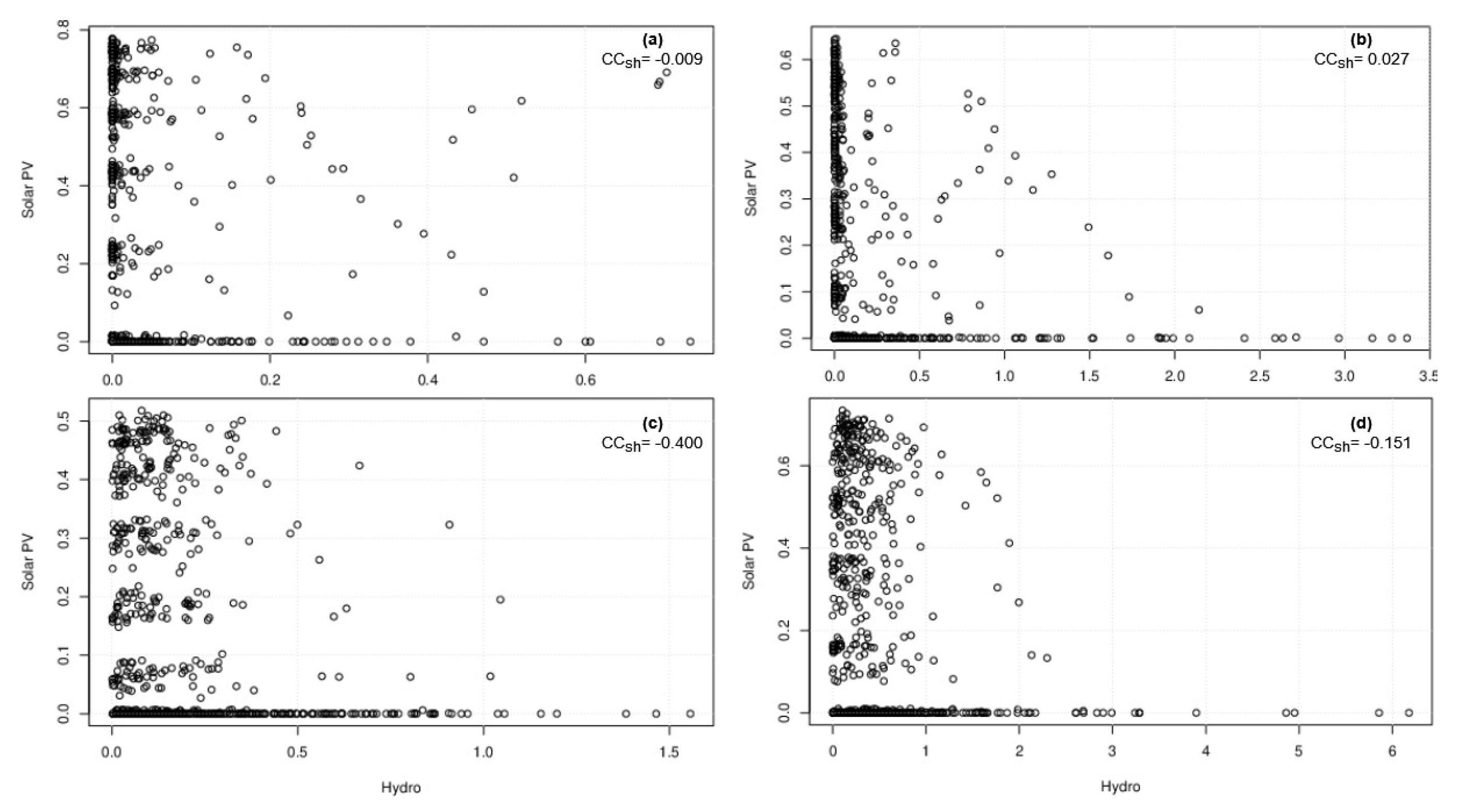
4.4. Complementary Characteristics of W-H-S on Daily Scale
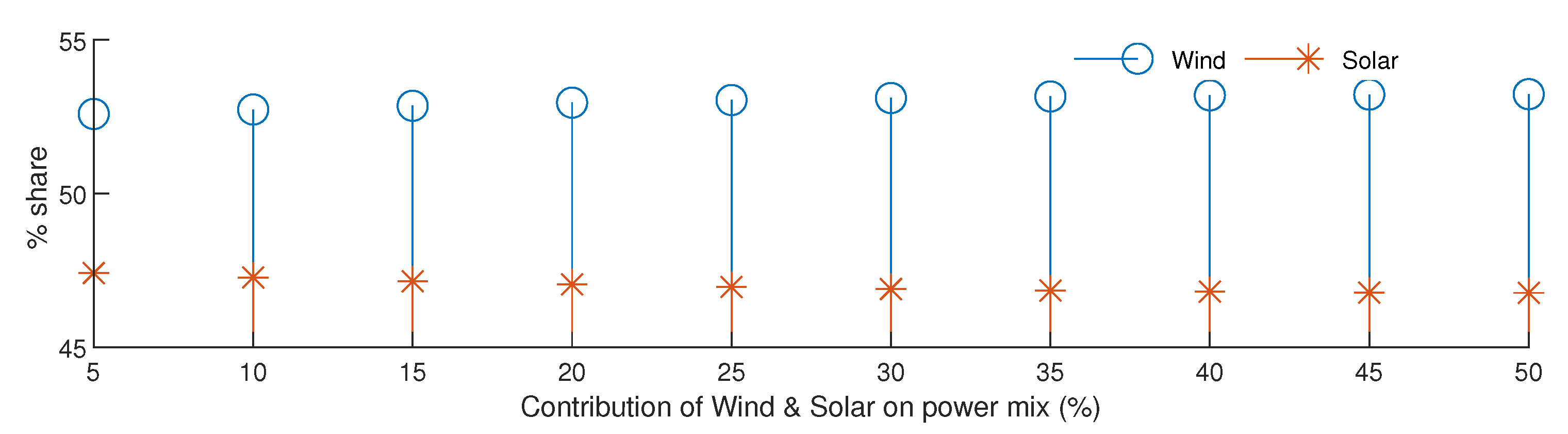
4.5. Temporo-Spatial Congruity between Wind/Solar and Hydropower Resources
5. Conclusions
- As the local electricity load demand continues to grow steadily, it is imperative to explore additional renewable energy options to meet this demand.
- The complementarity of VRE sources in the region is comparatively good, therefore, on appraising the power system flexibility in the region, it should be given utmost consideration when planning new power plants.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CC | Correlation Coefficients |
| CF | Capacity Factor |
| CSP | Concentrated Solar Power |
| GHG | Global Greenhouse Gas |
| GHI | Global Horizontal Irradiation |
| PV | Photovoltaic |
| RE | Renewable Energy |
| RE | Renewable Energy Sources |
| VRE | Variable Renewable Energy |
References
- Teske, S.; Giurco, D.; Morris, T.; Nagrath, K.; Mey, F.; Briggs, C.; Dominish, E.; Florin, N. Achieving the Paris Climate Agreement Goals: Global and Regional 100% Renewable Energy Scenarios to Achieve the Paris Agreement Goals with Non-Energy GHG Pathways for +1.5 °C and +2 °C; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Hirpa, F.A.; Dyer, E.; Hope, R.; Olago, D.O.; Dadson, S.J. Finding sustainable water futures in data-sparse regions under climate change: Insights from the Turkwel River basin, Kenya. J. Hydrol. Reg. Stud. 2018, 19, 124–135. [Google Scholar] [CrossRef]
- Hall, S. Power-Sector Emissions Are Set to Fall in 2022. Thanks to Renewable Energy. 2022. Available online: https://climatechampions.unfccc.int/power-sector-emissions-are-set-to-fall-in-2022-thanks-to-renewable-energy/ (accessed on 20 October 2022).
- Bogdanov, D.; Ram, M.; Aghahosseini, A.; Gulagi, A.; Oyewo, A.S.; Child, M.; Caldera, U.; Sadovskaia, K.; Farfan, J.; De Souza Noel Simas Barbosa, L.; et al. Low-cost renewable electricity as the key driver of the global energy transition towards sustainability. Energy 2021, 227, 120467. [Google Scholar] [CrossRef]
- Cheng, Q.; Liu, P.; Xia, J.; Ming, B.; Cheng, L.; Chen, J.; Xie, K.; Liu, Z.; Li, X. Contribution of complementary operation in adapting to climate change impacts on a large-scale wind-solar-hydro system: A case study in the Yalong River Basin, China. Appl. Energy 2022, 325, 119809. [Google Scholar] [CrossRef]
- Hunt, T. Has the International Energy Agency Finally Improved at Forecasting Solar Growth? 2020. Available online: https://pv-magazine-usa.com/2020/07/12/has-the-international-energy-agency-finally-improved-at-forecasting-solar-growth/ (accessed on 19 October 2022).
- Namahoro, J.P.; Wu, Q.; Xiao, H.; Zhou, N. The Impact of Renewable Energy, Economic and Population Growth on CO2 Emissions in the East African Region: Evidence from Common Correlated Effect Means Group and Asymmetric Analysis. Energies 2021, 14, 312. [Google Scholar] [CrossRef]
- Falchetta, G.; Gernaat, D.E.; Hunt, J.; Sterl, S. Hydropower dependency and climate change in sub-Saharan Africa: A nexus framework and evidence-based review. J. Clean. Prod. 2019, 231, 1399–1417. [Google Scholar] [CrossRef]
- Falchetta, G.; Pachauri, S.; Byers, E.; Danylo, O.; Parkinson, S.C. Satellite Observations Reveal Inequalities in the Progress and Effectiveness of Recent Electrification in Sub-Saharan Africa. One Earth 2020, 2, 364–379. [Google Scholar] [CrossRef]
- Oyewo, A.S.; Aghahosseini, A.; Ram, M.; Breyer, C. Transitions towards decarbonised power systems and its socio-economic impacts in West Africa. Renew. Energy 2020, 154, 1092–1112. [Google Scholar] [CrossRef]
- Alova, G.; Trotter, P.A.; Money, A. A machine-learning approach to predicting Africa’s electricity mix based on planned power plants and their chances of success. Nat. Energy 2021, 6, 158–166. [Google Scholar] [CrossRef]
- Sterl, S. A Grid for all Seasons: Enhancing the Integration of Variable Solar and Wind Power in Electricity Systems Across Africa. Curr. Sustain. Energy Rep. 2021, 8, 274–281. [Google Scholar] [CrossRef]
- Maulidi, B.; Dmitrii, B.; Solomon, O.A.; Christian, B. A cost optimal resolution for Sub-Saharan Africa powered by 100% renewables in 2030. Renew. Sustain. Energy Rev. 2018, 92, 440–457. [Google Scholar]
- IRENA. Planning and Prospects for Renewable Power: Eastern and Southern Africa, 2021. Available online: https://www.irena.org/publications/2021/Apr/Planning-and-prospects-for-renewable-power-Eastern-and-Southern-Africa (accessed on 20 October 2022).
- Wu, G.C.; Deshmukh, R.; Ndhlukula, K.; Radojicic, T.; Reilly-Moman, J.; Phadke, A.; Kammen, D.M.; Callaway, D.S. Strategic siting and regional grid interconnections key to low-carbon futures in African countries. Proc. Natl. Acad. Sci. USA 2017, 114, E3004–E3012. [Google Scholar] [CrossRef]
- Aghahosseini, A.; Bogdanov, D.; Breyer, C. Towards sustainable development in the MENA region: Analysing the feasibility of a 100% renewable electricity system in 2030. Energy Strategy Rev. 2020, 28, 100466. [Google Scholar] [CrossRef]
- Jurasz, J.; Canales, F.; Kies, A.; Guezgouz, M.; Beluco, A. A review on the complementarity of renewable energy sources: Concept, metrics, application and future research directions. Sol. Energy 2020, 195, 703–724. [Google Scholar] [CrossRef]
- Solomon, O.; Asfaw, S.; Bogdanov, D.; Aghahosseini, A.; Mensah, T.; Ram, M. Just transition towards defossilised energy systems for developing economies: A case study of Ethiopia. Renew. Energy 2021, 176, 346–365. [Google Scholar] [CrossRef]
- Bogdanov, D.; Aghahosseini, A.; Gulagi, A.; Child, M.; Solomon, O.; Farfan Orozco, F.; Sadovskaia, K.; Vainikka, P. Solar photovoltaics demand for the global energy transition in the power sector. Prog. Photovoltaics Res. Appl. 2018, 25, 523. [Google Scholar] [CrossRef]
- Elkadeem, M.R.; Younes, A.; Sharshir, S.W.; Campana, P.; Wang, S. Sustainable siting and design optimization of hybrid renewable energy system: A geospatial multi-criteria analysis. Appl. Energy 2021, 295, 117071. [Google Scholar] [CrossRef]
- Sterl, S.; Fadly, D.; Liersch, S.; Koch, H.; Thiery, W. Linking solar and wind power in eastern Africa with operation of the Grand Ethiopian Renaissance Dam. Nature Energy 2021, 6, 407–418. [Google Scholar] [CrossRef]
- Timmons, D.; Dhunny, A.; Elahee, K.; Havumaki, B.; Howells, M.; Khoodaruth, A.; Lema-Driscoll, A.; Lollchund, M.; Ramgolam, Y.; Rughooputh, S.; et al. Cost minimization for fully renewable electricity systems: A Mauritius case study. Energy Policy 2019, 133, 110895. [Google Scholar] [CrossRef]
- Oyewo, A.S.; Sterl, S.; Khalili, S.; Breyer, C. Highly renewable energy systems in Africa: Rationale, research, and recommendations. Joule 2023, 7, 1437–1470. [Google Scholar] [CrossRef]
- Nyenah, E.; Sterl, S.; Thiery, W. Pieces of a puzzle: Solar-wind power synergies on seasonal and diurnal timescales tend to be excellent worldwide. Environ. Res. Commun. 2022, 4, 055011. [Google Scholar] [CrossRef]
- Sterl, S.; Liersch, S.; Koch, H.; van Lipzig, N.P.; Thiery, W. A new approach for assessing synergies of solar and wind power: Implications for West Africa. Environ. Res. Lett. 2018, 13, 094009. [Google Scholar] [CrossRef]
- Škrbić, B.; Đurišić, Ž. Novel Planning Methodology for Spatially Optimized RES Development Which Minimizes Flexibility Requirements for Their Integration into the Power System. Energies 2023, 16, 3251. [Google Scholar] [CrossRef]
- Scott, I.J.; Carvalho, P.M.; Botterud, A.; Silva, C.A. Clustering representative days for power systems generation expansion planning: Capturing the effects of variable renewables and energy storage. Appl. Energy 2019, 253, 113603. [Google Scholar] [CrossRef]
- Geem, Z.W.; Kim, J.H. Optimal Energy Mix with Renewable Portfolio Standards in Korea. Sustainability 2016, 8, 423. [Google Scholar] [CrossRef]
- Cho, S.; Kim, H.; Lee, S.; Kim, S.; Jeon, E.C. Optimal energy mix for greenhouse gas reduction with renewable energy—The case of the South Korean electricity sector. Energy Env. 2020, 31, 1055–1076. [Google Scholar] [CrossRef]
- Huang, M.C.; Kim, C.J. Investigating Cost-Effective Policy Incentives for Renewable Energy in Japan: A Recursive CGE Approach for an Optimal Energy Mix. Singap. Econ. Rev. 2020, 66, 507–528. [Google Scholar] [CrossRef]
- Babonneau, F.; Barrera, J.; Toledo, J. Decarbonizing the Chilean Electric Power System: A Prospective Analysis of Alternative Carbon Emissions Policies. Energies 2021, 14, 4768. [Google Scholar] [CrossRef]
- Hussain, S.; Lai, C.; Eicker, U. Flexibility: Literature review on concepts, modeling, and provision method in smart grid. Sustain. Energy Grids Netw. 2023, 35, 101113. [Google Scholar] [CrossRef]
- Dong, J.; Chen, Z.; Dou, X. The Influence of Multiple Types of Flexible Resources on the Flexibility of Power System in Northwest China. Sustainability 2022, 14, 11617. [Google Scholar] [CrossRef]
- Wessa, P. Kendall tau Rank Correlation (v1.0.13) in Free Statistics Software (v1.2.1); Office for Research Development and Education: 2017. Available online: https://www.wessa.net/rwasp_kendall.wasp/ (accessed on 6 September 2023).
- Kendall, M.G. A new measure of rank correlation. Biometrika 1938, 30, 81–93. [Google Scholar] [CrossRef]
- Kendall tau Metric—Encyclopedia of Mathematics. 2023. Available online: https://encyclopediaofmath.org/wiki/Kendall_tau_metric (accessed on 6 September 2023).
- Canales, F.; Jurasz, J.; Beluco, A.; Kies, A. Assessing temporal complementarity between three variable energy sources through correlation and compromise programming. Energy 2019, 192, 116637. [Google Scholar] [CrossRef]
- Sharma, P.; Said, Z.; Kumar, A.; Nizetic, S.; Pandey, A.; Hoang, A.; Huang, Z.; Afzal, A.; Li, C.; Le Anh, T.; et al. Recent Advances in Machine Learning Research for Nanofluid-Based Heat Transfer in Renewable Energy System. Energy Fuels 2022, 36, 6626–6658. [Google Scholar] [CrossRef]
- Gershon, M.; Duckstein, L. Multiobjective Approaches to River Basin Planning. J. Water Resour. Plan. Manag. 1981, 109, 13–28. [Google Scholar] [CrossRef]
- Wang, S.; Jia, R.; Luo, C.; An, Y.; Guo, P. Spatiotemporal Complementary Characteristics of Large-Scale Wind Power, Photovoltaic Power, and Hydropower. Sustainability 2022, 14, 9273. [Google Scholar] [CrossRef]
- Liu, Y.; Xiao, L.; Wang, H.; Dai, S.; Qi, Z. Analysis on the hourly spatiotemporal complementarities between China’s solar and wind energy resources spreading in a wide area. Sci. China Technol. Sci. 2013, 56, 683–692. [Google Scholar] [CrossRef]
- Francois, B.; Borga, M.; Creutin, J.; Hingray, B.; Raynaud, D.; Sauterleute, J. Complementarity between solar and hydro power: Sensitivity study to climate characteristics in Northern-Italy. Renew. Energy 2016, 86, 543–553. [Google Scholar] [CrossRef]
- Gils, H.; Scholz, Y.; Pregger, T.; Luca de Tena, D.; Heide, D. Integrated modelling of variable renewable energy-based power supply in Europe. Energy 2017, 123, 173–188. [Google Scholar] [CrossRef]
- do Couto, A.F.; Estanqueiro, A. Exploring Wind and Solar PV Generation Complementarity to Meet Electricity Demand. Energies 2020, 13, 4132. [Google Scholar] [CrossRef]
- Ma, T.; Yang, H.; Lu, L. Optimal design of an autonomous solar–wind-pumped storage power supply system. Appl. Energy 2014, 160, 728–736. [Google Scholar] [CrossRef]
- Couto, A.; Estanqueiro, A. Assessment of wind and solar PV local complementarity for the hybridization of the wind power plants installed in Portugal. J. Clean. Prod. 2021, 319, 128728. [Google Scholar] [CrossRef]
- Huang, Y.; Chen, A.; Liu, T.; Wang, W.S. Assessment and Configuration of the Wind-PV-wave Complementary System for Improving the Stability and Power Generation Ability. In Proceedings of the 2022 4th International Conference on Smart Power & Internet Energy Systems (SPIES), Beijing, China, 9–12 December 2022; pp. 1344–1349. [Google Scholar]
- Sterl, S. Seasons of Power-Streamlining Strategies for Renewable Electricity Generation from Sun, Wind and Water in Sub-Saharan Africa. 2021. Available online: https://www.researchgate.net/publication/354758232_Seasons_of_Power_-_Streamlining_strategies_for_renewable_electricity_generation_from_sun_wind_and_water_in_sub-Saharan_Africa (accessed on 20 October 2022).
- Cantor, D.; Ochoa, A.; Mesa, O. Total Variation-Based Metrics for Assessing Complementarity in Energy Resources Time Series. Sustainability 2022, 14, 8514. [Google Scholar] [CrossRef]
- Iwueze, I.; Nwogu, E.; Nlebedim, V.; Imoh, J. Comparison of Two Time Series Decomposition Methods: Least Squares and Buys-Ballot Methods. Open J. Stat. 2016, 6, 1123–1137. [Google Scholar] [CrossRef][Green Version]
- Francois, B.; Martino, S.; Tofte, L.; Hingray, B.; Mo, B.; Creutin, J. Effects of Increased Wind Power Generation on Mid-Norway’s Energy Balance under Climate Change: A Market Based Approach. Energies 2017, 10, 227. [Google Scholar] [CrossRef]
- McPherson, M.; Sotiropoulos-Michalakakos, T.; Harvey, L.D.; Karney, B. An Open-Access Web-Based Tool to Access Global, Hourly Wind and Solar PV Generation Time-Series Derived from the MERRA Reanalysis Dataset. Energies 2017, 10, 1007. [Google Scholar] [CrossRef]
- Davis, P.J. Interpolation and Approximsation; Dover Publications: Mineola, NY, USA, 1975. [Google Scholar]
- Avery, S. Lake Turkana and the Lower Omo: Hydrological Impacts of Major Dam and Irrigation Developments. 2012. Available online: https://africanstudies.web.ox.ac.uk/sites/default/files/africanstudies/documents/media/executive_summary_introduction.pdf (accessed on 21 October 2022).
- Takase, M.; Kipkoech, R.; Essandoh, P.K. A comprehensive review of energy scenario and sustainable energy in Kenya. Fuel Commun. 2021, 7, 100015. [Google Scholar] [CrossRef]
- Staffell, I.; Pfenninger, S. Using bias-corrected reanalysis to simulate current and future wind power output. Energy 2016, 114, 1224–1239. [Google Scholar] [CrossRef]
- Pfenninger, S.; Staffell, I. Long-term patterns of European PV output using 30 years of validated hourly reanalysis and satellite data. Energy 2016, 114, 1251–1265. [Google Scholar] [CrossRef]
- Grams, C.; Beerli, R.; Pfenninger, S.; Staffell, I.; Wernli, H. Balancing Europes wind-power output through spatial deployment informed by weather regimes. Nat. Clim. Chang. 2017, 7, 557–562. [Google Scholar] [CrossRef]
- The Largest Wind Power Plant in Africa Has Opened in Kenya, 2023. Available online: https://www.weforum.org/agenda/2019/07/wind-power-project-opens-in-kenya/ (accessed on 22 April 2023).
- Bloomfield, H.C.; Wainwright, C.M.; Mitchell, N. Characterizing the variability and meteorological drivers of wind power and solar power generation over Africa. Meteorol. Appl. 2022, 29, e2093. [Google Scholar] [CrossRef]
- King, J.A.; Engelstaedter, S.; Washington, R.; Munday, C. Variability of the Turkana Low-Level Jet in Reanalysis and Models: Implications for Rainfall. J. Geophys. Res. Atmos. 2021, 126, e2020JD034154. [Google Scholar] [CrossRef]
- Gong, W.; Liu, P.; Cheng, L.; Li, H.; Yang, Z. A varying comprehensive hydropower coefficient for medium/long-term operation of a single reservoir. Hydrol. Res. 2020, 51, 686–698. [Google Scholar] [CrossRef]
- Jin, X.; Wu, Q. Local flexibility markets: Literature review on concepts, models and clearing methods. Appl. Energy 2020, 261, 114387. [Google Scholar] [CrossRef]
- Babatunde, O.; Munda, J.; Hamam, Y. Power system flexibility: A review. Energy Rep. 2020, 6, 101–106. [Google Scholar] [CrossRef]
- Akrami, A.; Doostizadeh, M.; Aminifar, F. Power system flexibility: An overview of emergence to evolution. J. Mod. Power Syst. Clean Energy 2019, 7, 987–1007. [Google Scholar] [CrossRef]
- Renewables.ninja. 2022. Available online: https://www.renewables.ninja/ (accessed on 21 October 2022).
- Kies, A.; Schyska, B.U.; Bilousova, M.; El Sayed, O.; Jurasz, J.; Stoecker, H. Critical review of renewable generation datasets and their implications for European power system models. Renew. Sustain. Energy Rev. 2021, 152, 111614. [Google Scholar] [CrossRef]
- Camberlin, P.; Wairoto, J.G. Intraseasonal wind anomalies related to wet and dry spells during the ‘long’ and ‘short’ rainy seasons in Kenya. Theor. Appl. Climatol. 1997, 58, 57–69. [Google Scholar] [CrossRef]
- Edwards, G.; Dent, C.J.; Wade, N. Assessing the Potential Impact of Grid-Scale Variable Renewable Energy on the Reliability of Electricity Supply in Kenya. IDS Bull. 2017, 48, 29–48. [Google Scholar] [CrossRef][Green Version]
- Funk, C.; Hoell, A.; Shukla, S.; Husak, G.; Michaelsen, J. The East African Monsoon System: Seasonal Climatologies and Recent Variations. In The Monsoons and Climate Change; Springer: Cham, Switzerland, 2016; pp. 163–185. [Google Scholar] [CrossRef]
- Jurasz, J.; Beluco, A.; Canales, F. The impact of complementarity on power supply reliability of small scale hybrid energy systems. Energy 2018, 161, 737–743. [Google Scholar] [CrossRef]
- Fant, C.; Gunturu, B.; Schlosser, A. Characterizing wind power resource reliability in southern Africa. Appl. Energy 2016, 161, 565–573. [Google Scholar] [CrossRef]








| Property | Correlation Coefficient Range | Implication |
|---|---|---|
| Similarity | 0.9 to 1.0 | Very strong |
| 0.6 to 0.9 | Strong | |
| 0.3 to 0.6 | Moderate | |
| 0.0 to 0.3 | Weak | |
| Complementary | −0.9 to 1.0 | Very strong |
| −0.6 to −0.9 | Strong | |
| −0.3 to −0.6 | Moderate | |
| 0.0 to −0.3 | Weak |
| Kendell Tau Correlation Coefficient—() | |
|---|---|
| Complementarity vector | −0.065− 0.198 − 0.123 |
| Compromise programming | 1.307 |
| Total temporal complementarity index— | 75.24% |
| Month | Complementary Vector c | Spatial Optimal Solution, | Total Complementary Index, |
|---|---|---|---|
| 1 | 0.261 − 0.009 − 0.029 | 1.611 | 61.74 |
| 2 | 0.233 − 0.142 − 0.020 | 1.536 | 65.08 |
| 3 | 0.244 − 0.343 − 0.106 | 1.398 | 71.20 |
| 4 | 0.027 − 0.249 − 0.212 | 1.283 | 76.31 |
| 5 | −0.357 + 0.021 − 0.061 | 1.302 | 75.47 |
| 6 | −0.481 + 0.030 − 0.209 | 1.170 | 81.33 |
| 7 | −0.400 + 0.080 − 0.182 | 1.249 | 77.84 |
| 8 | −0.381 + 0.016 − 0.210 | 1.213 | 79.44 |
| 9 | −0.441− 0.151 − 0.057 | 1.175 | 81.10 |
| 10 | −0.151 + 0.135 − 0.097 | 1.443 | 69.19 |
| 11 | 0.011 + 0.084 − 0.278 | 1.408 | 70.76 |
| 12 | 0.087 − 0.166 − 0.155 | 1.383 | 71.87 |
| Day of Month | Complementary Vector c | Spatial Optimal Solution, | Total Complementary Index, |
|---|---|---|---|
| 1/1 | 0.519 + 0.369 + 0.758 | 2.323 | 30.08% |
| 2/1 | 0.190 + 0.500 0.800 | 2.245 | 33.55% |
| 3/1 | 0.304 + 0.319 + 0.115 | 1.869 | 50.27% |
| 4/1 | 0.053 − 0.128 − 0.563 | 1.181 | 80.85% |
| 5/1 | −0.023 + 0.394 − 0.239 | 1.567 | 63.71% |
| 6/1 | −0.407 + 0.581 − 0.385 | 1.395 | 71.34% |
| 7/1 | −0.781 + 0.083 − 0.081 | 1.110 | 83.98% |
| 8/1 | −0.320 + 0.252 − 0.247 | 1.342 | 73.67% |
| 9/1 | 0.123 + 0.303 − 0.538 | 1.444 | 69.17% |
| 10/1 | 0.146 + 0.412 + 0.093 | 1.826 | 52.20% |
| 11/1 | −0.814 + 0.507 − 0.481 | 1.106 | 84.19% |
| 12/1 | 0.566 − 0.567 − 0.753 | 1.124 | 83.40% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Juma, D.; Munda, J.; Kabiri, C. Power-System Flexibility: A Necessary Complement to Variable Renewable Energy Optimal Capacity Configuration. Energies 2023, 16, 7432. https://doi.org/10.3390/en16217432
Juma D, Munda J, Kabiri C. Power-System Flexibility: A Necessary Complement to Variable Renewable Energy Optimal Capacity Configuration. Energies. 2023; 16(21):7432. https://doi.org/10.3390/en16217432
Chicago/Turabian StyleJuma, Denis, Josiah Munda, and Charles Kabiri. 2023. "Power-System Flexibility: A Necessary Complement to Variable Renewable Energy Optimal Capacity Configuration" Energies 16, no. 21: 7432. https://doi.org/10.3390/en16217432
APA StyleJuma, D., Munda, J., & Kabiri, C. (2023). Power-System Flexibility: A Necessary Complement to Variable Renewable Energy Optimal Capacity Configuration. Energies, 16(21), 7432. https://doi.org/10.3390/en16217432







