Partial Discharge Localization through k-NN and SVM
Abstract
1. Introduction
2. Summary of Detecting and Monitoring PD in Power Transformers
3. Sources of Insulation Degradation
3.1. Ageing Factor
- Thermal Stress: Transformers are designed to operate at specific temperature ranges, and when they are exposed to high temperatures, it can cause the insulation materials to age and break down. The aging of insulation materials can lead to reduced dielectric strength, resulting in insulation failure and reduced performance.
- Moisture: Infiltrate the transformer through leaks, condensation, or humidity, causing corrosion of internal components, insulation breakdown, and reduced performance. Over time, moisture can accumulate and lead to insulation failure, especially in high temperatures.
- Chemical Degradation: Chemical degradation can occur due to various factors, such as exposure to pollutants, acids, and other chemicals. Chemical degradation can cause the insulation material to soften or become brittle, leading to insulation breakdown and reduced performance.
- Electrical Stress: Electrical stress, such as voltage spikes, surges, or harmonics, can cause insulation breakdown and damage the transformer’s internal components. Electrical stress can weaken the insulation material, reducing dielectric strength and eventual insulation failure.
- Mechanical Stress: Mechanical stress, such as vibrations and mechanical impacts, can damage the transformer’s internal components, leading to insulation breakdown and reduced performance.
- Time: Over time, the materials used in transformers can undergo physical and chemical changes, leading to reduced performance and eventual failure. The rate of aging depends on the materials used, the operating conditions, and the maintenance practices.
3.2. Acoustic Factor
- Core Laminations: The core laminations inside a transformer can vibrate due to magnetic forces, creating a humming or buzzing noise. Over time, the vibration can cause the laminations to loosen, resulting in increased noise levels and reduced transformer efficiency.
- Winding Vibrations: Vibrations in the transformer windings can also create noise. The vibration can occur due to mechanical stress, high currents, or voltage fluctuations. The vibration can cause the winding conductors to rub against each other or the insulation, leading to insulation breakdown and reduced transformer performance.
- Mechanical Stress: Mechanical stress can cause deformation or misalignment of the transformer’s components, increasing noise levels. Mechanical stress can occur due to uneven terrain, seismic activity, or nearby construction.
- Insulation Degradation: Insulation degradation can also contribute to increased noise levels. The insulation materials can become brittle or crack over time due to thermal stress, moisture, and other factors. The degradation of insulation materials can lead to partial discharge, which creates noise.
- Loose Components: Loose components, such as fasteners or bolts, can cause vibration and noise in the transformer. Over time, the vibration can cause damage to the transformer components and lead to reduced performance.
3.3. Tapping Factor
- Mechanical Stress: The tapping mechanism involves moving parts that can experience mechanical stress, leading to wear and tear over time. The mechanical stress can cause misalignment or damage to the components, leading to reduced performance and potential failure.
- Corrosion: Corrosion can occur on the tapping mechanism due to exposure to moisture, chemicals, or other environmental factors. The corrosion can cause the mechanism to become stuck or seize, leading to reduced performance or complete failure.
- Electrical Stress: Electrical stress can also affect the tapping mechanism, such as voltage spikes or surges. The electrical stress can cause insulation breakdown or arcing, leading to reduced performance and potential failure.
- Age: The tapping mechanism can experience physical and chemical changes over time, leading to reduced performance and eventual failure. The rate of aging depends on the materials used, the operating conditions, and the maintenance practices.
4. Preparation for the Model and Construction
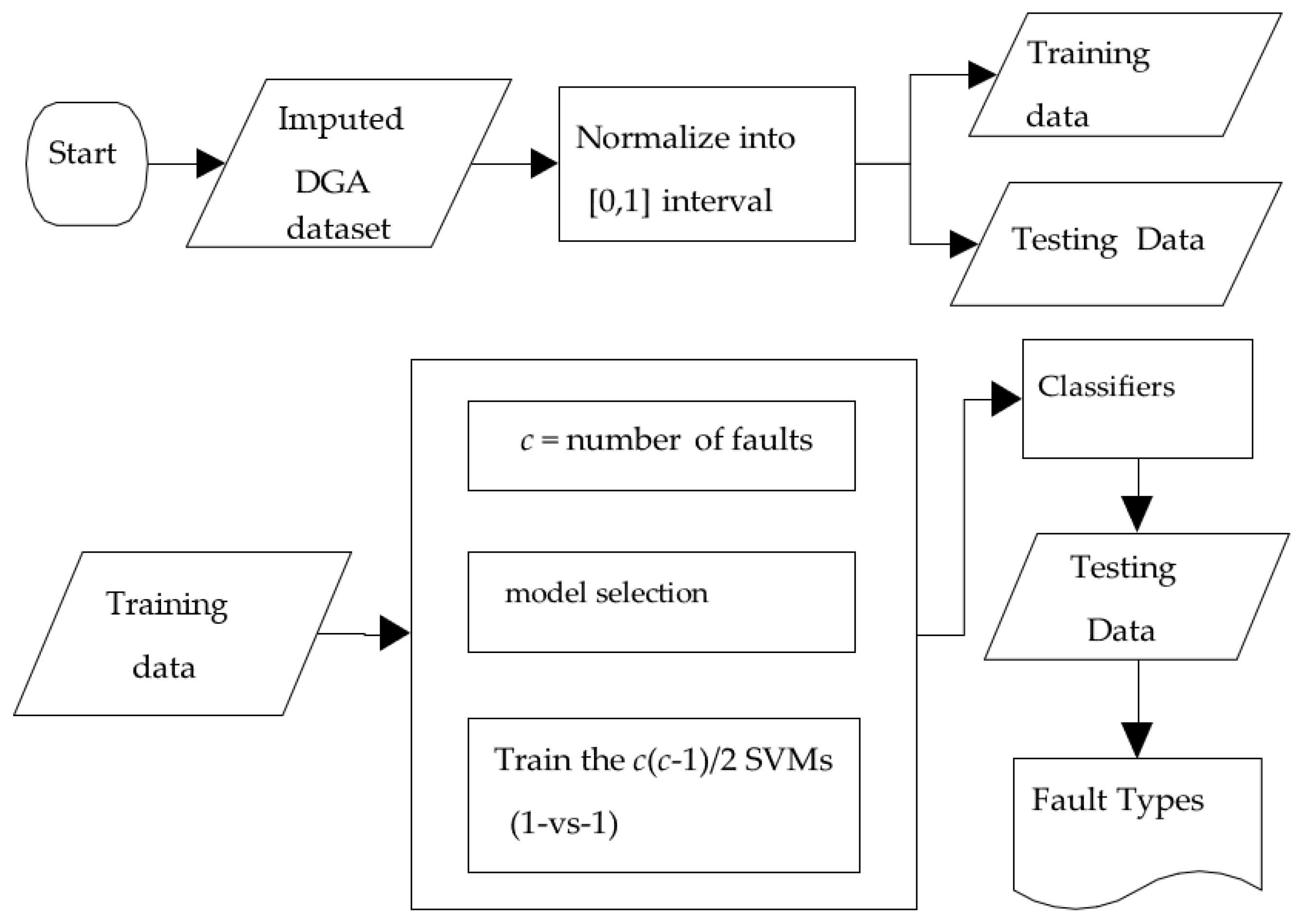
4.1. The Proposed Structure
4.2. Estimation of Missing Values Utilizing kNN
4.3. SVM Classification
- Polynomial: K() = ( ;
- Radial basic function: K() = ;
- Sigmoid: K() = tanh ().
5. Experimental Design and Results
5.1. Dataset
5.2. Experimental Setup
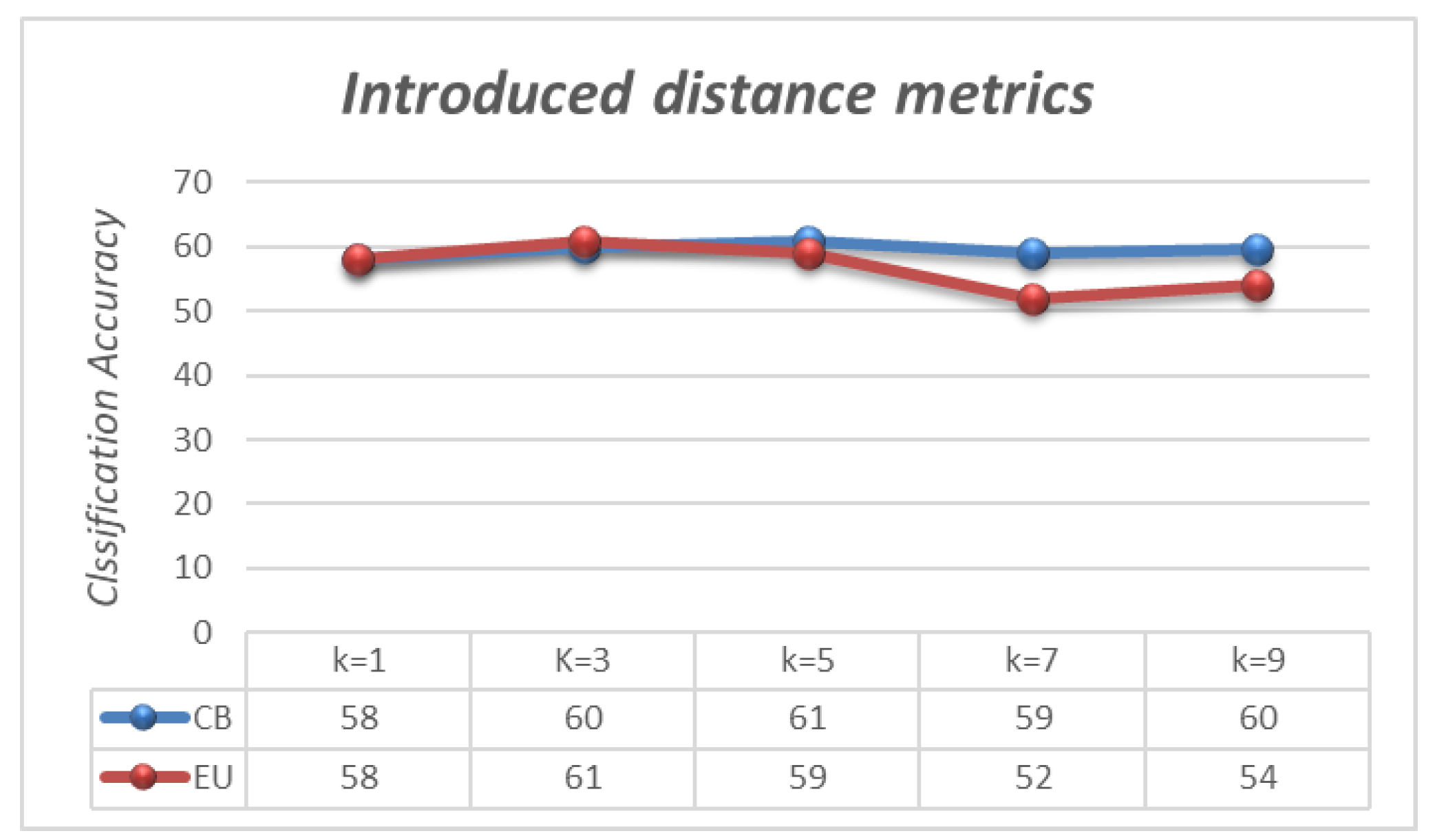
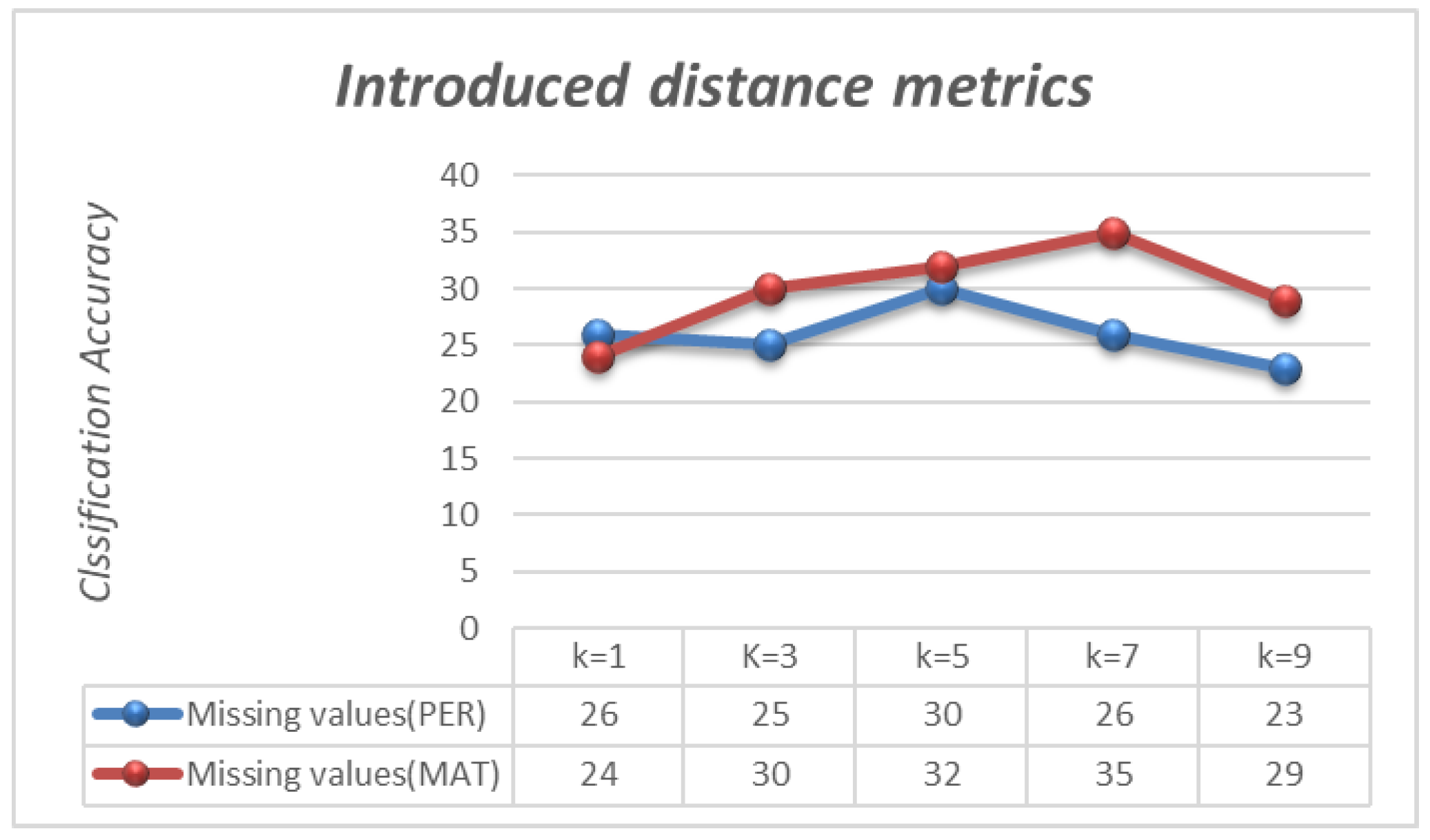
5.3. Case Study 1:PER_Dataset
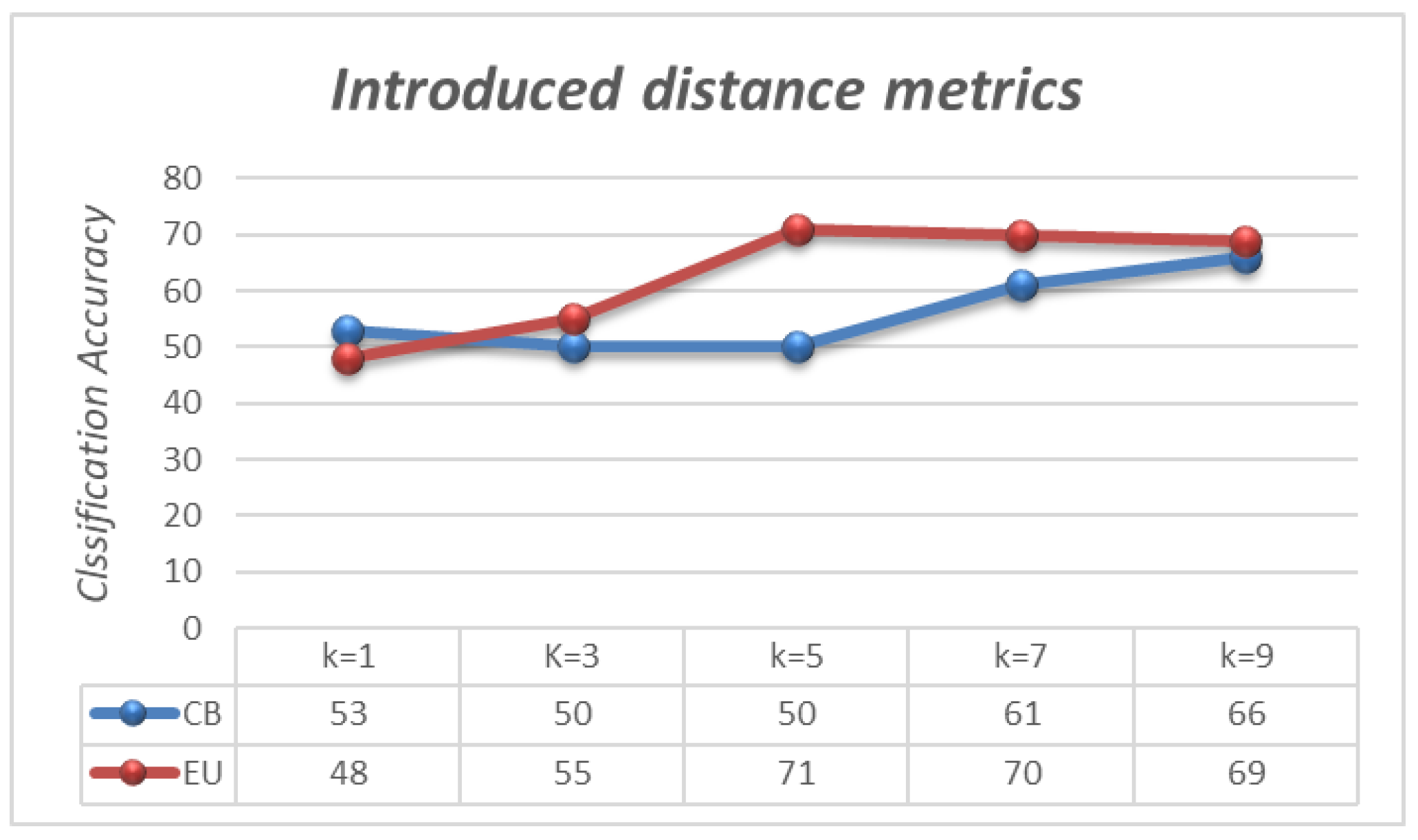
5.4. Case Study 2: MAT_Dataset
5.5. Case Study Discussion 1
5.6. Case Study Discussion 2
5.7. Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bartley, W. Analysis of Transformer Failures. In Proceedings of the 67th Annual International Conference of Doble Clients, Paper 8N, Watertown, MA, USA, 27–31 March 2000. [Google Scholar]
- Braunlich, R.; Hassig, M.; Fuhr, J.; Aschwanden, T. Assessment of insulation condition of large power transformers by on-site electrical diagnostic methods. In Proceedings of the Conference Record of the 2000 IEEE International Symposium on Electrical Insulation, Anaheim, CA, USA, 2–5 April 2000; pp. 368–372. [Google Scholar]
- Wang, X.; Li, B.; Roman, H.; Russo, O.; Chin, K.; Farmer, K. Acousto-optical PD Detection for Transformers. IEEE Trans. Power Deliv. 2006, 21, 1068–1073. [Google Scholar] [CrossRef]
- Sharkawy, R.M.; Ibrahim, K.; Salama, M.M.A.; Bartnikas, R. Particle swarm optimization feature selection for the classi-fication of conducting particles in transformer oil. IEEE Trans. Dielectr. Electr. Insul. 2011, 18, 1897–1907. [Google Scholar] [CrossRef]
- Rubio-Serrano, J.; Rojas-Moreno, M.V.; Posada, J.; Martínez-Tarifa, J.; Robles, J.; García-Souto, J. Electro-acoustic detection, identification and location of partial discharge sources in oil-paper insulation systems. IEEE Trans. Dielectr. Electr. Insul. 2012, 19, 1569–1578. [Google Scholar] [CrossRef]
- Coenen, S.; Tenbohlen, S. Location of PD sources in power transformers by UHF and acoustic measurements. IEEE Trans. Dielectr. Electr. Insul. 2012, 19, 1934–1940. [Google Scholar] [CrossRef]
- Li, J.; Jiang, T.; Wang, C.; Cheng, C. Optimization of UHF Hilbert Antenna for Partial Discharge Detection of Transformers. IEEE Trans. Antennas Propag. 2012, 60, 2536–2540. [Google Scholar] [CrossRef]
- Hooshmand, R.A.; Parastegari, M.; Yazdanpanah, M. Simultaneous location of two partial discharge sources in power transformers based on acoustic emission using the modified binary partial swarm optimization algorithm. IET Sci. Meas. Technol. 2012, 7, 119–127. [Google Scholar] [CrossRef]
- Zheng, S.; Li, C.; Tang, Z.; Chang, W.; He, M. Location of PDs inside transformer windings using UHF methods. IEEE Trans. Dielectr. Electr. Insul. 2014, 21, 386–393. [Google Scholar] [CrossRef]
- Sinaga, H.H.; Phung, B.; Blackburn, T.R. Recognition of single and multiple partial discharge sources in transformers based on ultra-high frequency signals. IET Gener. Transm. Distrib. 2014, 8, 160–169. [Google Scholar] [CrossRef]
- Cui, L.; Chen, W.; Xie, B.; Du, J.; Long, Z.; Li, Y. Characteristic information extraction and developing process recognizing method of surface discharge in oil immersed paper insulation. In Proceedings of the 2014 International Conference on High Voltage Engineering and Application (ICHVE), Poznan, Poland, 8–11 September 2014; pp. 3–6. [Google Scholar]
- Hall, M.A. Correlation-Based Feature Selection for Machine Learning. Ph.D. Thesis, University of Waikato, Waikato, New Zealand, 1999. [Google Scholar]
- Duval, M.; Depabla, A. Interpretation of gas-in-oil analysis using new IEC publication 60599 and IEC TC 10 databases. IEEE Electr. Insul. Mag. 2001, 17, 31–41. [Google Scholar] [CrossRef]
- Acuña, E.; Rodriguez, C. The Treatment of Missing Values and Its Effect on Classifier Accuracy. In Classification, Clustering, and Data Mining Applications; Banks, D., McMorris, F.R., Arabie, P., Gaul, W., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 639–647. [Google Scholar] [CrossRef]
- Liu, P.; Lei, L.; Wu, N. A Quantitative Study of the Effect of Missing Data in Classifiers. In Proceedings of the Fifth International Conference on Computer and Information Technology (CIT’05), Shanghai, China, 21–23 September 2005; pp. 28–33. [Google Scholar] [CrossRef]
- Ma, H.; Saha, T.K.; Ekanayake, C. Machine learning techniques for power transformer insulation diagnosis. In AUPEC 2011; IEEE: Brisbane, QLD, Australia, 2011; pp. 1–6. [Google Scholar]
- Guo, C.; Dong, M.; Wu, Z. Fault Diagnosis of Power Transformers Based on Comprehensive Machine Learning of Dissolved Gas Analysis. In Proceedings of the 2019 IEEE 20th International Conference on Dielectric Liquids (ICDL), Roma, Italy, 23–27 June 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Liang, Y.; Sun, X.; Liu, Q.; Bian, J.; Li, Y. Fault Diagnosis Model of Power Transformer Based on Combinatorial KFDA. In Proceedings of the 2008 International Conference on Condition Monitoring and Diagnosis, Beijing, China, 21–24 April 2008; pp. 956–959. [Google Scholar] [CrossRef]
- Rajesh, K.N.V.P.S.; Rao, U.M.; Fofana, I.; Rozga, P.; Paramane, A. Influence of Data Balancing on Transformer DGA Fault Classification with Machine Learning Algorithms. IEEE Trans. Dielectr. Electr. Insul. 2023, 30, 385–392. [Google Scholar] [CrossRef]
- Mehta, A.K.; Sharma, R.N.; Chauhan, S.; Saho, S. Transformer diagnostics under dissolved gas analysis using Support Vector Machine. In Proceedings of the 2013 International Conference on Power, Energy and Control (ICPEC), Dindigul, India, 6–8 February 2013; pp. 181–186. [Google Scholar] [CrossRef]
- Illias, H.A.; Choon, C.K.; Liang, W.Z.; Mokhlis, H.; Ariffin, A.M.; Yousof, M.F.M. Fault Identification in Power Transformers Using Dissolve Gas Analysis and Support Vector Machine. In Proceedings of the 2021 IEEE International Conference on the Properties and Applications of Dielectric Materials (ICPADM), Johor Bahru, Malaysia, 12–14 July 2021; pp. 33–36. [Google Scholar] [CrossRef]
- Raghuraman, R.; Darvishi, A. Detecting Transformer Fault Types from Dissolved Gas Analysis Data Using Machine Learning Techniques. In Proceedings of the 2022 IEEE 15th Dallas Circuit and System Conference (DCAS), Dallas, TX, USA, 17–19 June 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Patil, S.D.; Dharme, M.; Patil, A.J.; Gautam Chakrawarthy, A.K.; Jarial, R.K.; Singh, A. DGA Based Ensemble learning and Random Forest Models for Condition Assessment of Transformers. In Proceedings of the 2022 International Conference on Smart Generation Computing, Communication and Networking (SMART GENCON), Bangalore, India, 23–25 December 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Rao, U.M.; Fofana, I.; Rajesh, K.N.V.P.S.; Picher, P. Identification and Application of Machine Learning Algorithms for Transformer Dissolved Gas Analysis. IEEE Trans. Dielectr. Electr. Insul. 2021, 28, 1828–1835. [Google Scholar] [CrossRef]
- Laayati, O.; Bouzi, M.; Chebak, A. Design of an oil immersed power transformer monitoring and self diagnostic system integrated in Smart Energy Management System. In Proceedings of the 2021 3rd Global Power, Energy and Communication Conference (GPECOM), Antalya, Turkey, 5–8 October 2021; pp. 240–245. [Google Scholar] [CrossRef]
- Das, S.; Paramane, A.; Chatterjee, S.; Rao, U.M. Sensing Incipient Faults in Power Transformers Using Bi-Directional Long Short-Term Memory Network. IEEE Sens. Lett. 2023, 7, 7000304. [Google Scholar] [CrossRef]
- Souza, F.R.; Ramachandran, B. Dissolved gas analysis to identify faults and improve reliability in transformers using support vector machines. In Proceedings of the 2016 Clemson University Power Systems Conference (PSC), Clemson, SC, USA, 8–11 March 2016; pp. 1–4. [Google Scholar] [CrossRef]
- Saha, C.; Baruah, N.; Nayak, S.K. Implementation of Self-Organizing Map and Logistic Regression in Dissolved Gas Analysis of Transformer oils. In Proceedings of the 2021 IEEE International Conference on the Properties and Applications of Dielectric Materials (ICPADM), Johor Bahru, Malaysia, 12–14 July 2021; pp. 131–134. [Google Scholar] [CrossRef]
- Rediansyah, D.; Prasojo, R.A.; Suwarno; Abu-Siada, A. Artificial Intelligence-Based Power Transformer Health Index for Handling Data Uncertainty. IEEE Access 2021, 9, 150637–150648. [Google Scholar] [CrossRef]
- Zhang, Z.; Huang, W.-H.; Xiao, D.-M.; Liu, Y.-L. Fault detection of power transformers using genetic programming method. In Proceedings of the 2004 International Conference on Machine Learning and Cybernetics (IEEE Cat. No.04EX826), Shanghai, China, 26–29 August 2004; Volume 5, pp. 3018–3022. [Google Scholar] [CrossRef]
- Kumar, A.H.; Thind, B.S.; Reddy, C.C. Improving Reliability of Transformers based on DGA Analysis using Machine Learning Techniques. In Proceedings of the 2021 IEEE Conference on Electrical Insulation and Dielectric Phenomena (CEIDP), Vancouver, BC, Canada, 12–15 December 2021; pp. 151–154. [Google Scholar] [CrossRef]
- Ekanayake, C.; Ma, H.; Saha, T. Past experience and future developments toward the safeguarding of power transformers. In Proceedings of the International Conference on Electrical & Computer Engineering (ICECE 2010), Dhaka, Bangladesh, 18–20 December 2010; pp. 279–282. [Google Scholar] [CrossRef]
- Lopes, S.M.d.A.; Flauzino, R.A. A Novel Approach for Incipient Fault Diagnosis in Power Transformers by Artificial Neural Networks. In Proceedings of the 2021 IEEE PES Innovative Smart Grid Technologies Europe (ISGT Europe), Espoo, Finland, 18–21 October 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Tra, V.; Duong, B.-P.; Kim, J.-M. Improving diagnostic performance of a power transformer using an adaptive over-sampling method for imbalanced data. IEEE Trans. Dielectr. Electr. Insul. 2019, 26, 1325–1333. [Google Scholar] [CrossRef]
- Laayati, O.; El Hadraoui, H.; Bouzi, M.; Chebak, A. Smart Energy Management System: Oil Immersed Power Transformer Failure Prediction and Classification Techniques Based on DGA Data. In Proceedings of the 2022 2nd International Conference on Innovative Research in Applied Science, Engineering and Technology (IRASET), Meknes, Morocco, 3–4 March 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Boczar, T.; Cichon, A.; Borucki, S. Diagnostic expert system of transformer insulation systems using the acoustic emission method. IEEE Trans. Dielectr. Electr. Insul. 2014, 21, 854–865. [Google Scholar] [CrossRef]
- Bua-Nunez, I.; Posada-Roman, J.E.; Rubio-Serrano, J.; Garcia-Souto, J.A. Instrumentation System for Location of Partial Discharges Using Acoustic Detection with Piezoelectric Transducers and Optical Fiber Sensors. IEEE Trans. Instrum. Meas. 2014, 63, 1002–1013. [Google Scholar] [CrossRef]
- Chen, M.-K.; Chen, J.-M.; Cheng, C.-Y. Partial discharge detection by RF coil in 161 kV power transformer. IEEE Trans. Dielectr. Electr. Insul. 2014, 21, 1405–1414. [Google Scholar] [CrossRef]
- Harbaji, M.; Shaban, K.; El-Hag, A. Classification of common partial discharge types in oil-paper insulation system using acoustic signals. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 1674–1683. [Google Scholar] [CrossRef]
- Mirzaei, H.R.; Akbari, A.; Gockenbach, E.; Miralikhani, K. Advancing new techniques for UHF PDdetection and localization in the power transformers in the factory tests. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 448–455. [Google Scholar] [CrossRef]
- Sarkar, B.; Koley, C.; Roy, N.; Kumbhakar, P. Condition monitoring of high voltage transformers using Fiber Bragg Grating Sensor. Meas. J. Int. Meas. Confed. 2015, 74, 255–267. [Google Scholar] [CrossRef]
- Qi, Z.; Yi, Y.; Qiaohua, W.; Zhihao, W.; Zhe, L. Study on the Online Dissolved Gas Analysis Monitor based on the Photoacoustic Spectroscopy. In Proceedings of the 2012 IEEE International Conference on Condition Monitoring and Diagnosis (CMD), Bali, Indonesia, 23–27 September 2012; pp. 433–436. [Google Scholar]
- Seo, J.; Ma, H.; Saha, T. Probabilistic wavelet transform for partial discharge measurement of transformer. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 1105–1117. [Google Scholar] [CrossRef]
- Mitchell, S.D.; Siegel, M.; Beltle, M.; Tenbohlen, S. Discrimination of partial discharge sources in the UHF domain. IEEE Trans. Dielectr. Electr. Insul. 2016, 23, 1068–1075. [Google Scholar] [CrossRef]
- Rostaminia, R.; Saniei, M.; Vakilian, M.; Mortazavi, S.S.; Parvin, V. Accurate power transformer PD pattern recognition via its model. IET Sci. Meas. Technol. 2016, 10, 745–753. [Google Scholar] [CrossRef]
- Jahangir, H.; Akbari, A.; Werle, P.; Szczechowski, J. Possibility of PD calibration on power transformers using UHF probes. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 2968–2976. [Google Scholar] [CrossRef]
- Ghosh, R.; Chatterjee, B.; Dalai, S. A method for the localization of partial discharge sources using partial discharge pulse information from acoustic emissions. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 237–245. [Google Scholar] [CrossRef]
- Du, J.; Chen, W.; Cui, L.; Zhang, Z.; Tenbohlen, S. Investigation on the propagation characteristics of PD-induced elec-tromagnetic waves in an actual 110 kV power transformer and its simulation results. IEEE Trans. Dielectr. Electr. Insul. 2018, 25, 1941–1948. [Google Scholar] [CrossRef]
- Wang, Y.-B.; Fan, Y.-H.; Qin, S.-R.; Chang, D.-G.; Shao, X.-J.; Mu, H.-B.; Zhang, G.-J. Partial discharge localisation methodology for power transformers based on improved acoustic propagation route search algorithm. IET Sci. Meas. Technol. 2018, 12, 1023–1030. [Google Scholar] [CrossRef]
- Fabian, J.; Neuwersch, M.; Sumereder, C.; Muhr, M.; Schwarz, R. State of the Art and Future Trends of Unconventional PD-Measurement at Power Transformers. J. Energy Power Eng. 2014, 8, 1093–1098. [Google Scholar] [CrossRef][Green Version]
- Sinaga, H.H.; Phung, B.T.; Blackburn, T.R. Partial discharge localization in transformers using UHF detection method. IEEE Trans. Dielectr. Electr. Insul. 2012, 19, 1891–1900. [Google Scholar] [CrossRef]
- Jahangir, H.; Akbari, A.; Werle, P.; Szczechowski, J. UHF PD measurements on power transformers-advantages and limitations. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 3933–3940. [Google Scholar] [CrossRef]
- Ariannik, M.; Azirani, M.A.; Werle, P.; Azirani, A.A. UHF Measurement in Power Transformers: An Algorithm to Optimize Accuracy of Arrival Time Detection and PD Localization. IEEE Trans. Power Deliv. 2019, 34, 1530–1539. [Google Scholar] [CrossRef]
- Azadifar, M.; Karami, H.; Wang, Z.; Rubinstein, M.; Rachidi, F.; Karami, H.; Ghasemi, A.; Gharehpetian, G.B. Partial Discharge Localization Using Electromagnetic Time Reversal: A Performance Analysis. IEEE Access 2020, 8, 147507–147515. [Google Scholar] [CrossRef]
- Wang, Y.B.; Chang, D.G.; Fan, Y.H.; Zhang, G.J.; Zhan, J.Y.; Shao, X.J.; He, W.L. Acoustic localization of partial discharge sources in power transformers using a particle-swarmoptimization- route-searching algorithm. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 3647–3656. [Google Scholar] [CrossRef]
- Qian, S.; Chen, H.; Xu, Y.; Su, L. High sensitivity detection of partial discharge acoustic emission within power transformer by sagnac fiber optic sensor. IEEE Trans. Dielectr. Electr. Insul. 2018, 25, 2313–2320. [Google Scholar] [CrossRef]
- Gao, C.; Wang, W.; Song, S.; Wang, S.; Yu, L.; Wang, Y. Localization of partial discharge in transformer oil using Fabry-Pérot optical fiber sensor array. IEEE Trans. Dielectr. Electr. Insul. 2018, 25, 2279–2286. [Google Scholar] [CrossRef]
- Si, W.; Fu, C.; Yuan, P. An Integrated Sensor with AE and UHF Methods for Partial Discharges Detection in Transformers Based on Oil Valve. IEEE Sens. Lett. 2019, 3, 2019–2021. [Google Scholar] [CrossRef]
- Ansari, M.A.; Martin, D.; Saha, T.K. Investigation of Distributed Moisture and Temperature Measurements in Trans-formers Using Fiber Optics Sensors. IEEE Trans. Power Deliv. 2019, 34, 1776–1784. [Google Scholar] [CrossRef]
- Zhu, M.-X.; Wang, Y.-B.; Chang, D.-G.; Zhang, G.-J.; Shao, X.-J.; Zhan, J.-Y.; Chen, J.-M. Discrimination of three or more partial discharge sources by multi-step clustering of cumulative energy features. IET Sci. Meas. Technol. 2019, 13, 149–159. [Google Scholar] [CrossRef]
- Yaacob, M.M.; Alsaedi, M.A.; Rashed, J.R.; Dakhil, A.M.; Atyah, S.F. Review on partial discharge detection techniques related to high voltage power equipment using different sensors. Photonic Sens. 2014, 4, 325–337. [Google Scholar] [CrossRef]
- Karami, H.; Rachidi, F.; Azadifar, M.; Rubinstein, M. An Acoustic Time Reversal Technique to Locate a Partial Discharge Source: Two-Dimensional Numerical Validation. IEEE Trans. Dielectr. Electr. Insul. 2020, 27, 2203–2205. [Google Scholar] [CrossRef]
- Karami, H.; Azadifar, M.; Mostajabi, A.; Rubinstein, M.; Karami, H.; Gharehpetian, G.B.; Rachidi, F. Partial Discharge Localization Using Time Reversal: Application to Power Transformers. Sensors 2020, 20, 1419. [Google Scholar] [CrossRef]
- Karami, H.; Azadifar, M.; Mostajabi, A.; Favrat, P.; Rubinstein, M.; Rachidi, F. Localization of Electromagnetic Interference Sources Using a Time-Reversal Cavity. IEEE Trans. Ind. Electron. 2021, 68, 654–662. [Google Scholar] [CrossRef]
- Karami, H.; Aviolat, F.Q.; Azadifar, M.; Rubinstein, M.; Rachidi, F. Partial discharge localization in power transformers using acoustic time reversal. Electr. Power Syst. Res. 2022, 206, 107801. [Google Scholar] [CrossRef]
- Do, T.-D.; Tuyet-Doan, V.-N.; Cho, Y.-S.; Sun, J.-H.; Kim, Y.-H. Convolutional-Neural-Network-Based Partial Discharge Diagnosis for Power Transformer Using UHF Sensor. IEEE Access 2020, 8, 207377–207388. [Google Scholar] [CrossRef]
- Saleh, B.; Yousef, A.M.; Abo-Elyousr, F.K.; Mohamed, M.; Abdelwahab, S.A.M.; Elnozahy, A. Performance Analysis of Maximum Power Point Tracking for Two Techniques with Direct Control of Photovoltaic Grid-Connected Systems. Energy Sources Part A Recover. Util. Environ. Eff. 2021, 44, 413–434. [Google Scholar] [CrossRef]
- Eid, M.A.E.; Elbaset, A.A.; Ibrahim, H.A.; Abdelwahab, S.A.M. Modelling, Simulation of MPPT Using Perturb and Observe and Incremental Conductance techniques For Stand-Alone PV Systems. In Proceedings of the 2019 21st International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 17–19 December 2019; pp. 429–434. [Google Scholar] [CrossRef]
- Eid, M.A.E.; Abdelwahab, S.A.M.; Ibrahim, H.A.; Alaboudy, A.H.K. Improving the Resiliency of a PV Standalone System Under Variable Solar Radiation and Load Profile. In Proceedings of the 2018 Twentieth International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 18–20 December 2018; pp. 570–576. [Google Scholar] [CrossRef]
- Dessouky, S.S.; Abdellatif, W.S.E.; Abdelwahab, S.A.M.; Ali, M.A. Maximum Power Point Tracking Achieved of DFIG-Based Wind Turbines Using Perturb and Observant Method. In Proceedings of the 2018 Twentieth International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 18–20 December 2018; pp. 1121–1125. [Google Scholar] [CrossRef]

| Advantage | Drawbacks | |
|---|---|---|
| UHF technique [14,15,16] |
|
|
| Optical technique [17,18,19] |
|
|
| Acoustic technique [20] |
|
|
| Chemical technique [21] |
|
|
| Ref. | Objective | Technique | Methodology | Performance |
|---|---|---|---|---|
| [29] | Classifier | UHF | BPNN + FFT | Up to 97% |
| [30] | Classifier | UHF | Statistical features + OS-ELM | 91.5% |
| [31] | Detection | DGA | MLP + data augmentation + Non-code ratio | 85% to 96% overall |
| [31] | Classifier | PRPD | SVM + LBP&HOG | 99.3% |
| [32] | Classifier | acoustic | k-NN/SVM + DWT | SVM performs the better |
| [33] | Classifier | UHF | Statistical features + SVM | 99.14% |
| [34] | Classifier | HFCT | SVM + PSD-based features | Closer to perfect |
| [35] | Classifier | PRPD | SVM + PCA + Statistical features | 82% |
| [36] | Classifier | UHF | RVM + EEMD-sample entropy | 99% |
| [37] | Classifier | PRPD | FkNNC/BPNN/SVM + 2D PCA | 96/94/98% |
| [38] | Classifier | acoustic | k-NN + PCA | 94% (similar conditions) 90% (various conditions) |
| [39] | Classifier | acoustic | SVM + PSD | When there is variation in the dataset, SVM performs the worst. |
| [40,41,42] | Diagnosis | DGA | MLP-gas concentration | Not stated |
| [43,44,45] | Detection | DGA | DST + ANFIS | 77% for PD detection |
| [46] | Classifier | PRPD | RF + Statistical features | 98% |
| [47] | Classifier | PRPD | RF + Statistical features | 94% |
| [48] | Classifier | impedance | LSSVM | 70–74% |
| [49] | Detection | HFCT | ANN + Statistical features | 67% |
| [50] | Separation | acoustic | BSS | Successful under experimental conditions |
| [51] | Detection | DGA | Duval’s gas values + Gaussian BN | 96% for PD detection |
| [52] | Detection | impedance | Statistical features + KPLS | 88% |
| PER | MAT | |
|---|---|---|
| Number of samples | 101 | 315 |
| Amount of dissolved gases | 8 | 10 |
| Amount of fault type | 7 | 7 |
| Cases with missing values (%) | 30 | 57 |
| Missing values (%) | 6 | 20 |
| CO | H2 | C2O | C2H4 | CH4 | C2H6 | C2H2 | Fault |
|---|---|---|---|---|---|---|---|
| 190 | 11 | 2065 | 14 | 0 | 15 | 9 | PD Or Arc |
| 178 | 278 | 3040 | 1234 | 683 | 151 | 19 | |
| 230 | 429 | 4071 | 1640 | 965 | 230 | 31 | |
| 257 | 520 | 4159 | 1705 | 1037 | 233 | 25 | |
| 13 | 0 | 244 | 0 | 4 | 0 | 0 | |
| 35 | 3 | 541 | 18 | 11 | 1 | 1 | |
| 52 | 19 | 781 | 60 | 32 | 5 | 2 | |
| 70 | 0 | 1111 | 137 | 63 | 14 | 3 | |
| 75 | 25 | 1233 | 90 | 46 | 8 | 3 | |
| 96 | 48 | 1661 | 149 | 77 | 15 | 3 | |
| 0 | 43 | 0 | 218 | 101 | 21 | 3 | |
| 160 | 76 | 2661 | 299 | 0 | 31 | 0 |
| H2 | CO | CO2 | CH4 | C2H6 | C2H4 | C2H2 | Fault |
|---|---|---|---|---|---|---|---|
| 11 | 190 | 2065 | 20 | 15 | 14 | 9 | PD Or Arc |
| 278 | 178 | 3040 | 683 | 151 | 1234 | 19 | |
| 429 | 230 | 4071 | 965 | 230 | 1640 | 31 | |
| 520 | 257 | 4159 | 1037 | 233 | 1705 | 25 | |
| 76 | 13 | 244 | 4 | 16 | 115 | 10 | |
| 3 | 35 | 541 | 11 | 1 | 18 | 1 | |
| 19 | 52 | 781 | 32 | 5 | 60 | 2 | |
| 150 | 70 | 1111 | 63 | 14 | 137 | 3 | |
| 25 | 75 | 1233 | 46 | 8 | 90 | 3 | |
| 48 | 96 | 1661 | 77 | 15 | 149 | 3 | |
| 43 | 117 | 1749 | 101 | 21 | 218 | 3 | |
| 76 | 160 | 2661 | 176 | 31 | 299 | 5 |
| Approach | Accuracy | Precision | Recall | F1 Score | AUC |
|---|---|---|---|---|---|
| SVM without imputation | 0.6024 | 0.5964 | 0.5985 | 0.5975 | 0.6787 |
| kNN with imputation | 0.7012 | 0.6983 | 0.7037 | 0.7010 | 0.7731 |
| Proposed Approach | 0.7547 | 0.7552 | 0.7519 | 0.7532 | 0.7115 |
| Method | Accuracy: without k-NN Imputation | Accuracy: with k-NN Imputation |
|---|---|---|
| Support Vector Machines (SVM) | 0.60 | 0.75 |
| Random Forest | 0.46 | 0.57 |
| Convolutional Neural Networks (CNN) | 0.53 | 0.60 |
| Decision Trees | 0.48 | 0.63 |
| Artificial Neural Networks (ANNs) | 0.50 | 0.60 |
| With kNN Imputation | Without kNN Imputation | |
|---|---|---|
| Accuracy | 73.81% | 53.17% |
| Precision | 75. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sekatane, P.M.; Bokoro, P. Partial Discharge Localization through k-NN and SVM. Energies 2023, 16, 7430. https://doi.org/10.3390/en16217430
Sekatane PM, Bokoro P. Partial Discharge Localization through k-NN and SVM. Energies. 2023; 16(21):7430. https://doi.org/10.3390/en16217430
Chicago/Turabian StyleSekatane, Permit Mathuhu, and Pitshou Bokoro. 2023. "Partial Discharge Localization through k-NN and SVM" Energies 16, no. 21: 7430. https://doi.org/10.3390/en16217430
APA StyleSekatane, P. M., & Bokoro, P. (2023). Partial Discharge Localization through k-NN and SVM. Energies, 16(21), 7430. https://doi.org/10.3390/en16217430







