Abstract
In many industries, such as assembling, welding, packaging, quality control, loading, and wrapping, a specific operation is requested, which is to pick processed objects in a given area of the workspace and hold them there for a rather long time compared with picking. The current study aims to minimize the power consumed by robots in pick-and-place applications with long-term placing and short-term picking operations. The main contribution of the paper is in the development of an approach that ensures the low power required by the robot by selecting the best robot joint configuration for object placement and providing intelligent control of robot joints for object-picking. The proposed and tested methodology is based on the mutual solution of the forward kinematics, inverse kinematics, inverse statics, and reinforcement learning problems in robotics. An appropriate neural-network-based controller is designed. In this work, model development, simulation, and experimental stages are described. As a result, several MATLAB/Simulink™ models and simulation methods are designed for efficient robot control and an appropriate neural-network-based controller is developed. The experiment conducted on the IRB1600 robot demonstrates that up to 18% of the consumed power may be saved thanks to an optimally chosen joint configuration.
1. Introduction
Pick-and-place (PnP) robots that enable objects to be picked from one location, placed at other location, and held during the processing phase are widespread in a variety of fields [1]. As efficient manufacturing is an important part of sustainable development, power consumption is becoming one of the key quality indicators in such operations [2]. The most popular six-degrees-of-freedom robots from ABB, KUKA, PwrPack, River Systems, and other companies are usually equipped with inverter-fed electric actuators and control systems of 1–5 kW installation capacity. According to [3], the electrical energy consumed by robots in the production phase is about 8% of the total energy consumption in the lifecycle of products such as vehicles. According to the estimations of [4], the electricity consumption of robots will reach 0.5–0.8% of the total USA electricity demand in 2025 due to such factors as increases in robots’ power equipment, the introduction of robots in tasks previously performed by humans, the growing productivity of applications, and the involvement of robotics in more and more spheres. The same trend can be seen in industrial [5], aerial [6], floating [7], mobile [8], and professional [9] robotics.
Power consumption directly affects air pollution, climate change, water quality, thermal instability, waste disposal, and many other environmental issues. At present, global electricity generation per year is over 30,000 TWh [10], and this demand is growing annually. According to the International Energy Agency [11], the total global electricity capacity in 2022 was about 9 TW, having increased more than four times over the past 40 years.
Some measures to reduce power consumption are being taken by the suppliers of system components, while others are determined by appropriate technologies that allow for the actual energy to be captured, and can be used to try out various optimisation options. The deployment of enhanced electromechanical brakes, renewed highly efficient motors, capacity optimisation, gearless design, and creation of robot parts from novel light materials are the most popular methods applied in robotics to reduce the consumed power [12].
The present study addresses power management by means of the optimisation of joint configurations (JKs) that are permissible for placing, and torque control for picking, the articulated robots used in PnP applications. The concept of JK has several meanings in robotics. In this paper, the authors rely on the formulation widely used by the leading robotic companies, such as ABB [13,14], Siemens [15], and KUKA [16]. According to [17,18,19], JK is considered an arrangement of robot joints represented by a set of joint angles that are needed to locate the end effector (EE) in the target pose. The homogeneous topology of six-degrees-of-freedom robots ensures flexibility and versatility, making them suitable for gravity load decreases and torque reductions in joint actuators in statics (placing) and dynamics (picking).
There are at least two mandatory conditions for successful PnP performance:
- Any operation should start in the given home pose and be supported in the given target area;
- The robot shall be fully adjustable within the specified workspace, payload, velocity profile, and accuracy, considering the account inner and outer constraints.
In the presented approach, the design, planning, and managing of robot parts’ motion are composed for a complex task, during which the forward kinematics (FK), inverse kinematics (IK), inverse statics (IS), inverse dynamics (ID), and joint actuator control problems are solved within the scope of application requirements. The FK problem aims to find the EE pose and orientation, while the poses of all joints and orientations of all robot bodies are specified. The IK problem aims to estimate the poses and orientations of all robot parts that enable the target location of the EE. The IS problem aims to find torques in all joints when the steady forces on the EE are provided. The ID problem aims to find joint torque deviations in response to the changing EE forces, whereas the optimal joint actuator control aims to minimise these deviations.
As is known, all inverse robotics problems are challenging.
The IK problem solution yields multiple JKs. The case of a general serial manipulator with six revolute joints yields 16 different IK solutions of a 16th-degree polynomial [13]. This results in multiple JKs that are able to achieve the target [14], whereas the solutions to IS and ID problems greatly extend this multiplicity. Consequently, several additional conditions are formulated, such as selecting the first JK that is found, selecting the fastest path, and selecting the shortest movement, or the elimination of abrupt changes in JK during motion [19].
As these methods are not related to energy-saving demand, other criteria are put forward that affect power consumption. These include smoothing the EE trajectories [20], minimising robot joint movements [21], and finding energy-optimal parameters such as EE paths, object positions, and operating speeds [22].
One of the first studies that drew attention to the need to seek the best JKs came from [23]. There, the authors determine all attainable assembly JKs, calculate suitable forces and counter-torques on the joints and bodies, estimate the appropriate energy consumption, and select the JK with the lowest power demand. There is also other research that concerns energy-optimal techniques and motion profiles based on system dynamics [24,25]. They mainly refer to plant modifications, preliminarily planning robot motion, route optimisation, and helping shop-floor engineers to find object placements with minor power requirements. These approaches successfully lower the amount of power that is used while the robot moves along predefined trajectories.
However, none of these concepts addresses robots that have to hold processed objects in a given area of the workspace for applications such as assembling, welding, packaging, quality control, loading, or wrapping.
When focusing on PnP applications, research such as [26] attract attention, as they report on reductions in energy consumption at given pose profiles. Nevertheless, these results are primarily for the design of optimal operations based on the manufacturing effectiveness of strictly sequential operations, and only the second step is optimised in terms of overall power consumption.
The main novelty and originality of this paper is that it, for the first time, is devoted to the energy consumption of robots performing PnP tasks with long-term placing and short-term picking operations. Differently from many other solutions, the goal of the current study is to minimise the power consumed by robots in applications of this type. The main contribution of the paper is the development of an approach that ensures that low power is required by the robot to hold the processed object in a given place for rather long time comparing with when an object is delivered to that location. For this, the method is proposed and tested based on the need to find a mutual solution to the FK, IK, and IS problems for placing, as well as reinforcement learning (RL) for picking.
The remainder of the paper is organised as follows. Following the algorithmization of the offered methodology, the FK problem is resolved and the robot workspace is estimated. Then, a solution to the IK is given, followed by a resolution to the IS problem. Thereupon, the neural network (NN) based intelligent controller for the picking operation is presented. The following section contains a description of the case study, in which the IRB1600 robot is modelled, simulated, and analysed using the proposed method. After that, an experiment is outlined, and its results are compared with the simulation data. The paper is ended by presenting the outcomes, along with the discussion and conclusion.
2. The Method
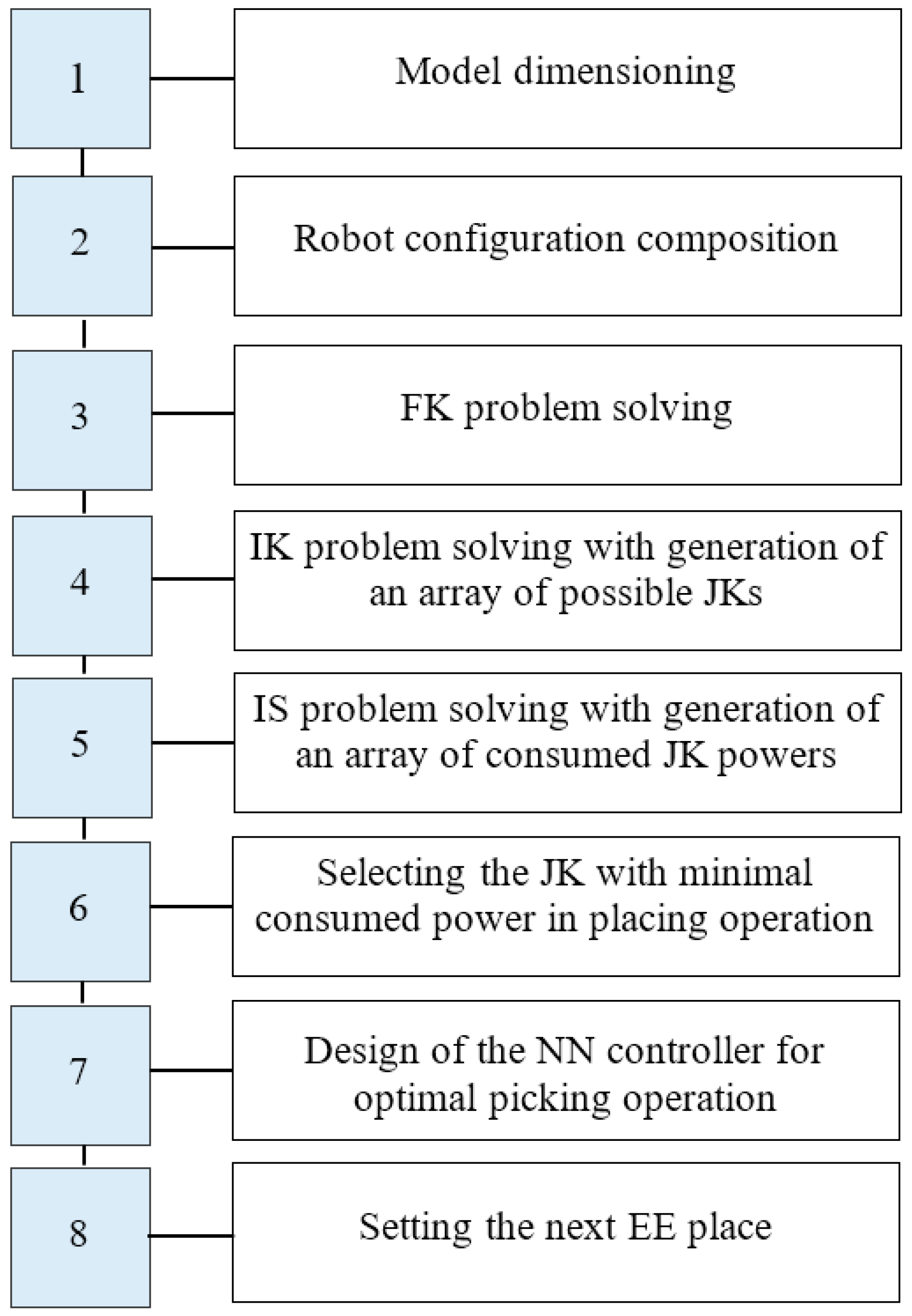
The described approach addresses homogeneous articulated robots, such as IRB 1600 (ABB), UR5 (Universal Robots), 1500 MM (KUKA), or RV1 (Mitsubishi), while they pick and hold processed objects in a given area of the workspace. The method includes a sequence of stages, as shown in Figure 1.
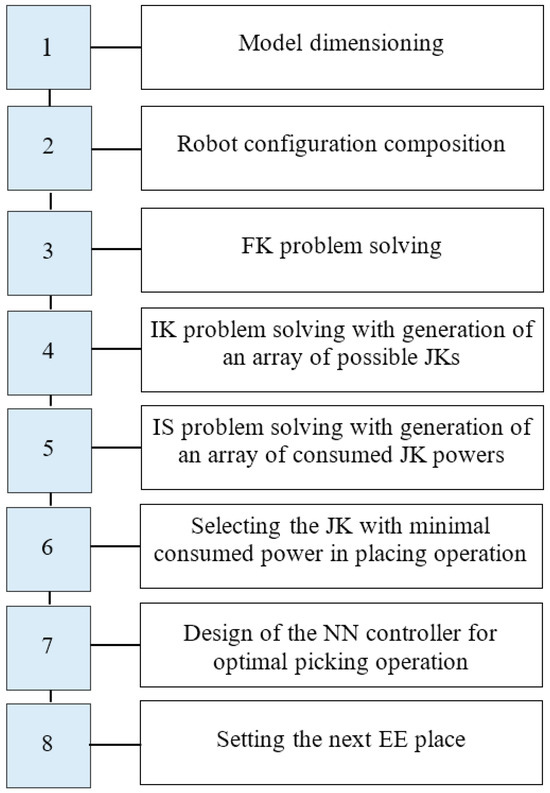
Figure 1.
GRAFCET chart of the proposed methodology.
2.1. FK Problem Solution and Finding a Workspace
After specifying the robot dimensions (body lengths and weights, joint angles, and so forth), an appropriate rigid body tree is developed by assembling separate rigid body-joint objects into a uniform computer model.
To create the FK solver, the frames of joints and adjacent bodies are referred via mutual frame transformations and mapped to the base coordinate system as follows:
where is a vector of body lengths , is a vector of joint angles , and is a vector of EE location in the base frame. Based on this transformation, the kinematics model in the DH-matrix form is generated [27].
Next, this solver is applied to estimations of the robot workspace, i.e., an area of all possible poses that the EE can reach. Herewith, restrictions are imposed, aiming to avoid body collisions and singularities. To identify the workspace, the FK problem is solved repeatedly while every joint cyclically increases its angle from minimal to maximal limits. At the end of each cycle, the obtained EE positions are saved. Lastly, the workspace diagram and its planar projections are plotted.
2.2. IK Problem Solution
A further step is devoted to the creation of an IK solver. Different IK algorithms may be applied to generate affordable JKs [18,28,29]. The Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm [30] and the Levenberg–Marquardt (LM) algorithm [31] were compared in this study. Both algorithms represent iterative-gradient-based optimization methods that start from an initial guess regarding the solution and seek to reduce a specific cost function. As soon as the cost of convergence of the algorithm to EE within a given tolerance becomes minimal, the IK problem is considered solved and the best JK found. Nevertheless, the algorithm fails in some combinations of initial guesses and desired EE poses. To handle this issue, several random restart mechanisms exist. Such restarts continue until either a qualifying IK solution is found, the maximum time has elapsed, or the iteration limit is reached.
The BFGS algorithm supports a quasi-Newton method that uses the gradients of the cost function from past iterations to generate an approximate second-derivative information to determine the next step for the current iteration. This helps deal with boundary limits on the cost function the robot model creates. The BFGS is often the default algorithm, since it is more robust at finding solutions and more effective for JKs that are close to the joint limits compared with the LM algorithm.
The LM algorithm is considered when either the initial guess is close to the solution, or a quicker solution is needed. This algorithm converges much more quickly when attempting to find a series of poses along a desired trajectory of the EE. Once a JK is found for one pose, this JK becomes a good initial guess for the next pose, etc.
In the system under discussion, the target may suddenly change, calling on the management system to make a prompt decision in real-time. Taking into account this factor, a simple iterative solution of the IK problem is applied in this work, which represents a very similar sequence of FK problem solutions to that used for the robot workspace estimation. Here, the FK solver runs repeatedly while the joints cyclically increase their angles by a specified increment. At the end of each iteration, the condition verifies if the EE is currently in its target position with an acceptable tolerance. If this condition is met, the revealed joint positions and appropriate body orientations are saved. The algorithm has tunable parameters, such as the maximal number of iterations, the maximal time during which the algorithm is executed before the timeout expires, the accuracy tolerance that specifies the error between the EE pose generated based on the solution and the target pose, and the minimal step size allowed by the solver. Due to its static nature and the absence of derivatives, the approach helps to drastically reduce the number of iterations required to estimate possible JKs. After all JKs are generated, at which point the EE can achieve the target, they are stored, and the revealed kinematics chains may be plotted.
2.3. IS Problem Solution
At the next step, the IS problem is solved for each JK, and the joint torques needed to hold this JK at the specified external forces are estimated. Hereinafter, the optimal JK is chosen to ensure minimal power consumption.
Robot rigid body dynamics are governed by the Newton–Euler equation [32]:
where is the joint torque applied to the th joint; is its fraction, which is dependent on external disturbances; is joint stiffness, which is dependent on the body mass friction; is the damping factor; is the moment of inertia; are vectors of joint poses, velocities, and accelerations.
Therefore, the torque transmitted from the actuator through the gear to drive the joint is composed of two parts [33], namely, the steady-state torque needed to withstand constant external and internal influences, and the dynamic torque which is required to accelerate and decelerate the motion due to robot inertia. Since the current study considers the retention of the processed object in the target pose, the ID problem is reduced to solving the IS part of the problem based on information.
The electromagnetic fraction of the torque is generated by the electric actuator made on the basis of a motor with flux linkage and supply current :
At the given supply voltage , this yields the following electrical power, which is required to maintain the joint:
with the following energy consumption during the placing cycle time :
This energy may be either negative (consumed) or positive (ready to be restored), depending on the robot mass distribution.
Nevertheless, the total power and energy consumption of the -degree-of-freedom robot depend not only on the common joint power and energy, but on the additional parts and , which are associated with losses in motors and gears, power converter, fans, sensors, control equipment, and other needs of the robot system:
This means that the power consumption of the robot depends on both the JK and other factors, and assessing the ratio of system and joint power and energy components is quite complex. In this research, this ratio is sought experimentally.
Once the consumed power (6) is found for each JK, the JK with the lowers amount of consumed power during the placing operation can be selected as follows:
2.4. Intelligent Control of Picking Operation
The optimal solution (7) for the placing operation can cause abrupt changes in JK, accompanied by either a prolonged or an oscillating picking process.
Therefore, a control system that is capable of maintaining the applied joint counter-torque in accordance with a reference torque T* generated by the controller is required to ensure both the static and dynamic stability. Considering the high-dimensional nonlinear robot model and actuator constraints [5], the use of traditional PID controllers is challenging. To overcome this obstacle, an intelligent-based controller of the joint drive is developed, which maintains the system stability during picking operations at a changing JK.
Many robot manufacturers, such as [28], consider a fuzzy logic controller (FLC) to be a suitable control tool due to their universality in tuning and simplicity when applying updates to commercially produced vehicles.
To get the most out of the FLCs, four specialists were recruited to set up such controllers in [34]. However, the results demonstrated that the transient quality significantly depends on the professionality of the experts who tune them.
As follows from [35,36], NN controllers successfully outperform human experts in managing quick and accurate robot motion.
Artificial NN is an adaptive system consisting of interconnected nodes called neurons in a layered structure that resembles a human brain. The main benefits of all NNs are fault tolerance, their suitability for real-time operation due to their high computational rates, and their remarkable ability to learn. NNs may learn from data, i.e., they can be trained to recognize patterns, classify data, or forecast future events. To implement this advantage, multiple single- and multilayer, feedforward and recurrent NNs were designed, including deep NNs with many hidden layers to support deep learning, feedforward (forward propagation) NNs, convolutional NNs that are suitable for image and audio processing and text recognition, and recurrent NNs with feedbacks (backward propagation) that model sequential dependencies in the inputs.
Together with unsupervised and supervised learning approaches, deep reinforcement learning (RL) is now considered the most progressive machine-learning methodology, during which the system is forcibly trained using a “stimulus–response” principle [37,38,39,40,41]. Unlike the previous two, RL does not rely on a static dataset, but operates in a dynamic environment and learns from collected experiences. This NN learning method uses the results of past actions to reinforce or weaken such actions depending on their success or failure. In robotics, the workspace feedback is applied for decision-making. During learning, the system tries to take actions and receives feedback, and then makes decisions based on the robot responses. With the right action, the algorithm gives the robot a positive reward, while, with the wrong action, the algorithm gives the robot a negative value. During the whole process, the robot strengthens its proper behaviour and weakens its improper behaviour. As a result, a rational solution is generated. This performance improves with experience.
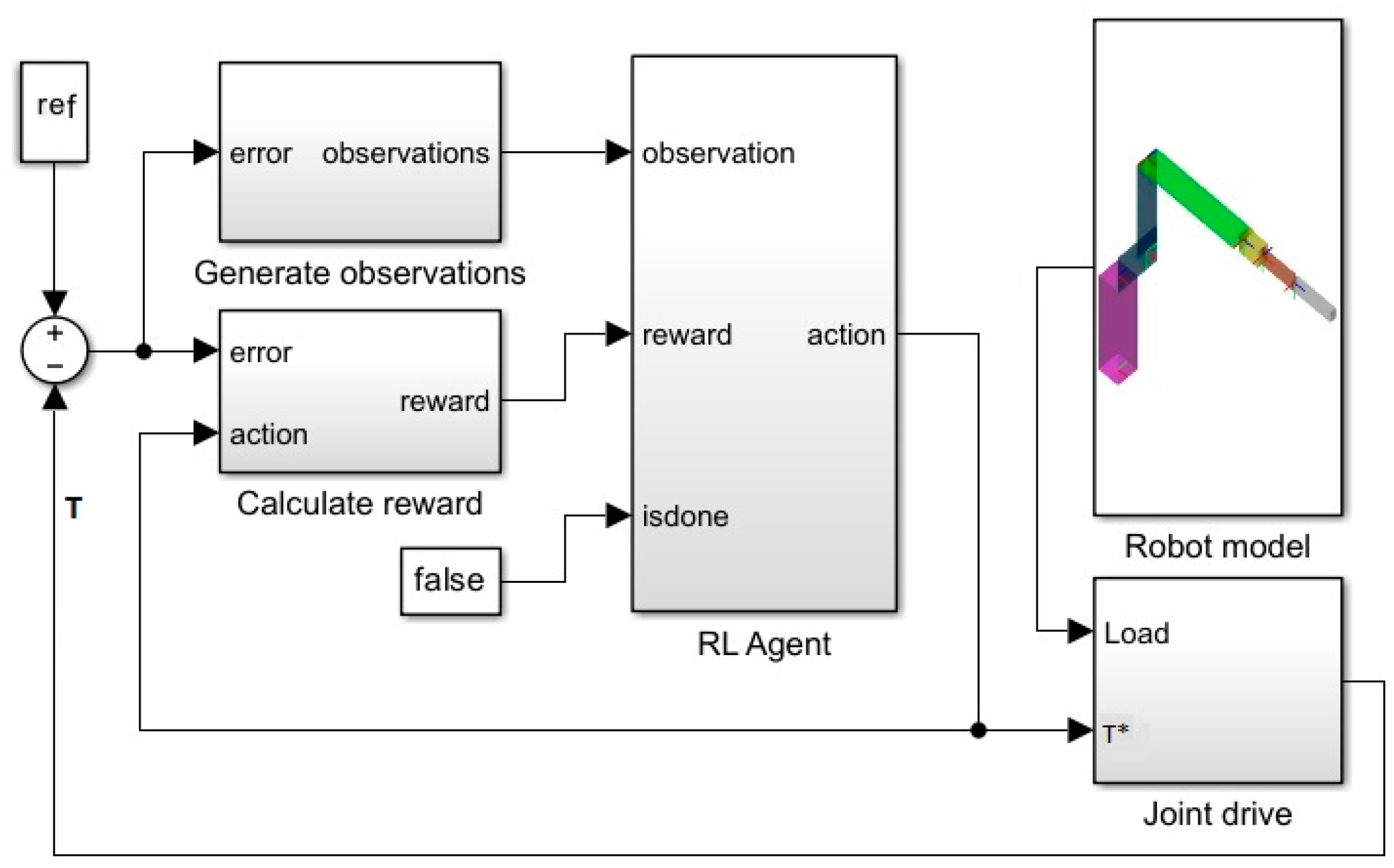
Therefore, to optimise transient shapes at changing JKs, an RL methodology was used to design the NN-based controller, which searches for a policy that could maximize the expected cumulative long-term reward. The model shown in Figure 2 interprets RL as a Markov decision-making process [42] denoted by a tuple {S,A,P,R}, where S is the state space of the joint drive, which plays the role of the control Environment, A relates to the control action space, P designates the state transition probability, and R is the reward function.
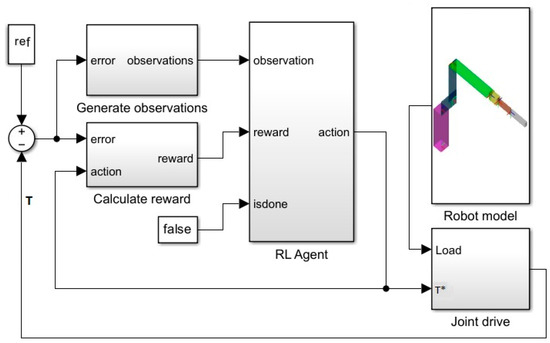
Figure 2.
RL system used in this study, in which a joint drive model acts as an environment and the robot model represents a changing load.
The control system contains the Agent block, the Observations block, the Reward block, and the Robot model block, which imitates the randomly changing load of the Joint drive corresponding to changing joint location at various JKs.
To represent state S of the Environment, the Observations block converts the error between the referred and joint application torque into a two-component vector and its integral:
The Reward block is intended to generate the total accumulated reward R as a negative of the linear quadratic Gaussian objective function:
where ei is the cumulative error in the ith time step and Ai is a cumulative penalty for an action of the Agent in this time step, matching each actuating torque T*.
To maximise a reward, a twin delayed (TD3) Agent [43] is used in the control system. This deep deterministic policy gradient (DDPG) class of agents [44] is suitable to support the actor–critic method of RL [45].
Agent contains two parts, namely the Actor NN and Critic NN. The Actor aims to choose an action A and apply it to the Environment, whereas the Critic evaluates A and predicts the action effect on the current state S. Actor and Critic search together for the reward from the Environment to estimate the prediction accuracy. At every step, Agent maps the states S to actions A in order to take an action from the available array of actions in accordance with its policy. Based on the action corresponding to the current state, Environment implements a transition to the next state with the transition dynamics of the transition probability P. To calculate P, the NN collects data reflecting the addressed situation, counts the number of transitions from one state to another, and normalises the measurements. Further, Agent observes the new state and receives a scalar reward according to the reward function (9).
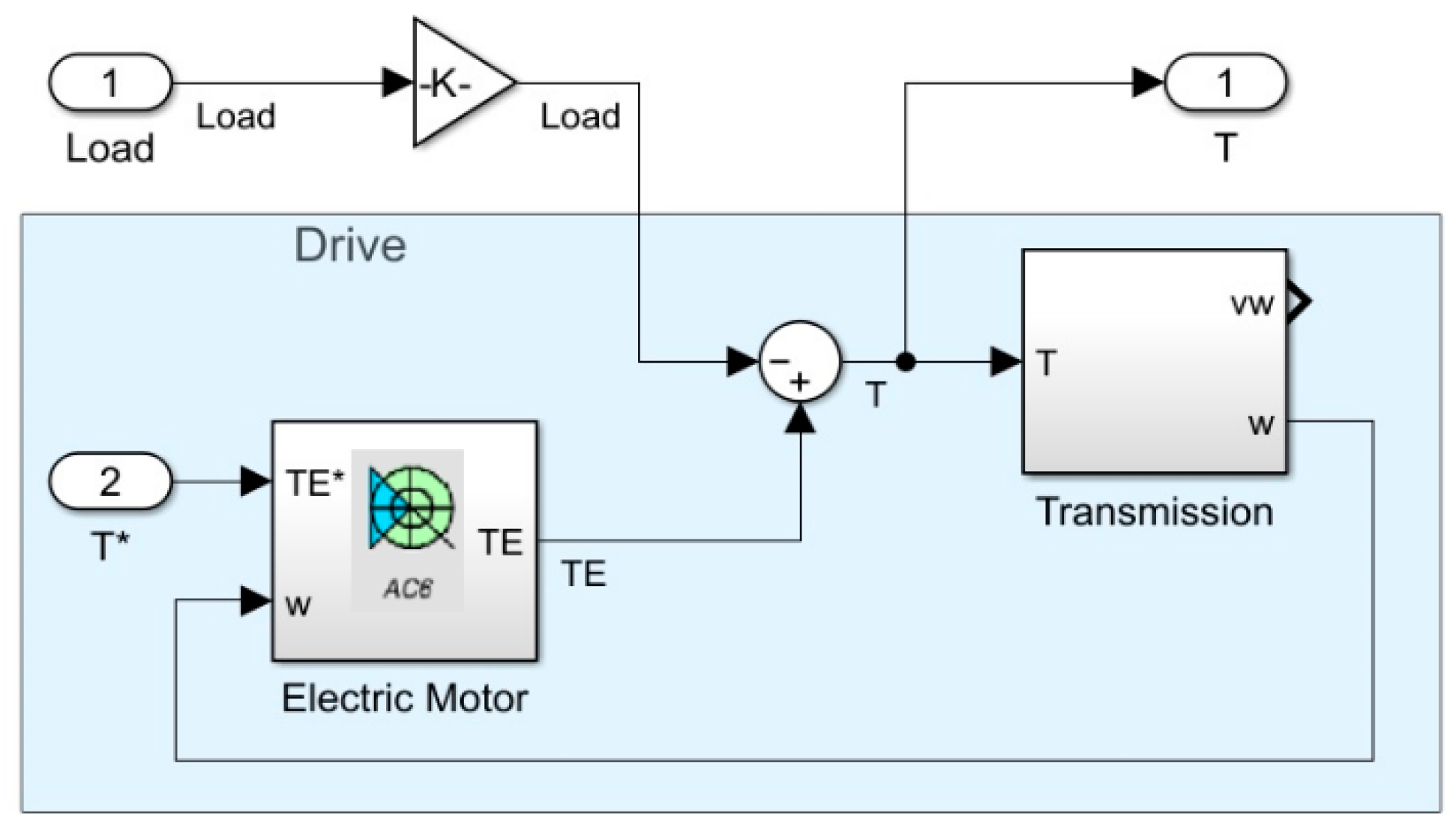
The environment model shown in Figure 3 is made up of several groups of blocks.
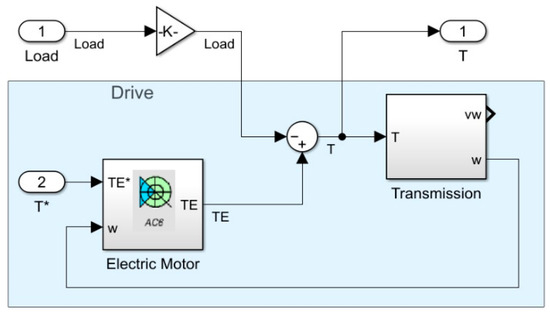
Figure 3.
MATLAB/Simulink™ model of the environment.
The Drive built on the permanent magnet synchronous Electric Motor block from the MATLAB/Simulink™ library implements battery-regenerative braking. The Electric Motor block additionally provides information regarding an electrical fraction of power consumed from and regenerated back to the supply source. Gear ratio and body inertia are calculated in the Transmission block. Normalised control signals are applied as the actuating torque T* and the randomly changed Load, whereas the feedback is presented by the joint application torque T.
3. Case Study
3.1. Robot Description
The IRB1600 [46] robot under study has a six-degrees-of-freedom spatial manipulator with revolute joints J1–J6 fed by Tamagawa servomotors 3HAC, with a total maximal power consumption of 0.58 kW. The payload capacity is 6 kg, reach distance is 1.2 m, robot weight is 250 kg, maximal force is 2500 N, bending XY torque is ±1700 Nm, and Z torque is ±855 Nm. The parameters of six robot bodies, B1–B6, are collected in Table 1.

Table 1.
IRB 1600 robot parameters used in simulation.
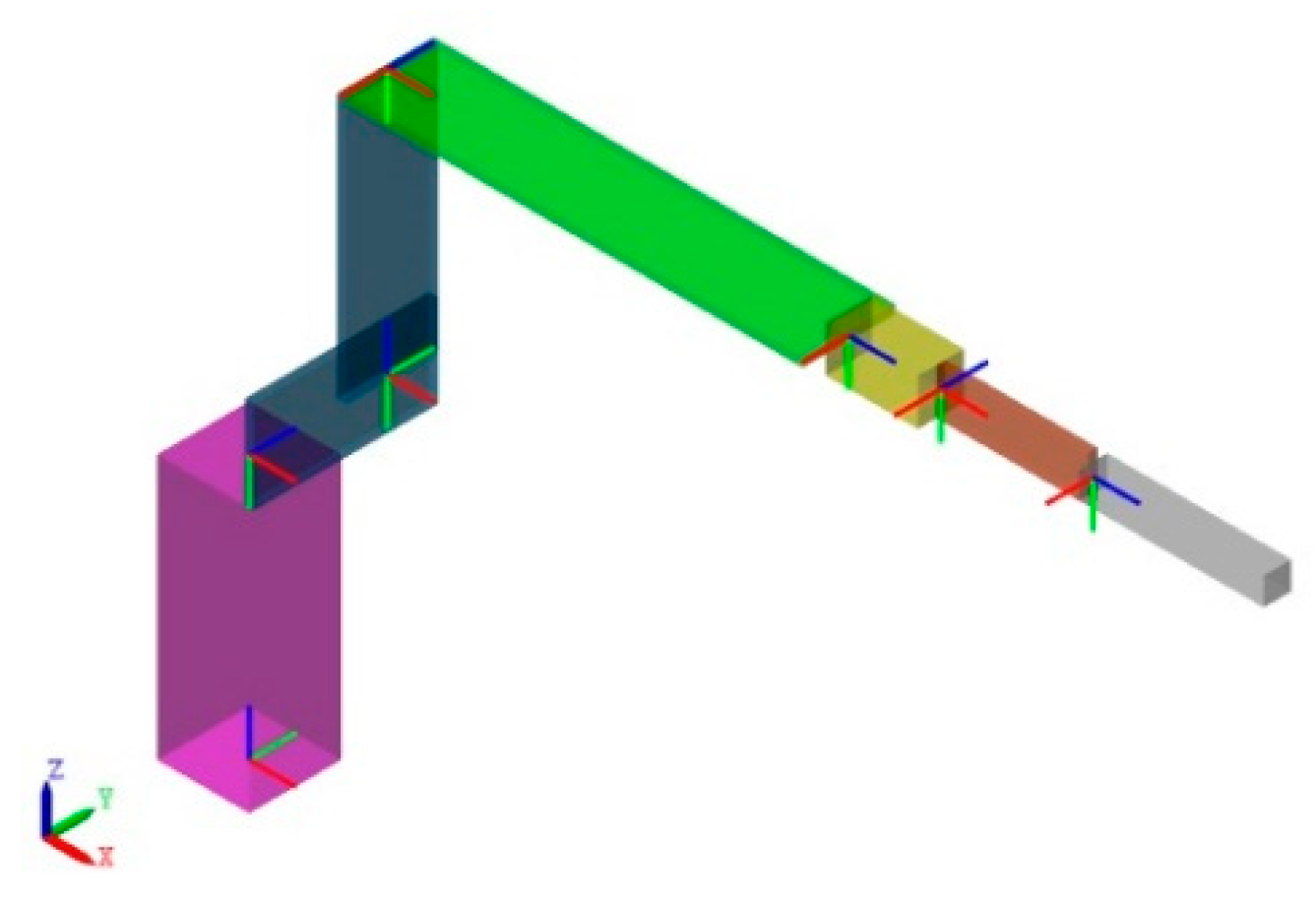
Robot configuration at the home state is presented in Figure 4.
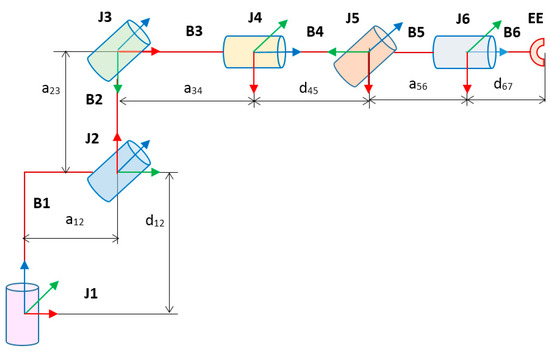
Figure 4.
Robot home configuration.
3.2. The Model
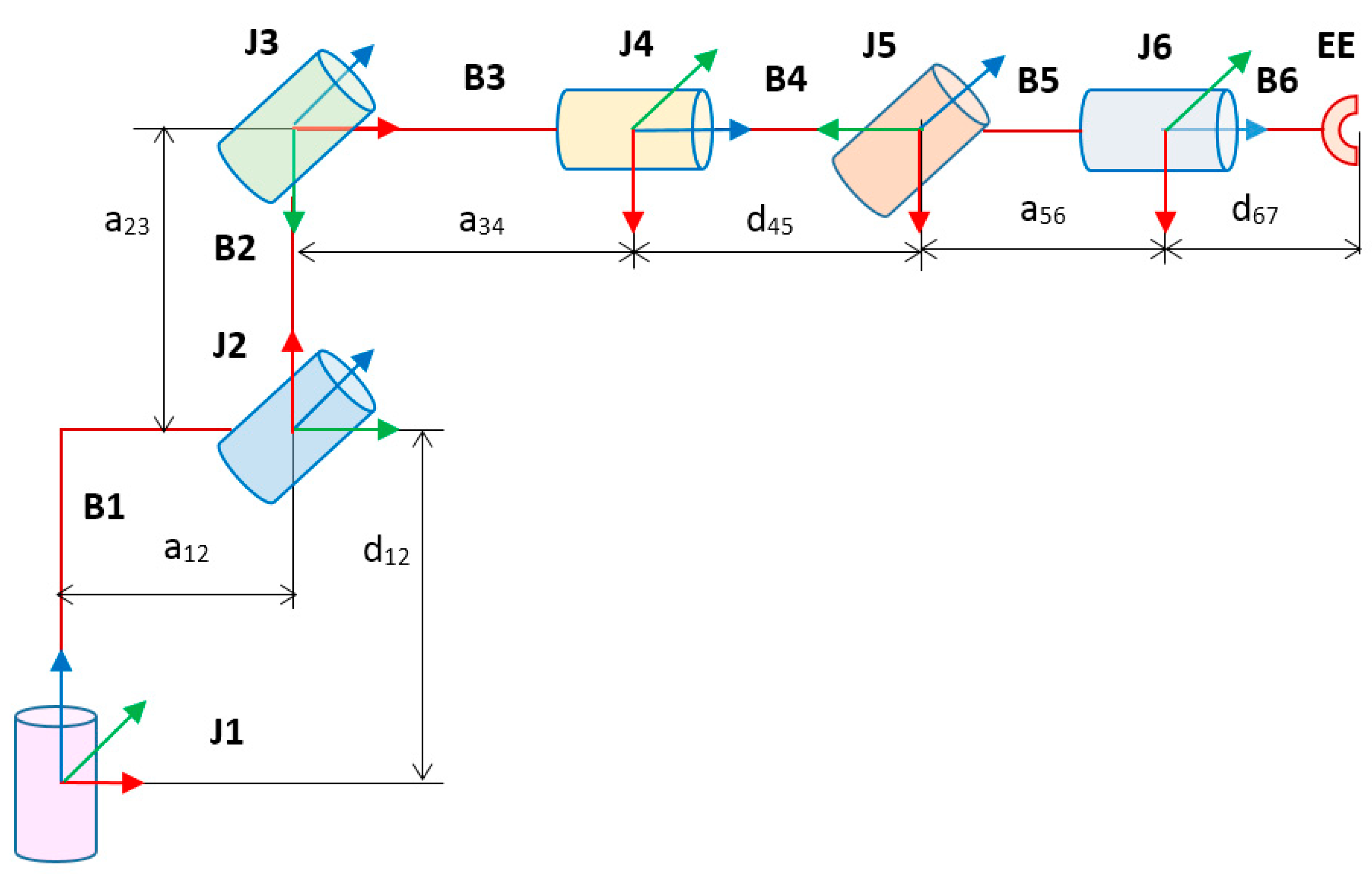
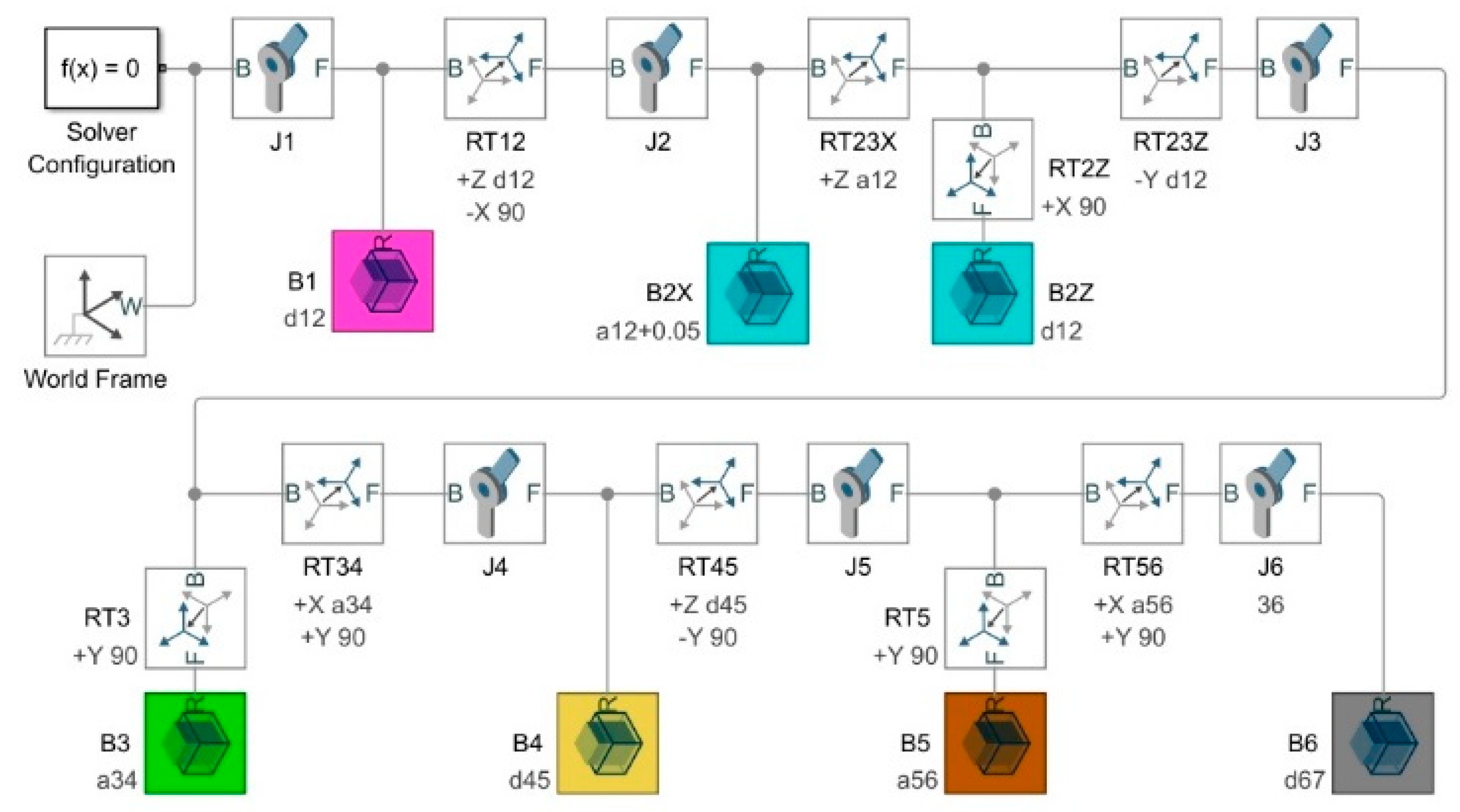
The Denavit–Hartenberg (DH) convention is applied to describe the topology and performance of the robot. To this aim, each joint is associated with its own frame, in which the z axis is guided in such a way that the joint rotates about z and other axes follow the right-hand rule.
Since the DH convention operates with x and z axes, six mandatory frame transforms (B1-B6) and two additional transforms (B4a and B6a) are applied. Therefore, both the robot topology and its performance are fully modelled by an eight-row, four-column DH matrix, in which the columns follow in the order [a, α, d, θ] and the rows follow from the base (top) to the end-effector (bottom). This DH matrix is introduced in Table 2.

Table 2.
DH matrix of the robot model with variable θ angles.
To describe robot topology, the following DH parameters are used here:
ai—(i + 1)th joint offset from zi measured along xi;
αi—(i + 1)th joint turn around xi between zi and zi+1 axes;
di—ith body length measured along zi between xi and xi+1 axes;
θi—ith body turn measured around zi between xi−1 and xi axes.
To consider robot performance, the θi parameter also describes the rotation of the revolute joint about zi between the xi−1 and xi axes.
In the Simulink™ model shown in Figure 5, each robot body is represented as a blockset composed of a joint, a variable mass, and rigid transform blocks that offset the joints and turn them relative to each other.
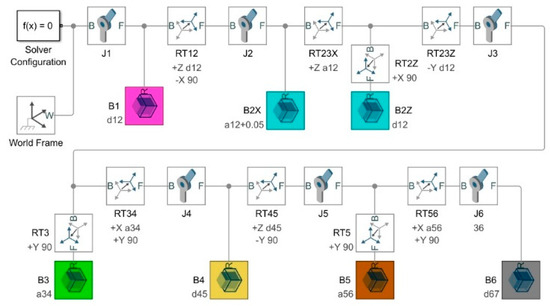
Figure 5.
Robot Simulink™ model built on the base of the DH matrix.
In Figure 6, the appropriate Simscape Multibody™ model that is upheld for animation is shown.
Figure 6.
Robot-animated Simscape Multibody™ model.
3.3. Simulation
To demonstrate the advantages of the method during the retention of the processed object in the specified target pose, the problem was aligned with the 2D task. The XZ Cartesian projection was chosen as the only permissible place for the EE, and variable displacements were set for three joints along this projection, whereas the other joints remained mechanically locked in the zero orientation without power consumption. This example shows how all PnP control problems can be resolved by exploring only a small part of the JK space.
First, the IK solver calculated the required joint poses and orientations to achieve the specified target in the XZ projection. To verify the solution, the robot was animated with the Simscape Multibody™ toolbox from MATLAB™.
To solve the IK problem, the following restrictions were set:
- Target EE pose TGT = [0.5 0 0.5];
- Positioning tolerance d = 0.01;
- Number of cycles N = 50;
- Iteration step dθ = 2 × pi/N.
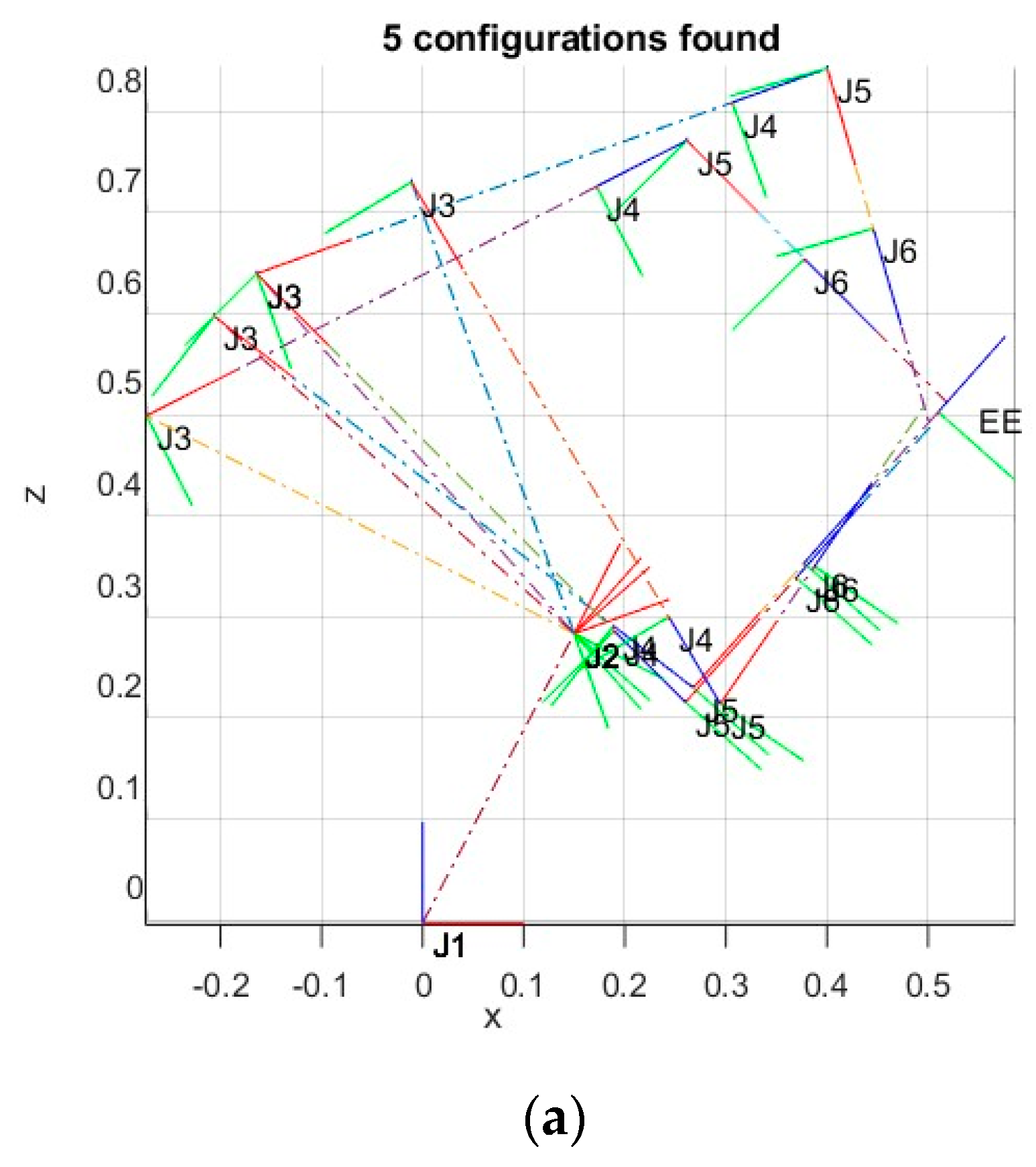
As a result, five permissible JKs were found and collected in Table 3.

Table 3.
Joint angles of five JKs.
Next, the IS solver was applied to evaluate joint torques at different JKs, aiming to select the best one. Five appropriate solutions of the IS problem are presented in Table 4, each column of which demonstrates the torques that the joints have to generate to keep the processed object.

Table 4.
Joint torques of five JKs.
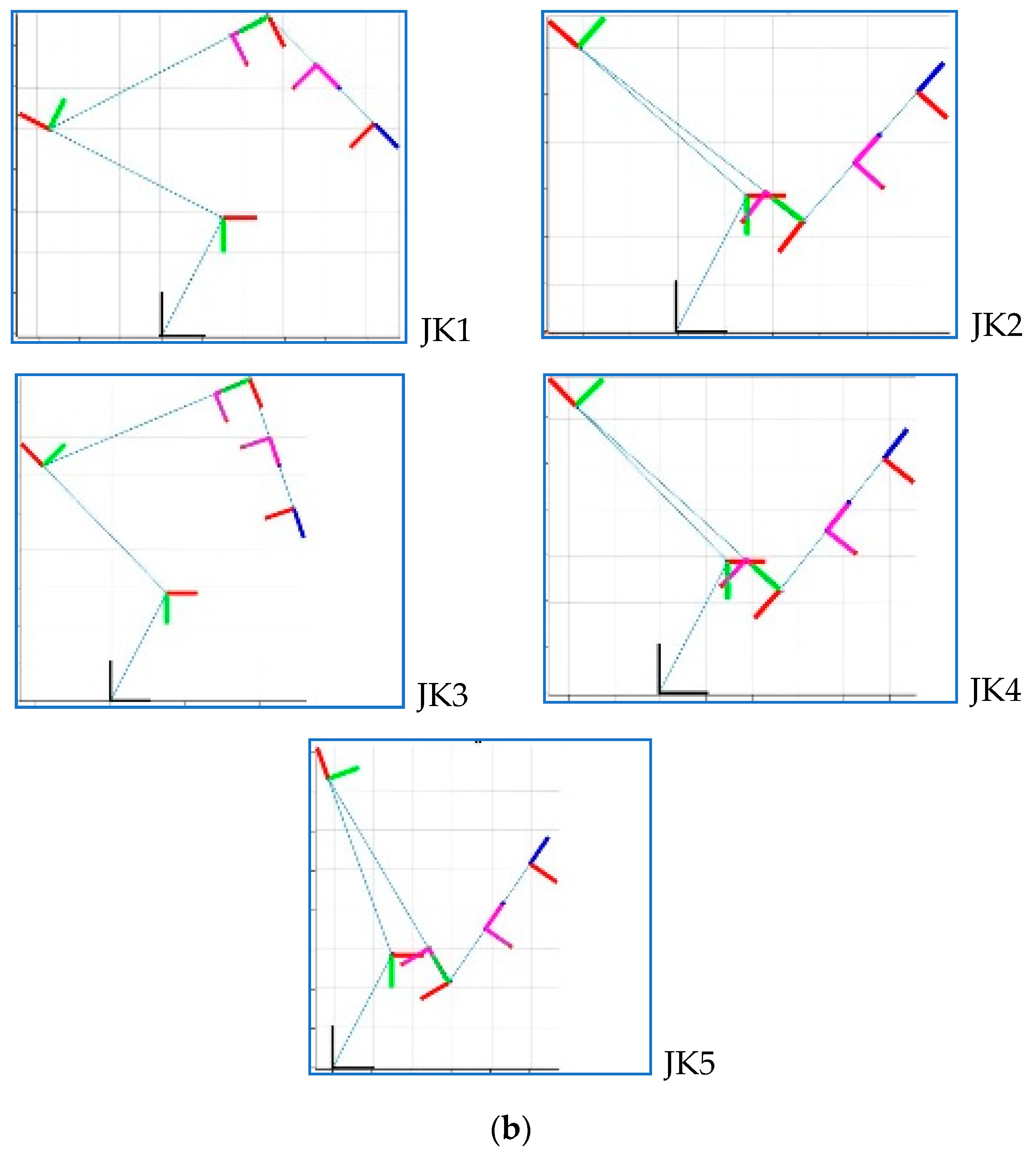
In Figure 7, five JKs that can be used to reach the target EE pose within the workspace are plotted.
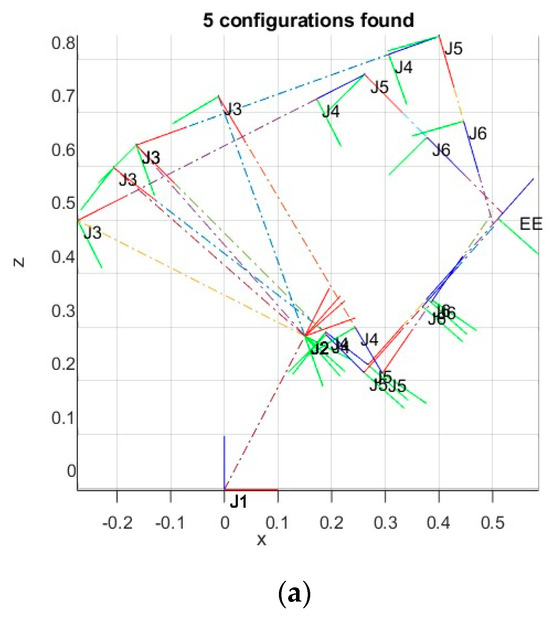
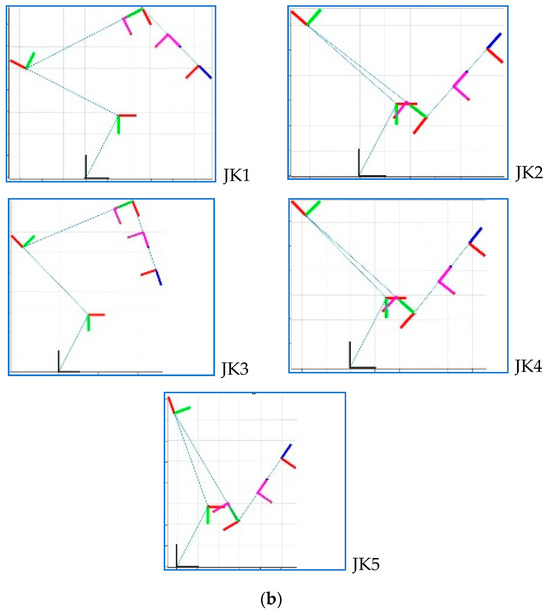
Figure 7.
Five JKs plotted in the XZ plane together (a) and separately (b).
In the last row of Table 4, the total JK torque values are summed. It is noteworthy that the ratio of torques generated at various JKs reaches 25%. Accordingly, the robot consumes the least electricity while keeping the object with JK5.
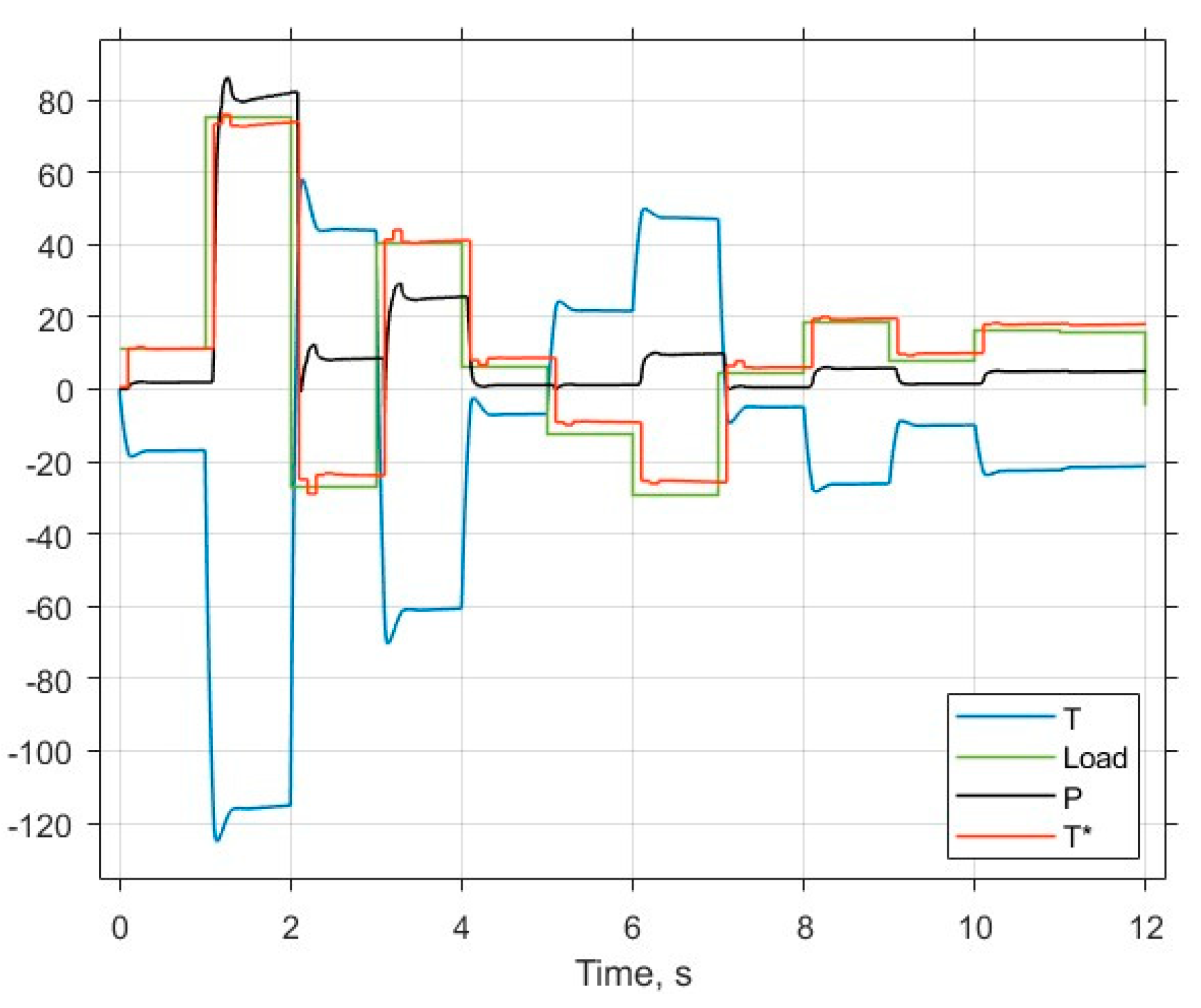
The assessment of separate joint behaviour in picking operations was made by simulation, during which the virtual load was minutely and randomly charged, as shown in Figure 8 in green for 12 optimal JKs, together with the actuating torque T* and joint application counter-torque T (Nm), as well as the power P (W) consumed by the joint.
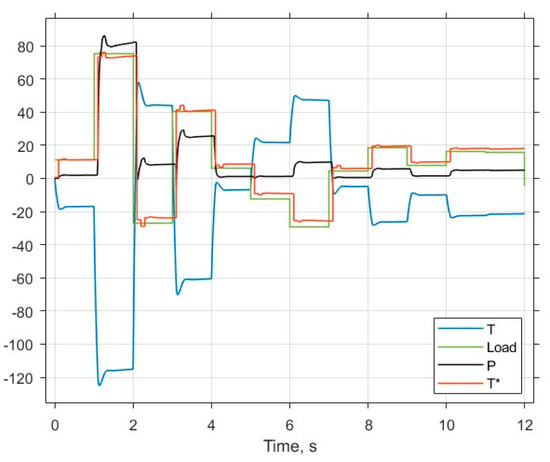
Figure 8.
Transients of a separate joint drive.
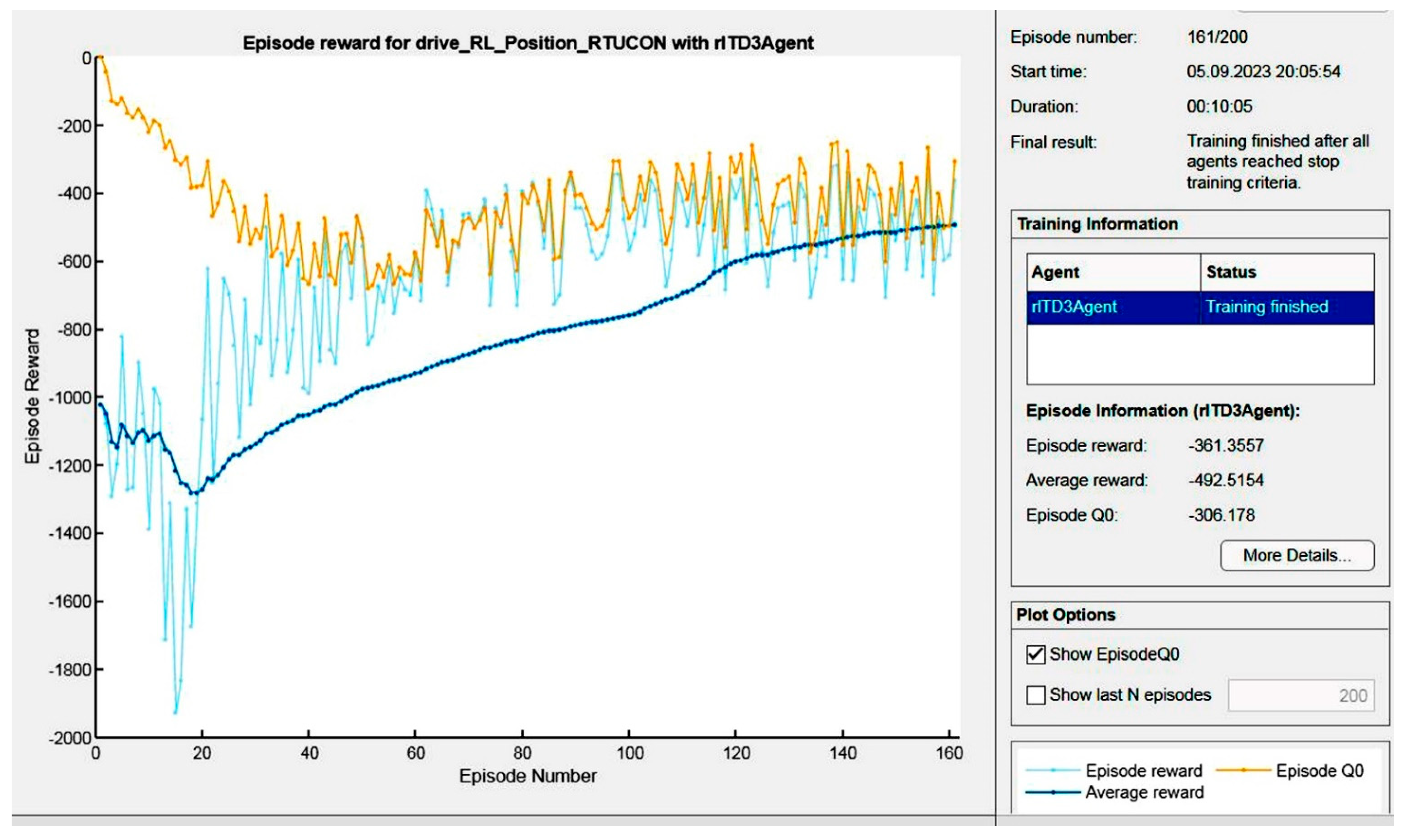
The model was trained for a maximal number of episodes of 200, and maximal number of steps of 100 at 160 ms each, and the average reward of −493 was used as a training termination criterion. Training parameters were tuned heuristically. The best episode was chosen considering the total accumulated reward value at the episode’s end. The parameters acquired in the best episode were used at the validation stage.
The generated episode reward diagram and statistics displayed by the Episode Manager are presented in Figure 9.
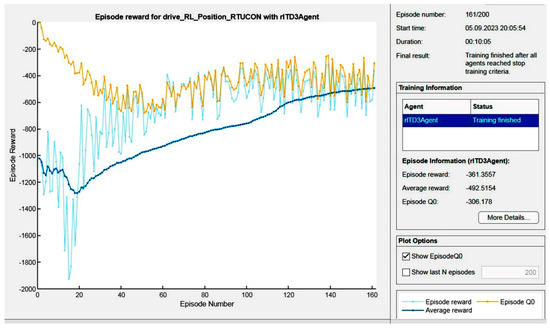
Figure 9.
Episode reward diagram and statistics.
After training, the model shown in Figure 1 and Figure 2 was studied under the condition of randomly changing joint poses. The plots of the actuating torque T*, joint application counter-torque T, changing load, and power P consumed by the joint are shown in Figure 8, together with the load diagram.
It follows from Figure 8 that the consumed power is proportional to the counter-torque generated by the joint drive, which, in turn, follows the load value, while the dynamical spikes are very short and small.
3.4. Experimentation
Finally, an assessment of the ratio of the system and joint power components was made experimentally. Herewith, the electrical power consumed by the robot was measured on the laboratory setup shown in Figure 10. This robot is equipped with one vertical and five horizontal active-motor-driven revolute joints that are suitable for setting multiple JKs. The common computer-fed supply module adjusts the drives under the ABB Robot Studio management. To avoid unpredictable collisions, the laboratory setup has a reliable fence, whereas electrical and mechanical protection is provided to prevent overpowering.

Figure 10.
Laboratory setup used for experimental study.
As the experimental IRB1600 robot was equipped with standard PID controllers, the intelligent control was not applied in this case.
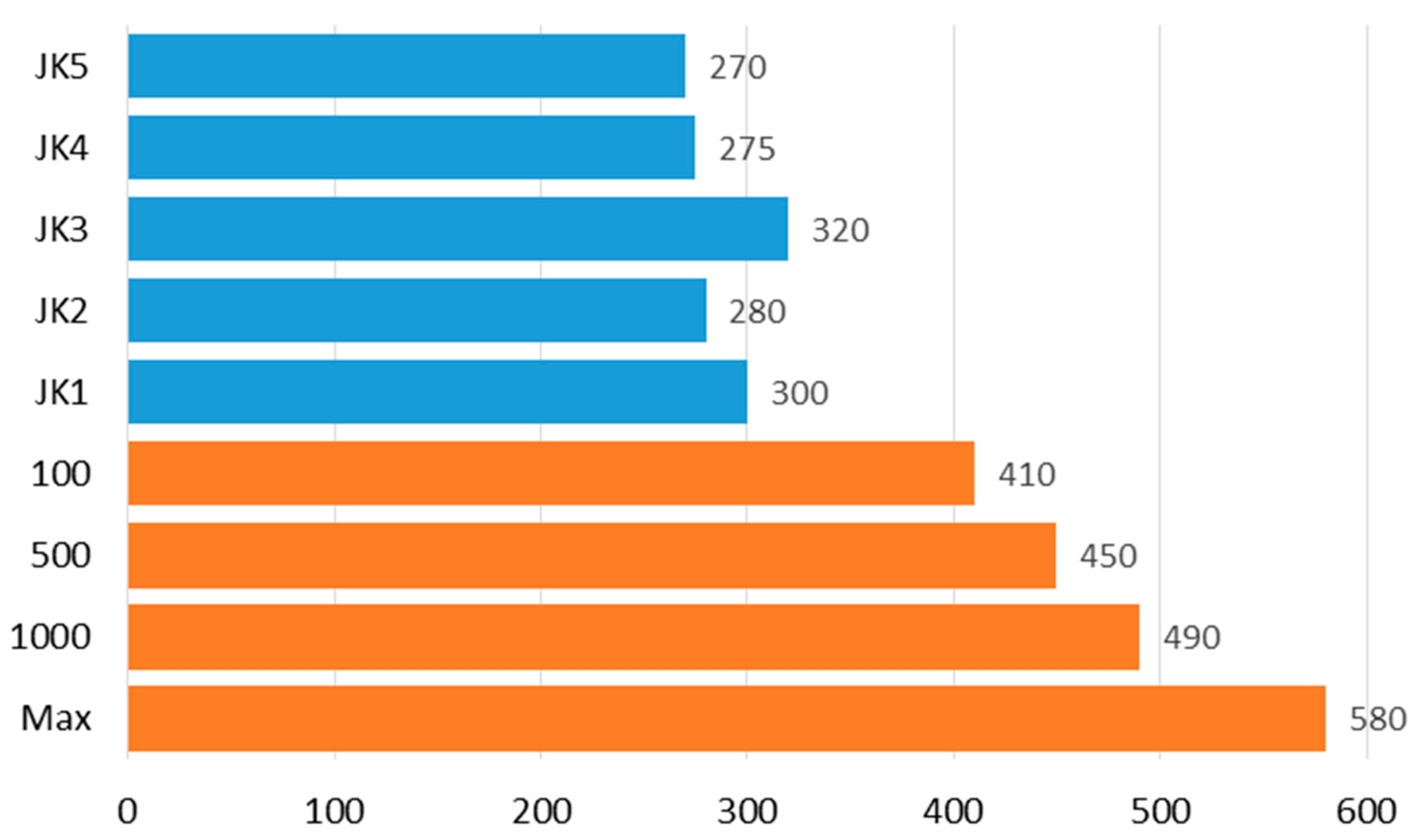
The amounts of experimentally measured electrical powers are shown in blue in Figure 11. The best JK occupies the upper bar. For comparison, the four orange bars display the passport powers published in [46] for different velocities (mm/s), namely 100, 500, 1000, and the maximal. The diagram proves that the holding power ranges from 55 to 75% of the total power consumed by the robot. Its value is proportional to the joint counter-torque developed at different JKs, whereas the difference in powers generated at various JKs is 50 W (18% of consumed power).
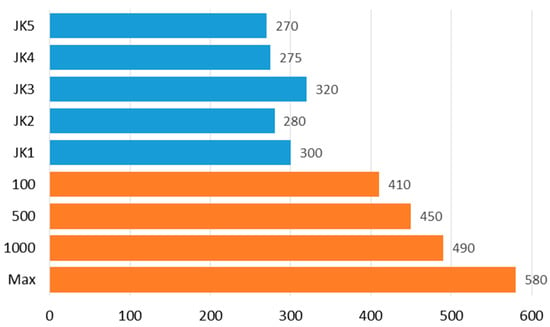
Figure 11.
Experimentally obtained (blue) and passport (orange) power consumption (W).
4. Discussion and Conclusions
As industrial robots consume the noticeable part of the generated energy, the power consumption of robots significantly affects industry effectiveness and natural resources’ preservation, as well as the product quality and the cost of living. The new approach developed in this research ensures that the minimal power required by robots is used in PnP applications with long-term placing and short-term picking operations. Control systems that support this methodology enable robots to hold the processed object in the given place, and deliver it to that location quickly and frugally. For that, a method is proposed and tested based on the mutual solution of the FK, IK, and IS problems for placing, as well as reinforcement learning for picking. As power consumption is defined by robot kinematics, statics, dynamics, workspace, and technical parameters, several MATLAB/Simulink™ models and simulation methods are designed for efficient robot control.
The designed forward kinematics solver provides the basis for estimating the robot workspace and easily solving the inverse kinematics problem. As a first result, several joint configurations can be found to be suitable for reaching the target area of the robot workspace. Next, for each configuration, a solution to the inverse statics problem is offered, which results in the joint configuration that requires the minimal torque to hold the processed object is chosen.
To assess the effectiveness of power-saving, the IRB1600 robot with a total maximal power consumption of 580 W was studied as an example. The experiment demonstrated that the holding power represents the largest portion of the total power consumed by the robot, and its value is proportional to the joint counter-torque generated at a particular configuration. A comparison of five permissible joint configurations shows that the differences in their holding torques can reach 53 Nm (25%), whereas the appropriate difference in the electrical power consumed at various configurations is 50 W (18% of consumed power, which means 8.6% of the maximal power at highest velocity and up to 12% at low velocities).
To optimise robot dynamics in the picking process, the reinforcement learning procedure and an appropriate NN-based control algorithm were designed. Although the latter one promises accurate and fast dynamics, it is sad to say that it could not be assessed during experimentation on the convenient IRB1600 robot equipped with standard PID controllers.
Therefore, an analysis of both the static and the dynamic power consumption components demonstrates that they may be successfully reduced with the help of the presented control method. This demonstrates how to search all possible alternative robot JKs and acquire them accurately to find the complete EE trajectories corresponding to the minimum power requested from the supply grid. The proposed approach can be recommended as a new mechanism for energy-saving and reducing negative environmental effects. The results of this study can be implemented in a wide range of industrial and domestic applications, without robot constructional modifications, plant updating, re-planning robot motions or routes in areas such as assembling, welding, packaging, quality control, loading, and wrapping.
Author Contributions
Conceptualization, methodology, software, writing, investigation, V.V.; validation, Z.R.; resources, V.V.; project administration, funding acquisition, E.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Estonian Research Council grant PRG 658.
Data Availability Statement
Data are contained within the article.
Acknowledgments
The authors express their gratitude to Madis Lehtla for his help in conducting the experiment.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| BFGS | Broyden–Fletcher–Goldfarb–Shanno |
| DDPG | deep deterministic policy gradient |
| DH | Denavit–Hartenberg |
| EE | end-effector |
| FK | forward kinematics |
| FLC | fuzzy logic controller |
| ID | inverse dynamics |
| IK | inverse kinematics |
| IS | inverse statics |
| JK | joint configuration |
| NN | neural network |
| PnP | pick-and-place |
| RL | reinforcement learning |
| LM | Levenberg–Marquardt |
| TD3 | twin-delayed |
References
- Robotics Capabilities; Bastian Solutions: Indianapolis, IN, USA, 2023; 11p, Available online: https://www.bastiansolutions.com/resources/downloads/brochures/robotics-brochure/ (accessed on 24 October 2023).
- Liu, A.; Liu, H.; Yao, B.; Xu, W.; Yang, M. Energy consumption modeling of industrial robot based on simulated power data and parameter identification. Adv. Mech. Eng. 2018, 10. [Google Scholar] [CrossRef]
- Meike, D.; Ribickis, L. Energy efficient use of robotics in the automobile industry. In Proceedings of the 5th International Conference on Advanced Robotics (ICAR), Tallinn, Estonia, 20–23 June 2011; pp. 507–511. [Google Scholar] [CrossRef]
- Barnett, N.; Costenaro, D.; Rohmund, I. Direct and indirect impacts of robots on future electricity load. ACEEE Summer Study on Energy Efficiency in Industry; 2017; pp. 1–9. Available online: https://www.aceee.org/files/proceedings/2017/data/polopoly_fs/1.3687904.1501159084!/fileserver/file/790278/filename/0036_0053_000029.pdf (accessed on 24 October 2023).
- Sabelhaus, A.P.; Li, A.H.; Sover, K.A.; Madden, J.; Barkan, A.; Agogino, A.K.; Agogino, A.M. Inverse statics optimization for compound tensegrity robots. IEEE Robot. Autom. Lett. 2020, 5, 3982–3989. Available online: https://alberthli.github.io/files/journal/invstatopt.pdf (accessed on 24 October 2023). [CrossRef]
- Siciliano, B.; Khatib, O. Springer Handbook of Robotics; Springer International Publishing: Berlin/Heidelberg, Germany, 2016; 2228p, Available online: https://www.academia.edu/26665877/Handbook_Springer_of_Robotics (accessed on 24 October 2023).
- Vodovozov, V.; Mjadzel, V.; Rassudov, L. Robots in Shipbuilding Manufactures; Shipbuilding: St. Petersburg, Russia, 1986; 248p, Available online: https://www.morkniga.ru/p839504.html (accessed on 24 October 2023).
- Vodovozov, V.; Raud, Z.; Petlenkov, E. Review on braking energy management in electric vehicles. Energies 2021, 14, 4477. [Google Scholar] [CrossRef]
- Rayyes, R.; Kubus, D.; Steil, J. Learning inverse statics models efficiently with symmetry-based exploration. Front. Neurorobot. 2018, 12, 68. [Google Scholar] [CrossRef] [PubMed]
- Electricity Generation Worldwide; Statista: New York, NY, USA, 2023; Available online: https://www.statista.com/statistics/270281/electricity-generation-worldwide/ (accessed on 24 October 2023).
- Electricity; International Energy Agency (IEA): Paris, France, 2023. Available online: https://www.iea.org/energy-system/electricity (accessed on 24 October 2023).
- Asada, M.; MacDorman, K.F.; Ishiguro, H.; Kuniyoshi, Y. Cognitive developmental robotics as a new paradigm for the design of humanoid robots. Rob. Auton. Syst. 2001, 37, 185–193. [Google Scholar] [CrossRef]
- Operating Manual RobotStudio; ABB: Zurich, Switzerland, 2011; Available online: https://library.e.abb.com/public/e5ad00148905fb58c1257b4b00523751/3HAC032104-001_revE_en.pdf (accessed on 24 October 2023).
- Technical Reference Manual. RAPID Instructions, Functions and Data Types; ABB: Zurich, Switzerland, 2010; Available online: https://library.e.abb.com/public/688894b98123f87bc1257cc50044e809/Technical%20reference%20manual_RAPID_3HAC16581-1_revJ_en.pdf (accessed on 24 October 2023).
- Tecnomatix Plant Simulation; Siemens: Munich, Germany, 2019; Available online: https://docs.plm.automation.siemens.com/content/plant_sim_help/15/plant_sim_all_in_one_html/en_US/tecnomatix_plant_simulation_help/tecnomatix_plant_simulation/tecnomatix_plant_simulation_help.html (accessed on 24 October 2023).
- Sharkawy, A.-N.; Koustoumpardis, P.; Aspragathos, N. Human-robot collisions detection for safe human-robot interaction using one multi-input-output neural network. Soft Comput. 2020, 24, 6687–6719. [Google Scholar] [CrossRef]
- McCarthy, J.M.; Soh, G.S. Geometric Design of Linkages, 2nd ed.; Springer: New York, NY, USA, 2010; 320p. [Google Scholar]
- Qiu, L.; Dong, L.; Gao, Y.; Wang, Z.; Tan, I.; Ji, Z. An enhanced approach for joint configuration of a robot performing in a repetitive task. J. Manuf. Syst. 2022, 64, 454–467. [Google Scholar] [CrossRef]
- Feng, Y.; Ji, Z.; Gao, Y.; Zheng, H.; Tan, J. An energy-saving optimization method for cyclic pick-and-place tasks based on flexible joint configurations. Robot. Comput.-Integr. Manuf. 2021, 67, 102037. [Google Scholar] [CrossRef]
- Gauthier, J.F.; Angeles, J.; Nokleby, S. Optimization of a test trajectory for SCARA systems. In Advances in Robot Kinematics: Analysis and Design; Lenarčič, J., Wenger, P., Eds.; Springer: Dordrecht, The Netherlands, 2008; pp. 225–234. [Google Scholar] [CrossRef]
- Gregory, J.; Olivares, A.; Staffetti, E. Energy-optimal trajectory planning for robot manipulators with holonomic constraints. Syst. Control Lett. 2012, 61, 279–291. [Google Scholar] [CrossRef]
- Rassõlkin, A.; Hõimoja, H.; Teemets, R. Energy saving possibilities in the industrial robot IRB 1600 control. In Proceedings of the 7th International Conference-Workshop Compatibility and Power Electronics (CPE), Tallinn, Estonia, 1–3 June 2011; pp. 226–229. [Google Scholar] [CrossRef]
- Mohammed, A.; Schmidt, B.; Wang, L. Energy-efficient robot configuration for assembly. J. Manuf. Sci. Eng. 2017, 139, 051007. [Google Scholar] [CrossRef]
- Park, J.S. Motion profile planning of repetitive point-to-point control for maximum energy conversion under acceleration conditions. Mechatronics 2006, 6, 649–663. [Google Scholar] [CrossRef]
- Hovgard, M.; Lennartson, B.; Bengtsson, K. Energy reduction of stochastic time-constrained robot stations. Robot. Comput.-Integr. Manuf. 2023, 81, 102511. [Google Scholar] [CrossRef]
- Pellicciari, M.; Berselli, G.; Leali, F.; Vergnano, A. A method for reducing the energy consumption of pick-and-place industrial robots. Mechatronics 2013, 23, 326–334. [Google Scholar] [CrossRef]
- Denavit, J.; Hartenberg, R.S. A kinematic notation for lower-pair mechanisms based on matrices. J. App. Mech. 1955, 22, 215–221. Available online: https://dokumen.tips/documents/a-kinematic-notation-for-lower-pair-mechanisms-based-on-matrices-denavit-hartenberg.html?page=2 (accessed on 24 October 2023). [CrossRef]
- Khanesar, M.A.; Branson, D. Robust sliding mode fuzzy control of industrial robots using an extended Kalman filter inverse kinematic solver. Energies 2022, 15, 1876. [Google Scholar] [CrossRef]
- Almaged, M.; Ismael, O. Forward and inverse kinematic analysis and validation of the ABB IRB 140 industrial robot. J. Mech. Eng. Technol. (JMET) 2017, 9, 1–20. [Google Scholar] [CrossRef]
- Aristidou, A.; Lasenby, J.; Chrysanthou, Y.; Shamir, A. Inverse kinematics techniques in computer graphics: A survey. Comput. Graph. Forum 2018, 37, 35–58. [Google Scholar] [CrossRef]
- Sugihara, T. Solvability-unconcerned inverse kinematics by the Levenberg–Marquardt method. IEEE Trans. Robot. 2011, 27, 984–991. [Google Scholar] [CrossRef]
- Featherstone, R. Rigid Body Dynamics Algorithms; Springer: New York, NY, USA, 2008; 272p. [Google Scholar] [CrossRef]
- Vodovozov, V. Electrical Drive: Performance, Design and Control; LAP Lambert Academic Publishing: Saarbrücken, Germany, 2014; 320p, Available online: https://www.amazon.co.uk/Electrical-Drive-Performance-Design-Control/dp/3659551910 (accessed on 24 October 2023).
- Vodovozov, V.; Aksjonov, A.; Petlenkov, E.; Raud, Z. Neural network-based model reference control of braking electric vehicles. Energies 2021, 14, 2373. [Google Scholar] [CrossRef]
- Tzafestas, S.G. Neural networks in robot control. In Artificial Intelligence in Industrial Decision Making, Control and Automation. Microprocessor-Based and Intelligent Systems Engineering; Tzafestas, S.G., Verbruggen, H.B., Eds.; Springer: Dordrecht, The Netherlands, 1995; Volume 14. [Google Scholar] [CrossRef]
- Khan, M.A.; Baig, D.-e.-Z.; Ali, H.; Ashraf, B.; Khan, S.; Wadood, A.; Kamal, T. Efficient system identification of a two-wheeled robot (TWR) using feed-forward neural networks. Electronics 2022, 11, 3584. [Google Scholar] [CrossRef]
- Han, Z.; Yang, L.; Zhang, Q.; Fan, J. Research on vehicle cruise control based on online asynchronous supervised reinforcement learning. J. Phys. 2021, 1873, 012023. [Google Scholar] [CrossRef]
- Mantripragada, V.K.T.; Kumar, R.K. Deep reinforcement learning-based antilock braking algorithm. Veh. Syst. Dyn. 2022, 61, 1410–1431. [Google Scholar] [CrossRef]
- Kuutti, S.; Bowden, R.; Fallah, S. Weakly supervised reinforcement learning for autonomous highway driving via virtual safety cages. Sensors 2021, 21, 2032. [Google Scholar] [CrossRef] [PubMed]
- Dubey, V.; Kasad, R.; Agrawal, K. Autonomous braking and throttle system: A deep reinforcement learning approach for naturalistic driving. In Proceedings of the 13th International Conference on Agents and Artificial Intelligence (ICAART), Vienna, Austria, 4–6 February 2021; Volume 1, pp. 173–180. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, G.; Wu, Y.; He, W.; Zhang, Y.; Chen, Z. Reinforcement-learning-based decision and control for autonomous vehicle at two-way single-lane unsignalized intersection. Electronics 2022, 11, 1203. [Google Scholar] [CrossRef]
- Otterlo, M.; Wiering, M. Reinforcement learning and Markov decision processes. In Reinforcement learning: State-of-the-Art; Springer: Berlin/Heidelberg, Germany, 2012; pp. 3–42. [Google Scholar] [CrossRef]
- Kim, M.; Han, D.-K.; Park, J.-H.; Kim, J.-S. Motion planning of robot manipulators for a smoother path using a twin delayed deep deterministic policy gradient with Hindsight experience replay. Appl. Sci. 2020, 10, 575. [Google Scholar] [CrossRef]
- Wang, D.; Hu, M. Deep deterministic policy gradient with compatible critic network. IEEE Trans. Neural Netw. Learn Syst. 2023, 34, 4332–4344. [Google Scholar] [CrossRef]
- Heredia, P.C.; Mou, S. Distributed multi-agent reinforcement learning by actor-critic method. IFAC-Pap. 2019, 52, 363–368. [Google Scholar] [CrossRef]
- Product Specification IRB 1600/1660; ABB Robotics: Zurich, Switzerland, 2022; 90p, Available online: https://library.e.abb.com/public/2f4a8db35722431abc41060243cd2c3d/3HAC023604%20PS%20IRB%201600-en.pdf?x-sign=I3H2UNs4L7trOkcrtkdMahcBVLt6z/Mzsyz+AYbdb0jEXXV2LbpjSSP/bTzJO27k (accessed on 24 October 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).