Abstract
The design process of a borehole heat exchanger (BHE) requires knowledge of building thermal loads, the expected heat pump’s COP and the ground’s thermophysical properties. The thermal response test (TRT) is a common experimental technique for estimating the ground’s thermal conductivity and borehole thermal resistance. In classic TRT, a constant heat transfer rate is provided above ground to the carrier fluid that circulates continuously inside a pilot BHE. The average fluid temperature is measured, and from its time-dependent evolution, it is possible to infer both the thermal resistance of the BHE and the thermal conductivity of the ground. The present paper investigates the possibility of a new approach for TRT with the continuous injection of heat directly into the BHE’s grouting by means of electrical resistance imparted along the entire BHE’s length, while local (along the depth) temperature measurements are acquired. This DTRT (distributed TRT) approach has seldom been applied and, in most applications, circulating hot fluid and optical fibers are used to infer depth-related temperatures. The distributed measurements allow the detection of thermal ground anomalies along the heat exchanger and even the presence of aquifer layers. The present paper investigates the new EDDTRT (electric depth-distributed TRT, under patenting) approach based on traditional instruments (e.g., RTD) or one-wire digital sensors. The accuracy of the proposed method is numerically assessed by Comsol Multiphysics simulations. The analysis of the data obtained from the “virtual” EDDTRT confirms the possibility of estimating within 10% accuracy both thermal ground and grout conductivities.
1. Introduction
In ground-coupled heat pumps (GCHPs), the plant is coupled with the soil by means of a buried system of pipes that allows the carrier fluid to extract heat from the ground. This system represents a very efficient solution for heating in buildings, especially in countries where climatic conditions are not favorable for other plant solutions, such as ASHPs (air source heat pumps). The undisturbed ground temperature indeed can be assumed to be equal (and even higher than, thanks to the geothermal gradient) to the annual average of the air temperature of the site; hence, it is significantly higher than the typical winter air temperatures of the selected location. Therefore, the coefficient of performance (COP) of a GCHP can be significantly higher than the corresponding value of an ASHP using the same operating conditions [1,2,3], provided that a correct design of the ground heat exchanger field is utilized.
In some countries, the diffusion of this efficient technology is limited for different reasons. Firstly, drilling and installation costs (especially for vertical borehole heat exchangers, BHEs) are relevant and represent an important capital cost, which is typically higher than the corresponding ASHP costs. Secondly, well-established engineering knowledge on correct BHE design procedures is still not so widespread in engineering communities: this can lead to reductions in the expected COP and an increase in the payback period of the plant. A third aspect, again related to the correct design of the BHE field, is related to the proper estimation of thermal ground properties and of the grouting material surrounding the heat exchanger pipes [4,5,6,7].
From the point of view of design strategies, the reference methods refer to the solution of the Fourier conduction equation in transient conditions. Such a complicated task, due to the geometrical complexity of the BHE field and the time-varying demand of heat by the building, is successfully accomplished by applying superposition techniques (in time and space) to reference pre-calculated solutions: the temperature response factors (TRFs), first introduced by Eskilson [8] and named “g-functions”. A series of scientific contributions have been provided in the last 20 years for calculating g-functions and tackling the same problem considered by Eskilson. To name a few of them, Hellstrom [9] and Spitler and co-workers [10,11] proposed a comparison between the accuracy of ten simplified approximations and the reference multipole algorithm aimed at calculating borehole thermal resistance. In addition, Javed and Claesson presented their analytical and numerical solutions for the short-term response of borehole heat exchangers in [12]; it is also worth mentioning the works by Bernier et al. [13,14], who considered the variability in heat extraction rates due to interactions between the boreholes, and they proposed a method for considering the time variation of heat extraction rates amidst the boreholes [15]. Beier and co-workers published several research papers on the topic [16,17] and developed a fast method for determining the minimum testing time in order to determine thermal ground conductivity, verifying their results against longer-period test results. Pasquier and Marcotte [18,19] introduced a novel algorithm to simulate a temperature signal by means of an analytical model, while the valuable research conducted by Lamarche and collaborators addressed the analytical evaluation of “g-functions” for both medium/long [20] and short time scales [21].
Based on the TRF approach and superposition techniques, the design method known as the ASHRAE method, first introduced by Kavanaugh and Rafferty [22], critically reformulated and improved by Bernier [13] and Ahmadfard and Bernier [23], has been made simple and accurate by introducing the “Tp8” temperature penalty model in [24], with the latter now being available as a web app calculation tool [25].
Any BHE field design procedure requires knowledge of thermal ground properties (thermal conductivity is the most important one) and possibly also the thermal conductivity of the cement filling surrounding the heat exchanger pipes.
The most reliable approach to ground property estimation is an experimental technique known as the thermal response test (TRT), which was first proposed and realized by Mogensen [26] and later applied and modeled by several researchers, including Gehlin [27], Pahud and Matthey [28], Fossa et al. [29], Galgaro et al. [30], and Morchio et al. [31].
During this test, the carrier fluid flows in a pilot BHE drilled into the ground in the selected location and fluid temperatures are measured outside the ground. A constant heat flux is typically provided to the fluid and the transient evolution of the average (inlet and outlet) fluid temperature is recorded, thus allowing a proper inverse technique to be applied for estimating the thermal ground properties [32].
The classic TRT experiment and its TRT machine have proven to provide accurate results on thermal ground conductivity as an average along the pilot BHE. The main drawbacks of this method are related to the obtained depth-averaged information, the cost of TRT equipment and its “bulky” size, often requiring a transportation cart.
Distributed thermal response tests (DTRTs) have been developed by the fundamental experimental investigations carried out by Acuña and co-workers [33,34], and they have been modeled by several authors, including the present research group [6]. This approach in the literature has been seldom applied and, in most applications, it is combined together with the use of optical fibers along the fluid carrier pipes [34] in order to obtain depth-related temperatures (distributed TRT). Optical fibers and related electronics, relying on Raman scattering technologies [35], comprise expensive sensors, and their use requires accurate calibrations.
The present paper investigates a new DTRT approach based on traditional sensors (e.g., RTDs or even single-wire digital sensors [36]) and uses an electric central cable for heating the core of the ground heat exchanger. The present investigation is addressed to simulate such electric depth-distributed TRTs (EDDTRT) and assess the effects on the ground property estimation of the position of sensors. This analysis is numerically carried out by Comsol Multiphysics simulations. The analysis of the data obtained from the “virtual” EDDTRT confirms the possibility of estimating both thermal ground and grout conductivities with 10% accuracy while low-cost temperature sensors are employed. This double estimation possibility during the same experiment represents an absolute novelty in the open literature relative to the authors’ knowledge.
2. Thermal Response Test: Theoretical Background
The thermal response test is an experimental procedure that estimates the average thermal ground conductivity and the effective thermal resistance of the BHE. The method was first introduced by Mogensen [26], and it is realized by means of suitable equipment on a pilot BHE that is drilled in the ground area of the future GCHP installation. The classic TRT [27,37,38,39] consists of continuously providing a constant heat transfer rate above ground to the carrier fluid that flows in the BHE. The inlet and outlet temperatures of the fluid are measured for the entire duration of the test, together with the fluid mass flow rate and the actual value of the provided electrical power (and the related heat transfer rate). The undisturbed ground temperature is evaluated at the beginning of the test by examining the temperature of the fluid that flows inside the BHE before the evaluation of the heat transfer rate.
The experimental data are then processed using the infinite line source (ILS) analytical model [40], which assumes pure heat transfer conduction in the ground and approximates the BHE as an infinite source of constant heat transfer rates relative to the unit’s length.
According to the ILS model, the ground temperature depends on time and on the radial distance from the linear heat source:
where E1 is the exponential integral, and For is the radius-based Fourier number For = ατ/r2.
The exponential integral can be approximated as
where γ is the Euler constant, and x = 1/4For.
Thus, the temperature in the medium evaluated at distance rb from the source, that is equal to the radius of the BHE, can be calculated as follows:
The effective thermal resistance of the BHE can be defined as a function of the average fluid and BHE temperatures:
where Tf is simply calculated as the average between the inlet’s and outlet’s fluid temperatures.
The BHE’s thermal resistance is assumed to be constant with respect to time and uniform for the entire length of the BHE and it depends on geometrical parameters (diameters, the number of pipes and pipe shank spacing), thermophysical properties of the materials (fluid, pipes and grout) and operating conditions (fluid mass flow rate). The BHE’s thermal performance increases for lower borehole resistance values [28].
Finally, the time-dependent evolution of the average fluid temperature can be written as follows:
For the constant heat transfer rate relative to unit length , this equation can be seen as a simple linear expression with respect to the logarithm of time:
Thus, by means of a (log)linear regression of the experimental TRT data of time-dependent fluid temperature, it is possible to infer slope S and intercept I and obtain an estimation of thermal ground conductivity kgr and effective BHE thermal resistance Rb.
It is worth noticing that the ILS model can estimate thermal conductivity using only slope S [27] irrespective of the correct determination of intercept I.
This classic approach allows estimating thermal ground conductivity as an average value, not taking into account the possible presence of ground layers with different thermophysical properties or the existence of groundwater movements at a particular depth.
It has to be noted that in the classic TRT, the assumption related to the constant heat transfer rate per unit length (as expected in the ILS model) is not completely satisfied in real experiments, since the local (along the depth) heat transfer rate depends on local fluid temperatures, which vary along the depth. To this extent, an experiment carried out with an electric heater along the BHE would much better fulfill the main assumption of the ILS model and ILS solution.
To infer the local value of thermal ground conductivity, it is possible to use the so-called distributed TRT (DTRT), during which the measured time-dependent temperature is not the average value of the carrier fluid but a local temperature in the grout or in the fluid (Fujii et al. [41,42]; Acuña et al. [33,43]). The data are collected by means of fiber optic cables that measure the temperature at various depths and can be located in different positions inside the BHE pilot installation. If the temperature of the fluid is locally measured, as well as the temperature of the borehole wall (Acuña et al. [33,43]), it is also possible to deduce an estimation of the BHE’s thermal resistance Rb. Pilot BHEs equipped with fiber optic cables also introduce the possibility of the continuous monitoring of the BHE field’s performance during the entire lifetime of the plant.
In either the classic TRT or the DTRT method, heat is provided above ground to the carrier fluid. An alternative solution is to use linear electrical resistance that delivers a uniform and constant in-time heat transfer rate per unit length directly inside the pilot BHE. This option represents a better approximation of the ILS model that is used to process experimental data.
The present paper investigates the opportunity to combine the use of a linear heat source, located in the middle of the borehole, with a system of distributed low-cost temperature sensors (e.g., single-wire digital sensors [36]) placed at selected depths and proper positions with respect to the U-pipes and the heater. It is worth noting that these instruments, installed before U-pipe placement, could be fixed using straightforward approaches: the relative position of the sensors with respect to the pipes and heater is not expected to be affected during the installation of U-pipes. However, a tailored solution for securing the thermoelements is detailed in [6]. The study analyzes the influence of the position of temperature sensors in the cross section of the BHE and the possibility of inferring both thermal ground and grout conductivities with suitable accuracy.
3. Distributed Thermal Response Test: The Numerical Model
The proposed EDDTRT geometry is based on the single U-pipe arrangement, which is the most popular and common configuration for ground heat exchangers. The borehole has a diameter of Db and a corresponding radius of rb, while pipes have an external radius of rp. The borehole is surrounded by the ground, and the inner borehole is supposed to be filled via a grouting material (the grout) that has different thermal properties compared to the ones of the ground. The axis of the borehole is fitted with an electric cable that acts as a heater when an electric current is applied.
The innovative EDDTRT process that includes the linear thermal source, and the distributed temperature sensors is numerically modeled by Comsol Multiphysics. The analysis refers to a single vertical U-pipe BHE in an ideally infinite ground volume. In particular, during the suggested EDDTRT procedure, pipes are filled with water, but the fluid is still and can be modeled with an equivalent solid medium. Thus, the problem involves transient 3D conduction in four different domains, i.e., the ground, grout, plastic pipes and water. The related geometrical parameters are presented in both Figure 1, representing the conceptual layout of the borehole heat exchanger, and Figure 2, while Table 1 summarizes the dimensions and the thermal property values adopted for simulations. The equation to be solved in the four different domains is the Fourier conduction equation:
where ρ and c are the density and specific heat of the analyzed domain, respectively.
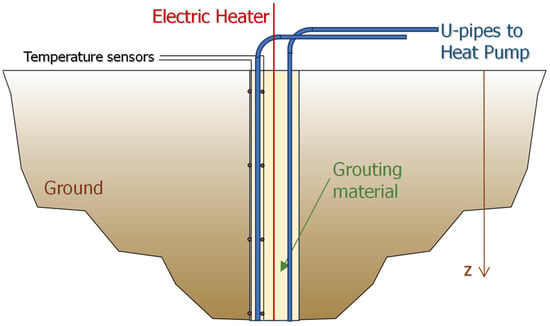
Figure 1.
Borehole heat exchanger schematics and position of heater and temperature sensors for EDDTRT analysis.
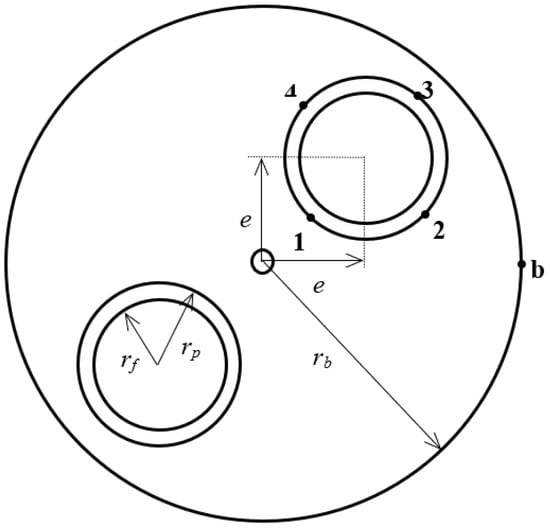
Figure 2.
Cross-section view of the borehole system, with temperature sensor positions.

Table 1.
Physical quantities in numerical simulations and their values for calculations.
The imposed temperature equal to the undisturbed ground value is both the initial condition applied everywhere in the calculation domain and the boundary condition on the external limits of the overall volume:
Linear electrical resistance is modeled as a thin cylindrical hole with radius rs that is located at the axis of the borehole, i.e., in the middle with respect to grout volume. This heater spans the entire depth of the BHE. The following Neumann boundary condition is imposed at the surface of the hole:
To reduce the effect of the great aspect ratio, the domain’s geometry has been rescaled relative to vertical coordinate z (Zanchini et al. [44]), with a consequent definition of anisotropic thermal conductivity in all different domains:
where a is a dimensionless scale factor; here, it is equal to 10.
All simulations were carried out starting with the above-described initial condition and “switching on” the heater, which comprised applying a depth constant heat flux along the hollow surface pertaining to the resistive cable.
The post-processing of numerical simulations includes the evaluation of time-dependent temperatures in the different locations of the grout domain; in particular, in the cross section of the BHE, four positions around the pipe perimeter and one on the BHE boundary have been considered. These reference positions (evaluation points), in any horizontal cross section, are those related to points 1, 2, 3, 4, and b, as described in Figure 2.
From the entire temperature field in space and time obtained with the Comsol simulations, reference positions relative to depths have been defined, and their temperatures have been stored as “local” (assigned depth) values; the distance step along the depth is not constant in order to take the edge effects into account. In detail, the considered depths are 1, 2, 5, 10, 20, 30, 40, 50, 60, 70, 80, 90, 95, 98 and 100 m. Moreover, for each evaluation position in the radial cross section, the average temperature along the entire BHE’s depth has been calculated.
In order to ensure that the results are independent of the domain’s extension, a preliminary analysis was conducted, and different radius and depth values of the cylindrical ground domain have been checked. In particular, the results obtained with boundary condition Tgr,∞ at the external vertical and bottom surfaces of the ground domain have been compared with those related to the boundary condition of adiabatic surfaces. For a cylindrical computational domain with a radius of rgr = 3 m and depth of Hgr = 110 m, the check produced the same results, and these dimensions were selected for all simulations. The values related to BHE geometry presented in Table 1 are in agreement with the current dimensions of the majority of existing vertical ground heat exchangers.
As can be observed in Table 1, the most important thermal properties (namely thermal ground conductivity and specific heat) have been selected with respect to the range of typical values in real applications.
A period of operation (duration of the EDDTRT experiment) of τ = 120 h was considered, and non-uniform time steps were adopted in the computations: 1 s for 0 < τ < 60 s, 5 s for 1 min < τ < 10 min, 1 min for 10 min < τ < 1 h, 10 min for 1 h < τ < 12 h, and 2 h for 12 h < τ < 120 h.
An extensive analysis of the independence from the selected mesh was performed by increasing the number of mesh elements until the stabilization of the results. Figure 3 reports the time evolution of the relative percentage error between the results obtained with two different meshes, namely with 745,431 and 1,267,402 elements, respectively. The error is related to the temperatures in the evaluation points (positions 1, 2, 3, 4, and b in Figure 2). As observed in Figure 3, the error is always lower than ±0.065%. Thus, as a compromise between accuracy and reduced computational times, the mesh with 745,431 was selected for the simulations.
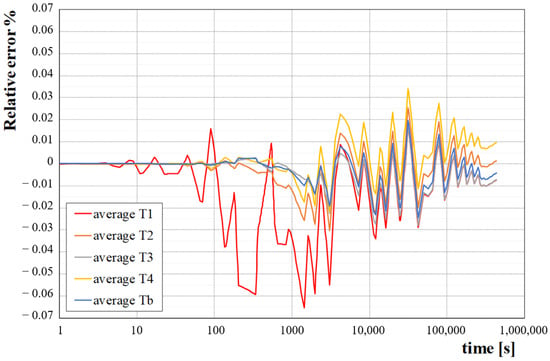
Figure 3.
Percentage error of temperatures as calculated in positions 1 to 4 and b (Figure 2) according to different meshes. The errors refer to depth-averaged temperatures, and their evolutions in time for a simulated EDDTRT experiment are plotted.
Finally, to show the capabilities of the distributed system of temperature sensors, further simulations were carried out with a ground volume composed of four layers with given thicknesses and different thermal conductivities (Table 2). Time-dependent temperature profiles as a function of the depth were obtained, and layer-related ground conductivities were estimated via ILS model analysis.

Table 2.
Layer vertical positions (ztop and zbottom) and related thermal properties as adopted in non-uniform thermal property simulations.
Numerical Model Validation against Experimental Results
The results obtained with the present numerical method were compared with the measurements obtained with a reduced-scale BHE and ground volume experimental setup [6]. The test section comprised an 800 kg rock volume (slate block) with a scaled U-pipe heat exchanger built via additive 3D-printing technology. The heat exchanger is equipped with temperature sensors (K-type thermocouples distributed along U-pipes). The measurements obtained with the scaled BHE setup refer to electric TRT experiments and estimate the (already known) rock’s thermal conductivity. The depth-related experimental temperature profiles reported in [6] were accurately replicated in [6] via the numerical model described in detail here. For further data and information about the comparison of measurements vs. numerical (present Comsol model) predictions, we refer the reader to the reduced scale experiment paper [6], which is intended as the first demonstrator of the innovative EDDTRT method to which the present paper is dedicated.
4. Numerical Results: Temperature Evolution in Time and Space and Their Processing for Thermal Property Estimation
The numerical results obtained from the simulations represent temperatures as they would have been measured during EDDTRT with the heat transfer rate provided by electric resistance along the BHE axis. The temperatures, in particular, refer to evaluation points in the cross section of the BHE (1, 2, 3, 4 and b, as shown in Figure 2), and the evolution in time of any such temperatures is analyzed with the ILS model (as a standard TRT experiment, but in that case, the time-dependent temperatures are the fluid ones outside the ground) in order to infer thermal ground (and grout) conductivities.
The innovative part of the present investigation and proposed EDDTRT method is that thermal grout conductivity can also be estimated from the same time series data provided that the temperature is measured (in this case, simulated) in the proper position inside the inner BHE’s volume (radius lower than rb).
The ILS solution can be reformulated as follows:
where Tx represents the measured temperature, and Rx represents the effective thermal resistance between Tx and the temperature at the BHE boundary, Tb.
In Equation (12), exponential integral E1 is approximated according to Equation (13) by Abramovitz and Stegun [45] and a set of coefficients listed in Table 3.

Table 3.
Values of numerical coefficients used in Equation (13).
For each of the four evaluation positions, numerical data are compared with the results obtained by solving Equation (12). Knowing the undisturbed ground temperature Tgr,∞ and the heat transfer rate per unit length, , Rx and kgr values are estimated by means of an optimum search that minimizes the root mean square error (Equation (14)). The solver algorithm comprises the GRG (generalized reduced gradient [45]) method, which is a robust method that is adopted in several calculation suites, including MS Excel.
Figure 4 presents a comparison between Comsol numerical results (average temperature along the entire BHE’s length) and ILS analytical solutions for the different evaluation positions, with a logarithmic scale on the x-axis and for the case of kgr = 2 W/mK.
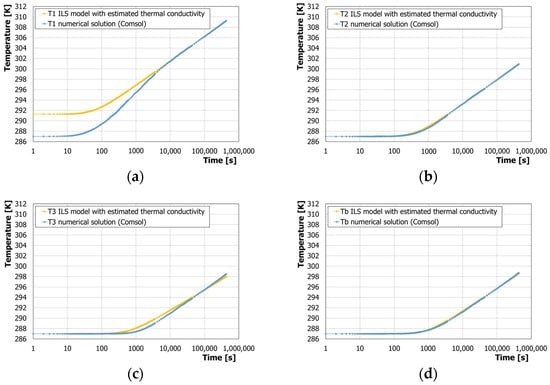
Figure 4.
Temperature profiles as a function of time in positions 1, 2, 3, b with reference to Figure 2 cross-section (a–d). Numerical Comsol results (kgr = 2 W/mK) vs. ILS model ones. Thermal conductivity in ILS temperatures is calculated from Equation (14) minimization process.
Figure 4 shows the best ILS profiles for the four evaluation positions once the minimum error solver is applied and the corresponding estimated ground conductivity is found.
The results for positions 2 and 4 are identical due to their symmetrical arrangement, and only the T2 temperature profile is presented for the sake of brevity. Thermal ground conductivity has been inferred for the different temperature positions via minimizazion procedure according to Equation (14). ILS-estimated conductivities have been finally compared with the real (as Comsol input) value and the estimated relative absolute percentage error (e%).
Table 4 summarizes the results of such comparisons among real and estimated conductivities for the four temperature positions. Positions 1 and 2 provide the best prediction in terms of the relative absolute percentage error with respect to thermal conductivity, whereas position 3 shows the largest error when estimating real (Comsol input) thermal ground conductivity.

Table 4.
Comparison between estimated thermal ground conductivities (ILS method and GRG minimization) and input conductivities (kgr = 2.00 W/mK) in Comsol simulations.
Hence the present results reveal that there are best positions inside the inner BHE where to measure (here simulate) temperatures in order to process them according to the ILS model.
Based on the very extensive experience of the present research group, the above finding is a complete novelty in the scientific literature that is related to BHE modeling, BHE measurements, and BHE theory. This finding opens new practical opportunities for realizing EDDTRT experiments with sensors located in the best positions for estimating thermal ground properties.
Again, in this analysis, Equations (12) to (14) were employed, but the goal here is to find grout conductivity, namely to iterate until the ILS-based profile has the same slope (also overlapping each other) as the Comsol one. It is important to notice that the minimization process (Equation (14)) finds another Rb value at which the slopes (which depend on thermal conductivity) are the same: this is the reason why Figure 4a and Figure 5 differ at the initial instants. Figure 5 shows some details related to the temperature profiles in position 1. It is possible to observe that the plot of time-dependent temperatures of position 1 (nearest to the center of the BHE and thus the linear heat source) presents two different slopes, one pertaining to approximately τ > 200 s and a second slope occurring at τ > 3600 s.
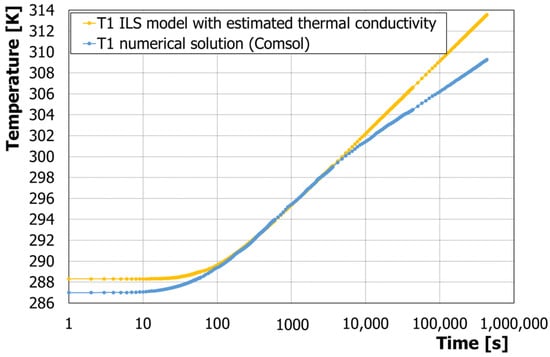
Figure 5.
Temperature profiles as a function of time in reference position 1 (Figure 2). Numerical Comsol results (kgr = 2 W/mK, kgt = 1.5 W/mK) vs. ILS model results. Thermal conductivity in ILS temperatures is calculated using Equation (14) minimization while simultaneously processing temperatures until the time point at which the change in slope occurs: (ρ · c)g = 2 × 106 (J/(m3 K)).
It should not be a surprise that the first slope within the range 200 s < τ < 3600 s provides thermal grout conductivity with good accuracies when processed according to the ILS method: the estimated kILS was equal to 1.32 W/mK and e% = 12.3% (Comsol input grout conductivity kgt is 1.5 W/mK).
The presence of two slopes in the temperature profile depends on the transient physics of the phenomenon; at the “beginning”, the thermal propagation of the heat pulse, which starts at instant zero at the BHE’s central axis, is “not yet affected” by the external ground medium (relative to its thermal properties); later on in the temperature profile and even inside the grout volume, it started to be controlled by ground transient behaviors, and ground properties started to dominate the process.
A general and very important result of the simulation is that, for a proper position at which temperatures inside the BHE core can be recorded when heating is provided at the BHE axis, it seems possible to infer (via ILS analysis) thermal grout and ground properties with the same measurements with high accuracy.
Temperature Distributions and Thermal Conductivity Estimation: Layered Ground with Different Thermal Properties
The present numerical model was applied to simulate the ground’s response to a constant heat transfer rate in time by assuming that the ground comprises four different layers of given thicknesses and thermal properties. Layer positions and the related thermal properties are given in Table 2.
Figure 6 and Figure 7 show the temperature evolution in time at sensor location #1, as indicated in Figure 2. The diagrams refer to different thermal property conditions in the ground volume: in Figure 6, the ground is uniform with respect to thermal conductivity along the depth, while Figure 7 shows a layered ground where each layer is assigned a given thickness (20 to 30 m) and a given thermal conductivity is applied as the Comsol input. In both cases, the ground’s heat capacity (density times specific heat) is set to 2.0 MJ/m3/K. It can be observed that in Figure 6, the temperature is always increasing in time (as an effect of the active heat source at the BHE’s axis) but is also substantially constant along the depth, with the exception of the top layer of the ground.
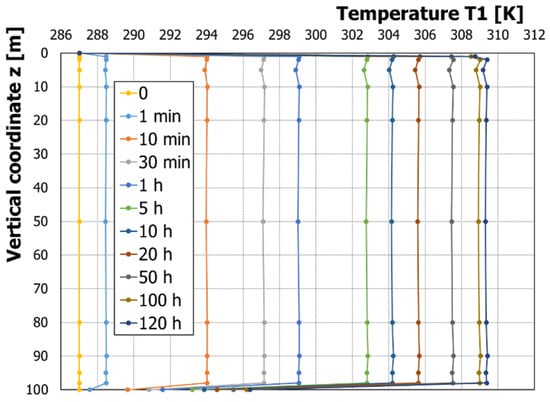
Figure 6.
Temperature distribution along the borehole depth for reference position 1 (Figure 2) at different time instants from 1 min to 120 h. Thermal ground capacity (density times specific heat) is 2.0 MJ/m3/K, and ground conductivity is constant along the depth at 2.0 W/m/K.
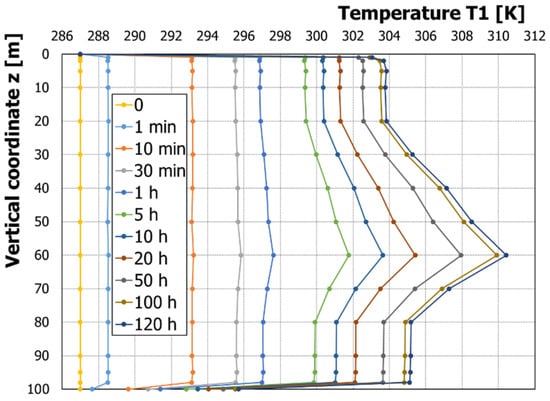
Figure 7.
Temperature distribution along the borehole’s depth for reference position 1 (Figure 2) at different time instants from 1 min to 120 h. Thermal ground capacity (density times specific heat) is 2.0 MJ/m3/K, and ground conductivity varies along the depth according to the layer description of Table 4.
In both the figures, it can be observed that the upper temperature (ground–external environment interface) remains constant since it refers to a constant temperature boundary condition, as assumed in such models since the very first study carried out by Eskilson [8]. On the other hand, the bottom BHE temperature is not imposed, but it is affected by the edge effects related to the ground underneath the U part of the heat exchanger, which is constrained at its lower surface (located at z = 110 m) by the undisturbed (and initial) temperature boundary condition.
In Figure 7, on the other hand, the temperature is affected by layered thermal conductivity. In the present layered case, there is a layer at which thermal conductivity is at the minimum (50 < z < 70 m, kgr = 1.5 W/mK).
As clearly observed in the area where conductivity is lower, the local temperature is higher at any given time, as noticed at depths of around 60 m.
Furthermore, the following is very important and novel: the increase rate of temperature vs. time in any ground layer can provide (with the present ILS approach) an accurate estimation of local ground conductivity: as an example, at layer A, z = 20 m, the estimation of the ground thermal conductivity provided kgr ext = 2.84 W/mK, with percentage error e% with respect to real (input) conductivity equal to 5.16%.
5. Conclusions
The present paper investigates a new approach for depth-distributed thermal response tests (EDDTRTs) based on the use of an electric central cable for heating the BHE and traditional sensors like RTDs for local temperature measurements. The aim of the study was to investigate the possibility of applying the ILS (infinite line source) model to transient temperature data and assess the best position of the sensors inside the inner borehole heat exchanger volume. The analysis was numerically carried out by Comsol Multiphysics and the validation of the numerical model was conducted using measurements in lab- and reduced-scale TRT ground volumes. The analysis of the data obtained from the numerical EDDTRT showed that there are best positions where to locate the temperature sensors in the BHE pipe’s neighborhood. At these positions, the present investigation shows that the ILS model and a minimization error method can be applied for inferring thermal ground conductivity with 10% uncertainty (and even less) in a variety of thermal property conditions related to the ground, also when the ground is not uniform along its depth. One of the novelties of the present study (to the authors’ knowledge, this has never been presented in the scientific literature) is that thermal grout conductivity can also be estimated during the same experiment with the same level of accuracy. Further simulations and measurements will be carried out to also compare the EDDTRT results against the corresponding ones pertaining to traditional TRT experiments with respect to the circulation of fluid and heat transfer rates that are supplied outside the ground.
The findings related to ground and grout estimations with the present EDDTRT approach have been submitted and accepted for patenting in selected countries.
6. Patents
This work is a part of a validation activity related to the Italian and Canadian Patent n. 102019000023082, “Method and device for measuring geothermal parameters for sizing and subsequent monitoring of geothermal heat pumps”.
Author Contributions
Conceptualization, M.F. and A.P.; methodology, M.F. and A.P.; Comsol analysis, A.P.; validation, A.P. and S.M.; formal analysis, all authors; investigation, M.F. and A.P.; resources, S.M. (Stefano Morchio) and S.M. (Samuele Memme); writing, all authors; review and editing, all authors; project administration, M.F.; measurements, S.M. (Stefano Morchio) and S.M. (Samuele Memme). All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Acknowledgments
This research study is a part of the Italian National Program PNRR—Raise PNRR—Ecosistema dell’Innovazione ECS00000035 “RAISE (Robotics and AI for Socio economic Empowerment)”—SPOKE 3 “Environmental Caring and Protection Technologies, towards a Zero Emission Environment”—Research Activity (Task) 3.2 “Technologies for energy storage”.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| a | rescaling factor (−) |
| c | specific heat (J/kg K) |
| E1 | exponential integral in ILS model (−) |
| e | center pipe coordinate (m) |
| e% | relative absolute percentage error (−) |
| Fo | Fourier number (−) |
| H | active depth of the BHE (m) |
| I | intercept (K) |
| k | thermal conductivity (W/(m·K)) |
| anisotropic thermal conductivity (W/(m·K)) | |
| matrix of thermal conductivity (W/(m·K)) | |
| heat transfer rate per unit length (W/m) | |
| heat transfer rate per unit area (W/m2) | |
| R | thermal resistance (m·K/W) |
| RMSE | root mean square error (K) |
| r | radial coordinate (m) |
| S | slope (K/cycles) |
| T | temperature (K) |
| z | vertical coordinate (m) |
| rescaled vertical coordinate (m) | |
| Greek letters | |
| α | thermal diffusivity (m2/s) |
| γ | Euler constant (−) |
| ρ | density (kg/m3) |
| π | pi constant (−) |
| τ | time (s) |
| Subscripts | |
| b | Borehole |
| ext | estimated value |
| f | heat carrier fluid |
| gr | of the ground medium and of the ground domain |
| gt | of the grout medium and of the grout domain |
| s | heat source |
| x | measured quantity |
| Comsol | Comsol Multiphysics numerical results |
| ILS | results from ILS analysis |
| ∞ | far-field undisturbed and initial condition |
References
- IEA. Heat Pumps; IEA: Paris, France, 2020; Available online: https://www.iea.org/reports/heat-pumps (accessed on 3 October 2023).
- Aresti, L.; Christodoulides, P.; Florides, G.A. An investigation on the environmental impact of various Ground Heat Ex-changers configurations. Renew. Energy 2021, 171, 592–605. [Google Scholar] [CrossRef]
- Bayer, P.; Saner, D.; Bolay, S.; Rybach, L.; Blum, P. Greenhouse gas emission savings of ground source heat pump systems in Europe: A review. Renew. Sustain. Energy Rev. 2012, 16, 1256–1267. [Google Scholar] [CrossRef]
- Spitler, J.D.; Gehlin, S.E.A. Thermal response testing for ground source heat pump systems—An historical review. Renew. Sustain. Energy Rev. 2015, 50, 1125–1137. [Google Scholar] [CrossRef]
- Wilke, S.; Menberg, K.; Steger, H.; Blum, P. Advanced thermal response tests: A review. Renew. Sustain. Energy Rev. 2020, 119, 109575. [Google Scholar] [CrossRef]
- Morchio, S.; Fossa, M.; Priarone, A.; Boccalatte, A. Reduced scale experimental modeling of distributed thermal response tests for the estimation of the ground thermal conductivity. Energies 2021, 14, 6955. [Google Scholar] [CrossRef]
- Minchio, F.; Cesari, G.; Pastore, C.; Fossa, M. Experimental hydration temperature increase in borehole heat exchangers during thermal response tests for geothermal heat pump design. Energies 2020, 13, 3461. [Google Scholar] [CrossRef]
- Eskilson, P. Thermal Analysis of Heat Extraction Boreholes. Ph.D. Thesis, Lund University, Lund, Sweden, 1987. [Google Scholar]
- Hellstrom, G. Borehole Heat Exchangers: State of the Art 2001. In Implementing Agreement on Energy Conservation through Energy Storage: Annex 13-Design, Construction and Maintenance of UTES Wells and Boreholes; Subtask 2; International Energy Agency (IEA): Paris, France, 2002. [Google Scholar]
- Javed, S.; Spitler, J.D.; Rees, S.J. Calculation of borehole thermal resistance. In Advances in Ground-Source Heat Pump Systems; Rees, S.J., Ed.; Woodhead Publishing: Duxford, UK, 2016; pp. 63–95. [Google Scholar]
- Javed, S.; Spitler, J.D. Accuracy of borehole thermal resistance calculation methods for grouted single U-tube ground heat exchangers. Appl. Energy 2017, 187, 790–806. [Google Scholar] [CrossRef]
- Javed, S.; Claesson, J. New analytical and numerical solutions for the short-term analysis of vertical ground heat exchangers. ASHRAE Trans. 2011, 117, 3–12. [Google Scholar]
- Bernier, M. Closed-Loop Ground-Coupled Heat Pump Systems. ASHRAE J. 2006, 48, 12–19. [Google Scholar]
- Cimmino, M.; Bernier, M.; Adams, F. A contribution towards the determination of g-functions using the finite line source. Appl. Therm. Eng. 2013, 51, 401–412. [Google Scholar] [CrossRef]
- Cimmino, M.; Bernier, M. A semi-analytical method to generate g-functions for geothermal bore fields. Int. J. Heat Mass Transf. 2014, 70, 641–650. [Google Scholar] [CrossRef]
- Beier, R.A.; Smith, M.D. Minimum duration of in-situ tests on vertical boreholes. ASHRAE Trans. 2003, 109, 475–486. [Google Scholar]
- Beier, R.A.; Fossa, M.; Morchio, S. Models of thermal response tests on deep coaxial borehole heat exchangers through multiple ground layers. Appl. Therm. Eng. 2021, 184, 116241. [Google Scholar] [CrossRef]
- Pasquier, P.; Marcotte, D. Efficient computation of heat flux signals to ensure the reproduction of prescribed temperatures at several interacting heat sources. Appl. Therm. Eng. 2013, 59, 515–526. [Google Scholar] [CrossRef]
- Marcotte, D.; Pasquier, P. Fast fluid and ground temperature computation for geothermal ground-loop heat exchanger systems. Geothermics 2008, 37, 651–665. [Google Scholar] [CrossRef]
- Lamarche, L.; Beauchamp, B. A new contribution to the finite line-source model for geothermal boreholes. Energy Build. 2007, 39, 188–198. [Google Scholar] [CrossRef]
- Lamarche, L. Short-term behavior of classical analytic solutions for the design of ground-source heat pumps. Renew. Energy 2013, 57, 171–180. [Google Scholar] [CrossRef]
- Kavanaugh, S.P.; Rafferty, K. Ground-Source Heat Pumps: Design of Geothermal Systems for Commercial and Institutional Buildings; ASHRAE: Atlanta, GA, USA, 1997. [Google Scholar]
- Ahmadfard, M.; Bernier, M. An Alternative to ASHRAE’s Design Length Equation for Sizing Borehole Heat Exchangers; American Society of Heating, Refrigerating, and Air-Conditioning Engineers, Inc. (ASHRAE): New York, NY, USA, 2014. [Google Scholar]
- Fossa, M. Correct design of vertical BHE systems through the improvement of the ASHRAE method. Sci. Technol. Built Environ. 2017, 23, 1080–1089. [Google Scholar] [CrossRef]
- GeoSensingDesign.org, (n.d.). Available online: https://www.geosensingdesign.org/ (accessed on 28 September 2023).
- Mogensen, P. Fluid to duct wall heat transfer in duct system heat storages. Doc. Swed. Counc. Build. Res. 1983, 16, 652–657. [Google Scholar]
- Gehlin, S. Thermal Response Test: Method Development and Evaluation. Ph.D. Thesis, Luleå Tekniska Universitet, Luleå, Sweden, 2002. [Google Scholar]
- Pahud, D.; Matthey, B. Comparison of the thermal performance of double U-pipe borehole heat exchangers measured in situ. Energy Build. 2001, 33, 503–507. [Google Scholar] [CrossRef]
- Fossa, M.; Rolando, D.; Pasquier, P. Pulsated Thermal Response Test experiments and modelling for ground thermal property estimation. In Proceedings of the IGSHPA Research Track, Stockholm, Sweden, 18–20 September 2018. [Google Scholar] [CrossRef]
- Galgaro, A.; Pasquier, P.; Schenato, L.; Cultrera, M.; Dalla Santa, G. Soil thermal conductivity from early TRT logs using an active hybrid optic fibre system. In Proceedings of the IGSHPA Research Track, Stockholm, Sweden, 18–20 September 2018; pp. 1–9. [Google Scholar] [CrossRef]
- Morchio, S.; Pasquier, P.; Fossa, M.; Beier, R.A. A spectral method aimed at explaining the role of the heat transfer rate when the Infinite Line Source model is applied to Thermal Response Test analyses. Geothermics 2023, 111, 102722. [Google Scholar] [CrossRef]
- Nguyen, A.; Pasquier, P.; Marcotte, D. Borehole thermal energy storage systems under the influence of groundwater flow and time-varying surface temperature. Geothermics 2017, 66, 110–118. [Google Scholar] [CrossRef]
- Acuña, J.; Mogensen, P.; Palm, B. Distributed Thermal Response Test on a U-Pipe Borehole Heat Exchanger. In Proceedings of the Effstock 2009, 11th International Conference on Thermal Energy Storage, Stockholm, Sweden, 14–17 June 2009. [Google Scholar]
- Acuña, J.; Palm, B. Distributed thermal response tests on pipe-in-pipe borehole heat exchangers. Appl. Energy 2013, 109, 312–320. [Google Scholar] [CrossRef]
- Li, J.; Zhang, M. Physics and applications of Raman distributed optical fiber sensing. Light Sci. Appl. 2022, 11, 128. [Google Scholar] [CrossRef] [PubMed]
- Vavrla, T.; Koziorek, J. Temperature Measurement in Boreholes by Programmable Logic Controller B&R and Temperature Sensors 1-Wire. IFAC Proc. 2012, 45, 382–387. [Google Scholar] [CrossRef]
- Eklöf, C.; Gehlin, S. TED—A Mobile Equipment for Thermal Response Test. Master’s Thesis, Lund University, Lund, Sweden, 1996. [Google Scholar]
- Austin, W.A. Development of an In Situ System for Measuring Ground Thermal Properties. Ph.D. Thesis, Oklahoma State University, Stillwater, OK, USA, 1998. [Google Scholar]
- Gehlin, S.; Hellstrom, G. Comparison of four models for thermal response test evaluation. ASHRAE Trans. 2003, 109, 131–142. [Google Scholar]
- Ingersoll, L.R. Heat Conduction: With Engineering, Geological, and Other Applications; University of Wisconsin Press: Madison, WI, USA, 1954. [Google Scholar]
- Fujii, H.; Okubo, H.; Itoi, R. Thermal response tests using optical fiber thermometers. Geotherm. Resour. Counc. Trans. 2006, 30, 545–551. [Google Scholar]
- Fujii, H.; Okubo, H.; Nishi, K.; Itoi, R.; Ohyama, K.; Shibata, K. An improved thermal response test for U-tube ground heat exchanger based on optical fiber thermometers. Geothermics 2009, 38, 399–406. [Google Scholar] [CrossRef]
- Acuña, J.; Mogensen, P.; Palm, B. Distributed thermal response tests on a multi-pipe coaxial borehole heat exchanger. HVACR Res. 2011, 17, 1012–1029. [Google Scholar]
- Zanchini, E.; Lazzari, S.; Priarone, A. Improving the thermal performance of coaxial borehole heat exchangers. Energy 2010, 35, 657–666. [Google Scholar] [CrossRef]
- Lasdon Leon, S.; Fox Richard, L.; Ratner Margery, W. Nonlinear optimization using the generalized reduced gradient method Revue française d’automatique, informatique, recherche opérationnelle. Rech. Oper. 1974, 8, 73–103. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).