Abstract
In offshore winch drive applications, determining the required number of pistons in digital displacement motors is critical for minimizing torque ripples. Digital displacement motors have shown promise for improving energy efficiency for offshore operations, such as placing equipment on the seabed or mineral drilling. However, they are known for exhibiting significant torque ripples, which can affect load-handling precision. This paper estimates the required number of pistons for realizing a digital hydraulic winch drive based on information from a commercial winch. The proposed drive employs full-stroke displacement strategies at high speeds and partial-stroke at low speeds. By simulating steady-state operations, this study correlates torque output with position oscillations. The results show that 37 pistons are required to keep position oscillations below a benchmark threshold of 10 mm throughout the drive’s operating range to avoid hindering the drive’s performance. However, such a high piston count could result in high costs due to the large, expensive valves required for partial-stroke operations. Therefore, this paper suggests an alternative drive topology for future research, which could potentially reduce the number of pistons that are operated with partial strokes.
1. Introduction
Operating within challenging maritime conditions, offshore cranes extensively employ winch drives for precise load handling. These loads often weigh several hundred tons and operate at relatively slow hoisting speeds, typically below 8 m/min. An example of a commercially available offshore knuckle-boom crane, with a load capacity of up to 150 t, is depicted in Figure 1. The winch drive controls the vertical position of the load, which is suspended from the hook and can be controlled by extending or retracting the wire. As the offshore industry endeavors to align with various environmental requirements, enhancing the energy efficiency of these drives is gaining increased significance. Hydraulic digital displacement motors (DDMs) have surfaced as potential solutions for augmenting the energy efficiency of offshore winch drives. DDMs are radial piston motors with the unique capability of individually controlling the flow to each piston through a pair of digital valves, which can significantly mitigate leakage, friction, and compressibility losses in comparison to their conventional counterparts, thus yielding much higher part load efficiency. Multiple research findings and practical implementations highlight their enhanced energy efficiency in areas like off-road vehicles, suspension mechanisms, and wave energy conversion systems [1,2,3,4,5,6,7].

Figure 1.
Offshore knuckle-boom crane from NOV, a globally known producer of offshore machinery. The crane is designed to handle loads of up to 150 t and it is placed on land for testing purposes.
Comprehensive descriptions of digital displacement pumps and motors are available in the existing literature [8,9,10,11,12]. The efficiency and response behavior of DDMs depend critically on the specifics of the valve timing control (VTC). The VTC strategy impacts the handling of piston strokes and, consequently, the displacement control strategy. Several displacement control strategies have been suggested, generally falling into three classifications: full-stroke displacement (FSD), partial-stroke displacement (PSD), and sequential partial-stroke displacement (SPD). The chosen displacement control strategy and the number of pistons that the DDM utilizes determine the motor’s response time and steady-state behavior as well as its energy efficiency. The response behavior and energy efficiency of the DDMs when utilizing these strategies have been explored in a range of studies [1,11,13,14,15]. However, these investigations primarily deal with digital displacement machines functioning at high speeds, typically above 500 rpm.
The response time of digital displacement motors is typically characterized as the duration required for the motor to increase its torque output from zero to peak value. An appraisal of the displacement strategies mentioned earlier by [16] demonstrated that the selection of the optimal displacement strategy is contingent upon the specifics of the application in question. The study found that for high-speed operations, a full-stroke displacement strategy provides short response times and high energy efficiency. For medium to low speeds, a partial-stroke displacement strategy facilitates faster responses at lower displacements since all cylinders are utilized to attain the desired displacement, albeit at the expense of energy efficiency. For extremely low speeds, the sequential partial-stroke displacement strategy delivers swift response times, limited only by the valve actuation time, but significantly increases energy losses.
Existing literature offers limited research on the steady-state oscillatory behavior of DDMs. Holland [17] proposed an algorithm enabling an FSD-controlled motor to achieve the smoothest possible output over a cycle. Merril [13] compared this algorithm with a PSD strategy and demonstrated that the latter produced the highest torque fluctuations at 50% displacement, while the FSD strategy exhibited the highest torque ripples below 30% displacement. Dumnov and Caldwell [18] introduced a combined FSD and PSD strategy that leveraged a quantization algorithm to prevent digital displacement pumps from generating low-frequency flow. Although this method enhanced the displacement resolution compared to an FSD strategy, it was unclear whether the same technique could be applied to a DDM. A unique method, termed ”creep mode“, was presented by Larsen et al. [19] for managing DDMs at exceptionally low speeds. This method, falling under the sequential partial-stroke category, relies on the gradual movement of the motor’s shaft from one-moment equilibrium to another by selectively pressurizing or depressurizing one chamber at a time. High positional accuracy can be achieved through this method, but Larsen et al. noted that the method can induce more wear on the valves and the electrical system due to frequent valve switching for small motions.
The work of Nordås et al. [20] critically analyzed the steady-state behavior and response times of digital displacement motors in the context of a winch drive. Their findings showed that both FSD and PSD strategies exhibited poor response rates for low-speed applications such as offshore winch drives. Although a sequential-stroke strategy presented a faster response, it necessitated a higher switching frequency of the digital valves. In response to these challenges, the authors put forward a simplified form of a sequential partial-stroke displacement strategy (s-SPD). This strategy closely mirrors a traditional partial-stroke strategy, but it allows any piston that can contribute torque towards the desired direction to change the states of the valves to pressurize the chamber, irrespective of the shaft position when the displacement reference is increased. This allows for a rapid motor response without requiring frequent valve actuation. However, the energy efficiency of this approach was not investigated in their study. This approach was further explored and refined by Farsakoglou et al. [21] in the context of an offshore winch drive actuated by DDMs, based on a commercial winch drive system by NOV. The conclusions of the paper suggested that the s-SPD strategy allows for a swift response time, which is crucial when the motors operate below 20 rpm. Above this operational speed, a PSD strategy can deliver an adequately low response time. However, it was demonstrated that the s-SPD strategy significantly compromises the motor’s energy efficiency. As a result, an alternative low-speed sequential partial-stroke displacement strategy (ls-SPD) was proposed, which led to high volumetric efficiency for the motor. With the s-SPD strategy, the motor can pressurize a chamber by switching the valve states simultaneously, which leads to high volumetric losses. The ls-SPD strategy counteracts this issue by introducing a minor time delay between the valves as they transition between states. This approach significantly enhanced the motor’s volumetric efficiency; however, it was deemed unsuitable for high-speed operations due to its strict timing requirements on the precision of valve actuation.
This paper aims to ascertain the required number of pistons for DDM technology in order to produce torque fluctuations that do not impede the accurate load-handling ability of the considered drive system. The analysis considers the resulting load position oscillation resulting from the torque pattern that is produced by different displacement control strategies, particularly at the slowest operational speed where torque ripples have their most extended duration. The investigation also considers a combination of full-stroke and partial-stroke strategies for controlling the torque output of the drive system. By implementing a full-stroke strategy alongside partial-stroke strategies, it is plausible to significantly reduce the need for costly large valves, which are mandatory for partial-stroke strategies, by substituting them with smaller, more affordable valves that a full-stroke strategy can employ. However, this approach is not explored further, and it is instead proposed for consideration in future research. The offshore winch drive being examined was originally presented by [22], and also considered in [21], and is designed following a commercial winch drive system by NOV, a globally recognized manufacturer of offshore cranes and winch drive systems [23]. In this context, traditional hydraulic motors and their associated gearboxes have been superseded by digital displacement motors.
This paper is structured as follows. Section 2 offers an overview of the commercially available winch drive system and the considered winch drive that makes use of digital displacement motors. Section 3 presents the methodology for modeling the DDMs. The considered displacement control strategies are subsequently detailed in Section 4. Section 5 outlines the methodology utilized to correlate torque fluctuations with oscillations in the load position. The results of the study are found in Section 6, which also presents the analysis for determining the necessary number of pistons. The conclusions derived from the study are finally summarized in Section 7.
2. Commercial and Digital Winch Drive Topologies
An illustration of the original winch drive is shown in Figure 2.
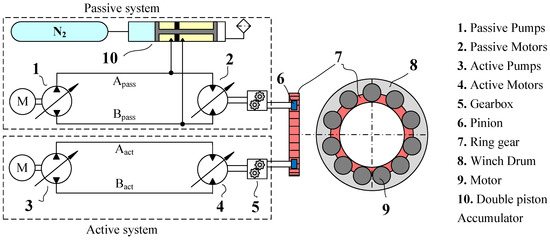
Figure 2.
A simplified depiction of the commercial offshore winch drive produced by NOV.
The drive system is composed of two interconnected systems: the active and passive systems, represented by the dashed line boxes. These systems work in tandem, both linked to the same ring gear. The passive system, through secondary control, maintains near-constant pressure levels. Its motors modify their output to yield a consistent torque that counteracts the gravitational pull on the load. Conversely, the active unit’s role is to match the velocity input from the crane operator, while also mitigating friction and external disturbances. As shown in Figure 1, the crane is equipped with an auxiliary winch that is rated for up to 20 t loads. Therefore, the main winch is utilized to lift loads over 20 t and up to its rated value of 150 t.
The proposed drive system, characterized as an offshore digital hydraulic winch drive, is depicted in Figure 3. Compared to the passive subsystem of the conventional drive, here, the motors are directly connected to the winch drum solely by a pinion-to-ring gear connection. Similarly, a digital displacement pump (DDP) and a double-piston accumulator are used to maintain a quasi-constant pressure in the high-pressure () and low-pressure () lines.
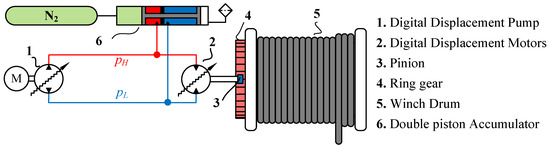
Figure 3.
Offshore digital hydraulic winch drive.
In order to evaluate the torque oscillations produced by the DDM, the study assumes constant pressures in the high- and low-pressure lines, thus discarding the pressure line dynamics. Therefore, the digital winch drive is simplified, as shown in Figure 4.
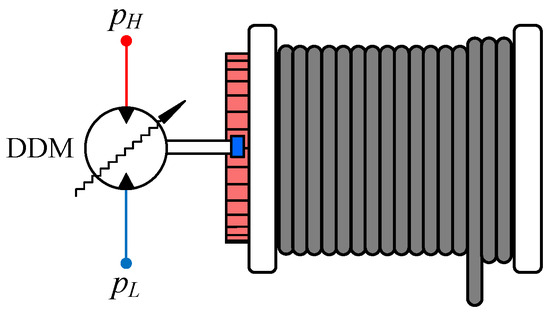
Figure 4.
A simplified representation of the proposed offshore digital winch drive.
A graphical illustration of a digital displacement motor equipped with five pistons is provided in Figure 5a. The pistons of a DDM are evenly arrayed around the motor’s shaft, as depicted in Figure 5b, and each piston chamber is controlled by a pair of digital valves.
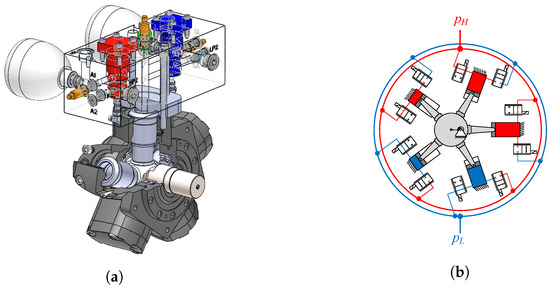
Figure 5.
(a) Basic depiction of a digital displacement motor featuring five pistons, inspired by [21]. (b) A 3D model showcasing a five-piston radial piston motor, with one chamber controlled by a pair of digital valves.
The focus of this paper is the torque output fluctuations exhibited by the DDM around the target value, which depend on the valve actuation strategy and the number of pistons utilized by the motor. The displacement control strategies under consideration are detailed in Section 4, while the torque oscillations are discussed and mitigated in Section 6. These torque ripples can compromise the control accuracy of the drive’s position as they can lead to load position errors. Consequently, it is crucial to choose an adequate number of pistons, ensuring that the position errors remain minimal. This allows the winch drive to precisely follow the reference input, irrespective of the employed displacement control strategy.
The main challenge that winch drives need to address in offshore operations is counteracting the disturbance of wave-induced heave motion, which causes vertical oscillations at the crane’s tip. This motion is typically modeled using the JONSWAP wave spectrum, as outlined by [24]. Figure 6 provides an illustration of a resultant wave-induced vertical motion at the crane tip, a disturbance the winch system is designed to compensate for.
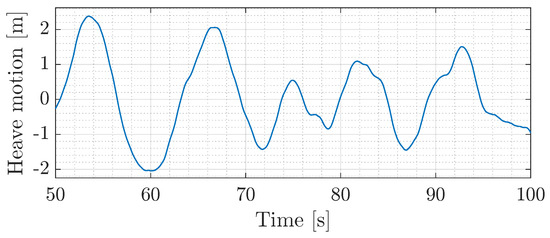
Figure 6.
Wave–induced vertical oscillation at the crane’s tip, simulated using the JONSWAP wave spectrum.
The control scheme utilized by the digital winch drive, shown in Figure 7, is similar to the one used by the active subsystem of the conventional drive [25]. Using the load’s position error, the controller adjusts the DDM’s displacement. This error is determined from the operator’s input, measured heave motion, and the position of the winch drum. Subsequently, the controller’s output is modulated through the displacement strategy to a stream of ones and zeros, actuating the digital valves accordingly. The displacement strategies are described in Section 4.
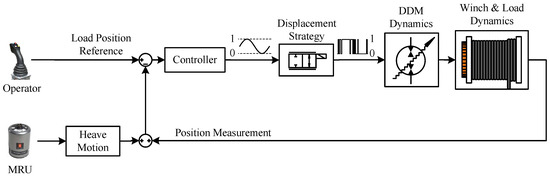
Figure 7.
Offshore digital hydraulic winch drive control scheme.
The offshore industry requires that winch drives must possess the capacity to compensate for heave motion to the extent that the load’s position deviates no more than mm from the reference point. This study does not consider heave compensation methods. Instead, the requirement for a position error margin below 100 mm during heave compensation is used as a point of reference for the purposes of the analysis to identify the optimal number of pistons. Thus, it is essential to ensure that position errors stemming from torque oscillations fall well below the aforementioned error margin. For this analysis, a maximum acceptable error of 10 mm is used as a benchmark for comparison purposes. Larger or lower values will thus influence the conclusions on how many pistons are required but not the general conclusions of the paper, as discussed at the end of the paper.
The parameters for the digital displacement motors and the digital winch drive are detailed in Table 1. As the objective of the paper is to identify the number of pistons required to achieve a position error below 10 mm, the piston displacement volume and the dead volume are provided as a total sum. These values represent the total displacement required to drive the drum, given the supply pressure, and are therefore distributed equally amongst the resulting number of pistons. The valve characteristics presented in Table 1 do not correspond to a specific valve. Rather, these parameters are used to ensure that the valve characteristics do not unduly influence the analysis by introducing significant pressure drops during high-flow conditions. The necessary valve characteristics for a specific number of pistons can be determined following a procedure akin to the one presented by [22].

Table 1.
Parameters for the digital displacement motors, digital valves, and winch drive.
3. DDM Model
Due to the uniform arrangement and identical nature of the cylinders, the operational attributes of the motor can be modeled based on Figure 8, and subsequently replicated for the remaining cylinders. This method of modeling the dynamics of DDMs is well established in the literature [13,17] and has been verified experimentally [20].
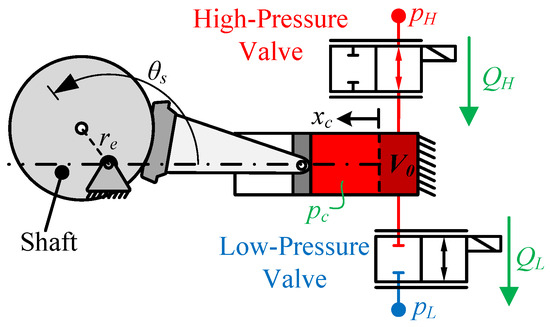
Figure 8.
Sketch of an individual piston from the digital displacement motor under consideration.
In this context, the pistons share a common shaft speed, denoted by , while the shaft angle introduces a relative phase shift for each piston, as expressed in Equation (1):
Here, and the subsequent parameters correspond to the parameters presented in Table 1. The piston’s displacement is a function of the shaft’s angle:
where is the eccentric radius of the shaft. The pressure dynamics of each chamber are given by the continuity Equation (3), which is dictated by the orifice equations for fluid flow via the high-pressure valve , low-pressure valve , and the displacement volume of the piston, as denoted in Equation (3):
and denote the normalized spool position of the high-pressure valve (HPV) and low-pressure valve, respectively (LPV). The cylinder’s volume , volumetric flow rate , and shaft torque are all geometric functions of the shaft’s angle, with the latter further influenced by the cylinder’s internal pressure.
The chamber’s displacement volume is given by:
where is the piston’s area. The total torque output of the winch drive is expressed as a sum of the individual piston torques:
The movement of the valves is modeled using a sigmoid function. Consequently, when a valve closes, it undergoes a constant negative acceleration during the first half of its switching time, and a constant positive acceleration for the second half, as illustrated in Equation (9). The signs in the piecewise function are inverted when the valve opens.
Here, denotes the normalized valve spool position, and denotes the spool acceleration.
4. Displacement Control Strategies
This section provides a brief overview of the three displacement control strategies under consideration, using Figure 9 for illustration. More detailed descriptions of these strategies are found in [13,26]. Figure 9 presents the simplified pressure and flow patterns of a single cylinder over a revolution, based on the valve actuation sequences produced by each displacement strategy. The states of the valves are displayed at the bottom of each figure, with the resultant flow and pressure depicted at the top.
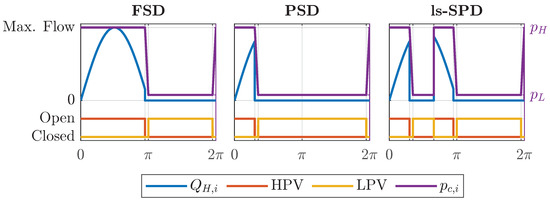
Figure 9.
Depiction of the contemplated displacement control strategies.
A full-stroke displacement strategy uses a specified number of cylinders in a single revolution to manage the displacement. The total displacement of the motor in one revolution corresponds to the number of active cylinders. For instance, if only one cylinder is activated, the motor’s displacement is equal to 14 % for . With this approach, the motor’s displacement manifests as discrete values, with intermediate displacement values achievable only across multiple rotations. An established method to generate signals for cylinder activation, aimed at attaining these intermediate displacement values, employs a first-order delta-sigma modulator. This method, depicted in Figure 10, was first put forth by [27].
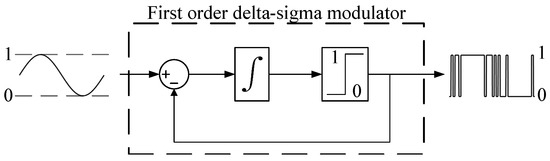
Figure 10.
Arrangement of a first-order delta-sigma modulator [20].
The modulator receives the desired displacement as input and generates a stream of ones and zeros. A bit with a value of one corresponds to an active cylinder and a zero to an idling cylinder. The term idling cylinder refers to a piston that remains connected to the low-pressure line over a full cycle. Given that the determination to activate a cylinder is resolved at a fixed angle, the sampling rate of the delta-sigma modulator demonstrates proportionality with both the number of pistons and the shaft speed .
In an active cylinder, the high-pressure valve opens when the shaft reaches , and the low-pressure valve opens at , corresponding to the points of minimum flow. To prevent valve openings against high pressure, the HPV and LPV close before the shaft reaches and 0, respectively, thereby allowing chamber pressurization or depressurization to balance the pressure across the HPV or LPV before opening. Idling cylinders keep the HPV closed and the LPV open throughout the entire stroke. As pressurization is not needed in an idling cycle, the decision to activate or idle a cylinder is made at a set angle before the angle at which the LPV closes.
A partial-stroke displacement strategy always activates all cylinders when a non-zero displacement is requested, but it varies the HPV closing angle () to regulate the displacement over a revolution. The HPV closing angle is given as a function of a normalized displacement input :
where is the motor’s displacement. This yields a continuous motor displacement relative to the HPV’s closing angle. At zero displacement, all HPVs stay closed, and LPVs open. Similar to FSD, the decision to close the LPV for chamber pressurization is made at a fixed angle before the LPV closing angle. Theoretically, a partial stroke can occur at any shaft position between 0 and . However, the described approach is predominantly favored as it minimizes volumetric losses due to the HPV opening at the lowest flow and chamber pressurization before HPV opening.
Sequential partial-stroke strategies involve multiple valve switches over a stroke to attain the desired displacement. This means any number of cylinders can be activated at any time to provide the required displacement. For a seven-cylinder motor, this equates to potential configurations of active and idle cylinders. However, past studies indicate this method results in frequent valve switching and substantial energy losses [16,20]. Consequently, a low-speed sequential partial-stroke displacement strategy, as proposed by Farsakoglou et al. [21], is considered. The strategy operates similarly to a partial-stroke strategy but permits the HPV to reopen when a larger displacement is needed. For instance, assuming the displacement reference is increased to 100 % at a shaft angle of , as shown in Figure 9, a partial-stroke strategy can only allow the HPV to open and flow into the chamber when the shaft reaches 0. However, the ls-SPD strategy allows the chamber to be pressurized in the same cycle by closing the LPV and opening the HPV after a small delay, thus allowing a nearly instantaneous displacement response.
Figure 11 depicts the torque output of a seven-piston DDM-driven winch when applying the previously mentioned control strategies with respect to the motor’s shaft angle. Solid lines represent the system’s torque response over the angular domain, while the dashed lines designate the displacement reference. The displacement reference signal initiates at in each figure. The drive’s transient response characteristics include response time and torque ripple amplitude which are indicated in the figure. The former is determined by the duration it takes for the drive to attain its peak displacement from a zero displacement, while the latter is quantified as the magnitude of torque oscillations around the reference value. As shown in Figure 11, for a given displacement, the torque profile remains fixed in the angular domain and, therefore, variable in the time domain as the motor’s speed changes.
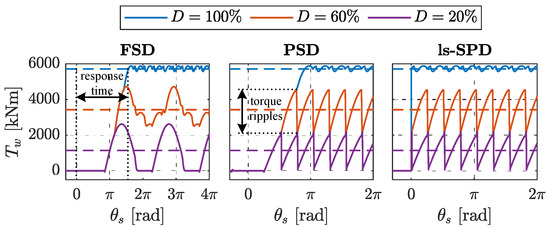
Figure 11.
Torque behavior of the examined displacement control strategies within the angular domain, featuring a seven-piston motor operating the winch [21].
The response time resulting from the application of various displacement control strategies for the considered digital winch drive has been studied by Farsakoglou et al. [21]. The authors identified specific operating speed ranges in which each of the three displacement strategies could be effectively employed. These ranges are illustrated in Figure 12, which encapsulates the findings. The appropriate operational range for each strategy was determined by comparing it to a benchmark response time of s, equivalent to the average response time of the traditional hydraulic motors utilized in the commercial drive. The figure depicts the resultant response time of the seven-piston DDM across the entire speed range for different strategies.
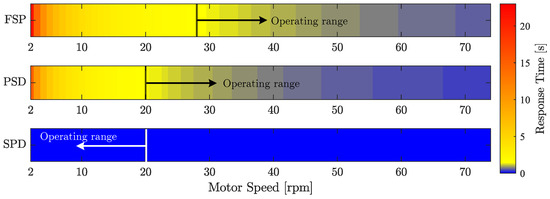
Figure 12.
Torque response time of the considered digital winch drive with each displacement control strategy in the whole operating speed range of the motors.
More specifically, the results showed that the ls-SPD strategy should be deployed in the operational speed range of 2 to 20 rpm. Beyond 20 rpm, the strategy necessitates stringent valve timing control requirements to avert cavitation. Contrary, both PSD and FSD strategies were found appropriate for usage at speeds exceeding 20 rpm and 28 rpm, respectively [21].
This paper continues to build upon the work of [21], specifically examining the influence of torque fluctuations on the positioning of the load. As the duration of these fluctuations is inversely proportional to the motor’s shaft speed while their amplitude remains fixed, the analysis focuses on the lowest operating speed for each strategy. Additionally, as observed in Figure 11, the torque responses of the PSD and ls-SPD strategies only differ in terms of their response times, while their steady-state responses are identical. Therefore, these strategies are jointly considered for the analysis of torque ripples. From Figure 11, it can be determined that with an FSD strategy, the torque ripples are significantly visible at low displacements where fewer cylinders are activated. For PSD and ls-SPD strategies, the most substantial torque fluctuations occur at 50% displacement.
5. Winch Drum Dynamics
To estimate the ensuing load oscillations based on the DDM’s torque output, it is necessary to consider the dynamics of the winch drum and the wire. Similar methods for modeling winch drum dynamics are available in the literature [28]. A simplified illustration of the winch and an attached load with a mass is seen in Figure 13a. The wire is wrapped around the winch drum in layers. Therefore, depending on the amount of wire that is released, the drum’s effective radius and inertia vary. The winch drum parameters that are used in this section are found in Table 2.
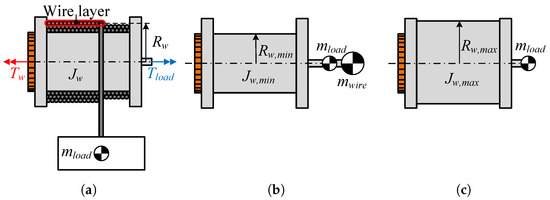
Figure 13.
(a) Illustration of the considered winch drum system. (b) Equivalent winch drum model with the wire fully paid out. (c) Equivalent winch drum model with the wire fully reeled in.

Table 2.
Winch drum parameters.
In this analysis, the wire is assumed to be rigid regardless of the amount of wire that is reeled out. Typically, wire dynamics can be modeled as a spring and damper system with parameters that vary depending on the length of wire that is paid out [24]. By assuming the wire to be rigid, the drum’s equivalent inertia, illustrated conceptually in Figure 13b,c, can be calculated for a given load as:
where denotes the mass of wire that is wrapped around the winch drum and the wire that has been released, so that the total wire mass is given as:
The effective drum inertia and radius as a function of the load’s position for a 20 ton load is depicted in Figure 14. The figure reveals that the winch manifests its greatest inertia when the wire is fully wound around the drum, corresponding to an expanded drum radius. As the wire unwinds and the load is lowered, the drum inertia decreases, with particularly rapid reductions occurring as the effective drum radius diminishes. It should be noted that in the real application, the radius transition is smoother. Thereby, the inertia is not reduced in a step-wise fashion but instead transitions with a small slope. However, this simplification does not affect the calculation of the maximum and minimum values of the drum’s inertia.
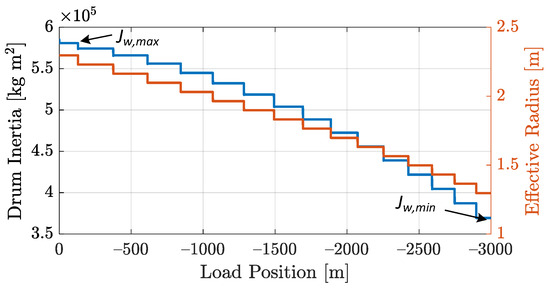
Figure 14.
Variation of equivalent drum inertia with respect to the load position for a load of 20 tons.
The load acceleration can be calculated directly from the winch drum’s acceleration , which obeys Newton’s second law:
where g is the gravitational acceleration, is the load’s gravity-induced torque, and is the torsional friction. To identify the highest position errors that can occur, the analysis is conducted with the motors operating at the lowest possible speed. This is depending on the utilized strategy, as indicated in Figure 12. From Equation (15), it is implied that in a steady state:
where is known and corresponds to the load’s gravitational torque on the drum. The precise value of is unknown; however, based on the friction model of the conventional model, which was presented by Moslått et al. [29], it can be estimated to be approximately:
at 2 rpm. When considering an FSD strategy, which exhibits the largest torque ripples at the lowest displacement, the motor displacement is chosen so that the average motor torque leads to a steady state as shown in Equation (16). However, for PSD and ls-SPD strategies, the largest torque ripples occur at 50% displacement as noted in Section 4. This value results in half the maximum torque output the drive can exhibit, which would accelerate the load. However, for the analysis, the simplification is made that the load is moving with constant velocity to simplify the analysis. This is a conservative assumption, thus overestimating the maximum position error when utilizing partial-stroke strategies. The load position error for one torque ripple period can be calculated as:
where is the torque’s period based on the utilized strategy. Equations (18) and (20) are illustrated graphically in Figure 15.
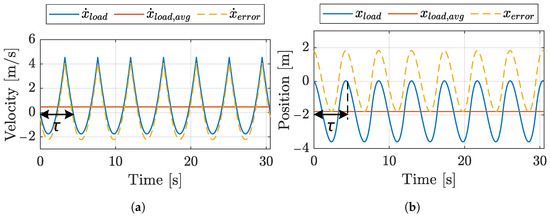
Figure 15.
(a) Calculation of load speed oscillations. (b) Calculation of load position oscillations.
As indicated by Equations (18) and (20), the most significant position oscillations are expected to occur when the winch drum possesses the minimum inertia. Consequently, the analysis is conducted using the smallest load that the crane is expected to handle, corresponding to 20 t, as discussed in Section 2. Notably, when the drum inertia is at its absolute minimum, corresponding to the smallest effective drum radius, the drum operates at roughly twice the speed compared to its operation at the maximum effective radius. This phenomenon occurs because the load’s minimum speed is always 2 m/min as noted in Table 2, while the drum’s effective radius varies. Therefore, at the initial stage of this analysis, it is required to determine which parameter, drum inertia or motor’s speed, has a more profound impact on the oscillations of the load’s position.
6. Torque Oscillations
The torque output of a DDM is inherently dependent on the shaft angle, which results in a consistent and predictable pattern within the angular domain. It is noted that torque ripples persist for a longer duration at the lowest load speed. Nevertheless, the minimum operating speed is contingent upon the displacement control strategy being employed, as shown in Figure 12.
6.1. Seven-Piston DDM Drive
Initially, the methodology described in Section 5 is utilized to calculate the position errors of the load that result from torque ripples, employing the seven-piston DDM model proposed by [21]. The purpose is to provide the reader with an initial understanding of how the different displacement control strategies affect torque oscillations. Furthermore, this subsection provides useful insights into how the different operating points affect the load’s position oscillations.
For an FSD strategy, pronounced torque fluctuations are predominantly observed at minimal displacements. The smallest displacement transpires when the motors generate an average torque that neutralizes the gravitational torque of the load. This situation corresponds to a displacement, , of 10% for the maximum drum radius , and 6% for the minimum radius . The percentage of the maximum displacement that is required to achieve a steady state can be calculated as follows:
The torque profile for a single period, , in the angular domain for the aforementioned cases is depicted in Figure 16a. The orange solid line signifies the torque output when the drum operates at its minimum radius, while the solid blue line represents the torque output at the maximum drum radius. The dashed lines depict the mean torque produced at these two operational points. Torque ripples, , are defined as the peak-to-peak amplitude. In this situation, the period of the torque exceeds a full revolution, or , due to the signals produced by the first-order delta-sigma modulator as explained in Section 4.
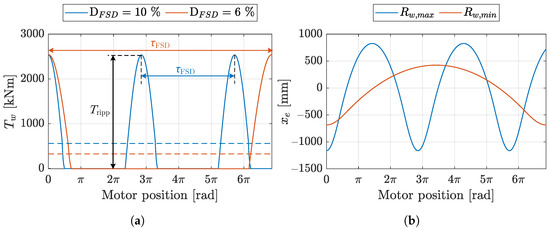
Figure 16.
FSD strategy. (a) Winch’s torque output for the maximum and minimum effective drum radii and . (b) Resulting load position error for the maximum and minimum effective drum radii.
The resulting position error for the load, , is displayed in Figure 16b. It is noted that the position errors reach an excessive height, surpassing 1100 mm, when the winch drum operates at its maximum radius. However, at the minimum winch drum radius, the maximum error decreases to 700 mm, a value that nonetheless hinders precise position control. The reduction in position error with the winch operating at its minimum radius can be attributed to the elevated motor speed, approximating 48 rpm. This speed considerably surpasses the 28 rpm observed when the drum radius is at its maximum, thereby diminishing the duration of the torque ripples and subsequently reducing the resultant position errors. From these observations, it can be deduced that the most substantial position errors occur when the winch operates at its maximum radius. Given this conclusion, the maximum radius and inertia are utilized to estimate the resulting position errors throughout the remaining sections of the paper.
For the PSD and ls-SPD strategies, the largest ripples are identified when the motor displacement is at 50 %. A partial-stroke strategy always activates all pistons for a non-zero displacement. Therefore, the torque profile is always fixed for a full motor revolution. The resulting torque over a revolution is seen in Figure 17a while the resulting position error is calculated with Equation (20) and depicted in Figure 17b for an angular motor speed of 2 rpm. It is seen that the position error oscillates with an amplitude of approximately 2000 mm, which is orders of magnitude higher than the required position of 10 mm.
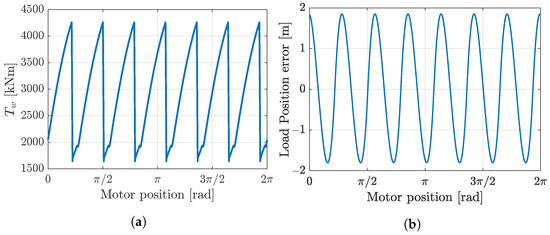
Figure 17.
PSD and ls-SPD strategies. (a) Winch’s torque output with a 50 % displacement and . (b) Load’s position error at 2 rpm for the maximum effective drum radius.
6.2. Analysis of the Number of Pistons
From Section 6.1, it is concluded that seven pistons are not sufficient for accurate control of the load. Therefore, it is required to identify the necessary number of pistons in order to reduce the effect of the torque ripples on the accurate positioning of the load. For that purpose, the methodology for producing Figure 16 and Figure 17 is repeated while the number of pistons is increased. The results are shown in Figure 18.
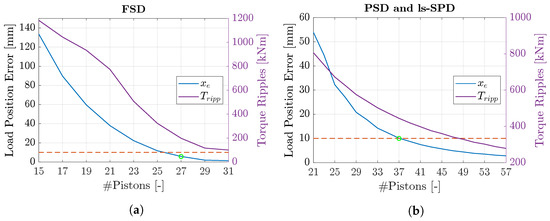
Figure 18.
Maximum load position error and torque ripples as a function of the number of cylinders. (a) FSD strategy operating at 28 rpm and with a 10 % displacement. (b) PSD and ls-SPD strategies operating at 2 rpm and with a 50 % displacement.
Figure 18a shows the resulting load position error and torque ripple peak-to-peak amplitude while controlling the displacement with FSD. It is seen that the position error drops below the desired value of 10 mm when utilizing pistons. With a partial-stroke strategy, Figure 18b, the number of required pistons is further increased to . The resulting torque and load position error with the chosen number of pistons, marked with green circles in Figure 18, are illustrated in Figure 19.
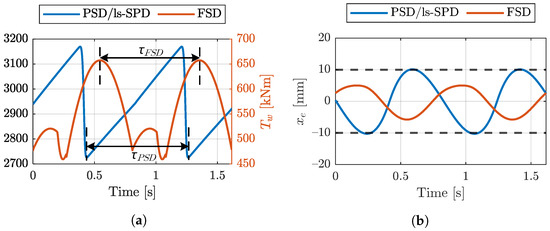
Figure 19.
(a) Torque ripples for PSD/ls-SPD with 37 pistons and FSD with 27 cylinders. (b) Resulting load position error from (a).
As PSD and ls-SPD strategies are required when operating at low speeds to achieve a fast motor response, ultimately, the number of required pistons will be determined based on the requirements of the partial-stroke strategies. It should be noted that if a larger maximum position error was allowed, then the number of pistons would increase, as observed in Figure 18. However, the total number of pistons would still remain high.
PSD and ls-SPD strategies impose strict requirements for valve specifications. A partial-stroke strategy requires valves with a higher flow rate and lower switching time compared to an FSD strategy [22]. In addition, the ls-SPD strategy further requires the valves to be capable of opening against large pressure drops. When considering the estimated number of pistons and that each piston requires two valves for its operation, the total number of valves reaches 74. Such valves are considerably costlier compared to those required for an FSD strategy. Based on the above, other methods may, therefore, be considered to reduce the number of pistons that utilize partial strokes. One such approach could be an active/passive topology similar to that of the commercial drive, which could reduce the displacement that is controlled with PSD and ls-SPD strategies. Such a method would result in reduced torque peaks, allowing for fewer pistons to be controlled with partial strokes, and subsequently, reducing the need for expensive valves. However, this consideration is not further explored in this work and is left for future research.
7. Conclusions
This study offers an analysis of the required number of pistons for a DDM in a winch drive application, with the aim of minimizing torque ripples and subsequent load oscillations in the steady state. The analysis was conducted via simulations that utilized information from a commercial winch drive system to determine the mechanical parameters of the winch drum. It was shown that the torque ripple effect on the load oscillations is most prominent when the winch operates with its maximum effective radius. Additionally, the torque ripple effect is highly dependent on the utilized displacement control strategy and operating speed. For an FSD strategy that is used for a speed above 28 rpm, the DDM required 27 pistons, while for PSD and ls-SPD strategies that were used at lower speeds, the DDM required 37 pistons. As the drive utilizes different displacement control strategies at different operating speeds, the number of required pistons was determined by the highest number, which corresponded to 37 pistons. It was noted that PSD and ls-SPD strategies require large and expensive valves to yield high volumetric efficiency. To reduce the need for utilizing these expensive valves, an active/passive topology could be considered, which separates the drive into two subsystems. Such a topology could limit the number of pistons that are operated with partial-stroke strategies and reduce valve-related costs. However, this concept was beyond the purview of the current study and is proposed to be explored in future work.
Author Contributions
Conceptualization, T.F., H.C.P., M.K.E. and T.O.A.; methodology, T.F.; investigation, T.F.; resources, T.F.; writing—original draft preparation, T.F.; writing—review and editing, T.F., H.C.P., M.K.E. and T.O.A.; visualization, T.F.; supervision, H.C.P., M.K.E. and T.O.A.; funding acquisition, T.O.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Research Council of Norway, SFI Offshore Mechatronics, project number 237896/O30.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DDM | digital displacement motor |
| FSD | full-stroke displacement |
| HPV | high-pressure valve |
| LPV | low-pressure valve |
| ls-SPD | low-speed sequential partial-stroke displacement |
| PSD | partial-stroke displacement |
| SPD | sequential partial-stroke displacement |
| s-SPD | simplified sequential partial-stroke displacement |
| VTC | valve timing control |
References
- Payne, G.S.; Kiprakis, A.E.; Ehsan, M.; Rampen, W.H.S.; Chick, J.P.; Wallace, A.R. Efficiency and Dynamic Performance of Digital Displacement™ Hydraulic Transmission in Tidal Current Energy Converters. Proc. Inst. Mech. Eng. Part J. Power Energy 2007, 221, 207–218. [Google Scholar] [CrossRef]
- Rydberg, K.E. Energy Efficient Hydraulic Hybrid Drives. In Proceedings of the 11: The Scandinavian International Conference on Fluid Power, SICFP’09, Linkoping, Sweden, 2–4 June 2009. [Google Scholar]
- Song, X. Modeling an Active Vehicle Suspension System with Application of Digital Displacement Pump Motor. In Proceedings of the ASME 2008 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, American Society of Mechanical Engineers Digital Collection, Washington, DC, USA, 2–4 July 2009; pp. 749–753. [Google Scholar] [CrossRef]
- Karvonen, M.; Heikkila, M.; Huova, M.; Linjama, M.; Huhtala, K. Simulation Study—Improving Efficiency in Mobile Boom by Using Digital Hydraulic Power Management System. In Proceedings of the Twelfth Scandinavian International Conference on Fluid Power, SICFP’11, Tampere, Finland, 18–20 May 2011; Volume 12, pp. 355–368. [Google Scholar]
- Heikkila, M.; Linjama, M. Displacement Control of a Mobile Crane Using a Digital Hydraulic Power Management System. Mechatronics 2013, 23, 452–461. [Google Scholar] [CrossRef]
- Chapple, P.; Lindholdt, P.N.; Larsen, H.B. An Approach to Digital Distributor Valves in Low Speed Pumps and Motors. In Proceedings of the ASME/BATH 2014 Symposium on Fluid Power and Motion Control, Bath, UK, 2–4 September 2014; p. V001T01A041. [Google Scholar] [CrossRef]
- Heikkila, M.; Linjama, M.; Huhtala, K. Digital Hydraulic Power Management System with Five Independent Outlets—Simulation Study of Displacement Controlled Excavator Crane. In Proceedings of the 9th International Fluid Power Conference, Aachen, Germany, 24–26 March 2014; pp. 455–465. [Google Scholar]
- Ehsan, M.; Rampen, W.H.S.; Salter, S.H. Modeling of Digital-Displacement Pump-Motors and Their Application as Hydraulic Drives for Nonuniform Loads. J. Dyn. Syst. Meas. Control 1997, 122, 210–215. [Google Scholar] [CrossRef]
- Payne, G.; Stein, U.; Ehsan, M.; Caldwell, N.; Rampen, W. Potential of Digital Displacement Hydraulics for Wave Energy Conversion. In Proceedings of the 6th European Wave and Tidal Energy Conference, 6th EWTEC: University of Strathclyde, Glasgow, UK, 29 August–2 September 2005. [Google Scholar]
- Rampen, W. Gearless Transmissions for Large Wind Turbines: The History and Future of Hydraulic Drives. In Proceedings of the DEWEK 2006, the International Technical Conference: 8th German Wind Energy Conference, Bremen, Germany, 22–23 November 2006. [Google Scholar]
- Heikkila, M.; Tammisto, J.; Huova, M.; Huhtala, K.; Linjama, M. Experimental Evaluation of a Piston-Type Digital Pump-Motor-Transformer with Two Independent Outlets. In Proceedings of the Fluid Power and Motion Control 2010, Bath, UK, 15–17 September 2010. [Google Scholar]
- Rampen, W. The Development of Digital Displacement Technology. In Proceedings of the Bath/ASME FPMC Symposium, Bath, UK, 15–17 September 2010; pp. 11–16. [Google Scholar]
- Merrill, K.J. Modeling and Analysis of Active Valve Control of a Digital Pump-Motor. Ph.D. Thesis, Purdue University, West Lafayette, IN, USA, 2012. [Google Scholar]
- Nørgård, C. Design, Optimization and Testing of Valves for Digital Displacement Machines. Ph.D. Thesis, Department of Energy Technology, Aalborg University, Aalborg, Denmark, 2017. [Google Scholar] [CrossRef]
- Williamson, C.; Manring, N. A More Accurate Definition of Mechanical and Volumetric Efficiencies for Digital Displacement® Pumps. In Proceedings of the ASME/BATH 2019 Symposium on Fluid Power and Motion Control, American Society of Mechanical Engineers Digital Collection, Washington, DC, USA, 12–14 December 2019. [Google Scholar] [CrossRef]
- Pedersen, N.H.; Johansen, P.; Andersen, T. Challenges with Respect to Control of Digital Displacement Hydraulic Units. Model. Identif. Control Nor. Res. Bull. 2018, 39, 91–105. [Google Scholar] [CrossRef]
- Holland, M.A. Design of Digital Pump/Motors and Experimental Validation of Operating Strategies. Ph.D. Thesis, Purdue University, West Lafayette, IN, USA, 2012. [Google Scholar]
- Dumnov, D.; Caldwell, N. A Cylinder Enabling Algorithm for Reduction in Low Frequency Pulsation From Digital Displacement Pumps. In Proceedings of the BATH/ASME 2022 Symposium on Fluid Power and Motion Control, Bath, UK, 7–15 September 2022; p. V001T01A010. [Google Scholar] [CrossRef]
- Larsen, H.B.; Kjelland, M.; Holland, A.; Lindholdt, P.N. Digital Hydraulic Winch Drives. In Proceedings of the BATH/ASME 2018 Symposium on Fluid Power and Motion Control, American Society of Mechanical Engineers Digital Collection, Washington, DC, USA, 13–17 November 2018. [Google Scholar] [CrossRef]
- Nordås, S.; Beck, M.M.; Ebbesen, M.K.; Andersen, T.O. Dynamic Response of a Digital Displacement Motor Operating with Various Displacement Strategies. Energies 2019, 12, 1737. [Google Scholar] [CrossRef]
- Farsakoglou, T.; Pedersen, H.C.; Ebbesen, M.K.; Andersen, T.O. Improving Energy Efficiency and Response Time of an Offshore Winch Drive with Digital Displacement Motors. MIC J. 2023, 2023, 1. [Google Scholar] [CrossRef]
- Farsakoglou, T.; Bhola, M.; Ebbesen, M.K.; Andersen, T.O.; Pedersen, H.C. Valve Specification Requirements for Digital Hydraulic Winch Drives. In Proceedings of the Digital Fluid Power Workshop DFP22, Edinburgh, UK, 7–15 September 2022; pp. 74–89. [Google Scholar]
- NOV. NOV Website. 2022. Available online: https://www.nov.com/ (accessed on 25 July 2022).
- DNV. DNV-RP-H103: Modelling and Analysis of Marine Operations. 2011. Available online: https://rules.dnv.com/docs/pdf/DNVPM/codes/docs/2012-12/RP-H103.pdf (accessed on 26 March 2021).
- Moslått, G.A.; Rygaard Hansen, M.; Padovani, D. Performance Improvement of a Hydraulic Active/Passive Heave Compensation Winch Using Semi Secondary Motor Control: Experimental and Numerical Verification. Energies 2020, 13, 2671. [Google Scholar] [CrossRef]
- Pedersen, N.H. Development of Control Strategies for Digital Displacement Units. Ph.D. Thesis, Department of Energy Technology, Aalborg University, Aalborg, Denmark, 2018. [Google Scholar]
- Johansen, P.; Roemer, D.B.; Andersen, T.O.; Pedersen, H.C. Delta-Sigma Modulated Displacement of a Digital Fluid Power Pump. In Proceedings of the 7th Workshop on Digital Fluid Power, Aalborg, Denmark, 7–8 February 2015; pp. 1–9. [Google Scholar]
- Huibert, K.; Raphael, S. Linear Optimal Control Systems; Wiley: New York, NY, USA, 1972; Volume 1. [Google Scholar]
- Moslått, G.A.; Hansen, M.R.; Karlsen, N.S. A Model for Torque Losses in Variable Displacement Axial Piston Motors. Model. Identif. Control 2018, 39, 107–114. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).