Sizing PV and BESS for Grid-Connected Microgrid Resilience: A Data-Driven Hybrid Optimization Approach

Abstract

This article presents a comprehensive data-driven approach on enhancing grid-connected microgrid grid resilience through advanced forecasting and optimization techniques in the context of power outages. Power outages pose significant challenges to modern societies, affecting various sectors such as industries, households, and critical infrastructures. The research combines statistical analysis, machine-learning algorithms, and optimization methods to address this issue to develop a holistic approach for predicting and mitigating power outage events. The proposed methodology involves the use of Monte Carlo simulations in MATLAB for future outage prediction, training a Long Short-Term Memory (LSTM) network for forecasting solar irradiance and load profiles with a dataset spanning from 2009 to 2018, and a hybrid LSTM-Particle Swarm Optimization (PSO) model to improve accuracy. Furthermore, the role of battery state of charge (SoC) in enhancing system resilience is explored. The study also assesses the techno-economic advantages of a grid-tied microgrid integrated with solar panels and batteries over conventional grid systems. The proposed methodology and optimization process demonstrate their versatility and applicability to a wide range of microgrid design scenarios comprising solar PV and battery energy storage systems (BESS), making them a valuable resource for enhancing grid resilience and economic efficiency across diverse settings. The results highlight the potential of the proposed approach in strengthening grid resilience by improving autonomy, reducing downtime by 25%, and fostering sustainable energy utilization by 82%.

1. Introduction

In today’s modern world, the continuous and reliable supply of electricity is of paramount importance, underscoring the critical significance of bolstering the resilience of electrical grid-connected microgrids to ensure the smooth functioning of societies, industries, and vital infrastructure [1,2]. The uninterrupted provision of electricity is indispensable for the effective operation of key institutions such as hospitals, communication networks, transportation systems, and numerous other sectors that constitute the backbone of our daily life [3]. However, the susceptibility of electrical grids to a wide array of disruptions, ranging from extreme weather events and cyberattacks to equipment failures, underscores the pressing need to develop strategies that enhance the resilience of microgrids tied to the main grid and mitigate the consequences of power interruptions [4,5,6]. Figure 1 illustrates common reasons for power outages in the United States.

Grid-connected microgrid resilience, a pivotal component of modern power systems, refers to the capacity of an electrical grid to endure and swiftly recover from disruptions, thereby ensuring a consistent and uninterrupted supply of electricity to consumers [7]. The primary impediment to microgrid resilience often arises from power outages, characterized by the abrupt interruption of electricity delivery to specific regions [8,9]. These outages encompass a broad spectrum in terms of duration and severity, spanning from momentary flickers to prolonged blackouts that impact entire areas [10,11]. The causes of power outages are diverse, encompassing natural disasters, equipment malfunctions, overloads, and deliberate attacks on infrastructure [12]. Consequently, a comprehensive comprehension of the underlying patterns and attributes of power outages is imperative for devising effective strategies to enhance grid resilience [13].

A thorough examination of the existing body of literature underscores the multifaceted challenges associated with grid-connected microgrid resilience and power outage prediction [14,15]. Research has established that accurate outage prediction models constitute essential tools for proactive microgrid management [2,16,17,18]. The integration of advanced machine-learning techniques, such as Long Short-Term Memory (LSTM) networks, has emerged as a promising approach for capturing temporal dependencies and augmenting the precision of forecasting models [19]. Furthermore, the incorporation of optimization methodologies like PSO has demonstrated significant potential in refining predictive models [2]. The choice of the PSO algorithm in this research is grounded in its efficient global search capabilities in complex, multidimensional solution spaces, rendering it particularly suitable for optimizing the sizing of photovoltaic (PV) systems and BESS within microgrids [2,9]. PSO’s rapid convergence towards near-optimal solutions, ease of implementation, versatility across various optimization problems, and scalability through parallel processing make it a practical choice for addressing microgrid design challenges [9]. While alternative optimization algorithms exist, the decision to employ PSO was driven by its effectiveness in achieving the research objectives related to microgrid resilience and economic efficiency [2].

To develop a comprehensive understanding of power outage occurrences and characteristics in the United States, a rigorous statistical analysis was conducted. The examination of historical outage data facilitated the identification of trends, frequency distributions, and correlations between outage events and influential factors. These insights provide valuable information for designing predictive models that anticipate and prepare for impending outage events [20,21]. Monte Carlo simulations, executed within the MATLAB environment, were employed to visualize future power outage events based on historical data and trends. This probabilistic approach takes into account the inherent uncertainties surrounding outage occurrences and generates a spectrum of potential scenarios. By considering diverse parameters and scenarios, the Monte Carlo method enhances the accuracy of outage predictions and contributes to the development of robust mitigation strategies [10]. The potential of Long Short-Term Memory (LSTM) networks, a subset of recurrent neural networks, was harnessed for the prediction of solar irradiance and load profiles within microgrids. Accurate solar irradiance prediction is critical for optimizing the utilization of renewable energy sources, while load forecasting facilitates the efficient allocation of energy resources [2,3,22]. The LSTM model’s innate ability to capture temporal dependencies within data significantly improves upon traditional methods, leading to heightened forecasting accuracy [23,24].

Recognizing the imperative to further enhance prediction accuracy, the hybrid LSTM-PSO model emerges as an innovative solution [3]. This hybridization leverages the strengths of both LSTM and PSO [25]. The PSO algorithm, typically utilized for optimization tasks, is adapted to fine-tune the parameters of the LSTM network, thereby enhancing the model’s performance [26,27,28]. The synergistic interplay between LSTM and PSO yields forecasts that are more precise, dependable, and adaptable [29]. On a different note, the state of charge (SoC) of batteries constitutes a pivotal factor in augmenting the resilience of microgrids during power outages [30]. Batteries, capable of storing surplus energy generated by solar panels and discharging it when needed, serve as a reliable source of backup power during disruptions [31]. The effective management of battery SoC ensures an uninterrupted power supply and minimizes downtime during outages [32]. A comparative evaluation between grid-tied microgrids featuring solar panels and battery storage and traditional grid systems highlights the techno-economic advantages of the former [33]. This assessment considers various factors, including reduced energy costs, decreased emissions, and increased energy self-sufficiency [34,35,36]. The results underscore the potential of microgrids as sustainable, cost-effective alternatives that enhance grid resilience and promote energy efficiency. The schematic of a grid-connected microgrid is shown in Figure 2.

The primary goal of this research is to present a comprehensive approach to improve microgrid resilience, integrating advanced prediction and optimization techniques. It encompasses statistical analysis, machine-learning methods, and hybrid models to address power outage impacts, alongside the incorporation of renewable energy sources and battery storage within microgrids for sustainability and economic benefits. The subsequent sections detail our data-driven approach, beginning with a decade-spanning dataset in the methodology section, followed by insights into solar irradiance and load profile forecasting in the optimization constraints section. Section 4 outlines the outage prediction process, while Section 5 introduces a cutting-edge optimization methodology, the modified PSO-LSTM algorithm, for sizing battery and solar PV systems. The final section comprehensively evaluates economic and environmental benefits, comparing our system with industry tools like HomerPro and ReOpt, culminating in a synthesis of findings showcasing the advantages of data-driven approaches in advancing grid-connected microgrid resilience and sustainable energy excellence [37,38,39].

2. Objective Function

The objective function in the context of this study serves as a critical mathematical construct, central to the optimization process for determining the ideal sizing of solar panels within a grid-connected microgrid. This function encapsulates the primary aim of the research, which is to maximize the energy production and overall efficiency of the microgrid while ensuring its resilience in the face of power outages.

The objective function strives to maximize the energy output of the microgrid. It achieves this by carefully considering various parameters, such as the size and placement of solar panels, which directly impact the amount of energy generated from renewable sources. This optimization objective aligns with the broader goal of promoting sustainable and eco-friendly energy solutions within the microgrid. $E$ is maximized by optimizing the solar panel capacity $P_s$ while considering the load profiles, solar irradiance data, and the system’s energy efficiency.

$$E_{max}={\int }_0^T[P_s\times {PV}_i\left(t\right)-L_p(t\left)\right]dt$$

(1)

where $E_{max}$ represents maximum energy, $P_s$ represents PV panel capacity in kW, ${PV}_i\left(t\right)$ represents solar irradiance over time, and $L_p\left(t\right)$ represents the load profile over time.

The objective function also seeks to enhance the resilience of the microgrid. This involves optimizing the sizing of solar panels in a way that ensures a continuous power supply, even during grid outages. By taking into account factors like battery SoC and energy storage, the objective function contributes to grid resilience, reducing the impact of power disruptions on critical infrastructure and ensuring an uninterrupted energy supply. The objective function achieves these goals by mathematically quantifying the trade-offs and interdependencies between various parameters, such as the capacity of solar panels, battery storage, and load profiles. Through iterative optimization, it strives to find the optimal configuration that strikes the right balance between maximizing energy production and enhancing grid resilience.

$$\sum {\xi }_{max}=\frac{\sum _0^T{L}_{cs}}{\sum _0^T{L}_{ds}}$$

(2)

where ${\xi }_{max}$ represents the grid resilience score, a dimensionless metric reflecting the microgrid’s ability to maintain a continuous power supply during outages, $L_{cs}$ and $L_{ds}$ represent the total critical load server and that demanded over time.

The overall objective function combines these two objectives into a multi-objective optimization problem,

$$\gamma ·E_{max}+\delta ·{\xi }_{max}$$

(3)

where $\gamma$ and $\delta$ are weight factors that represent the relative importance of energy production $E_{max}$ and grid resilience ${\xi }_{max}$ in the optimization process.

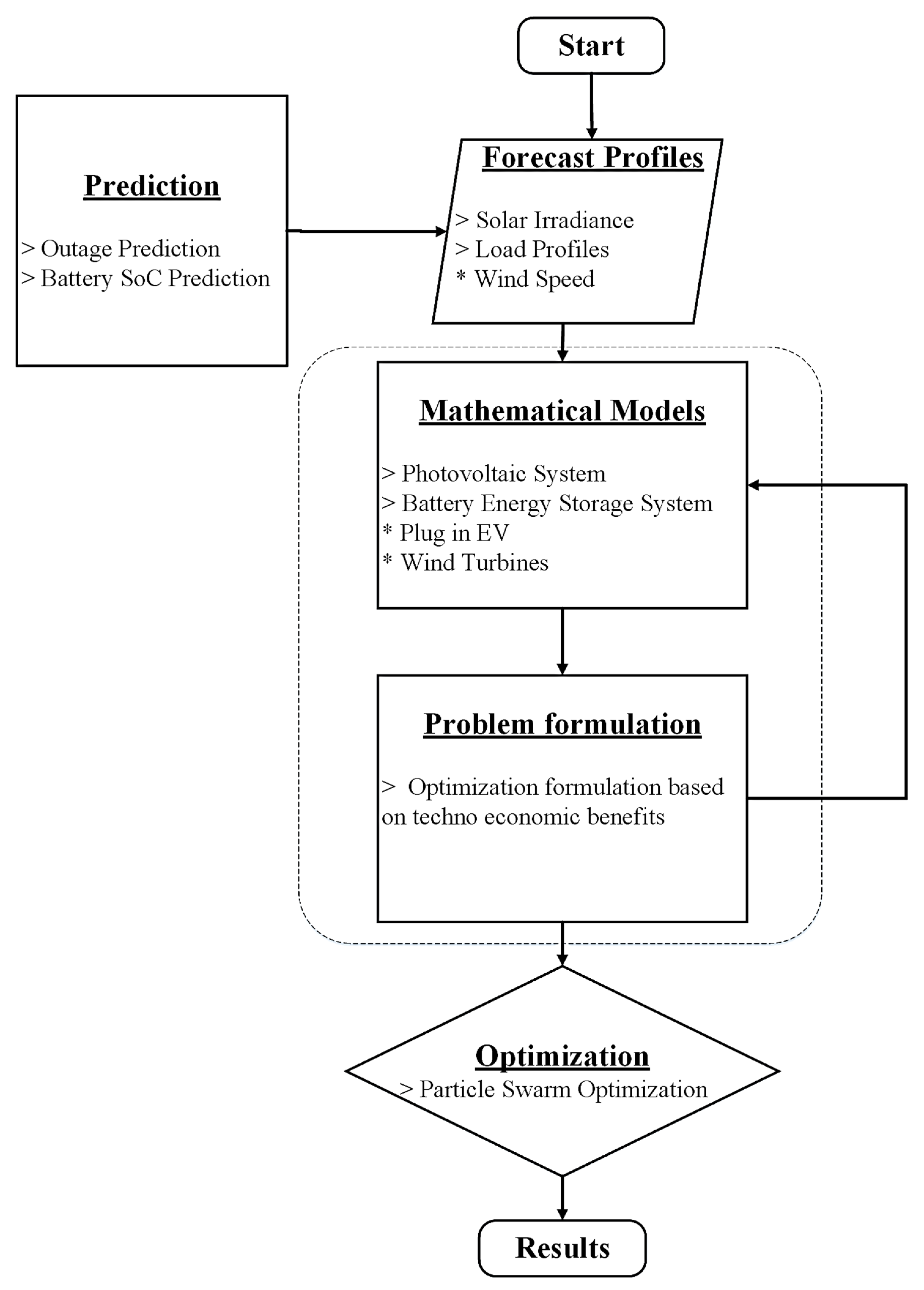
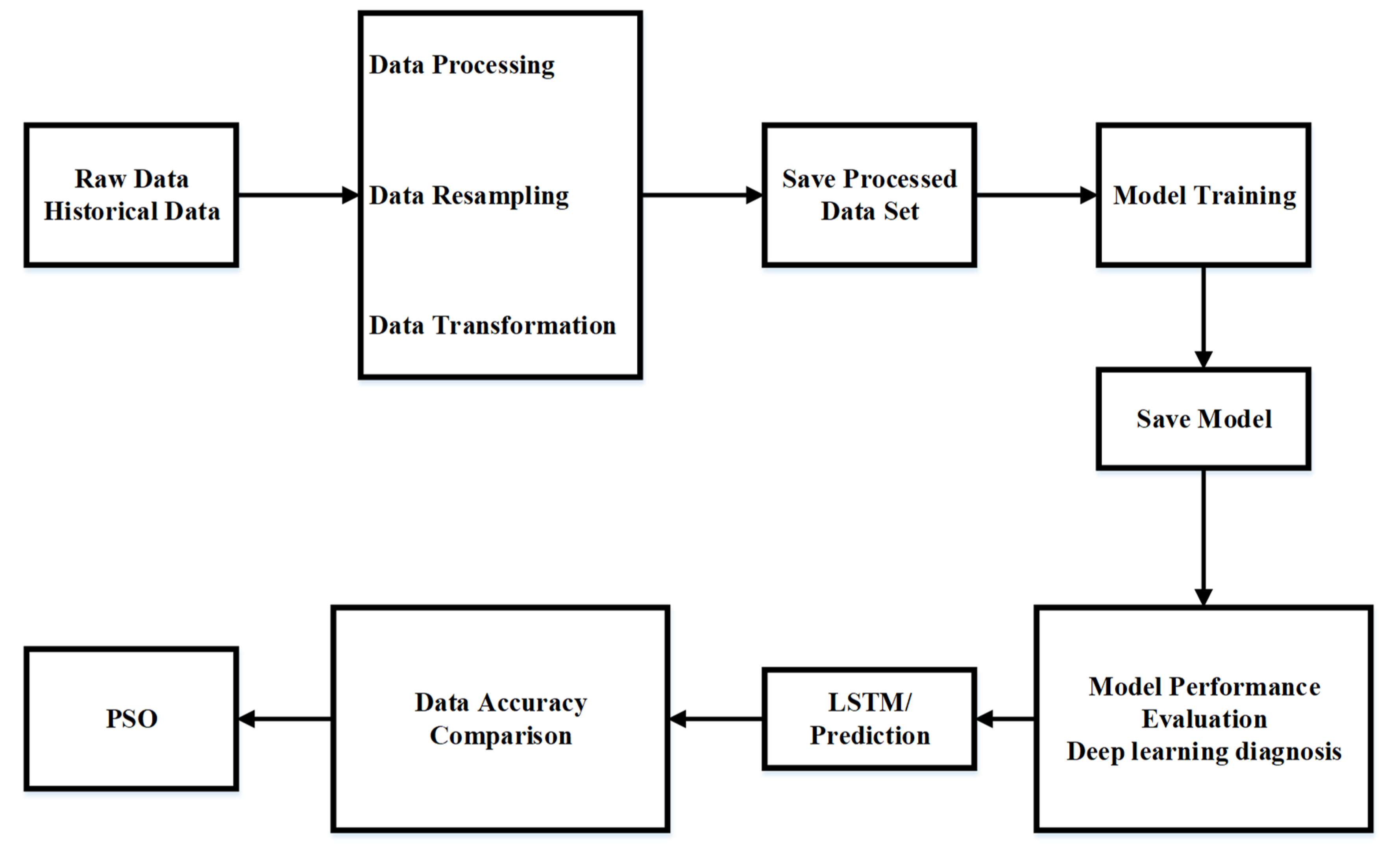
3. Methodology

The research methodology employs a systematic approach to enhance grid-tied microgrid resilience and optimize microgrid operations. The methodology encompasses several interconnected steps, leveraging predictive techniques, mathematical models, optimization algorithms, and results analysis. The proposed hybrid algorithm is shown in Figure 3.

The flowchart shows a six-step process for optimizing the resilience and economics of a microgrid. The first step is to predict outage events and battery state of charge using Monte Carlo simulation. The second step is to forecast energy profiles using hybrid-modified PSO-LSTM models. The third step is to formulate mathematical models for the various components of the microgrid. The fourth step is to formulate an optimization problem that maximizes microgrid resilience and economic benefits, subject to constraints such as energy generation, storage capacity, and load demand. The fifth step is to solve the optimization problem using particle swarm optimization. The sixth step is to analyze and interpret the results to identify the most resilient and economic microgrid configuration.

The flowchart is a comprehensive and systematic approach to optimizing the resilience and economics of a microgrid. It takes into account the uncertainty of future outage events and battery state of charge, and it uses state-of-the-art forecasting techniques to predict energy profiles. The optimization problem is formulated to maximize microgrid resilience and economic benefits, and it is solved using a powerful optimization algorithm. The flowchart is a valuable tool for microgrid operators looking to improve their systems’ resilience and economics.

By following this comprehensive methodology, the article’s approach ensures an integrated and optimized microgrid operation, considering both resilience and economic viability. The system overview is shown in Figure 4.

The combination of predictive techniques, mathematical models, optimization algorithms, and results analysis enables the microgrid to navigate uncertainties and challenges effectively while ensuring a reliable energy supply and efficient resource utilization.

4. Constraining Function for Optimization

The constraining functions used in the optimization problem play a vital role in ensuring that the solutions obtained are feasible and aligned with the objectives of the microgrid. These functions impose restrictions on various parameters and variables to ensure that the resulting configuration is practical and meets specific criteria. In the context of the article’s methodology, the constraining functions can be described as follows:

4.1. Energy Balance Constraint

This constraint ensures that the energy supplied by various sources within the microgrid matches the energy demand during an outage. It ensures that the energy generation (solar, wind, etc.), energy storage, and energy consumption (load demand) are balanced:

E_Gen + E_Storage = L_Demand

(4)

where, E_Gen, E_Storage, and L_Demand represents energy generation, energy storage, and load demand, respectively.

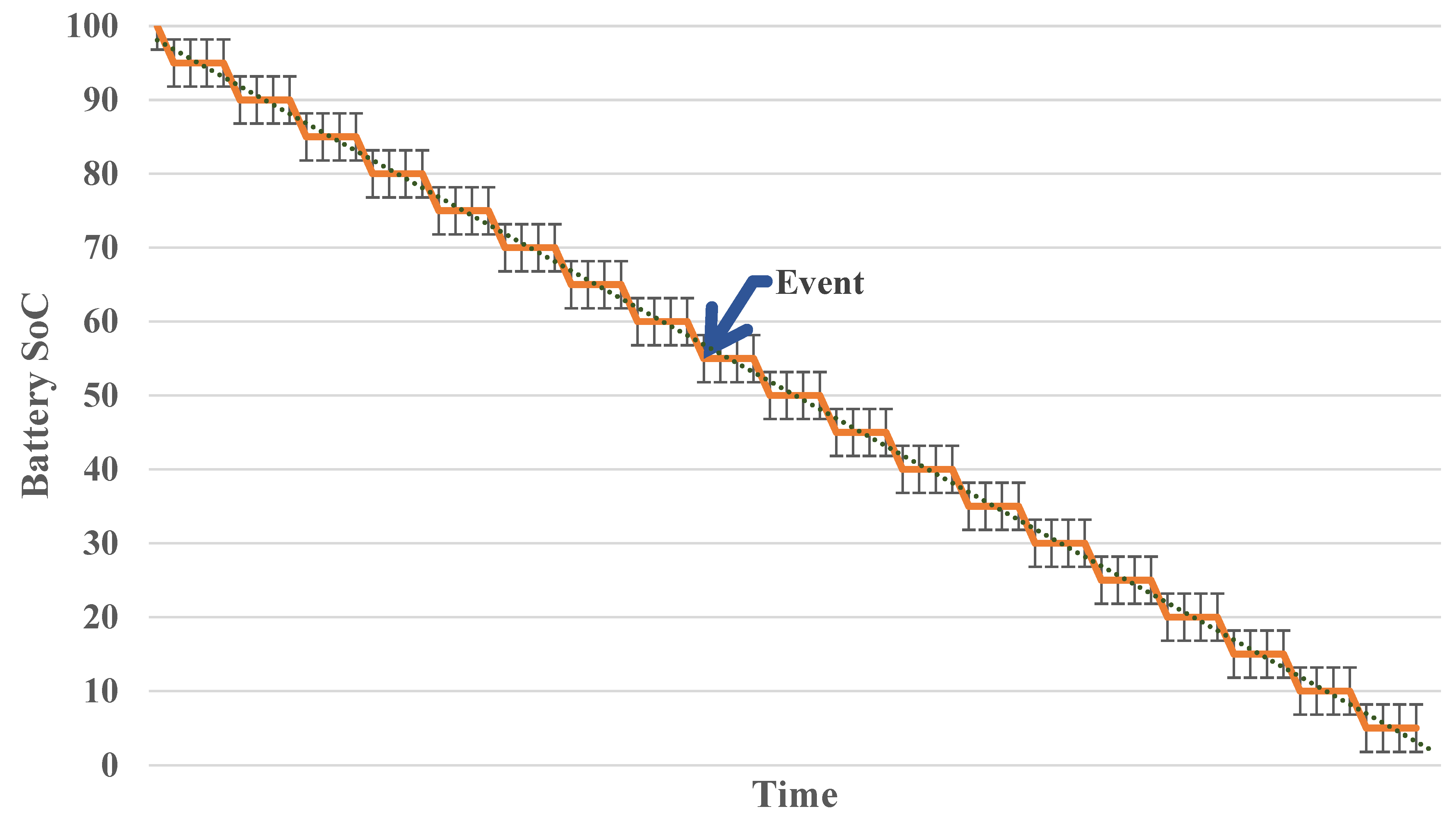
4.2. Battery State of Charge (SoC) Constraint

To maintain the reliability of the microgrid during outages, the battery SoC needs to be within a specific range. This constraint prevents overcharging or over-discharging of the battery, which can impact its efficiency and lifespan:

SoC_min ≤ SoC_battery ≤ SoC_max

(5)

where SoC_min and SoC_max represents the minimum and maximum state of charge for the battery, respectively, and SoC_battery represents the current state of charge for the battery.

4.3. Energy Storage Capacity Constraint

The energy stored in the existing battery should not exceed the storage capacity of the new battery system:

SoC_battery ≤ SoC_{new_max}

(6)

SoC_{new_max} represents the maximum state of charge for the new battery system.

4.4. Generation and Load Limits

Constraints are set on the maximum energy generation from different sources (solar panels, wind turbines) and the maximum allowable load demand to prevent exceeding the capacity of the microgrid components:

E_Gen ≤ G_max

(7)

L_Demand ≤ L_max

(8)

where G_max represents the maximum generation capacity, and L_max is the maximum load capacity.

4.5. Economic Constraints

If the analysis includes economic considerations, there may be budget limitations or cost-effectiveness constraints. These constraints ensure that the solution aligns with the available resources and budget:

C_total ≤ C_budget

(9)

where C_total represents the total cost, and C_budget represents the budget limit.

4.6. Environmental Constraints

In the case of a grid-connected microgrid with renewable sources, there might be constraints on minimizing carbon emissions or maximizing the utilization of renewable energy:

$${\mathrm{R}}_{\min }\le \frac{E_{Gen}}{E_{Gen}+E_{Srotage}}$$

(10)

where R_min is the minimum renewable energy ratio.

These constraining functions guide the optimization algorithm to search for solutions that satisfy both technical and economic requirements. The optimization aims to find a configuration that maximizes the microgrid’s resilience against outages while ensuring its efficient and cost-effective operation. The specific form and parameters of these constraints would depend on the microgrid’s characteristics, the objectives of the optimization, and the constraints imposed by the physical components and operational conditions.

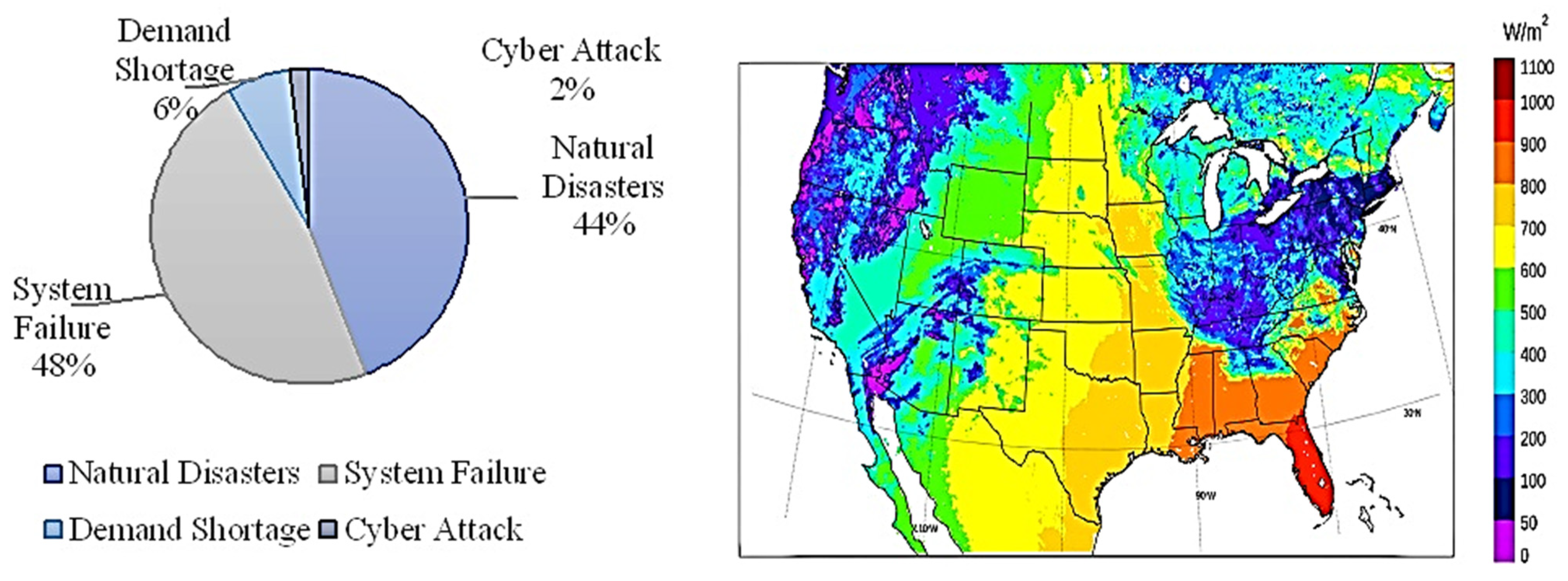
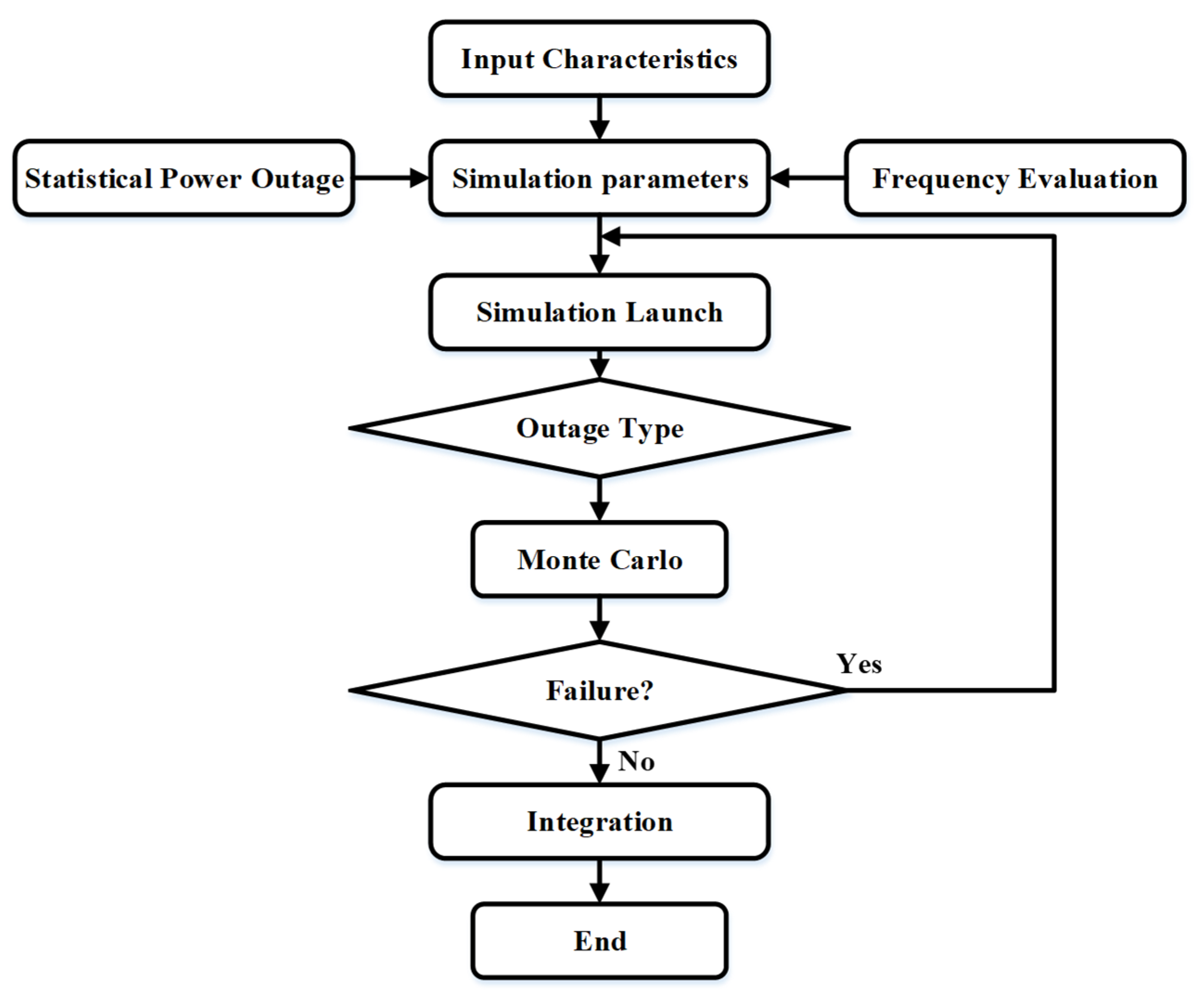
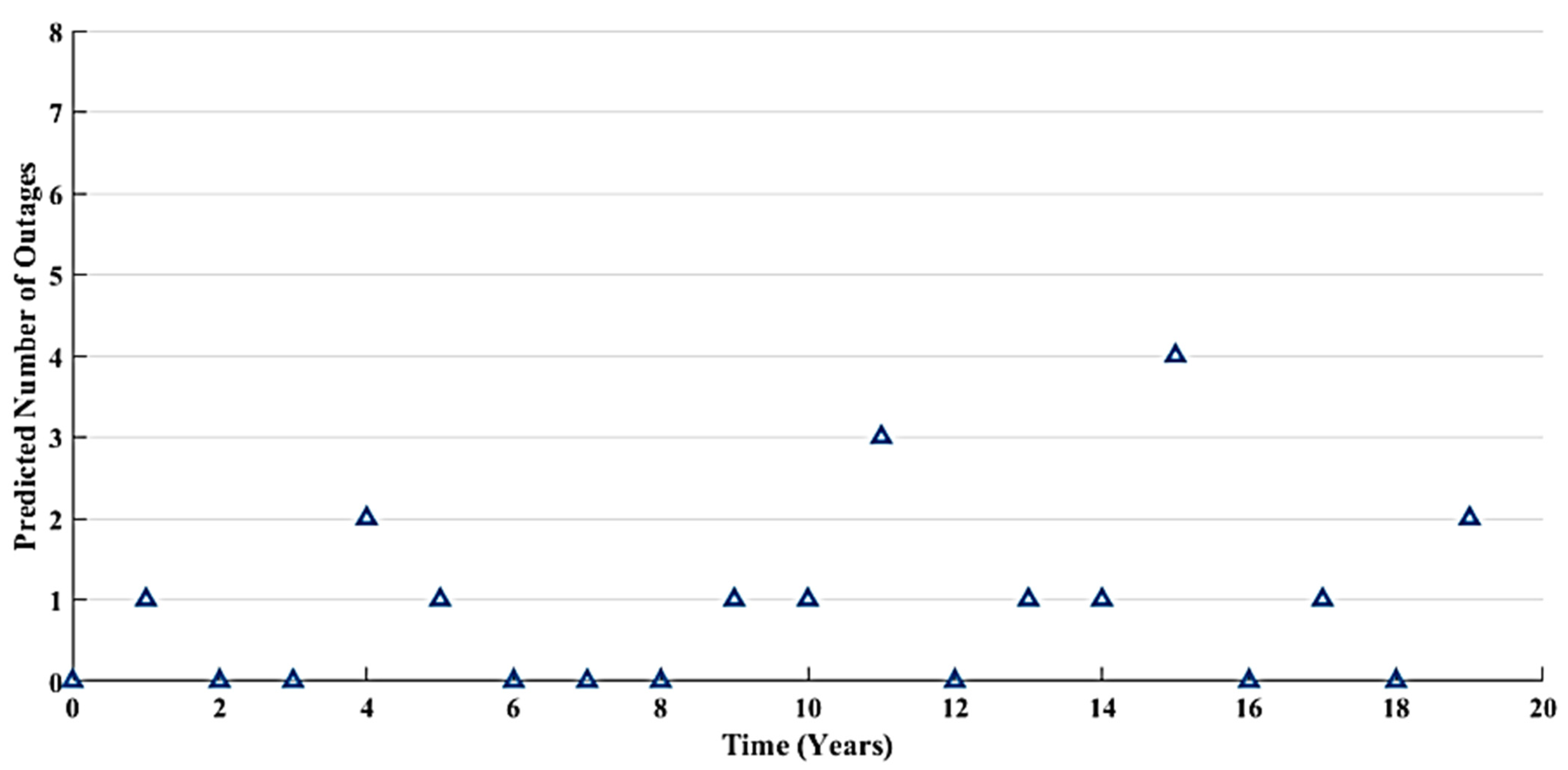
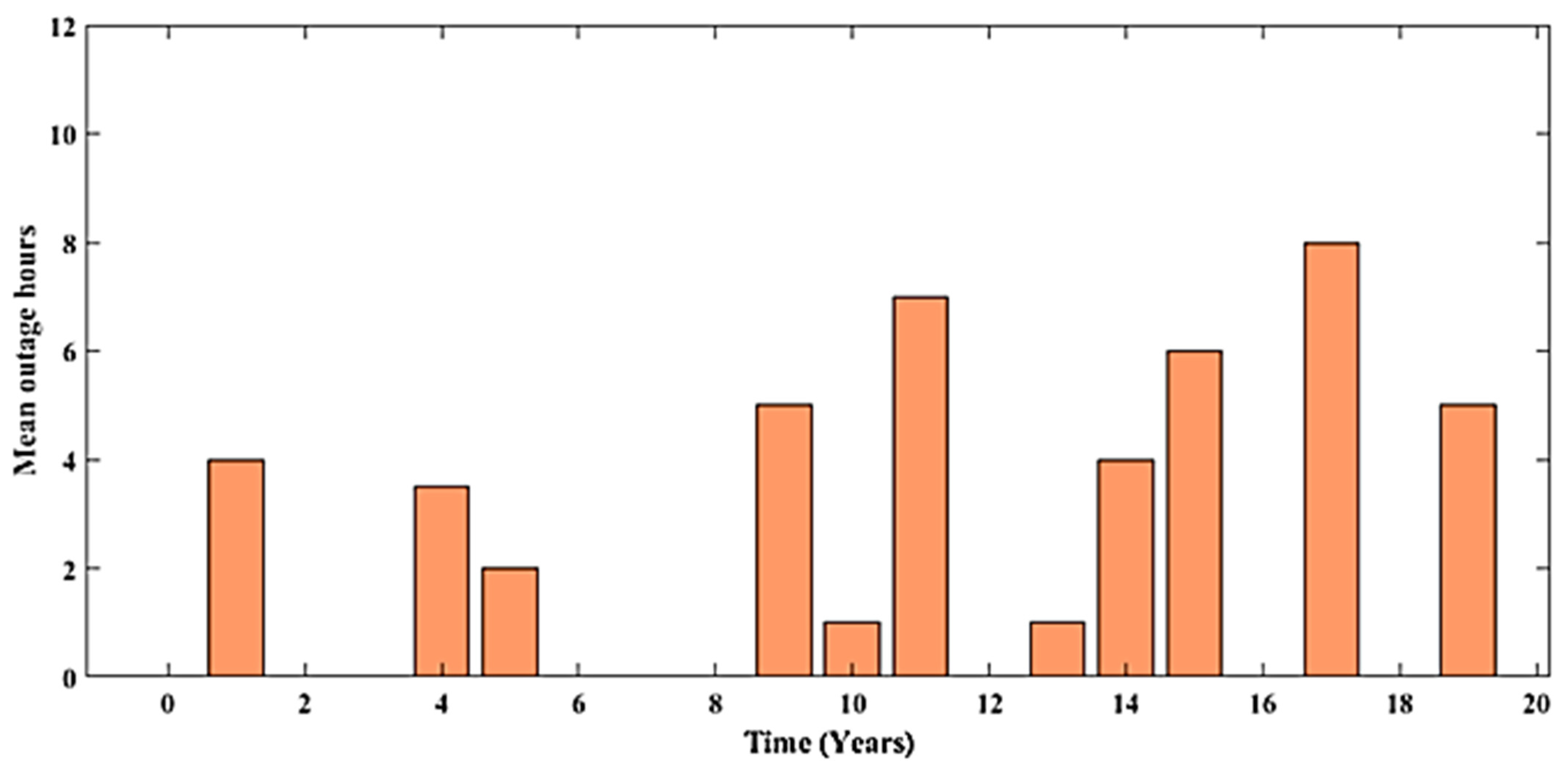
5. Outage and Battery SoC prediction

The role of battery SoC prediction, particularly during anticipated outage scenarios, is illuminated, emphasizing its integral contribution to the system’s overall performance. The article delves into the technical intricacies of SoC prediction, elucidating how it offers real-time insights into the battery’s stored energy relative to its total capacity [3,4,5,6,7,8,9,10,11]. This knowledge empowers informed decision-making during critical events such as grid failures or extreme weather conditions, ensuring efficient utilization of stored energy and minimizing downtime for vital loads. Additionally, the article emphasizes that battery SoC prediction plays a pivotal role in optimizing the BESS, tailoring it to the system’s specific requirements. This optimization not only enhances autonomy but also ensures the battery is appropriately sized. Overall, the study highlights that battery SoC prediction is a fundamental element of the microgrid resilience strategy, enabling data-driven decisions, system optimization, and the maintenance of a reliable, resilient, and sustainable energy system capable of withstanding various challenges and disruptions [2,10].

Monte Carlo simulation is a powerful technique used to model and analyze the behavior of complex systems through random sampling [10]. In the context of the article’s methodology, Monte Carlo simulation is applied to predict outage events and the battery state of charge (SoC). Figure 5 shows the flow chart to predict potential outages in a microgrid’s lifetime.

Here are the basic equations for performing Monte Carlo simulation: Outage prediction involves generating multiple scenarios of potential outage events based on historical data and probabilistic models.

Defining the probability distribution of outages, let P_outage be the probability of an outage occurring in a given time period. This probability can be estimated from historical outage data or other relevant sources.

A sequence of random numbers is generated between 0 and 1 using a random number generator.

Simulation of outage events: For each random number generated, compare it to the probability P_outage. If the random number is less than or equal to P_outage, an outage event is considered to have occurred in that scenario. This process is repeated for multiple random numbers to generate a set of outage scenarios in the lifetime of the microgrid, as shown in Figure 6 and Figure 7, respectively.

Similarly, battery SoC prediction involves assessing the batteries’ state of charge in different future scenarios.

Probability distributions are defined for battery charging and discharging rates based on historical data for an existing system and battery characteristics. Let P (charge) be the probability of the battery being charged, and P (discharge) be the probability of the battery being discharged.

Random numbers are generated to determine whether the battery will be charged or discharged in each outage scenario. The change in the battery SoC for each scenario is calculated based on the outcome of the random numbers generated. This change can be calculated as

ΔSoC = (C_rate − D_rate) × T_X

(11)

where C_rate and D_rate represent the charging and discharging rate of the battery, and T_X is the simulation time step.

The battery SoC is updated based on the calculated ΔSoC for each scenario. The initial SoC for each scenario can be set based on historical data or the current state of the battery. Figure 8 shows the discharging simulation using Monte Carlo, where a 1C-rated single-string battery has been considered.

By performing Monte Carlo simulations for both outage prediction and battery SoC prediction, it can generate a range of possible future scenarios considering uncertainties, providing valuable insights into the microgrid’s resilience and battery performance.

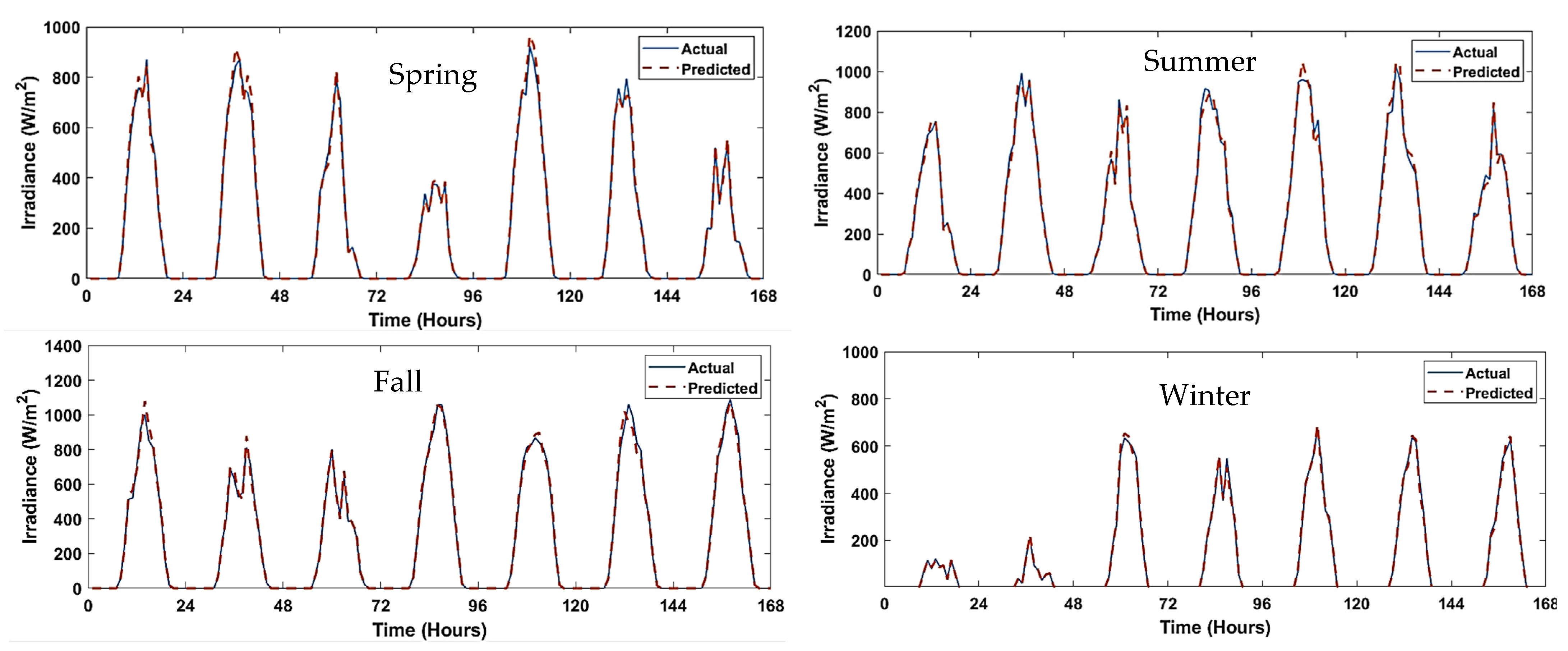
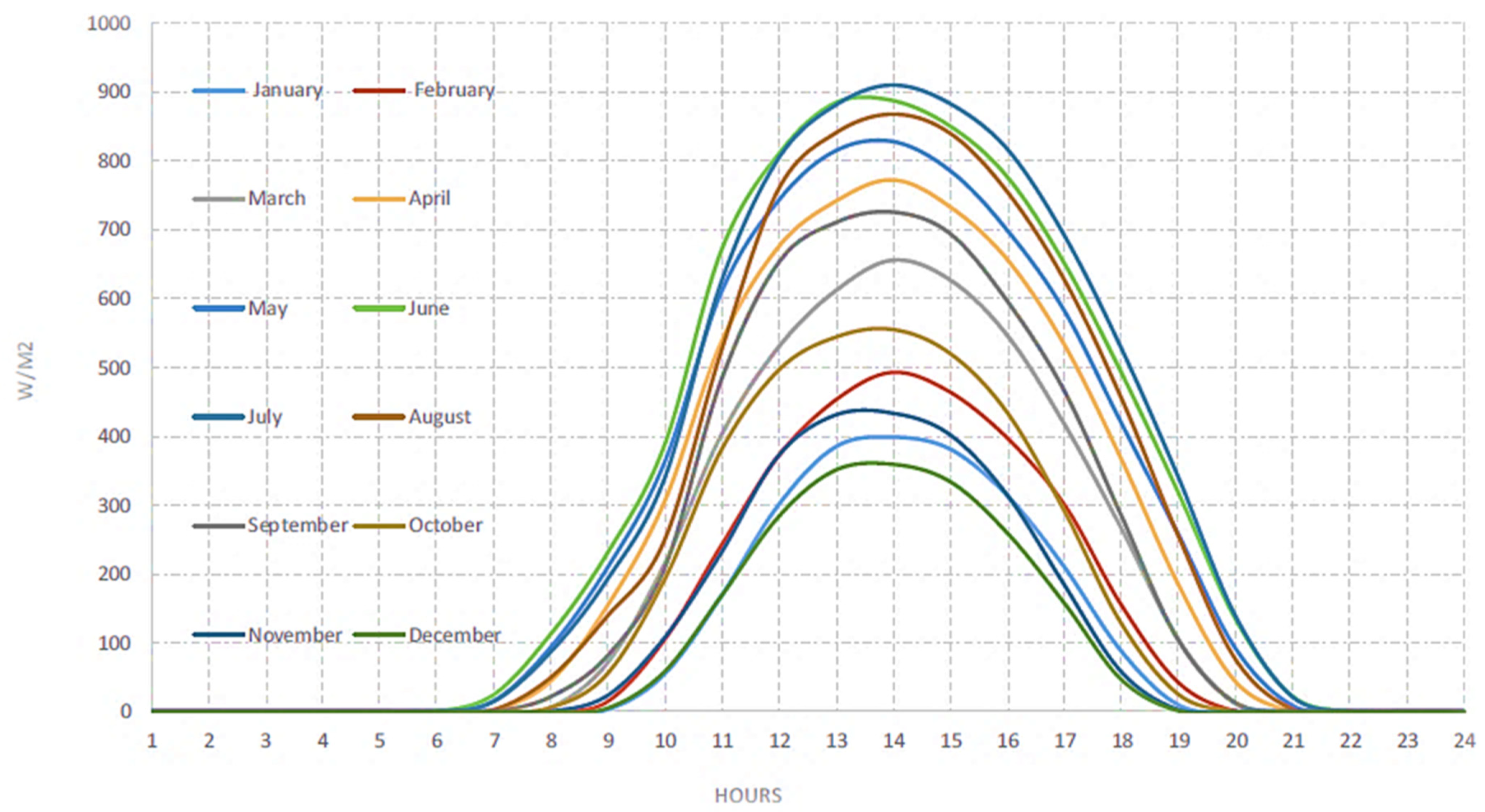
6. Load and Solar Irradiance Forecasting

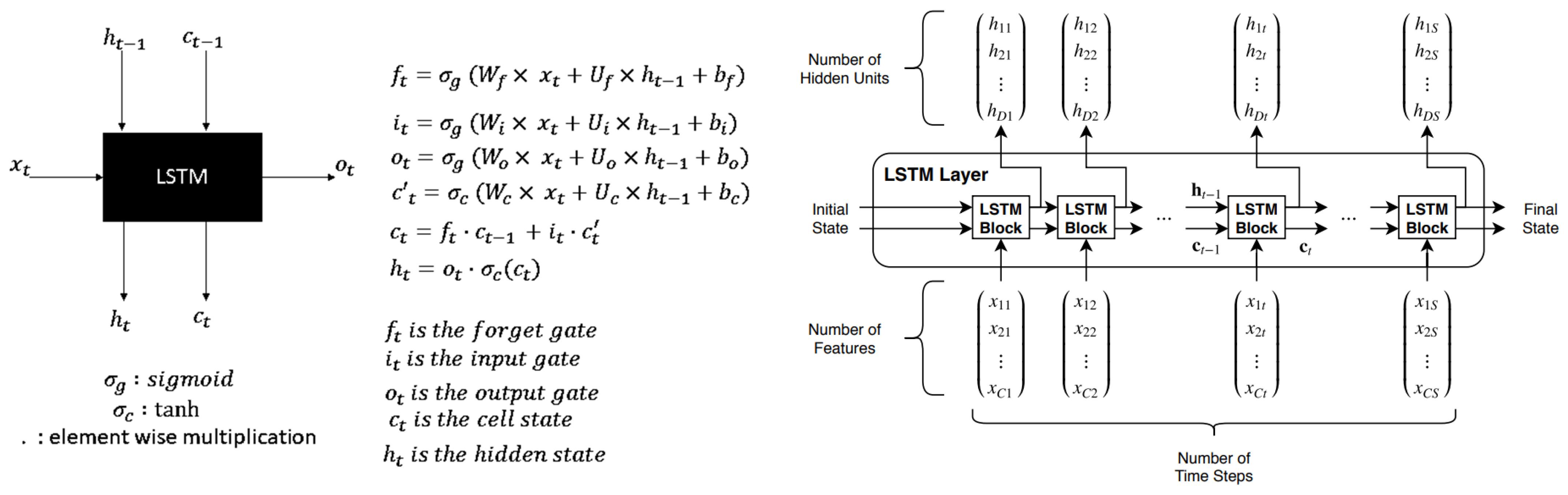
6.1. Long Short-Term Memory (LSTM)

Long Short-Term Memory (LSTM) networks, a type of recurrent neural network, were utilized to forecast solar irradiance and load profiles for a microgrid [2,3,4]. Solar irradiance prediction is crucial for managing renewable energy sources effectively, while load forecasting aids in optimizing energy distribution. The LSTM model captures temporal dependencies in the data and improves the accuracy of predictions compared to traditional methods. Figure 9 shows the standard LSTM block, LSTM gates, states, and time-series data accumulation process [40].

The LSTM equations below describe the forward propagation through the LSTM network. These equations calculate the values of the input, forget, cell, and output gates and the updated cell state and hidden state.

$$i_t=\sigma \left(W_{xi}{x}_t+W_{hi}{h}_{t-1}+b_i\right)$$

(12)

$$f_t=\sigma \left(W_{xf}{x}_t+W_{hf}{h}_{t-1}+b_f\right)$$

(13)

$$g_t=\tanh \left(W_{xg}{x}_t+W_{hg}{h}_{t-1}+b_g\right)$$

(14)

$$o_t=\sigma \left(W_{xo}{x}_t+W_{ho}{h}_{t-1}+b_o \right)$$

(15)

$$c_t=f_t\omega c_{t-1}+i_t\omega g_t$$

(16)

$$h_t=o_t\omega \tanh (c_t)$$

(17)

where,

• $x_t$ is the input at time;
• $i_t$, $f_t$, $g_t$, $o_t$ are the input, forget, cell, and output gates at time;
• $h_t$ is the hidden state at time;
• $c_t$ is the cell state at time;
• $W$ and $b$ are weight matrices and bias vectors;
• σ is the sigmoid activation function, and $\omega$ represents element-wise multiplication.

The forecasting process starts with the collection of raw historical data on solar irradiance and load profile, as shown in Figure 10. The data are then accumulated and preprocessed before being stored in a local storage device. The next step is to train a machine-learning model to learn the relationship between solar irradiance and load profile. The parameters of the trained model can then be modified to improve its accuracy. The trained model is then used to forecast solar irradiance and load profile for a future time period. The forecasted data are then compared with the actual data to assess the accuracy of the forecast. An accuracy improvement algorithm can then be used to improve the accuracy of the forecast. The final step is to obtain the results of the PSO algorithm. Figure 11 shows the comparisons of forecasted solar irradiance with real-time obtained solar irradiance.

The solar irradiance forecasting outcomes for Lubbock, Texas, utilizing a Long Short-Term Memory (LSTM) model and leveraging hourly historical data spanning from 2009 to 2018, offer a comprehensive insight into the model’s capability to predict solar irradiance patterns across diverse seasons. The analysis covers a week’s average profiles for each of the four seasons: spring, summer, fall, and winter, highlighting the accuracy of the LSTM model’s predictions, which achieved an impressive 92% accuracy rate when compared to the actual observed profiles.

Starting with the spring season, characterized by transitioning weather conditions and increasing sunlight hours, the LSTM model demonstrates its proficiency by accurately forecasting an average daily solar irradiance of 927 $\mathrm{W}/{\mathrm{m}}^2$. This prediction aligns closely with the actual solar irradiance profile for the week, confirming the model’s capacity to capture the evolving solar dynamics during this season.

Moving into the high-sunlight months of summer, the model maintains its precision, projecting an average daily solar irradiance of 981 $\mathrm{W}/{\mathrm{m}}^2$. This prediction mirrors the observed increase in solar radiation during this time, highlighting the model’s adeptness in anticipating intensified solar irradiance, which is crucial for optimizing energy generation and distribution strategies.

Transitioning to fall, as solar irradiance begins to taper off, the LSTM model maintains its accuracy by forecasting an average daily solar irradiance of 857 $\mathrm{W}/{\mathrm{m}}^2$. This prediction accurately mirrors the observed trends as the season progresses, underscoring the model’s adaptability to the changing solar dynamics and ensuring reliable forecasts throughout different conditions.

In the winter season, characterized by reduced daylight hours and lower sun angles, the LSTM model delivers accurate forecasts. It projects an average daily solar irradiance of 401 $\mathrm{W}/{\mathrm{m}}^2$, effectively capturing the diminished solar radiation characteristic of this season. The alignment between forecasted and observed profiles showcases the model’s robustness in navigating even challenging conditions. The consistent % accuracy rate of 82% across all seasons reinforces the LSTM model’s potential as a dependable tool for solar irradiance forecasting. This precision contributes significantly to the microgrid’s ability to optimize energy production, storage, and distribution strategies. By enabling informed decision-making and enhancing energy management, the LSTM model serves as a key enabler for resilient, cost-effective, and sustainable microgrid operations, particularly in regions with dynamic solar irradiance patterns like Lubbock, TX. Figure 12 shows the forecasted daily average of solar irradiance for every month.

The load profile forecasting results, utilizing an LSTM model trained on hourly historical load data from 2009 to 2018 and represented in a factorized form, provide a comprehensive understanding of the model’s performance across distinct seasons. A week’s average load profiles for each season, spring, summer, fall, and winter, offer insights into the LSTM model’s accuracy and its ability to anticipate load variations over time.

In the spring season, marked by changing weather conditions and varying energy demands, the LSTM model showcases its effectiveness by accurately predicting the factorized load profile as shown in Figure 13. When multiplied by the total building demand, this factorized representation yields the load curve. The average daily load profile for the week aligns closely with the actual observed load profile, reflecting the model’s capability to capture the evolving energy consumption patterns. The model’s accuracy of 81% reinforces its reliability in forecasting load profiles during this transitional season.

As summer arrives with increased energy usage due to cooling demands, the LSTM model continues to demonstrate its precision. The factorized load profile, transformed into the load curve, accurately captures the amplified energy consumption during peak hours. The average daily load profile for the week mirrors the observed load pattern, emphasizing the model’s competence in predicting the rising electricity demands of the season. The model’s 81% accuracy substantiates its ability to forecast load profiles in this high-demand period.

As temperatures moderate and energy consumption shifts in the fall season, the LSTM model remains reliable in load forecasting. When scaled by the total building demand, the factorized load profile represents the load curve effectively. The average daily load profile for the week closely mirrors the actual consumption pattern, underlining the model’s proficiency in capturing the transitioning energy demands. With an accuracy rate of 81%, the model consistently provides valuable insights into load fluctuations during this season.

During the winter season, characterized by heating-related electricity usage, the LSTM model maintains its accuracy in load forecasting. When transformed into the load curve, the factorized load profile accurately captures the increased energy demand during cold periods. The average daily load profile for the week closely tracks the actual observed load, underscoring the model’s aptitude in anticipating energy consumption shifts. With an accuracy of 81%, the model ensures reliable predictions of load profiles even during challenging conditions.

The consistent accuracy rate of 81% across all seasons highlights the LSTM model’s efficacy in forecasting load profiles. By understanding and anticipating load variations, the model effectively empowers microgrid operators to optimize energy distribution, storage, and management strategies. In scenarios where factorized representations are used, the model’s precision in capturing the load curve enables informed decision-making and contributes to resilient, cost-efficient, and sustainable microgrid operations.

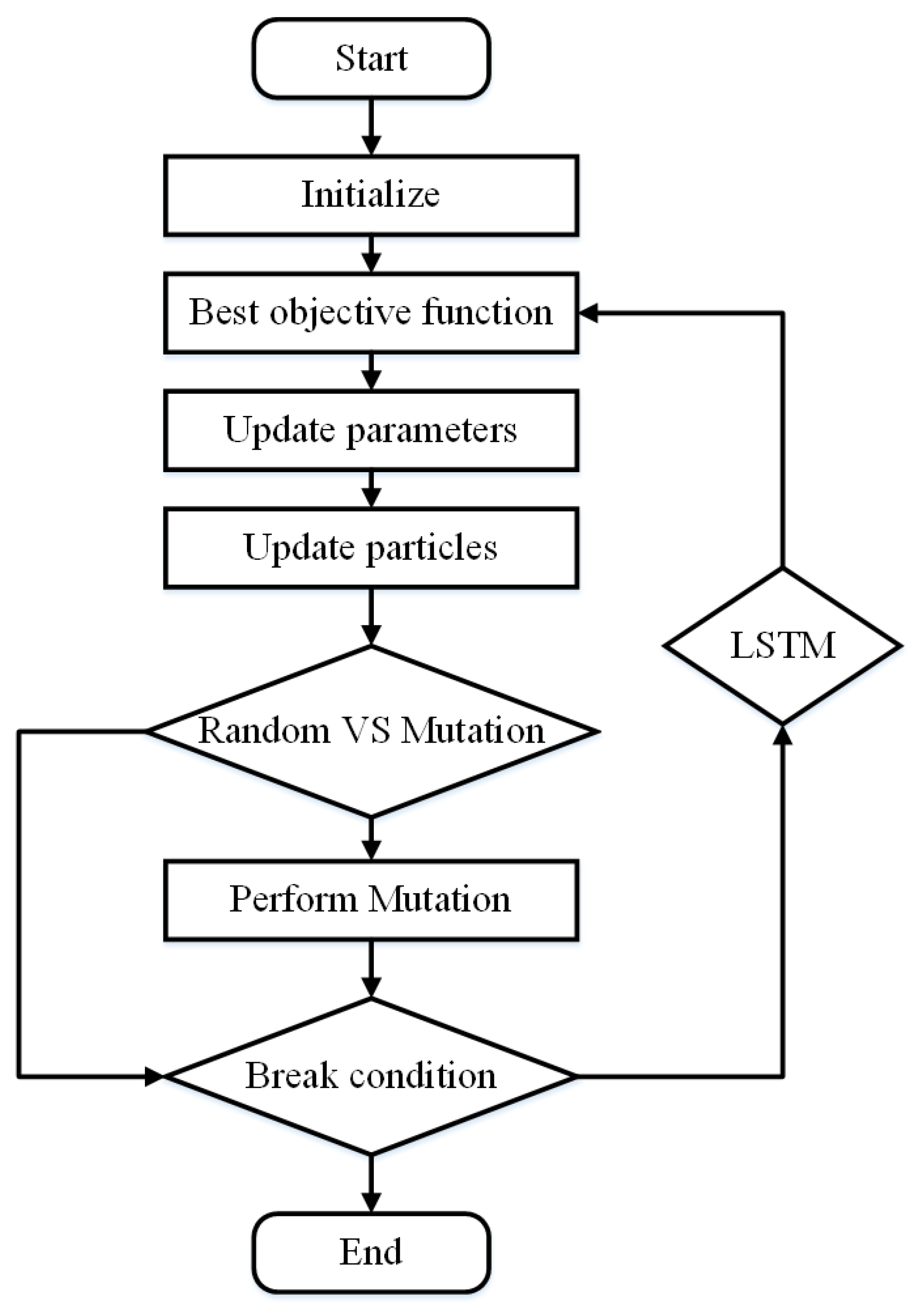
6.2. Modified Particle Swarm Optimization

The modified PSO algorithm works by initializing a swarm of particles in a search space. Each particle has a position and velocity. The velocity of a particle is updated at each iteration based on its own best position, the global best position, and a random number. The position of a particle is updated based on its velocity. The algorithm continues to iterate until a stopping criterion is met. Figure 14 shows the modified PSO-LSTM process.

The process starts with the initialization of the data. This includes the historical data on the variable being predicted, as well as any other relevant data. The data are then divided into two sets: a training set and a test set. The training set is used to train the LSTM model, and the test set is used to evaluate the accuracy of the model. The next step is to evaluate the optimum LSTM-driven objective function. The objective function is a mathematical expression that measures the accuracy of the LSTM model. The objective function is evaluated using the training set. The Pbest and gbest for resilience and the economic solution are then updated. The Pbest is the best position that a particle has achieved thus far, and the gbest is the best position that any particle has achieved thus far. The Pbest and gbest are updated using the objective function. The velocity and position of each particle are then updated. The velocity is a vector that determines how much a particle will move in the next iteration, and the position is the particle’s current location. The velocity and position are updated using the Pbest, gbest, and random variables.

Particle update rule,

$$p=p+v$$

(18)

with,

$$v=v+c1\times rand\times \left(pBest-p\right)+c2\times rnd\times \left(gBest-p\right)$$

(19)

where,

• p is the particle’ s position;
• v is the path direction;
• c1 is the weight of local information obtained from LSTM;
• c2 is the weight of global information;
• pBest is the best position of the particle;
• gBest is the best position of the swarm;
• rnd is the random variable.

Random variables are generated and compared with the mutation probability. A mutation is performed if the random variables are less than or equal to the mutation probability. Otherwise, the mutation is not performed. If the mutation probability is satisfied, a mutation is performed. A mutation is a change to the particle’s position or velocity. The mutation is performed using random variables. If the mutation result is not feasible, the initialization step with the LSTM model is restarted. A feasible result is a result that satisfies the constraints of the problem. The problem’s constraints may include the range of values the variable can take on. If the mutation result is feasible, the result is obtained. The result is the position of the particle that has the best objective function value. The flowchart continues to iterate until a stopping criterion is met. The stopping criterion may be a maximum number of iterations, a minimum error tolerance, or a combination of both. Figure 15 shows the hyperparameter convergence of the system.

The figures illustrating the modified PSO-LSTM algorithm’s application in determining the optimal sizing of battery and solar PV components provide a visual insight into the convergence and effectiveness of the optimization process. These figures highlight the algorithm’s ability to efficiently explore the solution space and identify the configurations that yield the best performance. The figure depicts the score plotted against the generation number. The scores represent the fitness of individual solutions evaluated during the optimization process. The fitness score measures the quality of a given solution, with lower values indicating better solutions. In this plot, the mean score over generations hovers around 0.0022, signifying that the algorithm consistently improves the solutions it explores. The algorithm’s ability to maintain a consistently low mean score is indicative of its efficiency in searching for optimal configurations. The figure showcases the best score achieved across generations. It illustrates the progressive improvement of solutions as the algorithm iteratively refines its search. The graph demonstrates that the best score achieved is 1.02021, indicating the top-performing solution identified by the algorithm. This representation underscores the algorithm’s capacity to identify highly competitive configurations within the solution space.

The 3D representation illustrates the convergence of the algorithms throughout generations. As generations progress, the algorithm converges towards a solution with a significantly improved score. The decreasing trend in scores indicates the algorithm’s ability to fine-tune solutions iteratively, reaching a point where the algorithm’s search becomes focused and refined. This convergence pattern reflects the algorithm’s efficacy in systematically exploring the solution space and narrowing down on optimal sizing configurations.

7. Result Analysis

The sizes of the photovoltaic (PV) system and battery, determined through the modified PSO-LSTM algorithm, were subjected to a comprehensive evaluation by comparing them with the economic and emission benefits obtained from two industry-standard tools: HOMER Pro version 3.14.7524 and REopt. This evaluation aims to validate the effectiveness of the algorithm in generating optimal sizing solutions that align with established commercial software results and further highlight the potential advantages of the proposed approach.

Comparing the sizing results with those obtained from HOMER Pro and REopt, we assess the economic viability of the microgrid system. HOMER Pro’s well-established optimization capabilities provide insights into the cost-effectiveness of different system configurations. REopt’s analysis further corroborates the economic benefits by identifying the sizing configurations that yield the lowest lifetime costs while meeting the desired energy requirements. Aligning the algorithm-generated sizes with the results from these tools reinforces the reliability of the hybrid approach in optimizing the microgrid’s economic performance.

The algorithm-derived sizing configurations are also evaluated for emission reduction benefits using both HOMER Pro and REopt. These tools quantify the environmental impact by estimating the reduction in greenhouse gas emissions associated with the optimal configurations. By comparing the emission benefits calculated by the algorithm with those from HOMER Pro and REopt, we ascertain the algorithm’s capability to generate sizing solutions that improve economic efficiency and reduce the microgrid’s carbon footprint.

To conduct the economic and environmental benefits, the listed equations are used.

• Total net present value,

$$\mathrm{N}\mathrm{P}\mathrm{V}={\sum }_{t=o}^T\frac{R_t-C_t}{{(1+r)}^t}$$

(20)

where $R_t$ is the revenue at time t, $C_t$ s the cost at time t, r is the discount rate, and T is the project’s lifetime.

• Levelized cost of energy,

$$LCOE=\frac{{\sum }_{t-0}^T{C}_t}{{\sum }_{t=0}^T{E}_t}$$

(21)

$E_t$ represents the total energy generated at time t.

The simple payback calculates the time it takes for the project’s cumulative benefits to offset the initial investment costs.

$$Simple Payback=\frac{Annual Net Cash Flow}{Initial Investment}$$

(22)

• Capital recovery factor,

$$CRF \left(i, N\right)=\frac{{i \left(1+i\right)}^N}{{(1+i)}^N-1}$$

(23)

where the discount rate is i, and N represents number of years.

• Reduction in CO₂ emissions compared to a baseline scenario, considering the energy mix and emissions factors.

CO₂ Reduction = Baseline Emissions − Microgrid Emissions

(24)

In the endeavor to propose a grid-connected microgrid solution, several critical aspects and input parameters have been carefully considered as shown in

Table 1. Considered input parameters of the proposed system and existing tools.

Aspects	Inputs
Microgrid lifetime	20 years
Discount rate	5%
Inflation rate	2%
Annual load demand	332 MWh
Average outage	7 h
Existing PV	0
Existing Battery	0
Criticality factor	50%

. The microgrid’s anticipated same load profile, outage frequency, average outage duration, and lifetime is set at 20 years, with a discount rate of 5% and an inflation rate of 2% accounted for in financial evaluations. The annual load demand, a pivotal factor in microgrid design, is projected at 332 MWh from the PSO-LSTM forecasting networks, while the average outage duration stands at 7 h, underscoring the need for resilience. Currently, there are no existing photovoltaic (PV) or battery systems in place. The criticality factor, set at 50%, highlights the importance of ensuring reliable power supply to critical loads. To analyze and determine the most resilient and cost-effective solution, advanced tools such as Homer Pro and ReOPT were employed, leveraging their capabilities to optimize the proposed microgrid topology. This meticulous consideration of inputs and the utilization of cutting-edge software tools were essential steps toward creating a sustainable and resilient energy solution for the envisioned microgrid.

The proposed system suggests a PV size of 88 kW and a battery size of 97 kWh as shown in

Table 2. Most resilient solution as calculated.

Aspects	Proposed System	Homer Pro	ReOPT
PV Size	88 kW	113 kW	102 kW
Battery Size	97 kWh	122 kWh	151 kWh
Levelized Cost of Energy	USD 0.39	USD 0.51	USD 0.47
Simple payback period	11 years	17 years	14 years
Resilience	10 h	19 h	15 h
Total Emission	188 tons	138 tons	151 tons
Cost Saving	USD 18,432	USD 762	USD 6103

. These sizing configurations are notably different from those obtained through HOMER Pro and REopt, highlighting the algorithm’s ability to explore alternative solutions that optimize the microgrid’s performance. The PSO-LSTM achieves a significantly lower levelized cost of energy (LCOE) of USD 0.39 compared to USD 0.51 from HOMER Pro and USD 0.47 from REopt. Additionally, the simple payback period for the proposed system is notably shorter at 11 years, outperforming both HOMER Pro (17 years) and REopt (14 years). The proposed system enhances the microgrid’s resilience with a backup duration of 10 h, surpassing HOMER Pro (19 h) and REopt (15 h). This underscores the algorithm’s ability to optimize system configurations that ensure a reliable energy supply during outages. It also demonstrates superior emission reduction, totaling 188 tons, compared to 138 tons from HOMER Pro and 151 tons from REopt. This signifies the algorithm’s ability to generate configurations aligning with sustainability goals. Finally, it yields significant cost savings of USD 18,432, which far exceed the savings of USD 762 from HOMER Pro and USD 6103 from REopt. This demonstrates the algorithm’s adeptness at identifying economically efficient solutions.

The proposed system maintains a competitive levelized cost of energy (LCOE) at USD 0.39, which compares favorably to HOMER Pro’s USD 0.46 and REopt’s USD 0.47 as shown in

Table 3. Most economic solutions are calculated.

Aspects	Proposed System	Homer Pro	ReOPT
PV size	102 kW	91 kW	75 kW
Battery size	42 kWh	18 kWh	0 kWh
Levelized Cost of Energy	USD 0.39	USD 0.46	USD 0.47
Simple payback period	11 years	9 years	8.25 years
Resilience	7 h	2 h	1 h (PV only)
Total Emission	159 tons	140 tons	185 tons
Cost Saving	USD 10,965	USD 21,354	USD 40,978

. The simple payback period of the proposed system is remarkably short, at just 11 h, demonstrating its immediate cost-effectiveness. In comparison, HOMER Pro requires 9 years, and REopt takes 8.25 years to achieve payback. The algorithm ensures a backup duration of 7 h during outages, enhancing the microgrid’s resilience. This surpasses HOMER Pro’s 2 h and REopt’s 1 h (for PV only), emphasizing the algorithm’s ability to optimize system configurations for reliable energy supply. It achieves substantial emission reduction, totaling 159 tons, compared to 140 tons from HOMER Pro and 185 tons from REopt. This showcases the algorithm’s capability to prioritize sustainability goals. The proposed system offers cost savings of USD 10,965, making it a financially efficient solution. While HOMER Pro provides savings of USD 21,354 and REopt offers significant savings of USD 40,978, the calculation maintains a competitive edge in cost-effectiveness.

The hybrid PSO-LSTM algorithm’s alternative sizing solutions outperform established tools across various metrics. The proposed approach consistently yields optimal configurations that balance economic viability, environmental impact, and resilience. The algorithm’s ability to provide immediate cost savings, achieve a remarkably simple payback period, enhance energy system resilience, and reduce emissions underscores its potential to revolutionize microgrid design and operation. By aligning economic efficiency with sustainability goals, the hybrid PSO-LSTM algorithm emerges as a powerful tool for creating resilient and sustainable energy systems.

The algorithm collectively showcases the modified PSO-LSTM algorithm’s effectiveness in determining the optimal sizing of battery and solar PV components. The consistently low mean score, the identification of the best-performing solution, and the convergence pattern underscore the algorithm’s ability to efficiently navigate a complex search space and identify configurations that enhance the microgrid’s performance. This hybrid approach improves the accuracy of predictions and contributes to the microgrid’s overall resilience, cost-efficiency, and sustainable energy utilization.

While the proposed method for optimal sizing of PV and BESS offers significant benefits in terms of enhancing microgrid resilience, it does come with certain drawbacks. namely, the computational complexity of the hybrid optimization techniques used can be relatively high, potentially requiring substantial computational resources and time for real-time implementation in practical microgrid settings. Also, the accuracy of the outage prediction models and renewable energy forecasts is contingent on the quality of the data and models employed, which may introduce uncertainties and errors in the sizing recommendations, affecting the system’s performance during actual power outages.

8. Conclusions

This research clearly indicates a significant step forward in the pursuit of enhanced grid-tied microgrid resilience through the synergistic integration of renewable energy resources and data-driven methodologies, which can be useful for any microgrid, DER-based system design consisting of solar PV and battery energy storage system. Leveraging a comprehensive ten-year dataset encompassing solar irradiance and load profiles, invaluable insights into the seasonal variabilities of solar energy potential have been revealed, coupled with impressive forecasting accuracies of 82% for solar irradiance and 81% for load profiles. The bottom line of this innovation lies in the development of a modified PSO-LSTM algorithm, a hybrid solution adeptly optimizing battery and solar PV system sizing, exemplified by a mean score of 0.0022 and the unequivocal convergence of these two potent techniques. Beyond the realm of numerical metrics, this optimization signifies a pivotal departure towards bespoke, efficient energy solutions tailored to harmonize seamlessly with the unique requisites of the microgrid. Furthermore, this research accentuates the tangible economic and environmental dividends ushered in by this approach. With cost savings amounting to USD 10,965, an 11 h payback period, and a substantial reduction of 159 tons in total emissions, the system not only shields businesses from the economic repercussions of power disruptions but also contributes substantially to a cleaner, more sustainable energy milieu. In essence, this work encapsulates a transformative journey toward a future where grid-connected microgrid resilience is not a theoretical concept but an actionable reality, where the fusion of renewable energy and data-driven acumen ensures an uninterrupted power supply. It extends a collective invitation to an odyssey where energy reliability, sustainability, and inclusivity stand as cornerstones of progress.