Enhancement Effect of a Diamond Network on the Flow Boiling Heat Transfer Characteristics of a Diamond/Cu Heat Sink
Abstract
:1. Introduction
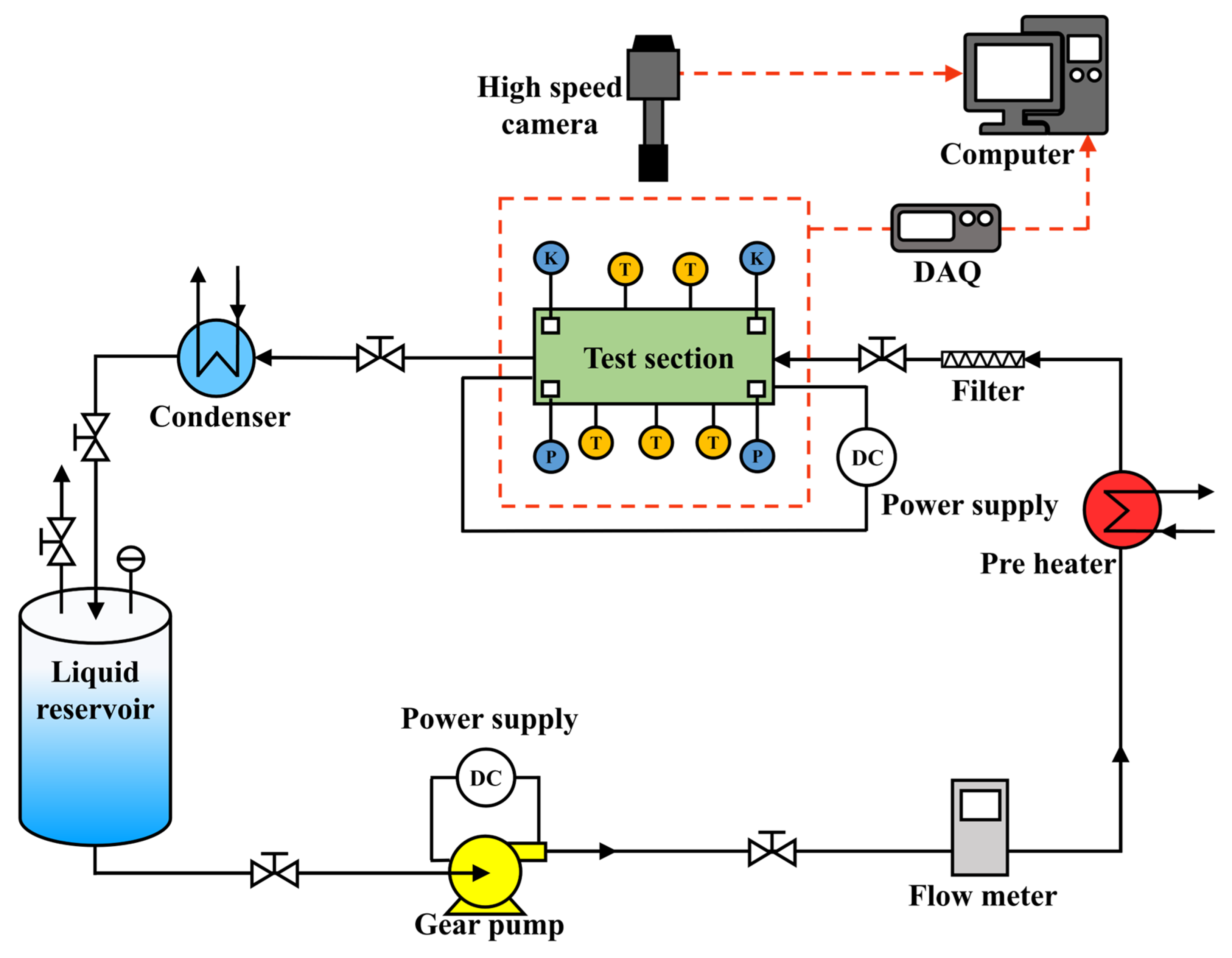
2. Experimental Setup
2.1. Flow Loop
2.2. Preparation of Diamond/Cu Composite
3. Heat Transfer Data Reduction
4. Results and Discussion
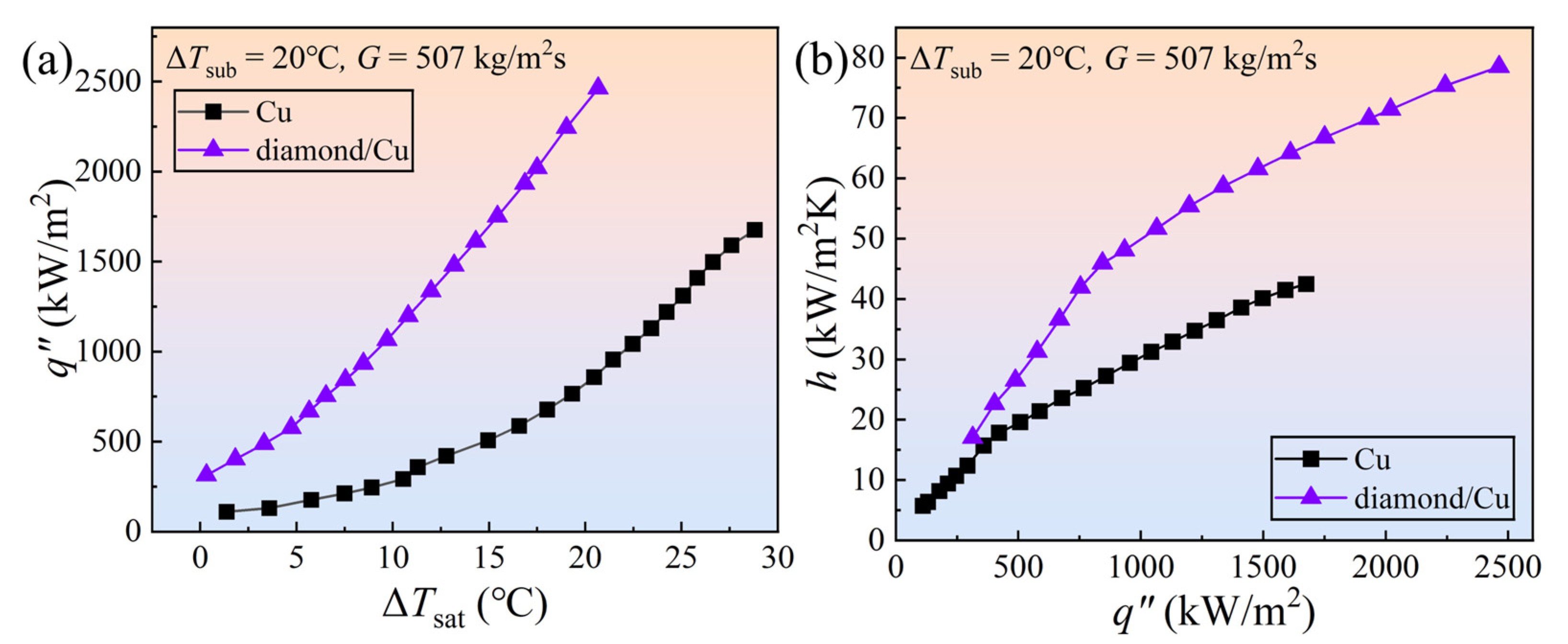
4.1. Flow Boiling Heat Transfer Performance
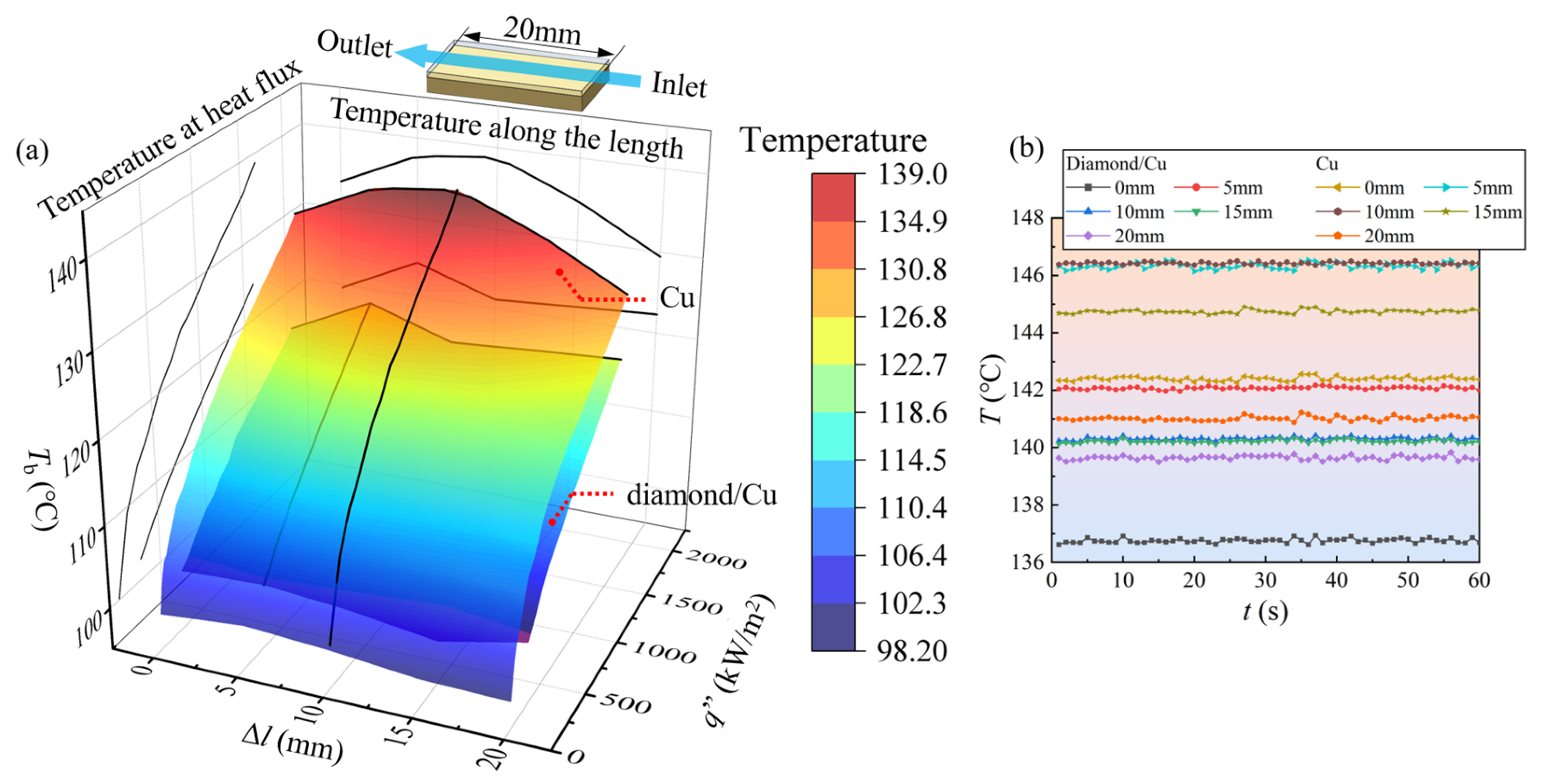
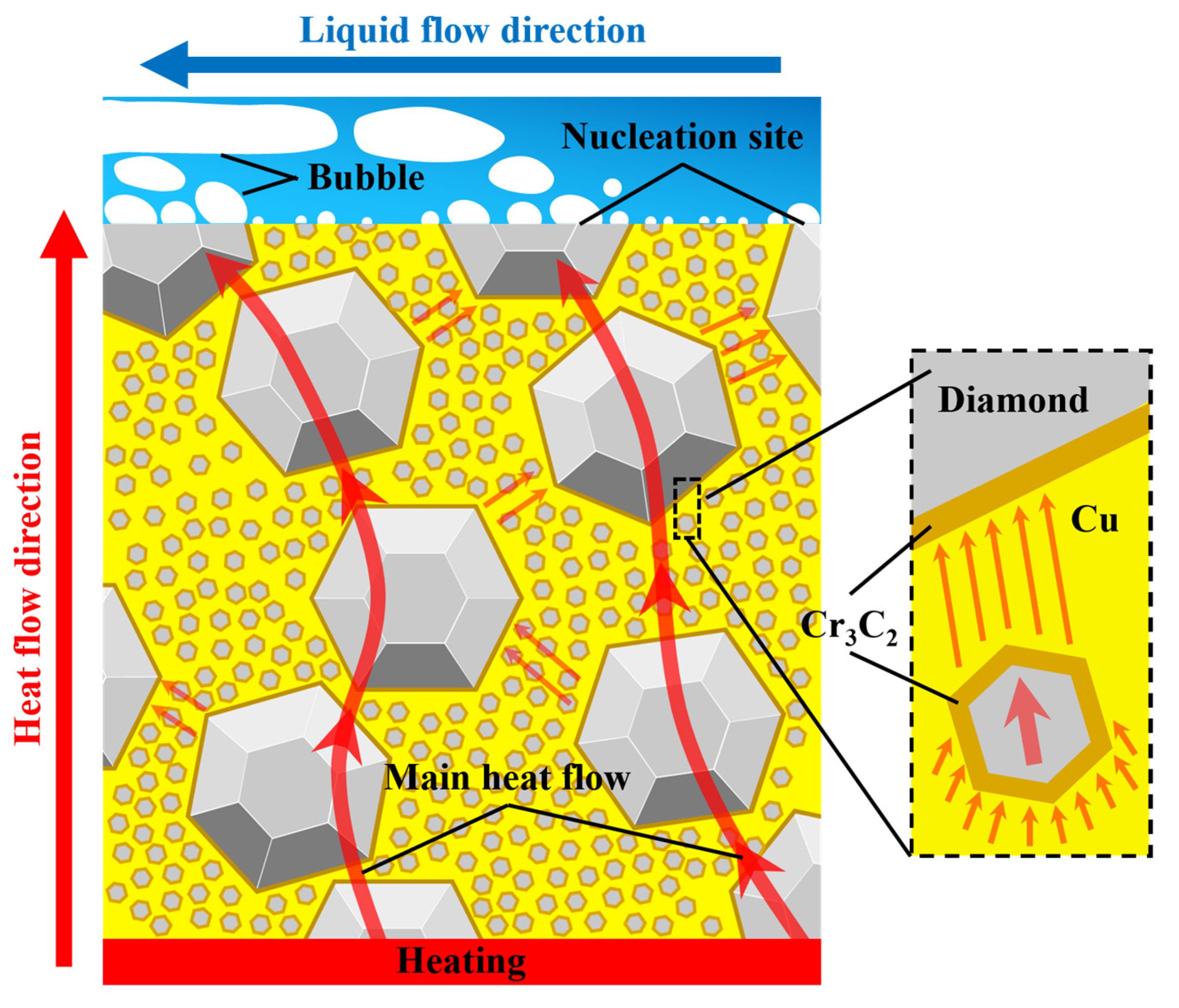
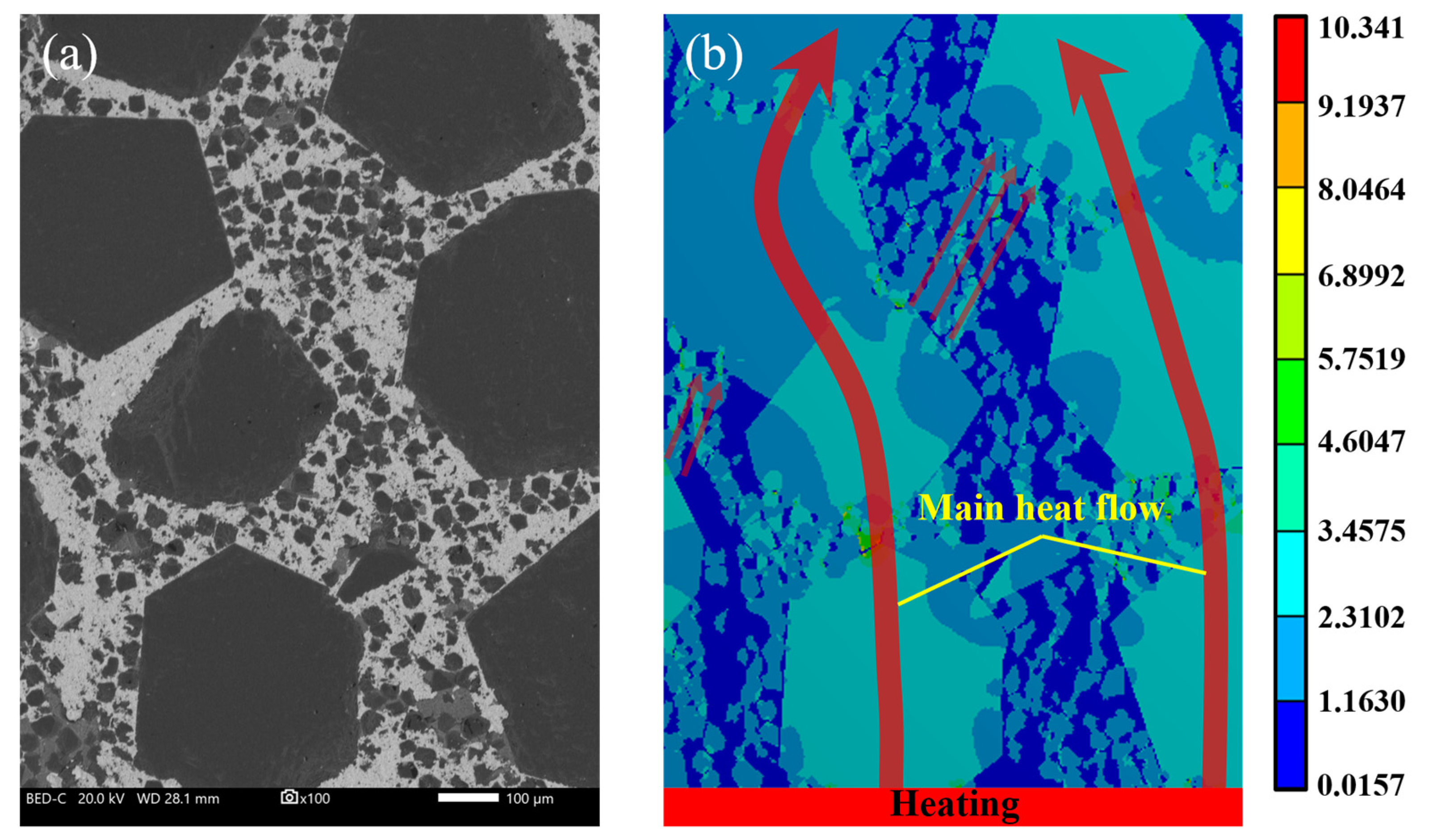
4.2. Enhanced Heat Transfer Mechanism of Diamond Network
4.3. Diamond/Cu Heat Sink Heat Transfer Model
5. Conclusions
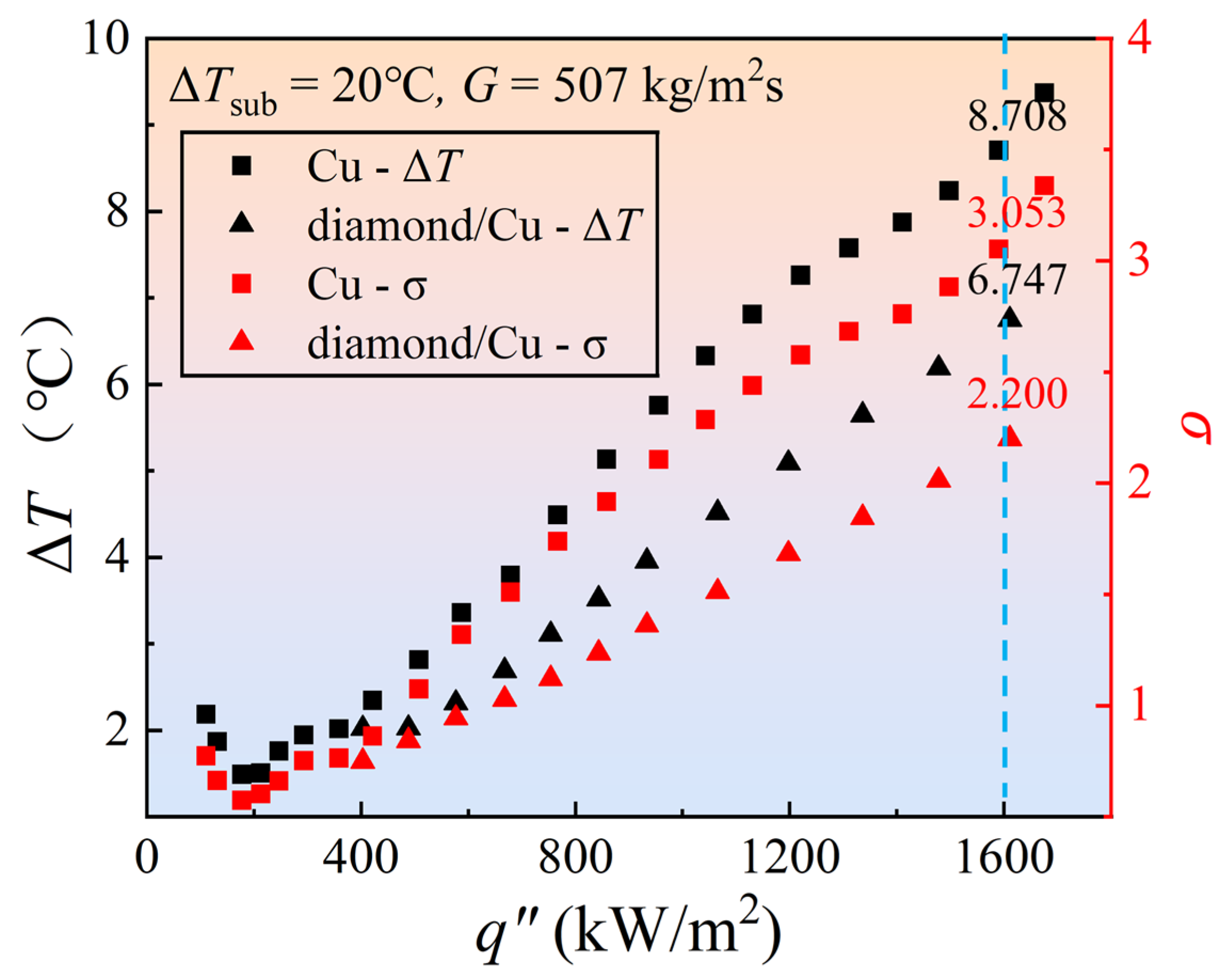
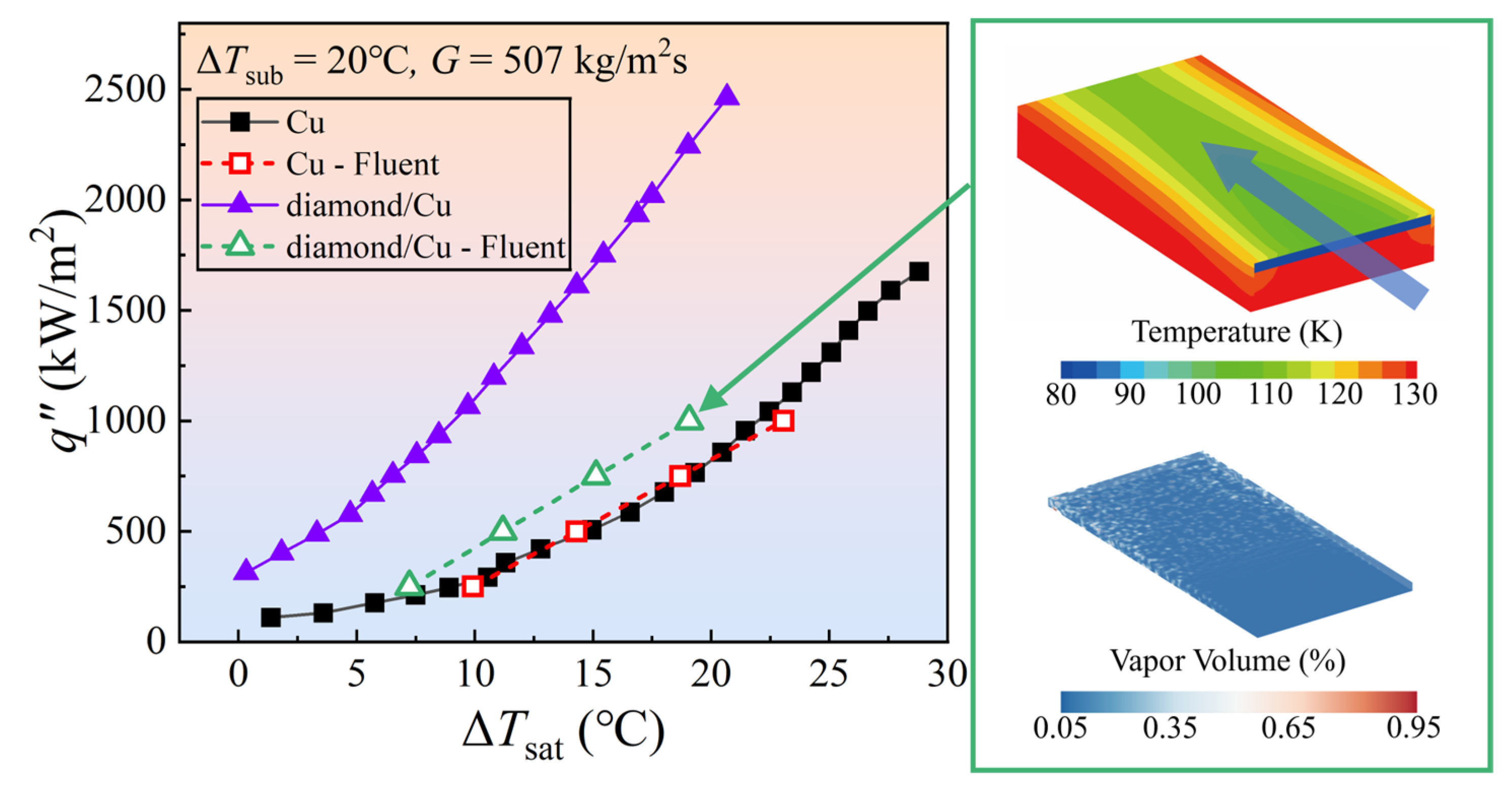
- At the same high temperature, the diamond/Cu heat sink exhibits higher boiling intensity and an improved heat transfer coefficient h of 38–51% compared to the Cu heat sink. At a high heat flux (q″) of approximately 1600 kW/m2, the diamond/Cu heat sink has a temperature difference that is 29% lower than that of the Cu heat sink. Moreover, the diamond/Cu heat sink demonstrates a temperature fluctuation amplitude (σ) reduction of 39% compared with the Cu heat sink.
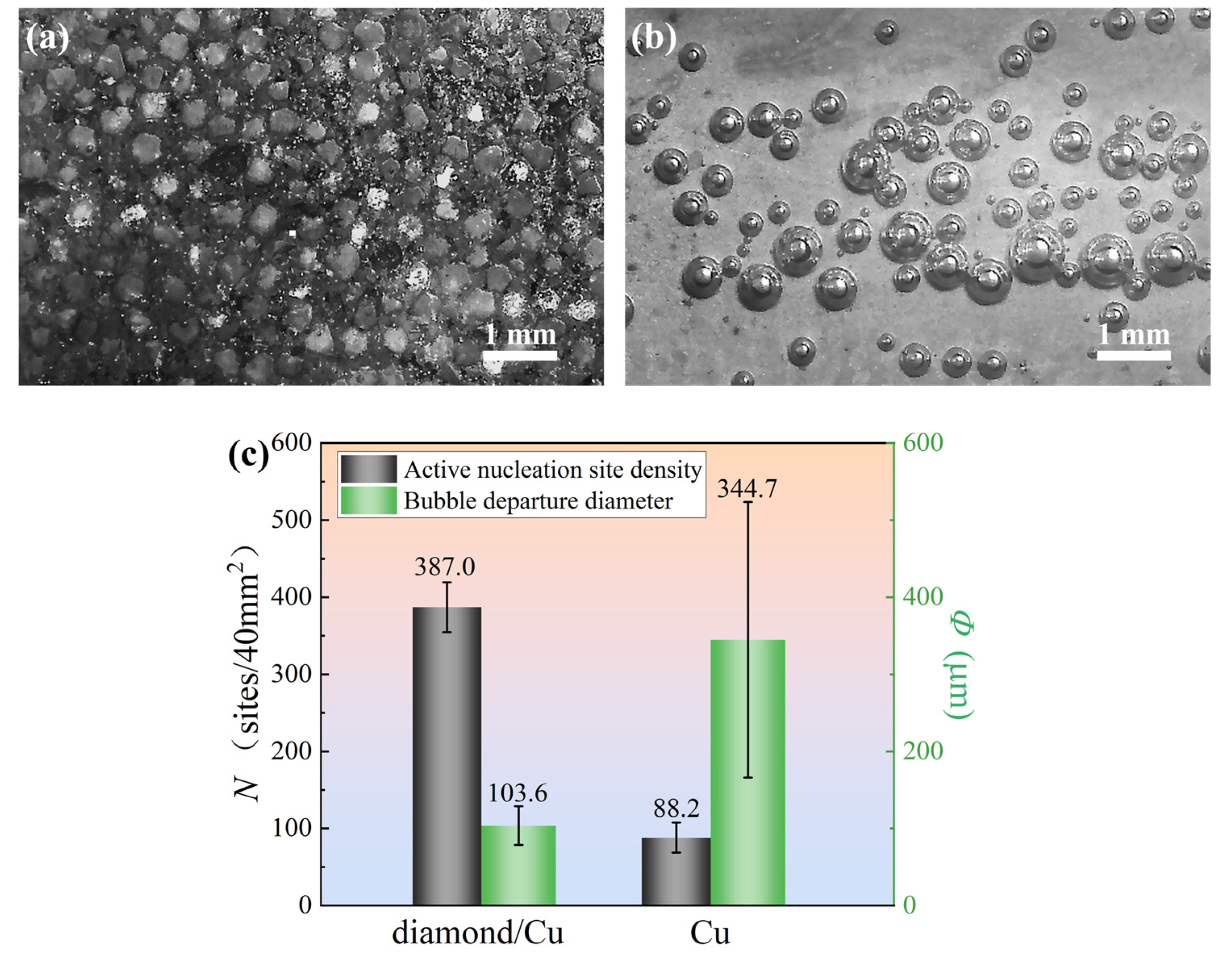
- The heat conduction network using diamonds is the main factor enhancing the heat transfer performance of the composite. The number of active nucleation sites on the diamond/Cu surface is much greater than that on the Cu surface. The bubble departure diameter is smaller. These factors contribute to the better flow boiling heat transfer performance of the diamond/Cu heat sink.
- The interfacial thermal conductivity between diamond and copper is crucial in studying the diamond network. The low thermal resistance of the interface significantly increases the internal heat flux of the material. Combining the transient thermal analysis model, which considers the thermal conduction network and the interfacial layer thermal conductivity, with the Fluent model allowed for a highly accurate simulation of the flow boiling heat transfer performance of the diamond/Cu composite heat sink.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kang, J.S.; Li, M.; Wu, H.; Nguyen, H.; Hu, Y. Experimental observation of high thermal conductivity in boron arsenide. Science 2018, 361, 575–578. [Google Scholar] [CrossRef]
- Ghani, I.A.; Kamaruzaman, N.; Sidik, N. Heat transfer augmentation in a microchannel heat sink with sinusoidal cavities and rectangular ribs. Int. J. Heat Mass Transf. 2017, 108, 1969–1981. [Google Scholar] [CrossRef]
- Lee, E.; Menumerov, E.; Hughes, R.A.; Neretina, S.; Luo, T.F. Low-cost nanostructures from nanoparticle-assisted large-scale lithography significantly enhance thermal energy transport across solid interfaces. ACS Appl. Mater. Interfaces 2018, 10, 34690–34698. [Google Scholar] [CrossRef] [PubMed]
- Mallik, S.; Ekere, N.; Best, C.; Bhatti, R. Investigation of thermal management materials for automotive electronic control units. Appl. Therm. Eng. 2011, 31, 355–362. [Google Scholar] [CrossRef]
- Moore, A.L.; Shi, L. Emerging challenges and materials for thermal management of electronics. Mater. Today 2014, 17, 163–174. [Google Scholar] [CrossRef]
- Kuddusi, L.; Denton, J.C. Analytical solution for heat conduction problem in composite slab and its implementation in constructal solution for cooling of electronics. Energy Convers. Manag. 2007, 48, 1089–1105. [Google Scholar] [CrossRef]
- Siddiqui, F.R.; Tso, C.-Y.; Qiu, H.; Chao, C.Y.H.; Fu, S.C. Hybrid nanofluid spray cooling performance and its residue surface effects: Toward thermal management of high heat flux devices. Appl. Therm. Eng. 2022, 211, 118454. [Google Scholar] [CrossRef]
- He, L.; Tang, X.; Luo, Q.; Liao, Y.; Luo, X.; Liu, J.; Ma, L.; Dong, D.; Gan, Y.; Li, Y. Structure optimization of a heat pipe-cooling battery thermal management system based on fuzzy grey relational analysis. Int. J. Heat Mass Transf. 2022, 182, 121924. [Google Scholar] [CrossRef]
- Deng, D.; Zeng, L.; Sun, W.; Pi, G.; Yang, Y. Experimental study of flow boiling performance of open-ring pin fin microchannels. Int. J. Heat Mass Transf. 2021, 167, 120829. [Google Scholar] [CrossRef]
- Molina, J.M.; Narciso, J.; Weber, L.; Mortensen, A.; Louis, E. Thermal conductivity of Al-SiC composites with monomodal and bimodal particle size distribution. Mater. Sci. Eng. A 2008, 480, 483–488. [Google Scholar] [CrossRef]
- Chen, P.; Luo, G.; Shen, Q.; Li, M.; Zhang, L. Thermal and electrical properties of W–Cu composite produced by activated sintering. Mater. Des. 2013, 46, 101–105. [Google Scholar] [CrossRef]
- Khanna, S.; Cluskey, P.M.; Cohen, A.B.; Yang, B.; Ohadi, M. Thin thermally efficient ICECool defense semiconductor power amplifiers. J. Microelectron. Electron. Packag. 2017, 14, 77–93. [Google Scholar] [CrossRef]
- Erp, R.V.; Soleimanzadeh, R.; Nela, L.; Kampitsis, G.; Matioli, E. Co-designing electronics with microfluidics for more sustainable cooling. Nature 2020, 585, 211–216. [Google Scholar] [CrossRef] [PubMed]
- Mohammed, H.A.; Gunnasegaran, P.; Shuaib, N.H. The impact of various nanofluid types on triangular microchannels heat sink cooling performance. Int. Commun. Heat Mass Transf. 2011, 38, 767–773. [Google Scholar] [CrossRef]
- Deng, D.; Zeng, L.; Sun, W. A review on flow boiling enhancement and fabrication of enhanced microchannels of microchannel heat sinks. Int. J. Heat Mass Transf. 2021, 175, 121332. [Google Scholar] [CrossRef]
- Wang, G.; Hao, L.; Cheng, P. An experimental and numerical study of forced convection in a microchannel with negligible axial heat conduction. Int. J. Heat Mass Transf. 2009, 52, 1070–1074. [Google Scholar] [CrossRef]
- Deng, D.; Chen, L.; Wan, W.; Fu, T.; Huang, X. Flow boiling performance in pin fin-interconnected reentrant microchannels heat sink in different operational conditions. Appl. Therm. Eng. 2019, 150, 1260–1272. [Google Scholar] [CrossRef]
- Qian, J.; Li, X.; Wu, Z.; Jin, Z.-J.; Sunden, B. A comprehensive review on liquid–liquid two-phase flow in microchannel: Flow pattern and mass transfer. Microfluid. Nanofluid. 2019, 23, 116. [Google Scholar] [CrossRef]
- McHale, J.P.; Garimella, S.V. Heat transfer in trapezoidal microchannels of various aspect ratios. Int. J. Heat Mass Transf. 2010, 53, 365–375. [Google Scholar] [CrossRef]
- Kandlikar, S.G.; Widger, T.; Kalani, A.; Mejia, V. Enhanced flow boiling over open microchannels with uniform and tapered gap manifolds. J. Heat Transf. 2013, 135, 061401. [Google Scholar] [CrossRef]
- Cheng, X.; Wu, H. Improved flow boiling performance in high-aspect-ratio interconnected microchannels. Int. J. Heat Mass Transf. 2021, 165, 120627. [Google Scholar] [CrossRef]
- Yin, L.; Jiang, P.; Xu, R.; Wang, W.; Jia, L. Visualization of flow patterns and bubble behavior during flow boiling in open microchannels. Int. Commun. Heat Mass Transf. 2017, 85, 131–138. [Google Scholar] [CrossRef]
- Gilmore, N.; Timchenko, V.; Menictas, C. Open manifold microchannel heat sink for high heat flux electronic cooling with a reduced pressure drop. Int. J. Heat Mass Transf. 2020, 163, 120395. [Google Scholar] [CrossRef]
- Yin, L.; Jiang, P.; Xu, R.; Hu, H.; Jia, L. Heat transfer and pressure drop characteristics of water flow boiling in open microchannels. Int. J. Heat Mass Transf. 2019, 137, 204–215. [Google Scholar] [CrossRef]
- Özdemir, M.R.; Mahmoud, M.M.; Karayiannis, T.G. Flow boiling of water in a rectangular metallic microchannel. Heat Transf. Eng. 2021, 42, 492–516. [Google Scholar] [CrossRef]
- Qi, Z.; Zheng, Y.; Zhu, X.; Wei, J.; Liu, J.; Chen, L.; Li, C. An ultra-thick all-diamond microchannel heat sink for single-phase heat transmission efficiency enhancement. Vacuum 2020, 177, 109377. [Google Scholar] [CrossRef]
- Yang, Q.; Zhao, J.; Huang, Y.; Zhu, X.; Fu, W.; Li, C.; Miao, J. A diamond made microchannel heat sink for high-density heat flux dissipation. Appl. Therm. Eng. 2019, 158, 113804. [Google Scholar] [CrossRef]
- Qi, X.; Zhang, L.; Ren, S. Review of metal matrix composites with high thermal conductivity for thermal management application. Prog. Nat. Sci. Mater. Int. 2011, 21, 189–197. [Google Scholar] [CrossRef]
- Xie, Z.; Guo, H.; Zhang, X.; Huang, S. Enhancing thermal conductivity of Diamond/Cu composites by regulating distribution of bimodal diamond particles. Diam. Relat. Mater. 2019, 100, 107564. [Google Scholar] [CrossRef]
- Xie, Z.; Guo, H.; Zhang, X.; Huang, S.; Mi, X. Tailoring the thermal and mechanical properties of diamond/Cu composites by interface regulation of Cr alloying. Diam. Relat. Mater. 2021, 114, 108309. [Google Scholar] [CrossRef]
- Yuan, M.; Tan, Z.; Fan, G.; Xiong, D.; Guo, Q.; Guo, Q.; Li, Z.; Zhang, D. Theoretical modelling for interface design and thermal conductivity prediction in diamond/Cu composites. Diam. Relat. Mater. 2018, 81, 38–44. [Google Scholar] [CrossRef]
- Every, A.G.; Tzou, Y.; Hasselman, D.P.H.; Raj, R. The effect of particle size on the thermal conductivity of ZnS/diamond composites. Acta Metall. Mater. 1992, 40, 123–129. [Google Scholar] [CrossRef]
- Molina-Jordá, J.M. Nano- and micro-/meso-scale engineered magnesium/diamond composites: Novel materials for emerging challenges in thermal management. Acta Mater. 2015, 96, 101–110. [Google Scholar] [CrossRef]
- Molina-Jordá, J.M. Design of composites for thermal management: Aluminum reinforced with diamond-containing bimodal particle mixtures. Compos. Part A 2015, 70, 45–51. [Google Scholar] [CrossRef]
- Li, Y.; Zhou, H.; Wu, C.; Yin, Z.; Liu, C.; Huang, Y.; Liu, J.; Shi, Z. The Interface and fabrication process of diamond/Cu composites with nanocoated diamond for heat sink applications. Metals 2021, 11, 196. [Google Scholar] [CrossRef]
- Gupta, S.K.; Misra, R.D. Experimental study of pool boiling heat transfer on copper surfaces with Cu-Al2O3 nanocomposite coatings. Int. Commun. Heat Mass Transf. 2018, 97, 47–55. [Google Scholar] [CrossRef]
- Buchling, P.; Kandlikar, S.G. Enhanced flow boiling of ethanol in open microchannels with tapered manifolds in a gravity-driven flow. J. Heat Transf. 2016, 138, 031503. [Google Scholar] [CrossRef]
- Weibel, J.A.; Garimella, S.V.; North, M.T. Characterization of evaporation and boiling from sintered powder wicks fed by capillary action. Int. J. Heat Mass Transf. 2010, 53, 4204–4215. [Google Scholar] [CrossRef]
- Deng, D.; Tang, Y.; Liang, D.; He, H.; Yang, S. Flow boiling characteristics in porous heat sink with reentrant microchannels. Int. J. Heat Mass Transf. 2014, 70, 463–477. [Google Scholar] [CrossRef]
- Yin, L.; Sun, M.; Jiang, P.; Dang, C.; Jia, L. Heat transfer coefficient and pressure drop of water flow boiling in porous open microchannels heat sink. Appl. Therm. Eng. 2023, 218, 119361. [Google Scholar] [CrossRef]
- Law, M.; Lee, P.S.; Balasubramanian, K. Experimental investigation of flow boiling heat transfer in novel oblique-finned microchannels. Int. J. Heat Mass Transf. 2014, 76, 419–431. [Google Scholar] [CrossRef]
- Moffat, R.J. Describing the uncertainties in experimental results. Exp. Therm Fluid. Sci. 1988, 1, 3–17. [Google Scholar] [CrossRef]
- Liu, X.; Sun, F.; Wang, L.; Wu, Z.; Wang, X.; Wang, J.; Kim, M.J.; Zhang, H. The role of Cr interlayer in determining interfacial thermal conductance between Cu and diamond. Appl. Surf. Sci. 2020, 515, 146046. [Google Scholar] [CrossRef]
- Monje, I.E.; Louis, E.; Molina, J.M. Role of Al4C3 on the stability of the thermal conductivity of Al/diamond composites subjected to constant or oscillating temperature in a humid environment. J. Mater. Sci. 2016, 51, 8027–8036. [Google Scholar] [CrossRef]
- Majumdar, A.; Reddy, P. Role of electron–phonon coupling in thermal conductance of metal–nonmetal interfaces. App. Phys. Lett. 2004, 84, 4768–4770. [Google Scholar] [CrossRef]
- Tan, Z.; Li, Z.; Xiong, D.; Fan, G.; Ji, G.; Zhang, D. A predictive model for interfacial thermal conductance in surface metallized diamond aluminum matrix composites. Mater. Des. 2014, 55, 257–262. [Google Scholar] [CrossRef]
- Hopkins, P.E.; Kassebaum, J.L.; Norris, P.M. Effects of electron scattering at metal-nonmetal interfaces on electron-phonon equilibration in gold films. J. App. Phys. 2009, 105, 023710. [Google Scholar] [CrossRef]




| Parameters | Maximum Relative Uncertainty |
|---|---|
| T (T-type) | ±0.30 °C |
| T (K-type) | ±0.20 °C |
| G | ±2.50% |
| U | ±0.50% |
| I | ±0.50% |
| q“ | ±1.78% |
| h | ±1.57% |
| Material | Density ρ (kg/m3) | Thermal Conductivity λ (W/mK) | Specific Heat c (J/kgK) | Phonon Velocity ν (m/s) |
|---|---|---|---|---|
| Cu | 8900 | 398 | 386 | 2881 |
| Cr3C2 | 6680 | 19 | 456 | 5628 |
| Diamond | 3520 | 1500 | 512 | 12,775 |
| Interface | Cu-Cr3C2 | Cr3C2-Diamond | Diamond-Cr3C2 | Cr3C2-Cu |
|---|---|---|---|---|
| hIF (W/m2K) | 5.138 × 108 | 6.966 × 108 | 4.820 × 109 | 1.955 × 109 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, N.; Sun, M.; Guo, H.; Xie, Z.; Du, S. Enhancement Effect of a Diamond Network on the Flow Boiling Heat Transfer Characteristics of a Diamond/Cu Heat Sink. Energies 2023, 16, 7228. https://doi.org/10.3390/en16217228
Wu N, Sun M, Guo H, Xie Z, Du S. Enhancement Effect of a Diamond Network on the Flow Boiling Heat Transfer Characteristics of a Diamond/Cu Heat Sink. Energies. 2023; 16(21):7228. https://doi.org/10.3390/en16217228
Chicago/Turabian StyleWu, Nan, Mingmei Sun, Hong Guo, Zhongnan Xie, and Shijie Du. 2023. "Enhancement Effect of a Diamond Network on the Flow Boiling Heat Transfer Characteristics of a Diamond/Cu Heat Sink" Energies 16, no. 21: 7228. https://doi.org/10.3390/en16217228
APA StyleWu, N., Sun, M., Guo, H., Xie, Z., & Du, S. (2023). Enhancement Effect of a Diamond Network on the Flow Boiling Heat Transfer Characteristics of a Diamond/Cu Heat Sink. Energies, 16(21), 7228. https://doi.org/10.3390/en16217228






