Heat Production Performance from an Enhanced Geothermal System (EGS) Using CO2 as the Working Fluid
Abstract
:1. Introduction
2. Numerical Method
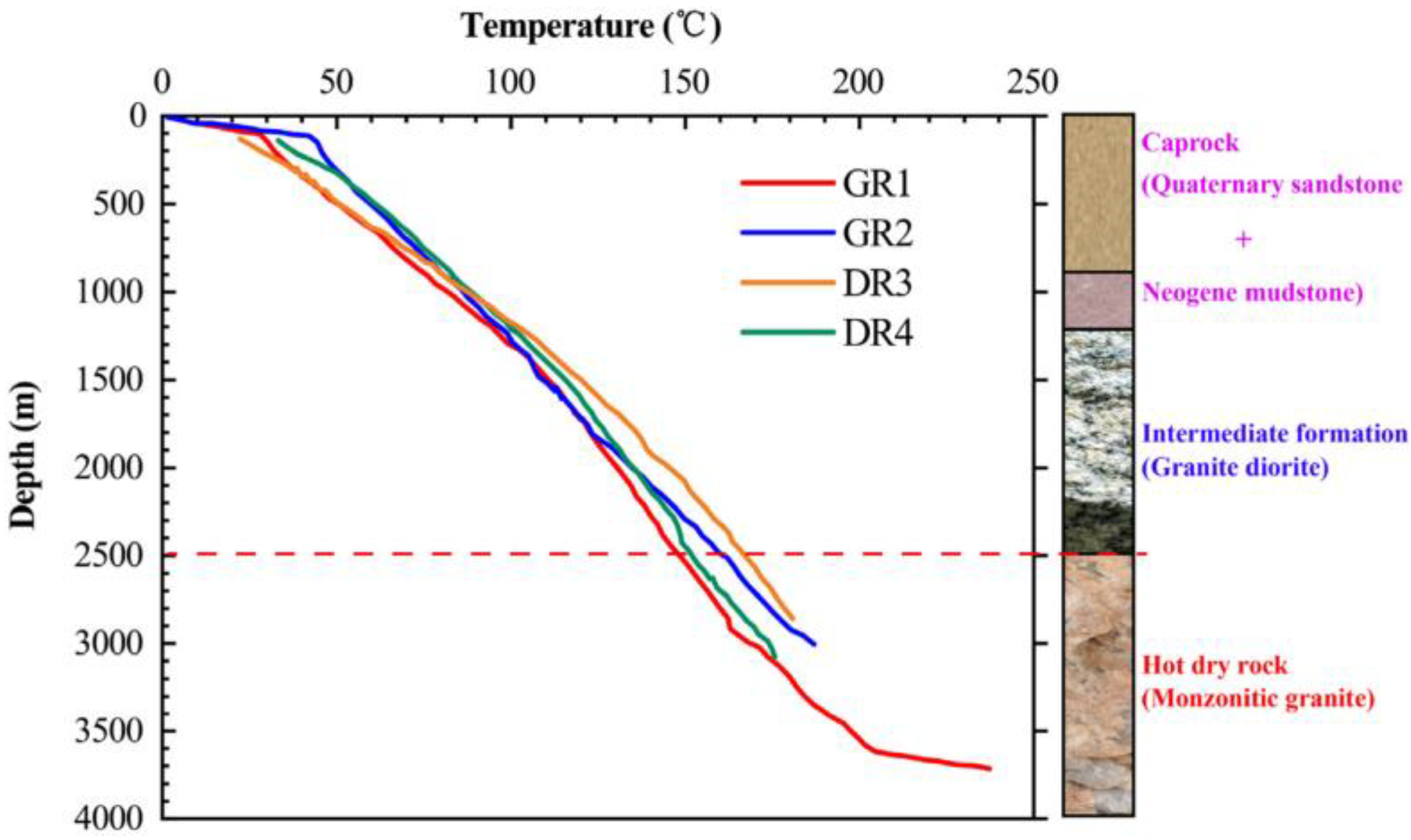
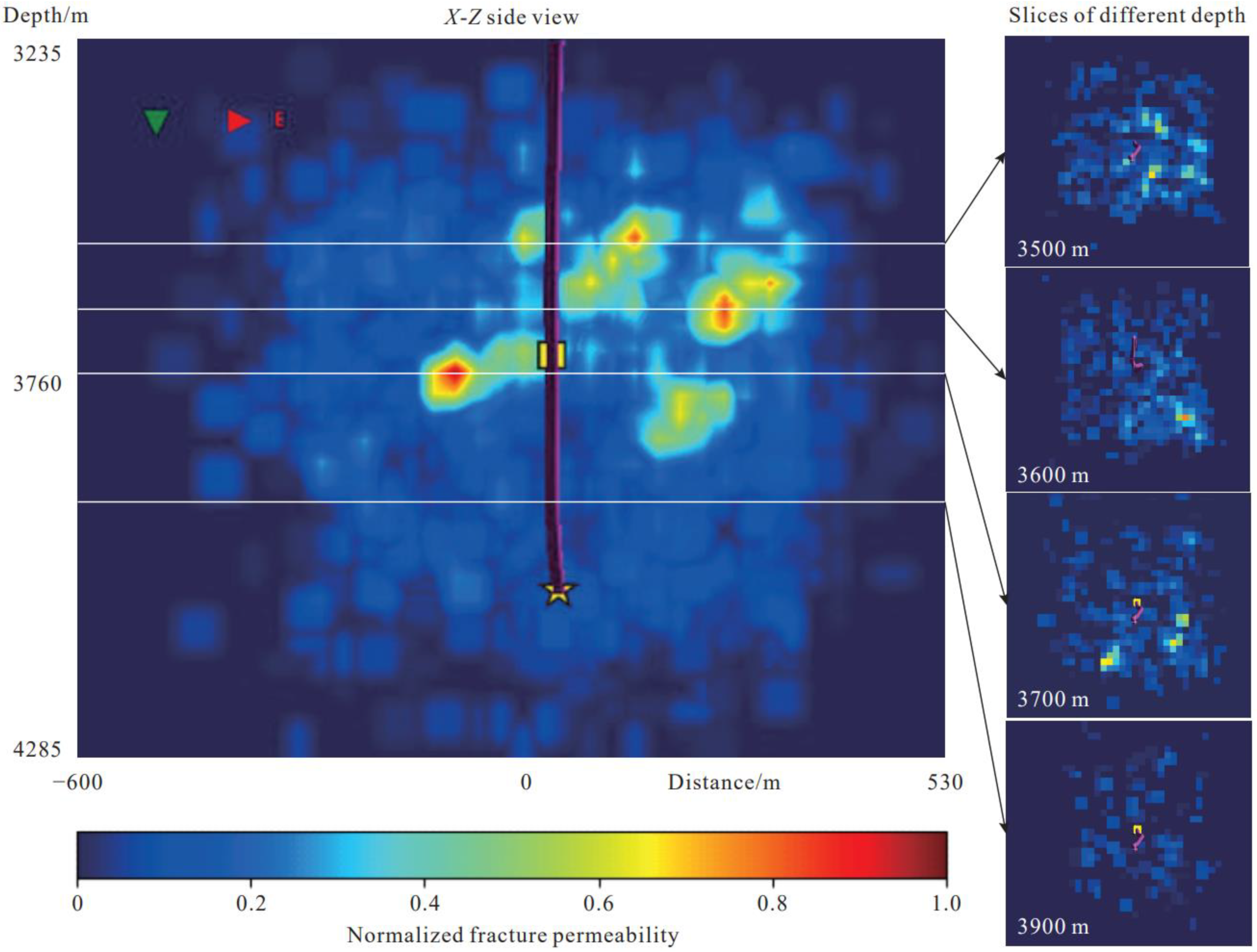
2.1. Geothermal Characteristics of the Gonghe Basin
2.2. Numerical Simulator
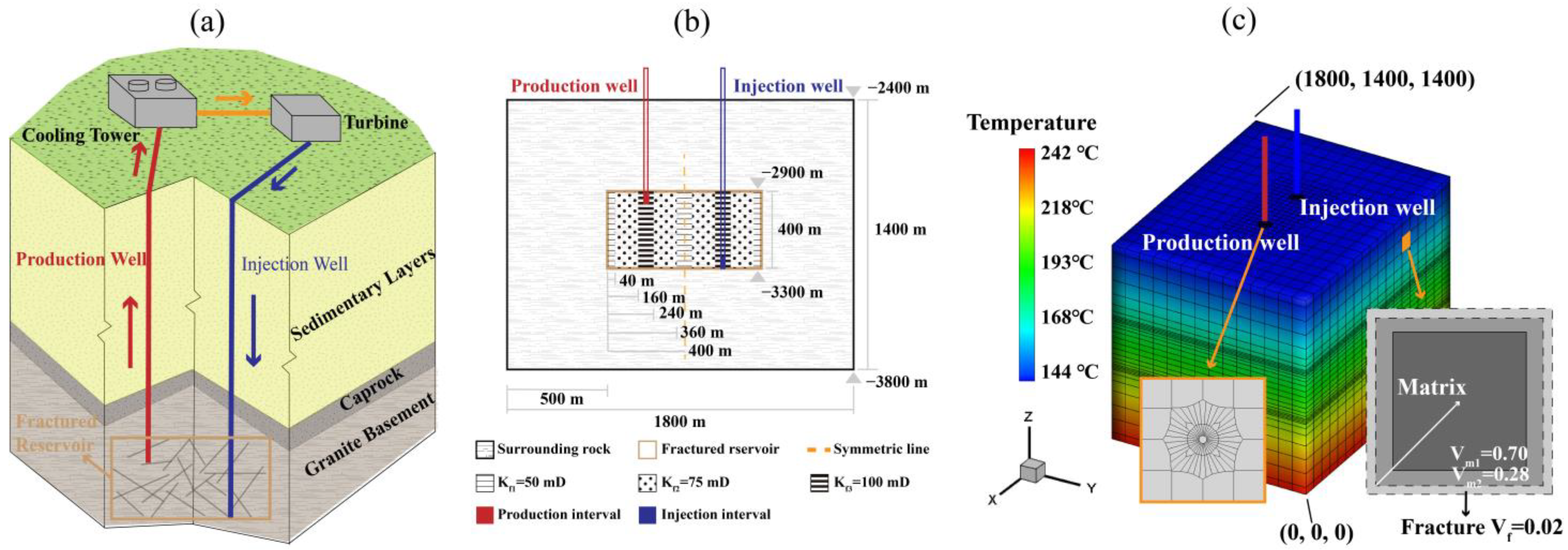
2.3. Model Geometry and Numerical Discretization
2.4. Model Parameters
2.5. Initial and Boundary Conditions
3. Results and Discussion
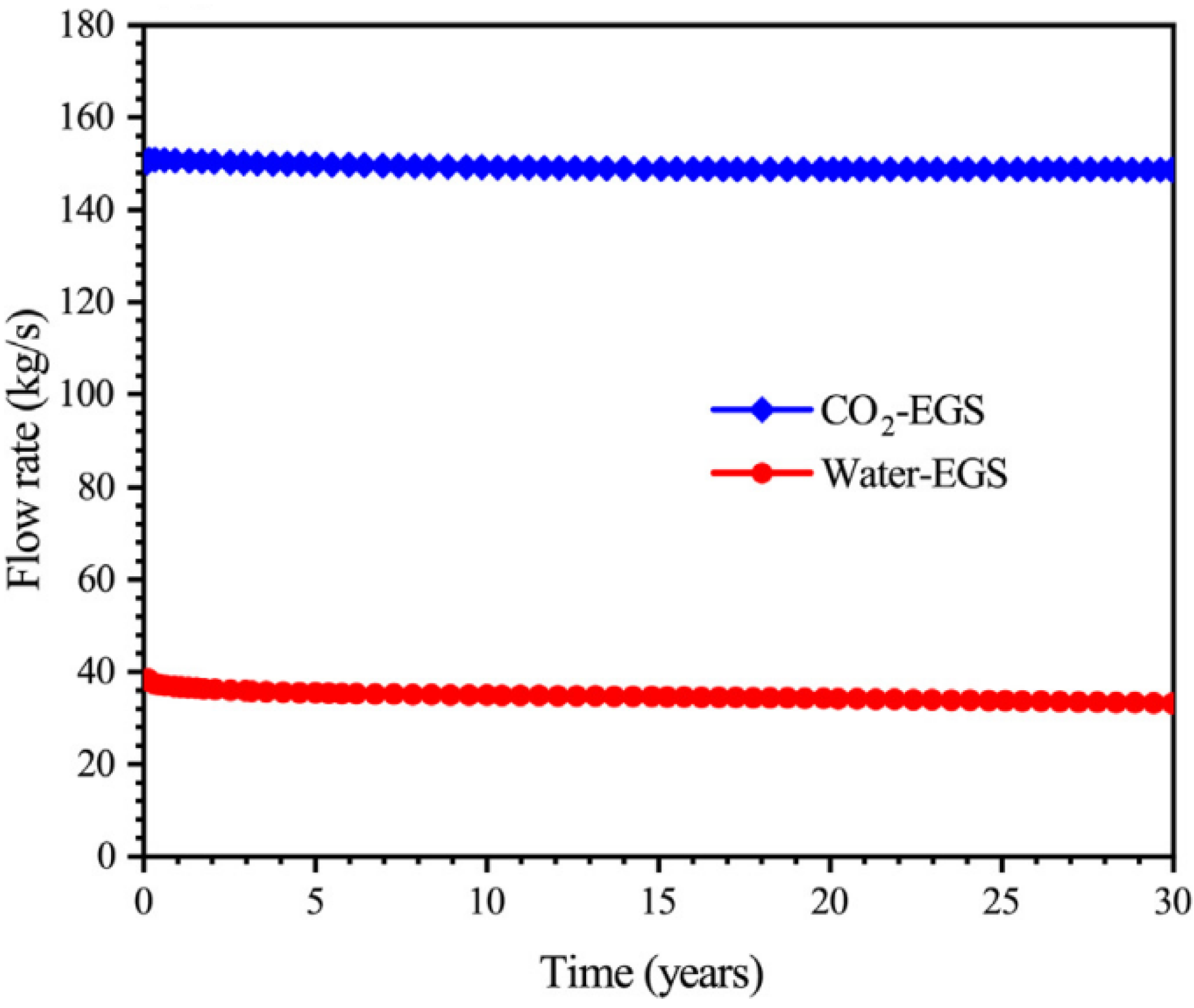
3.1. Production Temperature, Flow Rate, and Heat Extraction Rate
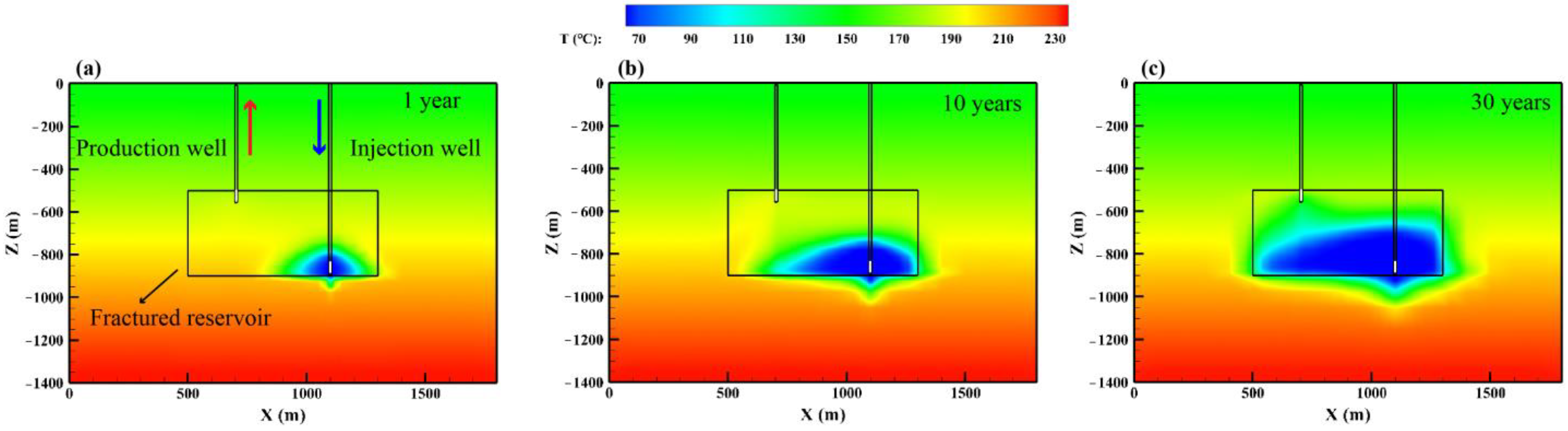
3.2. Spatial Distribution of Reservoir Temperature
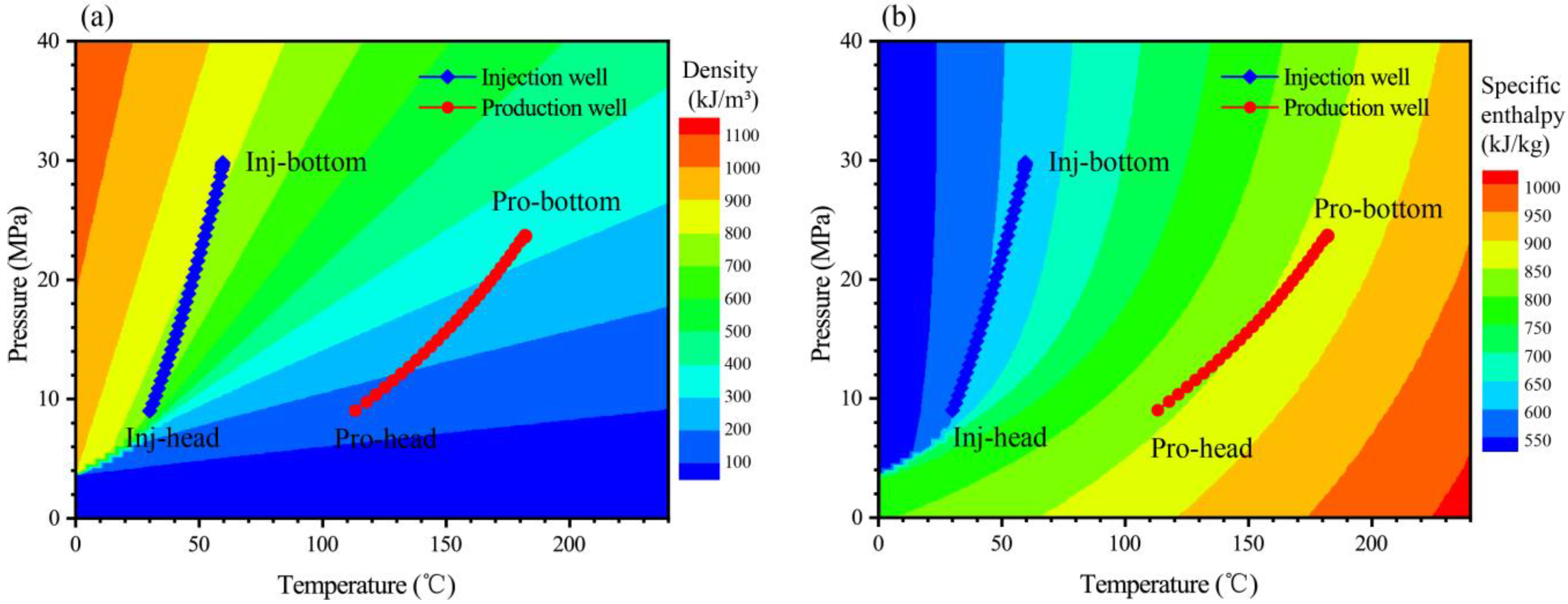
3.3. Changes in CO2 Velocity, Density, and Specific Enthalpy along the Wellbore
3.4. Evaluation of Heat Production Performance
3.5. Limitations of Using CO2 as the Working Fluid
4. Conclusions
- (1)
- The proposed CO2-EGS shows a promising heat production performance for the specified operating conditions using two vertical wells. The heat production processes of the proposed CO2-EGS include the ascending geothermal production stage in the first 9 years and the declining geothermal production stage in the following 21 years. The geothermal production temperature and heat extraction rate gradually increase during the ascending stage, while they drop by 20.0% and 14.3% during the declining stage. The heat extraction rate meets the commercial requirements throughout the 30-year production. In addition, the flow rate maintains a steady level of 150 kg/s throughout the entire production period.
- (2)
- The dual-vertical well pattern with height difference is a preferred well layout for the CO2-based enhanced geothermal systems. This is mainly because the optimal flow path can be obtained for the injected cold CO2 to extract more heat stored in the rock matrix, and thus a potential early thermal breakthrough can be avoided effectively. In addition, the trapezoid cold area occurs in the fractured geothermal reservoir due to the natural convection of CO2 fluid being significantly stronger than water. This further indicates that there must be a certain height difference in the perforation zone between the injection well and production well for the CO2-EGS.
- (3)
- The velocity and density of CO2 change significantly in the wellbore. The CO2 velocity increases from 12.29 m/s to 22.97 m/s during the upward process in the production well. The difference of the CO2 density between the well bottom and the wellhead reaches 426.92 kg/m3 in the production well. The significant density difference in the production well is the main reason for the CO2 velocity variation in the wellbore. In the production well, a significant Joule–Thomson effect coupled with a drastic temperature drop (e.g., about 62.61 °C) is observed based on the wellbore–reservoir coupled model. This is a critical defect of the proposed CO2-EGS for stable geothermal production. Therefore, pre-optimization analyses and physical material treatment (e.g., thermal insulation materials) are required to reduce this negative impact during the development of CO2-EGSs.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sowizdzal, A. Geothermal Systems—An Overview. Energies 2022, 15, 6377. [Google Scholar] [CrossRef]
- Yu, H.; Xu, T.F.; Yuan, Y.L.; Feng, B.; ShangGuan, S.T. Enhanced heat extraction performance from deep buried U-shaped well using the high-pressure jet grouting technology. Renew. Energy 2023, 202, 1377–1386. [Google Scholar] [CrossRef]
- Zhong, C.H.; Xu, T.F.; Gherardi, F.; Yuan, Y.L. Comparison of CO2 and water as working fluids for an enhanced geothermal system in the Gonghe Basin, northwest China. Gondwana Res. 2023, 122, 199–214. [Google Scholar] [CrossRef]
- Zhong, C.; Xu, T.; Yuan, Y.; Feng, B.; Yu, H. The feasibility of clean power generation from a novel dual-vertical-well enhanced geothermal system (EGS): A case study in the Gonghe Basin, China. J. Clean. Prod. 2022, 344, 131109. [Google Scholar] [CrossRef]
- Haraden, J. The status of hot dry rock as an energy source. Energy 1992, 17, 777–786. [Google Scholar] [CrossRef]
- Tester, J.W.; Anderson, B.J.; Batchelor, A.S.; Blackwell, D.D.; DiPippo, R.; Drake, E.M.; Garnish, J.; Livesay, B.; Moore, M.C.; Nichols, K.; et al. The Future of Geothermal Energy. Impact of Enhanced Geothermal Systems [EGS] on the United States in the 21st Century; Massachusetts Institute of Technology: Cambridge, MA, USA, 2006. [Google Scholar]
- Catalan, L.; Aranguren, P.; Araiz, M.; Perez, G.; Astrain, D. New opportunities for electricity generation in shallow hot dry rock fields: A study of thermoelectric generators with different heat exchangers. Energy Convers. Manag. 2019, 200, 112061. [Google Scholar] [CrossRef]
- Li, S.; Wang, S.; Tang, H. Stimulation mechanism and design of enhanced geothermal systems: A comprehensive review. Renew. Sustain. Energy Rev. 2022, 155. [Google Scholar] [CrossRef]
- Lu, S.M. A global review of enhanced geothermal system (EGS). Renew. Sustain. Energy Rev. 2018, 81, 2902–2921. [Google Scholar] [CrossRef]
- Duchane, D. (Ed.) Hot Dry Rock Flow Testing What Has It Use? What Questions Remain? Los Alamos National Lab. (LANL): Los Alamos, NM, USA, 1993.
- Brown, D.W. (Ed.) A hot dry rock geothermal energy concept utilizing supercritical CO2 instead of water. In The Twenty-Fifth Workshop on Geothermal Reservoir Engineering; Stanford University: Stanford, CA, USA, 2000. [Google Scholar]
- Mahmoodpour, S.; Singh, M.; Baer, K.; Sass, I. Thermo-hydro-mechanical modeling of an enhanced geothermal system in a fractured reservoir using carbon dioxide as heat transmission fluid—A sensitivity investigation. Energy 2022, 254, 124266. [Google Scholar] [CrossRef]
- Singh, M.; Mahmoodpour, S.; Ershadnia, R.; Soltanian, M.R.; Sass, I. Comparative study on heat extraction from Soultz-sous-Forêts geothermal field using supercritical carbon dioxide and water as the working fluid. Energy 2023, 266, 126388. [Google Scholar] [CrossRef]
- Olasolo, P.; Juárez, M.C.; Morales, M.P.; D’Amico, S.; Liarte, I.A. Enhanced geothermal systems (EGS): A review. Renew. Sustain. Energy Rev. 2016, 56, 133–144. [Google Scholar] [CrossRef]
- Pan, L.; Freifeld, B.; Doughty, C.; Zakem, S.; Sheu, M.; Cutright, B.; Terrall, T. Fully coupled wellbore-reservoir modeling of geothermal heat extraction using CO2 as the working fluid. Geothermics 2015, 53, 100–113. [Google Scholar] [CrossRef]
- Pruess, K. Enhanced geothermal systems (EGS) using CO2 as working fluid—A novel approach for generating renewable energy with simultaneous sequestration of carbon. Geothermics 2006, 35, 351–367. [Google Scholar] [CrossRef]
- Pan, L.; Doughty, C.; Freifeld, B. How to sustain a CO2-thermosiphon in a partially saturated geothermal reservoir: Lessons learned from field experiment and numerical modeling. Geothermics 2018, 71, 274–293. [Google Scholar] [CrossRef]
- Atrens, A.D.; Gurgenci, H.; Rudolph, V. CO2 Thermosiphon for Competitive Geothermal Power Generation. Energy Fuels 2009, 23, 553–557. [Google Scholar] [CrossRef]
- Atrens, A.D.; Gurgenci, H.; Rudolph, V. Electricity generation using a carbon-dioxide thermosiphon. Geothermics 2010, 39, 161–169. [Google Scholar] [CrossRef]
- Pan, C.; Romero, C.E.; Levy, E.K.; Wang, X.; Rubio-Maya, C.; Pan, L. Fully coupled wellbore-reservoir simulation of supercritical CO2 injection from fossil fuel power plant for heat mining from geothermal reservoirs. J. CO2 Util. 2018, 27, 480–492. [Google Scholar] [CrossRef]
- Wang, X.C.; Pan, C.J.; Romero, C.E.; Qiao, Z.L.; Banerjee, A.; Rubio-Maya, C.; Pan, L. Thermo-economic analysis of a direct supercritical CO2 electric power generation system using geothermal heat. Front. Energy 2022, 16, 246–262. [Google Scholar] [CrossRef]
- Hu, Z.X.; Xu, T.F.; Feng, B.; Yuan, Y.L.; Li, F.Y.; Feng, G.H.; Jiang, Z. Thermal and fluid processes in a closed-loop geothermal system using CO2 as a working fluid. Renew. Energy 2020, 154, 351–367. [Google Scholar] [CrossRef]
- Guo, T.; Gong, F.; Wang, X.; Lin, Q.; Qu, Z.; Zhang, W. Performance of enhanced geothermal system (EGS) in fractured geothermal reservoirs with CO2 as working fluid. Appl. Therm. Eng. 2019, 152, 215–230. [Google Scholar] [CrossRef]
- Xu, T.; Feng, G.; Hou, Z.; Tian, H.; Shi, Y.; Lei, H. Wellbore–reservoir coupled simulation to study thermal and fluid processes in a CO2-based geothermal system: Identifying favorable and unfavorable conditions in comparison with water. Environ. Earth Sci. 2015, 73, 6797–6813. [Google Scholar] [CrossRef]
- Zeng, L.; Zhang, K.-J.; Tang, X.-C.; Zhang, Y.-X.; Li, Z.-W. Mid-Permian rifting in central China; record of geochronology, geochemistry and Sr-Nd-Hf isotopes of bimodal magmatism on NE Qinghai-Tibetan Plateau. Gondwana Res. 2018, 57, 77–89. [Google Scholar] [CrossRef]
- Yan, W.D.; Wang, Y.X.; Gao, X.Z.; Zhang, S.; Ma, Y.; Shang, X.; Guo, S. Distribution and Aggregation Mechanism of Geothermal Energy in Gonghe Basin. Northwestern Geol. 2013, 46, 223–230. [Google Scholar]
- Lei, Z.; Zhang, Y.; Zhang, S.; Fu, L.; Hu, Z.; Yu, Z.; Li, L.; Zhou, J. Electricity generation from a three-horizontal-well enhanced geothermal system in the Qiabuqia geothermal field, China: Slickwater fracturing treatments for different reservoir scenarios. Renew. Energy 2020, 145, 65–83. [Google Scholar] [CrossRef]
- Yan, W.D. Characteristics of Gonghe Basin hot dry rock and its utilization prospects. Sci. Technol. Rev. 2015, 33, 54–57. [Google Scholar]
- Wang, B.; Zhang, G.; Li, S.; Yang, Z.; Roberts, A.P.; Zhao, Q.; Wang, Z. Early Carboniferous paleomagnetic results from the northeastern margin of the Qinghai–Tibetan plateau and their implications. Gondwana Res. 2016, 36, 57–64. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, S.; Li, S.; Jia, X.J.; Jiang, G.; Gao, P.; Wang, Y.; Hu, S. Geothermal characteristics of the Qiabuqia geothermal area in the Gonghe basin, northeastern Tibetan Plateau. Chin. J. Geophys. 2018, 61, 4545–4557. [Google Scholar]
- Xu, T.; Yuan, Y.; Jia, X.; Lei, Y.; Li, S.; Feng, B.; Hou, Z.; Jiang, Z. Prospects of power generation from an enhanced geothermal system by water circulation through two horizontal wells: A case study in the Gonghe Basin, Qinghai Province, China. Energy 2018, 148, 196–207. [Google Scholar] [CrossRef]
- Lei, Z.; Zhang, Y.; Yu, Z.; Hu, Z.; Li, L.; Zhang, S.; Fu, L.; Zhou, L.; Xie, Y. Exploratory research into the enhanced geothermal system power generation project: The Qiabuqia geothermal field, Northwest China. Renew. Energy 2019, 139, 52–70. [Google Scholar] [CrossRef]
- Zhang, C.; Jiang, G.; Jia, X.; Li, S.; Zhang, S.; Hu, D.; Hu, S.; Wang, Y. Parametric study of the production performance of an enhanced geothermal system: A case study at the Qiabuqia geothermal area, northeast Tibetan plateau. Renew. Energy 2019, 132, 959–978. [Google Scholar] [CrossRef]
- Ram Mohan, A.; Turaga, U.; Shembekar, V.; Elsworth, D.; Pisupati, S.V. Utilization of carbon dioxide from coal-based power plants as a heat transfer fluid for electricity generation in enhanced geothermal systems (EGS). Energy 2013, 57, 505–512. [Google Scholar] [CrossRef]
- Pruess, K.; Oldenburg, C.; Moridis, G. TOUGH2 User’s Guide Version 2; Lawrence Berkeley Natl Lab: Berkeley, CA, USA, 1999.
- Pan, L.; Oldenburg, C.M. T2Well—An integrated wellbore–reservoir simulator. Comput. Geosci. 2014, 65, 46–55. [Google Scholar] [CrossRef]
- Vasini, E.M.; Battistelli, A.; Berry, P.; Bonduà, S.; Bortolotti, V.; Cormio, C.; Pan, L. Interpretation of production tests in geothermal wells with T2Well-EWASG. Geothermics 2018, 73, 158–167. [Google Scholar] [CrossRef]
- Hu, L.; Pan, L.; Zhang, K. Modeling brine leakage to shallow aquifer through an open wellbore using T2WELL/ECO2N. Int. J. Greenh. Gas Control 2012, 9, 393–401. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, B.; Zhou, J.; Liu, H.; Zhou, L.; Wu, C. Research and Test on the Stimulated Reservoir Volume Technology of Hot Dry Rock. Pet. Drill. Tech. 2020, 48, 82–87. [Google Scholar]
- Liao, J.; Cao, C.; Hou, Z.; Mehmood, F.; Feng, W.; Yue, Y.; Liu, H. Field scale numerical modeling of heat extraction in geothermal reservoir based on fracture network creation with supercritical CO2 as working fluid. Environ. Earth Sci. 2020, 79, 1–22. [Google Scholar] [CrossRef]
- Farkas, M.P.; Hofmann, H.; Zimmermann, G.; Zang, A.; Bethmann, F.; Meier, P.; Cottrell, M.; Josephson, N. Hydromechanical analysis of the second hydraulic stimulation in well PX-1 at the Pohang fractured geothermal reservoir, South Korea. Geothermics 2021, 89, 101990. [Google Scholar] [CrossRef]
- Yuan, Y.; Xu, T.; Moore, J.; Lei, H.; Feng, B. Coupled Thermo–Hydro–Mechanical Modeling of Hydro-Shearing Stimulation in an Enhanced Geothermal System in the Raft River Geothermal Field, USA. Rock Mech. Rock Eng. 2020, 53, 5371–5388. [Google Scholar] [CrossRef]
- Yuan, Y.; Xu, T.; Jiang, Z.; Feng, B. Prospects of power generation from the deep fractured geothermal reservoir using a novel vertical well system in the Yangbajing geothermal field, China. Energy Rep. 2021, 7, 4733–4746. [Google Scholar] [CrossRef]
- Liu, G.; Zhou, C.; Rao, Z.; Liao, S. Impacts of fracture network geometries on numerical simulation and performance prediction of enhanced geothermal systems. Renew. Energy 2021, 171, 492–504. [Google Scholar] [CrossRef]
- Cladouhos, T.T.; Petty, S.; Swyer, M.W.; Uddenberg, M.E.; Grasso, K.; Nordin, Y. Results from Newberry Volcano EGS Demonstration, 2010–2014. Geothermics 2016, 63, 44–61. [Google Scholar] [CrossRef]
- Zhang, E.-Y.; Wen, D.-G.; Wang, G.-L.; Yan, W.-D.; Wang, W.-S.; Ye, C.-M.; Li, X.-F.; Wang, H.; Tang, X.-C.; Weng, W.; et al. The first power generation test of hot dry rock resources exploration and production demonstration project in the Gonghe Basin, Qinghai Province, China. JO-China Geol. 2022, 5, 372–382. [Google Scholar] [CrossRef]
- Liu, B.; Jin, H.; Sun, L.; Sun, Z.; Su, Z.; Zhang, C. Holocene climatic change revealed by aeolian deposits from the Gonghe Basin, northeastern Qinghai–Tibetan Plateau. Quat. Int. 2013, 296, 231–240. [Google Scholar] [CrossRef]
- Borgia, A.; Pruess, K.; Kneafsey, T.J.; Oldenburg, C.M.; Pan, L. Numerical simulation of salt precipitation in the fractures of a CO2-enhanced geothermal system. Geothermics 2012, 44, 13–22. [Google Scholar] [CrossRef]
- Sanyal, S.K.; Butler, S.J. (Eds.) An Analysis of Power Generation Prospects from Enhanced Geothermal Systems; Transactions Geothermal Resources Council: Reno, NV, USA, 2005. [Google Scholar]
- Keith, E. Enhanced/engineered geothermal systems: An introduction with overviews of deep systems built and circulated to date. In China Geothermal Development Forum Beijing; Geological Publishing House: Beijing, China, 2010; pp. 395–418. [Google Scholar]
- Cao, W.; Huang, W.; Jiang, F. Numerical study on variable thermophysical properties of heat transfer fluid affecting EGS heat extraction. Int. J. Heat Mass Transf. 2016, 92, 1205–1217. [Google Scholar] [CrossRef]
- Mathias, S.A.; Gluyas, J.G.; Oldenburg, C.M.; Tsang, C.-F. Analytical solution for Joule-Thomson cooling during CO2 geo-sequestration in depleted oil and gas reservoirs. Int. J. Greenh. Gas Control 2010, 4, 806–810. [Google Scholar] [CrossRef]
- Oldenburg, C.M. Joule-Thomson cooling due to CO2 injection into natural gas reservoirs. Energy Convers. Manag. 2007, 48, 1808–1815. [Google Scholar] [CrossRef]
- Zhang, X.X.; Wang, Z.P.; She, A.M.; Wei, Y.Q.; Zhu, Z.Y. Preparation and characterization of high-strength low-thermal-conductivity cement-based insulation materials. IOP Conf. Ser. Mater. Sci. Eng. 2019, 542, 012070. [Google Scholar] [CrossRef]



| Properties | Value |
|---|---|
| Reservoir | |
| Density (kg/m3) | 2623 |
| Specific heat (J/(kg·°C)) | 980 |
| Heat conductivity (W/(m·°C)) | 3 |
| Volume fraction of fracture | 0.02 |
| Fracture spacing (m) | 50 |
| Fracture porosity | 0.5 |
| Matrix porosity | 1 × 10−5 |
| Permeability in fractured reservoir | |
| kf1 (m2) | 50 × 10−15 |
| kf2 (m2) | 75 × 10−15 |
| kf3 (m2) | 100 × 10−15 |
| Matrix permeability (m2) | 9 × 10−19 |
| Wellbore | |
| Heat conductivity (W/(m·°C)) | 2.51 |
| Diameter (m) | 0.2 |
| Roughness (mm) | 0.046 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, W.; Yuan, Y.; Jing, T.; Zhong, C.; Wei, S.; Yin, Y.; Zhao, D.; Yuan, H.; Zheng, J.; Wang, S. Heat Production Performance from an Enhanced Geothermal System (EGS) Using CO2 as the Working Fluid. Energies 2023, 16, 7202. https://doi.org/10.3390/en16207202
Zhao W, Yuan Y, Jing T, Zhong C, Wei S, Yin Y, Zhao D, Yuan H, Zheng J, Wang S. Heat Production Performance from an Enhanced Geothermal System (EGS) Using CO2 as the Working Fluid. Energies. 2023; 16(20):7202. https://doi.org/10.3390/en16207202
Chicago/Turabian StyleZhao, Wentao, Yilong Yuan, Tieya Jing, Chenghao Zhong, Shoucheng Wei, Yulong Yin, Deyuan Zhao, Haowei Yuan, Jin Zheng, and Shaomin Wang. 2023. "Heat Production Performance from an Enhanced Geothermal System (EGS) Using CO2 as the Working Fluid" Energies 16, no. 20: 7202. https://doi.org/10.3390/en16207202
APA StyleZhao, W., Yuan, Y., Jing, T., Zhong, C., Wei, S., Yin, Y., Zhao, D., Yuan, H., Zheng, J., & Wang, S. (2023). Heat Production Performance from an Enhanced Geothermal System (EGS) Using CO2 as the Working Fluid. Energies, 16(20), 7202. https://doi.org/10.3390/en16207202







