High-Efficiency Sine-Wave Current Pulses Charging Method in Wireless Power-Transfer System Applications
Abstract
:1. Introduction
- In contrast to the square-wave pulse-charging method, this research demonstrates that the electrochemical reaction rate of the battery can catch up with the charging current. This novel charging method serves as an indirect safeguard for the battery, effectively prolonging its cycle life;
- Introducing interleaved charging technology allows for the simultaneous charging of multiple batteries, addressing the limitations of traditional single-output charging methods;
- The charger incorporates a small independent air-core inductor, eliminating the issue of difficult-to-control leakage inductance. This enhancement enhances design flexibility and enables the realization of the LLC-S charger;
- Compared to conventional LLC converters, the receiver side of the circuit features a reduced number of components, while soft switching technology further enhances the overall circuit efficiency. This results in a simple, cost-effective, and easily maintainable circuit, well-suited for high-power battery-charging applications;
- This research offers a comprehensive design process along with equipment brands and models, simplifying the replication and implementation of the proposed wireless circuit.
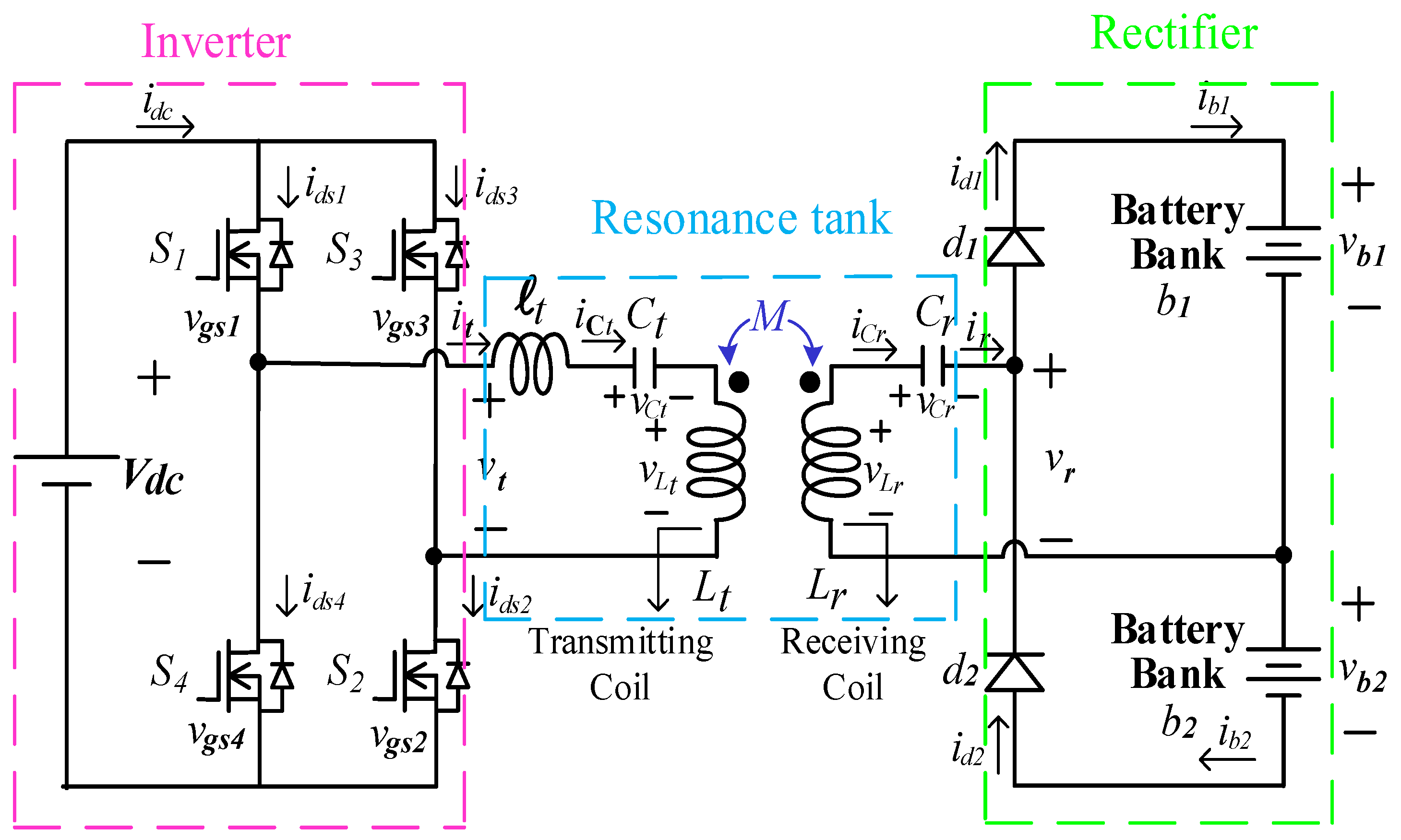
2. Operational Principle
- (1)
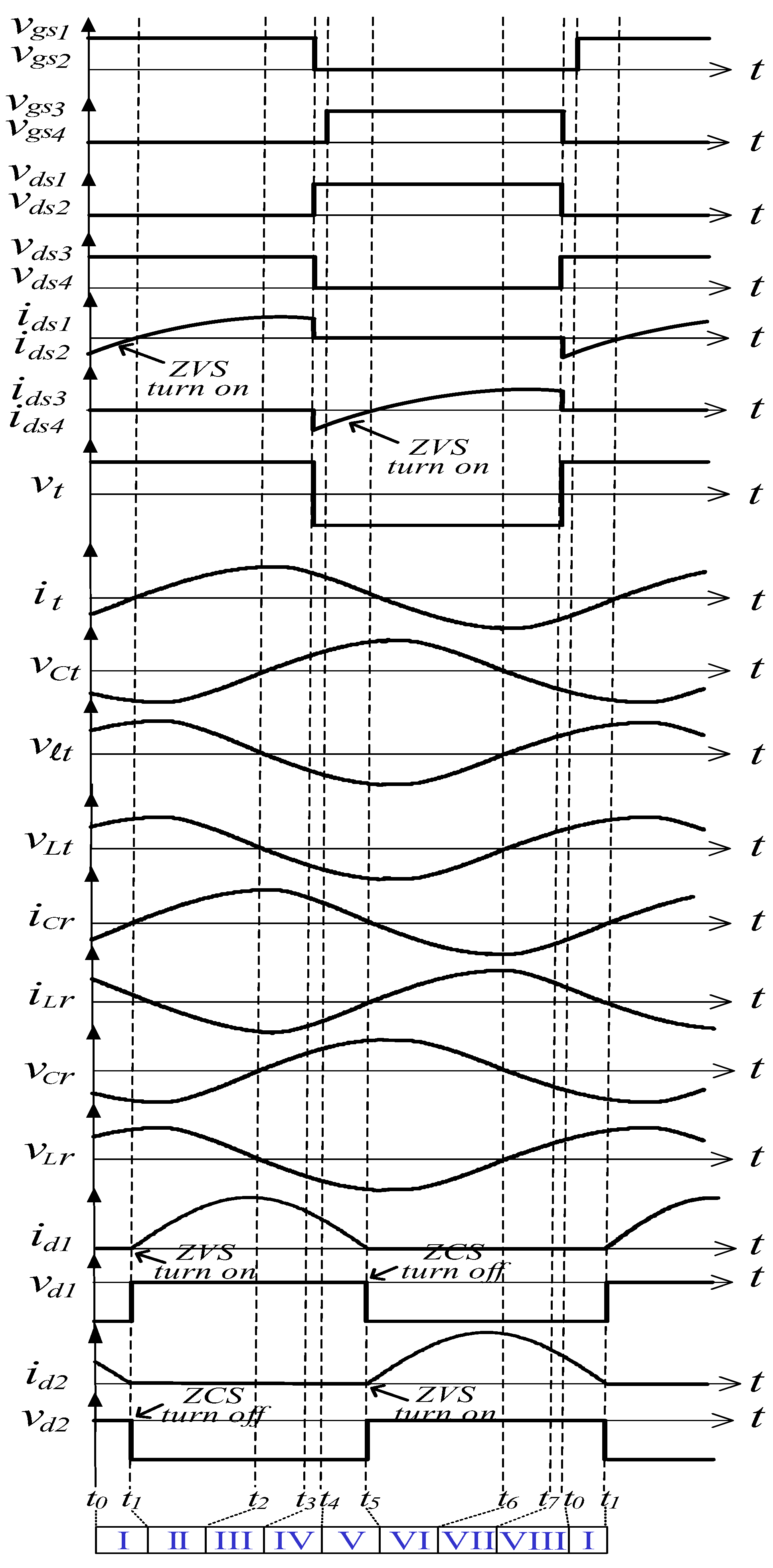
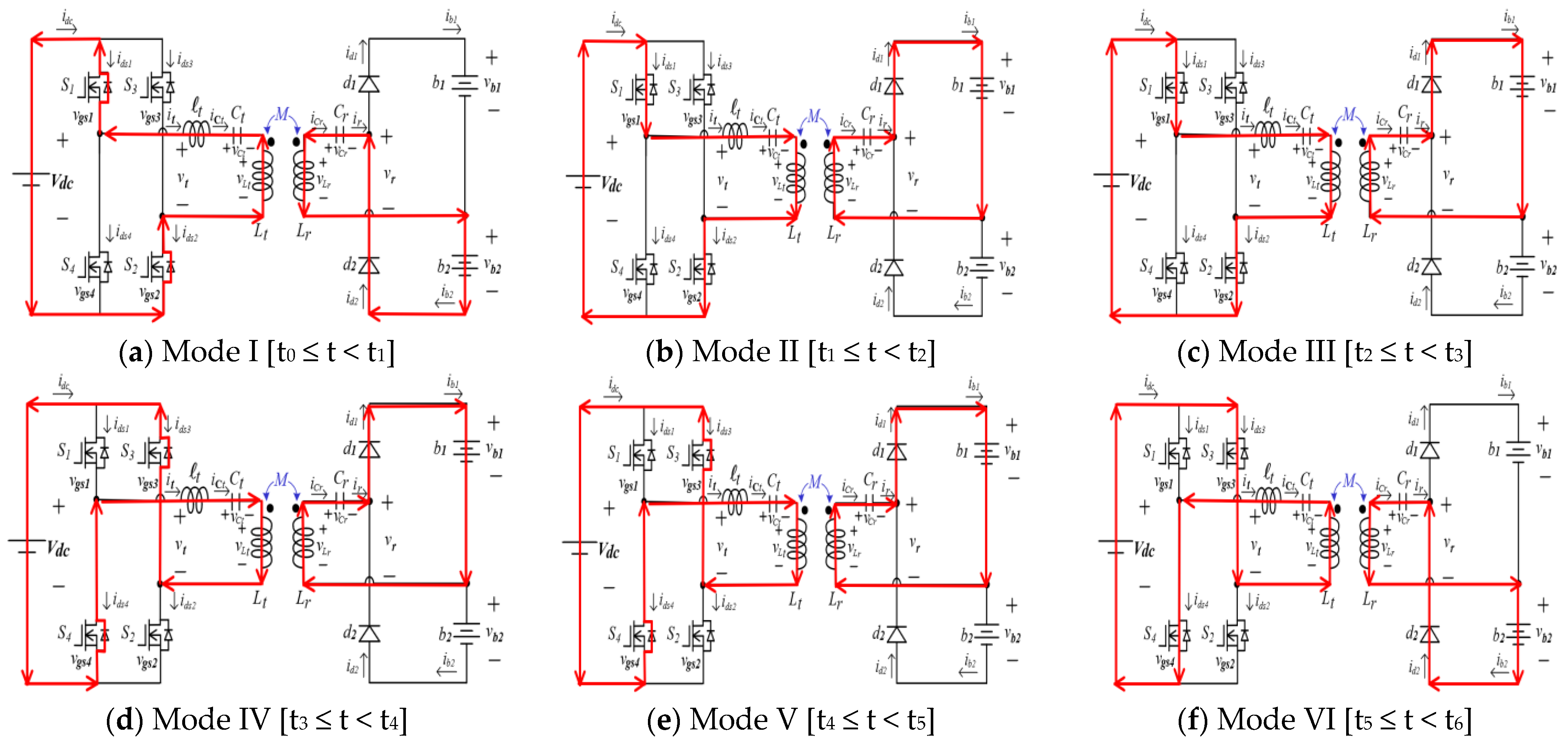
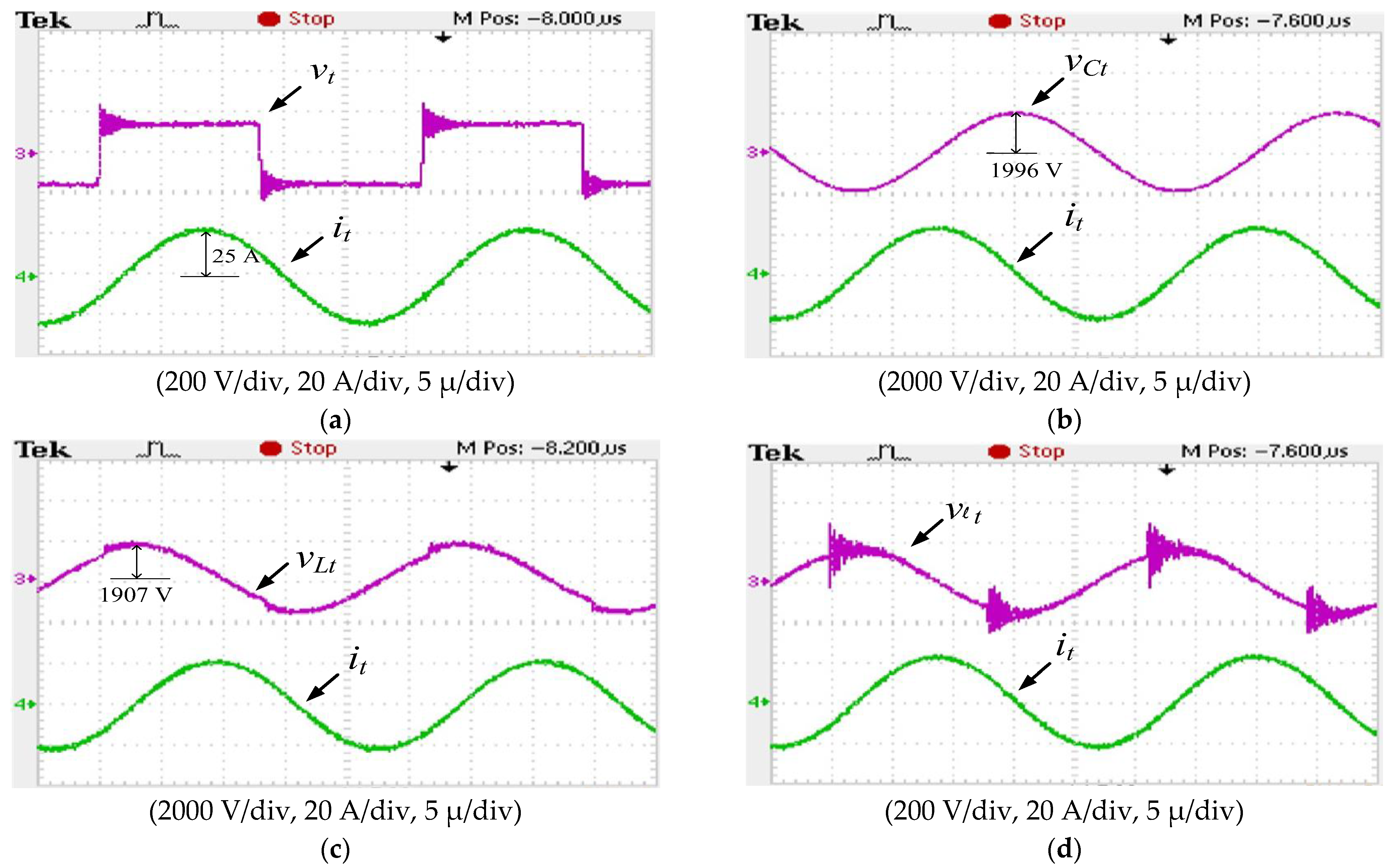
- Mode I [Figure 3a, t0 ≤ t < t1]: At t0, the resonant current it flows through the parasitic diodes of switches S1 and S2; therefore, the voltage of these switches can be reduced to 0 V to enable the switches to achieve ZVS in the next turn-on period. On the receiver side, the battery bank of b2 is in the charging state. The equivalent circuit for mode I operation is displayed in Figure 3a;
- (2)
- Mode II [Figure 3b, t1 ≤ t < t2]: Between t1 and t2, the current idc flows forward to switches S1 and S2; thus, these switches are turned on under the ZVS manner. In the resonance compensation network, the resonant inductor ℓt, the transmitting coil Lt, and the capacitor Ct are in resonance. Moreover, the current iCr charges the battery bank of b1. The equivalent circuit for mode II operation is in Figure 3b;
- (3)
- Mode III [Figure 3c, t2 ≤ t < t3]: Switches S1 and S2 remain turned on until t3 is reached. The resonant current reaches its maximum value at t2; therefore, the voltages of the inductor ℓt, Lt, and capacitor Ct begin to reverse in the resonance compensation network, and the voltage polarity across inductor Lr and capacitor Cr changes. The battery bank of b1 is continuously charging during mode III, and the equivalent circuit for mode III operation is shown in Figure 3c;
- (4)
- Mode IV [Figure 3d, t3 ≤ t < t4]: Between t3 and t4, all switches(S1–S4) are in the off state because of the deadtime process. Because the resonant current it flows in a freewheeling state through switches S3 and S4, the voltages vds3 and vds4 can be quickly reduced to 0 V to enable ZVS operation. Moreover, the resonance-tank voltage vt reverses polarity at t3. On the receiver side, current iCr continues to charge the battery bank of b1. The equivalent circuit for mode IV operation is shown in Figure 3d;
- (5)
- Mode V [Figure 3e, t4 ≤ t < t5]: Between t4 and t5, switches S3 and S4 are in a zero-voltage state because the resonant current it flows in a freewheeling state. The battery bank of b1 is charged continuously during mode V operation, and the equivalent circuit of mode V operation is illustrated in Figure 3e;
- (6)
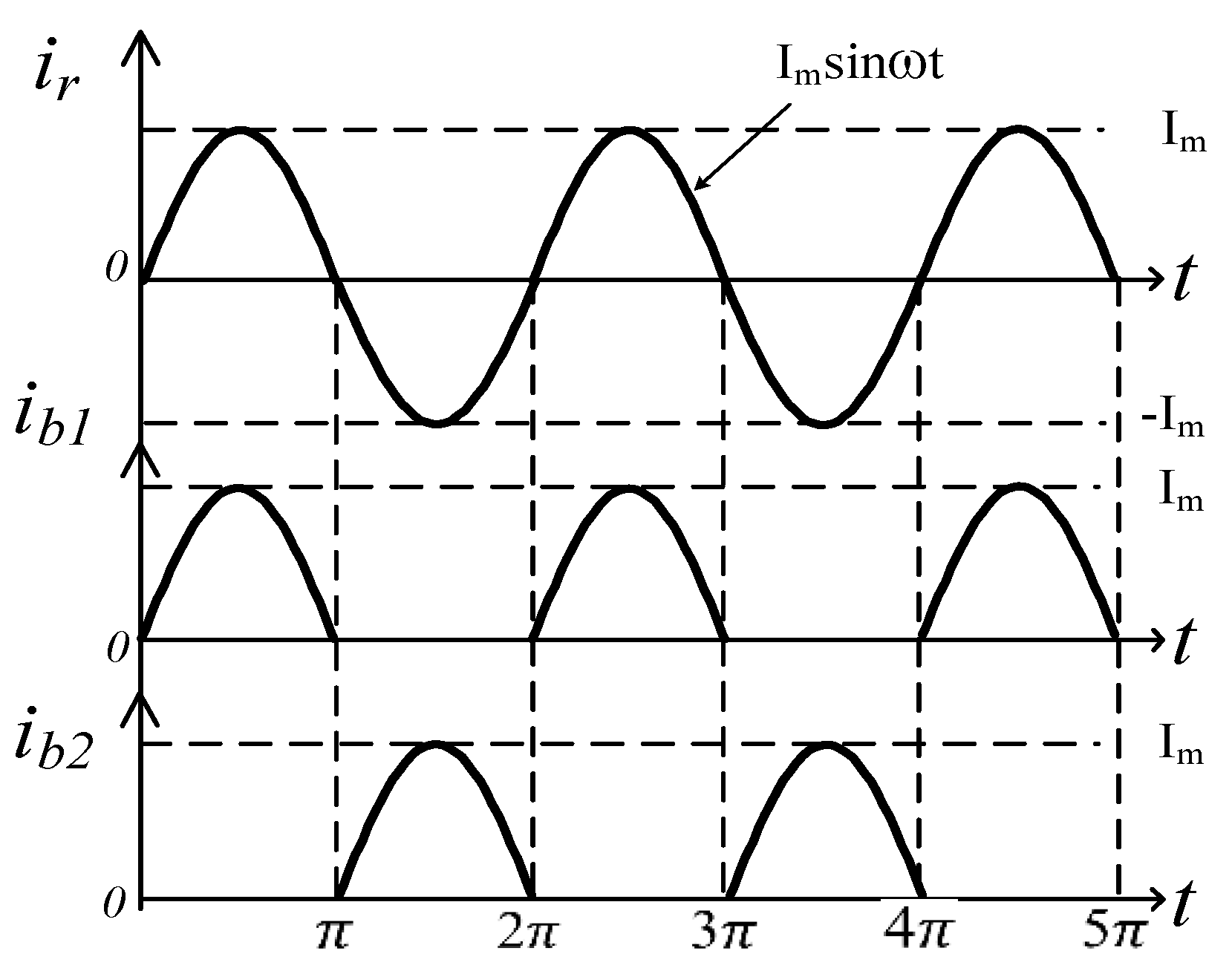
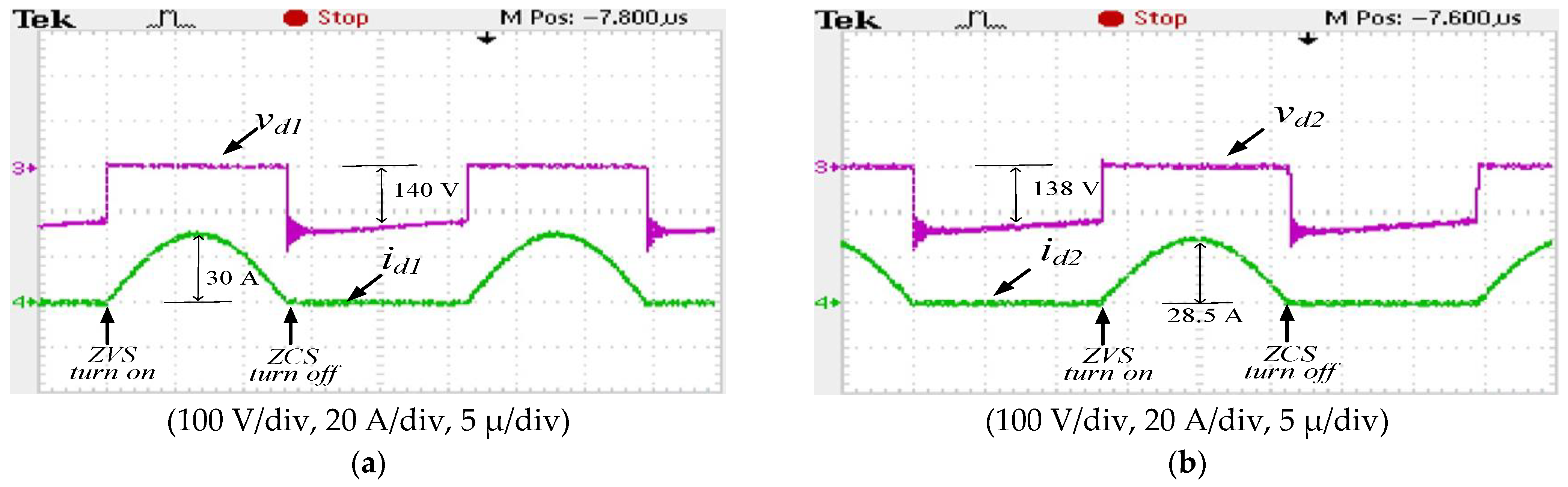
- Mode VI [Figure 3f, t5 ≤ t < t6]: At t5, the current it begins to commutate, and switches S3 and S4 are turned on under ZVS. On the receiver side, currents iCr and iLr also begin to, and rectifier diode d2 is turned on under ZVS; therefore, battery b2 begins charging. The equivalent circuit of mode VI operation is shown in Figure 3f;
- (7)
- Mode VII [Figure 3g, t6 ≤ t < t7]: Switches S3 and S4 are continuously turned on. At t6, multiple voltages, including the capacitor voltages vCt, and vCr, inductor voltage vℓt, and coil voltages vLt and vLr, are set to 0 V. Moreover, the currents, including the resonant current it, capacitor current iCr, and inductor current iLr, are in a peak value state. The battery bank of b2 continues to be charged until t7. The equivalent circuit of mode VII operation is displayed in Figure 3g;
- (8)
- Mode VIII [Figure 3h, t7 ≤ t < t0]: Between t7 and t0, switches S1–S4 are again switched off because of the deadtime process. The resonant current it flows through the parasitic diodes of switches S1 and S2, which forces the voltages vds1 and vds2 to decrease to 0 V; thus, a ZVS state is created in the next turn-on period. Furthermore, the polarity of the resonant tank voltage vt changes again. The resonant current ir on the receiver side still charges the battery bank of b2 to complete a cycle of interleaved charging. The equivalent circuit for mode VIII is presented in Figure 3h.
3. Circuit Characteristics and Charging Method Considerations
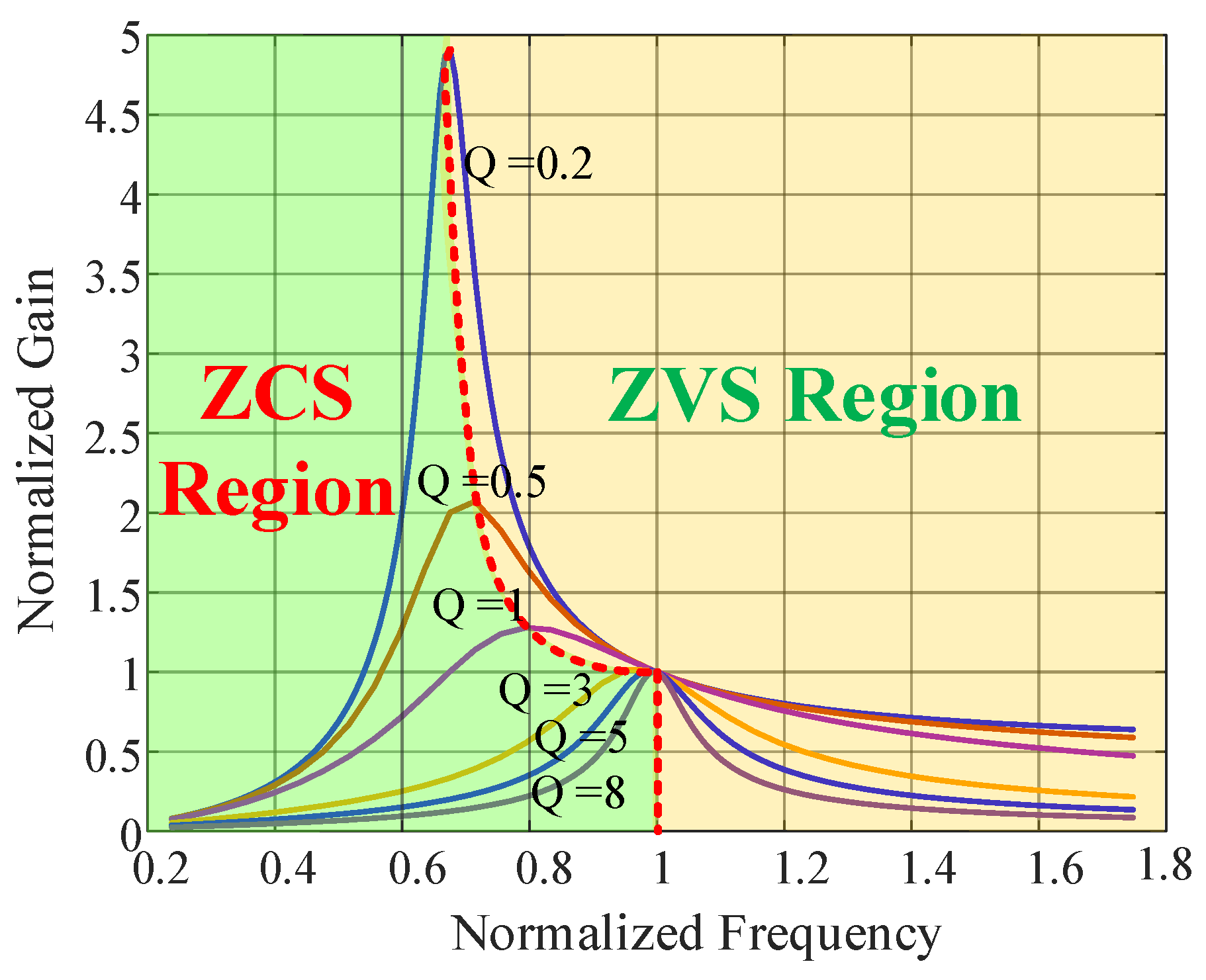
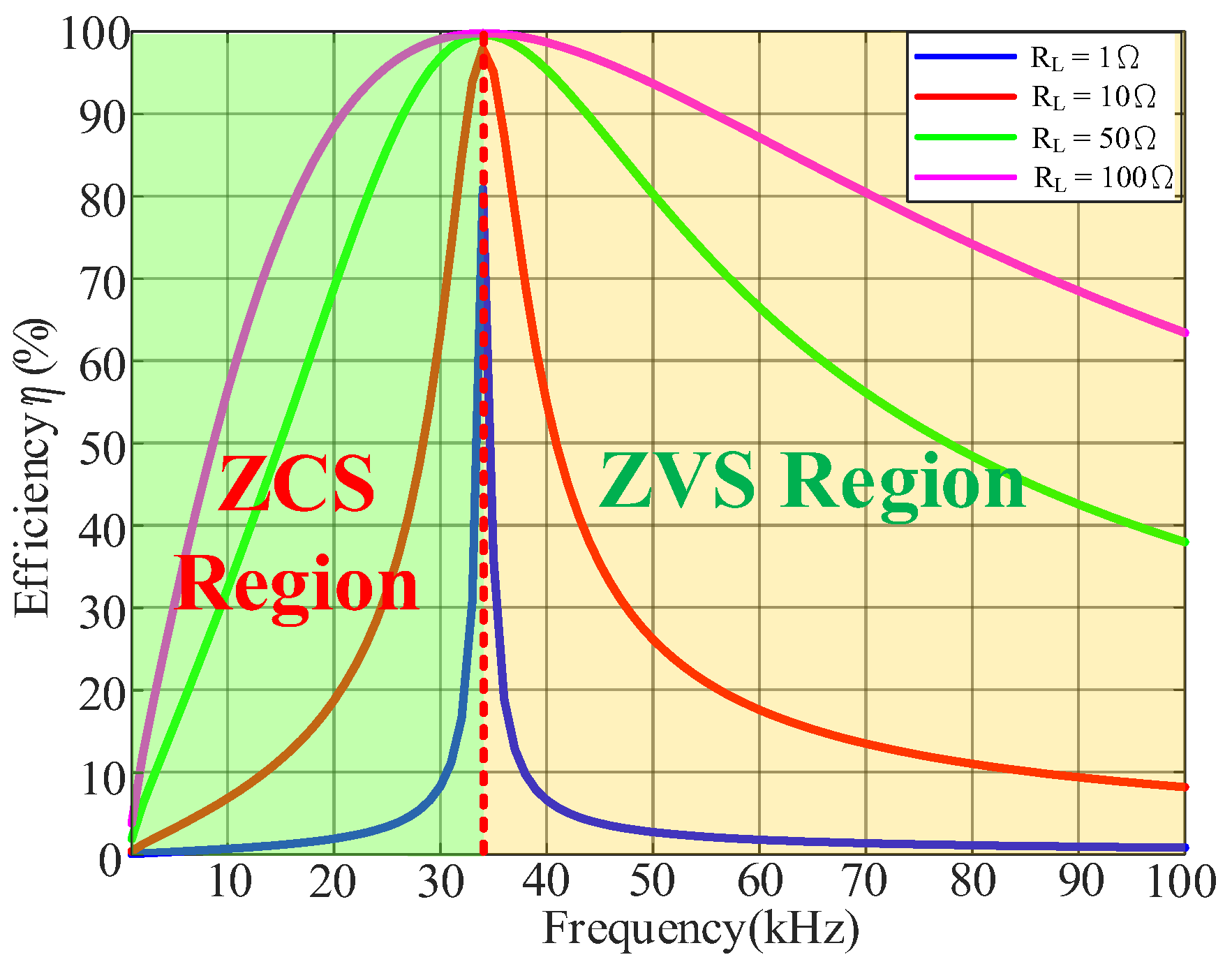
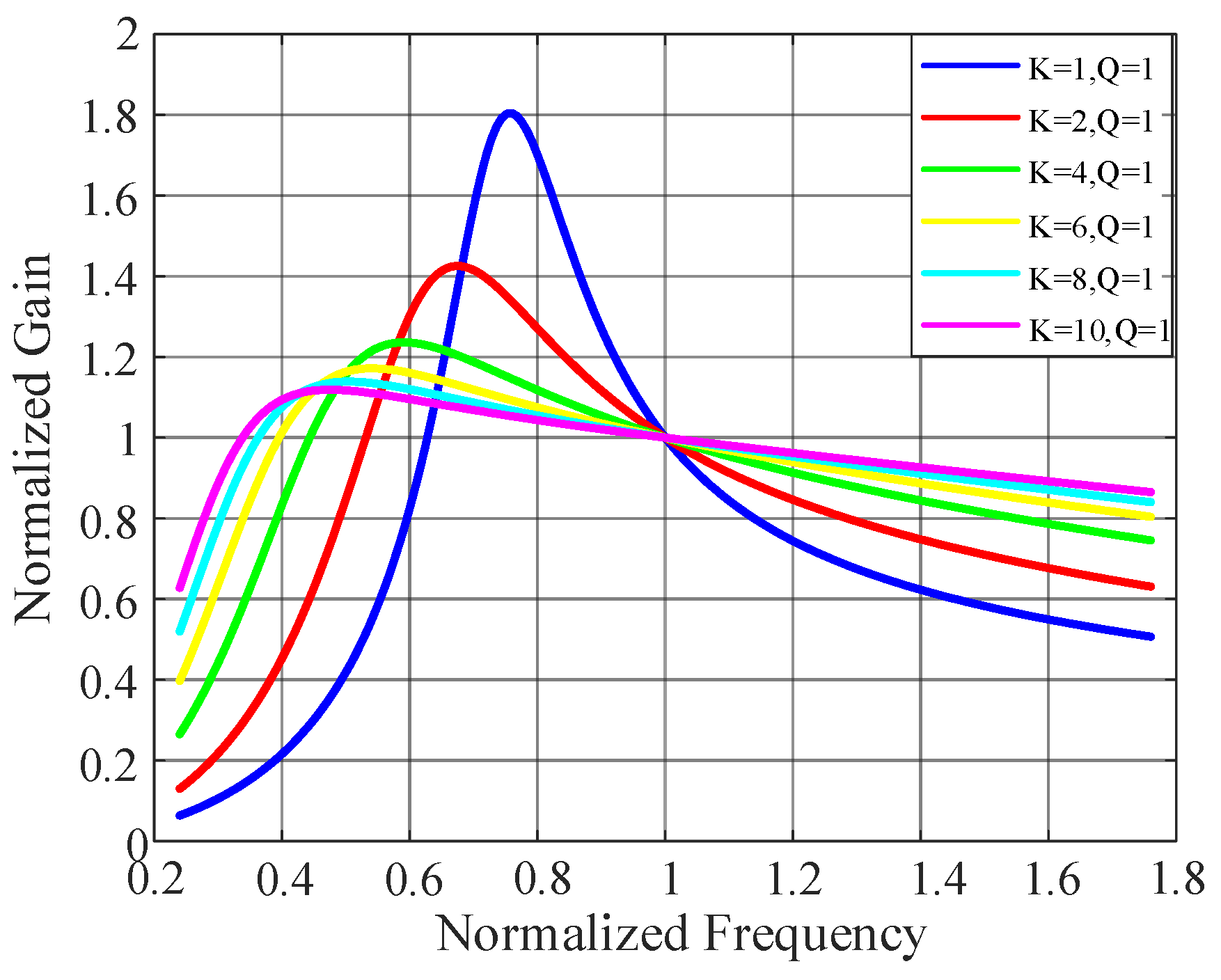
3.1. LLC-Converter Characteristics
3.2. Equivalent AC Circuit Analysis
3.3. Considerations Regarding the Charging Methods
4. Design Procedure
4.1. Design of the Resonance Compensation Network
4.2. Design of the Resonance Compensation Network
4.3. Rectifier Diodes
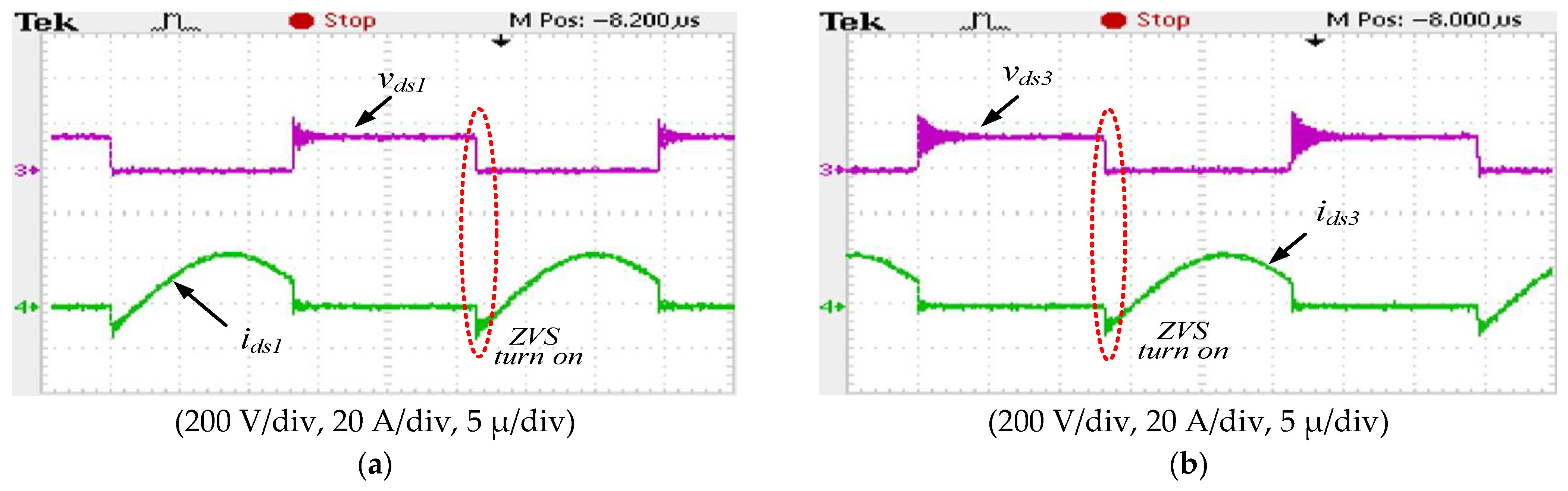
5. Experimental Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Brown, W.C. The history of power transmission by radio waves. IEEE Trans. Micro. Theory Tech. 1984, 32, 1230–1242. [Google Scholar] [CrossRef]
- Kurs, A.; Karalis, A.; Moffatt, R.; Joannopoulos, J.D.; Fisher, P.; Soljac, M. Wireless power transfer via strongly coupled magnetic resonances. Science 2007, 317, 83–86. [Google Scholar] [CrossRef] [PubMed]
- Karalis, A.; Joannopoulos, J.D.; Soljacicb, M. Efficient wireless non-radiative mid-range energy transfer. Ann. Phys. 2008, 323, 34–48. [Google Scholar] [CrossRef]
- Noeren, J.; Parspour, N. Lukas Elbracht, An Easily Scalable Dynamic Wireless Power Transfer System for Electric Vehicles. Energies 2023, 16, 3936. [Google Scholar] [CrossRef]
- Tran, D.H.; Vu, V.B.; Choi, W. Design of a High-Efficiency Wireless Power Transfer System with Intermediate Coils for the On-Board Chargers of Electric Vehicles. IEEE Trans. Power Electron. 2018, 33, 175–187. [Google Scholar] [CrossRef]
- Ramezani, A.; Farhangi, S.; Hossein, I.-E.; Farhangi, B.; Rahimi, R.; Moradi, G.R. Optimized LCC-Series Compensated Resonant Network for Stationary Wireless EV Chargers. IEEE Trans. Ind. Electron. 2019, 66, 2756–2765. [Google Scholar] [CrossRef]
- Park, Y.-J.; Jang, B.G.; Park, S.-M.; Ryu, H.-C.; Oh, S.J.; Kim, S.-Y.; Pu, Y.G.; Yoo, S.-S.; Hwang, K.C.; Yang, Y.; et al. A Triple-Mode Wireless Power-Receiving Unit With 85.5% System Efficiency for A4WP, WPC, and PMA Applications. IEEE Trans. Power Electron. 2018, 33, 175–187. [Google Scholar] [CrossRef]
- Yoo, J.-S.; Gil, Y.-M.; Ahn, T.-Y. High-Power-Density DC–DC Converter Using a Fixed-Type Wireless Power Transmission Transformer with Ceramic Insulation Layer. Energies 2022, 15, 9006. [Google Scholar] [CrossRef]
- Corti, F.; Reatti, A.; Nepote, A.; Pugi, L.; Pierini, M.; Paolucci, L.; Grasso, F.; Grasso, E.; Nienhause, M. A Secondary-Side Controlled Electric Vehicle Wireless Charger. Energies 2020, 13, 6527. [Google Scholar] [CrossRef]
- Nama, J.K.; Verma, A.K.; Srivastava, M.; Tomar, P.S. An Efficient Inductive Power Transfer Topology for Electric Vehicle Battery Charging. IEEE Trans. Ind. Appl. 2020, 56, 6925–6936. [Google Scholar] [CrossRef]
- Li, W.; Zhao, H.; Deng, J.; Li, S.; Mi, C.C. Comparison Study on SS and Double-Sided LCC Compensation Topologies for EV/PHEV Wireless Chargers. IEEE Trans. Veh. Technol. 2016, 65, 4429–4439. [Google Scholar] [CrossRef]
- Cui, S.; Liu, Z.Z.; Hou, Y.J.; Zeng, H.; Yue, Z.K.; Liang, L.H. Study on efficiency of different topologies of magnetic coupled resonant wireless charging system. Int. Conf. New Energy Future Energy Syst. 2017, 93, 012064. [Google Scholar] [CrossRef]
- Xu, S.; Wang, Z.; Chen, J.; Jiang, W. Research and Design of LC Series Resonant Wireless Power Transfer System with Modulation Control Method for Supercapacitor Charging in Linear Motion Systems. Energies 2022, 15, 6739. [Google Scholar] [CrossRef]
- Neto, P.B.L.; Saavedra, O.R.; Ribeiro, L.A.d.S. A Dual-Battery Storage Bank Configuration for Isolated Microgrids Based on Renewable Sources. IEEE Trans. Sustain. Energy 2018, 9, 1618–1626. [Google Scholar] [CrossRef]
- McKeon, B.B.; Furukawa, J.; Fenstermacher, S. Advanced Lead-Acid Batteries and the Development of Grid-Scale Energy Storage Systems. Proc. IEEE 2014, 102, 951–963. [Google Scholar] [CrossRef]
- Takeda, K.; Takahashi, C.; Arita, H.; Kusumi, N.; Amano, M.; Emori, A. Design of hybrid energy storage system using dual batteries for renewable applications. In Proceedings of the IEEE PES General Meeting Conference Exposition, National Harbor, MD, USA, 27–31 July 2014. [Google Scholar]
- Yang, Y.; Ye, Q.; Tung, L.J.; Greenleaf, M.; Li, H. Integrated Size and Energy Management Design of Battery Storage to Enhance Grid Integration of Large-Scale PV Power Plants. IEEE Trans. Ind. Electron. 2018, 65, 394–402. [Google Scholar] [CrossRef]
- Pablo, D.-C.; Jose Ignacio, M.-H.; Javier, C. A Microgrid Model with EV Demand Uncertainty and Detailed Operation of Storage Systems. IEEE Trans. Ind. Appl. 2022, 58, 2497–2511. [Google Scholar]
- Cheung, T.K.; Cheng, K.W.E.; Chan, H.L.; Ho, Y.L.; Chung, H.S.; Tai, K.P. Maintenance techiques for rechargeable battery using pulse charging. In Proceedings of the International Conference on Power Electronics Systems and Applications, Hong Kong, China, 12–14 November 2006; pp. 205–208. [Google Scholar]
- Lai, C.-M.; The, J.; Cheng, Y.-H.; Li, Y.-H. A reflex-charging based bidirectional DC charger for light electric vehicle and DC-microgrids. In Proceedings of the TENCON 2017–2017 IEEE Region 10 Conference, Penang, Malaysia, 5–8 November 2017. [Google Scholar]
- Lavety, S.; Keshri, R.K.; Chaudhari, M.A. Comparative Evaluation of Temperature Regulated Pulse and Reflex Charging. Annu. Conf. IEEE Ind. Electron. Soc. 2019, 1, 6337–6342. [Google Scholar]
- Bizhani, H.; Sani, S.K.H.; Rezazadeh, H.; Muyeen, S.M.; Rahmani, S. Modeling of an Optimum Fast Charging Multi-Step Constant Current Profile for Lead-Acid Batteries. IEEE Trans. Ind. 2023, 59, 2050–2060. [Google Scholar] [CrossRef]
- Alhaider, M.M.; Ahmed, E.M.; Aly, M.; Serhan, H.A.; Mohamed, E.A.; Ali, Z.M. New Temperature-Compensated Multi-Step Constant-Current Charging Method for Reliable Operation of Battery Energy Storage Systems. IEEE Access 2020, 8, 27961–27972. [Google Scholar] [CrossRef]
- Krieger, E.M.; Cannarella, J.; Arnold, C.B. A comparison of lead-acid and lithium-based battery behaviorand capacity fade in off-grid renewable charging applications. Energy 2013, 60, 492–500. [Google Scholar] [CrossRef]
- Al Zyoud, A.; Elhaija, W.A. Solar power lead battery storage solution using cycle recovery charging method. J. Energy Storage 2019, 25, 100843. [Google Scholar] [CrossRef]
- Kirchev, A.; Perrin, M.; Lemaire, E.; Karoui, F.; Mattera, F. Studies of the pulse charge of lead-acid batteries for PV applications Part I. Factors influencing the mechanism of the pulse charge of the positive plate. J. Power Sources 2008, 177, 217–225. [Google Scholar] [CrossRef]
- Mohamed, T.; Becetti, A.; Bayhan, S. Design and analysis of full bridge LLC resonant converter for wireless power transfer applications. In Proceedings of the IEEE International Conference on Compatibility Power Electronics Power Engineering, Doha, Qatar, 10–12 April 2018; pp. 1–5. [Google Scholar]
- Bosshard, R.; Kolar, J.W.; Mühlethaler, J.; Stevanović, I.; Wunsch, B.; Canales, F. Modeling and η-α-Pareto Optimization of Inductive Power Transfer Coils for Electric Vehicles. IEEE Trans. Emerg. Sel. Top. Power Electron. 2015, 3, 50–64. [Google Scholar] [CrossRef]
- Liao, C.; Li, J.; Li, S. Design of LCC impedance matching circuit for wireless power transfer system under rectifier load. IEEE Trans. Power Electron. Appl. 2017, 2, 237–245. [Google Scholar] [CrossRef]
- Ali, N.; Liu, Z.; Hou, Y.; Armghan, H.; Wei, X.; Armghan, A. LCC-S Based Discrete Fast Terminal Sliding Mode Controller for Efficient Charging through Wireless Power Transfer. Energies 2020, 13, 1370. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, X.; Zhang, K.; Cui, X.; Jiao, C.; Yang, X. Design of LCC-S Compensation Topology and Optimization of Misalignment Tolerance for Inductive Power Transfer. IEEE Access 2020, 8, 191309–191318. [Google Scholar] [CrossRef]
- Wang, X.; Xu, J.; Ma, H.; Yang, P. A High Efficiency LCC-S Compensated WPT System with Dual Decoupled Receive Coils and Cascaded PWM Regulator. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 3142–3146. [Google Scholar] [CrossRef]
- Krishnaswami, H.; Mohan, N. Three-Port Series-Resonant DC–DC Converter to Interface Renewable Energy Sources With Bidirectional Load and Energy Storage Ports. IEEE Trans. Power Electron. 2009, 24, 2289–2297. [Google Scholar] [CrossRef]
- Canales, F.; Barbosa, P.; Lee, F.C. A wide input voltage and load output variations fixed-frequency ZVS DC/DC LLC resonant converter for high-power applications. IEEE Ind. Appl. Conf. 2002, 4, 2306–2313. [Google Scholar]
- Roy, C.P. Control analysis of a high frequency resonant inverter for induction cooking application. Int. J. Res. Eng. Technol. 2015, 4, 340–348. [Google Scholar]






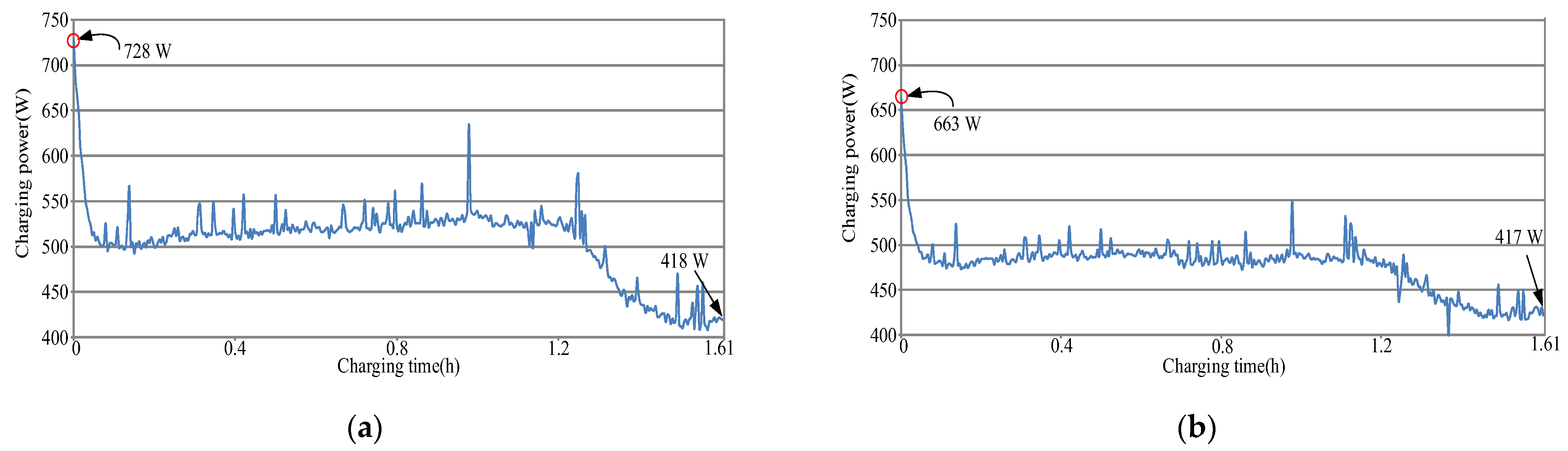
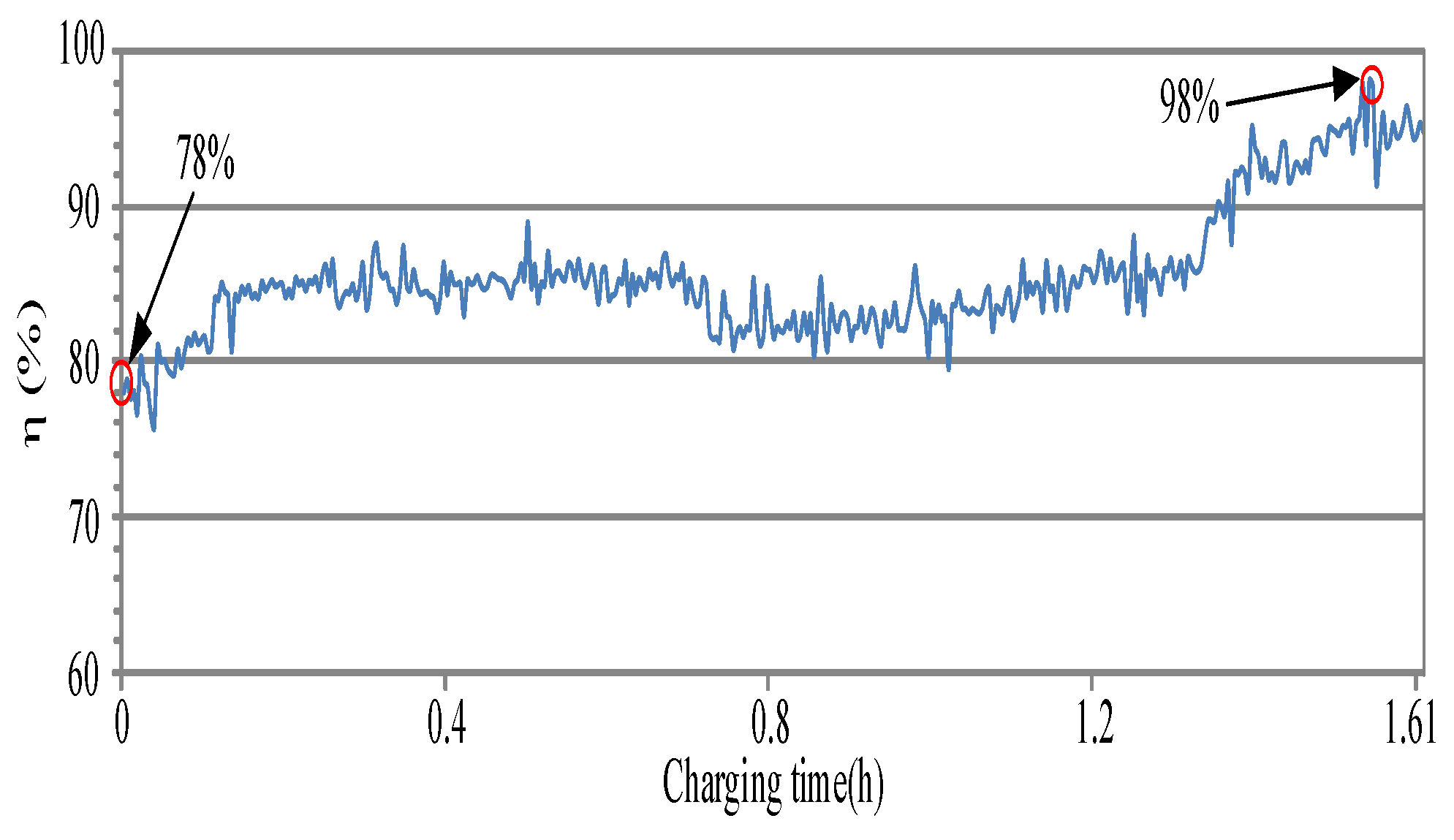
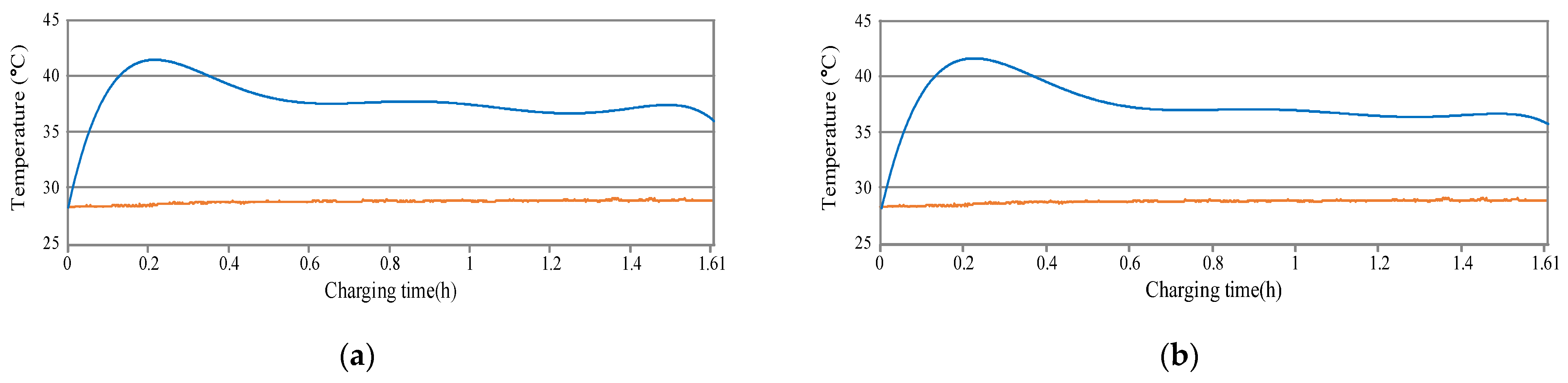


| Circuit Structure Performance Index | Half-Bridge Rectifier | Full-Bridge Rectifier |
|---|---|---|
| Charging method | Sine-wave current pulses | DC charging |
| Number of charging | 2 | 1 |
| Diode | 2 | 4 |
| LC filter | None | Need |
| Rest time | 50% period | None |
| Circuit structure | Double voltage | Rectifier |
| Cost | Low | High |
| Symbol | Parameter | Value |
|---|---|---|
| Vdc | Nominal input voltage | 155 V |
| fs | Switching frequency | 37.9 kHz |
| fm | Resonance frequency | 34 kHz |
| Hg | Air gap | 20 cm |
| Po | Rated output power | 1500 W |
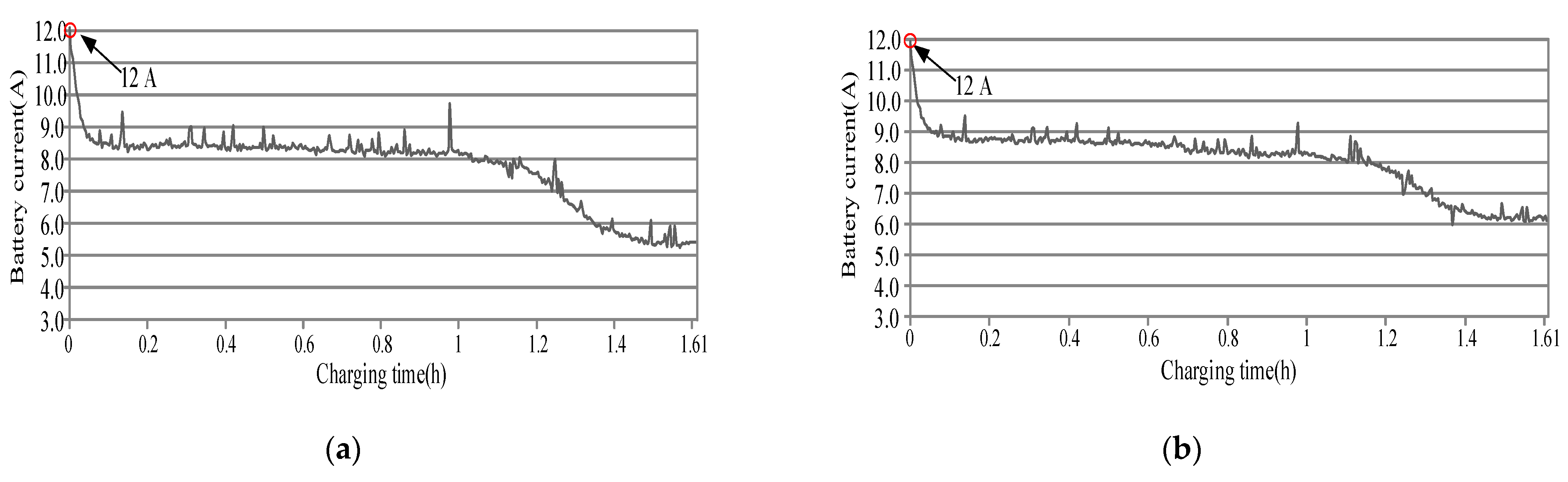
| ib1 | Charging current | 5.4~12.6 A |
| ib2 | Charging current | 6.2~12.48 A |
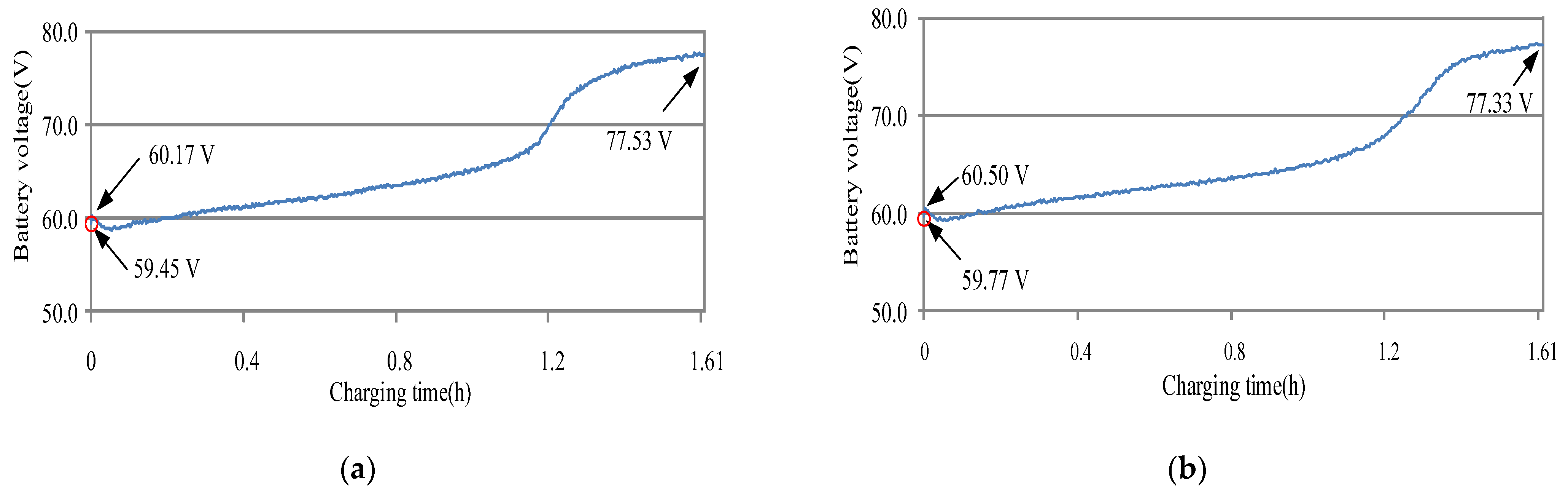
| vb1 | Battery voltage | 59.45~77.53 V |
| vb2 | Battery voltage | 59.77~77.33 V |
| Symbol | Parameter | Model/Value |
|---|---|---|
| S1–S4 | Active switch | IXTK120N65X2 |
| D1–D2 | Rectifier Diode | IQBD60E60A1 |
| Lt | Transmitting coil inductance | 400.4 H |
| Lr | Receiving coil inductance | 219.1 H |
| lt | Air-core inductance | 37 H |
| K | Inductance ratio | 10.82 |
| k | Coupling coefficient | 0.45 |
| Ct | Transmitting-side compensation capacitance | 0.05 |
| Cr | Receiving-side compensation capacitance | 0.1 |
| Option Equipment | Brand | Model |
|---|---|---|
| Power supply | Gitek | GR-15H20H |
| Oscilloscope | Tektronix | TDS 2024B |
| Differential probe | Sanhua | LDP6110 |
| Amplifier Current probe | Tektronix | TCPA300 TCP312A |
| LCR meter | Microtest | 6376 |
| Battery | Yuasa | REC14-12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, Y.-D.; Chuang, Y.-C.; Huang, Y.-S. High-Efficiency Sine-Wave Current Pulses Charging Method in Wireless Power-Transfer System Applications. Energies 2023, 16, 7102. https://doi.org/10.3390/en16207102
Chang Y-D, Chuang Y-C, Huang Y-S. High-Efficiency Sine-Wave Current Pulses Charging Method in Wireless Power-Transfer System Applications. Energies. 2023; 16(20):7102. https://doi.org/10.3390/en16207102
Chicago/Turabian StyleChang, Yong-Dong, Ying-Chun Chuang, and Yi-Shun Huang. 2023. "High-Efficiency Sine-Wave Current Pulses Charging Method in Wireless Power-Transfer System Applications" Energies 16, no. 20: 7102. https://doi.org/10.3390/en16207102
APA StyleChang, Y.-D., Chuang, Y.-C., & Huang, Y.-S. (2023). High-Efficiency Sine-Wave Current Pulses Charging Method in Wireless Power-Transfer System Applications. Energies, 16(20), 7102. https://doi.org/10.3390/en16207102






