Optimizing Energy Efficiency of Dielectric Materials’ Electrodischarge Dispersion as One Sustainable Development Green Trend
Abstract
1. Introduction
- the initial voltage U,
- storage capacitance C,
- circuit inductance L, and
- the length of the discharge gap l, but they come to the conclusion that “U, C, L, and l affect the characteristics of the channel in different and rather complex ways discharge, and for each specific type of electro-hydraulic installation, their combination must be selected separately experimentally”, which seems to be a cumbersome and very labor-intensive process.
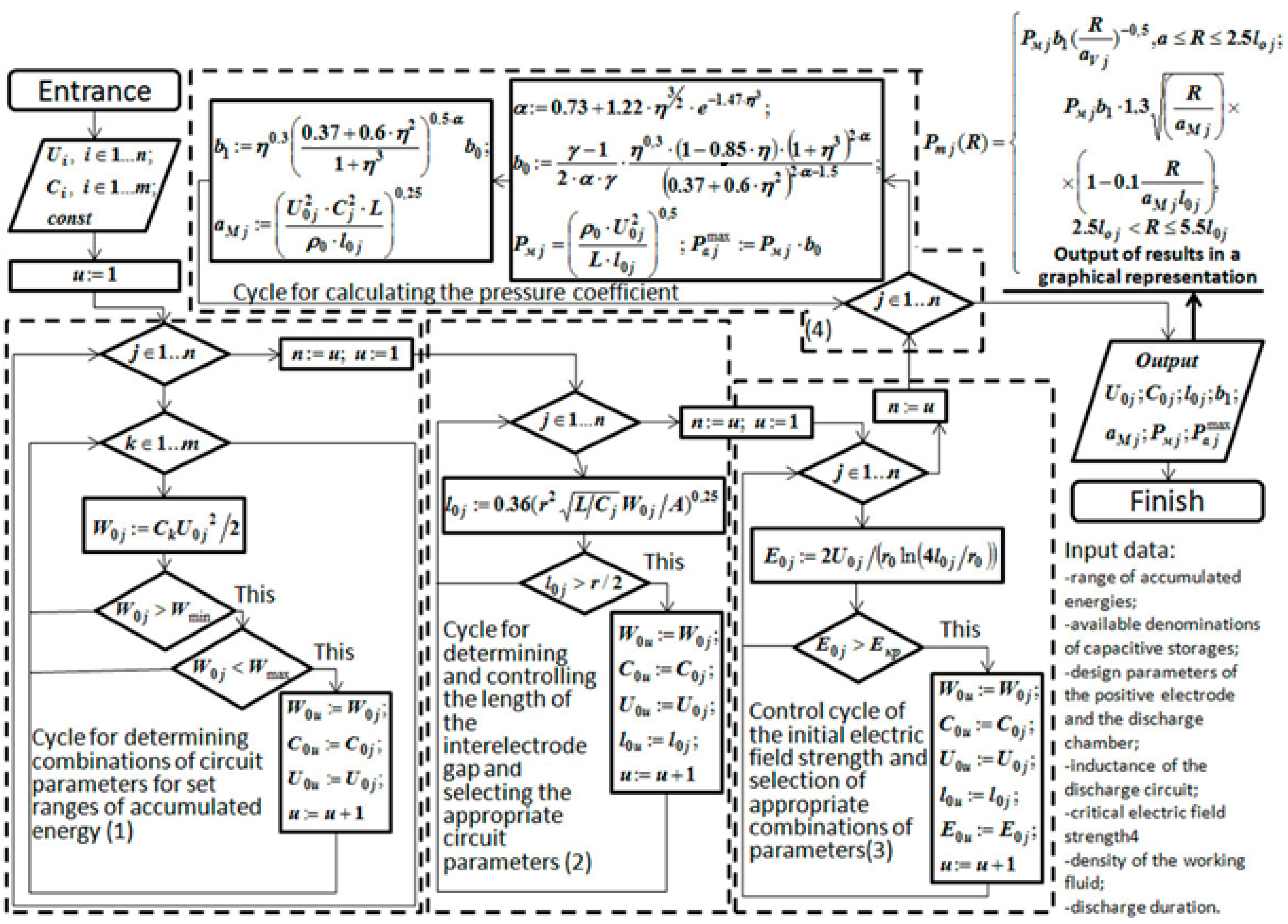
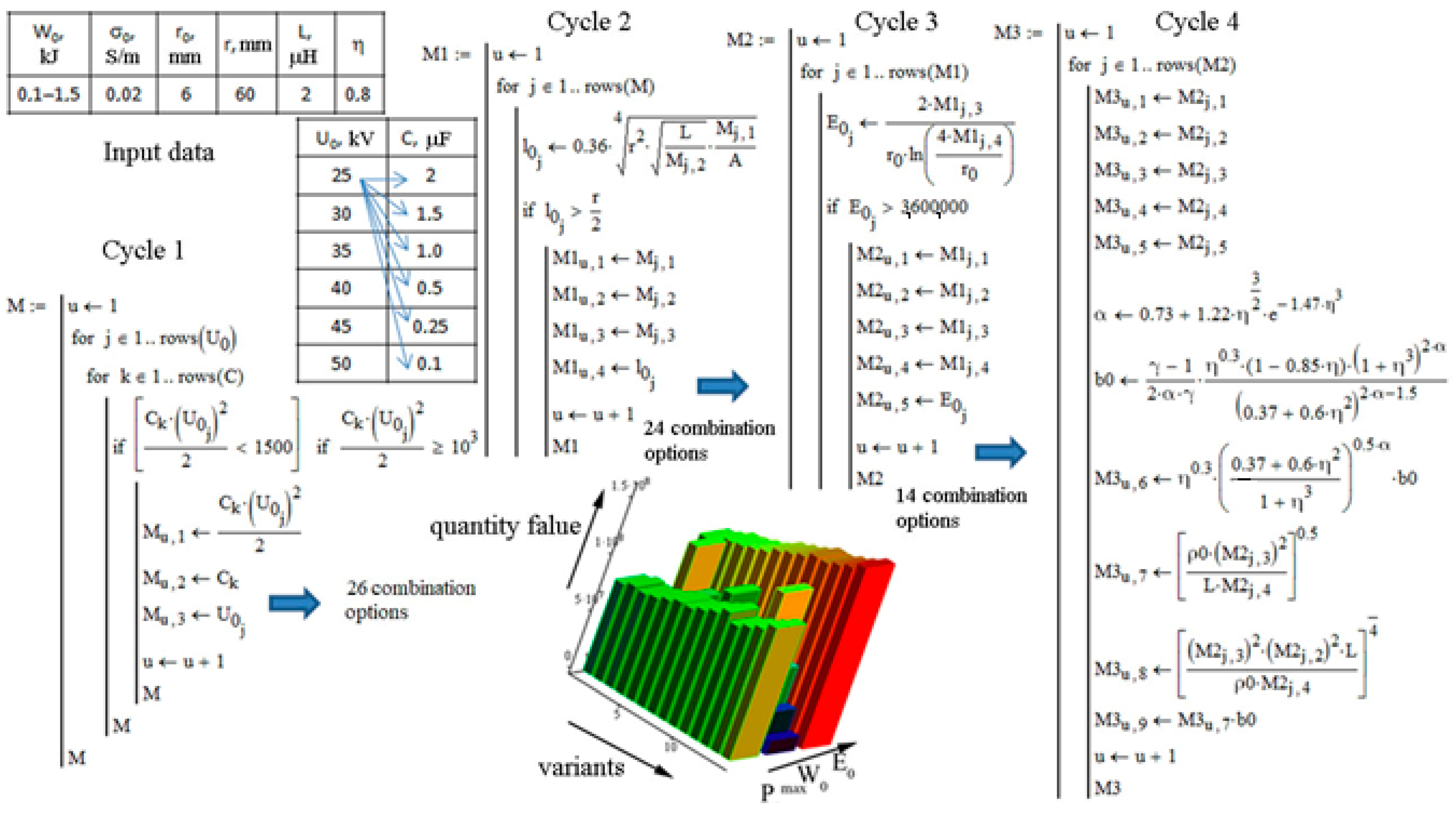
2. Materials and Methods
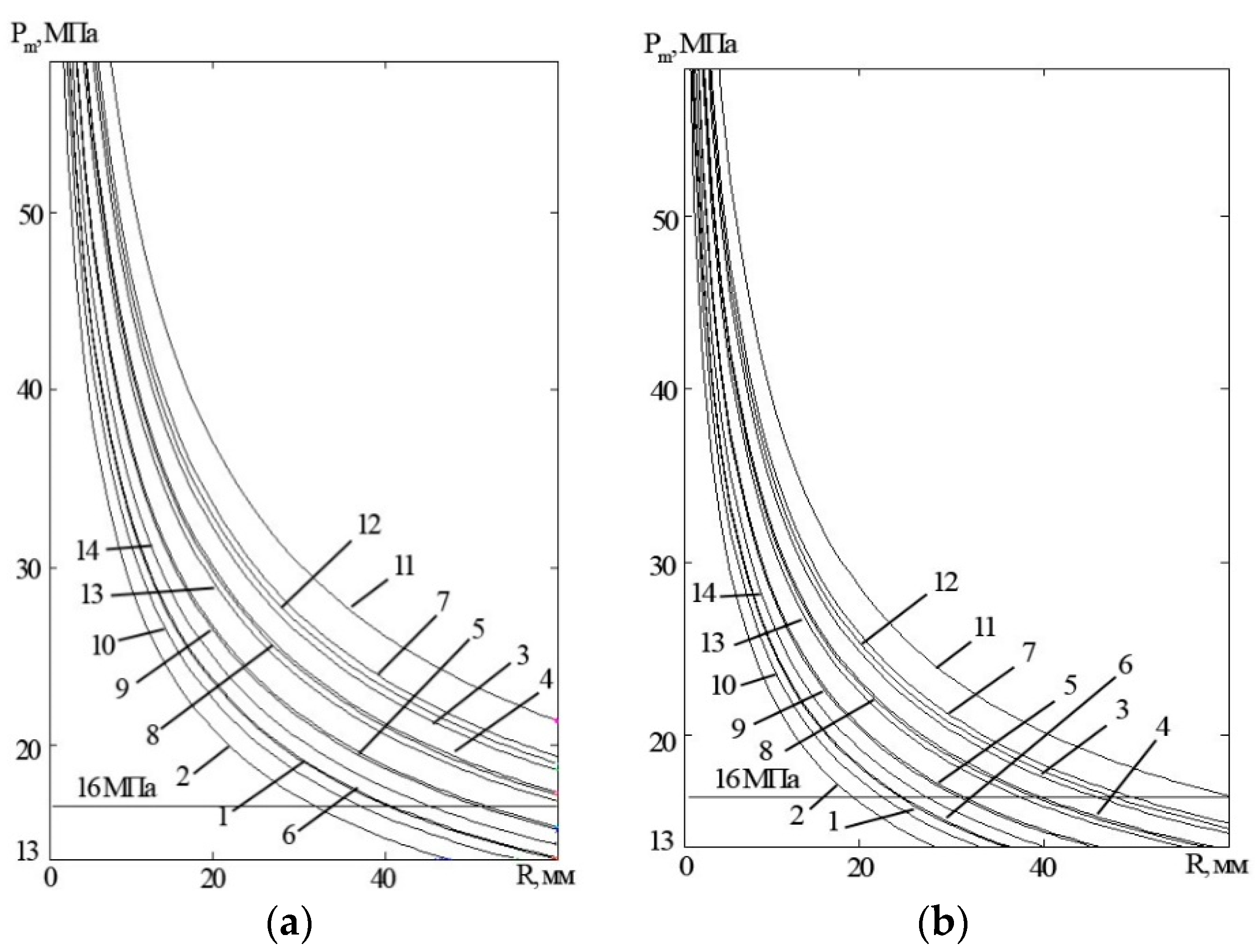
3. Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bezsonov, Y.; Mitryasova, O.; Smyrnov, V.; Smyrnova, S. Influence of the South-Ukraine electric power producing complex on the ecological condition of the Southern Bug River. East.-Eur. J. Enterp. Technol. 2017, 4, 20–28. [Google Scholar] [CrossRef][Green Version]
- Malyushevskaya, A.; Koszelnik, P.; Yushchishina, A.; Mitryasova, O.; Mats, A.; Gruca-Rokosz, R. Eco-friendly Principles on the Extraction of Humic Acids Intensification from Bio substrates. J. Ecol. Eng. 2023, 24, 317–327. [Google Scholar] [CrossRef] [PubMed]
- Malyushevskaya, A.; Koszelnik, P.; Yushchishina, A.; Mitryasova, O.; Mats, A.; Gruca-Rokosz, R. Synergy effect during water treatment by electric discharge and chlorination. Environments 2023, 10, 93. [Google Scholar] [CrossRef]
- Mitryasova, O.; Pohrebennyk, V.; Kochanek, A.; Stepanova, O. Environmental Footprint Enterprise as Indicator of Balance it’s Activity. In Proceedings of the 17th International Multidisciplinary Scientific Geoconference SGEM 2017, Albena, Bulgaria, 29 June–5 July 2017; Volume 51, pp. 371–378. [Google Scholar]
- Mitryasova, O.; Pohrebennyk, V.; Kardasz, P. Hydrochemical Aspects of Surface Water Quality Assessment. In Proceedings of the 18th International Multidisciplinary Scientific Geoconference SGEM 2018, Albena, Bulgaria, 30 June–9 July 2018; Volume 5.2, pp. 513–520. [Google Scholar]
- Phonphuak, N.; Chindaprasirt, P. Types of waste, properties, and durability of pore-forming waste-based fired masonrybricks. In Eco-Efficient Masonry Bricks and Blocks: Design, Properties and Durability; Woodhead Publishing: Sawston, UK, 2015; pp. 103–127. [Google Scholar] [CrossRef]
- Poklonov, S.G. Determination of the breakdown voltage of an aqueous interelectrode gap. Surf. Eng. Appl. Electrochem. 2010, 46, 64–69. [Google Scholar] [CrossRef]
- Pohrebennyk, V.; Cygnar, M.; Mitryasova, O.; Politylo, R.; Shybanova, A. Efficiency of Sewage Treatment of Company “Enzyme”. In Book 5, Ecology, Economics, Education and Legislation, Volume II, Ecology and Environmental Protection, Proceedings of the 16th International Multidisciplinary Scientific Geoconference SGEM 2016, Albena, Bulgaria, 30 June–6 July 2016; Curran Associates, Inc.: Red Hook, NY, USA, 2016; pp. 295–302. [Google Scholar]
- Kucharski, J. Fuzzy modelling of chosen electroheat systems. Prz. Elektrotechniczny (Electr. Rev.) 2008, 84, 189–192. [Google Scholar]
- Sundriyal, S.; Khan, M.Z.; Bundel, B.R.; Khan, I.A. Study on different types of electric discharge machining methods: A review. Mater. Today Proceeding 2021, 46, 6828–6834. [Google Scholar] [CrossRef]
- Smirnov, A.P.; Zhekul, V.G.; Mel’kher, Y.I.; Taftai, E.I.; Khvoshchan, O.V.; Shvets, I.S. Experimental Investigation of the Pressure Waves Generated by an Electric Explosion in a Closed Volume of a Fluid. Surf. Eng. Appl. Electrochem. 2018, 54, 475–480. [Google Scholar] [CrossRef]
- Ślot, K.; Kapusta, P.; Kucharski, J. Autoencoder-based image processing framework for object appearance modifications. Neural Comput. Appl. 2021, 33, 1079–1090. [Google Scholar] [CrossRef]
- Urbanek, P.; Kucharski, J. The algorithm for correction of emissivity variations of high-glittering moving surfaces for automatic temperature control systems. Prz. Elektrotechniczny (Electr. Rev.) 2008, 84, 100–102. [Google Scholar]
- Fiderek, P.; Kucharski, J.; Wajman, R. Fuzzy Regulator for Two-Phase Gas–Liquid Pipe Flows Control. Appl. Sci. 2022, 12, 399. [Google Scholar] [CrossRef]
- Frączyk, A.; Jaworski, T.; Urbanek, P.; Kucharski, J. The design for a smart high frequency generator for induction heating of loads. Prz. Elektrotechniczny (Electr. Rev.) 2014, 2, 20–23. [Google Scholar]
- Frączyk, A.; Kucharski, J. Surface temperature control of a rotating cylinder heated by moving inductors. Appl. Therm. Eng. 2017, 125, 767–779. [Google Scholar] [CrossRef]
- Hu, Z.; Bodyanskiy, Y.; Kulishova, N.; Tyshchenko, O. A Multidimensional Extended Neo-Fuzzy Neuron for Facial Expression Recognition. Int. J. Intell. Syst. Appl. (IJISA) 2017, 9, 29–36. [Google Scholar] [CrossRef]
- Hu, Z.; Dychka, I.; Sulema, Y.; Radchenko, Y. Graphical Data Steganographic Protection Method Based on Bits Correspondence Scheme. Int. J. Intell. Syst. Appl. (IJISA) 2017, 9, 34–40. [Google Scholar] [CrossRef]
- Hu, Z.; Dychka, I.; Onai, M.; Zhykin, Y. Blind Payment Protocol for Payment Channel Networks. Int. J. Comput. Netw. Inf. Secur. (IJCNIS) 2019, 11, 22–28. [Google Scholar] [CrossRef]
- Hu, Z.; Gnatyuk, S.; Okhrimenko, T.; Tynymbayev, S.; Iavich, M. High-Speed and Secure PRNG for Cryptographic Applications. Int. J. Comput. Netw. Inf. Secur. (IJCNIS) 2020, 12, 1–10. [Google Scholar] [CrossRef]
- Hu, Z.; Ivashchenko, M.; Lyushenko, L.; Klyushnyk, D. Artificial Neural Network Training Criterion Formulation Using Error Continuous Domain. Int. J. Mod. Educ. Comput. Sci. (IJMECS) 2021, 13, 13–22. [Google Scholar] [CrossRef]
- Hu, Z.; Khokhlachova, Y.; Sydorenko, V.; Opirskyy, I. Method for Optimization of Information Security Systems Behavior under Conditions of Influences. Int. J. Intell. Syst. Appl. (IJISA) 2017, 9, 46–58. [Google Scholar] [CrossRef]
- Hu, Z.; Mashtalir, S.; Tyshchenko, O.; Stolbovyi, M. Video Shots’ Matching via Various Length of Multidimensional Time Sequences. Int. J. Intell. Syst. Appl. (IJISA) 2017, 9, 10–16. [Google Scholar] [CrossRef]
- Hu, Z.; Odarchenko, R.; Gnatyuk, S.; Zaliskyi, M.; Chaplits, A.; Bondar, S.; Borovik, V. Statistical Techniques for Detecting Cyberattacks on Computer Networks Based on an Analysis of Abnormal Traffic Behavior. Int. J. Comput. Netw. Inf. Secur. (IJCNIS) 2020, 12, 1–13. [Google Scholar] [CrossRef]
- Hu, Z.; Tereykovskiy, I.; Tereykovska, L.; Pogorelov, V. Determination of Structural Parameters of Multilayer Perceptron Designed to Estimate Parameters of Technical Systems. Int. J. Intell. Syst. Appl. (IJISA) 2017, 9, 57–62. [Google Scholar] [CrossRef]
- Hu, Z.; Tereikovskyi, I.; Chernyshev, D.; Tereikovska, L.; Tereikovskyi, O.; Wang, D. Procedure for Processing Biometric Parameters Based on Wavelet Transformations. Int. J. Mod. Educ. Comput. Sci. (IJMECS) 2021, 13, 11–22. [Google Scholar] [CrossRef]
- Jaworski, T.; Kucharski, J. An algorithm for reconstruction of temperature distribution on rotating cylinder surface from a thermal camera video stream. Prz. Elektrotechniczny (Electr. Rev.) 2013, 2a, 91–94. [Google Scholar]
- Khanna, N.; Pusavec, F.; Agrawal, C.; Krolczyk, G.M. Measurement and evaluation of hole attributes for drilling CFRP composites using an indigenously developed cryogenic machining facility. Measurement 2020, 154, 107504. [Google Scholar] [CrossRef]
- Krolczyk, G.; Legutko, S.; Gajek, M. Predicting the surface roughness in the dry machining of duplex stainless steel (DSS). Metalurgija 2013, 52, 259–262. [Google Scholar]
- Krolczyk, G.M.; Legutko, S. Experimental analysis by measurement of surface roughness variations in turning process of duplex stainless steel. Metrol. Meas. Syst. 2014, 21, 759–770. [Google Scholar] [CrossRef]
- Łuczak, P.; Kucharski, P.; Jaworski, T.; Perenc, I.; Ślot, K.; Kucharski, J. Boosting intelligent data analysis in smart sensors by integrating knowledge and machine learning. Sensors 2021, 21, 6168. [Google Scholar] [CrossRef]
- Malyushevskij, P.P.; Levda, V.I.; Malyushevska, A.P. Electroexplosive nonlinear, volumetric cavitation in technological reactors. Part 1 (Electrodischarge generation of a gasphase—Nucleus of cavitation). Elektron. Process. Mater. 2004, 1, 40–46. [Google Scholar]
- Malyushevskij, P.P.; Levda, V.I.; Malyushevska, A.P. Electroexplosive nonlinear volumetric cavitation in technological reactors. Part II (Analysis of cavitation area structure). Elektron. Process. Mater. 2004, 2, 34–40. [Google Scholar]
- Malyushevskaya, A.; Koszelnik, P.; Yushchishina, A.; Mitryasova, O.; Gruca-Rokosz, R. Green Approach to Intensify the Extraction Processes of Substances from Plant Materials. J. Ecol. Eng. 2022, 23, 197–204. [Google Scholar] [CrossRef]
- Nathaniel, D.; Taylor, G.; Friedman, A.; Fridman, D. Non-equilibrium microsecond pulsed spark discharge in liquid as a source of pressure waves. Int. J. Heat Mass Transfer. 2018, 126 (Pt A), 1104–1110. [Google Scholar] [CrossRef]
- Ovchinnikova, L.E.; Kozyrev, S.S. Efficiency enhancement for discharge-pulse processing by adaptive control based on fuzzy models. Surf. Eng. Appl. Electrochem. 2012, 48, 332–338. [Google Scholar] [CrossRef]
- Michalowska, J.; Miaskowski, A.; Wac-Wlodarczyk, A. Numerical analysis of high frequency electromagnetic field distribution and specific absorption rate in realistic breast models. Prz. Elektrotechniczny (Electr. Rev.) 2012, 88, 97–99. [Google Scholar]
- Michałowska, J.; Wac-Włodarczyk, A.; Kozieł, J. Monitoring of the specific absorption rate in terms of electromagnetic hazards. J. Ecol. Eng. 2020, 21, 224–230. [Google Scholar] [CrossRef]
- Pytka, J.; Budzyński, P.; Tomiło, P.; Michałowska, J.; Gnapowski, E.; Błażejczak, D.; Łukaszewicz, A. IMUMETER—A Convolution Neural Network Based Sensor For Measurement of Aircraft Ground Performance. Sensors 2021, 21, 4726. [Google Scholar] [CrossRef]
- Twardowski, P.; Legutko, S.; Krolczyk, G.M.; Hloch, S. Investigation of wear and tool life of coated carbide and cubic boron nitride cutting tools in high speed milling. Adv. Mech. Eng. 2015, 7, 1687814015590216. [Google Scholar] [CrossRef]
- Yang, Y.; Friedman, A.; Cho, Y.I. Plasma Discharge in Water. Adv. Heat Transfer. 2010, 42, 179–292. [Google Scholar]
- Zgraja, J.; Lisowski, G.; Kucharski, J. Autonomous energy matching control in an LLC induction heating generator. Energies 2020, 13, 1860. [Google Scholar] [CrossRef]
- Zhekul, V.G.; Poklonov, S.G.; Trofimova, L.P.; Shvets, I.S. Formation of an electric discharge in water-oil emulsions at high pressures and temperatures. Electron. Process. Mater. 2001, 1, 37–43. [Google Scholar]
- Liu, Y.; Li, Z.-Y.; Li, X.-D.; Liu, S.; Zhou, G.-Y.; Lin, F.-C. Intensity improvement of shock waves induced by liquid electrical discharges. Phys. Plasmas 2017, 24, 043510. [Google Scholar] [CrossRef]
- Shamko, V.V. Investigation of the Conditions for Choosing the Optimal Parameters of the Discharge Circuit. Discharge-Pulse Technologies; Naukova Dumka: Kiev, Ukraine, 1978; pp. 21–28. [Google Scholar]
- Urbanek, P.; Kucharski, J.; Frączyk, A. Methods of determination of dynamic properties of induction heated multi input—Multi output system. Prz. Elektrotechniczny (Electr. Rev.) 2008, 84, 180–183. [Google Scholar]
- Vovchenko, A.I.; Demidenko, L.Y.; Kozyrev, S.S. Control of high voltage discharge-pulse installation for implementation of technological modes of electrochemical explosion. East.-Eur. J. Enterp. Technol. 2020, 2, 29–38. [Google Scholar] [CrossRef]
- Vovchenko, A.I.; Demidenko, L.Y.; Kozyrev, S.S.; Ovchinnikova, L.E. High voltage electrochemical explosion in discharge-pulse technologies. Surf. Eng. Appl. Electrochem. 2022, 58, 731–738. [Google Scholar] [CrossRef]
- Koji, U.; Naoyuki, S.; Shintaro, S.; Hiroshi, Y.; Junichiro, N. Controlled disintegration of reinforced concrete blocks based on wave and fracture dynamics. Procedia Struct. Integr. 2016, 2, 350–357. [Google Scholar] [CrossRef][Green Version]
- Kozyrev, S.S. Control system of discharge-pulse installation with elements of artificial intelligence. In Proceedings of the IEEE 2nd Ukraine Conference on Electrical and Computer Engineering UKRCON-2019, Lviv, Ukraine, 2–6 July 2019; pp. 513–517. [Google Scholar] [CrossRef]
- Kozyrev, S.S.; Nazarova, N.S.; Vinnychenko, D.V. Adaptive filter of input information signal for discharge pulse installation control system. In Proceedings of the IEEE 3rd International Conference on ntelligent Energy and Power Systems (IEPS), Kharkiv, Ukraine, 10–14 September 2018; Proceedings N° 8559558. pp. 343–346. [Google Scholar] [CrossRef]
- Rizun, A.R.; Denisyuk, T.D.; Golen, Y.V. Experimental study of electrodischarge powdering of brown coal as a constituent of coal-water fuel. Surf. Eng. Appl. Electrochem. 2009, 45, 256–258. [Google Scholar] [CrossRef]
- Rizun, A.R.; Golen, Y.V.; Denisyuk, T.D. Method for calculating the parameters of the electric discharge destruction of non-metallic materials. Electron. Process. Mater. 2003, 4, 74–84. [Google Scholar]
- Rizun, A.R.; Tsurkin, V.N. Electric discharge destruction of non-metallic materials. Electron. Process. Mater. 2002, 1, 83–85. [Google Scholar]
- Rizun, A.R.; Kosenkov, V.M. On the issue of determining the productivity of electric discharge destruction of brittle non-metallic materials. Electron. Process. Mater. 2001, 2, 45–50. [Google Scholar]
- Przystupa, K.; Petrichenko, S.; Yushchishina, A.; Mitryasova, O.; Pohrebennyk, V.; Kochan, O. Electric Spark Method of Purification of Galvanic Waste Waters. Prz. Elektrotechniczny (Electr. Rev.) 2020, 97, 230–233. [Google Scholar] [CrossRef]
- Petrov, O.; Petrichenko, S.; Yushchishina, A.; Mitryasova, O.; Pohrebennyk, V. Electrospark Method in Galvanic Wastewater Treatment for Heavy Metal Removal. Appl. Sci. 2020, 10, 5148. [Google Scholar] [CrossRef]
- Nusupbekov, B.R.; Kusaiynov, K.; Sakipova, S.; Khasenov, A.; Beisenbek, A. On the issue of improving the technology of complex extraction of rare and scattered metals by the electric pulse method. Met. Latest Technol./Metallofiz. Newishie Technol. 2014, 36, 275–286. [Google Scholar]
- Wei, H.; Yumeng, C. The application of high-voltage pulses in the mineral processing industry—A review. Powder Technol. 2021, 393, 116–130. [Google Scholar] [CrossRef]
- Barbashova, G.A.; Shomko, V.V. Influence of the discharge regime on the hydrodynamic parameters of an electric explosion. Electron. Process. Mater. 2007, 6, 64–70. [Google Scholar]
| Type of Coal | Compressive Strength, MPa | |
|---|---|---|
| Along the Fibers | Across the Fibers | |
| Spruce charcoal | 5.9–13.1 | 0.7–0.9 |
| Pine charcoal | 10.3–16.9 | 1.2–2.6 |
| birch charcoal | 19.5–33.4 | 2.1–4.4 |
| Aspen coal | 11.3–17.1 | 1.2–2.2 |
| No. Option | U0, kV | C, μF | W0, J | l0, mm | E0, V/m | Pamax, MPa |
|---|---|---|---|---|---|---|
| 1 | 35 | 0.5 | 306 | 36 | 36.8 × 105 | 80.4 |
| 2 | 35 | 0.25 | 153 | 33 | 37.9 × 105 | 83.9 |
| 3 | 40 | 1.5 | 1200 | 44 | 39.6 × 105 | 82.9 |
| 4 | 40 | 1.0 | 800 | 42 | 40.2 × 105 | 85.1 |
| 5 | 40 | 0.5 | 400 | 38 | 41.2 × 105 | 88.9 |
| 6 | 40 | 0.25 | 200 | 35 | 42.4 × 105 | 92.8 |
| 7 | 45 | 1 | 1012 | 44 | 44.4 × 105 | 92.9 |
| 8 | 45 | 0.5 | 506 | 40 | 45.6 × 105 | 97.1 |
| 9 | 45 | 0.25 | 253 | 37 | 46.8 × 105 | 101.4 |
| 10 | 45 | 0.1 | 101 | 33 | 48.5 × 105 | 107.4 |
| 11 | 50 | 1.0 | 1250 | 46 | 48.6 × 105 | 100.6 |
| 12 | 50 | 0.5 | 625 | 43 | 49.8 × 105 | 105.1 |
| 13 | 50 | 0.25 | 313 | 39 | 51.1 × 105 | 109.7 |
| 14 | 50 | 0.1 | 125 | 35 | 53.0 × 105 | 116.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malyushevskaya, A.; Petrychenko, S.; Przystupa, K.; Mitryasova, O.; Majka, M.; Kochan, O. Optimizing Energy Efficiency of Dielectric Materials’ Electrodischarge Dispersion as One Sustainable Development Green Trend. Energies 2023, 16, 7098. https://doi.org/10.3390/en16207098
Malyushevskaya A, Petrychenko S, Przystupa K, Mitryasova O, Majka M, Kochan O. Optimizing Energy Efficiency of Dielectric Materials’ Electrodischarge Dispersion as One Sustainable Development Green Trend. Energies. 2023; 16(20):7098. https://doi.org/10.3390/en16207098
Chicago/Turabian StyleMalyushevskaya, Antonina, Serhii Petrychenko, Krzysztof Przystupa, Olena Mitryasova, Michał Majka, and Orest Kochan. 2023. "Optimizing Energy Efficiency of Dielectric Materials’ Electrodischarge Dispersion as One Sustainable Development Green Trend" Energies 16, no. 20: 7098. https://doi.org/10.3390/en16207098
APA StyleMalyushevskaya, A., Petrychenko, S., Przystupa, K., Mitryasova, O., Majka, M., & Kochan, O. (2023). Optimizing Energy Efficiency of Dielectric Materials’ Electrodischarge Dispersion as One Sustainable Development Green Trend. Energies, 16(20), 7098. https://doi.org/10.3390/en16207098







