Priority of Wind Energy in West Coast of Southern Thailand for Installing the Water Pumping Windmill System with Combining of Entropy Weight Method and TOPSIS

Abstract

Wind energy potential or quality serve as the primary determinants influencing the decisions of Thai farmers regarding the installation of water-pumping windmills with heights ranging from 9 to 15 m and a cut-in wind speed requirement of 4 m/s, aimed at reducing their fuel costs. To introduce a simplified calculation method as one of their decision-making tools, the combined approach of the entropy weight method with TOPSIS has been introduced to assist them in prioritizing and assessing the wind quality in their respective areas. This study focuses on the western region of Southern Thailand, known for its high agricultural productivity. Initially, only 18 out of the 227 sub-districts with a minimum monthly wind speed exceeding 4 m/s were selected for thorough investigation. Subsequently, the entropy weight method was applied to the monthly wind speed data of these 18 chosen sub-districts to calculate their monthly weight values. These monthly weight values provide a quantifiable characterization of the wind quality in these specific sub-districts, revealing variations in wind quality between seasons, with superior quality during the summer season compared to the rainy season. Following the calculation of monthly weight values, the TOPSIS technique was applied to the wind data in conjunction with these monthly weight values, resulting in the determination of performance scores (P_i) for each of the 18 sub-districts. P_i values were found to vary from 0.0641 to 0.9006. In the final step of the analysis, these 18 sub-districts were ranked based on their respective P_i values, with the implication that sub-districts exhibiting higher P_i values are more suitable for the installation of water-pumping windmills with heights ranging from 9 to 15 m compared to those with lower P_i values.

1. Introduction

Thailand holds a prominent position as one of the leading global food exporters. Agriculture plays an important role in its economy, employing approximately 30% of the Thai workforce [1]. The country experiences three distinct seasons—summer (March to May), rainy (June to October) and winter (November to February)—driven by the influence of the southwest monsoon, northeast monsoon, and southeast monsoon. However, the extended mountainous terrain of the elongated southern peninsula, situated between the Andaman Sea and the Gulf of Thailand, divides the southern regions of Thailand into two principal zones: the western side, encompassing six provinces, and the eastern side, comprising eight provinces. This unique topography results in two primary seasons for these regions: (1) summer (November to April) and rainy (May to October) for the west side, and (2) summer (May to September) and rainy (October to April) for the eastern region. According to data from the Thailand Office of Agriculture Economics [2], five out of the six provinces in the western region are recognized for their high-quality agricultural production, positioning them within the top group of southern provinces for agriculture in 2022. Additionally, statistics from the Thailand Land Development Department [3] reveal that almost 54% of the land in the western region falls under the category of agricultural areas. Despite these favorable climate and agriculture-related indicators, farmers in these regions continue to incur high production costs, particularly in terms of fuel expenses for their water-pumping systems. Traditionally, Thai farmers have sought to mitigate these costs by transitioning from conventional water-pumping systems to water-pumping windmills, with heights typically ranging from 10 to 15 m. These windmills are designed to draw water from natural sources for irrigating their agricultural areas. However, a crucial prerequisite for the effective installation of such water-pumping windmills is a comprehensive understanding of the wind potential within the agricultural areas. Regrettably, most Thai farmers lack access to analyzed wind data for their specific locales. Wind energy data from the Department of Alternative Energy Development and Efficiency (DEDE) [4] in Thailand indicate an average wind speed range of approximately 3–5 m/s, characterized as low to moderate. This wind speed range is deemed adequate for continuous electricity generation throughout the day. Previous research by Thitipong et al. [5] involved the collection of hourly wind speed data spanning the years 2008 to 2010, recorded at heights of 10 m, 30 m, and 40 m in Ubonratchathani province, Thailand. The primary objective was to assess wind power generation potential in relation to varying wind speeds at different altitudes. Meanwhile, Sakkarin et al. [6] conducted a comprehensive review of the state of wind energy in Thailand. The collective findings underscored that while wind energy resources in Thailand were not exceptionally high, they still represented a valuable renewable energy source for electricity generation. Pham et al. [7] conducted a statistical analysis of one year’s worth of wind measurement data collected from three sites, aiming to investigate wind energy potential at higher altitudes, specifically at 65 m, 90 m, and 120 m. Their findings strongly recommended the installation of wind turbines with low cut-in wind speeds at these locations. Additionally, Chamlong et al. [8] examined the correlation between average wind speed and the discharge capacity of water-pumping windmills with a height of 12 m at the Ayutthaya site. Their recorded data demonstrated an increase in pump discharge with rising wind speeds, with a cut-in speed of 2 m/s. It is important to note that these previous researchers [5,6,7,8] encountered significant challenges in their endeavors, including the need to independently collect and measure wind data over extended periods, coupled with substantial budget requirements. These hurdles cause considerable impediments for Thai farmers who lack access to wind measurement instruments and face budget constraints when contemplating the adoption of water-pumping windmill systems in the western regions of Southern Thailand.

Based on the mentioned research findings, it is advisable to introduce methods for prioritizing wind quality across all western regions of Southern Thailand, utilizing monthly wind data and sub-district information obtained from secondary data sources. Sakon et al. [9,10] previously applied the analytical hierarchy process (AHP) and the complete linkage clustering method to secondary wind data. The outcomes of their calculations indicated that AHP effectively prioritized wind energy potential across different areas, while the complete linkage clustering method efficiently grouped areas with similar wind quality into three categories: low quality, medium quality, and high quality. However, these two methods were not straightforward to apply to wind datasets. Numerous studies have explored the application of simpler techniques such as the entropy weight method and the technique for order preference similarity to the ideal solution (TOPSIS) to address various decision-making challenges, providing a rational basis for selecting the most suitable alternatives. Jingwen [11] applied the combination of the entropy weight and TOPSIS methods to select a suitable management information system (MIS) in the purchasing process, considering five purchasing criteria weighted using the entropy weight method. Xiangxin et al. [12] assigned weight values to ten evaluation indexes related to safety conditions in coal mines using the entropy weight method, subsequently employing TOPSIS to assess the safety conditions of four coal mines based on these weights. Jia et al. [13] prioritized three cold-chain logistics and distribution center locations using a combination of 11 indexes, with weight values assigned by the entropy weight method, followed by ranking using TOPSIS. In a different context, Fu et al. [14] aimed to identify the best wastewater pollution control technology among three alternatives. They initially applied the entropy method to assign weights to four investment and operation cost indexes and one process efficiency index. Subsequently, TOPSIS was employed, considering all five indexes’ weight values, to select the most suitable wastewater pollution control technology. Salehi et al. [15] evaluated the quality of management systems in five petrochemical plants using the Entropy-TOPSIS method. Data were collected through a well-designed questionnaire covering organizational, human, and technical aspects from 34 employees within these plants. The collected data were analyzed using the entropy method to determine weight values for each aspect, and then the management system quality of the five petrochemical plants was assessed and ranked using TOPSIS. Tien-Chin et al. [16] ranked 45 private universities in Vietnam using three criteria for publication conditions to ensure the quality of education, three criteria for the publication of actual education quality, and one criterion for financial revenue and expenditure publication. This study began by calculating the weighted values of all seven criteria using the entropy method. Subsequently, these 45 universities were ranked based on the weight values of these seven criteria for the years 2018 to 2019 and 2019 to 2020 using TOPSIS. Finally, the ranking order of the 45 universities for the years 2018 to 2019 and 2019 to 2020 was grouped into four categories, and the university ranking results for these two years were compared. Yushan et al. [17] evaluated and ranked the quality development level of nine cities in the Pearl River Delta using four criteria in the economic development dimension, three criteria in the innovative development dimension, three criteria in the coordination and sharing dimension, three criteria in the green development dimension, and three criteria in the open development dimension. This evaluation began by calculating the weighting values of all 16 criteria. Finally, the quality development level of the nine cities was ranked based on data from the years 2013 to 2020 using TOPSIS. Fu et al. [18] assigned weight values to 10 secondary-level indicators for four groups of first-level indicators, including access openness, transaction openness, exit openness, and transfer openness, using the entropy method. They then evaluated and ranked 22 digital platforms in China using TOPSIS. These platforms were subsequently grouped into three categories: four digital platforms in the top 20% group, seven digital platforms in the middle 20–50% group, and eleven digital platforms in the lower 50% group. Wang et al. [19] applied the entropy method and TOPSIS to select suitable green retrofitting options for old multi-story houses in severe cold regions. They established 16 evaluation indicators across five dimensions, including energy savings, environmental benefits, economic benefits, thermal performance, and building fire protection. The weight values for all 16 indicators were determined using the entropy method. Using these weight values and TOPSIS, they evaluated various green retrofitting plans. With the best retrofitting plan, old multi-story houses in severe cold regions could be renovated to significantly reduce energy consumption and pollutant gas emissions. Wang et al. [20] assessed and ranked the maturity of urban energy internet (UEI) development for five first-tier cities in China. Firstly, they defined evaluation indexes based on three dimensions: development status, development benefits, and development prospects. The weighting values were assigned using the AHP-entropy weighting method. Finally, the maturity of UEI development for the five first-tier cities in China was prioritized using GRA-KL-TOPSIS. Alghassab [21] studied suitable sustainable energy sources for the Kingdom of Saudi Arabia based on six criteria: environmental impact, cost-effectiveness, energy efficiency, scalability and reliability, social acceptance and equity, and technological maturity and innovation potential. By employing fuzzy TOPSIS, the results showed that the final ranking of suitable sustainable energy sources, from the best energy source to the least, was as follows: solar energy, wind energy, energy storage technologies, hydropower, biomass energy, geothermal energy, and ocean energy. Research works [11,12,13,14,15,16,17,18,19,20,21] have shown that the combination of the entropy weight method and TOPSIS is one of the most popular methods for prioritizing or ranking alternatives based on the related criteria. This combination method is straightforward to calculate, and the results are reasonably explainable. Moreover, this combination method can be applied to various problems.

For this study, the main purpose is to apply the entropy weight method and TOPSIS to prioritize and rank secondary wind datasets for the western region of Southern Thailand [22]. This combining method should be expected to be one of the simple methods to inform the suitable areas for installing water-pumping windmill systems with heights ranging from 9 to 15 m for Thai farmers to reduce fuel cost in their agriculture farms.

2. Materials and Methods

To rank all alternative areas based on the quality of monthly wind speed data, this study should follow three main steps as outlined below: (1) Preliminary assessment of suitable areas for the water-pumping windmill with heights ranging from 9 to 15 m, (2) assignment of monthly weight values using the entropy weight method and (3) ranking of qualified areas using TOPSIS.

2.1. Preliminary Assessment of Suitable Areas for the Water Pumping Windmill with Heights Ranging from 9 to 15 m

In this step, the secondary dataset of monthly wind speeds at a height of 10 m for 271 sub-districts in the western region of southern Thailand is collected [22]. Since water-pumping windmills with heights ranging from 9 to 15 m can operate at high performance when the wind speed is faster than 4 m/s [8], all sub-districts with a minimum monthly wind speed faster than 4 m/s are initially selected.

2.2. Assignment of Monthly Weight Values with the Entropy Weight Method

In this step, all monthly wind speed data for the qualified sub-districts are organized in tabular form, as illustrated in

Table 1. Monthly wind speed data for the m sub-districts.

Sub-District	Wind Speed (m/s)
	January	February	March	…	December
A1	x1,1	x1,2	x1,3	…	x1,12
A2	x2,1	x2,2	x2,3	…	x2,12
A3	x3,1	x3,2	x3,3	…	x3,12
⋮	⋮	⋮	⋮	⋮	⋮
Am	xm,1	xm,2	xm,3	…	xm,12

. Here, A_i represents sub-district i, and x_i,j represents the wind speed of sub-district i (m/s) for the jth month.

Subsequently, all values of x_i,j should be normalized using their respective column sum (${{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{m}}{\mathrm{x}}_{\mathrm{i},\mathrm{j}}$) so that each normalized value of r_i,j corresponding to its value of x_i,j, is derived with Equation (1). Then, all normalized values of r_i,j are organized into tabular form, as shown in Table 2.

$${\mathrm{r}}_{\mathrm{i},\mathrm{j}}=\frac{{\mathrm{x}}_{\mathrm{i},\mathrm{j}}}{{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{m}}{\mathrm{x}}_{\mathrm{i},\mathrm{j}}}, \mathrm{i}=1 \mathrm{to} \mathrm{m} \mathrm{and} \mathrm{j}=1 \mathrm{to} 12$$

(1)

Table 2. Normalized values of monthly wind speed.

Sub-District	Normalized Values of Monthly Wind Speed
	January	February	March	…	December
A1	r1,1	r1,2	r1,3	…	r1,12
A2	r2,1	r2,2	r2,3	…	r2,12
A3	r3,1	r3,2	r3,3	…	r3,12
⋮	⋮	⋮	⋮	⋮	⋮
Am	rm,1	rm,2	rm,3	…	rm,12

Table 2. Normalized values of monthly wind speed.

Sub-District	Normalized Values of Monthly Wind Speed
	January	February	March	…	December
A1	r1,1	r1,2	r1,3	…	r1,12
A2	r2,1	r2,2	r2,3	…	r2,12
A3	r3,1	r3,2	r3,3	…	r3,12
⋮	⋮	⋮	⋮	⋮	⋮
Am	rm,1	rm,2	rm,3	…	rm,12

Subsequently, the monthly entropy values of e_j for 12 months (January, February, March, April, May, June, July, August, September, October, November, and December) are calculated using Equation (2). Then, all monthly weight values of w_j for the 12 months are determined with Equation (3) to assess the monthly effects on wind speeds in different areas. Finally, the initial data for TOPSIS as shown in Table 3 are generated from monthly wind speed data in Table 1 by adding the values of w_j with their corresponding month names, for example, w₁ for Jan, w₂ for Feb, etc., and then adding the values of RMS from the values of x_i,j in each column.

$${\mathrm{e}}_{\mathrm{j}}=-\frac{{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{m}}{\mathrm{r}}_{\mathrm{i},\mathrm{j}}\ln ({\mathrm{r}}_{\mathrm{i},\mathrm{j}})}{\ln \left(\mathrm{m}\right)}, \mathrm{i}=1 \mathrm{to} \mathrm{m} \mathrm{and} \mathrm{j}=1 \mathrm{to} 12$$

(2)

$${\mathrm{w}}_{\mathrm{j}}=\frac{1-{ \mathrm{e}}_{\mathrm{j}}}{{{\displaystyle \sum }}_{\mathrm{j}=1}^{12}\left(1-{\mathrm{e}}_{\mathrm{j}}\right)}, \mathrm{i}=1 \mathrm{to} 12$$

(3)

Table 3. The initial data table for TOPSIS.

Sub-District	Wind Speed (m/s)
	January w1	February w2	March w3	…	December w12
A1	x1,1	x1,2	x1,3	…	x1,12
A2	x2,1	x2,2	x2,3	…	x2,12
A3	x3,1	x3,2	x3,3	…	x3,12
⋮	⋮	⋮	⋮	⋮	⋮
Am	xm,1	xm,2	xm,3	…	xm,12
	$\sqrt{{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{m}}{\mathrm{x}}_{\mathrm{i},1}^2}$	$\sqrt{{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{m}}{\mathrm{x}}_{\mathrm{i},2}^2}$	$\sqrt{{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{m}}{\mathrm{x}}_{\mathrm{i},3}^2}$	…	$\sqrt{{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{m}}{\mathrm{x}}_{\mathrm{i},12 }^2}$

Table 3. The initial data table for TOPSIS.

Sub-District	Wind Speed (m/s)
	January w1	February w2	March w3	…	December w12
A1	x1,1	x1,2	x1,3	…	x1,12
A2	x2,1	x2,2	x2,3	…	x2,12
A3	x3,1	x3,2	x3,3	…	x3,12
⋮	⋮	⋮	⋮	⋮	⋮
Am	xm,1	xm,2	xm,3	…	xm,12
	$\sqrt{{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{m}}{\mathrm{x}}_{\mathrm{i},1}^2}$	$\sqrt{{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{m}}{\mathrm{x}}_{\mathrm{i},2}^2}$	$\sqrt{{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{m}}{\mathrm{x}}_{\mathrm{i},3}^2}$	…	$\sqrt{{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{m}}{\mathrm{x}}_{\mathrm{i},12 }^2}$

2.3. Ranking of Qualified Areas with TOPSIS

In this part, the data in Table 3 is analyzed using TOPSIS to calculate the performance score (P_i) for each qualified sub-district. This step involves calculating the TOPSIS-normalized values of b_i,j from the values of x_i,j in Table 3 using Equation (4), and then transferring all TOPSIS-normalized values (b_i,j) into tabular form, as shown in Table 4.

$${\mathrm{b}}_{\mathrm{i},\mathrm{j}}=\frac{{\mathrm{x}}_{\mathrm{i},\mathrm{j}}}{\sqrt{{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{m}}{\mathrm{x}}_{\mathrm{i},\mathrm{j}}^2}}, \mathrm{i}=1 \mathrm{to} \mathrm{m} \mathrm{and} \mathrm{j}=1 \mathrm{to} 12$$

(4)

Table 4. TOPSIS-normalized values of monthly wind speed with the monthly weight values (w_j).

Sub-District	TOPSIS-Normalized Values
	January w1	February w2	March w3	…	December w12
A1	b1,1	b1,2	b1,3	…	b1,12
A2	b2,1	b2,2	b2,3	…	b2,12
A3	b3,1	b3,2	b3,3	…	b3,12
⋮	⋮	⋮	⋮	⋮	⋮
Am	bm,1	bm,2	bm,3	…	bm,12

Table 4. TOPSIS-normalized values of monthly wind speed with the monthly weight values (w_j).

Sub-District	TOPSIS-Normalized Values
	January w1	February w2	March w3	…	December w12
A1	b1,1	b1,2	b1,3	…	b1,12
A2	b2,1	b2,2	b2,3	…	b2,12
A3	b3,1	b3,2	b3,3	…	b3,12
⋮	⋮	⋮	⋮	⋮	⋮
Am	bm,1	bm,2	bm,3	…	bm,12

Subsequently, the entire set of values for b_i,j in Table 4 is multiplied by their corresponding w_j to derive the TOPSIS-weighted normalized values of V_i,j as per the formula in Equation (5). These resulting TOPSIS-weighted normalized values (V_i,j) are then organized into tabular form, as displayed in

Table 5. TOPSIS-weighted normalized values of monthly wind speed with the monthly weight values (w_j).

Sub-District	TOPSIS-Weighted Normalized Values
	January w1	February w2	March w3	…	December w12
A1	V1,1	V1,2	V1,3	…	V1,12
A2	V2,1	V2,2	V2,3	…	V2,12
A3	V3,1	V3,2	V3,3	…	V3,12
⋮	⋮	⋮	⋮	⋮	⋮
Am	Vm,1	Vm,2	Vm,3	…	Vm,12
Vj+	V1+	V2+	V3+	…	V12+
Vj−	V1−	V2−	V3−	…	V12−

. All the values of V_j⁺ in Table 5 represent the monthly ideal best values, with each V_j⁺ selected from the maximum values of V_i,j in the jth column. Conversely, all the values of V_j⁻ in Table 5 serve as the monthly ideal worst values, with each V_j⁻ chosen from the minimum values of V_i,j in the jth column. To simplify the calculation of values for V_j⁺ and V_j⁻, it is necessary to carry out Equations (6) and (7).

V_i,j = w_j × b_i,j

(5)

V_j⁺ = max (V_1,j, V_2,j, V_3,j, …, V_12,j)

(6)

V_j⁻ = min (V_1,j, V_2,j, V_3,j, …, V_12,j)

(7)

Now, the Euclidean distance from the monthly ideal best for each sub-district (S_i⁺) and the Euclidean distance from the monthly ideal worst for each sub-district (S_i⁻) are computed using Equations (8) and (9). Finally, the performance scores (P_i) are calculated using Equation (10). Sub-districts with higher P_i values are more suitable for confidently installing water-pumping windmills with heights ranging from 9 to 15 m than sub-districts with lower P_i values.

$${\mathrm{S}}_{{\mathrm{i}}^{+}}=\sqrt{{{\displaystyle \sum }}_{\mathrm{j}=1}^{12}{\left({\mathrm{V}}_{\mathrm{i},\mathrm{j}}-{ \mathrm{V}}_{\mathrm{j}}^{+}\right)}^2}$$

(8)

$${\mathrm{S}}_{{\mathrm{i}}^{-}}=\sqrt{{{\displaystyle \sum }}_{\mathrm{j}=1}^{12}{\left({\mathrm{V}}_{\mathrm{i},\mathrm{j}}-{ \mathrm{V}}_{\mathrm{j}}^{-}\right)}^2}$$

(9)

$${\mathrm{P}}_{\mathrm{i}}=\frac{{\mathrm{S}}_{\mathrm{i}}^{-}}{\left({\mathrm{S}}_{\mathrm{i}}^{+}+{\mathrm{S}}_{\mathrm{i}}^{-}\right)}$$

(10)

3. Results

Most agricultural farms in Thailand have adopted water-pumping windmills with heights ranging from 9 to 15 m, which can operate efficiently at a relatively low cut-in wind speed of 3 m/s. However, Chamlong et al. [8] observed that for optimal performance and efficiency, the suitable cut-in wind speed for this type of water-pumping windmill should be faster than 4 m/s. Based on this criterion, only 18 out of 271 sub-districts in the western region of southern Thailand meet this initial requirement. The positions of all 18 sub-districts and their respective monthly wind speeds at a height of 10 m are detailed in

Table 6. Latitude and longitude of 18 sub-districts with minimum monthly wind speed faster than 4 m/s.

Sub-District	A1	A2	A3	A4	A5	A6	A7	A8	A9
Lat. (°N)	10.0479	10.1292	10.1811	10.0292	10.0307	9.6173	10.3016	8.4155	8.6056
Long. (°E)	98.8086	98.7269	98.7849	98.8527	98.8839	98.6201	98.8484	98.5702	98.5508
Sub-District	A10	A11	A12	A13	A14	A15	A16	A17	A18
Lat. (°N)	8.5464	8.1901	8.0256	7.8118	7.7311	7.8471	7.8688	7.8086	7.5404
Long. (°E)	98.5796	99.2521	99.3696	99.6936	99.7218	99.6623	99.7274	99.4625	99.7879

and

Table 7. The monthly wind speed at a height of 10 m of 18 sub-districts with minimum monthly wind speed faster than 4 m/s [22].

Alternative Areas	Monthly Wind Speed (m/s) at a Height of 10 m
	January	February	March	April	May	June	July	August	September	October	November	December
A1	6.15	6.03	5.48	4.67	4.51	4.61	4.58	4.91	4.89	4.21	4.81	5.83
A2	5.29	5.29	4.83	4.35	4.41	4.46	4.48	4.69	4.71	4.09	4.29	4.97
A3	6.10	6.04	5.51	4.70	4.31	4.25	4.26	4.57	4.69	4.17	4.80	5.70
A4	6.88	6.74	6.19	5.15	4.67	4.77	4.74	5.16	5.16	4.45	5.26	6.37
A5	6.56	6.43	5.96	5.08	4.69	4.79	4.75	5.21	5.28	4.58	5.2	6.15
A6	5.96	5.63	5.39	4.83	4.91	4.79	4.88	4.82	4.62	4.25	4.62	5.60
A7	5.35	5.36	5.00	4.45	4.14	4.10	4.09	4.42	4.52	4.15	4.47	5.01
A8	4.57	4.55	4.25	4.19	4.18	4.19	4.26	4.48	4.54	4.54	4.51	4.75
A9	5.28	5.08	4.51	4.22	4.44	4.54	4.56	4.90	4.93	4.41	4.52	5.52
A10	4.67	4.68	4.73	4.61	4.53	4.59	4.74	5.01	4.79	4.74	4.75	5.04
A11	4.63	4.56	4.33	4.29	4.69	4.75	4.78	4.95	4.93	4.39	4.05	4.36
A12	5.17	5.04	4.74	4.26	4.36	4.40	4.44	4.59	4.58	4.19	4.24	4.85
A13	5.12	5.01	4.62	4.30	4.52	4.55	4.57	4.79	4.78	4.26	4.35	5.03
A14	5.58	5.41	4.92	4.23	4.31	4.38	4.36	4.67	4.64	4.08	4.48	5.39
A15	4.72	4.65	4.29	4.13	4.38	4.40	4.42	4.59	4.58	4.16	4.08	4.63
A16	6.42	6.23	5.67	5.02	5.32	5.39	5.40	5.69	5.67	4.97	5.30	6.33
A17	6.20	5.92	5.40	4.57	4.51	4.52	4.54	4.84	4.94	4.53	4.92	6.06
A18	6.77	6.47	5.90	4.82	4.80	4.79	4.80	5.08	5.09	4.61	5.28	6.64
Col. Sum	101.42	99.11	91.72	81.87	81.67	82.28	82.64	87.37	87.35	78.78	83.93	98.24

.

Next, all the monthly wind speed values are normalized with respect to their respective column sums using Equation (1). This normalization process results in the creation of a table displaying the normalized monthly wind speeds at a height of 10 m for the 18 sub-districts where the minimum monthly wind speed exceeds 4 m/s, as presented in

Table 8. The normalized values of monthly wind speed at a height of 10 m of 18 sub-districts with minimum monthly wind speed faster than 4 m/s.

Alternative Areas	Normalized Values of Monthly Wind Sat a Height of 10 m
	January	February	March	April	May	June	July	August	September	October	November	December
A1	0.0606	0.0609	0.0597	0.0571	0.0552	0.0560	0.0555	0.0562	0.056	0.0535	0.0573	0.0594
A2	0.0522	0.0534	0.0527	0.0531	0.0540	0.0542	0.0542	0.0537	0.0539	0.0519	0.0511	0.0506
A3	0.0601	0.0609	0.0600	0.0575	0.0528	0.0517	0.0515	0.0523	0.0537	0.0530	0.0572	0.0581
A4	0.0678	0.0680	0.0674	0.0629	0.0571	0.0580	0.0574	0.0591	0.0591	0.0565	0.0627	0.0649
A5	0.0647	0.0649	0.0650	0.0621	0.0574	0.0582	0.0574	0.0597	0.0605	0.0581	0.0620	0.0626
A6	0.0588	0.0568	0.0587	0.0590	0.0601	0.0582	0.0590	0.0552	0.0529	0.0539	0.0551	0.0570
A7	0.0527	0.0540	0.0545	0.0544	0.0507	0.0499	0.0494	0.0506	0.0518	0.0527	0.0532	0.0510
A8	0.0451	0.0459	0.0463	0.0511	0.0511	0.0509	0.0516	0.0513	0.0520	0.0576	0.0537	0.0484
A9	0.0520	0.0512	0.0492	0.0516	0.0544	0.0552	0.0552	0.0560	0.0564	0.0560	0.0539	0.0562
A10	0.0460	0.0473	0.0516	0.0563	0.0555	0.0558	0.0573	0.0574	0.0548	0.0602	0.0566	0.0513
A11	0.0457	0.0460	0.0472	0.0524	0.0574	0.0578	0.0578	0.0567	0.0565	0.0557	0.0483	0.0443
A12	0.0510	0.0509	0.0516	0.0520	0.0534	0.0535	0.0537	0.0525	0.0524	0.0532	0.0506	0.0494
A13	0.0505	0.0505	0.0504	0.0525	0.0554	0.0553	0.0553	0.0548	0.0547	0.0541	0.0518	0.0512
A14	0.0550	0.0546	0.0537	0.0516	0.0527	0.0532	0.0528	0.0534	0.0531	0.0518	0.0534	0.0548
A15	0.0465	0.0469	0.0468	0.0504	0.0536	0.0535	0.0535	0.0525	0.0525	0.0528	0.0486	0.0472
A16	0.0633	0.0629	0.0619	0.0613	0.0652	0.0655	0.0654	0.0651	0.0649	0.0631	0.0631	0.0644
A17	0.0612	0.0597	0.0589	0.0559	0.0552	0.0550	0.0550	0.0554	0.0566	0.0574	0.0586	0.0617
A18	0.0668	0.0653	0.0644	0.0589	0.0588	0.0583	0.0580	0.0582	0.0582	0.0585	0.0628	0.0676

. Subsequently, the monthly entropy values (e_j) for each month are calculated using Equation (2), and the monthly weight values (w_j) are assigned based on Equation (3), as depicted in

Table 9. The monthly entropy values (e_j) and the monthly weight values (w_j) of monthly wind speed at a height level of 10 m of 18 sub-districts with minimum monthly wind speed faster than 4 m/s.

	Entropy Values (ej) and Weight Values (wj) of Monthly Wind Speed at a Height of 10 m
	January	February	March	April	May	June	July	August	September	October	November	December
ej	0.9970	0.9973	0.9977	0.9991	0.9994	0.9993	0.9993	0.9993	0.9994	0.9995	0.9988	0.9975
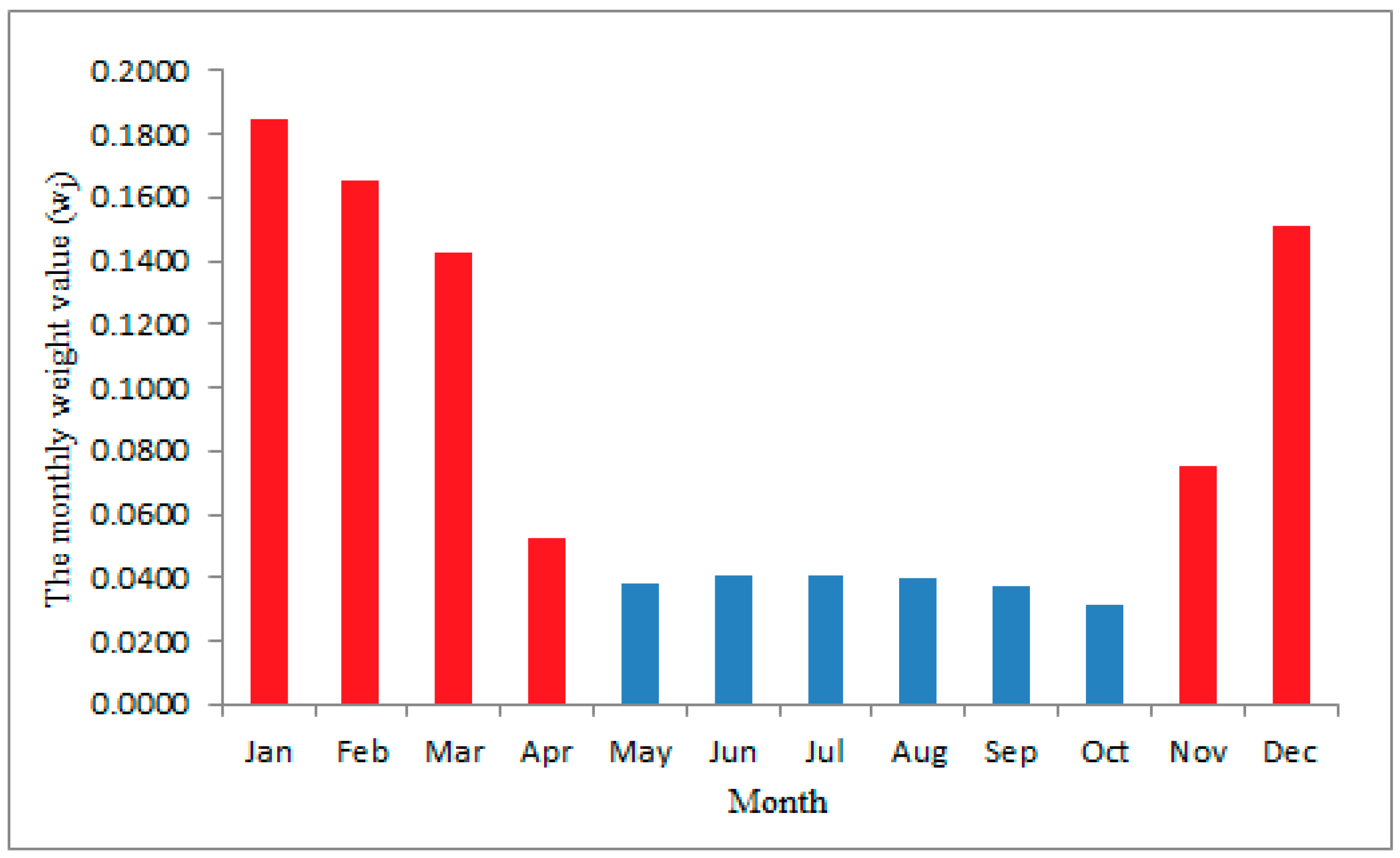
wj	0.1848	0.1653	0.1424	0.0522	0.0384	0.0407	0.0407	0.0401	0.0376	0.0316	0.0753	0.1509
Season	Summer season				Rainy season						Summer season

and Figure 1. Now, the monthly weight values of w_j can be analyzed in conjunction with the monthly wind speeds at a height level of 10 m for all 18 sub-districts using TOPSIS to prioritize or rank the wind quality of these 18 sub-districts. The initial data for TOPSIS is organized and all values within

Table 10. The initial data for TOPSIS for values of monthly wind speed at a height level of 10 m of 18 sub-districts with minimum monthly wind speed faster than 4 m/s.

Alternative Areas	Monthly Wind Speed (m/s) at a Height of 10 m
	January	February	March	April	May	June	July	August	September	October	November	December
	w1	w2	W3	w4	w5	w6	w7	w8	w9	w10	w11	w12
	0.1848	0.1653	0.1424	0.0522	0.0384	0.0407	0.0407	0.0401	0.0376	0.0316	0.0753	0.1509
A1	6.15	6.03	5.48	4.67	4.51	4.61	4.58	4.91	4.89	4.21	4.81	5.83
A2	5.29	5.29	4.83	4.35	4.41	4.46	4.48	4.69	4.71	4.09	4.29	4.97
A3	6.10	6.04	5.51	4.70	4.31	4.25	4.26	4.57	4.69	4.17	4.80	5.70
A4	6.88	6.74	6.19	5.15	4.67	4.77	4.74	5.16	5.16	4.45	5.26	6.37
A5	6.56	6.43	5.96	5.08	4.69	4.79	4.75	5.21	5.28	4.58	5.2	6.15
A6	5.96	5.63	5.39	4.83	4.91	4.79	4.88	4.82	4.62	4.25	4.62	5.60
A7	5.35	5.36	5.00	4.45	4.14	4.10	4.09	4.42	4.52	4.15	4.47	5.01
A8	4.57	4.55	4.25	4.19	4.18	4.19	4.26	4.48	4.54	4.54	4.51	4.75
A9	5.28	5.08	4.51	4.22	4.44	4.54	4.56	4.90	4.93	4.41	4.52	5.52
A10	4.67	4.68	4.73	4.61	4.53	4.59	4.74	5.01	4.79	4.74	4.75	5.04
A11	4.63	4.56	4.33	4.29	4.69	4.75	4.78	4.95	4.93	4.39	4.05	4.36
A12	5.17	5.04	4.74	4.26	4.36	4.40	4.44	4.59	4.58	4.19	4.24	4.85
A13	5.12	5.01	4.62	4.30	4.52	4.55	4.57	4.79	4.78	4.26	4.35	5.03
A14	5.58	5.41	4.92	4.23	4.31	4.38	4.36	4.67	4.64	4.08	4.48	5.39
A15	4.72	4.65	4.29	4.13	4.38	4.40	4.42	4.59	4.58	4.16	4.08	4.63
A16	6.42	6.23	5.67	5.02	5.32	5.39	5.40	5.69	5.67	4.97	5.30	6.33
A17	6.20	5.92	5.40	4.57	4.51	4.52	4.54	4.84	4.94	4.53	4.92	6.06
A18	6.77	6.47	5.90	4.82	4.80	4.79	4.80	5.08	5.09	4.61	5.28	6.64

are normalized through Equation (4). Consequently, the TOPSIS-normalized values for the monthly wind speeds at a height of 10 m for the 18 sub-districts are generated, as illustrated in

Table 11. TOPSIS-normalized values of monthly wind speed at a height level of 10 m of 18 sub-districts with minimum monthly wind speed faster than 4 m/s.

Alternative Areas	TOPSIS-Normalized Values of Monthly Wind at a Height of 10 m
	January	February	March	April	May	June	July	August	September	October	November	December
	w1	w2	W3	w4	w5	w6	w7	w8	w9	w10	w11	w12
	0.1848	0.1653	0.1424	0.0522	0.0384	0.0407	0.0407	0.0401	0.0376	0.0316	0.0753	0.1509
A1	1.5679	1.5466	1.3773	1.1283	1.0537	1.0916	1.0762	1.1678	1.1602	0.9545	1.1658	1.4595
A2	1.1623	1.1888	1.0731	0.9767	1.0068	1.0247	1.0282	1.0665	1.0765	0.8994	0.9259	1.0612
A3	1.5419	1.5492	1.3928	1.1440	0.9626	0.9307	0.9278	1.0102	1.0654	0.9370	1.1619	1.3952
A4	1.9617	1.9269	1.7581	1.3705	1.1291	1.1733	1.1512	1.2919	1.2915	1.0638	1.3955	1.7420
A5	1.7852	1.7556	1.6321	1.3343	1.1398	1.1798	1.1537	1.3166	1.3536	1.1267	1.3632	1.6222
A6	1.4725	1.3446	1.3328	1.2080	1.2512	1.1797	1.2177	1.1281	1.0358	0.9704	1.0766	1.3454
A7	1.1853	1.2184	1.1489	1.0237	0.8888	0.8659	0.8555	0.9485	0.9907	0.9258	1.0043	1.0765
A8	0.8665	0.8799	0.8291	0.9055	0.9044	0.9043	0.9319	0.9736	0.9986	1.1088	1.0237	0.9679
A9	1.1546	1.0941	0.9365	0.9220	1.0233	1.0618	1.0677	1.1620	1.1762	1.0469	1.0296	1.3058
A10	0.9042	0.9322	1.0275	1.0979	1.0658	1.0832	1.1499	1.2184	1.1121	1.2080	1.1368	1.0880
A11	0.8905	0.8817	0.863	0.9501	1.1403	1.1634	1.1702	1.1883	1.1800	1.0345	0.8263	0.8133
A12	1.1097	1.0808	1.0305	0.9383	0.9846	0.9973	1.0101	1.0209	1.0167	0.9446	0.9075	1.0082
A13	1.0860	1.0649	0.9815	0.9554	1.0600	1.0657	1.0684	1.1108	1.1065	0.9775	0.9514	1.0839
A14	1.2920	1.2444	1.1131	0.9237	0.9624	0.9857	0.9759	1.0555	1.0449	0.8949	1.0120	1.2442
A15	0.9227	0.9176	0.8459	0.8811	0.9943	0.9961	1.0005	1.0191	1.0185	0.9304	0.8397	0.9208
A16	1.7111	1.6492	1.4790	1.3027	1.4698	1.4940	1.4947	1.5685	1.5583	1.3306	1.4149	1.7165
A17	1.5956	1.4887	1.3418	1.0811	1.0558	1.0520	1.0581	1.1349	1.1850	1.1010	1.2178	1.5769
A18	1.9032	1.7792	1.6019	1.2020	1.1946	1.1824	1.1787	1.2518	1.2551	1.1424	1.4015	1.8931

. With the data from Table 11 and the utilization of Equation (5) through Equation (7), the weighted normalized values (V_i,j), the monthly ideal best values (V_j+), and the monthly ideal worst values (V_j−) can be computed, as detailed in

Table 12. The weighted normalized values V_i,j, the monthly ideal best value V_j⁺ and the monthly ideal worst value V_j⁻ of monthly wind speed at a height level of 10 m of 18 sub-districts with minimum monthly wind speed faster than 4 m/s.

Alternative Areas	TOPSIS-Normalized Values of Monthly Wind Speed (m/s) at a Height of 10 m
	January	February	March	April	May	June	July	August	September	October	November	December
	w1	w2	w3	w4	w5	w6	w7	w8	w9	w10	w11	w12
	0.1848	0.1653	0.1424	0.0522	0.0384	0.0407	0.0407	0.0401	0.0376	0.0316	0.0753	0.1509
A1	0.2897	0.2556	0.1961	0.0589	0.0405	0.0444	0.0438	0.0468	0.0437	0.0302	0.0878	0.2203
A2	0.2147	0.1965	0.1528	0.0510	0.0387	0.0417	0.0418	0.0427	0.0405	0.0284	0.0698	0.1602
A3	0.2849	0.2561	0.1983	0.0597	0.0370	0.0378	0.0377	0.0405	0.0401	0.0296	0.0876	0.2106
A4	0.3624	0.3185	0.2503	0.0715	0.0434	0.0477	0.0468	0.0518	0.0486	0.0336	0.1051	0.2630
A5	0.3298	0.2902	0.2324	0.0696	0.0438	0.0480	0.0469	0.0527	0.0509	0.0356	0.1027	0.2449
A6	0.2721	0.2222	0.1898	0.0631	0.0481	0.0480	0.0495	0.0452	0.0390	0.0307	0.0811	0.2031
A7	0.2190	0.2014	0.1636	0.0534	0.0342	0.0352	0.0348	0.0380	0.0373	0.0293	0.0757	0.1625
A8	0.1601	0.1454	0.1180	0.0473	0.0348	0.0368	0.0379	0.0390	0.0376	0.0350	0.0771	0.1461
A9	0.2133	0.1808	0.1333	0.0481	0.0393	0.0432	0.0434	0.0465	0.0443	0.0331	0.0776	0.1971
A10	0.1671	0.1541	0.1463	0.0573	0.0410	0.0440	0.0468	0.0488	0.0419	0.0382	0.0857	0.1642
A11	0.1645	0.1457	0.1229	0.0496	0.0438	0.0473	0.0476	0.0476	0.0444	0.0327	0.0623	0.1228
A12	0.2050	0.1786	0.1467	0.0490	0.0379	0.0405	0.0411	0.0409	0.0383	0.0299	0.0684	0.1522
A13	0.2007	0.1760	0.1397	0.0499	0.0408	0.0433	0.0435	0.0445	0.0416	0.0309	0.0717	0.1636
A14	0.2387	0.2057	0.1585	0.0482	0.0370	0.0401	0.0397	0.0423	0.0393	0.0283	0.0763	0.1878
A15	0.1705	0.1517	0.1204	0.0460	0.0382	0.0405	0.0407	0.0408	0.0383	0.0294	0.0633	0.1390
A16	0.3162	0.2726	0.2106	0.0680	0.0565	0.0607	0.0608	0.0628	0.0586	0.0421	0.1066	0.2591
A17	0.2948	0.2461	0.1910	0.0564	0.0406	0.0428	0.0430	0.0455	0.0446	0.0348	0.0918	0.2380
A18	0.3517	0.2941	0.2281	0.0627	0.0459	0.0481	0.0480	0.0501	0.0472	0.0361	0.1056	0.2858
Vj+	0.3624	0.3185	0.2503	0.0715	0.0565	0.0607	0.0608	0.0628	0.0586	0.0421	0.1066	0.2858
Vj−	0.1601	0.1454	0.118	0.046	0.0342	0.0352	0.0348	0.038	0.0373	0.0283	0.0623	0.1228

. Subsequently, the performance scores (P_i) for each sub-district are assigned using Equation (8) through Equation (10). Finally, the ranking of wind speed quality among the 18 sub-districts based on their performance scores (P_i) is compared with their average wind speeds, as shown in

Table 13. Comparison of wind speed quality ranking of 18 sub-districts with minimum monthly wind speed faster than 4 m/s base on their performance scores (P_i) and their average wind speed.

Ranking Based on Performance Scores (Pi)					Ranking Based on Average Wind Speed
Alternative Areas	Si+	Si−	Pi	Rank with Pi	Alternative Areas	Average Wind Speed (m/s)	Rank with Average Wind Speed
A4	0.0368	0.3336	0.9006	1	A16	5.62	1
A18	0.0453	0.3169	0.875	2	A4	5.46	2
A5	0.0678	0.2843	0.8074	3	A18	5.42	3
A16	0.081	0.2706	0.7697	4	A5	5.39	4
A17	0.1323	0.2195	0.6239	5	A17	5.08	5
A1	0.1357	0.2138	0.6116	6	A1	5.06	6
A3	0.1456	0.207	0.587	7	A6	5.03	7
A6	0.1728	0.177	0.506	8	A3	4.93	8
A14	0.2231	0.1263	0.3615	9	A9	4.75	9
A7	0.2477	0.1024	0.2925	10	A10	4.74	10
A9	0.2561	0.102	0.2848	11	A14	4.70	11
A2	0.2564	0.0918	0.2637	12	A2	4.66	12
A13	0.2773	0.0713	0.2044	13	A13	4.65	13
A12	0.2776	0.0704	0.2022	14	A7	4.59	14
A10	0.3044	0.0618	0.1688	15	A12	4.57	15
A8	0.3346	0.0288	0.0791	16	A11	4.56	16
A11	0.3396	0.0249	0.0684	17	A15	4.42	17
A15	0.3284	0.0225	0.0641	18	A8	4.41	18

.

4. Discussion

After careful consideration of the data in Table 9 and Figure 1, it becomes evidences that all w_j values are notably high during the summer season (November, December, January, February, March, and April). Interestingly, these wj values exhibit a continuous increase, starting from w₁₁ = 0.0753 in November (the first month of the summer season), reaching their peak at w₁ = 0.1848 in January (the middle of the summer season), and then gradually decreasing to w₄ = 0.0522 in April (the last month of the summer season). In contrast, during the rainy season from May to October, the w_j values remain consistently low and hover around 0.0316 and 0.0407. This pattern indicates that the monthly wind speeds during the summer season are higher than those during the rainy season, and the variation in monthly wind speeds across these 18 sub-districts is more noticeable in the summer season. This observation aligns with the monthly wind speed data presented in Table 7. For example, the w₁ = 0.1848 in January (the maximum value) implies that the wind speed values across these 18 sub-districts in this month exhibit significant variation (with a minimum wind speed of 4.57 m/s at area A₈ and a maximum wind speed of 6.88 m/s at area A₄, resulting in a range of 2.31 m/s). Conversely, the w₁₀ = 0.0316 in October (the minimum value) suggests that the wind speed values across these 18 sub-districts in this month show less variation (with a minimum wind speed of 4.08 m/s at area A14 and a maximum wind speed of 4.97 m/s at area A₁₆, resulting in a range of 0.89 m/s). With the performance scores of P_i presented in Table 13, it is evident that the sub-districts with higher P_i values are more suitable for the installation of water-pumping windmills with heights ranging from 9 to 15 m than those with lower P_i values. Therefore, the 18 sub-districts can be ranked based on their performance scores or wind speed quality as follows: A₄, A₁₈, A₅, A₁₆, A₁₇, A₁, A₃, A₆, A₁₄, A₇, A₉, A₂, A₁₃, A₁₂, A₁₀, A₈, A₁₁, and A₁₅. This ranking suggests that agriculture farms in sub-district A₄ are the most suitable areas for installing water-pumping windmills with heights ranging from 9 to 15 m, as it has the highest P_i value of 0.9006. Intriguingly, among the top 10 sub-districts with the highest P_i values, six of them (A₁, A₃, A₄, A₅, A₆, and A₇) are located in the same province, while the remaining four (A₁₄, A₁₆, A₁₇, and A₁₈) are also grouped within the same province. Furthermore, the values of w_j indicate that wind speeds in all sub-districts exhibit more significant variation and are generally faster during the summer season (November, December, January, February, March, and April) compared to the rainy season (May, June, July, August, September, and October). When comparing the results of ranking wind speed quality for these 18 sub-districts based on the performance scores (P_i) with the results based on the values of average wind speed, a conventional method commonly used by most Thai farmers and presented in Table 13, it is noteworthy that the results from both methods are quite similar. For the classification of wind speed quality into three groups based on performance scores (P_i), Group A (comprising the six highest Pi values) includes sub-districts A₄, A₁₈, A₅, A₁₆, A₁₇, and A₁; Group B consists of sub-districts A₃, A₆, A₁₄, A₇, A₉, and A₂; and Group C (comprising the six lowest P_i values) consists of sub-districts A₁₃, A₁₂, A₁₀, A₈, A₁₁, and A₁₅. Similarly, for the classification based on the values of average wind speed, Group A (comprising the six highest average wind speed values) includes sub-districts A₁₆, A₄, A₁₈, A₅, A₁₇, and A₁; Group B consists of sub-districts A₆, A₃, A₉, A₁₀, A₁₄, and A₂; and Group C (comprising the six lowest average wind speed values) consists of sub-districts A₁₃, A₇, A₁₂, A₁₁, A₁₅, and A₈. Although these two methods yield similar results, the combining method of the entropy weight method and TOPSIS may provide more reasonable results, as it takes into account multiple factors and considers the effect of seasonality, unlike the conventional method, which relies solely on the average wind speed and disregards seasonal variations.

5. Conclusions

This study aims to introduce an agile method for evaluating, prioritizing, and ranking the wind quality of sub-districts in the western region of Southern Thailand. By combining the entropy weight method and TOPSIS, this approach can be easily applied to the secondary data of monthly wind speeds throughout the year. The primary objective is to identify suitable areas for installing water-pumping windmill systems with heights ranging from 9 to 15 m. Initially, 18 sub-districts with minimum monthly wind speeds exceeding 4 m/s are selected, as this range of wind speed ensures optimal performance and high efficiency for such water-pumping windmills. The calculation results indicate that all 18 sub-districts can be effectively ranked based on wind quality, ranging from low-quality areas to high-quality areas. Furthermore, this combined method reveals that wind speeds during the summer season are faster than those during the rainy season. This study also highlights the utility of this combined method as one of the valuable decision-making tools for farmers considering investments in water-pumping windmill systems with heights ranging from 9 to 15 m to reduce their current fuel cost of water-pumping systems. Even farmers with access to monthly wind speed data spanning more than 12 months can apply this method by utilizing the average monthly wind speed values for each month, instead of relying on the specific monthly wind speed values. Then, all three main steps of this combining method (preliminary assessment of suitable areas, assignment of monthly weight values using the entropy weight method, and ranking of qualified areas using TOPSIS) can be orderly applied to these data so that all qualified areas are simply ranked from low-quality areas to high-quality areas based on wind quality.