Modeling of Biomass Gasification: From Thermodynamics to Process Simulations
Abstract
:1. Introduction
2. Biomass Gasification Principle and Technology
- ○
- Drying. Occurring at 100–200 °C, the drying stage reduces the moisture content of biomass below 5%.
- ○
- Devolatilization (pyrolysis). In this step, the thermal decomposition of biomass occurs in the absence of oxygen or air. The volatile matter is decreased, releasing hydrocarbon gases from biomass, and is then reduced to solid charcoal.
- ○
- Oxidation. In this stage, CO2 is produced from the reaction of solid carbonized biomass and oxygen in the air. H2 present in the biomass is oxidized to produce water. Then, if oxygen is present in sub-stoichiometric quantities, partial oxidation of carbon may happen, producing CO.
- ○
- Reduction. At high temperatures (800–950 °C) several reduction reactions occur in the absence (or sub-stoichiometric presence) of oxygen, i.e., water–gas reaction, Boudouard reaction, water–gas shift reaction, and methane reaction.
3. Thermodynamic Models
- Stoichiometric models, which are based on equilibrium constants: the specific chemical reactions of the process must be declared;
- Non-stoichiometric models, which are based on minimization of Gibbs free energy, neglecting the chemical reactions involved. Only the definition of a set of chemical compounds that are expected at equilibrium is needed.
- (a)
- All the reactions considered are at thermodynamic equilibrium equivalent to an infinite residence time.
- (b)
- All the carbon is gasified and is not present among the reaction products.
- (c)
- The products leaving the gasifier, except for the ashes in the solid phase, are in the gaseous phase and consist of CO, CO2, H2O, H2, CH4, N2.
- (d)
- Among the reaction products, there is no tar.
4. Kinetic Models
5. CFD Models
- ▪
- The Eulerian–Lagrangian discrete particle model (DPM), which considers gas a continuous and particle a discrete phase. It is used where there are diluted particle conditions, such as in the freeboard of the reactor. CFD DPMs consider particle trajectory in a continuous phase of fluid and take into account the interaction between particles by means of the heat and mass transfer as the governing phenomena [86,87]. The main advantage is the simple accounting of the particle size, allowing us to track the changes in physicochemical characteristics of the biomass particles during conversion along their path through the reactor.
- ▪
- The Eulerian–Eulerian two-fluid model (TFM), which is used to investigate both the gaseous and solid (particle) phase. Interaction of granular and continuous phases is considered via momentum transfer contribution based on drag models [88]. The CFD TFM approach has the disadvantages of high computational demand when a wide range of particle sizes has to be investigated because each size fraction of the distribution is counted as a separated phase. Moreover, another drawback of these models is that they are poor in recognizing the discrete character of the particle phase, so they are consequently poor in modeling flows of wide particles and in tracking movement and conversion of single particles.
- ▪
- The Eulerian–Eulerian discrete element model (DEM) within the Eulerian–Lagrangian framework, which uses the Eulerian method for the gas phase and discrete element method for the particle phase, tracking individually each particle and associating it with multiple physical (size, density, composition, and temperature) and thermochemical (reactive or inert) properties [89,90]. The main disadvantage of this method is the extremely small-time steps required, making this approach highly computationally demanding and thus best avoided for design and optimization of industrial scale facilities [91].
6. Process Modeling
- The whole process is taken into account (e.g., separators, mixers, heat exchangers, pumps, etc.) and not only the reaction unit.
- Overall energy duty of the process is estimated.
- Optimization to improve CAPEX and OPEX is allowed.
- The main assumptions for process modeling in Aspen Plus are:
- Process is steady-state and isothermal [104].
- Volatile products are H2, CO, CO2, CH4 and H2O [105].
- Char is 100% carbon [106].
- All gas mixtures are supposed to behave as perfect gases.
- Pressure drops and heat losses are neglected.
7. Multivariate Data Analysis (MVDA) and Model Validation
- Reducing the number of variables while maintaining the system’s descriptive capacity.
- Grouping variables into categories.
- Utilizing correlations between variables to characterize system behavior.
Black-Box Approaches
8. Discussion
9. An Overview on Tar Modeling Approach
10. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Acronyms | ||
| ANN | artificial neural network | |
| CCA | canonical correlation analysis | |
| CFD | computational fluid dynamics | |
| CSTR | continuous-flow stirred-tank reactor | |
| DEM | discrete element method | |
| DPM | discrete particle model | |
| GMM | Gibbs free-energy gradient method model | |
| LHV | low heating value | |
| MVDA | multivariate data analysis | |
| QET | quasi-equilibrium temperature | |
| PCA | principal component analysis | |
| TFM | two-fluid model | |
| Symbols | Unit | Description |
| Cp,i | J/(mol·k) | specific heat at constant pressure of the i-component |
| H | kJ/mol | enthalpy |
| kJ/mol | enthalpy formation | |
| G | kJ/mol | Gibbs free energy |
| kJ/mol | Gibbs energy formation | |
| ni | mol | number of moles of the i-component |
| nT | mol | total moles of produced gas |
| P | Pa | pressure |
| Pi | Pa | partial pressure of i-component |
| P0 | Pa | operative pressure of the system |
| R | J/(mol·k) | universal constant of gas |
| T | K | temperature |
| Greek Letters | ||
| α | reaction coordinate of water–gas shift reaction | |
| β | reaction coordinate of steam-reforming reaction | |
| µi | chemical potential | |
| standard chemical potential of the i-component | ||
References
- Pala, L.P.R.; Wang, Q.; Kolb, G.; Hessel, V. Steam gasification of biomass with subsequent syngas adjustment using shift reaction for syngas production: An Aspen Plus model. Renew. Energy 2017, 101, 484–492. [Google Scholar] [CrossRef]
- Chang, W.-R.; Hwang, J.-J.; Wu, W. Environmental impact and sustainability study on biofuels for transportation applications. Renew. Sustain. Energy Rev. 2017, 67, 277–288. [Google Scholar] [CrossRef]
- Biagini, E.; Barontini, F.; Tognotti, L. Gasification of agricultural residues in a demonstrative plant: Vine pruning and rice husks. Bioresour. Technol. 2015, 194, 36–42. [Google Scholar] [CrossRef] [PubMed]
- Ritslaid, K.; Küüt, A.; Olt, J. State of the Art in Bioethanol Production. Agron. Res. 2010, 8, 236–254. [Google Scholar]
- Kuchler, M.; Linnér, B. Challenging the food vs. fuel dilemma: Genealogical analysis of the biofuel discourse pursued by international organizations. Food Policy 2012, 37, 581–588. [Google Scholar] [CrossRef]
- Antizar-Ladislao, B.; Turrion-Gomez, J.L. Second-generation biofuels and local bioenergy systems. Biofuels Bioprod. Biorefin. 2008, 2, 455–469. [Google Scholar] [CrossRef]
- Oliveira, W.E.; Franca, A.S.; Oliveira, L.S.; Rocha, S.D. Untreated coffee husks as biosorbents for the removal of heavy metals from aqueous solutions. J. Hazard. Mater. 2008, 152, 1073–1081. [Google Scholar] [CrossRef]
- Bolívar Caballero, J.J.; Zaini, I.N.; Yang, W. Reforming processes for syngas production: A mini-review on the current status, challenges, and prospects for biomass conversion to fuels. Appl. Energy Combust. Sci. 2022, 10, 100064. [Google Scholar] [CrossRef]
- Pande, M.; Bhaskarwar, A.N. Biomass conversion to energy. In Biomass Conversion; Springer: Berlin/Heidelberg, Germany, 2012; pp. 1–90. [Google Scholar] [CrossRef]
- Yilmaz, S.; Selim, H. A review on the methods for biomass to energy conversion systems design. Renew. Sustain. Energy Rev. 2013, 25, 420–430. [Google Scholar] [CrossRef]
- Ramzan, N.; Ashraf, A.; Naveed, S.; Malik, A. Simulation of hybrid biomass gasification using Aspen plus: A comparative performance analysis for food, municipal solid and poultry waste. Biomass Bioenergy 2011, 35, 3962–3969. [Google Scholar] [CrossRef]
- Liao, C.; Summers, M.; Seiser, R.; Cattolica, R.; Herz, R. Simulation of a pilot-scale dual-fluidized-bed gasifier for biomass. Environ. Prog. Sustain. Energy 2014, 33, 732–736. [Google Scholar] [CrossRef]
- Baldinelli, A.; Cinti, G.; Desideri, U.; Fantozzi, F. Biomass integrated gasifier-fuel cells: Experimental investigation on wood syngas tars impact on NiYSZ-anode Solid Oxide Fuel Cells. Energy Convers. Manag. 2016, 128, 361–370. [Google Scholar] [CrossRef]
- Arteaga-Pérez, L.E.; Casas-Ledón, Y.; Pérez-Bermúdez, R.; Peralta, L.M.; Dewulf, J.; Prins, W. Energy and exergy analysis of a sugar cane bagasse gasifier integrated to a solid oxide fuel cell based on a quasi-equilibrium approach. Chem. Eng. J. 2013. [CrossRef]
- Sikarwar, V.S.; Zhao, M.; Clough, P.; Yao, J.; Zhong, X.; Memon, M.Z.; Shah, N.; Anthony, J.; Fennell, P. An overview of advances in biomass gasification. Energy Envrion. Sci. 2016, 9, 2939–2977. [Google Scholar] [CrossRef]
- Parvez, A.M.; Hafner, S.; Hornberger, M.; Schmid, M.; Scheffknecht, G. Sorption enhanced gasification (SEG) of biomass for tailored syngas production with in-situ CO2 capture: Current status, process scale-up experiences and outlook. Renew. Sustain. Energy Rev. 2021, 141, 110756. [Google Scholar] [CrossRef]
- Dascomb, J.; Krothapalli, A.; Fakhrai, R. Thermal conversion efficiency of producing hydrogen enriched syngas from biomass steam gasification. Int. J. Hydrogen Energy 2013, 38, 11790–11798. [Google Scholar] [CrossRef]
- Hamel, S.; Krumm, W. Mathematical modelling and simulation of bubbling fluidised bed gasifiers. Powder Technol. 2001, 120, 105–112. [Google Scholar] [CrossRef]
- Ahmed, T.Y.; Ahmad, M.M.; Yusup, S.; Inayat, A.; Khan, Z. Mathematical and computational approaches for design of biomass gasification for hydrogen production: A review. Renew. Sustain. Energy Rev. 2012, 16, 2304–2315. [Google Scholar] [CrossRef]
- Patra, T.K.; Sheth, P.N. Biomass gasification models for downdraft gasifier: A state-of-the-art review. Renew. Sustain. Energy Rev. 2015, 50, 583–593. [Google Scholar] [CrossRef]
- Canneto, G.; Freda, C.; Braccio, G. Numerical simulation of gas-solid flow in an interconnected fluidized bed. Therm. Sci. 2015, 19, 317–328. [Google Scholar] [CrossRef]
- Ajorloo, M.; Ghodrat, M.; Scott, J.; Strezov, V. Recent advances in thermodynamic analysis of biomass gasification: A review on numerical modelling and simulation. J. Energy Inst. 2022, 102, 395–419. [Google Scholar] [CrossRef]
- Mazaheri, N.; Akbarzadeh, A.H.; Madadian, E.; Lefsrud, M. Systematic review of research guidelines for numerical simulation of biomass gasification for bioenergy production. Energy Convers. Manag. 2019, 183, 671–688. [Google Scholar] [CrossRef]
- Basu, P. Biomass Gasification and Pyrolysis: Practical Design and Theory; Academic Press: Cambridge, MA, USA, 2010. [Google Scholar]
- Ahmed, A.M.A.; Salmiaton, A.; Choong, T.S.Y.; Azlina, W.A.K.G.W. Review of kinetic and equilibrium concepts for biomass tar modeling by using Aspen Plus. Renew. Sustain. Energy Rev. 2015, 52, 1623–1644. [Google Scholar] [CrossRef]
- Baruah, D.; Baruah, D.C. Modeling of biomass gasification: A review. Renew. Sustain. Energy Rev. 2014, 39, 806–815. [Google Scholar] [CrossRef]
- Marcantonio, V.; Bocci, E.; Monarca, D. Development of a chemical quasi-equilibrium model of biomass waste gasification in a fluidized-bed reactor by using Aspen plus. Energies 2019, 13, 53. [Google Scholar] [CrossRef]
- Ramos, A.; Monteiro, E.; Rouboa, A. Numerical approaches and comprehensive models for gasification process: A review. Renew. Sustain. Energy Rev. 2019, 110, 188–206. [Google Scholar] [CrossRef]
- Li, Y.; Yan, L.; Yang, B.; Gao, W.; Farahani, M.R. Simulation of biomass gasification in a fluidized bed by artificial neural network (ANN). Energy Sources Part A Recov. Util. Environ. Eff. 2018, 40, 544–548. [Google Scholar] [CrossRef]
- Puig-Arnavat, M.; Hernández, J.A.; Bruno, J.C.; Coronas, A. Artificial neural network models for biomass gasification in fluidized bed gasifiers. Biomass Bioenergy 2013, 49, 279–289. [Google Scholar] [CrossRef]
- Safarian, S.; Unnþórsson, R.; Richter, C. A review of biomass gasification modelling. Renew. Sustain. Energy Rev. 2019, 110, 378–391. [Google Scholar] [CrossRef]
- Naaz, Z.; Ravi, M.R.; Kohli, S. Modelling and simulation of downdraft biomass gasifier: Issues and challenges. Biomass Bioenergy 2022, 162, 106483. [Google Scholar] [CrossRef]
- Nunes, L.J.R.; Rodrigues, A.M.; Matias, J.C.O.; Ferraz, A.I.; Rodrigues, A.C. Production of Biochar from Vine Pruning: Waste Recovery in the Wine Industry. Agriculture 2021, 11, 489. [Google Scholar] [CrossRef]
- Puig-Arnavat, M.; Bruno, J.C.; Coronas, A. Review and analysis of biomass gasification models. Renew. Sustain. Energy Rev. 2010, 14, 2841–2851. [Google Scholar] [CrossRef]
- Review of Technologies for Gasification of Biomass and Wastes. Final Report; E4tech. 2009. Available online: https://www.erm.com/service/low-carbon-economy-transition/ (accessed on 1 August 2023).
- Bridgwater, T. Biomass for energy. J. Sci. Food Agric. 2006, 86, 1755–1768. [Google Scholar] [CrossRef]
- Puig-Gamero, M.; Argudo-Santamaria, J.; Valverde, J.L.; Sánchez, P.; Sanchez-Silva, L. Three integrated process simulation using aspen plus®: Pine gasification, syngas cleaning and methanol synthesis. Energy Convers. Manag. 2018, 177, 416–427. [Google Scholar] [CrossRef]
- Eisavi, B.; Chitsaz, A.; Hosseinpour, J.; Ranjbar, F. Thermo-environmental and economic comparison of three different arrangements of solid oxide fuel cell-gas turbine (SOFC-GT) hybrid systems. Energy Convers. Manag. 2018, 168, 343–356. [Google Scholar] [CrossRef]
- Wang, J.; Diao, M.; Yue, K. Optimization on pinch point temperature difference of ORC system based on AHP-Entropy method. Energy 2016, 98, 790–797. [Google Scholar] [CrossRef]
- Wan, W.; Engvall, K.; Yang, W. Model investigation of condensation behaviors of alkalis during syngas treatment of pressurized biomass gasification. Chem. Eng. Process—Process Intensif. 2018, 129, 28–36. [Google Scholar] [CrossRef]
- Li, X.T.; Grace, J.R.; Lim, C.J.; Watkinson, A.P.; Chen, H.P.; Kim, J.R. Biomass gasification in a circulating fluidized bed. Biomass Bioenergy 2004, 26, 171–193. [Google Scholar] [CrossRef]
- Aydin, E.S.; Yucel, O.; Sadikoglu, H. Numerical and experimental investigation of hydrogen-rich syngas production via biomass gasification. Int. J. Hydrogen Energy 2018, 43, 1105–1115. [Google Scholar] [CrossRef]
- González-Vázquez, M.P.; Rubiera, F.; Pevida, C.; Pio, D.T.; Tarelho, L.A.C. Thermodynamic analysis of biomass gasification using aspen plus: Comparison of stoichiometric and non-stoichiometric models. Energies 2021, 14, 189. [Google Scholar] [CrossRef]
- Fiori, L.; Castello, D. Thermodynamic Analysis of the Supercritical Water Gasification of Biomass. In Near-Critical and Supercritical Water and Their Applications for Biorefineries. Biofuels and Biorefineries; Springer: Dordrecht, The Netherlands, 2014; pp. 99–129. [Google Scholar] [CrossRef]
- Barba, D.; Prisciandaro, M.; Salladini, A.; Mazziotti Di Celso, G. The Gibbs Free Energy Gradient Method for RDF gasification modelling. Fuel 2011, 90, 1402–1407. [Google Scholar] [CrossRef]
- Marcantonio, V.; De Falco, M.; Capocelli, M.; Bocci, E.; Colantoni, A.; Villarini, M. Process analysis of hydrogen production from biomass gasification in fluidized bed reactor with different separation systems. Int. J. Hydrogen Energy 2019, 44, 10350–10360. [Google Scholar] [CrossRef]
- Barba, D.; Capocelli, M.; Cornacchia, G.; Matera, D.A. Theoretical and experimental procedure for scaling-up RDF gasifiers: The Gibbs Gradient Method. Fuel 2016, 179, 60–70. [Google Scholar] [CrossRef]
- Gumz, W. Gas Producers and Blast Furnaces; Wiley: Hoboken, NJ, USA, 1950. [Google Scholar]
- Gambarotta, A.; Morini, M.; Zubani, A. A non-stoichiometric equilibrium model for the simulation of the biomass gasification process. Appl. Energy 2018, 227, 119–127. [Google Scholar] [CrossRef]
- Doherty, W.; Reynolds, A.; Kennedy, D.; Doherty, W.; Reynolds, A.; Kennedy, D. Simulation of a Circulating Fluidised Bed Biomass Gasifier using ASPEN Plus: A Performance Analysis. In Proceedings of the 21st International Conference on Efficiency, Cost, Optimization, Simulation and Environmental Impact of Energy Systems, Krakow, Poland, 24–27 June 2008; pp. 1241–1248. [Google Scholar]
- Mckeen, L.W.; Taylor, J.W. A study of the input data selection on the qet calculated intensities of ethylene and propane ions. Int. J. Mass Spectrom. Ion Phys. 1980, 33, 167–185. [Google Scholar] [CrossRef]
- Marcantonio, V.; Monforti Ferrario, A.; Di Carlo, A.; Del Zotto, L.; Monarca, D.; Bocci, E. Biomass Steam Gasification: A Comparison of Syngas Composition between a 1-D MATLAB Kinetic Model and a 0-D Aspen Plus Quasi-Equilibrium Model. Computation 2020, 8, 86. [Google Scholar] [CrossRef]
- Buekens, A.G.; Schoeters, J.G. Modelling of Biomass Gasification. In Fundamentals of Thermochemical Biomass Conversion; Overend, R.P., Milne, T.A., Mudge, L.K., Eds.; Springer: Dordrecht, The Netherlands, 1985; pp. 619–689. [Google Scholar]
- Loha, C.; Chatterjee, P.K.; Chattopadhyay, H. Performance of fluidized bed steam gasification of biomass—Modeling and experiment. Energy Convers. Manag. 2011, 52, 1583–1588. [Google Scholar] [CrossRef]
- Loha, C.; Chattopadhyay, H.; Chatterjee, P.K. Thermodynamic analysis of hydrogen rich synthetic gas generation from fluidized bed gasification of rice husk. Energy 2011, 36, 4063–4071. [Google Scholar] [CrossRef]
- Kaya, E.; Koksal, M. Investigation of the predicting ability of single-phase chemical equilibrium modeling applied to circulating fluidized bed coal gasification. J. Energy Resour. Technol. Trans. ASME 2016, 138, 032203. [Google Scholar] [CrossRef]
- Ramanan, M.V.; Lakshmanan, E.; Sethumadhavan, R.; Renganarayanan, S. Modeling and Experimental Validation of Cashew Nut Shell Char Gasification Adopting Chemical Equilibrium Approach. Energy Fuels 2008, 22, 2070–2078. [Google Scholar] [CrossRef]
- Bridgwater, A.V. The technical and economic feasibility of biomass gasification for power generation. Fuel 1995, 74, 631–653. [Google Scholar] [CrossRef]
- Basu, P.; Kaushal, P. Modeling of pyrolysis and gasification of biomass in fluidized beds: A review. Chem. Prod. Process Model. 2009, 4. [Google Scholar] [CrossRef]
- Castello, D.; Fiori, L. Kinetics modeling and main reaction schemes for the supercritical water gasification of methanol. J. Supercrit. Fluids 2012, 69, 64–74. [Google Scholar] [CrossRef]
- Ranzi, E.; Dente, M.; Goldaniga, A.; Bozzano, G.; Faravelli, T. Lumping procedures in detailed kinetic modeling of gasification, pyrolysis, partial oxidation and combustion of hydrocarbon mixtures. Prog. Energy Combust. Sci. 2001, 27, 99–139. [Google Scholar] [CrossRef]
- Resende, F.L.P.; Savage, P.E. Kinetic model for noncatalytic supercritical water gasification of cellulose and lignin. AIChE J. 2010, 56, 2412–2420. [Google Scholar] [CrossRef]
- Guan, Q.; Wei, C.; Savage, P.E. Kinetic model for supercritical water gasification of algae. Phys. Chem. Chem. Phys. 2012, 14, 3140–3147. [Google Scholar] [CrossRef] [PubMed]
- Jin, H.; Guo, L.; Guo, J.; Ge, Z.; Cao, C.; Lu, Y. Study on gasification kinetics of hydrogen production from lignite in supercritical water. Int. J. Hydrogen Energy 2015, 40, 7523–7529. [Google Scholar] [CrossRef]
- Iwaszenko, S.; Howaniec, N.; Smoliński, A. Determination of random pore model parameters for underground coal gasification simulation. Energy 2019, 166, 972–978. [Google Scholar] [CrossRef]
- Experimental Investigation on the Gasification Kinetic Model of a Char Particle in Supercritical Water n.d. Available online: https://agris.fao.org/agris-search/search.do?recordID=US201700052980 (accessed on 19 May 2023).
- Vostrikov, A.A.; Psarov, S.A.; Dubov, D.Y.; Fedyaeva, O.N.; Sokol, M.Y. Kinetics of coal conversion in supercritical water. Energy Fuels 2007, 21, 2840–2845. [Google Scholar] [CrossRef]
- Sharma, A.K. Modeling Drying and Pyrolysis of Moist Wood Particles at Slow Heating Rates. Int. J. Energy Environ. Eng. 2019, 13, 243–250. [Google Scholar] [CrossRef]
- Di Carlo, A.; Borello, D.; Bocci, E. Process simulation of a hybrid SOFC/mGT and enriched air/steam fluidized bed gasifier power plant. Int. J. Hydrogen Energy 2013, 38, 5857–5874. [Google Scholar] [CrossRef]
- Fercher, E.; Hofbauer, H.; Fleck, T.; Rauch, R.; Veronik, G. Two years experience with the ficfb-gasification process. In Proceedings of the 10th European Conference and Technology Exhibition Biomass for Energy and Industry, Würzburg, Germany, 8–11 June 1998. [Google Scholar]
- Pfeifer, C.; Rauch, R.; Hofbauer, H. In-Bed Catalytic Tar Reduction in a Dual Fluidized Bed Biomass Steam Gasifier. Ind. Eng. Chem. Res. 2004, 43, 1634–1640. [Google Scholar] [CrossRef]
- Kunii, D.; Levenspiel, O. Fluidized reactor models. 1. For bubbling beds of fine, intermediate, and large particles. 2. For the lean phase: Freeboard and fast fluidization. Ind. Eng. Chem. Res. 1990, 29, 1226–1234. [Google Scholar] [CrossRef]
- Nikoo, M.B.; Mahinpey, N. Simulation of biomass gasification in fluidized bed reactor using ASPEN PLUS. Biomass Bioenergy 2008, 32, 1245–1254. [Google Scholar] [CrossRef]
- Roy, P.C.; Datta, A.; Chakraborty, N. Assessment of cow dung as a supplementary fuel in a downdraft biomass gasifier. Renew. Energy 2010, 35, 379–386. [Google Scholar] [CrossRef]
- Roy, P.C.; Datta, A.; Chakraborty, N. An assessment of different biomass feedstocks in a downdraft gasifier for engine application. Fuel 2013, 106, 864–868. [Google Scholar] [CrossRef]
- Jia, J.; Xu, L.; Abudula, A.; Sun, B. Effects of operating parameters on performance of a downdraft gasifier in steady and transient state. Energy Convers. Manag. 2018, 155, 138–146. [Google Scholar] [CrossRef]
- Kaushal, P.; Tyagi, R. Advanced simulation of biomass gasification in a fluidized bed reactor using ASPEN PLUS. Renew. Energy 2017, 101, 629–636. [Google Scholar] [CrossRef]
- Lu, Y.; Huang, J.; Zheng, P. Fluid hydrodynamic characteristics in supercritical water fluidized bed: A DEM simulation study. Chem. Eng. Sci. 2014, 117, 283–292. [Google Scholar] [CrossRef]
- Gómez-Barea, A.; Leckner, B. Modeling of biomass gasification in fluidized bed. Prog. Energy Combust. Sci. 2010, 36, 444–509. [Google Scholar] [CrossRef]
- Xue, Q.; Fox, R.O. Reprint of: Multi-fluid CFD modeling of biomass gasification in polydisperse fluidized-bed gasifiers. Powder Technol. 2014, 265, 23–34. [Google Scholar] [CrossRef]
- Hassen, W.; Dhrioua, M.; Kolsi, L.; Anbumalar, V.; Al-Rashed, A.A.A.A.; Borjini, M.N. CFD modeling of gas-particles flow in a circulating fluidized G-Volution gasification reactor. Int. J. Mech. Sci. 2018, 144, 438–451. [Google Scholar] [CrossRef]
- Papadikis, K.; Gu, S.; Bridgwater, A.V.; Gerhauser, H. Application of CFD to model fast pyrolysis of biomass. Fuel Process Technol. 2009, 90, 504–512. [Google Scholar] [CrossRef]
- Xue, Q.; Dalluge, D.; Heindel, T.J.; Fox, R.O.; Brown, R.C. Experimental validation and CFD modeling study of biomass fast pyrolysis in fluidized-bed reactors. Fuel 2012, 97, 757–769. [Google Scholar] [CrossRef]
- Nguyen, T.D.B.; Seo, M.W.; Lim YIl Song, B.H.; Kim, S.D. CFD simulation with experiments in a dual circulating fluidized bed gasifier. Comput. Chem. Eng. 2012, 36, 48–56. [Google Scholar] [CrossRef]
- Herce, C.; Cortés, C.; Stendardo, S. Numerical simulation of a bubbling fluidized bed reactor for sorption-enhanced steam methane reforming under industrially relevant conditions: Effect of sorbent (dolomite and CaO-Ca 12 Al 14 O 33 ) and operational parameters. Fuel Process Technol. 2019, 186, 137–148. [Google Scholar] [CrossRef]
- Barik, H.; Bhattacharya, S.; Bose, M. CFD-DPM-based numerical simulation for char gasification in an entrained flow reactor: Effect of residence time distribution. Can. J. Chem. Eng. 2023, 101, 2286–2306. [Google Scholar] [CrossRef]
- Salem, A.M.; Paul, M.C. CFD modelling of spatiotemporal evolution of detailed tar species in a downdraft gasifier. Biomass Bioenergy 2023, 168, 106656. [Google Scholar] [CrossRef]
- von Berg, L.; Anca-Couce, A.; Hochenauer, C.; Scharler, R. Multi-scale modelling of fluidized bed biomass gasification using a 1D particle model coupled to CFD. Fuel 2022, 324, 124677. [Google Scholar] [CrossRef]
- Wang, S.; Luo, K.; Fan, J. CFD-DEM coupled with thermochemical sub-models for biomass gasification: Validation and sensitivity analysis. Chem. Eng. Sci. 2020, 217, 115550. [Google Scholar] [CrossRef]
- Ku, X.; Li, T.; Løvås, T. CFD–DEM simulation of biomass gasification with steam in a fluidized bed reactor. Chem. Eng. Sci. 2015, 122, 270–283. [Google Scholar] [CrossRef]
- Lungu, M.; Siame, J.; Mukosha, L. Comparison of CFD-DEM and TFM approaches for the simulation of the small scale challenge problem 1. Powder Technol. 2021, 378, 85–103. [Google Scholar] [CrossRef]
- Yu, L.; Lu, J.; Zhang, X.; Zhang, S. Numerical simulation of the bubbling fluidized bed coal gasification by the kinetic theory of granular flow (KTGF). Fuel 2007, 86, 722–734. [Google Scholar] [CrossRef]
- Armstrong, L.M.; Gu, S.; Luo, K.H. Parametric Study of Gasification Processes in a BFB Coal Gasifier. Ind. Eng. Chem. Res. 2011, 50, 5959–5974. [Google Scholar] [CrossRef]
- Armstrong, L.M.; Gu, S.; Luo, K.H. Effects of limestone calcination on the gasification processes in a BFB coal gasifier. Chem. Eng. J. 2011, 168, 848–860. [Google Scholar] [CrossRef]
- Yang, S.; Liu, X.; Wang, S. CFD simulation of air-blown coal gasification in a fluidized bed reactor with continuous feedstock. Energy Convers. Manag. 2020, 213, 112774. [Google Scholar] [CrossRef]
- Xia, Z.; Fan, Y.; Wang, T.; Guo, X.; Chen, C. A TFM-KTGF jetting fluidized bed coal gasification model and its validations with data of a bench-scale gasifier. Chem. Eng. Sci. 2015, 131, 12–21. [Google Scholar] [CrossRef]
- Adnan, M.; Sun, J.; Ahmad, N.; Wei, J.J. Comparative CFD modeling of a bubbling bed using a Eulerian–Eulerian two-fluid model (TFM) and a Eulerian-Lagrangian dense discrete phase model (DDPM). Powder Technol. 2021, 383, 418–442. [Google Scholar] [CrossRef]
- Song, T.; Wu, J.; Shen, L.; Xiao, J. Experimental investigation on hydrogen production from biomass gasification in interconnected fluidized beds. Biomass Bioenergy 2012, 36, 258–267. [Google Scholar] [CrossRef]
- Li, T.; Pannala, S.; Shahnam, M. Reprint of "CFD simulations of circulating fluidized bed risers, part II, evaluation of differences between 2D and 3D simulations. Powder Technol. 2014, 265, 13–22. [Google Scholar] [CrossRef]
- Tokmurzin, D.; Nam, J.Y.; Park, S.J.; Yoon, S.J.; Mun, T.Y.; Yoon, S.M.; Moon, J.H.; Lee, J.G.; Lee, D.H.; Ra, H.W.; et al. Three-Dimensional CFD simulation of waste plastic (SRF) gasification in a bubbling fluidized bed with detailed kinetic chemical model. Energy Convers. Manag. 2022, 267, 115925. [Google Scholar] [CrossRef]
- Han, S.W.; Lee, J.J.; Tokmurzin, D.; Lee, S.H.; Nam, J.Y.; Park, S.J.; Ra, H.W.; Mun, T.Y.; Yoon, S.J.; Yoon, S.M.; et al. Gasification characteristics of waste plastics (SRF) in a bubbling fluidized bed: Effects of temperature and equivalence ratio. Energy 2022, 238, 121944. [Google Scholar] [CrossRef]
- Doherty, W.; Reynolds, A.; Kennedy, D. Aspen Plus Simulation of Biomass Gasification in a Steam Blown Dual Fluidised Bed. In Materials and Processes for Energy: Communicating Current Research and Technological Developments; Formatex Research Centre: Badajoz, Spain, 2013. [Google Scholar]
- Mutlu, Ö.Ç.; Zeng, T. Challenges and Opportunities of Modeling Biomass Gasification in Aspen Plus: A Review. Chem. Eng. Technol. 2020, 43, 1674–1689. [Google Scholar] [CrossRef]
- Ye, G.; Xie, D.; Qiao, W.; Grace, J.R.; Lim, C.J. Modeling of fluidized bed membrane reactors for hydrogen production from steam methane reforming with Aspen Plus. Int. J. Hydrogen Energy 2009, 34, 4755–4762. [Google Scholar] [CrossRef]
- Sadaka, S.S.; Ghaly, A.E.; Sabbah, M.A. Two phase biomass air-steam gasification model for fluidized bed reactors: Part I—Model development. Biomass Bioenergy 2002, 22, 439–462. [Google Scholar] [CrossRef]
- Demirbaş, A. Carbonization ranking of selected biomass for charcoal, liquid and gaseous products. Energy Convers. Manag. 2001, 42, 1229–1238. [Google Scholar] [CrossRef]
- Doherty, W.; Reynolds, A.; Kennedy, D. Computer simulation of a biomass gasification-solid oxide fuel cell power system using Aspen Plus. Energy 2010, 27, 415–427. [Google Scholar] [CrossRef]
- Batista, F.R.M.; Follegatti-Romero, L.A.; Bessa, L.C.B.A.; Meirelles, A.J.A. Computational simulation applied to the investigation of industrial plants for bioethanol distillation. Comput. Chem. Eng. 2012, 46, 1–16. [Google Scholar] [CrossRef]
- Detchusananard, T.; Ponpesh, P.; Saebea, D.; Authayanun, S.; Arpornwichanop, A. Modeling and analysis of sorption enhanced chemical looping biomass gasification. Chem. Eng. Trans. 2017, 57, 103–108. [Google Scholar] [CrossRef]
- Marcantonio, V.; De Falco, M.; Capocelli, M.; Amado-Fierro, Á.; Centeno, T.A.; Bocci, E. Modelling and assessment of a sorption enhanced gasification system coupled with hydrothermal carbonization, hot gas cleaning, and plasma to produce pure H2 from biomass. Int. J. Hydrogen Energy 2023, 48, 32672–32685. [Google Scholar] [CrossRef]
- Dang, Q.; Zhang, X.; Zhou, Y.; Jia, X. Prediction and optimization of syngas production from a kinetic-based biomass gasification process model. Fuel Process Technol. 2021, 212, 106604. [Google Scholar] [CrossRef]
- Peters, J.F.; Banks, S.W.; Bridgwater, A.V.; Dufour, J. A kinetic reaction model for biomass pyrolysis processes in Aspen Plus. Appl. Energy 2017, 188, 595–603. [Google Scholar] [CrossRef]
- Di Blasi, C. Modeling chemical and physical processes of wood and biomass pyrolysis. Prog. Energy Combust. Sci. 2008, 34, 47–90. [Google Scholar] [CrossRef]
- Krijnen, W.P.; Wit, E. Computational and Statistical Methods for Chemical Engineering; Chapman and Hall/CRC: New York, NY, USA, 2022. [Google Scholar]
- Ge, Z.; Song, Z. Process Monitoring Based on Independent Component Analysis−Principal Component Analysis (ICA−PCA) and Similarity Factors. Ind. Eng. Chem. Res. 2007, 46, 2054–2063. [Google Scholar] [CrossRef]
- Williams, C.L.; Westover, T.L.; Emerson, R.M.; Tumuluru, J.S.; Li, C. Sources of Biomass Feedstock Variability and the Potential Impact on Biofuels Production. Bioenergy Res. 2016, 9, 1–14. [Google Scholar] [CrossRef]
- Resch, M.G.; Ladisch, M.R. Analysis, Impacts, and Solutions to Biomass Variability for Production of Fuels and Value-Added Products. ACS Sustain. Chem. Eng. 2020, 8, 15375–15377. [Google Scholar] [CrossRef]
- Martínez, M.G.; Floquet, P.; Dupont, C.; da Silva Perez, D.; Meyer, X.M. Assessing the impact of woody and agricultural biomass variability on its behaviour in torrefaction through Principal Component Analysis. Biomass Bioenergy 2020, 134, 105474. [Google Scholar] [CrossRef]
- Multivariate Statistical Process Control and Industrial Applications—ProQuest n.d. Available online: https://www.proquest.com/openview/207b6bafd5110b23915b2f4994723514/1?pq-origsite=gscholar&cbl=39817 (accessed on 31 July 2023).
- Clark, V. Multivariate data analysis in industrial practice: By Paul J. LEWI John Wiley and Sons, Chichester, 1982 (256 pp., $29.95/£13.75, ISBN 0471 10466 3). Comput. Stat. Data Anal. 1983, 1, 289–290. [Google Scholar] [CrossRef]
- Jolliffe, I.T. Principal Component Analysis for Special Types of Data. In Principal Component Analysis; Springer: New York, NY, USA, 2002; pp. 338–372. [Google Scholar] [CrossRef]
- Thompson, B. Canonical Correlation Analysis: Uses and Interpretation. Available online: https://books.google.com.hk/books?hl=en&lr=&id=Dk0XINOvsw8C&oi=fnd&pg=PA11&dq=Canonical+Correlation+Analysis:+Uses+and+Interpretation&ots=3bDBW84Vpj&sig=kIJ6zi3v3HqI-8sDHWjFINPB7ks&redir_esc=y#v=onepage&q=Canonical%20Correlation%20Analysis%3A%20Uses%20and%20Interpretation&f=false (accessed on 31 July 2023).
- Nachtergaele, P.; Thybaut, J.; De Meester, S.; Drijvers, D.; Saeys, W.; Dewulf, J. Multivariate Analysis of Industrial Biorefinery Processes: Strategy for Improved Process Understanding with Case Studies in Fatty Acid Production. Ind. Eng. Chem. Res. 2020, 59, 7732–7745. [Google Scholar] [CrossRef]
- Li, J.; Xu, K.; Yao, X.; Chen, S. Prediction and optimization of syngas production from steam gasification: Numerical study of operating conditions and biomass composition. Energy Convers. Manag. 2021, 236, 114077. [Google Scholar] [CrossRef]
- Meuzelaar, H.L.C.; Hoesterey, B.L.; Windig, W.; Hill, G.R. Prediction and modeling of coal conversion reactions by pyrolysis mass spectrometry and multivariate statistical analysis. Fuel Process Technol. 1987, 15, 59–70. [Google Scholar] [CrossRef]
- Tiong, L.; Komiyama, M. Statistical analysis of microalgae supercritical water gasification: Reaction variables, catalysis and reaction pathways. J. Supercrit. Fluids 2022, 183, 105552. [Google Scholar] [CrossRef]
- Dellavedova, M.; Derudi, M.; Biesuz, R.; Lunghi, A.; Rota, R. On the gasification of biomass: Data analysis and regressions. Process Saf. Environ. Prot. 2012, 90, 246–254. [Google Scholar] [CrossRef]
- Motta, I.L.; Marchesan, A.N.; Maciel Filho, R.; Wolf Maciel, M.R. Correlating biomass properties, gasification performance, and syngas applications of Brazilian feedstocks via simulation and multivariate analysis. Ind. Crops Prod. 2022, 181, 114808. [Google Scholar] [CrossRef]
- Baggio, P.; Baratieri, M.; Fiori, L.; Grigiante, M.; Avi, D.; Tosi, P. Experimental and modeling analysis of a batch gasification/pyrolysis reactor. Energy Convers. Manag. 2009, 50, 1426–1435. [Google Scholar] [CrossRef]
- Adeyemi, I.; Janajreh, I.; Arink, T.; Ghenai, C. Gasification behavior of coal and woody biomass: Validation and parametrical study. Appl. Energy 2017, 185, 1007–1018. [Google Scholar] [CrossRef]
- Gil, M.V.; González-Vázquez, M.P.; García, R.; Rubiera, F.; Pevida, C. Assessing the influence of biomass properties on the gasification process using multivariate data analysis. Energy Convers. Manag. 2019, 184, 649–660. [Google Scholar] [CrossRef]
- Obafemi, O.; Stephen, A.; Ajayi, O.; Nkosinathi, M. A survey of Artificial Neural Network-based Prediction Models for Thermal Properties of Biomass. Procedia Manuf. 2019, 33, 184–191. [Google Scholar] [CrossRef]
- George, J.; Arun, P.; Muraleedharan, C. Assessment of producer gas composition in air gasification of biomass using artificial neural network model. Int. J. Hydrogen Energy 2018, 43, 9558–9568. [Google Scholar] [CrossRef]
- Ranade, N.V.; Nagarajan, S.; Sarvothaman, V.; Ranade, V.V. ANN based modelling of hydrodynamic cavitation processes: Biomass pre-treatment and wastewater treatment. Ultrason. Sonochem. 2021, 72, 105428. [Google Scholar] [CrossRef]
- Brown, D.; Fuchino, T.; Maréchal, F. Solid fuel decomposition modelling for the design of biomass gasification systems. Comput. Aided Chem. Eng. 2006, 21, 1661–1666. [Google Scholar] [CrossRef]
- Sreejith, C.C.; Muraleedharan, C.; Arun, P. Performance prediction of fluidised bed gasification of biomass using experimental data-based simulation models. Biomass Convers. Biorefinery 2013, 3, 283–304. [Google Scholar] [CrossRef]
- Begum, S.; Rasul, M.G.; Akbar, D.; Ramzan, N. Performance analysis of an integrated fixed bed gasifier model for different biomass feedstocks. Energies 2013, 6, 6508–6524. [Google Scholar] [CrossRef]
- Hussain, M.; Tufa, L.D.; Yusup, S.; Zabiri, H. A kinetic-based simulation model of palm kernel shell steam gasification in a circulating fluidized bed using Aspen Plus®: A case study. Biofuels 2018, 9, 635–646. [Google Scholar] [CrossRef]
- Furusawa, T.; Saito, K.; Kori, Y.; Miura, Y.; Sato, M.; Suzuki, N. Steam reforming of naphthalene/benzene with various types of Pt- and Ni-based catalysts for hydrogen production. Fuel 2013, 103, 111–121. [Google Scholar] [CrossRef]
- Herrmann, T.; Dillig, M.; Hauth, M.; Karl, J. Conversion of tars on solid oxide fuel cell anodes and its impact on voltages and current densities. Energy Sci. Eng. 2017, 5, 194–207. [Google Scholar] [CrossRef]
- Font Palma, C. Modelling of tar formation and evolution for biomass gasification: A review. Appl. Energy 2013, 111, 129–141. [Google Scholar] [CrossRef]
- Zhao, B.; Zhang, X.; Chen, L.; Qu, R.; Meng, G.; Yi, X.; Sun, L. Steam reforming of toluene as model compound of biomass pyrolysis tar for hydrogen. Biomass Bioenergy 2010, 34, 140–144. [Google Scholar] [CrossRef]
- Serrano, D.; Castelló, D. Tar prediction in bubbling fluidized bed gasification through artificial neural networks. Chem. Eng. J. 2020, 402, 126229. [Google Scholar] [CrossRef]
- Damartzis, T.; Michailos, S.; Zabaniotou, A. Energetic assessment of a combined heat and power integrated biomass gasification–internal combustion engine system by using Aspen Plus®. Fuel Process Technol. 2012, 95, 37–44. [Google Scholar] [CrossRef]
- Rapagnà, S.; Orazio, A.D.; Gallucci, K.; Ugo, P. Hydrogen Rich Gas from Catalytic Steam Gasification of Biomass in a Fluidized Bed Containing Catalytic Filters. Chem. Eng. Trans. 2014, 37, 157–162. [Google Scholar]
- Marcantonio, V.; Bocci, E.; Ouweltjes, J.P.; Del Zotto, L.; Monarca, D. Evaluation of sorbents for high temperature removal of tars, hydrogen sulphide, hydrogen chloride and ammonia from biomass-derived syngas by using Aspen Plus. Int. J. Hydrogen Energy 2020, 45, 6651–6662. [Google Scholar] [CrossRef]
- Pauls, J.H.; Mahinpey, N.; Mostafavi, E. Simulation of air-steam gasification of woody biomass in a bubbling fluidized bed using Aspen Plus: A comprehensive model including pyrolysis, hydrodynamics and tar production. Biomass Bioenergy 2016, 95, 157–166. [Google Scholar] [CrossRef]
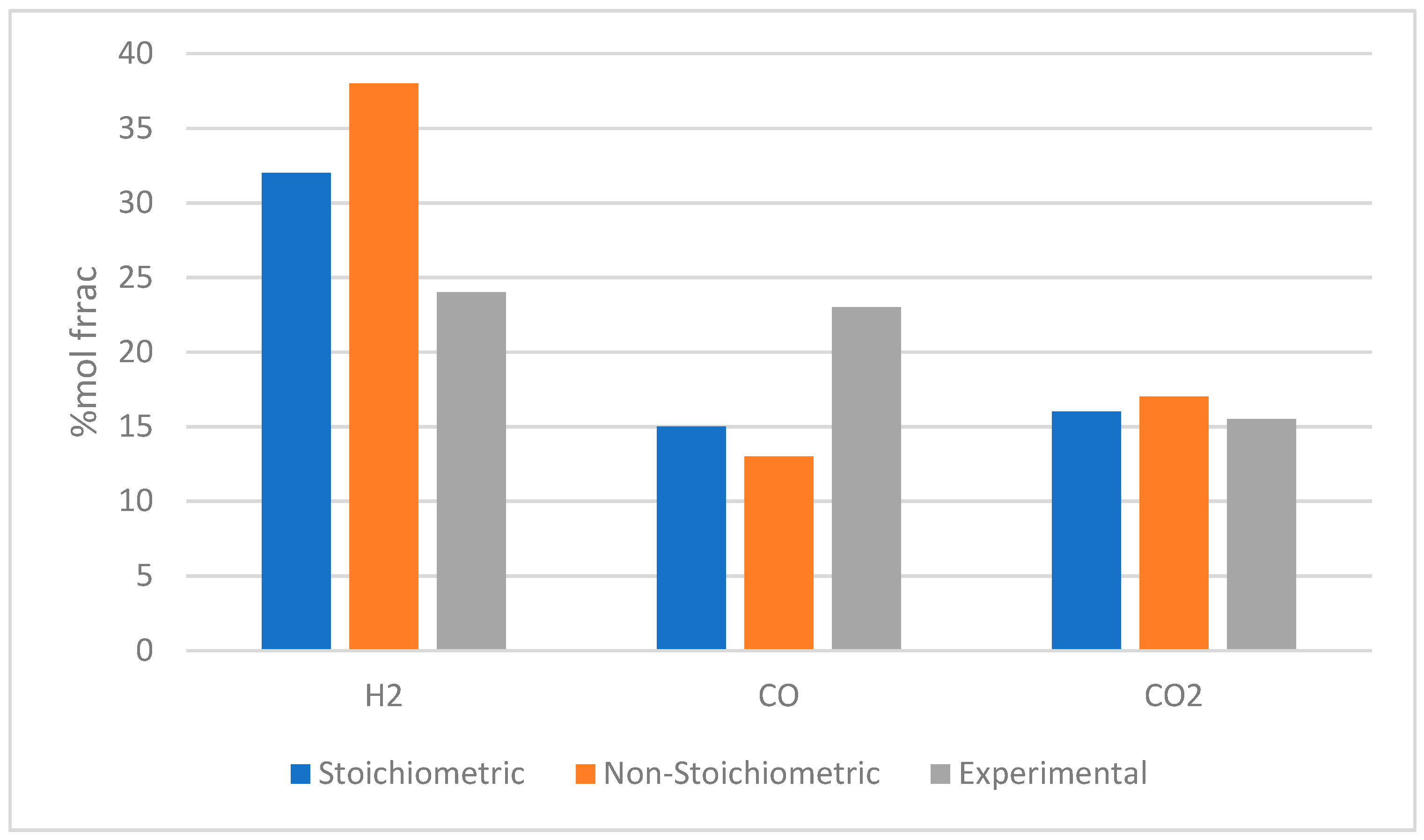
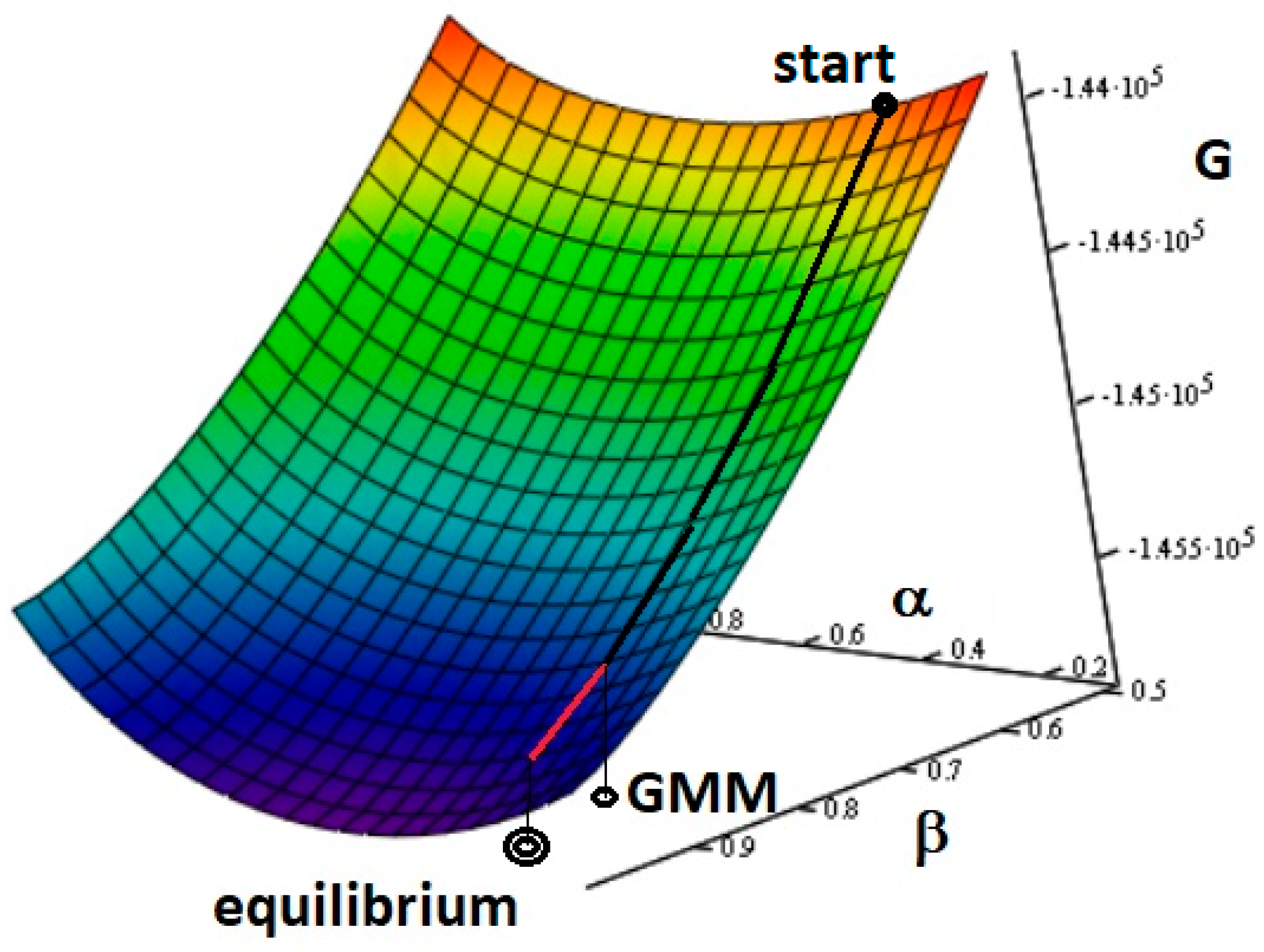
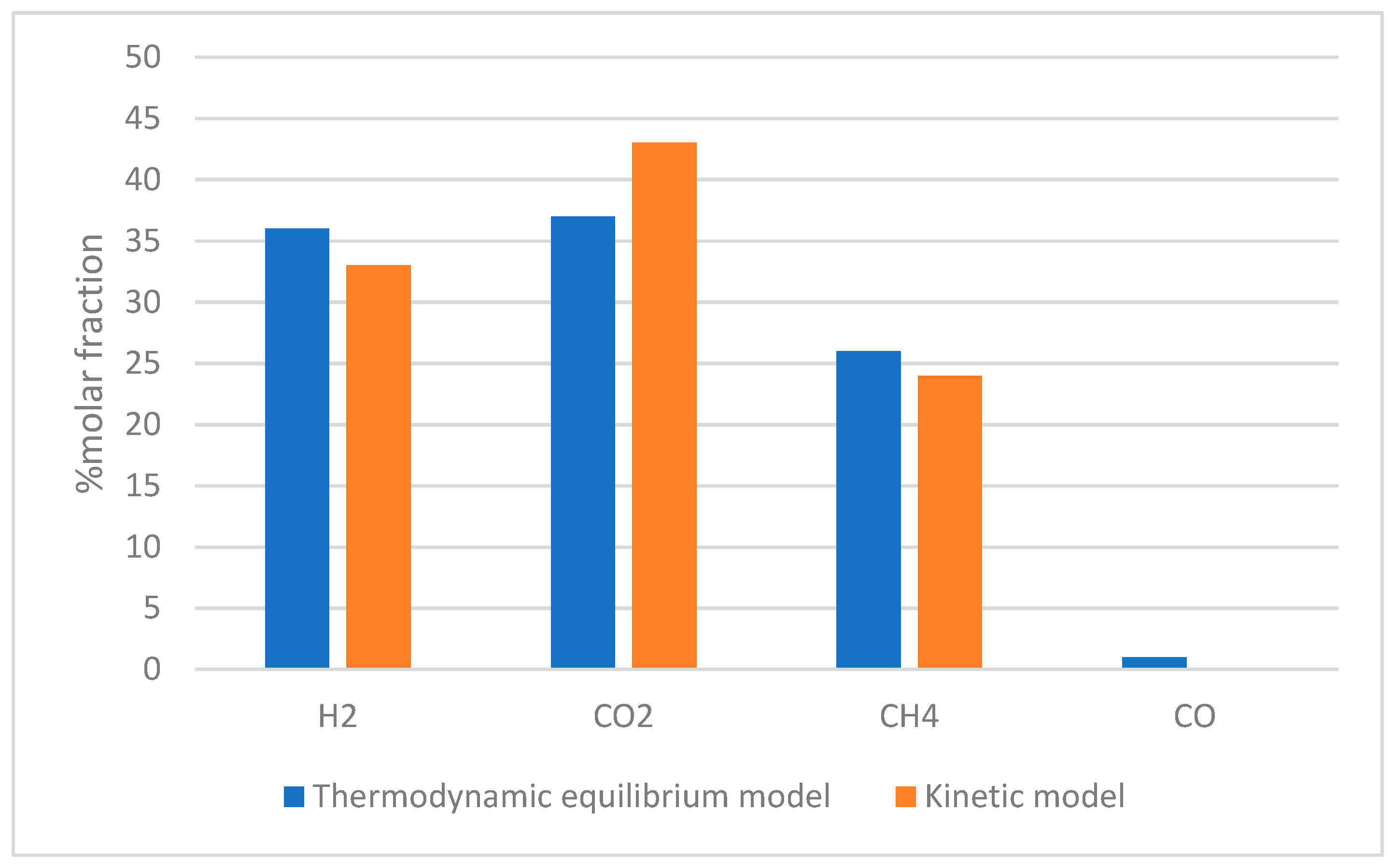
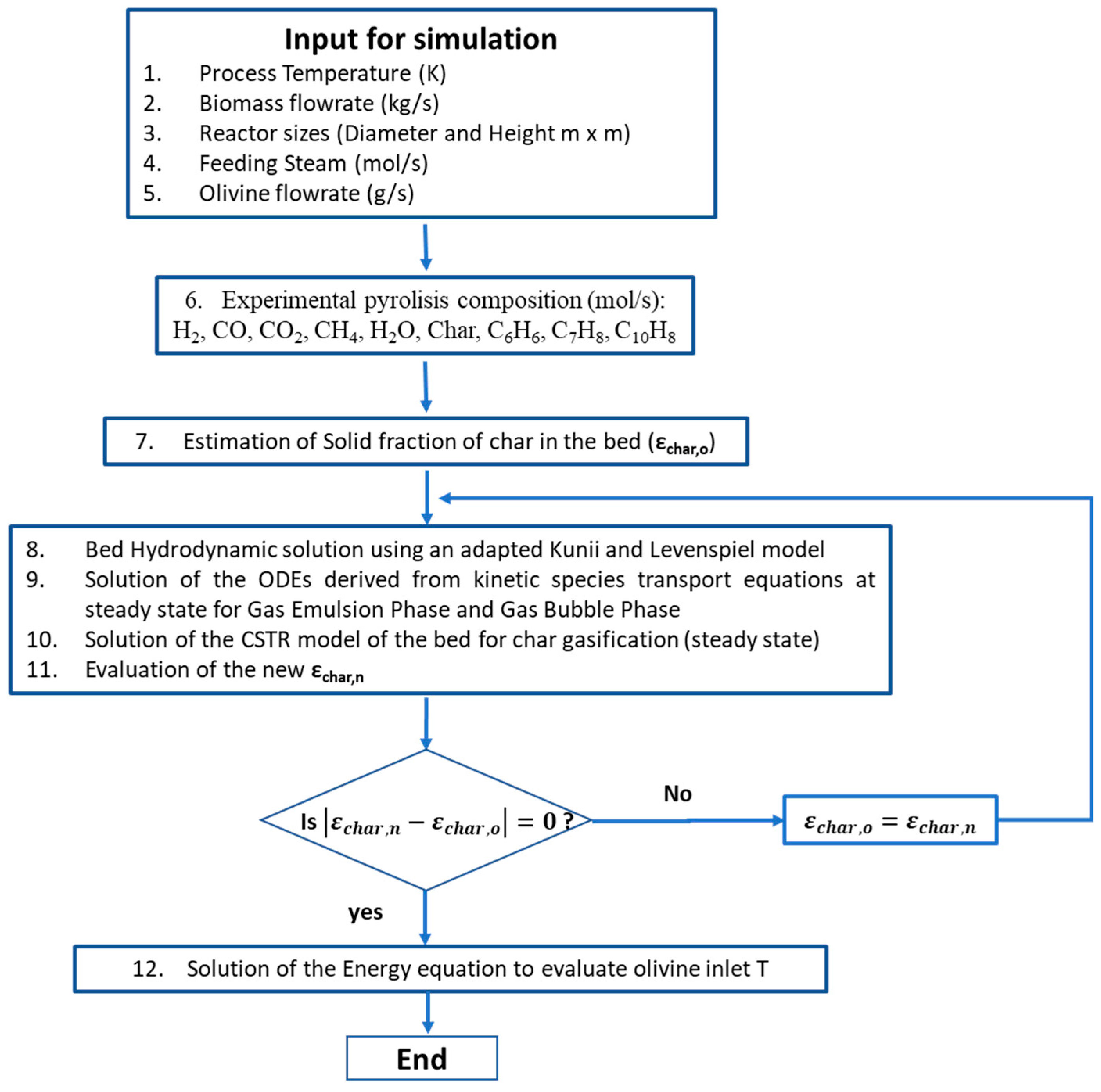

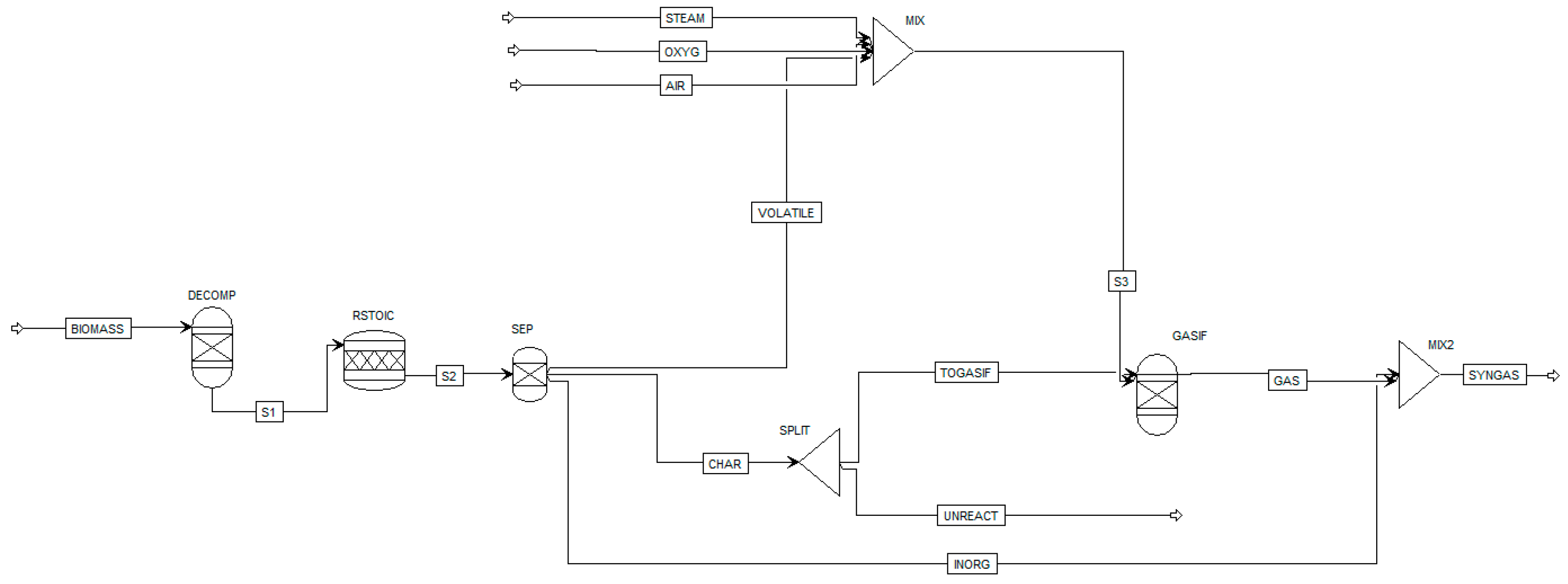
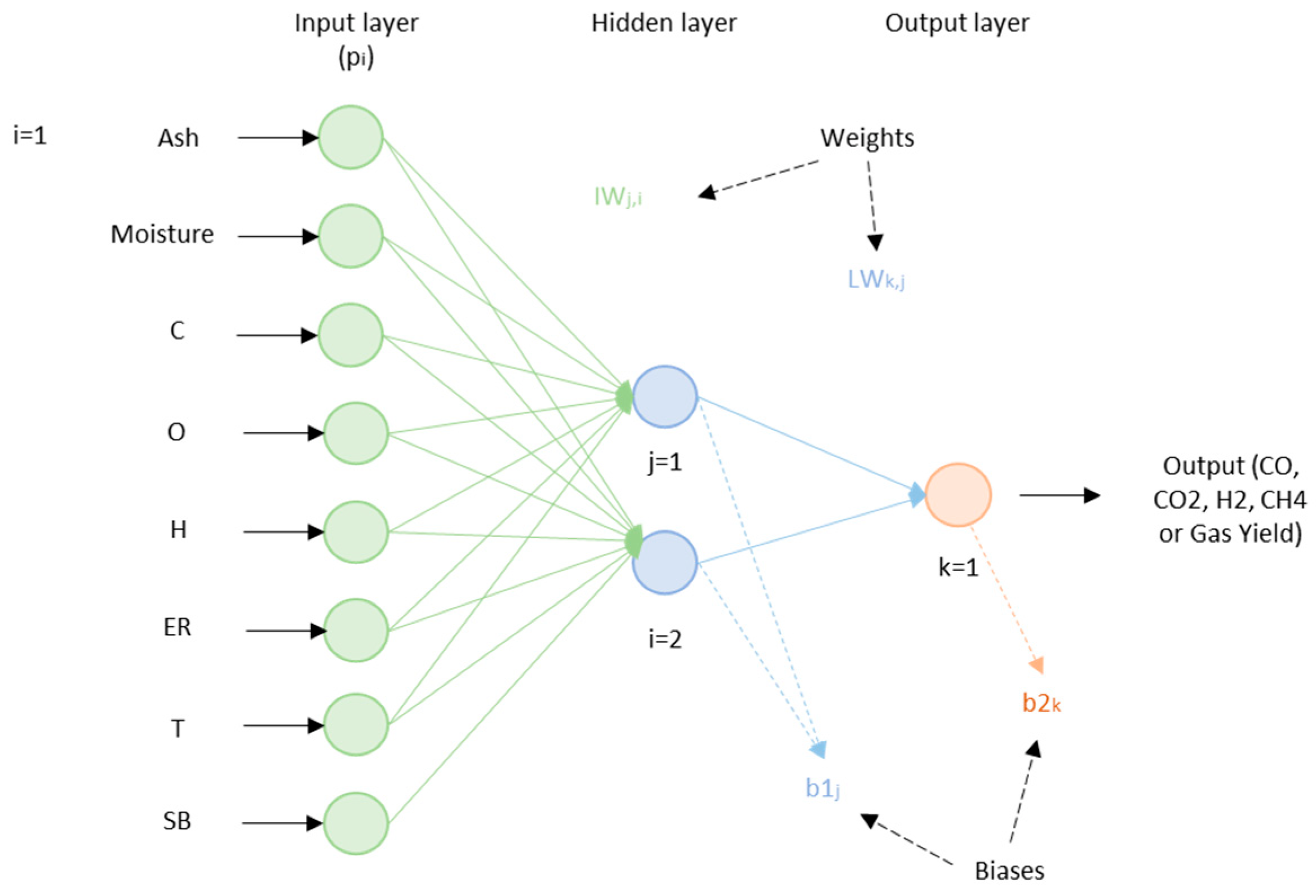
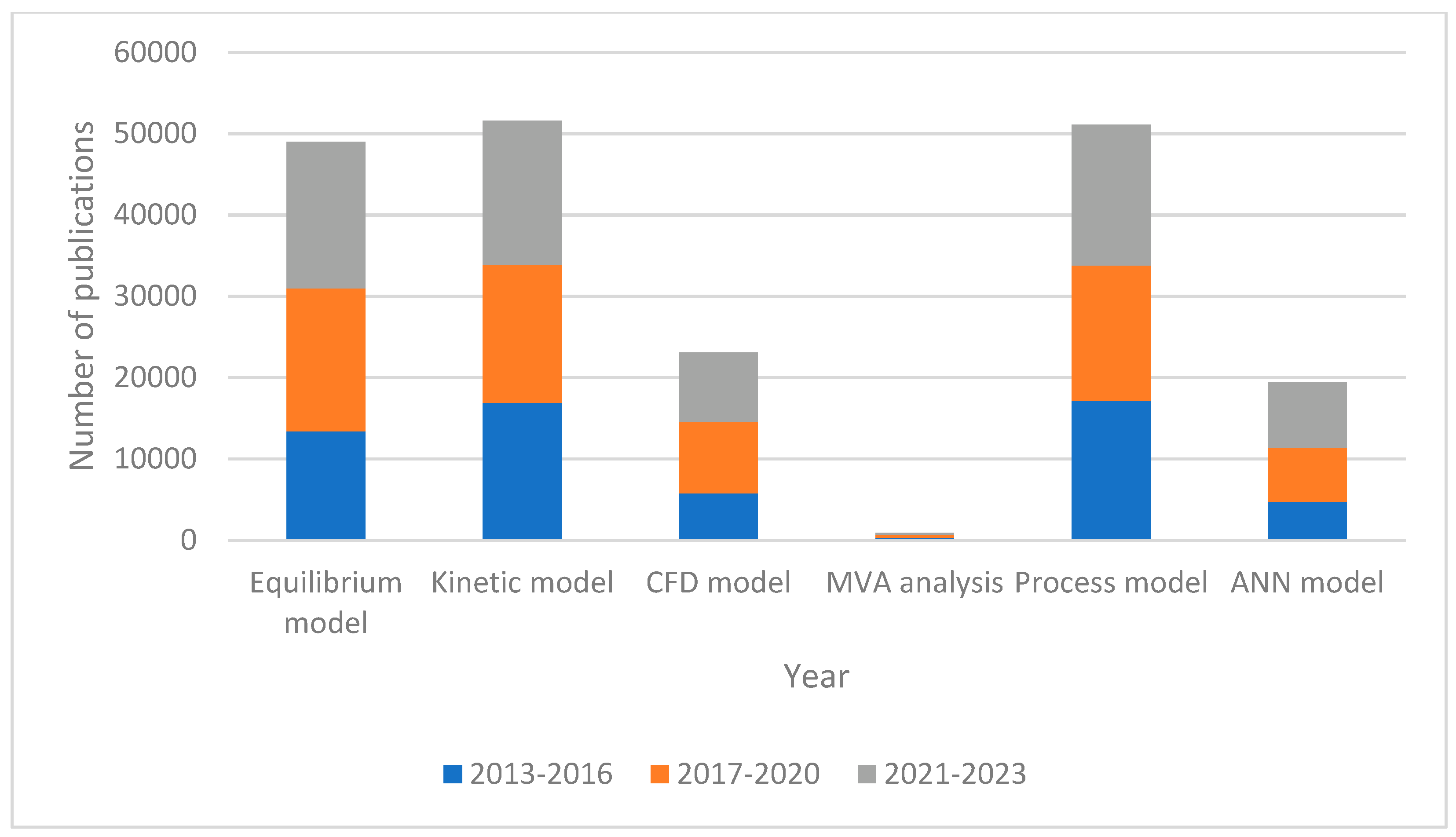
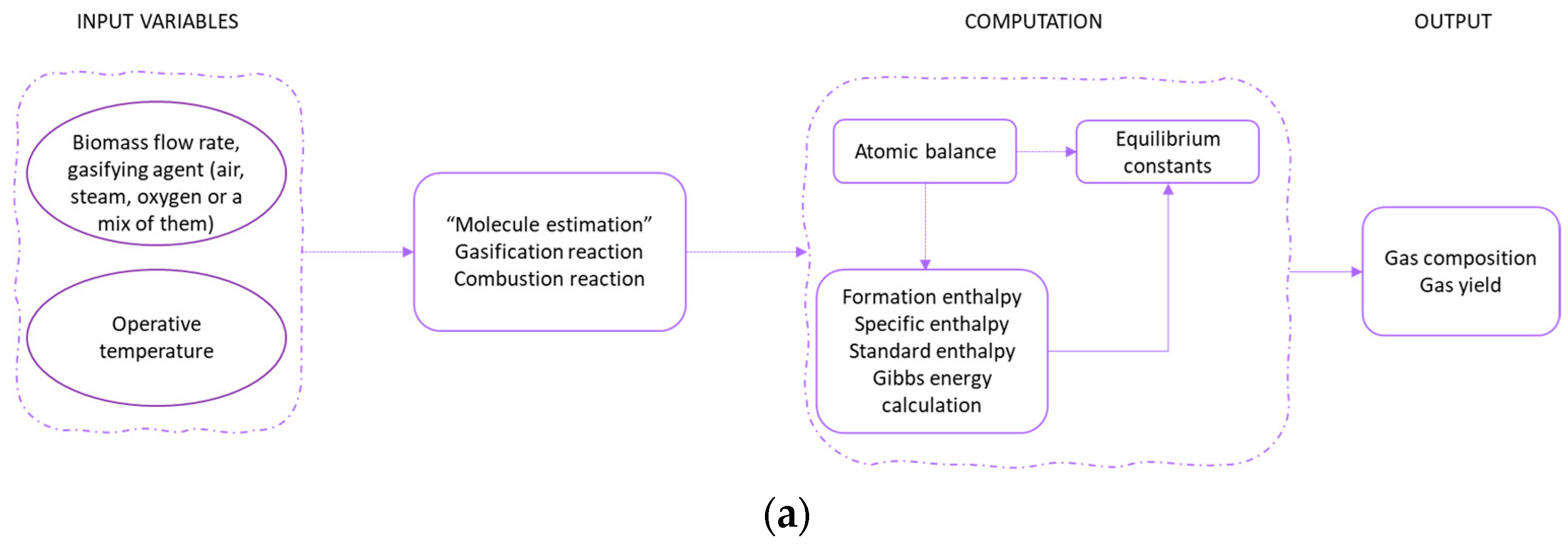
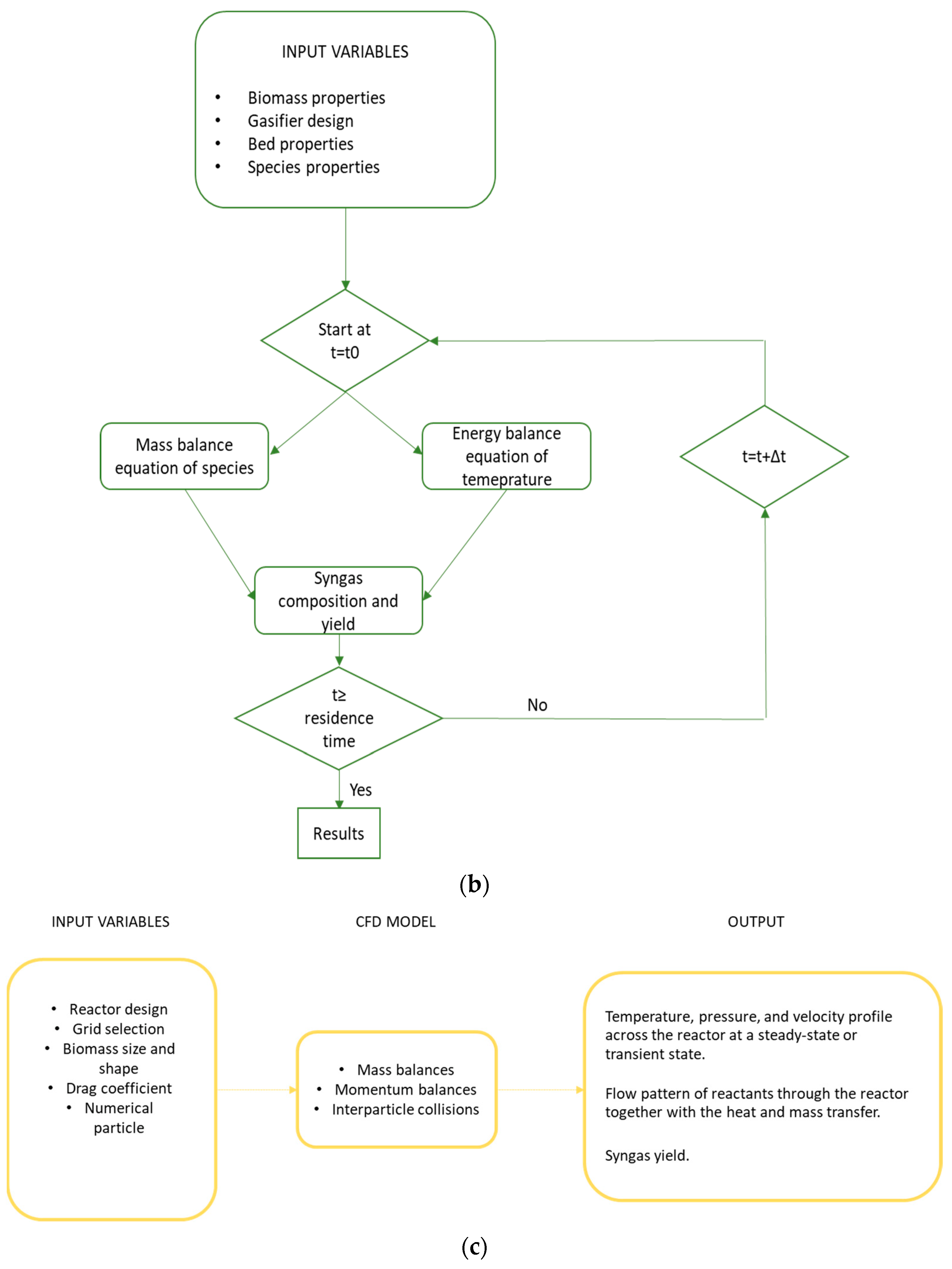
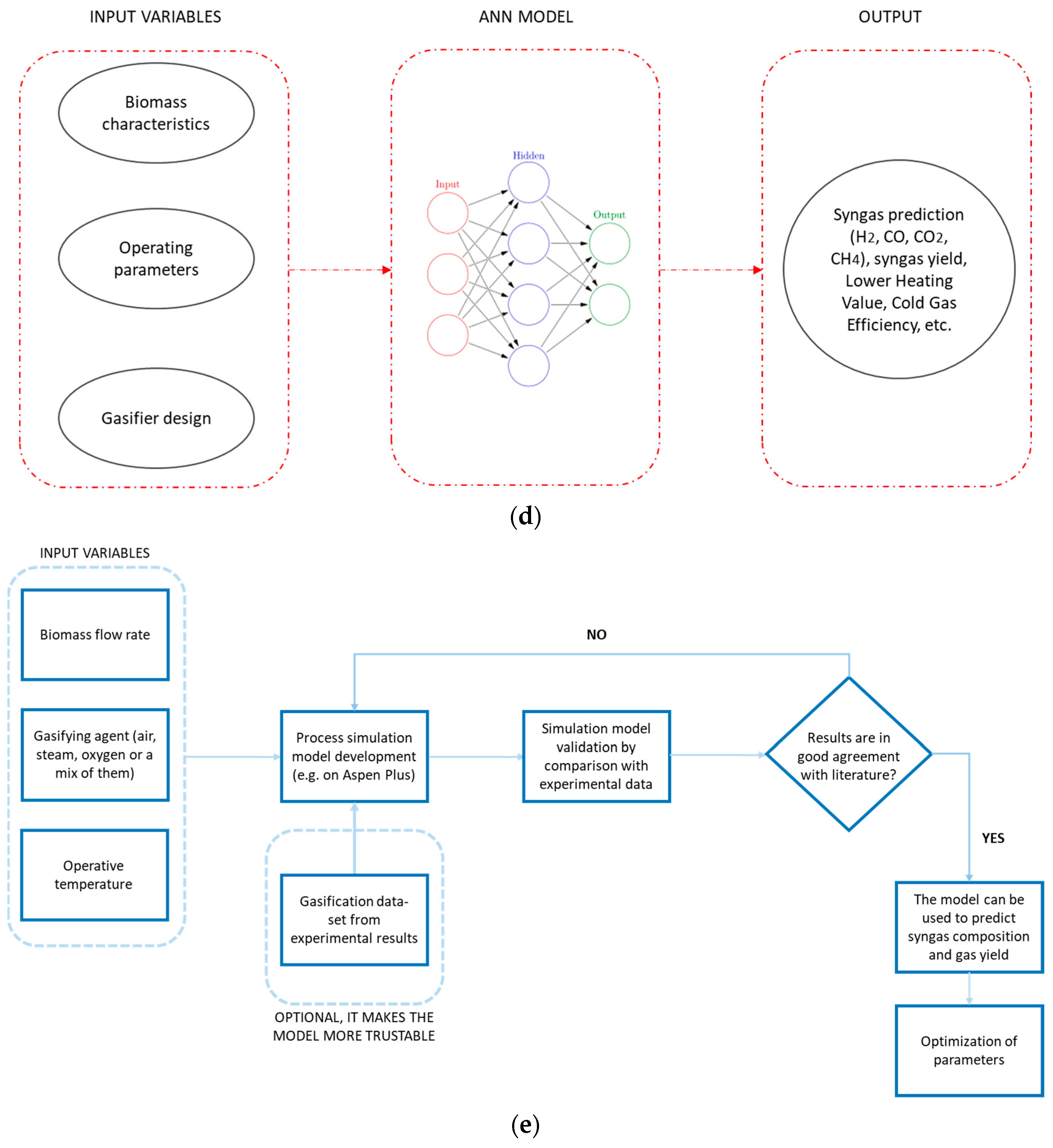
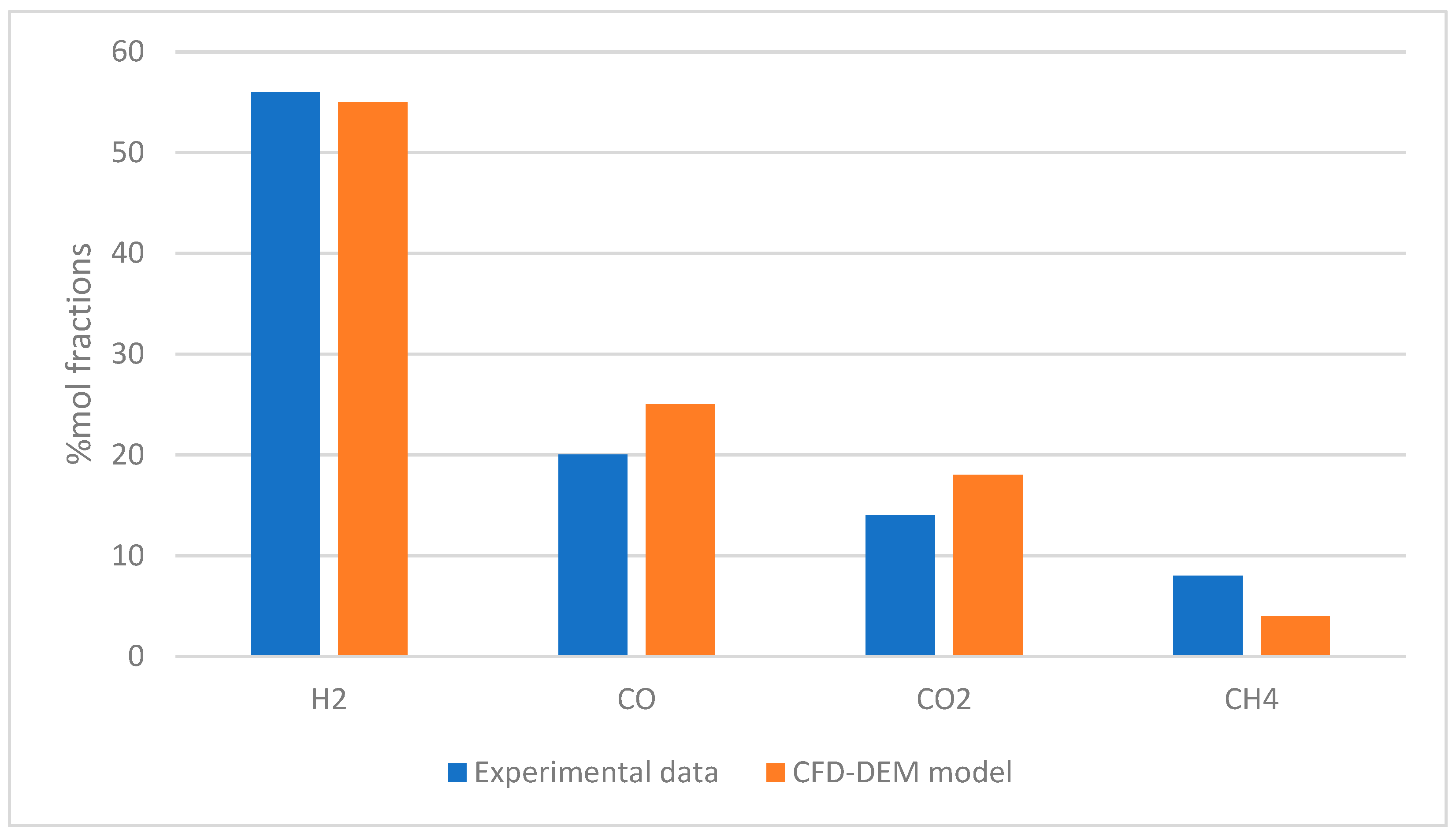
| Gasifying Agent | H2 (%mol) | CO2 (%mol) | CO (%mol) | CH4 (%mol) | N2 (%mol) | LHV (MJ/kg) |
|---|---|---|---|---|---|---|
| Air | 3–13 | 10–18 | 5–28 | 0–7 | 40–50 | 4–6 |
| Oxygen | 20–30 | 25–40 | 20–30 | 5–10 | 0–1 | 7–8 |
| Steam | 30–50 | 8–25 | 20–40 | 6–15 | 0–1 | 9–11 |
| Oxidation Reaction | |
|---|---|
| Volatiles | Char |
| (1) ΔH = −283 kJ/mol | (2) ΔH = −111 kJ/mol |
| (3) ΔH = −242 kJ/mol | (4) ΔH = −394 kJ/mol |
| Boudouard reaction | |
| (5) ΔH = −172 kJ/mol | |
| Water-Gas reaction | |
| Primary | Secondary |
| (6) ΔH = −131 kJ/mol | (7) ΔH = −90 kJ/mol |
| Methanation reaction | |
| (8) ΔH = −75 kJ/mol | |
| Water–gas shift reaction | |
| (9) ΔH = −41 kJ/mol | |
| Steam-reforming reaction | |
| (10) ΔH = 206 kJ/mol (11) | |
| Dry reforming reaction | |
| (12) ΔH = 247 kJ/mol | |
| (13) | |
| Compound | (kJ/mol) | (kJ/mol) |
|---|---|---|
| CH4 | −75.51 | −50.45 |
| H2O(gas) | −241.83 | −228.59 |
| CO | −110.52 | −137.27 |
| CO2 | −393.51 | −394.38 |
| H2 | 0 | 0 |
| C(solid) | 0 | 0 |
| Experimental Data [70,71] | Aspen Plus Model | MATLAB Model | |
|---|---|---|---|
| H2 (%dry mole fraction) | 42 | 34 | 39 |
| CO (%dry mole fraction) | 17 | 33 | 30 |
| CO2 (%dry mole fraction) | 31 | 21 | 17 |
| CH4 (%dry mole fraction) | 9 | 12 | 14 |
| LHV (MJ/kg) dry | 14–15 | 13 | 15 |
| 0.85 | 1.40 | 1.25 | |
| Cold gas efficiency | 0.87–0.96 | 0.88 | 0.92 |
| Aspen Plus Block Name | Description |
|---|---|
| Thermodynamic equilibrium approach [27,110] | |
RYield | Usually called DECOMP block (DECOMP stays for decomposition), it is a yield reactor which converts the non-conventional inlet stream of biomass into its conventional components (carbon, hydrogen, oxygen, sulfur, nitrogen, and ash) by specifying the yield distribution according to the biomass ultimate analysis. |
RStoic | Stoichiometric reactor, used to simulate the production of inorganic compounds. Indeed, DECOMP block creates N, Cl and S as elemental components that are known to produce mainly HCl, NH3 and H2S, and the results of the real fractional conversion model are closer to the experimental data than that of the chemical equilibrium. This is why a stoichiometric reactor is needed to simulate the production of H2S, NH3 and HCl specifying the proper reactions and the fractional conversion for S, Cl2 and N. |
RGibbs | Gibbs free-energy reactor, which simulates drying, pyrolysis, partial oxidation, and gasification. It is possible to let the software individuate all the possible products without specifying any reactions or products by means of the option “Calculate phase equilibrium and chemical equilibrium.” Otherwise, it is also possible using the QET approach of the specified reactions to set the syngas composition by specifying a temperature approach for individual reactions by means of the option “Restrict chemical equilibrium—specify temperature approach or reaction extents.” |
| Total kinetic approach [111,112] | |
RYield | Yield reactor represents the virtual reaction step that decomposes the biomass into its three principal biochemical building blocks: cellulose, hemicellulose, and lignin. This reaction step does not represent any part of the actual pyrolysis reaction mechanism, but is necessary for the following interlinked reaction model. The yields are calculated iteratively by an embedded Excel worksheet that determines the cellulose, hemicellulose, and lignin composition of the biomass according to its elemental composition. |
RCSTR or RBatch | In the second phase, a kinetic reaction model is implemented for the primary pyrolysis reactions. It is an interlinked model of individual decomposition reactions of cellulose, hemicellulose, and lignin, according to [61,113]. The reactor type can be chosen according to the pyrolysis reactor that needs to be modeled. For fast pyrolysis, the RCStir reactor is used, while the RBatch-type reactor is more suitable for slow pyrolysis modeling. |
RYield | The secondary vapor reactions at longer residence times are implemented in Aspen Plus as an embedded Excel sheet that determines the yields of the RYield type secondary reaction reactor. The complete methodology and the corresponding equations are generated. |
| Range | |
|---|---|
| Input variables | |
| Ash content of dry biomass (g/kg) | 5.5–11.0 |
| Moisture content of wet biomass (g/kg) | 62.8–25.0 |
| Carbon content of dry biomass (g/kg) | 458.9–505.4 |
| Oxygen content of dry biomass (g/kg) | 411.1–471.8 |
| Hydrogen content of dry biomass (g/kg) | 56.4–70.8 |
| Equivalence ratio (ER) | 0.19–0.47 |
| Gasification temperature (T) (°C) | 700–900 |
| Steam to dry biomass ratio (SB) (kg/kg) | 0–0.04 |
| Output variables | |
| Gas yield (m3/kg) | 1.17–3.42 |
| H2 volume fraction, dry basis (%) | 4.97–26.17 |
| CO volume fraction, dry basis (%) | 10–29.47 |
| CO2 volume fraction, dry basis (%) | 9.82–18.60 |
| CH4 volume fraction, dry basis (%) | 2.40–6.07 |
| Approach | Features | Pros | Cons |
|---|---|---|---|
| Kinetic modeling |
|
|
|
| Thermodynamic modeling |
|
|
|
| CFD modeling |
|
|
|
| MVA analysis |
|
|
|
| Process simulation modeling with commercial software |
|
|
|
| Artificial neural network modeling |
|
|
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marcantonio, V.; Di Paola, L.; De Falco, M.; Capocelli, M. Modeling of Biomass Gasification: From Thermodynamics to Process Simulations. Energies 2023, 16, 7042. https://doi.org/10.3390/en16207042
Marcantonio V, Di Paola L, De Falco M, Capocelli M. Modeling of Biomass Gasification: From Thermodynamics to Process Simulations. Energies. 2023; 16(20):7042. https://doi.org/10.3390/en16207042
Chicago/Turabian StyleMarcantonio, Vera, Luisa Di Paola, Marcello De Falco, and Mauro Capocelli. 2023. "Modeling of Biomass Gasification: From Thermodynamics to Process Simulations" Energies 16, no. 20: 7042. https://doi.org/10.3390/en16207042
APA StyleMarcantonio, V., Di Paola, L., De Falco, M., & Capocelli, M. (2023). Modeling of Biomass Gasification: From Thermodynamics to Process Simulations. Energies, 16(20), 7042. https://doi.org/10.3390/en16207042