Numerical and Techno-Economic Analysis of Batch Annealing Performance Improvements in Tinplate Manufacturing
Abstract
1. Introduction
2. Materials and Methods
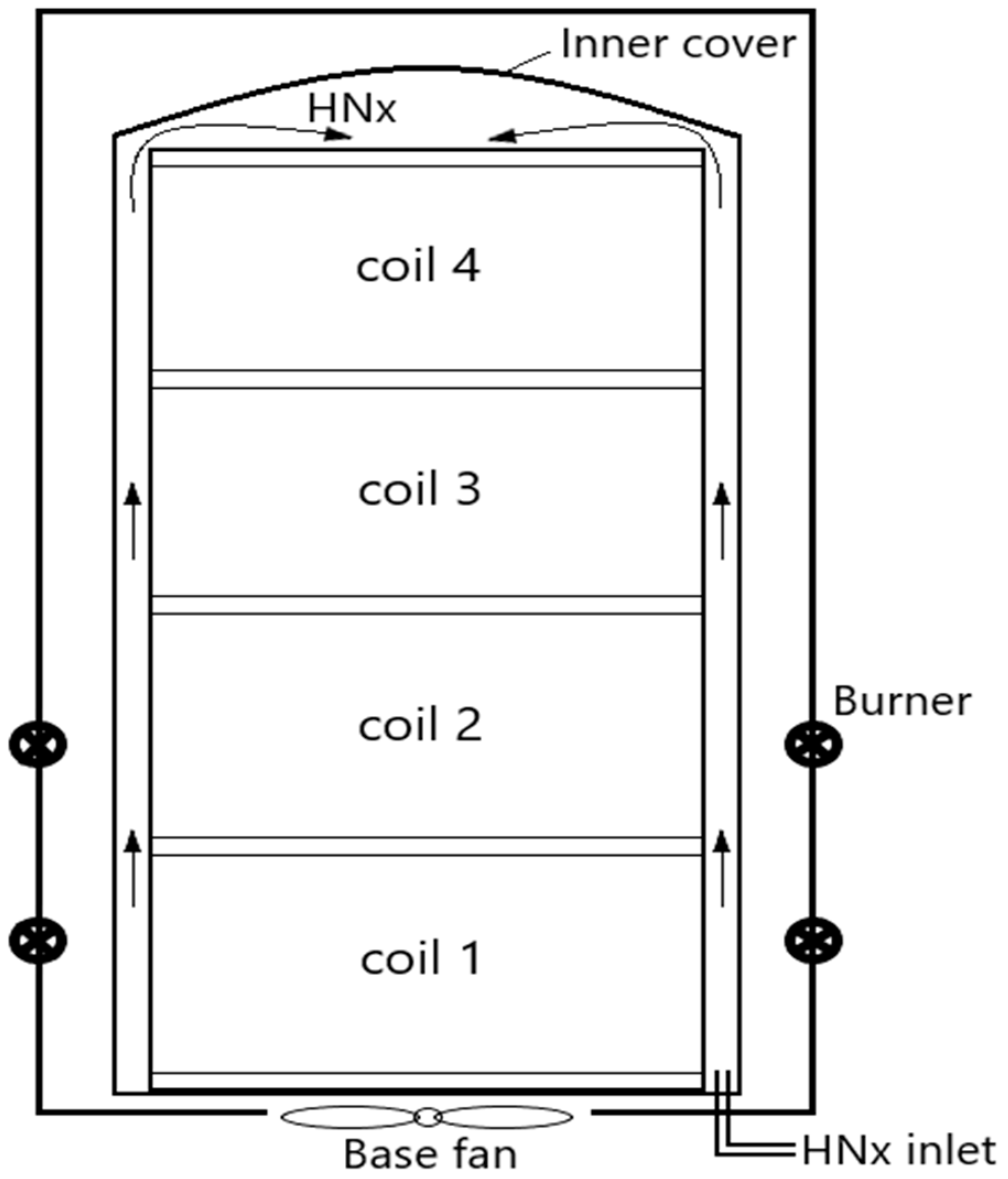
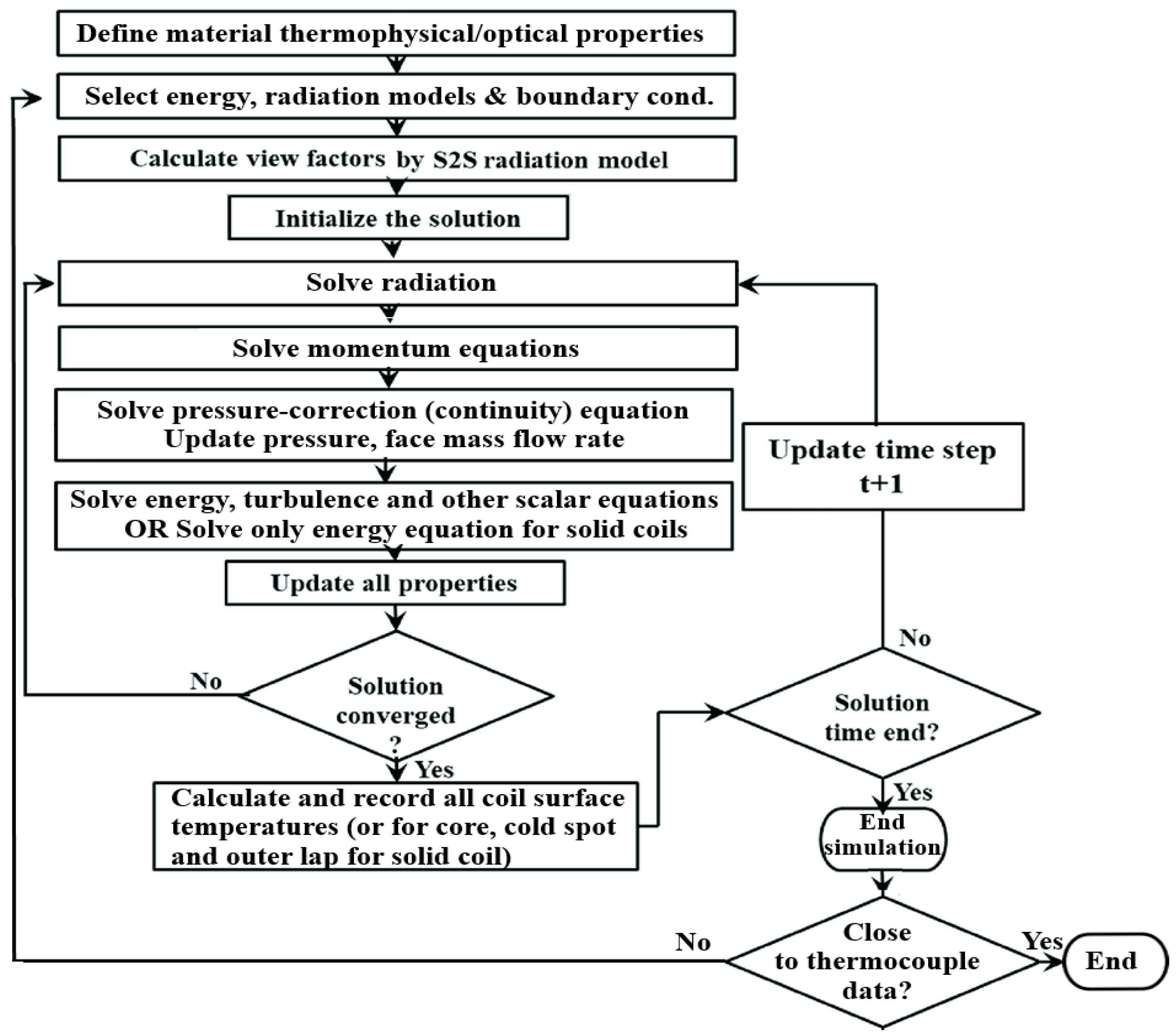
2.1. Computational Fluid Dynamics (CFD) Analysis
2.1.1. Transient CFD Analysis of Current Furnace and Model Validation
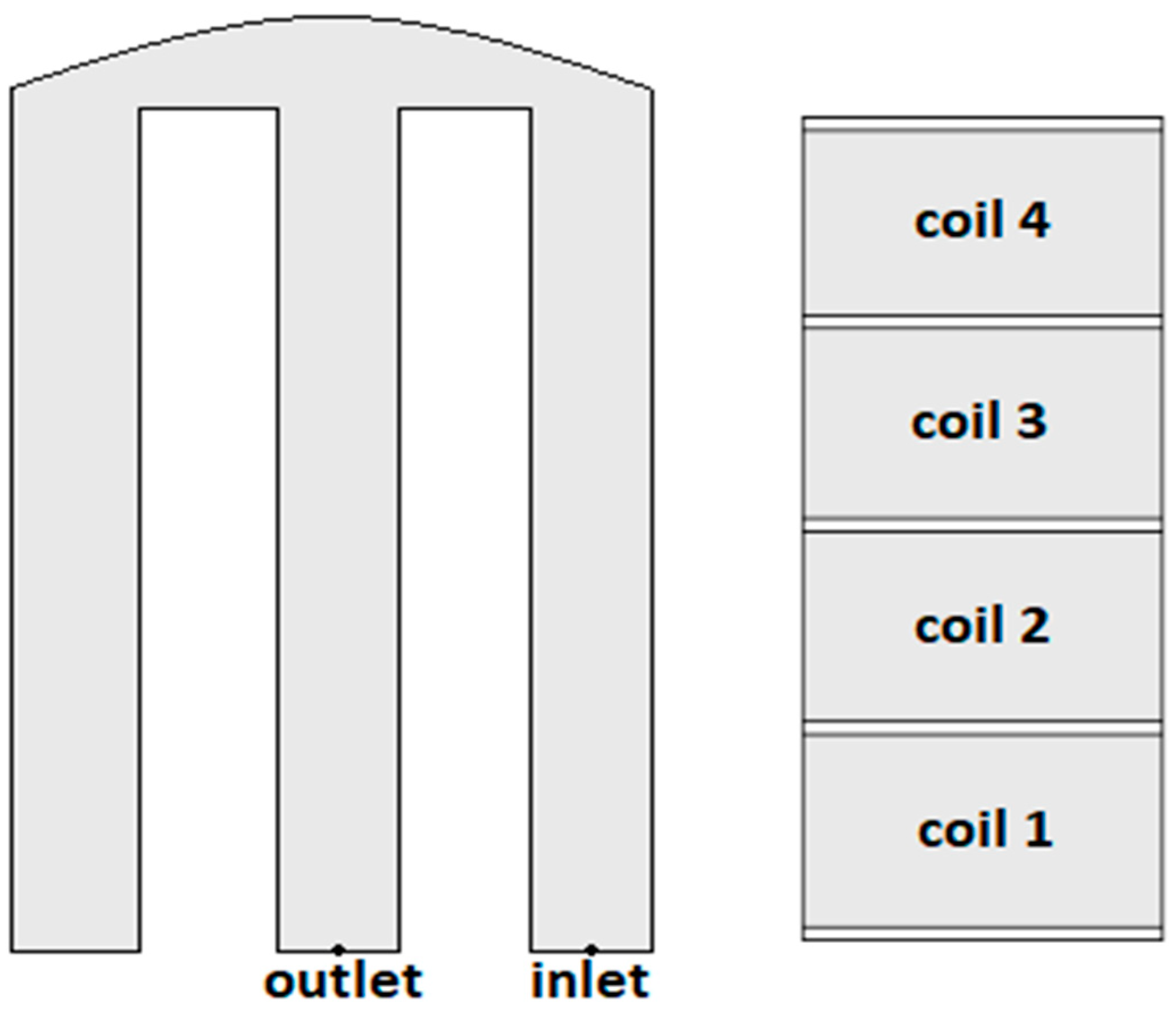
Fluid-Only CFD Model
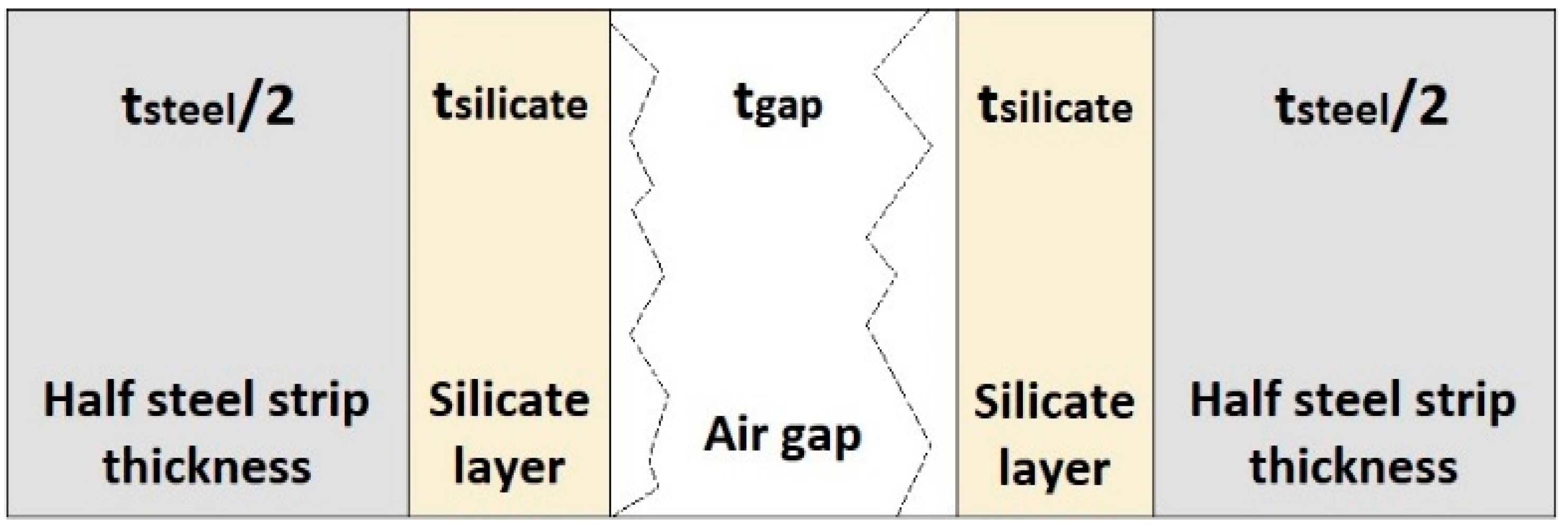
Solid-Only CFD Model
Validation of CFD Models
- Outer thermocouple—3 cm from coil outer edge and depth of 19.5 cm into coil
- Middle thermocouple—32 cm in from coil outer edge and depth of 32 cm into coil
- Core thermocouple—7 cm in from coil core edge and depth of 18.5 cm into coil
2.1.2. Grid and Time-Step Independency Study
2.1.3. Transient CFD Analysis of Furnace Improvement Scenarios
2.2. Technoeconomic Analysis of Promising Improvement Scenarios
3. Results
3.1. Computational Fluid Dynamics (CFD) Analysis
3.1.1. Transient CFD Analysis of Current Furnace and Model Validation
3.1.2. Grid and Time-Step Independence Study
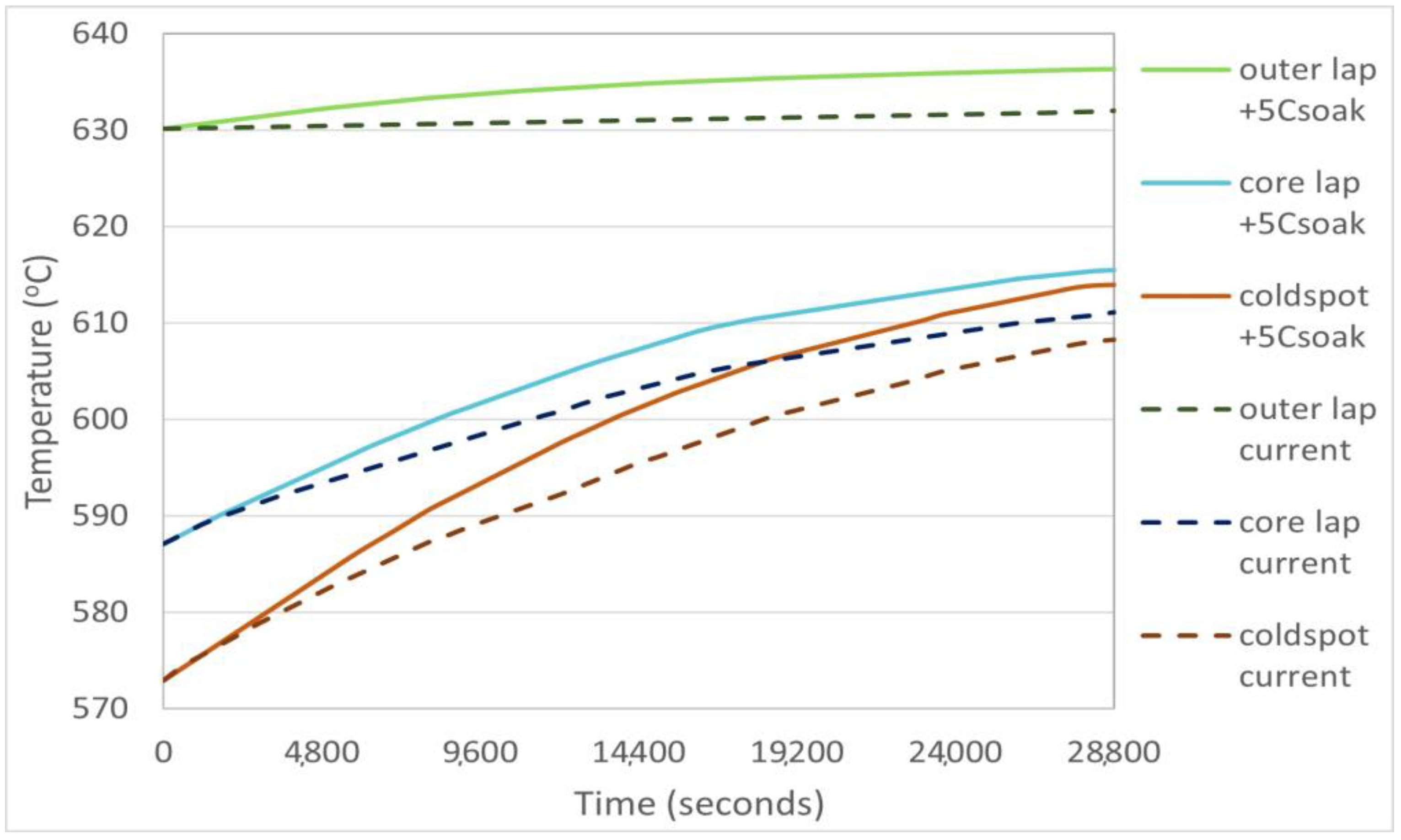
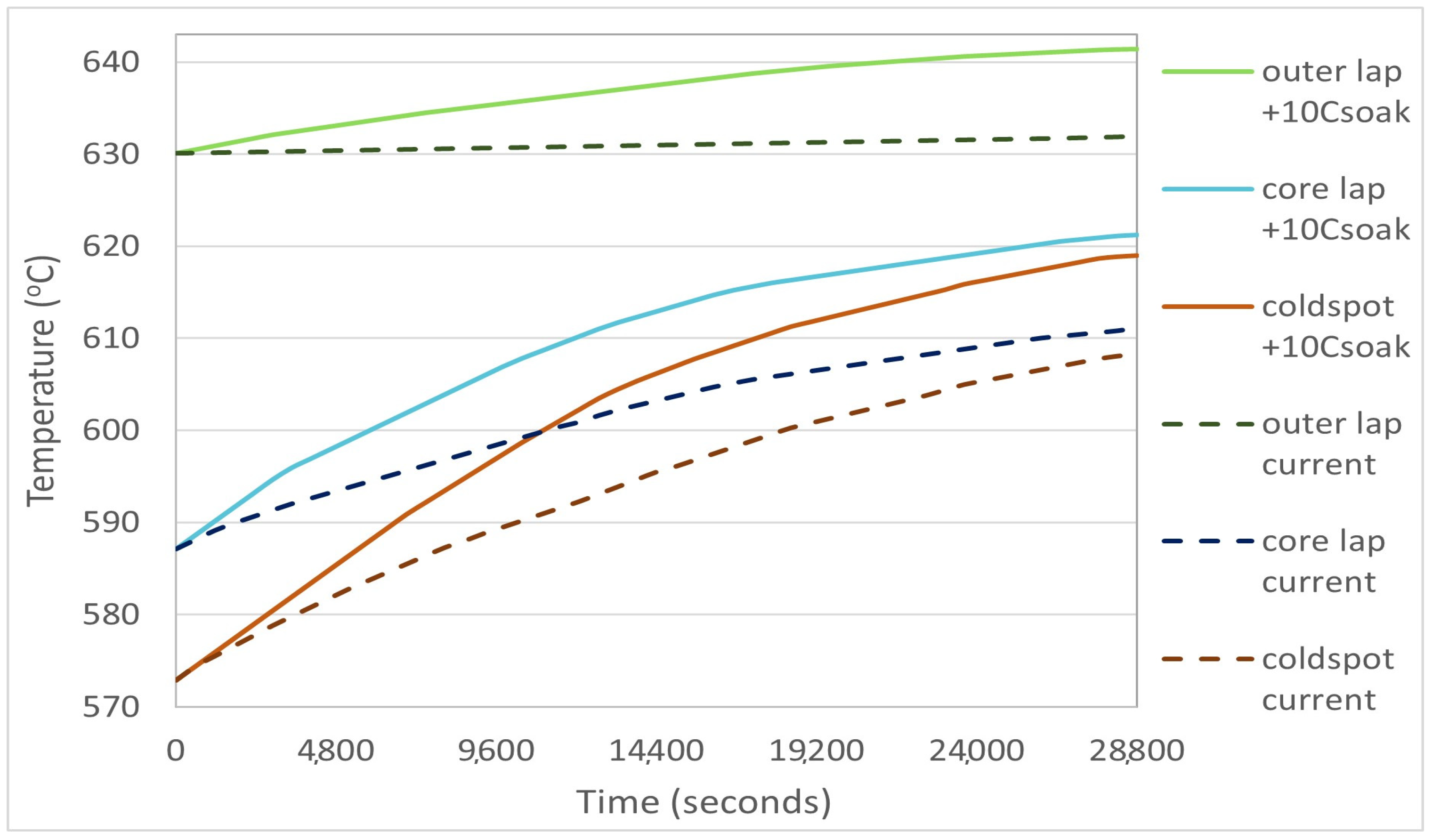
3.1.3. Furnace Improvement Scenario 1: Increased Soaking Temperature
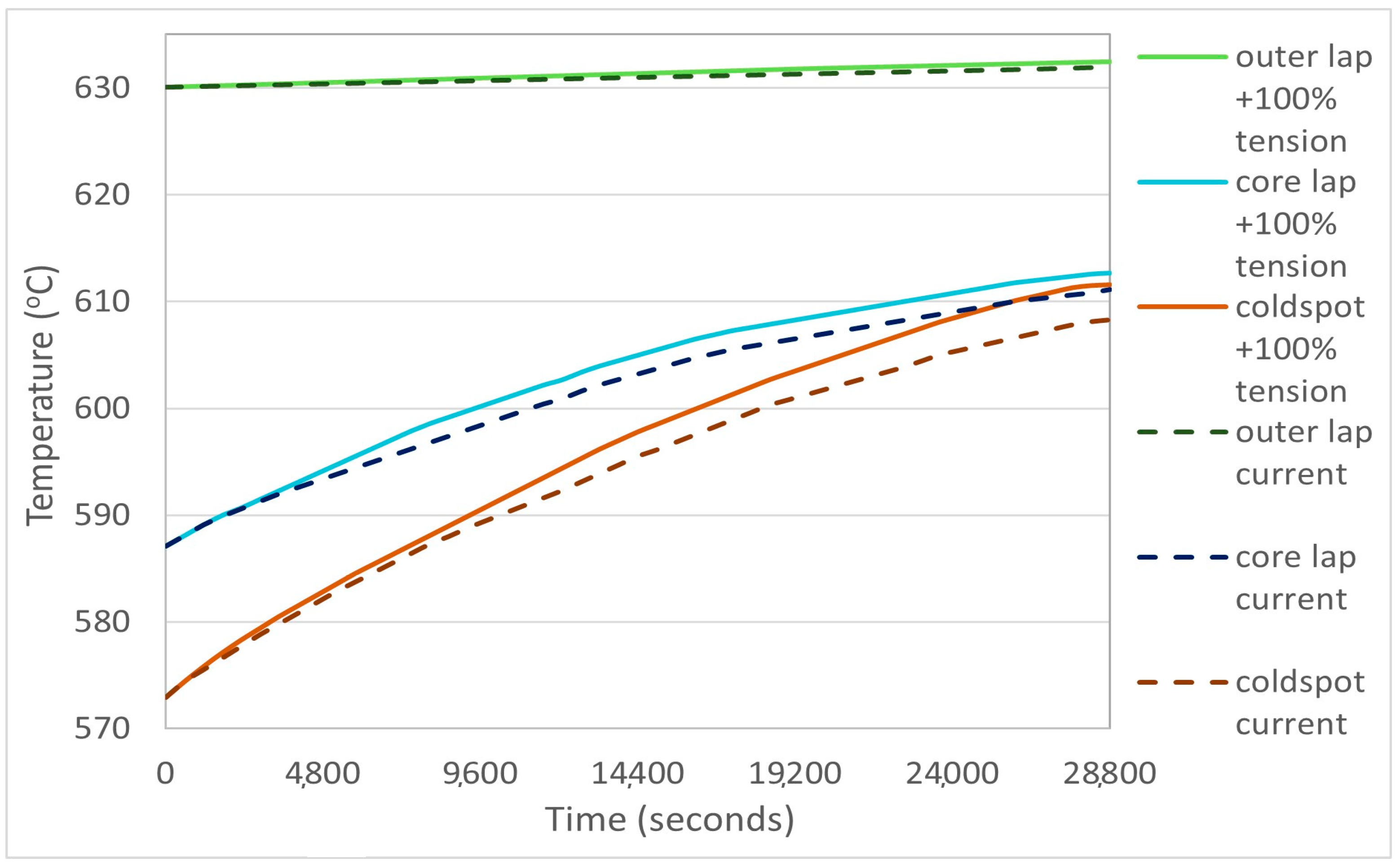
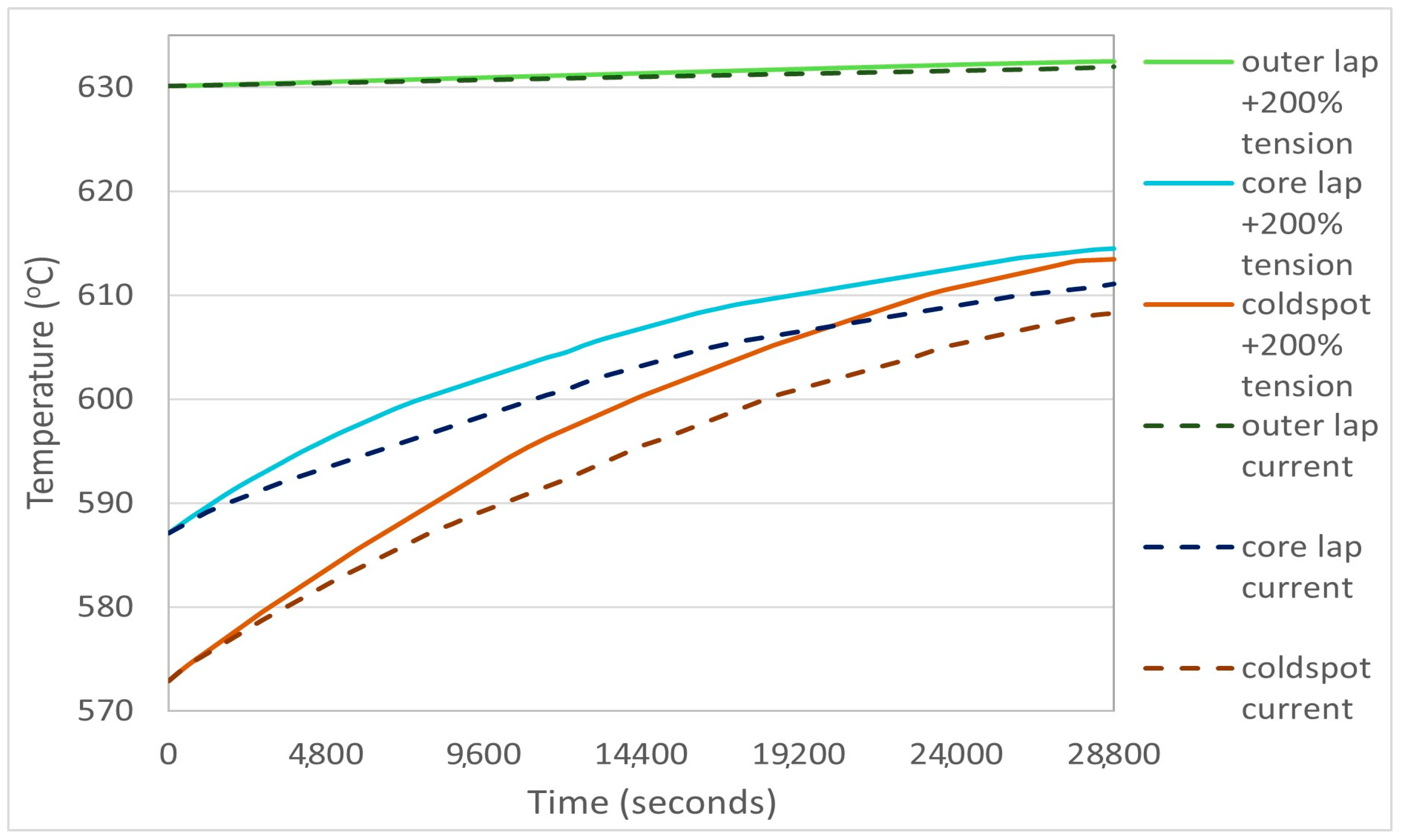
3.1.4. Furnace Improvement Scenario 2: Increased Coiling Tension
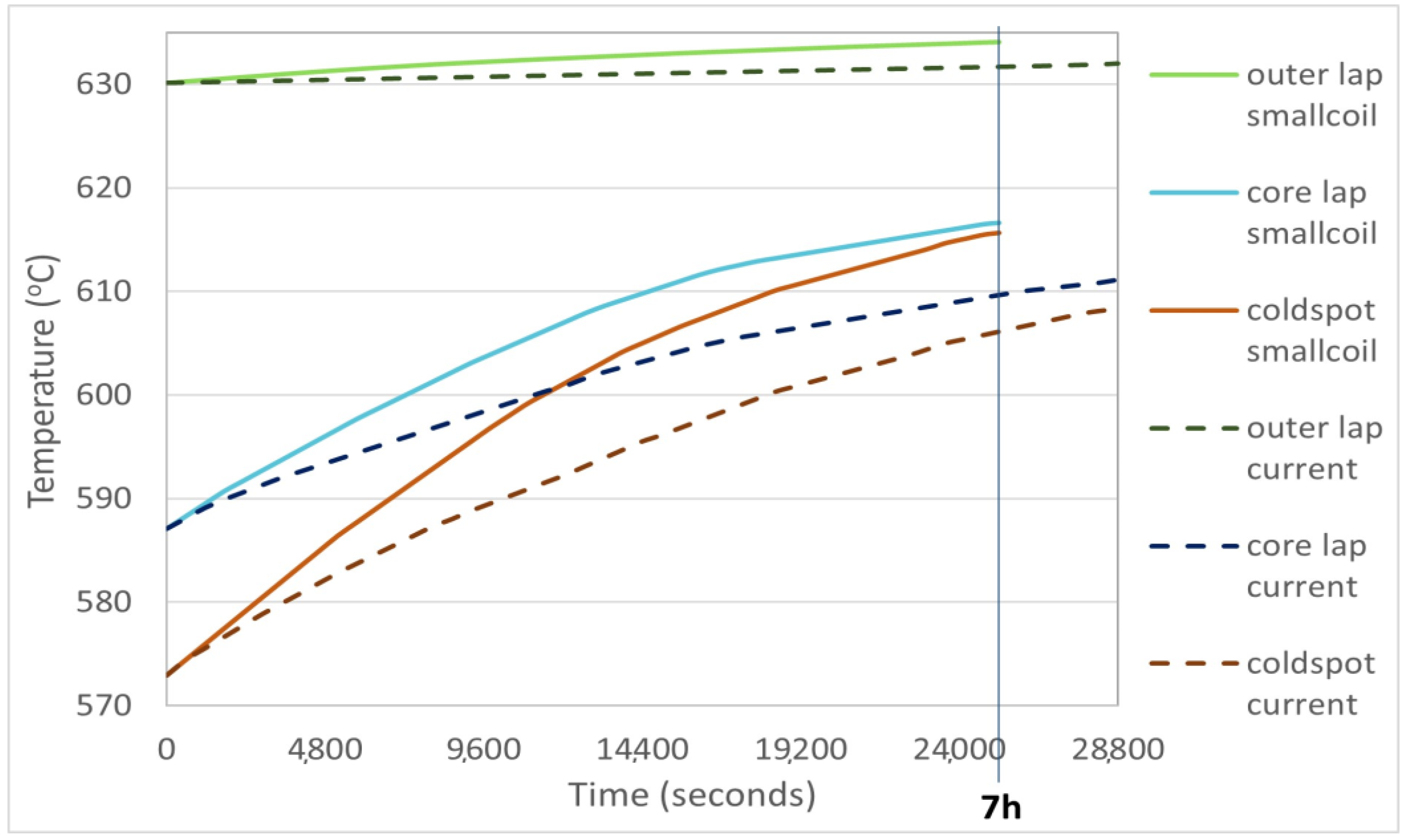
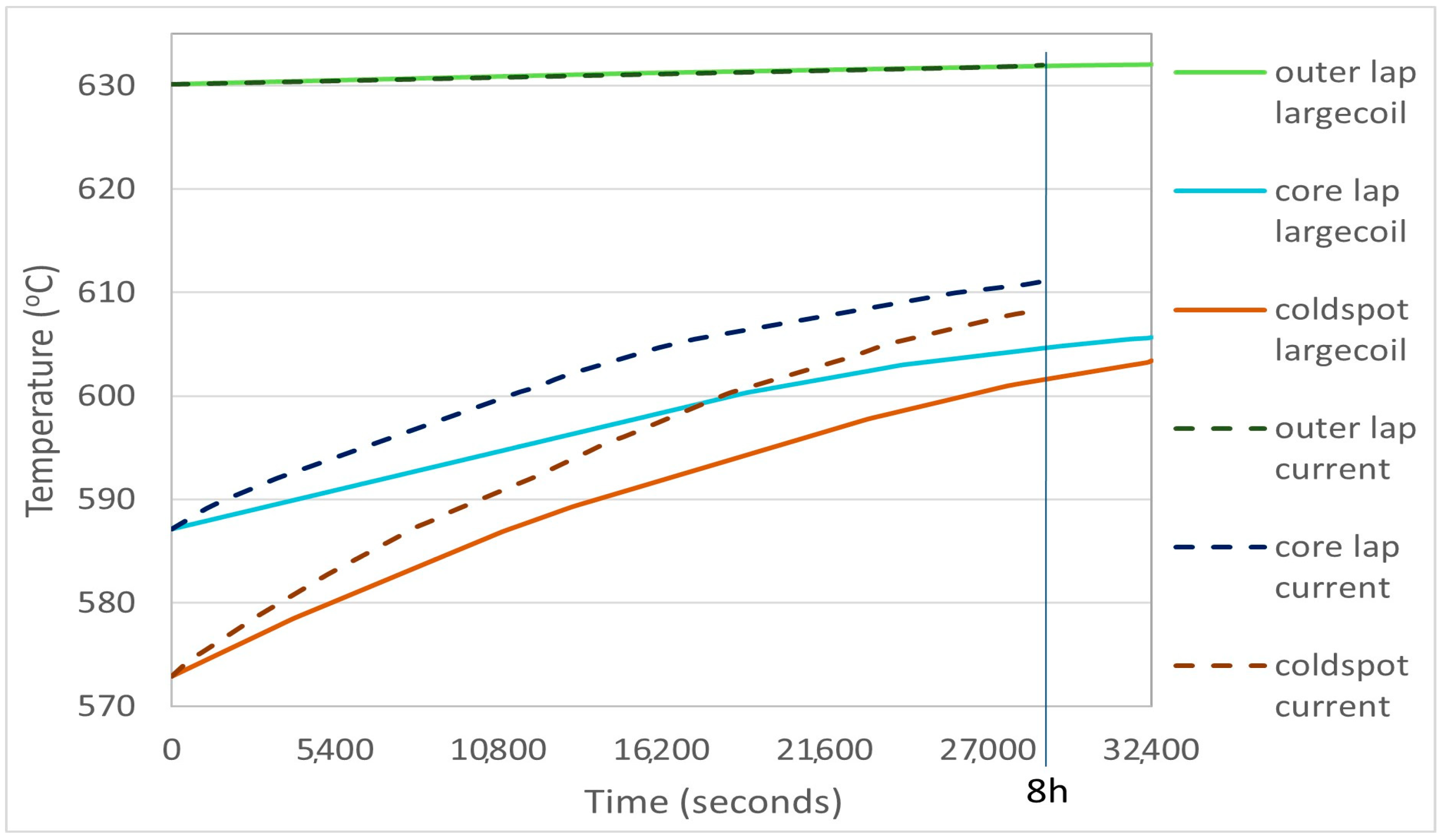
3.1.5. Furnace Improvement Scenario 3: Altered Coil Size
3.1.6. Furnace Improvement Scenario 4: Extended Soaking Time
3.1.7. Comparison of Temperature Profiles and Temperature Uniformity
3.2. Technoeconomic Analysis of Promising Improvement Scenarios
4. Discussion
5. Conclusions
- The 10 °C increased soaking temperature case resulted in the highest inner coil temperatures, possibly ensuring successful steel recrystallisation across the coil;
- The 4 h extended soaking time case showed the highest temperature uniformity, closely followed by small coil batch and the 200% increased tension cases;
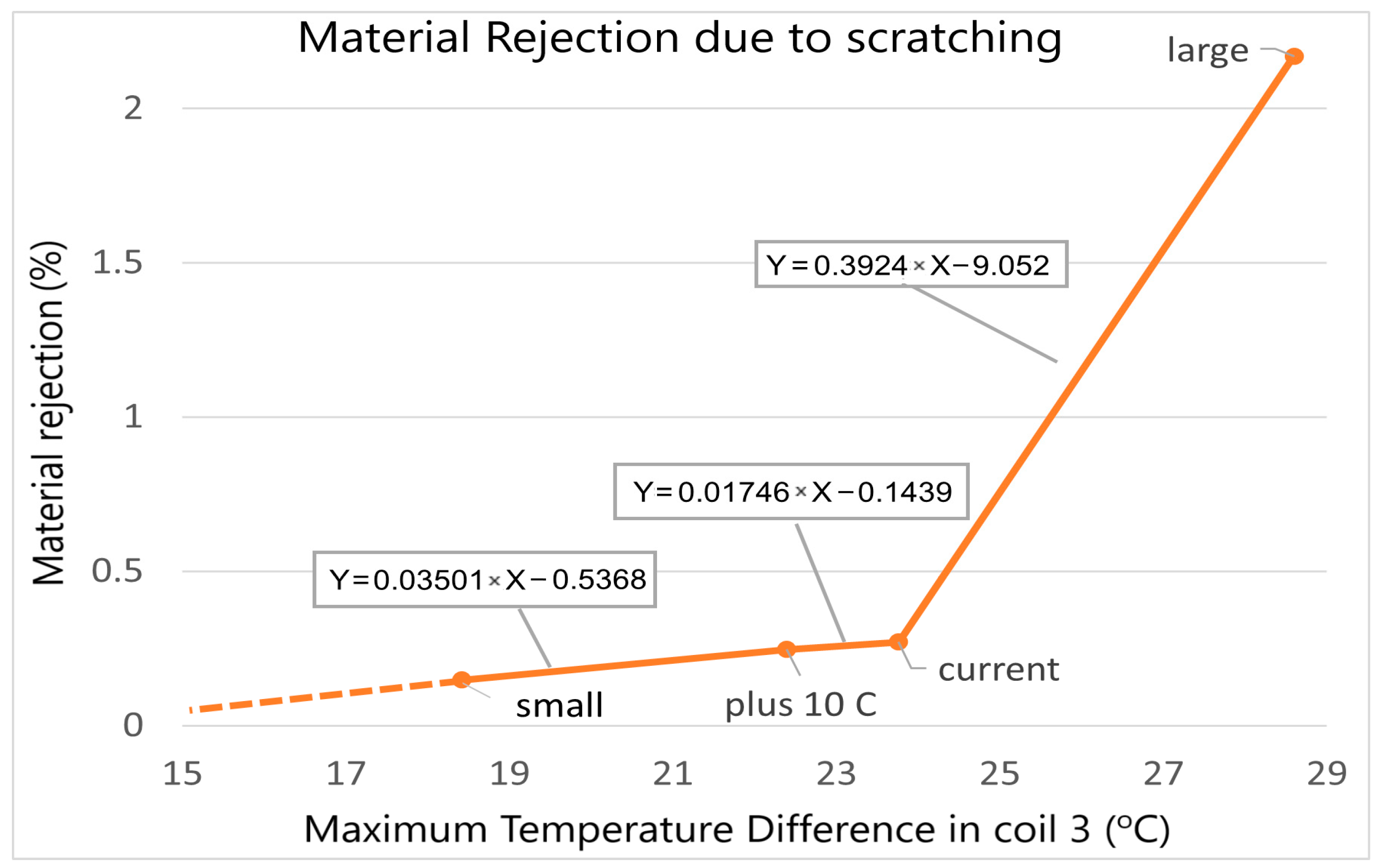
- The lowest material rejection was shown by the small coil batch case, followed by the 4 h extended soaking time and 200% increased coiling tension cases, whereas the highest rejection was presented by the large coil batch case;
- The highest total net cost for one heating cycle was exhibited by the small coil case. The lowest total net cost was shown by the large coil batch case, followed by the 200% increased coiling tension case;
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| CFD | Computational Fluid Dynamics |
| NG | Natural Gas |
| Nitrogen | |
| Hydrogen | |
| Variables | |
| Ρ | Pressure (Pa) |
| u, v, w | Three-dimensional fluid velocities (m/s) |
| ρ (Du,v,w/Dt) | Rates of change of momentum in 3 dimensions (N) |
| ρf | Body forces on the fluid (N) |
| μ | ) |
| τ | Shear stress (Pa) |
| Rate of change of energy (W) | |
| T | Temperature (°C or K) |
| k | Thermal conductivity (W/mK) |
| Net rate of heat conduction through boundaries in 3 dimensions (W) | |
| Other sources of energy (W) | |
| Total thickness (m) | |
| Total equivalent coil radial thermal conductivity (W/mK) | |
| Thickness of steel strip (m) | |
| Thickness of silicate layer deposit (m) | |
| Thickness of air gap between coil laps (m) | |
| Thermal conductivity of steel (W/mK) | |
| Thermal conductivity of silicates (W/mK) | |
| Thermal conductivity of protective atmosphere gas (W/mK) | |
| Percentage contact between coil laps (%) | |
| Maximum temperature difference inside coil (°C) | |
| Maximum and minimum temperatures inside coil (°C) | |
| C | Cost (£) |
| Sum of heating and soaking segment time (hours) | |
| W | Furnace equipment capacity (kW) |
| Unit cost of electricity (£/kWh) and gas (£/m3) | |
| Unit cost of nitrogen and hydrogen gases (£/m3) | |
| N | Number of burners in Batch annealing furnace |
| η | Burner efficiency (%) |
| q | Specific calorific value of natural gas (kWh/m3) |
| Volumetric flow (m3/h) | |
| Time added to annealing cycle (hours) | |
| L | Coil batch load (tonnes) |
| Unit price of tin coated steel (£/tonne) |
References
- Morgan, E. Tinplate Manufacture. In Tinplate & Modern Canmaking Technology, 1st ed.; Pergamon Press: Exeter, UK, 1985; pp. 5–73+200–222. [Google Scholar]
- JFE Steel Corporation. Tin Mill Products; JFE Steel Corporation: Tokyo, Japan, 2020; Available online: https://www.jfe-steel.co.jp/en/products/sheets/catalog/b1e-006.pdf (accessed on 8 June 2020).
- ITRA Ltd. Guide to Tinplate, 2nd ed.; ITRA Ltd.: Uxbridge, UK, 2000. [Google Scholar]
- SMS Group GmbH. Efficient Production of Tinplate Packaging Material out of Cold-Strip; SMS Group GmbH: Hilden, Germany, 2015. [Google Scholar]
- ASM International. Subject Guide: Heat Treating; ASM International: Novelty, OH, USA, 2015; Available online: www.asminternational.org (accessed on 23 March 2020).
- Llewellyn, D.T.; Hudd, R.C. Low-carbon strip steels. In Steels, 3rd ed.; Llewellyn, D.T., Hudd, R.C., Eds.; Butterworth-Heinemann: Swansea, UK, 1998; pp. 1–136. [Google Scholar]
- Alaneme, K.K.; Okotete, E.A. Recrystallization mechanisms and microstructure development in emerging metallic materials: A review. J. Sci. Adv. Mater. Devices 2019, 4, 19–33. [Google Scholar] [CrossRef]
- Trostre Works Tata Steel Packagigng. Personal Communication. Llanelli, 2020. [Google Scholar]
- Eurotherm Limited. Single and Multi-Stack batch Annealing; Eurotherm Limited: Worthing, UK, 2006; Available online: https://www.eurotherm.com/download/ht-single-multi-stack-batch-annealing-app-note-hr084054u003/ (accessed on 20 March 2020).
- Sahay, S.S.; Mehta, R.; Raghavan, S.; Roshan, R.; Dey, S.J. Process analytics, modeling, and optimization of an industrial batch annealing operation. Mater. Manuf. Process. 2009, 24, 1459–1466. [Google Scholar] [CrossRef]
- Clifford, J.A. The Partial Annealing of Low-Carbon Steel Strip. Master’s Thesis, McGill University, Montreal, QC, Canada, 1969. [Google Scholar]
- Bertrandie, J.J.; Bordignon, L.; Putz, P.D.; Volger, G. Hot and Cold Rolling Processes—Sticking and Scratching Problems after Batch Annealing, Including Coil Compression Stress Effects; European Commission: Luxembourg, 2006. [Google Scholar]
- Saboonchi, A.; Hassanpour, S. Simulation of cold rolled steel coil heating during batch annealing process. Heat Transf. Eng. 2008, 29, 893–901. [Google Scholar] [CrossRef]
- Mazur, V.L.; Timoshenko, V.I.; Prikhodko, I.Y. Efficient Cold Rolling and Coiling Modes. Steel Transl. 2019, 49, 548–558. [Google Scholar] [CrossRef]
- Buckley, A.; Moses, A.J.; Trollope, L. Study and redesign of high temperature batch annealing furnace for production of grain oriented electrical steel. Ironmak. Steelmak. 1999, 26, 477–482. [Google Scholar] [CrossRef]
- Sahay, S.S.; Kumar, B.V.H.; Krishnan, S.J. Microstructure evolution during batch annealing. J. Mater. Eng. Perform. 2003, 12, 701–707. [Google Scholar] [CrossRef]
- Zuo, Y.; Wu, W.F.; Zhang, X.X.; Lin, L.; Xiang, S.H.; Liu, T.S.; Niu, L.Y.; Huang, X.L. A study of heat transfer in high-performance hydrogen bell-type annealing furnaces. Heat Transf. Asian Res. 2001, 30, 615–623. [Google Scholar] [CrossRef]
- Schoina, L.; Jones, R.; Burgess, S.; Vaughan, D.; Andrews, L.; Foley, A. Impact of annealing cycle parameters on Batch Annealing process performance in tinplate manufacturing. In Proceedings of the 13th European Conference on Industrial Furnace and Boilers, Algarve, Portugal, 19–22 April 2022; pp. 1–12. Available online: https://orca.cardiff.ac.uk/id/eprint/150121/ (accessed on 1 August 2022).
- Roache, P.J. Computational Fluid Dynamics, 1st ed.; Hermosa Publishers: Albuquerque, NM, USA, 1972. [Google Scholar]
- Anderson, J.D. Governing equations of fluid dynamics. In Computational Fluid Dynamics, 1st ed.; Wendt, J.F., Ed.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 15–51. [Google Scholar]
- Childs, P.R.N. Rotating Flow, 1st ed.; Elsevier: Oxford, UK, 2011. [Google Scholar]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method, 2nd ed.; Pearson Education Limited: Harlow, UK, 2007. [Google Scholar]
- Ferziger, J.H.; Peric, M. Computational Methods for Fluid Dynamics, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Hadawi Fatla Oula, M. Development of Convection in High-Temperature Coil Annealing Furnaces Using Rotating Cylinders Technique. Ph.D. Thesis, Cardiff University, Cardiff, UK, 2019. [Google Scholar]
- Hân, T. ANSYS Fluent Theory Guide 15.0; ANSYS Inc.: Canonsburg, PA, USA, 2013. [Google Scholar]
- ANSYS Inc. Temporal Discretization. afs.enea.it. 2023. Available online: https://www.afs.enea.it/project/neptunius/docs/fluent/html/th/node367.htm (accessed on 28 February 2023).
- ANSYS Inc. ANSYS Fluent Getting Started Lecture 10: Transient Flow Modeling; ANSYS Inc.: Canonsburg, PA, USA, 2019. [Google Scholar]
- Ideal Simulations. Courant Number. Ideal Simulations.com. 2020. Available online: https://www.idealsimulations.com/resources/courant-number-cfd/#:~:text=The%20CFL%20condition,-Let%27s%20discuss%20the&text=Roughly%20speaking%2C%20in%20explicit%20schemes,the%20solution%20of%20an%20ODE (accessed on 17 February 2023).
- ANSYS Inc. ANSYS Fluent Getting Started Lecture 9: Turbulence; ANSYS Inc.: Canonsburg, PA, USA, 2019. [Google Scholar]
- ANSYS Inc. ANSYS Fluent Heat Trnasfer Modeling Lecture 02: Conduction Heat Transfer; ANSYS Inc.: Canonsburg, PA, USA, 2017. [Google Scholar]
- Barry, S.I.; Sweatman, W.L. Modelling heat transfer in steel coils. ANZIAM J. 2008, 50, 668–681. [Google Scholar] [CrossRef][Green Version]
- Karlberg, M. Thermo-Mechanical Modelling of Hot Strip Coil Cooling Process, 1st ed.; Lulea University of Technology: Lulea, Sweden, 2014. [Google Scholar]
- Yoshioka, N. Elastic behavior of contacting surfaces under normal loads: A computer simulation using three-dimensional surface topographies. J. Geophys. Res. 1994, 99, 15549–15560. [Google Scholar] [CrossRef]
- Fluent Inc. Fluent 6.1 User’s Guide. 2003; Fluent Inc.: Lebanon NH, USA; Available online: https://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=&ved=2ahUKEwjK-ZfEl7yBAxXfQEEAHWgwDcIQFnoECBgQAQ&url=https%3A%2F%2Fwww.researchgate.net%2Ffile.PostFileLoader.html%3Fid%3D570bb021cbd5c2adcc30fdfb%26assetKey%3DAS%3A349689057693697%401460383776597&usg=AOvVaw3MmjRwYgddamPvQfnNQhV3&opi=89978449 (accessed on 13 September 2021).
- Ahmed, M.; Radwan, A.; Serageldin, A.; Memon, S.; Katsura, T.; Nagano, K. Thermal analysis of a new sliding smart window integrated with vacuum insulation, photovoltaic, and phase change material. Sustainability 2002, 12, 7846. [Google Scholar] [CrossRef]
- Ajotikar, N.A. Synthesis of Computations and Experiments for Obtaining Pulsatile Gas Flow Rates from Dynamic Pressure Difference Measurements across an Orifice-plate Meter. Michigan. 2011. Available online: https://digitalcommons.mtu.edu/cgi/viewcontent.cgi?article=1563&context=etds (accessed on 1 September 2022).
- Leap Australia. Tips and Tricks: Convergence and Mesh Independece Study. Leading Engineering Application Providers. 2021. Available online: https://www.computationalfluiddynamics.com.au/convergence-and-mesh-independent-study/ (accessed on 8 November 2021).
- Supercomputing Wales Portal. Guidance for Completing the Project Application Form on MySCW. Supercomputing Wales Portal: Cardiff, UK, 2021. Available online: https://portal.supercomputing.wales/index.php/getting-access/guidance-for-completing-the-project-application-form-on-myscw/ (accessed on 8 November 2021).
- Herring, D.H. Saving Money by Maximizing Furnace Uptime Productivity. Industral Heating, Elmhurst, p. 1, June 2013. Available online: https://www.industrialheating.com/articles/90856-saving-money-by-maximizing-furnace-uptime-productivity (accessed on 4 May 2020).
- Office of Energy Efficiency & Renewable Energy. Estimating Appliance and Home Electronic Energy Use. US Department of Energy. Available online: https://www.energy.gov/energysaver/estimating-appliance-and-home-electronic-energy-use (accessed on 10 September 2022).
- U.S. Department of Energy. A BestPractices Steam Technical Brief—How To Calculate The True Cost of Steam; U.S. Department of Energy: Washington, DC, USA, 2003.
- Borutsky, V. How Much Gas a Gas Stove Consumes: Gas Flow Calculation Procedure. 2019. Available online: https://engineer.decorexpro.com/en/gaz/standart/skolko-gaza-potreblyaet-gazovaya-plita.html (accessed on 20 September 2022).
- Fives North American Combustion UK Ltd. FRG Series Gas Burners; Fives North American Combustion UK Ltd.: Wolverhampton, UK, 2009; pp. 1–4. Available online: https://manualzz.com/doc/37339056/frg-series-gas-burners-bulletin-1.1 (accessed on 24 August 2023).
- Mickey, S.R.; Efficient Gas Heating of Industrial Furnaces. Thermal Processing, Pelham, p. 1, January 2017. Available online: https://thermalprocessing.com/efficient-gas-heating-of-industrial-furnaces/ (accessed on 12 November 2022).
- Rohsenow, W.M.; Hartnett, J.P.; Cho, Y.I. (Eds.) Handbook of Heat Transfer, 3rd ed.; McGraw-Hill: New York, NY, USA, 1998. [Google Scholar]
- Can Tech International. Trostre Tinplate Works Celebrates Milestone Anniversary; Bell Publishing Ltd.: Gravesend, UK, 2022; Available online: https://www.cantechonline.com/news/28844/trostre-tinplate-works-celebrates-milestone-anniversary/ (accessed on 20 September 2022).
- Javed, R.; Payback Method. Accounting for Management. 2022. Available online: https://www.accountingformanagement.org/payback-method/ (accessed on 20 September 2022).
- Qilin, L.; Kai, D.; Weining, L.; Linglei, K.; Jiajia, C.; Daping, S.; Xichao, W. Temperature uniformity of profiled grinding wheel under high-frequency induction brazing. Int. J. Adv. Manuf. Technol. 2021, 117, 1091–1099. [Google Scholar] [CrossRef]
- Department for Business Energy and Industrial Strategy. Quarterly Energy Prices June 2022. London. 2022. Available online: https://assets.publishing.service.gov.uk/government/uploads/system/uploads/attachment_data/file/1086569/quarterly_energy_prices_uk_june_2022.pdf (accessed on 30 September 2022).
- BOC Ltd. Hydrogen Gas; BOC Ltd.: Guildford, UK, 2022; Available online: https://www.boconline.co.uk/shop/en/uk/gas-a-z/hydrogen (accessed on 1 September 2022).
- BOC Ltd. Nitrogen Gas Cylinders; BOC Ltd.: Guildford, UK, 2022; Available online: https://www.boconline.co.uk/shop/en/uk/gas-a-z/nitrogen (accessed on 1 September 2022).
- U.S. Environmental Protection Agency. Natural Gas Combustion. U.S. Environmental Protection Agency: Durham, NC, USA, 2020. Available online: https://www.epa.gov/sites/default/files/2020-09/documents/1.4_natural_gas_combustion.pdf (accessed on 17 February 2022).
- Testo Ltd. Calculation Formulae, Fuels and Testo Flue Gas Analyzers; Testo Ltd.: Alton, UK, 2020; Available online: https://static-int.testo.com/media/de/3b/f57704ebe71e/testo-Calculation-formulae-fuels-and-parameters-testo-flue-gas-analyzers.pdf (accessed on 11 February 2023).
- Arkhazlooa, N.B.; Bouissaa, Y.; Bazdidi-Tehranib, F.; Jadidib, M.; Morinc, J.-B.; Jahazia, M. Experimental and unsteady CFD analyses of the heating process of large size forgings in a gas-fired furnace. Case Stud. Therm. Eng. 2019, 14, 1–12. [Google Scholar] [CrossRef]
- Filipponi, M.; Rossi, F.; Presciutti, A.; De Ciantis, S.; Castellani, B.; Carpinelli, A. Thermal analysis of an industrial furnace. Energies 2016, 9, 833. [Google Scholar] [CrossRef]
- Transmetra GmbH. Table of Emissivity of Various Surfaces; Transmetra GmbH: Flurlingen, Switzerland, 2020; Available online: https://www.transmetra.ch/images/transmetra_pdf/publikationen_literatur/pyrometrie-thermografie/emissivity_table.pdf (accessed on 17 January 2022).


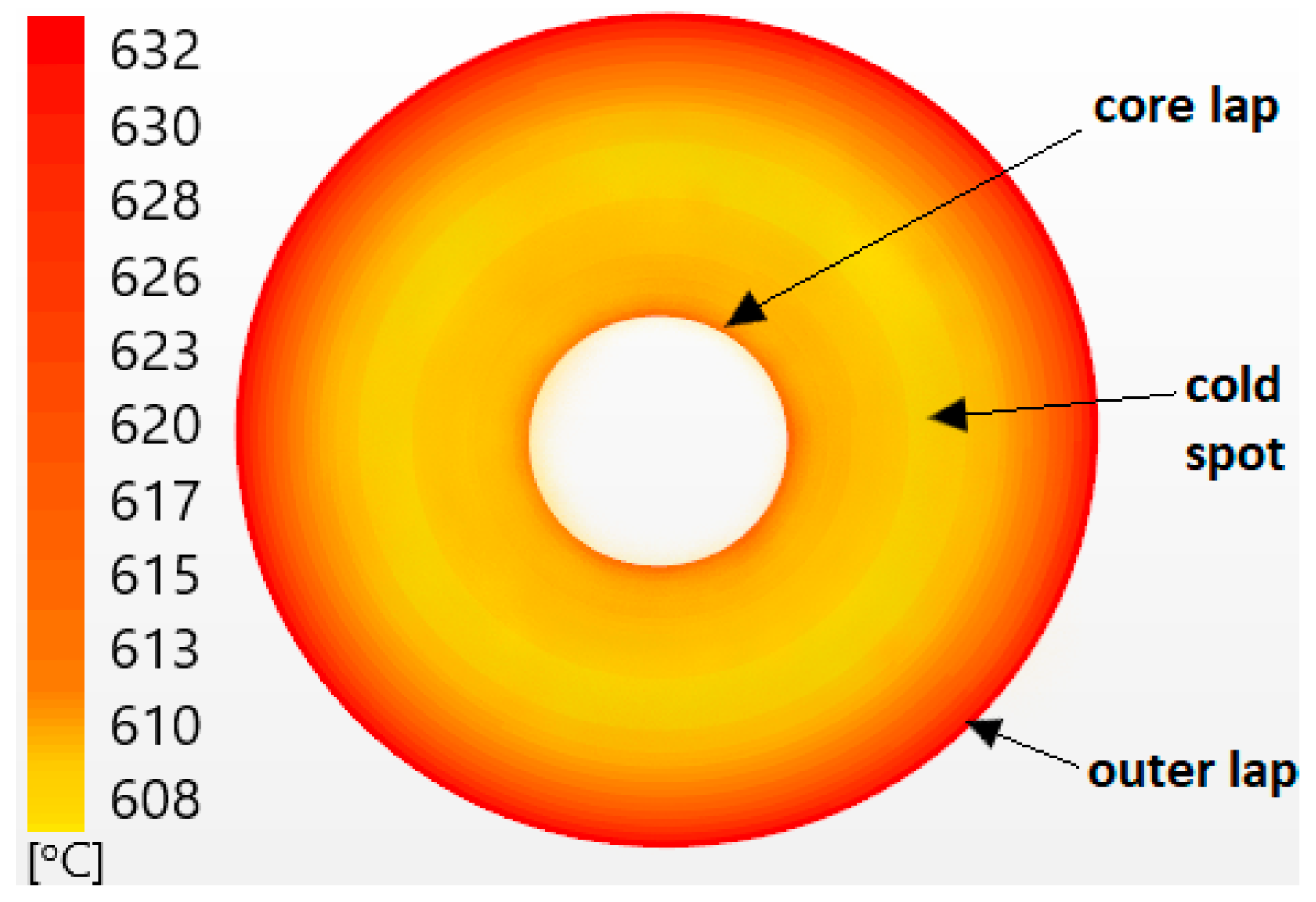
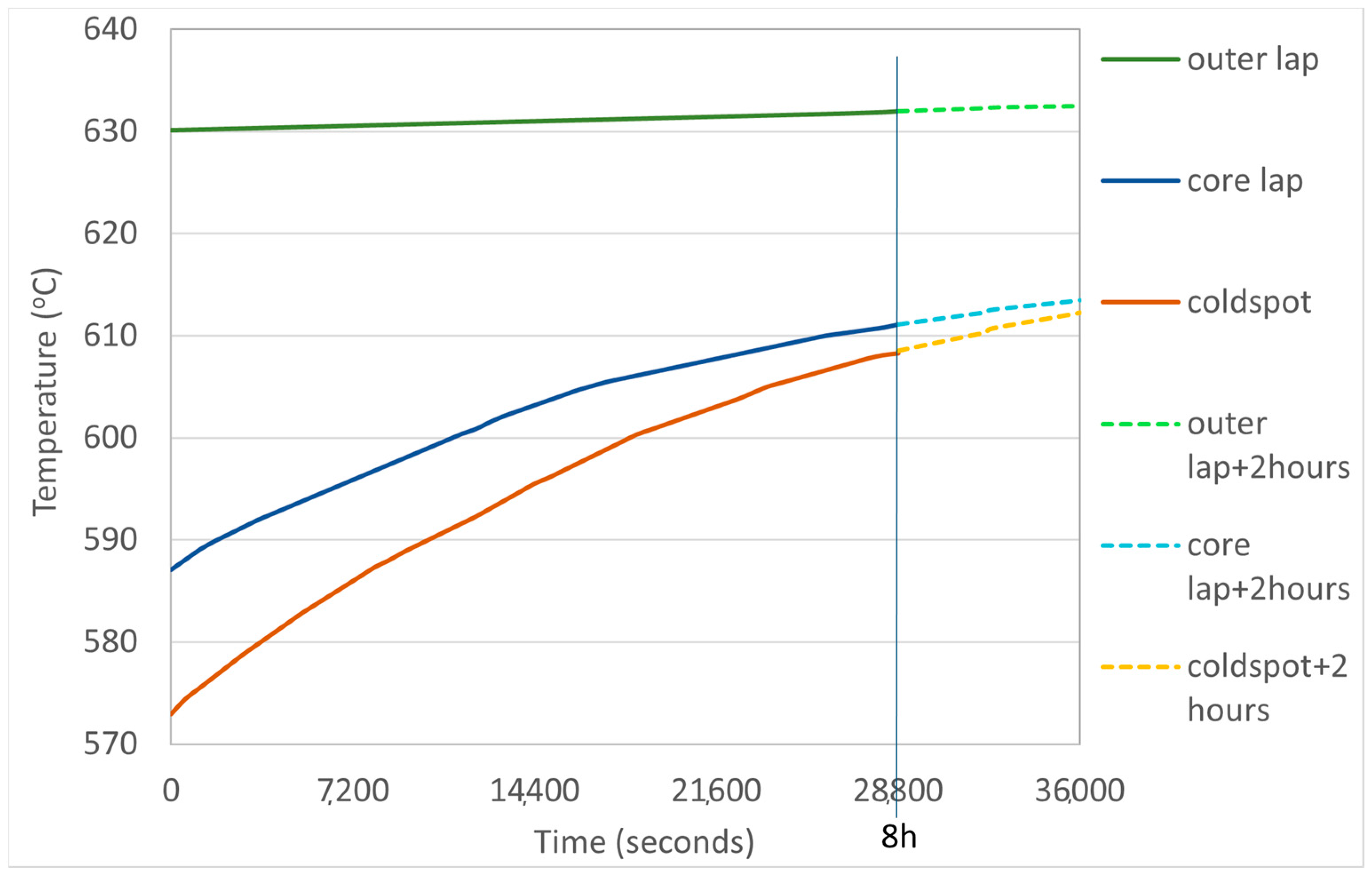
| Temperatures (°C) | Thermocouple Data | CFD Model |
|---|---|---|
| Coil 3—outer lap | 631.91 | 632 |
| Coil 3—core lap | 610.72 | 611.1 |
| Coil 3—cold spot | 608.23 | av. 608.27 |
| Mesh Size | Number of Elements | Outlet Temperature (°C) | Coil 3 Outer Lap Temperature (°C) | Coil 3 Core Lap Temperature (°C) | Running Time (hours) |
|---|---|---|---|---|---|
| Coarse | 6.36 million | 547.9 | 628.68 | 610.651 | 57 |
| Medium | 8.74 million | 566.89 | 632 | 611.1 | 84.5 |
| Fine | 12.71 million | 566.97 | 632.02 | 611.09 | 146.5 |
| Mesh Size | Number of Elements | Coil 3 Outer Lap Temperature (°C) | Coil 3 Core Lap Temperature (°C) | Coil 3 Average Cold Spot Temperature (°C) | Running Time (hours) |
|---|---|---|---|---|---|
| Coarse | 2.02 million | 628.69 | 610.65 | 597.98 | 15.5 |
| Medium | 3.46 million | 632.002 | 611.101 | 608.27 | 24.5 |
| Fine | 6.51 million | 632.01 | 611.093 | 608.28 | 48.4 |
| Time Step Size (s) | Number of Steps | Outlet Temperature (°C) | Coil 3 Outer Lap Temperature (°C) | Coil 3 Core Lap Temperature (°C) |
|---|---|---|---|---|
| 0.001 | 28.8 mil | 565.91 | 631.86 | 610.95 |
| 0.0006 | 48 mil | 566.89 | 632 | 611.1 |
| 0.0003 | 96 mil | 566.901 | 632.002 | 611.102 |
| Time Step Size (s) | Number of Steps | Coil 3 Outer Lap Temperature (°C) | Coil 3 Core Lap Temperature (°C) | Coil 3 Average Cold Spot Temperature (°C) |
|---|---|---|---|---|
| 18 | 1600 | 631.89 | 610.93 | 608.03 |
| 12 | 2400 | 632.002 | 611.101 | 608.27 |
| 6 | 4800 | 632.004 | 611.105 | 608.272 |
| Enhancement Scenarios | Coil 3 Outer Lap Temperature (°C) | Coil 3T Core Lap Temperature (°C) | Coil 3Average T Cold Spot (°C) | ΔΤ = Max − Min (°C) |
|---|---|---|---|---|
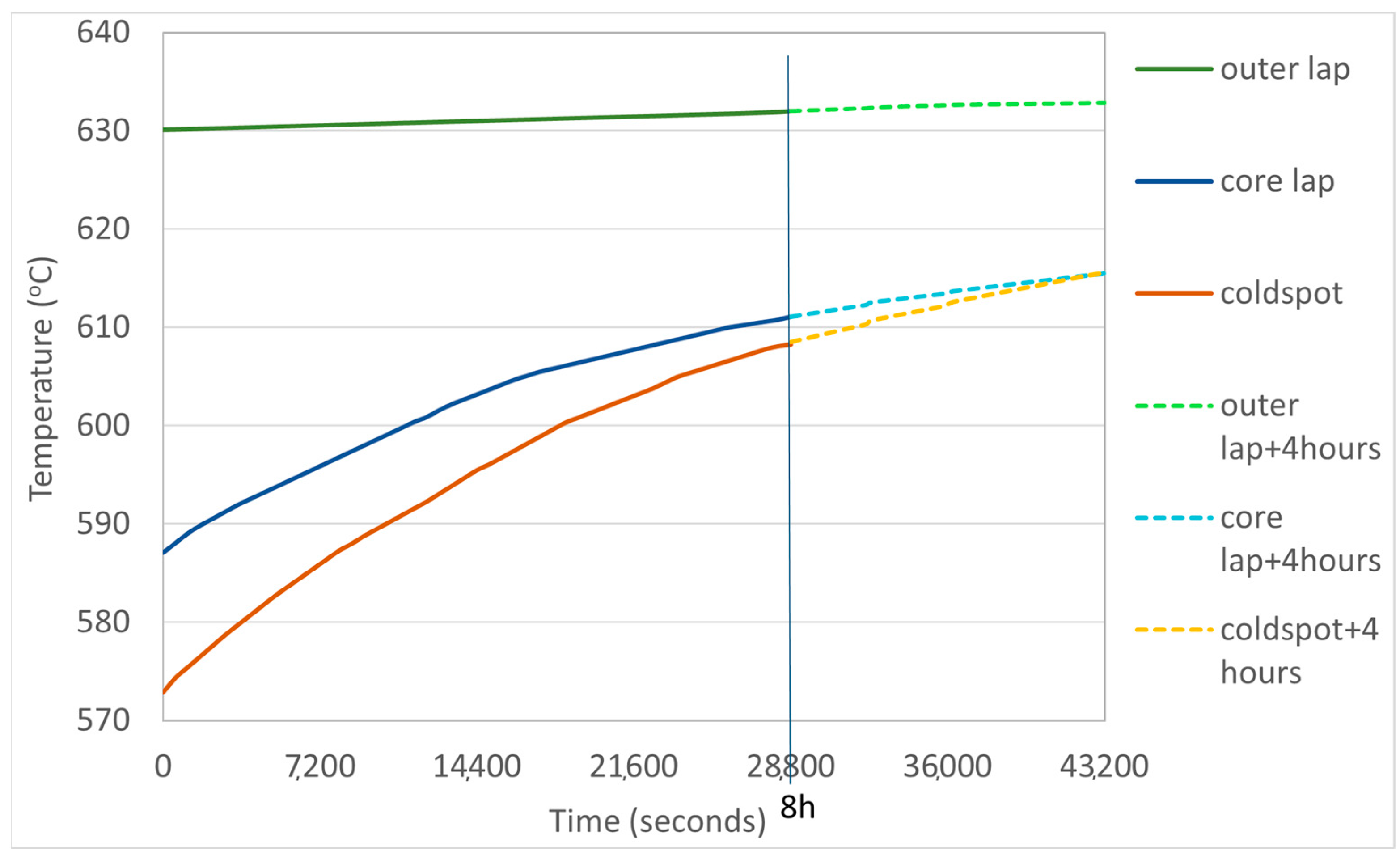
| Current furnace + 4 h | 632.89 | 615.5 | 615.5 | 17.34 |
| Small coil | 634.09 | 616.62 | 615.66 | 18.43 |
| Coiling tension + 200% | 632.5 | 614.5 | 613.48 | 19.02 |
| Current furnace + 2 h | 632.51 | 613.5 | 612.25 | 20.26 |
| Coiling tension + 100% | 632.43 | 612.7 | 611.58 | 20.85 |
| +10 °C soaking T | 641.4 | 621.2 | 619.02 | 22.38 |
| +5 °C soaking T | 636.32 | 615.44 | 613.92 | 22.4 |
| Current furnace | 632 | 611.1 | 608.27 | 23.73 |
| Large coil | 632.05 | 605.65 | 603.43 | 28.62 |
| Cases | Material Rejection Due to Scratching (%) | Total Operational Cost (1 Heating Cycle) (GBP) | Total Furnace Availability Cost (1 Heating Cycle) (GBP) | Material Rejection Cost from 1 Batch (GBP) | Total Cost per Heating Cycle (GBP) |
|---|---|---|---|---|---|
| Current furnace | 0.2709 | 179.25 | - | 118.93 | 298.18 |
| +5 °C soaking T | 0.24737 | 185.03 | 544.36 | 108.60 | 837.99 |
| +10 °C soaking T | 0.24698 | 190.83 | 1088.72 | 108.43 | 1387.98 |
| +100% tension | 0.1774 | 179.25 | - | 77.88 | 257.13 |
| +200% tension | 0.09804 | 179.25 | - | 43.04 | 222.29 |
| Small coils | 0.07 | 173.66 | 4255.65 | 27.41 | 4456.72 |
| Large coils | 2.17 | 184.86 | −2953.01 | 1029.48 | −1738.67 |
| Current furnace + 2 h | 0.15199 | 190.46 | 1088.73 | 66.72 | 1345.91 |
| Current furnace + 4 h | 0.0702 | 201.66 | 2177.45 | 30.82 | 2409.93 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schoina, L.; Jones, R.; Burgess, S.; Vaughan, D.; Andrews, L.; Foley, A.; Valera Medina, A. Numerical and Techno-Economic Analysis of Batch Annealing Performance Improvements in Tinplate Manufacturing. Energies 2023, 16, 7040. https://doi.org/10.3390/en16207040
Schoina L, Jones R, Burgess S, Vaughan D, Andrews L, Foley A, Valera Medina A. Numerical and Techno-Economic Analysis of Batch Annealing Performance Improvements in Tinplate Manufacturing. Energies. 2023; 16(20):7040. https://doi.org/10.3390/en16207040
Chicago/Turabian StyleSchoina, L., R. Jones, S. Burgess, D. Vaughan, L. Andrews, A. Foley, and A. Valera Medina. 2023. "Numerical and Techno-Economic Analysis of Batch Annealing Performance Improvements in Tinplate Manufacturing" Energies 16, no. 20: 7040. https://doi.org/10.3390/en16207040
APA StyleSchoina, L., Jones, R., Burgess, S., Vaughan, D., Andrews, L., Foley, A., & Valera Medina, A. (2023). Numerical and Techno-Economic Analysis of Batch Annealing Performance Improvements in Tinplate Manufacturing. Energies, 16(20), 7040. https://doi.org/10.3390/en16207040








