Voltage Stability and Power Sharing Control of Distributed Generation Units in DC Microgrids
Abstract
:1. Introduction
| Control Methods | Hierarchy of Control for Voltage Regulation | Voltage Regulation | Communication | Parameter Estimation Required | Control Complexity |
|---|---|---|---|---|---|
| Decentralized control [9] | Secondary control | Very good | Low-bandwidth communication | Yes | Medium |
| Improved droop control [11] | Primary | Good | Low-bandwidth communication | No | Medium |
| Feed-forward control [25] | Primary control | Precise | No | No | Low |
| Virtual resistance control [26] | Secondary control | Very good | Low-bandwidth communication | Yes | Medium |
| Control Methods | Hierarchy of Control for Voltage Regulation | Power Sharing | Communication | Parameter Estimation Required | Control Complexity |
|---|---|---|---|---|---|
| Droop control [12] | Secondary | Good | Yes | No | Medium |
| Improved droop control [13] | Primary | Good | Yes | No | Low |
| Virtual negative line resistance [27] | Secondary control | Very good | Yes | No | Medium |
| Virtual resistance [28] | Primary | Good | Yes | Yes | Low |
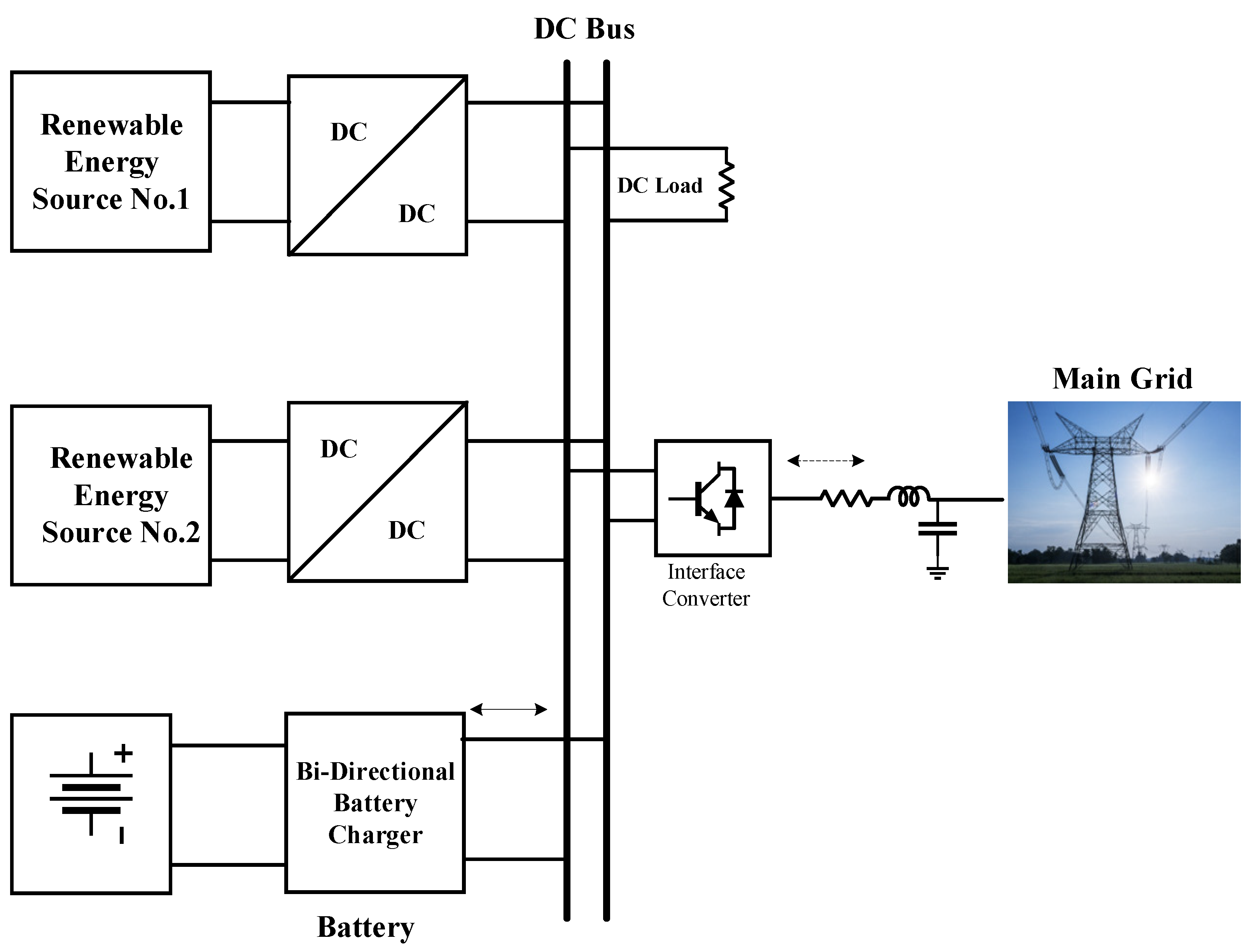
2. Mathematical Model
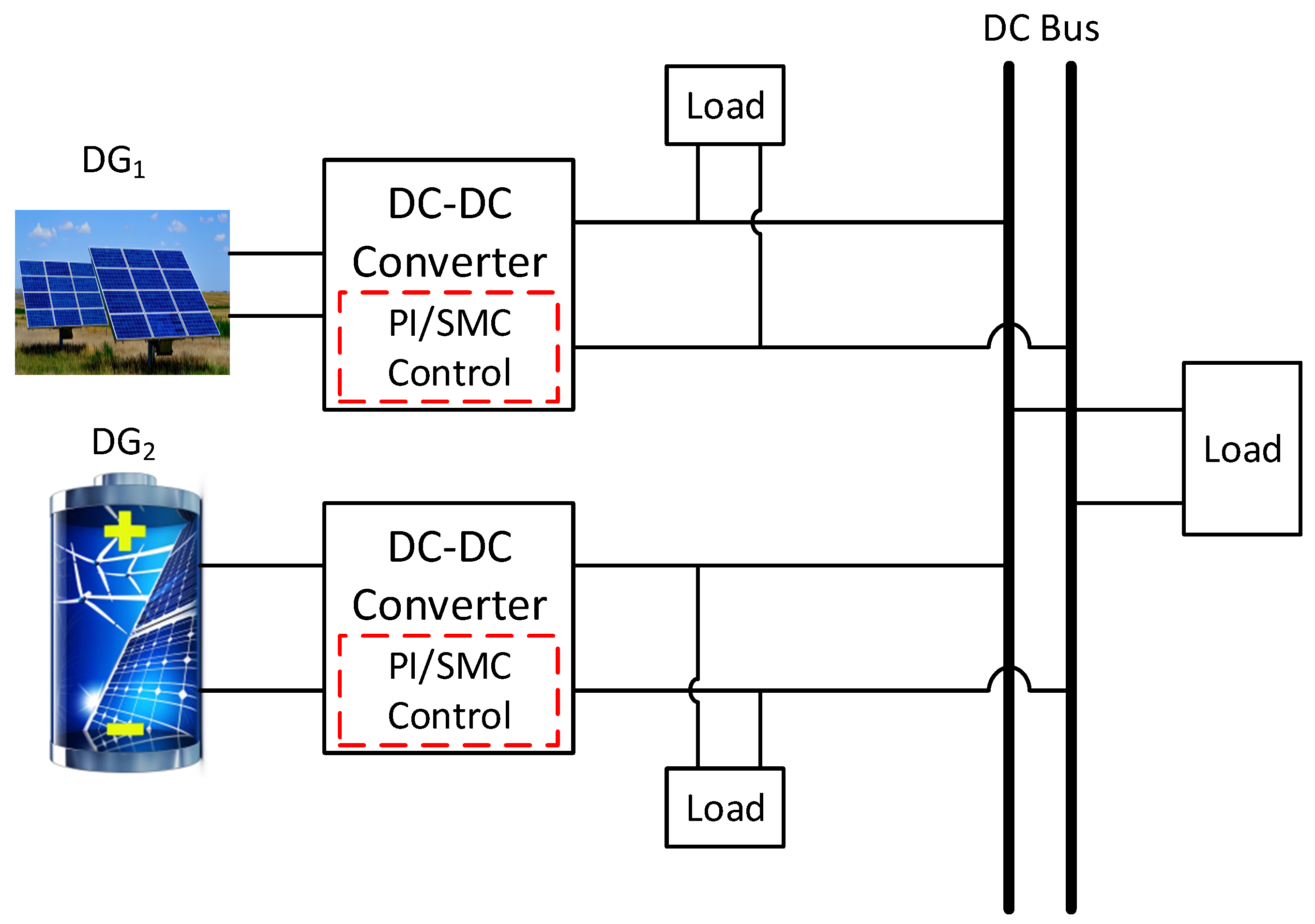
2.1. Control of Distributed Generation Units
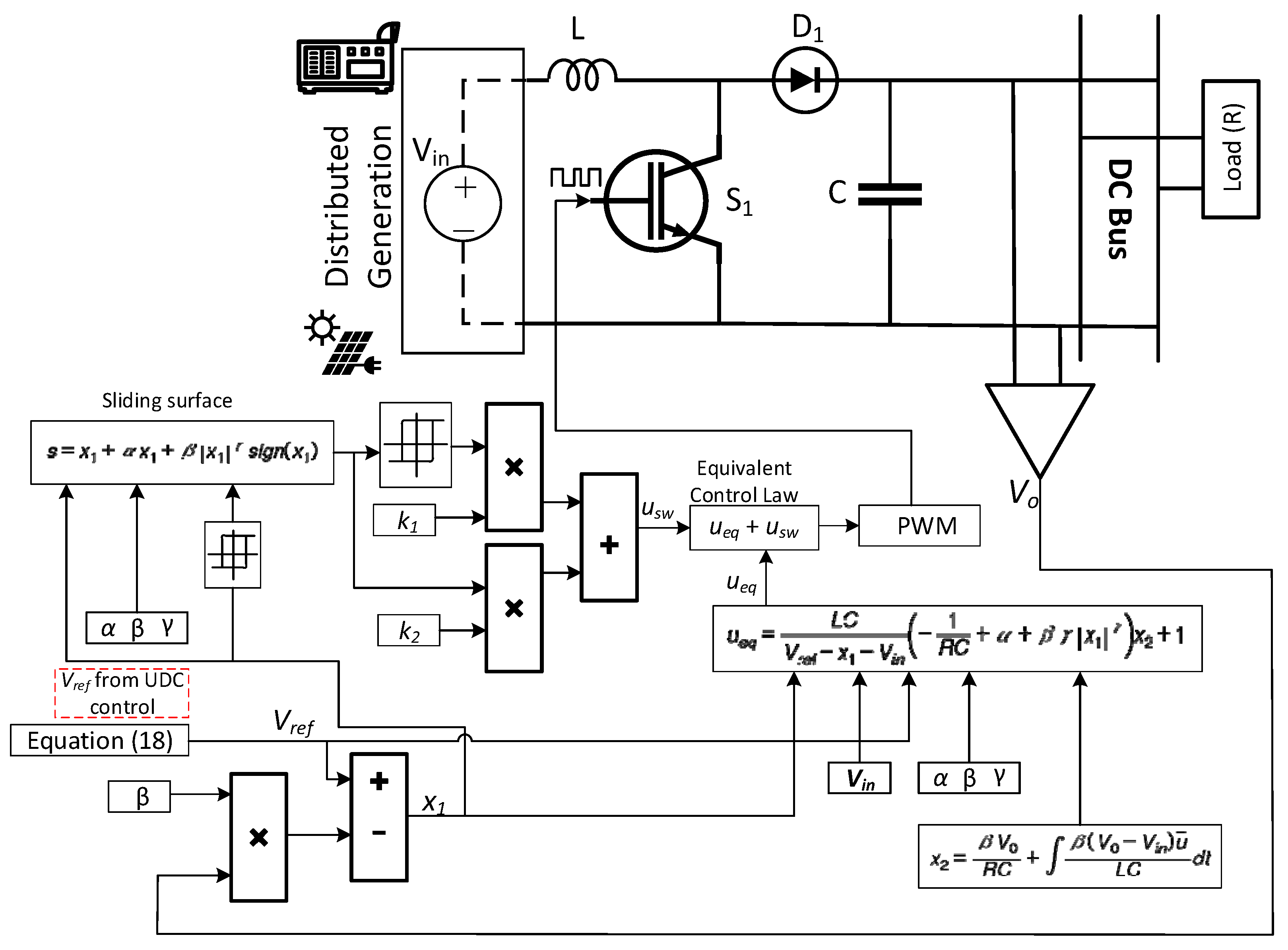
2.1.1. Sliding Mode Control for DC–DC Converters
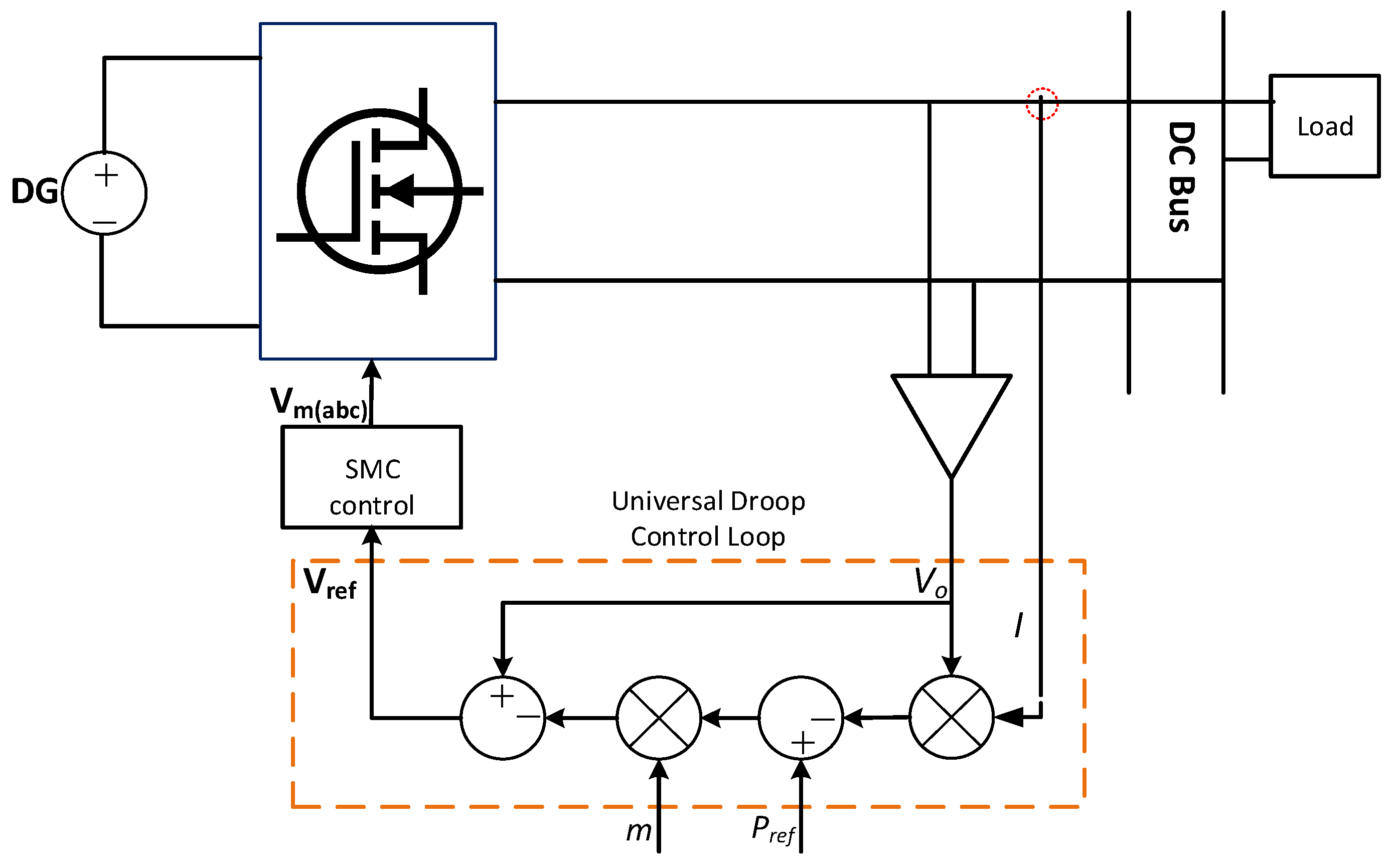
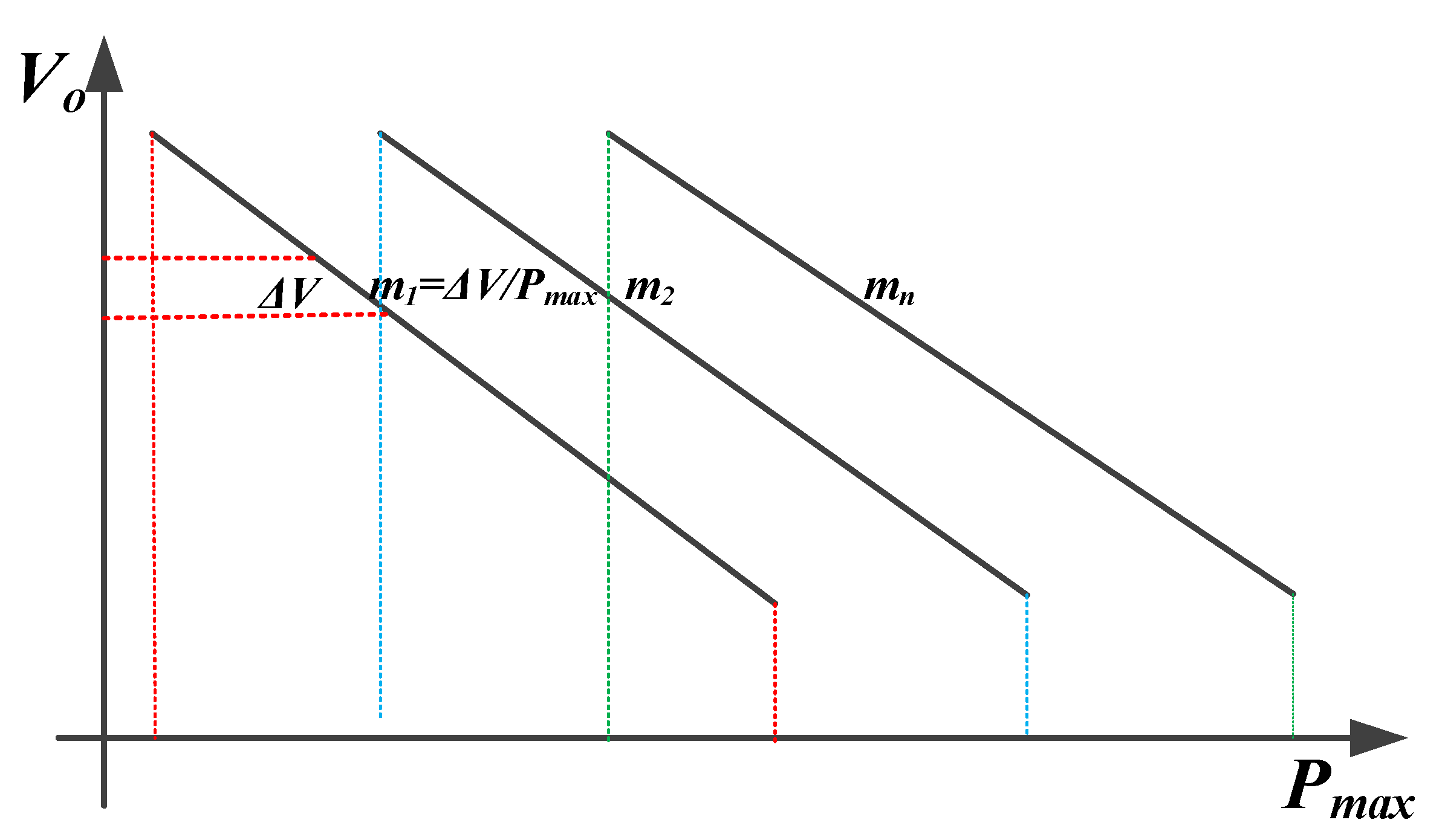
2.1.2. Universal Droop Control
3. Simulation of Proposed Control System and Results
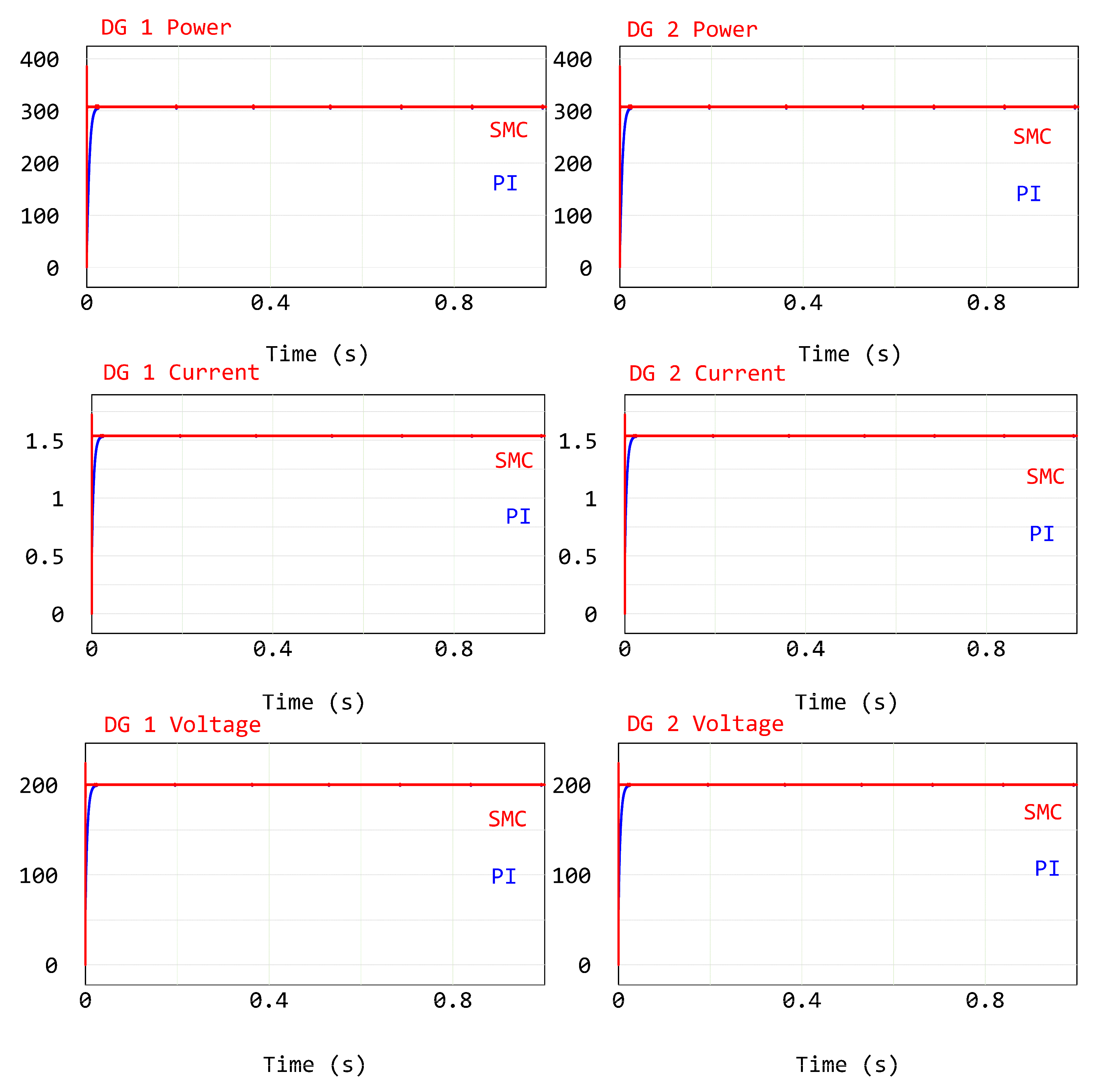
3.1. Steady-State Analysis
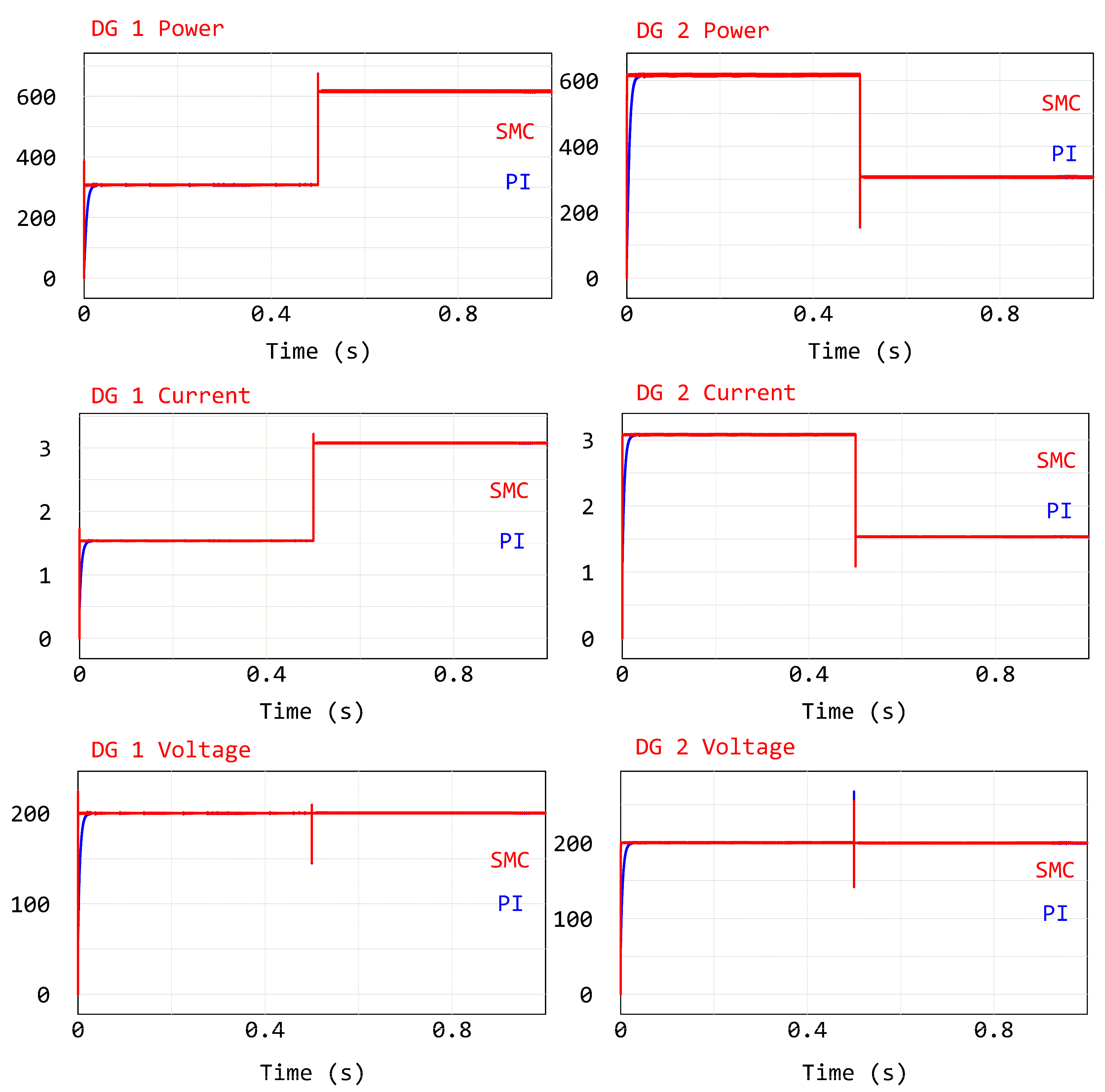
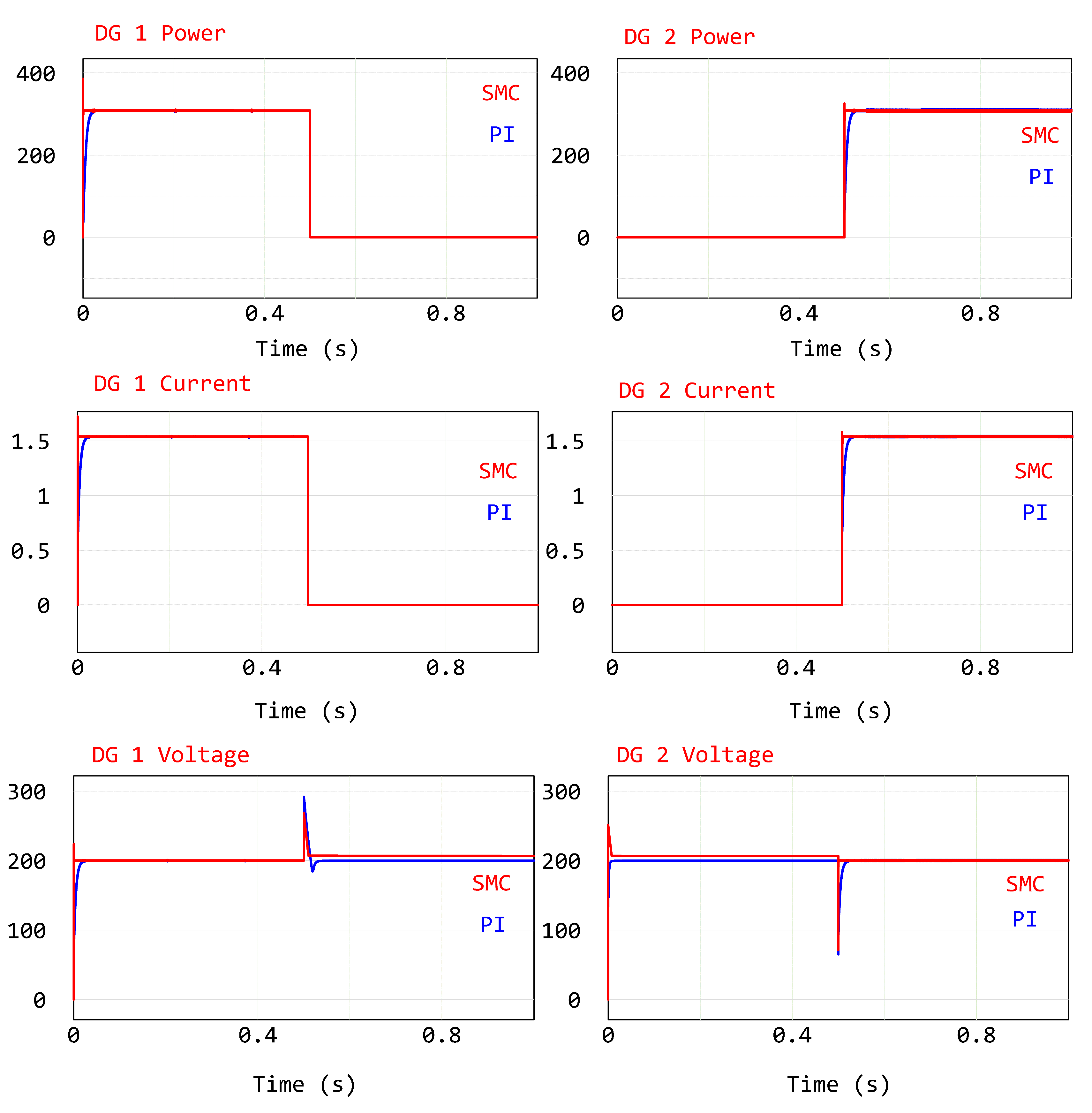
3.2. Transient State Analysis
3.2.1. Study I: Dynamic Load Changes
3.2.2. Study II: Load Shifting
4. Experimental Set-Up and Results
4.1. Experimental Set-Up
4.1.1. Steady-State Analysis
4.1.2. Transient State Analysis
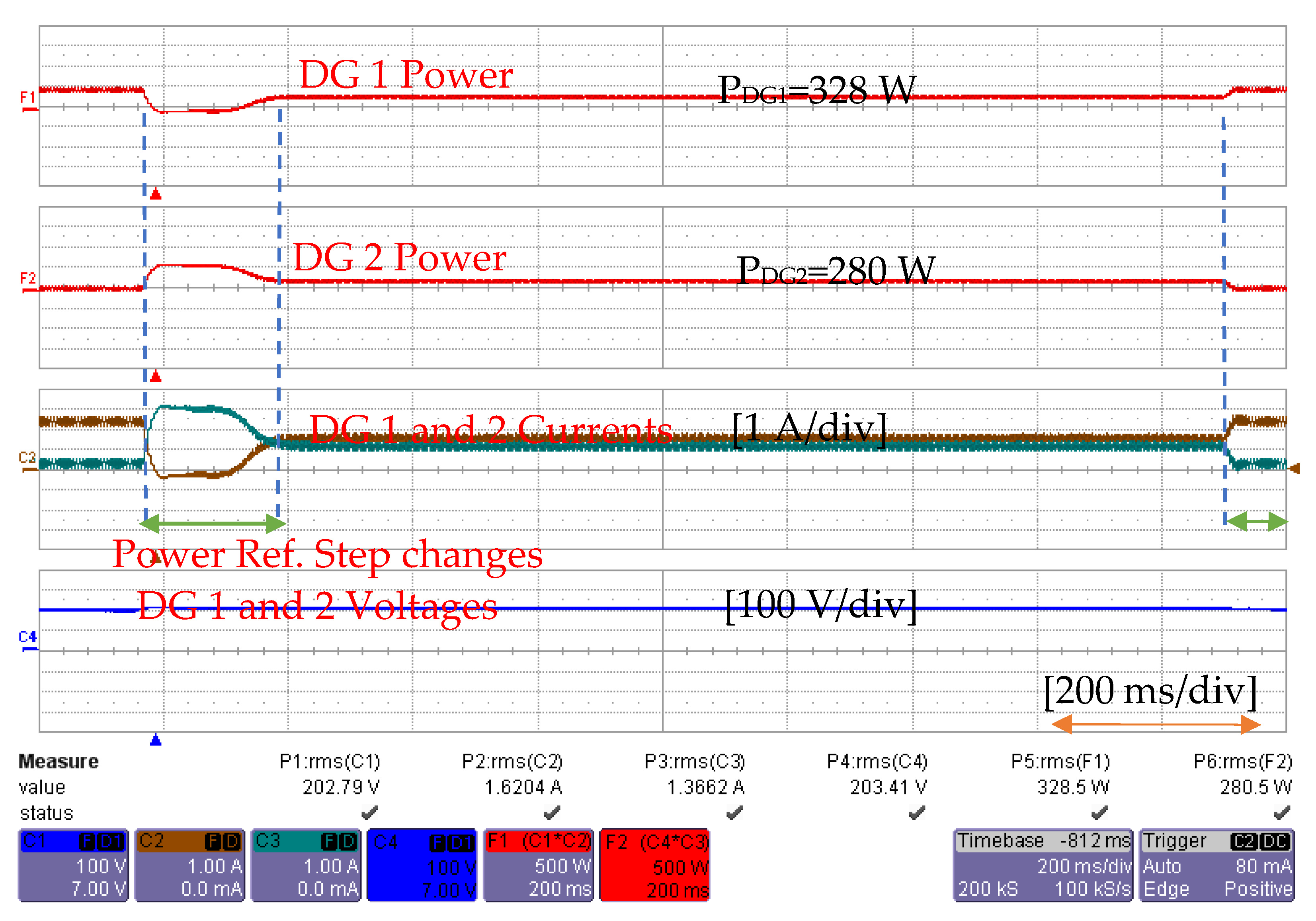
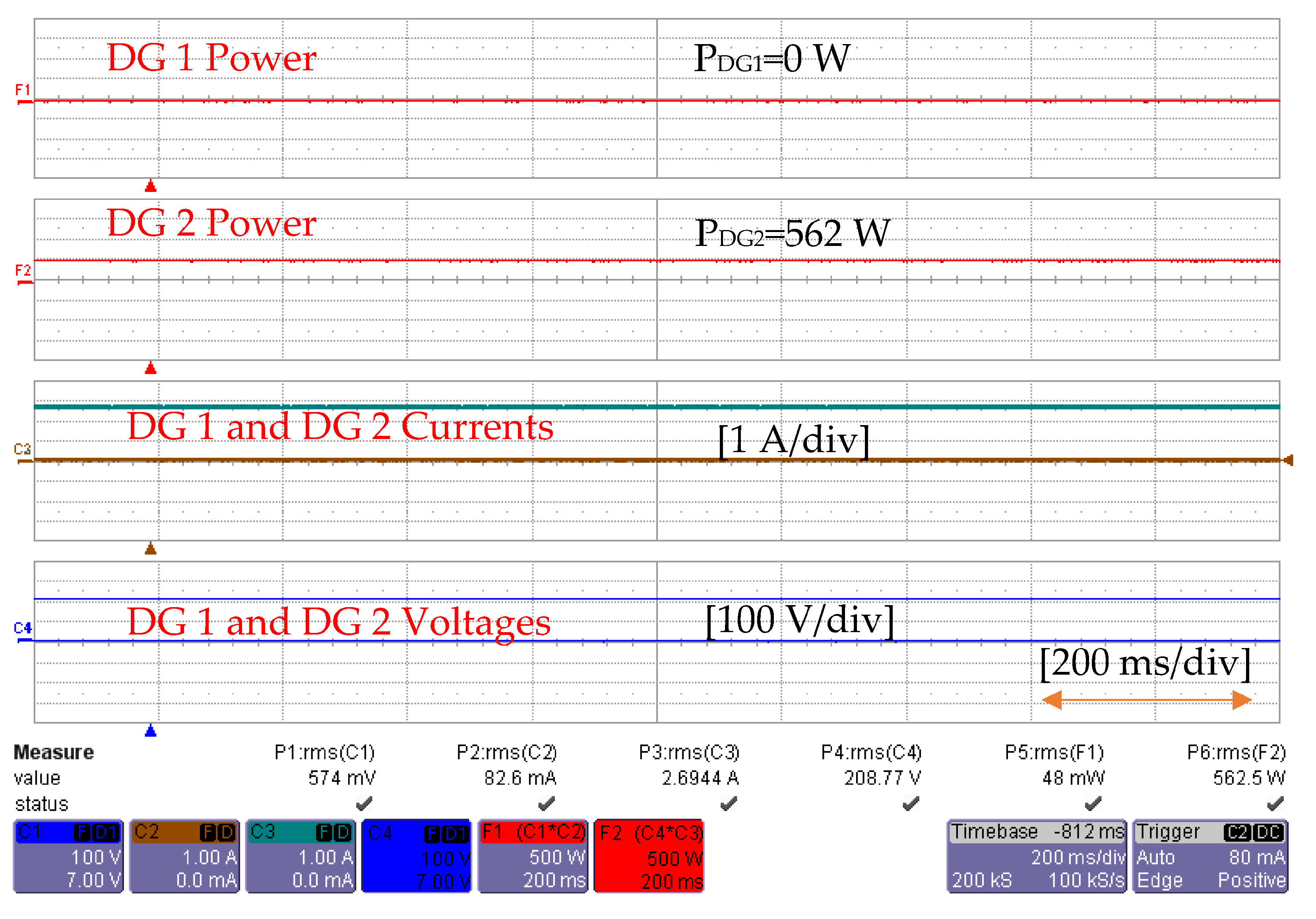
Study I: Load Dynamics
Study II: Load Transfer
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hatziargyriou, N.; Dimeas, A.; Tsikalakis, A. Centralized and decentralized control of microgrids. Int. J. Distrib. Energy Resour. 2005, 1, 197–212. [Google Scholar]
- Muhammad, R.; Muhammad, A.; Bhatti, A.I.; Minhas, D.M. Mathematical modeling and stability analysis of DC microgrid using SM hysteresis controller. Int. J. Electr. Power Energy Syst. 2018, 95, 507–522. [Google Scholar] [CrossRef]
- Chang, F.; O’Donnell, J.; Su, W. Voltage Stability Assessment of AC/DC Hybrid Microgrid. Energies 2023, 16, 399. [Google Scholar] [CrossRef]
- AlLee, G.; Tschudi, W. Edison redux: 380 Vdc brings reliability and efficiency to sustainable data centers. IEEE Power Energy Mag. 2012, 10, 50–59. [Google Scholar] [CrossRef]
- Dragicevic, T.; Vasquez, J.C.; Guerrero, J.M.; Skrlec, D. Advanced LVDC Electrical Power Architectures and Microgrids: A step toward a new generation of power distribution networks. IEEE Electrif. Mag. 2014, 2, 54–65. [Google Scholar] [CrossRef]
- Liu, S.; Miao, H.; Li, J.; Yang, L. Voltage control and power sharing in DC Microgrids based on voltage-shifting and droop slope-adjusting strategy. Electr. Power Syst. Res. 2023, 214, 108814. [Google Scholar] [CrossRef]
- Flourentzou, N.; Agelidis, V.G.; Demetriades, G.D. VSC-based HVDC power transmission systems: An overview. IEEE Trans. Power Electron. 2009, 24, 592–602. [Google Scholar] [CrossRef]
- Cucuzzella, M.; Rosti, S.; Cavallo, A.; Ferrara, A. Decentralized sliding mode voltage control in DC microgrids. In Proceedings of the 2017 American Control Conference (ACC), Seattle, WA, USA, 24–26 May 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 3445–3450. [Google Scholar]
- Anand, S.; Fernandes, B.G.; Guerrero, J. Distributed control to ensure proportional load sharing and improve voltage regulation in low-voltage DC microgrids. IEEE Trans. Power Electron. 2012, 28, 1900–1913. [Google Scholar] [CrossRef]
- Zhao, E.; Han, Y.; Zeng, H.; Li, L.; Yang, P.; Wang, C.; Zalhaf, A.S. Accurate Peer-to-Peer Hierarchical Control Method for Hybrid DC Microgrid Clusters. Energies 2022, 16, 421. [Google Scholar] [CrossRef]
- Lu, X.; Guerrero, J.M.; Sun, K.; Vasquez, J.C. An improved droop control method for dc microgrids based on low bandwidth communication with dc bus voltage restoration and enhanced current sharing accuracy. IEEE Trans. Power Electron. 2013, 29, 1800–1812. [Google Scholar] [CrossRef]
- Yang, N.; Paire, D.; Gao, F.; Miraoui, A.; Liu, W. Compensation of droop control using common load condition in DC microgrids to improve voltage regulation and load sharing. Int. J. Electr. Power Energy Syst. 2015, 64, 752–760. [Google Scholar] [CrossRef]
- Mi, Y.; Guo, J.; Yu, S.; Cai, P.; Ji, L.; Wang, Y.; Yue, D.; Fu, Y.; Jin, C. A power sharing strategy for islanded DC microgrid with unmatched line impedance and local load. Electr. Power Syst. Res. 2021, 192, 106983. [Google Scholar] [CrossRef]
- Cucuzzella, M.; Trip, S.; De Persis, C.; Cheng, X.; Ferrara, A.; van der Schaft, A. A robust consensus algorithm for current sharing and voltage regulation in DC microgrids. IEEE Trans. Control Syst. Technol. 2018, 27, 1583–1595. [Google Scholar] [CrossRef]
- Guerrero, J.M.; Vasquez, J.C.; Matas, J.; De Vicuña, L.G.; Castilla, M. Hierarchical control of droop-controlled AC and DC microgrids—A general approach toward standardization. IEEE Trans. Ind. Electron. 2010, 58, 158–172. [Google Scholar] [CrossRef]
- Hamzeh, M.; Ghazanfari, A.; Mohamed, Y.A.-R.I.; Karimi, Y. Modeling and design of an oscillatory current-sharing control strategy in DC microgrids. IEEE Trans. Ind. Electron. 2015, 62, 6647–6657. [Google Scholar] [CrossRef]
- Liu, X.; Wang, P.; Loh, P.C. A hybrid AC/DC microgrid and its coordination control. IEEE Trans. Smart Grid 2011, 2, 278–286. [Google Scholar]
- Tan, S.-C.; Lai, Y.-M.; Chi, K.T.; Martinez-Salamero, L.; Wu, C.-K. A fast-response sliding-mode controller for boost-type converters with a wide range of operating conditions. IEEE Trans. Ind. Electron. 2007, 54, 3276–3286. [Google Scholar] [CrossRef]
- Tan, S.-C.; Lai, Y.; Tse, C.K.; Cheung, M.K. Adaptive feedforward and feedback control schemes for sliding mode controlled power converters. IEEE Trans. Power Electron. 2006, 21, 182–192. [Google Scholar]
- Tan, S.-C.; Lai, Y.-M.; Chi, K.T. General design issues of sliding-mode controllers in DC–DC converters. IEEE Trans. Ind. Electron. 2008, 55, 1160–1174. [Google Scholar]
- Fan, J.-C.; Kobayashi, T. A simple adaptive pi controller for linear systems with constant disturbances. IEEE Trans. Autom. Control 1998, 43, 733–736. [Google Scholar] [CrossRef]
- Hussaini, H.; Yang, T.; Bai, G.; Urrutia-Ortiz, M.; Bozhko, S. Artificial Intelligence-Based Hierarchical Control Design for Current Sharing and Voltage Restoration in DC Microgrid of the More Electric Aircraft. IEEE Trans. Transp. Electrif. 2023. [Google Scholar] [CrossRef]
- Sabanovic, A.; Fridman, L.M.; Spurgeon, S.; Spurgeon, S.K. Variable Structure Systems: From Principles to Implementation; IET: London, UK, 2004; Volume 66. [Google Scholar]
- Wai, R.-J.; Shih, L.-C. Design of voltage tracking control for DC–DC boost converter via total sliding-mode technique. IEEE Trans. Ind. Electron 2010, 58, 2502–2511. [Google Scholar] [CrossRef]
- Li, X.; Guo, L.; Zhang, S.; Wang, C.; Li, Y.W.; Chen, A.; Feng, Y. Observer-based DC voltage droop and current feed-forward control of a DC microgrid. IEEE Trans. Smart. Grid 2017, 9, 5207–5216. [Google Scholar] [CrossRef]
- Meng, L.; Dragicevic, T.; Vasquez, J.; Guerrero, J.; Sanseverino, E.R. Hierarchical control with virtual resistance optimization for efficiency enhancement and State-of-Charge balancing in DC microgrids. In Proceedings of the 2015 IEEE First International Conference on DC Microgrids (ICDCM), Atlanta, GA, USA, 7–10 June 2015; pp. 1–6. [Google Scholar]
- Li, F.; Lin, Z.; Xu, H.; Wang, F. Comprehensive local control design for eliminating line resistance effect on power sharing degradation in DC microgrids. IET Power Electron. 2022, 15, 11–22. [Google Scholar] [CrossRef]
- Mohammed, N.; Callegaro, L.; Ciobotaru, M.; Guerrero, J.M. Accurate power sharing for islanded DC microgrids considering mismatched feeder resistances. Appl. Energy 2023, 340, 121060. [Google Scholar] [CrossRef]
- Batiyah, S.; Sharma, R.; Abdelwahed, S.; Zohrabi, N. An MPC-based power management of standalone DC microgrid with energy storage. Int. J. Electr. Power Energy Syst. 2020, 120, 105949. [Google Scholar] [CrossRef]




| Parameters | Values |
|---|---|
| DC source voltage (input voltage) | Vin = 96 V |
| Output voltage | Vo = 200 V |
| Beta | β = 1/6 |
| LC values | C = 220 µF, L = 450 µH |
| Switching frequency | 50 kHz |
| Droop coefficient | m = 0.02 |
| Proportional gain | Kp = 0.382 |
| Integral gain | KI = 0.0127 |
| Control Technique | Voltage Deviation: ΔV = Vo (200 Ω) − Vo(20 Ω) | Percentage Change: (∆Vo)/Vo (nominal) × 100% |
|---|---|---|
| PI | 3.76 V | 1.88% |
| SMC | 1.1 V | 0.5% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, K.; Hussain, I.; Seyedmahmoudian, M.; Stojcevski, A.; Mekhilef, S. Voltage Stability and Power Sharing Control of Distributed Generation Units in DC Microgrids. Energies 2023, 16, 7038. https://doi.org/10.3390/en16207038
Ahmed K, Hussain I, Seyedmahmoudian M, Stojcevski A, Mekhilef S. Voltage Stability and Power Sharing Control of Distributed Generation Units in DC Microgrids. Energies. 2023; 16(20):7038. https://doi.org/10.3390/en16207038
Chicago/Turabian StyleAhmed, Kafeel, Irfan Hussain, Mehdi Seyedmahmoudian, Alex Stojcevski, and Saad Mekhilef. 2023. "Voltage Stability and Power Sharing Control of Distributed Generation Units in DC Microgrids" Energies 16, no. 20: 7038. https://doi.org/10.3390/en16207038
APA StyleAhmed, K., Hussain, I., Seyedmahmoudian, M., Stojcevski, A., & Mekhilef, S. (2023). Voltage Stability and Power Sharing Control of Distributed Generation Units in DC Microgrids. Energies, 16(20), 7038. https://doi.org/10.3390/en16207038









