Numerical Investigation of Aerodynamic Performance and Structural Analysis of a 3D J-Shaped Based Small-Scale Vertical Axis Wind Turbine

Abstract

Small vertical axis wind turbines (VAWTs) are often considered suitable for use in urban areas due to their compact design. However, they are also well known to offer poor performance at low wind speeds, which is a common situation in such environments. An optimised 3D J-shaped VAWT was designed from standard NACA 0015 blades and analysed numerically through computational fluid dynamics (CFD). A finite element analysis (FEA) was also carried out to ensure the model’s structural integrity. Optimal results were obtained with aluminium alloy hollow blades and stainless-steel struts with X-shaped beams, with internal ribs. Numerical results showed that the J-shaped VAWT achieved an 18.34% higher moment coefficient compared to a NACA 0015-based VAWT, indicating better self-starting abilities.

1. Introduction

The UK government aims to achieve net zero greenhouse gas emissions by 2050 by transitioning to an electricity production system that is 100% renewable. Wind is currently a major source of energy in the UK, with its average wind speed among the highest in Europe, mainly in the North Sea but also throughout the country [1]. As exposed through the total energy generation mix in 2022 [2], 26.8% of the country’s electricity was generated by wind, compared to 5.2%, 4.4% and 1.8%, respectively, for biomass, solar and hydro generation.

However, according to [3], the British population is ambivalent regarding the installation of wind energy technologies, the deployment of wind turbines in natural landscapes and the power production of these technologies. Small-scale wind turbines appear to be a good compromise to maximise the national wind power capacity while reducing their impact on the landscape. Small-scale vertical axis wind turbines (VAWTs) are deemed better suited than horizontal axis wind turbines (HAWTs) in urban environments, having the advantage of catching the wind from any direction [4], thus limiting the need for complex and onerous control systems. VAWTs are also known for their low manufacturing and maintenance costs and their capacity to produce less noise than HAWTs [5]. One of the main limitations of VAWTs is, however, their difficulties in starting at low wind speeds, which often necessitates electrical means.

Many computational fluid dynamics (CFD)-based studies on VAWTs are reported in the literature. For instance, URANS ($k\text{-}\omega$ SST model) and large eddy simulation (LES) CFD simulations were performed with 2D, 2.5D and 3D models and the results were compared with wind tunnel measurements [6]. The 2.5D LES, 3D LES and URANS-based simulations provided the best results for a range of tip speed ratios ($TSRs$) defined as

$$TSR=\frac{\omega R_T}{V}$$

(1)

where $\omega$ is the VAWT angular velocity, $R_T$ is the VAWT radius and V is the wind velocity at the inlet of the numerical domain. The 3D model was considered the preferred option to study the self-starting characteristics of the turbine.

The starting torque of a Darrieus-type VAWT can potentially be improved through the use of J-shaped blades. A J-shape is obtained by removing a section of a standard NACA airfoil from the trailing edge of the blade, either on the pressure or the suction side. Such shape modification has been shown to increase the acquirable energy by improving the self-starting and power generation capabilities of a wind turbine subject to low wind speeds, as the turbine can use both lift and drag forces [7]. The authors investigated numerically a VAWT built with J-shaped blades generated from NACA 0015 airfoils with a transient solver and the $k\text{-}\omega$ SST turbulence model [7]. A blade chord length of 0.4 m and a rotor diameter of 2.5 m were considered. Results showed that the J-profile improved the VAWT self-starting capabilities, with the torque and power coefficients improved for $TSR$ values ranging from $0.6$ to $1.6$, outperforming standard NACA 0015-based blades.

Previous investigations within the Energy & Sustainability Department at Cranfield University (UK) and reported in [8] considered an optimisation procedure to improve the VAWT starting torque through 2D CFD also for both J-shaped and NACA 0015-based blades. The model tested numerically displayed a rotor diameter of 2.5 m and three blades of 0.4 m chord length. Out of the six geometries investigated by the authors, the best performance was obtained with the J1 airfoil, which showed the starting torque to increase by a factor of $2.35$ when compared to the NACA 0015-based case.

For a 3D model to be accurate, all components constituting the geometry of a wind turbine should be considered. A numerical analysis of a VAWT based on a NACA 0021 profile was performed to study the effects of the struts and tower [9]. The model was of diameter 6.5 m with a blade chord length of 25 cm. The $k\text{-}ϵ$ turbulence model was considered with the PIMPLE algorithm as the main solver. The study showed that the tower did not account for any significant changes in force distribution or power, but struts had a negative influence on the power coefficient, with values being lowered from 0.28 to 0.16 when struts were present. The authors suggested that the strut design should be optimised to reduce power losses and increase efficiency. In the current study, the tower will not be accounted for, but the struts will be optimised to reduce adverse effects on the turbine.

This study extends the preliminary research reported in [8]. A comparison was performed between the 2D results obtained previously and the new 3D-based simulation results. For such a comparison to be valid, most parameters remained identical. Unsteady Reynolds-averaged Navier–Stokes (URANS) equations were considered with the $k\text{-}\omega$ SST turbulence model, and the SIMPLE algorithm was used for the pressure velocity coupling, with a second-order upwind discretization method. The power and torque coefficients were used to monitor the performance of the wind turbine.

A structural integrity analysis is necessary to avoid any breakage of a wind turbine structure that is subjected to different loads, including lift, drag and centrifugal forces, which can create important bending moments [10]. In the current work, the aforementioned forces are accounted for in the static structural modelling of the blades, and the weight of the blades is included in the struts analysis. Three blades are considered as described in [8] to reduce the structural loads without reducing the performance of the Darrieus rotor [11].

Based on the above-cited literature, a 3D model is recommended for the numerical study, and both CFD and FEA should be investigated. J-shaped-based VAWTs have the potential to shape the future of small wind turbines deployed in urban areas, due to their efficiency in low-speed conditions compared to traditional turbines. This work includes (1) an FEA of each component to check the structural integrity of the novel J-shaped turbine and (2) the development of a CFD model to evaluate the effects of the blade shape on the VAWT performance and compare the newly generated 3D numerical results with previous 2D studies.

The numerical analysis is divided into two main sections, the first one covering the structural integrity assessment of parts of the VAWT and the second one dealing with the CFD study of the starting torque performance of the J-shape-based VAWT.

2. Structural Integrity Analysis

A VAWT consists mainly of blades, struts and a hub. The dimensions and parameters of the developed J-shaped design are provided in

Table 1. Design parameters of the VAWT.

Parameter	Value/Dimension	Literature Reference
Blade airfoil	J-shape	[8]
Number of blades	3 blades	[12]
Blade span	3 m	[13]
Chord length	0.4 m	[8]
VAWT diameter	2.5 m	[8]
VAWT configuration	H-type straight	[14]
Pitch angle	Fixed at 0${}^{\circ }$	[14]
Number of struts per blade	2	[14]
Strut shape	Streamlined	[15]
Strut airfoil	E862	[16]
Support type of blade on strut	Cantilever	[14]
Angle between strut and blade	0${}^{\circ }$	[14]
Span position of top struts	0.63 m from blade tip	[14]
Span position of bottom struts	0.63 m from blade tip	[14]
Shape of struts lengthwise	Linearly tapered	[17]
Chord length on hub	80 mm	[18]
Chord length on blade	60 mm	[18]
Strut length	1150 mm	[14]
Hub height	3 m	[18]
Hub cross-section	Circular	[18]
Hub diameter	150 mm	[18]

. In addition to the J-shaped VAWT, a NACA 0015-based VAWT was also developed to compare the effect of the blades and assess the ability of both VAWTs to self-start. To ensure a proper comparison of blade performance, all parameters and dimensions of the VAWTs other than the blade profiles remained identical.

Different internal structures of the blade and struts were designed and studied through FEA. Four cases were considered for the blade study: (1) fully solid blades, (2) hollow blades with thickness, (3) hollow blades with ribs positioned on the outside and (4) hollow blades with internal ribs. Three strut cases were considered: (1) full solid struts, (2) hollow struts with thickness and (3) hollow struts consisting of ‘X’ beams with ribs throughout their cross-section.

In addition to assessing the structural integrity of the above-designed parts of the VAWT, the FEA also enabled the testing of various materials for the internal structure of the blades and struts, reducing the model’s weight and therefore the manufacturing costs. Four different alternative designs of the internal structure were developed, for both blades and struts. In the case of the blade, a preliminary study was conducted to define the aerodynamic loads experienced by the blades when in operation; this is further detailed in Section. For the struts, the stress generated could be approximated by a cantilever, since the influence of the blade weight is higher than the lift and drag generated.

ANSYS Meshing and ANSYS Mechanical (2023 R2 version) were considered, respectively, for the mesh generation and FEA of each component. The materials considered were tested numerically and the resistance of the parts against the loads was evaluated.

2.1. Blade Cases

The method described in [19] and explained below was considered to obtain the main loads (lift and drag) on the blade, which, here, were obtained from the previous 2D study [8]. During the rotation of the turbine, both the angle of attack ($\alpha$) and the relative velocity seen by the blade vary as a function of the azimuthal angle, changing accordingly the coefficients and the resulting aerodynamic forces. The obtained lift (L) and drag (D) for each azimuthal increment in the revolution can thus be transformed into normal (N) and axial (A) forces on the airfoil [20]:

$$N=Lcos\alpha +Dsin\alpha$$

(2)

$$A=Dcos\alpha -Lsin\alpha$$

(3)

The 2D-based forces were then applied linearly on the 3D blade with respect to the aerodynamic centre of the blade, located at $x=0.25$ times the chord length and measured from the leading edge. As the full blade was made of multiple 2D airfoils, the 2D-based axial and normal forces could be applied to the blade. The resulting loads are shown in Figure 1, where A and B are the normal and axial forces, respectively, and E is the acceleration due to gravity. The C and D labels show the fixed supports for the strut connections.

All four blade cases investigated in this work are summarised in

Table 2. Cases studied for the structural analysis of the J-shaped blade.

Case ID	Internal Structure	Material	Mass (kg)
1	Solid blade	Carbon Fibre	35.516
		Aluminium Alloy	53.872
2	Hollow blade	Carbon Fibre	12.016
		Aluminium Alloy	18.227
3	Hollow blade with ribs outside	Carbon Fibre	12.626
		Aluminium Alloy	19.152
4	Hollow blade with ribs inside	Carbon Fibre	12.181
		Aluminium Alloy	18.477

, including the materials tested, carbon fibre and aluminium alloy. An axial force value of A = 416 N and a normal force value of N = 1216 N were applied linearly onto the blade. These values depict the worst-case scenario, corresponding to the maximum forces that a blade would sustain in a complete revolution. The blade can thus be considered structurally safe if it withstands these loads.

Table 3. Results from the FEA study for the VAWT blades. Studied cases from Table 2.

Case ID	Max ${\mathit{\sigma }}_{\mathit{V}\mathit{M}}$ (MPa)		Max Deflection (mm)
	Carbon Fibre	Al Alloy	Carbon Fibre	Al Alloy
1	$6.1069$	$5.6910$	$0.1815$	$0.0589$
2	$105.1900$	$78.5500$	$1.8879$	$2.2032$
3	$140.6600$	$119.4800$	$1.6469$	$1.8951$
4	$59.0650$	$37.3490$	$0.8874$	$0.4262$

summarises the outcomes of the FEA carried out on the blade. The maximum Von Mises stress (${\sigma }_{VM}$ stress) and the maximum deflection obtained for all four cases are provided. The lowest deflection, 0.0589 mm, and the lowest maximum stress, 5.691 MPa, were obtained for Case 1 with aluminium alloy (solid blade). Case 4 with aluminium alloy (hollow blade with internal ribs) resulted in 0.4262 mm for the deflection and 37.349 MPa for the $VM$ stress. Based on this deflection, Case 1 thus seems the best choice. However, the weight of the solid blade (35.5 kg) makes it unfavourable to use. Case 4, therefore, appears as a more suitable option, where the deflection and maximum stress for carbon fibre are 0.8874 mm and 59.065 MPa, and they are 0.42615 mm and 37.349 MPa for aluminium alloy, respectively. Considering the price of each material, and their mass provided in Table 2, a cost-effective choice would be Case 4 for hollow blades with internal ribs in aluminium alloy, with a weight of 18.477 kg each.

Figure 2 shows the blade deformation for Case 4, with aluminium alloy. The effect due to the fixed supports can be seen, with the blade being deformed in the normal direction in the middle and end sections of the blade. The maximum deformation is found along the trailing edge; this is a consequence of the combined effects of the thin blade thickness in this region and the axial force.

2.2. Strut Cases

The struts are only subjected to a bending force; the bending was thus generated by the weight of the blades only. The strut shown in Figure 3 was attached to the tower using the fixed support A, and the bending force represented by the B label was applied on the opposite side. Three cases were investigated, modifying the internal parts of these struts to be either solid, hollow or hollow with X beams, with stainless steel (SS 316) or aluminium alloy materials; see

Table 4. Cases studied for the structural analysis of the VAWT struts.

Case ID	Internal Structure	Material
1	Solid strut	Stainless Steel
		Aluminium Alloy
2	Hollow strut	Stainless Steel
		Aluminium Alloy
3	Hollow strut with ribs and X beam	Stainless Steel
		Aluminium Alloy

.

The load corresponding to the blade weight is applied where the blade is attached to the struts. According to the above results, the best case to consider is for blades made of aluminium with internal hollow ribs. A blade weighs 18.477 kg, which corresponds to a force of 185 N. As each blade is held in place by two struts, the total load to be sustained by each strut will be half, bringing the load to 92.5 N on each strut.

Table 5. Results from FEA study for VAWT struts. Studied cases presented in Table 4.

Case ID	Max Von Mises Stress (MPa)		Max Deflection (mm)
	Al Alloy	SS 316	Al Alloy	SS 316
1	$72.900$	$74.589$	$13.023$	$4.755$
2	$41.053$	$40.810$	$19.830$	$7.235$
3	$100.860$	$31.088$	$2.898$	$3.409$

shows the outcome of the structural analysis on the strut. Here, the lowest maximum deflection was obtained for Case 3 in aluminium alloy (hollow strut with X beam), with only 2.898 mm. The lowest maximum Von Mises stress was also achieved for Case 3, with 31.088 MPa, but with stainless steel 316.

The total deformation of the strut obtained for Case 3 is shown in Figure 4. It can be seen that the maximum deformation is obtained in the region where the blade is mounted, with a deformation of 3.40 mm. The deformation increases gradually through the length of the strut, from the point of connection with the hub. This is, as expected, similar to the behaviour of a cantilever.

To check the structural integrity of a new structure, the maximum stress of this structure should be compared with the real equivalent one, considering a safety factor. Structural parts are thus resistant when the following condition is met:

$${\sigma }_{VM}<R_{pe}$$

(4)

where ${\sigma }_{VM}$ is the obtained maximum Von Mises stress obtained from the FEA analysis, $R_{pe}$ is the practical resistance to extension and is defined as $R_{pe}=R_e/S_f$, $R_e$ is the elastic resistance of the material and $S_f$ is the desired safety factor. A safety factor of $2.5$ was considered for both the blades and struts. Usually, the range of typical safety factors is between 2 and 3 for regular and known structure loads [21]. The corresponding practical resistance results are summarised in

Table 6. Structural integrity analysis for Case 3—struts.

	${\mathit{S}}_{\mathit{f}}=2.5$	${\mathit{S}}_{\mathit{f}}=2.5$
	Stainless Steel 316	Aluminium Alloy
Maximum ${\sigma }_{VM}$ (MPa)	$31.088$	$100.860$
Shear stress (MPa)	$27.700$	$28.100$
Elastic limit (MPa)	$170.000$	$150.000$
$R_{pe}$ (MPa)	$68.000$	$60.000$

, where the best strut option is a hollow one with ribs and an X-beam, made of stainless steel 316, for which the VM stress is 31.088 MPa.

The structural analysis performed on the blades and struts of the J-shaped VAWT has shown that hollow blades with internal ribs in aluminium alloy and hollow struts with ribs and an X-beam, made of stainless steel 316, should be considered for the manufacturing of this VAWT. To establish how the turbine behaved under low wind conditions, a CFD study was next carried out.

3. Computational Fluid Dynamics Study

The CFD study was performed to analyse the performance of the newly designed J-shaped VAWT. This analysis was carried out with the commercial flow solver ANSYS Fluent.

3.1. Computational Domain

A C-shaped computational domain was considered, consisting of a stationary outer region and a rotating inner region containing the VAWT, with both regions linked by an interface. To ensure that the results near the turbine were not affected by the domain’s boundaries, the domain limits listed in

Table 7. Limits of the computational domain considered in this work.

Dimension ID	Dimension Based on VAWT Diameter	Dimension (m)
$D_T$	$1D_T$	$2.50$
$L_1$	$10D_T$	$25.00$
$L_2$	$14.4D_T$	$36.00$
$L_3$	$20D_T$	$50.00$
$L_4$	$1.2D_T$	$3.00$
$L_5$	$1.5D_T$	$3.75$
$L_6$	$8D_T$	$20.00$

were applied, following recommendations from [6,22]. These dimensions are shown in Figure 5.

3.2. Solver Settings and Numerical Approach

The $k\text{-}\omega$ SST turbulence model is commonly used in CFD simulations dealing with VAWTs [6,7,8,23], and the corresponding equations can be found in the Appendix A [24]. When using this model, the computational cost per simulation is usually increased due to the fine mesh needed at the walls (ideally $y^{+}<1$) when compared to the realizable $k\text{-}ϵ$ model with standard wall functions, where a coarser grid is considered at the walls ($30<y^{+}<300$). Researchers [25] have, however, reported that the use of the realizable $k\text{-}ϵ$ with wall functions provides similar results as experimental data when the $TSR$ is lower than $0.6$. In the current study, both turbulence models have been tested and compared, to establish whether the realizable $k\text{-}ϵ$ turbulence model with wall functions is indeed suitable at low $TSR$.

An incompressible flow was assumed, as the Mach number considered here was less than $0.3$ [26]. Furthermore, as the VAWT was to be placed near the ground (less than 10 m high), the density $\rho$ and dynamic viscosity $\mu$ of the air were taken at sea level; hence, $\rho$ = 1.225 kg/m${}^3$ and $\mu =1.8·{10}^{-5}$ kg/(m·s). A 10 m/s wind velocity was specified at the inlet boundary of the external computational domain. The internal domain, which included the VAWT model, was run at $TSR=0.2$, which was equivalent to an angular velocity of 1.6 rad/s. The fixed time step $\Delta t$ of a transient VAWT simulation is related to the azimuthal increment $\Delta \theta$ provided in Equation (5) [22], where $\omega$ is the angular velocity.

$$\Delta t=\frac{\pi }{180}·\frac{\Delta \theta }{\omega }$$

(5)

In addition, to ensure that the time resolution did not affect the simulation results, the angular velocity increment had to be such that $\Delta \theta \le 0.5$ deg [22]. Taking this value into account, and considering the above operating conditions, the fixed time step applied here was thus $\Delta t$ = 0.00545415 s. The SIMPLE scheme was selected for the pressure–velocity coupling and a second-order discretization was applied for all equations [6,8,9]. In addition, a ${10}^{-5}$ convergence criterion was applied for all equations [27].

3.3. CFD-Based Results

3.3.1. Mesh Independence Study

A mesh independence study was performed to ensure that the numerical results did not depend on the mesh density. This was carried out for the domain that included the J-shaped blade profile, under self-starting conditions at $TSR=0.2$. The study was performed with the realizable $k\text{-}ϵ$ turbulence model with wall functions. Five unstructured meshes were tested, comprising around 1 to 5 million (1 M to 5 M) cells. The resulting mean power coefficients $C_p$ for these cases are presented in

Table 8. Summary—mesh independence study. Relative error based on the finest 5 M mesh.

Mesh ID	Number of Cells	Mean ${\mathit{C}}_{\mathit{p}}$ per Revolution	Relative Error ${\mathit{C}}_{\mathit{p}}$ (%)
1 M	$\mathrm{858,660}$	$0.00585$	23.414
2 M	$\mathrm{1,942,407}$	$0.00657$	14.075
3 M	$\mathrm{2,993,119}$	$0.00728$	4.788
4 M	$\mathrm{3,830,635}$	$0.00764$	0.007
5 M	$\mathrm{4,814,656}$	$0.00765$	0.000

. It can be seen that the 3 M cell mesh was suitable for the CFD study as the relative error on $C_p$ between the 3 M and 4 M cell meshes was less than 5%. When considering the $k\text{-}\omega$ SST turbulence model, a more refined mesh is needed at the wall. An unstructured mesh comprising 34 M cells was deemed suitable for the study.

3.3.2. Time Independence Study

A time independence study shows the flow behaviour with time, defining a time value from which the flow is stabilised, ensuring that the simulated results remain constant after a suitable number of blade revolutions. Figure 6 shows the effect of the number of revolutions required for the mean $C_p$ to stabilise for both the newly designed J-shaped and the base NACA 0015 blades, with both turbulence models used in this work. Only two revolutions are required to obtain time-independent solutions at $TSR=0.2$. This result is useful when setting up simulations as it helps to optimise the computational time and resources needed, preventing any waste of resources while ensuring that the numerical results are converged.

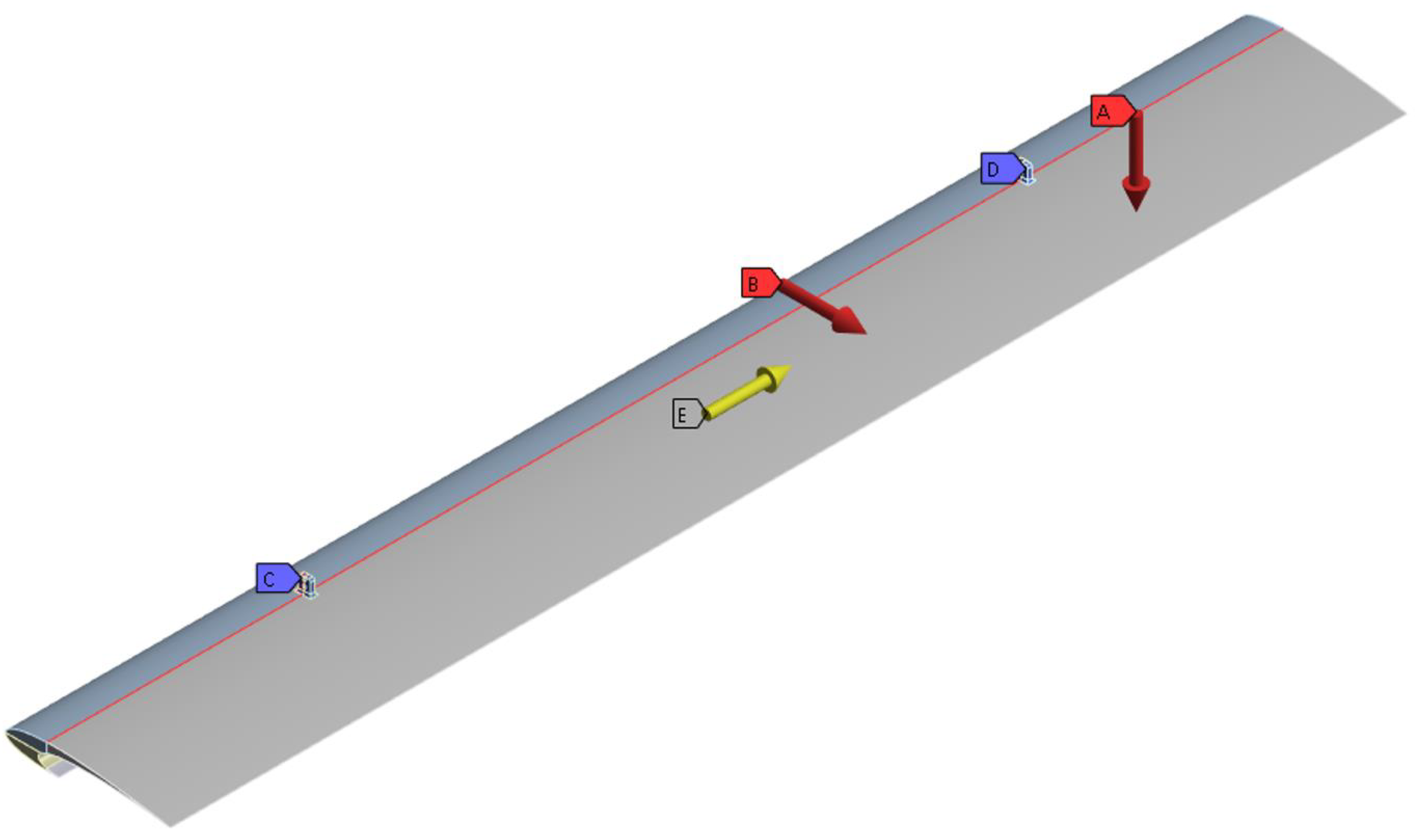
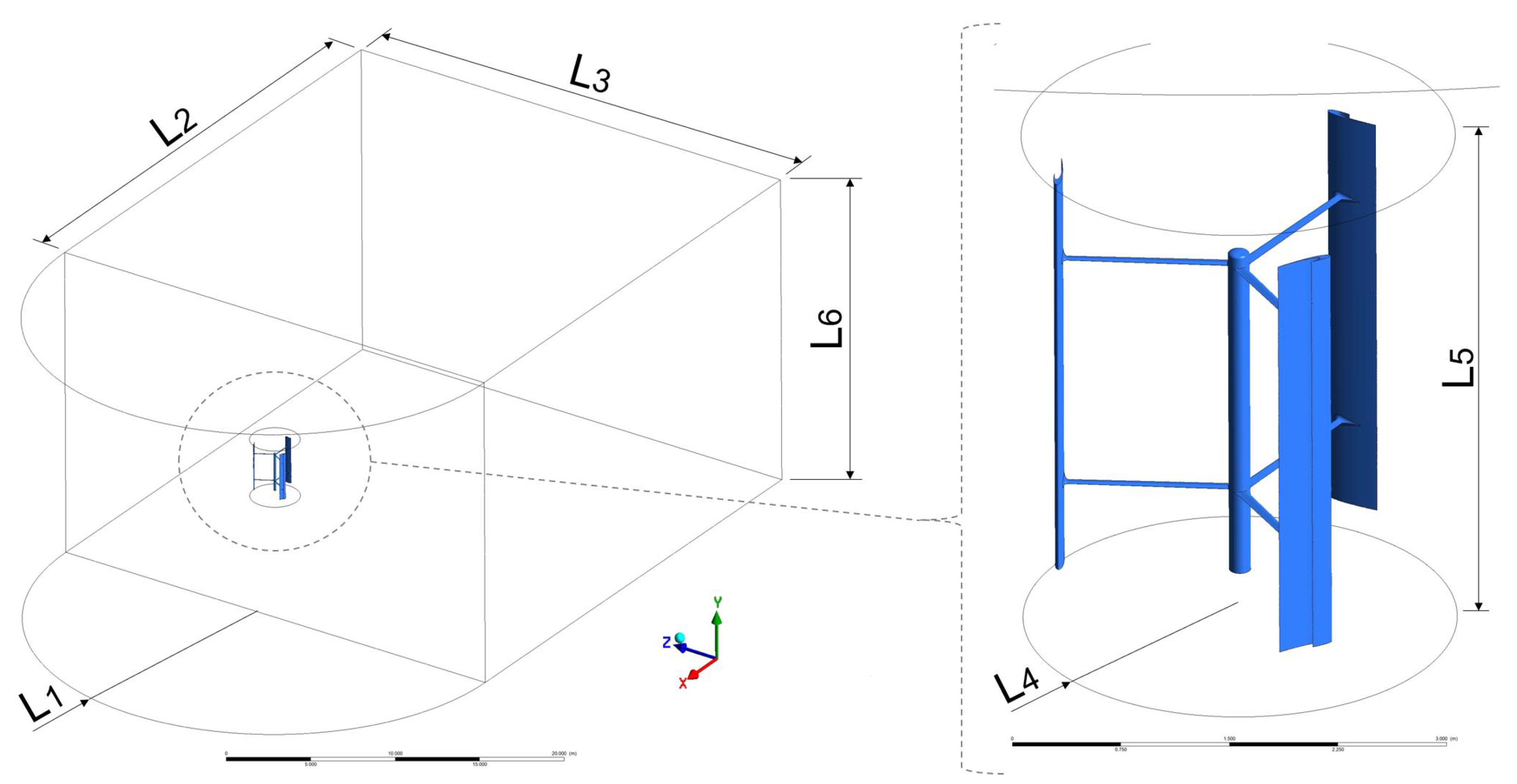
3.3.3. Flow Analysis

The flow distribution for the J-shaped-based VAWT at $TSR=0.2$ using the $k\text{-}\omega$ SST turbulence model is studied. Figure 7 shows the turbulent intensity field in the $XZ$ plane for different azimuthal angles during one ‘converged’ revolution of the VAWT. Figure 8 presents the same flow behaviour but in its 3D form, showing the velocity magnitude field and pathlines. The effect of the airfoil dynamic stall is clearly noticeable in regions where the turbulent intensity levels are high in Figure 7. Tip vortices generated as a consequence of the 3D design are also visible.

• Starting torque comparison between 3D J-shape and NACA 0015 cases

Figure 9 shows the evolution of the moment coefficient over one revolution for the J-shaped and NACA 0015 cases at $TSR=0.2$, with both the $k\text{-}ϵ$ and $k\text{-}\omega$ SST turbulence models. As can be seen, small differences are present. With both turbulence models, the NACA 0015 profile shows higher and lower peak values of the moment coefficient compared to the J-shape profile. It can also be seen that the curve of the moment coefficient for the J-shape displays a higher number of relative peaks.

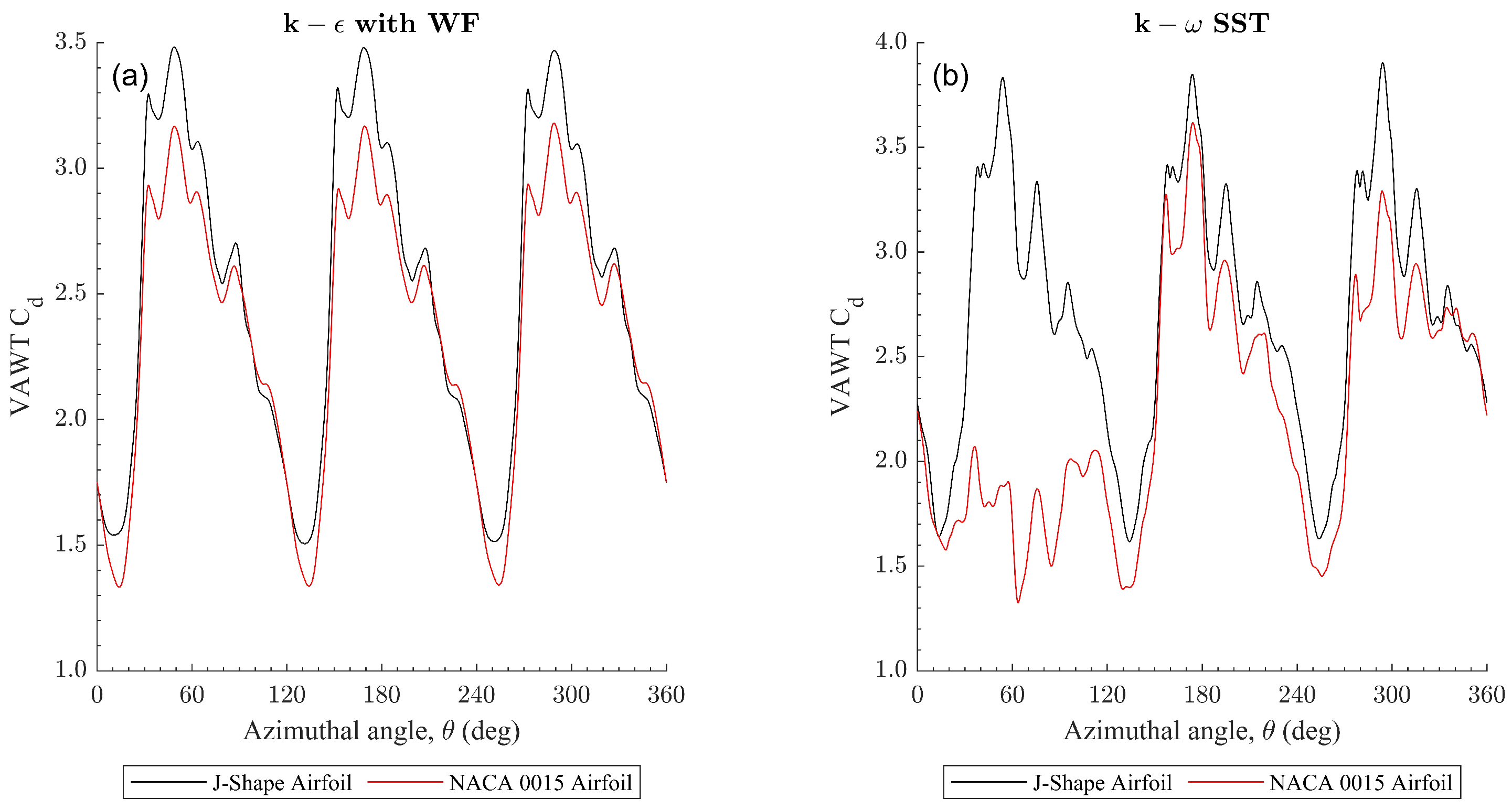
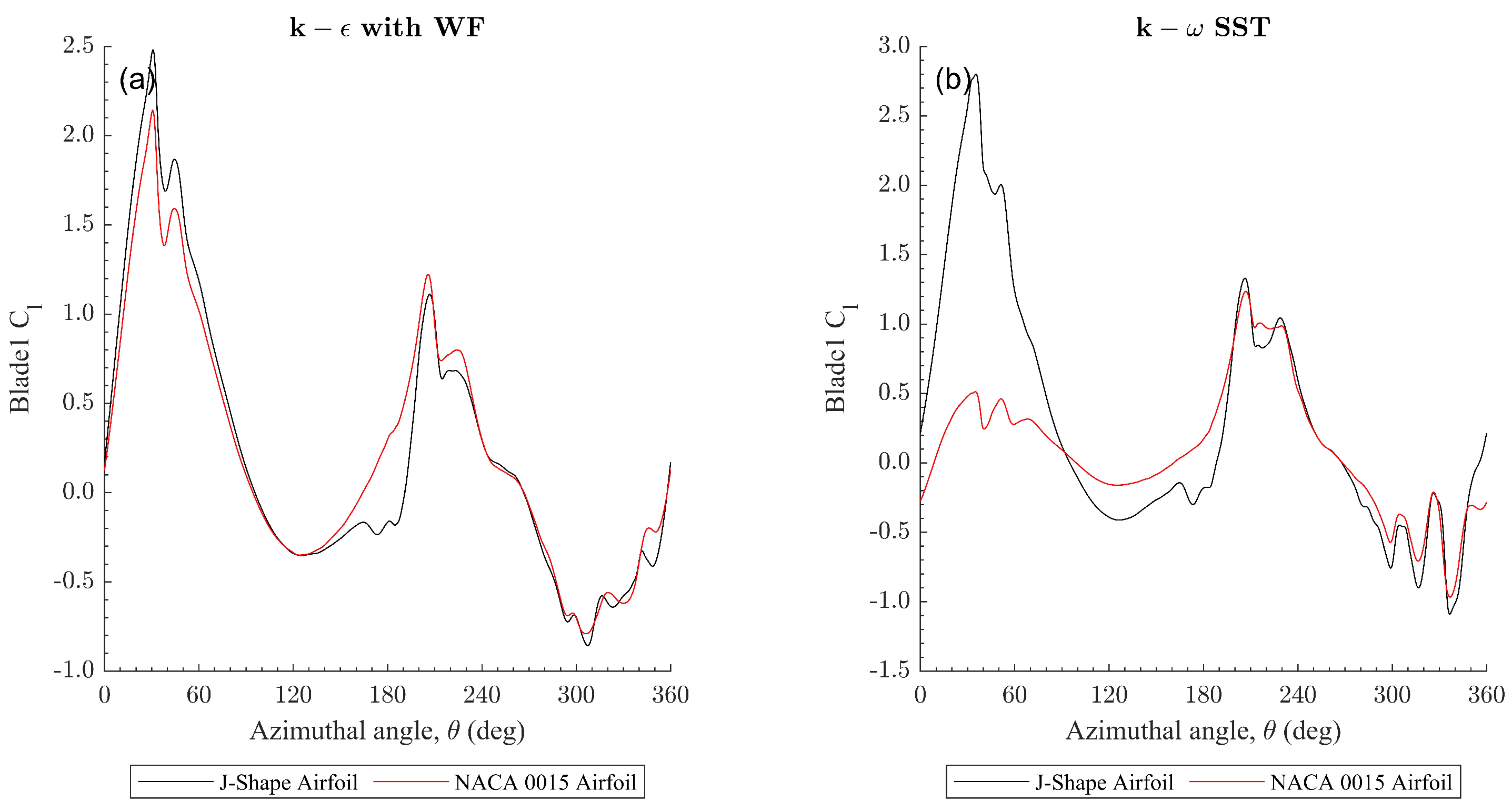
To understand better the difference in the performance of the J-shaped and NACA 0015-based VAWTs, the drags for both airfoil-based VAWTs are plotted in Figure 10. It can be seen that the J-shaped-based VAWT displays a higher drag coefficient for $TSR=0.2$. Similarly, the lift coefficients produced by one blade during one revolution with both turbulence models are plotted in Figure 11.

To identify more clearly which airfoil provides the best starting torque, the average values of the moment coefficient in one revolution were calculated for both airfoils and turbulence models; see

Table 9. Comparison between the mean moment coefficient for one revolution ($TSR=0.2$) of the VAWT with J-shape and NACA 0015 3D cases.

Airfoil	Turbulence Model	Mean ${\mathit{C}}_{\mathit{m}}$	$\mathbf{\Delta }{\mathit{C}}_{\mathit{m}}$ (%)
3D J-shape	$k\text{-}ϵ$	$0.0279$	$+5.84$
	$k\text{-}\omega$ SST	$0.0329$	$+24.60$
3D NACA 0015	$k\text{-}ϵ$	$0.0264$	Reference
	$k\text{-}\omega$ SST	$0.0281$	$+6.26$

. A comparison between all cases is also provided, through the difference in percentage between the values of the 3D NACA 0015 and the $k\text{-}ϵ$ model as a reference. The result obtained with the $k\text{-}ϵ$ turbulence model shows that the starting torque of the VAWT improves by 5.84% with the J-shaped profile compared to NACA 0015. This difference is significantly higher when the $k\text{-}\omega$ SST model is used as a reference, showing an 18.34% increase with the J-shaped profile. These results will be discussed further in Section 3.3.4.

• Starting torque comparison between 2D and 3D J-shape cases

The 2D outputs obtained by García Auyanet et al. [8] and the current 3D results can now be compared. The two main geometrical difference between the current and previously published studies is the 3D nature of the geometry not accounted for in [8] and the fact that the struts and hub were not considered either in the original study. The mean moment coefficient during an entire revolution of the VAWT is shown for both the 2D and 3D J-shaped cases in

Table 10. Comparison of the mean $C_m$ (one revolution) at $TSR=0.2$ between 2D J-shape [8] and the current 3D J-shape.

Airfoil	Turbulence Model	Mean ${\mathit{C}}_{\mathit{m}}$	$\mathbf{\Delta }{\mathit{C}}_{\mathit{m}}$ (%)
2D J-shape	$k\text{-}\omega$ SST	$0.0538$	Reference
3D J-shape	$k\text{-}\omega$ SST	$0.0329$	$-38.94$
	$k\text{-}ϵ$	$0.0279$	$-48.15$

. The mean moment coefficient appears lower for the 3D case than for the 2D case. This is discussed in more detail in Section 3.3.4.

3.3.4. Discussion

An aerodynamic and performance study was carried out to identify which airfoil offered optimum self-start capabilities. For both the J-shaped and NACA 0015 cases, under starting torque conditions, the angular velocity is so low that the case is nearly static, with the relative velocity of the profile itself being of similar value and direction as the speed imposed at the inlet. Therefore, during the rotation, there are regions where the airfoil angle of attack in absolute value is elevated, reaching dynamic stall ranges (see Figure 7), implying a high loss of lift and a high drag in comparison to cases with greater $TSR$. Under these conditions, as this VAWT is of the lift type, it has a lower moment to enable VAWT rotation. Due to the stall of the airfoil itself, a large wake is generated. This wake length and the airfoil’s dynamic stall are important to consider if a small wind farm of VAWTs is to be placed in an urban area, as it leads to a significant turbulent intensity, being in certain areas higher than 40%, as illustrated in Figure 7. This can also cause fatigue problems in the connection region between the struts and the blade, but also in the struts, as reported by [28,29]. At a structural level, this means that these regions need to be strengthened, and a structural fatigue analysis should be performed, in addition to experimental tests.

An important point highlighted in the CFD study is the design of the strut. As can be seen in Figure 7, the presence of a strut generates very little or no wake at all under the conditions of study, thus minimising the turning resistance and reducing possible effects due to turbulence, including noise.

In terms of flow behaviour, no major difference is seen between the J-shape and NACA 0015 cases (see Figure 7 and Figure 8). Both the turbulence intensity levels and the magnitude and direction of the wind speed are nearly identical throughout the revolution of the VAWT. The only difference is found, logically, around the airfoil geometry. In Figure 8, the formation of a vortex can be seen in the bitten region of the J-shaped airfoil, where the low velocity leads to high static pressure on this surface. Such pressure is responsible for an additional drag force, pushing the VAWT tangentially to its trajectory in certain azimuthal regions. Consequently, the drag of this profile is higher, as demonstrated in Figure 10, acting more like a Savonius VAWT compared to the NACA 0015 profile.

Theoretically, the moment causing a VAWT’s rotation is mainly a consequence of the generated lift, as per its design (H-type). The maximum moment occurs as many times as the number of blades in the model, on a periodic basis, and under the azimuthal angle where the generated lift is maximum (due to the angle of attack between the airfoil and the relative wind velocity direction). At low $TSR$, this is not noticeable, however, as several peaks are present. This is due to the high azimuthal range where the dynamic stall of the airfoil is produced, as the relative wind velocity direction and magnitude are almost constant and equal to the velocity inlet conditions. The generated lift is also reduced, increasing the drag, which is the main aerodynamic moment generator.

Figure 9 does not show clearly which airfoil provides higher performance. In Figure 10, it can be seen that the J-shaped-based VAWT displays a higher drag coefficient at $TSR=0.2$. The most remarkable fact is the comparison of the orders of magnitude between $C_d$ and $C_l$ in Figure 10 and Figure 11, respectively. In both cases, the magnitude of the drag coefficient is higher, although of a similar order, which is uncommon in lift-based VAWTs, where $C_l$ is usually one order of magnitude higher than $C_d$ [30]. This fact leads to a less harmonic (although periodic) result for the moment coefficient evolution (see Figure 9). Therefore, it appears that under starting torque conditions, it is as important that the airfoil can generate a lift coefficient at high angles of attack (late stall in the late windward region, 0${}^{\circ }$ < $\theta$ < 45${}^{\circ }$) as it is to generate sufficiently high drag in the upwind region (45${}^{\circ }$ < $\theta$ < 135${}^{\circ }$).

From Table 9, it appears that the 3D J-shape is able to provide a 5.84% higher moment coefficient than the 3D NACA 0015 when using the realizable $k\text{-}ϵ$ turbulence model with wall functions, which is 18.34% higher than when the $k\text{-}\omega$ SST turbulence model is used, under the same conditions. In all cases, this result is promising, since it would improve the VAWT’s ability to self-start at low wind speeds, thus reducing the initial energy consumption to start its movement. Likewise, the power generated at low $TSR$ conditions would also be higher, since the $C_p$ is proportional to the calculated $C_m$, with $C_p=TSR\times C_m$. As discussed in Section 1, the most commonly used turbulence model in CFD simulations of VAWTs is the $k\text{-}\omega$ SST. This is due to the better representation of this model in complex boundary layer flows under adverse pressure gradients and separation, as in VAWT cases, obtaining results more similar to the experimental ones [22]. The results obtained with this turbulence model are therefore a priori more reliable, pending experimental validation.

In the 2D case developed in [8], the authors concluded that the same J-shape profile improved the self-starting ability by 135% compared to the NACA 0015 profile. However, the present study demonstrated that this improvement is reduced to 18.34% when 3D cases are considered, resulting in a performance reduction between the 2D and 3D J-shaped VAWT of 38.94%. This difference may be due to two main factors: the three-dimensional effects caused by the tip vortices and/or the inclusion of the struts and hub in the current 3D model. In this study, it was found that, on average, the starting torque of the developed 3D design was 48.15% lower than in the 2D study performed by [8]. According to [31], in an H-type Darrieus small vertical wind turbine operating at $TSR=1.35$, the difference in the power coefficients of the simulated 2D and 3D cases is 21.4%, without the consideration of the struts. However, to study the specific influence on the VAWT performance loss due to tip vortices, a CFD study should be performed, considering only the 3D blades, studying the addition of end plates to avoid the flow moving from high to low pressure in the tips and to create such vortices. This will be considered in future work.

4. Conclusions

Based on initial 2D numerical studies of a J-shaped based VAWT [8], the design and simulation of the 3D J-shaped VAWT were carried out. Several structural and functional aspects of the 3D development of the turbine were investigated. The following conclusions can be drawn from this work.

• From the structural assessment, it was established that aluminium alloy hollow blades with ribs and stainless-steel struts with X-shaped beams with internal ribs provide the best structural integrity for the model.
• The 3D J-shaped VAWT showed a promising improvement in the moment coefficient compared to the 3D NACA 0015, with a potential increase of 5.84% as established with the realizable $k\text{-}ϵ$ turbulence model or 18.34% as established with the $k\text{-}\omega$ SST model. This enhances the VAWT’s self-starting ability and power generation at low $TSR$. The $k\text{-}ϵ$ turbulence model with the wall function can be considered a suitable option if a lower computational cost is required, knowing that the $k\text{-}\omega$ SST model is most certainly more accurate. This would, however, need to be validated with experimental data.
• The performance gain obtained with the 2D J-shaped VAWT in terms of self-starting ability is significantly reduced to 18.34% when a 3D model is used. This decrease may be attributed to 3D effects from tip vortices and the inclusion of the struts and hub in the 3D model.

Future studies will focus on wind tunnel testing and validation of the CFD results, additional CFD studies without the struts and hub to further improve the J-shaped blade, additional study of the effect of tip vortices and the evaluation of blade tip element implementation.