Modeling and Experimental Studies of the Photovoltaic System Performance in Climate Conditions of Poland
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Setup
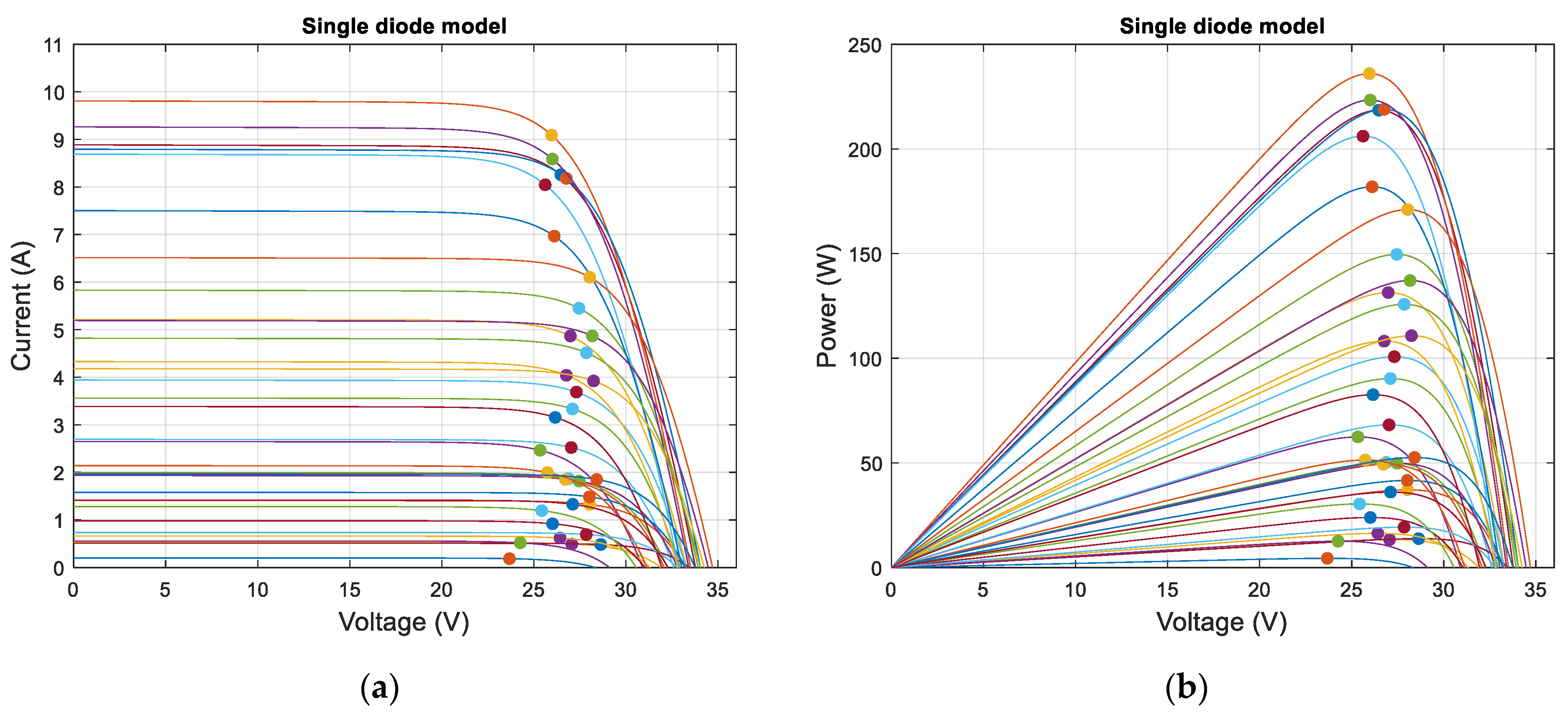
2.2. Single-Diode (SD) Model
2.3. Osterwald Model (OM)
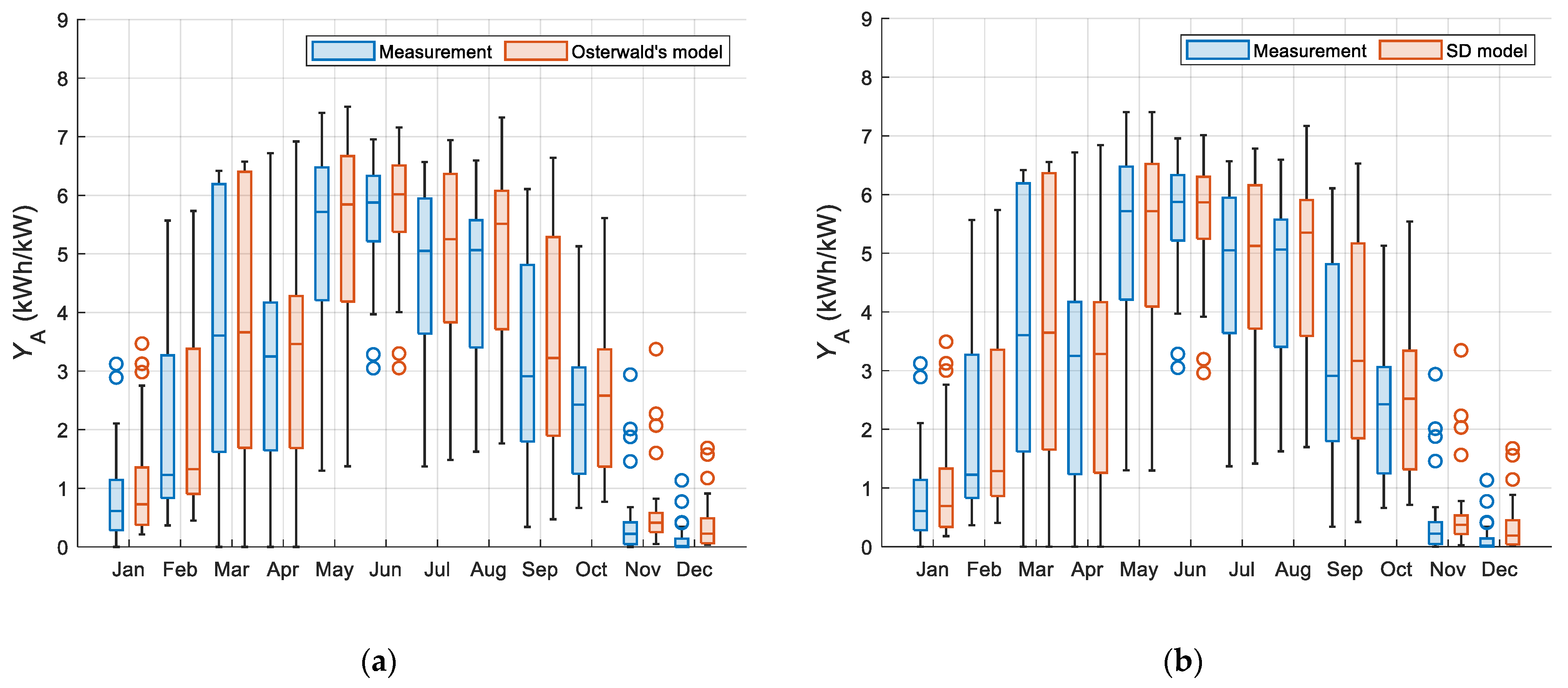
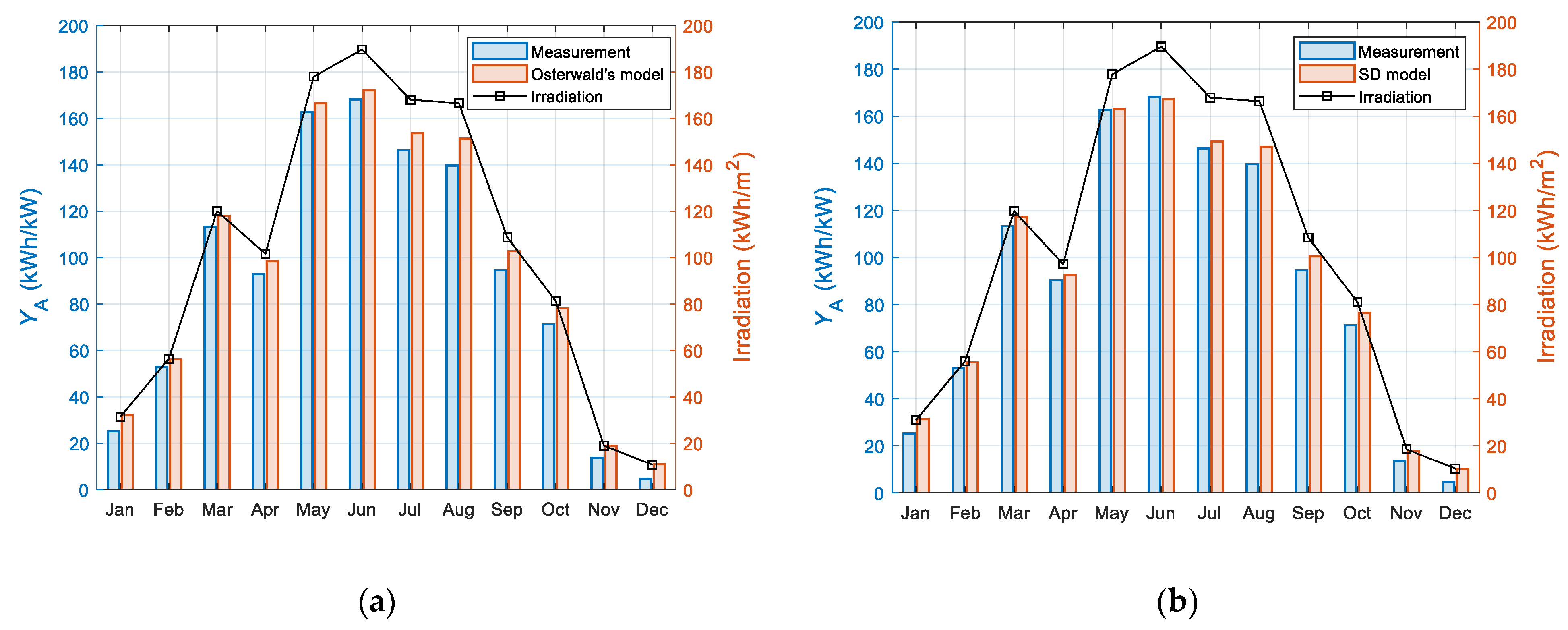
2.4. Performance Metrics
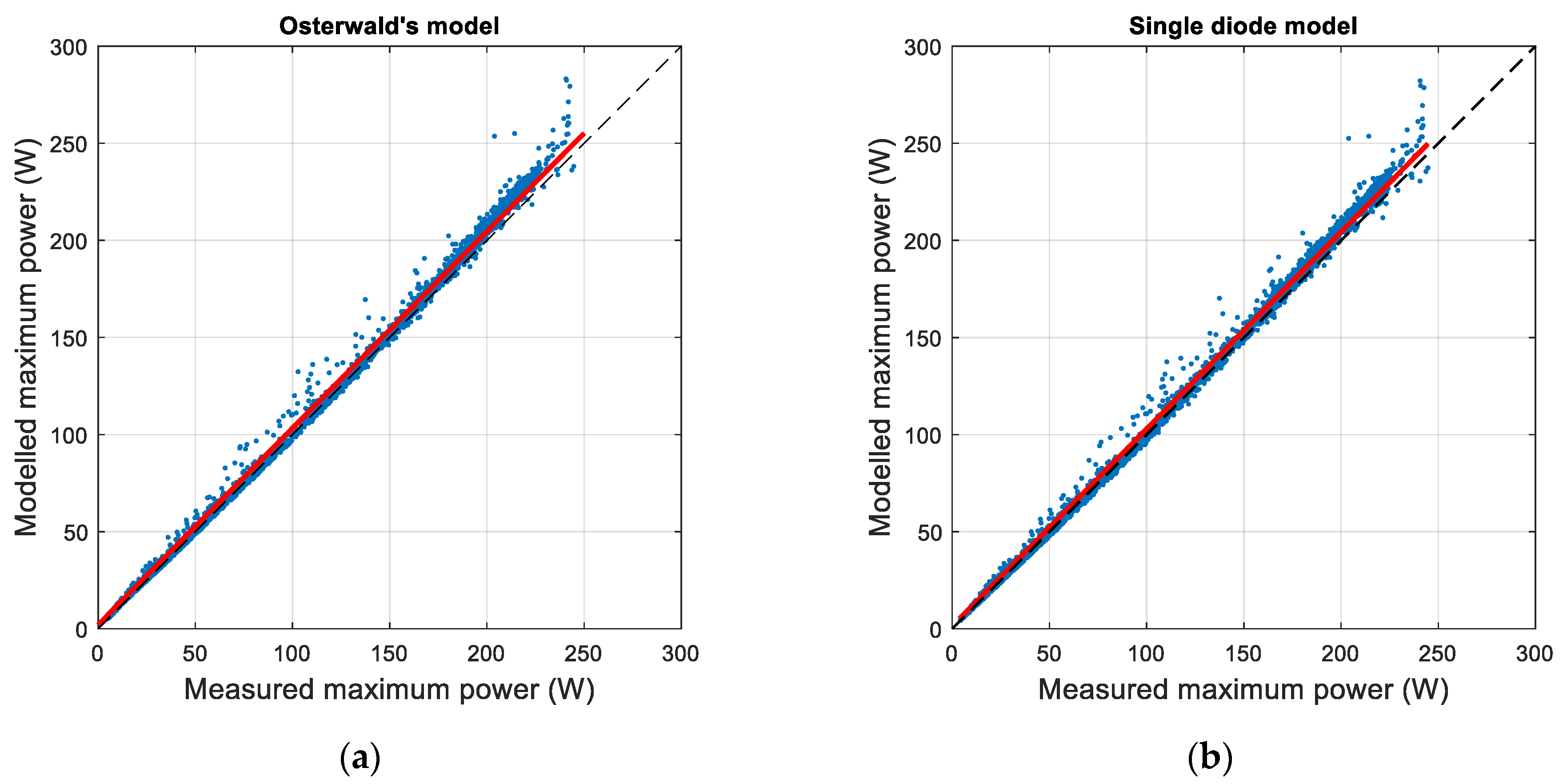
2.5. Experimental vs. Modeling Analysis
3. Results and Discussion
4. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Humada, A.M.; Hojabri, M.; Mekhilef, S.; Hamada, H.M. Solar Cell Parameters Extraction Based on Single and Double-Diode Models: A Review. Renew. Sustain. Energy Rev. 2016, 56, 494–509. [Google Scholar] [CrossRef]
- Kumar, M.; Kumar, A. An Efficient Parameters Extraction Technique of Photovoltaic Models for Performance Assessment. Sol. Energy 2017, 158, 192–206. [Google Scholar] [CrossRef]
- Massi Pavan, A.; Mellit, A.; Lughi, V. Explicit Empirical Model for General Photovoltaic Devices: Experimental Validation at Maximum Power Point. Sol. Energy 2014, 101, 105–116. [Google Scholar] [CrossRef]
- Attivissimo, F.; Adamo, F.; Carullo, A.; Lanzolla, A.M.L.; Spertino, F.; Vallan, A. On the Performance of the Double-Diode Model in Estimating the Maximum Power Point for Different Photovoltaic Technologies. Measurement 2013, 46, 3549–3559. [Google Scholar] [CrossRef]
- Cuce, E.; Cuce, P.M.; Bali, T. An Experimental Analysis of Illumination Intensity and Temperature Dependency of Photovoltaic Cell Parameters. Appl. Energy 2013, 111, 374–382. [Google Scholar] [CrossRef]
- Roberts, J.J.; Mendiburu Zevallos, A.A.; Cassula, A.M. Assessment of Photovoltaic Performance Models for System Simulation. Renew. Sustain. Energy Rev. 2017, 72, 1104–1123. [Google Scholar] [CrossRef]
- Dolara, A.; Leva, S.; Manzolini, G. Comparison of Different Physical Models for PV Power Output Prediction. Sol. Energy 2015, 119, 83–99. [Google Scholar] [CrossRef]
- Bader, S.; Ma, X.; Oelmann, B. One-Diode Photovoltaic Model Parameters at Indoor Illumination Levels—A Comparison. Sol. Energy 2019, 180, 707–716. [Google Scholar] [CrossRef]
- Chin, V.J.; Salam, Z.; Ishaque, K. Cell Modelling and Model Parameters Estimation Techniques for Photovoltaic Simulator Application: A Review. Appl. Energy 2015, 154, 500–519. [Google Scholar] [CrossRef]
- Ciulla, G.; Lo Brano, V.; Di Dio, V.; Cipriani, G. A Comparison of Different One-Diode Models for the Representation of I–V Characteristic of a PV Cell. Renew. Sustain. Energy Rev. 2014, 32, 684–696. [Google Scholar] [CrossRef]
- Jordehi, A.R. Parameter Estimation of Solar Photovoltaic (PV) Cells: A Review. Renew. Sustain. Energy Rev. 2016, 61, 354–371. [Google Scholar] [CrossRef]
- Lim, L.H.I.; Ye, Z.; Ye, J.; Yang, D.; Du, H. A Linear Method to Extract Diode Model Parameters of Solar Panels from a Single I–V Curve. Renew. Energy 2015, 76, 135–142. [Google Scholar] [CrossRef]
- Ortiz-Conde, A.; García-Sánchez, F.J. A New Approach to the Extraction of Single Exponential Diode Model Parameters. Solid-State Electron. 2018, 144, 33–38. [Google Scholar] [CrossRef]
- Yıldıran, N.; Tacer, E. Identification of Photovoltaic Cell Single Diode Discrete Model Parameters Based on Datasheet Values. Sol. Energy 2016, 127, 175–183. [Google Scholar] [CrossRef]
- Abbassi, A.; Ben Mehrez, R.; Touaiti, B.; Abualigah, L.; Touti, E. Parameterization of Photovoltaic Solar Cell Double-Diode Model Based on Improved Arithmetic Optimization Algorithm. Optik 2022, 253, 168600. [Google Scholar] [CrossRef]
- Chin, V.J.; Salam, Z.; Ishaque, K. An Accurate Modelling of the Two-Diode Model of PV Module Using a Hybrid Solution Based on Differential Evolution. Energy Convers. Manag. 2016, 124, 42–50. [Google Scholar] [CrossRef]
- El Ainaoui, K.; Zaimi, M.; Assaid, E.M. Innovative Approaches to Extract Double-Diode Model Physical Parameters of a PV Module Serving Outdoors under Real-World Conditions. Energy Convers. Manag. 2023, 292, 117365. [Google Scholar] [CrossRef]
- Yahya-Khotbehsara, A.; Shahhoseini, A. A Fast Modeling of the Double-Diode Model for PV Modules Using Combined Analytical and Numerical Approach. Sol. Energy 2018, 162, 403–409. [Google Scholar] [CrossRef]
- Ćalasan, M.; Abdel Aleem, S.H.E.; Zobaa, A.F. A New Approach for Parameters Estimation of Double and Triple Diode Models of Photovoltaic Cells Based on Iterative Lambert W Function. Sol. Energy 2021, 218, 392–412. [Google Scholar] [CrossRef]
- Houssein, E.H.; Zaki, G.N.; Diab, A.A.Z.; Younis, E.M.G. An Efficient Manta Ray Foraging Optimization Algorithm for Parameter Extraction of Three-Diode Photovoltaic Model. Comput. Electr. Eng. 2021, 94, 107304. [Google Scholar] [CrossRef]
- Gulkowski, S.; Muñoz Diez, J.V.; Aguilera Tejero, J.; Nofuentes, G. Computational Modeling and Experimental Analysis of Heterojunction with Intrinsic Thin-Layer Photovoltaic Module under Different Environmental Conditions. Energy 2019, 172, 380–390. [Google Scholar] [CrossRef]
- Khezzar, R.; Zereg, M.; Khezzar, A. Modeling Improvement of the Four Parameter Model for Photovoltaic Modules. Sol. Energy 2014, 110, 452–462. [Google Scholar] [CrossRef]
- Bana, S.; Saini, R.P. A Mathematical Modeling Framework to Evaluate the Performance of Single Diode and Double Diode Based SPV Systems. Energy Rep. 2016, 2, 171–187. [Google Scholar] [CrossRef]
- De Soto, W.; Klein, S.A.; Beckman, W.A. Improvement and Validation of a Model for Photovoltaic Array Performance. Sol. Energy 2006, 80, 78–88. [Google Scholar] [CrossRef]
- Ma, T.; Yang, H.; Lu, L. Solar Photovoltaic System Modeling and Performance Prediction. Renew. Sustain. Energy Rev. 2014, 36, 304–315. [Google Scholar] [CrossRef]
- Celik, A.N.; Acikgoz, N. Modelling and Experimental Verification of the Operating Current of Mono-Crystalline Photovoltaic Modules Using Four- and Five-Parameter Models. Appl. Energy 2007, 84, 1–15. [Google Scholar] [CrossRef]
- Eke, R.; Demircan, H. Performance Analysis of a Multi Crystalline Si Photovoltaic Module under Mugla Climatic Conditions in Turkey. Energy Convers. Manag. 2013, 65, 580–586. [Google Scholar] [CrossRef]
- Senturk, A.; Eke, R. A New Method to Simulate Photovoltaic Performance of Crystalline Silicon Photovoltaic Modules Based on Datasheet Values. Renew. Energy 2017, 103, 58–69. [Google Scholar] [CrossRef]
- Gulkowski, S.; Zdyb, A.; Dragan, P. Experimental Efficiency Analysis of a Photovoltaic System with Different Module Technologies under Temperate Climate Conditions. Appl. Sci. 2019, 9, 141. [Google Scholar] [CrossRef]
- Zdyb, A.; Gulkowski, S. Performance Assessment of Four Different Photovoltaic Technologies in Poland. Energies 2020, 13, 196. [Google Scholar] [CrossRef]
- Dane Publiczne. Instytut Meteorologii i Gospodarki Wodnej-Państwowy Instytut Badawczy. Available online: https://danepubliczne.imgw.pl/ (accessed on 23 August 2023).
- Dobos, A.P. An Improved Coefficient Calculator for the California Energy Commission 6 Parameter Photovoltaic Module Model. J. Sol. Energy Eng. 2012, 134, 021011. [Google Scholar] [CrossRef]
- National Renewable Energy Laboratory Golden. System Advisor Model Version 2022.11.29. Available online: https://sam.nrel.gov/ (accessed on 26 July 2023).
- Holmgren, W.F.; Hansen, C.W.; Mikofski, M.A. Pvlib Python: A Python Package for Modeling Solar Energy Systems. J. Open Source Softw. 2018, 3, 884. [Google Scholar] [CrossRef]
- Osterwald, C.R. Translation of Device Performance Measurements to Reference Conditions. Sol. Cells 1986, 18, 269–279. [Google Scholar] [CrossRef]
- IEC 61724-1:2021; Photovoltaic System Performance—Part 1: Monitoring. International Electrotechnical Commission: London, UK, 2021. Available online: https://webstore.iec.ch/publication/65561 (accessed on 10 September 2023).
- Romero-Fiances, I.; Muñoz-Cerón, E.; Espinoza-Paredes, R.; Nofuentes, G.; De la Casa, J. Analysis of the Performance of Various PV Module Technologies in Peru. Energies 2019, 12, 186. [Google Scholar] [CrossRef]
- Adaramola, M.S.; Vågnes, E.E.T. Preliminary Assessment of a Small-Scale Rooftop PV-Grid Tied in Norwegian Climatic Conditions. Energy Convers. Manag. 2015, 90, 458–465. [Google Scholar] [CrossRef]
- Malvoni, M.; Kumar, N.M.; Chopra, S.S.; Hatziargyriou, N. Performance and Degradation Assessment of Large-Scale Grid-Connected Solar Photovoltaic Power Plant in Tropical Semi-Arid Environment of India. Sol. Energy 2020, 203, 101–113. [Google Scholar] [CrossRef]
- The MathWorks Inc. MATLAB Version: 9.13.0 (R2022b); The MathWorks Inc.: Natick, MA, USA, 2023; Available online: https://www.mathworks.com/ (accessed on 23 August 2023).
- Torres-Ramírez, M.; Nofuentes, G.; Silva, J.P.; Silvestre, S.; Muñoz, J.V. Study on Analytical Modelling Approaches to the Performance of Thin Film PV Modules in Sunny Inland Climates. Energy 2014, 73, 731–740. [Google Scholar] [CrossRef]
- Kottek, M.; Grieser, J.; Beck, C.; Rudolf, B.; Rubel, F. World Map of the Köppen-Geiger Climate Classification Updated. Meteorol. Z. 2006, 15, 259–263. [Google Scholar] [CrossRef]
- Gulkowski, S. Specific Yield Analysis of the Rooftop PV Systems Located in South-Eastern Poland. Energies 2022, 15, 3666. [Google Scholar] [CrossRef]
- Kausika, B.B.; van Sark, W.G.J.H.M. Calibration and Validation of ArcGIS Solar Radiation Tool for Photovoltaic Potential Determination in the Netherlands. Energies 2021, 14, 1865. [Google Scholar] [CrossRef]
- Øgaard, M.B.; Riise, H.N.; Haug, H.; Sartori, S.; Selj, J.H. Photovoltaic System Monitoring for High Latitude Locations. Sol. Energy 2020, 207, 1045–1054. [Google Scholar] [CrossRef]
- Olczak, P.; Żelazna, A.; Stecuła, K.; Matuszewska, D.; Lelek, Ł. Environmental and Economic Analyses of Different Size Photovoltaic Installation in Poland. Energy Sustain. Dev. 2022, 70, 160–169. [Google Scholar] [CrossRef]
- Santhakumari, M.; Sagar, N. A Review of the Environmental Factors Degrading the Performance of Silicon Wafer-Based Photovoltaic Modules: Failure Detection Methods and Essential Mitigation Techniques. Renew. Sustain. Energy Rev. 2019, 110, 83–100. [Google Scholar] [CrossRef]
- Kaplanis, S.; Kaplani, E.; Kaldellis, J.K. PV Temperature and Performance Prediction in Free-Standing, BIPV and BAPV Incorporating the Effect of Temperature and Inclination on the Heat Transfer Coefficients and the Impact of Wind, Efficiency and Ageing. Renew. Energy 2022, 181, 235–249. [Google Scholar] [CrossRef]
- Murat Ates, A.; Singh, H. Rooftop Solar Photovoltaic (PV) Plant—One Year Measured Performance and Simulations. J. King Saud Univ. Sci. 2021, 33, 101361. [Google Scholar] [CrossRef]
- Drouiche, I.; Harrouni, S.; Arab, A.H. A New Approach for Modelling the Aging PV Module upon Experimental I–V Curves by Combining Translation Method and Five-Parameters Model. Electr. Power Syst. Res. 2018, 163, 231–241. [Google Scholar] [CrossRef]
- Krawczak, E. A Comparative Analysis of Measured and Simulated Data of PV Rooftop Installations Located in Poland. Energies 2023, 16, 5975. [Google Scholar] [CrossRef]
- Sarniak, M.T. Researches of the Impact of the Nominal Power Ratio and Environmental Conditions on the Efficiency of the Photovoltaic System: A Case Study for Poland in Central Europe. Sustainability 2020, 12, 6162. [Google Scholar] [CrossRef]
- Ritzen, M.J.; Vroon, Z.A.E.P.; Rovers, R.; Lupíšek, A.; Geurts, C.P.W. Environmental Impact Comparison of a Ventilated and a Non-Ventilated Building-Integrated Photovoltaic Rooftop Design in the Netherlands: Electricity Output, Energy Payback Time, and Land Claim. Sol. Energy 2017, 155, 304–313. [Google Scholar] [CrossRef]
- te Heesen, H.; Herbort, V.; Rumpler, M. Performance of Roof-Top PV Systems in Germany from 2012 to 2018. Sol. Energy 2019, 194, 128–135. [Google Scholar] [CrossRef]




| Module Characteristics | Inverter Characteristics | ||
|---|---|---|---|
| Maximum power under STC (Wp) | 250 (0%/+2%) | Nominal DC power (kW) | 21.4 |
| Open-circuit voltage Voc (V) | 37.4 | Nominal AC power (kVA) | 21 |
| Nominal voltage Vmpp (V) | 30.1 | Maximum DC Voltage (V) | 1000 |
| Short-circuit current Isc (A) | 8.83 | DC operating voltage range (V) | 200–1000 |
| Nominal current Impp (A) | 8.31 | MPPT DC operating voltage range (V) | 350–800 |
| Efficiency (%) | 15.4 | Maximum efficiency (%) | 98 |
| Temperature coefficient of Voc (%/°C) | −0.30 | ||
| Temperature coefficient of Voc (V/°C) | −0.1122 | ||
| Temperature coefficient of Isc (%/°C) | 0.04 | ||
| Temperature coefficient of Isc (A/°C) | 0.0035 | ||
| Temperature coefficient of power (%/°C) | −0.40 | ||
| Temperature coefficient of power (W/°C) | 1.00 | ||
| Nominal operating cell temperature (NOCT) (°C) | 45 °C ± 2% | ||
| PV panel area (m2) | 1.63 | ||
| PV panel weight (kg) | 19 | ||
| Ref. parameters | IL,ref (A) | I0,ref (A) | aref | Rs,ref (Ω) | Rsh,ref (Ω) |
| 8.8330 | 6.893 × 10−10 | 1.6073 | 0.3180 | 844.04 |
| Month | Osterwald Model | Single-Diode Model |
|---|---|---|
| 1 | 0.862 | 0.860 |
| 2 | 0.974 | 0.973 |
| 3 | 0.983 | 0.983 |
| 4 | 0.935 | 0.934 |
| 5 | 0.965 | 0.966 |
| 6 | 0.966 | 0.967 |
| 7 | 0.971 | 0.972 |
| 8 | 0.967 | 0.968 |
| 9 | 0.976 | 0.976 |
| 10 | 0.971 | 0.972 |
| 11 | 0.941 | 0.938 |
| 12 | 0.627 | 0.623 |
| Month | Osterwald Model | Single-Diode Model | ||
|---|---|---|---|---|
| RMSE | MBE | RMSE | MBE | |
| 1 | 0.349 | 0.159 | 0.351 | 0.145 |
| 2 | 0.074 | 0.032 | 0.068 | 0.023 |
| 3 | 0.054 | 0.026 | 0.050 | 0.021 |
| 4 | 0.135 | 0.031 | 0.119 | 0.015 |
| 5 | 0.064 | 0.015 | 0.050 | −0.007 |
| 6 | 0.064 | 0.020 | 0.048 | −0.010 |
| 7 | 0.091 | 0.043 | 0.062 | 0.011 |
| 8 | 0.118 | 0.072 | 0.082 | 0.040 |
| 9 | 0.126 | 0.078 | 0.101 | 0.055 |
| 10 | 0.130 | 0.083 | 0.115 | 0.065 |
| 11 | 0.236 | 0.127 | 0.201 | 0.090 |
| 12 | 0.756 | 0.399 | 0.748 | 0.355 |
| Month | Osterwald Model | Single-Diode Model |
|---|---|---|
| 1 | 0.275 | 0.244 |
| 2 | 0.065 | 0.049 |
| 3 | 0.042 | 0.034 |
| 4 | 0.060 | 0.025 |
| 5 | 0.024 | 0.003 |
| 6 | 0.023 | −0.005 |
| 7 | 0.051 | 0.022 |
| 8 | 0.083 | 0.053 |
| 9 | 0.088 | 0.065 |
| 10 | 0.097 | 0.075 |
| 11 | 0.387 | 0.308 |
| 12 | 1.362 | 1.177 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gulkowski, S. Modeling and Experimental Studies of the Photovoltaic System Performance in Climate Conditions of Poland. Energies 2023, 16, 7017. https://doi.org/10.3390/en16207017
Gulkowski S. Modeling and Experimental Studies of the Photovoltaic System Performance in Climate Conditions of Poland. Energies. 2023; 16(20):7017. https://doi.org/10.3390/en16207017
Chicago/Turabian StyleGulkowski, Slawomir. 2023. "Modeling and Experimental Studies of the Photovoltaic System Performance in Climate Conditions of Poland" Energies 16, no. 20: 7017. https://doi.org/10.3390/en16207017
APA StyleGulkowski, S. (2023). Modeling and Experimental Studies of the Photovoltaic System Performance in Climate Conditions of Poland. Energies, 16(20), 7017. https://doi.org/10.3390/en16207017





