Simulation and Research of Methane Premixed Combustion Characteristics Based on Constant Volume Combustion Chamber with Different Ignition Modes
Abstract
1. Introduction
2. The Numerical Simulation Model
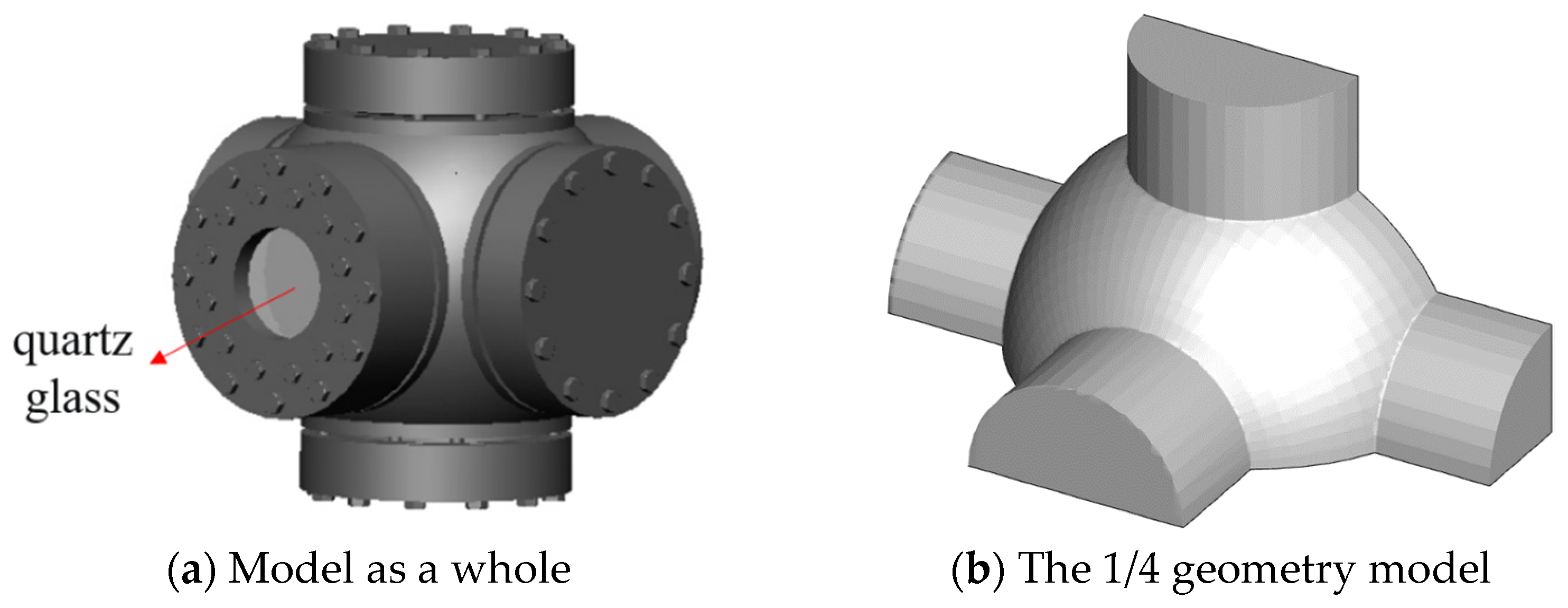
2.1. Geometric Model
2.2. Numerical Set Up
2.2.1. Mathematical Model
- (1)
- Turbulence model
- (2)
- Combustion model
- (3)
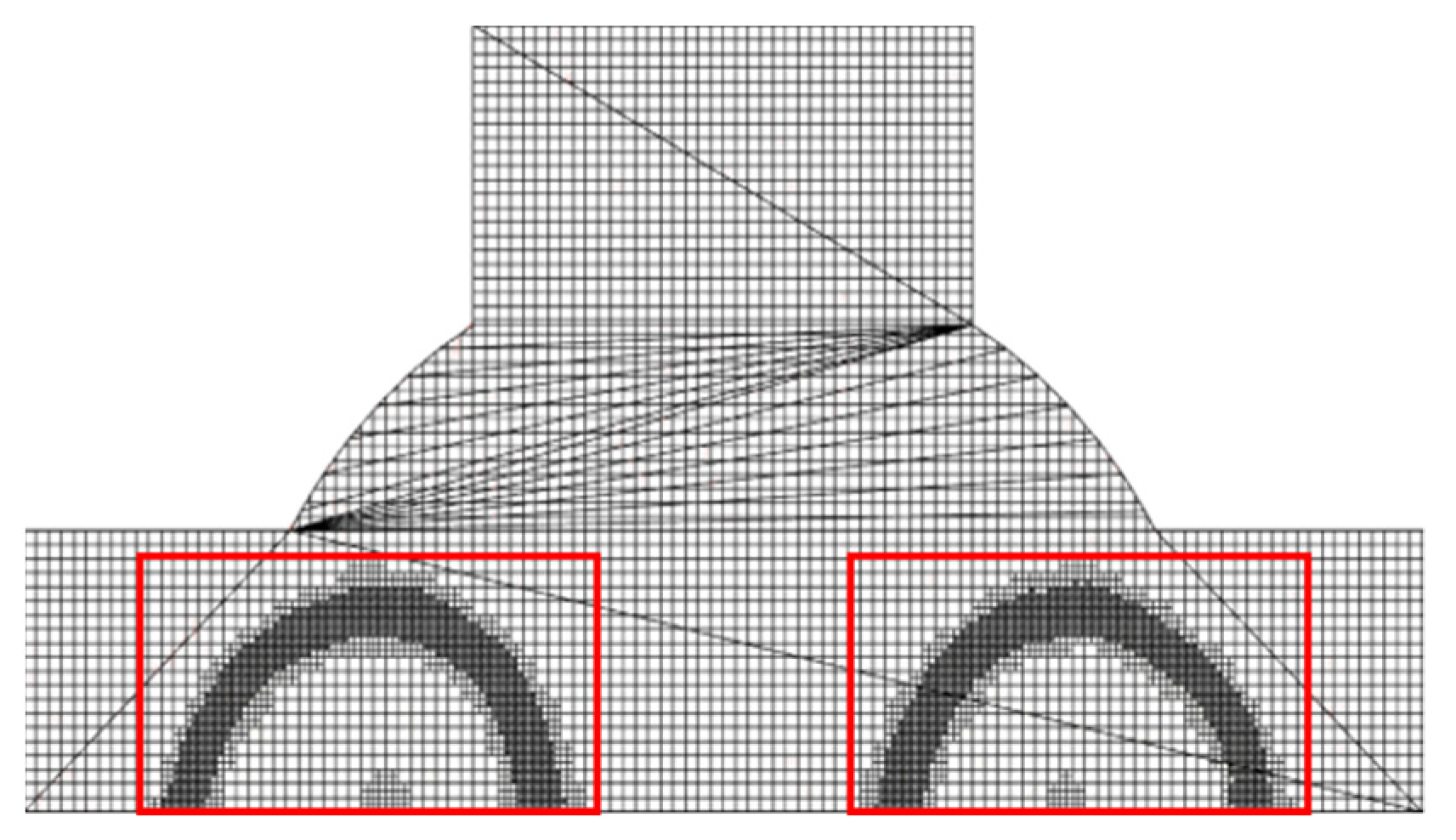
- Calculation grid
- (4)
- Parameter definition
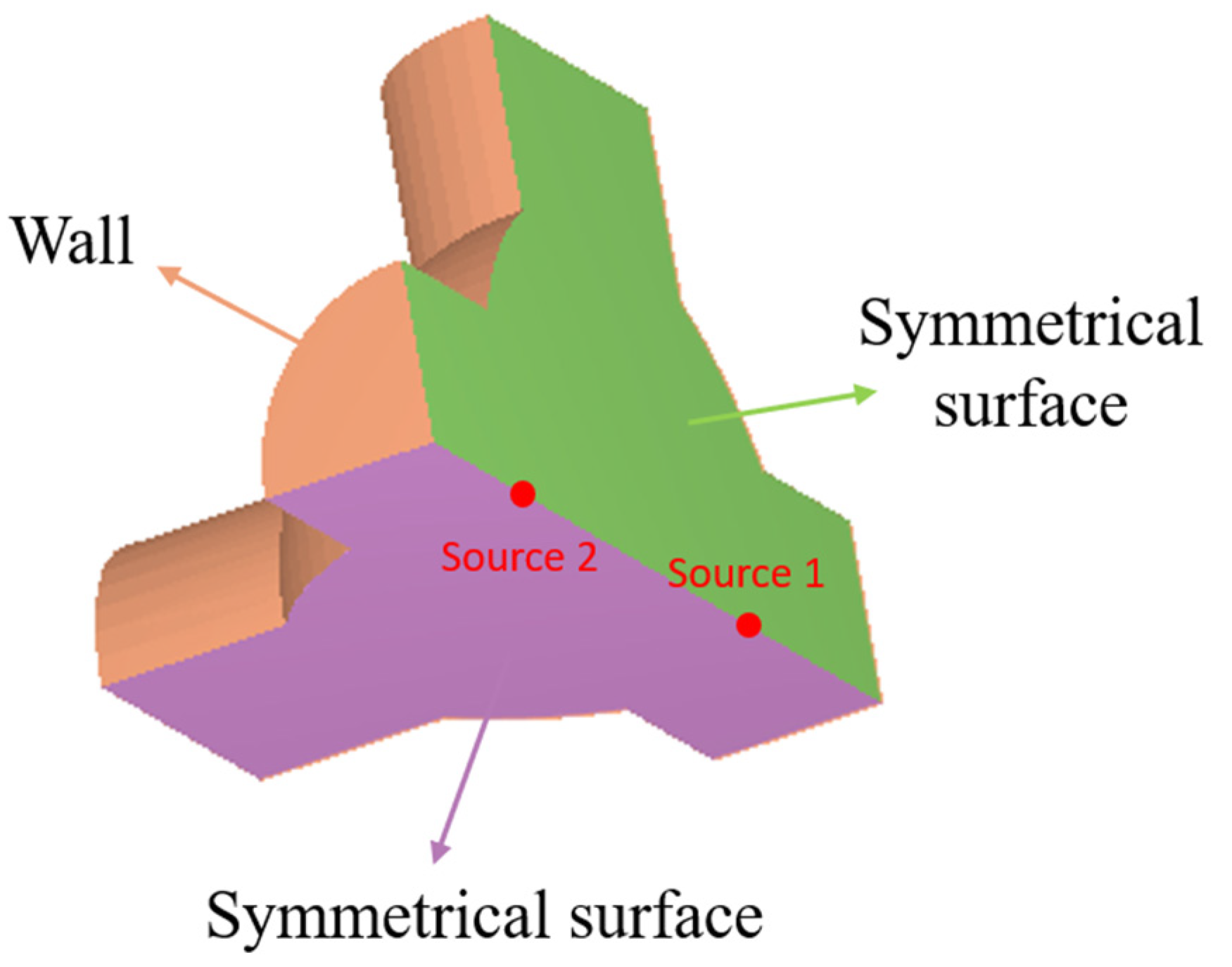
2.2.2. Boundary Conditions and Initial Conditions
2.3. Test and Model Verification
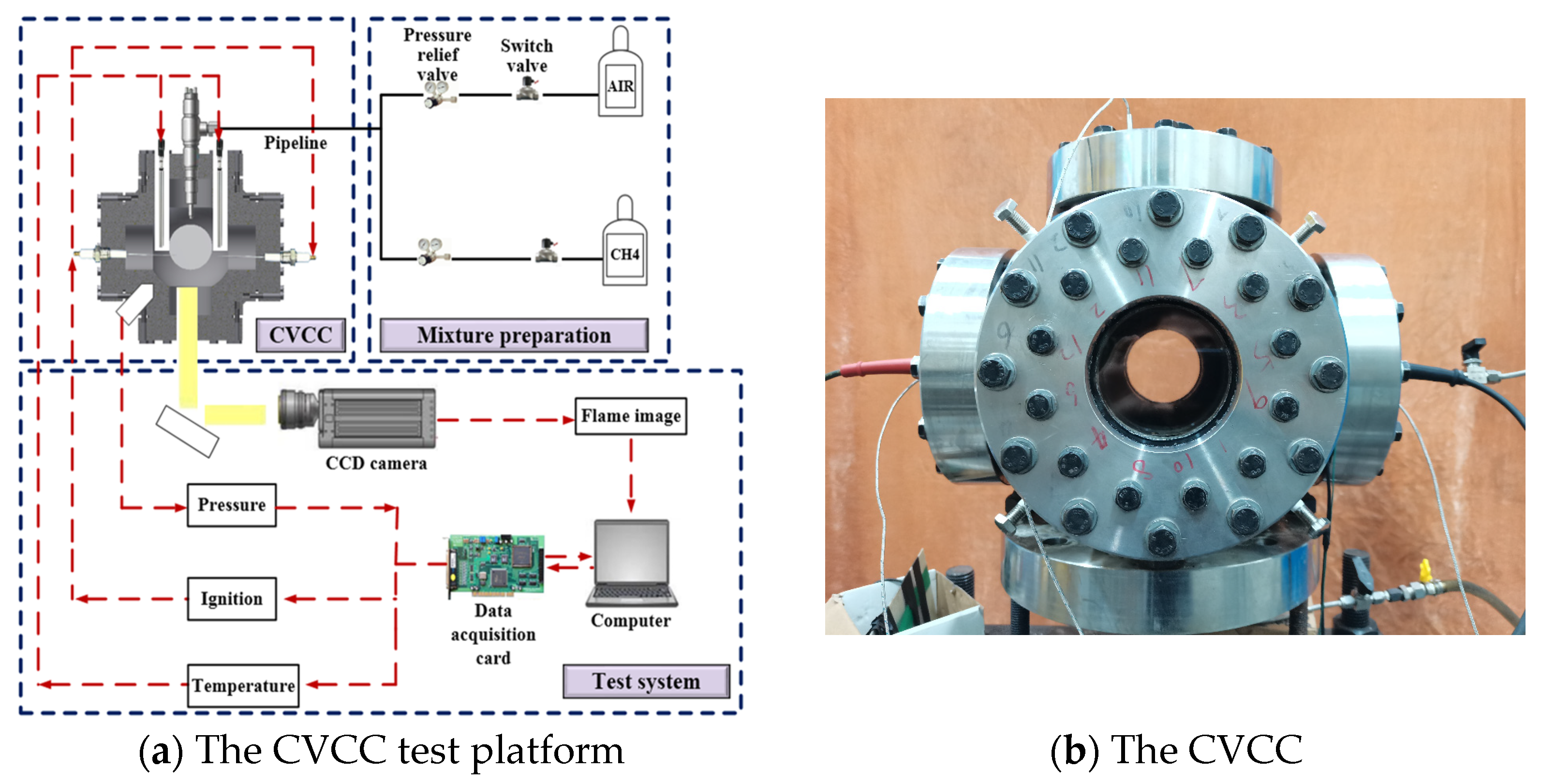
2.3.1. Experiment Setup
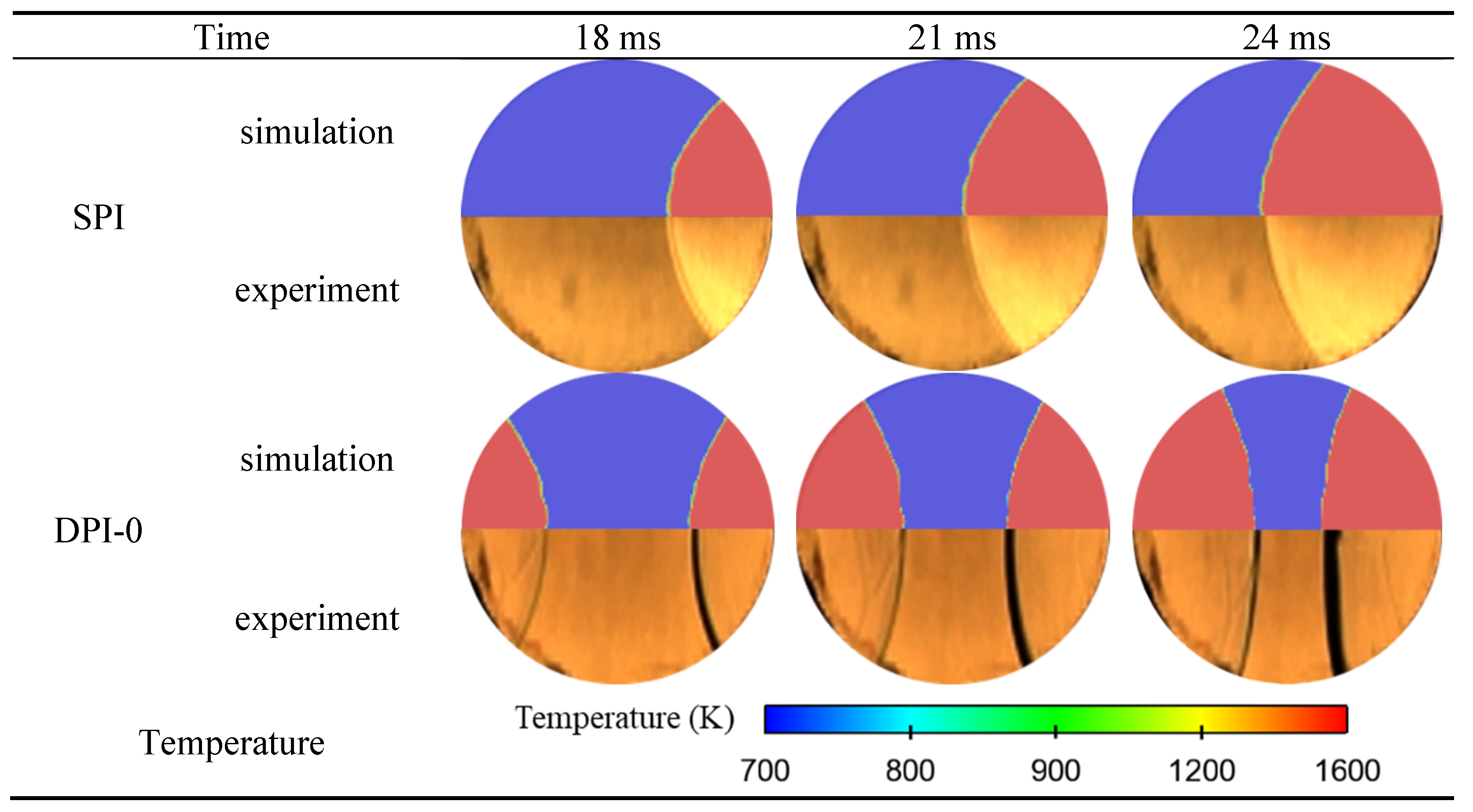
2.3.2. Validation of the Model
3. Results
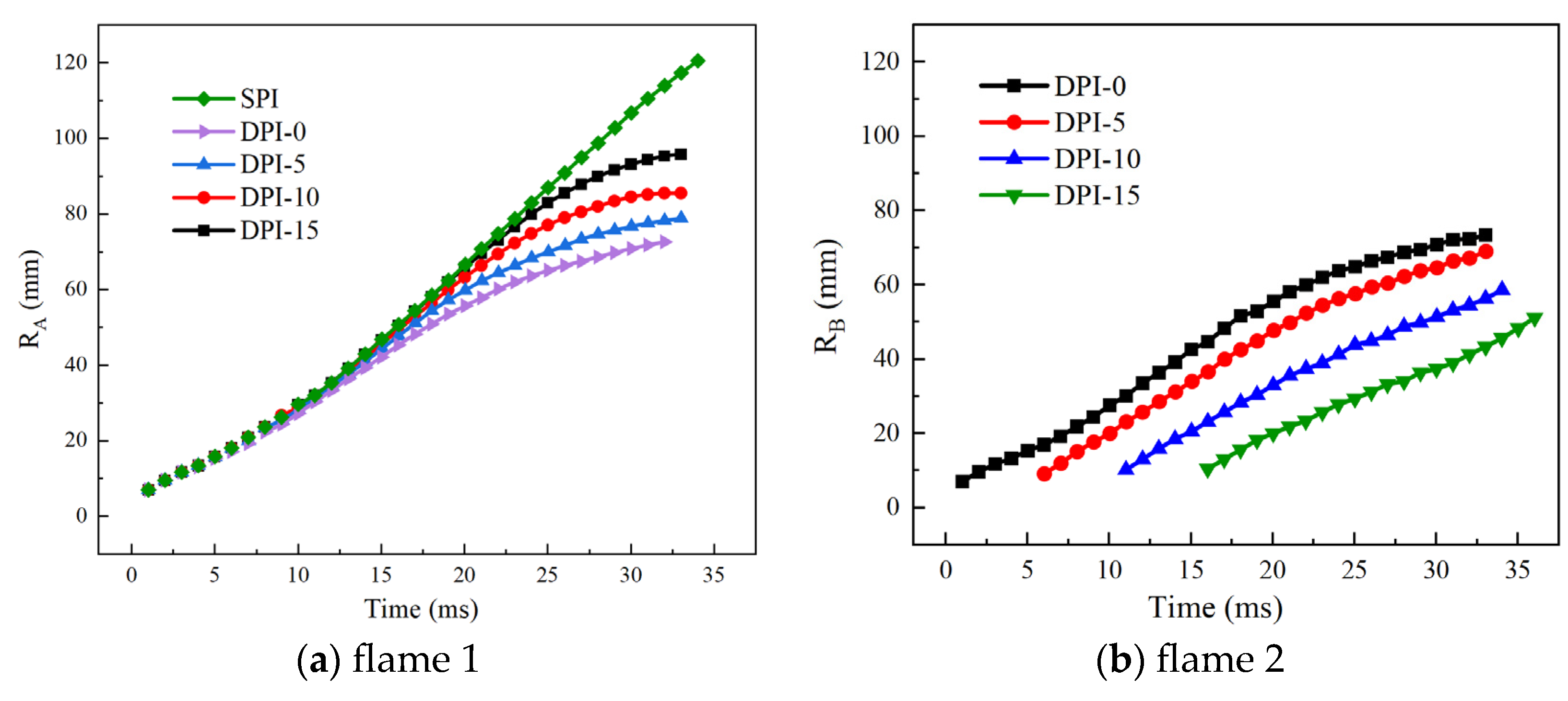
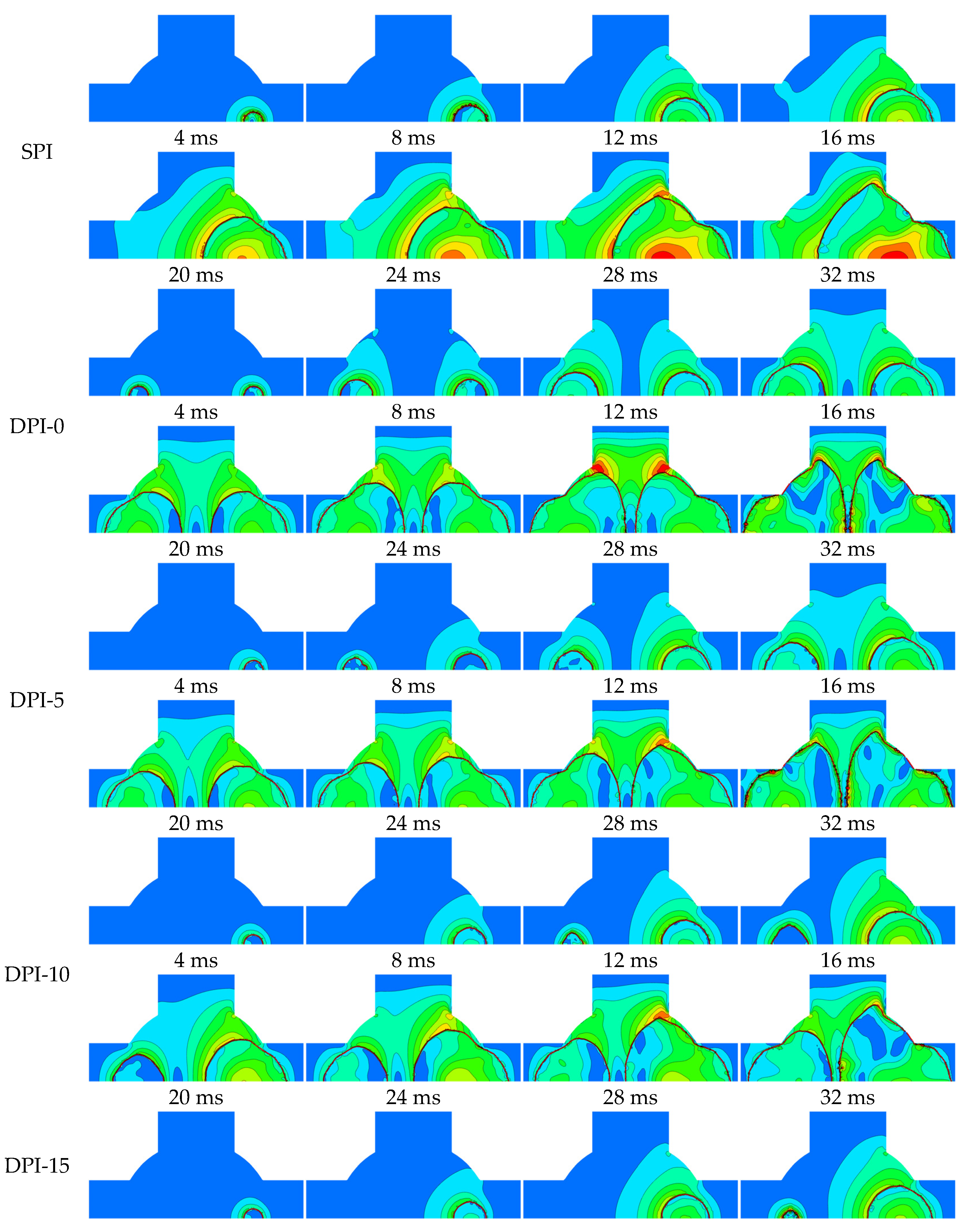
3.1. Flame Propagation Characteristics
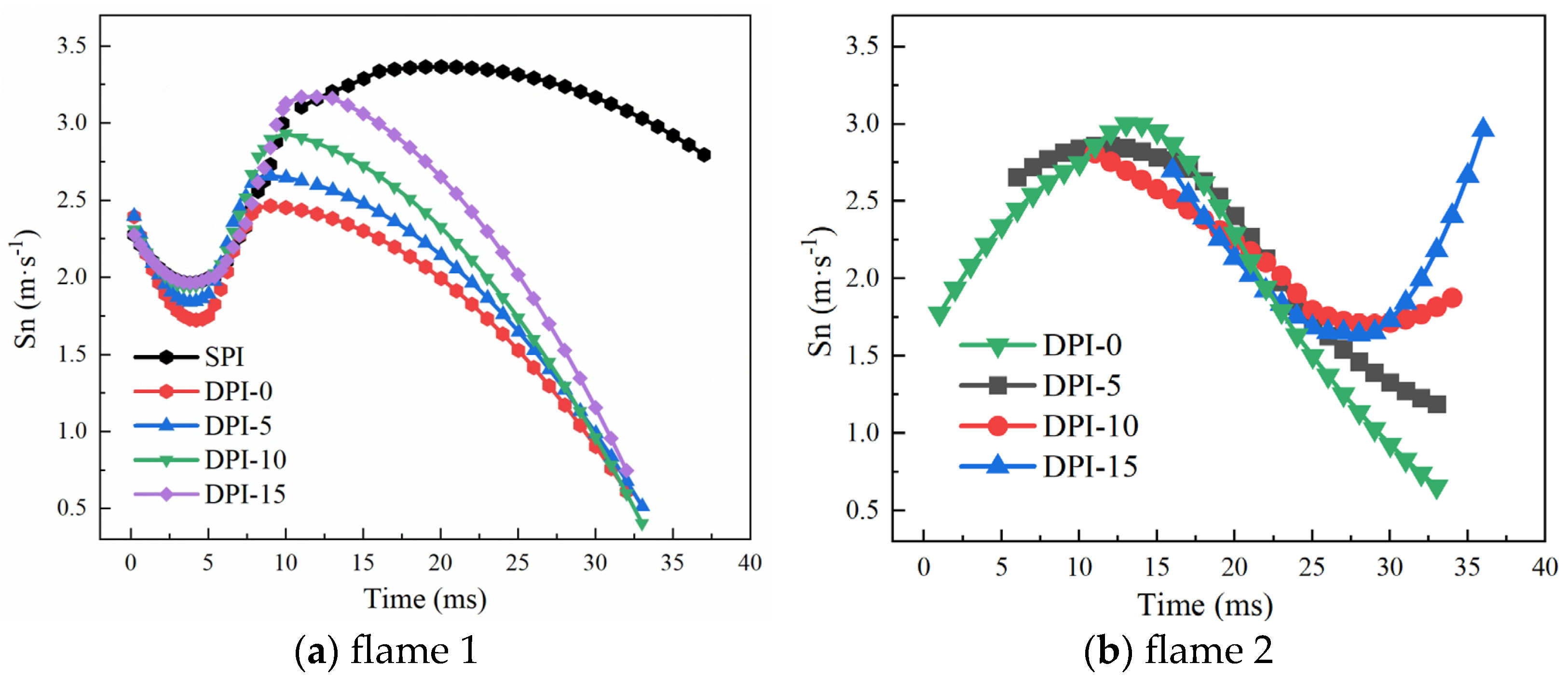
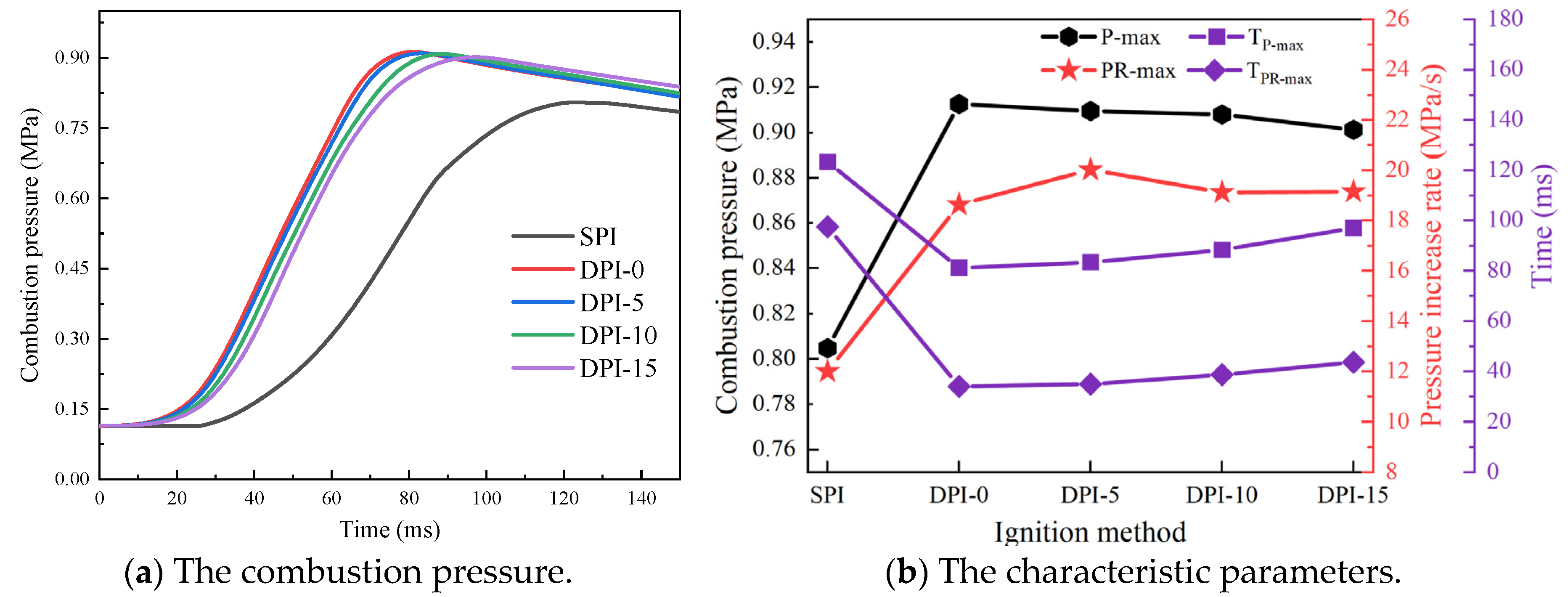
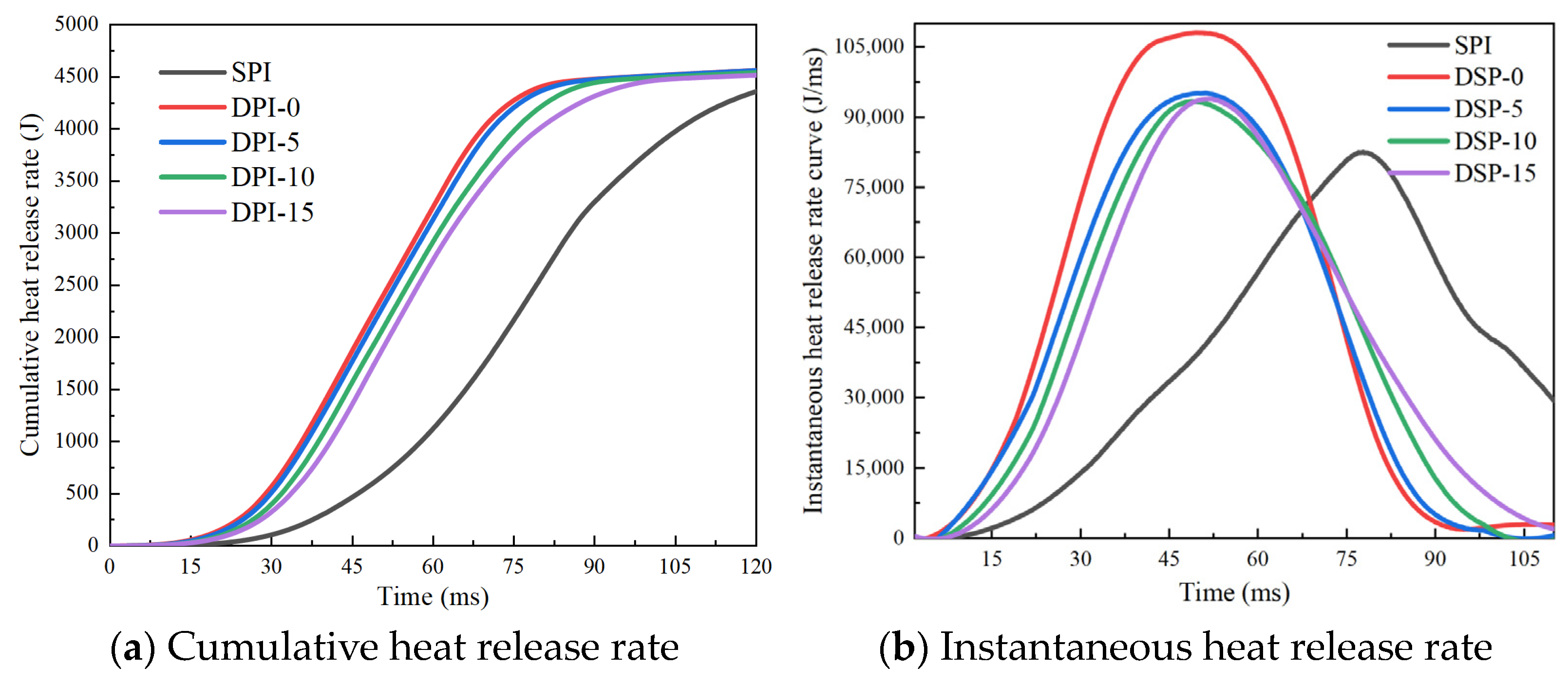
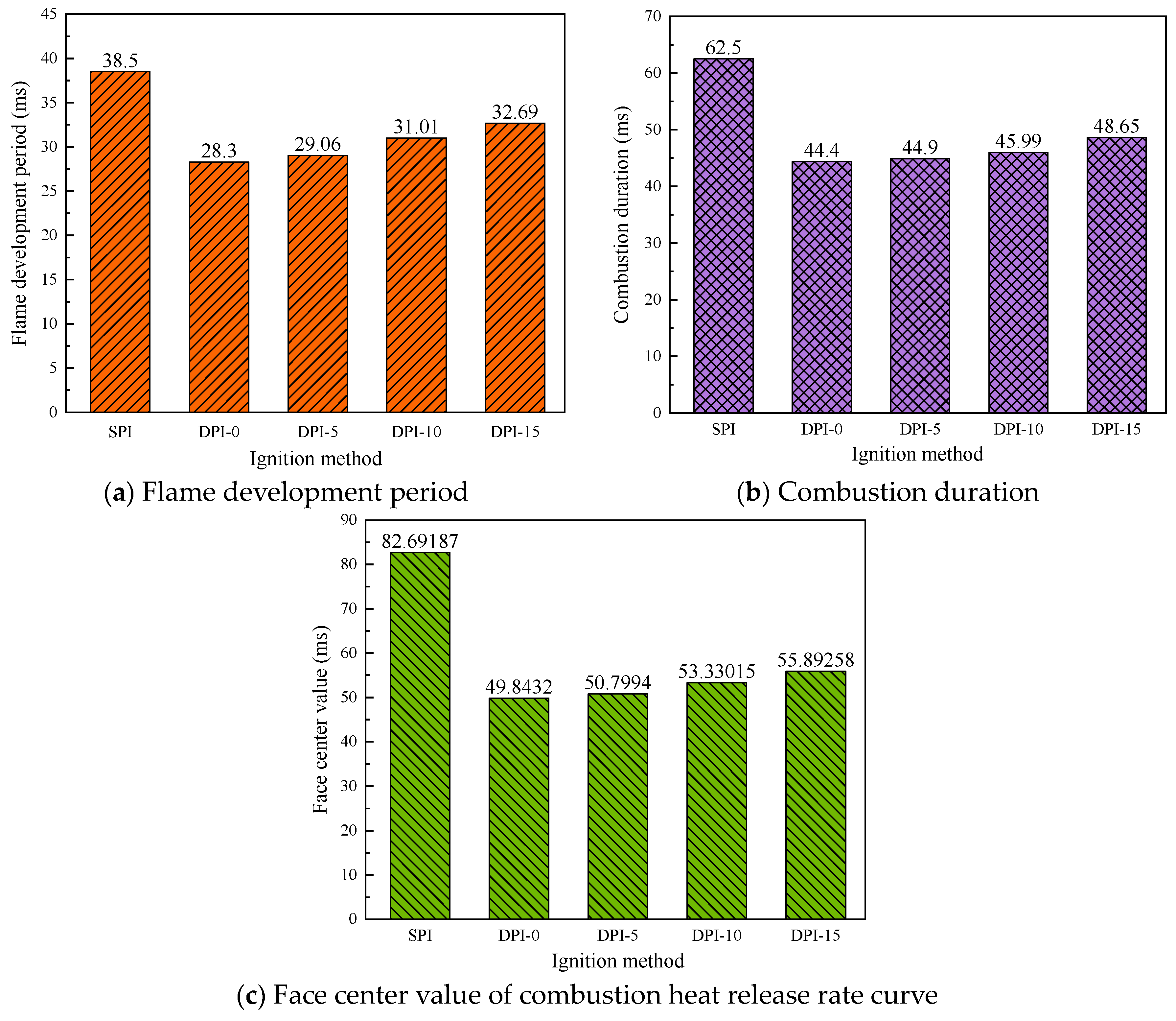
3.2. Combustion Characteristics
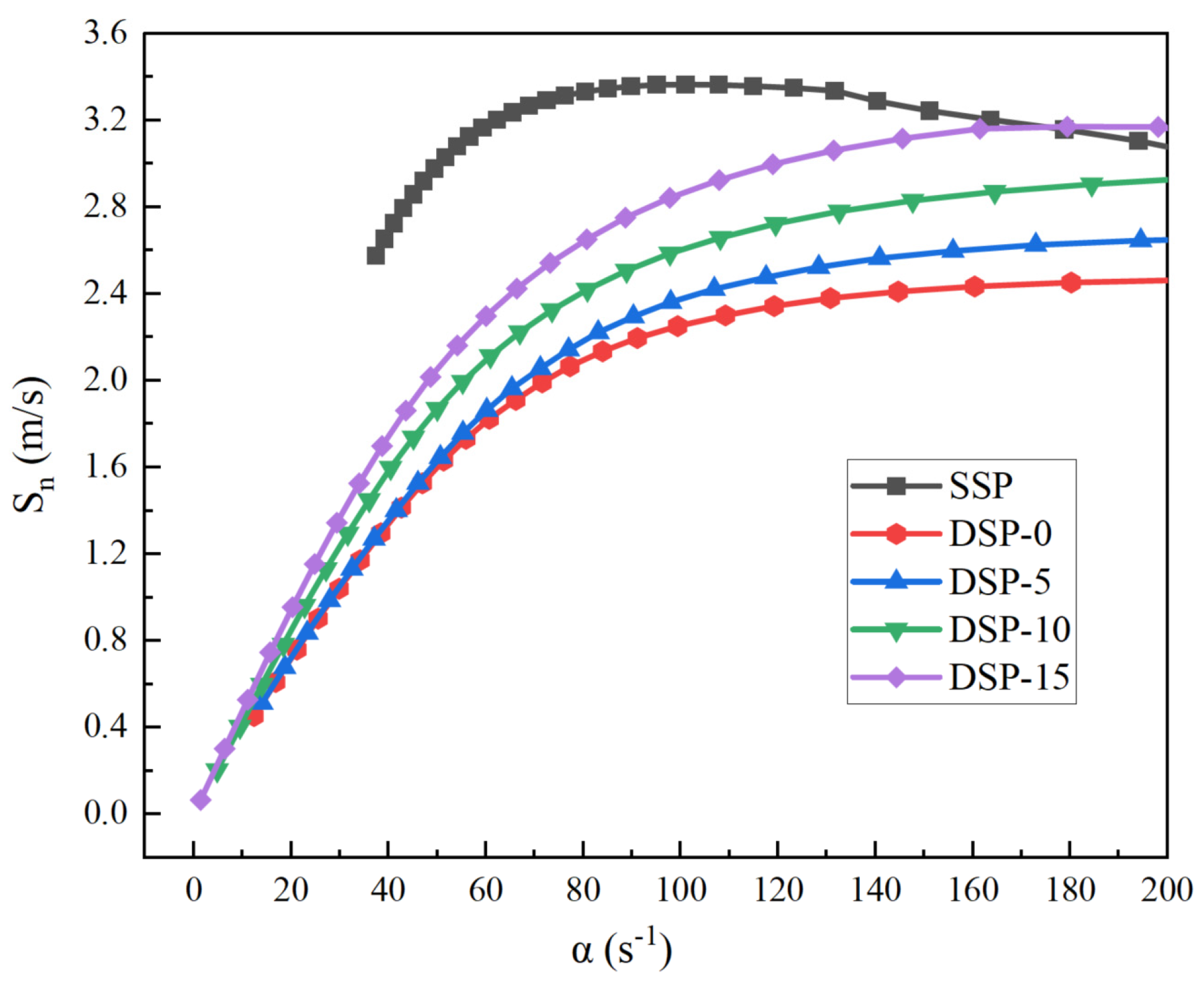
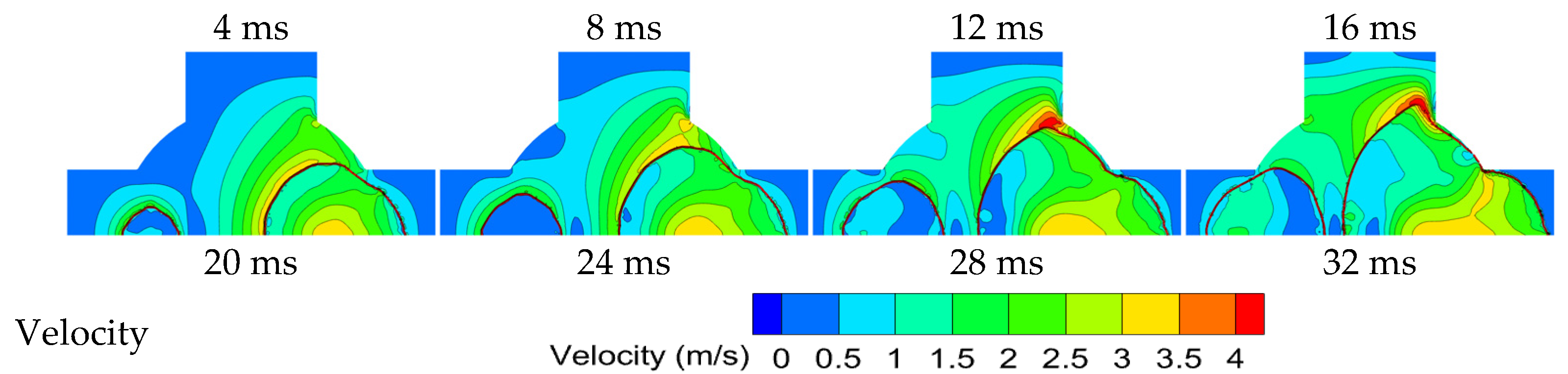
3.3. Interaction between Turbulence and Flame
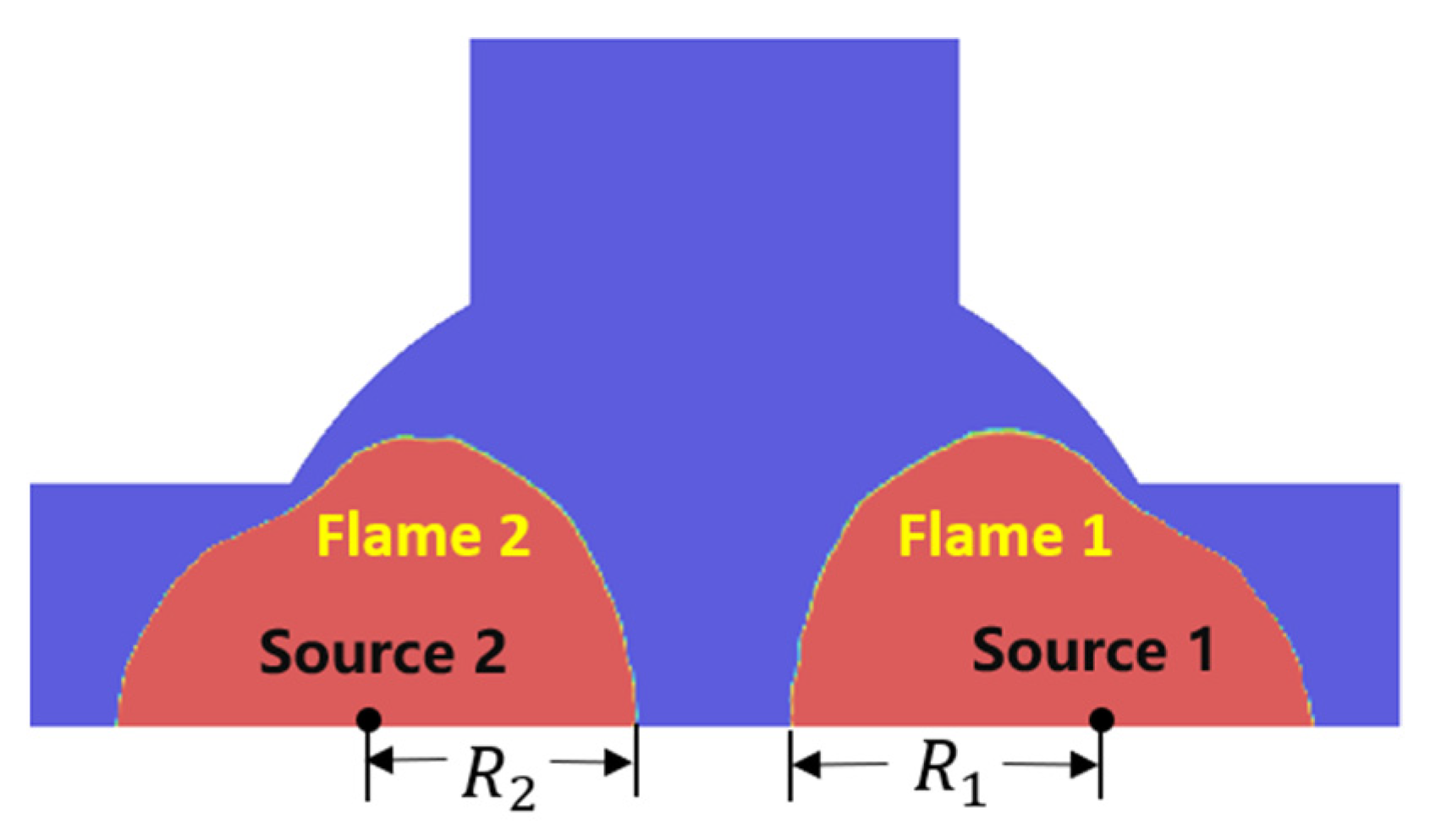
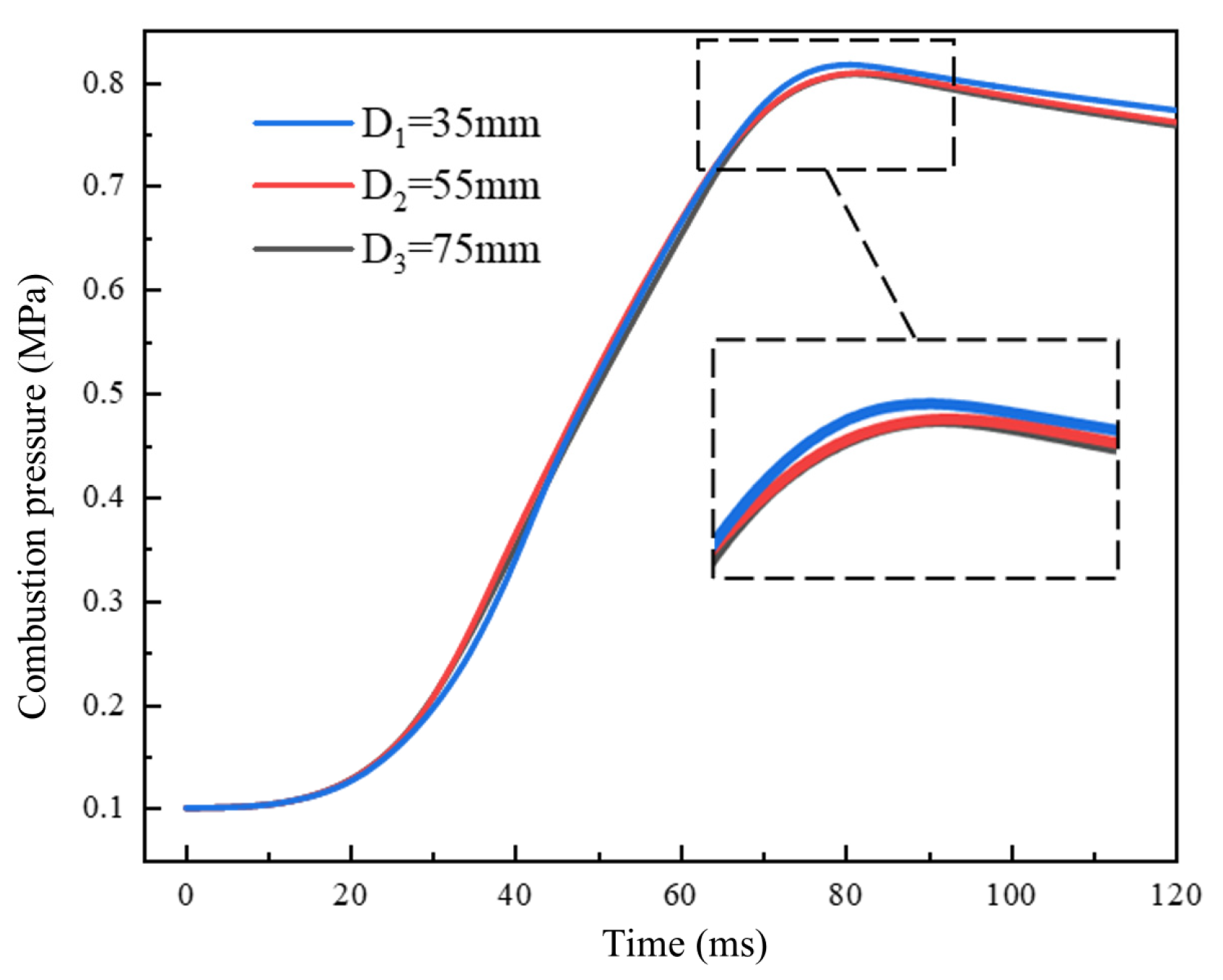
3.4. Influence of Ignition Position on Premixed Combustion Characteristics of Dual Spark-Ignition
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Symbol | Name | Unit |
| SPI | Single point ignition | |
| DPI | Dual point ignition | |
| CVCC | Constant volume combustion chamber | |
| Equal area radius | mm | |
| Flame propagation rate | m/s | |
| Flame surface stretch rate | 1/s | |
| Unstretched flame propagation speed | m/s | |
| Markstein length | m | |
| Instantaneous heat release rate | KJ/s | |
| Cumulative heat release rate | J | |
| Pressure | MPa | |
| P-max | Maximum combustion pressure | MPa |
| PR-max | Maximum pressure increase rate | MPa/s |
| Tp-max | Moment of peak combustion pressure | |
| TPR-max | Moment of maximum pressure increase rate |
References
- Tian, Z.; Wang, Y.; Zhen, X.; Liu, Z. The effect of methanol production and application in internal combustion engines on emissions in the context of carbon neutrality: A review. Fuel 2022, 320, 123902. [Google Scholar] [CrossRef]
- Li, M.; Wu, H.; Zhang, T.; Shen, B.; Zhang, Q.; Li, Z. A comprehensive review of pilot ignited high pressure direct injection natural gas engines: Factors affecting combustion, emissions and performance. Renew. Sustain. Energy Rev. 2020, 119, 109653. [Google Scholar] [CrossRef]
- Cong, X.; Ji, C.; Wang, S. Investigation into engine performance of a hydrogen-dimethyl ether spark-ignition engine under various dimethyl ether fractions. Fuel 2021, 306, 121429. [Google Scholar] [CrossRef]
- Shu, J.; Fu, J.Q.; Liu, J.P.; Wang, S.Q.; Yin, Y.S.; Deng, B.L.; Becker, S.M. Influences of excess air coefficient on combustion and emission performance of diesel pilot ignition natural gas engine by coupling computational fluid dynamics with reduced chemical kinetic model. Energy Convers. Manag. 2019, 187, 283–296. [Google Scholar] [CrossRef]
- Benajes, J.; García, A.; Monsalve-Serrano, J.; Boronat, V. Achieving clean and efficient engine operation up to full load by combining optimized RCCI and dual-fuel diesel-gasoline combustion strategies. Energy Convers. Manag. 2017, 136, 142–151. [Google Scholar] [CrossRef]
- Gong, C.; Sun, J.; Liu, F. Numerical study of twin-spark plug arrangement effects on flame, combustion and emissions of a medium compression ratio direct-injection methanol engine. Fuel 2020, 279, 118427. [Google Scholar] [CrossRef]
- Altin, İ.; Sezer, İ.; Bilgin, A. Effects of the Stroke/Bore Ratio on the Performance Parameters of a Dual-Spark-Ignition (DSI) Engine. Energy Fuels 2009, 23, 1825–1831. [Google Scholar] [CrossRef]
- Altın, İ.; Bilgin, A. A parametric study on the performance parameters of a twin-spark SI engine. Energy Convers. Manag. 2009, 50, 1902–1907. [Google Scholar] [CrossRef]
- Altın, İ.; Bilgin, A. Quasi-dimensional modeling of a fast-burn combustion dual-plug spark-ignition engine with complex combustion chamber geometries. Appl. Therm. Eng. 2015, 87, 678–687. [Google Scholar] [CrossRef]
- Altın, İ.; Bilgin, A.; Sezer, İ. Theoretical investigation on combustion characteristics of ethanol-fueled dual-plug SI engine. Fuel 2019, 257, 116068. [Google Scholar] [CrossRef]
- Chen, W.; Pan, J.; Fan, B.; Otchere, P.; Miao, N.; Lu, Y. Numerical investigation of dual-fuel injection timing on air-fuel mixing and combustion process in a novel natural gas-diesel rotary engine. Energy Convers. Manag. 2018, 176, 334–348. [Google Scholar] [CrossRef]
- Ji, C.W.; Shi, C.; Wang, S.F.; Yang, J.X.; Su, T.; Wang, D. Effect of dual-spark plug arrangements on ignition and combustion processes of a gasoline rotary engine with hydrogen direct-injection enrichment. Energy Convers. Manag. 2019, 181, 372–381. [Google Scholar] [CrossRef]
- Shi, C.; Ji, C.; Wang, S.; Yang, J.; Li, X.; Ge, Y. Numerical simulation on combustion process of a hydrogen direct-injection stratified gasoline Wankel engine by synchronous and asynchronous ignition modes. Energy Convers. Manag. 2019, 183, 14–25. [Google Scholar] [CrossRef]
- Chang, K.; Ji, C.; Wang, S.; Yang, J.; Wang, H.; Meng, H.; Liu, D. Numerical investigation of the synchronous and asynchronous changes of ignition timing in a double spark plugs direct injection rotary engine. Energy 2023, 268, 126688. [Google Scholar] [CrossRef]
- Gong, C.; Sun, J.; Chen, Y.; Liu, F. Numerical study of cold-start performances of a medium compression ratio direct-injection twin-spark plug synchronous ignition engine fueled with methanol. Fuel 2021, 285, 119235. [Google Scholar] [CrossRef]
- Gong, C.; Sun, J.; Liu, F. Numerical research on combustion and emissions behaviors of a medium compression ratio direct-injection twin-spark plug synchronous ignition methanol engine under steady-state lean-burn conditions. Energy 2021, 215, 119193. [Google Scholar] [CrossRef]
- Yan, X.; Feng, H.; Zuo, Z.; Jia, B.; Zhang, Z.; Wu, L. Research on the influence of dual spark ignition strategy at combustion process for dual cylinder free piston generator under direct injection. Fuel 2021, 299, 120911. [Google Scholar] [CrossRef]
- Lauvergne, R.; Hallot, J. Investigation of the Effect of Double Ignition on the Combustion Processes in a 2-valves Gasoline Engine Through 3D Simulation. SAE Trans. 2003, 112, 87–99. [Google Scholar]
- Hwang, P.W.; Chen, X.C.; Cheng, H.C. Influences of Ignition Timing, Spark Plug and Intake Port Locations on the Combustion Performance of a Simulated Rotary Engine. J. Mech. 2016, 32, 579–591. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, A.; Deng, B.; Xu, Z.; Feng, R.; Fu, J.; Liu, X.; Zhang, G.; Zhou, L. The influences of ignition modes on the performances for a motorcycle single cylinder gasoline engine at lean burn operation: Looking inside interaction between flame front and turbulence. Energy 2019, 179, 528–541. [Google Scholar] [CrossRef]
- Duan, X.; Zhang, S.; Liu, Y.; Li, Y.; Liu, J.; Lai, M.-C.; Deng, B. Numerical investigation the effects of the twin-spark plugs coupled with EGR on the combustion process and emissions characteristics in a lean burn natural gas SI engine. Energy 2020, 206, 118181. [Google Scholar] [CrossRef]
- Deng, B.; Li, Q.; Chen, Y.; Li, M.; Liu, A.; Ran, J.; Xu, Y.; Liu, X.; Fu, J.; Feng, R. The effect of air/fuel ratio on the CO and NOx emissions for a twin-spark motorcycle gasoline engine under wide range of operating conditions. Energy 2019, 169, 1202–1213. [Google Scholar] [CrossRef]
- Forte, C.; Bianchi, G.M.; Corti, E.; Fantoni, S.; Costa, M. CFD Methodology for the Evaluation of Knock of a PFI Twin Spark Engine. Energy Procedia 2014, 45, 859–868. [Google Scholar] [CrossRef][Green Version]
- Forte, C.; Bianchi, G.M.; Corti, E.; Fantoni, S. Evaluation of the Effects of a Twin Spark Ignition System on Combustion Stability of a High Performance PFI Engine. Energy Procedia 2015, 81, 897–906. [Google Scholar] [CrossRef]
- Chen, L.; Pan, J.; Liu, C.; Shu, G.; Wei, H. Effect of rapid combustion on engine performance and knocking characteristics under different spark strategy conditions. Energy 2020, 192, 116706. [Google Scholar] [CrossRef]
- Zou, R.; Li, Y.; Liu, J.; Wang, N.; Zeng, Q.; Li, J. Numerical study on the effects of spark strategies on knocking combustion in a downsized gasoline rotary engine. Energy 2023, 263, 125770. [Google Scholar] [CrossRef]
- Lee, S.W.; Choi, W.; Cho, Y.S. Characterization of HCNG combustion and emission characteristics in a constant volume chamber with a single and a dual spark plug configuration. Int. J. Hydrog. Energy 2012, 37, 682–690. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, X.; Wang, Y.; Sun, J.; Fan, X. Experimental study on premixed combustion characteristics of methane-air under dual spark plug ignition strategy in a closed spherical chamber. Fuel 2022, 314, 123093. [Google Scholar] [CrossRef]
- Lim, M.T.; Anderson, R.W.; Arpaci, V.S. Prediction of spark kernel development in constant volume combustion. Combust. Flame 1987, 69, 303–316. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, X.; Li, Y.; Qin, S. Experimental study on premixed turbulent flame of methane/air in a spherical closed chamber. Energy Convers. Manag. 2020, 222, 113219. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, X.; Wang, Y. Experimental study on the combustion characteristics of premixed methane-hydrogen-air mixtures in a spherical closed chamber. Fuel 2021, 299, 120885. [Google Scholar] [CrossRef]
- Basha, S.A.; Raja Gopal, K. In-cylinder fluid flow, turbulence and spray models—A review. Renew. Sustain. Energy Rev. 2009, 13, 1620–1627. [Google Scholar] [CrossRef]
- Han, Z.; Reitz, R.D. Turbulence Modeling of Internal Combustion Engines Using RNG κ-ε Models. Combust. Sci. Technol. 1995, 106, 267–295. [Google Scholar] [CrossRef]
- Smith, L.M. Renormalization-Group Analysis of Turbulence. Annu. Rev. Fluid Mech. 1998, 30, 275–310. [Google Scholar] [CrossRef]
- Amsden, A.A.; Orourke, P.J.; Butler, T.D. KIVA-2: A Computer Program for Chemically Reactive Flows with Sprays; Los Alamos National Lab. (LANL): Los Alamos, NM, USA, 1989; p. 27975. [Google Scholar]
- O’Rourke, P.J.; Amsden, A.A. A Spray/Wall Interaction Submodel for the KIVA-3 Wall Film Model; SAE International: Warren, PA, USA, 2000. [Google Scholar]
- Sazhin, S.S.; Sazhina, E.M.; Heikal, M.R.; Marooney, C.; Mikhalovsky, S.V. The shell autoignition model: A new mathematical formulation. Combust. Flame 1999, 117, 529–540. [Google Scholar] [CrossRef]
- Schneider, E.; Maltsev, A.; Sadiki, A.; Janicka, J. Study on the potential of BML-approach and G-equation concept-based models for predicting swirling partially premixed combustion systems: URANS computations. Combust. Flame 2008, 152, 548–572. [Google Scholar] [CrossRef]
- Williams, F.A. Spray combustion theory. Combust. Flame 1959, 3, 215–228. [Google Scholar] [CrossRef]
- Peters, N. Turbulent Combustion; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Zhang, Z.; Tian, J.; Xie, G.; Li, J.; Xu, W.; Jiang, F.; Huang, Y.; Tan, D. Investigation on the combustion and emission characteristics of diesel engine fueled with diesel/methanol/n-butanol blends. Fuel 2022, 314, 123088. [Google Scholar] [CrossRef]
- Lu, T.; Law, C.K. A criterion based on computational singular perturbation for the identification of quasi steady state species: A reduced mechanism for methane oxidation with NO chemistry. Combust. Flame 2008, 154, 761–774. [Google Scholar] [CrossRef]
- Senecal, P.K.; Pomraning, E.; Richards, K.J.; Briggs, T.E.; Choi, C.Y.; McDavid, R.M.; Patterson, M.A. Multi-Dimensional Modeling of Direct-Injection Diesel Spray Liquid Length and Flame Lift-Off Length using CFD and Parallel Detailed Chemistry; SAE International: Warren, PA, USA, 2003. [Google Scholar]





| Test Parameters | Value |
|---|---|
| Initial temperature | 300 K |
| Initial pressure | 0.1 MPa |
| The equivalence ratio | 1.0 |
| Ignition distance | 150 mm |
| Ignition energy | 200 mJ |
| High speed camera frequency | 5000 Hz |
| High speed camera pixel | 512 × 512 |
| Pressure acquisition frequency | 5000 Hz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Zhang, X.; Fan, X.; Li, Y. Simulation and Research of Methane Premixed Combustion Characteristics Based on Constant Volume Combustion Chamber with Different Ignition Modes. Energies 2023, 16, 7016. https://doi.org/10.3390/en16207016
Wang Y, Zhang X, Fan X, Li Y. Simulation and Research of Methane Premixed Combustion Characteristics Based on Constant Volume Combustion Chamber with Different Ignition Modes. Energies. 2023; 16(20):7016. https://doi.org/10.3390/en16207016
Chicago/Turabian StyleWang, Yue, Xin Zhang, Xinmiao Fan, and Yanfei Li. 2023. "Simulation and Research of Methane Premixed Combustion Characteristics Based on Constant Volume Combustion Chamber with Different Ignition Modes" Energies 16, no. 20: 7016. https://doi.org/10.3390/en16207016
APA StyleWang, Y., Zhang, X., Fan, X., & Li, Y. (2023). Simulation and Research of Methane Premixed Combustion Characteristics Based on Constant Volume Combustion Chamber with Different Ignition Modes. Energies, 16(20), 7016. https://doi.org/10.3390/en16207016






