Comparison of Wavelet Artificial Neural Network, Wavelet Support Vector Machine, and Adaptive Neuro-Fuzzy Inference System Methods in Estimating Total Solar Radiation in Iraq
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Artificial Neural Network (ANN)
2.3. Support Vector Machine (SVM)
2.4. Wavelet Transform
2.5. Adaptive Neural Fuzzy Inference System (ANFIS)
- Layer 1: Every node in this layer is equal to a fuzzy set, Equation (8).
- Layer 2: The input signals are multiplied and create output, Equation (9).
- Layer 3: This layer calculates the proportion of the activity grade of the i-th rule to the sum of the activity degrees of all the rules, Equation (10).
- Layer 4: The result of every node in this layer is as seen in Equation (11).
- Layer 5: Each node in this layer, which is displayed as ∑, calculates the last output value in the form of Equation (12).
2.6. Criteria for Evaluating
2.7. Training, Validation, and Testing Sets
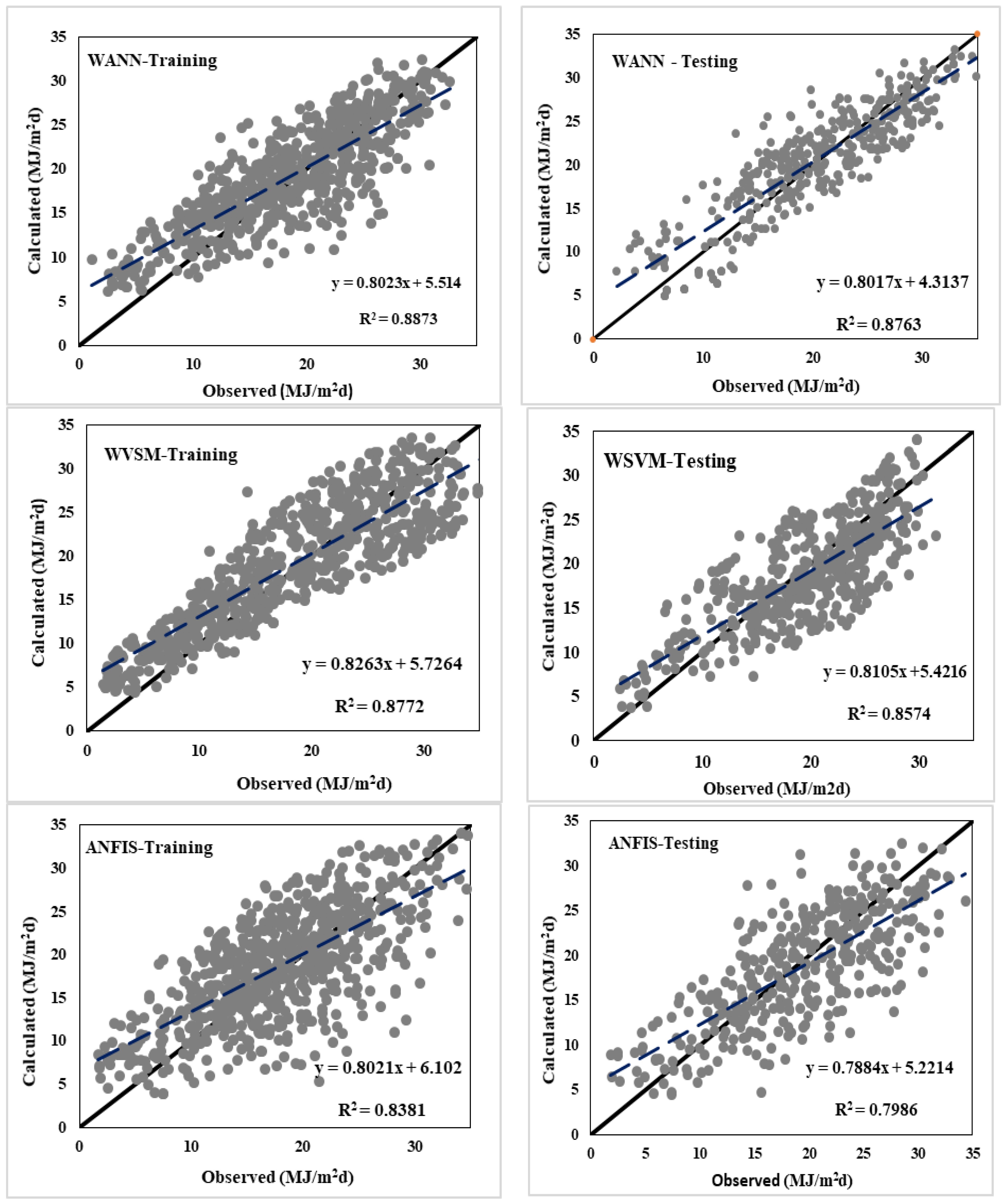
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Symbols | definition | Unit |
| ANN | Artificial Neural Network | - |
| SVM | Support Vector Machine | - |
| ANFIS | Adaptive Neuro-Fuzzy Inference System | - |
| WANN | Wavelet Artificial Neural Network | - |
| WSVM | Wavelet Support Vector Machine | - |
| Rs | solar radiation | MJ/m2 d |
| TWh | Terawatt-hour | - |
| GIS | Geographic Information System | - |
| T max | Maximum Temperature | °C |
| T min | Minimum Temperature | °C |
| H ave | Average Humidity | % |
| T avg | Average Temperature | °C |
| The Connection Weight of Neuron j to Neuron i | - | |
| a Kernel Function | - | |
| The Bias of Neuron i | - | |
| ψ (x) | Wavelet Function | - |
| The Output of The Third layer in ANFIS Model | - | |
| Set of Adaptive parameters | - | |
| RMSE | Root Mean Square Error | - |
| MAE | Mean Absolute Error | - |
| IA | Index of Agreement | - |
| R2 | Coefficient of Determination | - |
| The Predicted Radiation Intensity | MJ/m2 d | |
| The Mean Predicted Radiation Intensity | MJ/m2 d | |
| The Measured Radiation Intensity | MJ/m2 d | |
| The Mean Measured Radiation Intensity | MJ/m2 d | |
| The Number of Recorded Data | - |
References
- Guedri, K.; Salem, M.; Assad, M.E.H.; Rungamornrat, J.; Malek Mohsen, F.; Buswig, Y.M. PV/Thermal as Promising Technologies in Buildings: A Comprehensive Review on Exergy Analysis. Sustainability 2022, 14, 12298. [Google Scholar] [CrossRef]
- Molajou, A.; Afshar, A.; Khosravi, M.; Soleimanian, E.; Vahabzadeh, M.; Variani, H.A. A new paradigm of water, food, and energy nexus. Environ. Sci. Pollut. Res. 2021, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Vahabzadeh, M.; Afshar, A.; Molajou, A. Energy simulation modeling for water-energy-food nexus system: A systematic review. Environ. Sci. Pollut. Res. 2022, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Sharifpur, M.; Ahmadi, M.H.; Rungamornrat, J.; Malek Mohsen, F. Thermal Management of Solar Photovoltaic Cell by Using Single Walled Carbon Nanotube (SWCNT)/Water: Numerical Simulation and Sensitivity Analysis. Sustainability 2022, 14, 11523. [Google Scholar] [CrossRef]
- Afshar, A.; Soleimanian, E.; Akbari Variani, H.; Vahabzadeh, M.; Molajou, A. The conceptual framework to determine interrelations and interactions for holistic Water, Energy, and Food Nexus. Environ. Dev. Sustain. 2022, 24, 10119–10140. [Google Scholar] [CrossRef]
- Asgher, U.; Babar Rasheed, M.; Al-Sumaiti, A.S.; Ur-Rahman, A.; Ali, I.; Alzaidi, A.; Alamri, A. Smart Energy Optimization Using Heuristic Algorithm in Smart Grid with Integration of Solar Energy Sources. Energies 2018, 11, 3494. [Google Scholar] [CrossRef]
- Parimita Panigrahi, S.; Kumar Maharana, S.; Rajashekaraiah, T.; Gopalashetty, R.; Sharifpur, M.; Ahmadi, M.H.; Saleel, C.A.; Abbas, M. Flat Unglazed Transpired Solar Collector: Performance Probability Prediction Approach Using Monte Carlo Simulation Technique. Energies 2022, 15, 8843. [Google Scholar] [CrossRef]
- Şenkal, O. Solar Radiation and Precipitable Water Modeling for Turkey Using Artificial Neural Networks. Meteorol. Atmos. Phys. 2015, 127, 481–488. [Google Scholar] [CrossRef]
- Sivaneasan, B.; Yu, C.Y.; Goh, K.P. Solar Forecasting Using ANN with Fuzzy Logic Pre-Processing. Energy Procedia 2017, 143, 727–732. [Google Scholar] [CrossRef]
- Fourcade, Y.; Besnard, A.G.; Secondi, J. Paintings Predict the Distribution of Species, or the Challenge of Selecting Environmental Predictors and Evaluation Statistics. Glob. Ecol. Biogeogr. 2018, 27, 245–256. [Google Scholar] [CrossRef]
- Anwar, K.; Deshmukh, S. Assessment and Mapping of Solar Energy Potential Using Artificial Neural Network and GIS Technology in the Southern Part of India. Int. J. Renew. Energy Res. 2018, 8, 974–985. [Google Scholar]
- Voyant, C.; Notton, G.; Kalogirou, S.; Nivet, M.-L.; Paoli, C.; Motte, F.; Fouilloy, A. Machine Learning Methods for Solar Radiation Forecasting: A Review. Renew. Energy 2017, 105, 569–582. [Google Scholar] [CrossRef]
- Chen, J.-L.; Li, G.-S. Evaluation of Support Vector Machine for Estimation of Solar Radiation from Measured Meteorological Variables. Theor. Appl. Climatol. 2014, 115, 627–638. [Google Scholar] [CrossRef]
- Olatomiwa, L.; Mekhilef, S.; Shamshirband, S.; Mohammadi, K.; Petković, D.; Sudheer, C. A Support Vector Machine–Firefly Algorithm-Based Model for Global Solar Radiation Prediction. Sol. Energy 2015, 115, 632–644. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Nazari, M.A.; Mahariq, I.; Assad, M.E.H.; Ali, M.E.; Almuzaiqer, R.; Nuhait, A.; Murshid, N. Thermophysical Properties of Hybrid Nanofluids and the Proposed Models: An Updated Comprehensive Study. Nanomaterials 2021, 11, 3084. [Google Scholar] [CrossRef]
- Ghebrezgabher, M.G.; Weldegabir, A.K. Estimating Solar Energy Potential in Eritrea: A GIS-Based Approach. Renew. Energy Res. Appl. 2022, 3, 155–164. [Google Scholar]
- Dos Santos, C.M.; Escobedo, J.F.; Teramoto, E.T.; da Silva, S.H.M.G. Assessment of ANN and SVM Models for Estimating Normal Direct Irradiation (Hb). Energy Convers. Manag. 2016, 126, 826–836. [Google Scholar] [CrossRef]
- Ferrero Bermejo, J.; Gómez Fernández, J.F.; Olivencia Polo, F.; Crespo Márquez, A. A Review of the Use of Artificial Neural Network Models for Energy and Reliability Prediction. A Study of the Solar PV, Hydraulic and Wind Energy Sources. Appl. Sci. 2019, 9, 1844. [Google Scholar] [CrossRef]
- IAC Iraqi Agrometeorological Center, Baghdad, Iraq. 2020. Available online: https://www.agromet.gov.iq (accessed on 9 December 2022).
- Sharghi, E.; Nourani, V.; Najafi, H.; Molajou, A. Emotional ANN (EANN) and Wavelet-ANN (WANN) Approaches for Markovian and Seasonal Based Modeling of Rainfall-Runoff Process. Water Resour. Manag. 2018, 32, 3441–3456. [Google Scholar] [CrossRef]
- Molajou, A.; Nourani, V.; Afshar, A.; Khosravi, M.; Brysiewicz, A. Optimal design and feature selection by genetic algorithm for emotional artificial neural network (EANN) in rainfall-runoff modeling. Water Resour. Manag. 2021, 35, 2369–2384. [Google Scholar] [CrossRef]
- Samadi, M.; Afshar, M.H.; Jabbari, E.; Sarkardeh, H. Prediction of Current-Induced Scour Depth around Pile Groups Using MARS, CART, and ANN Approaches. Mar. Georesour. Geotechnol. 2021, 39, 577–588. [Google Scholar] [CrossRef]
- Wu, W.; Zhou, H. Data-Driven Diagnosis of Cervical Cancer with Support Vector Machine-Based Approaches. IEEE Access 2017, 5, 25189–25195. [Google Scholar] [CrossRef]
- Mohan, L.; Pant, J.; Suyal, P.; Kumar, A. Support Vector Machine Accuracy Improvement with Classification. In Proceedings of the 2020 12th International Conference on Computational Intelligence and Communication Networks (CICN), Bhimtal, India, 25–26 September 2020; IEEE: Manhattan, NY, USA, 2020; pp. 477–481. [Google Scholar]
- Zhang, D. Wavelet Transform. In Fundamentals of Image Data Mining; Springer: Berlin/Heidelberg, Germany, 2019; pp. 35–44. [Google Scholar]
- Abbate, A.; Koay, J.; Frankel, J.; Schroeder, S.C.; Das, P. Signal Detection and Noise Suppression Using a Wavelet Transform Signal Processor: Application to Ultrasonic Flaw Detection. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1997, 44, 14–26. [Google Scholar] [CrossRef]
- Kharb, R.K.; Shimi, S.L.; Chatterji, S.; Ansari, M.F. Modeling of Solar PV Module and Maximum Power Point Tracking Using ANFIS. Renew. Sustain. Energy Rev. 2014, 33, 602–612. [Google Scholar] [CrossRef]
- Jang, J.-S. Input Selection for ANFIS Learning. In Proceedings of the IEEE 5th International Fuzzy Systems, New Orleans, LA, USA, 11 September 1996; IEEE: Manhattan, NY, USA, 1996; Volume 2, pp. 1493–1499. [Google Scholar]
- Meenal, R.; Selvakumar, A.I. Assessment of SVM, Empirical and ANN Based Solar Radiation Prediction Models with Most Influencing Input Parameters. Renew. Energy 2018, 121, 324–343. [Google Scholar] [CrossRef]
- Breck, E.; Polyzotis, N.; Roy, S.; Whang, S.; Zinkevich, M. Data Validation for Machine Learning. In Proceedings of the MLSys, Stanford, CA, USA, 31 March–2 April 2019. [Google Scholar]
- Quej, V.H.; Almorox, J.; Arnaldo, J.A.; Saito, L. ANFIS, SVM and ANN Soft-Computing Techniques to Estimate Daily Global Solar Radiation in a Warm Sub-Humid Environment. J. Atmos. Sol. Terr. Phys. 2017, 155, 62–70. [Google Scholar] [CrossRef]
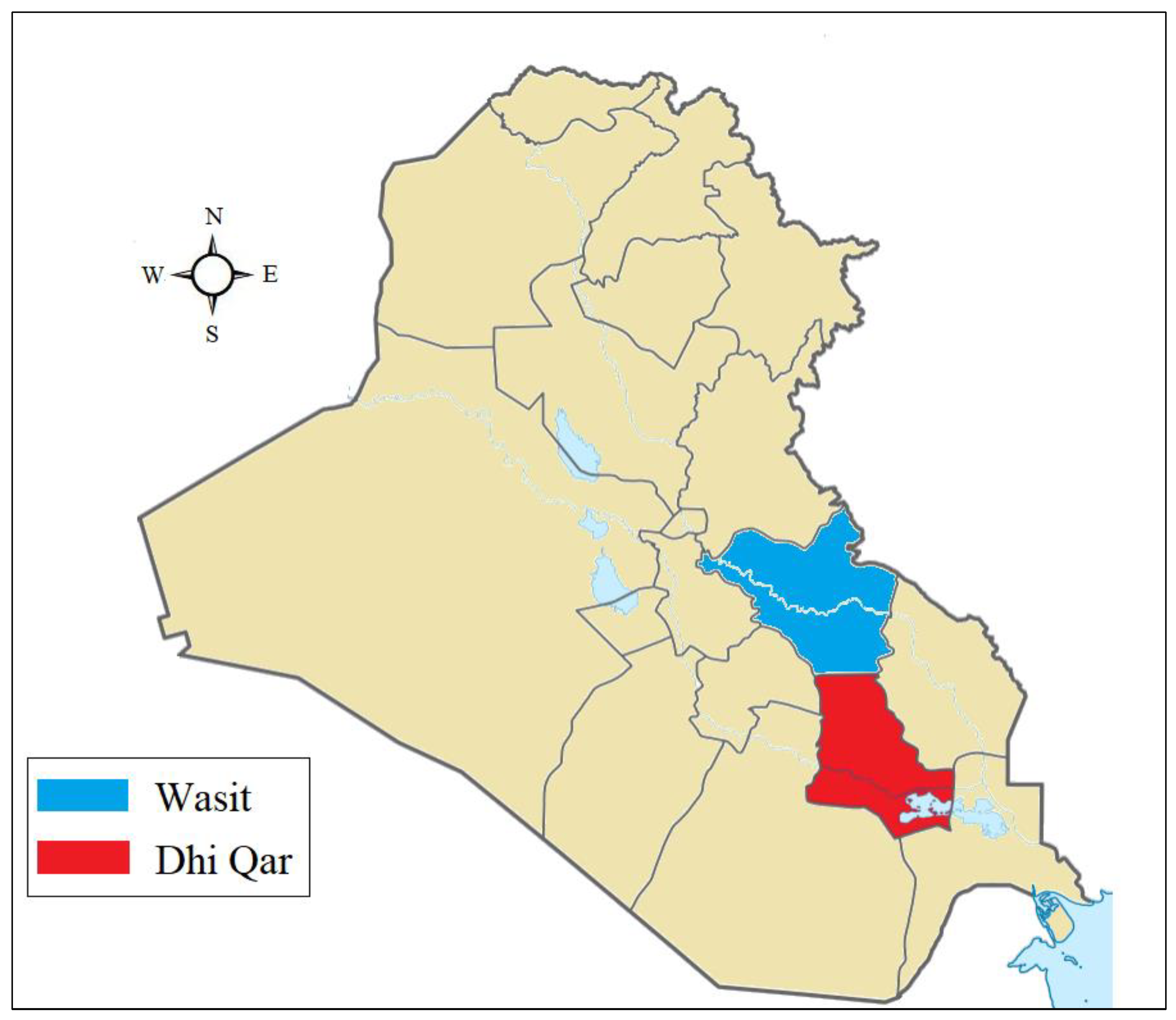

| Station | Wasit | Dhi Qar | ||||
|---|---|---|---|---|---|---|
| Max | Min | Average | Max | Min | Average | |
| T max (°C) | 43.5 | 17.8 | 31.2 | 44.8 | 17.3 | 32.4 |
| T min (°C) | 25.4 | 5.7 | 15.6 | 28.1 | 6.2 | 17.1 |
| H avg (%) | 95.6 | 3.7 | 28.4 | 97.2 | 5.4 | 29.2 |
| S (h) | 13.8 | 0.0 | 9.7 | 13.4 | 0.0 | 9.2 |
| Rs (MJ/m2 d) | 41.7 | 3.1 | 22.8 | 40.2 | 2.7 | 21.6 |
| Station | Dhi Qar | Wasit | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Model | WANN-1 | WANN-2 | WANN-3 | WANN-4 | WANN-1 | WANN-2 | WANN-3 | WANN-4 | |
| Training phase | RMSE | 3.10 | 2.76 | 3.00 | 3.08 | 3.01 | 3.40 | 2.42 | 3.21 |
| MEA | 2.24 | 2.09 | 2.20 | 2.18 | 2.02 | 2.21 | 1.80 | 2.07 | |
| R2 | 0.82 | 0.86 | 0.77 | 0.78 | 0.82 | 0.76 | 0.89 | 0.79 | |
| IA | 0.96 | 0.97 | 0.96 | 0.95 | 0.95 | 0.95 | 0.98 | 0.96 | |
| Validation Phase | RMSE | 3.18 | 2.83 | 3.20 | 3.36 | 3.08 | 3.38 | 2.59 | 3.22 |
| MEA | 2.28 | 2.07 | 2.28 | 2.38 | 2.15 | 2.21 | 2.04 | 2.13 | |
| R2 | 0.80 | 0.85 | 0.77 | 0.76 | 0.79 | 0.77 | 0.88 | 0.74 | |
| IA | 0.96 | 0.95 | 0.95 | 0.93 | 0.93 | 0.94 | 0.96 | 0.95 | |
| Testing Phase | RMSE | 3.39 | 2.93 | 3.24 | 3.47 | 3.1 | 3.30 | 2.84 | 3.20 |
| MEA | 2.33 | 2.09 | 2.31 | 2.43 | 2.14 | 2.23 | 2.05 | 2.14 | |
| R2 | 0.79 | 0.85 | 0.76 | 0.74 | 0.80 | 0.79 | 0.88 | 0.76 | |
| IA | 0.94 | 0.96 | 0.93 | 0.93 | 0.95 | 0.95 | 0.97 | 0.96 | |
| Station | Dhi Qar | Wasit | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Model | WSVM-1 | WSVM-2 | WSVM-3 | WSVM-4 | WSVM-1 | WSVM-2 | WSVM-3 | WSVM-4 | |
| Training phase | RMSE | 2.88 | 3.06 | 2.45 | 3.13 | 2.67 | 3.02 | 3.00 | 2.69 |
| MEA | 2.04 | 2.08 | 1.92 | 2.12 | 1.58 | 1.91 | 1.90 | 1.84 | |
| R2 | 0.82 | 0.79 | 0.87 | 0.78 | 0.88 | 0.79 | 0.80 | 0.86 | |
| IA | 0.96 | 0.96 | 0.97 | 0.95 | 0.97 | 0.96 | 0.96 | 0.96 | |
| Validation Phase | RMSE | 3.07 | 3.57 | 2.49 | 3.52 | 2.45 | 3.86 | 3.38 | 2.99 |
| MEA | 2.18 | 2.19 | 2.11 | 2.21 | 1.67 | 3.84 | 3.19 | 1.98 | |
| R2 | 0.75 | 0.66 | 0.85 | 0.74 | 0.86 | 0.77 | 0.88 | 0.82 | |
| IA | 0.94 | 0.94 | 0.96 | 0.94 | 0.93 | 0.95 | 0.94 | 0.95 | |
| Testing Phase | RMSE | 3.37 | 3.77 | 2.54 | 3.68 | 2.45 | 3.92 | 3.42 | 3.27 |
| MEA | 2.22 | 2.37 | 2.18 | 2.30 | 1.81 | 2.22 | 2.06 | 2.21 | |
| R2 | 0.74 | 0.67 | 0.85 | 0.69 | 0.86 | 0.72 | 0.76 | 0.81 | |
| IA | 0.95 | 0.92 | 0.97 | 0.93 | 0.95 | 0.93 | 0.94 | 0.96 | |
| Station | Dhi Qar | Wasit | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Model | ANFIS-1 | ANFIS-2 | ANFIS-3 | ANFIS-4 | ANFIS-1 | ANFIS-2 | ANFIS-3 | ANFIS-4 | |
| Training phase | RMSE | 2.94 | 2.62 | 2.85 | 2.92 | 2.86 | 3.23 | 3.04 | 2.70 |
| MEA | 2.12 | 1.98 | 2.09 | 2.07 | 1.91 | 2.10 | 1.96 | 1.91 | |
| R2 | 0.74 | 0.83 | 0.73 | 0.77 | 0.80 | 0.72 | 0.75 | 0.84 | |
| IA | 0.91 | 0.94 | 0.93 | 0.90 | 0.89 | 0.92 | 0.93 | 0.95 | |
| Validation Phase | RMSE | 3.18 | 2.59 | 2.94 | 3.19 | 2.89 | 3.17 | 3.00 | 2.65 |
| MEA | 2.14 | 2.08 | 2.11 | 2.24 | 2.00 | 2.09 | 2.17 | 2.10 | |
| R2 | 0.71 | 0.81 | 0.73 | 0.75 | 0.84 | 0.69 | 0.71 | 0.81 | |
| IA | 0.90 | 0.93 | 0.91 | 0.85 | 0.86 | 0.88 | 0.91 | 0.94 | |
| Testing Phase | RMSE | 3.22 | 2.64 | 3.07 | 3.29 | 2.94 | 3.13 | 3.03 | 2.69 |
| MEA | 2.21 | 2.13 | 2.19 | 2.31 | 2.03 | 2.11 | 2.15 | 2.11 | |
| R2 | 0.70 | 0.78 | 0.72 | 0.70 | 0.76 | 0.70 | 0.72 | 0.80 | |
| IA | 0.89 | 0.92 | 0.90 | 0.88 | 0.87 | 0.89 | 0.91 | 0.92 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anupong, W.; Jweeg, M.J.; Alani, S.; Al-Kharsan, I.H.; Alviz-Meza, A.; Cárdenas-Escrocia, Y. Comparison of Wavelet Artificial Neural Network, Wavelet Support Vector Machine, and Adaptive Neuro-Fuzzy Inference System Methods in Estimating Total Solar Radiation in Iraq. Energies 2023, 16, 985. https://doi.org/10.3390/en16020985
Anupong W, Jweeg MJ, Alani S, Al-Kharsan IH, Alviz-Meza A, Cárdenas-Escrocia Y. Comparison of Wavelet Artificial Neural Network, Wavelet Support Vector Machine, and Adaptive Neuro-Fuzzy Inference System Methods in Estimating Total Solar Radiation in Iraq. Energies. 2023; 16(2):985. https://doi.org/10.3390/en16020985
Chicago/Turabian StyleAnupong, Wongchai, Muhsin Jaber Jweeg, Sameer Alani, Ibrahim H. Al-Kharsan, Aníbal Alviz-Meza, and Yulineth Cárdenas-Escrocia. 2023. "Comparison of Wavelet Artificial Neural Network, Wavelet Support Vector Machine, and Adaptive Neuro-Fuzzy Inference System Methods in Estimating Total Solar Radiation in Iraq" Energies 16, no. 2: 985. https://doi.org/10.3390/en16020985
APA StyleAnupong, W., Jweeg, M. J., Alani, S., Al-Kharsan, I. H., Alviz-Meza, A., & Cárdenas-Escrocia, Y. (2023). Comparison of Wavelet Artificial Neural Network, Wavelet Support Vector Machine, and Adaptive Neuro-Fuzzy Inference System Methods in Estimating Total Solar Radiation in Iraq. Energies, 16(2), 985. https://doi.org/10.3390/en16020985






