Heat and Mass Transfer Analysis of a Fluid Flow across the Conical Gap of a Cone-Disk Apparatus under the Thermophoretic Particles Motion
Abstract
1. Introduction
2. Mathematical Formulation
3. Numerical Procedure
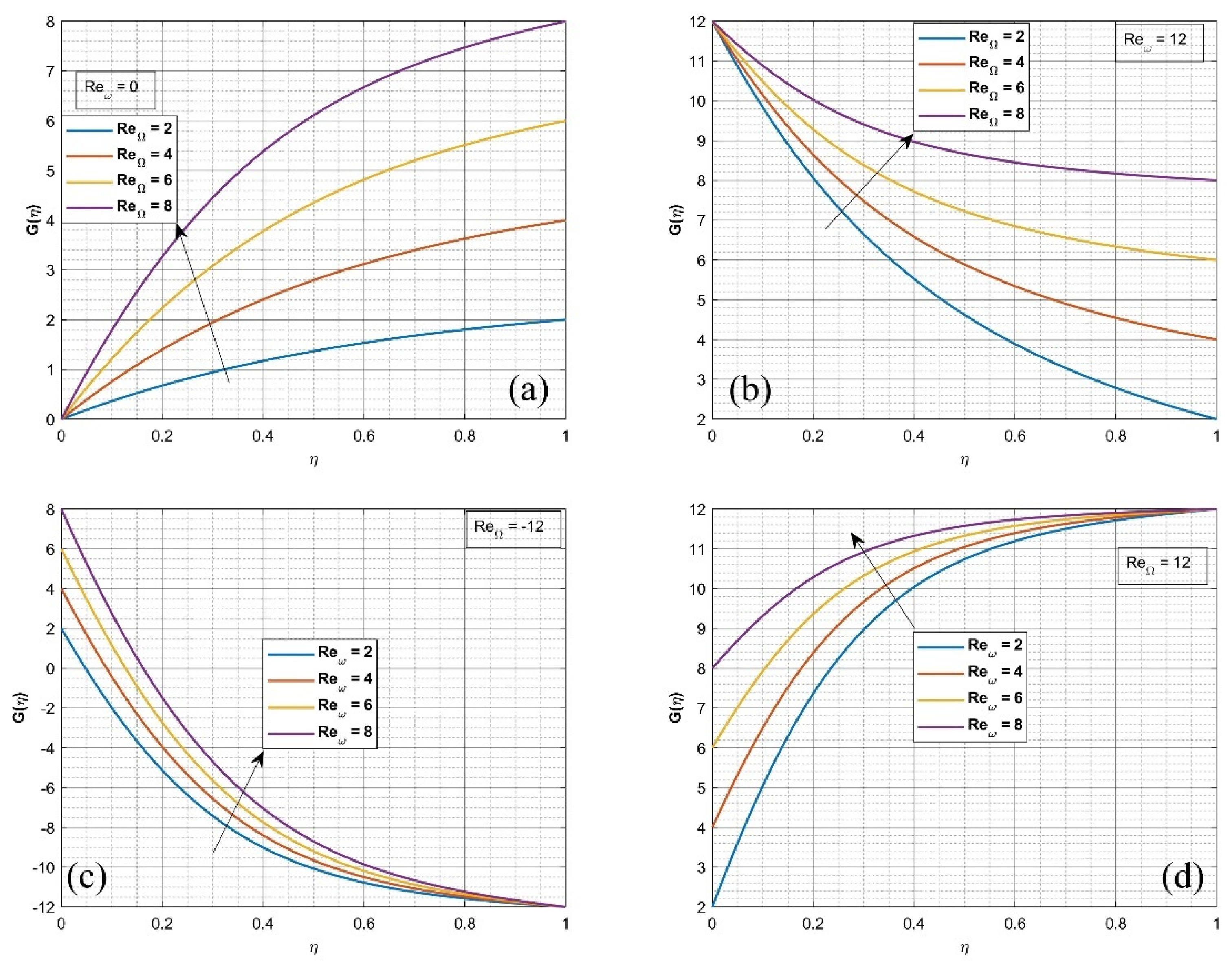
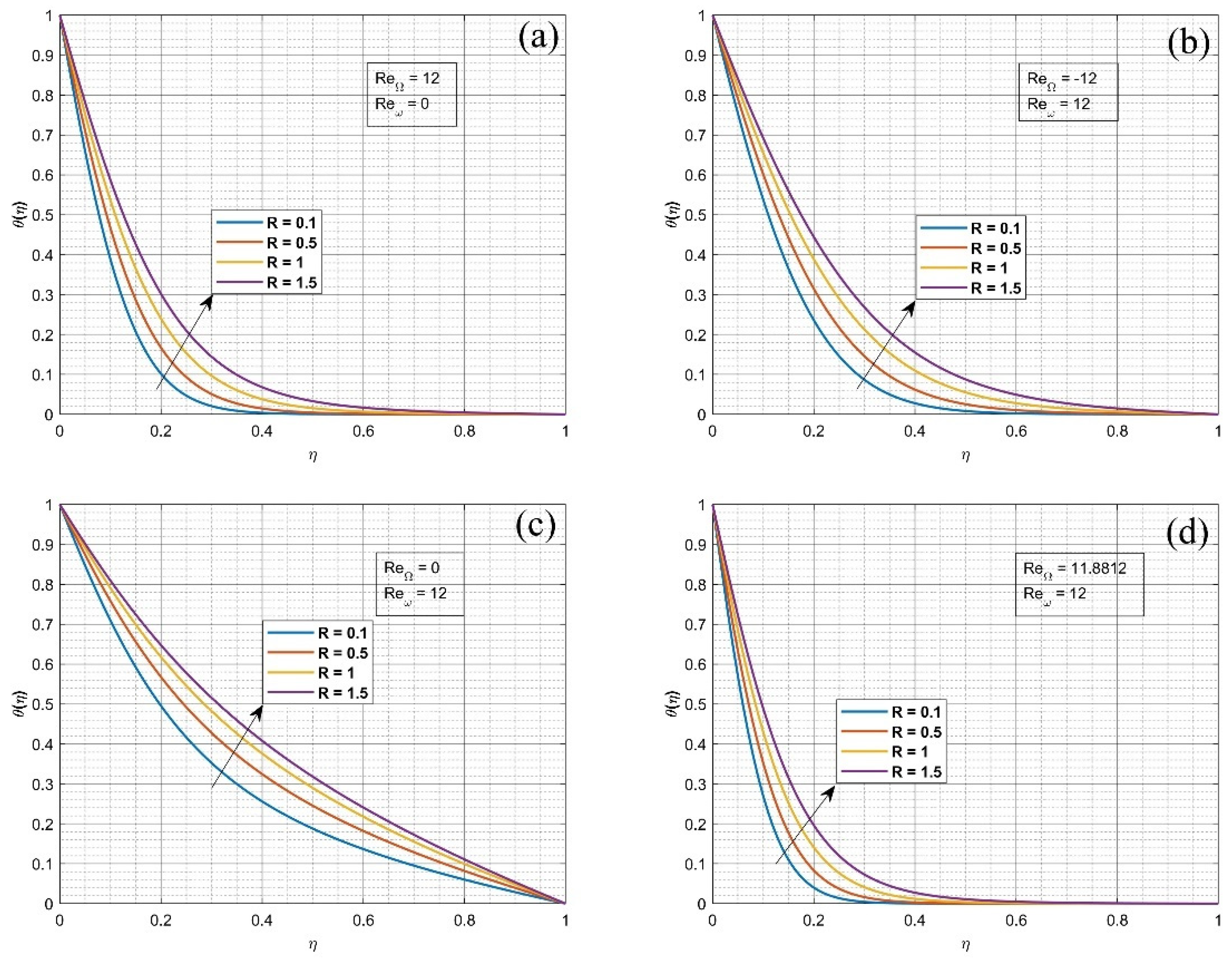
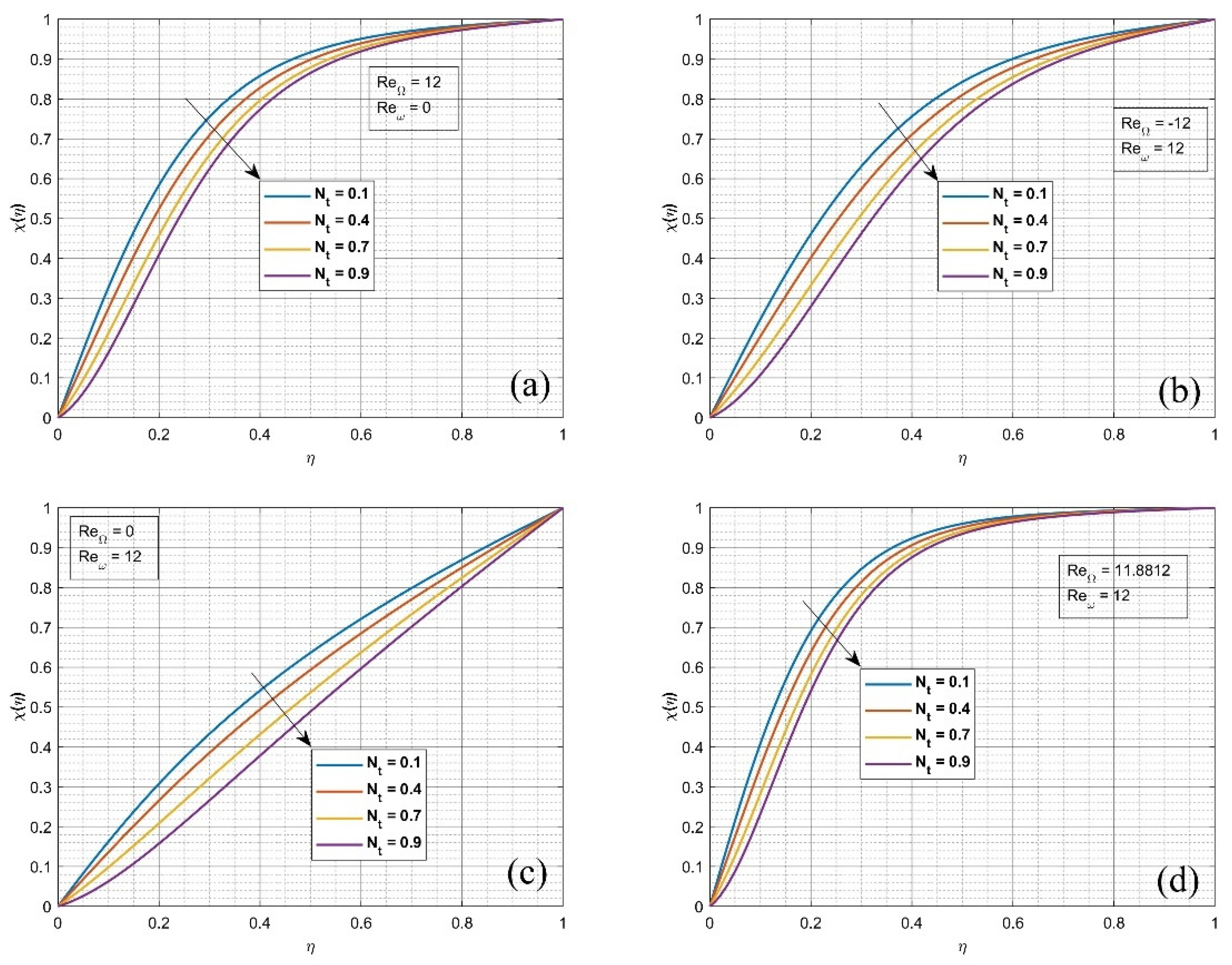
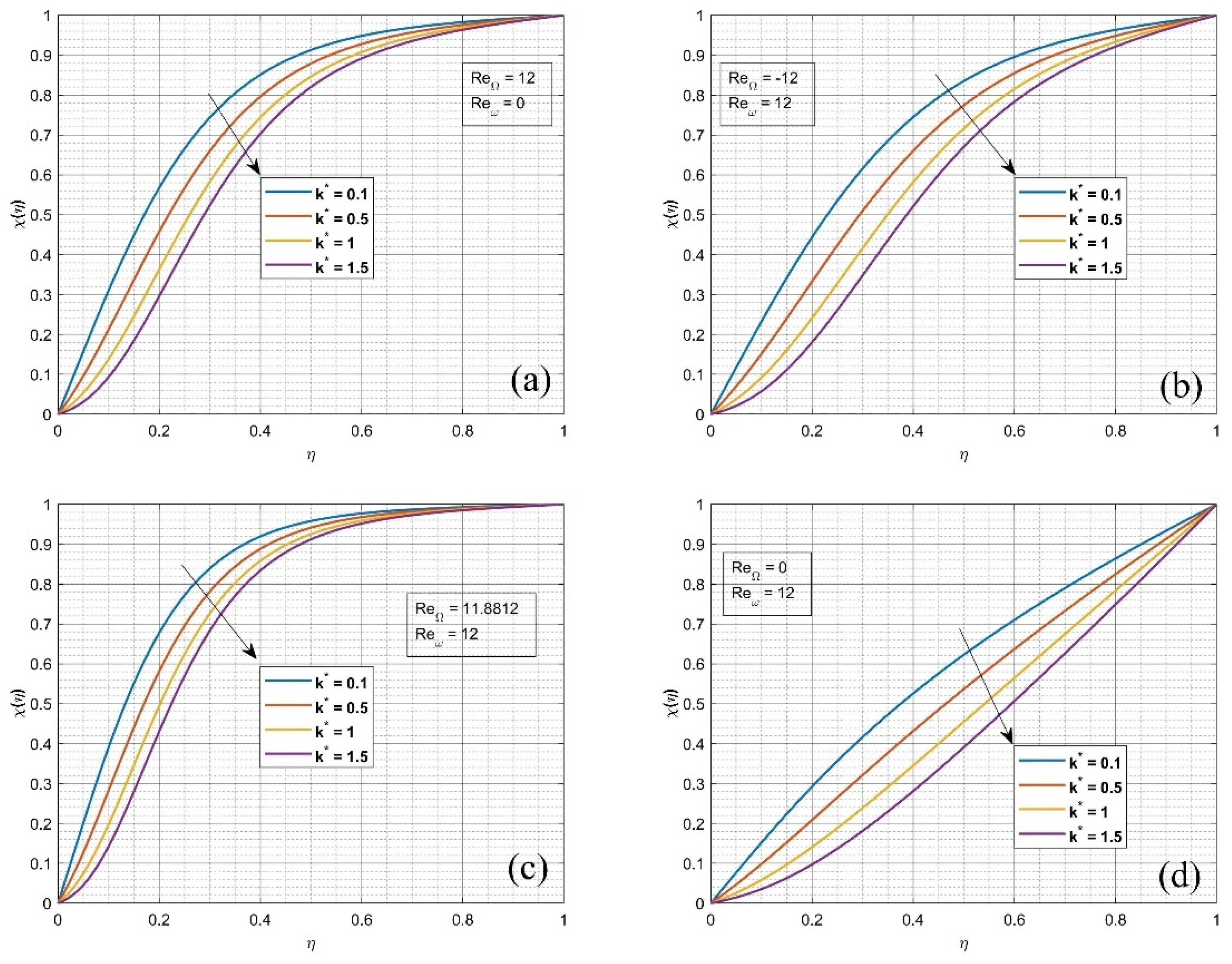
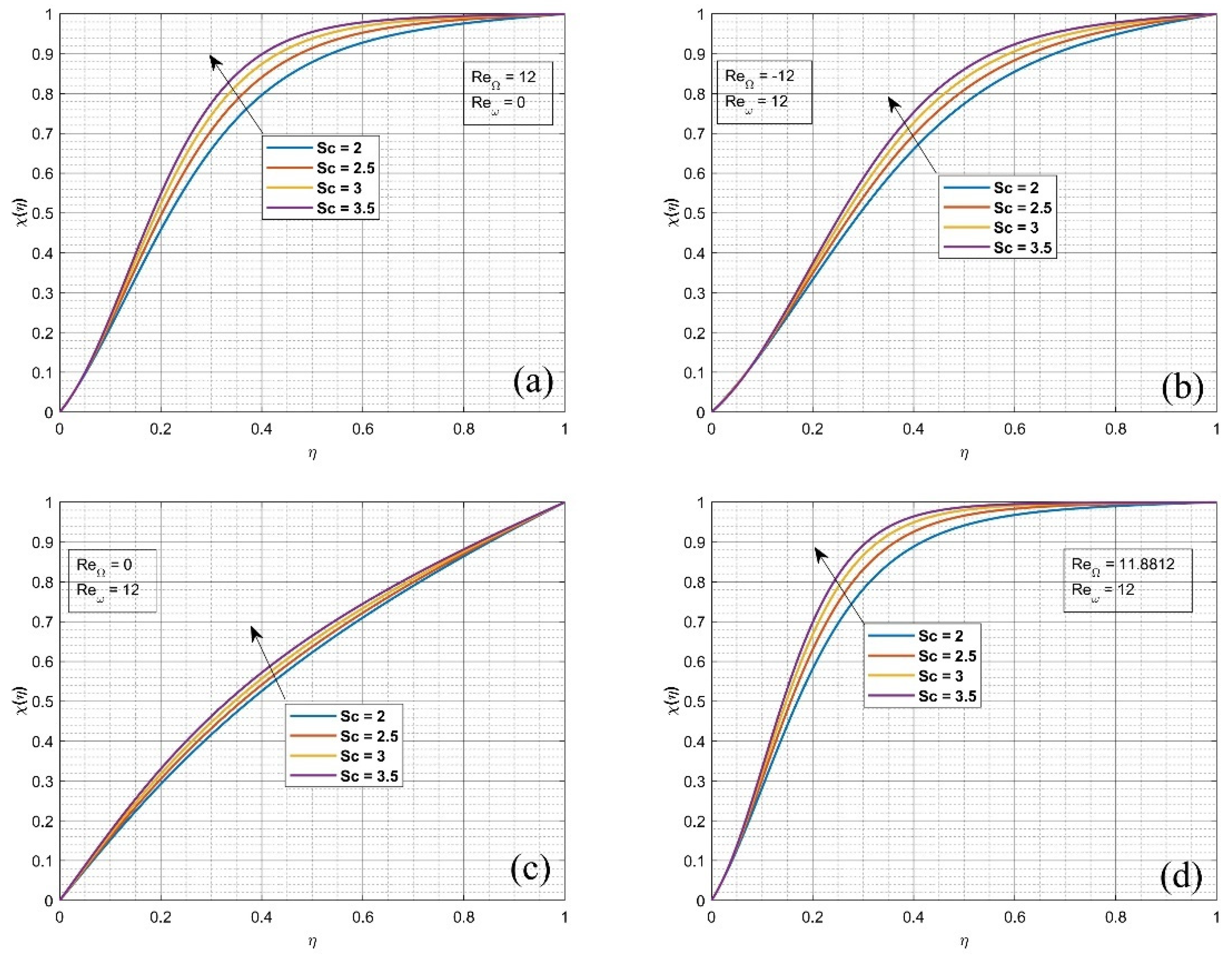
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Radiation parameter | Pressure | ||
| Cylindrical coordinates | Temperature of the surface | ||
| Nusselt number at the disk’s surface | Velocity profiles | ||
| Ambient temperature | Schmidt number | ||
| Thermal conductivity | Kinematic viscosity of the fluid | ||
| Gap angle | Stefan–Boltzmann constant | ||
| Volume fraction | Concentration | ||
| Temperature | Ψ | Stream function | |
| Power index of wall temperature | Dimensionless thermal profile | ||
| Ambient concentration | Local Reynolds number | ||
| Angular velocities | Mean absorption coefficient | ||
| Concentration of the surface | and | Thermophoretic velocities | |
| Constituents of velocity | Dynamic viscosity | ||
| Prandtl number | Thermophoretic co-efficient | ||
| Density | Thermophoretic parameter | ||
| Nusselt number at cone’s surface | Dimensionless concentration profile | ||
| Constant | Heat capacitance |
References
- Phan-Thien, N. Cone-and-plate flow of the Oldroyd-B fluid is unstable. J. Non-Newton. Fluid Mech. 1985, 17, 37–44. [Google Scholar] [CrossRef]
- Mooney, M.; Ewart, R.H. The Conicylindrical Viscometer. Physics 1934, 5, 350–354. [Google Scholar] [CrossRef]
- Buschmann, M.H.; Dieterich, P.; Adams, N.A.; Schnittler, H.-J. Analysis of flow in a cone-and-plate apparatus with respect to spatial and temporal effects on endothelial cells. Biotechnol. Bioeng. 2005, 89, 493–502. [Google Scholar] [CrossRef]
- Shevchuk, V. A Self-Similar Solution of Navier–Stokes and Energy Equations for Rotating Flows between a Cone and a Disk. High Temp. 2004, 42, 104–110. [Google Scholar] [CrossRef]
- Basavarajappa, M.; Bhatta, D. Study of flow of Buongiorno nanofluid in a conical gap between a cone and a disk. Phys. Fluids 2022, 34, 112004. [Google Scholar] [CrossRef]
- Wang, F.; Rani, S.P.; Sarada, K.; Gowda, R.P.; Khan, U.; Zahran, H.Y.; Mahmoud, E.E. The effects of nanoparticle aggregation and radiation on the flow of nanofluid between the gap of a disk and cone. Case Stud. Therm. Eng. 2022, 33, 101930. [Google Scholar] [CrossRef]
- Alrabaiah, H.; Bilal, M.; Khan, M.A.; Muhammad, T.; Legas, E.Y. Parametric estimation of gyrotactic microorganism hybrid nanofluid flow between the conical gap of spinning disk-cone apparatus. Sci. Rep. 2022, 12, 59. [Google Scholar] [CrossRef] [PubMed]
- Gul, T.; Kashifullah; Bilal, M.; Alghamdi, W.; Asjad, M.I.; Abdeljawad, T. Hybrid nanofluid flow within the conical gap between the cone and the surface of a rotating disk. Sci. Rep. 2021, 11, 1180. [Google Scholar] [CrossRef] [PubMed]
- de Gans, B.-J.; Kita, R.; Wiegand, S.; Luettmer-Strathmann, J. Unusual Thermal Diffusion in Polymer Solutions. Phys. Rev. Lett. 2003, 91, 245501. [Google Scholar] [CrossRef]
- Podolny, A.; Oron, A.; Nepomnyashchy, A.A. Long-wave Marangoni instability in a binary-liquid layer with deformable interface in the presence of Soret effect: Linear theory. Phys. Fluids 2005, 17, 104104. [Google Scholar] [CrossRef]
- Sarma, R.; Mondal, P.K. Marangoni instability in a viscoelastic binary film with cross-diffusive effect. J. Fluid Mech. 2021, 910, A30. [Google Scholar] [CrossRef]
- Gowda, R.P.; Kumar, R.N.; Aldalbahi, A.; Issakhov, A.; Prasannakumara, B.; Rahimi-Gorji, M.; Rahaman, M. Thermophoretic particle deposition in time-dependent flow of hybrid nanofluid over rotating and vertically upward/ downward moving disk. Surf. Interfaces 2021, 22, 100864. [Google Scholar] [CrossRef]
- Khan, N.S.; Gul, T.; Islam, S.; Khan, W. Thermophoresis and thermal radiation with heat and mass transfer in a magnetohydrodynamic thin-film second-grade fluid of variable properties past a stretching sheet. Eur. Phys. J. Plus 2017, 132, 11. [Google Scholar] [CrossRef]
- Alhadhrami, A.; Alzahrani, H.A.H.; Kumar, R.N.; Gowda, R.J.P.; Sarada, K.; Prasanna, B.M.; Madhukesh, J.K.; Madhukeshwara, N. Impact of thermophoretic particle deposition on Glauert wall jet slip flow of nanofluid. Case Stud. Therm. Eng. 2021, 28, 101404. [Google Scholar] [CrossRef]
- Abbas, A.; Ashraf, M.; Chamkha, A.J. Combined effects of thermal radiation and thermophoretic motion on mixed convection boundary layer flow. Alex. Eng. J. 2021, 60, 3243–3252. [Google Scholar] [CrossRef]
- Shah, N.A.; Yook, S.-J.; Tosin, O. Analytic simulation of thermophoretic second grade fluid flow past a vertical surface with variable fluid characteristics and convective heating. Sci. Rep. 2022, 12, 5445. [Google Scholar] [CrossRef]
- Kármán, T.V. Über laminare und turbulente Reibung. Z. Angew. Math. Mech. 1921, 1, 233–252. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. On the fluid flow and heat transfer between a cone and a disk both stationary or rotating. Math. Comput. Simul. 2020, 177, 329–340. [Google Scholar] [CrossRef]
- Shevchuk, V. Laminar Heat and Mass Transfer in Rotating Cone-and-Plate Devices. J. Heat Transf. 2011, 133, 024502. [Google Scholar] [CrossRef]
- Tassaddiq, A.; Khan, S.; Bilal, M.; Gul, T.; Mukhtar, S.; Shah, Z.; Bonyah, E. Heat and mass transfer together with hybrid nanofluid flow over a rotating disk. AIP Adv. 2020, 10, 055317. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M.; Senel, P. Heat and mass transfer of the flow due to a rotating rough and porous disk. Int. J. Therm. Sci. 2013, 63, 146–158. [Google Scholar] [CrossRef]
- Shevchuk, V. Concerning the effect of radial thermal conductivity in a self-similar solution for rotating cone-disk systems. Int. J. Numer. Methods Heat Fluid Flow 2022, 33, 204–225. [Google Scholar] [CrossRef]
- Kumar, R.N.; Suresha, S.; Gowda, R.J.P.; Megalamani, S.B.; Prasannakumara, B.C. Exploring the impact of magnetic dipole on the radiative nanofluid flow over a stretching sheet by means of KKL model. Pramana—J. Phys. 2021, 95, 180. [Google Scholar] [CrossRef]
- Kumar, R.N.; Gamaoun, F.; Abdulrahman, A.; Chohan, J.S.; Gowda, R.J.P. Heat transfer analysis in three-dimensional unsteady magnetic fluid flow of water-based ternary hybrid nanofluid conveying three various shaped nanoparticles: A comparative study. Int. J. Mod. Phys. B 2022, 36, 2250170. [Google Scholar] [CrossRef]
- Alzahrani, H.A.H.; Alsaiari, A.; Madhukesh, J.K.; Kumar, R.N.; Prasanna, B.M. Effect of thermal radiation on heat transfer in plane wall jet flow of Casson nanofluid with suction subject to a slip boundary condition. Waves Random Complex Media 2022, 1–18. [Google Scholar] [CrossRef]
- Jayaprakash, M.C.; Sarada, K.; Gowda, R.J.P.; Kumar, R.; Fareeduddin, M.; Ibrahim, T.K.; Suresha, S. Three-dimensional unsteady flow of second-grade magnetic nanofluid with KKL correlation model. Int. J. Mod. Phys. B 2022, 36, 2250188. [Google Scholar] [CrossRef]
- Rahman, M.; Postelnicu, A. Effects of thermophoresis on the forced convective laminar flow of a viscous incompressible fluid over a rotating disk. Mech. Res. Commun. 2010, 37, 598–603. [Google Scholar] [CrossRef]
- Talbot, L.; Cheng, R.K.; Schefer, R.W.; Willis, D.R. Thermophoresis of particles in a heated boundary layer. J. Fluid Mech. 1980, 101, 737–758. [Google Scholar] [CrossRef]
- Wang, C. Combined effects of inertial and thermophoresis on particle deposition onto a wafer with wavy surface. Int. J. Heat Mass Transf. 2006, 49, 1395–1402. [Google Scholar] [CrossRef]
- Chu, Y.-M.; Hashmi, M.S.; Khan, N.; Khan, S.U.; Khan, M.I.; Kadry, S.; Abdelmalek, Z. Thermophoretic particles deposition features in thermally developed flow of Maxwell fluid between two infinite stretched disks. J. Mater. Res. Technol. 2020, 9, 12889–12898. [Google Scholar] [CrossRef]

| Models | Shevchuk [19] | Turkyilmazoglu [18] | Basavarajappa and Bhatta [5] | Present Results | |
|---|---|---|---|---|---|
| I. Rotating cone with a stationary disk. | 2463 | 13.401 | 13.4006970 | 13.40069715 | 13.40069716 |
| 12 | 0.954 | 0.95405487 | 0.95405477 | 0.954054771 | |
| II. Stationary cone with a rotating disk. | 2463 | 15.353 | 15.3528734 | 15.35287341 | 15.35287342 |
| 12 | 1.041 | 1.04080471 | 1.04080467 | 1.040804672 | |
| III. Co-rotating cone and disk. | 2463 | 14.346 | 14.3466439 | 14.34664704 | 14.34664705 |
| 12 | 1.001 | 1.00087052 | 1.00087491 | 1.000874913 | |
| IV. Counter-rotating cone and disk. | 2463 | 14.440 | 14.4395241 | 14.43952407 | 14.43952409 |
| 12 | 0.989 | 0.98884832 | 0.98884832 | 0.988848323 |
| Models | Turkyilmazoglu [18] | Basavarajappa and Bhatta [5] | Present Results | |
|---|---|---|---|---|
| I | 0.83028093 | 0.83028103 | 0.83028104 | |
| 1.09328442 | 1.09328437 | 1.09328437 | ||
| II | 0.78069847 | 0.78069848 | 0.78069849 | |
| 1.17198527 | 1.17198529 | 1.17198530 | ||
| III | 0.80178312 | 0.80177021 | 0.80177022 | |
| 1.13538224 | 1.13540222 | 1.13540222 | ||
| IV | 0.81339331 | 0.81339331 | 0.81339332 | |
| 1.12618149 | 1.12618149 | 1.12618150 |
| 0.4 | −0.9422 | −0.9483 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Srilatha, P.; Remidi, S.; Nagapavani, M.; Singh, H.; Prasannakumara, B.C. Heat and Mass Transfer Analysis of a Fluid Flow across the Conical Gap of a Cone-Disk Apparatus under the Thermophoretic Particles Motion. Energies 2023, 16, 952. https://doi.org/10.3390/en16020952
Srilatha P, Remidi S, Nagapavani M, Singh H, Prasannakumara BC. Heat and Mass Transfer Analysis of a Fluid Flow across the Conical Gap of a Cone-Disk Apparatus under the Thermophoretic Particles Motion. Energies. 2023; 16(2):952. https://doi.org/10.3390/en16020952
Chicago/Turabian StyleSrilatha, Pudhari, Srinivas Remidi, Mulupuri Nagapavani, Harjot Singh, and B. C. Prasannakumara. 2023. "Heat and Mass Transfer Analysis of a Fluid Flow across the Conical Gap of a Cone-Disk Apparatus under the Thermophoretic Particles Motion" Energies 16, no. 2: 952. https://doi.org/10.3390/en16020952
APA StyleSrilatha, P., Remidi, S., Nagapavani, M., Singh, H., & Prasannakumara, B. C. (2023). Heat and Mass Transfer Analysis of a Fluid Flow across the Conical Gap of a Cone-Disk Apparatus under the Thermophoretic Particles Motion. Energies, 16(2), 952. https://doi.org/10.3390/en16020952






