ARX-GARCH Probabilistic Price Forecasts for Diversification of Trade in Electricity Markets—Variance Stabilizing Transformation and Financial Risk-Minimizing Portfolio Allocation
Abstract
1. Introduction
2. Datasets
3. Models
3.1. The Mean Model
3.2. The Variance Models
3.3. Variance Stabilizing Transformation
3.4. Model in-Sample Evaluation
4. Price Forecasts
4.1. Point Forecasts
4.2. Probabilistic Forecasts
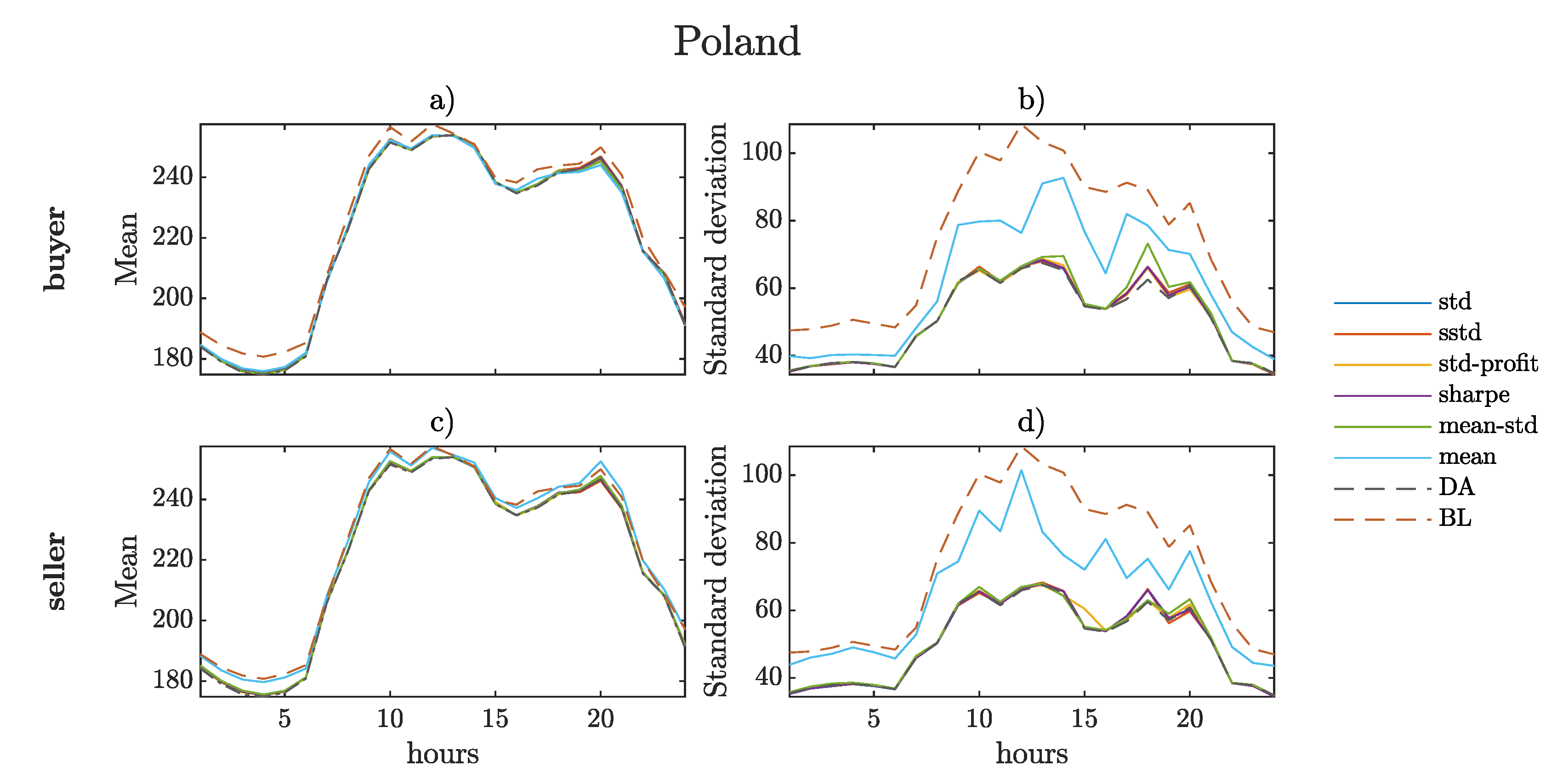
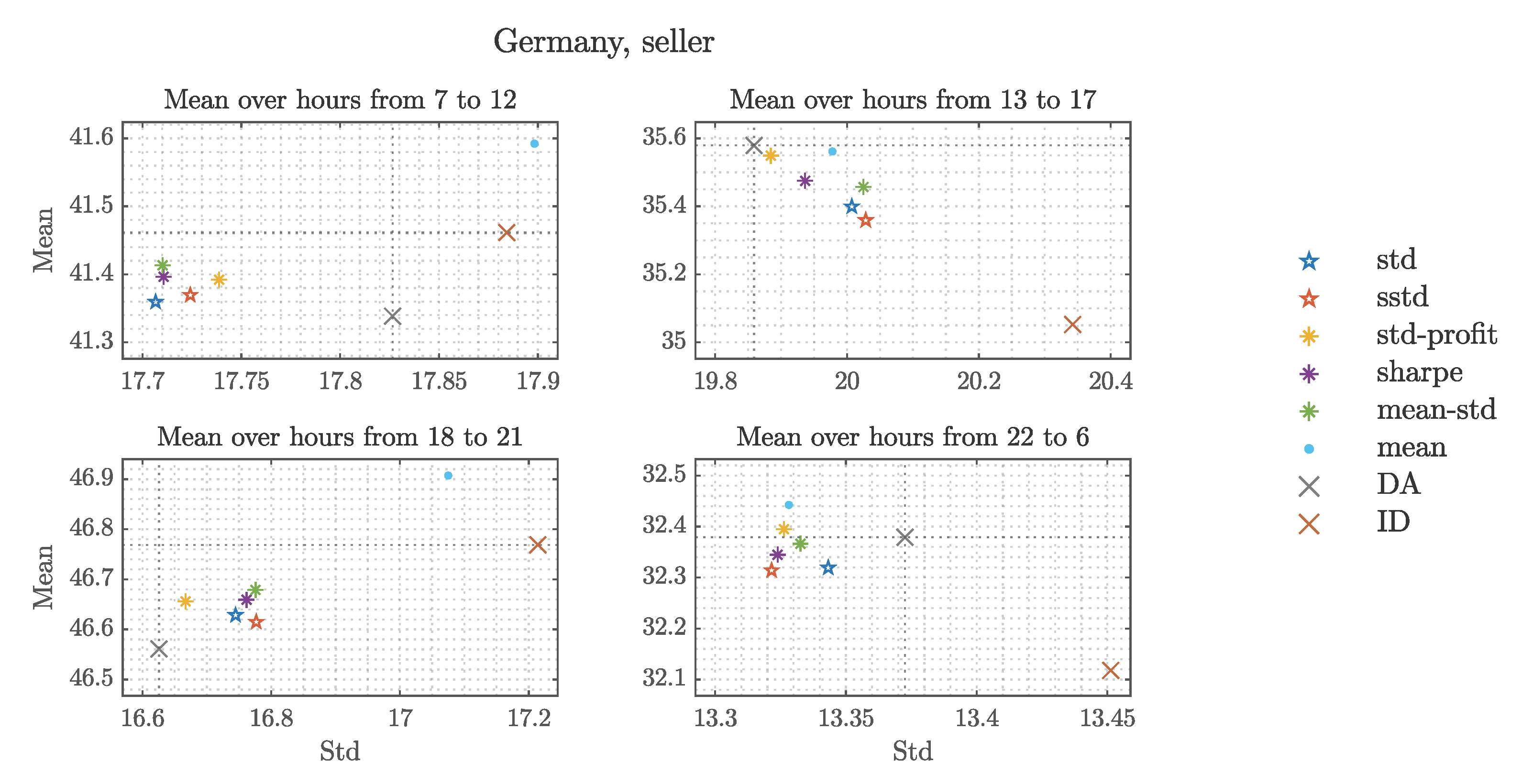
5. Portfolio Selection Based on Probabilistic Forecasts
5.1. Strategies
5.2. Evaluation of the Obtained Portfolios
6. Summary and Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Additional Figures
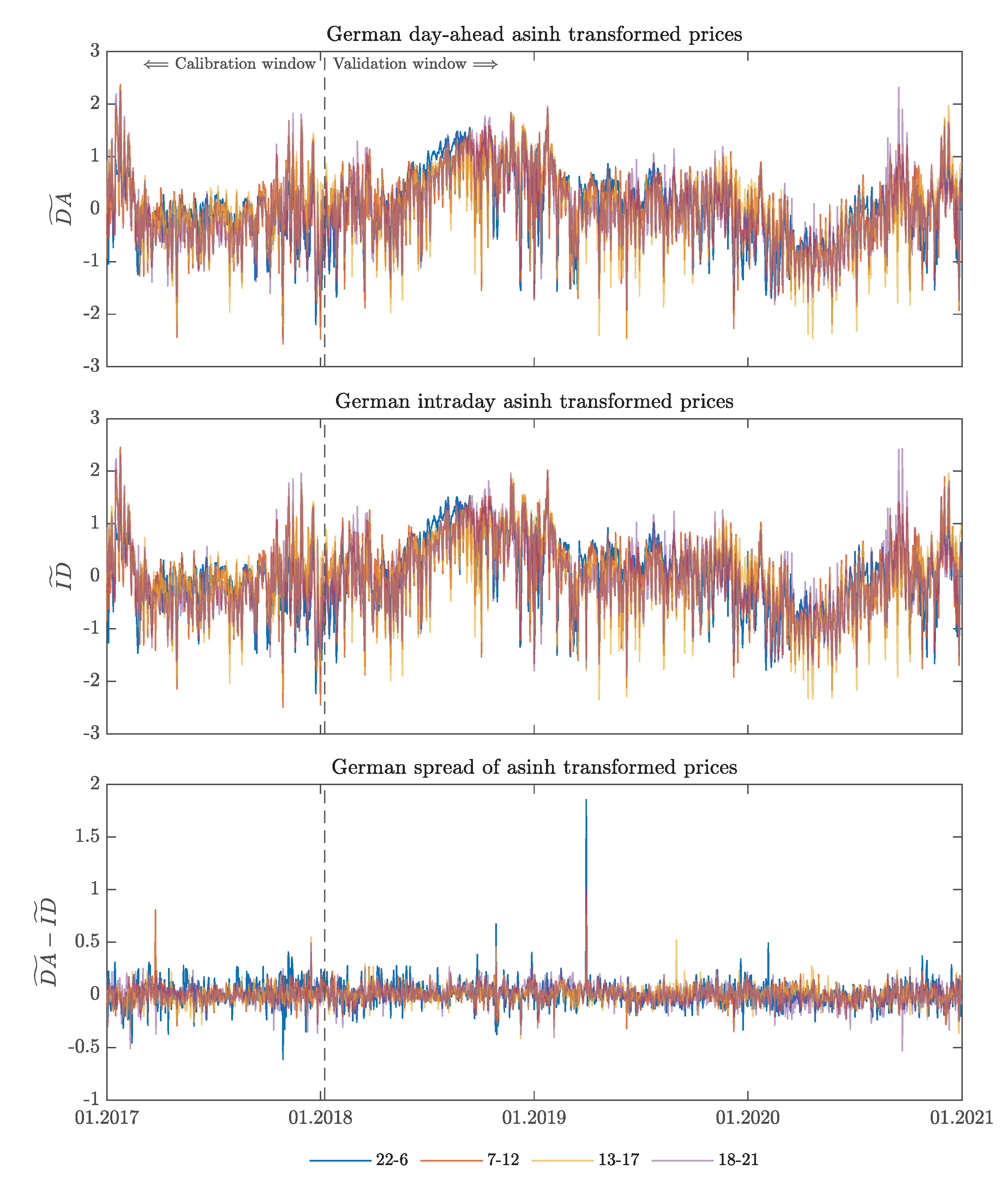
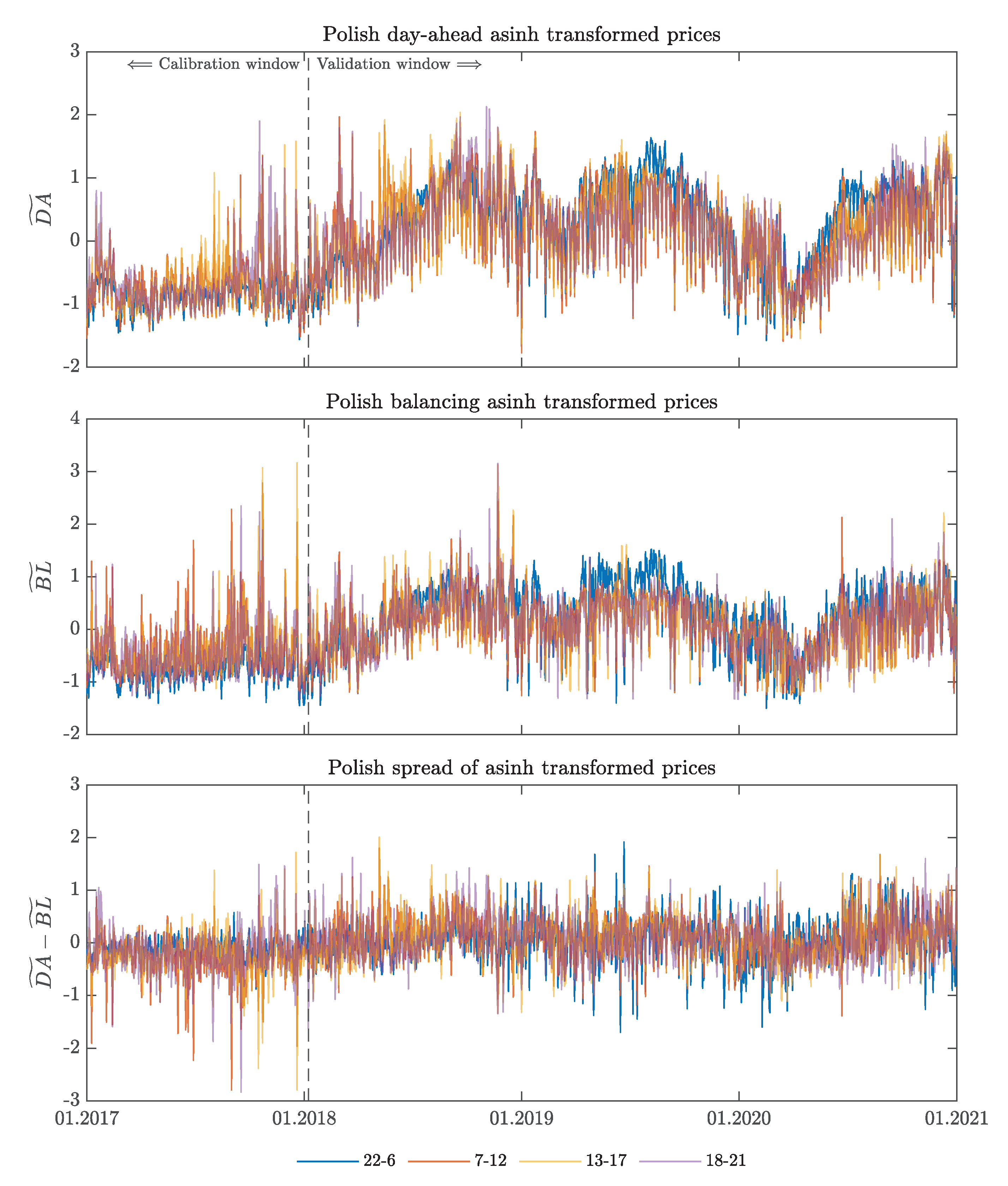
Appendix B. Misspecification Testing
References
- Burger, B. Energy-Charts. 2022. Available online: https://www.energy-charts.info (accessed on 25 July 2022).
- Martinez-Anido, C.B.; Brinkman, G.; Hodge, B. The impact of wind power on electricity prices. Renew. Energy 2016, 94, 474–487. [Google Scholar] [CrossRef]
- Gianfreda, A.; Parisio, L.; Pelagatti, M. The impact of RES in the Italian day-ahead and balancing markets. Energy J. 2016, 37, 161–184. [Google Scholar] [CrossRef]
- Maciejowska, K. Assessing the impact of renewable energy sources on the electricity price level and variability—A quantile regression approach. Energy Econ. 2020, 85, 104532. [Google Scholar] [CrossRef]
- Kulakov, S.; Ziel, F. The impact of renewable energy forecasts on intraday electricity prices. Econ. Energy Environ. Policy 2021, 10. [Google Scholar] [CrossRef]
- Gholami, M.; Shahryari, O.; Rezaei, N.; Bevrani, H. Optimum storage sizing in a hybrid wind-battery energy system considering power fluctuation characteristics. J. Energy Storage 2022, 52, 104634. [Google Scholar] [CrossRef]
- de Siqueira, L.M.S.; Peng, W. Control strategy to smooth wind power output using battery energy storage system: A review. J. Energy Storage 2021, 35, 102252. [Google Scholar] [CrossRef]
- Maciejowska, K.; Nitka, W.; Weron, T. Day-ahead vs. intraday—Forecasting the price spread to maximize economic benefits. Energies 2019, 12, 631. [Google Scholar] [CrossRef]
- Janczura, J.; Michalak, A. Optimization of electric energy sales strategy based on probabilistic forecasts. Energies 2020, 13, 1045. [Google Scholar] [CrossRef]
- Janczura, J.; Wójcik, E. Dynamic short-term risk management strategies for the choice of electricity market based on probabilistic forecasts of profit and risk measures. The German and the Polish market case study. Energy Econ. 2022, 110, 106015. [Google Scholar] [CrossRef]
- Markowitz, H. Portfolio selection. J. Financ. 1952, 7, 77–91. [Google Scholar]
- Elton, E.J.; Gruber, M.J. Modern portfolio theory, 1950 to date. J. Bank. Financ. 1997, 21, 1743–1759. [Google Scholar] [CrossRef]
- Liu, M.; Wu, F.F. Risk management in a competitive electricity market. Int. J. Electr. Power Energy Syst. 2007, 29, 690–697. [Google Scholar] [CrossRef]
- Garcia, R.C.; González, V.; Contreras, J.; Custodio, J.E. Applying modern portfolio theory for a dynamic energy portfolio allocation in electricity markets. Electr. Power Syst. Res. 2017, 150, 11–23. [Google Scholar] [CrossRef]
- Roques, F.A.; Newbery, D.M.; Nuttall, W.J. Fuel mix diversification incentives in liberalized electricity markets: A Mean–Variance Portfolio theory approach. Energy Econ. 2008, 30, 1831–1849. [Google Scholar] [CrossRef]
- Bollerslev, T. Generalized autoregressive conditional heteroskedasticity. J. Econom. 1986, 31, 307–327. [Google Scholar] [CrossRef]
- Hickey, E.; Loomis, D.G.; Mohammadi, H. Forecasting hourly electricity prices using ARMAX–GARCH models: An application to MISO hubs. Energy Econ. 2012, 34, 307–315. [Google Scholar] [CrossRef]
- Garcia, R.; Contreras, J.; van Akkeren, M.; Garcia, J. A GARCH forecasting model to predict day-ahead electricity prices. IEEE Trans. Power Syst. 2005, 20, 867–874. [Google Scholar] [CrossRef]
- Tehrani, S.; Juan, J.; Caro, E. Electricity spot price modeling and forecasting in European markets. Energies 2022, 15, 5980. [Google Scholar] [CrossRef]
- Karakatsani, N.V.; Bunn, D.W. Fundamental and behavioural drivers of electricity price volatility. Stud. Nonlinear Dyn. Econom. 2010, 14. [Google Scholar] [CrossRef]
- Billé, A.G.; Gianfreda, A.; Del Grosso, F.; Ravazzolo, F. Forecasting electricity prices with expert, linear, and nonlinear models. Int. J. Forecast. 2022, in press. [Google Scholar] [CrossRef]
- Tan, H.; Li, Z.; Wang, Q.; Mohamed, M.A. A novel forecast scenario-based robust energy management method for integrated rural energy systems with greenhouses. Appl. Energy 2023, 330, 120343. [Google Scholar] [CrossRef]
- Chen, Z.; Jin, T.; Zheng, X.; Liu, Y.; Zhuang, Z.; Mohamed, M.A. An innovative method-based CEEMDAN–IGWO–GRU hybrid algorithm for short-term load forecasting. Electr. Eng. 2022, 104, 3137–3156. [Google Scholar] [CrossRef]
- European Energy Exchange. 2021. Available online: https://www.epexspot.com (accessed on 12 April 2021).
- Towarowa Giełda Energii. 2021. Available online: https://tge.pl/ (accessed on 12 April 2021).
- Lago, J.; Marcjasz, G.; De Schutter, B.; Weron, R. Forecasting day-ahead electricity prices: A review of state-of-the-art algorithms, best practices and an open-access benchmark. Appl. Energy 2021, 293, 116983. [Google Scholar] [CrossRef]
- Commission, T.E. Commission Regulation (EU) 2017/2195 of 23 November 2017 establishing a guideline on electricity balancing. Off. J. Eur. Union 2017, 312, 6–53. [Google Scholar]
- Polskie Sieci Energetyczne. 2021. Available online: http://www.pse.pl (accessed on 12 April 2021).
- Karakatsani, N.V.; Bunn, D.W. Forecasting electricity prices: The impact of fundamentals and time-varying coefficients. Int. J. Forecast. 2008, 24, 764–785. [Google Scholar] [CrossRef]
- Uniejewski, B.; Marcjasz, G.; Weron, R. Understanding intraday electricity markets: Variable selection and very short-term price forecasting using LASSO. Int. J. Forecast. 2019, 35, 1533–1547. [Google Scholar] [CrossRef]
- Kiesel, R.; Paraschiv, F. Econometric analysis of 15-minute intraday electricity prices. Energy Econ. 2017, 64, 77–90. [Google Scholar] [CrossRef]
- Luo, S.; Weng, Y. A two-stage supervised learning approach for electricity price forecasting by leveraging different data sources. Appl. Energy 2019, 242, 1497–1512. [Google Scholar] [CrossRef]
- Weron, R. Electricity price forecasting: A review of the state-of-the-art with a look into the future. Int. J. Forecast. 2014, 30, 1030–1081. [Google Scholar] [CrossRef]
- Petropoulos, F.; Apiletti, D.; Assimakopoulos, V.; Babai, M.Z.; Barrow, D.K.; Ben Taieb, S.; Bergmeir, C.; Bessa, R.J.; Bijak, J.; Boylan, J.E.; et al. Forecasting: Theory and practice. Int. J. Forecast. 2022, 38, 705–871. [Google Scholar] [CrossRef]
- Glosten, L.R.; Jagannathan, R.; Runkle, D.E. On the relation between the expected value and the volatility of the nominal excess return on stocks. J. Financ. 1993, 48, 1779–1801. [Google Scholar] [CrossRef]
- Janczura, J.; Trück, S.; Weron, R.; Wolff, R.C. Identifying spikes and seasonal components in electricity spot price data: A guide to robust modeling. Energy Econ. 2013, 38, 96–110. [Google Scholar] [CrossRef]
- Uniejewski, B.; Weron, R.; Ziel, F. Variance Stabilizing Transformations for Electricity Spot Price Forecasting. IEEE Trans. Power Syst. 2018, 33, 2219–2229. [Google Scholar] [CrossRef]
- Engle, R.F. Autoregressive conditional heteroscedasticity with estimates of the variance of United Kingdom inflation. Econometrica 1982, 50, 987–1007. [Google Scholar] [CrossRef]
- Maki, D.; Ota, Y. Robust tests for ARCH in the presence of a misspecified conditional mean: A comparison of nonparametric approaches. Cogent Econ. Financ. 2021, 9, 1862445. [Google Scholar] [CrossRef]
- Lumsdaine, R.L.; Ng, S. Testing for ARCH in the presence of a possibly misspecified conditional mean. J. Econom. 1999, 93, 257–279. [Google Scholar] [CrossRef]
- Narajewski, M.; Ziel, F. Econometric modelling and forecasting of intraday electricity prices. J. Commod. Mark. 2020, 19, 100107. [Google Scholar] [CrossRef]
- Diebold, F.; Mariano, R. Comparing predictive accuracy. J. Bus. Econ. Stat. 1995, 13, 253–263. [Google Scholar]
- Nowotarski, J.; Weron, R. Recent advances in electricity price forecasting: A review of probabilistic forecasting. Renew. Sustain. Energy Rev. 2018, 81, 1548–1568. [Google Scholar] [CrossRef]
- Alexander, C. Market Risk Analysis, Value at Risk Models; The Wiley Finance Series; Wiley: Hoboken, NJ, USA, 2009. [Google Scholar]
- Gneiting, T. Quantiles as optimal point forecasts. Int. J. Forecast. 2011, 27, 197–207. [Google Scholar] [CrossRef]
- Sharpe, W.F. Mutual Fund Performance. J. Bus. 1966, 39, 119–138. [Google Scholar] [CrossRef]
- Fabozzi, F.; Focardi, S.; Kolm, P.; Pachamanova, D. Robust Portfolio Optimization and Management; Frank J. Fabozzi Series; Wiley: Hoboken, NJ, USA, 2007. [Google Scholar]
- Waltz, R.; Morales, J.; Nocedal, J.; Orban, D. An interior algorithm for nonlinear optimization that combines line search and trust region steps. Math. Program. 2006, 107, 391–408. [Google Scholar] [CrossRef]
- Ascencio-Vásquez, J.; Osorio-Aravena, J.C.; Brecl, K.; Muñoz-Cerón, E.; Topič, M. Typical Daily Profiles, a novel approach for photovoltaics performance assessment: Case study on large-scale systems in Chile. Solar Energy 2021, 225, 357–374. [Google Scholar] [CrossRef]
- Pryor, S.C.; Barthelmie, R.J.; Shepherd, T.J. Wind power production from very large offshore wind farms. Joule 2021, 5, 2663–2686. [Google Scholar] [CrossRef]
- Maciejowska, K. A portfolio management of a small RES utility with a Structural Vector Autoregressive model of German electricity markets. arXiv 2022, arXiv:2205.00975. [Google Scholar]
- Adamska, J.; Bielak, Ł.; Janczura, J.; Wyłomańska, A. From multi- to univariate: A product random variable with an application to electricity market transactions: Pareto and Student’s t-distribution case. Mathematics 2022, 10, 3371. [Google Scholar] [CrossRef]
- Janczura, J.; Puć, A.; Bielak, .; Wyłomańska, A. Dependence structure for the product of bi-dimensional finite-variance VAR(1) model components. An application to the cost of electricity load prediction errors. arXiv 2022, arXiv:2203.02249. [Google Scholar]
- Shah, I.; Lisi, F. Forecasting of electricity price through a functional prediction of sale and purchase curves. J. Forecast. 2020, 39, 242–259. [Google Scholar] [CrossRef]
- Kulakov, S. X-Model: Further development and possible modifications. Forecasting 2020, 2, 20–35. [Google Scholar] [CrossRef]
- Mestre, G.; Portela, J.; Muñoz San Roque, A.; Alonso, E. Forecasting hourly supply curves in the Italian Day-Ahead electricity market with a double-seasonal SARMAHX model. Int. J. Electr. Power Energy Syst. 2020, 121, 106083. [Google Scholar] [CrossRef]
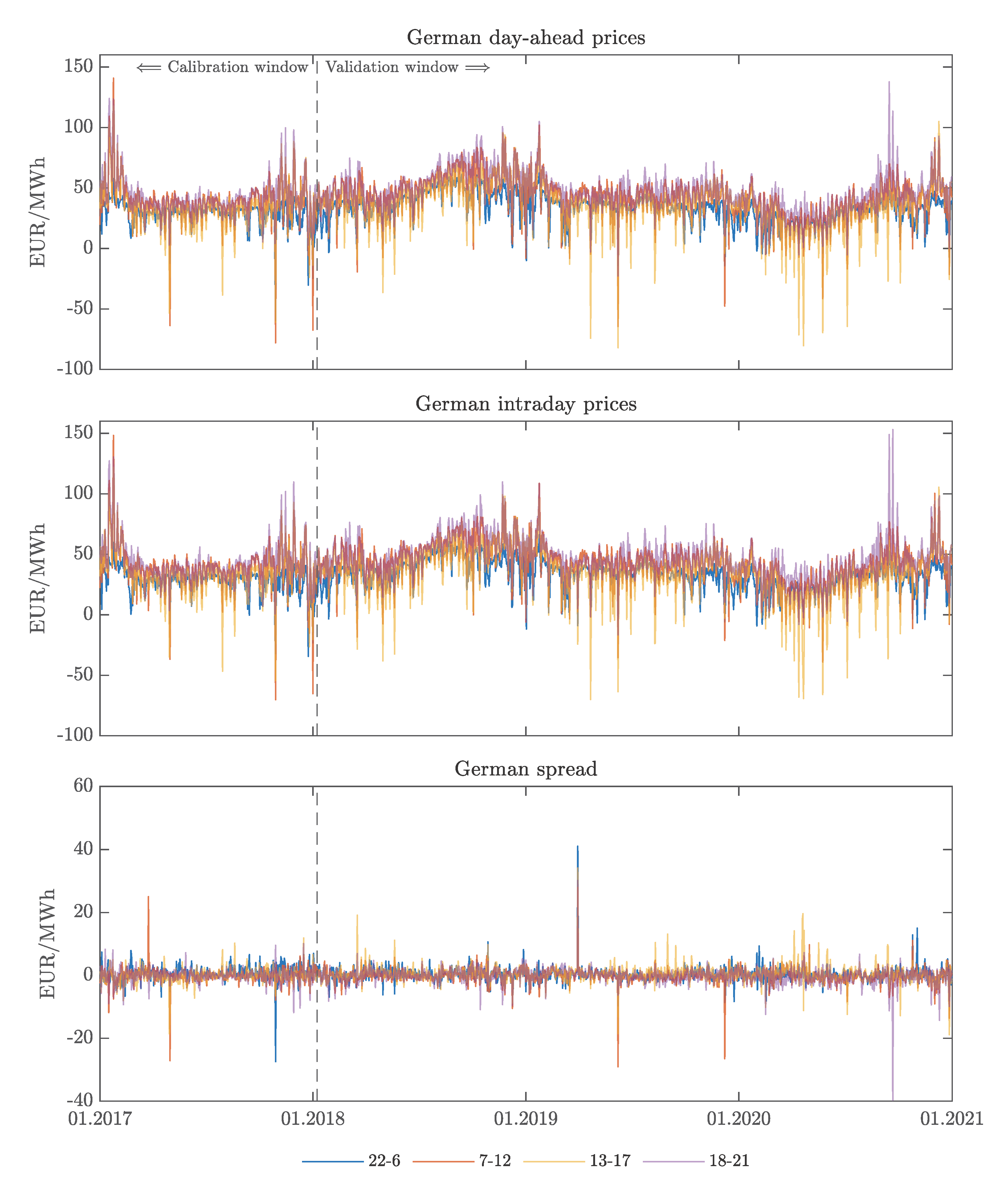
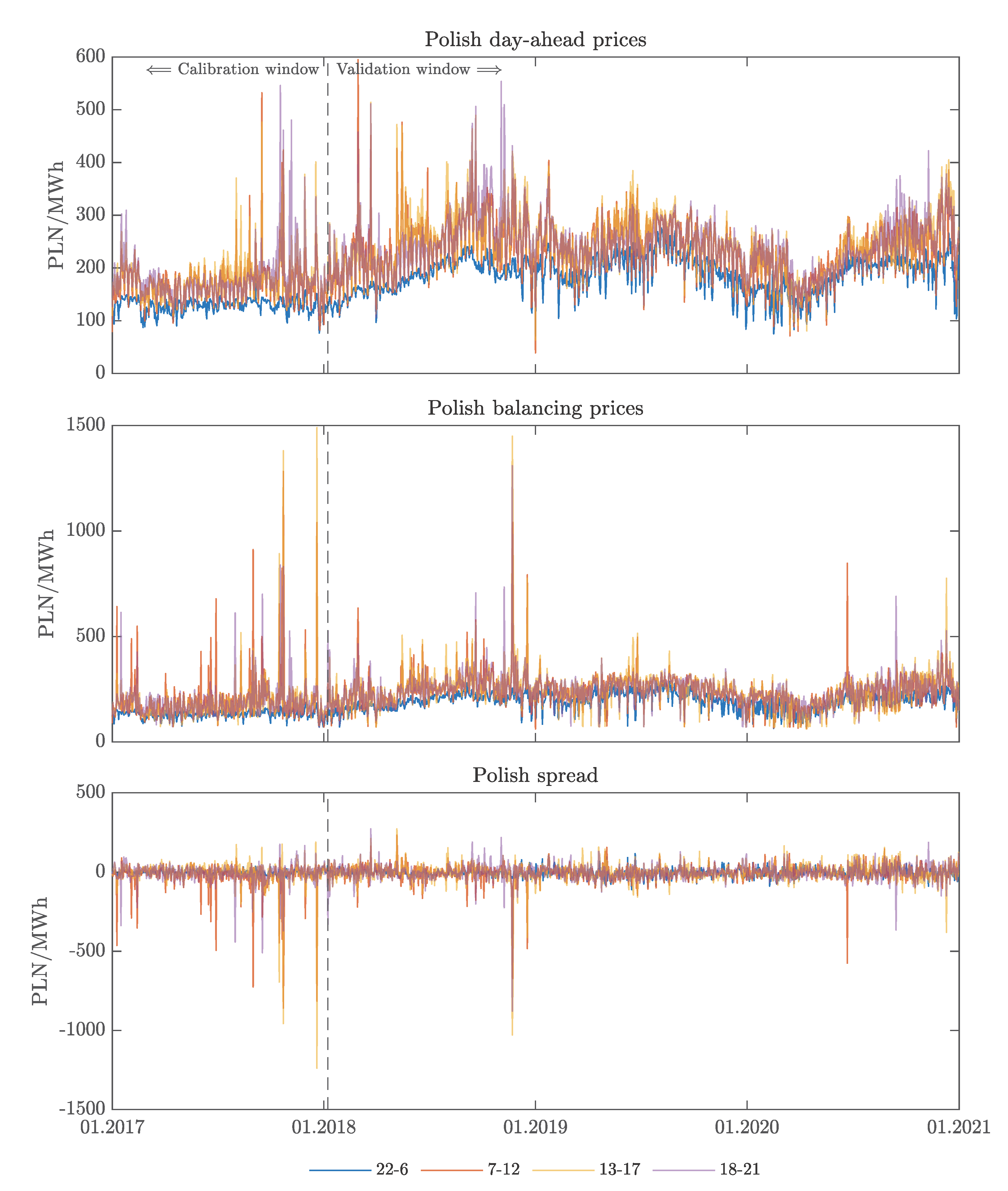






| Data | Unit | Notation | Frequency | Source |
|---|---|---|---|---|
| Germany | ||||
| Day-ahead prices | [EUR/MWh] | hourly | EPEX SPOT | |
| Intraday prices | [EUR/MWh] | hourly | EPEX SPOT | |
| Forecasted generation | [MWh] | hourly | ENTSO-E | |
| Forecasted wind generation | [MWh] | hourly | ENTSO-E | |
| Forecasted load | [MWh] | hourly | ENTSO-E | |
| Forecasted solar generation | [MWh] | hourly | ENTSO-E | |
| CO emission prices | [EUR/Mg CO] | daily | CFI2Z1, investing.com | |
| Gas prices | [EUR/MWh] | daily | Börse Frankfurt | |
| Poland | ||||
| Day-ahead prices | [PLN/MWh] | hourly | TGE [25] | |
| Balancing prices | [PLN/MWh] | hourly | PSE [28] | |
| Forecasted demand | [MWh] | hourly | PSE [28] | |
| Forecasted wind generation | [MWh] | hourly | PSE [28] | |
| Forecasted reserves | [MWh] | hourly | PSE [28] | |
| Imbalance | [MWh] | hourly | PSE [28] | |
| CO emission prices | [PLN/Mg CO] | daily | PSE [28] | |
| Gas prices | [PLN/MWh] | daily | cire.pl | |
| Temperature | [C] | daily | imgw.pl | |
| Poland | Germany | |||||||
|---|---|---|---|---|---|---|---|---|
| Day-Ahead | Balancing | Day-Ahead | Intraday | |||||
| Transformation | — | Asinh | — | Asinh | — | Asinh | — | Asinh |
| no ARCH | 15% | 9% | 25% | 36% | 20% | 32% | 16% | 15% |
| Gaussian | 36% | 23% | 64% | 33% | 55% | 3% | 42% | 2% |
| Student’s t | 1% | 1% | 2% | 6% | 0% | 0% | 0% | 0% |
| Germany | Poland | |||||||
|---|---|---|---|---|---|---|---|---|
| Day-Ahead | Intraday | Day-Ahead | Balancing | |||||
| Hour | — | Asinh | — | Asinh | — | Asinh | — | Asinh |
| 1 | 4.23 | 4.12 * | 4.57 | 4.64 | 13.43 | 13.65 | 27.44 | 27.24 |
| 2 | 4.38 | 4.19 * | 4.6 | 4.58 | 13.61 | 13.76 | 26.87 | 26.98 |
| 3 | 4.56 | 4.36 * | 5.01 | 4.91 | 13.53 * | 13.84 | 28.22 | 28.44 |
| 4 | 4.45 | 4.38 | 4.98 | 4.94 | 13.33 * | 13.77 | 28.63 | 28.66 |
| 5 | 4.44 | 4.38 | 4.68 | 4.77 | 12.98 * | 13.48 | 28.01 | 27.91 |
| 6 | 4.28 | 4.16 * | 4.43 | 4.53 | 12.94 * | 13.3 | 27.43 | 27.46 |
| 7 | 4.9 | 4.62 * | 5 | 4.83 * | 14.97 | 15.03 | 29.65 | 28.77 * |
| 8 | 5.37 | 5.13 * | 5.52 | 5.4 | 17.1 | 17.42 | 41.74 | 38.87 * |
| 9 | 5.41 | 5.31 | 5.68 | 5.6 | 22.63 | 23.03 | 48.76 | 44.98 * |
| 10 | 5.1 | 5.06 | 5.23 | 5.27 | 25.19 * | 25.98 | 55.45 | 51.64 * |
| 11 | 5.17 | 5.08 | 5.39 | 5.37 | 24.09 | 24.62 | 56.15 | 51.52 * |
| 12 | 5.56 | 5.23 * | 5.68 | 5.47 * | 26.77 | 27.3 | 61.01 | 56.09 * |
| 13 | 5.91 | 5.32 * | 6.22 | 5.74 * | 26.81 * | 27.56 | 55.91 | 52.17 * |
| 14 | 6.51 | 5.67 * | 7.12 | 6.28 * | 25.33 | 25.95 | 55.19 | 51.61 * |
| 15 | 6.78 | 5.96 * | 7.34 | 6.49 * | 19.21 * | 20.74 | 51.27 | 47.7 * |
| 16 | 6.3 | 5.6 * | 6.77 | 5.96 * | 18.19 * | 19.86 | 50.56 | 46.32 * |
| 17 | 5.96 | 5.42 * | 6.24 | 5.69 * | 20.42 * | 21.19 | 50.14 | 46.7 * |
| 18 | 5.53 | 5.15 * | 6.07 | 5.6 * | 24.4 | 23.62 | 52.36 | 46.46 * |
| 19 | 5.25 | 5.07 * | 5.8 | 5.54 * | 23.09 | 23.61 | 45.89 | 42.98 * |
| 20 | 5.93 | 5.72 * | 6.4 | 6.13 * | 24.82 | 23.68 * | 43.63 | 41.13 * |
| 21 | 4.93 * | 5.06 | 5.49 | 5.53 | 19.4 | 19.72 | 39.09 | 38.17 * |
| 22 | 4.16 | 4.28 | 4.53 | 4.65 | 12.86 * | 13.35 | 35.63 * | 36.55 |
| 23 | 3.81 | 3.84 | 4.06 | 3.96 | 13.52 * | 13.8 | 27.85 * | 28.19 |
| 24 | 4.04 | 3.98 | 4.73 | 4.41 * | 13.32 * | 13.79 | 27.61 | 27.66 |
| Avg. | 5.12 | 4.88 * | 5.48 | 5.26 * | 18.83 | 19.25 | 41.44 | 39.34 * |
| Germany | Poland | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Strategy | Seller | Buyer | Seller | Buyer | ||||||||
| p-DA | p-ID | std | p-DA | p-ID | std | p-DA | p-BL | std | p-DA | p-BL | std | |
| std | −1135 | 2583 | 16.39 | 1135 | −2583 | 16.39 | 7371 | −88,569 | 50.89 | −7371 | 88,569 | 50.89 |
| sstd | −1397 | 2320 | 16.4 | 874 | −2844 | 16.38 | 6808 | −89,132 | 50.83 | −8787 | 87,153 | 51.03 |
| std-profit | 754 | 4471 | 16.35 | 1988 | −1729 | 16.42 | 8322 | −87,617 | 50.98 | −102 | 95,838 | 50.87 |
| sharpe | −97 | 3620 | 16.37 | 2906 | −811 | 16.45 | 9220 | −86,720 | 50.86 | −5522 | 90,418 | 50.95 |
| mean-std | 213 | 3930 | 16.4 | 2482 | −1236 | 16.42 | 14,611 | −81,328 | 51.18 | −131 | 95,809 | 51.78 |
| mean | 3686 | 7403 | 16.48 | 7403 | 3686 | 16.52 | 91,829 | −4111 | 64.72 | −4111 | 91,829 | 61.36 |
| Strategy | |||||||
|---|---|---|---|---|---|---|---|
| Risk Minimization | Optimal Strategies | Profit Maximization | |||||
| std | sstd | std-Profit | Sharpe | Mean-std | Mean | ||
| Germany | seller | 2.29 | 2.29 | 2.30 | 2.30 | 2.30 | 2.29 |
| buyer | −2.29 | −2.30 | −2.29 | −2.28 | −2.29 | −2.26 | |
| Poland | seller | 4.34 | 4.35 | 4.33 | 4.34 | 4.32 | 3.46 |
| buyer | −4.34 | −4.33 | −4.34 | −4.33 | −4.26 | −3.60 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Janczura, J.; Puć, A. ARX-GARCH Probabilistic Price Forecasts for Diversification of Trade in Electricity Markets—Variance Stabilizing Transformation and Financial Risk-Minimizing Portfolio Allocation. Energies 2023, 16, 807. https://doi.org/10.3390/en16020807
Janczura J, Puć A. ARX-GARCH Probabilistic Price Forecasts for Diversification of Trade in Electricity Markets—Variance Stabilizing Transformation and Financial Risk-Minimizing Portfolio Allocation. Energies. 2023; 16(2):807. https://doi.org/10.3390/en16020807
Chicago/Turabian StyleJanczura, Joanna, and Andrzej Puć. 2023. "ARX-GARCH Probabilistic Price Forecasts for Diversification of Trade in Electricity Markets—Variance Stabilizing Transformation and Financial Risk-Minimizing Portfolio Allocation" Energies 16, no. 2: 807. https://doi.org/10.3390/en16020807
APA StyleJanczura, J., & Puć, A. (2023). ARX-GARCH Probabilistic Price Forecasts for Diversification of Trade in Electricity Markets—Variance Stabilizing Transformation and Financial Risk-Minimizing Portfolio Allocation. Energies, 16(2), 807. https://doi.org/10.3390/en16020807






