Theoretical and Experimental Study on Cementing Displacement Interface for Highly Deviated Wells
Abstract
1. Introduction
2. Theoretical Model
2.1. Theoretical Basis
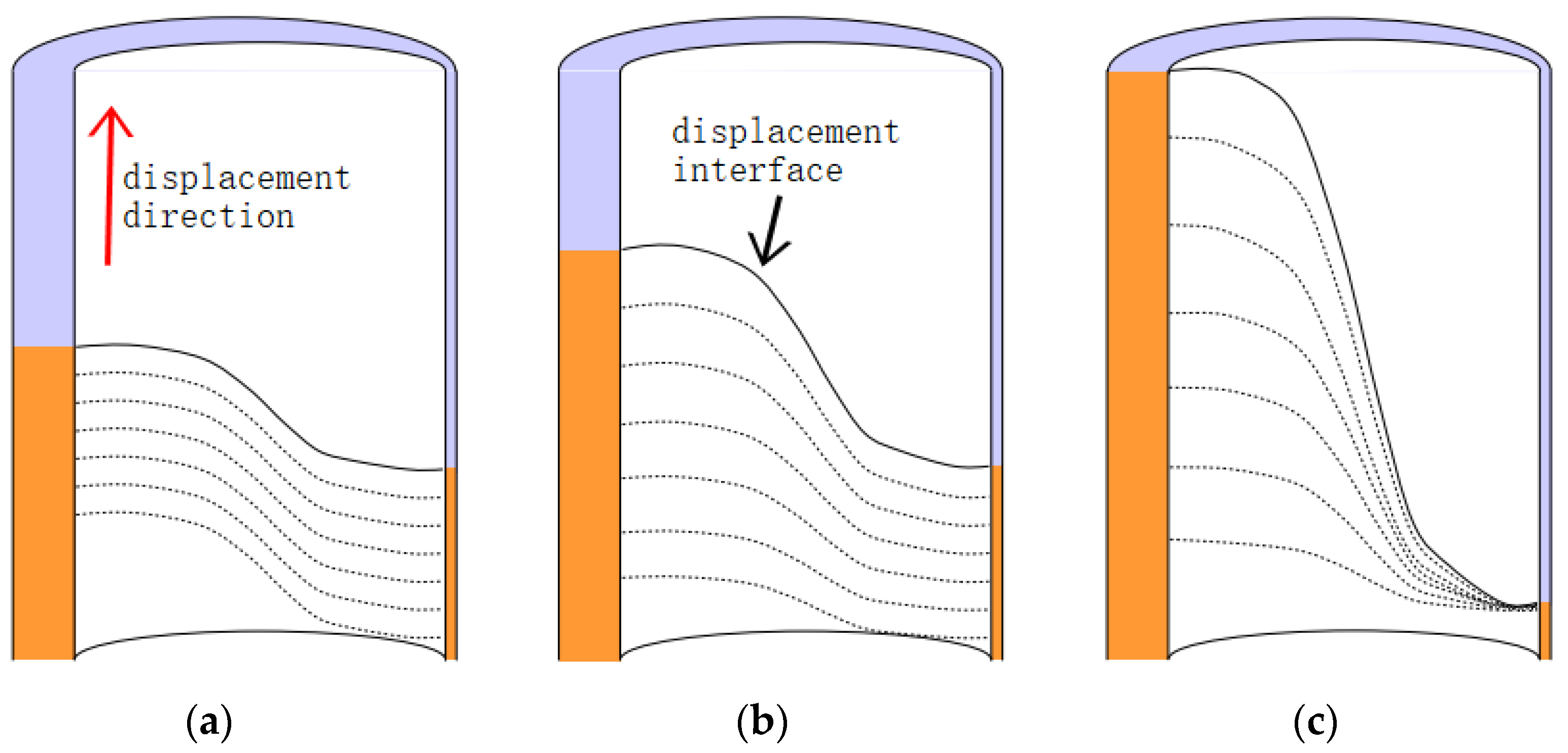
2.2. Model Development for Displacement Interface
- (1)
- The displacement interface completely separates the drilling fluid and cement slurry, and there is no obvious mixing and diffusion between them.
- (2)
- The shape of the displacement interface gradually changes from unstable to stable ones after the cement slurry is pumped into the annulus. The length of annulus is much larger than the extension length of displacement interface, so the object of study is determined as the stable displacement interface after long enough displacement time.
- (3)
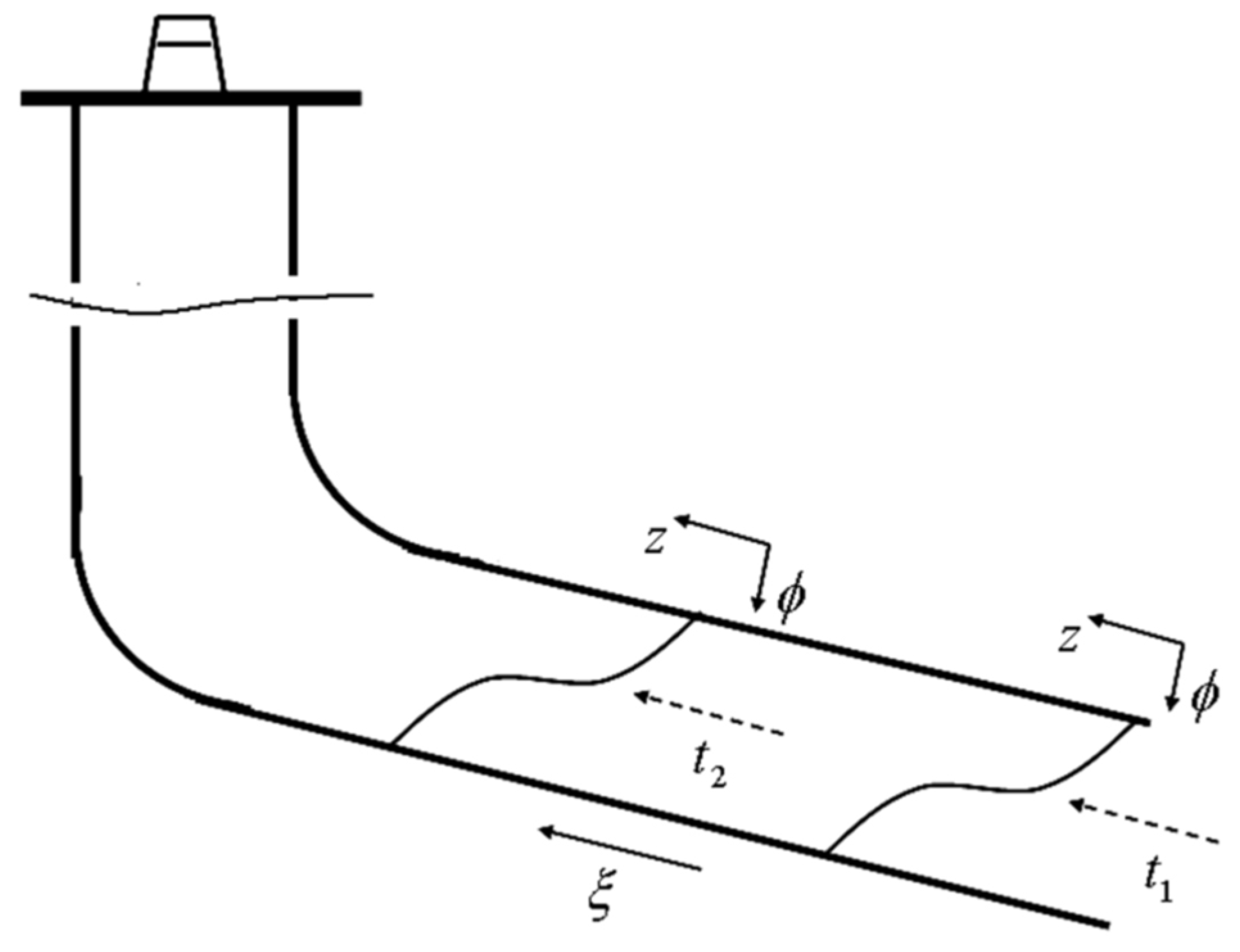
- Take a wellbore annulus section with a length of . In the annulus area of this section, the borehole is regular; the well deviation angle and casing eccentricity are constant (i.e., and are constant), and the flow rate of cement slurry in annulus is constant.
- (4)
- In the practice of on-site cementing, especially in highly deviated wells and horizontal wells, it is difficult for the flow state of cement slurry to achieve turbulent flow. In addition to the pressure bearing capacity of on-site equipment, it is easy for turbulent displacement to cause formation fracture. Thus, on-site cementing displacement is still dominated by laminar flow. Thus, the displacement interface model studied by the author is aimed at the situation of laminar flow.
- (1)
- The displacement interface expression for : ;
- (2)
- The stream function for and the stream function for satisfy the following relations: . This is due to the following relations: , ;
- (3)
- The motion equation for is: ;
- (4)
- The continuity equation for is:
- (5)
- The boundary condition for :; .
2.3. Solution of Model
- (1)
- Stream function expressions for zone and are converted into:
- (2)
- The continuity equation at the displacement interface is transformed into:
- (3)
- Transformation form of definite solution condition is: ; .Where and denote partial derivative of to and , respectively.
3. Experiment Verification of Model
3.1. Experimental Research Device and Method
- (1)
- The inner diameter of PVC pipe is 70 mm, the outer diameter of steel pipe is 30 mm, the annular space gap is 20 mm, and the total length is 4.2 m. The PVC pipe simulates wellbore, and steel pipe simulates casing;
- (2)
- Through the lifting system on the support, the deviation angle of the well can be adjusted between 80–90°;
- (3)
- The maximum displacement of the liquid pump is 10 L/min. By reasonably adjusting the rheological parameters of the fluid, the flow state of the fluid in the annulus can be obtained as laminar flow;
- (4)
- The eccentricity of the steel pipe can be changed by adjusting the flange combination on the plexiglass pipe.
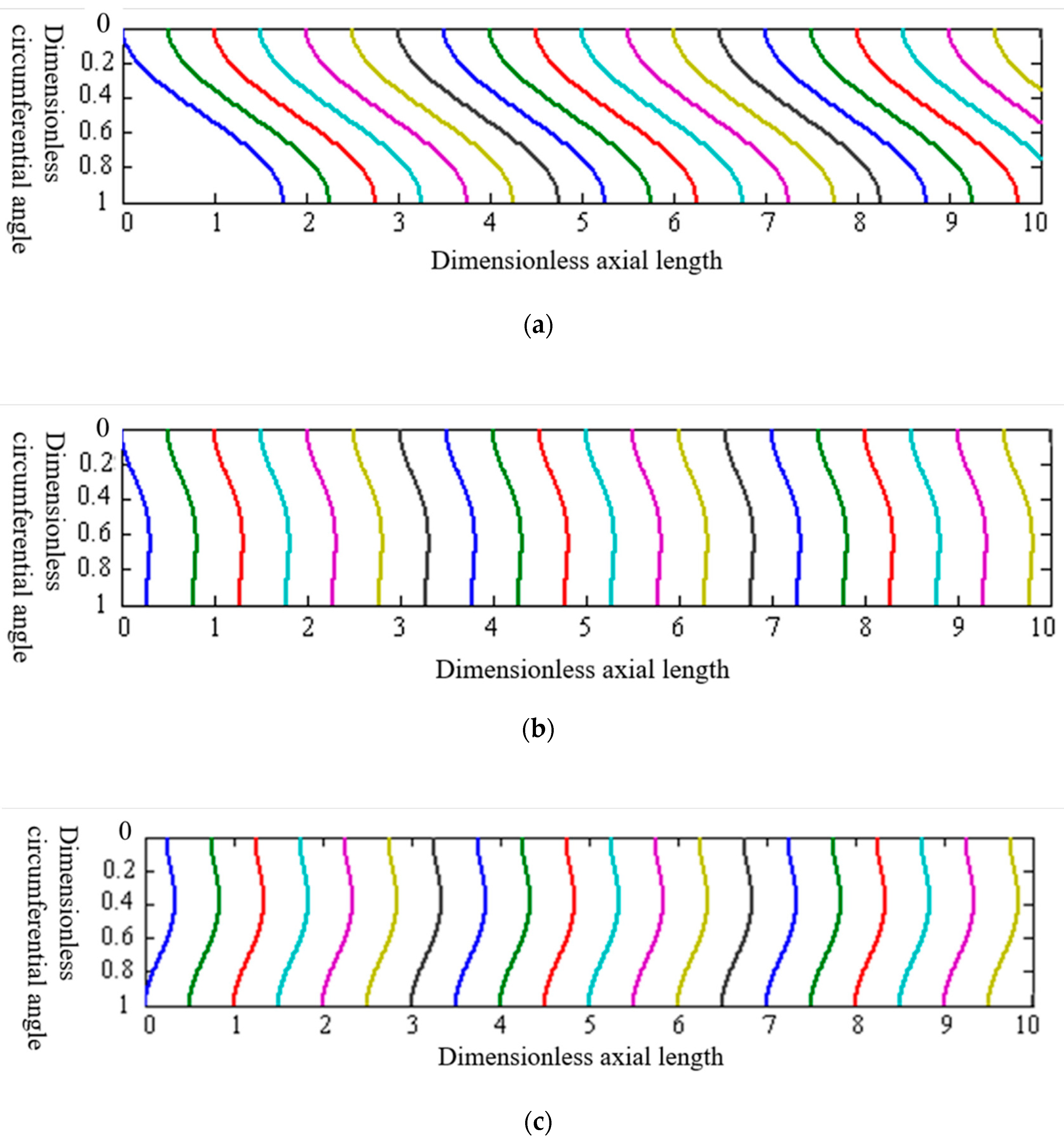
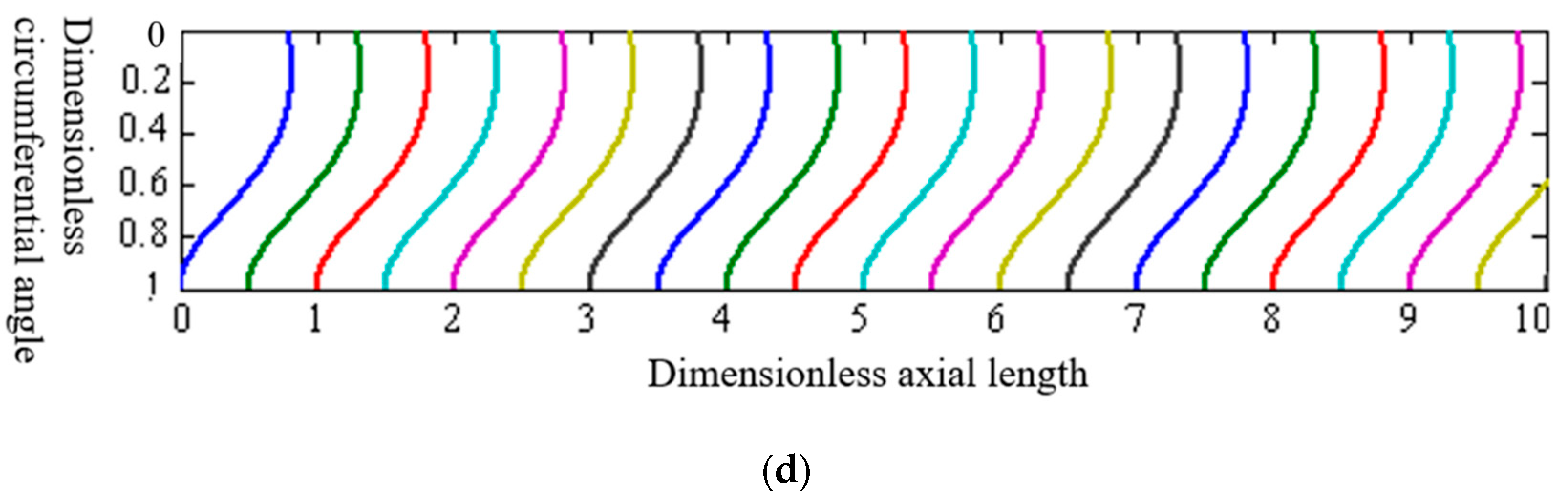
3.2. Results and Discussion
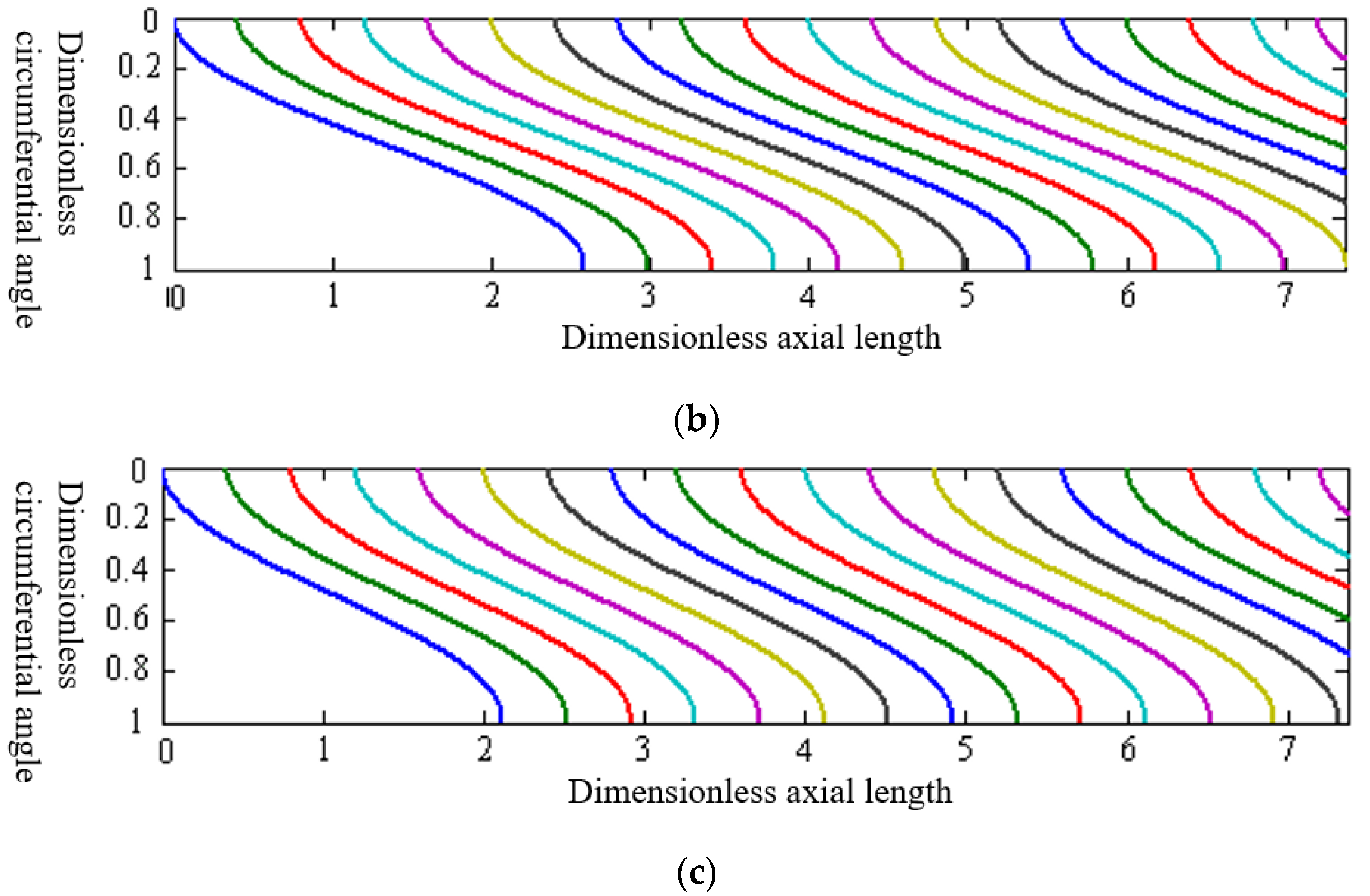
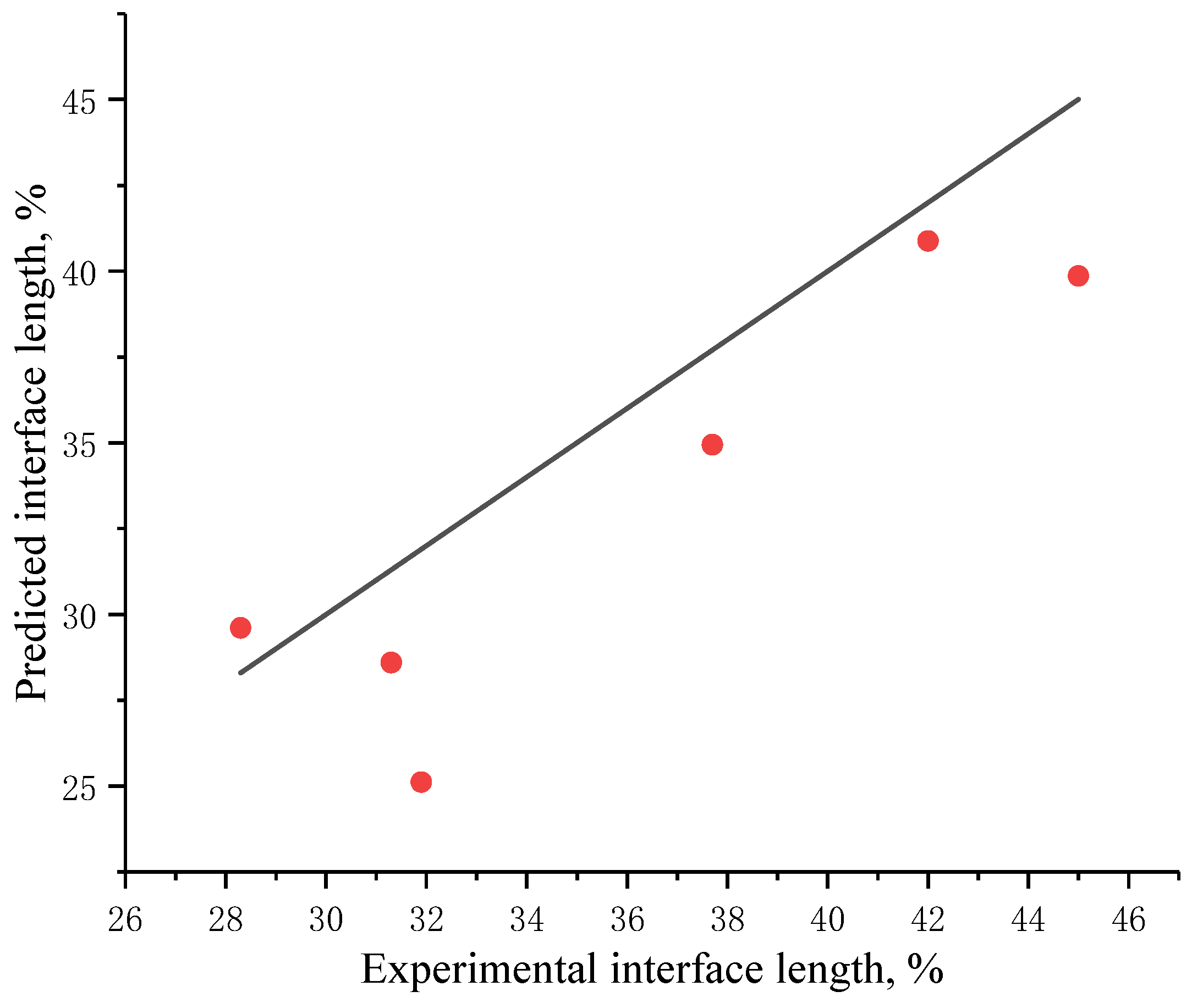
3.3. Model Validation
4. Application of Theoretical Model
5. Conclusions
- (1)
- A theoretical model for cement displacement interface is established, and the theoretical model is verified by the experiments which investigate influence of well deviation angle, casing eccentricity, and cement slurry formulations on the displacement interface. The new model is not limited to the well deviation angle, and can simulate the cement displacement interface morphology in concentric annulus and eccentric annulus.
- (2)
- The finite difference method can effectively solve the theoretical model. The analysis shows that: with the increase of well deviation angle, the cement displacement interface length gradually extends, and under the same injection conditions, the well with a larger well deviation angle has a poor cement displacement effect. Increasing the apparent viscosity of cement slurry is beneficial to improve the stability of displacement interface. In highly deviated wells, a certain casing eccentricity can inhibit the uneven penetration of cement slurry in the annulus, which is conducive to maintaining the stability of the displacement interface.
Author Contributions
Funding
Conflicts of Interest
References
- Lockyear, C.F.; Hibbert, A.P. Integrated primary cementing study defines key factors for field success. J. Pet. Technol. 1989, 41, 1320–1325. [Google Scholar] [CrossRef]
- Lockyear, C.F.; Ryan, D.F.; Gunningham, D.F. Cement channeling: How to predict and prevent. SPE Drill. Complet. 1989, 5, 201–208. [Google Scholar] [CrossRef]
- Frigaard, I.A.; Allouche, M.; Gabardcuoq, C. Setting rheological targets for chemical solutions in mud removal and cement slurry design. In Proceedings of the SPE International Symposium on Oilfield Chemistry, Houston, TX, USA, 13–16 February 2001. [Google Scholar] [CrossRef]
- Frigaard, I.A.; Pelipenko, S. Effective and ineffective strategies for mud removal and cement slurry design. In Proceedings of the SPE Latin American and Caribbean Petroleum Engineering Conference, Port-of-Spain, Trinidad and Tobago, 27–30 April 2003. [Google Scholar] [CrossRef]
- Su, Y.; Dou, X. General condition and technical difficulties of extended reach drilling and rrs requirements on tools and instrument. J. Oil Drill. Prod. Technol. 2003, 25, 6–10. [Google Scholar] [CrossRef]
- Keller, S.R.; Crook, R.J.; Haut, R.C.; Kulakofsky, D.S. Problems associated with deviated-wellbore. In Proceedings of the SPE Annual Technical Conference, San Francisco, CA, USA, 5 October 1983. [Google Scholar]
- Couturier, M.; Guillot, D.; Hendriks, H.; Callet, F. Design rules and associated spacer properties for optimal mud removal in eccentric annuli. In Proceedings of the CIM/SPE International Technical Meeting, Calgary, AB, Canada, 10–13 June 1990. [Google Scholar] [CrossRef]
- Li, M.; Wang, C.; Wang, C.; Guo, S.; Fang, Q. Numerical simulation of cement displacement in eccentric annulus at highly deviated wells. J. Pet. Drill. Tech. 2012, 40, 40–44. [Google Scholar] [CrossRef]
- Li, M.; Wang, R.; Wang, C.; Fang, Q.; Xue, Y. Study on Flow Characteristic of Non-newtonian fluid in Eccentric Annulus. Res. J. Appl. Sci. Eng. Technol. 2013, 13, 2451–2458. [Google Scholar] [CrossRef]
- Pelipenko, S.; Frigaard, I.A. Visco-plastic fluid displacements in near-vertical narrow eccentric annuli: Prediction of travelling-wave solutions and interfacial instability. J. Fluid Mechematics 2004, 520, 343–377. [Google Scholar] [CrossRef]
- Moyers-Gonzalez, M.A.; Frigaard, I.A. Kinematic instabilities in two-layer eccentric annular flows, part 1: Newtonian fluids. J. Eng. Math. 2007, 62, 103–131. [Google Scholar] [CrossRef]
- Moyers-Gonzalez, M.A.; Frigaard, I.A. Kinematic instabilities in two-layer eccentric annular flows, part 2: Shear-thinning and yield-stress effects. J. Eng. Math. 2009, 65, 25–52. [Google Scholar] [CrossRef]
- Liu, C.; Huang, B.; Xue, T. Theories and Applications of Oil and Gas Well Cementing; China Petroleum Industry Press: Beijing, China, 2001; pp. 295–297. [Google Scholar]
- Beirute, R.M.; Flumerfelt, R.W. Mechanics of the displacement process of drilling muds by cement slurries using an accurate rheological model. In Proceedings of the SPE Annual Fall Technical Conference and Exhibition, San Antonio, TX, USA, 9–12 October 1977. [Google Scholar] [CrossRef]
- Flumerfelt, R.W. Laminar displacement of Non-newtonian fluids in parallel plate and narrow gap annular geometries. SPE J. 1975, 5, 169–180. [Google Scholar] [CrossRef]
- Liao, H.; Li, G.; Zhang, S. Theoretical analysis of cementing displacement mechanics of laminar flow for slim-hole. J. Pet. Drill. Tech. 2003, 31, 30–32. [Google Scholar]
- Zheng, Y. The Non-Newtonian Fluid Flow Mechanics and Application in the Petroleum Industry; Petroleum Industry Press: Beijing, China, 1990. [Google Scholar]
- Zheng, Y. Displacement mechanical of laminar flow cementing in deviated wells. Acta Pet. Sin. 1995, 16, 133–138. [Google Scholar] [CrossRef]
- Tehrani, A.; Ferguson, J.; Bittleston, S.H. Laminar displacement in annuli: A combined experimental and theroretical study. In Proceedings of the SPE Annual Technical Conference and Exhibition, Washington, DC, USA, 4–7 October 1992. [Google Scholar] [CrossRef]
- Bittleston, S.H.; Ferguson, J.; Frigaard, I.A. Mud removal and cement placement during primary cementing of an oil well: Laminar non-Newtonian displacements in an eccentric annular Hele-Shaw cell. J. Eng. Math. 2002, 43, 229–253. [Google Scholar] [CrossRef]
- Bittleston, S.H.; Frigaard, I.A. Mud removal and cement placement during primary cementing of an oil well—Part 2; Steady-state displacements. J. Eng. Math. 2004, 48, 1–26. [Google Scholar] [CrossRef]
- Zhou, H. Parameter unfolded asymptotic technique. J. Acta Math. Sci. 1983, 3, 71–80. [Google Scholar]
- Zheng, Y.; Fang, D.; Hao, J. A theoretical and experimental study of cementing for horizontal well. J. Hydrodyn. 1996, 11, 19–23. [Google Scholar]
- Malekmohammadi, S.; Carrasco-Teja, M.; Storey, S. An experimental study of laminar displacement flows in narrow vertical eccentric annuli. J. Fluid Mech. 2010, 649, 371–398. [Google Scholar] [CrossRef]



| Borehole Parameters | Length of Videoed Well Section/m | Well Deviation Angle/° | Eccentricity | ||
| 0.84 | 83°/80°/85° | 0/0.4 | |||
| Displacement parameters | Displacement capacity/L/min | ||||
| 10 | |||||
| Drilling fluid parameters | Drilling fluid density/kg/m3 | Liquidity index | Consistency coefficient/Pa·sn | Yield stress/Pa | |
| 1030 | 0.8562 | 0.0250 | 0.1180 | ||
| Cement slurry parameters | Formulation number | Cement slurry density/kg/m3 | Liquidity index | Consistency coefficient/Pa·sn | Yield stress/Pa |
| #1 | 1150 | 0.9563 | 0.0459 | 1 | |
| #2 | 1150 | 0.8969 | 0.0541 | 0.7132 | |
| #3 | 1150 | 0.9038 | 0.1073 | 1.4277 | |
| Experimental Conditions (Model Solving Conditions) | Experimental Result (%) | Theoretical Results (%) | Relative Error (%) |
|---|---|---|---|
| Well deviation angle = 85°, Casing centered, Cement slurry: Formula 1 | 42 | 40.88 | 2.667 |
| Well deviation angle = 83°, Casing centered, Cement slurry: Formula 1 | 37.7 | 34.94 | 7.409 |
| Well deviation angle = 80°, Casing centered, Cement slurry: Formula 1 | 31.3 | 28.6 | 8.626 |
| Well deviation angle = 83°, Casing eccentricity = 0.4, Cement slurry: Formula 1 | 28.3 | 29.61 | 4.622 |
| Well deviation angle = 83°, Casing centered, Cement slurry: Formula 2 | 45 | 39.86 | 11.422 |
| Well deviation angle = 83°, Casing centered, Cement slurry: Formula 3 | 31.9 | 25.12 | 20.254 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Z.; Chen, Z.; Zhao, Y.; Xue, Y.; Wang, C.; Xiong, C.; Chen, S. Theoretical and Experimental Study on Cementing Displacement Interface for Highly Deviated Wells. Energies 2023, 16, 733. https://doi.org/10.3390/en16020733
Wu Z, Chen Z, Zhao Y, Xue Y, Wang C, Xiong C, Chen S. Theoretical and Experimental Study on Cementing Displacement Interface for Highly Deviated Wells. Energies. 2023; 16(2):733. https://doi.org/10.3390/en16020733
Chicago/Turabian StyleWu, Zhiqiang, Zehua Chen, Yipeng Zhao, Yucheng Xue, Chengwen Wang, Chao Xiong, and Shunli Chen. 2023. "Theoretical and Experimental Study on Cementing Displacement Interface for Highly Deviated Wells" Energies 16, no. 2: 733. https://doi.org/10.3390/en16020733
APA StyleWu, Z., Chen, Z., Zhao, Y., Xue, Y., Wang, C., Xiong, C., & Chen, S. (2023). Theoretical and Experimental Study on Cementing Displacement Interface for Highly Deviated Wells. Energies, 16(2), 733. https://doi.org/10.3390/en16020733






