Anomaly Detection for Wind Turbines Using Long Short-Term Memory-Based Variational Autoencoder Wasserstein Generation Adversarial Network under Semi-Supervised Training
Abstract
:1. Introduction
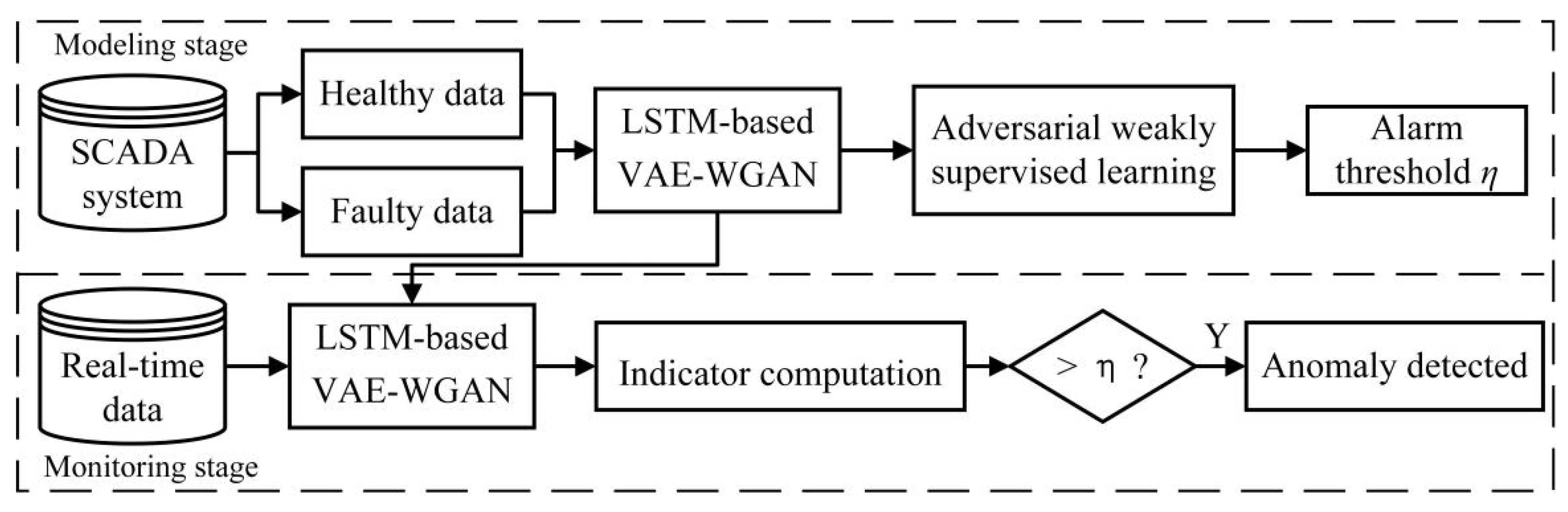
2. Model Description
2.1. SCADA Data
2.2. LSTM-Based VAE-WGAN
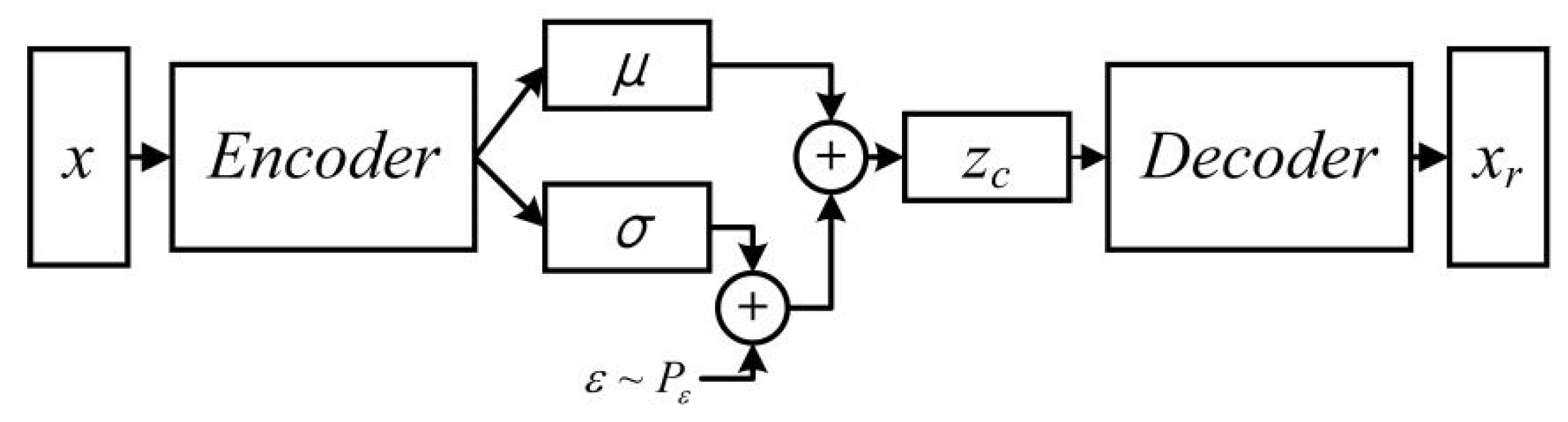
2.2.1. Variational Autoencoder (VAE)
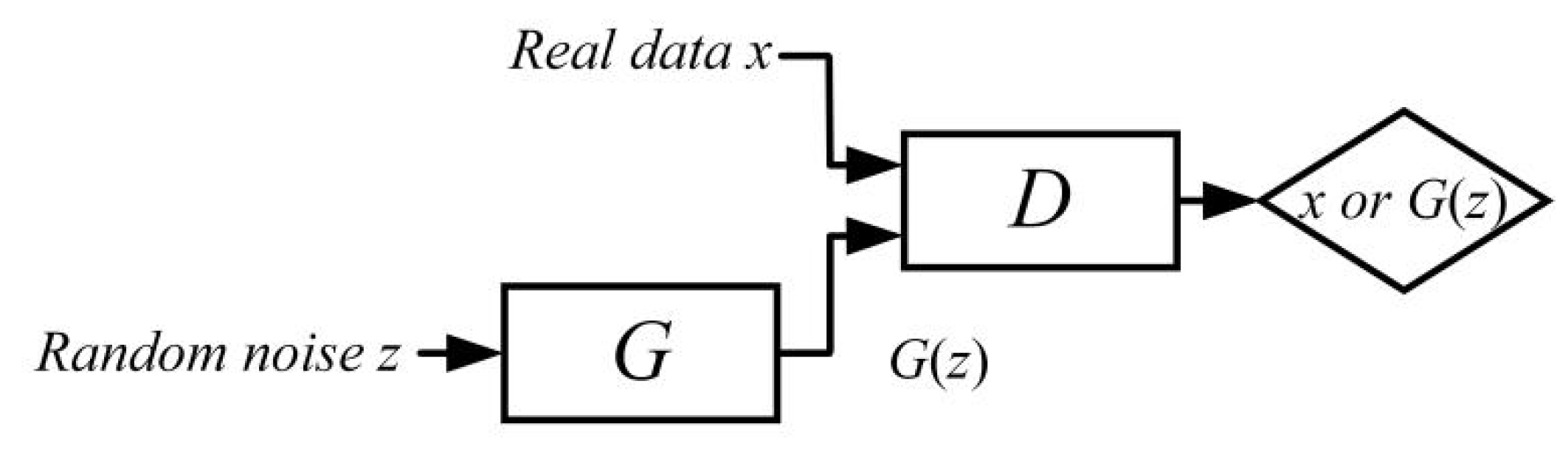
2.2.2. Wasserstein Generative Adversarial Network (WGAN)
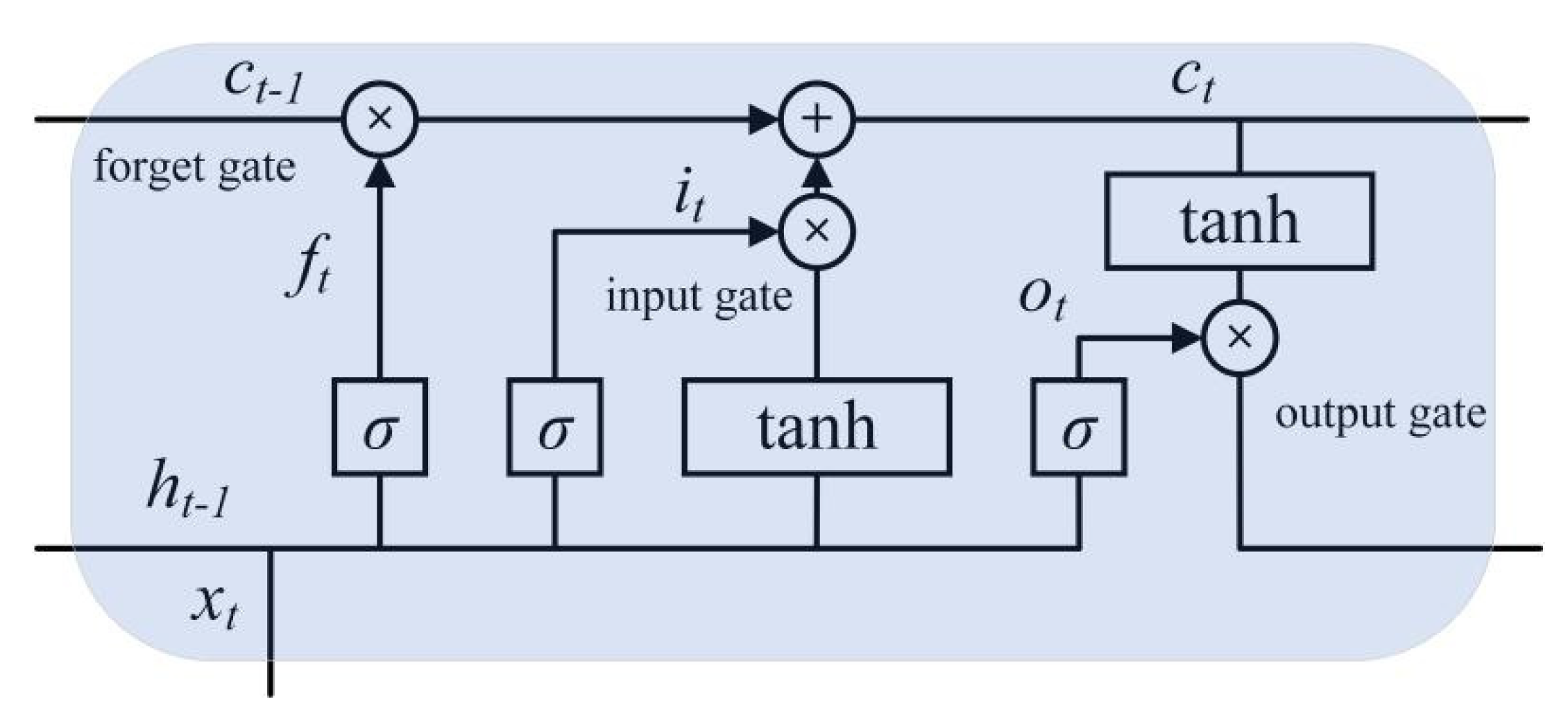
2.2.3. Long Short-Term Memory (LSTM)
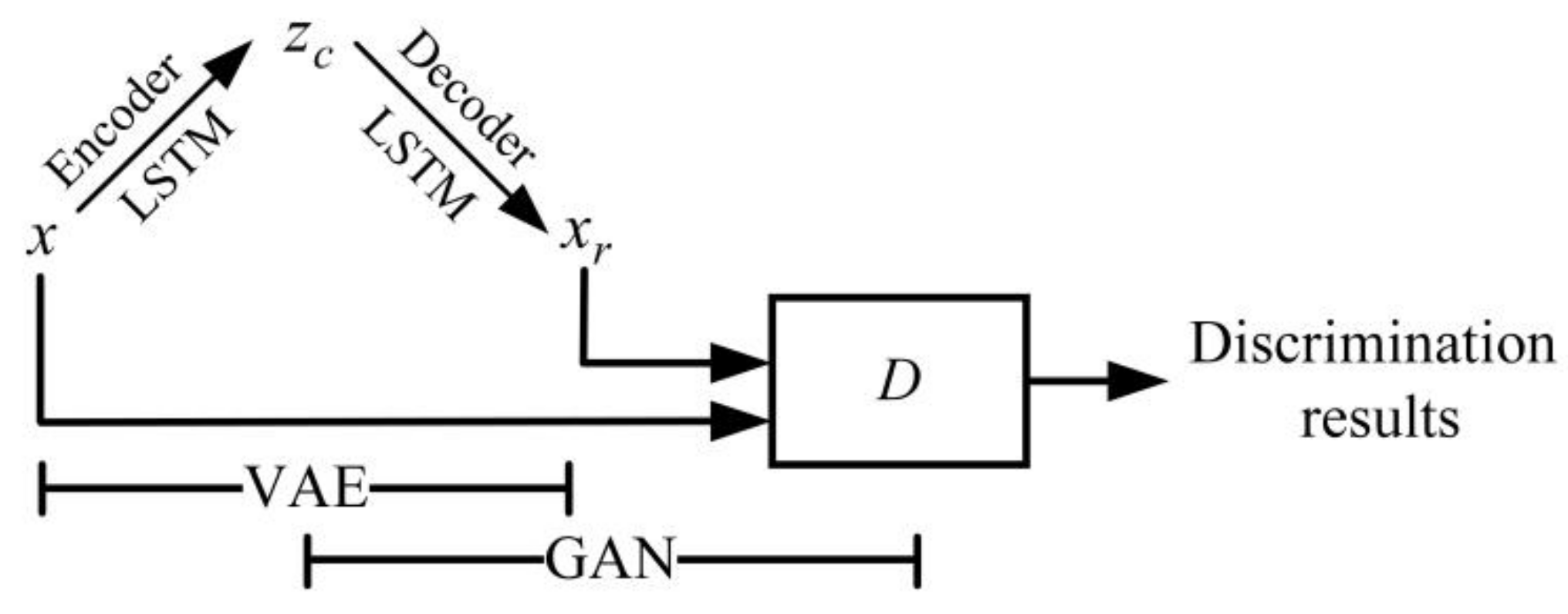
2.2.4. LSTM-Based VAE-WGAN
2.2.5. Adversarial Semi-Supervised Training
| Algorithm 1: LSTM-based VAE-WGAN with normal samples. |
| Initialization: Network parameters for encoder and decoder . Input: Maximum training epoch , batch size , clipping parameter , number of iterations of the discriminator per generator iteration , RMSProp learning rate , gradient penalty weight , VAE hyperparameter , and network parameters for the discriminator . while the training epoch is not satisfied do for do for do Sample real data , a random number . , , Update parameters of discriminator according to gradient: end for Update parameters of encoder and decoder according to gradient: end for end while |
2.3. Anomaly Detection
3. Results
3.1. Generator Input Bearing Wear for Wind Turbine YD37
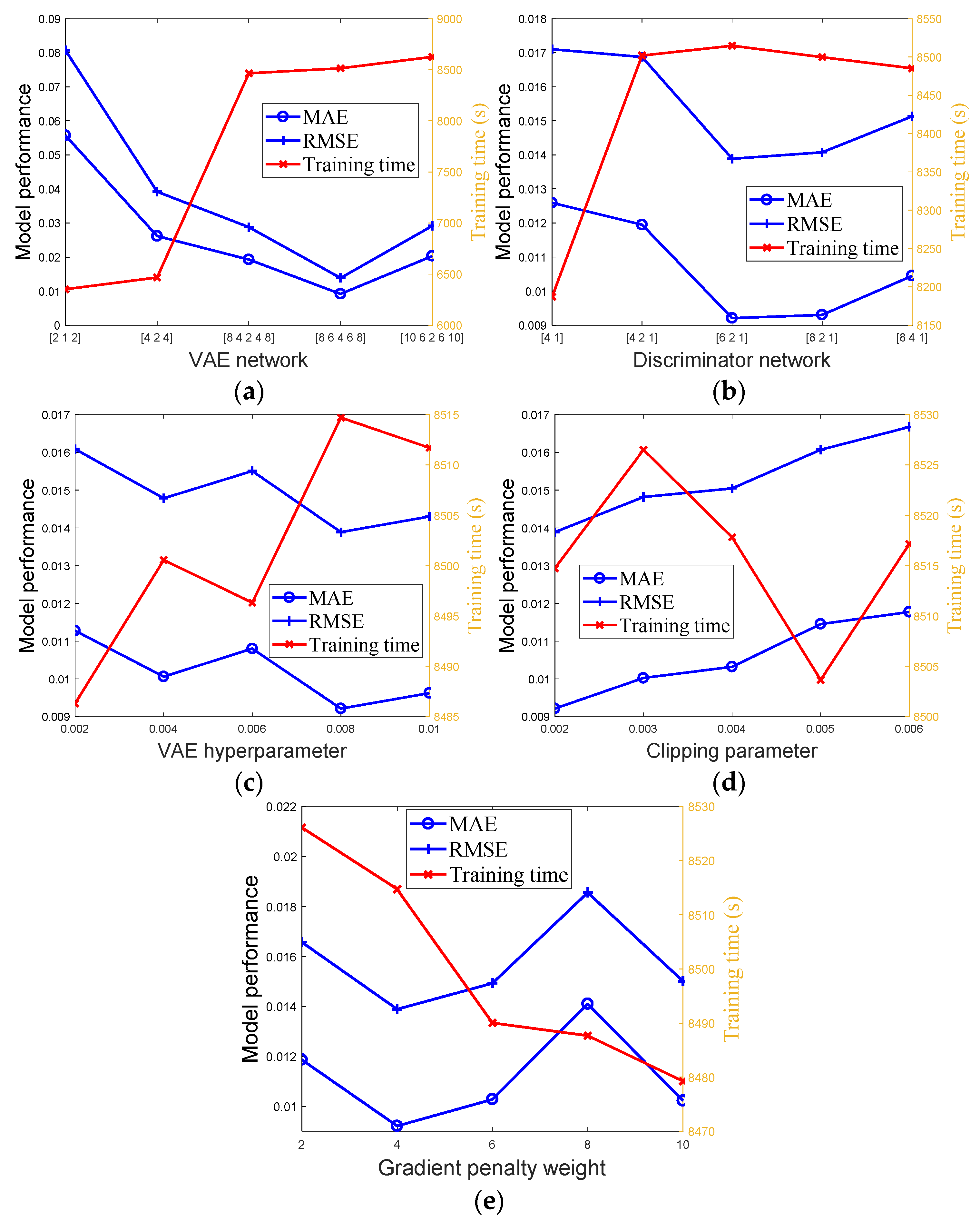
3.1.1. Model Performance
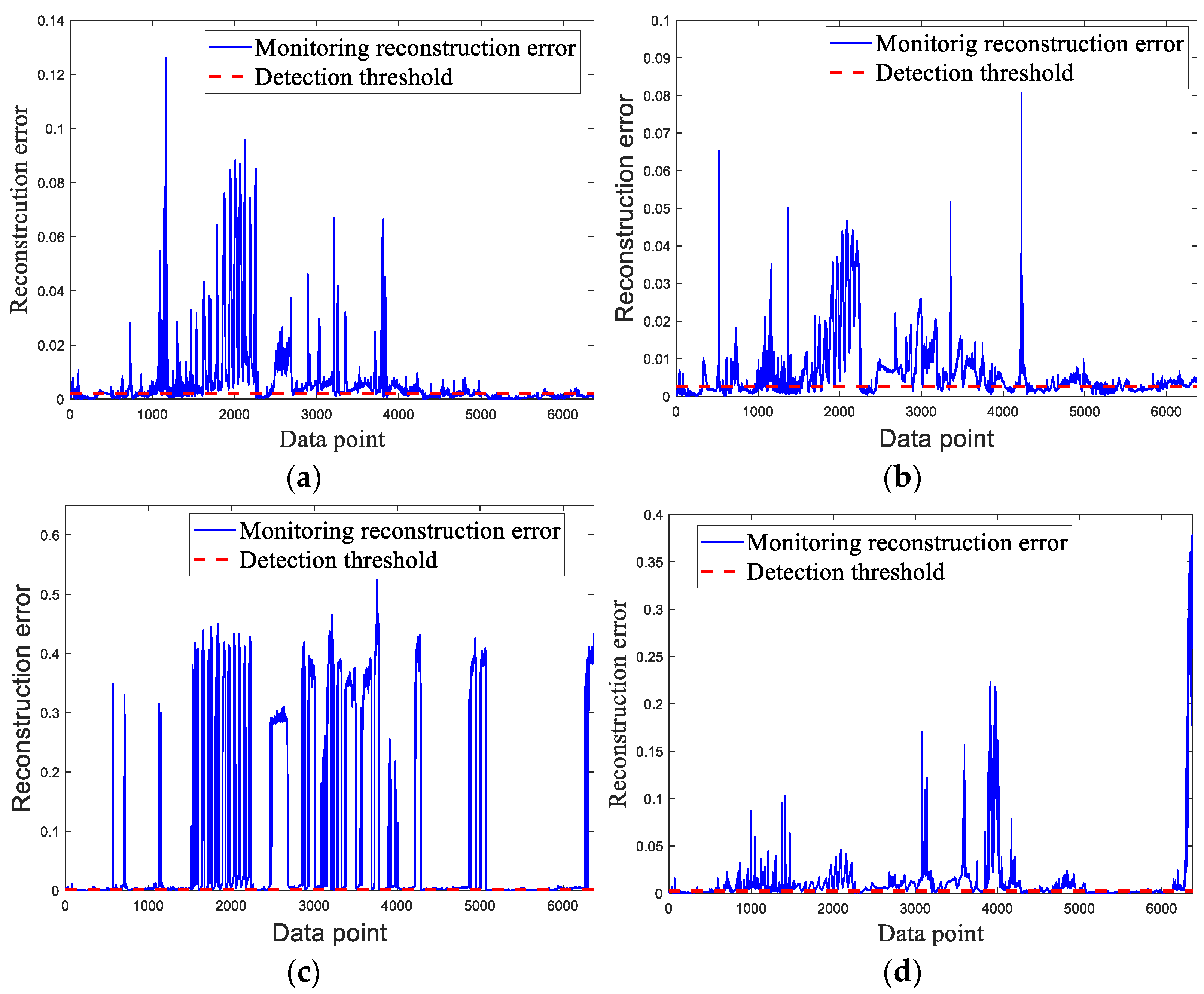
3.1.2. Anomaly Detection
3.1.3. Comparative Experiments
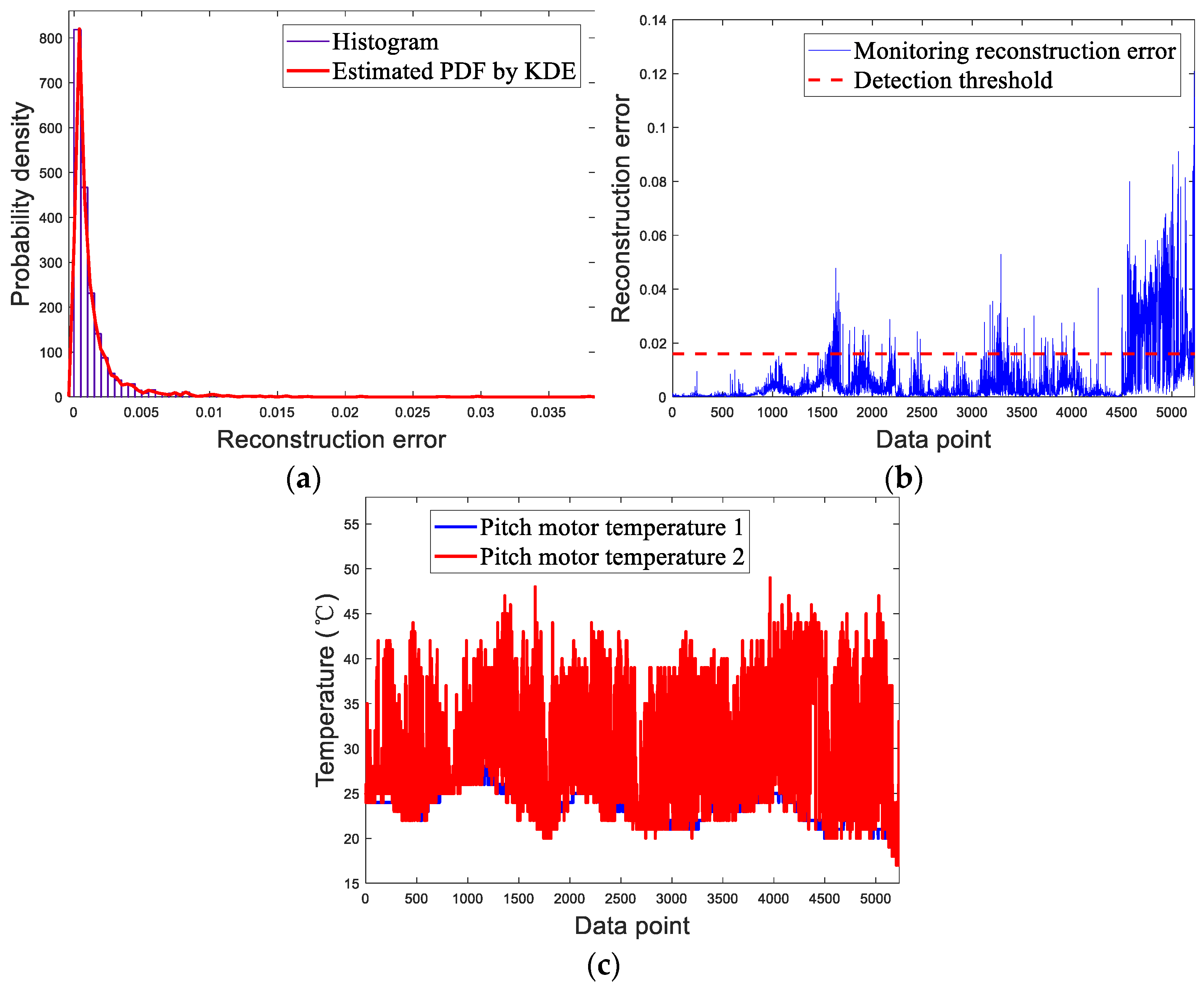
3.2. Sensor Failure of Pitch Motor Temperature 2 for Wind Turbine YD28
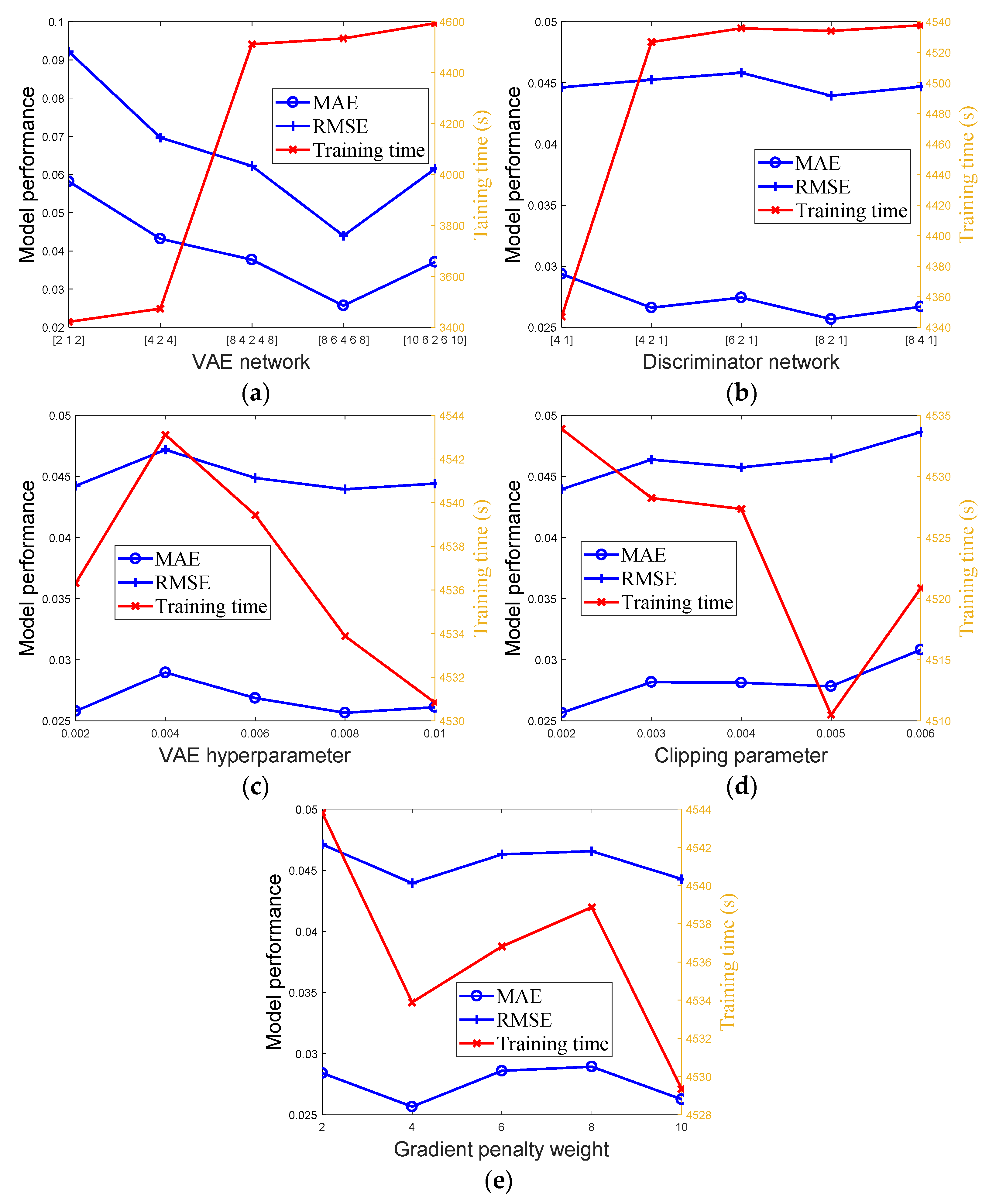
3.2.1. Model Performance
3.2.2. Anomaly Detection
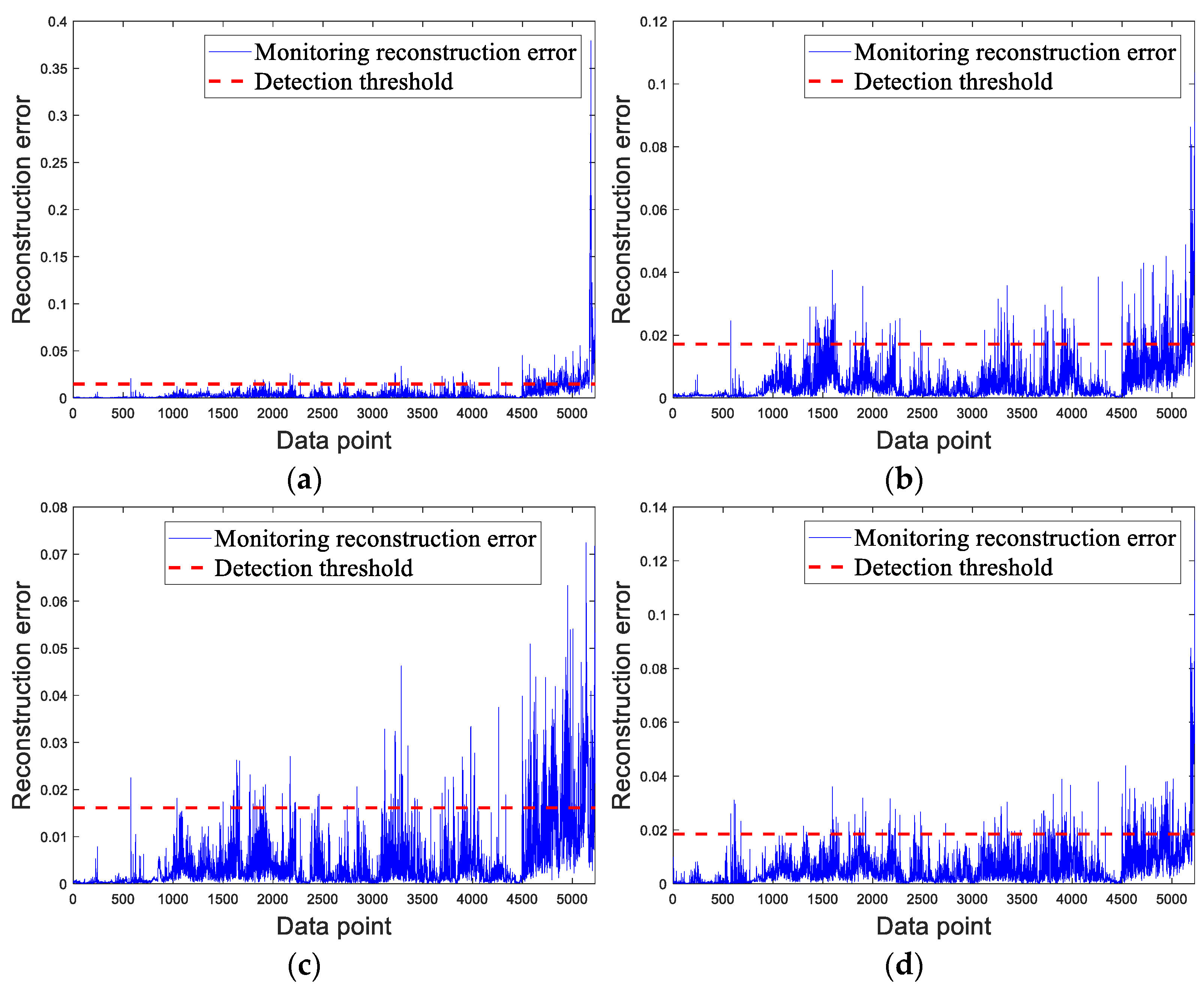
3.2.3. Comparative Experiments
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Abbreviations | |||
| LSTM | Long short-term memory | SCADA | Supervisory control and data acquisition |
| VAE | Variational autoencoder | CMS | Condition monitoring system |
| WGAN | Wasserstein generation adversarial network | AE | Autoencoder |
| KDE | Kernel density estimation | GAN | Generative adversarial network |
| GWEC | Global Wind Energy Council | RNN | Recurrent neural network |
| O&M | Operation and maintenance | Probability density function | |
| Parameters | |||
| The predefined alarm threshold | The bias of forget gate | ||
| The input data/real data | The bias of input gate | ||
| The reconstructed data | The bias of output gate | ||
| The latent variable | The bias of cell | ||
| The mean of a normal distribution | The sigmoid activation function | ||
| The standard deviation of a normal distribution | The element-wise multiplication | ||
| The parameter of the encoder | The learning rate for optimizer RMSProp | ||
| The parameter of the decoder | The input abnormal data | ||
| The random noise | The hyperparameter that weights reconstruction versus discrimination. | ||
| The distribution of real samples | The maximum training epoch | ||
| The data generated by the generator | The batch size | ||
| The set of all possible joint distributions of and | The number of iterations of the discriminator per generator iteration | ||
| The set of 1-Lipschitz functions | The network parameters for discriminator | ||
| The clipping parameter | The network parameters for encoder | ||
| The random number | The network parameters for decoder | ||
| The mixed sample | The kernel function | ||
| The gradient penalty weight | The window width | ||
| The weight of forget gate | The given confidence interval | ||
| The weight of input gate | TP | The number of cases that are correctly labeled as positive | |
| The weight of output gate | FP | The number of cases that are incorrectly labeled as positive | |
| The weight of cell | FN | The number of cases that are positive but are labeled as negative | |
References
- Mcmorland, J.; Collu, M.; Mcmillan, D.; Carroll, J. Operation and maintenance for floating wind turbines: A review. Renew. Sustain. Energy Rev. 2022, 163, 112499. [Google Scholar] [CrossRef]
- Global Wind Report 2023. Available online: https://gwec.net/globalwindreport2023/ (accessed on 1 May 2023).
- Bakir, I.; Yildirim, M.; Ursavas, E. An integrated optimization framework for multi-component predictive analytics in wind farm operations & maintenance. Renew. Sustain. Energy Rev. 2021, 138, 110639. [Google Scholar]
- Zhu, Y.; Zhu, C.; Tan, J.; Song, C.; Chen, D.; Zheng, J. Fault detection of offshore wind turbine gearboxes based on deep adaptive networks via considering Spatio-temporal fusion. Renew. Energy 2022, 200, 1023–1036. [Google Scholar] [CrossRef]
- Dhiman, H.S.; Deb, D.; Muyeen, S.M.; Kamwa, I. Wind Turbine Gearbox Anomaly Detection based on Adaptive Threshold and Twin Support Vector Machines. IEEE Trans. Energy Convers. 2021, 36, 3462–3469. [Google Scholar] [CrossRef]
- Benammar, S.; Tee, K.F. Failure Diagnosis of Rotating Machines for Steam Turbine in Cap-Djinet Thermal Power Plant. Eng. Fail. Anal. 2023, 149, 107284. [Google Scholar] [CrossRef]
- Nick, H.; Aziminejad, A.; Hosseini, M.H.; Laknejadi, L. Damage identification in steel girder bridges using modal strain energy-based damage index method and artificial neural network. Eng. Fail. Anal. 2021, 119, 105010. [Google Scholar] [CrossRef]
- Li, H.; Huang, J.; Ji, S. Bearing Fault Diagnosis with a Feature Fusion Method Based on an Ensemble Convolutional Neural Network and Deep Neural Network. Sensors 2019, 19, 2034. [Google Scholar] [CrossRef] [PubMed]
- Zhou, D.; Yao, Q.; Wu, H.; Ma, S.; Zhang, H. Fault diagnosis of gas turbine based on partly interpretable convolutional neural networks. Energy 2020, 200, 117467. [Google Scholar] [CrossRef]
- Kong, Z.; Tang, B.; Deng, L.; Liu, W.; Han, Y. Condition monitoring of wind turbines based on spatio-temporal fusion of SCADA data by convolutional neural networks and gated recurrent units. Renew. Energy 2020, 146, 760–768. [Google Scholar] [CrossRef]
- Yang, Z.; Baraldi, P.; Zio, E. A method for fault detection in multi-component systems based on sparse autoencoder-based deep neural networks. Reliab. Eng. Syst. Saf. 2022, 220, 108278. [Google Scholar] [CrossRef]
- Xiang, L.; Yang, X.; Hu, A.; Su, H.; Wang, P. Condition monitoring and anomaly detection of wind turbine based on cascaded and bidirectional deep learning networks. Appl. Energy 2022, 305, 117925. [Google Scholar] [CrossRef]
- Chen, H.; Liu, H.; Chu, X.; Liu, Q.; Xue, D. Anomaly detection and critical SCADA parameters identification for wind turbines based on LSTM-AE neural network. Renew. Energy 2021, 172, 829–840. [Google Scholar] [CrossRef]
- Zhang, C.; Hu, D.; Yang, T. Anomaly detection and diagnosis for wind turbines using long short-term memory-based stacked denoising autoencoders and XGBoost. Reliab. Eng. Syst. Saf. 2022, 222, 108445. [Google Scholar] [CrossRef]
- Khan, P.W.; Yeun, C.Y.; Byun, Y.C. Fault detection of wind turbines using SCADA data and genetic algorithm-based ensemble learning. Eng. Fail. Anal. 2023, 148, 107209. [Google Scholar] [CrossRef]
- Liu, X.; Teng, W.; Wu, S.; Wu, X.; Liu, Y.; Ma, Z. Sparse Dictionary Learning based Adversarial Variational Auto-encoders for Fault Identification of Wind Turbines. Measurement 2021, 183, 109810. [Google Scholar] [CrossRef]
- Dao, P.B. Condition monitoring and fault diagnosis of wind turbines based on structural break detection in SCADA data. Renew. Energy 2021, 185, 641–654. [Google Scholar] [CrossRef]
- Morrison, R.; Liu, X.; Lin, Z. Anomaly detection in wind turbine SCADA data for power curve cleaning. Renew. Energy 2022, 184, 473–486. [Google Scholar] [CrossRef]
- Morshedizadeh, M.; Rodgers, M.; Doucette, A.; Schlanbusch, P. A case study of wind turbine rotor over-speed fault diagnosis using combination of SCADA data, vibration analyses and field inspection. Eng. Fail. Anal. 2023, 146, 107056. [Google Scholar] [CrossRef]
- Shen, X.; Fu, X.; Zhou, C. A combined algorithm for cleaning abnormal data of wind turbine power curve based on change point grouping algorithm and quartile algorithm. IEEE Trans. Sustain. Energy 2019, 10, 46–54. [Google Scholar] [CrossRef]
- Chen, J.; Li, J.; Chen, W.; Wang, Y.; Jiang, T. Anomaly detection for wind turbines based on the reconstruction of condition parameters using stacked denoising autoencoders. Renew. Energy 2020, 147, 1469–1480. [Google Scholar] [CrossRef]
- Thill, M.; Konen, W.; Wang, H.; Bäck, T. Temporal convolutional autoencoder for unsupervised anomaly detection in time series. Appl. Soft Comput. 2021, 112, 107751. [Google Scholar] [CrossRef]
- Yong, B.X.; Brintrup, A. Bayesian autoencoders with uncertainty quantification: Towards trustworthy anomaly detection. Expert Syst. Appl. 2022, 209, 118196. [Google Scholar] [CrossRef]
- Jin, U.K.; Na, K.; Oh, J.S.; Kim, J.; Youn, B.D. A new auto-encoder-based dynamic threshold to reduce false alarm rate for anomaly detection of steam turbines. Expert Syst. Appl. 2022, 189, 116094. [Google Scholar]
- Sun, C.; He, Z.; Lin, H.; Cai, L.; Cai, H.; Gao, M. Anomaly detection of power battery pack using gated recurrent units based variational autoencoder. Appl. Soft Comput. 2023, 132, 109903. [Google Scholar] [CrossRef]
- Gulrajani, I.; Ahmed, F.; Arjovsky, M.; Dumoulin, V.; Courville, A.C. Improved Training of Wasserstein GANs. In Proceedings of the 31st International Conference on Neural Information Processing Systems (NIPS’17), Long Beach, CA, USA, 4–9 December 2017; Curran Associates Inc.: Red Hook, NY, USA, 2017; pp. 5769–5779. [Google Scholar]
- Hu, D.; Zhang, C.; Yang, T.; Chen, G. Anomaly Detection of Power Plant Equipment Using Long Short-Term Memory Based Autoencoder Neural Network. Sensors 2020, 20, 6164. [Google Scholar] [CrossRef]
- Lin, S.; Clark, R.; Birke, R.; Schonborn, S.; Trigoni, N.; Roberts, S. Anomaly Detection for Time Series Using VAE-LSTM Hybrid Model. In Proceedings of the ICASSP 2020—2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020. [Google Scholar]
- Hu, D.; Zhang, C.; Yang, T.; Chen, G. An Intelligent Anomaly Detection Method for Rotating Machinery Based on Vibration Vectors. IEEE Sens. J. 2022, 22, 14294–14305. [Google Scholar] [CrossRef]

| Training Network | Value |
|---|---|
| VAE network | [8 6 4 6 8] |
| Discriminator network | [6 2 1] |
| Batch size | 64 |
| Epoch size | 2000 |
| Delay time for LSTM [14] | 10 |
| Learning rate | 0.001 |
| Clipping parameter | 0.002 |
| Discriminator iterations | 5 |
| VAE hyperparameter | 0.008 |
| Gradient penalty weight | 4 |
| Training Network | MAE | RMSE | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Random Seed | 1 | 2 | 3 | 4 | 5 | 1 | 2 | 3 | 4 | 5 |
| VAE | 0.02062 | 0.01999 | 0.02106 | 0.01989 | 0.01815 | 0.02760 | 0.02683 | 0.02794 | 0.02670 | 0.02448 |
| VAE-GAN | 0.02333 | 0.01997 | 0.02090 | 0.02300 | 0.02288 | 0.03058 | 0.02718 | 0.02772 | 0.03063 | 0.02963 |
| VAE-WGAN | 0.01725 | 0.01844 | 0.01976 | 0.02197 | 0.02017 | 0.02335 | 0.02442 | 0.02618 | 0.02939 | 0.02632 |
| LSTM-based VAE | 0.01475 | 0.01428 | 0.01490 | 0.01832 | 0.01220 | 0.02011 | 0.02022 | 0.01989 | 0.02513 | 0.01691 |
| LSTM-based VAE-GAN | 0.01006 | 0.01218 | 0.01172 | 0.01556 | 0.01384 | 0.01482 | 0.01671 | 0.01653 | 0.02092 | 0.01891 |
| LSTM-based VAE-WGAN | 0.00921 | 0.01287 | 0.01059 | 0.01062 | 0.01053 | 0.01389 | 0.01790 | 0.01543 | 0.01539 | 0.01525 |
| Model | Alarm Point | Precision | Recall | F1 Score |
|---|---|---|---|---|
| LSTM-based AE | 343rd point | 0.9886 | 0.5476 | 0.7048 |
| LSTM-based VAE | 322nd point | 0.9967 | 0.5944 | 0.7447 |
| LSTM-based VAE-GAN | 320th point | 0.9942 | 0.7118 | 0.8296 |
| LSTM-based VAE-WGAN(without supervised pre-training) | 325th point | 0.9944 | 0.7018 | 0.8229 |
| LSTM-based VAE-WGAN (with supervised pre-training) | 314th point | 0.9952 | 0.7238 | 0.8381 |
| Training Network | Value |
|---|---|
| VAE network | [8 6 4 6 8] |
| Discriminator network | [8 2 1] |
| Batch size | 64 |
| Epoch size | 2000 |
| Delay time for LSTM [14] | 10 |
| Learning rate | 0.001 |
| Clipping parameter | 0.002 |
| Discriminator iterations | 5 |
| VAE hyperparameter | 0.008 |
| Gradient penalty weight | 4 |
| Training Network | MAE | RMSE | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Random Seed | 1 | 2 | 3 | 4 | 5 | 1 | 2 | 3 | 4 | 5 |
| VAE | 0.03907 | 0.03640 | 0.03749 | 0.03913 | 0.03539 | 0.06099 | 0.05785 | 0.05682 | 0.05965 | 0.05827 |
| VAE-GAN | 0.03358 | 0.03443 | 0.03438 | 0.03517 | 0.03389 | 0.05635 | 0.05533 | 0.05489 | 0.05627 | 0.05652 |
| VAE-WGAN | 0.03243 | 0.03434 | 0.03490 | 0.03725 | 0.03238 | 0.05586 | 0.05593 | 0.05635 | 0.05765 | 0.05600 |
| LSTM-based VAE | 0.02861 | 0.02913 | 0.03011 | 0.02992 | 0.02663 | 0.04648 | 0.04664 | 0.04761 | 0.04704 | 0.04453 |
| LSTM-based VAE-GAN | 0.02592 | 0.02600 | 0.02934 | 0.02755 | 0.02719 | 0.04209 | 0.04294 | 0.04619 | 0.04419 | 0.04500 |
| LSTM-based VAE-WGAN | 0.02566 | 0.02737 | 0.02846 | 0.02648 | 0.02565 | 0.04395 | 0.04480 | 0.04621 | 0.04330 | 0.04405 |
| Model | Alarm Point | Precision | Recall | F1 Score |
|---|---|---|---|---|
| LSTM-based AE | 4867th point | 0.6582 | 0.5746 | 0.6136 |
| LSTM-based VAE | 5140th point | 0.2386 | 0.7640 | 0.3636 |
| LSTM-based VAE-GAN | 4812th point | 0.5670 | 0.4365 | 0.4933 |
| LSTM-based VAE-WGAN (without supervised pre-training) | 4933th point | 0.3450 | 0.3007 | 0.3213 |
| LSTM-based VAE-WGAN (with supervised pre-training) | 4639th point | 0.6938 | 0.6220 | 0.6559 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Yang, T. Anomaly Detection for Wind Turbines Using Long Short-Term Memory-Based Variational Autoencoder Wasserstein Generation Adversarial Network under Semi-Supervised Training. Energies 2023, 16, 7008. https://doi.org/10.3390/en16197008
Zhang C, Yang T. Anomaly Detection for Wind Turbines Using Long Short-Term Memory-Based Variational Autoencoder Wasserstein Generation Adversarial Network under Semi-Supervised Training. Energies. 2023; 16(19):7008. https://doi.org/10.3390/en16197008
Chicago/Turabian StyleZhang, Chen, and Tao Yang. 2023. "Anomaly Detection for Wind Turbines Using Long Short-Term Memory-Based Variational Autoencoder Wasserstein Generation Adversarial Network under Semi-Supervised Training" Energies 16, no. 19: 7008. https://doi.org/10.3390/en16197008
APA StyleZhang, C., & Yang, T. (2023). Anomaly Detection for Wind Turbines Using Long Short-Term Memory-Based Variational Autoencoder Wasserstein Generation Adversarial Network under Semi-Supervised Training. Energies, 16(19), 7008. https://doi.org/10.3390/en16197008






