Abstract
A ground-source heat pump (GSHP) system is a renewable energy technology that effectively reduces greenhouse gas emissions and consequently mitigates the progression of global warming. The thermal efficiency of ground heat exchangers (GHEs) is a critical component in the GSHP system that must be accurately estimated for its long-term operationality. Therefore, in this study, the thermal performance of double-spiral GHEs incorporated within the thermal piles of a zero-energy building in Sapporo, Japan, was investigated using the actual measured data obtained from the site and a novel metric, namely, the coefficient of heat extraction/injection, for a more precise evaluation. Moreover, this study assessed the coefficient of performance (COP) of the GSHP units during various periods of cooling or heating. The temperature of the circulating fluid remained within an ideal operational range over an operational period of 2 years, and the COP calculations indicated a high operational efficiency. The results derived in this study substantially exceeded those of traditional U-tube GHEs, indicating the enhanced efficiency and superior performance of large-diameter thermal piles with augmented thermal capacity. Our findings suggest that GSHP systems with double-spiral-tube GHEs have superior efficiency than conventional GHEs.
1. Introduction
Currently, the most substantial environmental issue for humankind is global warming, which is primarily driven by the greenhouse effect owing to carbon dioxide (CO2) emissions. These considerable CO2 emissions are primarily caused by the extensive use of fossil fuels to fulfill the energy demand required for various anthropogenic activities. Energy demand from buildings, including residential and commercial structures, currently accounts for approximately 40% and 30% of global energy consumption and CO2 emissions, respectively [1], and this proportion is projected to increase.
Approximately 80% of the energy demand in residential and commercial buildings is owing to air conditioning and hot water generation, with space cooling demonstrating rapid growth in recent years [2]. Compared with 2021, the energy consumption in buildings and the use of fossil fuels under the net-zero scenario are projected to decline by 25% and over 40% by 2030, respectively [3]. The residential sector, which comprises three-quarters of the total energy consumption in the building sector [4], can substantially enhance energy efficiency. Thus, it is essential to adopt renewable energy technologies to promote energy conservation within these buildings.
To fulfill the demand for space heating and cooling loads in buildings, various efforts are being made to develop alternative energy sources, in which the shallow ground is an excellent low-temperature heat source. Recently, ground-source heat pump (GSHP) systems have gained popularity in the residential and commercial building sectors globally owing to their considerably higher energy efficiency (than that of widely used air-source heat pumps), environmental sustainability, continuous operationality (unlike intermittent functioning systems), and seamless integrability with complementary energy systems, such as photovoltaic (PV) systems. As illustrated in Figure 1, because the shallow ground temperature (i.e., in the undisturbed layer) remains nearly constant throughout the year [5], the ground can facilitate the heating and cooling of buildings via heat pump units using ground heat exchangers (GHEs) and a circulating fluid (e.g., ethylene glycol); in addition, compared to conventional air conditioning methods, this approach would facilitate a significant reduction in CO2 emissions. In 2020, the thermal capacity of GSHP systems and the energy usage reached 77,547 MWt and 599,981 TJ/year, respectively, indicating a 54% increase in the number of installed units compared with 2015, and more than double the number of units reported in 2010 [6].

Figure 1.
A typical ground-source heat pump (GSHP) system providing space cooling and heating in a building.
Although GSHP systems have several advantages, their large-scale implementation faces a substantial obstacle, as an extensive land area is required for boreholes during multiple GHE installations. Therefore, the innovative use of thermal piles in energy-efficient buildings has emerged in recent years (Figure 2), eliminating the need for additional installation space by integrating building piles with GHEs. These dual-purpose elements not only provide structural support to buildings but also act as efficient heat exchangers [7], effectively addressing the land requirement issues associated with traditional borehole heat exchangers (BHEs).
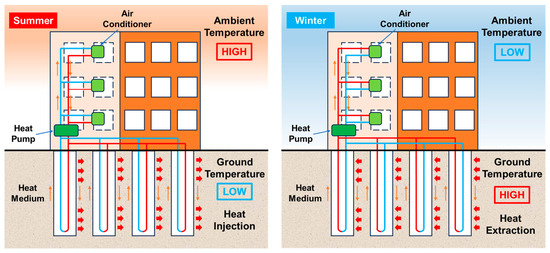
Figure 2.
Operation of a building equipped with thermal piles during summer and winter.
In the context of GHEs, traditionally, U-tube GHEs have been predominantly used. Their widespread use can be attributed to the ease with which they can be manufactured. However, the installation of U-tube GHEs requires deep-borehole drilling, which is very costly. To address this issue, the Japan Pile Corporation, a Japanese construction company, not only designed a novel GHE (i.e., consisting of double spiral pipes), but it also developed a technique (i.e., the Geothermal Tornado Method) for its installation [8]. Figure 3 illustrates the three types of GHEs: single and double U-shaped and double spiral pipes. At an equivalent borehole depth, the double-spiral pipe has a higher extended length than that of the conventional U-tube configuration, implying a larger heat transfer surface area between the ground and fluid circulating inside this GHE. Additionally, compared with traditional borehole GHEs, the larger diameter of the double spiral GHE thermal piles yields a higher thermal capacity, thereby allowing for increased heat exchange with the ground. Overall, this results in a significant boost in efficiency.
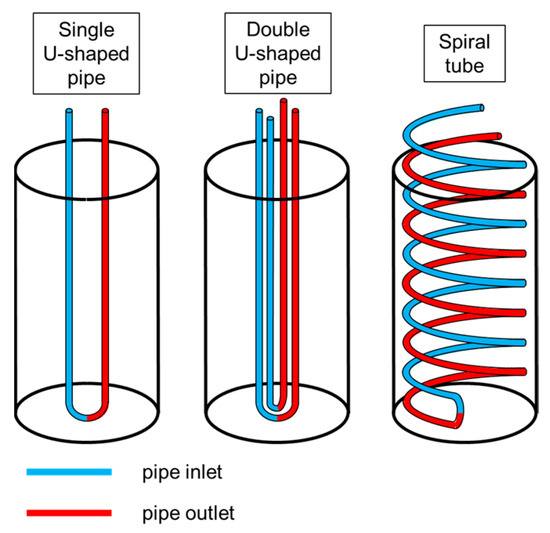
Figure 3.
Ground heat exchanger (GHE) configurations: single U-tube, double U-tube, and double spiral.
The thermal efficiency of the GHEs is a critical component in the GSHP system and, therefore, must be accurately estimated for the long-term operationality of the system. The overall performance of the system is determined by GHEs’ ability to exchange heat between the ground and circulating fluid. Numerous studies, comprising both numerical simulations and experimental tests (laboratory and field studies), have examined the heat transfer behavior in and around GHEs and addressed various concerns related to their performance measurement and analysis. Moreover, several studies evaluated the efficiency of GHEs using various parameters and methodologies, as follows:
- Material of ground and grout: The temperature difference between the circulating fluid and ground substantially affects heat transfer, which is determined by factors such as the medium, undisturbed ground temperature, and thermal conductivity. While a larger temperature difference may contribute to a more efficient heat exchange, it is also essential for sustaining the ground temperature within acceptable limits to prevent any degradation in the long-term performance of the system.
Chen et al. [9] constructed a numerical model to conduct a thorough analysis of a deep BHE (DBHE) system and revealed that the thermal conductivity of the ground soil substantially affects the specific heat extraction rate (W/m). Tang et al. [10] used numerical simulations to identify the key factors influencing the coefficient of performance (COP) of a GSHP system and observed that transitioning from clay to sand and operating in warmer climates (meteorological conditions) can substantially enhance the performance of the system. Cao et al. [11] conducted experimental tests to analyze the performance of flat-panel GHEs and reported that the choice of the backfilling material substantially affects the overall operating efficiency of the system, and the water–sand mixture considerably improves the heat transfer rate (W) compared with dry sand. Zhang et al. [12] investigated a DBHE system and observed that an increase in the thermal conductivity of a geological formation led to high heat extraction and injection rates during winter and summer, respectively. Congedo et al. [13] used FLUENT to examine horizontal GHEs and reported that the thermal conductivity of the ground surrounding the GHEs is the most crucial parameter affecting the heat transfer performance of the system, and the optimal ground type has the highest thermal conductivity. Zhang et al. [14] combined field experiments and numerical simulations to explore the long-term thermal properties of a precast high-strength concrete (PHC) energy pile in a layered foundation and demonstrated that the heat exchange rate (W/m) of a PHC energy pile can be enhanced by increasing the thermal conductivity of the backfill soil.
- Temperature of the pipe inlet and outlet: The temperatures of the fluids entering and exiting the heat exchanger considerably affect the heat exchange capacity of the system.
Jalaluddin et al. [15] investigated the thermal performance (W/m) of spiral GHEs and revealed that variations in inlet temperature can cause substantial changes in the heat exchange rate. Huang et al. [16] and Cai et al. [17] proposed an analytical model to assess the heat exchange efficiency of deep geothermal systems under nonuniform ground conditions based on reliability theory and demonstrated that an increase in the temperature difference between the pipe inlet and undisturbed layer ground can substantially enhance the heat exchange efficiency.
- Configurations and materials of GHEs: The design and materials used in GHEs substantially influence their performance. Optimal designs can maximize the surface contact between the ground and circulating fluid. Meanwhile, the selected materials also possess high thermal conductivity.
Serageldin et al. [18] introduced an oval U-tube GHE and used computational fluid dynamics simulations to demonstrate that this design can reduce thermal resistance and enhance the COP of GHEs. Jahanbin [19] developed a single U-tube GHE design to improve the thermal efficiency of ground-coupled heat pump systems and used three-dimensional finite element simulations to demonstrate that elliptical U-tubes can substantially enhance heat transfer and reduce borehole thermal resistance compared with conventional single U-tubes. Majeed et al. [20] evaluated GHEs comprising various pipe materials, such as polyvinyl chloride (PVC), copper, and galvanized materials, and elucidated that the copper pipes have the highest heat exchange rate (W/m), whereas the PVC pipes have the lowest rate. Li et al. [21] investigated the heat injection and extraction capabilities of single- and double-pipe BHEs under different operating conditions and reported that the heat injection and extraction rates (W/m) of the BHEs are 50% and 45% higher, respectively, than those of a conventional single U-tube GHE. Kerme and Fung [22] compared the performances of single U-tube and double U-tube BHEs and concluded that double U-tube BHEs have better performance and lower resistance than single U-tube BHEs. Luo et al. [23] analyzed the thermal load of a BHE installed in a GSHP with three borehole diameters and revealed that an increase in the borehole diameter could slightly improve the thermal performance of the BHE. Kim et al. [24] developed a stainless-steel BHE and elucidated that it has a 160% and four times higher maximum heat capacity and gain (kW), respectively, when compared with conventional GHEs made of high-density polyethylene, implying a high heat extraction capacity from the ground. Zou et al. [25] developed a three-dimensional heat transfer model for three types of horizontal GHEs (HGHEs) and demonstrated that spiral-coil HGHEs exhibit the best performance with respect to the COP and heat transfer rate (W/m).
- Diameter and depth of borehole: The borehole depth and diameter can substantially enhance the thermal capacity and performance of GHEs, thereby improving heat transfer. However, the escalating costs of drilling must also be considered.
Dehghan [26] experimentally and computationally investigated the thermal performance of spiral GHEs and observed a high dependence of heat transfer rate on the vertical length of the borehole. Furthermore, the distances between the GHEs cause thermal interactions, thereby leading to a minor impact. Li et al. [27] investigated different factors influencing the energy performance of a GSHP system and revealed that the operation mode and depth of the buried tube have a greater effect than other factors, and the intermittent operation of the GSHP system can promote a highly efficient heat exchange within the buried pipes. Furthermore, the deeper the pipe is buried, the higher the energy efficiency coefficient of the GSHP system.
In addition to these factors, other influential variables must be considered. Walch et al. [28] quantified the potential (kWh/m2) of GSHP systems for district heating and cooling and observed that seasonal regeneration, which considerably decreases the thermal interference between boreholes, exerts a substantial impact on the achievable maximum geothermal potential. Guo et al. [29] analyzed the impact of groundwater flow on the thermal performance of BHEs in Tangshan, China, revealing that natural groundwater can barely enhance heat transfer. Tu et al. [30] developed a thermal resistance and capacity model to investigate the heat transfer between vertical single U-tube GHEs and frozen soil in severely cold climate zones and demonstrated that frozen soil can increase the heat transfer capacity (W/m) of the GHE by 30%.
Numerous studies have been conducted on this subject; however, they predominantly emphasize and are restricted to laboratory tests and computer simulations, with only a few ventures into real-life applications. The principal shortcomings of these studies are their short duration and assumption of idealized conditions rather than actual use conditions. Consequently, the resulting operational data are mostly restricted to laboratory and simulation environments. Furthermore, many of the evaluation methods used in these studies do not accurately depict the heat exchange capabilities of GHEs, with most studies relying on units of W or W/m to assess the thermal performance of GHEs, thereby neglecting the impact of the temperature difference between the ground and circulating fluid within the GHEs. Finally, these studies often consider substantial ground depths, which is inconsistent with the actual conditions of large-scale applications that primarily use shallow ground layers.
In addition, only a few studies have focused on the performance of thermal piles and spiral-tube GHEs, which are predominantly installed on shallow ground. Therefore, accurately evaluating the thermal performance of spiral-tube GHEs has become critical for practical applications owing to the recent large-scale use of GSHP systems facilitated by thermal piles.
In this study, we investigated the thermal performance of double-spiral GHEs incorporated within the thermal piles of an energy-efficient building in Sapporo, Japan, using the actual measured data obtained from the site and a novel metric, namely, the coefficient of heat extraction/injection, for a more precise evaluation and demonstrated the superiority of the thermal piles and double-spiral GHEs. Additionally, we highlight the benefits of using this novel GHE for real-world applications. Our findings suggest that GSHP systems with double-spiral-tube GHEs have superior efficiency than conventional GHEs. Moreover, they do not suffer efficiency losses from long-term operation, and the circulating fluid maintains thermal balance, avoiding performance deterioration even in heat-dominant cold regions.
2. Material and Methods
2.1. Overview of the GSHP System
This study conducted measurements in an energy-efficient, i.e., nearly zero energy building (ZEB), located in Sapporo, Japan, as per the Japanese standards. This three-story building is a company office and integrates various energy-saving technologies. The first, second, and third floors accommodate stores and control rooms for the entire system, office rooms, and conference meeting rooms, respectively. The building has been in operation since July 2021 and includes the following energy-saving technologies: PV panels for electricity supply, fan coil units, high thermal insulation building materials, heat recovery ventilation, GSHP systems, and radiant air-conditioning systems, which are listed in Table 1.

Table 1.
Basic information about the building.
Three GSHP units (rated power of 10 kW) provide space heating and cooling in all the rooms on each floor and facilitate snow melting around the building during winter. During operation, the indoor temperatures in all the rooms were maintained at 22 °C and 26 °C in winter and summer, respectively, and the GSHP systems were operated only when needed (e.g., during working hours). When the rooms were unoccupied at night or on weekends and holidays, the corresponding GSHP system was not operated until required. Figure 4 shows the GSHP system diagram for each floor.
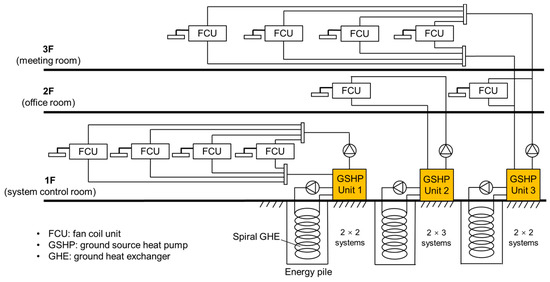
Figure 4.
Schematic diagram of the three-story building.
For the GHEs, 24 thermal piles were installed underneath the building at an underground depth of 20 m, according to the “Geothermal Tornado Method” developed by the Japan Pile Corporation. The configuration of the thermal piles on each floor was as follows: four (two series × two parallel), six (two series × three parallel), four (1 + 1 + 2), and ten for the first, second, and third floors and snowmelt systems, respectively (Figure 5).
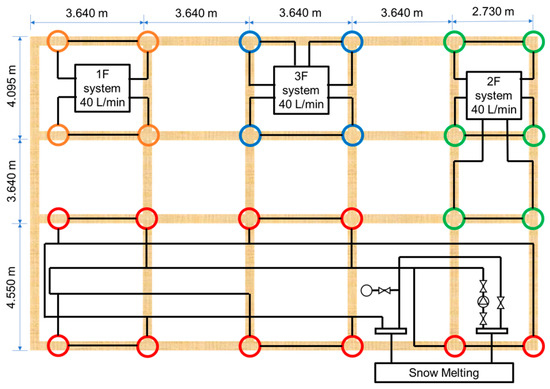
Figure 5.
Layout diagram of thermal piles installed underneath the building (orange circle: first floor system; green circle: second floor system; blue circle: third system; red circle: snowmelt system).
All energy piles used double-spiral GHEs with a pitch (spiral distance) of 250 mm. Figure 6 illustrates the sectional and top views of a thermal pile. The thermal pile can be divided into three parts: the grouting material (cement and soil), the spiral tube with a circulating fluid flowing inside, and the pile material (concrete). Table 2 lists the details of the thermal piles, double-spiral GHEs, and surrounding ground soil. The undisturbed ground temperature was set at 12 °C, according to the in situ underground temperature measurements conducted prior to the commencement of construction [31].
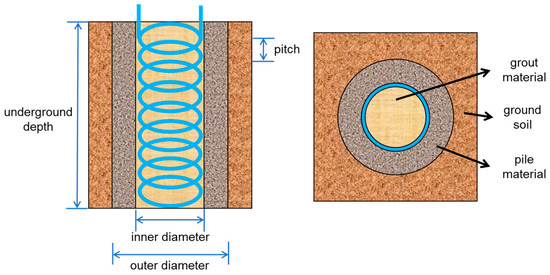
Figure 6.
Sectional and top views of a thermal pile.

Table 2.
Specifications of ground source heat pump (GSHP) units, thermal piles, and spiral tube ground heat exchangers (GHEs).
2.2. Measurement and Performance Evaluation of the GSHP System
Each GSHP unit comprised temperature sensors (Pt100) and electromagnetic flow meters that collected real-time measurements of the pipe inlet and outlet temperatures, circulating fluid flow rate , and power consumption of the heat pump unit . The measurement was started on 27 August 2021. All measured data were collected using a real-time measurement system, and measurements per minute were available for download in .csv (comma-separated values) file format. Figure 7 shows a schematic diagram of the GSHP system and its associated measurements.
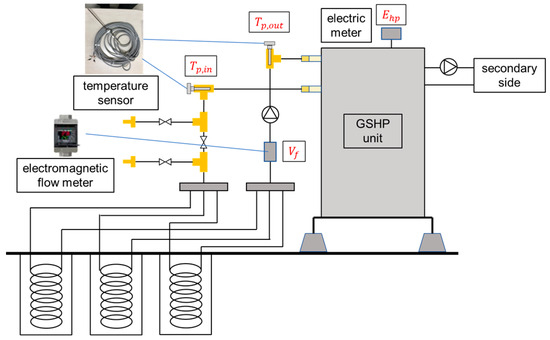
Figure 7.
Schematic diagram of the ground-source heat pump (GSHP) system and its associated measuring points.
Figure 8 illustrates a schematic diagram of the GSHP system examined in this study. The key parameters of the system, such as the primary and secondary loads, the temperature of the circulating fluid, and COP, were calculated using hourly measured data, as illustrated in Figure 8.
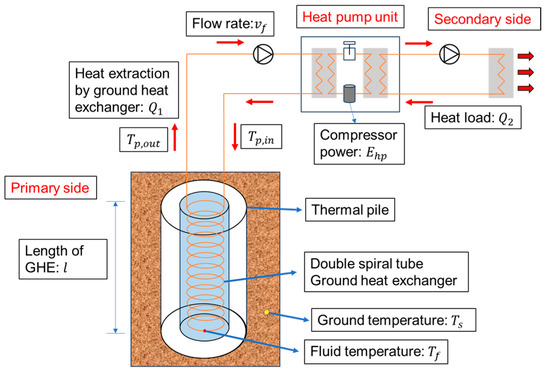
Figure 8.
Schematic of the ground-source heat pump (GSHP) system examined in this study.
In summer, the heat injection (primary load ) from the indoor environment to the ground (heat sink) were obtained using the temperature difference between the pipe inlet and outlet as follows.
where , and are the density, specific heat capacity, and flow rate of the circulating fluid, respectively.
Subsequently, the heat removed from the indoor environment (secondary load ) was equal to the amount remaining after subtracting the power consumption .
In winter, the heat extraction (primary load ) from the ground (heat source) to the indoor environment was calculated by reversing the order as follows.
The heat supplied to the indoor environment (secondary load ) was equal to the heat extracted by adding the power consumption .
2.3. Coefficient of Heat Extraction/Injection
GHEs have been used to extract/discharge heat from/to the ground [32]. The heat extraction/injection performance of GHEs is influenced by several factors, including the composition of the surrounding soil, the design and materials of the GHEs, and the flow rate of the circulating fluid inside the GHEs, of which the temperature of the circulating fluid is the most important. For example, in winter heat extraction scenarios, lowering the temperature of the circulating fluid, which is already considerably lower than the underground temperature, increases the temperature difference between the underground and the circulating fluid, thus enhancing the amount of extractable heat. However, the temperature of the circulating fluid should not be altered excessively, as it is crucial that the temperature of the circulating fluid remains within its operational range. If the operating temperature falls below the acceptable range, it can compromise the performance of the heat pump unit and lead to reliability issues.
The heat extraction/injection performance of the GHEs can be determined by calculating the heat extraction/injection per unit length and dividing it by the difference between the undisturbed ground temperature and the temperature of the circulating fluid [31]. The calculated heat extraction/injection rate of the GHEs per unit length and the temperature difference are defined as the coefficient of heat extraction/injection. Compared with the heat transfer rate, the coefficient of heat extraction/injection is more useful for assessing the performance of GHEs as it considers both the heat extracted/injected per unit length and the temperature difference between the ground and circulating fluid, thereby accurately depicting the capability of different GHEs to exchange heat between the circulating fluid and ground under the same temperature difference. Therefore, this value can be effectively used to evaluate different GHEs.
The circulating fluid temperature was regarded as the average of the pipe inlet and outlet temperatures.
The coefficient of heat extraction/injection (W/(m∙K)) was then calculated using Equation (6) as follows.
where is the heat extraction/injection rate (W), is the borehole length of the GHEs (m), and is the undisturbed ground temperature (K). Using the equations outlined above, we analyzed the measured data.
2.4. Simplification of Large Quantities of Data
The data were measured every minute, resulting in over 880,000 datasets until 31 May 2023. However, analyzing this extensive volume of data was impractical because of the presence of invalid entries, measurement errors, and null values, which primarily occurred when the devices were not monitored during holidays, rest days, and night-time hours.
To mitigate the impact of erroneous data, we represented the hourly measurement values using the 60 min measured data average. This method effectively reduced the dataset to approximately 15,000 sets. For example, on 19 January 2022, there were 60 datasets representing the pipe inlet temperature, flow rate of the circulating fluid, energy consumption of the heat pump unit, and heat extraction rate of GSHP unit 1 every minute (calculated by Equation (3)) from 16:00 to 17:00; therefore, the average value of each variable was used to represent the entire hour, as illustrated in Figure 9.
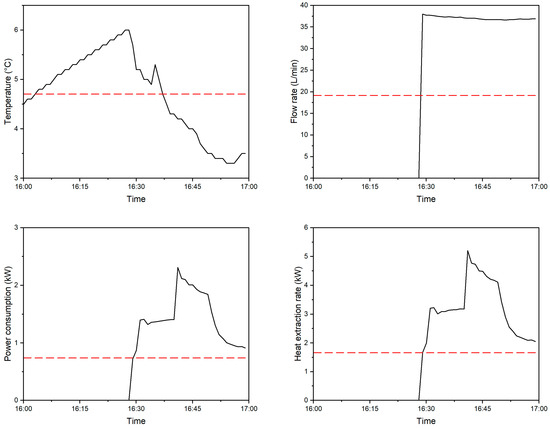
Figure 9.
Average values (red dotted line) of measured data from 16:00 to 17:00, 19 January 2022.
However, 15,000 datasets were too vast for precise analysis. To further reduce the volume of data, we used measured data from a specific hour to represent the operation for an entire day, which reflected typical uninterrupted system operations to ensure data validity and representation.
To identify the most representative hour, we analyzed the hourly changes in the flow rate of the circulating fluid during four distinct time periods, as illustrated in Figure 10. Whether it was a working day or holiday, the system generally began operating after 6:00 every day and ceased at approximately 18:00, or the flow rate dropped to a considerably low level, which continued until the system restarted after 6:00 the following day. Based on this operational pattern, the measured data from 16:00 to 17:00 best represented the operating conditions for an entire day.
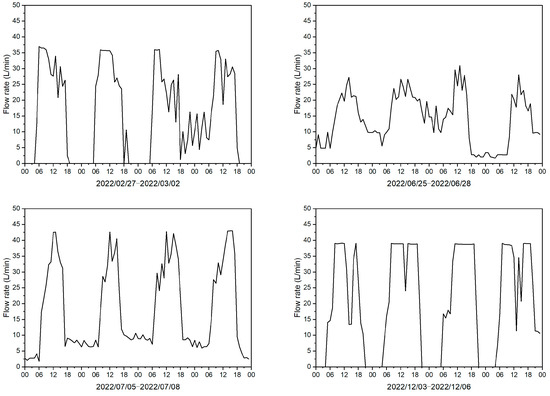
Figure 10.
Hourly fluctuations in the flow rate of the circulating fluid during four different periods.
2.5. Calculation of the Heat Extraction Rate and Fluid Temperature
Daily heat extraction rate was calculated as the sum of the primary loads of the GSHP units over a 24 h period. For example, we calculated the hourly heat extraction rate (kW) for GSHP unit 1 on 27 February 2022 using Equation (3), as illustrated in Figure 11. Therefore, the total heat extraction for the entire day, expressed in kWh/d, can be derived as follows.
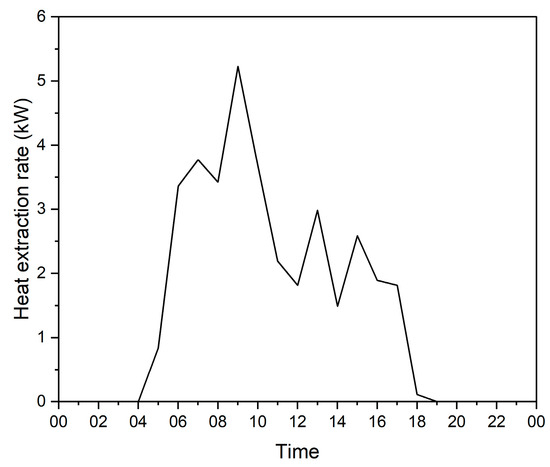
Figure 11.
Hourly variations in the heat extraction rate during the day.
The daily temperature of the circulating fluid was determined by averaging the temperature fluctuations in the fluid over a 24 h period.
2.6. Data Visualization
Though the measured data can be reduced to 643 sets, corresponding to 643 days, this data is still too large to allow for intuitive judgments to be made about the patterns nested within it. Therefore, to visualize this data, we used linear regression analysis and histograms.
By plotting the temperature difference, , between the undisturbed ground temperature and representative fluid temperatures for each ground source heat pump unit on the x-axis and the representative heat extraction rate per unit length of the borehole on the y-axis, the coefficient of heat extraction/injection can be obtained using linear regression analysis.
Histograms provide a visual representation of the distribution of data points. Thus, we used histogram methods to derive an approximate value for the coefficient of heat extraction/injection for the spiral GHEs and further verify the reliability of linear regression analysis. This methodology was used to calculate the coefficients of heat extraction/injection for GSHP units 1 and 2 using hourly measured data, totaling 15,418 sets. The data ranged from 1.5 to 6.0 W/m∙K and were sectioned into intervals of 0.25 to facilitate detailed analysis.
The daily COP calculations for the GSHP system show considerable variation between workdays and holidays due to differing operational times. To minimize errors that could stem from not taking into account long operational times, we introduced a new method in this study. Briefly, by summing the hourly values (secondary load and power consumption ) over these periods, we calculated the seasonal COP. This approach offers a more accurate representation of real-life performance by evaluating the efficiency of a heat pump unit throughout an entire cooling or heating season. As detailed in Section 2.6, the seasonal COP for a given duration is obtained by summing up over a heating/cooling season and then dividing it by the total power consumption for that period. This calculation was conducted as follows:
In this study, due to budget constraints, measurements are constrained by costs. We were unable to measure the power consumption of the GSHP system’s circulation pump. As highlighted in Table 2, the GSHP system’s circulation pump has a rated power of 0.4 kW and a rated flow rate of 40 L/min. During the measurement period, the power consumption of the circulating pump, denoted as , can be approximately determined based on fluctuations in the flow rate of the circulating fluid. The assessment of the can be expressed as:
By summing up the electricity consumption of both the heat pump and circulation pump, we can calculate the System’s Coefficient of Performance (SCOP):
Considering that people largely transitioned to remote work and reduced their office attendance during the pandemic until the restrictions eased (i.e., in May 2022), the heat extraction/injection values before May 2022 may not accurately represent the actual usage of the GSHP systems. Consequently, we used data from June 2022 to May 2023 to accurately characterize annual operational conditions. Figure 12 illustrates the workflow used for analyzing the measured data to assess the performance of the GHEs.
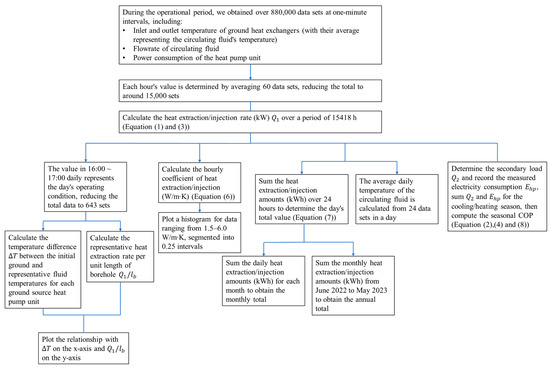
Figure 12.
Flow chart of data processing.
2.7. Uncertainty Analysis
The uncertainty of the coefficient of heat extraction/injection is a cumulative uncertainty derived from the propagation of individual uncertainties. It can be calculated using the subsequent equation. Table 3 lists the experimentally measured parameters, , along with their uncertainties, .

Table 3.
Experimental uncertainties.
3. Results
3.1. Monthly and Annual Heat Extraction/Injection Amount of the GHEs
Figure 13, Figure 14 and Figure 15 show the monthly heat extraction/injection amounts and the annual primary load from August 2021 to May 2023 and June 2022 to May 2023, respectively, of the three GSHP units. The transition between space heating and cooling operations occurred in October and May, resulting in simultaneous heat extraction and injection.
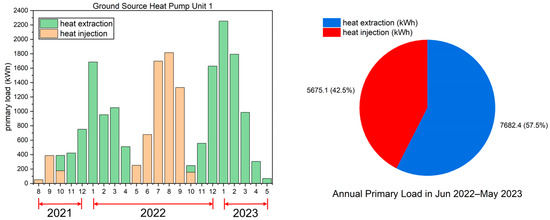
Figure 13.
Monthly heat extraction/injection amount and the annual primary load of ground-source heat pump (GSHP) unit 1 from June 2022 to May 2023.
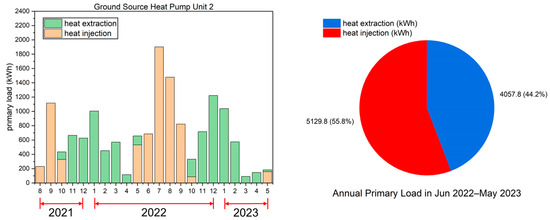
Figure 14.
Monthly heat extraction/injection amount and the annual primary load of ground-source heat pump (GSHP) unit 2 from June 2022 to May 2023.
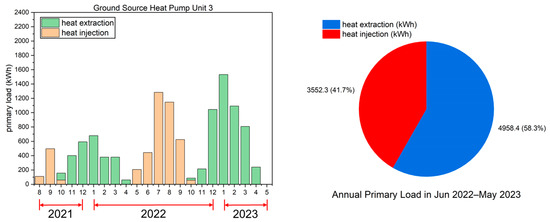
Figure 15.
Monthly heat extraction/injection amount and the annual primary load of ground-source heat pump (GSHP) unit 3 from June 2022 to May 2023.
As illustrated in Figure 13, the first floor of the building has the highest occupancy, with people present virtually every day throughout the year. This constant occupancy led to relatively balanced heating and cooling demands for the stores and central control room of the system. The amount of heat extracted from the ground surpassed the heat injected back into it throughout the year, highlighting the predominant trend in cold regions: the demand for heating far outweighs that for cooling.
As illustrated in Figure 14, the second floor houses offices that require space heating and cooling only on workdays. Owing to the high level of airtightness in the building, the demand for heating was not particularly high during winter. However, because of the continuous rise in summer temperatures in recent years, the demand for space cooling was particularly high in the summer of 2022, which was considerably higher than the demand for space heating during winter. Furthermore, the amount of heat discharged into the ground annually exceeded the amount of heat extracted. As shown in Figure 15, the third floor houses conference rooms that require space heating and cooling only when meetings are underway. Thus, its heating and cooling demands were similar to those of the first floor, and the heating demand during winter was higher than the cooling demand during summer.
3.2. Daily Heat Extraction/Injection Rate of the GHEs and the Average Temperature of the Circulating Fluid
Figure 16a shows the daily variation in the heat extraction rate for the GHEs of GSHP unit 1 over a 643 d measurement period, whereas Figure 16b illustrates the annual fluctuation in the daily average temperature of the circulating fluid within the GHEs from June 2022 to May 2023 (the data points corresponding to zero heat extraction/injection days were removed). The heat extraction rate was negative and positive during the cooling period in summer (heat injected into the ground) and the heating period in winter, respectively.
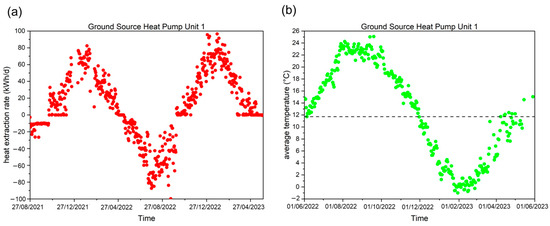
Figure 16.
Daily variations in the (a) heat extraction amount (red dots) and (b) daily average temperature (green dots) of the circulating fluid for the ground heat exchangers (GHEs) of ground-source heat pump (GSHP) unit 1.
The first floor, which houses the stores and central control rooms of the system, has a high occupancy rate. Therefore, it required a great amount of space heating and cooling. As illustrated in Figure 16, the heat extraction amount for GSHP unit 1 peaked during the heating periods of December 2021–February 2022 and December 2022–February 2023, whereas the circulating fluid temperature decreased correspondingly.
During both the winter heating periods, the heat extraction rate consistently exceeded 60 kWh/d, reaching over 80 and 100 kWh/d at the beginning of 2022 and 2023, respectively. This caused the fluid temperature to drop below 0 °C, but it did not exceed −2 °C. In contrast, during the summer cooling period from July 2022 to September 2022, the heat injected into the ground consistently exceeded 60 kWh/d, whereas the temperature of the circulating fluid remained below 26 °C, maintaining a favorable operating temperature.
Figure 17 and Figure 18 demonstrate the operational conditions for GSHP units 2 and 3, respectively. The second and third floors experience less frequent usage as they are only required during workdays and meetings. Consequently, their space-heating demands were much lower than those of the first floor during winter, with the maximum winter heat injection barely exceeding 60 kWh/d. Over a 1-year period, the fluid temperature remained within the range of 8–24 °C. However, the highest heat injection reached 100 kWh/d during summer, indicating a high need for space cooling, even in cold regions. Hokkaido experienced unusually hot weather in the summer of 2021. Considering that the heat injection and extraction will remain unbalanced over the years, it is essential to address not only the anti-freeze properties of the circulating fluid during winters but also the temperature increase of the circulating fluid during the space cooling periods in summers.
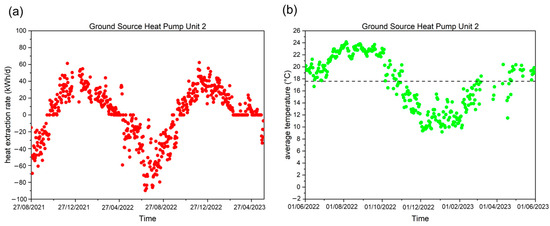
Figure 17.
Daily variations in the (a) heat extraction amount (red dots) and (b) daily average temperature (green dots) of the circulating fluid for the ground heat exchangers (GHEs) of ground-source heat pump (GSHP) unit 2.
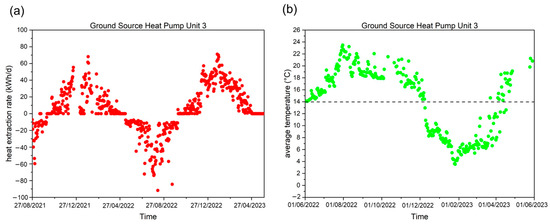
Figure 18.
Daily variations in the (a) heat extraction amount (red dots) and (b) daily average temperature (green dots) of the circulating fluid for the ground heat exchangers (GHEs) of ground-source heat pump (GSHP) unit 3.
Theoretically, long-term operation can cause the ground temperature to increase continuously, potentially affecting the efficiency of the system. However, the temperature of the circulating fluid in 3 GSHP systems was within the operational range in this study, demonstrating the strong adaptability of the system.
3.3. Calculation and Comparison of the Coefficient of Heat Extraction/Injection of the GHEs
Figure 19, Figure 20 and Figure 21 plot the data points (red) of corresponding (the temperature difference between the undisturbed ground temperature and fluid temperatures) and the heat extraction rate per unit length of the borehole (80 m and 120 m for the GHEs of GSHP units 1 and 3 and unit 2, respectively).
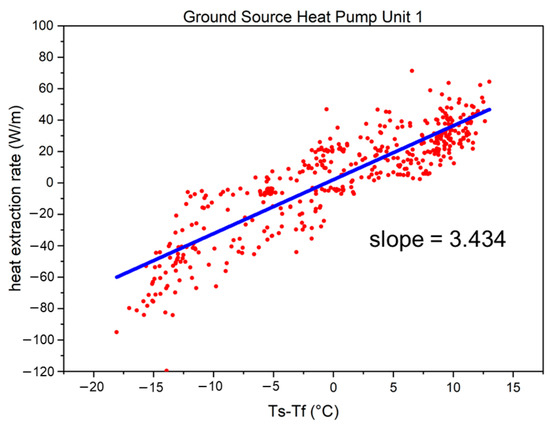
Figure 19.
The relationship between the heat extraction rate per length and temperature difference between the undisturbed ground temperature and fluid temperatures for ground-source heat pump (GSHP) unit 1 (red dots) and regression line (blue).
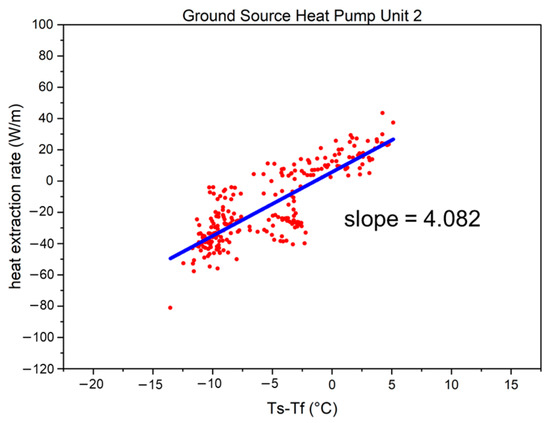
Figure 20.
The relationship between the heat extraction rate per length and temperature difference between the undisturbed ground temperature and fluid temperatures for ground-source heat pump (GSHP) unit 2 (red dots) and regression line (blue).
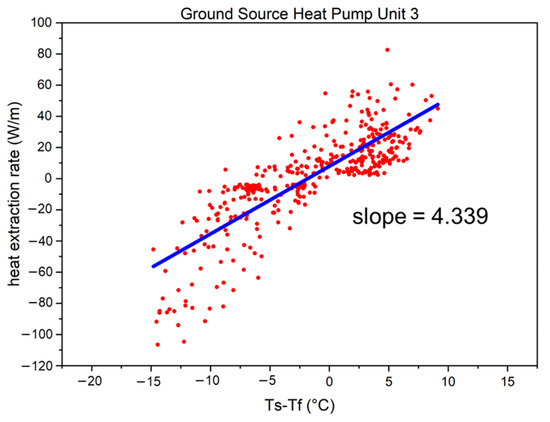
Figure 21.
The relationship between the heat extraction rate per length and temperature difference between the undisturbed ground temperature and fluid temperatures for ground-source heat pump (GSHP) unit 3 (red dots) and regression line (blue).
As illustrated in Figure 19, Figure 20 and Figure 21, the data visualization method of linear regression analysis is applied. Based on the slope of the regression line (blue), we observed that the coefficient of heat extraction/injection for double spiral GHEs exceeded 3.4 W/m∙K, even reaching values higher than 4.3 W/m∙K.
For another data visualization method, as shown in Figure 22 and Figure 23, based on histograms of calculated coefficient of heat extraction/injection for each hour, frequency analysis revealed that the most frequently occurring approximate representation was within the range of 3.5–4.0 W/m∙K for GSHP unit 1, whereas GSHP unit 2 exhibited a range of 3.75–5.0 W/m∙K (the peak of the histogram was not pronounced, possibly because the large heat capacity of the thermal pile caused some deviations and the operation time was not long enough). These results are consistent with the slopes of the regression lines calculated above.
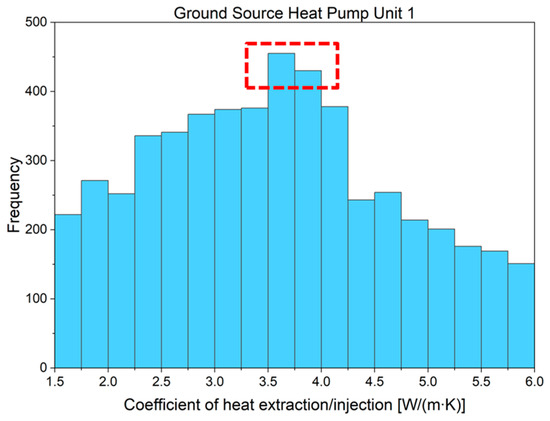
Figure 22.
Distribution of hourly coefficient of extraction/injection for ground-source heat pump (GSHP) unit 1 (red box highlights the value with the highest frequency).
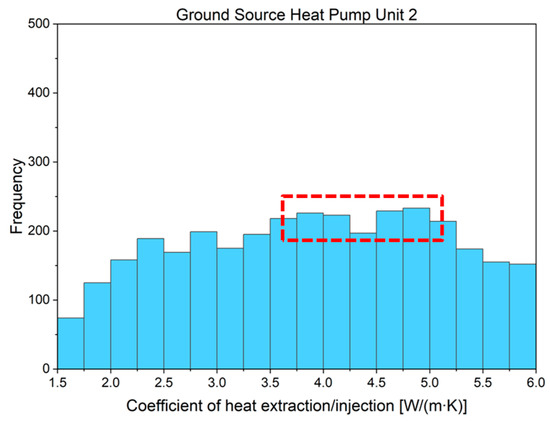
Figure 23.
Distribution of hourly coefficient of extraction/injection for ground-source heat pump (GSHP) unit 2 (red box highlights the value with the highest frequency).
3.4. Performance Evaluation of the GSHP System
According to the measured data, two periods of space cooling were observed during summer: 27 August–18 October 2021 and 6 May–5 October 2022. Similarly, two periods of space heating were observed during winter: 18 October–6 May 2022 and 5 October–25 May 2023. Seasonal COP for each of these periods is depicted in Figure 24.
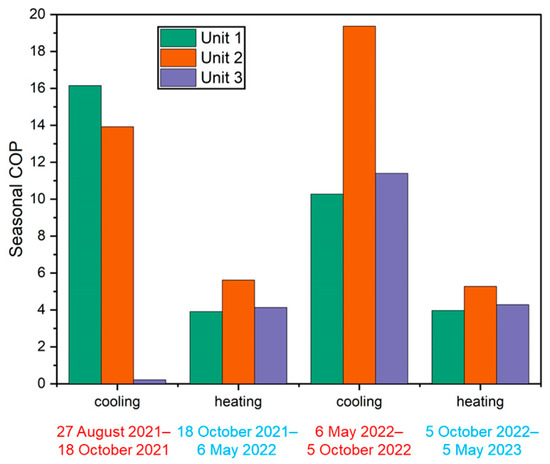
Figure 24.
Seasonal coefficient of performance (COP) of three ground-source heat pump (GSHP) units during four periods (red: summer cooling; blue: winter heating).
Except for the seasonal COP of GSHP unit 3 during the first cooling period, the seasonal COP of all GSHP units exceeded 10 in the summers of both 2021 and 2022, with the seasonal COP of unit 2 reaching 20 in the summer of 2022. This elevated performance can be attributed to two primary factors. First, the ambient temperature in cold regions, such as Sapporo, Japan, is remarkably lower than those of other areas and rarely exceeds 30 °C. This results in a reduced temperature difference between the set indoor (26 °C) and outdoor temperatures, diminishing the need for intensive space cooling and thereby alleviating the continuous high-demand operation of the GSHP system. Second, the building uses the free cooling method, which reduces the air temperature in a building using naturally cool air or water rather than mechanical refrigeration. When the ambient temperature is low, the outdoor air cools the indoor environment, effectively decreasing the indoor temperature with minimal electrical consumption. This approach can considerably enhance the COP.
In winter, all GSHP units maintained a COP of more than four during the cooling periods in both 2022 and 2023. This performance is impressive, especially considering the extreme weather conditions in Sapporo during winters when temperatures remain below 0 °C for a long time, creating a considerable temperature difference with the indoor setting of 22 °C. Compared with a typical air source heat pump system, which has a COP of approximately 2, or a conventional GSHP system with borehole GHEs, which has a COP of approximately 3, the GSHP systems equipped with double spiral-tube GHEs in this energy-efficient building demonstrated far superior efficiency.
In Section 2.6, the calculation of SCOP is thoroughly discussed. When accounting for the electricity consumed by the circulation pump of the GSHP system, the results are derived using Equation (10) and depicted in Figure 25. When compared to the seasonal COP, there is a notable decrease in the SCOP for each unit. This decline is especially pronounced during the summer cooling period. Despite employing free cooling, the power consumption of the circulation pumps due to circulating fluid movement results in a large drop in SCOP. However, during the winter, the SCOP decreases but not as dramatically. This aligns with the design specifications of the GSHP unit, highlighting the GSHP system’s exceptional thermal efficiency. Importantly, these results align well with the heating COP of the GSHP system listed in Table 2.
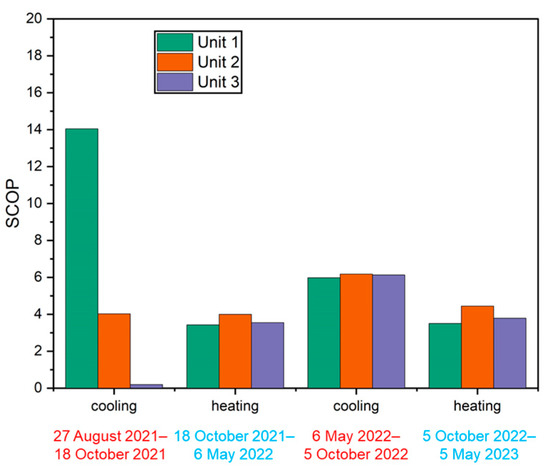
Figure 25.
System coefficient of performance (SCOP) of three ground-source heat pump (GSHP) units during four periods (red: summer cooling; blue: winter heating).
3.5. Uncertainty Analysis
To analyze the uncertainty of the coefficient of heat extraction/injection , we examined a 4 h operational dataset from GSHP unit 1 on 31 July 2022; the pipe inlet/outlet temperature and flow rate were recorded every minute. Using this data, we calculated for each minute. Table 4 presents the hourly averages of these values. Using Equation (11), the uncertainty of for each hour was determined. From the results, it is evident that due to the slightly larger margin of error in the temperature measuring equipment used in this experiment, the cumulative uncertainty is amplified. However, the uncertainty still remains within an acceptable range. Moreover, when the GSHP system operates continuously, in the short-term aligns closely with the results derived in Section 3.3.

Table 4.
Pipe inlet/out temperature, fluid flowrate, coefficient and its uncertainty during a 4 h operational period.
4. Discussion
4.1. Comparison with Traditional U-Tube GHEs
U-tube GHEs have been used in GSHP systems for decades and commonly feature in many energy-efficient homes. However, because thermal piles and double-spiral tube GHEs had large borehole diameters and surface areas, respectively, for heat exchange in this study, they exhibited a thermal performance greater than that of U-tube GHEs.
A residential house in Sapporo, Japan, adopted conventional U-tube GHEs and has been under observation since 2005. The specific details of the house are listed in Table 5.

Table 5.
Basic information on the residential house in Sapporo, Japan.
The GSHP system in the abovementioned house is used solely for space heating. Using data measured hourly, the coefficient of heat extraction was calculated every hour from October 2006 to May 2007, totaling 4714 h. The distribution of data points characterizing this period is shown in Figure 26. Specifically, most of the values were within the range of 1.8–2.2 W/m∙K, indicating that the typical value of the coefficient of heat extraction/injection for the U-tube GHEs is approximately 2 W/m∙K. On comparing this value with that of the double spiral tube GHEs (approximately 3.5–4.5 W/m∙K), the superior performance of double-spiral GHEs was clearly demonstrated. Additionally, when comparing results from a prior study that utilized a simulation tool to forecast the long-term thermal efficiency of GHEs, the simulated coefficient of heat extraction/injection for the double spiral tube GHE was approximately 4 W/m∙K, compared to about 2 W/m∙K for the conventional U-tube GHE [31]. These simulation outcomes align closely with the results derived from the present study.
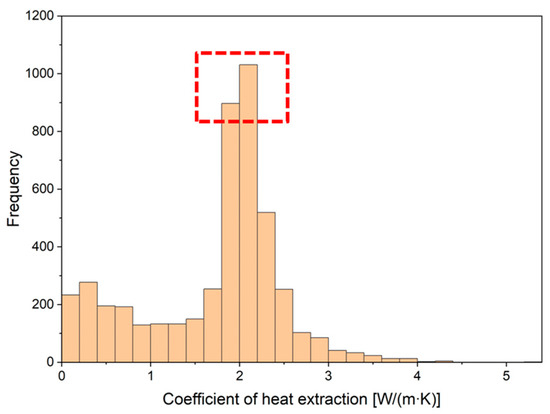
Figure 26.
Distribution of the hourly coefficient of extraction for the residential house using U-tube ground heat exchangers (GHEs) (red box highlights the value with the highest frequency).
4.2. Pressure Drop of Different Types of GHE
The pressure drop of the double spiral tube GHEs examined in this study was compared to that of the conventional U-tube GHEs. Due to budgetary limitations, we were unable to conduct long-term measurements for the pressure drop inside the pipe continuously. Instead, based on specifications provided by the manufacturing company [33] for the U-tube GHEs and recent data we obtained from on-site measurements at the ZEB building, the comparison of pressure drops for these two types of GHEs when using anti-freeze fluid at 0 °C for various flow rates is depicted in Figure 27. The double spiral GHEs in this study have an underground depth of 20 m and a total pipe length of 95 m. In contrast, the U-tube GHEs is a commonly adopted design with an underground depth of 40 m and a pipe length of 80 m.
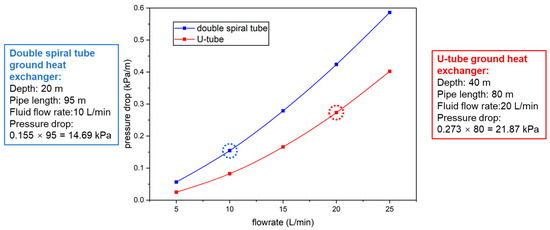
Figure 27.
Pressure drop in double spiral GHEs and U-tube GHEs with anti-freeze fluid at 0 °C across different flow rates.
As shown in Figure 27, the double spiral GHE exhibits a pressure drop of 14.69 kPa at a fluid flow rate of 10 L/min. Our findings in Section 4.1 indicate that the double spiral GHEs achieve roughly double the heat extraction/injection per unit length and temperature difference than U-tube GHEs. To match the heat extraction/injection rate of the double spiral GHEs, the circulation flow rate for the U-tube GHEs needs to be set at 20 L/min, resulting in a pressure drop of 21.87 kPa. This comparison indicates the efficiency of the spiral tube GHEs: it can achieve the same heat extraction/injection amount as the U-tube GHEs but at half the underground depth while also benefiting from a reduced pressure drop.
Additionally, when the circulation flow rate of the U-tube GHEs is set to a lower value, like 10 L/min, the Reynolds number drops to 2100 or below, transitioning to a laminar flow regime. This would inherently diminish the heat exchange efficiency between the circulating fluid and the ground. Based on these findings, it’s clear that the double spiral GHEs offer superior performance, both in terms of minimizing pressure drop and maximizing heat exchange capacity.
4.3. Cooling Demands of Places in Cold Region
Sapporo, the capital of Hokkaido, Japan, is a generally cold region, largely due to its extremely cold winters and high seasonal snowfall. Despite this information, our findings in Section 3.4 indicate that the Seasonal COP in this region during summer was unexpectedly high. This can be attributed to Sapporo’s relatively mild summer conditions, which are characterized by fewer hot days and considerably cooler temperatures than those of other parts of Japan. Overall, the reduced temperature gap between the indoor and outdoor environments enhanced the efficiency of the GSHP system in the context of efficient space cooling.
This study unveiled an unexpected result: Despite Sapporo’s cold climate and its general classification as a heating-dominant region, the cooling demand during summer was higher than the heating demand during winter in some office buildings. This is largely because previously cold locations are experiencing a growing demand for cooling as summer temperatures continue to increase annually due to global warming. In the long term, these changes could culminate in prolonged thermal imbalances in the soil. Therefore, it will be necessary to address this issue through the implementation of various measures (e.g., the installation of cooling towers or sharing the cooling load with other devices); these measures would improve the resiliency of the abovementioned systems under ongoing climate change.
4.4. Study Limitations
This study emphasizes the long-term practical application of GSHP systems using innovative GHEs rather than computer simulations or experimental results obtained via laboratory-based studies. Although this study provides a more realistic reflection of the thermal performance of double-spiral tube GHEs under real-use conditions, it does have some limitations.
First, some of the holiday-linked data is missing owing to the temporary suspension of the measurement system during the study. In addition, unnecessary power consumption occurred during periods when there was no heating or cooling demand. Moreover, the system did not operate continuously; instead, its operations had frequent starts and stops. Contrary to the steady and continuous operation observed in a laboratory setting, the intermittent nature of the real-world functioning of the system resulted in discontinuous measurements, which may explain the different coefficients of heat extraction/injection among the GSHP units. This variation may also be attributed to distinctive room occupancy levels and operational durations for each floor. Moreover, the daily operation times influenced the thermal performance of the GSHP systems; the influence of this factor needs to be investigated in future studies.
We did not conduct long-term measurements of the power consumption of the circulation pump and the pressure drop within the double spiral GHEs. Though these factors were not the primary focus of this study, incorporating them would have improved the accuracy of our findings. We acknowledge this limitation and aim to address and enhance it in future research.
5. Conclusions
In this study, we investigated the thermal performance of thermal piles with double-spiral GHEs based on the actual measured data of a GSHP system installed in a ZEB. The findings of this study are as follows.
- In contrast to the traditional U-shaped pipe GHEs, the double spiral pipe GHEs have shorter underground boreholes but larger areas for heat exchange between the ground and circulating fluid without additional drilling work, thereby reducing the initial costs of the GSHP system and promoting its future use;
- For the most frequently used first-floor GSHP system, the temperature of the circulating fluid remained above −2 °C during winter and did not exceed 26 °C during summer, whereas the circulating fluid temperatures for other GSHP systems were within a range of 4–24 °C. Furthermore, the coefficient of heat extraction/injection of double spiral GHEs was more than 3.4 W/m∙K, with the GHEs of GSHP unit 3 even exceeding 4.3 W/m∙K. The use of histograms further confirmed these findings;
- On the second and third floors, there was an imbalance between the heat extraction and injection amounts, which may lead to a soil thermal imbalance in the long term. However, the temperature of the circulating fluid remained within an acceptable range over a period of approximately 2 years, indicating the feasibility of long-term operation and the robustness of the system to climate change;
- Seasonal COP calculations indicated a high operational efficiency, with values surpassing 10 and 4 during the summer cooling and winter heating periods, respectively. These results highlight the advantages of using GSHP systems with double-spiral GHEs. After evaluating the power consumption of the circulation pump, we calculated the SCOP. Although there was a decrease compared to COP, these results are consistent with the heating COP of the GSHP system listed in Table 2;
- The pressure drop in the double spiral GHE has not been continuously measured, but verification from the on-site measurements has been carried out. Results from this verification suggest that this innovative design can effectively decrease the pressure drop and boost heat exchange efficiency;
- Considering that many ZEBs without GSHP systems in cold regions rely primarily on kerosene or gas for winter heating and rarely consider summer cooling, this study demonstrates that GSHP systems, which offer both efficient heating and cooling, are a promising choice that should be widely adopted in the future.
Author Contributions
Conceptualization, K.Y. and T.K.; methodology, K.Y.; data curation, K.Y.; writing—original draft preparation, K.Y.; writing—review and editing, T.K.; supervision, T.K., S.N. and K.N.; funding acquisition, T.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by JST SPRING, grant number JPMJSP2119.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available because the original data volume is too large and complex, making it difficult to understand.
Acknowledgments
This study is based on the results obtained from the project “Renewable energy heat utilization technology development for cost reduction,” commissioned by the Japanese national agency NEDO. The authors also thank M’s Industry Co., Ltd. and Japan Pile Corporation for their assistance in this research project.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of this study, in the collection, analyses, or interpretation of data, in the writing of the manuscript, or in the decision to publish the results.
Nomenclature
| Symbols | |
| c | specific heat capacity, J/kg∙K |
| E | power consumption, kW |
| l | length/depth, m |
| q’ | coefficient of heat extraction/injection, W/m∙K |
| Q | heating/cooling load, kW |
| T | temperature, ℃ |
| U | daily primary load, kWh |
| u | uncertainty |
| v | flow rate, m3/s |
| ρ | density, kg/m3 |
| Subscripts | |
| 1 | primary side |
| 2 | secondary side |
| b | borehole of energy pile |
| f | circulating fluid |
| hp | heat pump |
| pump | circulation pump |
| p,in | pipe inlet |
| p,out | pipe outlet |
| s | soil |
| Abbreviations | |
| BHE | borehole heat exchanger |
| COP | coefficient of performance |
| DBHE | deep borehole heat exchanger |
| FCU | fan coil unit |
| GHE | ground heat exchanger |
| GSHP | ground source heat pump |
| HGHE | horizontal ground heat exchanger |
| PHC | precast high-strength concrete |
| PV | photovoltaic |
| PVC | polyvinyl chloride |
| SCOP | system coefficient of performance |
| ZEB | zero energy building |
References
- Aggarwal, V.; Meena, C.S.; Kumar, A.; Alam, T.; Kumar, A.; Ghosh, A.; Ghosh, A. Potential and future prospects of geothermal energy in space conditioning of buildings: India and worldwide review. Sustainability 2020, 12, 8428. [Google Scholar] [CrossRef]
- Sarbu, I.; Sebarchievici, C. General review of ground-source heat pump systems for heating and cooling of buildings. Energy Build. 2014, 70, 441–454. [Google Scholar] [CrossRef]
- IEA. Buildings; IEA: Paris, France, 2022; Available online: https://www.iea.org/reports/buildings (accessed on 8 August 2023).
- Nejat, P.; Jomehzadeh, F.; Taheri, M.M.; Gohari, M.; Muhd, M.Z. A global review of energy consumption, CO2 emissions and policy in the residential sector (with an overview of the top ten CO2 emitting countries). Renew Sustain. Energy Rev. 2015, 43, 843–862. [Google Scholar] [CrossRef]
- Florides, G.; Kalogirou, S. Ground heat exchangers-A review of systems, models and applications. Renew Energy 2007, 32, 2461–2478. [Google Scholar] [CrossRef]
- Lund, J.W.; Toth, A.N. Direct utilization of geothermal energy 2020 worldwide review. Geothermics 2021, 90, 101915. [Google Scholar] [CrossRef]
- Wang, D.; Lu, L.; Zhang, W.; Cui, P. Numerical and analytical analysis of groundwater influence on the pile geothermal heat exchanger with cast-in spiral coils. Appl. Energy 2015, 160, 705–714. [Google Scholar] [CrossRef]
- Zero-Emission by Low Cost Construction Method of Geothermal Heat Collection. Challenge Zero. Available online: https://www.challenge-zero.jp/en/casestudy/673 (accessed on 8 August 2023).
- Chen, C.; Shao, H.; Naumov, D.; Kong, Y.; Tu, K.; Kolditz, O. Numerical investigation on the performance, sustainability, and efficiency of the deep borehole heat exchanger system for building heating. Geotherm. Energy 2019, 7, 18. [Google Scholar] [CrossRef]
- Tang, F.; Nowamooz, H. Factors influencing the performance of shallow Borehole Heat Exchanger. Energy Convers. Manag. 2019, 181, 571–583. [Google Scholar] [CrossRef]
- Cao, J.; Bottarelli, M.; Bortoloni, M.; Pei, G. Small-scale lab analysis of the ground freezing effect on the thermal performance of a Flat-Panel ground heat exchanger. Geothermics 2018, 74, 247–254. [Google Scholar] [CrossRef]
- Zhang, J.; Lu, X.; Zhang, W.; Liu, J.; Yue, W.; Ma, F. Investigation of a Novel Deep Borehole Heat Exchanger for Building Heating and Cooling with Particular Reference to Heat Extraction and Storage. Processes 2022, 10, 888. [Google Scholar] [CrossRef]
- Congedo, P.M.; Colangelo, G.; Starace, G. CFD simulations of horizontal ground heat exchangers: A comparison among different configurations. Appl. Therm. Eng. 2012, 33, 24–32. [Google Scholar] [CrossRef]
- Zhang, G.; Cao, Z.; Liu, Y.; Chen, J. Field test and numerical simulation on the long-term thermal response of phc energy pile in layered foundation. Sensors 2021, 21, 3873. [Google Scholar] [CrossRef] [PubMed]
- Jalaluddin; Miyara, A.; Tarakka, R.; Mochtar, A.A.; Muhammad Anis, I.R. Thermal performance of shallow spiral-tube ground heat exchanger for ground-source cooling system. IOP Conf. Ser. Mater. Sci. Eng. 2019, 619, 012012. [Google Scholar] [CrossRef]
- Huang, X.; Yao, Z.; Cai, H.; Li, X.; Chen, H. Performance evaluation of coaxial borehole heat exchangers considering ground non-uniformity based on analytical solutions. Int. J. Therm. Sci. 2021, 170, 107162. [Google Scholar] [CrossRef]
- Cai, W.; Wang, F.; Chen, C.; Chen, S.; Liu, J.; Ren, Z.; Shao, H. Long-term performance evaluation for deep borehole heat exchanger array under different soil thermal properties and system layouts. Energy. 2022, 241, 122937. [Google Scholar] [CrossRef]
- Serageldin, A.A.; Sakata, Y.; Katsura, T.; Nagano, K. Thermo-hydraulic performance of the U-tube borehole heat exchanger with a novel oval cross-section: Numerical approach. Energy Convers. Manag. 2018, 177, 406–415. [Google Scholar] [CrossRef]
- Jahanbin, A. Thermal performance of the vertical ground heat exchanger with a novel elliptical single U-tube. Geothermics 2020, 86, 101804. [Google Scholar] [CrossRef]
- Majeed, S.H.; Abdul-Zahra, A.S.; Mutasher, D.G. Performance evaluation of different types of ground source heat exchangers in a hot and dry climate. Heat Transfer. 2022, 51, 5700–5722. [Google Scholar] [CrossRef]
- Li, X.; Chen, Y.; Chen, Z.; Zhao, J. Thermal performances of different types of underground heat exchangers. Energy Build. 2006, 38, 543–547. [Google Scholar] [CrossRef]
- Kerme, E.D.; Fung, A.S. Heat transfer analysis of single and double U-tube borehole heat exchanger with two independent circuits. J. Energy Storage 2021, 43, 103141. [Google Scholar] [CrossRef]
- Luo, J.; Rohn, J.; Bayer, M.; Priess, A. Thermal performance and economic evaluation of double U-tube borehole heat exchanger with three different borehole diameters. Energy Build. 2013, 67, 217–224. [Google Scholar] [CrossRef]
- Kim, J.W.; Kim, Y.M.; Ko, Y.J.; Chen, Q.; Xin, C.; Oh, S.J. Study on an advanced borehole heat exchanger for ground source heat pump operating in volcanic island: Case study of Jeju island, South Korea. Front. Built. Environ. 2022, 8, 1061760. [Google Scholar] [CrossRef]
- Zou, H.; Pei, P.; Wang, C.; Hao, D. A numerical study on heat transfer performances of horizontal ground heat exchangers in ground-source heat pumps. PLoS ONE 2021, 6, e0250583. [Google Scholar] [CrossRef] [PubMed]
- Dehghan, B.B. Experimental and computational investigation of the spiral ground heat exchangers for ground source heat pump applications. Appl. Therm. Eng. 2017, 121, 908–921. [Google Scholar] [CrossRef]
- Li, B.; Zheng, M.; Shahrestani, M.; Zhang, S. Driving factors of the thermal efficiency of ground source heat pump systems with vertical boreholes in Chongqing by experiments. J. Build. Eng. 2020, 28, 101049. [Google Scholar] [CrossRef]
- Walch, A.; Li, X.; Chambers, J.; Mohajeri, N.; Yilmaz, S.; Patel, M.; Scartezzini, J.L. Shallow geothermal energy potential for heating and cooling of buildings with regeneration under climate change scenarios. Energy 2022, 244, 123086. [Google Scholar] [CrossRef]
- Guo, L.; Zhang, J.; Li, Y.; McLennan, J.; Zhang, Y.; Jiang, H. Experimental and numerical investigation of the influence of groundwater flow on the borehole heat exchanger performance: A case study from Tangshan, China. Energy Build. 2021, 248, 111199. [Google Scholar] [CrossRef]
- Tu, S.; Yang, X.; Zhou, X.; Luo, M.; Zhang, X. Experimenting and modeling thermal performance of ground heat exchanger under freezing soil conditions. Sustainability 2019, 11, 5738. [Google Scholar] [CrossRef]
- Yang, K.; Katsura, T.; Nagasaka, S.; Nagano, K. Development and application of a new calculation method for double spiral ground heat exchangers. Energy Build. 2023, 291, 113144. [Google Scholar] [CrossRef]
- Katsura, T.; Nagano, K.; Nakamura, Y. A study on design method for the ground heat exchanger’s specification of ground source heat pump system. J. Environ. Eng. 2011, 76, 59Y66. [Google Scholar] [CrossRef]
- Products/INOAC Housing & Construction Materials Co., Ltd. Available online: https://www.inoac-juukan.co.jp/en/product/ (accessed on 27 September 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).