New Modular Multilevel DC–DC Converter Derived from Modified Buck–Boost DC–DC Converter
Abstract
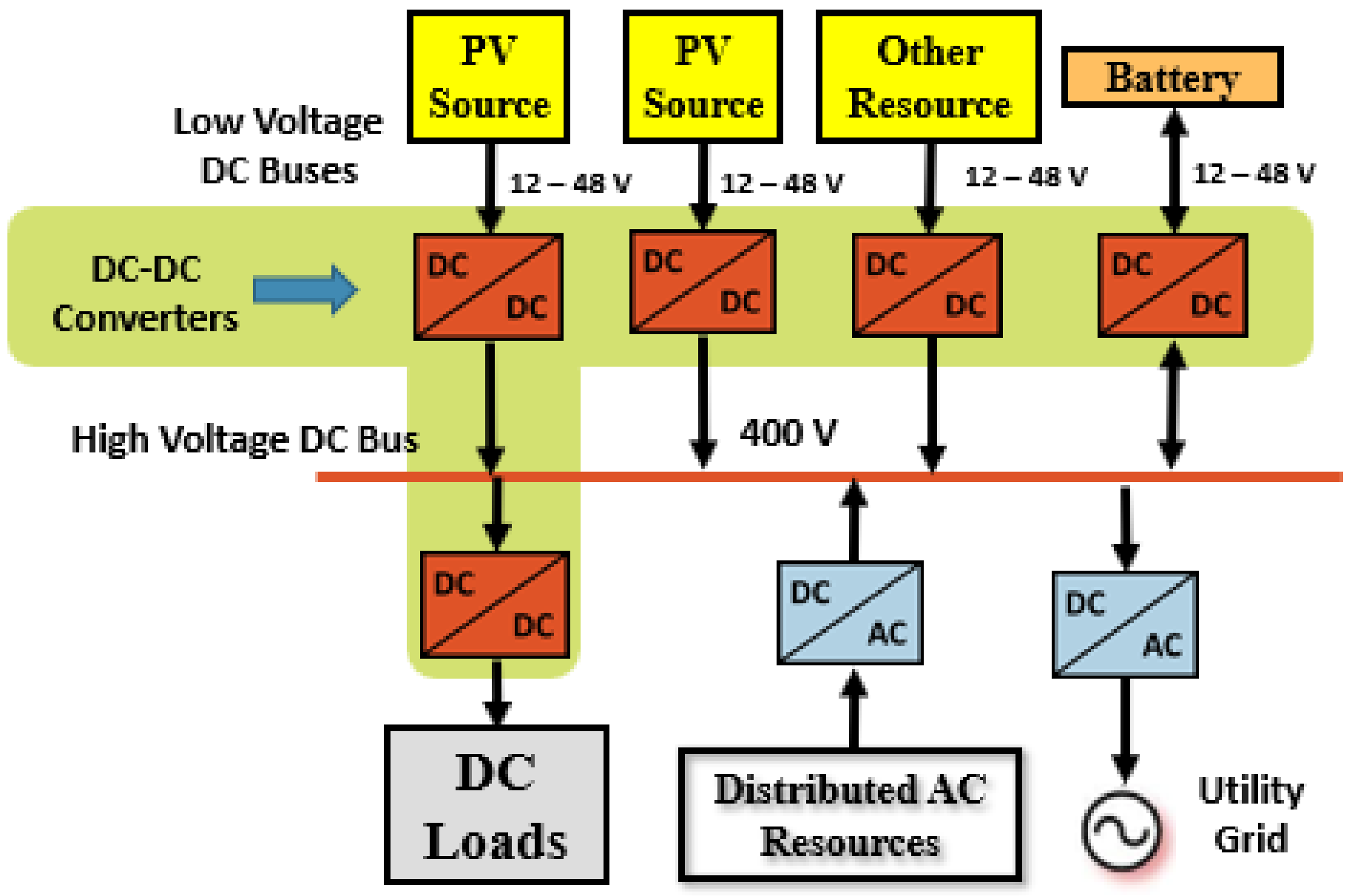
:1. Introduction
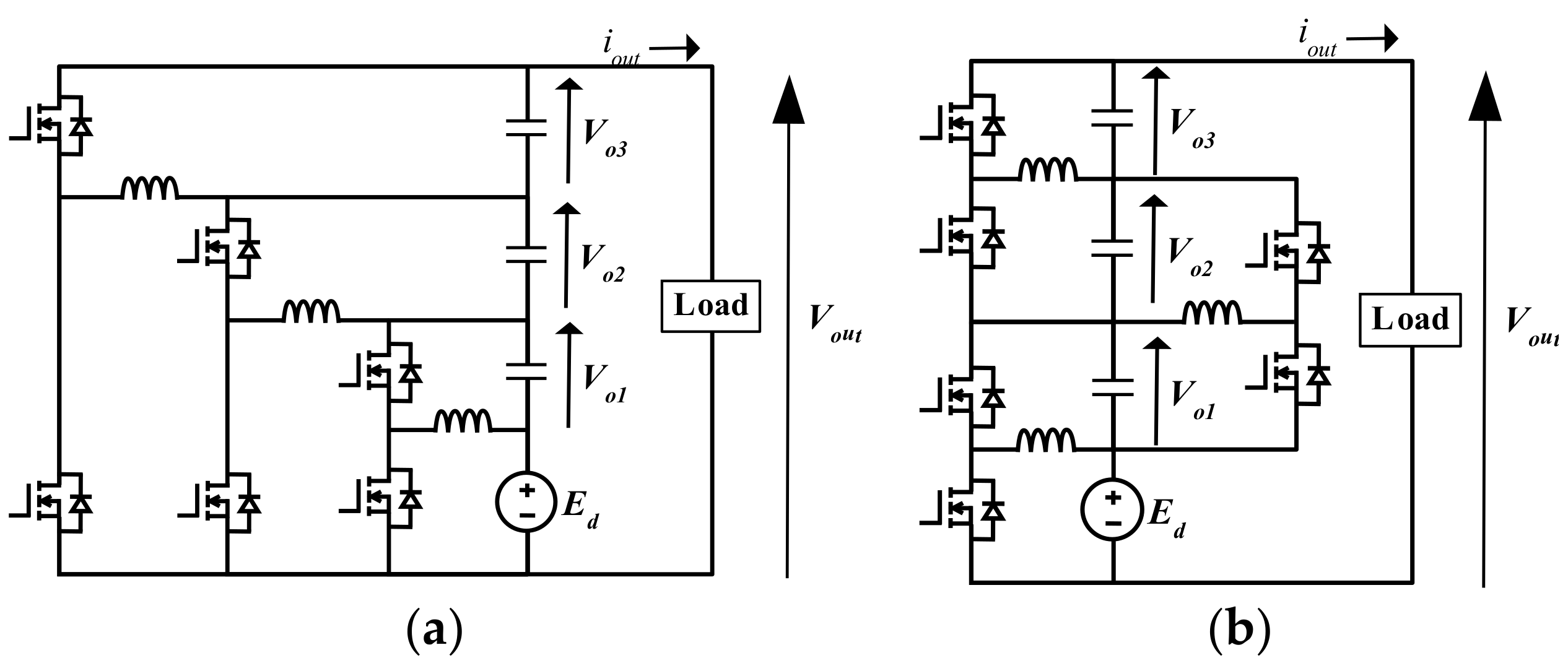
2. New Modular Multilevel DC–DC Converter
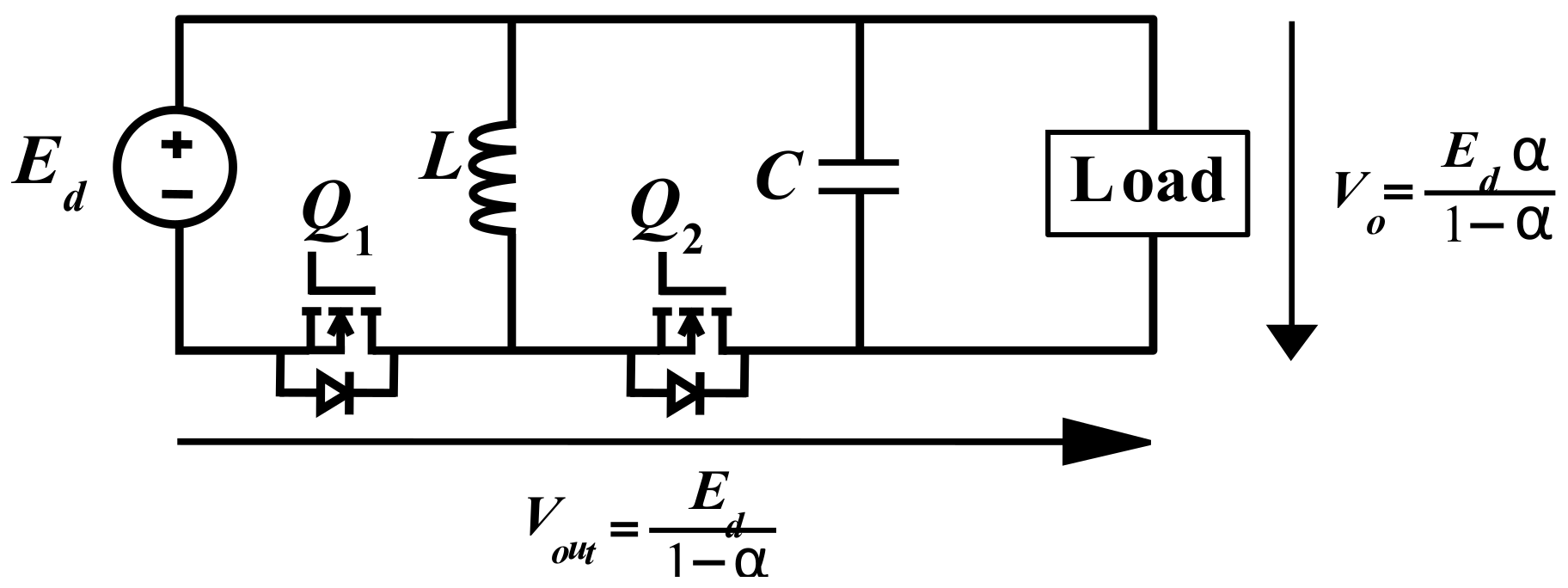
2.1. Modified Buck–Boost DC–DC Converter
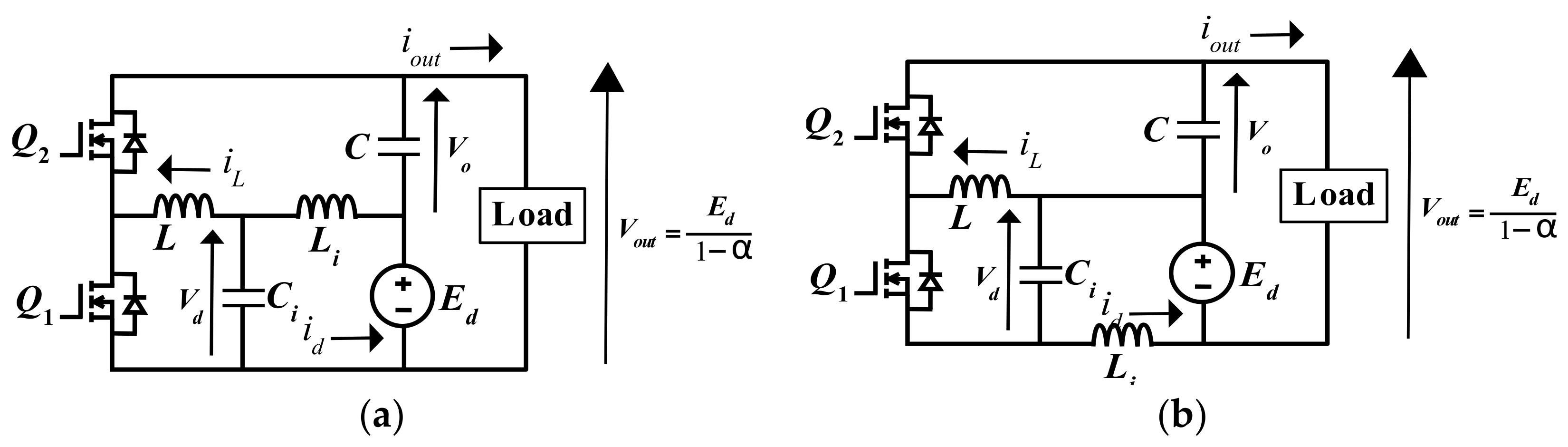
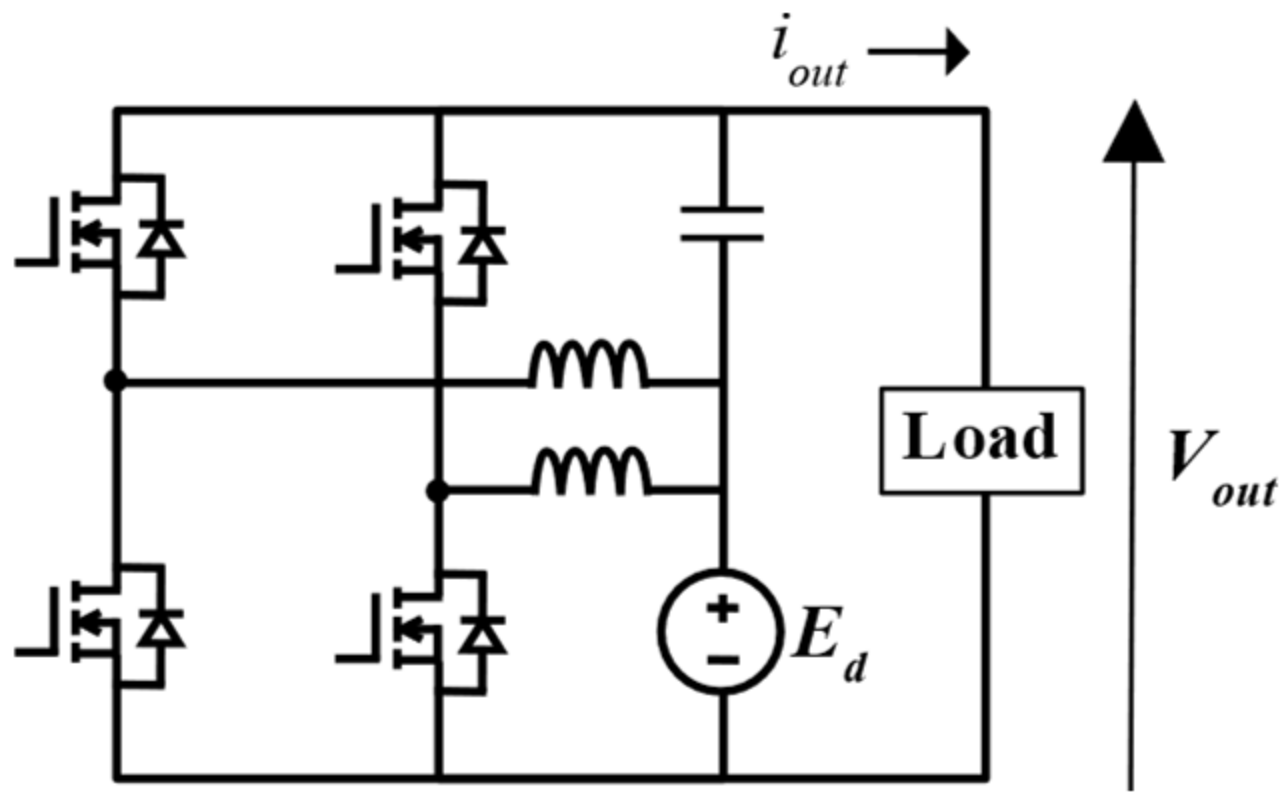
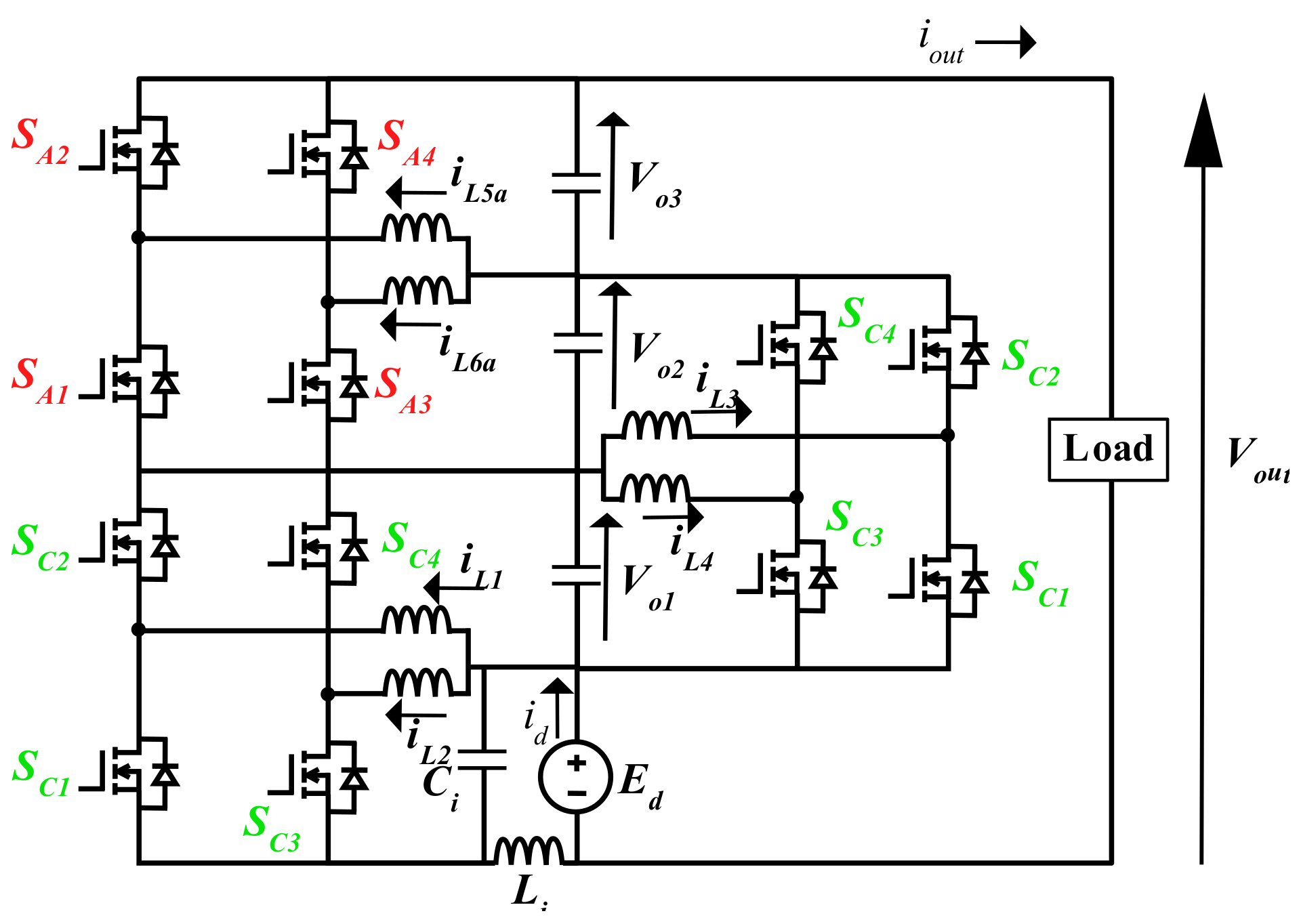
2.2. Modular Multilevel DC–DC Converter
2.3. Operational Mode of Proposed Multilevel DC–DC Converter
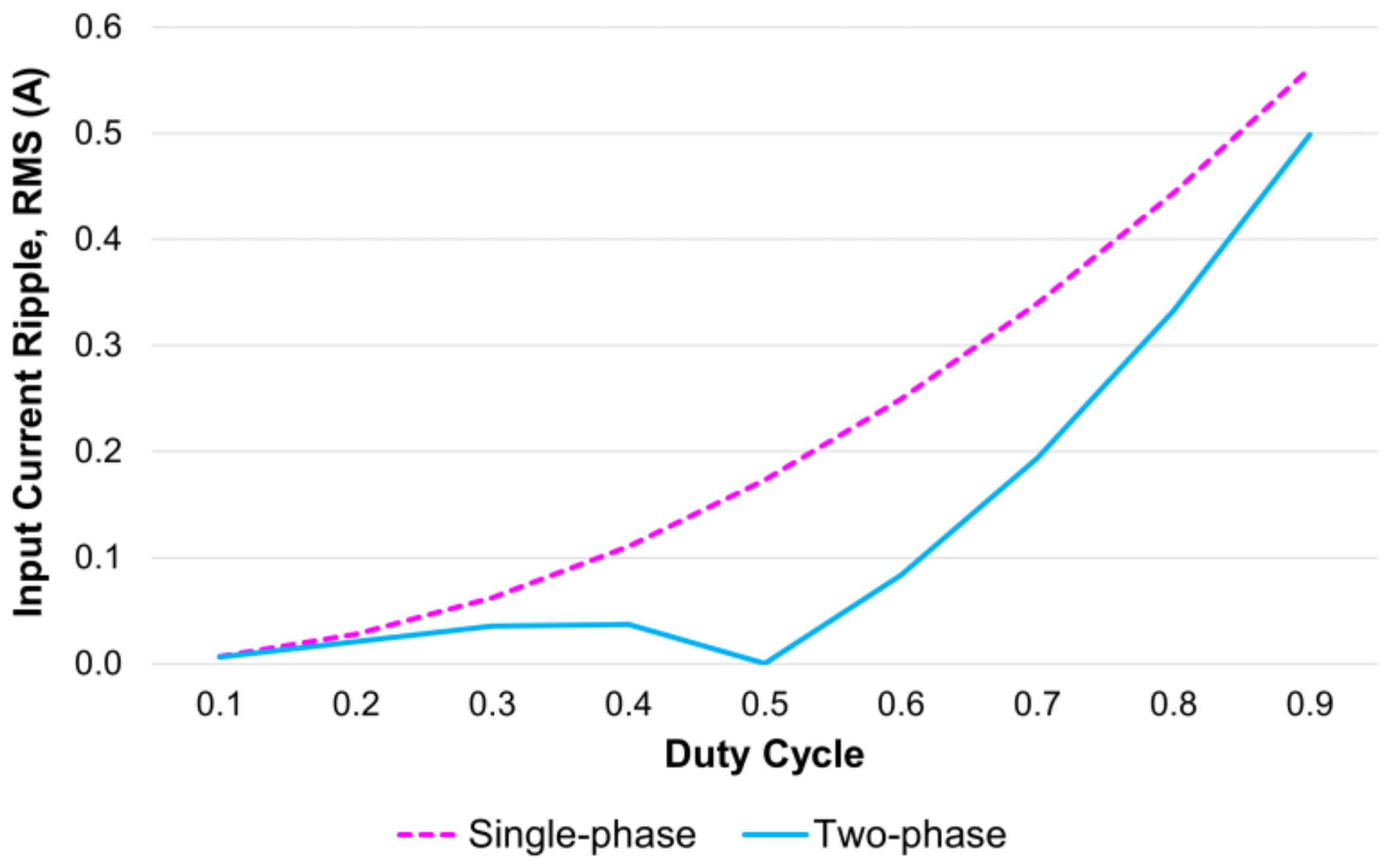
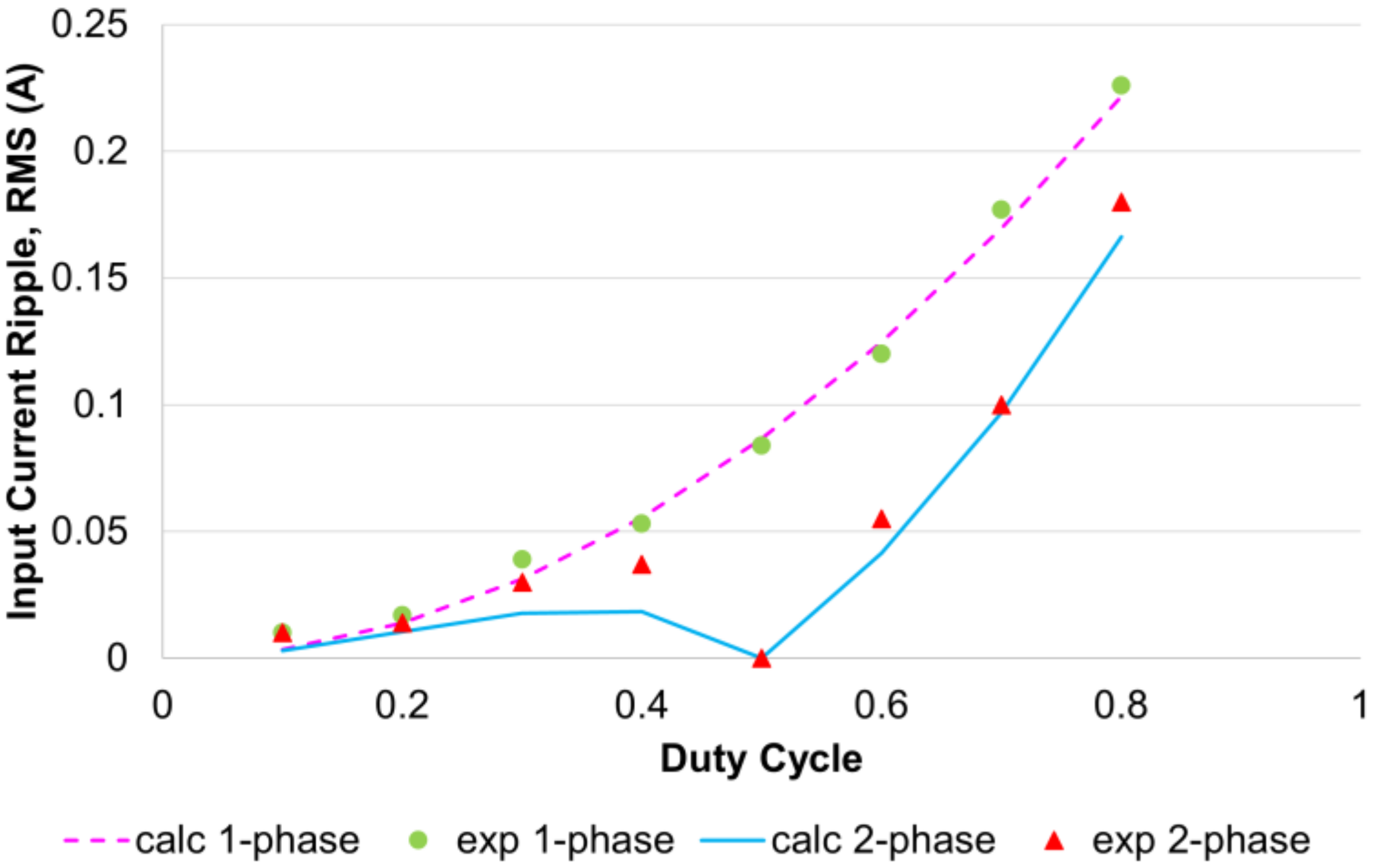
3. Ripple Current and Output Voltage Analysis
3.1. Ripple Current Analysis
3.2. Output Voltage Analysis
3.2.1. Controlling the First Cell
3.2.2. Controlling the Last Cell
3.3. Comparison with Previous Topology
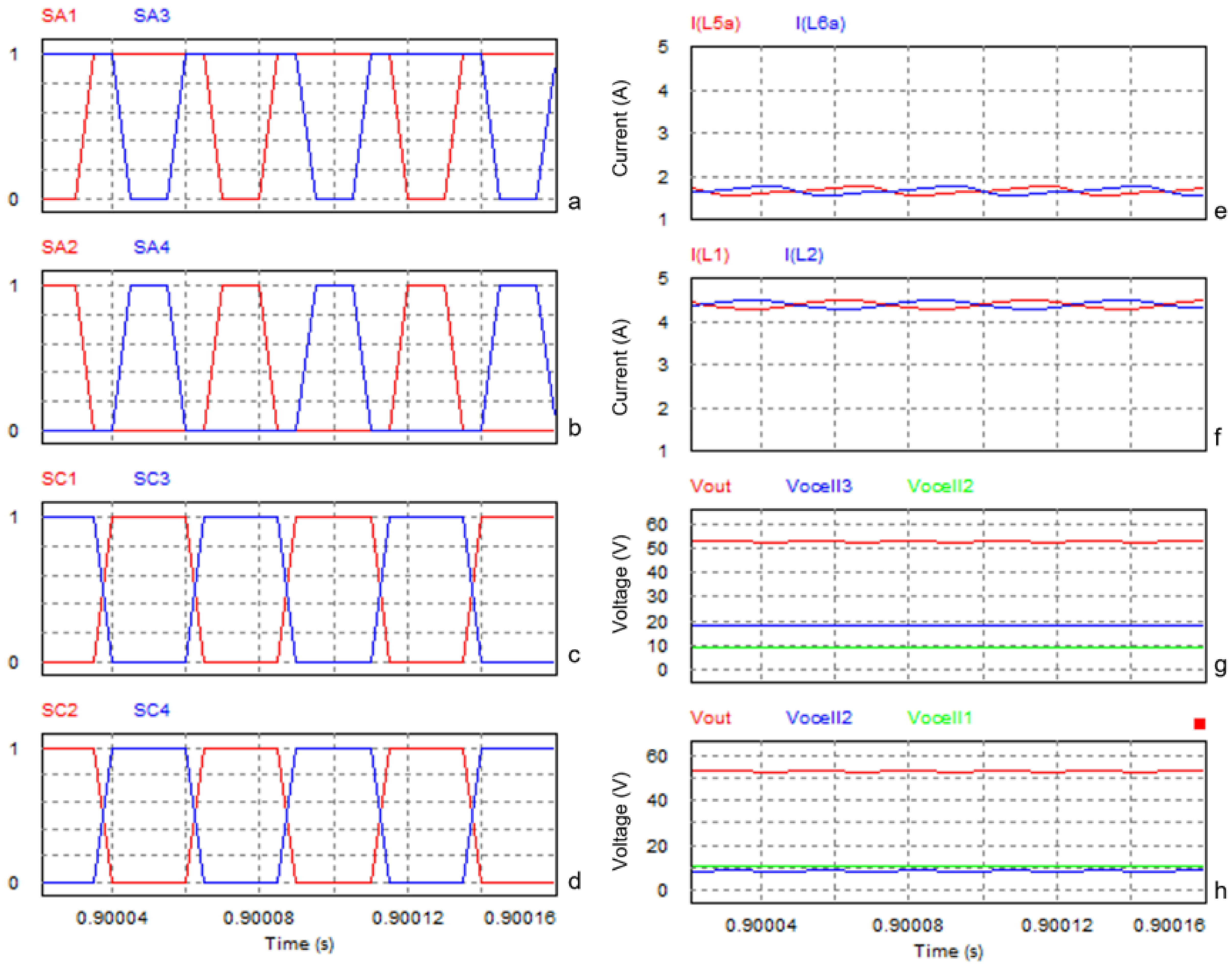
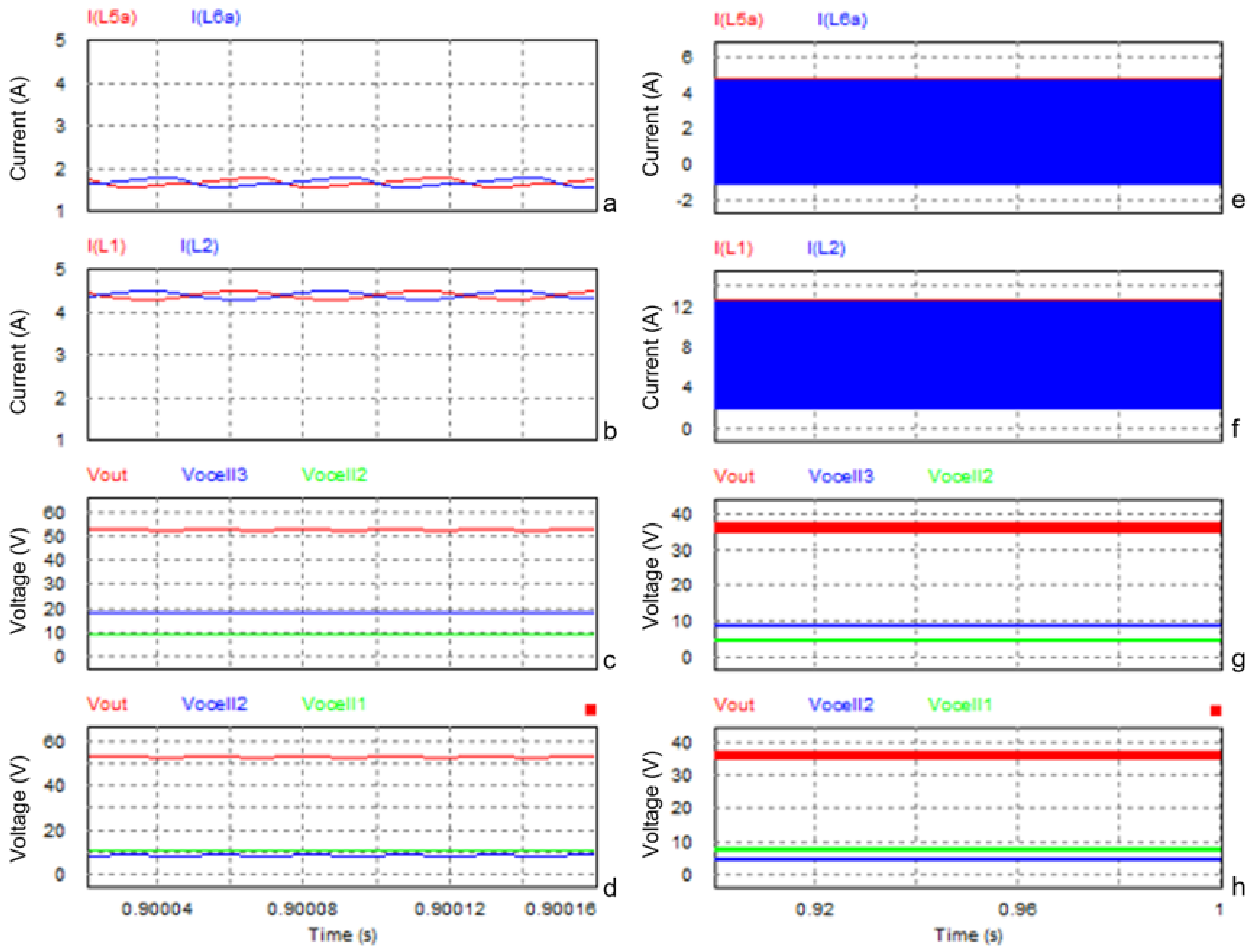
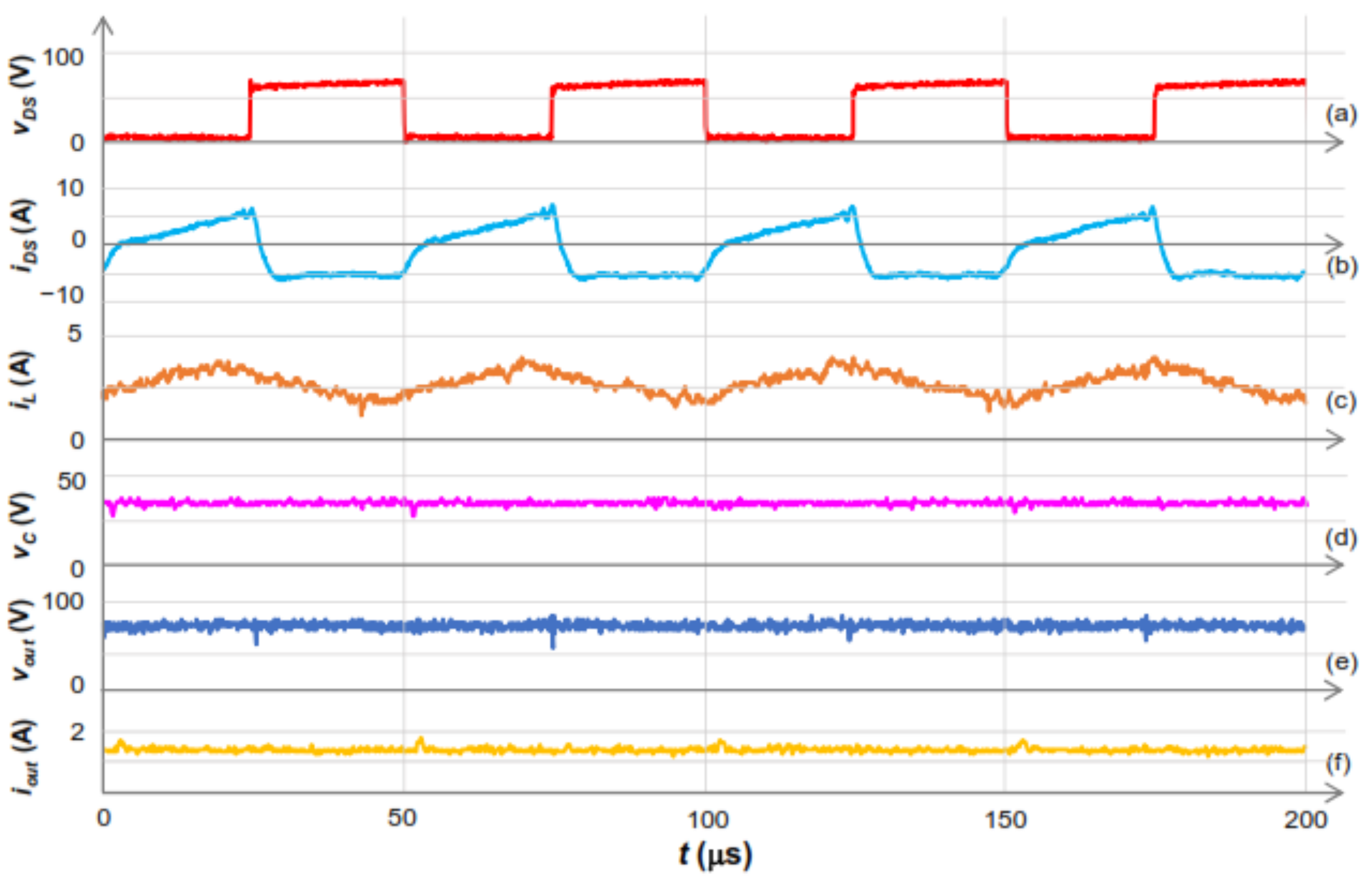
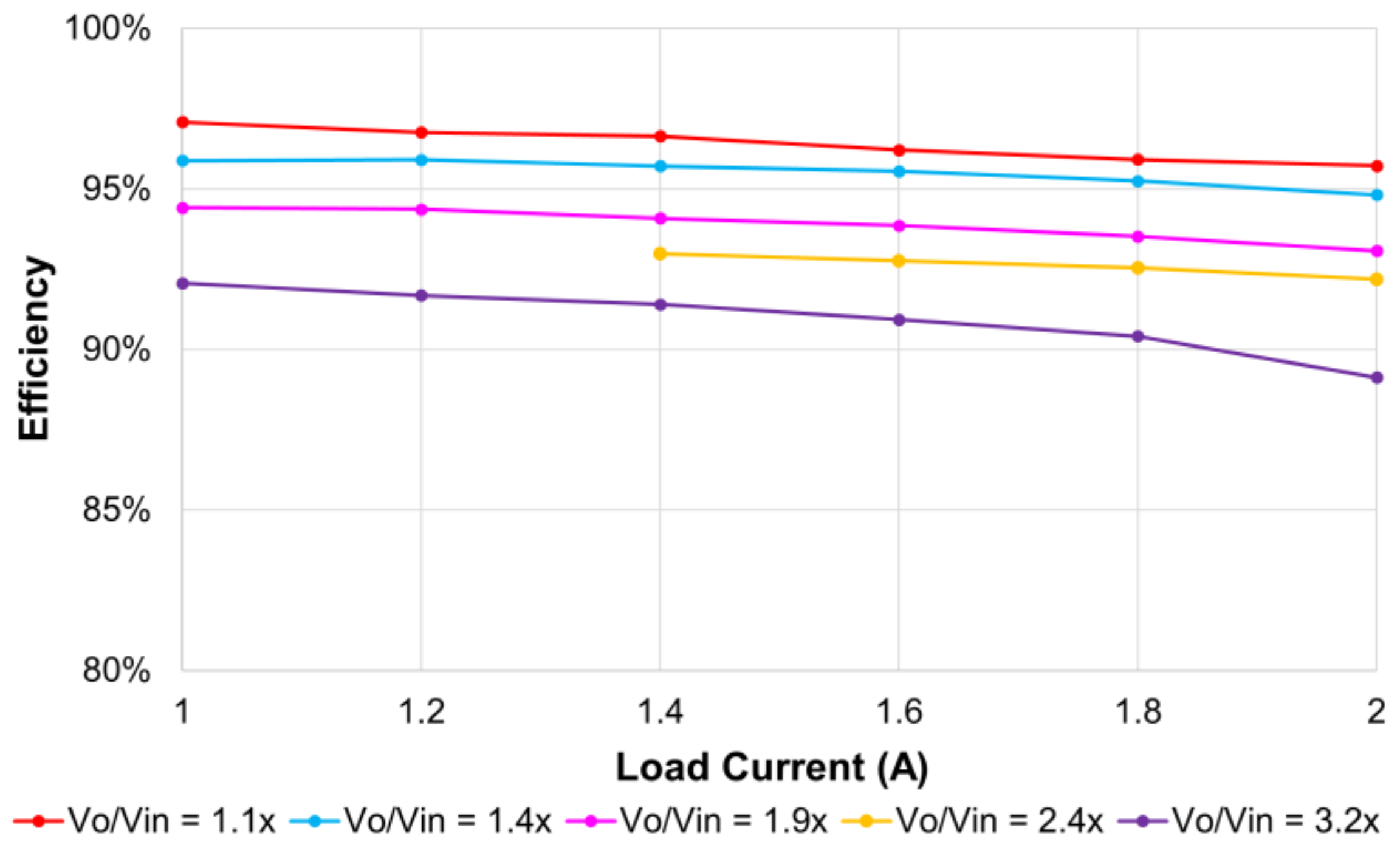
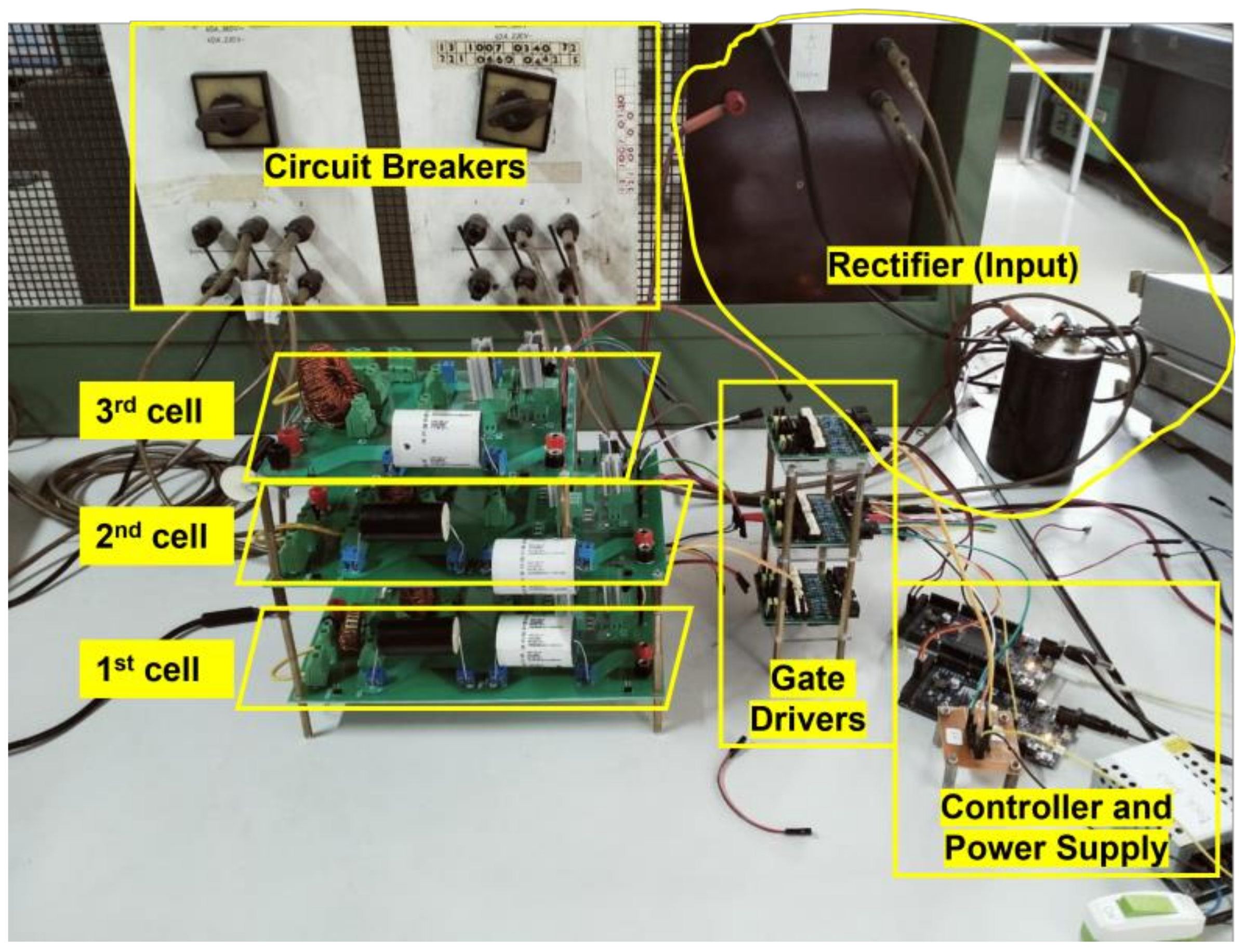
4. Experimental Results
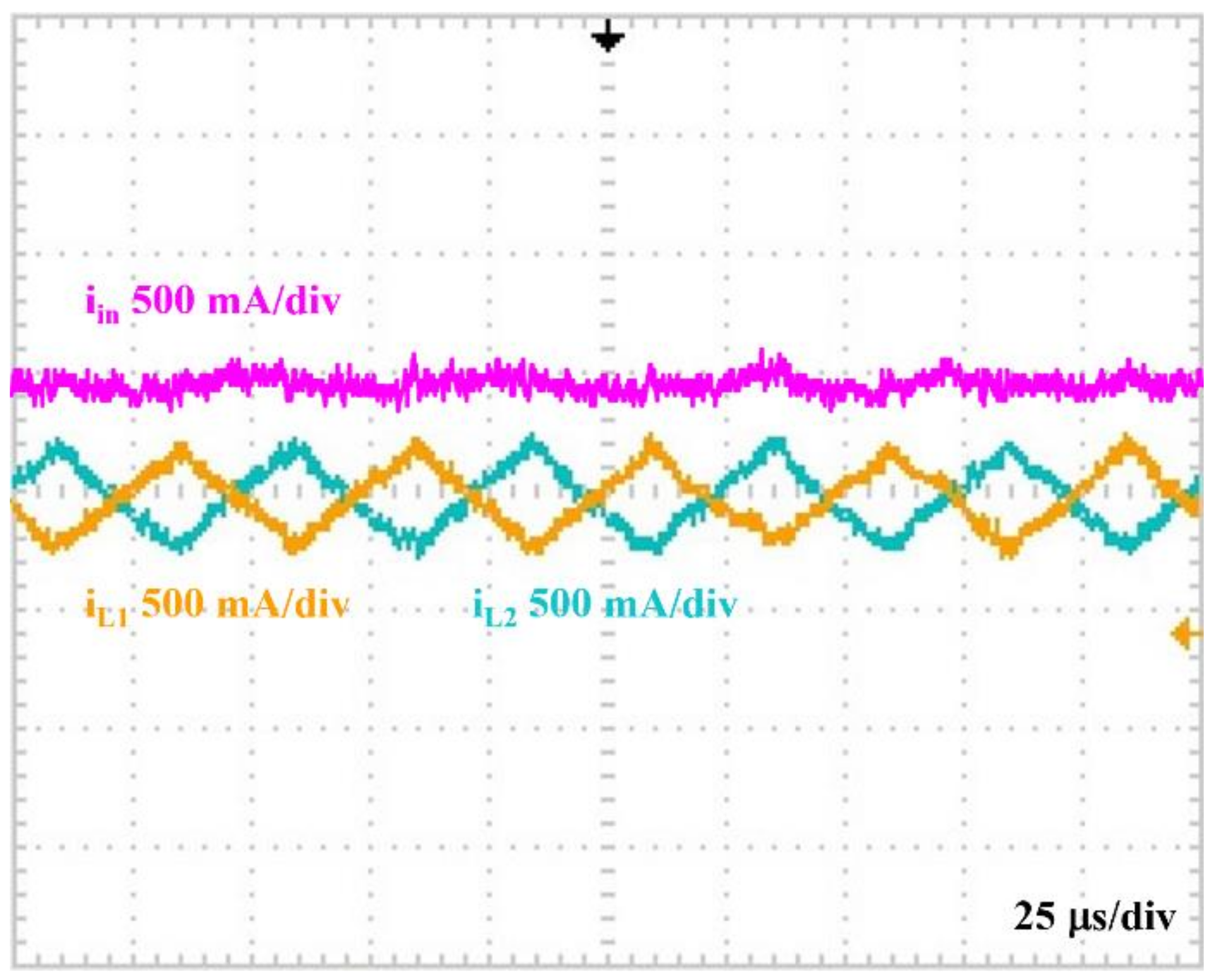
4.1. Ripple Current Verification
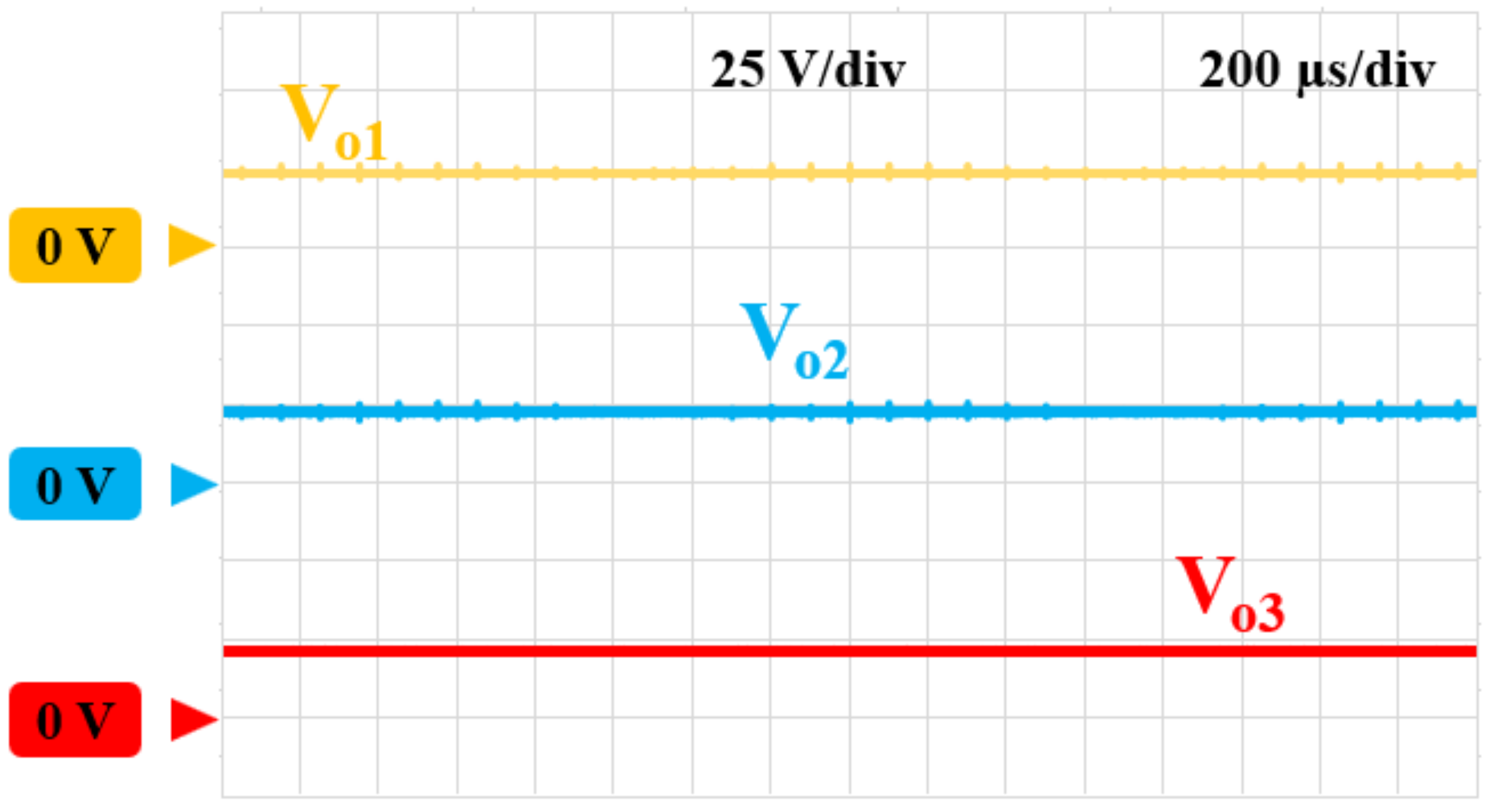
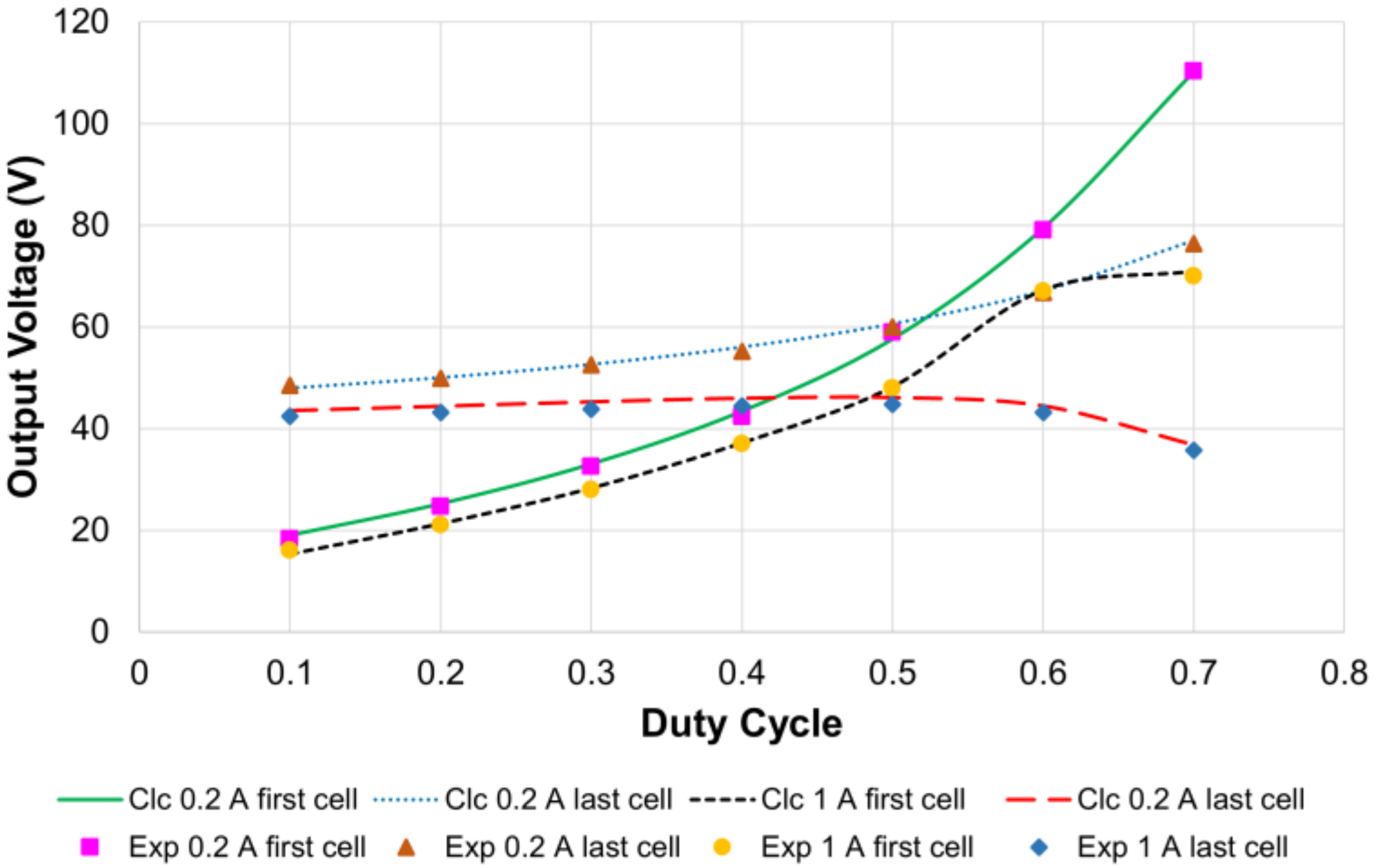
4.2. Output Voltage Verification
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| CCM | Continuous conduction mode |
| DCM | Discontinuous conduction mode |
| ESR | Equivalent series resistance |
| EV | Electric Vehicle |
| HVDC | High Voltage DC |
| PCB | Printed circuit board |
| PV | Photovoltaic |
| RMS | Root mean square |
References
- Debnath, D.; Chatterjee, K. Two-Stage Solar Photovoltaic-Based Stand-Alone Scheme Having Battery as Energy Storage Element for Rural Deployment. IEEE Trans. Ind. Electron. 2015, 62, 4148–4157. [Google Scholar] [CrossRef]
- Wu, H.; Sun, K.; Chen, L.; Zhu, L.; Xing, Y. High Step-Up/Step-Down Soft-Switching Bidirectional DC–DC Converter with Coupled-Inductor and Voltage Matching Control for Energy Storage Systems. IEEE Trans. Ind. Electron. 2016, 63, 2892–2903. [Google Scholar] [CrossRef]
- Mahmood, A.; Zaid, M.; Ahmad, J.; Khan, M.A.; Khan, S.; Sifat, Z.; Lin, C.-H.; Sarwar, A.; Tariq, M.; Alamri, B. A Non-Inverting High Gain DC–DC Converter with Continuous Input Current. IEEE Access 2021, 9, 54710–54721. [Google Scholar] [CrossRef]
- Kim, J.; Kwon, I. Design of a High-Efficiency DC–DC Boost Converter for RF Energy Harvesting IoT Sensors. Sensors 2022, 22, 10007. [Google Scholar] [CrossRef] [PubMed]
- Sharma, R.; Gao, H. Low cost high efficiency DC–DC converter for fuel cell powered auxiliary power unit of a heavy vehicle. IEEE Trans. Power Electron. 2006, 21, 587–591. [Google Scholar] [CrossRef]
- Yang, J.; He, Z.; Pang, H.; Tang, G. The Hybrid-Cascaded DC–DC Converters Suitable for HVdc Applications. IEEE Trans. Power Electron. 2015, 30, 5358–5363. [Google Scholar] [CrossRef]
- Gontijo, G.F.; Wang, S.; Kerekes, T.; Teodorescu, R. Novel Converter Topology With Reduced Cost, Size and Weight for High-Power Medium-Voltage Machine Drives: 3x3 Modular Multilevel Series Converter. IEEE Access 2021, 9, 49082–49097. [Google Scholar] [CrossRef]
- Askarian, I.; Pahlevani, M.; Knight, A.M. Three-Port Bidirectional DC/DC Converter for DC Nanogrids. IEEE Trans. Power Electron. 2021, 36, 8000–8011. [Google Scholar] [CrossRef]
- Palumbo, G.; Pappalardo, D. Charge Pump Circuits: An Overview on Design Strategies and Topologies. IEEE Circuits Syst. Mag. 2010, 10, 31–45. [Google Scholar] [CrossRef]
- Li, S.; Zheng, Y.; Wu, B.; Smedley, K.M. A Family of Resonant Two-Switch Boosting Switched-Capacitor Converter with ZVS Operation and a Wide Line Regulation Range. IEEE Trans. Power Electron. 2018, 33, 448–459. [Google Scholar] [CrossRef]
- Qian, W.; Cao, D.; Cintron-Rivera, J.G.; Gebben, M.; Wey, D.; Peng, F.Z. A Switched-Capacitor DC–DC Converter with High Voltage Gain and Reduced Component Rating and Count. IEEE Trans. Ind. Appl. 2012, 48, 1397–1406. [Google Scholar] [CrossRef]
- Li, S.; Xie, W.; Smedley, K.M. A Family of an Automatic Interleaved Dickson Switched-Capacitor Converter and Its ZVS Resonant Configuration. IEEE Trans. Ind. Electron. 2019, 66, 255–264. [Google Scholar] [CrossRef]
- Xie, H.; Li, R. A Novel Switched-Capacitor Converter with High Voltage Gain. IEEE Access 2019, 7, 107831–107844. [Google Scholar] [CrossRef]
- Nguyen, M.-K.; Duong, T.-D.; Lim, Y.-C. Switched-Capacitor-Based Dual-Switch High-Boost DC–DC Converter. IEEE Trans. Power Electron. 2018, 33, 4181–4189. [Google Scholar] [CrossRef]
- Fardahar, S.M.; Sabahi, M. New Expandable Switched-Capacitor/Switched-Inductor High-Voltage Conversion Ratio Bidirectional DC–DC Converter. IEEE Trans. Power Electron. 2020, 35, 2480–2487. [Google Scholar] [CrossRef]
- Forouzesh, M.; Siwakoti, Y.P.; Gorji, S.A.; Blaabjerg, F.; Lehman, B. Step-Up DC–DC Converters: A Comprehensive Review of Voltage-Boosting Techniques, Topologies, and Applications. IEEE Trans. Power Electron. 2017, 32, 9143–9178. [Google Scholar] [CrossRef]
- Prudente, M.; Pfitscher, L.L.; Emmendoerfer, G.; Romaneli, E.F.; Gules, R. Voltage Multiplier Cells Applied to Non-Isolated DC–DC Converters. IEEE Trans. Power Electron. 2008, 23, 871–887. [Google Scholar] [CrossRef]
- Meraj, M.; Bhaskar, M.S.; Iqbal, A.; Al-Emadi, N.; Rahman, S. Interleaved Multilevel Boost Converter with Minimal Voltage Multiplier Components for High-Voltage Step-Up Applications. IEEE Trans. Power Electron. 2020, 35, 12816–12833. [Google Scholar] [CrossRef]
- Azizkandi, M.E.; Sedaghati, F.; Shayeghi, H.; Blaabjerg, F. A High Voltage Gain DC–DC Converter Based on Three Winding Coupled Inductor and Voltage Multiplier Cell. IEEE Trans. Power Electron. 2020, 35, 4558–4567. [Google Scholar] [CrossRef]
- Barreto, L.H.S.C.; Praca, P.P.; Henn, G.A.L.; Silva, R.N.A.L.; Oliveira, D.S. Single stage high voltage gain boost converter with voltage Multiplier Cells for battery charging using photovoltaic panels. In Proceedings of the 2012 Twenty-Seventh Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Orlando, FL, USA, 5–9 February 2012; pp. 364–368. [Google Scholar] [CrossRef]
- Tofoli, F.L.; De Souza Oliveira, S.; Torrico-Bascopé, R.P.; Alcazar, Y.J.A. Novel Nonisolated High-Voltage Gain DC–DC Converters Based on 3SSC and VMC. IEEE Trans. Power Electron. 2012, 27, 3897–3907. [Google Scholar] [CrossRef]
- Zhu, B.; Wei, Z.; Chen, Y.; Wang, H.; Vilathgamuwa, D.M. Multiple Input-Terminal Voltage Multiplier Circuit. IEEE Trans. Ind. Appl. 2020, 56, 5075–5082. [Google Scholar] [CrossRef]
- Park, K.-B.; Moon, G.-W.; Youn, M.-J. Nonisolated High Step-Up Stacked Converter Based on Boost-Integrated Isolated Converter. IEEE Trans. Power Electron. 2011, 26, 577–587. [Google Scholar] [CrossRef]
- Lu, Y.; Liu, H.; Hu, H.; Wu, H.; Xing, Y. Single-switch high step-up converter with coupled-inductor and built-in transformer. In Proceedings of the 2015 IEEE 10th Conference on Industrial Electronics and Applications (ICIEA), Auckland, New Zealand, 15–17 June 2015; pp. 1181–1186. [Google Scholar] [CrossRef]
- Li, F.; Liu, H. A Cascaded Coupled Inductor-Reverse High Step-Up Converter Integrating Three-Winding Coupled Inductor and Diode–Capacitor Technique. IEEE Trans. Ind. Informatics 2017, 13, 1121–1130. [Google Scholar] [CrossRef]
- Wu, H.; Lu, J.; Shi, W.; Xing, Y. Nonisolated Bidirectional DC–DC Converters with Negative-Coupled Inductor. IEEE Trans. Power Electron. 2012, 27, 2231–2235. [Google Scholar] [CrossRef]
- Chen, S.-M.; Lao, M.-L.; Hsieh, Y.-H.; Liang, T.-J.; Chen, K.-H. A Novel Switched-Coupled-Inductor DC–DC Step-Up Converter and Its Derivatives. IEEE Trans. Ind. Appl. 2015, 51, 309–314. [Google Scholar] [CrossRef]
- Liu, H.; Hu, H.; Wu, H.; Xing, Y.; Batarseh, I. Overview of High-Step-Up Coupled-Inductor Boost Converters. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 689–704. [Google Scholar] [CrossRef]
- Chen, S.-M.; Liang, T.-J.; Yang, L.-S.; Chen, J.-F. A Cascaded High Step-Up DC–DC Converter with Single Switch for Microsource Applications. IEEE Trans. Power Electron. 2011, 26, 1146–1153. [Google Scholar] [CrossRef]
- Sulthon, M.; Damanik, O.A.; Efraim; Rizqiawan, A.; Dahono, P.A. A new simplified cascaded boost converter for high ratio and low ripple application. In Proceedings of the 2017 4th International Conference on Electric Vehicular Technology (ICEVT), Bali, Indonesia, 2–5 October 2017; pp. 117–124. [Google Scholar] [CrossRef]
- Ai, J.; Lin, M.; Yin, M. A Family of High Step-Up Cascade DC–DC Converters with Clamped Circuits. IEEE Trans. Power Electron. 2020, 35, 4819–4834. [Google Scholar] [CrossRef]
- Hu, X.; Liu, X.; Zhang, Y.; Yu, Z.; Jiang, S. A Hybrid Cascaded High Step-Up DC–DC Converter with Ultralow Voltage Stress. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 1824–1836. [Google Scholar] [CrossRef]
- Kasper, M.; Bortis, D.; Kolar, J.W. Novel high voltage conversion ratio “Rainstick” DC/DC converters. In Proceedings of the 2013 IEEE Energy Conversion Congress and Exposition, Denver, CO, USA, 15–19 September 2013; pp. 789–796. [Google Scholar] [CrossRef]
- Elserougi, A.; Abdelsalam, I.; Massoud, A.; Ahmed, S. A modular multilevel DC–DC converter with self-energy equalization for DC grids. IET Renew. Power Gener. 2021, 15, 1736–1747. [Google Scholar] [CrossRef]
- Zhang, X.; Green, T.C. The Modular Multilevel Converter for High Step-Up Ratio DC–DC Conversion. IEEE Trans. Ind. Electron. 2015, 62, 4925–4936. [Google Scholar] [CrossRef]
- Elserougi, A.A.; Massoud, A.M.; Abdelsalam, I.A.; Ahmed, S. A Self-Balanced Bidirectional Medium-/High-Voltage Hybrid Modular DC–DC Converter with Low-Voltage Common DC-Link and Sequential Charging/Discharging of Submodules Capacitors. IEEE Trans. Ind. Electron. 2019, 66, 2714–2725. [Google Scholar] [CrossRef]
- Elserougi, A.; Abdelsalam, I.; Massoud, A.; Ahmed, S. Modular multilevel DC–DC converter with arm interchange concept. IET Gener. Transm. Distrib. 2020, 14, 564–576. [Google Scholar] [CrossRef]
- Peng, F.Z.; Zhang, F.; Qian, Z. A magnetic-less DC–DC converter for dual-voltage automotive systems. IEEE Trans. Ind. Appl. 2003, 39, 511–518. [Google Scholar] [CrossRef]
- Costa, L.F.; Mussa, S.A.; Barbi, I. Multilevel Buck/Boost-Type DC–DC Converter for High-Power and High-Voltage Application. IEEE Trans. Ind. Appl. 2014, 50, 3931–3942. [Google Scholar] [CrossRef]
- Gandomkar, A.; Parastar, A.; Seok, J.-K. High-Power Multilevel Step-Up DC/DC Converter for Offshore Wind Energy Systems. IEEE Trans. Ind. Electron. 2016, 63, 7574–7585. [Google Scholar] [CrossRef]
- You, H.; Cai, X. Stepped Two-Level Operation of Nonisolated Modular DC/DC Converter Applied in High-Voltage DC Grid. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 1540–1552. [Google Scholar] [CrossRef]
- Lai, J.-S.; Peng, F.Z. Multilevel converters–A new breed of power converters. IEEE Trans. Ind. Appl. 1996, 32, 509–517. [Google Scholar] [CrossRef]
- Aditama, R.D.N.; Ramadhani, N.; Furqani, J.; Rizqiawan, A.; Dahono, P.A. New bidirectional step-up DC–DC converter derived from buck- boost DC–DC converter. Int. J. Power Electron. Drive Syst. 2021, 12, 1699–1707. [Google Scholar] [CrossRef]
- Dahono, P.A.; Dahono, A. A Family of Modular Multilevel Bidirectional DC–DC Converters for High Voltage-Ratio and Low-Ripple Applications. In Proceedings of the 2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 11–15 October 2020; pp. 3934–3940. [Google Scholar] [CrossRef]
- Kazimiercuk, M. Pulse Width Modulated DC–DC Power Converters; Wiley: Chichester, UK, 2008. [Google Scholar]
- Dahono, P.; Riyadi, S.; Mudawari, A.; Haroen, Y. Output ripple analysis of multiphase DC–DC converters. In Proceedings of the IEEE 1999 International Conference on Power Electronics and Drive Systems, PEDS’99 (Cat. No.99TH8475). Hong Kong, China, 27–29 July 1999; Volume 2, pp. 626–631. [Google Scholar] [CrossRef]



| Components | Value | Unit |
|---|---|---|
| Inductors | 1 | mH |
| Capacitors | 30 | µF |
| Filter inductor | 46 | µH |
| Filter capacitor | 10 | µF |
| ESR of inductors | 0.3 | Ω |
| MOSFET On-resistance | 0.04 | Ω |
| Topology | Application | No. of Components | Bidirectional | Voltage Gain | Current Ripple |
|---|---|---|---|---|---|
| [12] | Auxiliary power supplies | 2N switches 2(N − 1) diodes 2(N − 1) capacitors | No | N(2N) for even N(2N + 1) for odd | Moderate |
| [13] | High-voltage-gain application | N × M + (2N − 2) switches N × M capacitors | No | (N − 1) M + 1 N = number of cap. in each stage M = number of stages | High |
| [18] | DC Link, hybrid PV systems | 2 switches 2 inductors N capacitors N diodes | No | Zero | |
| [25] | High step-up applications | 1 switch 5 diodes 4 inductors (3-coupled) 4 capacitors | No | . n2 = turns ratio inductor 2 n3 = turns ratio inductor 3 | Moderate |
| [32] | Grid-connected PV/fuel cell systems | 2 switches 6 diodes 2 coupled inductors 6 capacitors | No | Zero | |
| [44] | DC microgrid | 2N switches 2N inductors 2N capacitors | Yes | Low | |
| Proposed | DC microgrid, distributed generation | 4N switches 2N inductors 2N capacitors | Yes | Zero |
| No | Parameter | Value |
|---|---|---|
| 1 | MOSFET type | IRFP260N |
| 2 | Li | 47.8 μH |
| 3 | Ci | 10 μF, film capacitor |
| 4 | L | 1 mH, ensures CCM |
| 5 | C | 30 μF, film capacitor |
| 6 | fs | 20 kHz |
| 7 | Ed | 24 VDC |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aditama, R.D.N.; Ramadhani, N.; Ardriani, T.; Furqani, J.; Rizqiawan, A.; Dahono, P.A. New Modular Multilevel DC–DC Converter Derived from Modified Buck–Boost DC–DC Converter. Energies 2023, 16, 6950. https://doi.org/10.3390/en16196950
Aditama RDN, Ramadhani N, Ardriani T, Furqani J, Rizqiawan A, Dahono PA. New Modular Multilevel DC–DC Converter Derived from Modified Buck–Boost DC–DC Converter. Energies. 2023; 16(19):6950. https://doi.org/10.3390/en16196950
Chicago/Turabian StyleAditama, Ridha D. N., Naqita Ramadhani, Tri Ardriani, Jihad Furqani, Arwindra Rizqiawan, and Pekik Argo Dahono. 2023. "New Modular Multilevel DC–DC Converter Derived from Modified Buck–Boost DC–DC Converter" Energies 16, no. 19: 6950. https://doi.org/10.3390/en16196950
APA StyleAditama, R. D. N., Ramadhani, N., Ardriani, T., Furqani, J., Rizqiawan, A., & Dahono, P. A. (2023). New Modular Multilevel DC–DC Converter Derived from Modified Buck–Boost DC–DC Converter. Energies, 16(19), 6950. https://doi.org/10.3390/en16196950







