Investigation of the Performance of Thermodynamic Analysis Models for a Cryocooler PPG-102 Stirling Engine
Abstract
:1. Introduction
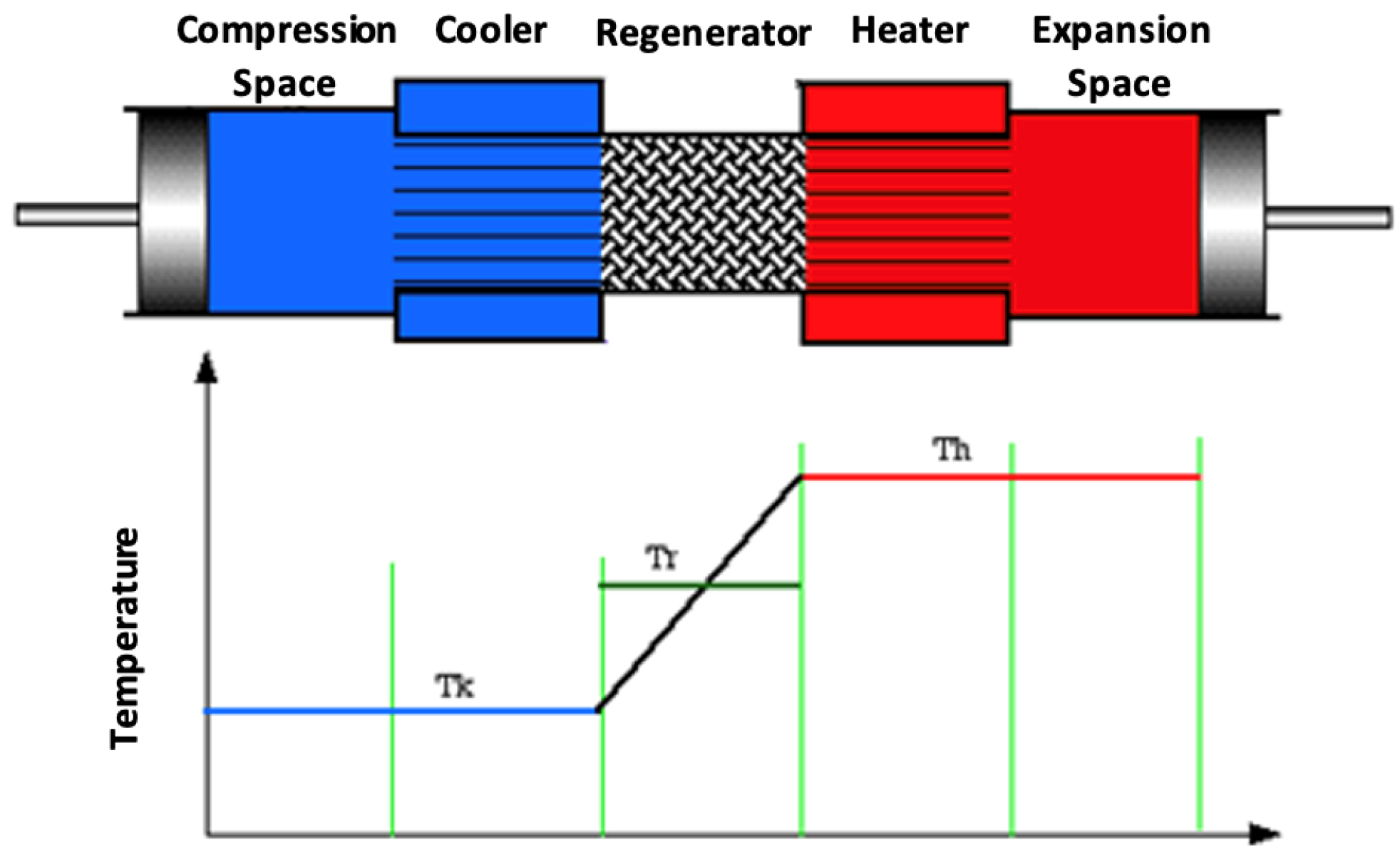
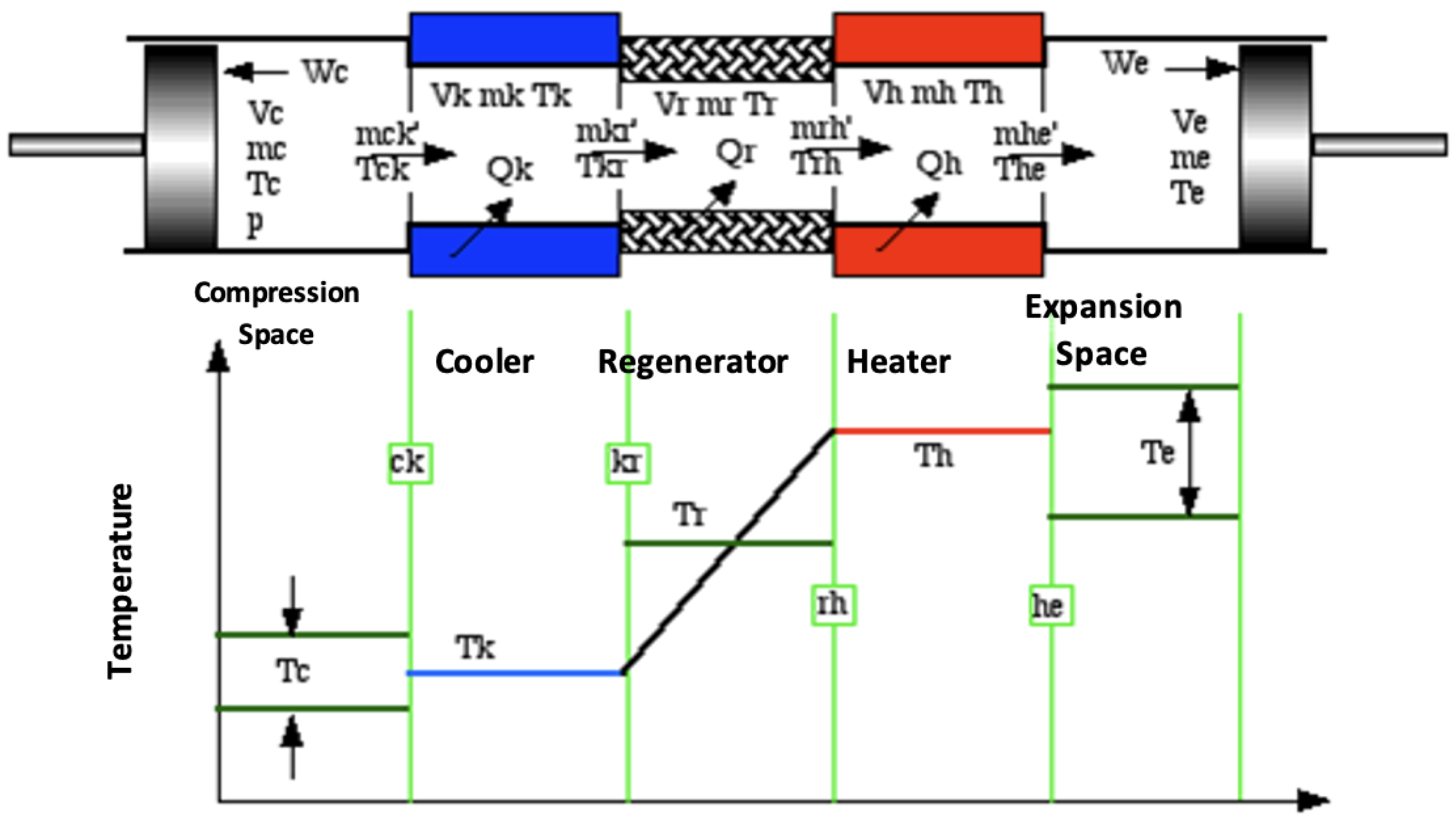
2. Thermodynamic Analysis Models
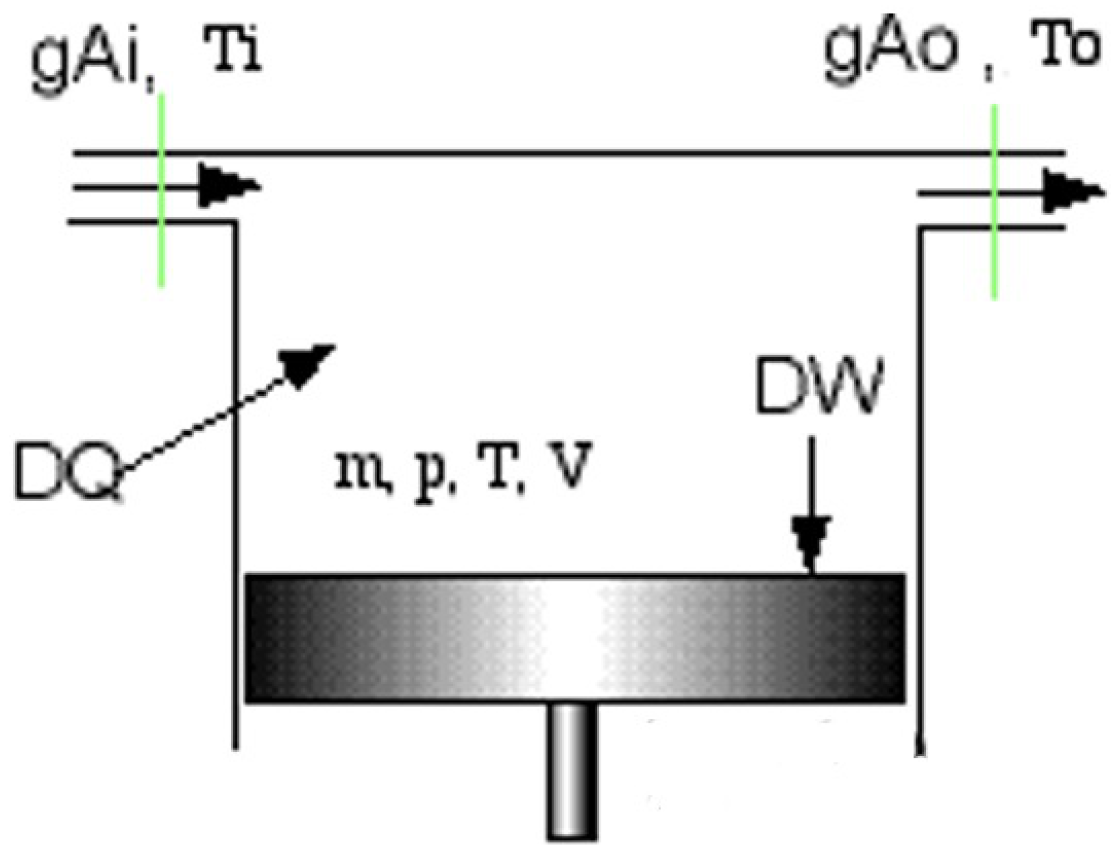
2.1. Isothermal Analysis
- The mass of the working fluid is constant, meaning there are no losses.
- The ideal gas equation holds true.
- The speed (frequency) of the engine is constant.
- Cyclical thermodynamic variation.
- The kinetic and dynamic energy of the gases is neglected.
2.2. Schmidt Analysis
2.3. Adiabatic Analysis
3. PPG-102 Cryocooler
4. Results of Thermodynamic Analysis Models
4.1. Isothermal Analysis Results
4.2. Schmidt Analysis Results
4.3. Adiabatic Analysis Results
4.4. Comparison of Computational Results of Thermodynamic Analysis
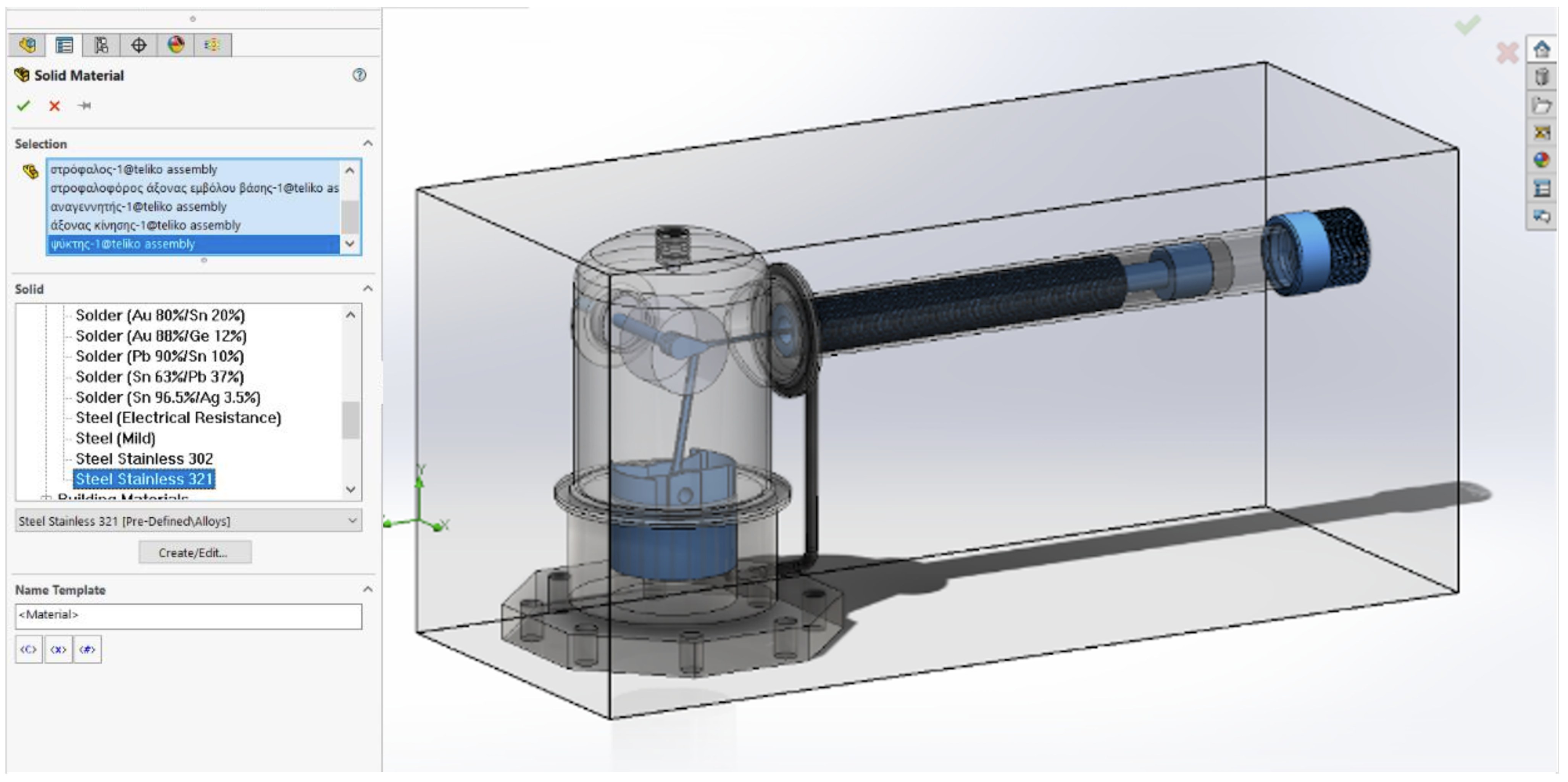
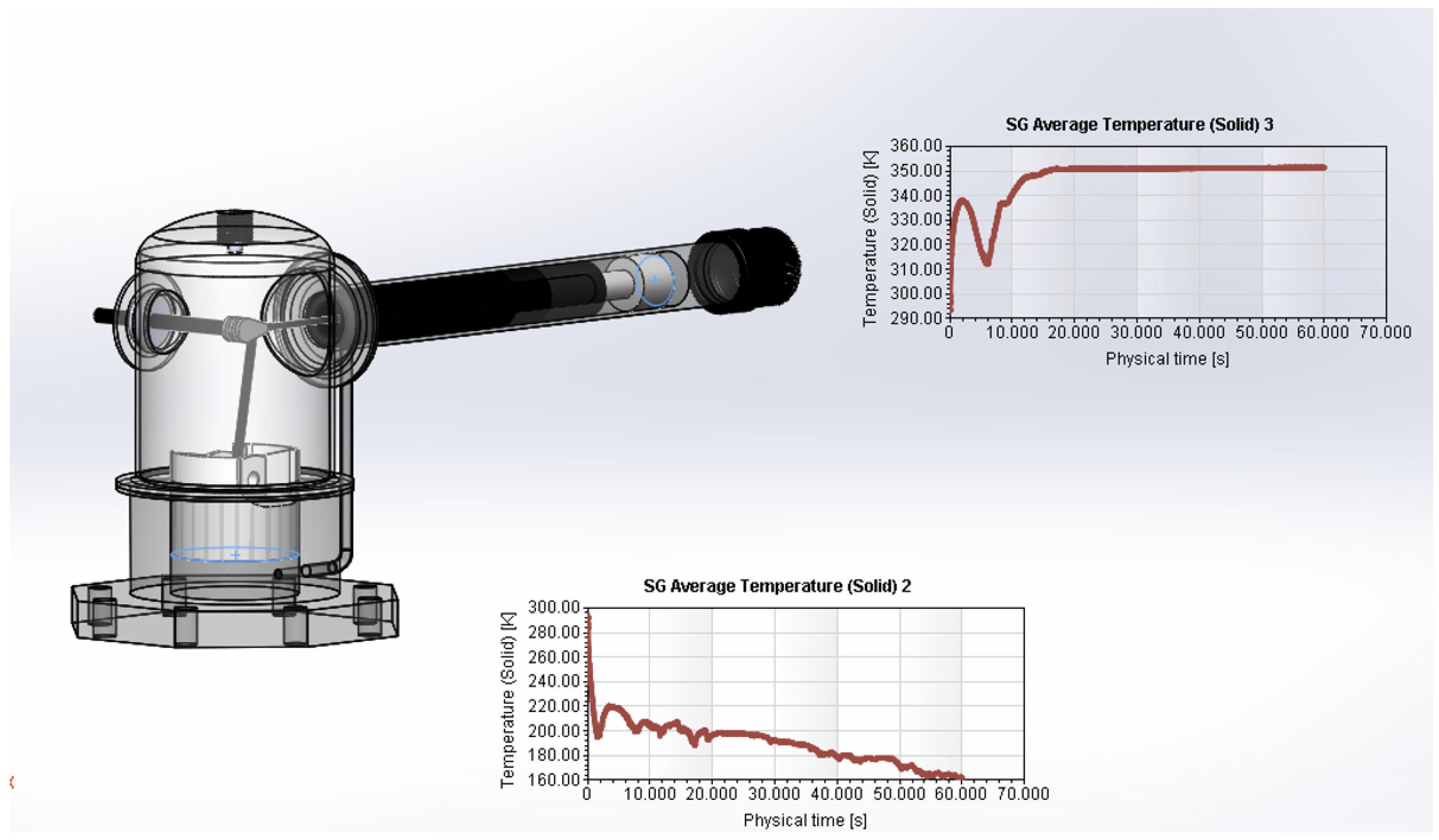
5. Thermal Behavior Simulation of the PPG-102 Thermal Performance in Solidworks Environment
- Power piston and cylinder;
- Displacer and crankshaft with a phase angle of 90 degrees;
- Regenerator;
- Piston housings (base and cylinder);
- External engine casing;
- Cooler;
- Power delivery system;
- Engine supports.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| mass flow rate () | |
| T | working gas temperature (K) |
| Q | heat rate (W) |
| W | work () |
| consumed work by the displacer piston per cycle () | |
| P | power output (W) |
| M | working gas total mass () |
Appendix A
| General | |
|---|---|
| Machine Type (Configuration) | B |
| Number of Cylinders | 1 |
| Piston Drive Mechanism | Philips-crankshaft |
| Working Fluid | Helium |
| Mass of He | g |
| Mean Pressure | bar |
| Frequency | Hz |
| Mean Phase Difference between Pistons | |
| Active Exhaust Space Temperature | K |
| Cold Metal Temperature | K |
| Exhaust Temperature Difference | K |
| Active Compression Space Temperature | K |
| Cooling Water Temperature | K |
| Compression Temperature Difference | K |
| Displacement Volume of Compression | cc |
| Displacement Volume of Exhaust | cc |
| Swept Volume in Compression | cc |
| Swept Volume in Exhaust | cc |
| Maximum “Dead” Volume | cm |
| Minimum “Dead” Volume | cm |
| Cooler Volume | cc |
| - Regenerator Volume | = 379.463 cc |
| - Condenser Volume | = 12.668 cc |
| - Cylinder Diameter | 7.00 cm |
| - Displacer Clearance Diameter | 0.500 cm |
| - Clearance at End of Piston | 0.050 cm |
| - Clearance at End of Displacer | 0.050 cm |
| - Clearance Gap of Exhaust Cover | 0.040 cm |
| - Length of Exhaust Cover | 10.000 cm |
| - Clearance Volume of Exhaust Cylinder | 1.924 cc |
| - Clearance Volume of Compression Cylinder | 1.924 cc |
| - Bugger Factor | 1.000 |
| - Cold Water Flow Rate | 1.000 L/s |
| - Thermal Conductivity of Metal | 0.010 W/m·K |
| - Mechanical Efficiency | 70% |
| - Thickness of Exhaust Cylinder Wall | 0.250 cm |
| - Thickness of Exhaust Cover Wall | 0.250 cm |
| - Thickness of Regenerator Protective Cover | 0.250 cm |
| - Internal Diameter of Cooler Tubes | 0.160 cm |
| - Length of Cooler Tubes | 10.00 cm |
| - Length of Heat Transfer | 10.00 cm |
| - Number of Cooler Tubes per Cylinder | 200 |
| - External Diameter of Regenerator | 12.700 cm |
| - Internal Diameter of Regenerator | 7.620 cm |
| - Length of Regenerator | 7.620 cm |
| - Number of Regenerators per Cylinder | 1 |
| - Diameter of Wire Mesh | 0.008 cm |
| - Void Fraction | 0.400 |
| - Surface Area per Unit Volume | 179.000 cm/cm |
| - Weave Density (Threads per cm) | 63.662 |
| - Internal Diameter of Freezer Tubes | 0.100 cm |
| - Length of Freezer Tubes | 7.600 cm |
| - Length of Heat Transfer | 7.600 cm |
| - Number of Freezer Tubes per Cylinder | 180 |
| - Length of Connecting Displacer | 15.000 cm |
| Length of Pulley | 2.650 cm |
3D Schematics


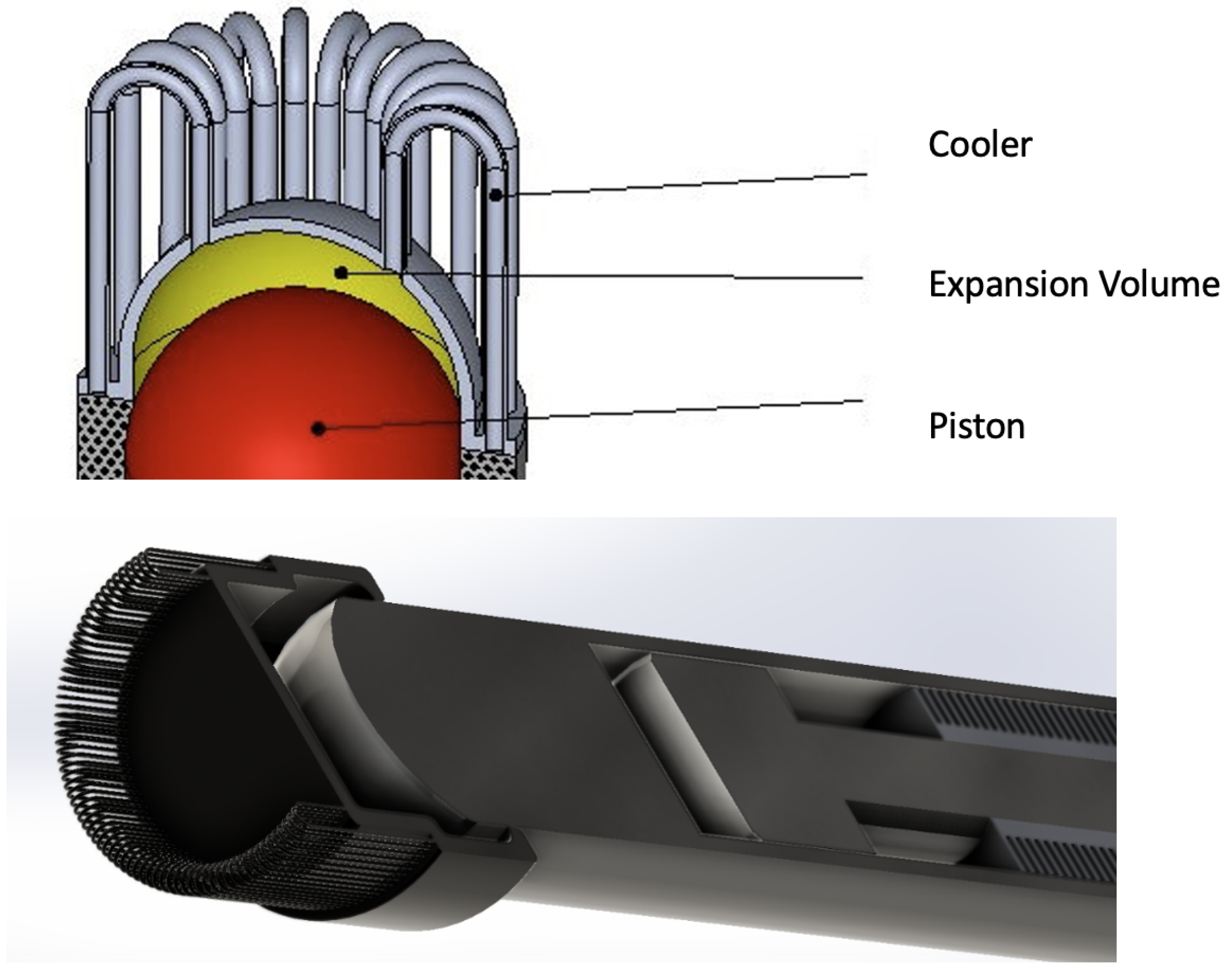

References
- Walker, G. Cryocoolers; Springer: New York, NY, USA, 1990. [Google Scholar]
- Chen, N.C.; Griffin, F.P. Review of Stirling-Engine Mathematical Models; Oak Ridge National Lab. (ORNL): Oak Ridge, TN, USA, 1983. [CrossRef]
- Kongtragool, B.; Wongwises, S. A review of solar-powered Stirling engines and low temperature differential Stirling engines. Renew. Sustain. Energy Rev. 2003, 7, 131–154. [Google Scholar] [CrossRef]
- Collins, S.C.; Cannaday, R.L. Expansion Machines for Low Temperature Processes; Oxford University Press: London, UK, 1958. [Google Scholar]
- Martini, W. Stirling Engine Design Manual; Technical Report; NASA National Technical Information Services, US Department of Commerce: Spring Field, VA, USA, 1978.
- Martini, W. A non-proprietary nonsecret program for calculating Stirling cryocoolers. In Proceedings of the Third Cryocooler Conference, Boulder, CO, USA, 17–18 September 1984; NBS Spec. Pub 698. NTIS: Springfield, VA, USA, 1984. [Google Scholar]
- Walker, G.; Weiss, M.; Fauvel, R.; Reader, G. Microcomputer simulation of Stirling cryocoolers. Cryogenics 1989, 29, 846–849. [Google Scholar] [CrossRef]
- Atrey, M.D.; Bapat, S.; Narayankhedkar, K. Cyclic simulation of Stirling cryocoolers. Cryogenics 1990, 30, 341–347. [Google Scholar] [CrossRef]
- Li, R.; Grosu, L. Parameter effect analysis for a Stirling cryocooler. Int. J. Refrig. 2017, 80, 92–105. [Google Scholar] [CrossRef]
- Rogdakis, E.D.; Borbilas, N.A. Second Law Analysis of a Stirling Cryocooler with Optimal Design of the Regenerator and Losses. In Proceedings of the IMCE ASME International Mechanical Engineering Congress and Exposition, New York, NY, USA, 11–16 November 2001. [Google Scholar]
- Urieli, I.; Berchowitz, D. Stirling Cycle Engine Analysis; Adam Hilger Ltd.: Bristol, UK, 1984. [Google Scholar]
- Schmidt, G. The theory of Lehmann’s Calorimetric Machine. Z. Ver. Dtsch. Ing. 1871, 15, 98–112. [Google Scholar]
- Domenikos, G.R.; Bitsikas, P.; Rogdakis, E. Thermodynamic Modelling of Superfluid Stirling Cryocoolers. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Salt Lake City, UT, USA, 11–14 November 2019; American Society of Mechanical Engineers: New York, NY, USA, 2019; Volume 59438, p. V006T06A069. [Google Scholar]
- Rogdakis, E.; Bitsikas, P.; Dogkas, G.; Antonakos, G. Three-dimensional CFD study of a β-type Stirling Engine. Therm. Sci. Eng. Prog. 2019, 11, 302–316. [Google Scholar] [CrossRef]
- Bitsikas, P.; Rogdakis, E.; Dogkas, G. CFD study of heat transfer in Stirling engine regenerator. Therm. Sci. Eng. Prog. 2020, 17, 100492. [Google Scholar] [CrossRef]
- Domenikos, G.R.; Bitsikas, P.; Rogdakis, E. Computational Analysis of Cryogenic Stirling Refrigerator. In Proceedings of the ASME 2019 International Mechanical Engineering Congress and Exposition, Salt Lake City, UT, USA, 11–14 November 2019; American Society of Mechanical Engineers Digital Collection: Lawrence, KS, USA. [Google Scholar]
- Domenikos, G.R.; Rogdakis, E.; Koronaki, I. Computational Analysis, Three-Dimensional Simulation, and Optimization of Superfluid Stirling Cryocooler. J. Energy Resour. Technol. 2023, 145, 111701. [Google Scholar] [CrossRef]
- Amundsen, T.; Furuseth, O.; Sovik, R. The lattice thermal conductivity of aluminium at low temperatures (and dilute aluminium-copper alloys). J. Phys. F Met. Phys. 1977, 7, L159. [Google Scholar] [CrossRef]
- Domenikos, G.; Rogdakis, E.; Koronaki, I. Continuous equation of state and thermodynamic maps for cryogenic helium 4. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Virtual, 1–5 November 2021; American Society of Mechanical Engineers: New York, NY, USA, 2021; Volume 85642, p. V08BT08A009. [Google Scholar]
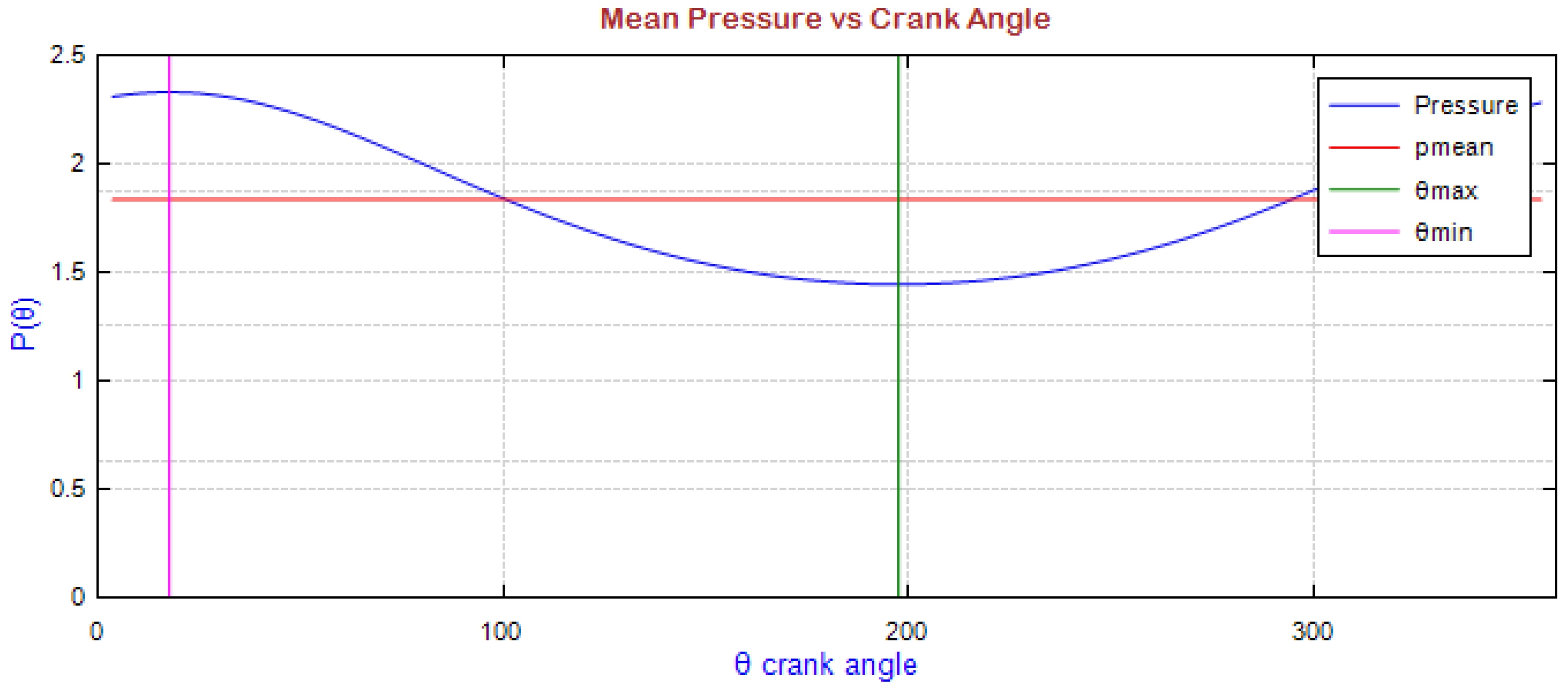
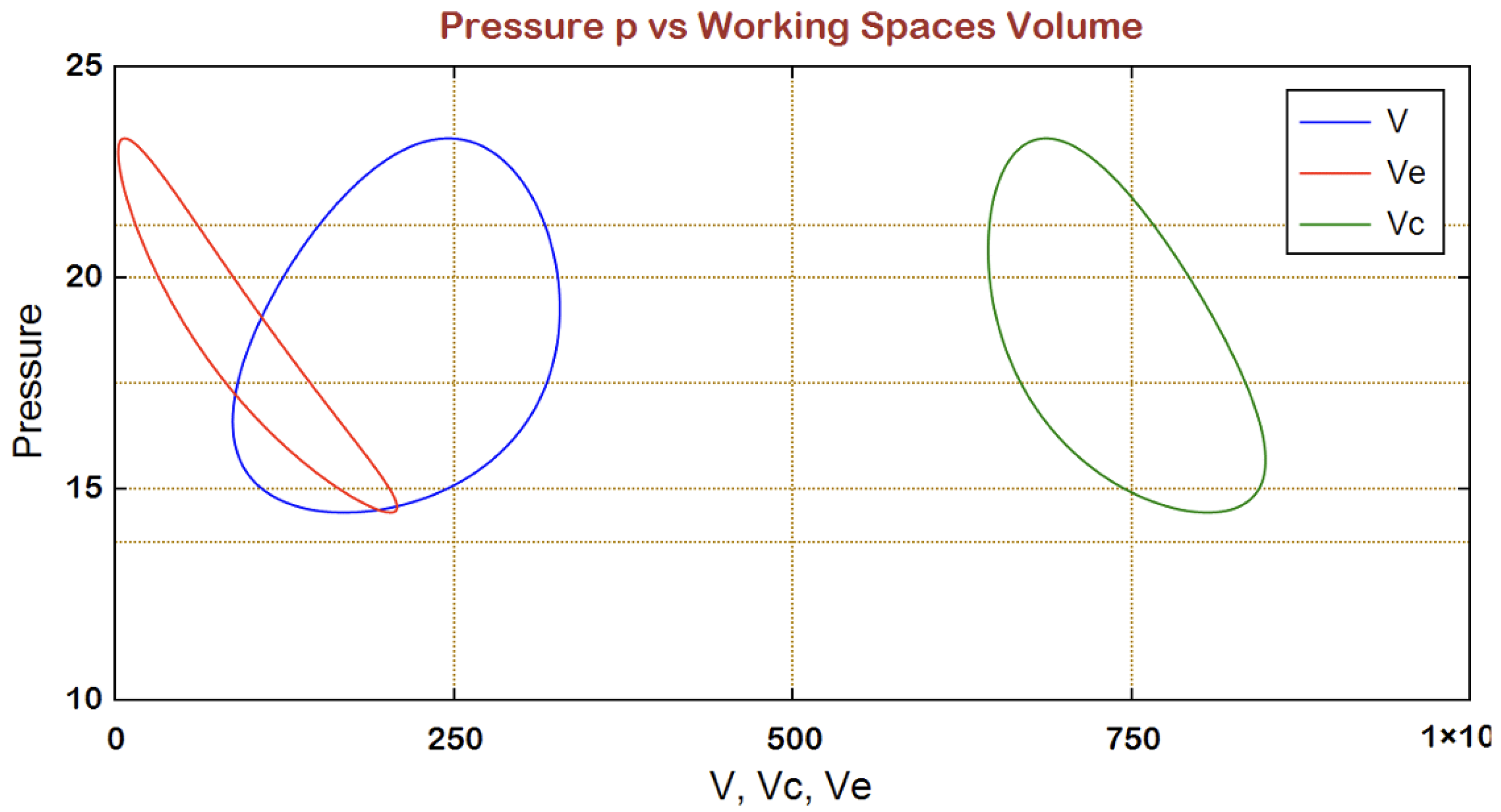
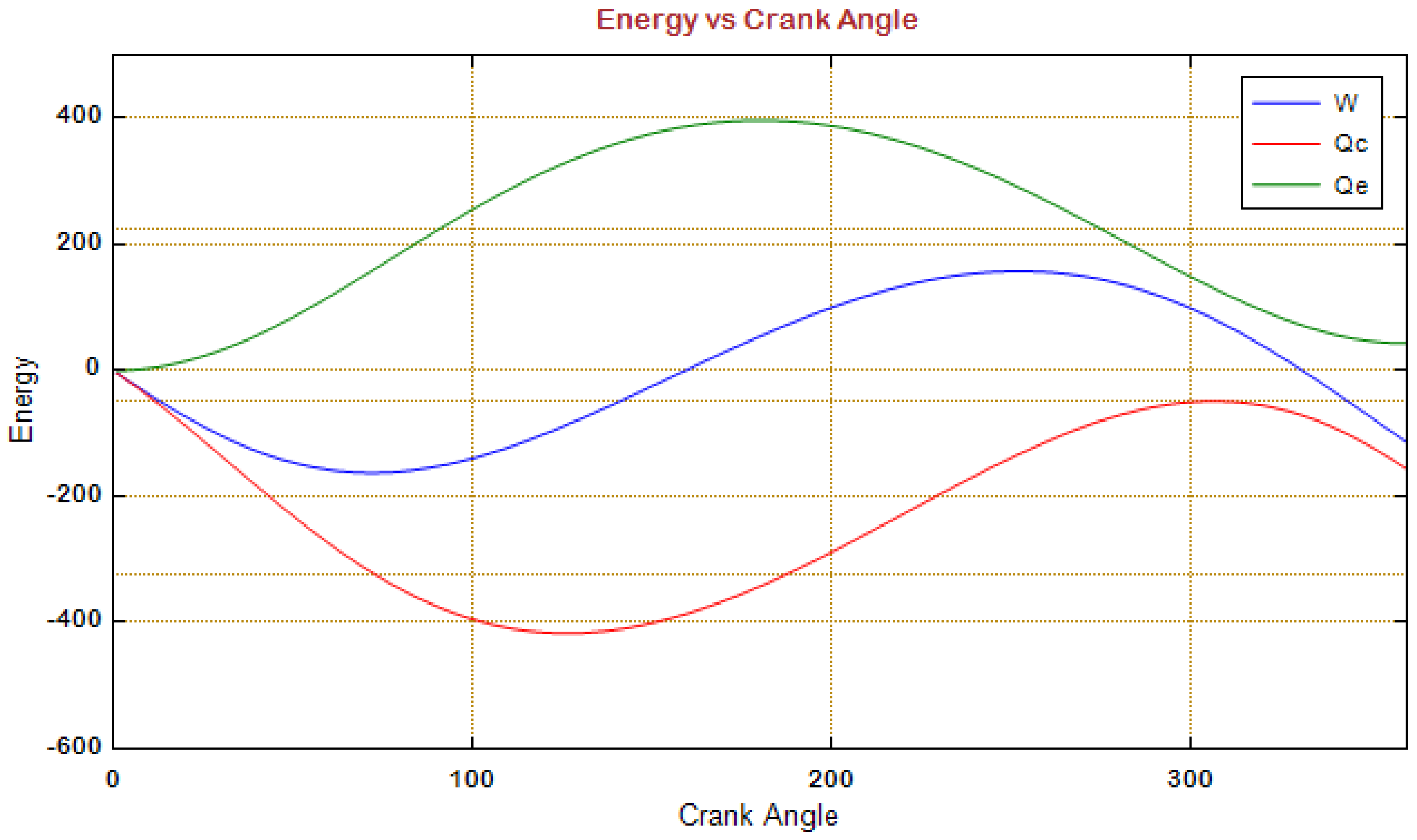
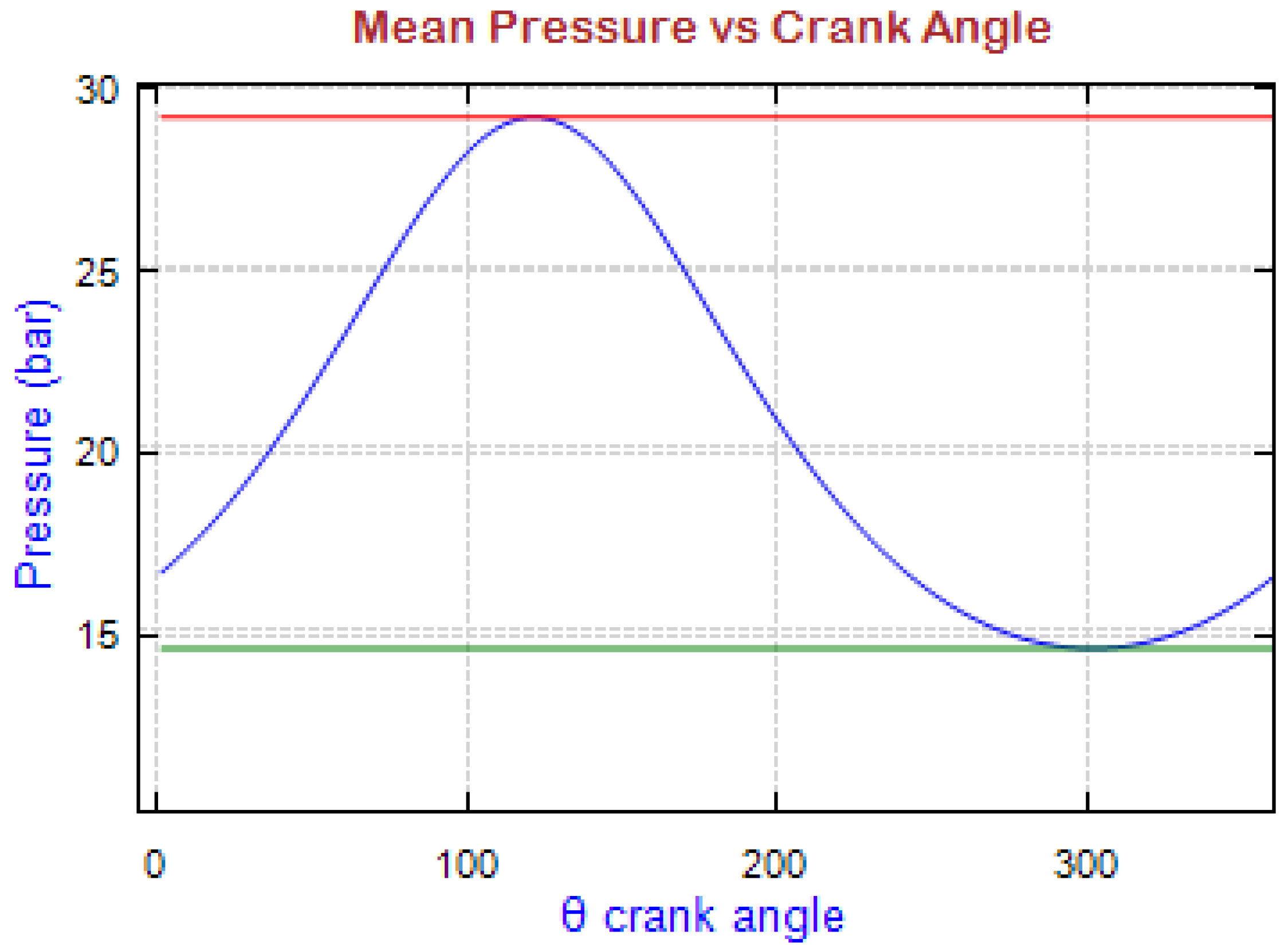
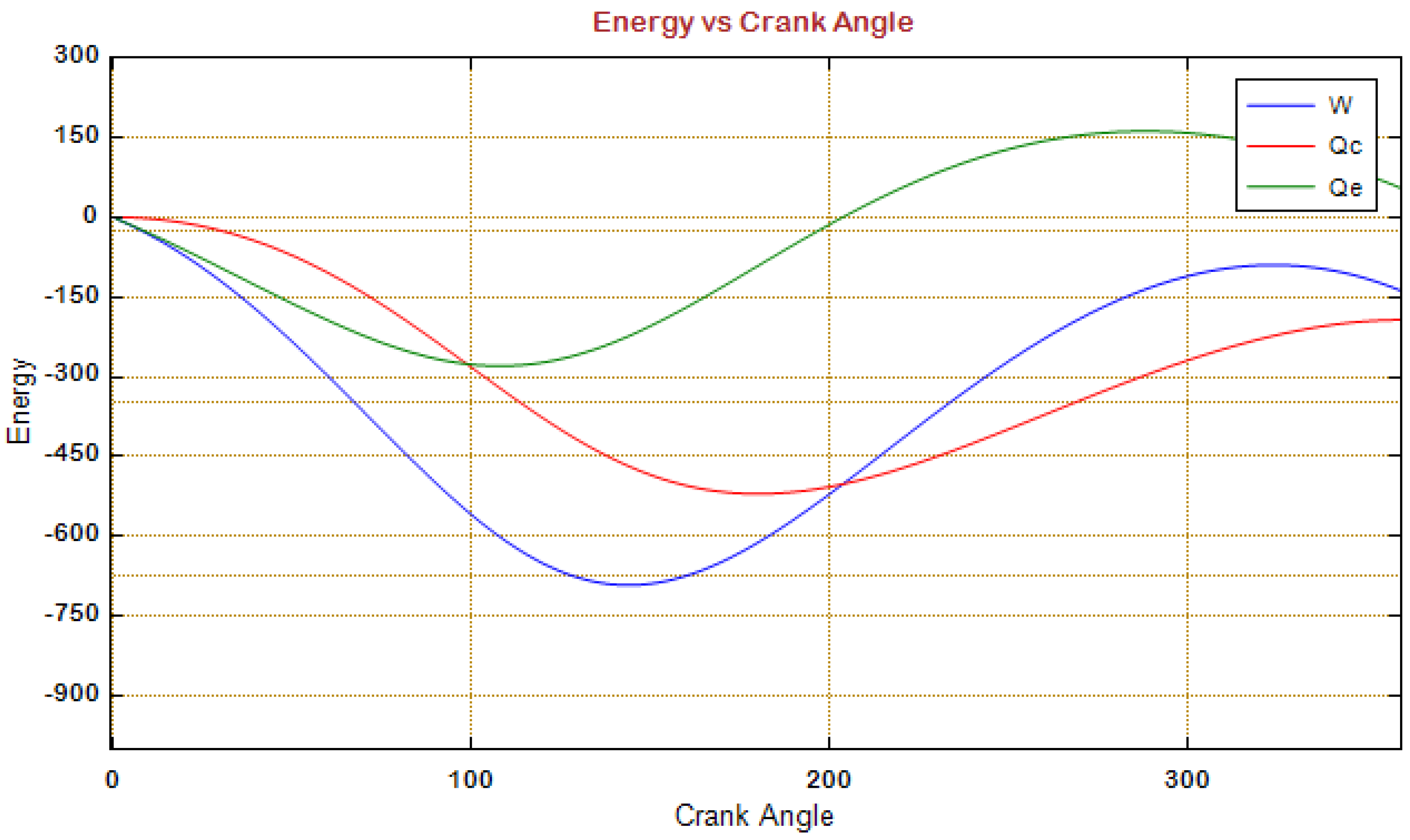
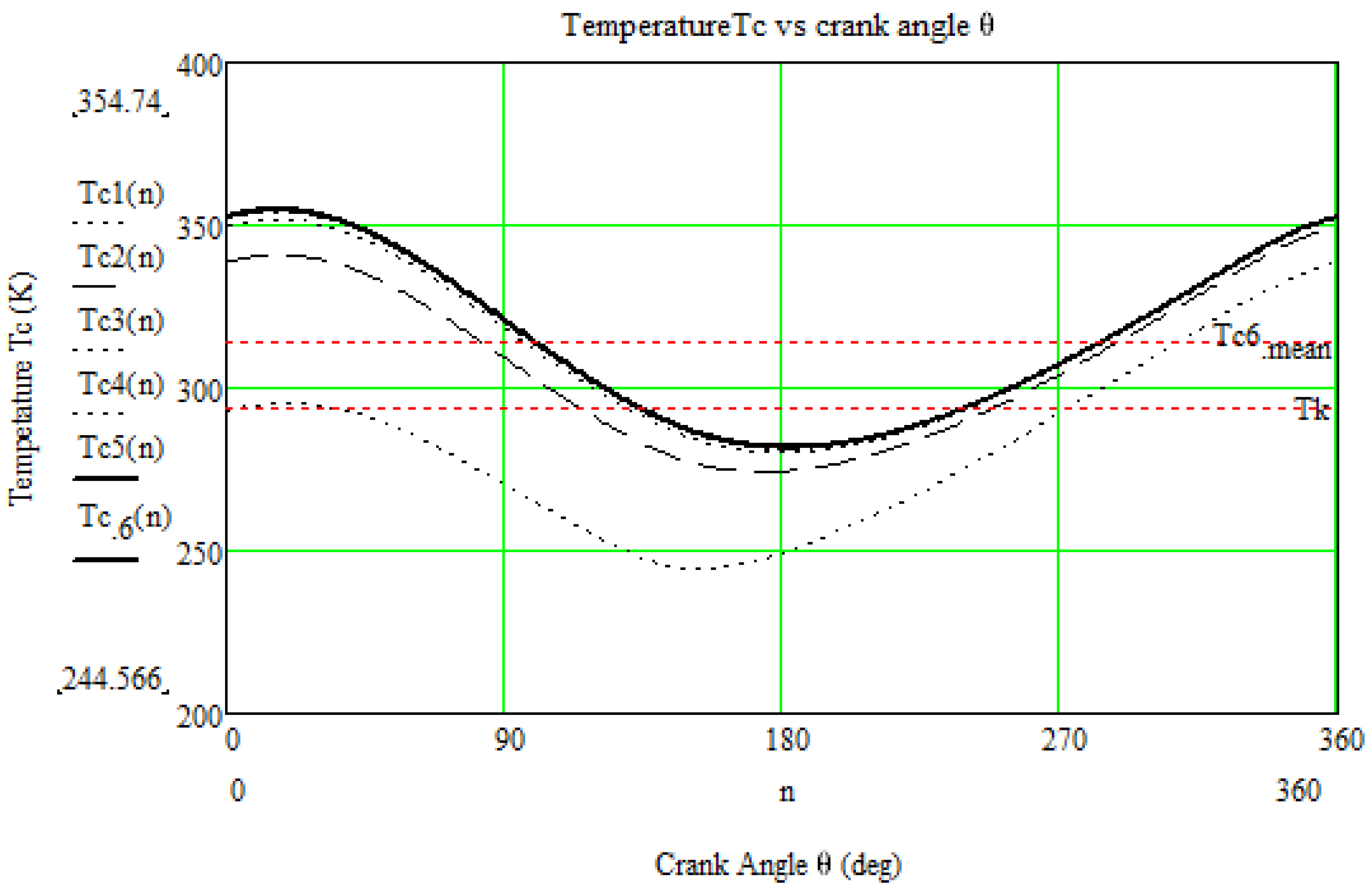
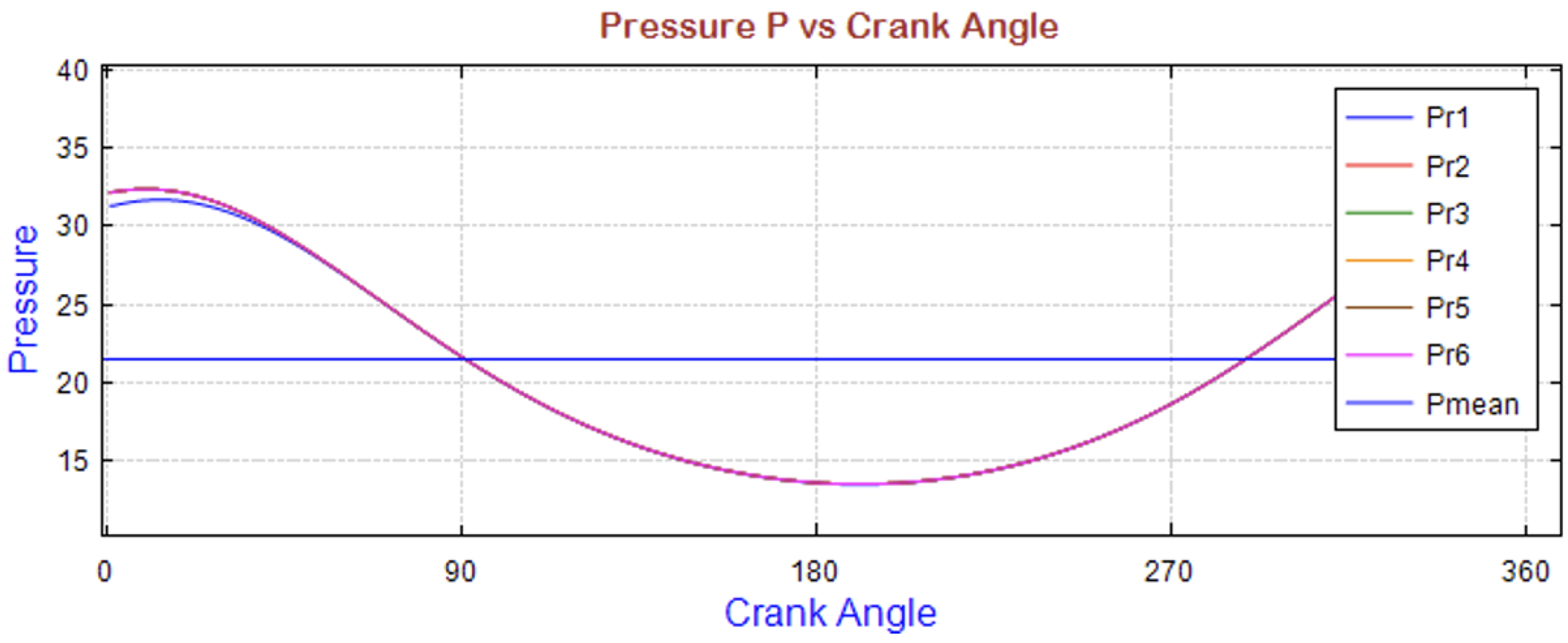

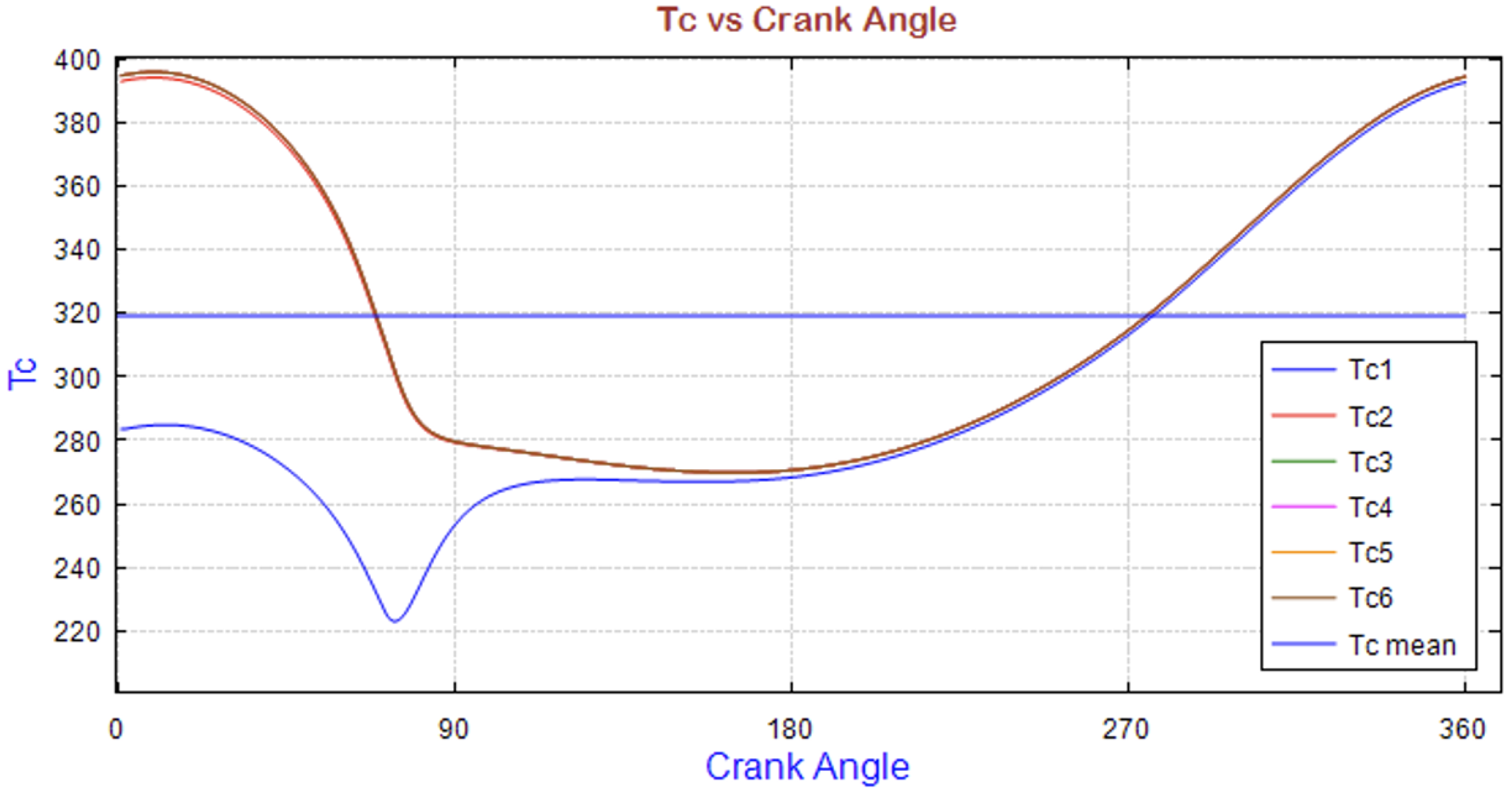
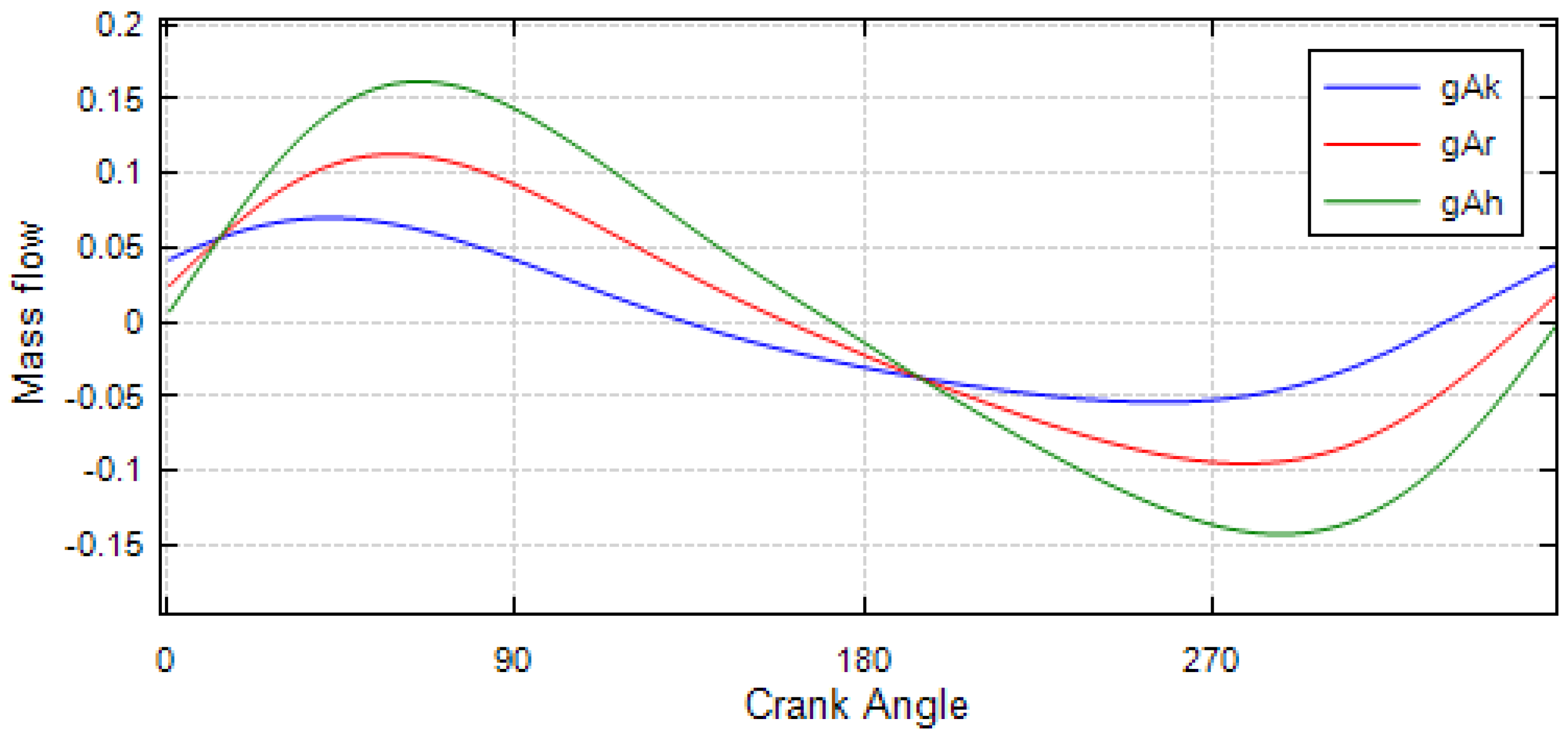
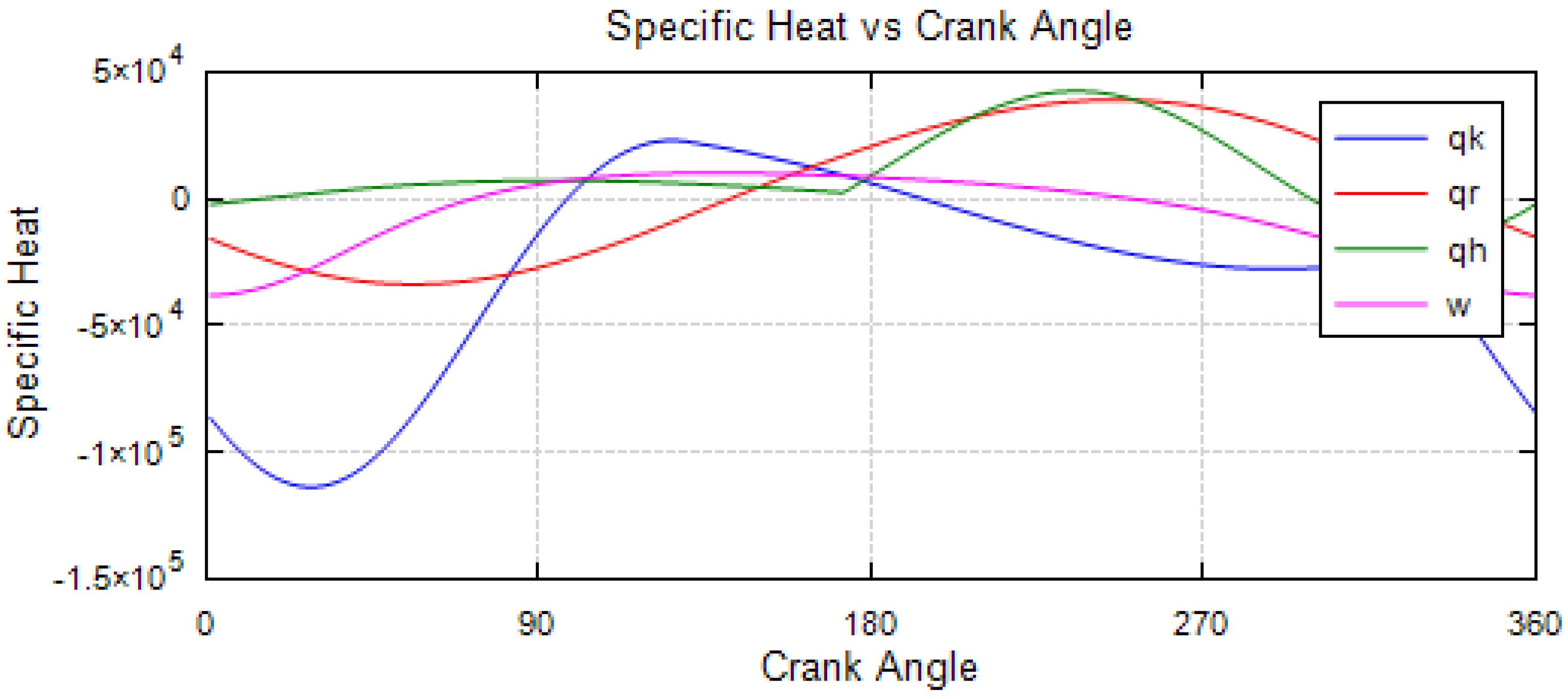
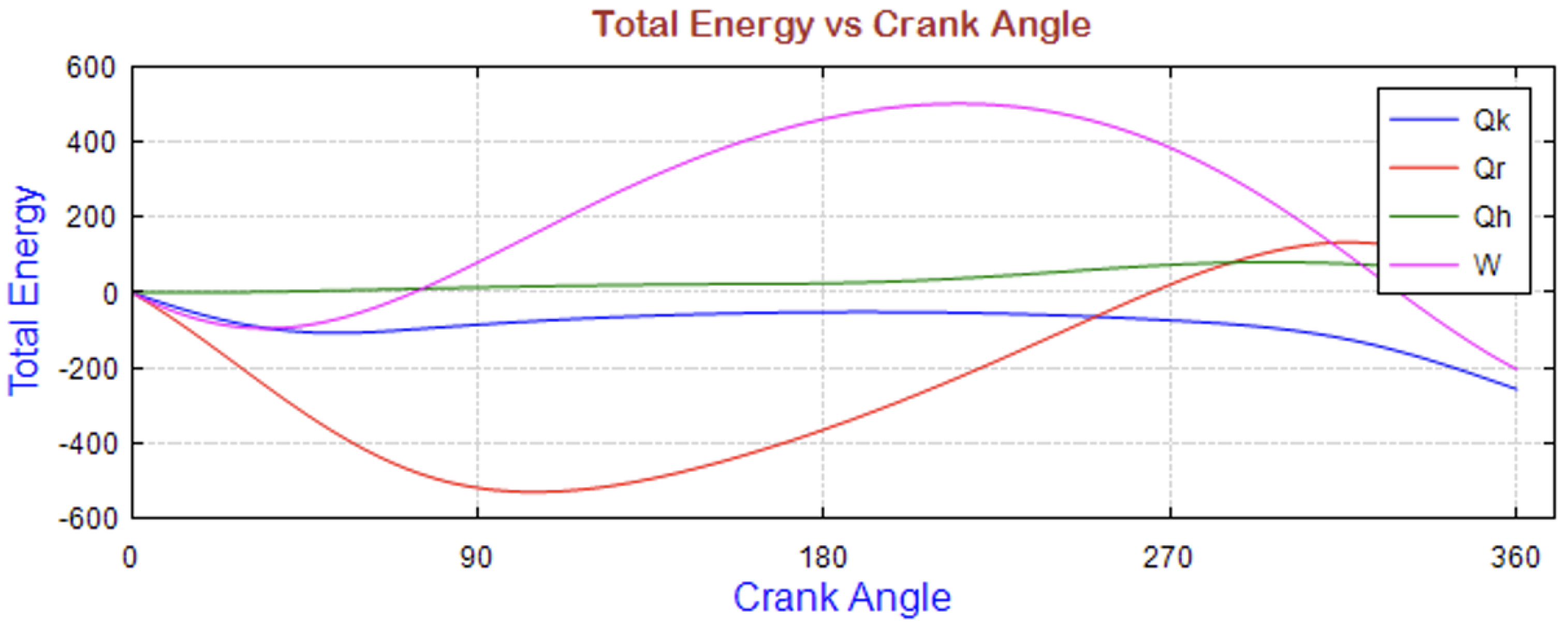
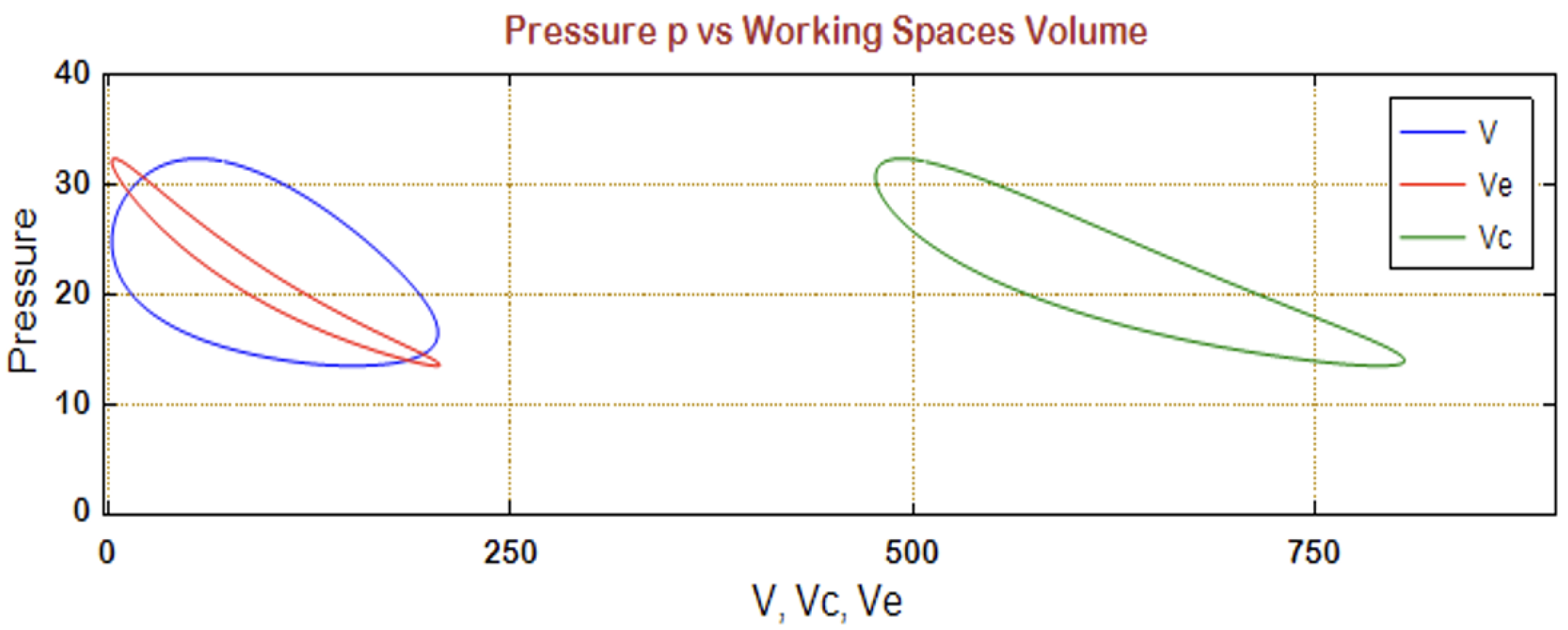
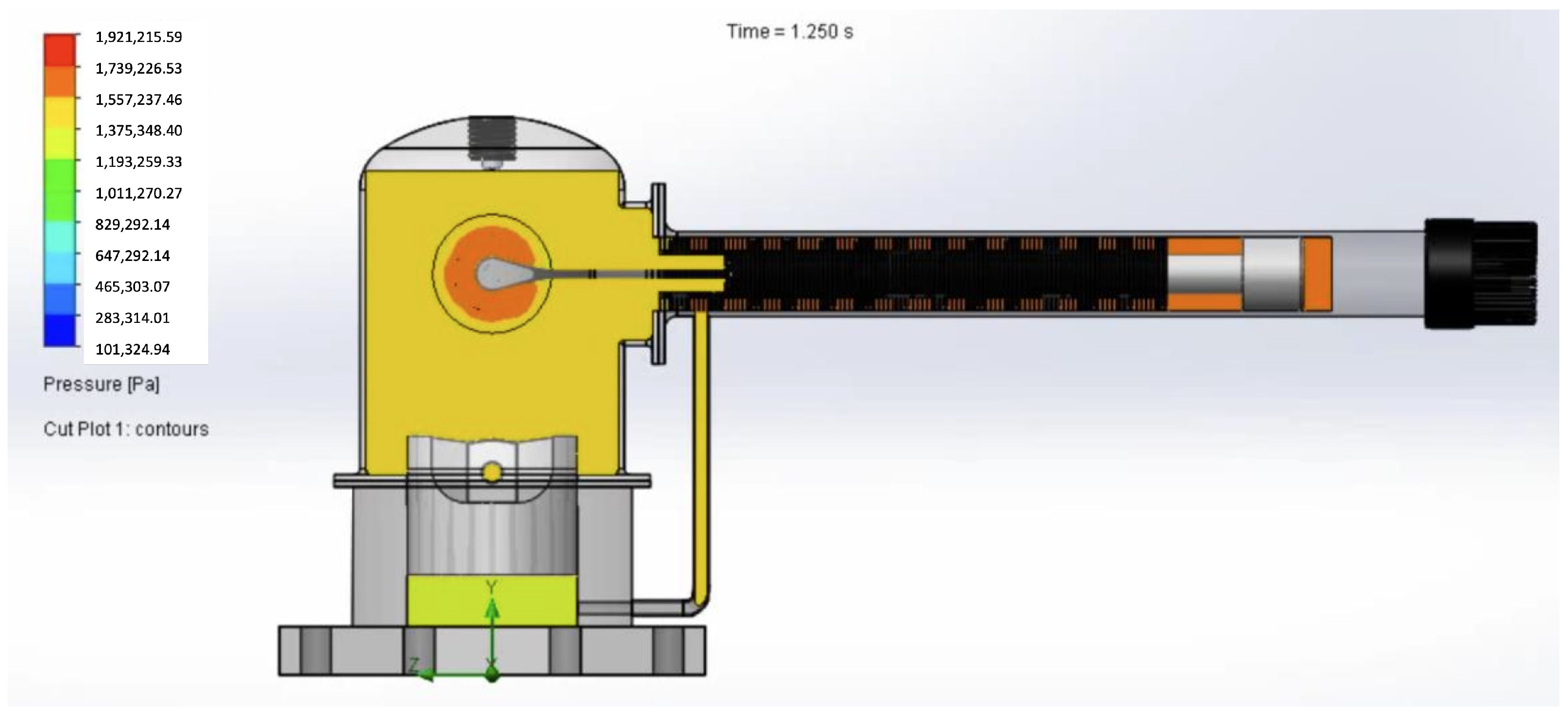
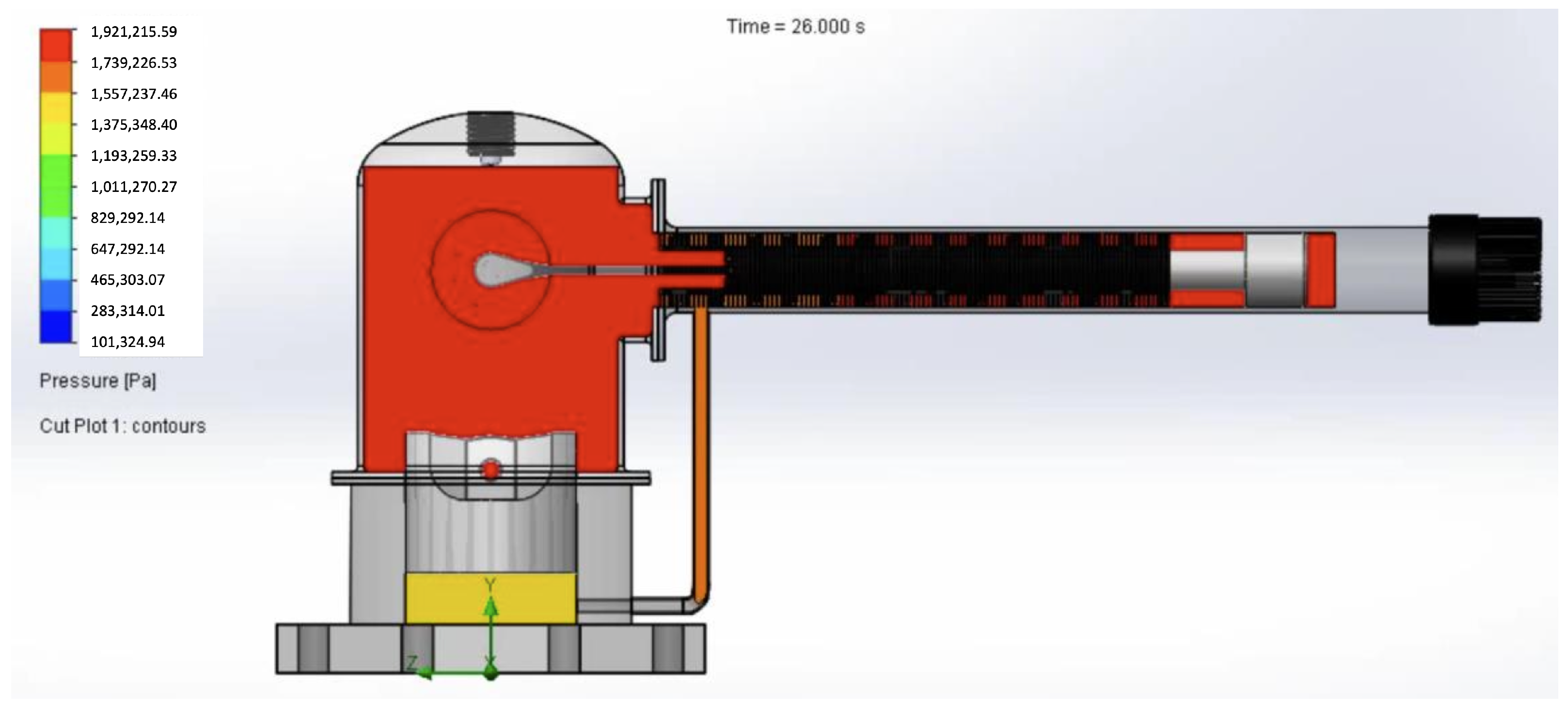
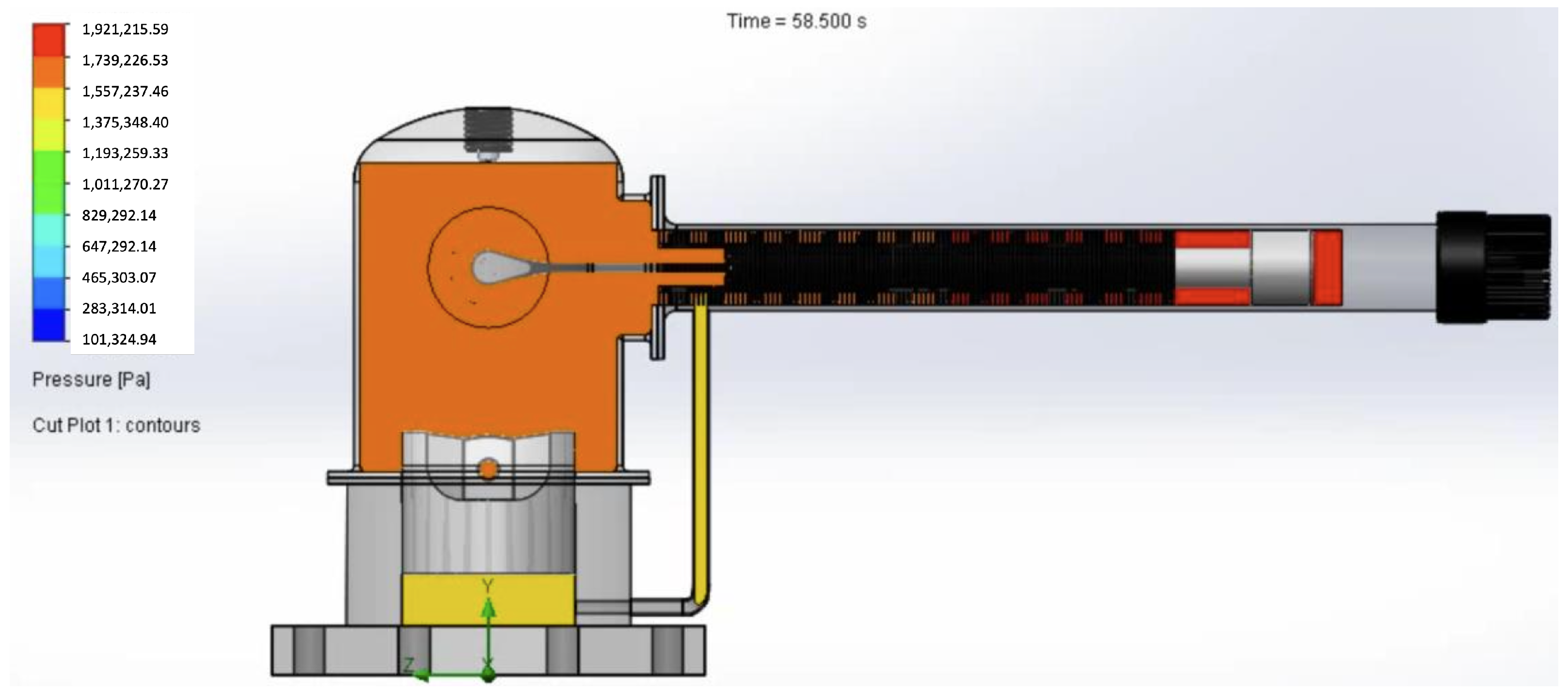

| Pressure | |
| Transferred heat to the expansion space | |
| Transferred heat to the compression space | |
| Required work | |
| Coefficient of performance (COP) |
| Required work | J/cycle |
| Useful heat in the expansion | J/cycle |
| Rejected heat in the compression | J/cycle |
| Coefficient of performance (COP) | |
| Indicated cooling power | P = 1035.8 kW at 1450 rpm |
| Mean pressure | MPa |
| Required work | J/cycle |
| Schmidt equation | J/cycle |
| Useful heat in expansion | J/cycle |
| Rejected heat in compression | J/cycle |
| Coefficient of performance (COP) | |
| Indicative cooling power | P = 1272.54 kW at 1450 rpm |
| Mean pressure | MPa |
| Engine Model | Schmidt Analysis | |
| Power | Coefficient of Performance COP | |
| (kW) | ||
| PPG – 102 Cryocooler | 1.272 | 37.55% |
| Engine Model | Isothermal Analysis | |
| Power | Coefficient of Performance COP | |
| (kW) | ||
| PPG – 102 Cryocooler | 1.035 | 37.56% |
| Required work | − J/cycle |
| Required heat from the refrigerant | − J/cycle |
| Transferred heat in the regenerator | J/cycle |
| Supplied heat in the freezer | = 55.625 J/cycle |
| Useful heat in the expansion | − J/cycle |
| Rejected heat in the compression | kW at 1450 rpm |
| Coefficient of performance (COP) | |
| Indicative refrigerating power | kW at 1450 rpm |
| Mean pressure | MPa |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Antonakos, G.; Koronaki, I.; Domenikos, G.-R.; Baltadouros, S. Investigation of the Performance of Thermodynamic Analysis Models for a Cryocooler PPG-102 Stirling Engine. Energies 2023, 16, 6815. https://doi.org/10.3390/en16196815
Antonakos G, Koronaki I, Domenikos G-R, Baltadouros S. Investigation of the Performance of Thermodynamic Analysis Models for a Cryocooler PPG-102 Stirling Engine. Energies. 2023; 16(19):6815. https://doi.org/10.3390/en16196815
Chicago/Turabian StyleAntonakos, George, Irene Koronaki, George-Rafael Domenikos, and Serafeim Baltadouros. 2023. "Investigation of the Performance of Thermodynamic Analysis Models for a Cryocooler PPG-102 Stirling Engine" Energies 16, no. 19: 6815. https://doi.org/10.3390/en16196815
APA StyleAntonakos, G., Koronaki, I., Domenikos, G.-R., & Baltadouros, S. (2023). Investigation of the Performance of Thermodynamic Analysis Models for a Cryocooler PPG-102 Stirling Engine. Energies, 16(19), 6815. https://doi.org/10.3390/en16196815








