Design and Analysis of an Axial Center-Piercing Hydrocyclone
Abstract
:1. Introduction
2. Structure and Working Principle
3. Research Methods
3.1. Mathematical Model Method
Boundary Conditions and Efficiency
3.2. Optimal Design of Response Surface
3.2.1. Basic Principles of Response Surface
3.2.2. Response Surface Optimization Design
4. Results and Discussion
4.1. Model Optimization Result
4.2. Analysis of Variance
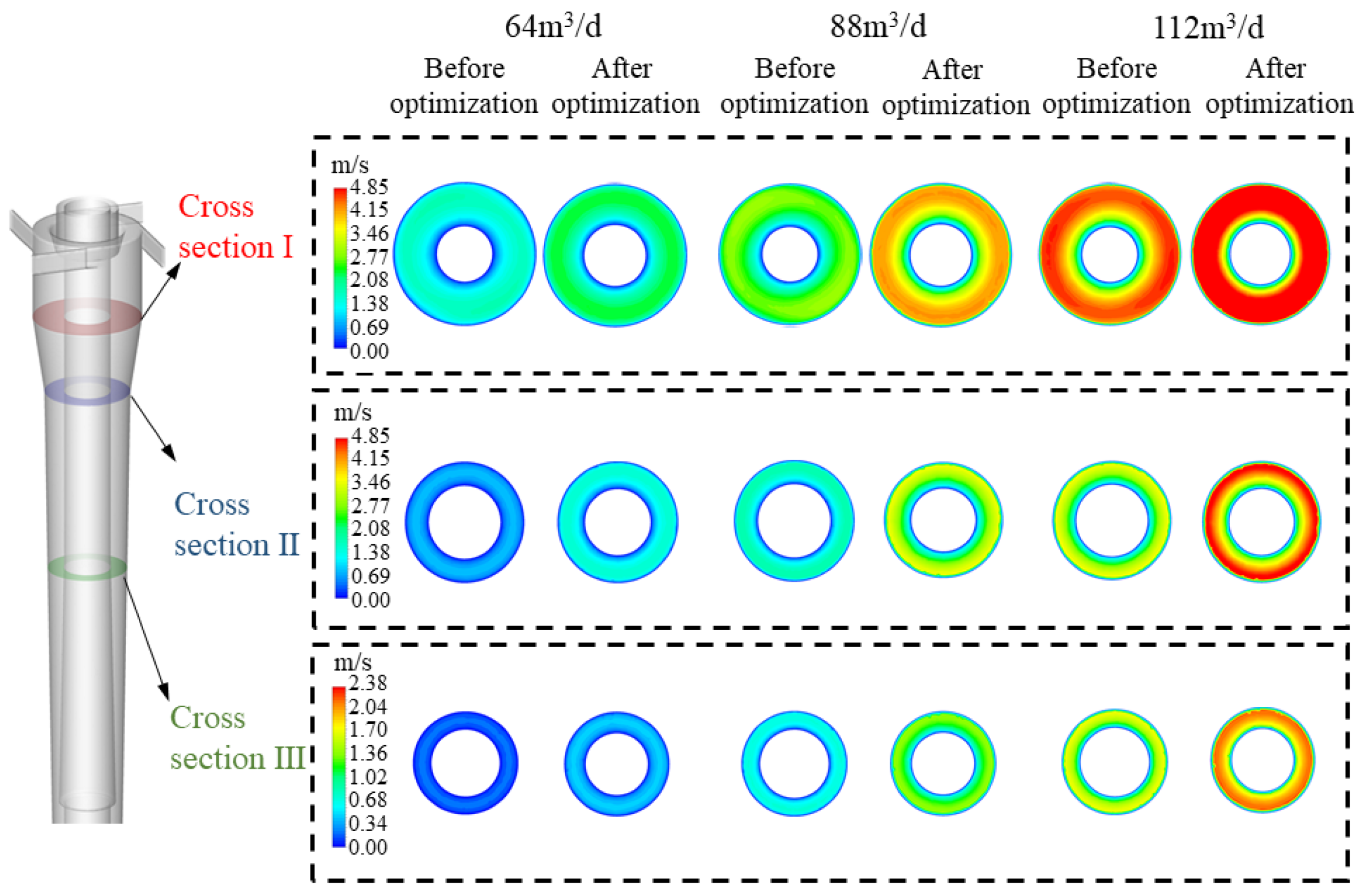
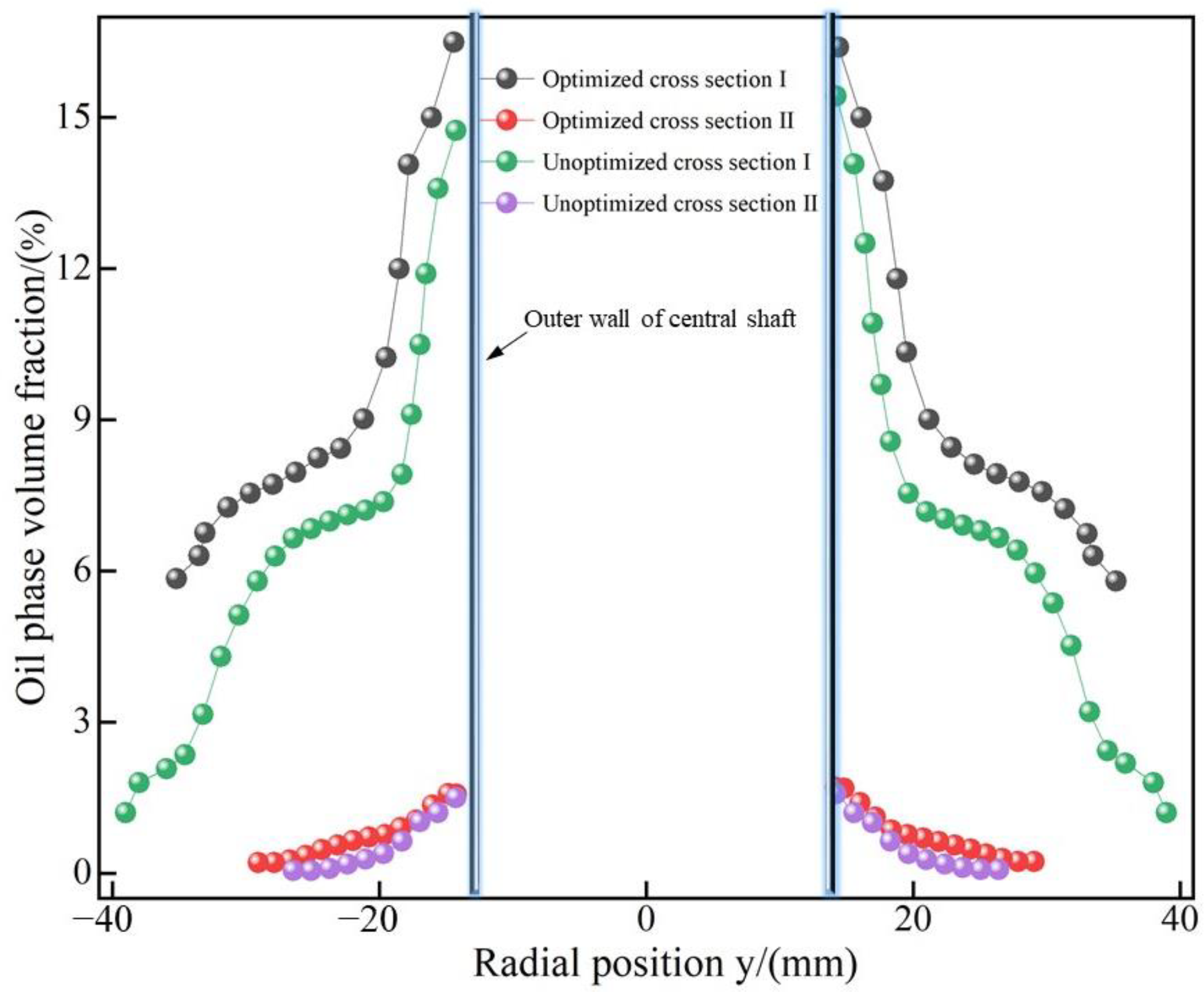
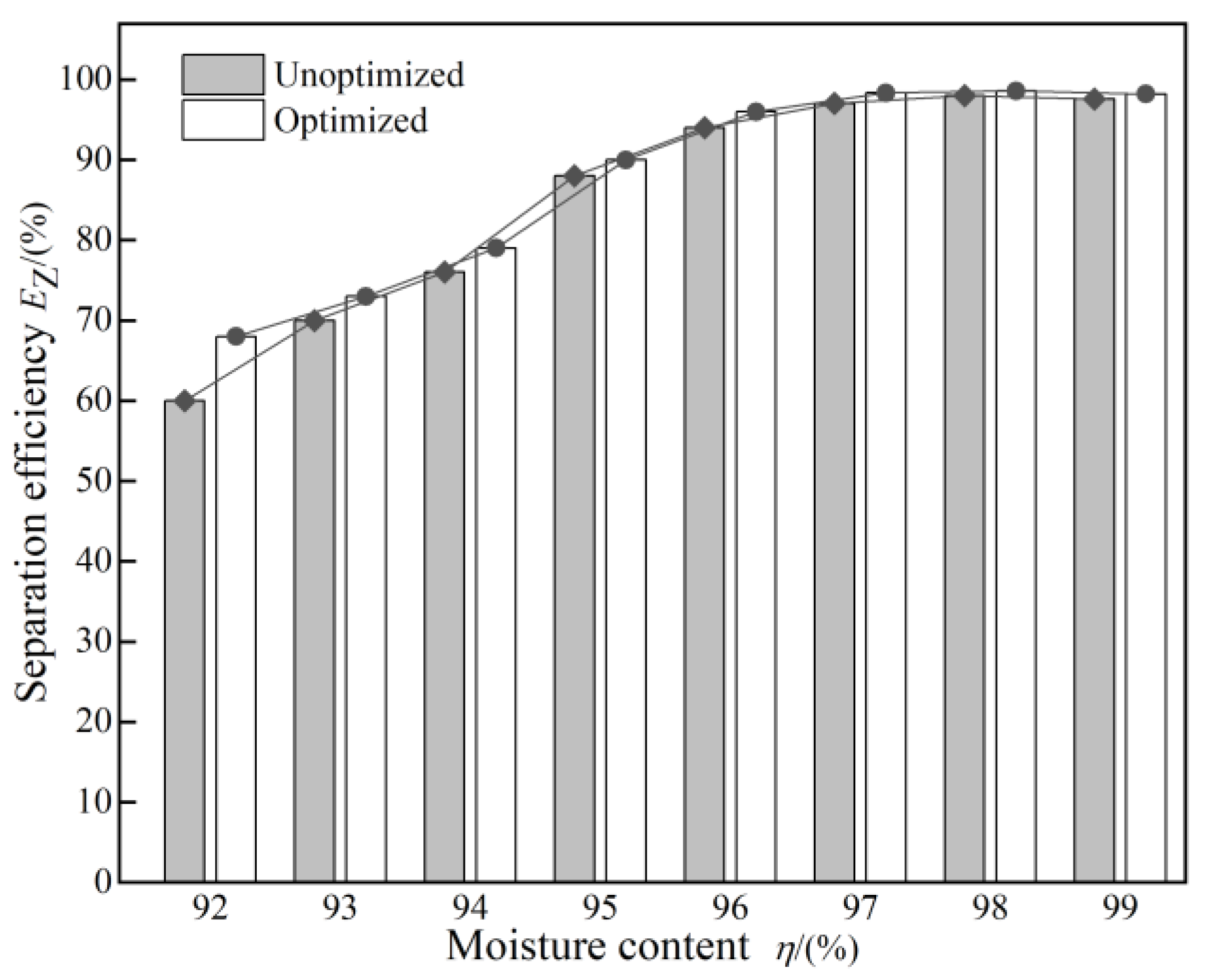
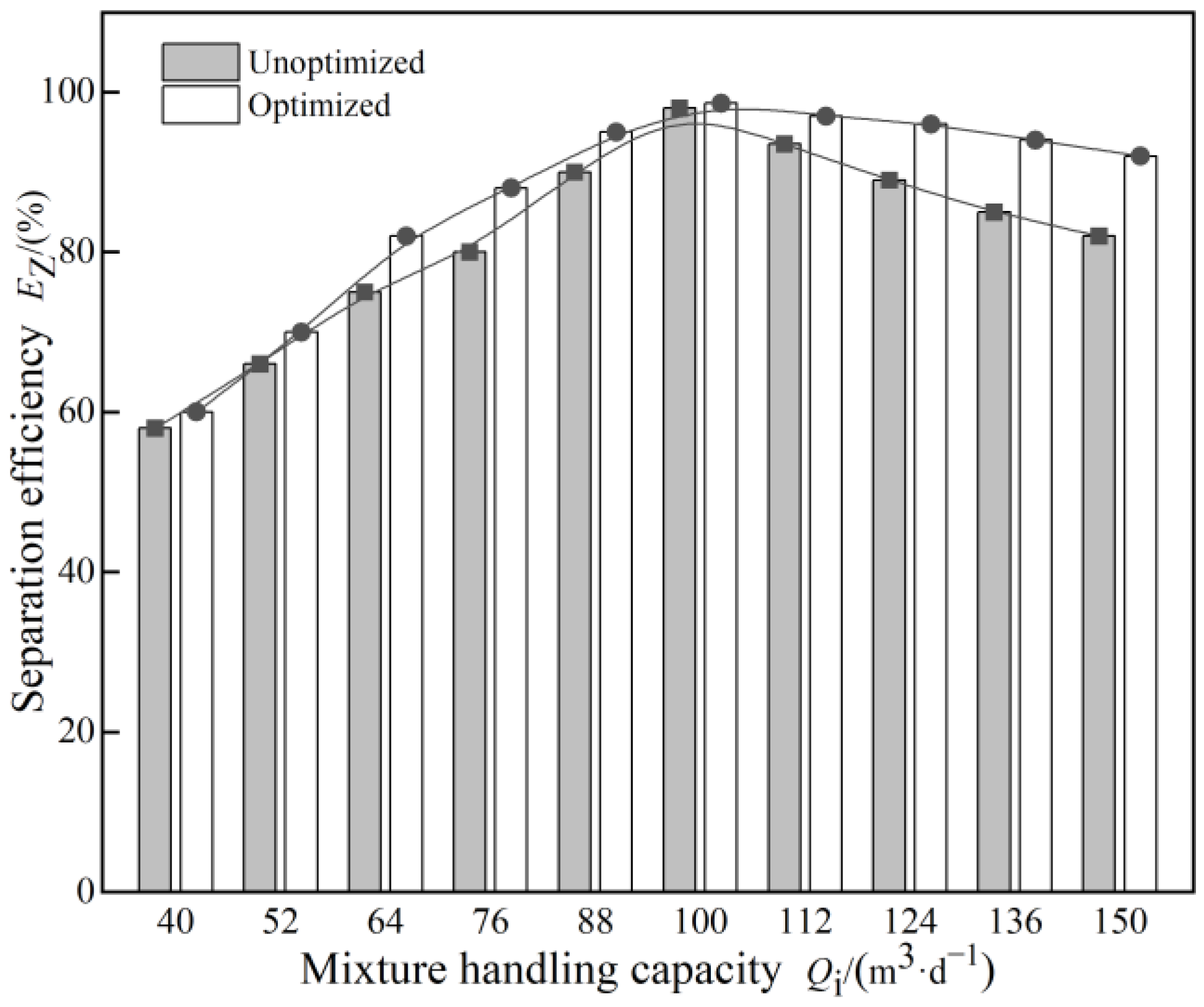
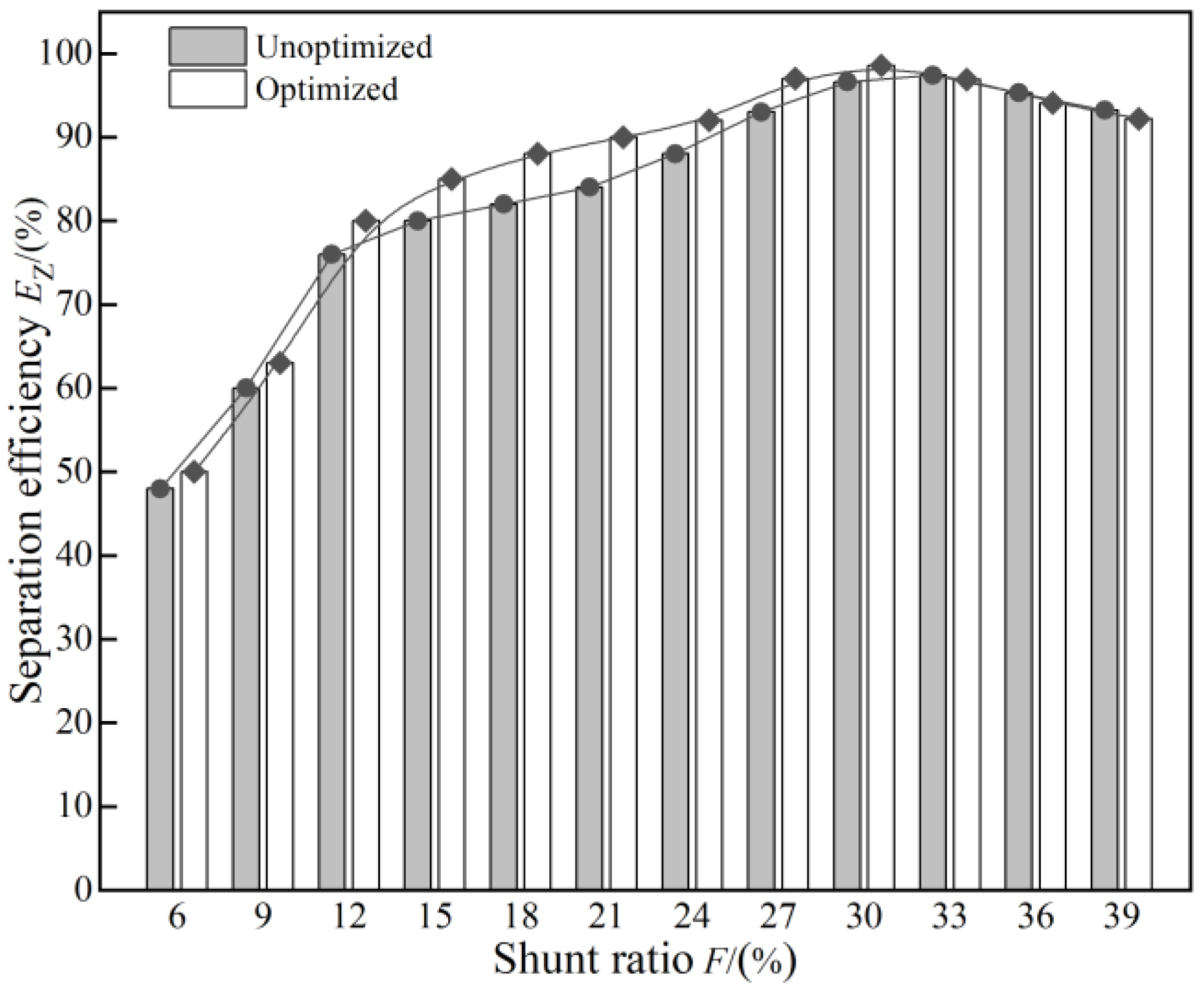
4.3. Comparison of Structural Shunt Performance before and after Optimization
4.4. Experimental Verification
5. Conclusions
- According to the downhole working conditions of injection and production in the same well, a novel axial center-piercing hydrocyclone structure was proposed. The optimal structural parameters were determined through the response surface method, as follows: main diameter D = 70.4 mm, large cone angle α1 = 32.4°, small cone angle α2 = 3.9°, bottom flow tube length L3 = 311.7 mm, and inverted cone length L4 = 166.0 mm.
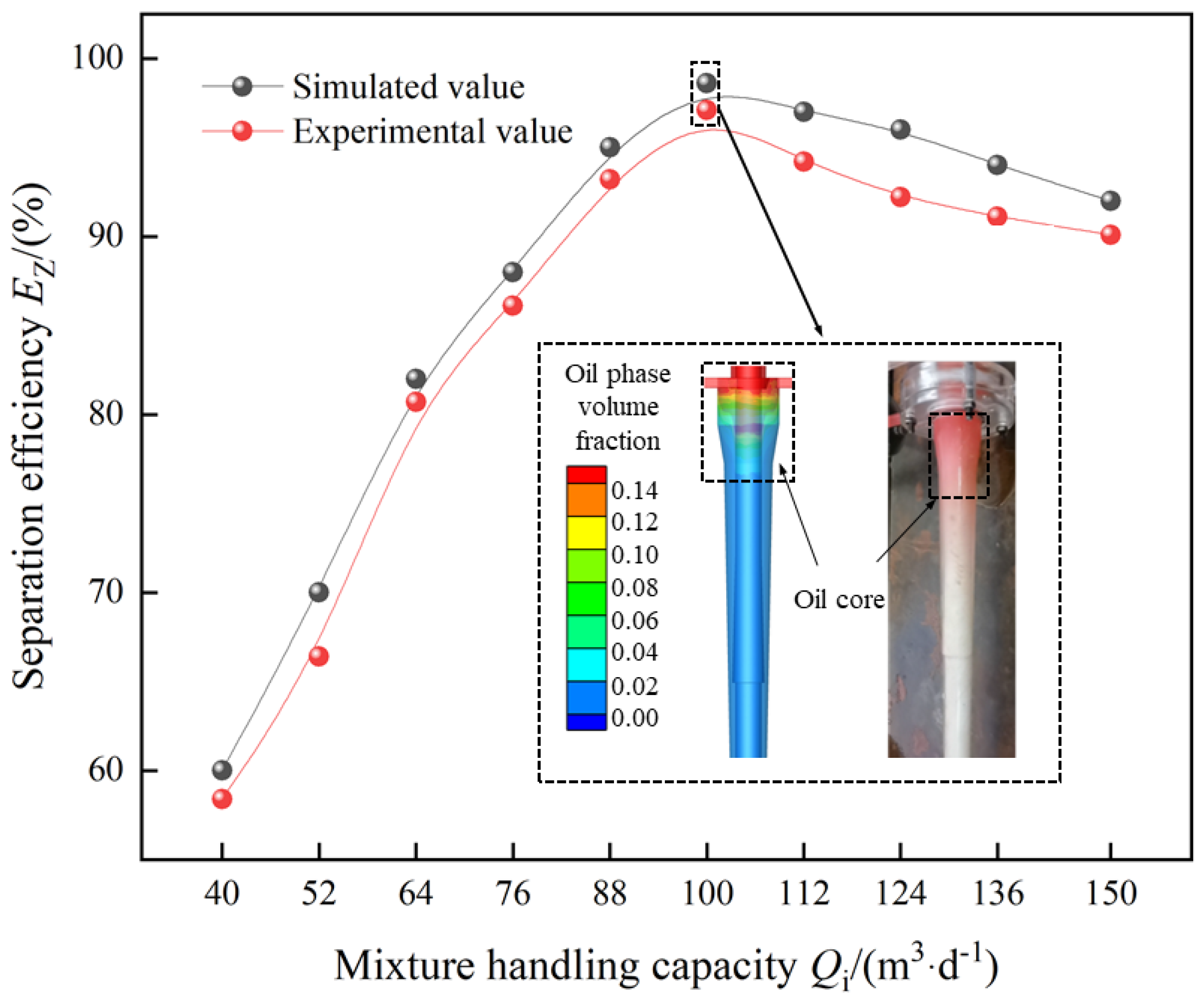
- The reliability of the optimized structure was validated through a comparison of internal tangential velocity cloud images and the distribution of the oil-phase volume fraction before and after optimization. Numerical simulations of the optimized structure demonstrated that the separation efficiency after optimization surpassed that before optimization under equivalent parameter conditions, confirming the enhanced efficiency of the optimized structure. The optimal operational parameters for the optimized over-axis cyclone were determined. At a treatment capacity of 100 m3/d, water content of 98%, and a shunt ratio of 30%, the separation efficiency reached its peak at 98.6%, a 2% improvement over the pre-optimized configuration.
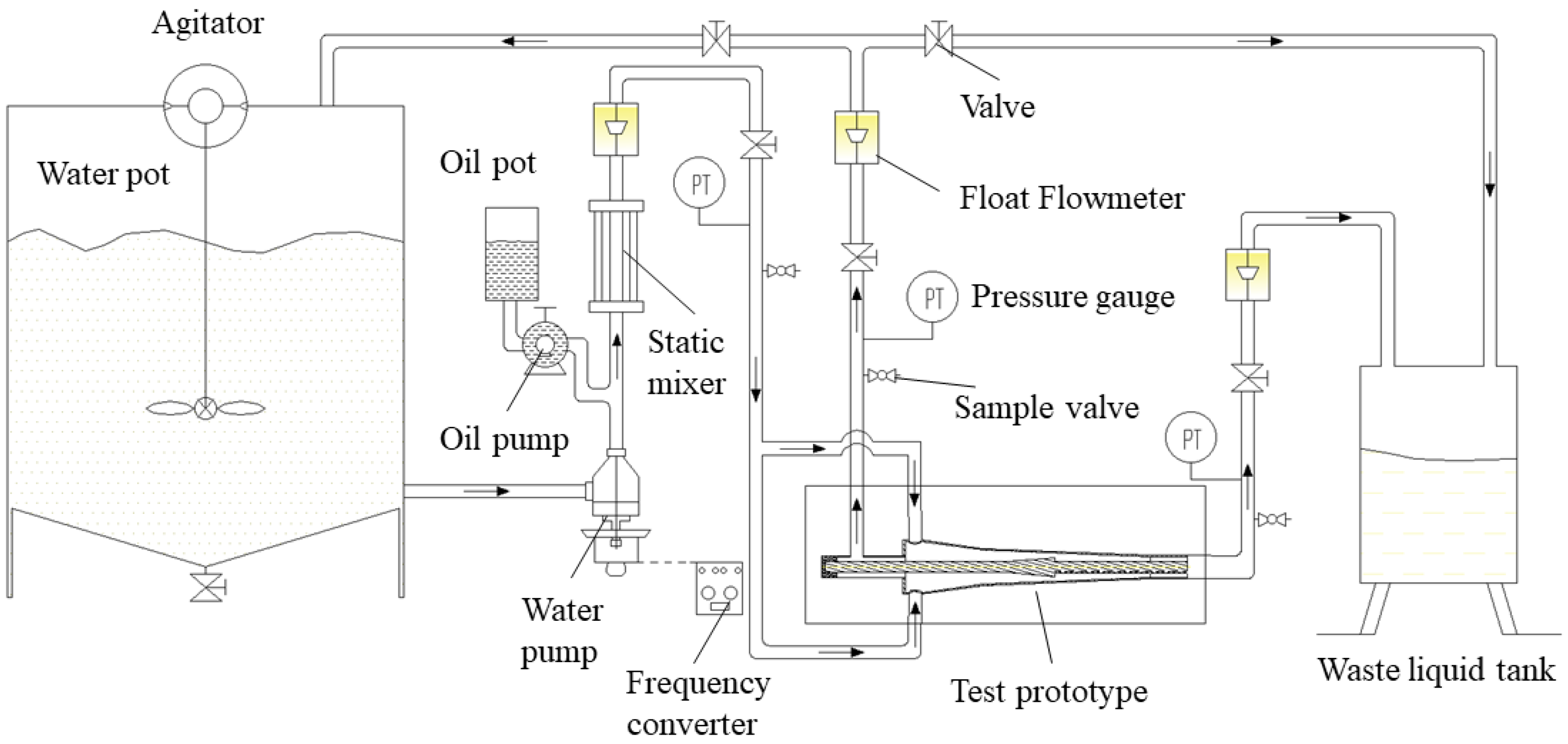
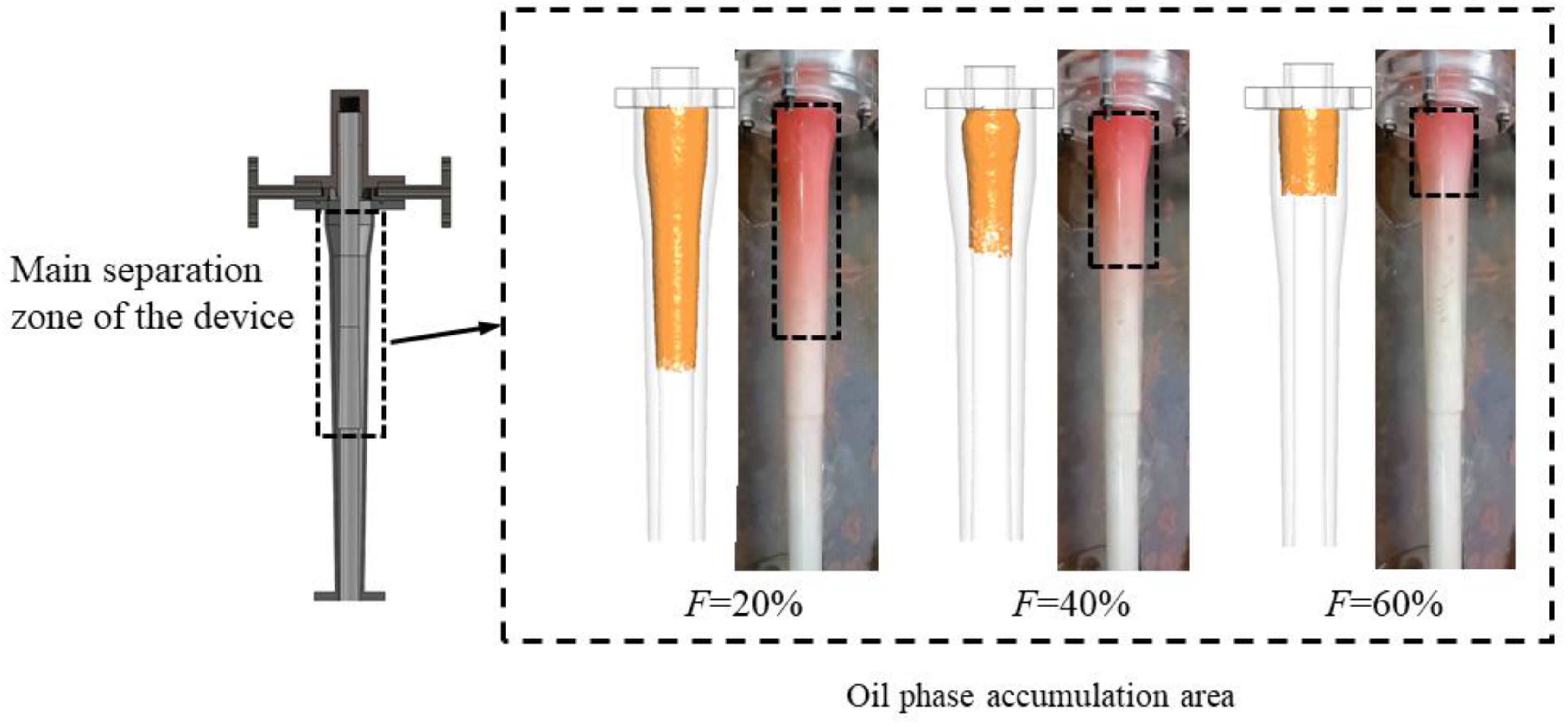
- Reliability verification of the experiments was conducted under various shunt ratios and processing capacities. The experimental results showed close agreement with the numerical simulation results.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, H.; Gao, Y.; Pei, X.H.; Zheng, G.; Lichen, Z. Progress and prospect of downhole cycloneoil-water separation with single-well injection-production technology. Acta Pet. Sin. 2018, 39, 463–471. [Google Scholar]
- Wang, D.M.; Wang, Y.; Zhang, L.L.; Liu, J.T.; Zhang, H.Y.; He, Z.G.; Zhang, Y. Matching technology and application effect of injection-production in the same well. J. China Univ. Pet. 2023, 47, 64–72. [Google Scholar]
- Liu, H.Y.; Han, T.L.; Wang, Y.; Huang, Q. Influence of new outlet configurations with baffle on hydrocycloneon separation performance. CIESC J. 2018, 69, 2081–2088. [Google Scholar]
- Gao, Y.; Pei, X.; Cao, G.; Yu, J.; Zhao, X.; Li, F. Effect of collision of particles on migration behaviour in hydrocyclone. J. Phys. Conf. Ser. 2023, 2441, 012040. [Google Scholar] [CrossRef]
- Zhang, Y.K.; Ge, J.B.; Liu, P.K.; Yang, X.G. Flow field characteristics and separation performance of multi-inlet hydrocyclone. Chem. Ind. Eng. Prog. 2022, 41, 86–94. [Google Scholar]
- Liu, L.; Zhao, L.; Yang, X.; Wang, Y.; Xu, B.; Liang, B. Innovative design and study of an oil-water coupling separation magnetic hydrocyclone. Sep. Purif. Technol. 2019, 213, 389–400. [Google Scholar] [CrossRef]
- Slot, J.J.; Campen, L.; Hoeijmakers, H.W.M.; Mudde, R.F. In-line oil-water separation in swirling flow. In Proceedings of the 8th International Conference on CFD in Oil & Gas, Metallurgical and Process Industries, Trondheim, Norway, 21–23 June 2011; pp. 21–23. [Google Scholar]
- Tian, J.; Wang, H.; Lv, W.; Huang, Y.; Fu, P.; Li, J.; Liu, Y. Enhancement of pollutants hydrocyclone separation by adjusting back pressure ratio and pressure drop ratio. Sep. Purif. Technol. 2020, 240, 116604. [Google Scholar] [CrossRef]
- Yan, Y.J.; Shang, Y.X.; Wang, Z.C.; Tian, M.; Wang, Y. The Structure Design and Numerical Simulation Research on Downhole Hydrocyclone Desander. Adv. Mater. Res. 2014, 933, 434–438. [Google Scholar] [CrossRef]
- Xing, L.; Guan, S.; Gao, Y.; Jiang, M. Measurement of a Three-Dimensional Rotating Flow Field and Analysis of the Internal Oil Droplet Migration. Energies 2023, 16, 5094. [Google Scholar] [CrossRef]
- Al-Kayiem, H.H.; Osei, H.; Hashim, F.M.; Hamza, J.E. Flow structures and their impact on single and dual inlets hydrocyclone performance for oil–water separation. J. Pet. Explor. Prod. Technol. 2019, 9, 2943–2952. [Google Scholar] [CrossRef]
- Xing, L.; Zhang, Y.; Jiang, M.H.; Gao, Y. Flow Filed Analysis and Performance Evaluationon Axis-in Dual-Stage Tandem Hydrocyclones. China Mech. Eng. 2018, 29, 1927–1935. [Google Scholar]
- Zhao, C.W.; Li, Z.L.; Deng, L.J.; Wu, H.Y. Study on working characteristics of downhole two-stage series oil-water separator. J. Mech. Eng. 2014, 50, 177–185. [Google Scholar] [CrossRef]
- Zhao, C.W.; Li, Z.L.; Dong, X.W.; Zhang, X.L. Numerical simulation and experiment of downhole two-stage tandem hydrocyclone. Acta Pet. Sin. 2014, 35, 551–557. [Google Scholar]
- Wang, Z.C.; Zhang, J.L.; Kong, L.Z.; Xu, Y. Numerical simulation of the flow field in aixial rotating Hydrocyclone. J. Harbin Inst. Technol. 2011, 43, 126–130. [Google Scholar]
- Bai, C.L.; Wang, C.S.; Chen, J.Q.; Shang, C.; Zhang, M.; Liu, M.L.; Zheng, X.P. Experimental study of axial hydrocyclone for pre-dehydration from wellstream. Chem. Ind. Eng. Prog. 2020, 39, 1649–1656. [Google Scholar]
- Ding, W.G.; Liu, L.; Du, X.X.; Zhang, B.L.; Yang, G.W.; Wu, G.; Zhao, L.X. Structure Design and Optimization of Offshore Downhole Oil-Water Separation Hydrocyclone. China Pet. Mach. 2020, 48, 69–76. [Google Scholar]
- Gao, Y.; Han, Q.Q.; Su, J.; Wang, W.C.; Ma, Z.Q. Numerical Simulation of Downhole Axial-flow Oil-Water Separator in Rod-pumped Well. Chem. Eng. Mach. 2021, 48, 683–690+749. [Google Scholar]
- Xu, B.R.; Jiang, M.H.; Zhao, L.X. CFD simulation and PIV test of water flow characteristics in helix separator. Acta Pet. Sin. 2018, 39, 223–231. [Google Scholar]
- Gao, Y.; Liu, H.; Zhang, Y. Effect of separation performance of downhole hydrocyclones in series on different sand content. J. Northeast Pet. Univ. 2018, 42, 112–120+128. [Google Scholar]
- Wang, Z.J.; Li, F.; Zhao, L.X. Numerical simulation and experimental study on the effect of polymer concentration on hydrocyclone performance. Chem. Ind. Eng. Prog. 2019, 38, 5287–5296. [Google Scholar]
- Liu, P.K.; Niu, Z.Y.; Yang, X.H. Separation performance contrastive study of micro hydrocyclone for ultrafine particles. China Powder Sci. Technol. 2016, 22, 1–6. [Google Scholar]
- Zhang, Y.; Xing, L.; Zhang, Y.; Jiang, M.H. Effects of Discrete Phase Entering Positions on Separation Performance of a Hydrocyclone. J. Chem. Eng. Chin. Univ. 2017, 31, 1311–1317. [Google Scholar]
- Hwang, K.J.; Chou, S.P. Designing vortex finder structure for improving the particle separation efficiency of a hydrocyclone. Sep. Purif. Technol. 2017, 172, 76–84. [Google Scholar] [CrossRef]
- Xing, L.; Li, J.Y.; Zhao, L.X.; Jiang, M.G.; Han, G.X. Structural Optimization of Downhole Hydrocyclones Based onResponse Surface Methodology. China Mech. Eng. 2021, 32, 1818–1826. [Google Scholar]
- Liu, M.; Chen, J.; Cai, X.; Han, Y.; Xiong, S. Oil-water pre-separation with a novel axial hydrocyclone. Chin. J. Chem. Eng. 2018, 26, 60–66. [Google Scholar] [CrossRef]
- Li, F.; Liu, H.L.; Xing, L.; Zhu, Y.M.; Gao, J.M. Influence of Gas Intake on the Performance of Gas Lift Cocurrent Outflow Cyclone. China Pet. Mach. 2021, 49, 100–106+141. [Google Scholar]
- Jiang, M.H.; Zhao, L.X.; Li, F.; Zunce, W. Cyclone Separation Technology; Press of Harbin Institute of Technology: Harbin, China, 2000. [Google Scholar]
- Bezerra, M.A.; Santelli, R.E.; Oliveira, E.P.; Villar, L.S.; Escaleira, L.A. Response surface methodology (RSM) as a tool for optimization in analytical chemistry. Talanta 2008, 76, 965–977. [Google Scholar] [CrossRef]

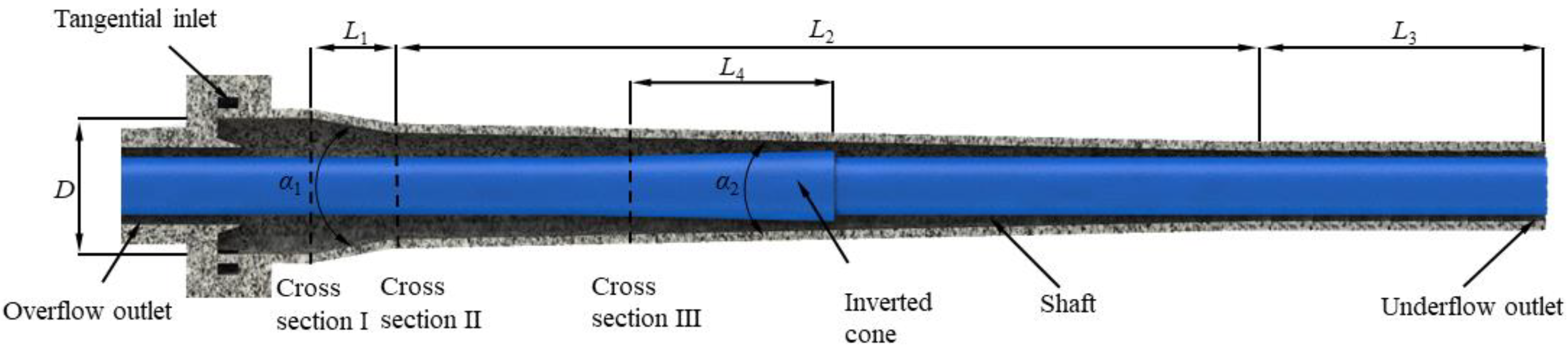

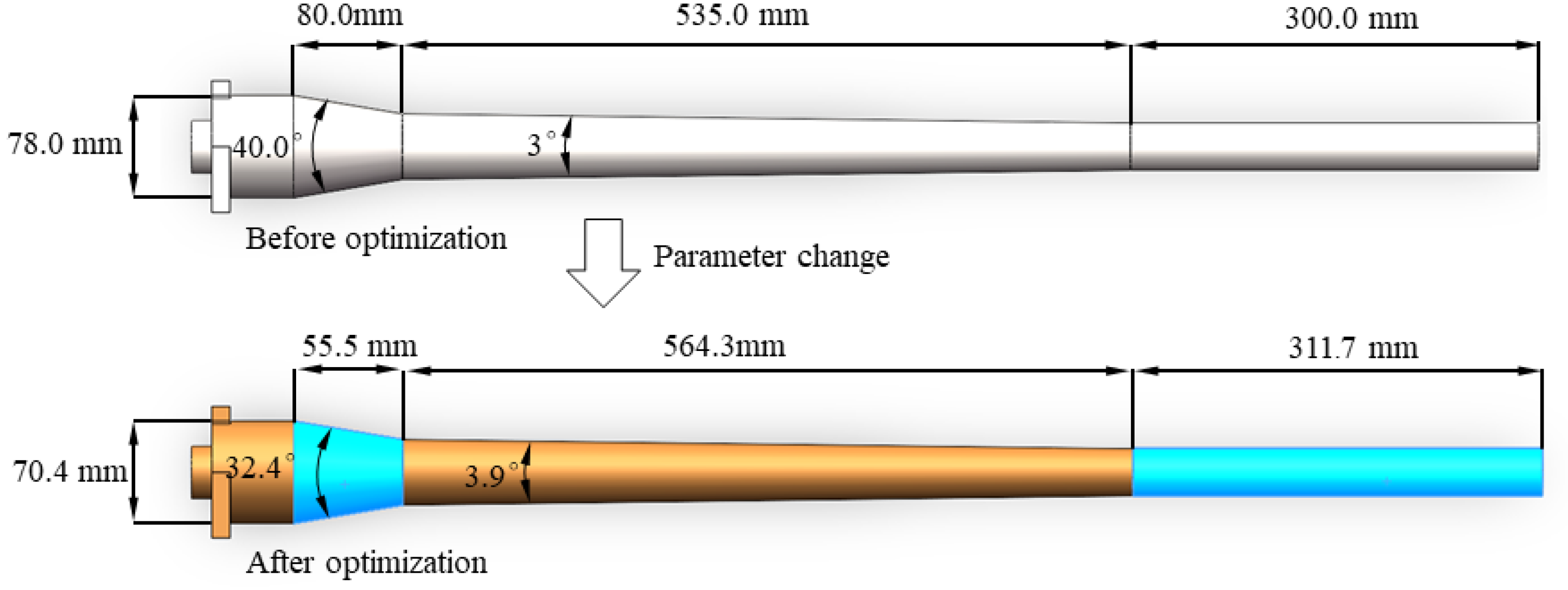

| Parameters | D | L1 | L2 | L3 | L4 | α1 | α2 |
| Numerical value | 78 mm | 80.0 mm | 535.0 mm | 300.0 mm | 166.0 mm | 40.0° | 3.0° |
| Factors | Symbol | Horizontal | ||
|---|---|---|---|---|
| Lower Limit (−1) | Upper Limit (1) | Central Point (0) | ||
| Length of inverted cone L1/mm | x1 | 100 | 200 | 150 |
| Angle of the large cone α1/° | x2 | 32 | 48 | 40 |
| Angle of the small cone α2/° | x3 | 2 | 4 | 3 |
| Length of underflow pipe L2/mm | x4 | 250 | 350 | 300 |
| Principal diameter L3/mm | x5 | 70 | 86 | 78 |
| Serial Number | x1 | x2 | x3 | x4 | x5 | Ez/% |
|---|---|---|---|---|---|---|
| 1 | 150 | 20 | 1.5 | 250 | 35 | 94.36 |
| 2 | 100 | 20 | 1.5 | 250 | 39 | 93.96 |
| 3 | 200 | 24 | 1.5 | 300 | 39 | 92.49 |
| 4 | 150 | 20 | 1 | 250 | 39 | 93.56 |
| 5 | 150 | 16 | 1.5 | 300 | 35 | 96.13 |
| 6 | 150 | 20 | 1 | 350 | 39 | 94.04 |
| 7 | 150 | 16 | 2 | 300 | 39 | 96.7 |
| 8 | 100 | 20 | 2 | 300 | 39 | 96.12 |
| 9 | 150 | 16 | 1.5 | 250 | 39 | 95.69 |
| 10 | 150 | 20 | 1 | 300 | 43 | 92.72 |
| 11 | 150 | 20 | 1.5 | 250 | 43 | 92.45 |
| 12 | 150 | 24 | 2 | 300 | 39 | 95.5 |
| 13 | 200 | 20 | 1.5 | 300 | 35 | 95.2 |
| 14 | 150 | 20 | 1.5 | 300 | 39 | 94.41 |
| 15 | 200 | 20 | 1.5 | 300 | 43 | 93.02 |
| 16 | 200 | 20 | 1.5 | 250 | 39 | 94.13 |
| 17 | 150 | 20 | 1.5 | 300 | 39 | 94.42 |
| 18 | 150 | 20 | 1.5 | 300 | 39 | 94.42 |
| 19 | 150 | 20 | 1.5 | 300 | 39 | 94.42 |
| 20 | 150 | 20 | 1.5 | 350 | 35 | 94.95 |
| 21 | 200 | 20 | 2 | 300 | 39 | 96.23 |
| 22 | 200 | 20 | 1 | 300 | 39 | 94.11 |
| 23 | 150 | 20 | 2 | 350 | 39 | 96.28 |
| 24 | 150 | 20 | 1.5 | 350 | 43 | 92.99 |
| 25 | 150 | 16 | 1.5 | 350 | 39 | 95.97 |
| 26 | 150 | 16 | 1.5 | 300 | 43 | 95.24 |
| 27 | 150 | 20 | 2 | 250 | 39 | 96.01 |
| 28 | 100 | 20 | 1.5 | 300 | 43 | 92.86 |
| 29 | 150 | 24 | 1 | 300 | 39 | 91.66 |
| 30 | 100 | 20 | 1.5 | 350 | 39 | 94.42 |
| 31 | 150 | 20 | 2 | 300 | 35 | 97.55 |
| 32 | 150 | 20 | 2 | 300 | 43 | 93.3 |
| 33 | 150 | 24 | 1.5 | 300 | 35 | 93.87 |
| 34 | 150 | 20 | 1 | 300 | 35 | 94.03 |
| 35 | 200 | 20 | 1.5 | 350 | 39 | 93.33 |
| 36 | 150 | 20 | 1.5 | 300 | 39 | 94.42 |
| 37 | 150 | 24 | 1.5 | 250 | 39 | 92.1 |
| 38 | 150 | 24 | 1.5 | 350 | 39 | 91.43 |
| 39 | 150 | 24 | 1.5 | 300 | 43 | 92.63 |
| 40 | 100 | 20 | 1 | 300 | 39 | 93.9 |
| 41 | 150 | 16 | 1 | 300 | 39 | 95.88 |
| 42 | 100 | 20 | 1.5 | 300 | 35 | 92.55 |
| 43 | 100 | 24 | 1.5 | 300 | 39 | 91.49 |
| 44 | 200 | 16 | 1.5 | 300 | 39 | 94.17 |
| 45 | 150 | 20 | 1.5 | 300 | 39 | 94.42 |
| 46 | 100 | 16 | 1.5 | 300 | 39 | 94.4 |
| Types | Sum of Squares of Deviation | Degree of Freedom | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 84.43 | 20 | 4.22 | 9.36 | <0.0001 |
| A—Inverted cone length | 0.56 | 1 | 0.56 | 1.23 | 0.2778 |
| B—Angle of the large cone | 33.09 | 1 | 33.09 | 73.37 | <0.0001 |
| C—Angle of the small cone | 19.78 | 1 | 19.78 | 43.86 | <0.0001 |
| D—Length of underflow pipe | 0.083 | 1 | 0.083 | 0.18 | 0.6722 |
| E—Principal diameter | 11.27 | 1 | 11.27 | 24.99 | <0.0001 |
| AB | 0.38 | 1 | 0.38 | 0.84 | 0.3685 |
| AC | 2.500 × 10−3 | 1 | 2.500 × 10−3 | 5.543 × 10−3 | 0.9412 |
| AD | 0.40 | 1 | 0.40 | 0.88 | 0.3572 |
| AE | 1.55 | 1 | 1.55 | 3.44 | 0.0756 |
| BC | 2.28 | 1 | 2.28 | 5.06 | 0.0336 |
| BD | 0.23 | 1 | 0.23 | 0.50 | 0.4859 |
| BE | 0.031 | 1 | 0.031 | 0.068 | 0.7965 |
| CD | 0.011 | 1 | 0.011 | 0.024 | 0.8770 |
| CE | 2.16 | 1 | 2.16 | 4.79 | 0.0382 |
| DE | 6.250 × 10−4 | 1 | 6.250 × 10−4 | 1.386 × 10−3 | 0.9706 |
| A2 | 2.17 | 1 | 2.17 | 4.81 | 0.0377 |
| B2 | 0.55 | 1 | 0.55 | 1.22 | 0.2796 |
| C2 | 5.16 | 1 | 5.16 | 11.44 | 0.0024 |
| D2 | 0.44 | 1 | 0.44 | 0.98 | 0.3327 |
| E2 | 1.24 | 1 | 1.24 | 2.74 | 0.1104 |
| Residual | 11.28 | 25 | 0.45 | ||
| Lack of Fit | 11.28 | 20 | 0.56 | 33825.40 | <0.0001 |
| Pure Error | 8.333 × 10−5 | 5 | 1.667 × 10−5 | ||
| Cor Total | 95.70 | 45 |
| Statistical Item | Value | Statistical Item | Value |
|---|---|---|---|
| Std. Dev. | 0.67 | R-squared | 0.8822 |
| Mean | 94.22 | Adj R-squared | 0.7879 |
| C.V. % | 0.71 | Pred R-squared | 0.5287 |
| PRESS | 45.10 | Adeq Precision | 13.380 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, Y.; Liu, H.; Yu, J.; Zhao, X.; Cao, G.; Yang, Q.; Jia, D.; Zheng, L. Design and Analysis of an Axial Center-Piercing Hydrocyclone. Energies 2023, 16, 6800. https://doi.org/10.3390/en16196800
Gao Y, Liu H, Yu J, Zhao X, Cao G, Yang Q, Jia D, Zheng L. Design and Analysis of an Axial Center-Piercing Hydrocyclone. Energies. 2023; 16(19):6800. https://doi.org/10.3390/en16196800
Chicago/Turabian StyleGao, Yang, He Liu, Jiaqing Yu, Xiaojie Zhao, Gang Cao, Qinghai Yang, Deli Jia, and Lichen Zheng. 2023. "Design and Analysis of an Axial Center-Piercing Hydrocyclone" Energies 16, no. 19: 6800. https://doi.org/10.3390/en16196800
APA StyleGao, Y., Liu, H., Yu, J., Zhao, X., Cao, G., Yang, Q., Jia, D., & Zheng, L. (2023). Design and Analysis of an Axial Center-Piercing Hydrocyclone. Energies, 16(19), 6800. https://doi.org/10.3390/en16196800





