Wind Turbine Gearbox Condition Monitoring Using Hybrid Attentions and Spatio-Temporal BiConvLSTM Network
Abstract
:1. Introduction
- (1)
- Existing condition monitoring approaches primarily incorporate attention mechanisms in the following two ways: (a) Introducing the feature attention mechanism on the model-input variables dimension to assign attention weights according to the impact of different model input features on model output; (b) Introducing the time attention mechanism on the time dimension to assign larger attention weights to time steps that are highly correlated with the current prediction. However, these approaches often lack consideration for a multi-dimensional attention fusion.
- (2)
- The network structures of spatio-temporal models in the previous studies have inherent disadvantages, specifically the issues of non-interactivity and non-synchronicity when attempting to extract spatio-temporal features from SCADA time series data. These limitations can have adverse effects on model performance.
- (1)
- This study proposed a multi-dimensional hybrid-attention mechanism (HA). By introducing attention mechanisms into the spatial-dimension and temporal-dimension of model input data matrices produced by the sliding window approach, multi-dimensional attention weights can be calculated and assigned to input matrices to increase key feature weights and weaken or discard redundant features. The experimental results showed that the hybrid-attention mechanism can significantly improve the model performance.
- (2)
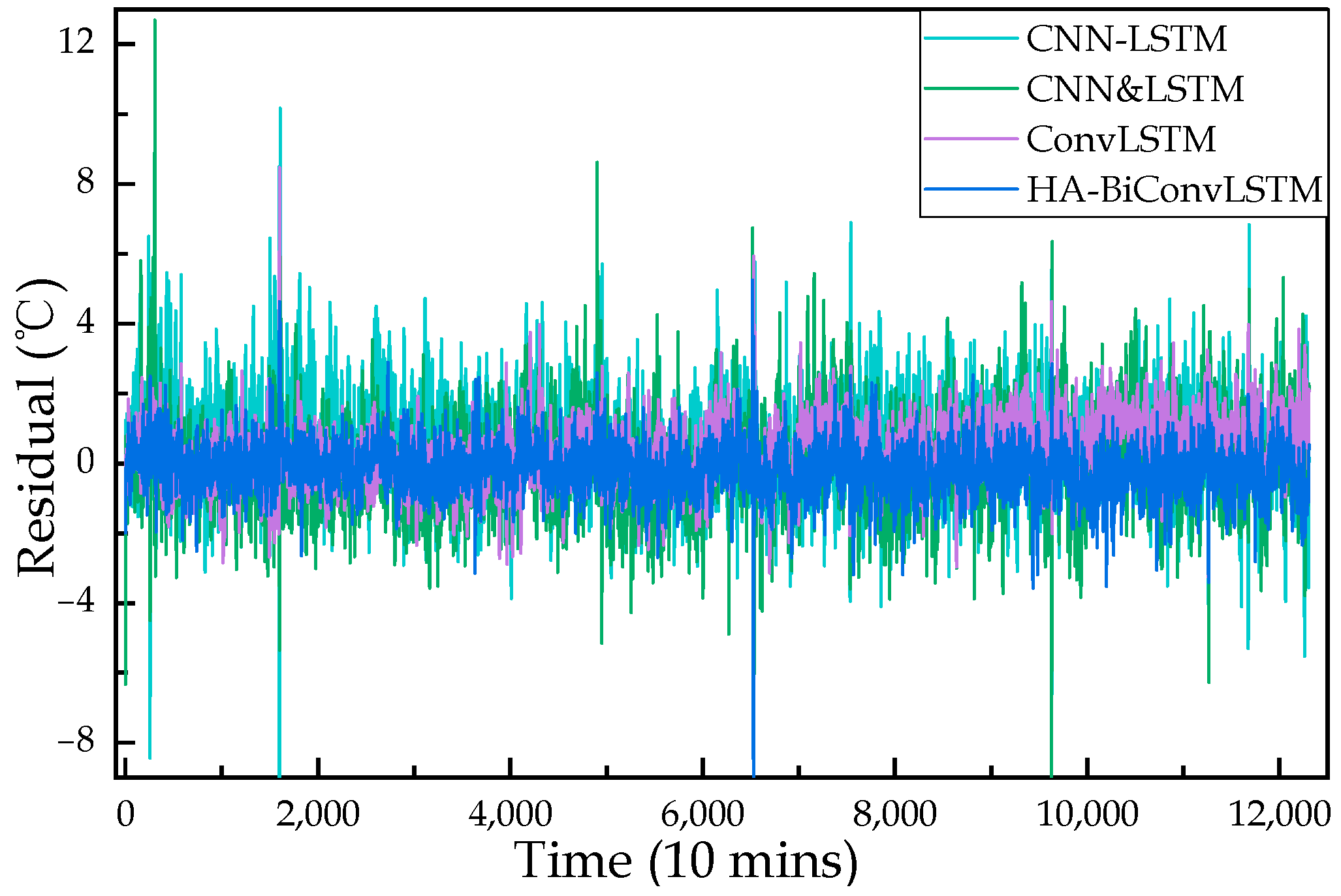
- We constructed a novel HA-BiConvLSTM spatio-temporal normal behavior model (NBM) for a wind turbine gearbox. Convolutional long short-term memory (ConvLSTM) perfectly integrates the powerful local spatial-feature extractive capability of CNN and the efficient time series processing capability of LSTM, the embedded network structure of which compensates disadvantages of conventional parallel or sequential structures (denoted as CNN-LSTM and CNN&LSTM) to some extent. Compared with CNN-LSTM and CNN&LSTM, the constructed HA-BiConvLSTM model achieved better valuation result in terms of RMSE, MAE, MAPE, and R2 metrics.
- (3)
- We designed an improved EWMA-based dynamic anomaly detection approach. Based on the exponentially weighted moving-average algorithm (EWMA), the adaptive outlier thresholds of prediction residuals of different well-trained gearbox NBMs can be calculated to identify outliers. To reduce false alarms caused by some isolated outliers, an anomaly detection index, i.e., the outlier ratio within a sliding window, was proposed to improve the reliability of early gearbox faults. Results of the case study illustrated that the proposed HA-BiConvLSTM-iEWMA (HBCE) method can detect gearbox deteriorated conditions earlier than conventional CNN-LSTM and CNN&LSTM models, which verified the effectiveness, superiority, and robustness of the constructed HA-BiConvLSTM model.
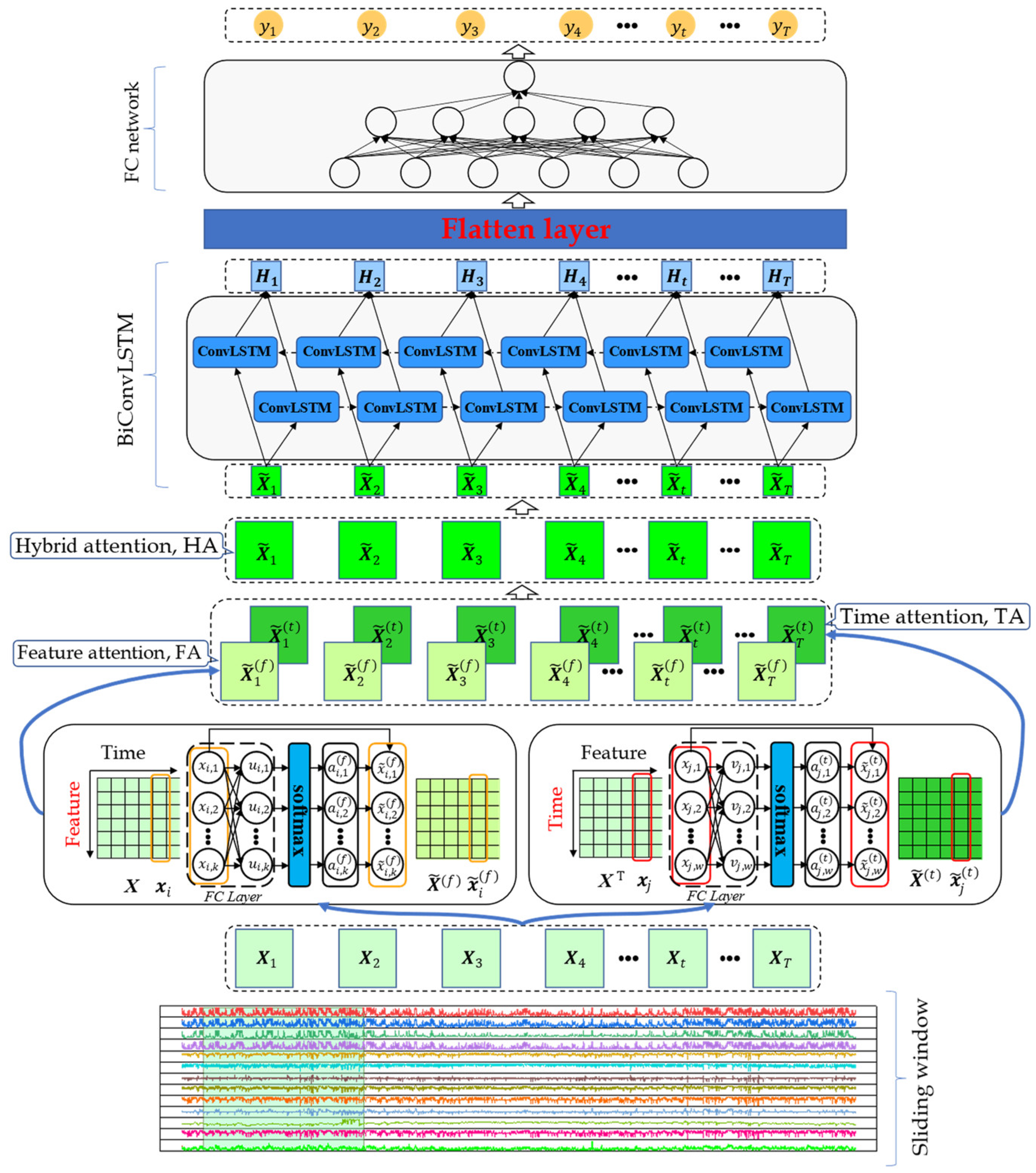
2. Framework of the Proposed HBCE Method
3. Constructed HA-BiConvLSTM Model
3.1. Data Preprocessing
3.1.1. Data Cleaning
3.1.2. Data Normalization
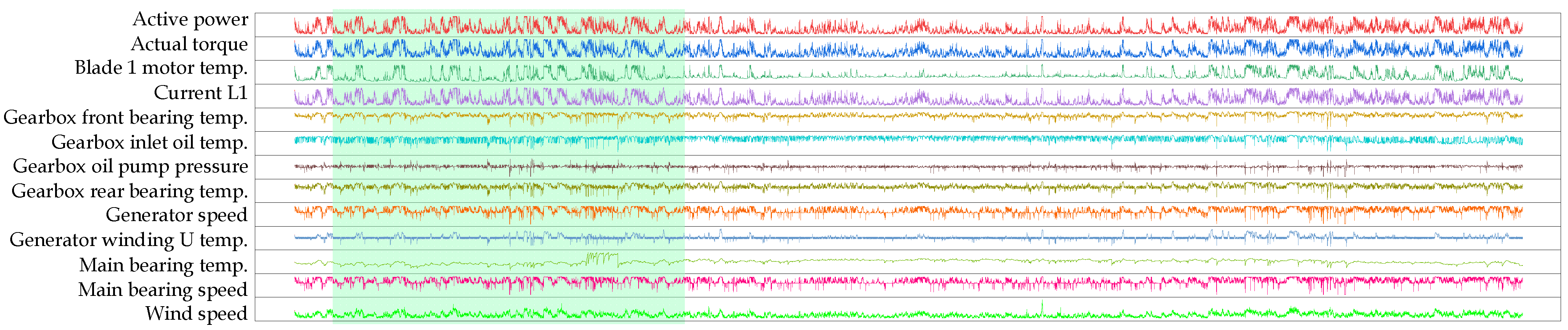
3.1.3. Variable Selection
3.1.4. Model Input Matrices Based on the Sliding Window Algorithm
3.2. Spatio-Temporal Hybrid Attention Mechanism
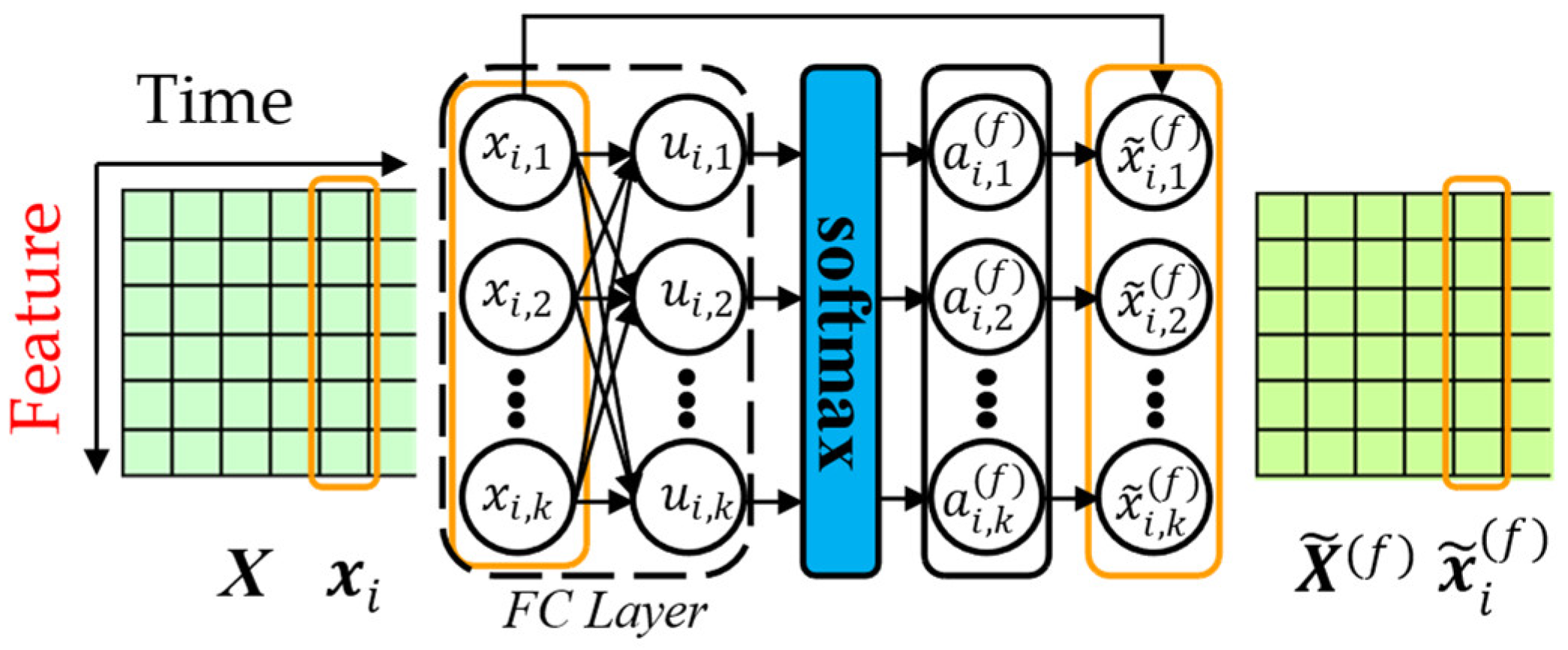
3.2.1. Feature Attention
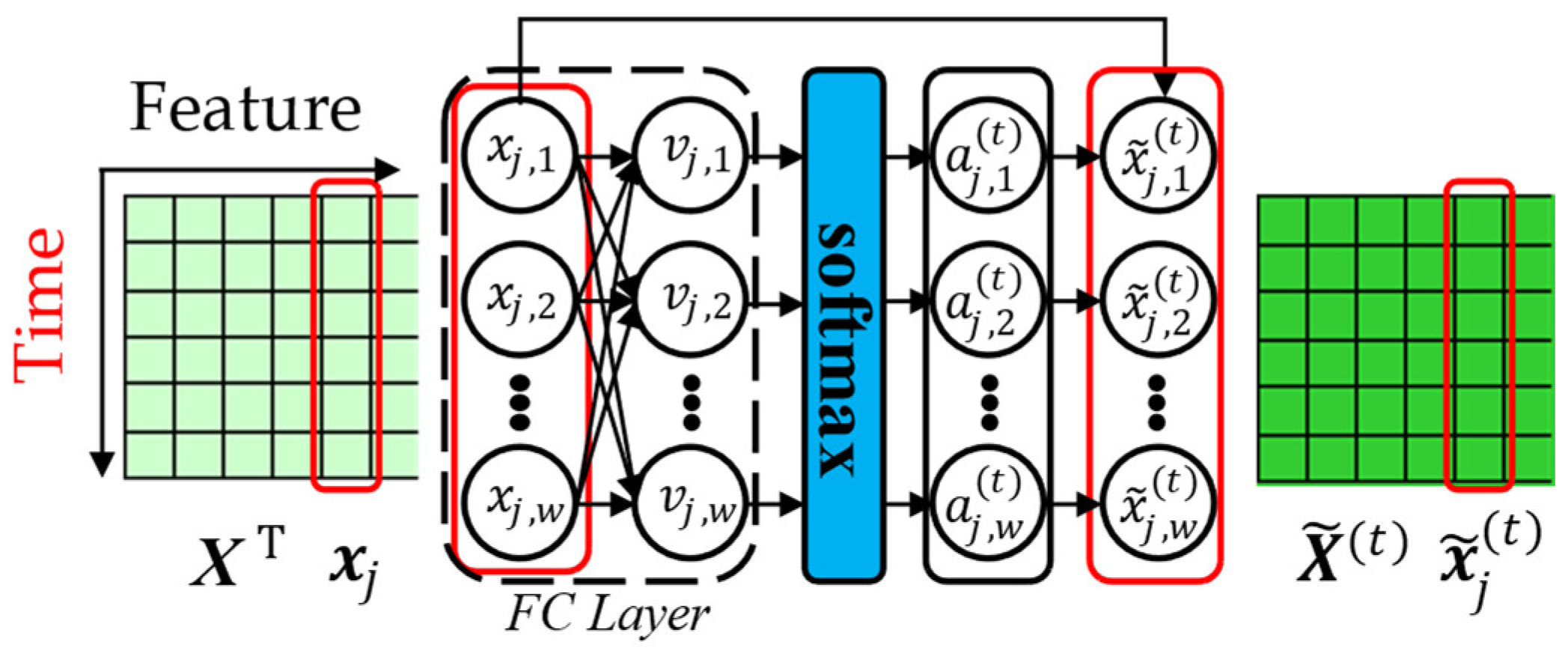
3.2.2. Time Attention
3.2.3. Hybrid Attention
3.3. Bidirectional Conventional Long Short-Term Memory Network
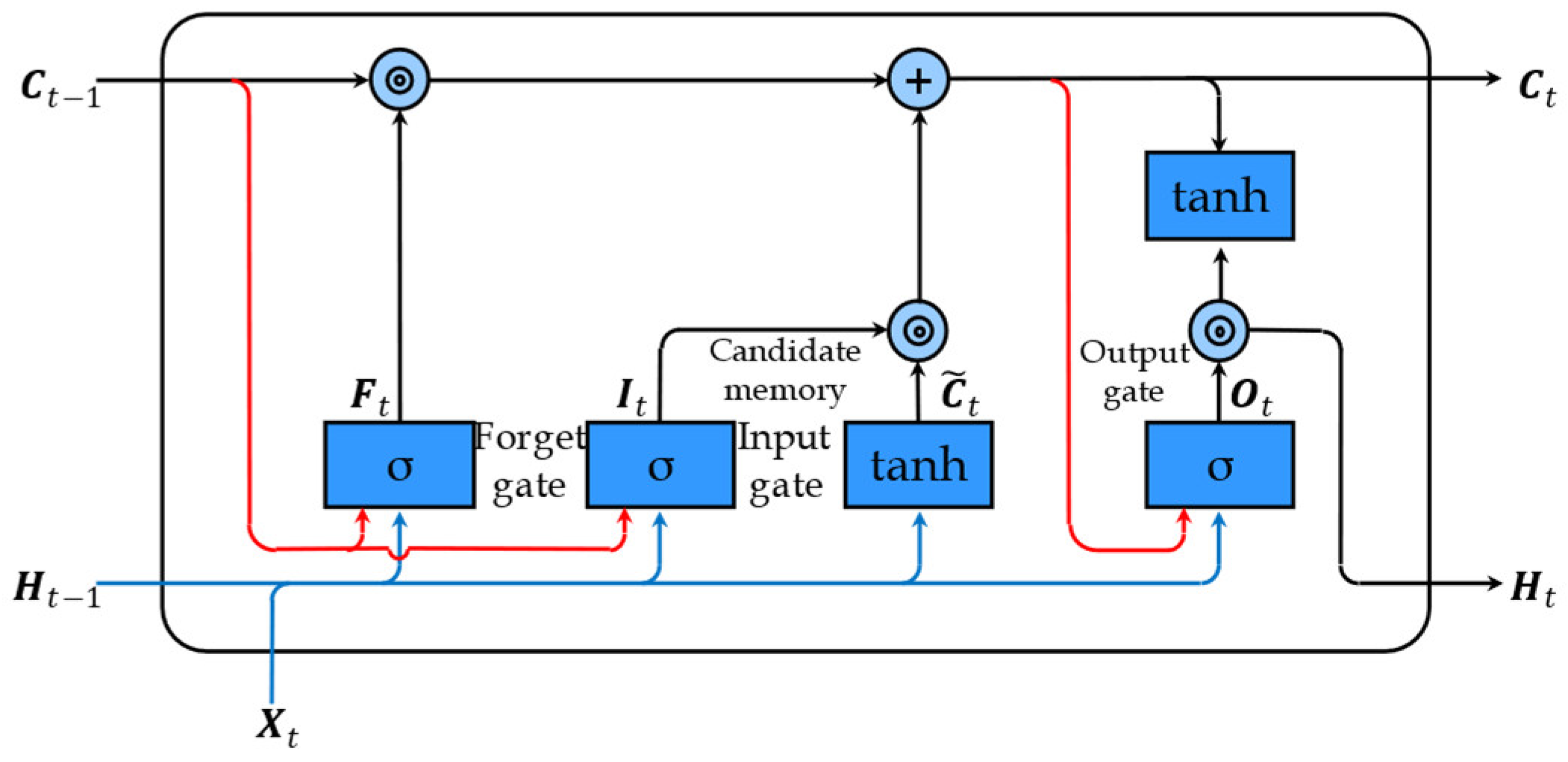
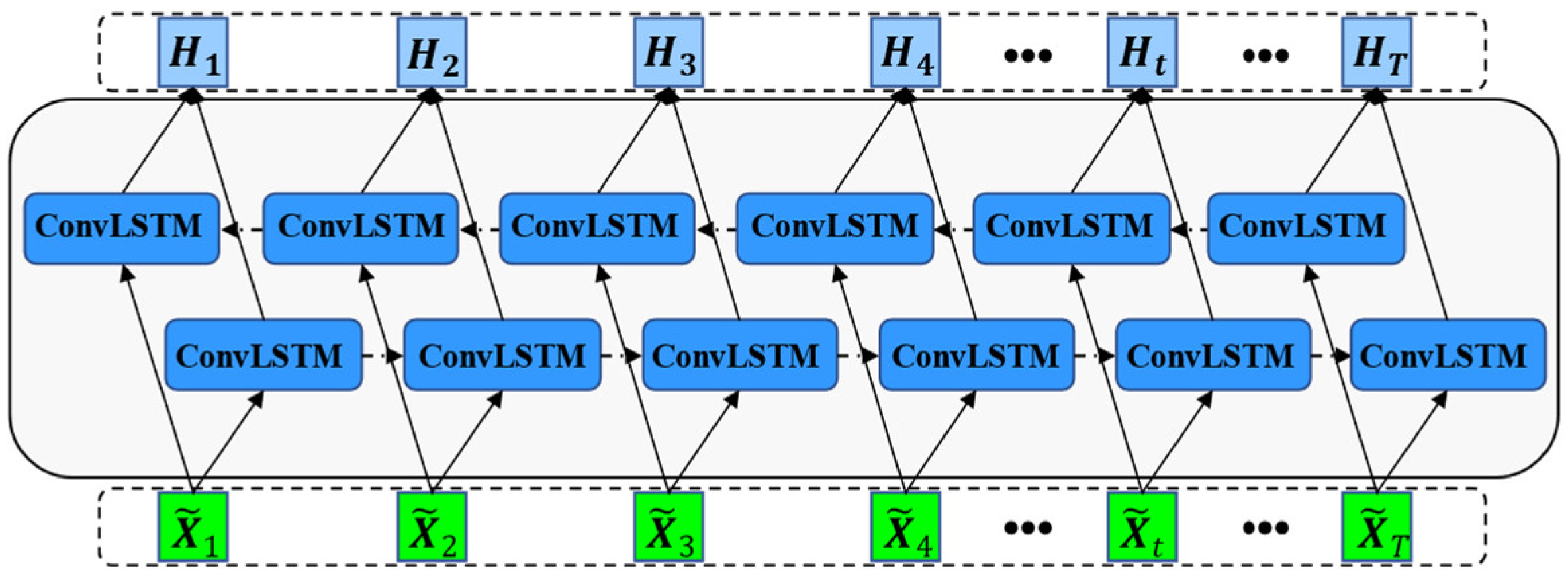
3.3.1. ConvLSTM
3.3.2. BiConvLSTM
3.4. Structure of the Constructed HA-BiConvLSTM Model
3.5. Evaluation Metrics
4. Condition Monitoring
5. Case Study
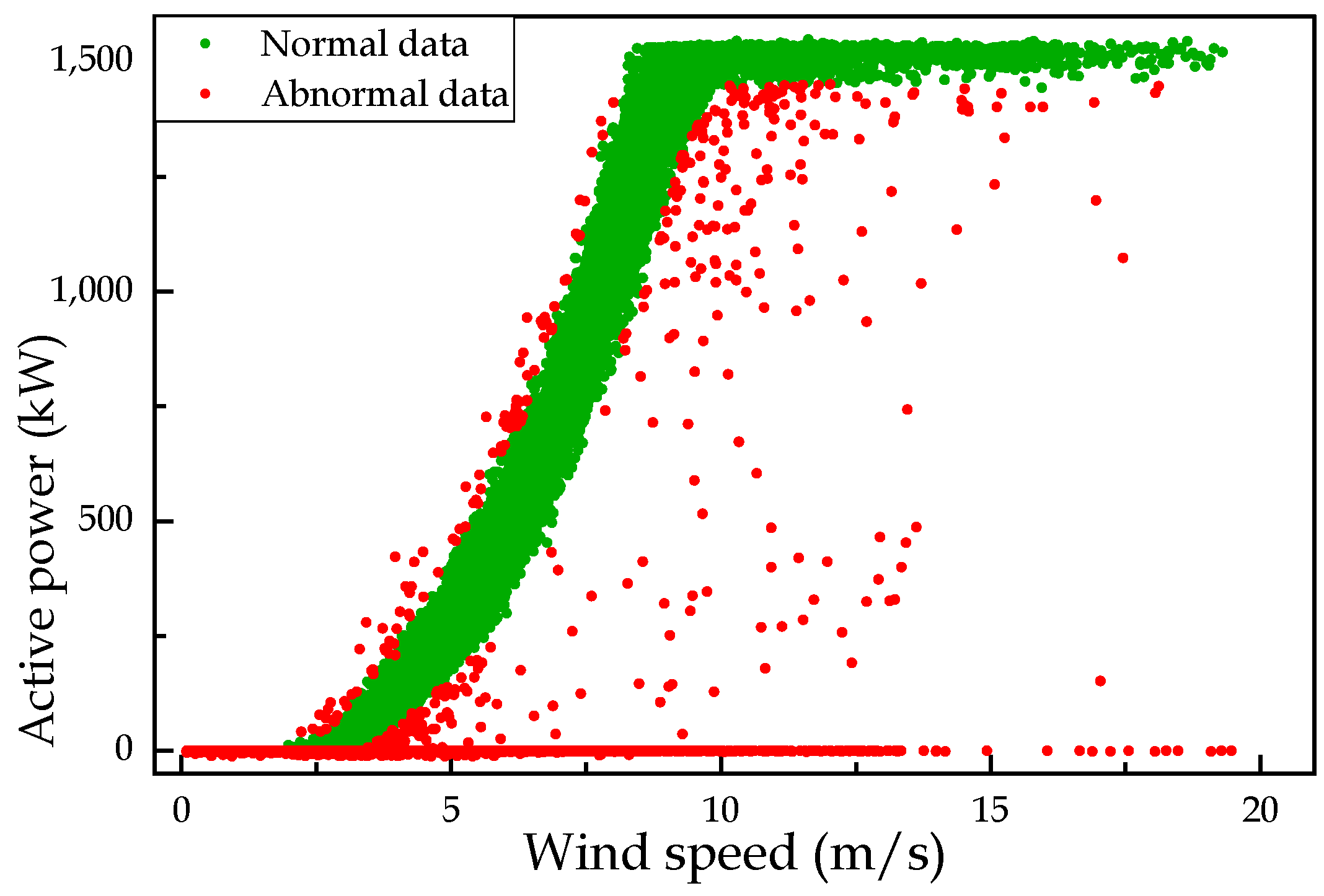
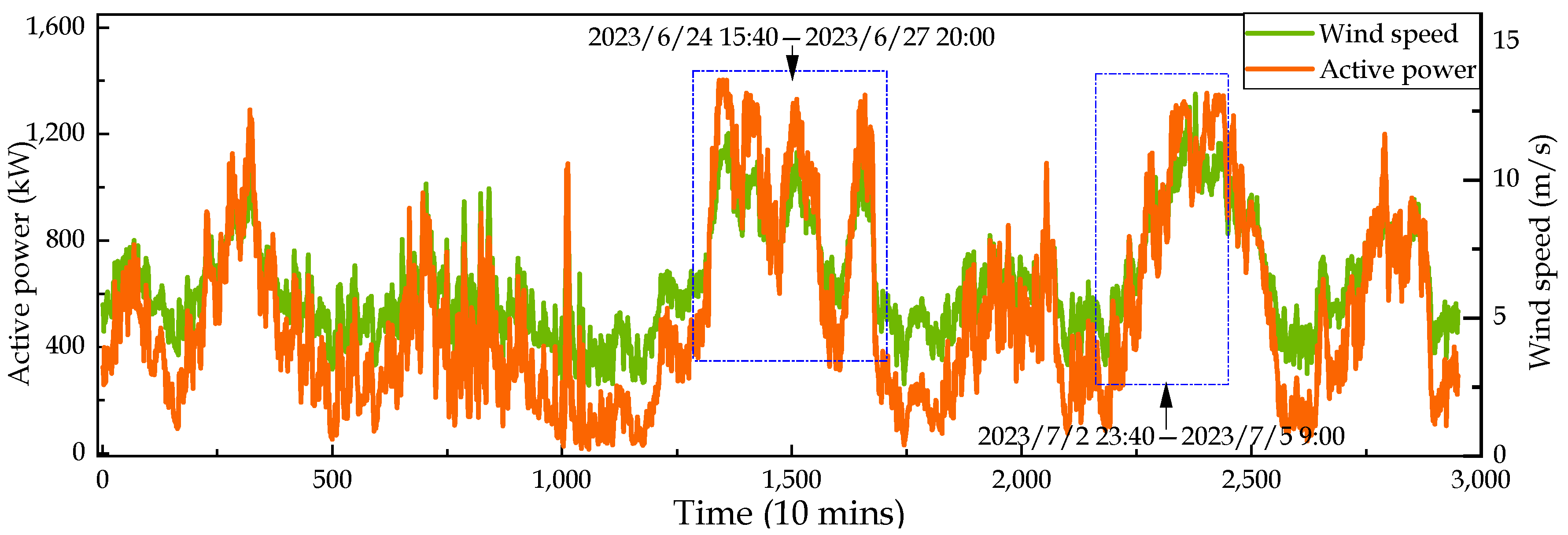
5.1. Data Description
5.2. Data Preprocessing
5.3. Variable Selection
5.4. Model Train and Test
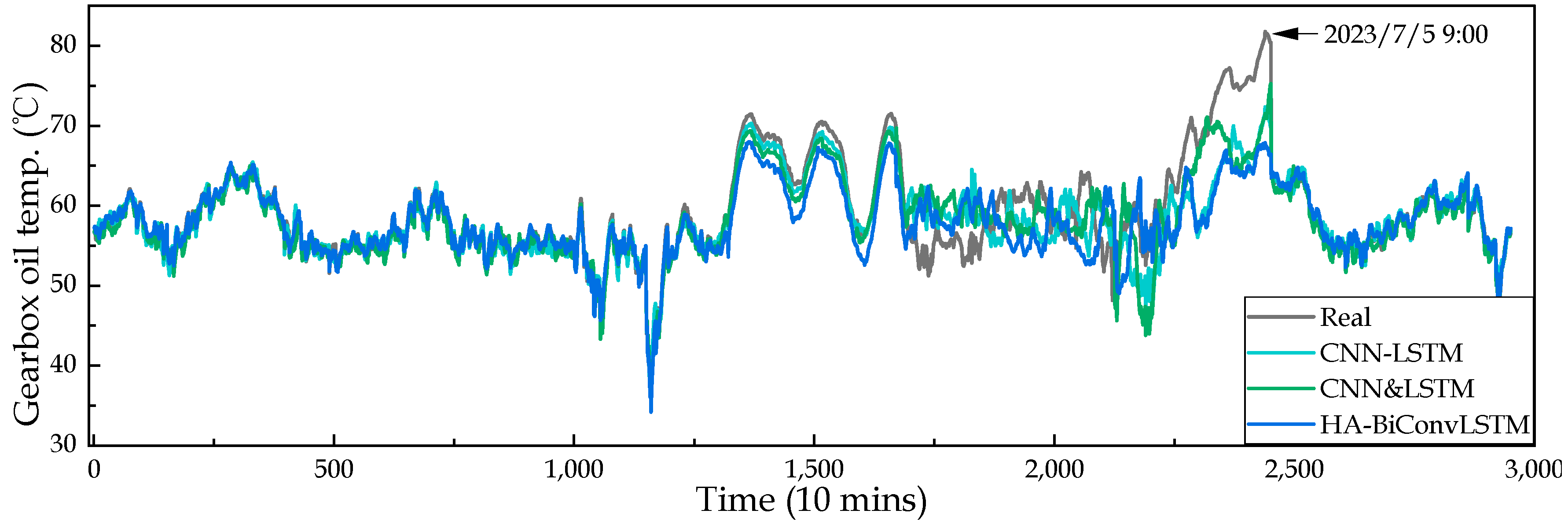
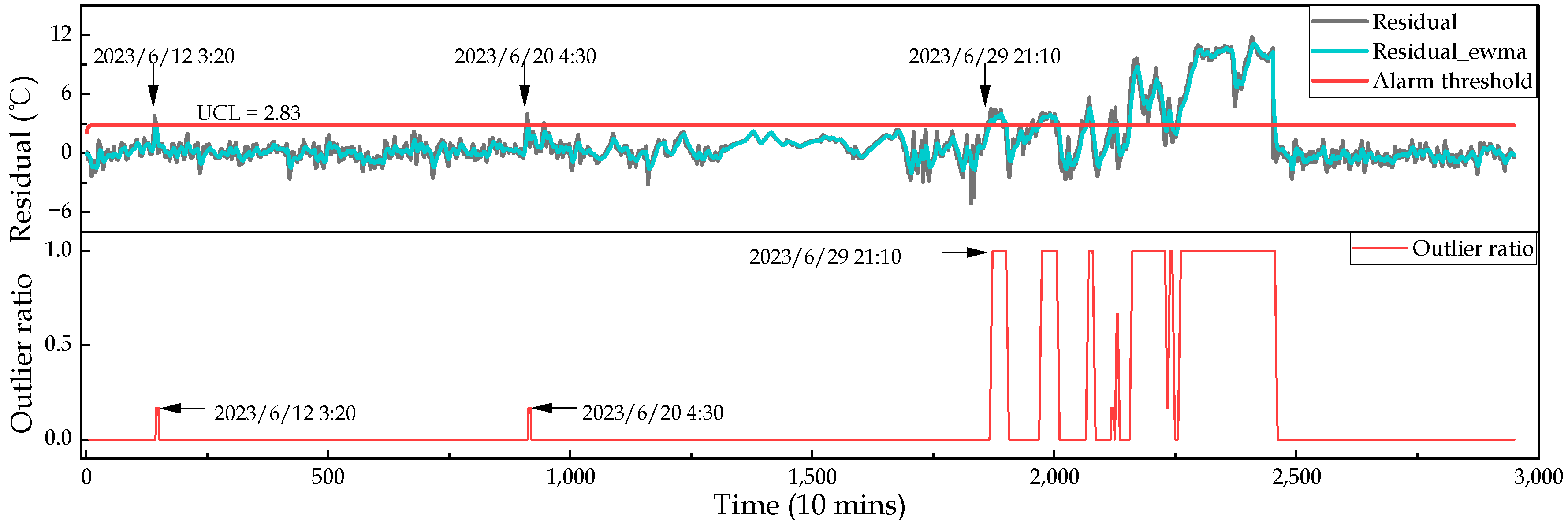
5.5. Condition Monitoring
6. Conclusions
- (1)
- The ConvLSTM model efficiently integrates CNN and LSTM through an embedded network structure, and overcomes the non-interactive or non-synchronous problems of conventional models when extracting spatio-temporal features. Compared with CNN-LSTM and CNN&LSTM, the ConvLSTM model presented better performance with lower RMSE, MAE, and MAPE values and a higher R2 value.
- (2)
- The introduced hybrid attention mechanism can significantly enhance the model performance by calculating and assigning different attention weights from the spatio-temporal dimension for model input features. The constructed HA-BiConvLSTM model achieved the RMSE, MAE, and MAPE reductions by about 21.27%, 23.75%, and 23.97%, and the R2 improvement by 1.06%, in comparison with the ConvLSTM model.
- (3)
- The proposed HBCE method has superior and robust early fault warning capabilities, which can efficiently identify early deteriorated conditions of a wind turbine gearbox 253.17 h in advance of the actual failure time, and 121.34 h, 33.67 h earlier than CNN-LSTM and CNN&LSTM.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, J.; Liang, Y.; Zheng, Y.; Gao, R.X.; Zhang, F. An Integrated Fault Diagnosis and Prognosis Approach for Predictive Maintenance of Wind Turbine Bearing with Limited Samples. Renew. Energy 2020, 145, 642–650. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, C. Wind Turbine Condition Monitoring Based on a Novel Multivariate State Estimation Technique. Measurement 2021, 168, 108388. [Google Scholar] [CrossRef]
- Park, J.; Kim, C.; Dinh, M.-C.; Park, M. Design of a Condition Monitoring System for Wind Turbines. Energies 2022, 15, 464. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhu, C.; Song, C.; Li, Y.; Chen, X.; Yong, B. Improvement of Reliability and Wind Power Generation Based on Wind Turbine Real-Time Condition Assessment. Int. J. Electr. Power Energy Syst. 2019, 113, 344–354. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhu, C.; Tan, J.; Wang, Y.; Tao, J. Operational State Assessment of Wind Turbine Gearbox Based on Long Short-Term Memory Networks and Fuzzy Synthesis. Renew. Energy 2022, 181, 1167–1176. [Google Scholar] [CrossRef]
- Pérez-Pérez, E.-J.; López-Estrada, F.-R.; Puig, V.; Valencia-Palomo, G.; Santos-Ruiz, I. Fault Diagnosis in Wind Turbines Based on ANFIS and Takagi–Sugeno Interval Observers. Expert Syst. Appl. 2022, 206, 117698. [Google Scholar] [CrossRef]
- Cho, S.; Choi, M.; Gao, Z.; Moan, T. Fault Detection and Diagnosis of a Blade Pitch System in a Floating Wind Turbine Based on Kalman Filters and Artificial Neural Networks. Renew. Energy 2021, 169, 1–13. [Google Scholar] [CrossRef]
- Su, H.; Zhao, Y.; Wang, X. Analysis of a State Degradation Model and Preventive Maintenance Strategies for Wind Turbine Generators Based on Stochastic Differential Equations. Mathematics 2023, 11, 2608. [Google Scholar] [CrossRef]
- Jiang, G.; Jia, C.; Nie, S.; Wu, X.; He, Q.; Xie, P. Multiview Enhanced Fault Diagnosis for Wind Turbine Gearbox Bearings with Fusion of Vibration and Current Signals. Measurement 2022, 196, 111159. [Google Scholar] [CrossRef]
- Pandit, R.K.; Infield, D. SCADA-Based Wind Turbine Anomaly Detection Using Gaussian Process Models for Wind Turbine Condition Monitoring Purposes. IET Renew. Power Gener. 2018, 12, 1249–1255. [Google Scholar] [CrossRef]
- Sun, P.; Li, J.; Wang, C.; Lei, X. A Generalized Model for Wind Turbine Anomaly Identification Based on SCADA Data. Appl. Energy 2016, 168, 550–567. [Google Scholar] [CrossRef]
- Xie, T.; Xu, Q.; Jiang, C.; Lu, S.; Wang, X. The Fault Frequency Priors Fusion Deep Learning Framework with Application to Fault Diagnosis of Offshore Wind Turbines. Renew. Energy 2023, 202, 143–153. [Google Scholar] [CrossRef]
- Zhang, J.; Xu, B.; Wang, Z.; Zhang, J. An FSK-MBCNN Based Method for Compound Fault Diagnosis in Wind Turbine Gearboxes. Measurement 2021, 172, 108933. [Google Scholar] [CrossRef]
- Liu, X.; Guo, H.; Liu, Y. One-Shot Fault Diagnosis of Wind Turbines Based on Meta-Analogical Momentum Contrast Learning. Energies 2022, 15, 3133. [Google Scholar] [CrossRef]
- López de Calle, K.; Ferreiro, S.; Roldán-Paraponiaris, C.; Ulazia, A. A Context-Aware Oil Debris-Based Health Indicator for Wind Turbine Gearbox Condition Monitoring. Energies 2019, 12, 3373. [Google Scholar] [CrossRef]
- Fuentes, R.; Dwyer-Joyce, R.S.; Marshall, M.B.; Wheals, J.; Cross, E.J. Detection of Sub-Surface Damage in Wind Turbine Bearings Using Acoustic Emissions and Probabilistic Modelling. Renew. Energy 2020, 147, 776–797. [Google Scholar] [CrossRef]
- Ma, Z.; Zhao, M.; Luo, M.; Gou, C.; Xu, G. An Integrated Monitoring Scheme for Wind Turbine Main Bearing Using Acoustic Emission. Signal Process. 2023, 205, 108867. [Google Scholar] [CrossRef]
- Attallah, O.; Ibrahim, R.A.; Zakzouk, N.E. CAD System for Inter-Turn Fault Diagnosis of Offshore Wind Turbines via Multi-CNNs & Feature Selection. Renew. Energy 2023, 203, 870–880. [Google Scholar] [CrossRef]
- Attallah, O.; Ibrahim, R.A.; Zakzouk, N.E. Fault Diagnosis for Induction Generator-Based Wind Turbine Using Ensemble Deep Learning Techniques. Energy Rep. 2022, 8, 12787–12798. [Google Scholar] [CrossRef]
- Heydari, A.; Garcia, D.A.; Fekih, A.; Keynia, F.; Tjernberg, L.B.; De Santoli, L. A Hybrid Intelligent Model for the Condition Monitoring and Diagnostics of Wind Turbines Gearbox. IEEE Access 2021, 9, 89878–89890. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhu, C.; Tan, J.; Tan, Y.; Rao, L. Anomaly Detection and Condition Monitoring of Wind Turbine Gearbox Based on LSTM-FS and Transfer Learning. Renew. Energy 2022, 189, 90–103. [Google Scholar] [CrossRef]
- McKinnon, C.; Carroll, J.; McDonald, A.; Koukoura, S.; Plumley, C. Investigation of Isolation Forest for Wind Turbine Pitch System Condition Monitoring Using SCADA Data. Energies 2021, 14, 6601. [Google Scholar] [CrossRef]
- Tao, T.; Liu, Y.; Qiao, Y.; Gao, L.; Lu, J.; Zhang, C.; Wang, Y. Wind Turbine Blade Icing Diagnosis Using Hybrid Features and Stacked-XGBoost Algorithm. Renew. Energy 2021, 180, 1004–1013. [Google Scholar] [CrossRef]
- Guo, P.; Fu, J.; Yang, X. Condition Monitoring and Fault Diagnosis of Wind Turbines Gearbox Bearing Temperature Based on Kolmogorov-Smirnov Test and Convolutional Neural Network Model. Energies 2018, 11, 2248. [Google Scholar] [CrossRef]
- Wang, D.; Cao, C.; Chen, N.; Pan, W.; Li, H.; Wang, X. A Correlation-Graph-CNN Method for Fault Diagnosis of Wind Turbine Based on State Tracking and Data Driving Model. Sustain. Energy Technol. Assess. 2023, 56, 102995. [Google Scholar] [CrossRef]
- Yang, W.; Liu, C.; Jiang, D. An Unsupervised Spatiotemporal Graphical Modeling Approach for Wind Turbine Condition Monitoring. Renew. Energy 2018, 127, 230–241. [Google Scholar] [CrossRef]
- Wang, H.; Wang, H.; Jiang, G.; Wang, Y.; Ren, S. A Multiscale Spatio-Temporal Convolutional Deep Belief Network for Sensor Fault Detection of Wind Turbine. Sensors 2020, 20, 3580. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, S.; Wang, P.; Jiang, P.; Zhou, H. Research on Fault Early Warning of Wind Turbine Based on IPSO-DBN. Energies 2022, 15, 9072. [Google Scholar] [CrossRef]
- Jia, X.; Han, Y.; Li, Y.; Sang, Y.; Zhang, G. Condition Monitoring and Performance Forecasting of Wind Turbines Based on Denoising Autoencoder and Novel Convolutional Neural Networks; Social Science Research Network: Rochester, NY, USA, 2021. [Google Scholar]
- Zhang, C.; Hu, D.; Yang, T. Anomaly Detection and Diagnosis for Wind Turbines Using Long Short-Term Memory-Based Stacked Denoising Autoencoders and XGBoost. Reliab. Eng. Syst. Saf. 2022, 222, 108445. [Google Scholar] [CrossRef]
- Wu, Y.; Ma, X. A Hybrid LSTM-KLD Approach to Condition Monitoring of Operational Wind Turbines. Renew. Energy 2022, 181, 554–566. [Google Scholar] [CrossRef]
- Li, G.; Wang, C.; Zhang, D.; Yang, G. An Improved Feature Selection Method Based on Random Forest Algorithm for Wind Turbine Condition Monitoring. Sensors 2021, 21, 5654. [Google Scholar] [CrossRef] [PubMed]
- Xiao, X.; Liu, J.; Liu, D.; Tang, Y.; Qin, S.; Zhang, F. A Normal Behavior-Based Condition Monitoring Method for Wind Turbine Main Bearing Using Dual Attention Mechanism and Bi-LSTM. Energies 2022, 15, 8462. [Google Scholar] [CrossRef]
- Xiang, L.; Wang, P.; Yang, X.; Hu, A.; Su, H. Fault Detection of Wind Turbine Based on SCADA Data Analysis Using CNN and LSTM with Attention Mechanism. Measurement 2021, 175, 109094. [Google Scholar] [CrossRef]
- Pang, Y.; He, Q.; Jiang, G.; Xie, P. Spatio-Temporal Fusion Neural Network for Multi-Class Fault Diagnosis of Wind Turbines Based on SCADA Data. Renew. Energy 2020, 161, 510–524. [Google Scholar] [CrossRef]
- Zhu, A.; Zhao, Q.; Yang, T.; Zhou, L.; Zeng, B. Condition Monitoring of Wind Turbine Based on Deep Learning Networks and Kernel Principal Component Analysis. Comput. Electr. Eng. 2023, 105, 108538. [Google Scholar] [CrossRef]
- Kong, Z.; Tang, B.; Deng, L.; Liu, W.; Han, Y. Condition Monitoring of Wind Turbines Based on Spatio-Temporal Fusion of SCADA Data by Convolutional Neural Networks and Gated Recurrent Units. Renew. Energy 2020, 146, 760–768. [Google Scholar] [CrossRef]
- Xiang, L.; Yang, X.; Hu, A.; Su, H.; Wang, P. Condition Monitoring and Anomaly Detection of Wind Turbine Based on Cascaded and Bidirectional Deep Learning Networks. Appl. Energy 2022, 305, 117925. [Google Scholar] [CrossRef]
- Zhan, J.; Wu, C.; Yang, C.; Miao, Q.; Wang, S.; Ma, X. Condition Monitoring of Wind Turbines Based on Spatial-Temporal Feature Aggregation Networks. Renew. Energy 2022, 200, 751–766. [Google Scholar] [CrossRef]
- Bahdanau, D.; Cho, K.; Bengio, Y. Neural Machine Translation by Jointly Learning to Align and Translate. arXiv 2016, arXiv:1409.0473. [Google Scholar]
- Werbos, P.J. Backpropagation through Time: What It Does and How to Do It. Proc. IEEE 1990, 78, 1550–1560. [Google Scholar] [CrossRef]
- Kolen, J.F.; Kremer, S.C. Gradient Flow in Recurrent Nets: The Difficulty of Learning LongTerm Dependencies. In A Field Guide to Dynamical Recurrent Networks; IEEE: New York, NY, USA, 2001; pp. 237–243. ISBN 978-0-470-54403-7. [Google Scholar]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.-Y.; Wong, W.; Woo, W. Convolutional LSTM Network: A Machine Learning Approach for Precipitation Nowcasting. Adv. Neural Inf. Process. Syst. 2015, 28. [Google Scholar]
- Graves, A. Generating Sequences with Recurrent Neural Networks. arXiv 2014, arXiv:1308.0850. [Google Scholar]

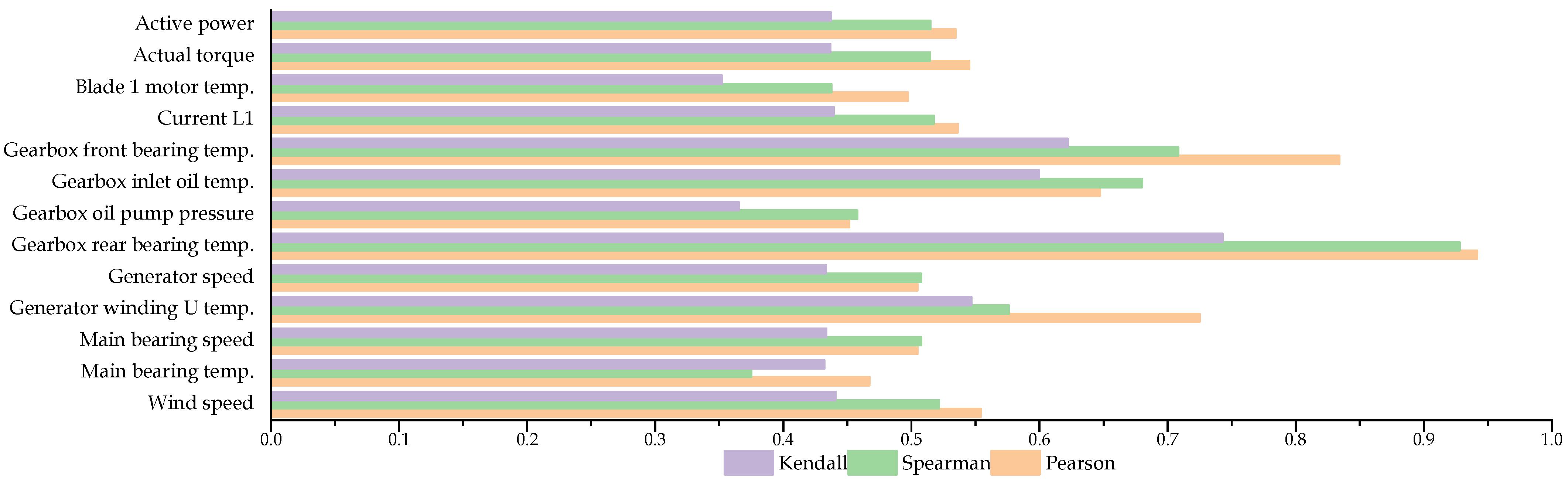




| Dataset | WT Number | Time Range | Data Size | Fault Time | Fault Type |
|---|---|---|---|---|---|
| Health dataset H | #23 | 1 January 2020–31 December 2020 | 51,451 | —— | —— |
| Fault dataset F | #17 | 10 June 2020–11 July 2020 | 2983 | 5 July 2023 9:00 | Gearbox oil overtemperature |
| Original Health Dataset | Model Dataset | Train Set | Test Set |
|---|---|---|---|
| 51,451 | 43,167 | 30,217 | 12,950 |
| Model | RMSE | MAE | MAPE | R2 |
|---|---|---|---|---|
| CNN-LSTM | 1.5003 | 1.1395 | 0.0196 | 0.9533 |
| CNN&LSTM | 1.3537 | 1.0252 | 0.0176 | 0.9669 |
| ConvLSTM | 0.9759 | 0.7471 | 0.0129 | 0.9814 |
| HA-BiConvLSTM | 0.7683 | 0.5696 | 0.0098 | 0.9918 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, J.; Liu, Y.; Ren, X.; Li, L. Wind Turbine Gearbox Condition Monitoring Using Hybrid Attentions and Spatio-Temporal BiConvLSTM Network. Energies 2023, 16, 6786. https://doi.org/10.3390/en16196786
Yan J, Liu Y, Ren X, Li L. Wind Turbine Gearbox Condition Monitoring Using Hybrid Attentions and Spatio-Temporal BiConvLSTM Network. Energies. 2023; 16(19):6786. https://doi.org/10.3390/en16196786
Chicago/Turabian StyleYan, Junshuai, Yongqian Liu, Xiaoying Ren, and Li Li. 2023. "Wind Turbine Gearbox Condition Monitoring Using Hybrid Attentions and Spatio-Temporal BiConvLSTM Network" Energies 16, no. 19: 6786. https://doi.org/10.3390/en16196786
APA StyleYan, J., Liu, Y., Ren, X., & Li, L. (2023). Wind Turbine Gearbox Condition Monitoring Using Hybrid Attentions and Spatio-Temporal BiConvLSTM Network. Energies, 16(19), 6786. https://doi.org/10.3390/en16196786






