Abstract
Currently, the integration of new energy sources into the power system poses a significant challenge to frequency stability. To address the issue of capacity sizing when utilizing storage battery systems to assist the power grid in frequency control, a capacity optimal allocation model is proposed for the primary frequency regulation of energy storage. Due to the requirement of a large number of actual parameters for the optimal allocation model, a simulation model of energy storage capacity is constructed based on the characteristics of primary frequency control to provide the necessary parameters. Subsequently, the primary frequency modulation output model of energy storage is established by considering the basic action output, the action in the frequency modulation dead zone, and a certain capacity margin. The antlion algorithm is employed to solve the capacity optimal allocation model. Finally, three groups of experiments are designed and compared to demonstrate the effectiveness of the proposed method in setting the capacity margin, which can increase profit to a certain extent.
1. Introduction
With the advent of the electric power revolution, the use of thermal power generation has led to significant environmental damage, making it imperative to shift towards clean energy sources such as wind and solar power. However, the inherent stochastic nature of these resources makes it difficult to maintain a stable frequency of energy generation [1]. To address this issue, researchers propose combining battery energy storage technology with new energy generation technology. This approach involves storing excess energy from natural resources and releasing it when needed, thereby improving the efficiency of the new energy generation system and reducing the negative impact of traditional power systems on the environment. Additionally, energy-storage-assisted grid frequency regulation can enhance the stability of the power system frequency [2].
At the macro level, the literature [3] proposes development strategies for China based on the current status of the energy storage FM market in major countries such as the United States, the United Kingdom, and Australia. Specifically, [4] analyzes the current situation of FM in China and national policies in recent years, concluding that independent energy storage power stations have a promising future. On the user side, [5] highlights the benefits of multi-scenario analysis, suggesting that user groups can complement each other, and with a reasonable operating mechanism, this approach is expected to become a future development trend.
Regarding the application scope, primary FM is crucial for frequency adjustment in the power system [6]. The literature [7] optimizes capacity by integrating economic and technical indexes, while [8] comprehensively discusses the control method by modeling and simulating the process of energy storage participating in frequency regulation. In foreign literature, research mainly focuses on the battery energy storage system’s peak and frequency regulation of the grid. For instance, [9] presents a case of combining the antlion optimizer and grey wolf optimizer to optimize the objective function of the hybrid power generation system (HPGS) for power system peaking. S. Zhang et al. propose a two-stage capacity allocation optimization scheme to improve the power system’s frequency response, where the first stage determines the capacity based on the activated energy storage’s critical frequency, and the second stage optimizes the capacity based on the energy storage’s charging rate [10].
This paper investigates the capacity allocation problem when the storage battery assists the primary frequency regulation of the power grid using the antlion algorithm. Firstly, an evaluation model for capacity optimization is constructed based on the energy storage system’s net benefit over its life cycle. Secondly, an output model mimicking the energy storage action situation is constructed for the missing parameters in the evaluation model. Finally, the antlion algorithm is used to find the optimal solution for the model’s variables, followed by an analysis and discussion.
2. Evaluation Model for Optimal Allocation of Energy Storage Capacity
2.1. Lifetime Estimation of Energy Storage Battery
The cost of the energy storage system is significantly impacted by the battery life’s duration [11]. Therefore, it is necessary to simulate the battery life estimation, which is based on the state of charge estimation [12]. The following steps are taken: the sequence of the equivalent depth of discharge is obtained based on the measured state of charge sequence. The relationship between the number of charging and discharging times and the depth of discharge is used, combined with the rated number of times, to obtain the equivalent number of charge and discharge times. When the equivalent number of charge and discharge times reaches the rated value, the battery is considered to have reached its life limit.
The depth of discharge () is the difference between the battery’s charge state () discharged from 100% to a certain charge state. The rainflow counting method [13] is used to convert it to an equivalent depth of discharge (), which describes the effect of small-amplitude frequent charging and discharging behaviors on battery life. It can be expressed by Equation (1):
where in the above equation is the sequence of charging states during the sampling period; and , which is derived by the rainflow counting method, is the sequence of equivalent discharge depths during that sampling period.
The energy storage system adopts lithium-ion batteries, and the relationship between the depth of discharge and the number of charges/discharges [14] is shown in Table 1.

Table 1.
Relationship between discharge depth and charging and discharging times of lithium-ion batteries.
According to practice, the data in Table 1 are fitted with a type II power function, which can approximate the number of charging and discharging times corresponding to any discharge depth. The fitting results are shown in Figure 1 and the fitted function is shown in Equation (2):
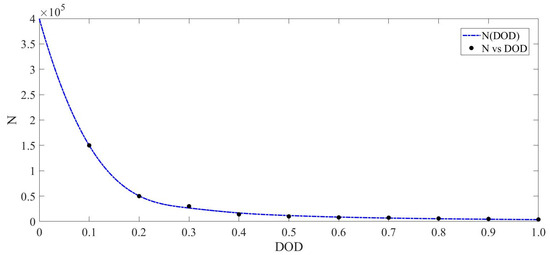
Figure 1.
Curve of lithium-ion battery discharge depth versus charge/discharge times.
The rated charging and discharging times of the energy storage battery are generally taken as the charging and discharging times when , and the charging and discharging times are set to 4000.
According to Equation (1), Equation (2) combined with the rated number of charging and discharging times can be obtained in 1 year the total equivalent number of charging and discharging times , described by Equation (3) as:
where is the number of after counting the sequence of charge states in the sampling period by the rainfall counting method; and is the conversion factor of the sampling period into 1 year. When reaches the rated charging and discharging times of 4000 after the energy storage battery needs to be replaced, then its life can be calculated as , and the unit is years.
2.2. Calculation of the Cost Model
During the life cycle, all costs of the energy storage battery system are mainly generated by the pre-installation, mid-term operation and maintenance, and post-recovery, in addition to other penalty costs due to FM non-compliance and so on.
2.2.1. Construction Cost
This type of cost mainly includes the construction cost of power conversion equipment and the construction cost of the energy storage battery pack. The construction cost of the energy storage battery system can be described by Equation (4):
where denotes the ratio coefficient between the construction cost of the power conversion equipment and the rated power of the battery system in ; denotes the rated power in ; denotes the cost per unit of the rated capacity of the energy storage in ; denotes the rated capacity in ; denotes the discount rate; and denotes the life cycle of the energy storage system.
2.2.2. Operation and Maintenance Cost
The operation and maintenance cost of the storage battery is the maintenance cost of the PCS system and the maintenance cost of the storage battery pack during the life cycle. It can be described by Equation (5):
where denotes the operation and maintenance cost per MW in , denotes the operation and maintenance cost per MW·h of the battery in , and denotes the total annual charge/discharge in .
2.2.3. Recycling Costs
After the end of the life cycle of the energy storage system, the energy storage battery system equipment and battery packs must be recycled to avoid environmental pollution. Therefore, this cost can be expressed by Equation (6):
where denotes the cost of recovering a unit of power of a PCS device in ; and denotes the cost of recovering a unit of capacity in .
2.2.4. Other Costs
There are other costs for normal operation over the years, such as a battery pack charge state does not meet the specific practical needs of the cost of power shortage and abandoned power costs. This part of the cost consumption can be described by Equation (7):
where , denote annual power shortage and annual power abandonment, respectively, both in ; and , denote the cost per unit of power shortage and per unit of power abandonment, respectively, both in .
2.2.5. Comprehensive Cost Model
Based on the analysis of the cost consumption of the energy storage battery, a comprehensive cost model is derived, as shown in Equation (8):
2.3. Calculation of the Revenue Model
All the benefits of the energy storage battery system in the life cycle are generally composed of FM power benefits, standby power benefits, and environmental benefits.
2.3.1. FM Power Gain
The FM power gain of the energy storage battery system is mainly related to its charging and discharging power, which can be expressed by Equation (9):
where represents a day of charging and discharging power, depicted in units of ; represents the energy storage frequency regulation and the price of electricity, depicted in units of ; represents the number of days of operation of an energy storage battery system in a year., taking into account the existence of fault maintenance, planned shutdowns, and other factors, generally taking the impact of 300.
2.3.2. Standby Power Gain
The backup power gain of the energy storage battery system refers to its real-time power output, the surplus power as a power system backup, and the revenue generated. The standby power of the energy storage system can be divided into upper standby power and lower standby power . The calculation method is shown in Equation (10):
where is the actual output power of the energy storage battery system at a certain moment, is the rated discharge power, and is the rated charging power.
Assuming that the energy storage battery system is used as the upper and lower standby time and each accounted for half of the total working time, the energy storage battery system standby power gains can be expressed by Equation (11):
where , denote the upper and lower standby prices during the FM time period, respectively, and the unit is taken as ; and denotes the total number of sampling points in a day.
2.3.3. Environmental Benefits
The input of energy storage equipment reduces the consumption of conventional thermal power units, the consumption of primary energy, and the generation of exhaust gases, and the resulting cost savings are called environmental benefits, which can be described by Equation (12):
where denotes the unit cost of the i-th substance in , denotes the consumption or emission per unit of electricity of the i-th substance in , and denotes the total discharge of the energy storage battery system in a day in .
2.3.4. Comprehensive Benefit Model
Based on the aforementioned analysis of the benefits over the life cycle of the energy storage battery, a comprehensive benefit model is derived, as shown in Equation (13):
2.4. Objective Function
Based on the analysis of Equations (8) and (13), the net benefit over the life cycle of the energy storage battery is derived, as shown in Equation (14):
This equation represents the correlation between various parameters, including rated capacity, rated power, charging and discharging power, and net benefits of energy storage during grid FM participation. Therefore, it can serve as an evaluation model for determining the optimal allocation of energy storage capacity. The objective function of the optimal capacity allocation, which involves finding the optimal combination solution of multiple independent variables in the evaluation model to achieve the maximum benefit, can be expressed using Equation (15):
3. Output Modelling
3.1. Objective Function
In the process of energy storage output, it is necessary to constrain its charge state; the so-called charge state () can be described by Equation (16), where is the actual remaining power:
Assuming that the initial charging state of the energy storage battery is , and the output curve of the energy storage battery is , the charging state of the energy storage battery at the i-th moment is shown in Equation (17):
To calculate the sequence of the state of charge () of the storage battery during the sampling time period, Equation (17) can be used. However, it is crucial to ensure that (1) the units of the upper and lower parts of Equation (17) are consistent, and (2) the output power curve () indicates positive output power and negative input power. Additionally, determining the charging state relies on the storage battery’s rated capacity (), so it is necessary to determine the battery’s capacity beforehand.
3.2. Calculation of Rated Capacity
In the charge state curve calculated by Equation (17), there must be a peak () and a valley (). In order to ensure the use of storage battery safety and adequate life, its state of charge will generally set an upper limit value () and a lower limit value (), and requires that the peak value of the state of charge curve shall not exceed the upper limit value, and the valley value shall not exceed the lower limit value. This relationship is shown in Equation (18):
Equation (18) is also known as the constraints of the charge state of the storage battery, and the calculated value of the rated capacity of the storage battery can be solved by associating Equations (17) and (18), and the result is shown in Equation (19):
The energy storage battery’s rated capacity must fulfill the grid’s electrical energy demand at any given moment. This means that the energy storage battery’s charge state must be maintained at a high level whenever the grid requires electrical energy from the energy storage system. Conversely, when the grid needs to store electrical energy in the energy storage system, the battery’s charge state must be maintained at a relatively low level.
3.3. Basic Action Output
The action of energy storage when it participates in the grid primary FM is shown in Figure 2.
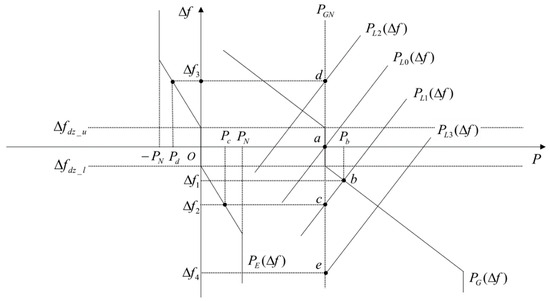
Figure 2.
Schematic diagram of energy storage participating in primary frequency modulation of power grid.
In Figure 2, the horizontal axis denotes the power , the vertical axis denotes the frequency deviation , and along the direction of the arrow indicates the gradual increase of this variable; denotes the upper limit of the FM dead zone, and denotes the lower limit of the FM dead zone; the curve represents the relationship between output power and frequency deviation of a conventional thermal power unit; the curve denotes the relationship between load power change and frequency deviation, and the numerical corner scale denotes the curve after a sudden increase or decrease change in load power; and the curve represents the relationship between the input and output power and frequency deviation of the energy storage battery system. The intersection point a of curve and curve is the initial operating point, where the power consumed by the load is balanced with the power issued by the conventional thermal power unit, both of which are .
At this point, the energy storage battery system is not involved in frequency regulation. When the load obtains an increment so that the load curve changes from to —due to the thermal power unit to maintain being unchanged at this time, the operating point is point c, and the frequency deviation is —the frequency deviation has crossed the lower limit of the FM dead zone. According to the curve , it can be known that at this time the output power of the energy storage is . Similar to the load increase, when the load is reduced to , the frequency deviation rises to ; at this time the power absorbed by the energy storage is . If the amount of change in the load is large, resulting in frequency deviation corresponding to the power exceeding the limit of the storage battery, the energy storage can only be rated power output, as shown in the curve . This situation is also known as the power constraints of the storage battery.
In power grids that incorporate energy storage, the primary frequency modulation (FM) task can be assigned to the energy storage system, as the FM power required for primary FM is typically not substantial. This can be achieved by simulating the FM characteristics of a conventional thermal power unit, where the thermal power unit maintains its rated output power while the energy storage battery system undertakes the FM power. To implement this scheme, the storage battery system must be assigned a simulated unit regulation power () to ensure that its FM characteristics are comparable to those of a thermal power unit.
3.4. Additional Output in the FM Deadband
To further increase the yield, the following scheme is implemented when the frequency change falls within the FM deadband:
As depicted in Figure 3, a high-level charge state () is established between the upper limit value () and the initial value () of the charge state, while a low-level charge state () is established between the lower limit value () and the initial value () of the charge state. When the frequency deviation falls within the FM dead zone, i.e., , the energy storage system is controlled to sell electrical energy () to other power systems or vendors at a power level () if the charge state is above the HCS. Conversely, if the charge state is below the LLS, the energy storage system is controlled to repurchase electrical energy () from the power grid at a power level (). The values of and are calculated using Equation (20):
where , denote the proportion of this power to the rated power.
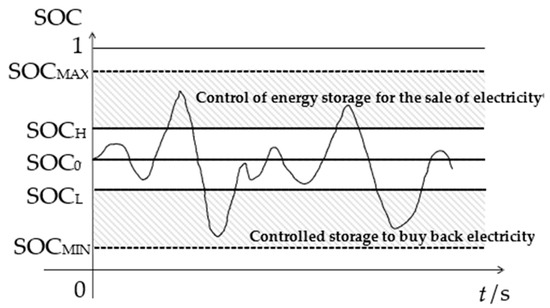
Figure 3.
Schematic diagram of energy storage in FM deadband.
The calculation of the additional revenue generated after the above operation is shown in Equation (21), and the calculation of Equation (13) should be added in the optimization simulation:
3.5. Construction Method of Output Model
Firstly, it is necessary to obtain a set of frequency deviation sequences for a certain sampling time period, and then according to this set of frequency deviation sequences combined with the regulation effect of the load, the output sequence of the storage battery in the ideal case can be obtained, as shown in Equation (22):
According to this set of output power sequence , the size of the rated capacity can be initially determined by using Equation (19), which is an important parameter for the next step of calculating the load sequence of the energy storage battery.
The next step is the calculation of all sampling points. This process requires judging the constraints as shown in Equation (23) before each calculation:
where k denotes the total number of sampling points; and is given by the optimization algorithm before each iteration.
Combined with the previous description of the energy storage output, Equation (24) can be used to calculate the actual energy storage output:
It is important to note that the initial state of charge () of the energy storage battery must be specified before optimization. This ensures that the SOC at the first sampling point satisfies the constraints, and the power output of the energy storage battery at that point is obtained by calculating and considering the power constraints at the first sampling point using Equation (24). Using the power at the first sampling point and the initial calculation of the rated capacity (), the charging state at the next point can be calculated using Equation (17). The constraints can then be used to calculate the power at the next point, and so on until the last sampling point is reached. This process yields the actual power sequence and the charging state sequence () of the energy storage battery. The rated capacity is updated to based on the actual output , and the charging state sequence is updated to based on . The actual output also needs to be updated because may be smaller than , which could cause to reach the constraint limit and affect the actual output.
However, the rated capacity , determined from the actual output as per Equation (19), may be small, resulting in large fluctuations in the state of charge and reduced economic efficiency. To address this, the standard deviation of the state of charge () is introduced, and the rated capacity is appropriately increased based on . The state of charge and output at this capacity are then calculated. When satisfies the given reference value , the capacity of this load state is calculated, which is the rated capacity at the given power of the optimization algorithm. The formula for calculating the standard deviation of the load state is shown in Equation (25).
In all power-related calculations, the output power of the stored energy during the sampling interval is assumed to remain constant from the previously calculated value. As such, it can be obtained by multiplying the output power related to the requested power with the sampling interval time.
4. Principle of Antlion Algorithm
The antlion algorithm is a novel optimization algorithm proposed by scholars in 2015 [15]. To use this algorithm, the number of antlions and the number of iterations must be specified. The optimization principle of the antlion algorithm is illustrated in Figure 4. During the first iteration, the positions of ants and antlions are initialized, and the fitness is calculated. Elite antlions are then selected. From the second iteration onwards, the ants traverse all points in the search space, and the antlion algorithm enters the optimization search process. It is important to note that all ants are linearly independent of each other, and each ant exists in multiple dimensions. Each dimension corresponds to an independent variable, which can be thought of as each ant carrying all independent variables for computing the objective function.
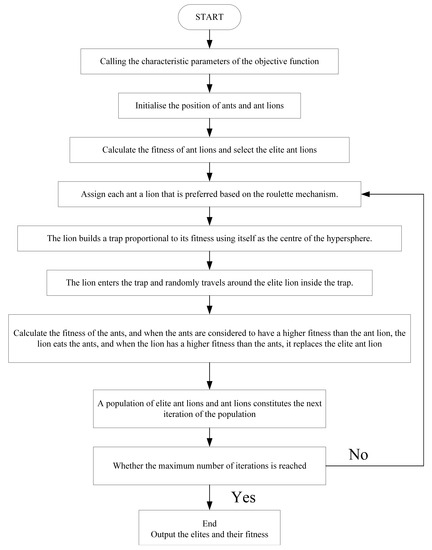
Figure 4.
Flow chart of antlion algorithm iteration.
5. Example Simulation
For the optimization of the energy storage capacity of the primary FM, the independent variables are set as rated power , high-level charging state , low-level charging state , and scaling factors and . The antlion algorithm, combined with the established optimization model, is used to search for the optimization of these five variables, and the result of the search for optimization is carried out into the established power model to obtain the optimal capacity of the primary FM.
5.1. Parameter Setting
The frequency deviation of a regional power grid with a capacity of 250 MW is sampled to obtain the original data, the sampling period is set to 1 h, the sampling period is set to 2 s, and the sampling results are shown in Figure 5, in which the peak value of the frequency deviation is 0.47 Hz.
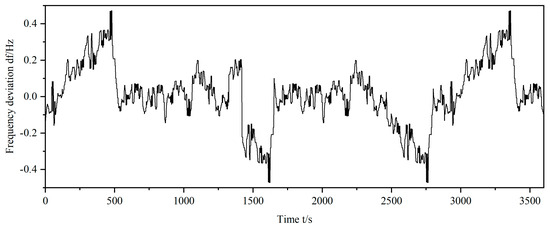
Figure 5.
Frequency deviation of a regional grid within one hour.
The specific parameters calculated by the simulation [16] are shown in Table 2.

Table 2.
The primary frequency modulation parameters of the power grid involved in energy storage.
5.2. Optimization Process
The optimization process is mainly based on the process represented in Figure 4, in which the characteristic parameters of the objective function tuned by the antlion algorithm mainly include the number of independent variables and their upper and lower limits. The number of variables has been described in the previous section, and the selection of upper and lower limits is described as follows:
For the rated power , according to the maximum frequency deviation combined with the simulation of unit regulation power , determine its base value of 7 , considering a certain margin will be set to the upper limit of 12 . According to the actual situation of the high level of charge state , the optimization interval is set to 0.55–0.9, the low level of charge state optimization interval is set to 0.1–0.45, and the optimization interval for the ratio coefficients and is set to 0–1.
In order to verify that the capacity margin can actually improve the revenue, three sets of comparison experiments are proposed in this section:
Experiment 1: In the solution process, the action of the energy storage in the FM dead zone is not considered, and the capacity reserve of the energy storage battery is not considered;
Experiment 2: During the solution process, only the action of the energy storage within the FM dead zone is considered, and still the capacity backup of the energy storage battery is not considered;
Experiment 3: In the solution process, both the action within the FM dead zone and the capacity backup of the energy storage battery are considered.
5.3. Optimization Results
After the optimization solution of the antlion algorithm, the optimization results of each experiment are shown in Table 3.

Table 3.
Optimization results of experiments 1, 2, and 3.
Since experiment 1 does not consider the action of the energy storage in the dead zone, the four terms , , , and in the optimization variables are redundant and an optimization search for them is not meaningful in this experiment.
The results of experiment 2 compared to experiment 1 are the following: in terms of the parameters of the energy storage battery system, the rated power determined by the antlion algorithm is increased, the rated capacity is decreased, and the unit service life of the storage battery is decreased; in terms of cost and benefit, the total cost does not change much, but the total benefit increases due to the action in the dead zone, which in turn increases the net benefit, so it makes sense to set up an additional action within the dead zone of the frequency modulation.
A comparison of the FM results, energy storage output, and state of charge for the three sets of experiments is shown below:
Upon comparing Figure 5 and Figure 6, it can be observed that the involvement of energy storage in the FM process of experiment 1 and experiment 3 resulted in a reduction in the value of the frequency deviation. The frequency deviation in the results of experiment 2 is similar to that of experiment 3, with only a few moments not involved in FM. It was found that these moments were not involved in FM due to the constraints of reaching the lower limit of the charge state, as seen in Figure 7.
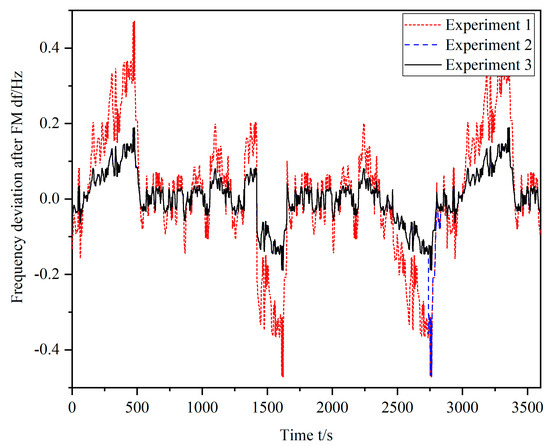
Figure 6.
Frequency modulation result comparison of three experiments.
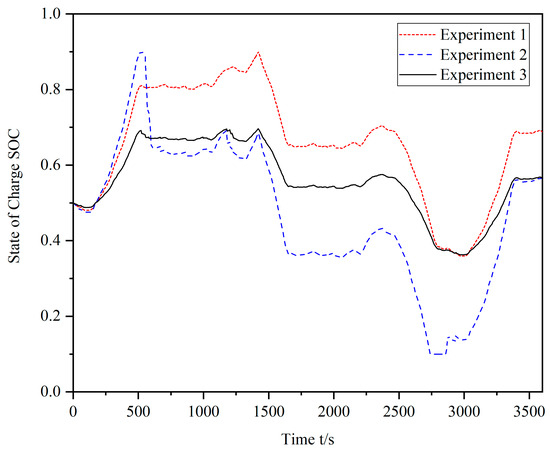
Figure 7.
State of charge comparison of three experiments.
Based on the simulation results presented in Figure 7 and Figure 8, along with the rated capacity data in Table 3, it can be concluded that the charge state fluctuates the most in experiment 2, which has the smallest rated capacity. This results in the shortest service life of the storage battery unit in experiment 2. On the other hand, experiment 3 has appropriately increased the capacity margin and reduced the amplitude of the output power in the dead zone of the FM, resulting in the smoothest charge state curve and the longest service life of the storage battery. Therefore, experiment 3 has the longest service life compared to the other two experiments.
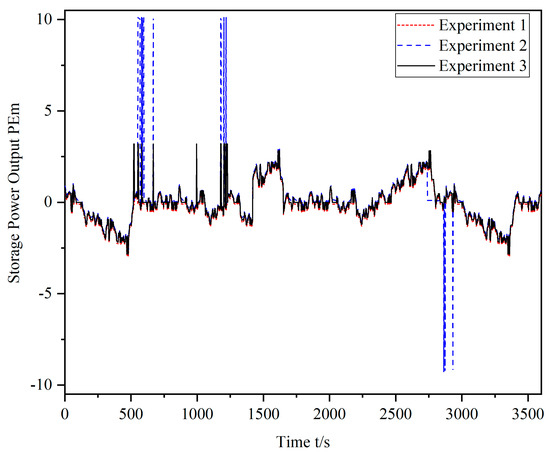
Figure 8.
Energy storage output comparison of three experiments.
5.4. Calculation Analysis
A longitudinal comparison of the data of the three sets of experiments shows that the present value of the net benefit of the energy storage battery system increases gradually over the whole life cycle, which shows that the optimization model proposed in this paper can achieve the optimal allocation of energy storage capacity. According to the various results in Table 3, the discussion is as follows:
By comparing experiment 1 and experiment 2, it is found that the additional action of the energy storage in the dead zone can increase the benefit, which is specifically manifested in the three items , , and . Although there is a certain degree of decline in the rated capacity, there is no more obvious reduction in the various costs of consumption, mainly due to the fact that the action in the dead zone increases the amplitude of the action of the energy storage battery, so that the unit life of the battery is reduced to a certain degree, which increases the number of replacements.
A comparison of experiments 2 and 3 shows that after taking into account a certain margin of rated capacity according to the standard deviation of the state of charge, increases slightly; decreases slightly; and and , the proportionality coefficients, decrease to different degrees. This indicates that in order to further increase the net benefit, it is necessary to limit the action amplitude of the energy storage in the FM dead zone; although this reduces the benefit to a certain extent, it obviously prolongs the unit life of the battery and reduces the cost of and . At the same time, due to the consideration of a certain margin, the penalty type of cost in experiment 2 is eliminated in experiment 3, which leads to the improvement of the net benefit.
6. Conclusions
In the context of the “dual carbon” goal gradually taking root in people’s hearts, with the extensive access of new energy generation to the power grid, the fatigue of the traditional FM, mainly thermal power units, begins to appear gradually. Therefore, this paper researches the capacity allocation of energy storage in the primary frequency regulation of the power grid, and the main contents and results are as follows:
- (1)
- The cost and revenue of energy storage battery systems are analyzed, modeled, and simulated throughout their life cycle. The simulation results show that increasing the capacity margin can increase revenue by extending the service life of the energy storage unit and reducing investment.
- (2)
- A model is developed for the participation of energy storage in the primary frequency regulation process of the power grid, providing essential data for optimal capacity allocation. An antlion algorithm is proposed to optimize storage battery capacity, and the results are simulated and discussed.
- (3)
- Based on the findings from three sets of comparative experiments, it has been demonstrated that augmenting the motion within the deadband effectively enhances the gain. Additionally, restraining the magnitude of energy storage action within the FM deadband exhibits a notable extension of the battery unit’s operational lifespan.
In terms of constructing the discharge model of the energy storage battery, the idealized battery characteristics can be studied by considering its discharge multiplier characteristics [17].
Author Contributions
Conceptualization, H.Y.; methodology, R.H.; software, H.Y. and R.H.; validation, H.Y., R.H., and Z.Y.; formal analysis, R.H. and Z.Y.; investigation, M.S.; resources, H.Y.; data curation, R.H.; writing—original draft preparation, R.H., M.S., and Z.Y.; writing—review and editing, H.Y., R.H., M.S., Z.Y., and L.Y.; visualization, M.S. and Z.Y.; supervision, H.Y. and L.Y.; project administration, H.Y. and L.Y.; funding acquisition, L.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the Shanxi Development and Reform Commission’s Special Project for Mass Entrepreneurship and Innovation (137541005), the Shanxi Postgraduate Innovation Project (2022Y156), and the Ministry of Education University-Industry Cooperation Collaborative Education Project (221002262073019).
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhu, T. Research Review on Related Issues of Wind Power Connection System. China South. Power Grid Technol. 2009, 3, 58–63. [Google Scholar]
- Liu, H.; Peng, G.; Zhang, C.; Zhang, S. Overview of Wind Power Participation in Power System Frequency Regulation Control Strategy. Electr. Power Autom. Equip. 2021, 41, 81–92. [Google Scholar]
- Zhang, H.; Wang, Y. The mechanism experience of foreign grid-side energy storage power stations participating in the frequency regulation auxiliary service market and its enlightenment to my country. Energy Storage Sci. Technol. 2021, 10, 766–773. [Google Scholar]
- Liu, B.; Zhang, J.; Li, D.; Ning, N. Application status and prospect analysis of energy storage in power generation side peak regulation and frequency regulation services. Energy Storage Sci. Technol. 2016, 5, 909–914. [Google Scholar]
- Yu, S.; Su, H.; Fang, C.; Gui, Q.; Zhou, Y.; Feng, D. Review of user-side energy storage benefit analysis and economic operation research. Power Demand Side Manag. 2021, 23, 2–7. [Google Scholar]
- Huang, J. Study on Optimal Allocation and Control Strategy Design of Battery Energy Storage System for Power Grid Frequency Regulation. Ph.D. Thesis, Hunan University, Changsha, China, 2015. [Google Scholar]
- Huang, J.; Li, X.; Chang, M.; Li, S.; Liu, W. Capacity allocation method considering energy storage battery participating in primary frequency modulation technical and economic model. J. Electrotech. Technol. 2017, 32, 112–121. [Google Scholar]
- Deng, X.; Sun, W.; Xiao, H. Comprehensive control method of energy storage battery participating in primary frequency modulation. High Volt. Technol. 2018, 44, 1157–1165. [Google Scholar]
- Algabalawy, M.A.; Abdelaziz, A.Y.; Mekhamer, S.F.; Badr, M.A.L. Optimal multi-criteria design of a new hybrid power generation system using ant lion and grey wolf optimizers. In Proceedings of the Eighteenth International Middle East Power Systems Conference, Cairo, Egypt, 27–29 December 2016; pp. 138–146. [Google Scholar]
- Zhang, S.; Mishra, Y.; Ledwich, G. Battery energy storage systems to improve power system frequency response. In Proceedings of the Australasian Universities Power Engineering Conference, Perth, Australia, 28 September–1 October 2014; pp. 1–5. [Google Scholar]
- Xiu, X.; Li, X.; Wang, J.; Xie, Z.; Lv, X. Research on generalized cost of energy storage power station based on equivalent efficiency conversion. China Electr. Power 2022, 55, 192–202. [Google Scholar]
- Han, X.; Cheng, C.; Ji, T.; Ma, H. Capacity optimization model of hybrid energy storage system considering battery life. Chin. J. Electr. Eng. 2013, 33, 91–97+16. [Google Scholar]
- Xe, Z.; Wang, J.; Li, D.; Meng, T. Research on Economic Evaluation of Energy Storage System Participating in Frequency Regulation of Power System. Electr. Appl. Energy Effic. Manag. Technol. 2020, 5, 14–20. [Google Scholar]
- Li, J. Battery Energy Storage System Frequency Regulation Technology; Energy Storage Science and Technology Series; Mechanical Industry Press: Beijing, China, 2018; Volume 9, p. 141. [Google Scholar]
- Mirjalili, S. The Ant Lion Optimizer. Adv. Eng. Softw. 2015, 83, 80–98. [Google Scholar] [CrossRef]
- Jie, T. Research on Capacity Allocation and Control Strategy of BESS Participating in Secondary Frequency Regulation of Power Grid. Ph.D. Thesis, Hunan University, Changsha, China, 2019. [Google Scholar]
- Li, S.; Li, X.; Huang, J.; Liu, W.; Meng, Y.; Xie, Y. Optimal configuration of energy storage batteries for frequency modulation considering rate characteristics. J. Sol. Energy 2020, 41, 127–132. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).