Abstract
For recycling waste batteries, high-gain DC-DC provides a great solution. In this article, the design and optimization of a high-gain converter–synchronous rectification low-inductance current secondary boost converter (SLIC-QBC) is studied. The optimization objective of this article is to propose an automatic design method for passive components and the switching frequency of the converter to improve efficiency and power density. A machine learning-integrated optimization method is proposed to minimize the converter mass and power loss of the converter. In this method, first, a component-based automatic design model is built with embedded SLIC-QBC simulation. Then, a series of design schemes is generated within a large parameter range, and training data for machine learning are collected. Support vector machine (SVM) and artificial neural network (ANN) are used to validate the converter design scheme, where ANN establishes the mapping relationship from design parameters to optimization objectives. After the optimization, an experimental prototype is built for experimental verification. The simulation and experimental results verify the practicability of the proposed method.
1. Introduction
With the increasing awareness of green environmental protection, the new energy-friendly vehicle industry has been developed rapidly in many countries [1], which has led to a large amount of residual energy from recyclable batteries for energy storage to meet other applications [2]. Therefore, the recycling and utilization of waste batteries have attracted much attention in the past several years [3]. DC-DC converter is a key component for the reuse and reliable management of waste batteries [4]. Due to the low output voltage of the battery, a high-gain DC-DC boost is usually required to meet the voltage requirements of the power supply. In addition, high-gain DC-DC converters are also widely used in fields such as DC micro-grids [5] and photovoltaic power generation [6].
With the development of power electronics technology, DC-DC converters have become popular recently due to their high-efficiency character in high-power applications [7]. To maintain the efficiency advantage, on the one hand, the design of passive components is important for DC-DC converters. This is because the inductor and capacitor, which are common components in DC-DC converters, have relatively large volumes and masses. With a reasonable design, the required space can be minimized to effectively improve the power density of the converter. On the other hand, high efficiency (with a small loss) in the energy-transfer process of the converter is directly determined by the switching frequency, which also affects the design process of passive components. Therefore, the switching frequency, as well as passive components, should be optimized for high-efficiency DC-DC converters.
Reference [8] traversed the conversion ratio, operation frequency, and Leakage inductance of the coupling inductance within a certain range to optimize the efficiency of the boost converter, but it only considered the efficiency; the mass of this converter was not included. Reference [9] used multi-objective optimization algorithms to design the inductance and capacitance of BUCK circuits, but the switching frequency was subjectively set and thus might not be optimal, and the influence of internal resistance was not considered. Reference [10] comprehensively considers efficiency, volume, and ripple in the optimization process of inductance, capacitance, and switching frequency of BUCK converters, achieving the optimal efficiency of the converter. In this article, for an optimal converter design, the inductance and switching frequency are considered design variables aimed at finding the best solution with high performance, high efficiency, and high power density.
In the past two decades, computer technology has developed rapidly, and many scholars have studied the optimization of circuit parameters. For example, Reference [11] used a multi-objective optimization algorithm based on a genetic algorithm to design LC-filter parameters for aircraft DC power supply systems, but it took about 9 h to terminate; Reference [12] applied the NSGA-II algorithm to design the parameters of the laser equivalent circuit model. Although it only took 1.5 s, the solving process was relatively complex, and its applicability in other circuits still needs to be studied further.
Machine learning (ML) technology has provided new ideas for breakthroughs in the field of power electronics. The artificial neural network (ANN), one of the most popular ML techniques, has shown unique advantages in short-term prediction compared to other ML methods, mainly due to its fast learning ability and adaptability [13]. Reference [14] used an ANN for the open-circuit fault diagnosis of three-phase converters, demonstrating a good example of a data-model-hybrid-driven method. In [15,16], an ANN was trained to explicitly map the parameters of power electronic systems into lifetime consumption. Reference [17] compared the traditional finite element analysis method of permanent magnet synchronous motors with the ANN-aided analysis model, which can speed up the optimization process with a high accuracy. In a similar way, [18] utilized an ANN to overcome the limitations of traditional motor loss estimation.
Another supervised ML method, Support Vector Machine (SVM), can achieve the classification of data into two categories based on given features. It has been applied to fault diagnosis of rotation machinery [19], signal classification for epilepsy detection [20], smart emotion recognition [21], etc. It has been proved that applying filtered data to ANNs can help achieve better prediction results [22]. Reference [23] used SVM-ANN integration to predict the mass and loss of aircraft drive system filters, demonstrating good predictive performance. Reference [24] optimized the membership function of fuzzy controllers in the same way, which greatly improved the efficiency of energy management systems
At present, the integration of SVM and ANN in the design of circuit parameters is still relatively rare. References [25,26] adopted the SVM-ANN integration method to optimize the design of filter inductance and capacitors at different frequencies and verified the advanced nature of this method through simulation experiments and hardware experiments. Inspired by these articles [25,26], this article focuses on a high-gain boost converter–synchronous rectification low-inductance current secondary boost converter (SLIC-QBC) and uses SVM and ANN integration to optimize the design of inductance and switching frequency to achieve optimal converter mass and efficiency. Due to the use of chip capacitors in the design process, the changes in capacitor mass and power loss are relatively small and can be ignored, so there is no optimization design for capacitors. However, it is important to note that this multi-parameter optimization method can cover both the inductor and capacitor and is also applicable to other circuits.
The remaining part of this paper is organized as follows: In the Section 2 of this article, the topology and working principle of the converter, as well as the traditional design method, are introduced. The Section 3 introduces the design principle and general design process of the converter. The Section 4 introduces the parameter design scheme of the converter based on machine learning. The Section 5 includes the experimental verification, and the Section 6 summarizes and draws conclusions.
2. Topology and Traditional Converter Design Method
Based on the low-inductance current secondary boost converter [27], two MOSFETs with low conduction resistances are used to replace the diodes to reduce the loss of the converter. To achieve synchronous rectification, the driving signals of these MOSFETs are synchronized with the current flowing through them. That is why this topology is called a synchronous rectification low-inductance current secondary boost converter (SLIC-QBC), and the topology is shown in Figure 1. Vin is the input voltage, Vo is the output voltage, and S1~S4 are four MOSFETs. Due to the consideration of actual dead time, these MOSFETs are combined with diodes to continue the current during the dead time. S2 and S4 are the two MOSFETs that replace diodes. L1, C1, S1, and S2 form the first-stage boost circuit, while L2, C2, S3, and S4 form the second-stage boost circuit. RL is the load resistance.
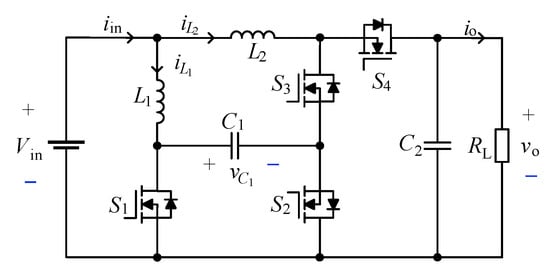
Figure 1.
Topology of SLIC-QBC.
Figure 2 shows the ideal working waveforms of the converter under steady-state conditions. In order to reduce the ripple of input current, the circuit adopts a phase-shifted control method. The driving signals of switch S1 and S2 complement each other, and the driving signals of switch S3 and S4 complement each other. T represents one working cycle. The driving signal of S1 is a square wave with a duty cycle of DA, while the driving signal of S3 is a square wave with a duty cycle of DB. The driving signal phase of S1 is ahead of S3.
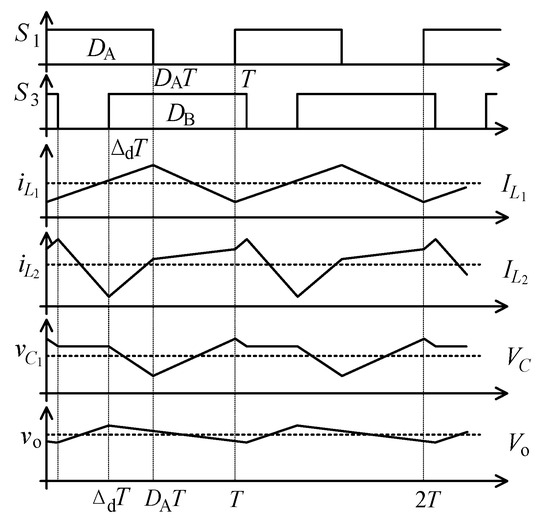
Figure 2.
Working waveforms of SLIC-QBC.
In order to balance the currents of two inductors during converter operation, the following equation needs to be set:
2.1. Traditional Design Method for Inductor and Capacitor of Converter
According to the working waveform of the converter, the expression for voltage, current, and their ripple are as follows:
where ΔiL1 is the current ripple of iL1, ΔiL2 is the current ripple of iL2, ΔvC1 is the voltage ripple of vC1, and Δvo is the voltage ripple of vo.
The value range of inductance (L1, L2) and capacitance (C1, C2) in the converter is traditionally determined by the current ripple ratios ( and ) and voltage ripple ratios ( and ) [27].
The design specification of the current ripple ratio and voltage ripple ratio is shown in Table 1.

Table 1.
Design specification of current ripple ratio and voltage ripple ratio.
Based on Formulas (10)–(13) and Table 1, the conditions for the inductance value and capacitance value can be deduced as follows:
In traditional design method [25], firstly, select the magnetic core model based on the current. Then, the number of wire reaches , AL is the nominal inductance coefficient of the magnetic core; under DC current, the magnetic field intensity of magnetic core is biased to . le is the length of the magnetic circuit. According to the percentage permeability-DC bias curve γ(H), determine the percentage decrease in magnetic permeability. After increasing the number of wire turns to make the inductance value close to the target value, select the wire type according to the winding table. The traditional design scheme is L1 = 150 μH; the magnetic core is made of Hi Lux material, model 58195, and is wound with AWG12 wire for 30 turns. The DC resistance of the winding is 0.013 Ω. L2 is chosen to be 300 μH; the magnetic core is made of Hi Lux material, model 58438, and is wound with AWG12 wire for 65 turns. Its DC resistance of the winding is 0.023 Ω. Capacitor C1 is chosen to be 176 μF; C2 is chosen to be 88 μF.
2.2. Transformer Loss Analysis
The loss of this converter mainly includes the loss of magnetic components and switches. The loss of switches includes turn-on loss, turn-off loss, and conduction loss.
The turn-on and turn-off loss of the switch are approximately as follows:
where f is the switching frequency, Vds(on) represents the drain source voltage before opening, Vds(off) represents the drain source voltage after shutdown, Ids(on) represents the current when the switch is turned on, ton represents the opening time, and toff represents the closing time.
The conduction loss of MOSFET () is as follows:
The loss of magnetic components is divided into core loss and winding loss. Based on the core loss density (PL), magnetic circuit length (le), and cross-sectional area (Ae), the core loss (PFe) can be calculated as follows:
In the above equations, a, b, and c are constants obtained by curve fitting, and Bpk represents half of the change in AC magnetic flux.
The winding loss of magnetic components (Pwind) can be divided into AC loss Pac and DC loss Pdc. The calculation formula for the winding loss of inductance is as follows:
where Rdc represents the DC resistance of the winding, and Rac represents the AC resistance of the winding.
A simulation model for SLIC-QBC was built using PLECS 4.5 software. The following Table 2 shows the circuit parameters of the simulation model.

Table 2.
Circuit parameters of the simulation model.
Based on the simulated current data and the Formulas (18)–(26), the loss of each part is shown in Table 3. The total loss of the converter is 4.25 W, the loss of the switches is 3.42 W, and the loss of the inductor is 0.8 W.

Table 3.
Loss of each part of traditional method.
The pie chart of converter loss distribution with the traditional method is shown in Figure 3. With traditional design method, the selection of inductance and capacitance is mainly based on empirical data and manual adjustment; thus, it may not be optimal. As shown in Figure 3, switching loss accounts for 60% of the total converter loss, and it is necessary to optimize the switching frequency of the converter.
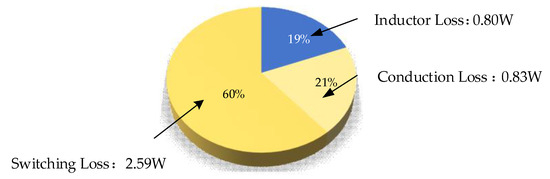
Figure 3.
Pie chart of converter loss distribution with traditional method.
Based on the design and calculation results, the traditional design result is shown in Table 4. Below is an optimization design method based on machine learning.

Table 4.
Traditional design result.
3. Converter Modeling and Design Process
This section introduces a design model for converter parameters with embedded simulation, which uses data from Magnetics’ data book. It is an independent size estimation method that lays the foundation for optimization design.
3.1. Design Model of Inductor
This article selects the Hi-Flux material from Magnetics as the magnetic core. The Hi-Flux magnetic core has many advantages in applications under high power and high-DC-bias voltage. Its saturated magnetic flux density is twice that of MPP alloy and more than three times that of ferrite, providing higher DC bias current and AC magnetic flux density. According to the normal working conditions of the converter, the AWG12 line is selected to load the corresponding inductance current. The inductor design flowchart is shown in Figure 4.
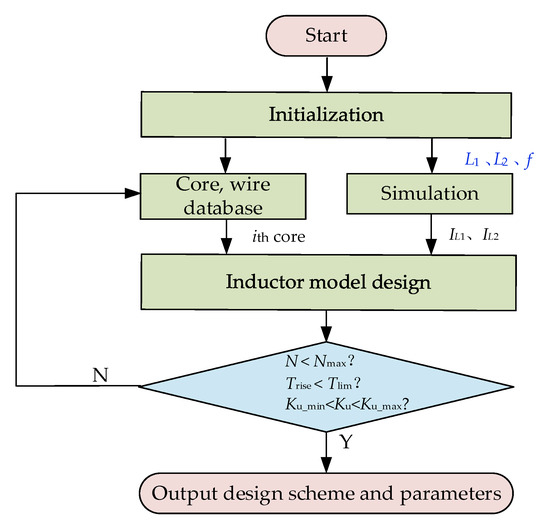
Figure 4.
Inductor design flowchart.
Firstly, an optional inductance core library needs to be established. This article does not simply use the same magnetic core to design L1 and L2 but various cores instead. Due to the significant difference between L1 and L2, magnetic core databases with permeability of 60 and 125 were created for L1 and L2, respectively. In summary, the core libraries of L1 and L2 contain 21 and 30 alternative cores, respectively. The magnetic core database contains information such as the model, size, magnetic circuit length, window area, volume, weight, etc. Then, select the magnetic core to design the input inductance value, and then input the value of inductances L1 and L2 with their internal resistance and switching frequency f. The current data of the converter can be obtained by the simulation model. The operating condition of the simulation model has been shown in Table 2.
Finally, the design scheme, loss, and mass can be obtained after checking the limited conditions. The conditions considered in the design model include the maximum number of turns of winding (Nmax), maximum temperature rise (Tlim), and winding factor (Ku). The specific calculation formula is as follows:
where dcore represents the inner diameter of the magnetic core, and dw represents the diameter of the wire. λ is the limiting factor, λ = 0.8.
where AL is the nominal inductance coefficient of the magnetic core.
where Awire is the cross-sectional area of the wire, and AW is the window area of the magnetic core, and 0.3 < Ku < 0.45.
where AS is the surface area of the winding element. Tlim is set to 50 °C.
where ML is the mass of inductance, Mcore is the mass of the magnetic core, and is the density of the wire. = 0.008 kg/m3. MLT is the average length of turns.
The internal resistance (R1, R2) of both inductors can be calculated as follows:
where α is the correction factor for different winding factors. LR is the resistance of unit-length winding.
3.2. Component-Based Design Model of Converter
The component-based design flow chart of the converter is shown in Figure 5.
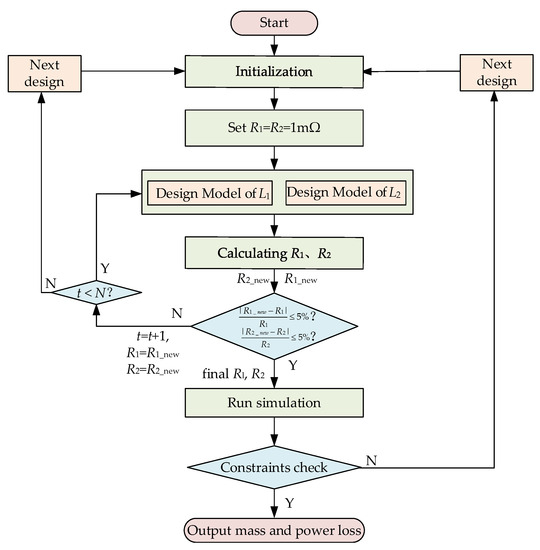
Figure 5.
Component-based design flow chart of the converter.
In Figure 5, the total mass and power loss are first initialized and assume that the initial internal resistance of both inductors is 1 mΩ. In the methodology, currents of inductors and capacitors should be obtained before giving their inner resistance and judgment for constraints. However, the issue is that the current can only be generated by simulating the system with resistance beforehand input. To address that, an integrated and recurrent approach is used here, which combines the filter component model with the built circuit simulation. When starting the approach, the initial resistances R1 and R2 should be given. Then, the whole filter design is updated in a loop.
Then, input the value of inductances L1 and L2 with their internal resistance and switching frequency f into the design model of the inductor to obtain the design scheme of the inductance. After calculating according to the Formulas (27)–(32), update the internal resistance until the internal resistance error is less than 5%. If the result cannot be obtained after 10 iterations, the set of parameters is considered invalid. Finally, input the final R1 and R2 into the simulation to recheck. Output mass and power loss after meeting the constraints of the converter. The constraints of the converter include the ripple ratio of the inductor current (ρL1, ρL2) being 10%, the ripple ratio of the capacitor voltage (ρo) being 10%, and the output voltage drop affected by internal resistance does not exceed 1 V.
In addition, considering the impact of switching frequency on the range of inductance values, before initializing a new set of circuit parameters, based on the minimum value of inductance under switching frequency in this set of parameters, if the inductance value is much smaller than the limit value, this set of circuit parameters will be infeasible.
4. Optimal Converter Design Method Based on Machine Learning
On the basis of Section 3, this study adopts an integrated approach of two machine learning methods to optimize the design of converter circuit parameters. The flow chart of this ML optimization structure implementation scheme is shown in Figure 6.
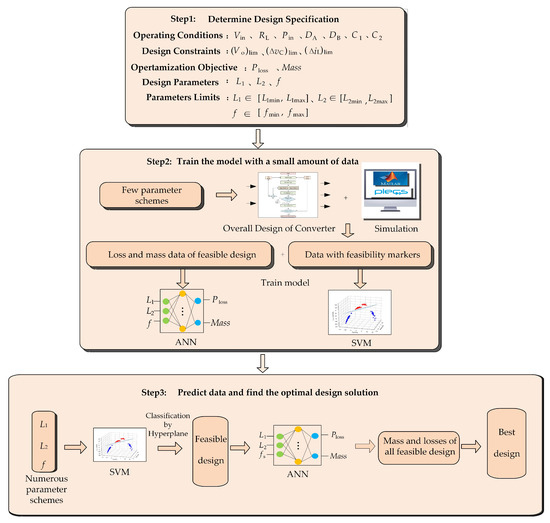
Figure 6.
Flow chart of ML optimization structure implementation scheme.
The specific steps are as follows:
Step 1: The first step is to determine the design specifications. The design specifications include the operating conditions, optimization objectives, design constraints, design parameters, and parameter limits. This method optimizes L1, L2, and switching frequency f for the mass and loss of the converter. Their optimization limits have different settings at different stages. The constraints and operating conditions of the converter have been mentioned in Section 3.2.
Step 2: The second step is to train the model with a small amount of data. At this step, this method firstly relies on the overall design flow chart of the converter shown in Figure 5 and combines circuit simulation to obtain a small amount of data with feasibility marks. These feasible design schemes also contain the corresponding loss and mass data. Then, use these few design schemes and their feasibility markers to train the support vector machine (SVM) classification model. After training the SVM-constrained classification model, these feasible designs, along with their corresponding mass and loss data, are used as training sets for ANN to map circuit parameters to optimization objectives.
Step 3: The third step is to predict data and find the optimal design solution. This step is based on the trained SVM classification model and ANN prediction model to classify and predict numerous circuit parameter design schemes and then find the optimal circuit parameter design scheme from the predicted results. Firstly, the SVM classification model is used to screen feasible design schemes, and then ANN is used to predict the loss and mass of feasible design schemes. Finally, find the optimal design based on comprehensive index ri.
The main motivation for using ML is that, after training ML models with a small dataset, the final optimal design can be quickly found using the exhausted algorithm rather than running the time-consuming simulations over and over again. More details about the use of SVM and ANN will be given below.
4.1. Support Vector Machine for Classification
In this article, SVM is used to classify circuit parameter schemes. The hyperplane in this classification problem refers to the interface that can divide the data in the data space into two categories according to its characteristics in a broad sense. After visualization, it is a line for data containing two characteristics/inputs and a surface for data containing three. The principle of SVM is finding the maximum hyperplane between two types of data, which is in the middle of the interval between two types of data. This optimal hyperplane is unique.
During the training step, the range of inductance L1 values is set as [20 μH, 420 μH], with a total of 21 discrete values taken at intervals of 20 μH. The value range of inductance L2 is [50 μH, 1050 μH], with a total of 21 discrete values taken at intervals of 50 μH. The value range of switching frequency f is [25,000 Hz, 100,000 Hz], with a total of 11 discrete values taken at an interval of 7500 Hz. This generates a total of 4851 points of circuit parameter design schemes to be verified. For the three-dimensional feature space in this article, the original data of SVM is filtered according to the model in Section 3, where feasible designs are marked as 1 and infeasible designs are marked as 0. Among these 4851 points of circuit parameter schemes, 1816 schemes are feasible, and 3035 schemes are not.
Using these 4851 data points with feasibility markers for SVM model training, in order to improve the accuracy of the SVM model, the raw data are normalized and then input into the model for training. The SVM model is implemented using the ‘fitcsvm’ function in MATLAB 2021b, and its related settings are shown in Table 5. Calculate the validation loss of the SVM model based on ‘kfoldloss’ to reflect the performance of the SVM model. The smaller its value, the more accurate the model is.

Table 5.
Fitcsvm function parameters.
Use 3500 random data points from the original 4851 as the training set and the remaining data as the test set. The training time of the SVM model is 1.84 s, the computational cross-validation takes 14.34 s, and the computational validation loss takes 0.06898 s. The training results show that the validation loss of the model is 0.7%, indicating that the model has good classification performance. Comparing the training results with the actual results, the accuracy of model classification reaches 98%. The training result of the SVM model is shown in Figure 7.
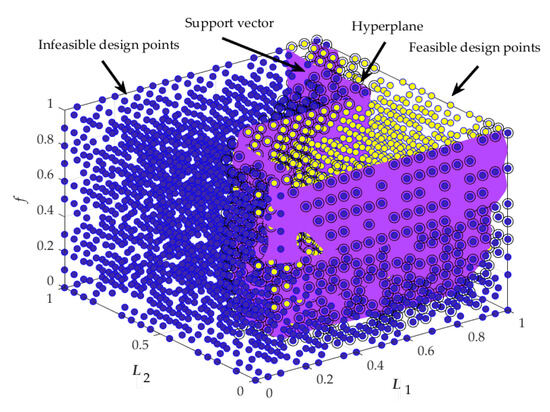
Figure 7.
SVM training model.
In Figure 7, the yellow points are feasible design points, the blue points are infeasible design points, the points surrounded by black circles are support vectors, and the purple surface is the hyperplane of the SVM model.
Generate more parameter schemes in the design space, with 51 values of inductance L1 taken at intervals of 8 μH in the range of [20 μH, 420 μH]. Inductance L2 should be uniformly taken as 51 values with intervals of 20 μH in the range of [50 μH, 1050 μH]. In the same way, there are a total of 76 uniform values for switching frequency f within the range of [25,000 Hz, 100,000 Hz] with an interval of 1000 Hz. In this way, a total of 197,676 data points of parameter schemes are generated in the design space. These parameter schemes are input into the SVM model to obtain their feasibility prediction results, which take about 5 min to predict. Among these 197,676 parameter design schemes, there are 88,591 feasible design schemes. The SVM prediction result is shown in Figure 8.
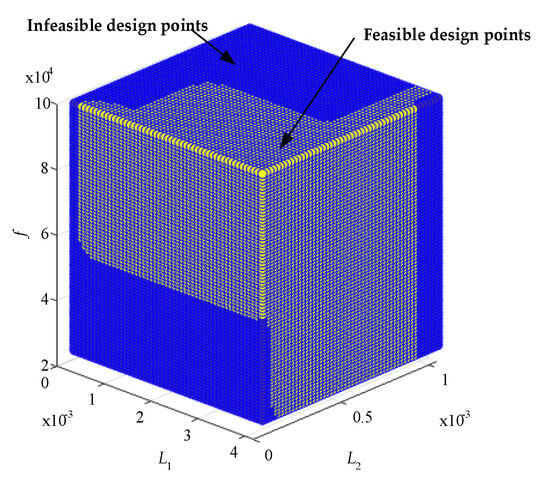
Figure 8.
SVM prediction result.
4.2. Artificial Neural Network for Mapping
An artificial neural network (ANN) is an algorithm used for information processing. It simulates the way the brain processes information, consisting of a large number of highly interconnected neurons. It solves specific problems by changing the structure, weight, and bias of the network.
Figure 9 shows the ANN structural model used in this article. The input design parameters are normalized and fed into an artificial neural network. Then, after anti-normalization, corresponding mass and loss can be obtained. The established ANN is divided into three parts, including one input layer, one output layer, and two hidden layers. After trial and error in setting ANN hidden layers, it is found that the training performance would be quite good and robust as long as there are two hidden layers and more than three neurons in each layer. Here, the number of neurons in the two hidden layers is 10 and 3, respectively. The ‘logsig’ function is selected as the transfer function of the hidden layer, the ‘purelin’ function is selected as the transfer function of the output layer, and the ‘traingdx’ function is selected as the function of backpropagation.
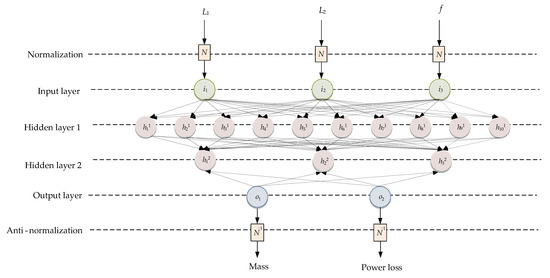
Figure 9.
ANN structural model.
Use 1816 feasible data points from the training step mentioned in Section 4.1, along with corresponding mass and loss data, to train the ANN model. The training goal is set to 0.0001, the learning rate to 0.01, and the maximum number of training epochs to 1000. It takes 2.35 s, and the actual training uses 266 iteration cycles. The root mean square error is only 0.0003.
Input 88,591 feasible parameter design schemes obtained from the SVM classification model into the trained ANN model, predict the loss and mass of these schemes, and then select the optimal design scheme based on the comprehensive index ri from the predicted results. When the comprehensive index ri reaches the minimum value, the parameter design is considered to achieve the optimal solution. The comprehensive index ri is defined as follows:
where Mi is the mass obtained by the ith solution, Mmax is the maximum mass, Plossi is the loss obtained by the ith solution, and Plossmax is the maximum loss.
Input the optimized parameter design scheme into the design model of the inductor to obtain the revised design scheme, and then substitute the obtained inductance internal resistance value into the simulation model. Finally, calculate the loss of each part of the converter under the optimized parameter scheme. The design and calculation result are shown in Table 6.

Table 6.
ML design result.
It can be seen in Table 6 that compared with the traditional design in Table 4, although the inductance value of L1 and L2 increases, the use of more suitable magnetic cores reduces the total mass.
After optimization, the loss of each part is shown in Table 7. Compared with Table 3, the loss of each switch tube and inductance are reduced.

Table 7.
Loss of each part of ML method.
The pie chart of converter loss distribution with the ML method is shown in Figure 10. Compared with the pie chart of the traditional method shown in Figure 3, the parameter scheme obtained by the optimization design method reduces the total loss of the converter by about 1.44 W, with a switching loss reduction of about 1.31 W.
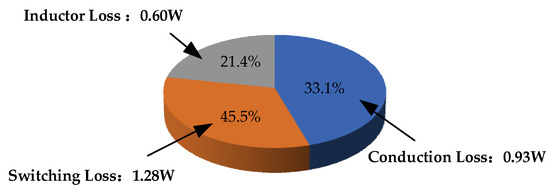
Figure 10.
Pie chart of converter loss distribution with ML method.
5. Experimental Result
According to the results obtained in Section 2.2 and Section 4.2, the converter parameters design results based on the traditional method and ML method are shown in Table 8.

Table 8.
Design results of Traditional and ML method.
Through simulation analysis, the loss of the optimized converter was reduced from 4.21 W to 2.81 W, and the total mass of the inductor was reduced from 0.19 kg to 0.12 kg. In order to verify the proposed optimization design method, an experimental prototype was built. The rated output voltage is 24 V. The picture of the prototype is shown in Figure 11.

Figure 11.
Picture of experimental prototype.
The prototype includes a main circuit module, a driver circuit module, and a control circuit module.The main circuit module corresponds to the circuit in Figure 1, achieving power conversion. The driver module used a Si271 isolated gate driver chip and Mornsun’s module power supply to provide sufficient driving energy for the MOSFET. The control module used the DSP28335 chip as the control chip to output the required PWM signal.
It can be seen that capacitors C1 and C2 are composed of patch capacitors in parallel. The switches were selected as IRF3205ZPBF model N-channel MOSFET, with a drain source rated voltage of 55 V, a drain current of 75 A, and a conduction resistance of 7.5 mΩ.
Design the inductance according to the data in Table 4 and Table 6. The physical photos of the inductors are shown in Figure 12; the total mass of the inductors with the ML method is 0.29 kg, which is less than the mass of the inductor with the traditional method of 0.45 kg. Although there is some error between the ML method’s predicted results and the actual values, the mass was reduced by 35.6%.

Figure 12.
Traditonal and ML designed inductor.
The converter is designed based on the indicators shown in Table 9. Different from simulation, by changing the load resistance to ensure the same boost ratio, we can compare the mass and power loss of the two schemes via experiments. The voltage waveforms and switching drive waveforms with the two methods are shown in Figure 13. The yellow waveform represents the driving signal of S1, the green waveform represents the driving signal of S3, the blue waveform represents the output voltage vo, and the pink waveform represents the input voltage vin.The input voltage Vin and output voltage Vo of the converter with the two methods are the same. Due to the reduced switching frequency, the voltage ripple of the converter with ML increases from 1.12 V to 1.56 V, but the voltage ripple ratio ρo still meets the constraints mentioned in Section 3.2.

Table 9.
Technical indicators of the converter with two methods.
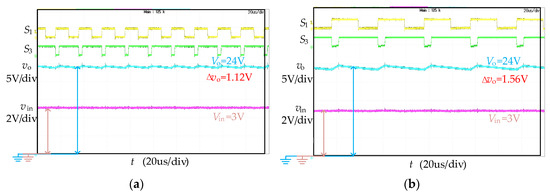
Figure 13.
Voltage and switching drive waveforms of the converter with two methods: (a) waveforms with traditional method; (b) waveforms with ML method.
The current waveforms and the ripple of the converter with two methods are shown in Figure 14. The yellow waveform represents the driving signal of S3, the green waveform represents the input current iin, the blue waveform represents i1, and the pink waveform represents i2.Similar to the conclusion of the voltage waveform, the current ripple of the converter with the ML method increases, but the current ripple ratio ρL1, ρL2 still meets the constraints mentioned in Section 3.2.
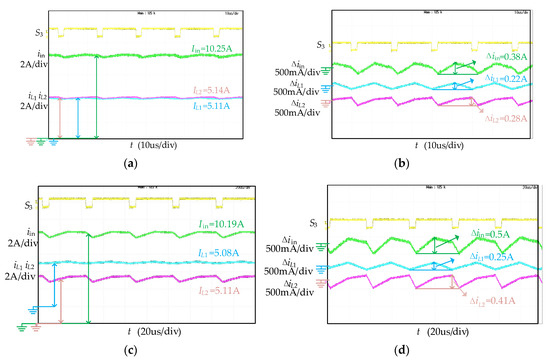
Figure 14.
Current and their ripple waveforms of the converter with two methods: (a) Current waveforms with traditional method; (b) Current ripple waveforms with traditional method; (c) Current waveforms with ML method; (d) Current ripple waveforms with ML method.
The experimental results show that under the same input voltage and power, the converter can operate stably and maintain a constant boost ratio under the set optimization parameters. Due to the decrease in switching frequency, the voltage and current ripple of the converter with the ML method increase but still remain within the constraint range mentioned in Section 3.2. After calculation, the loss of the converter with the traditional method is 6.55 W, while the ML method is 4.39 W. The loss of the converter was reduced by 32.9%.
6. Conclusions
In this article, a machine learning-based integrated optimization method for SLIC-QBC is proposed to minimize the mass and power loss. This method can automatically use Magnetics’ data to design the inductance model and select the design scheme with the best mass and power loss from all feasible design methods. It has two outstanding advantages: (1) High design accuracy due to the used components’ data; (2) This method avoids the repetitive running process of traditional complex algorithms and saves a lot of time in running simulations.
In the proposed method, based on a component-based inductance design model, SVM and ANN are used to map design parameters to the mass and power loss of the converter. The optimal design scheme is selected using the value of the comprehensive index r. The simulation and experimental results show that the proposed optimized design method can reduce the mass of the converter by 35.6% and power loss by 32.9% compared with the traditional design method in the range of voltage and current ripple.
The main implications of this study are as follows:
(1) Research on the design and optimization of high-gain DC-DC converters for the recycling and utilization of waste batteries.
(2) Proposal of a machine learning-based integrated optimization method to automatically design passive components and switching frequency.
(3) The scheme designed by this method has been verified through simulation and experiments to achieve the optimal combination of converter mass and power loss.
Although this method achieves optimal design for mass and power loss by optimizing inductance and switching frequency, this method relies on a large amount of data to train the neural network, and the lack of data may not achieve the desired training effect. Also, this optimization is achieved within a certain limited design space. If it exceeds this design space, new data need to be collected again. In future research, as this method only targets the passive components of the converter and has no limitation to the topology structure of the converter, we will consider using this method in the topology of other converters to achieve optimal design. Also, more accurate inductance design models can be further established to cover more alternative inductance cores. On this basis, we will research circuit parameter optimization methods with wider applicability.
Author Contributions
Conceptualization, G.L.; methodology, G.L., L.K. and Y.G.; software, L.K., Y.G. and F.L.; validation, L.K., F.L. and W.C.; formal analysis, W.W. and Y.G.; investigation, G.L. and W.W.; resources, G.L.; data curation, L.K.; writing—original draft preparation, L.K. and G.L.; writing—review and editing, L.K., G.L. and Y.G.; visualization, L.K.; supervision, G.L., Y.G. and W.W.; project administration, G.L.; funding acquisition, G.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China under Grants 51977045.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Falvo, M.C.; Manganelli, M.; Moscatiello, C.; Vellucci, F. Electrical Vehicles and Charging Stations: State of Art and Future Perspectives. In Proceedings of the 2022 IEEE International Conference on Environment and Electrical Engineering and 2022 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Prague, Czech Republic, 28 June–1 July 2022; pp. 1–7. [Google Scholar]
- Bhatt, A.; Tiwari, S.; Ongsakul, W. A Review on Re-Utilization of Electric Vehicle’s Retired Batteries. In Proceedings of the 2018 International Conference and Utility Exhibition on Green Energy for Sustainable Development (ICUE), Phuket, Thailand, 24–26 October 2018; pp. 1–5. [Google Scholar]
- Pool, R. The multi-million-tonne scrap heap: As sales of electric vehicles start to soar, the thorny issue of what to do with end-of-life lithium-ion batteries isn’t going away. We look at the problem and explore the solutions. Eng. Technol. 2020, 15, 38–42. [Google Scholar] [CrossRef]
- Chen, B. Repurposition of Lithium ion Battery Packs from Electric Vehicles to Energy Storage Systems: The challenge and cost effective solutions. In Proceedings of the 2018 IEEE Symposium on Product Compliance Engineering—Asia (ISPCE-CN), Shenzhen, China, 5–7 December 2018; pp. 1–2. [Google Scholar]
- Pratama, A.P.; Rahman, I.; Zain, A.A.; Fadlika, I.; Afandi, A.N. A New Transformerless High Voltage Gain DC-DC Converter for DC Microgrid. In Proceedings of the 2020 International Conference on Sustainable Energy Engineering and Application (ICSEEA), Tangerang, Indonesia, 18–20 November 2020; pp. 197–203. [Google Scholar]
- Karthikeyan, V.; Kumaravel, S.; Gurukumar, G. High Step-Up Gain DC–DC Converter with Switched Capacitor and Regenerative Boost Configuration for Solar PV Applications. IEEE Trans. Circuits Syst. II Express Briefs 2019, 66, 2022–2026. [Google Scholar] [CrossRef]
- Lu, S.; Sun, K.; Cao, G.; Yi, Z.; Liu, H.; Li, Y. A High Efficiency and High Power SiC DC-DC Converter Based on Interleaved-Boost and Full-bridge LLC Integration for PV Applications. In Proceedings of the 2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 11–15 October 2020; pp. 4822–4827. [Google Scholar]
- Yao, R.; Zheng, Z.; Li, Y. Parameter Optimization Design Method of the Interleaved Isolated Boost Converter with Coupled Inductors. In Proceedings of the 2020 IEEE Transportation Electrification Conference & Expo (ITEC), Chicago, IL, USA, 23–26 June 2020; pp. 715–722. [Google Scholar]
- Liu, Y.; Huang, M.; Liu, Y.; Zha, X. Reliability-oriented design of LC filter in buck DC-DC converter with multi-objective optimization. In Proceedings of the 2016 IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 18–22 September 2016; pp. 1–6. [Google Scholar]
- Li, X.; Zhang, X.; Lin, F.; Blaabjerg, F. Artificial-Intelligence-Based Design for Circuit Parameters of Power Converters. IEEE Trans. Ind. Electron. 2020, 69, 11144–11155. [Google Scholar] [CrossRef]
- Gao, Y.; Yang, T.; Dragičević, T.; Bozhko, S.; Wheeler, P.; Zheng, C. Optimal Filter Design for Power Converters Regulated by FCS-MPC in the MEA. IEEE Trans. Power Electron. 2021, 36, 3258–3268. [Google Scholar] [CrossRef]
- Ding, Q.-A.; Cheng, X.D.; Liu, H.X.; Wang, X.J.; Guo, X.H. Optimizing Equivalent Circuit Model Parameters of DFB Lasers with RSM Model and NSGA-II Algorithm. IEEE Photonics J. 2022, 14, 1–9. [Google Scholar] [CrossRef]
- Aljarrah, R.; Al-Omary, M.; Alshabi, D.; Salem, Q.; Alnaser, S.; Ćetenović, D.; Karimi, M. Application of Artificial Neural Network-Based Tool for Short Circuit Currents Estimation in Power Systems with High Penetration of Power Electronics-Based Renewables. IEEE Access 2023, 11, 20051–20062. [Google Scholar] [CrossRef]
- Li, Z.; Gao, Y.; Zhang, X.; Wang, B.; Ma, H. A Model-Data-Hybrid-Driven Diagnosis Method for Open-Switch Faults in Power Converters. IEEE Trans. Power Electron. 2021, 36, 4965–4970. [Google Scholar] [CrossRef]
- Dragičević, T.; Wheeler, P.; Blaabjerg, F. Artificial Intelligence Aided Automated Design for Reliability of Power Electronic Systems. IEEE Trans. Power Electron. 2019, 34, 7161–7171. [Google Scholar] [CrossRef]
- Xu, Q.; Dragicevic, T.; Xie, L.; Blaabjerg, F. Artificial Intelligence-Based Control Design for Reliable Virtual Synchronous Generators. IEEE Trans. Power Electron. 2021, 36, 9453–9464. [Google Scholar] [CrossRef]
- Gao, Y.; Yang, T.; Bozhko, S.; Wheeler, P.; Dragicevic, T.; Gerada, C. Neural network aided PMSM multi-objective design and optimization for more-electric aircraft applications. Chin. J. Aeronaut. 2022, 35, 233–246. [Google Scholar] [CrossRef]
- Gao, Y.; Yang, T.; Wang, X.; Bozhko, S.; Wheeler, P. Machine Learning Based Correction Model in PMSM Power Loss Estimation for More-Electric Aircraft Applications. In Proceedings of the 2020 23rd International Conference on Electrical Machines and Systems (ICEMS), Hamamatsu, Japan, 24–27 November 2020; pp. 1940–1944. [Google Scholar]
- Zhu, X.; Xiong, J.; Liang, Q. Fault Diagnosis of Rotation Machinery Based on Support Vector Machine Optimized by Quantum Genetic Algorithm. IEEE Access 2018, 6, 33583–33588. [Google Scholar] [CrossRef]
- Su, Y.; Shi, W.; Hu, L.; Zhuang, S. Implementation of SVM-Based Low Power EEG Signal Classification Chip. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 4048–4052. [Google Scholar] [CrossRef]
- Yan, X.; Lin, Z.; Lin, Z.; Vucetic, B. A Novel Exploitative and Explorative GWO-SVM Algorithm for Smart Emotion Recognition. IEEE Internet Things J. 2023, 10, 9999–10011. [Google Scholar] [CrossRef]
- Xu, Z.; Gao, Y.; Wang, X.; Tao, X.; Xu, Q. Surrogate Thermal Model for Power Electronic Modules using Artificial Neural Network. In Proceedings of the IECON 2019—45th Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 14–17 October 2019; pp. 3160–3165. [Google Scholar]
- Gao, Y.; Yang, T.; Bozhko, S.; Wheeler, P.; Dragičević, T. Filter Design and Optimization of Electromechanical Actuation Systems Using Search and Surrogate Algorithms for More-Electric Aircraft Applications. IEEE Trans. Transp. Electrif. 2020, 6, 1434–1447. [Google Scholar] [CrossRef]
- Liu, G.-H.; Huang, X.-C.; Gao, Y.; Wang, W. An Optimization Energy Management Strategy for Hybrid Emergency Power Supply System of More Electric Aircraft Based on Machine Learning. In Proceedings of the 2022 IEEE International Power Electronics and Application Conference and Exposition (PEAC), Guangzhou, China, 4–7 November 2022; pp. 1336–1341. [Google Scholar]
- Liu, G.-H.; Chen, Y.-B.; Gao, Y.; Zhu, J.-N.; Wang, B.-X.; Yang, T. Component Based and Machine Learning Aided Optimal Filter Design for Full-Bridge Current Doubler Rectifier. In Proceedings of the IECON 2021—47th Annual Conference of the IEEE Industrial Electronics Society, Toronto, ON, Canada, 13–16 October 2021; pp. 1–6. [Google Scholar]
- Liu, G.-H.; Qu, W.-Q.; Wang, X.-Y.; Wang, W. An Integrated Optimization Design Method of Single-Phase PV Inverter Based on Machine Learning. In Proceedings of the 2022 IEEE 5th International Electrical and Energy Conference (CIEEC), Nangjing, China, 27–29 May 2022; pp. 4363–4368. [Google Scholar]
- Li, G.; Jin, X.; Chen, X.; Mu, X. A novel quadratic boost converter with low inductor currents. CPSS Trans. Power Electron. Appl. 2020, 5, 1–10. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).